Perception of Human Motion with Different Geometric Models
Abstract
Human figures have been animated using a variety of geometric models including stick figures, polygonal models, and NURBS-based models with muscles, flexible skin, or clothing. This paper reports on experimental results indicating that a viewer’s perception of motion characteristics is affected by the geometric model used for rendering. Subjects were shown a series of paired motion sequences and asked if the two motions in each pair were the same or different. The motion sequences in each pair were rendered using the same geometric model. For the three types of motion variation tested, sensitivity scores indicate that subjects were better able to observe changes with the polygonal model than they were with the stick figure model.
Index Terms:
Motion perception, motion sensitivity, computer animation, geometric model, perceptual study, biological motion stimuli, light-dot display.I Introduction
Few movements are as familiar and recognizable as human walking and running. Almost any collection of dots, lines, or shapes attached to an unseen walking figure is quickly identified and understood as human. Studies in human perception have displayed walking motion using only dots of light located at the joints and have found test subjects quite adept at assessing the nature of the underlying motion[1]. In particular, subjects can identify the gender of a walker and recognize specific individuals from light-dot displays even when no other cues are available[2, 3, 4].
In part because people are skilled at detecting subtleties in human motion, the animation of human figures has long been regarded as an important, but difficult, problem in computer animation. Recent publications have presented a variety of techniques for creating animations of human motion. Promising approaches include techniques for manipulating keyframed or motion capture data[5, 6, 7, 8], control systems for dynamic simulations[9, 10, 11, 12, 13], and other procedural or hybrid approaches[14, 15, 16, 17, 18, 19, 20]. Each method has its own strengths and weaknesses, making the visual comparison of results essential, especially for the evaluation of such subjective qualities as naturalness and emotional expression. The research community has not yet adopted a standard set of models and there is currently enormous variety in the models and rendering styles used to present results.
Our ability to make judgments about human motion from displays as rudimentary as dot patterns raises an important question: Does the geometric model used to render an animation affect a viewer’s judgment of the motion or can a viewer make accurate judgments independent of the geometric model? There are three plausible but contradictory answers to this question.
Possibility 1. Simple representations may allow finer distinctions when judging human motion. Simpler models may be easier to comprehend than more complex ones, allowing the viewer’s attention to focus more completely on the details of the movement rather than on the details of the model. For example, a stick figure is an obvious abstraction and rendering flaws may be easily ignored. When more detailed models are used, subtle flaws in rendering, body shape, posture, or expression may draw attention away from the movements themselves. Complex models may also obscure the motion. For example, the movement of a jacket sleeve might hide subtle changes to the motion of the arm underneath.
Possibility 2. Complex, accurate representations may allow finer distinctions. People have far more experience judging the position and movement of actual human shapes than they do judging abstract representations such as stick figures. A viewer, therefore, may be able to make finer distinctions when assessing the motion of more human-like representations. Furthermore, complex representations provide more features to identify and track. Each body segment in a polygonal human model has a distinctive, familiar shape, making it easier to gauge fine variations in both position and rotation.
Possibility 3. Both simple and complex representations may allow equally fine distinctions. The human visual system may use a displayed image only to maintain the positions of a three-dimensional mental representation. Judgments about the motion may be made from this mental representation rather than directly from the viewed image. Displayed images must of course supply enough cues to keep the mental representation accurate, but additional detail and accuracy may be irrelevant. Just as joint positions shown by light dots are sufficient to control the mental representation, connecting the dots with a stick figure might not improve the viewer’s perception. Similarly, encasing a stick figure within a detailed human body shape might likewise prove unnecessary.
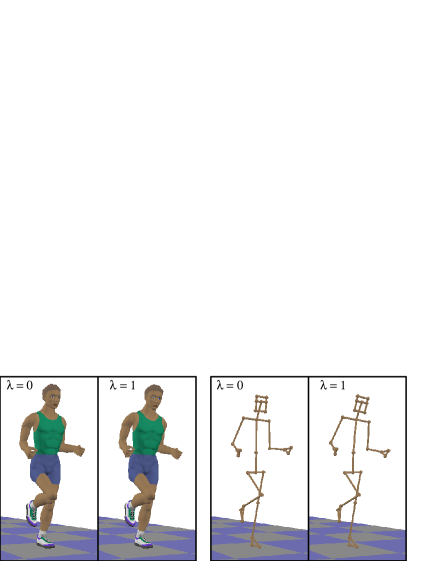
Objective evidence is needed to determine which of these possibilities is correct. We argue that definitive experiments to select between possibilities 1 and 2 are impractical. The question of which style of geometric model is more useful for judging motion is likely to be highly complex and context dependent, affected by all of the variables of both the motion and the rendering. If possibility 3 were correct and model style were largely irrelevant, then we would be able to perform critical comparisons of the motion synthesis techniques in the literature by direct comparison of the substantially different geometric models used in each publication. This paper provides experimental evidence to disprove possibility 3 by showing that viewer sensitivities to variations in motion are significantly different for the stick figure model and the polygonal model shown in Fig. 1. In particular, for the types of motion variation we tested, viewers were more sensitive to motion changes displayed through the polygonal model than through the stick figure model. This result suggests that stick figures may not always have the required complexity to ensure that the subtleties of the motion are apparent to the viewer.
II Background
Several researchers have used light-dot displays, also referred to as biological motion stimuli, to study perception of human movements and to investigate the possibility of dynamic mental models[21]. The light-dot displays show only dots or patches of light that move with the main joints of walking figures (Fig. 2), but even these minimal cues have been shown to be sufficient for viewers to make detailed assessments of the nature of both the motion and the underlying figure.

The ability to perceive human gaits from light-dot displays has been widely reported to be acute and robust. Early experiments by Johansson reported that 10-12 light dots “evoke a compelling impression of human walking, running, dancing, etc.”[1]. Because such displays provide motion cues independent of form or outline, other investigators have used them to study human motion perception. Work by Cutting and Kozlowski showed that viewers easily recognized friends by their walking gaits on light-dot displays[2]. They also reported that the gender of unfamiliar walkers was readily identifiable, even after the number of lights had been reduced to just two located on the ankles[3]. In a published note, they later explained that the two light-dot decisions were probably attributable to stride length[4]. Continuing this work, Barclay, Cutting, and Kozlowski showed that gender recognition based on walking gait required between 1.6 and 2.7 seconds of display, or about two step cycles[22]. Our experiments used pairs of running stimuli 4 seconds in duration that displayed about six strides. We noticed that test subjects often marked their answer sheets near the midpoint of the second stimuli which is consistent with Barclay’s results.
Motion is apparently essential for identifying human figures on light-dot displays. The Cutting studies reported that while moving light-dot displays were recognized immediately, still light-dot displays of a walking figure were not recognized as human. Poizner and colleagues also noted that movement is required for accurately reading American Sign Language gestures[23].
This capacity to recognize moving figures was shown to be robust in the presence of masking by additional light points. In a modified experiment, subjects were shown light-dot displays of walkers facing either left or right and asked to determine walking direction. Only complex masks of extraneous light dots moving in patterns that were similar to those of the walking figure were able to disrupt viewer judgments[24].
Appropriate synthetic movements are easily accepted as human when rendered as light-dot displays. Cutting and colleagues found that apparent torso structure and rotation were strongly correlated with judgments of walker gender[25]. Cutting then constructed a simple mathematical model of light-dot motion for human walkers and computed displays of synthetic walkers. Viewers easily identified the synthetic displays as human walkers and accurately determined the intended gender of the walkers. These experiments clearly showed that variations in torso rotation are important for gender judgments. Accordingly, we chose to measure viewer sensitivity to torso rotations in one of our experiments.
Proffitt and colleagues found that occlusion of light dots by clothing or human body segments plays an important role in gait judgment and may also provide information about body outlines[26]. Synthetic displays without occlusion yielded poorer subject performance. These experimental observations suggest that extremely simple models of human figures, such as thin stick figures, may present similar difficulties for the viewer.
Surprisingly, the perception of rigid body segments between moving light dots at joints does not generalize to movements of isolated pairs of light dots. Ishiguchi showed test subjects one fixed light dot and a second one that moved on an arc of degrees as if it were on the end of a pendulum with the first light dot as the pivot joint[27]. Viewers perceived the dots as attached to a flexible bar held fixed at the first light dot rather than as a rigid bar moving as a pendulum. Thus the perception of rigid body segments in the largely pendulum-like movements of human walking is exceptional; perhaps the ensemble of dots is important, or perhaps the movements are so intimately familiar that the perception of an assembly of flexible bars is overridden.
III Experimental Methods


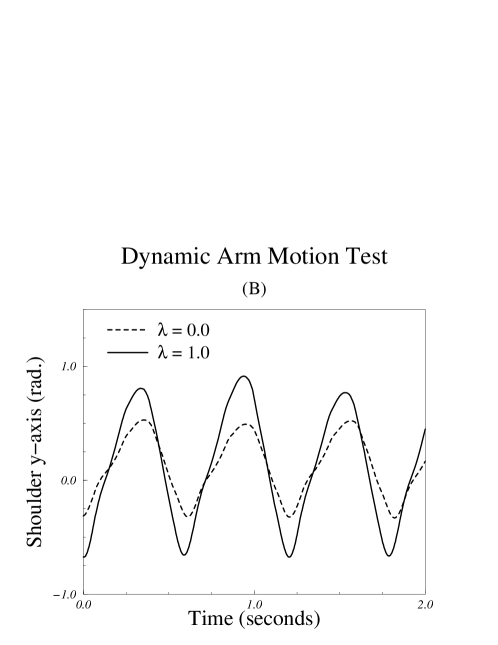
While it is impossible to exhaustively test all of the variables that may affect a perceived motion, we can use A/B comparison tests to form a preliminary assessment of whether the geometric model affects a viewer’s perception of motion. We evaluated three different types of motion variation in separate experiments described below: torso rotation, dynamic arm motion, and additive noise. For each experiment, the modifications to the motion were controlled by a normalized parameter, , that varied between and . Figs. 3 and 4 show sequences of images excerpted from the base motion sequence, , and the modified sequences, , used in all three experiments. Joint angle trajectories are shown in Fig. 6 to illustrate the key components of the base motion and the modified motions created by setting .
In each of the three tests, subjects viewed pairs of animated sequences rendered using the same geometric model and were asked whether the motions in the two sequences were the same or different. We then computed a sensitivity measure for each type of geometric model. The difference between the sensitivity values is a measure of whether a particular subject was better able to discriminate between the motions when they were rendered with a polygonal model or with a stick figure model.
III-A Experiment One: Torso Rotation
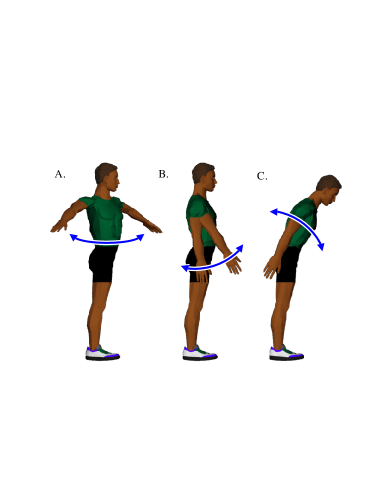
This experiment measured whether a subject’s ability to differentiate between larger and smaller yaw rotations of a runner’s torso was affected by the geometric model used for rendering. The motion sequences were generated by making kinematic modifications to data obtained from a physically based dynamic simulation of a human runner[9]. The torso’s rotation about the longitudinal axis, or yaw relative to the pelvis, was exaggerated (Fig. 5–A). The neck was counter-rotated to compensate for the torso rotation so that the facing direction of the head remained unchanged.
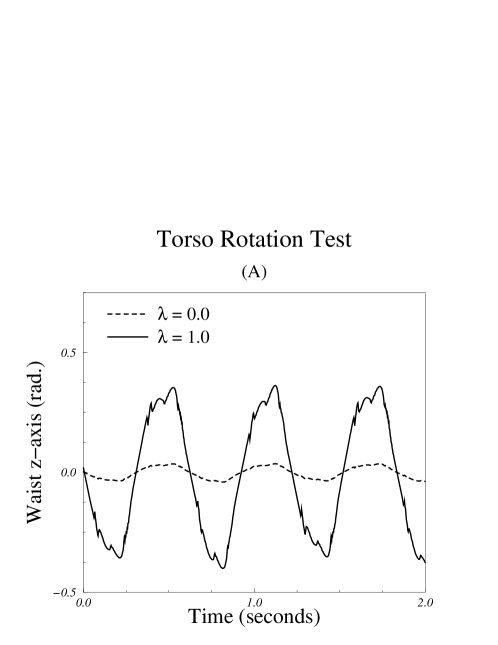

The magnitude of the exaggeration in torso rotation was controlled by a normalized parameter, . A value of gave a magnification factor of so that the modified motion was identical to that of the original data. Larger values of correspond linearly to higher magnification factors, with yielding a magnification of the torso rotation. The motion of body segments below the waist was left unchanged (Figs. 3, 4, and 6–A).
The test consisted of a series of 40 pairs of motion sequences divided into two sets of 20 pairs each. One set was rendered with the stick figure model and the other with the polygonal model (Fig. 1). All other parameters used to render the animations, such as lighting, ground models, and camera motion, were identical for the two sets. Within each set, half of the pairs were randomly selected to show two different motion sequences (different values). Of those that were different, the pairs with the largest disparity in were placed toward the beginning of each set so that the questions became progressively more difficult. To minimize bias due to fatigue or learning effects, we varied the order in which the two sets were presented. Asymmetric learning effects would not necessarily be minimized by this ordering.
Twenty-six student volunteers who were not familiar with the animations served as subjects. All had normal or corrected-to-normal vision. Subjects were tested in groups of two or three in a quiet room. They were instructed to remain silent and not to collaborate during the test. The test stimulus was presented on a 20-inch monitor approximately three feet from the subjects. All animations were prerendered and shown at 30 frames per second in NTSC resolution. These experimental conditions were selected because they match the viewing conditions commonly encountered when watching animated motion.
Subjects were told that they would be shown a series of 4-second computer-generated animations of a human runner and that the animations would be grouped in A/B pairs with 5 seconds of delay between the presentation of each pair. Subjects were asked to view each pair and then indicate on a response sheet whether the two motions were the same or different. They were also informed that the variations would be confined to the motion of the runner’s upper body and that the questions would become progressively more difficult. A monetary reward for the highest percentage of correct responses was offered as an incentive to all test subjects. Subjects were not told the purpose of the experiment.
III-B Experiment Two: Dynamic Arm Motion
This experiment measured whether a subject’s ability to differentiate between larger and smaller arm motions was affected by the geometric model used for rendering. The motion sequences were generated by modifying the desired fore-aft rotation about the transverse axis at the shoulder joint in the dynamic simulation of the human runner (Fig. 5–B). The control routines then computed torques based on the desired value of the shoulder joint. These torques were applied to the dynamic model. The resulting motion is shown in Figs. 3, 4, and 6–B. Because the motion was dynamically simulated, the exaggerated arm motion also had subtle effects on other aspects of the running motion.
The magnitude of the exaggeration in arm motion was controlled by a normalized parameter, . A value of gave a magnification factor of so that the modified motion was identical to that of the original data. Larger values of correspond linearly to higher magnification factors, with yielding a magnification of the shoulder rotation.
Twenty-four student volunteers who had not participated in the first experiment were subjects for this second experiment. Testing procedures and format were identical to those used in the first experiment.
III-C Experiment Three: Additive Noise
The format of this experiment was identical to that of the first two, except for the manner in which the running motion was modified. For this experiment, time-varying noise was added to the joint angles for the waist, shoulders, and neck. The noise was generated using a sinusoidal wave generator[28] with frequency varying randomly about that of the runner’s gait at approximately 3 Hz. The amplitude of the additive noise was controlled by a normalized parameter, , as in the torso rotation test. A value of resulted in motion data that was identical to the original data (zero noise amplitude). The maximum noise amplitude used, given by , produced a variation of radians about the original joint angles (Figs. 3 and 4). One representative joint angle, rotation of the torso at the waist about the transverse axis, is shown in Figs. 5–C and 6–C.
Twenty-six student volunteers who had not participated in the previous experiments were selected as subjects. Testing procedures were identical to those used in the first and second experiments.
IV Results
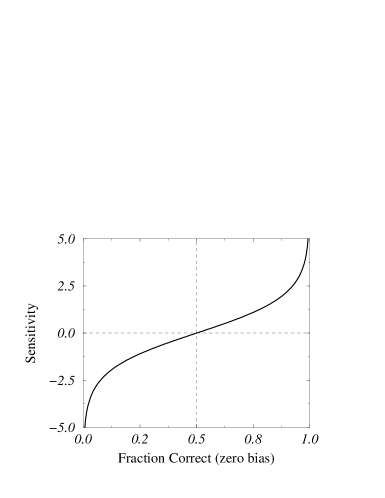
To analyze the data from the experiments, we used the responses to compute the Choice Theory sensitivity measure for each subject on each test set. The sensitivity measure, , is defined as
| (1) |
where is the fraction of pairs in a set that were different and which the subject labeled correctly, and is the fraction of pairs in a section that were the same and which the subject labeled incorrectly[29]. This measure is zero when the subject’s responses are uncorrelated with the correct responses to cause a correct score, and increases as response correlation improves, as illustrated in Fig. 7. Additionally, the measure is symmetric, naturally invariant with respect to response bias, and suitable for use as a distance metric[29].
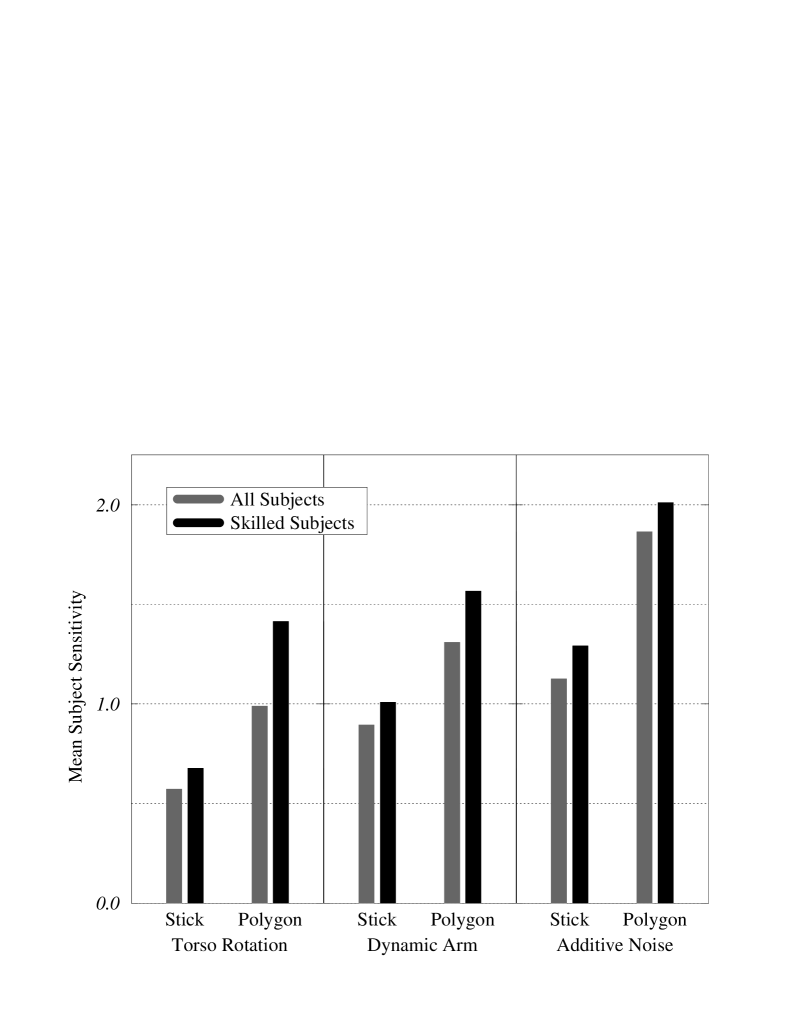
After sensitivity scores had been determined, a post hoc selection criteria was used to build a subgroup of “skilled” subjects who had achieved a sensitivity score indicating performance significantly better than chance with either the polygonal or the stick figure models. Significantly better than chance was defined as at least correct, which corresponds to a sensitivity score of . Analysis was computed both for the group of all subjects and for the group of skilled subjects. Sensitivity scores for each experiment averaged within subject groups are shown in Fig. 8.
In Section I, we proposed three possible answers to the question of whether the geometric model used for rendering affects a viewer’s perception of motion. The third possible answer implied that subjects would achieve similar sensitivity measures when asked identical questions about the motion of stick figure models or polygonal models. To test this hypothesis, we computed the difference in sensitivity for each subject:
| (2) |
The results from the three tests are summarized in Table I. For the torso rotation test, the mean of the difference in sensitivities across all subjects was with a standard deviation of . Student’s –test for paired samples[30] shows this difference to be significant, . For the group of skilled subjects, the mean rose to while the standard deviation fell to . The –test for paired samples shows this difference to be significant, .
For the dynamic arm motion test, the mean of the difference in sensitivities across all subjects was with a standard deviation of , a difference significant at . For the group of skilled subjects, the mean was and the standard deviation was , a difference significant at .
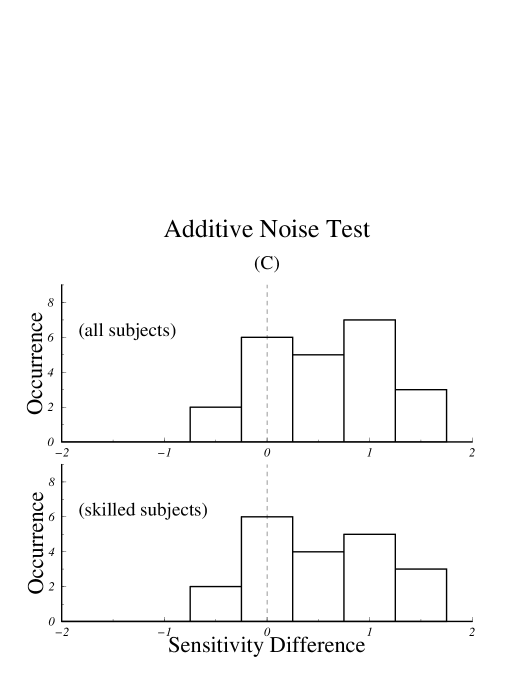
For the additive noise test, the mean of the difference in sensitivities across all subjects was with a standard deviation of , a difference significant at . For the group of skilled subjects, the mean was and the standard deviation was , a difference significant at .
All Subjects Skilled Subjects Mean Std. Dev. Prob. Err. Mean Std. Dev. Prob. Err. Torso Rotation Dynamic Arm Additive Noise
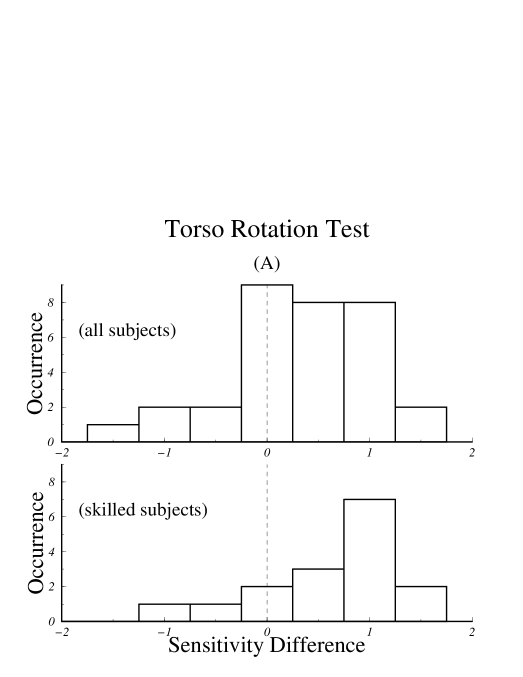
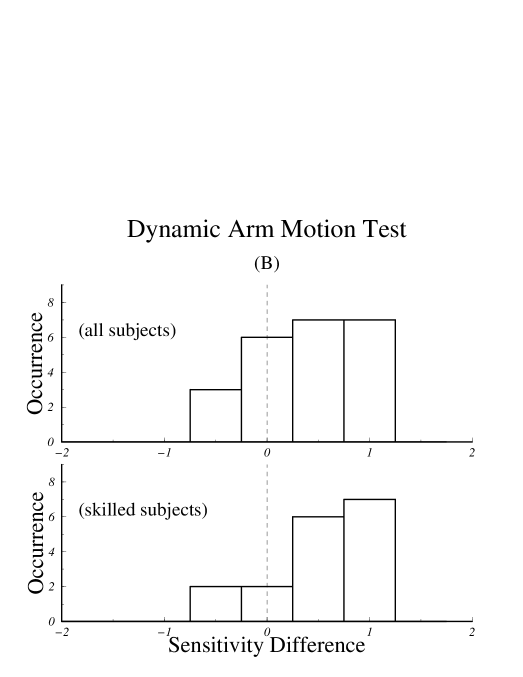
Fig. 9 shows histograms of the sensitivity differences, , for the three test conditions. Positive values correspond to higher sensitivity for the set rendered with the polygonal model.
Our results indicate that, for the three types of motion variation tested, subjects were better able to discriminate motion variations using the polygonal model than they were with the stick figure model. This result holds to a high level of significance both for the analyses computed on the group of all subjects and for the group of skilled subjects, although the magnitude of the differences are, in general, greater within the group of skilled subjects.
V Discussion
Although the differences in sensitivity measures show that our subjects were more sensitive to motion changes when a polygonal model was used for rendering, our results can not be generalized to say that polygonal models are always better than stick figure models for perceiving motions. Rather, the two types of geometric models are distinctly different and, in the cases we tested, polygonal models allowed better discrimination. There may be variations for which the difference in sensitivity has the opposite sign, implying that stick figures might be a better model for making fine discriminations about that particular motion variation.
Our results, however, do show that stick figures and polygonal models are not equivalent for tasks that require making fine discriminations about motion. This observation implies that any useful comparison of motion sequences requires that the same models and rendering methods be used for each and might indicate that the community would benefit from adopting a standard set of human models. In particular, comparing motions of a stick figure model to those of a more complex model may be meaningless because viewer sensitivities can differ substantially. As a practical matter, animators may want to avoid conducting preliminary tests only with stick figures or other simple models because it is likely that viewers would have different sensitivities to the more complex models that would be used in the final rendering.
Considerable familiarity with the motion appears to make differences in the geometric models less significant. For example, when the authors of this paper took the tests, they answered nearly all questions correctly. Of course, the authors were not included among the subjects whose data are reported above. If a larger subject pool showed that subjects who were very familiar with particular animated motions showed equal sensitivity to the two models, then we would have evidence that using stick figures for preliminary pencil tests of motion sequences will provide good information about the motion. The subject, in this case the animator, is very familiar with the motion and may be able to make subtle observations independent of the geometric models used for rendering.
Our results do not conflict with the findings discussed in Section II. Previous studies have found that subjects were able to use a variety of models to make judgments about human motion, these studies did not address how the subject’s proficiency might be affected. As can be seen from Fig. 8, the subjects we tested were able to make distinctions using both polygonal and stick figure models; however they were better able to make these distinctions when viewing motion rendered with the polygonal model.
For the two models used in these experiments, the more complex model was also more human-like but that may not always be the case. Complex but abstract models may be useful for making particular features of the motion visible in some applications. For example, crash test dummies have markings for the center of mass of each body segment and other visualization techniques such as force vectors have been used successfully in biomechanics research.
We used simulation combined with kinematic modifications to generate the motion for these studies because it allowed us to control the variations explicitly. Motion capture data would be an interesting source for this kind of study because it more closely matches human motion. However, even two consecutive captures of an actor performing a simple task will have significant differences because of the variability of human motion. Capturing a set of consecutive motions with a controlled variation for sensitivity tests would be difficult because of this variability.
The three techniques used to modify the motion were chosen both for their relevance to current animation techniques and for their perceptual significance. We chose torso rotation because previous studies have shown that the motion of the torso provides important cues for gender determination and subject recognition[25]. The kinematic modification used for the torso rotation test is also similar to the modifications an animator might make when keyframing motion or adjusting motion capture data. Similarly, the adjustments of the desired shoulder joint angles used in the dynamic arm motion test are typical of the adjustments that an animator might make to a dynamic simulation in order to change the style of the resulting motion. Finally, noise is found in naturally occurring motions, and additive noise generators have been used to synthesize natural and appealing human motion[20].
A potential problem with the experimental design used in this study is that the test must be of an appropriate difficulty. If the test is too difficult, then subject responses will be guesses regardless of which model is presented. Conversely, if the test is too easy, then all subject responses will be correct. In either case, the data gathered will not be useful. We can increase or decrease the difficulty of a test by changing the spacing of the values for the trials or the amount of information given to the subjects about the alterations to the motion. Unfortunately, it can be difficult to devise a test sequence of appropriate difficulty. This problem could be overcome by using tests that adaptively adjust difficulty level by selecting subsequent questions based on past responses. Alternatively, selection criteria can be used to cull subjects whose responses are not significantly correlated with the test stimuli.
While our assessment that the polygonal models allow greater sensitivity holds irrespective of culling, it is interesting to note how selection based on performance criteria does affect the data. As can be seen from the average scores shown in Fig. 8, subjects who took the torso rotation test achieved lower scores than did those who took the additive noise test, probably because the torso rotation test was more difficult. Comparing the results of the torso rotation test before and after culling shows that the mean of as well as the shape of the histograms in Fig. 9.A were notably different between the group of all subjects and the group of skilled subjects. For the easier, additive noise test, the selection criteria has essentially no effect. Moreover, the effect of the selection criteria on the torso rotation data appears to make it more closely resemble the data from the additive noise test, thereby supporting the notion that lowering the difficulty of the test and selecting subjects based on performance criteria are approximately equivalent.
Although we did not formally measure the subjects’ perceptions of how well they did on the test, it appeared that their perceptions did not always match their performance. Several subjects were certain that they had scored higher on the section with the stick figure model when in fact they had a higher sensitivity to motion changes with the polygonal model.
To create the animation sequences for these tests, we altered only the motion and the geometric models used; all other aspects of the rendering were held constant. It would be interesting to explore whether, and how, other aspects of the rendering affect the perception of motion as well as whether these results hold for behaviors other than running. For example, we have informally observed that the motion of the simulated runner appears more natural when the tracking camera has a constant velocity rather than one that matches the periodic accelerations of the runner’s center of mass. When the camera motion matches the acceleration of the center of mass exactly, the running motion appears jerky. More sophisticated models that incorporate clothing and skin may help to smooth out rapid accelerations of the limbs and make the motion appear more natural. Motion blur probably plays a similar role. Textured ground planes and shadows help to determine motion of the feet with respect to the ground and may provide important clues about the details of the motion.
If we had enough psychophysical results to build a model of how people perceive motion, we could optimize the rendering of animated sequences by emphasizing those factors that would make the greatest differences in how a viewer perceives the sequence either consciously or unconsciously. This approach of using results from the psychophysical literature to refine rendering techniques has already been used successfully for still images[31, 32, 33].
Acknowledgments
The authors would like to thank Jacquelyn Gray, John Pani, Neff Walker, and the reviewers for their valuable comments. This project was supported in part by NSF NYI Grant No. IRI-9457621, Mitsubishi Electric Research Laboratory, and a Packard Fellowship. An earlier version of this work, reporting preliminary results, appeared in The Conference Proceedings of Graphics Interface ’97.
References
- [1] G. Johansson, “Visual perception of biological motion and a model for its analysis,” Perception & Psychophysics, vol. 14, no. 2, pp. 201–211, 1973.
- [2] J. E. Cutting and L. T. Kozlowski, “Recognizing friends by their walk: Gait perception without familiarity cues,” Bulletin of the Psychonomic Society, vol. 9, no. 5, pp. 353–356, 1977.
- [3] L. T. Kozlowski and J. E. Cutting, “Recognizing the sex of a walker from a dynamic point-light display,” Perception & Psychophysics, vol. 21, no. 6, pp. 575–580, 1977.
- [4] L. T. Kozlowski and J. E. Cutting, “Recognizing the gender of walkers from point-lights mounted on ankles: Some second thoughts,” Perception & Psychophysics, vol. 23, no. 5, pp. 459, 1978.
- [5] A. Bruderlin and L. Williams, “Motion signal processing,” in SIGGRAPH ’95 Conference Proceedings. ACM SIGGRAPH, Aug. 1995, Annual Conference Series, pp. 97–104, Held in Los Angeles, California, 6–11 August 1995.
- [6] C. F. Rose, B. Guenter, B. Bodenheimer, and M. F. Cohen, “Efficient generation of motion transitions using spacetime constraints,” in SIGGRAPH ’96 Conference Proceedings. ACM SIGGRAPH, Aug. 1996, Annual Conference Series, pp. 155–162, Held in New Orleans, Louisiana, 4–9 August 1996.
- [7] M. Unuma, K. Anjyo, and R. Takeuchi, “Fourier principles for emotion-based human figure animation,” in SIGGRAPH ’95 Conference Proceedings. ACM SIGGRAPH, Aug. 1995, Annual Conference Series, pp. 91–96, Held in Los Angeles, California, 6–11 August 1995.
- [8] A. Witkin and Z. Popović, “Motion warping,” in SIGGRAPH ’95 Conference Proceedings. ACM SIGGRAPH, Aug. 1995, Annual Conference Series, pp. 105–108, Held in Los Angeles, California, 6–11 August 1995.
- [9] J. K. Hodgins, W. L. Wooten, D. C. Brogan, and J. F. O’Brien, “Animating human athletics,” in SIGGRAPH ’95 Conference Proceedings. ACM SIGGRAPH, Aug. 1995, Annual Conference Series, pp. 71–78, Held in Los Angeles, California, 6–11 August 1995.
- [10] J. Laszlo, M. van de Panne, and E. Fiume, “Limit cycle control and its application to the animation of balancing and walking,” in SIGGRAPH ’96 Conference Proceedings. ACM SIGGRAPH, Aug. 1996, Annual Conference Series, pp. 155–162, Held in New Orleans, Louisiana, 4–9 August 1996.
- [11] J. Thomas Ngo and J. Marks, “Spacetime constraints revisited,” in SIGGRAPH ’93 Conference Proceedings. ACM SIGGRAPH, Aug. 1993, vol. 27 of Annual Conference Series, pp. 343–350, Held in Anaheim, California, 1–6 August 1993.
- [12] M. van de Panne and A. Lamouret, “Guided optimization for balanced locomotion,” in Eurographics Workshop on Computer Animation and Simulation ’95, 1995, pp. 165–177.
- [13] M. van de Panne and E. Fiume, “Sensor-actuator networks,” in SIGGRAPH ’93 Conference Proceedings. ACM SIGGRAPH, Aug. 1993, vol. 27 of Annual Conference Series, pp. 335–342, Held in Anaheim, California, 1–6 August 1993.
- [14] N. I. Badler, C. B. Phillips, and B. L. Webber, Simulating Humans: Computer Graphics Animation and Control, Oxford University Press, New York, 1993.
- [15] A. Bruderlin and T. W. Calvert, “Goal-directed, dynamic animation of human walking,” in SIGGRAPH ’89 Conference Proceedings. ACM SIGGRAPH, July 1989, vol. 23 of Annual Conference Series, pp. 233–242, Held in Boston, Massachusetts, 31 July – 4 Agust 1992.
- [16] M. F. Cohen, “Interactive spacetime control for animation,” in SIGGRAPH ’92 Conference Proceedings. ACM SIGGRAPH, July 1992, vol. 26 of Annual Conference Series, pp. 293–302, Held in Chicago, Illinois, 226–31 July 1992.
- [17] M. Girard and A. A. Maciejewski, “Computational modeling for the computer animation of legged figures,” in SIGGRAPH ’85 Conference Proceedings. ACM SIGGRAPH, July 1985, vol. 19 of Annual Conference Series, pp. 263–270.
- [18] H. Ko and N. I. Badler, “Straight line walking animation based on kinematic generalization that preserves the original characteristics,” in Proceedings of Graphics Interface ’93, Toronto, Ontario, Canada, May 1993, Canadian Information Processing Society, pp. 9–16.
- [19] B. Laurent, B. Ronan, and N. Magnenat-Thalmann, “An interactive tool for the design of human free-walking trajectories,” in Proceedings of Computer Animation ’92, 1992, pp. 87–104.
- [20] K. Perlin, “Real time responsive animation with personality,” IEEE Transactions on Visualization and Computer Graphics, vol. 1, no. 1, pp. 5–15, Mar. 1995.
- [21] J. Freyd, “Dynamic mental representations,” Psychological Review, vol. 94, no. 4, pp. 427–438, 1987.
- [22] C. D. Barclay, J. E. Cutting, and L. T. Kozlowski, “Temporal and spatial factors in gait perception that influence gender recognition,” Perception & Psychophysics, vol. 23, no. 2, pp. 145–152, 1978.
- [23] H. Poizner, U. Bellugi, and V. Lutes-Driscoll, “Perception of american sign language in dynamic point-light displays,” Journal of Experimental Psychology: Human Perception and Performance, vol. 7, pp. 430–440, 1981.
- [24] J. E. Cutting, C. Moore, and R. Morrison, “Masking the motions of human gait,” Perception & Psychophysics, vol. 44, no. 4, pp. 339–347, 1988.
- [25] J. E. Cutting, D. R. Proffitt, and L. T. Kozlowski, “A biomechanical invariant for gait perception,” Journal of Experimental Psychology: Human Perception and Performance, vol. 4, no. 3, pp. 357–372, 1978.
- [26] D. R. Proffitt, B. I. Bertenthal, and R. J. Roberts Jr., “The role of occlusion in reducing multistability in moving point-light displays,” Perception & Psychophysics, vol. 36, no. 4, pp. 315–323, 1984.
- [27] A. Ishiguchi, “The effect of orientation on interpolated elastic structure from dot motion: Its occurrence and persistence,” Perception & Psychophysics, vol. 44, no. 4, 1988.
- [28] C. Schlick, “Wave generators for computer graphics,” in Graphics Gems 5, Alan Paeth, Ed., pp. 367–374. Academic Press, 1995.
- [29] N. A. Macmillan and C. D. Creelman, Detection Theory: A User’s Guide, Cambridge University Press, New York, 1991.
- [30] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C, Cambridge University Press, New York, 1992.
- [31] J. A. Ferwerda, S. N. Pattanaik, P. Shirley, and D. P. Greenberg, “A model of visual adaptation for realistic image synthesis,” in SIGGRAPH ’96 Conference Proceedings. ACM SIGGRAPH, Aug. 1996, Annual Conference Series, pp. 249–258, Held in New Orleans, Louisiana, 4–9 August 1996.
- [32] J. K. Kawai, J. S. Painter, and M. F. Cohen, “Radioptimization - goal based rendering,” in SIGGRAPH ’93 Conference Proceedings. ACM SIGGRAPH, Aug. 1993, Annual Conference Series, pp. 147–154, Held in Anaheim, California, 1–6 August 1993.
- [33] P. Teo and D. Heeger, “Perceptual image distortion,” in First IEEE International Conference on Image Processing, Nov. 1994, pp. 982–986, Held in Los Alamitos, California, 11–16 November 1994.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/def0e477-502b-43df-bf40-a938482aca4e/x14.png) Jessica K. Hodgins
received her Ph.D. from the Computer Science Department at Carnegie
Mellon University in 1989. From 1989 to 1992, Hodgins was a
postdoctoral researcher in the MIT Artificial Intelligence Laboratory
and the IBM Thomas J. Watson Research Center. She is currently an
associate professor in the College of Computing at the Georgia
Institute of Technology and a member of the Graphics, Visualization
and Usability Center. Her research explores techniques that may
someday allow robots and animated creatures to plan and control their
actions in complex and unpredictable environments. In 1994 she
received an NSF Young Investigator Award and was awarded a Packard
Fellowship. In 1995 she received a Sloan Foundation Fellowship. She
is on the Editorial Board of the Journal of Autonomous Robots, the
IEEE Magazine on Robotics and Automation and ACM Transactions on
Graphics.
Jessica K. Hodgins
received her Ph.D. from the Computer Science Department at Carnegie
Mellon University in 1989. From 1989 to 1992, Hodgins was a
postdoctoral researcher in the MIT Artificial Intelligence Laboratory
and the IBM Thomas J. Watson Research Center. She is currently an
associate professor in the College of Computing at the Georgia
Institute of Technology and a member of the Graphics, Visualization
and Usability Center. Her research explores techniques that may
someday allow robots and animated creatures to plan and control their
actions in complex and unpredictable environments. In 1994 she
received an NSF Young Investigator Award and was awarded a Packard
Fellowship. In 1995 she received a Sloan Foundation Fellowship. She
is on the Editorial Board of the Journal of Autonomous Robots, the
IEEE Magazine on Robotics and Automation and ACM Transactions on
Graphics.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/def0e477-502b-43df-bf40-a938482aca4e/x15.png) James F. O’Brien
is a doctoral student in the College of Computing at the Georgia
Institute of Technology, and a member of the Graphics, Visualization,
and Usability Center. He received a M.S. in Computer Science from the
Georgia Institute of Technology in 1996 and a B.S. in Computer Science
from Florida International University in 1992. His research interests
include physically based animation and geometric modeling. In 1997 he
received a graduate fellowship from the Intel Foundation.
James F. O’Brien
is a doctoral student in the College of Computing at the Georgia
Institute of Technology, and a member of the Graphics, Visualization,
and Usability Center. He received a M.S. in Computer Science from the
Georgia Institute of Technology in 1996 and a B.S. in Computer Science
from Florida International University in 1992. His research interests
include physically based animation and geometric modeling. In 1997 he
received a graduate fellowship from the Intel Foundation.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/def0e477-502b-43df-bf40-a938482aca4e/x16.png) Jack Tumblin
is a PhD candidate in computer science. His research interests
include computer graphics, visual perception and image processing.
After graduating from Georgia Tech with a BSEE in 1979, he worked as a
television broadcast engineer and later designed flight simulator
image-generating hardware, resulting in four patents. He returned to
Georgia Tech and in 1990 earned an MS (EE) degree.
Jack Tumblin
is a PhD candidate in computer science. His research interests
include computer graphics, visual perception and image processing.
After graduating from Georgia Tech with a BSEE in 1979, he worked as a
television broadcast engineer and later designed flight simulator
image-generating hardware, resulting in four patents. He returned to
Georgia Tech and in 1990 earned an MS (EE) degree.