Performance of the upgraded ultracold neutron source at Los Alamos National Laboratory and its implication for a possible neutron electric dipole moment experiment

Ultracold neutrons (UCN) Ign90 ; Gol91 are defined to be neutrons of sufficiently low kinetic energies that they can be confined in material and magnetic bottles, corresponding to kinetic energies below about 340 neV. UCN are playing increasingly important roles in the study of fundamental physical interactions (see e.g. Refs. Dub11 ; You14 ). Searches for a non-zero electric dipole moment of the neutron (nEDM), which are performed almost exclusively using UCN Khr97 ; Lam09 ; ILL ; Ser15 , probe new sources of time reversal symmetry violation Pos05 ; Eng13 and may give clues to the puzzle of the matter-antimatter asymmetry in the Universe Cir10 ; Mor13 . The free neutron lifetime, which is measured using UCN Ser08 ; Pat17 or beams of cold neutrons Yue13 , is an important input parameter needed to describe Big-Bang nucleosynthesis. Measurements of neutron decay correlation parameters performed using UCN Pat09 ; Liu10 ; Pla12 ; Men13 ; Bro17 as well as cold neutrons Mun13 , along with measurement of the free neutron lifetime, test the consistency of the standard model of particle physics and probe what may lie beyond it Cir13 . Precision studies of bound quantum states of the neutron in gravitational fields are performed to search for new interactions Jen11 .

For decades, the turbine UCN source Ste86 at the PF2 Facility of Institut Laue-Langevin (ILL) provided UCN to various experiments as the world’s only UCN source with sufficient UCN density and flux. Ultimately the performance of the UCN experiments performed there was limited by the available UCN density and flux. This led to development of many new UCN sources around the world based on the superthermal process Gol75 in either liquid helium (LHe) Gol77 or solid deuterium (SD₂, where ‘D’ denotes deuterium ‘²H’ ) Gol83 ; Yu85 ; Mor03 ; Sau04 coupled to spallation or reactor neutrons. See e.g. Ref. You14 for a list of operational and planned UCN sources around the world.

At Los Alamos National Laboratory (LANL) a UCN source based on a SD₂ converter driven by spallation neutrons has been operated successfully for over 10 years Sau13 . This was the first production UCN source based on superthermal UCN production. As the only operational UCN source in the US and as one of the two multi-experiment UCN facilities in the world (along with the ILL turbine source), it has provided UCN to various experiments including the UCNA Pat09 ; Liu10 ; Pla12 ; Men13 ; Bro17 , UCNB Bro16 , and UCN$\tau$ Pat17 experiments as well as development efforts for the nEDM and Nab experiments at SNS Tan16 ; Bro16 .

This source has recently undergone a major upgrade, primarily motivated by the desire to perform a new nEDM experiment with improved sensitivity Ito14 . The current upper limit on the nEDM, set by an experiment performed more than a decade ago at the ILL turbine UCN source, is $d_{n}<3.0\times 10^{-26}$ $e\cdot$cm (90% C.L.)ILL , which was statistics limited. Further improvement on the sensitivity of experiments to the nEDM, currently attempted by many efforts worldwide, has been hindered by the lack of sufficiently strong sources of UCN, although it has been shown through various efforts that the necessary control for known systematic effects at the necessary level is likely to be achievable. An estimate Ito14 indicated that an upgrade of the LANL UCN source would provide a sufficient UCN density for an nEDM experiment with a sensitivity of $\sigma(d_{n})\sim 3\times 10^{-27}$ $e\cdot$cm, which formed the basis of the source upgrade reported here.

The basic design of the source, which was unchanged through the upgrade, is as follows. Spallation neutrons produced by a pulsed 800-MeV proton beam striking a tungsten target were moderated by beryllium and graphite moderators at ambient temperature and further cooled by a cold moderator that consisted of cooled polyethylene beads. The cold neutrons were converted to UCN by downscattering in an SD₂ crystal at 5 K. UCN were directed upward 1 m along a vertical guide coated with ⁵⁸Ni, to compensate for the 100-neV boost that UCN receive when leaving the SD₂, and then 6 m along a horizontal guide made of stainless steel (and coated with nickel phosphorus for the upgraded source) before exiting the biological shield. At the bottom of the vertical UCN guide was a butterfly valve that remained closed when there was no proton beam pulse striking the spallation target, in order to keep the UCN from returning to the SD₂ where they would be absorbed.

When in production, the peak proton current from the accelerator was typically 12 mA, delivered in bursts of 10 pulses each 625-$\mu$s long at 20 Hz, with a gap between bursts of 5 s. The total charge delivered per burst was $\sim$45 $\mu$C in 0.45 s. The time averaged current delivered to the target was $\sim$9 $\mu$A.

Details of the design and performance of the LANL UCN source before the upgrade are described in Ref. Sau13 . Figures 1 and 2 show the layout of the LANL UCN facility and the details of the source after the upgrade.

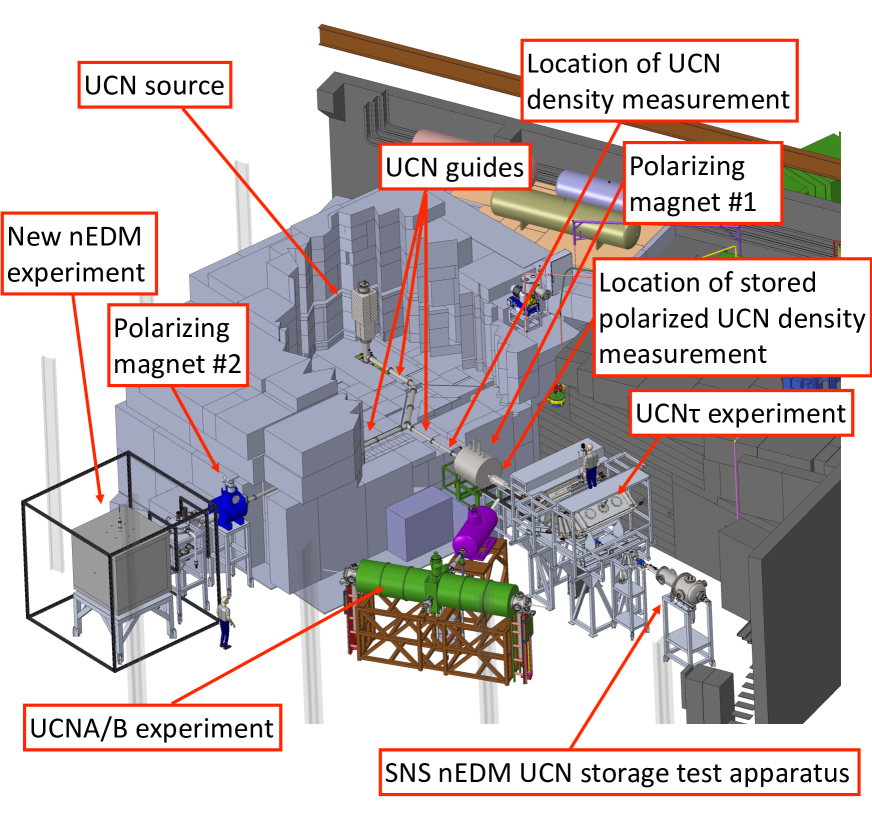
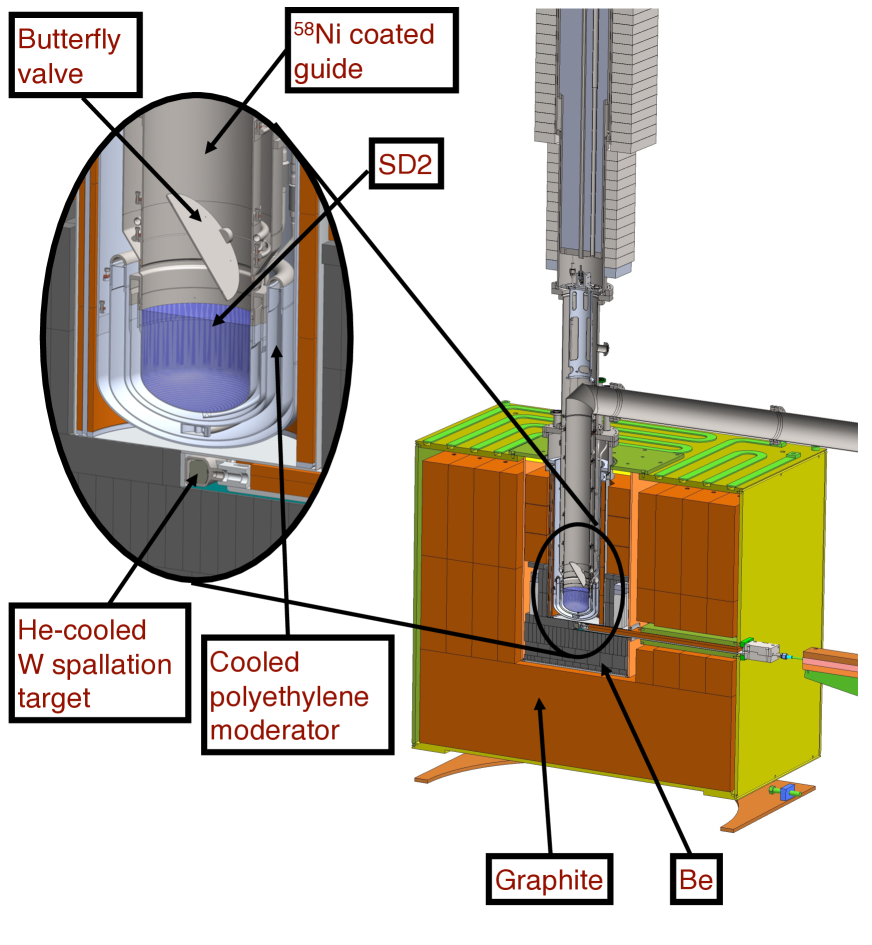
Because of the budgetary and schedule constraints, the scope of the UCN source upgrade work was limited to replacing the so-called “cryogenic insert” and the horizontal UCN guide. The cryogenic insert is the cryostat that houses the ⁵⁸Ni-coated vertical guide, the bottom of which is the SD₂ volume separated from the rest of the vertical guide by the butterfly valve, and the cold moderator volume. The scope of the upgrade work also included installing an additional new UCN guide, which guides UCN to a location envisioned for the new nEDM experiment (see Fig. 1).

The design of the new cryogenic insert was optimized to maximize the stored UCN density in the nEDM cell at the envisioned location of the experiment. The optimization variables were the geometry of the cryogenic insert, including the SD₂ volume, the cold moderator, and the vertical and horizontal UCN guides, as well as the material and temperature of the cold moderator. Considerations were given to both the specific UCN production in the SD₂ volume and the UCN transport from the SD₂ volume to the experiment. The specific UCN production $P_{\rm UCN}$, the number of UCN produced per unit incident proton beam charge per unit volume in the SD₂, is given by

where $\rho_{\rm SD2}$ is the number density of D₂ molecules, $\Phi_{\rm CN}(E)$ is the cold neutron flux in the volume element under consideration (per unit incident proton beam charge) at energy $E$, and $\sigma_{\rm UCN}(E)$ is the UCN production cross section per deuterium (D₂) molecule for cold neutrons at energy $E$. $\sigma_{\rm UCN}(E)$ was taken from Ref. Fre10 . $\Phi_{\rm CN}(E)$ was evaluated using MCNP6 MCNP6 . As seen in Fig. 6 of Ref. Fre10 , $\sigma_{\rm UCN}(E)$ has a peak at $E\sim 6$ meV. The task was to maximize the overlap integral in Eq. (1). For the cold moderator material, we considered polyethylene, liquid hydrogen, solid and liquid methane, and mesitylene. The following thermal neutron scattering cross section files were used in addition to the standard MCNP6 distribution: Ref. Gra09 for ortho-SD₂ at 5 K, Ref. Lav13 for polyethylene at 5, 77, and 293 K, Ref. Shi10 for solid methane at 20 K, and Ref. Can06 for mesitylene at 20 K. Polyethylene at 45 K, liquid methane at 100 K, and mesitylene at 20 K gave equally good results. Solid methane at 20 K made the cold neutron spectrum too cold. Taking engineering consideration into account, we decided to use polyethylene beads cooled to 45 K.

Our study showed that making the diameter of the SD₂ volume (and the vertical guide and the opening of the cold moderator) smaller increases the specific UCN production by confining the cold neutron flux. However, the UCN transport study we performed using an in-house developed UCN transport code indicated that by doing so, we lost in UCN transport efficiency. As a compromise, we made the diameter of the SD₂ volume somewhat smaller (15 cm) than that of the previous source (20 cm). This allowed us to place the mechanism for the butterfly valve outside the vertical guide, reducing the possible UCN loss due to UCN interacting with potentially UCN-removing surfaces. Furthermore, we increased the diameter of the horizontal guide (up to the branch point at which the new UCN guide starts) to 15 cm from the previous 10 cm, further improving the UCN transport efficiency. The horizontal UCN guides were all coated with nickel phosphorus, which we measured to have a high Fermi potential [213(5) neV] and low UCN loss ($1.6\times 10^{-4}$ per bounce) Pat17b .

The commissioning of the upgraded source started in November 2016. We performed a series of measurements to characterize the performance of the upgraded source. In order to make a direct comparison of the performance of the upgraded source to that of the source before the upgrade, these measurements were performed with the system disconnected from the new UCN guide designed to send UCN to the new nEDM experiment. The measured para fraction in the SD₂ was $2-3$% for these measurements.

The performance of SD₂-based UCN sources is known to depend on the quality of the SD₂ crystal, as observed in our previous source Mak17 and others Fre07 ; Lau16 . For the measurements reported in this paper, the source was prepared following our standard procedure, that is, the SD₂ crystal was grown directly from D₂ gas at vapor pressures of $50-130$ mbar. With this source, as well as with our previous source, we observed that the UCN production degraded with time, and the crystal was therefore periodically rebuilt. The source performance results presented in this paper were typical.

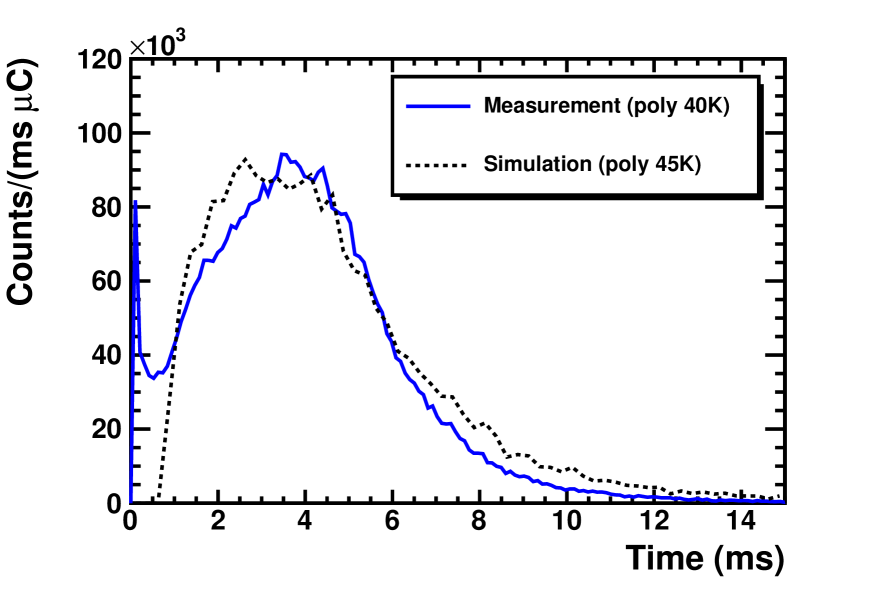
We first measured the time of arrival (TOA) distribution of cold neutrons at a detector placed 3.6 m above the 1-liter SD₂ volume, with the timing of the proton pulse giving the start time. In order not to blind the cold neutron detector (described below), these measurements were performed with the proton beam pulsed at 1 Hz with each pulse containing $\sim$1.5$\times 10^{-3}$ $\mu$C of protons.

The obtained TOA distributions give us information on the energy spectra of the cold neutrons at the location of the SD₂, which we can compare with our predictions from our MCNP6 model. If all cold neutrons left the SD₂ volume at $t=0$, there would be a trivial one-to-one correspondence between the neutron’s energy and the TOA; for example, it takes 3.4 ms for a 6-meV neutron to travel 3.6 m. However, our MCNP6 study showed that there is a broad emission time distribution as is typical for cold neutron moderators. Therefore a comparison between the experimental results and the simulations was made using the TOA distributions, shown in Fig. 3. The overall scale of the predicted spectrum was adjusted to reflect the detection efficiency of the cold neutron detectors, which was measured offline as described below. In the TOA range of $1.4-6.5$ ms, which corresponds to neutron energies of $1.6-34$ meV in the absence of delayed emission, the agreement between the measurement and model prediction is better than 20%, well within the expected model uncertainty. However, the model clearly overpredicts for TOA $>6.5$ ms, the cause of which is a subject of further investigation, along with a closer comparison between the measurement and model for TOA $<6.5$ ms. The same simulation predicts a specific UCN production of 478 UCN/cm³/$\mu$C near the bottom of the SD₂ volume and 290 UCN/cm³/$\mu$C near the top of the SD₂ volume.

The cold neutron detector consisted of an Eljen-426HD2 scintillator sheet directly coupled to a Hamamatsu R1355 photomultiplier tube (PMT). The scintillator consisted of a homogeneous matrix of particles of ⁶LiF and ZnS:Ag dispersed in a colorless binder Eljen . In this scintillator sheet, while the ⁶LiF particles provided neutron sensitivity through the neutron capture reaction ⁶Li($n$,$\alpha$)$t$, the ZnS:Ag particles provided light output by emitting scintillation light in response to alphas and tritons traversing them. The alphas and tritons depositing part of their energy in ⁶LiF particles or the binder produced a continuous energy deposition spectrum, causing the detector efficiency to depend strongly on the electronic threshold and to be lower than the probability of neutron capture by ⁶Li. For the TOA measurement describe above, the electronic threshold was adjusted so that the detector was not blinded by the initial fast particles from the proton pulse hitting the target. The efficiency of the cold neutron detector with the same threshold setting was measured offline using a monoenergetic neutron beam of 37 meV at the Neutron Powder Diffraction Facility at the PULSTAR Reactor at North Carolina State University. The detection efficiency was determined to be $0.53(2)$ of the probability of neutron capture by ⁶Li in the sheet. The quoted uncertainty is dominated by the systematic uncertainty associated with the determination of the neutron flux.

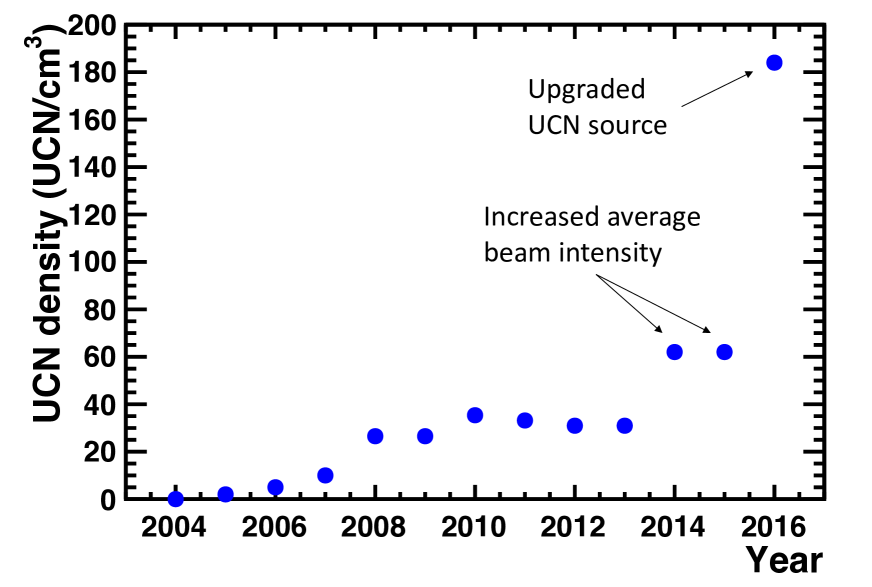
We also measured the UCN density at two different locations using the production proton beam described earlier. We first measured the unpolarized UCN density at the exit of the biological shield (see Fig. 1). The measurement was performed using a small vanadium foil fixed to the inner wall of the UCN guide, following the method described in our earlier publication Sau13 . The excited ⁵²V formed in the neutron capture reaction on ⁵¹V undergoes $\beta$-decay to ⁵²Cr and subsequently emits a 1.4-MeV $\gamma$ ray. At saturation, the rate of UCN capture equals the rate of 1.4-MeV $\gamma$ emission, and the UCN capture rate can be related to the UCN density by the kinetic theory formula $R=\frac{1}{4}\langle v\rangle A\rho$, where $R$ is the capture rate, $A$ is the area of the foil, $\langle v\rangle$ is the average UCN velocity, and $\rho$ is the UCN density. A UCN transport Monte Carlo simulation study showed that the UCN angular distribution is sufficiently isotropic at the location where the density was measured and in the condition in which the measurement was made to use this formula. The $\gamma$ rays were detected by a germanium detector placed outside the UCN guide. The detection efficiency (including the detector solid angle) was calibrated using a ⁶⁰Co source of known activity placed at the location of the vanadium foil. The UCN density was $184(32)$ UCN/cm³. The quoted uncertainty is dominated by the systematic uncertainty associated with the correction for the effect of the oxide layer, as described in Ref. Sau13 .

Note that for this UCN density measurement, the UCN spectrum was cut off by a stainless steel guide component used in the system. Figure 4 shows a comparison of this result with ones from the previous source. Together with the higher average proton current made possible by an improved proton beam current monitor (a more accurate beam current integration allowed us to run closer to the allowed limit), the UCN source upgrade project improved the source performance relevant for filling the UCN chamber of a neutron EDM experiment by a factor of $\sim$5.

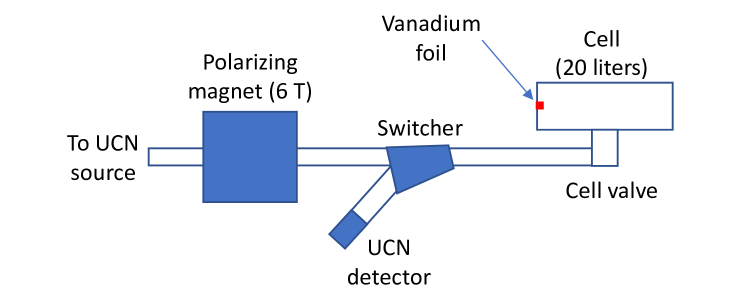
We measured the density of spin-polarized UCN stored in a prototype nEDM cell located downstream of polarizing magnet #1 (see Fig. 1). A schematic of the experimental setup is shown in Fig. 5. The prototype nEDM cell had an inner diameter of 50 cm and a height of 10 cm, giving a total volume of 20 liters. The inner surface was coated with nickel phosphorus. Note that for this UCN density measurement, in which high field seeking UCN were stored in the cell, the UCN spectrum was cut off by a stainless steel guide component used upstream in the system and further softened by the $\sim$10 cm climb needed to enter the chamber. The polarized UCN density was measured using the vanadium foil method described above. The measured density at this location was $39(7)$ UCN/cc. Here also, the quoted uncertainty is dominated by the systematic uncertainty associated with the correction for the effect of the oxide layer, as described in Ref. Sau13 .

We also measured the stored spin-polarized UCN density in the prototype nEDM cell using the so-called “fill-and-dump” method, in which (i) the cell is first filled with UCN, then (ii) the cell valve is closed to store UCN for a certain holding time, and finally (iii) the cell valve is opened and the remaining UCN are counted by a detector mounted on a UCN switcher. This measurement is repeated for various holding times. After holding times of 20 s and 150 s, we detected $\sim$200,000 UCN and $\sim$45,000 UCN, respectively. Figure 6 shows the detected UCN counts, normalized to the UCN monitor detector near the exit of the biological shield, as a function of the holding time. Normalization was necessary to make a storage time curve because the UCN source output had some fluctuations because the proton bursts from the accelerator were separated by 10 s. The stored UCN density extrapolated to $t=0$ was $13.6(0.9)$ UCN/cc, with the quoted uncertainty dominated by the fluctuation of the UCN source output mentioned above. The difference between this density and the density obtained by the vanadium method can be attributed to the loss of UCN through the UCN switcher as well as the finite UCN detection efficiency. The curve in Fig. 6 is well described by the UCN spectrum having the form $\frac{dN}{dv}\propto v^{2.9(0.6)}$ with a cutoff velocity of 5.7 m/s and the cell having an average storage time of 181(7) s.

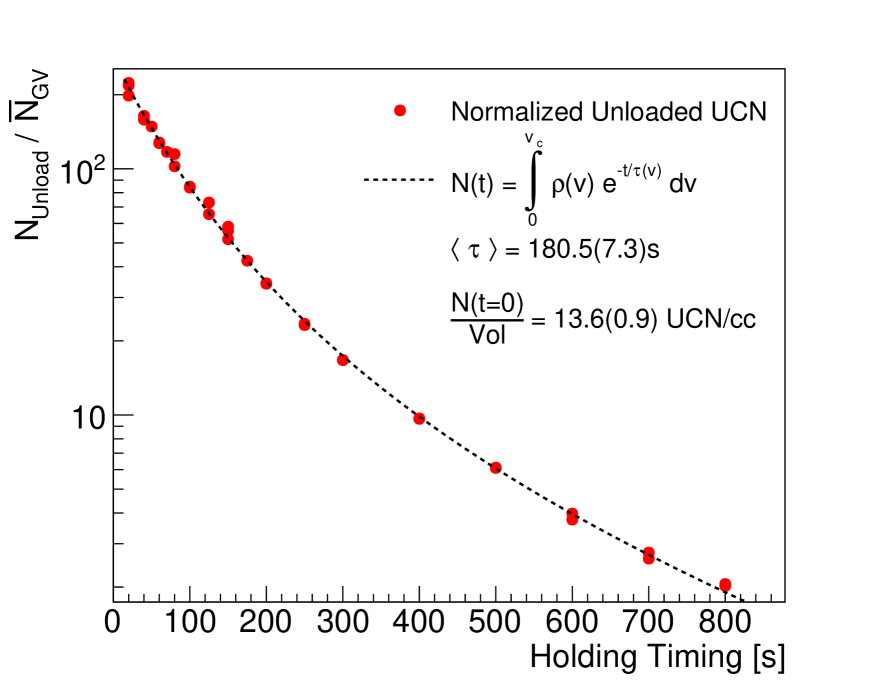
The system lifetime of the UCN source with the butterfly valve closed was measured to be 84.2(1.9) s.

Using the measured spin polarized UCN density stored in the prototype nEDM cell, we can estimate the statistical sensitivity of a possible nEDM experiment mounted at the upgraded UCN source. When an nEDM experiment based on Ramsey’s separated oscillatory field method Ram56 is performed using stored UCN, the statistical sensitivity is given by

where $\alpha$ is the polarization product (the product of the analyzing power and the UCN polarization), $E$ is the strength of the electric field, $T_{\rm free}$ is the free precession time, and $N_{T}$ is the total number of the detected neutrons over the duration of the experiment. If the number of detected neutron per measurement cycle is given by $N$, and the number of the performed measurement cycles is given by $M$, then $N_{T}=NM$. Therefore, the cycle time $T_{\rm cycle}$, the time it takes to perform a measurement, is also an important parameter. For the purpose here, we use the detected number of UCN at 180 s holding time, which is 39,000 per cell, for $N$. We further assume $\alpha=0.8$, $E=12$ kV/cm, $T_{\rm free}=180$ s, and $T_{\rm cycle}=300$ s, all of which have been demonstrated by other collaborations (see e.g. Ref. Bon16 ). Furthermore, we assume a double chamber configuration Ser15 . Then we expect to achieve a per-day one-standard-deviation statistical sensitivity of $\delta d_{n}=4.0\times 10^{-26}$ $e\cdot$cm/day. With an assumed data taking efficiency of 50% and the nominal LANSCE accelerator running schedule, we expect to achieve a one standard deviation statistical sensitivity of $\delta d_{n}=2.1\times 10^{-27}$ $e\cdot$cm in 5 calendar years. If the systematic uncertainty is equal to the statistical, then the total one-standard-deviation sensitivity is $\sigma(d_{n})=3\times 10^{-27}$ $e\cdot$cm. Note that this is a conservative estimate, as it is expected that we can further improve the detected number of UCN by using a switcher with an improved design, which will result in fewer years needed to achieve this sensitivity.

In conclusion, we have successfully upgraded the LANL UCN source. Its performance, as evaluated by the measured equilibrium UCN density in the UCN guide at the exit of the biological shield [184(32) /cm³] and the CN TOA distributions measured by a CN detector located 3.6 m above the source, is consistent with the prediction based on MCNP6 neutron moderation simulation and an in-house UCN transport simulation. The measured polarized UCN density stored in an nEDM-like chamber indicate that an nEDM experiment based on the room temperature Ramsey’s separated oscillatory field method with a one-standard-deviation sensitivity of $\sigma(d_{n})=3\times 10^{-27}$ $e\cdot$cm is possible with a running time of five calendar years (possibly fewer years with the switcher transmission issues addressed). In addition, with the upgraded LANL UCN source, the UCN$\tau$ experiment now routinely collects data sufficient for a 1-s statistical uncertainty in the free neutron lifetime in an actual running time of $\sim$60 hours Pat17 . The upgraded LANL UCN source will enable other UCN based experiments such as improved measurements of the neutron $\beta$-asymmetry.

This work was supported by Los Alamos National Laboratory LDRD Program (Project No. 20140015DR), the US Department of Energy (contract numbers DE-AC52-06NA25396 and DE-FG02-97ER41042) and the US National Science Foundation (Grant No. PHY1615153). We gratefully acknowledge the support provided by the LANL Physics and AOT Divisions. We thank M. Mocko and his team for allowing us to use their computer cluster for the mcnp6 simulation presented in this paper. We thank E. Brosha, S. Satjija, and G. Yuan for their help with characterizing the ⁵⁸Ni coating.