Persistence of cluster structure in the ground state of
Abstract
The persistence of cluster configuration in the ground state of is discussed. The particles emitted from excited states of could be utilized for cancer treatment, where the cluster states are created by a clinical proton beam on the target. Although the cross section has been already available, for the nuclear structure side, whether the ground state of contains the seeds of the cluster states is a crucial question, since the cluster structure may be washed out by the spin-orbit interaction, which has been known as a driving force to break the clusters. For this purpose, in addition to the basis states with cluster configurations, we include their breaking effects by employing the antisymmetrized quasi cluster model (AQCM). The inclusion of the breaking effect of cluster structure is found to contribute to the lowering of the ground-state energy by about . Assuming the typical three- cluster state of as an equilateral triangular configuration with the relative distances of , the ground state of is found to have a certain squared overlap with such state when a proton approaches. The third state has been suggested as a cluster state both theoretically and experimentally, and we confirmed the well-developed clustering.
I Introduction
In describing the structure of light nuclei, the nucleus is often treated as a subsystem called cluster due to its large binding energy in the free space. The most famous example of the state comprised of clusters is the second state of called the Hoyle state, which is a three state with large relative distances between clusters [1, 2]. The cluster models have been found to be quite effective in describing various properties of such state [3, 4].
Cluster states of , which are located higher than Hoyle state in energy, are recently utilized for cancer treatment. A clinical proton beam on the target induces excited states of with three configurations above the three- threshold energy and emitted particles from these states as their decay are used for destroying cancer cells [5]. For , the threshold corresponds to the excitation energy of , well above three threshold energy of , but the neutron threshold () is not opened. Therefore, the excited states decay by emitting particles. This method is called Proton Boron Capture Therapy (PBCT). The three- cluster states of in this energy region have been investigated for decades [6], and the data of – scattering cross section has been accumulated.
For the nuclear structure side, it would be still intriguing to investigate whether structure persists in the ground state of . The fact that this method work means that the ground state of contains enough component of the cluster configurations, which is the seed of the three states of . It has been discussed in that the third state is a candidate for the state with a cluster structure [7], but it is considered that in the ground state, the cluster structure is washed out to some extent as in the case of . Indeed, the spin-orbit interaction is known to work as a driving force to break the clusters [8].
In most of the conventional cluster models, the contribution of the non-central interactions (spin-orbit and tensor interactions) vanishes. If non-central interaction acts attractively by incorporating shell-model states in the model space, we must extend the model space and break the cluster structure. As well known, the spin-orbit interaction is important in the shell model; the observed magic numbers of , , and correspond to the subclosure configurations of , , and of the -coupling shell model [9].
This spin-orbit contribution is included by extending the cluster model; we have developed the antisymmetrized quasi cluster model (AQCM) [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]. This method allows us to smoothly transform -cluster model wave functions to -coupling shell model ones, and we call the clusters that feel the effect of the spin-orbit interaction owing to this model quasi clusters. We have previously introduced AQCM to and discussed the competition between the cluster states and -coupling shell model state [18]. The consistent description of and , which has been a long-standing problem of microscopic cluster models, has been achieved. Also, not only the competition between the cluster states and the lowest shell-model configuration, the effect of single-particle excitation was further included for the description of the ground state [23].
For , until now, various cluster models [24, 25, 26, 27] and antisymmetrized molecular dynamics (AMD) [28, 29] have been applied, where the main focus was the clustering in the excited states. In this paper, however, we couple cluster model space and shell-model one and investigate the persistence of cluster configuration in the ground state of . In addition to the basis states with cluster configurations, cluster breaking ones are prepared with AQCM, where the contribution of the spin-orbit interaction plays an important role. Furthermore, the basis states with the configurations are generated. All of these basis states are superposed based on the framework of the generator coordinate method (GCM), and cluster-shell competition is microscopically investigated. The interactions used are the same as those in our previous analysis on [23]. For the central part, the Tohsaki interaction [30], which has finite range three-body terms, is adopted. There is no free parameter to be adjusted. For the spin-orbit part, we use the spin-orbit term of the G3RS interaction [31], whose strength is set to give consistent description of and [18].
II framework
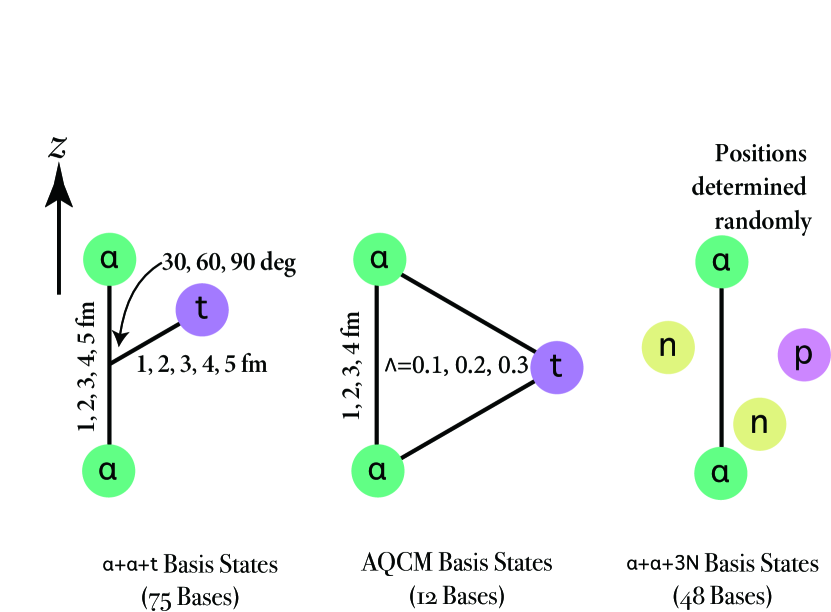
The wave function is fully antisymmetrized, and we superpose three kinds of the basis states: basis states (75 bases), AQCM basis states (12 bases), and basis states (48 bases), whose schematic figure is shown in Fig. 1. All these states are superposed based on the GCM after the angular momentum projection and amplitude for each basis state is determined by diagonalizing the norm and Hamiltonian matrices.
II.1 Single-particle wave function
In our framework, each single particle is described by a Gaussian form as in many other cluster models including the Brink model [32],
| (1) |
where the Gaussian center parameter is related to the expectation value of the position of the nucleon, and is the spin-isospin part of the wave function. For the size parameter , here we use , which gives the optimal energy of within a single AQCM basis state. The Slater determinant is constructed from these single-particle wave functions by antisymmetrizing them.
II.2 Basis states of cluster configurations
When four single-particle wave functions with different spin and isospin share a common value, an cluster is formed. Similarly, when two neutrons with opposite spin orientations and a proton share the same , a triton cluster is formed. We prepare 75 basis states with different configurations. The distance between two clusters is changed from to in the step of . The triton is set at the places with the distance of – from the center of two clusters, which is changed in the step of , and the axis measured from the – axis is set to , , and . In all these states, the values in Eq. (1) are real numbers.
II.3 Basis states of AQCM
This cluster wave function is transformed into -coupling shell model based on the AQCM, by which the contribution of the spin-orbit interaction due to the breaking of clusters is included. Here the values in Eq. (1) are changed to complex numbers. When the original value of the Gaussian center parameter is , which is real and related to the spatial position of this nucleon, it is transformed by adding the imaginary part as
| (2) |
where is a unit vector for the intrinsic-spin orientation of this nucleon. The control parameter is associated with the breaking of the cluster, and two nucleons with opposite spin orientation have values that are complex conjugate to each other. This situation corresponds to the time-reversal motion of two nucleons. After this transformation, the clusters are called quasi clusters.
In our previous analysis on , we have prepared three quasi clusters with an equilateral triangular shape. We introduced two parameters, representing the – distances and for the breaking of the clusters. The subclosure configuration of of the -coupling shell model can be obtained at the limit of and .
For , we remove one spin-down proton from a quasi cluster. The and values are taken as , , , and , , ( states are not necessary because they have large overlaps with the basis states).
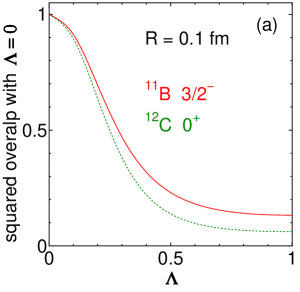
It has been discussed that the cluster model space covers the model space of the shell model, if the wave function is antisymmetrized and we take the small-distance limit between clusters. This statement is correct when the term of the “shell model” is used in the sense of the three-dimensional harmonic oscillator. The cluster-model wave function becomes the three-dimensional harmonic oscillator one at the limit of the small relative distances. However, the three-dimensional harmonic oscillator wave function (corresponding to in AQCM) is quite different from the -coupling shell-model one (corresponding to in AQCM), as we can easily assess using our AQCM. Figure 2(a) shows the squared overlap between the three-dimensional harmonic oscillator (cluster model with small distances) and AQCM as functions of the value. The dotted line is for with equilateral triangular configuration and very small distances between three quasi clusters. The vertical axis shows the squared overlap between and finite states. The angular momentum and parity are projected to . The dotted line rapidly drops and the state with (identical to the three-dimensional harmonic oscillator one) has very small squared overlap with the subclosure configuration of the -coupling shell model () of about at . The solid line is for the of . Since one proton is missing compared with , the squared overlap between the three-dimensional harmonic oscillator and -coupling shell model increases, but the value is still quite small (slightly above ).
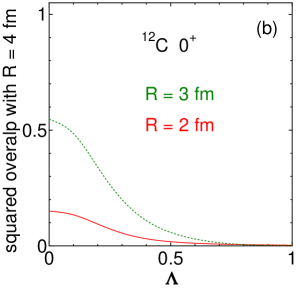
Next, the squared overlaps between a typical three- cluster state and AQCM basis states are shown in Fig. 2(b). Here, the typical three- cluster state means an equilateral triangular configuration with the – distance () of . The solid and dotted lines are for the squared overlap with this typical cluster state and the AQCM basis states with and as functions of , respectively. In our previous work, we have discussed that and is the optimal AQCM basis state, which is found have the squared overlap of with the typical cluster state.
II.4 Basis states of
To describe the single-particle nature of three nucleons outside two clusters, we prepare basis states, where – distance is determined using the random number (between – with equal probability) and positions of three nucleons (a spin-up proton and two neutrons with opposite spin directions) are also determined randomly. We generate 48 basis states and include them in the diagonalization process of the norm and Hamiltonian matrices.
II.5 projection and GCM
As we have mentioned before, totally we generate 135 intrinsic states. The basis states from 1 to 75 are states with various configurations, those from 76 to 87 are AQCM basis states with , , , and , and those from 88 to 135 are configurations with the – distance of –. These 135 basis states are numerically projected to eigenstates of angular momentum and parity. After the angular momentum projection, different number states are generated from the same intrinsic basis state. Here, the direction of the intrinsic frame is parallel to the axis of two (quasi) clusters. These different states are treated independently when we determine the coefficients for the linear combination of the basis states based on GCM. Therefore, after the angular momentum projection, the number of the basis states increases to 540, the basis states of 1–135, 136–270, 271–405, and 406–540 are , , , and , respectively.
II.6 Hamiltonian
The Hamiltonian consists of the kinetic energy and potential energy terms. For the potential part, the interaction consists of the central, spin-orbit, and Coulomb terms. The interactions are the same as those in our previous analysis on [23]. For the central part, the Tohsaki interaction [30] is adopted. This interaction has finite-range three-body terms in addition to two-body terms, which is designed to reproduce both saturation properties and scattering phase shifts of two clusters. For the spin-orbit part, There is no free parameter left for each nucleus for this interaction. For the spin-orbit part, we use the spin-orbit term of the G3RS interaction [31], which is a realistic interaction originally developed to reproduce the nucleon-nucleon scattering phase shifts. The strength of the spin-orbit interactions is set to , which allows consistent description of and [18].
III Results
III.1 Energy levels of
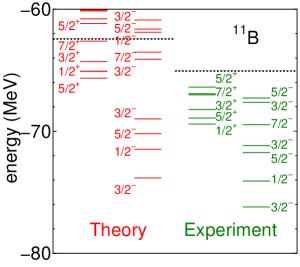
We project 135 basis states to the eigenstates of angular momentum and parity, and basis states with , , , and are independently treated. Thus, based on GCM, we diagonalize the norm and Hamiltonian matrices with the dimension of 540. The obtained energy levels of are listed in Fig. 3, where dotted lines are threshold energies of . The ground state is obtained at , compared with the experimental value of . Although we have no adjustable parameter for the central interaction and the spin-orbit strength is determined in our previous work for , the absolute value of the calculated energy is quite reasonable.
The theoretical binding energy underestimates the experimental one by , but the agreement between theoretical and experimental binding energies becomes even better if we measure them from the threshold. This is because the underestimate can be absorbed in the internal energies of the clusters; the theoretical value of (triton) energy is (), compared with the experimental value of (). The ground-state energy of is from the threshold compared with the experimental value of .
III.2 Energy convergence of the states
The energy convergence of the states of is shown in Fig. 4(a). The horizontal axis shows the number of the basis states superposed in the GCM calculation. As mentioned before, we generated 135 basis states, which are projected to the eigenstates with , , , and , and thus we diagonalize the norm and Hamiltonian with the dimension of . From this figure, the first and third states are found to have predominantly the component, whereas the second state has mainly the component. Figure 4(b) is the excerpt of the part. Here the first 75 basis states (136–210 on the horizontal axis) are basis states with the cluster configurations, the next 12 basis states (211–222) are AQCM, and the last 48 basis states (223–270) are configurations.
From these figures, we can confirm that the inclusion of the breaking effect of cluster structure contributes to the lowering of the ground-state energy by about 2 MeV (for instance, we can compare the energies at 210 and 270 on the horizontal axis of Fig. 4(b)). The decrease of the energy when cluster breaking is incorporated is about half compared with , where the spin-orbit effect decreases the ground-state energy by several MeV (the same interaction is applied to in Ref. [18]). This is because the spin-orbit acts for a proton in the triton cluster already within the model space; the antisymmetrization effect excites the triton cluster with the configuration to the -shell and the angular momentum projection allows the change of this proton wave function to . Anyhow, two clusters and di-neutron cluster in the triton cluster are free from the spin-orbit interaction, and breaking these clusters based on AQCM has a certain effect of decreasing the ground state of about .


III.3 Squared overlap with each basis state
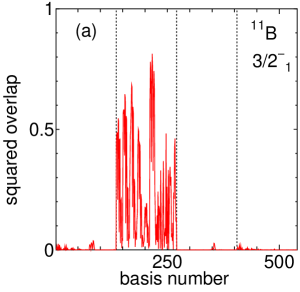
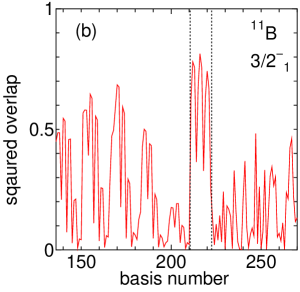
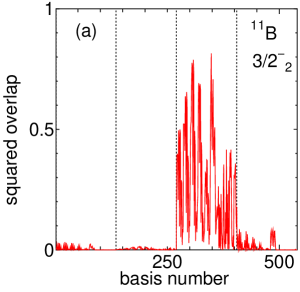
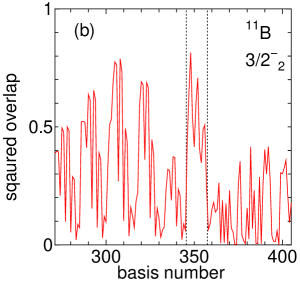
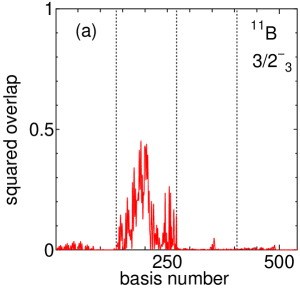
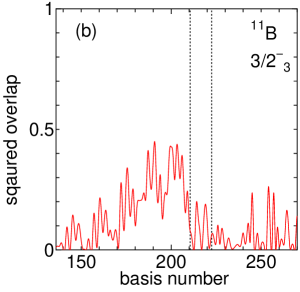
Figure 5(a) shows the squared overlap between the ground state and each basis state. Here, basis states with correspond to 1–135 on the horizontal axis, and , , and correspond to 136–270, 271–405, and 406–540 on the horizontal axis. As expected, the contribution of is dominant in the ground state.
Figure 5(b) is the excerpt of the part. As in the previous figure, the first 75 basis states (136–210 on the horizontal axis) are basis states with the cluster configurations, the next 12 basis states (211–222) are AQCM, and the last 48 basis states (223–270) are configurations. For the cluster configurations basis states (136–210), we see five peak structures, and the basis states are classified into five groups with the interval of 15 basis states (136–150, 151–165, 166–180, 181–195, and 196–210). These five groups correspond to the basis states with the – distances of , , , , and , and as we can see, – distance of 3 fm contributes the most importantly (166–180). These 15 basis states are further classified into five groups with the interval of three (166–168, 169–171, 172–174, 175–177, and 178–180) corresponding to the position of the triton at , , , , and form the center of –. The largest squared overlap of within the cluster configurations is given for the basis state 170 on the horizontal axis, which corresponds to the – distance is , and the triton is located at from the center of – with the angle of . Therefore, the ground state is found to have the component of about .
Furthermore, we can get insight about the overlap with the higher excited cluster states of when a proton is added, which is important medically, as explained in the introduction. Such cluster states can be characterized as a state with the three clusters with the relative distances of , since the – system has the minimum energy with such relative distance in the free space. In our calculation, the basis states 181–195 correspond to the – distance of , and in the basis states 190–192, the last cluster is placed at 4 fm from the center of two clusters. We can confirm that the ground state has the squared overlap of about with those basis states proving it contains enough amount of seeds for the Hoyle state of .
However, the figures show that the AQCM basis states (211–222) describe the ground state better than the cluster configuration and they are more important. These AQCM basis states are classified into three groups with the interval of four, and basis states 211–214 are for (215–218 are for and 219–222 are for ). The largest squared overlap of 0.81 is given for the basis state 216 on the horizontal line corresponding to the basis states with and , where represents the distances between quasi clusters with equilateral triangular shape. The AQCM basis states with finite values have larger squared overlaps than the cluster configurations, and this means that the breaking of clusters due to the spin-orbit contribution is important. In our previous work on with the same interaction, similarly, was found to give the optimal energy, where the – distance was reduced to owing to the strong attraction of three quasi clusters.
Figure 6(a) shows the squared overlap between the second state and each basis state. The orders of the basis states are the same as in the previous figures, and it is obvious that is important for this state. In our basis states, the spin direction of a valence proton is set to spin-up, thus means that the orbital angular momentum of the proton and its spin are antiparallel, for which the spin-orbit interaction acts repulsively. Figure 6(b) is the excerpt of the part. The squared overlaps with the cluster states (271–345 on the horizontal axis) are increases compared with the previous cases of the ground state, and again, the – distance of 3 fm is found to be most important among them. However, the squared overlaps with the AQCM basis states (346–357 on the horizontal axis) have even larger overlaps. Contrary to the ground-state case, the basis state with has the largest squared overlap.
Figure 7(a) shows the squared overlap between the third state, which has been suggested as a candidate for the cluster state both theoretically and experimentally, and each basis state. Here, we find that the contribution of is dominant, and Figure 7(b) is the excerpt of the part. The squared overlaps with the cluster states (136–210 on the horizontal axis) are much larger than those of the AQCM basis states (211–222). We can confirmed that the breaking effect of clusters is small and this state is really a cluster state as expected. The – distance of is found to have the largest overlap, which can be considered as well developed clustering.
Summarizing, one can find that contributes dominantly to the ground , where AQCM states dominates the most, especially with , while the cluster states, especially with – distance , contributes largely as well; contributes dominantly to the second , where AQCM states dominates the most, especially with , while the cluster states, especially with – distance , contributes largely as well; contributes dominantly to the third , where the cluster states, especially with – distance , dominates.
III.4 Squared overlap between and
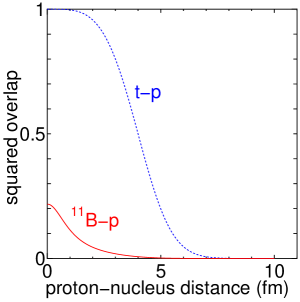
We have shown how the components of the configurations are mixed in the ground state of . Here, finally, we discuss the squared overlap with the three- cluster configuration when a proton approaches . We start with the case of single- formation. The dotted line in Fig. 8 shows the squared overlap between an cluster and as a function of the distance between the triton cluster and the proton. The total angular momentum is projected to . Here the spin orientations of the proton and the one in the triton cluster are assumed to be anti-parallel. The squared overlap becomes zero when they are parallel. Therefore, we need an additional factor of , which is not considered in Fig. 8, in the real situation of the proton scattering, where spin orientations are not fixed. The squared overlap between and is unity at zero-distance and gradually drops as the distance increases.
Next, the solid line shows the squared overlap between and three--cluster state as a function of the distance between the proton and . In the real situation of the proton scattering, various three- cluster states of are created when the proton meets , and in this calculation, such three--cluster states are represented by a single configuration of an equilateral triangular shape with the relative – distance of (optimal – distance of in the free space). The target nucleus, , is represented by the most important basis state in the previous subsection; AQCM basis state with and . To compare with the real situation of the proton scattering, the target nucleus of should be angular momentum projected to and the relative angular momentum between and also must be treated as a good quantum number. However, here these are approximated as the total angular momentum projection, and the proton is assumed to approach from the perpendicular direction to the three quasi clusters. The threshold energy of corresponds to in , and the resonances slightly above this energy are clinically important sources of the -cluster emission. According to the database at National Nuclear Data Center, the resonance state of at decays with the branching ratio of . Therefore, here we project the angular momentum to , and in this case, the relative wave function between the proton and dominantly has the -wave component. Again the spin orientations of the incident proton and that in the target nucleus are assumed to be antiparallel, and thus we need an additional factor of , which is not considered in Fig. 8, to compare with the real situation. We can see the squared overlap of – at small distances. The value is not very large, but the proton scattering on is considered tot have a sizeable branching ratio for creating the three- cluster states.
IV Conclusions
We have discussed the persistence of cluster configuration is discussed in the ground state of . The highly excited three- cluster states of are recently used for cancer treatment. The proton scattering on creates excited states of with three configurations much above the three- threshold energy and emitted particles after the decay destroy cancer cells. From the nuclear structure point of view, it would be intriguing to investigate whether structure persist in the ground state of ; this spin-orbit interaction is known to work as a driving force to break the clusters and it is considered that the cluster structure is washed out to some extent as in the case of . Although this effect is not investigated within the traditional cluster models, the antisymmetrized quasi cluster model (AQCM) allows as to transform cluster model wave functions to -coupling shell-model ones, by which the contribution of the spin-orbit interaction can be included. All of these basis states are superposed based on the framework of the generator coordinate method (GCM), and cluster-shell competition is microscopically investigated.
It is confirmed that the inclusion of the breaking effect of cluster structure contributes to the lowering of the ground-state energy by about . The decrease of the energy when cluster breaking is incorporated is about half compared with , where the spin-orbit effect decreases the ground-state energy by several MeV, and this is because the spin-orbit acts for a proton in the triton cluster already within the model space; the antisymmetrization effect the triton cluster to the -shell and the angular momentum projection allows the change of this proton wave function to . Anyway, two clusters and di-neutron cluster in the triton cluster are free from the spin-orbit interaction, and breaking these clusters based on AQCM has a certain effect. Nevertheless, the ground state has the component of about . Furthermore, we can get insight that contains the seeds of the Hoyle state of when a proton is added. The three- cluster state in highly excited states can be characterized as a state with the three clusters with the relative distances of (optimal – distance of in the free space). We can confirm that the ground state of has a certain squared overlap (–) with the state having the – distance of when a proton approaches.
The third state has been suggested as a cluster state both theoretically and experimentally. The squared overlaps with the cluster states are much larger than the AQCM basis states. The – distance of is found to have the largest overlap, which can be considered as well developed clustering.
Acknowledgements.
This work was supported by JSPS KAKENHI Grant Number 19J20543. The numerical calculations have been performed using the computer facility of Yukawa Institute for Theoretical Physics, Kyoto University (Yukawa-21).References
- Hoyle [1954] F. Hoyle, On Nuclear Reactions Occuring in Very Hot STARS.I. the Synthesis of Elements from Carbon to Nickel., Astrophys. J. Suppl. 1, 121 (1954).
- Freer and Fynbo [2014] M. Freer and H. O. U. Fynbo, The Hoyle state in , Prog. Part. Nucl. Phys. 78, 1 (2014).
- Fujiwara et al. [1980] Y. Fujiwara, H. Horiuchi, K. Ikeda, M. Kamimura, K. Katō, Y. Suzuki, and E. Uegaki, Chapter II. Comprehensive Study of Alpha-Nuclei, Prog. Theor. Phys. Supplement 68, 29 (1980).
- Tohsaki et al. [2001] A. Tohsaki, H. Horiuchi, P. Schuck, and G. Röpke, Alpha Cluster Condensation in and , Phys. Rev. Lett. 87, 192501 (2001).
- A. P. Cirrone et al. [2018] G. A. P. Cirrone, L. Manti, D. Margarone, et al., First experimental proof of Proton Boron Capture Therapy (PBCT) to enhance protontherapy effectiveness., Sci Rep 8, 1141 (2018).
- Stave et al. [2011] S. Stave, M. W. Ahmed, R. H. France, S. S. Henshaw, B. Müller, B. A. Perdue, R. M. Prior, M. C. Spraker, and H. R. Weller, Understanding the reaction at the resonance, Phys. Lett. B 696, 26 (2011).
- Kawabata et al. [2007] T. Kawabata, H. Akimune, H. Fujita, Y. Fujita, M. Fujiwara, K. Hara, K. Hatanaka, M. Itoh, Y. Kanada-En’yo, S. Kishi, K. Nakanishi, H. Sakaguchi, Y. Shimbara, A. Tamii, S. Terashima, M. Uchida, T. Wakasa, Y. Yasuda, H. Yoshida, and M. Yosoi, cluster structure in , Physics Letters B 646, 6 (2007).
- Itagaki et al. [2004] N. Itagaki, S. Aoyama, S. Okabe, and K. Ikeda, Cluster-shell competition in light nuclei, Phys. Rev. C 70, 054307 (2004).
- Mayer and Jensen [1955] M. G. Mayer and H. G. Jensen, “Elementary theory of nuclear shell structure”, John Wiley, Sons, New York, Chapman, Hall, London (1955).
- Itagaki et al. [2005] N. Itagaki, H. Masui, M. Ito, and S. Aoyama, Simplified modeling of cluster-shell competition, Phys. Rev. C 71, 064307 (2005).
- Masui and Itagaki [2007] H. Masui and N. Itagaki, Simplified modeling of cluster-shell competition in carbon isotopes, Phys. Rev. C 75, 054309 (2007).
- Yoshida et al. [2009] T. Yoshida, N. Itagaki, and T. Otsuka, Appearance of cluster states in , Phys. Rev. C 79, 034308 (2009).
- Itagaki et al. [2011] N. Itagaki, J. Cseh, and M. Płoszajczak, Simplified modeling of cluster-shell competition in and , Phys. Rev. C 83, 014302 (2011).
- Suhara et al. [2013] T. Suhara, N. Itagaki, J. Cseh, and M. Płoszajczak, Novel and simple description for a smooth transition from -cluster wave functions to -coupling shell model wave functions, Phys. Rev. C 87, 054334 (2013).
- Itagaki et al. [2016] N. Itagaki, H. Matsuno, and T. Suhara, General transformation of cluster model wave function to jj-coupling shell model in various 4n nuclei, Prog. Theor. Exp. Phys. 2016, 093D01 (2016).
- Matsuno et al. [2017] H. Matsuno, N. Itagaki, T. Ichikawa, Y. Yoshida, and Y. Kanada-En’yo, Effect of clustering on the transition in , Prog. Theor. Exp. Phys. 2017, 063D01 (2017).
- Matsuno and Itagaki [2017] H. Matsuno and N. Itagaki, Effects of cluster-shell competition and BCS-like pairing in 12C, Prog. Theor. Exp. Phys. 2017, 123D05 (2017).
- Itagaki [2016] N. Itagaki, Consistent description of and using a finite-range three-body interaction, Phys. Rev. C 94, 064324 (2016).
- Itagaki and Tohsaki [2018] N. Itagaki and A. Tohsaki, Nontrivial origin for the large nuclear radii of dripline oxygen isotopes, Phys. Rev. C 97, 014307 (2018).
- Itagaki et al. [2018] N. Itagaki, H. Matsuno, and A. Tohsaki, Explicit inclusion of the spin-orbit contribution in the tohsaki-horiuchi-schuck-röpke wave function, Phys. Rev. C 98, 044306 (2018).
- Itagaki et al. [2020a] N. Itagaki, A. V. Afanasjev, and D. Ray, Possibility of cluster as a building block of medium-mass nuclei, Phys. Rev. C 101, 034304 (2020a).
- Itagaki et al. [2020b] N. Itagaki, T. Fukui, J. Tanaka, and Y. Kikuchi, and cluster structures in light nuclei, Phys. Rev. C 102, 024332 (2020b).
- Itagaki and Naito [2021] N. Itagaki and T. Naito, Consistent description for cluster dynamics and single-particle correlation, Phys. Rev. C 103, 044303 (2021).
- Nishioka et al. [1979] H. Nishioka, S. Saito, and M. Yasuno, Structure Study of System by the Orthogonality Condition Model, Progress of Theoretical Physics 62, 424 (1979).
- Descouvemont [1995] P. Descouvemont, The and reactions in a microscopic three-cluster model, Nuclear Physics A 584, 532 (1995).
- Yamada and Funaki [2010] T. Yamada and Y. Funaki, cluster structures and ()-analog states in , Phys. Rev. C 82, 064315 (2010).
- Zhou and Kimura [2018] B. Zhou and M. Kimura, cluster structure in , Phys. Rev. C 98, 054323 (2018).
- Kanada-En’yo [2007] Y. Kanada-En’yo, Negative parity states of and and the similarity with , Phys. Rev. C 75, 024302 (2007).
- Suhara and Kanada-En’yo [2012] T. Suhara and Y. Kanada-En’yo, Cluster structures in 11B, Phys. Rev. C 85, 054320 (2012).
- Tohsaki [1994] A. Tohsaki, New effective internucleon forces in microscopic -cluster model, Phys. Rev. C 49, 1814 (1994).
- Tamagaki [1968] R. Tamagaki, Potential Models of Nuclear Forces at Small Distances, Prog. Theor. Phys. 39, 91 (1968).
- Brink [1966] D. M. Brink, Proc. Int. School Phys.“Enrico Fermi” XXXVI, 247 (1966).