Corresponding author: ]leishu@fudan.edu.cn
Persistent spin dynamics and absence of spin freezing in the - phase diagram of the 2D triangular antiferromagnet YbMgGaO4
Abstract
We report results of muon spin relaxation and rotation (SR) experiments on the spin-liquid candidate YbMgGaO4. No static magnetism per Yb ion, ordered or disordered, is observed down to 22 mK, a factor of two lower in temperature than previous measurements. Persistent (temperature-independent) spin dynamics are observed up to 0.20 K and at least 1 kOe, thus extending previous zero-field SR results over a substantial region of the - phase diagram. Knight shift measurements in a 10-kOe transverse field reveal two lines with nearly equal amplitudes. Inhomogeneous muon depolarization in a longitudinal field, previously characterized by stretched-exponential relaxation due to spatial inhomogeneity, is fit equally well with two exponentials, also of equal amplitudes. We attribute these results to two interstitial muon sites in the unit cell, rather than disorder or other spatial distribution. Further evidence for this attribution is found from agreement between the ratio of the two measured relaxation rates and calculated mean-square local Yb3+ dipolar fields at candidate muon sites. Zero-field data can be understood as a combination of two-exponential dynamic relaxation and quasistatic nuclear dipolar fields.
I INTRODUCTION
In 1973 Anderson Anderson (1973) proposed an exotic magnetic state in the two-dimensional (2D) triangular-lattice Heisenberg antiferromagnet where local spins are highly entangled with no spin freezing. A clear experimental identification of such a quantum spin liquid (QSL) material is much desired, for its own sake and for potential applications in quantum computation and possible relation to novel phenomena such as high-temperature superconductivity, topological order, and Mott insulators Anderson (1987); Lee (2008); Balents (2010); Savary and Balents (2017); Zhou et al. (2017). Many materials with geometrically-frustrated lattices have been proposed as candidate spin liquids (see, e.g., Uemura et al. (1994); Shimizu et al. (2003); Nakatsuji et al. (2006); Helton et al. (2007); Okamoto et al. (2007); Itou et al. (2008); Li et al. (2015a)). Whether there is a QSL among these candidates remains controversial, however.
YbMgGaO4 is a quasi-2D triangular-lattice antiferromagnet that has attracted considerable attention as a QSL candidate Li et al. (2015a, b, 2016a); Xu et al. (2016); Shen et al. (2016); Paddison et al. (2017); Li et al. (2017a, b); Shen et al. (2018); Zhang et al. (2018); Ma et al. (2018); Li et al. (2019). No spin ordering was observed down to 0.06 K from thermodynamic and transport measurements Li et al. (2015a); Xu et al. (2016). The low-temperature heat capacity exhibits a power-law temperature dependence with an exponent close to the theoretical value of 2/3 for a QSL. An anisotropic spin interaction was observed and discussed as important to stabilize a possible QSL ground state Li et al. (2015b). Inelastic neutron scattering measurements Shen et al. (2016); Paddison et al. (2017); Li et al. (2017b, 2019) provided evidence for a QSL state with a spinon Fermi surface by observing continuous spin excitations. High-field time-domain terahertz spectroscopy measurements Zhang et al. (2018) characterized YbMgGaO4 as an easy-plane XXZ antiferromagnet. Theoretical treatments predict a proposed spinon Fermi surface spin liquid Li et al. (2016b, 2017c); Li and Chen (2017).
Whether or not there is a QSL state in YbMgGaO4 is still under debate. Evidence against a QSL includes thermal conductivity measurements that did not observe the expected magnetic excitation contribution down to 0.050 K Xu et al. (2016). Furthermore, a frequency-dependent cusp was observed at 0.1 K in ac susceptibility measurements Ma et al. (2018), suggesting a spin-glass-like transition, although the dc magnetization saturates at low temperatures with no evidence for spin freezing up to 10 kOe Li et al. (2019). Proposed alternative ground states Luo et al. (2017); Zhu et al. (2017); Parker and Balents (2018); Kimchi et al. (2018) involve various forms of ordered or disordered static magnetism, but without definite predictions for transition temperatures.
Muon spin rotation and relaxation (SR) Schenck (1985); *Blundell99; *Brewer03; *Yaouanc11 is a powerful technique to probe local magnetism in solids, and has been widely used to study spin-liquid candidates (e.g., Uemura et al. (1994); Bert et al. (2009); Pratt et al. (2011); Clark et al. (2013); Khuntia et al. (2016); Li et al. (2016a); Pratt (2018)). A SR study of YbMgGaO4 by Y. Li et al. Li et al. (2016a) showed no static or long-range magnetic order in zero field (ZF) down to 0.048 K, which was taken as evidence for a QSL ground state. Below 10 K the ZF muon spin polarization exhibited so-called stretched-exponential relaxation , where is a characteristic relaxation rate and is the stretching exponent. Stretched exponentials are used as phenomenological models for spatially inhomogeneous distributions of relaxation rates Johnston (2006). In YbMgGaO4 at 10 K Li et al. (2016a); the ZF relaxation was nearly exponential. With decreasing temperature decreased considerably, suggesting the onset of spatial inhomogeneity. At 70 mK was continuously suppressed by an applied longitudinal field (LF) up to 1.8 kOe. The field dependence of was not reported.
This article reports SR experiments on single-crystalline YbMgGaO4 that extend the work of Li et al. Li et al. (2016a). Positive-muon () frequency and relaxation measurements were carried out for temperatures down to 22 mK and applied fields up to 10 kOe. Fourier transforms of SR data taken in a transverse field (TF) kOe (Sec. III.1) reveal two lines with equal amplitudes but significantly different frequency (Knight) shifts. We attribute the lines to two distinct interstitial stopping sites near the two inequivalent oxygen ions in the YbMgGaO4 unit cell, as previously suggested Li et al. (2016a). The corrected Knight shifts are nearly temperature-independent below 1 K, as is the bulk susceptibility at this field (Ref. Li et al. (2019), supplement). The ratio is roughly consistent with calculated Yb3+ dipolar fields at candidate sites.
spin relaxation data were taken for longitudinal fields up to 8 kOe at 22 mK, 0.20 K, and 5.83 K (Sec. III.2), and in ZF over the temperature range 22 mK–5.8 K (Sec. III.3). In light of the TF-SR results summarized above, LF asymmetry spectra for mK and Oe, where the relaxation is purely dynamic Schenck (1985); *Blundell99; *Brewer03; *Yaouanc11, were fit by a sum of two exponentials (rates and ), rather than the stretched exponential used previously Li et al. (2016a). A sum of two exponentials and a stretched exponential are both sub-exponential forms (i.e., exhibit upward curvature on a log-linear plot), and can be difficult to distinguish [See; forexample; ]Johnston06.
With equal amplitudes of the two exponentials, the observed ratio is field-independent and in rough agreement with the ratio of calculated mean-square Yb3+ dipolar fields. This is expected if the sub-exponential relaxation is due to differences in coupling fields rather than inhomogeneity in the spin dynamics. It is additional evidence for the two-site scenario.
For lower the contributions of static nuclear dipolar fields must be considered (stretched-exponential fits alone mix the static and dynamic contributions). Fits of relaxation functions appropriate to this situation Schenck (1985); *Blundell99; *Brewer03; *Yaouanc11 (Sec. III.2) to the data then allow determination of down to .
The paper is organized as follows. Section II describes the YbMgGaO4 sample and its crystal structure, briefly summarizes the SR technique, and gives details of the experiment. Results of TF, LF, and ZF experiments are reported in Sec. III and are discussed in Sec. IV. Section V summarizes our conclusions.
II EXPERIMENT
II.1 Sample
Plate-like high-quality single crystals of YbMgGaO4 were grown by a floating-zone method and characterized as reported previously Ma et al. (2018). Figure 1
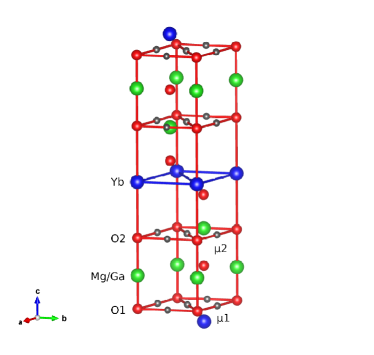
shows two-thirds of a hexagonal unit cell of YbMgGaO4 (space group , No. 166) Li et al. (2015a, b). Mg and Ga ions are distributed randomly on the indicated sites, leading to unavoidable local disorder in the structure. There are two inequivalent oxygen locations (O1 and O2) in the unit cell. The triangular 2D Yb3+ layers are well separated by two Mg/Ga planes and four O1/O2 planes (Yb3+ layer spacing 8.377 Å), and inter-layer magnetic interaction is weak.
Implanted positive muons in oxides are likely to stop near O2- ions. To date there are no reported calculations of site locations in YbMgGaO4 [Forareview; see]Bonfa16. In lieu of such information, we consider candidate sites that are centered with respect to oxygen nearest neighbors. There are two such crystallographically inequivalent sites (1 and 2), shown in Fig. 1. Dipolar magnetic fields from neighboring Yb3+ ions and nuclei are unlikely to be very different if the actual sites are closer to O2- ions.
II.2 The SR technique
In a typical SR experiment Schenck (1985); *Blundell99; *Brewer03; *Yaouanc11, 100% spin-polarized positive muons are implanted into the sample and stop at interstitial sites. Each precesses in the (in general fluctuating) local field at its site, and at the time of its decay (mean lifetime s) emits a positron preferentially in the direction of the spin. Positrons are detected by an array of scintillation counters, and a histogram of count rate vs time after implantation is obtained from each counter.
For two identical counters on opposite sides of the sample, the SR asymmetry time spectrum is proportional to the component of the ensemble spin polarization along the axis joining the counters and the sample. Corrections for differences in counter geometries and efficiencies are straightforward Schenck (1985); Blundell (1999); Brewer (2003); Yaouanc and Dalmas de Réotier (2011). Unlike its cousin NMR, which, apart from NQR and field-cycling techniques, requires a strong applied magnetic field to polarize the nuclear spins, the polarized beam allows SR to be carried out in arbitrary fields.
Experiments may be considered in three classes:
-
•
In high TF-SR, the precession frequency in a paramagnet is shifted from its value in vacuo. The fractional frequency shift (often called the Knight shift after its discoverer Knight (1949)) and its inhomogeneous distribution (often the main contribution to the linewidth) provide a microscopic characterization of the field-induced static magnetization.
-
•
In sufficiently strong LF-SR, the resultant of applied and any local static fields is essentially parallel to the initial spin orientation. This results in “decoupling” of the static fields, and the remaining relaxation is purely dynamic in origin Hayano et al. (1979).
-
•
In ZF- and weak LF-SR, the time evolution of is due to either or both of two mechanisms: (1) decay due to dynamic fluctuations of the local fields, and (2) spin precession in the resultant of a distribution of (quasi)static local fields and the applied field, if any (static Kubo-Toyabe (KT) relaxation Hayano et al. (1979)). The latter are normally due to nuclear dipolar fields.
This situation can be modeled by a dynamically-damped static KT function :
(1) where the dynamic damping function is often a simple exponential but can be more complex (as in the present work). Choices of are discussed below in Sec. III.2.2. It is, however, often difficult to disentangle static and dynamic relaxation contributions from ZF-SR data alone; this is one reason why strong LF-SR is valuable.
II.3 Experimental details
A mosaic of YbMgGaO4 single crystals (total mass g) was mounted on a pure silver sample holder using diluted GE varnish, with the crystal axes parallel to the beam direction. SR experiments were carried out using the dilution refrigerator spectrometer at the M15 beam line of TRIUMF, Vancouver, Canada. Field zeroing to mOe was achieved using a variation of the method of Morris and Heffner Morris and Heffner (2003).
Data were taken over the temperature range 22 mK–8 K. Due to the large low-temperature specific heat of YbMgGaO4 Xu et al. (2016), temperatures were stabilized for 15 minutes before taking data. ZF- and LF-SR data were taken with the initial ensemble spin polarization parallel to the crystal axes. For TF-SR the spins were rotated by before implantation. Data were analyzed using the Paul Scherrer Institute musrfit fitting program Suter and Wojek (2012) and the TRIUMF physica programming environment 111http://computing.triumf.ca/legacy/physica/.
III RESULTS
III.1 Transverse-field SR
TF-SR experiments were carried out in YbMgGaO4 over the temperature range 26 mK–0.825 K in a transverse applied field kOe. Representative Fourier transforms of TF asymmetry time spectra are shown in Fig. 2.
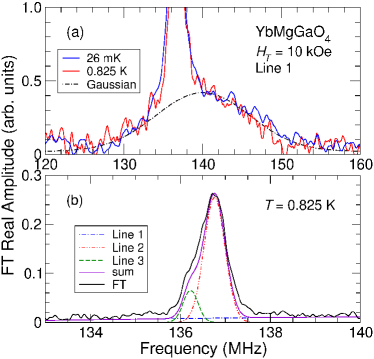
They exhibit three lines: line 1 [Fig. 2(a)], which is very broad and shifted to higher frequency, and lines 2 and 3 [Fig. 2(b)], which are narrow and overlap considerably.
The original TF asymmetry time spectra (not shown) were therefore fit by a sum of three Gaussian-damped oscillating components:
| (2) |
where a common phase was assumed. Parameter values for mK are listed in Table 1.
| line | 222From lattice sums of nuclear dipolar fields. | |||||
|---|---|---|---|---|---|---|
| (MHz) | () | (mol/emu) | (kOe/ per Yb) | (kOe/ per Yb) | ||
| 1 | 0.140(7) | 140.2(3) | 32.5(1.3) | 0.23(1) | 1.26(6) | 1.174 (1) |
| 2 | 0.149(5) | 136.760(5) | 1.47(2) | 0.13(1) | 0.73(5) | 0.897 (2) |
| 3 | 0.027(5) | 136.23(1) | 1.04(5) | – | – | – |
Amplitudes and from the fits are nearly equal and considerably larger than . The curves in Fig. 2 are Fourier transforms of the Gaussian asymmetry terms in Eq. (2), with parameters from the fits: frequencies , widths , and areas proportional to . Their sum is normalized to the experimental Fourier transform in Fig. 2(b).
One of the three lines arises from muons that miss the sample and stop in the silver sample holder, and the other two are from the sample. Line 3, which is the narrowest, is assumed to be the “silver” signal, and is used as the reference frequency for the Knight shifts of the other two components. Additional evidence for this attribution is discussed below in Sec. III.2.1. The sample lines are numbered in order of their shifts (Fig. 2), consistent with the site numbering in order of their distance from the nearest Yb3+ layer (Fig. 1).
In order for Knight shifts to reflect local magnetism, a correction must be made for the contributions to the raw shift from macroscopic Lorentz and demagnetizing fields Carter et al. (1977); *Akashin92:
| (3) |
where , is the molar bulk susceptibility, is the sample demagnetization coefficient, and is the molar volume (50.6 cm3/mol for YbMgGaO4). For field normal to the thin mosaic samples, is estimated to be 0.8(1), so that mol emu-1. This correction can be important in SR shift measurements.
The rates in Table 1 are faster than the dynamic rates discussed below in Secs. III.2 and III.3, particularly for line 3. is therefore attributed to static distributions of TF frequencies, most likely related to the crystalline-electric-field randomness observed in neutron scattering Li et al. (2017a), which lead to rms widths of Knight shift distributions. We do not fully understand the large difference between and .
The temperature dependencies of , , and for lines 1 and 2 are given in Fig. 3.
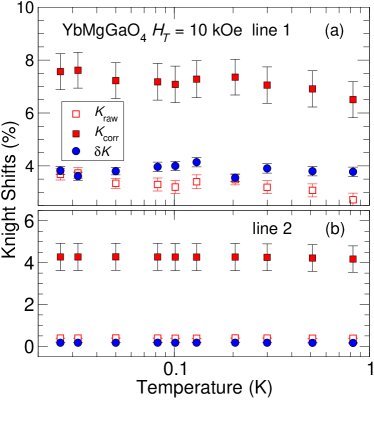
The error in is largely due to uncertainty in [Eq. (3)]. Over the temperature range of the data both the Knight shifts and in 10 kOe Li et al. (2019) are practically constant.
The relation between the Knight shift and is often analyzed using the Clogston-Jaccarino relation Clogston and Jaccarino (1961)
| (4) |
where is the hyperfine coupling constant and temperature is an implicit variable. In the present case there is not enough temperature dependence to either quantity for this procedure to be reliable. Instead, we assume in Eq. (4) is negligible, as would be expected in a magnetic insulator, so that . The hyperfine field (the local field at a site per of paramagnetic moment on the local-moment sites) is given by , where is Avogadro’s number.
Values of and for the two lines are given in Table 1. Also included in Table 1 are calculated Yb3+ dipolar hyperfine fields at each of the two candidate sites discussed in Sec. II.1 (Appendix A); local-moment/ coupling fields are expected to be predominantly dipolar in insulators Schenck (1985). The calculated and measured values are of the same order of magnitude, but with a discrepancy in sign for line 1. This is not understood, but it may mean that the location of site 1 is incorrect.
III.2 Longitudinal-field SR
III.2.1 Oe; two-exponential relaxation
We first consider data for strong enough to decouple any nuclear dipolar fields at sites. Then the relaxation is purely dynamic, and its analysis is simplified.
The observation of two sample lines in TF-SR and their identification with distinct sites motivates fitting the data to a sum of two exponentials
| (5) |
rather than the stretched exponential used previously Li et al. (2016a). Here is the initial sample asymmetry, and are the fast and slow relaxation rates, respectively, is the asymmetry of the background silver signal noted above in Sec. III.1, and . Good fits to the data (Appendix B) were obtained using Eq. (5) with fixed at 0.52 from the amplitudes of the TF lines (Table 1). This is a posteriori justification for the assumption that lines 1 and 2 arise from the sample; the amplitude of line 3 is too small to produce significantly sub-exponential relaxation.
The field dependencies of the fast rate and the ratio at mK are shown in Fig. 4 for intermediate fields.
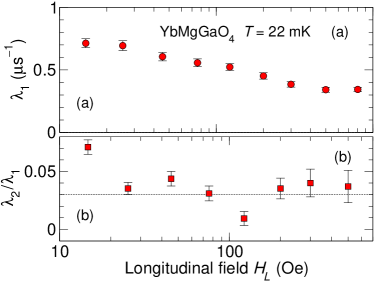
For , the ratio is basically constant, and agrees roughly with the value 0.021 from a lattice sum of uncorrelated mean-square Yb3+ dipolar fields at the candidate sites (Appendix A). This is expected in the fast-fluctuation (motionally narrowed) limit if the fluctuation rates at the two sites are the same and the correlation length for the fluctuations is short Miao et al. (2016).
Its small value makes difficult to measure accurately. Furthermore, for Oe, becomes too slow to permit distinguishing the two components from data in the SR time window (Appendix B), so that cannot be determined at high fields. This together with its observed proportionality to (Fig. 4) justifies consideration only of the latter in the following.
The increase of at 14 Oe (Fig. 4) signals the onset of static relaxation at low fields. As discussed below in Sec. IV, in zero and low fields a static (Gaussian) local-field component reduces the sub-exponential character of the relaxation, thereby increasing in the now-incorrect two-exponential fit.
III.2.2 kOe; two-exponential + KT static relaxation
In the presence of static nuclear dipolar local fields, both static and dynamic processes contribute to relaxation at low LF. For the two-site scenario, the asymmetry function becomes
| (6) | |||||
where is the static KT function for Gaussian local-field distributions Hayano et al. (1979). Here is the rms width of the Gaussian field distribution, where is the gyromagnetic ratio. In YbMgGaO4 we attribute this distribution to nuclear dipolar fields: .
Equation (6) is also valid for , where it is most sensitive to the values of the . These were determined by fits of Eq. (6) to ZF data, discussed in more detail in Sec. III.3. For fits to the LF data, and the were fixed at 0.03 and their ZF values, respectively.
Figure 5
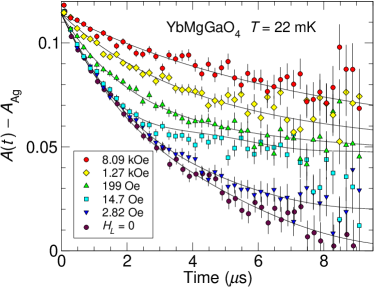
shows asymmetry spectra for representative values of . At low fields the field dependence is dominated by decoupling of the static relaxation, with its characteristic field independence at early times. At higher fields the predominantly dynamic relaxation becomes slower with increasing field as previously reported Li et al. (2016a).
The field dependencies of at temperatures of 22 mK, 0.20 K, and 5.83 K are shown in Fig. 6,
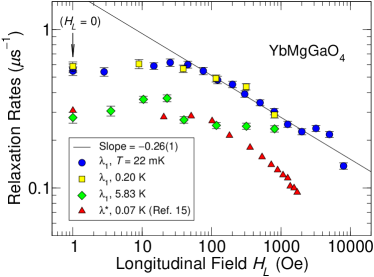
together with stretched-exponential rates for mK from Ref. Li et al. (2016a). The values for 22 mK are in agreement with the two-exponential fit results for Oe, since for . and follow the same trend, but do not agree quantitatively because the assumed relaxation functions are different.
The straight line in Fig. 6 is a power-law fit to the 22-mK data for kOe, almost two decades of field values. Power-law behavior is a form of time-field scaling Keren and Bazalitsky (2000), since for . Time-field scaling is in general indicative of long-lived spin correlations with a power-law divergence in the noise spectrum as . This result is consistent with the conclusion of Li et al. Li et al. (2016a) from a more detailed analysis.
At 5.83 K the rates are reduced, and exhibit a plateau for Oe. The rather abrupt crossover may be to a normal paramagnetic state, in which local-moment fluctuations are independent of both field and temperature Moriya (1956).
III.3 Zero-field SR
III.3.1 ZF asymmetry spectra
Extraction of parameters in Eq. (6) from fits in ZF and weak LF that include static nuclear dipolar relaxation is difficult, because the data are smooth and without distinguishing features (Figs. 5 and 7). Fits with all parameters free lead to excessive scatter, so that it is necessary to fix as many parameters as possible.
Fixing and have been discussed above. The were then allowed to vary, leading to fits (not shown) with excessive scatter but reasonably temperature-independent values below 0.5 K. The data were finally refit with fixed at their averages and . No temperature dependence of the nuclear dipolar relaxation is expected in the absence of diffusion, which is unlikely at low temperatures Schenck (1985).
ZF-SR asymmetry spectra for mK, 0.17 K, and 6.00 K are shown in Fig. 7,
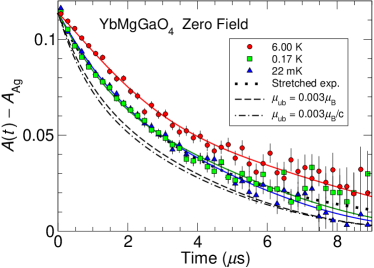
again with the silver background signal subtracted. The solid curves are fits of Eq. (6) to the data. The temperature dependence of the overall relaxation over this range is weak because of the temperature-independent static KT contribution, and there is essentially no temperature dependence between 0.17 K and 22 mK. We observe no oscillating signal due to long-range magnetic order and no initial rapid relaxation or asymmetry loss due to short-range magnetic order Miao et al. (2016) down to 22 mK. The dotted curve is a stretched-exponential fit for mK, illustrating the similarity between it and the two-exponential fit. The dashed and dash-dot curves are discussed in the next section.
III.3.2 Limits on static magnetism
To determine upper bounds on static magnetism in YbMgGaO4, two scenarios are considered: equal (small) moments on all Yb3+ ions (moment concentration ), and the dilute spin-glass limit for small . For each of these we begin with the ZF data and fit to Eq. (6) for mK. Upper bounds on the static moment per Yb ion are chosen, and the corresponding calculated asymmetry spectra are compared with the data. The upper bounds are then adjusted to yield well-resolved increases in relaxation. The results are shown in Fig. 7 for the and dilute limits by the dashed and dash-dot curves, respectively.
For the Yb3+ dipolar field contribution from disordered Yb3+ moments is Gaussian Uemura et al. (1985), and additional ZF relaxation below a transition temperature increases the values of the Gaussian rates in Eq. (6) 333Long-range magnetic order gives rise to oscillation, which for low frequency varies quadratically with time and cannot be distinguished from a slow Gaussian. The disordered estimate therefore also applies to this case.. Gaussian rms field widths per Yb ion were calculated from dipole-field lattice sums (Appendix A) at the candidate sites 1 and 2 of Fig. 1, yielding and .
An upper bound on the static moment per Yb ion is found by comparing Eq. (6) with increased rates to the data. The choice per Yb ion results in the dashed curve in Fig. 7, which exhibits a well-resolved increase. For comparison, dc susceptibility measurements in YbMgGa)4 Ma et al. (2018); Li et al. (2019), which, like SR, probe the bulk magnetization, yield paramagnetic Curie-Weiss and saturated moments per Yb ion.
We next consider dilute (disordered) static Yb3+ moments. The Lorentzian ZF KT relaxation function Uemura et al. (1985)
| (7) |
is expected from dipolar coupling to a static random spin system in the dilute limit. Here is the half-width of the Lorentzian dipolar field distribution Uemura et al. (1985);
| (8) |
where is the moment per (dilute) Yb ion per Bohr magneton. The resulting relaxation function is derived from Eq. (6) by multiplying each term by . We choose a value (e.g., for concentration per Yb ion) and determine the from Eq. (8), resulting in the dash-dot curve in Fig. 7. Again, the increase is well resolved.
Somewhat surprisingly, the sample-average and dilute bounds are identical. The results cannot be taken as quantitative, however, since they involve the assumed sites and do not employ a well-defined resolution criterion. They are solely intended to demonstrate the basic sensitivity of the SR technique to weak static magnetism.
III.3.3 Temperature dependence of zero-field rates
Figure 8
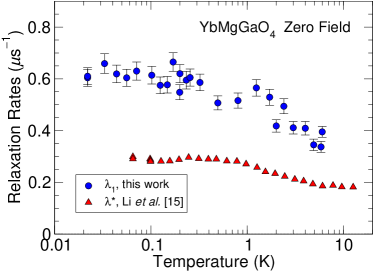
shows the temperature dependence of the ZF dynamic relaxation rate (circles) from fits of Eq. (6) to the data discussed above, and also gives from Li et al. Li et al. (2016a) (triangles). With decreasing temperature, the rates increase and saturate below 0.5 K, exhibiting persistent spin dynamics down to the lowest temperatures. The scatter in is mainly due to the fact that in ZF the dynamic relaxation is only a fraction of the total relaxation.
The difference between and is again a consequence of the different assumed relaxation functions. Furthermore, as noted above, in ZF and weak LF “pure” stretched-exponential fits [i.e., without the factor of Eq. (6)] mix the static and dynamic contributions.
IV DISCUSSION
Our SR study extends previous results Li et al. (2016a) concerning the nature of the ground state and low-lying excitations in YbMgGaO4. The observation of the same field dependence at 22 mK and 0.20 K for fields up to 0.8 kOe (Fig. 6) complements the previously-reported temperature independence of ZF relaxation below 0.4 K Li et al. (2016a), and is strong evidence that the system is in a temperature-independent state over this region in the - phase diagram.
IV.1 Limits on spin freezing
SR experiments are extremely sensitive to static magnetism, ordered or disordered Schenck (1985), in the present case with an upper limit per Yb ion on any sample-average static Yb3+ moment down to 22 mK (Sec. III.3.2). This is a strong constraint on proposals involving magnetic ground states Luo et al. (2017); Zhu et al. (2017); Parker and Balents (2018); Kimchi et al. (2018), although in the disordered local-singlet valence solid Kimchi et al. (2018) the “ultimate fate of the …defect spins is unknown.”
The lack of spin freezing is in apparent contradiction with the observation of a cusp in the low-field ac susceptibility of YbMgGaO4 at 0.1 K Ma et al. (2018), and the conclusion that a spin-glass-like transition occurs there. We note that suppression of static order by the muon itself, a possible explanation of this discrepancy, has been shown to be unlikely Keren (2004). We also note that large static Yb3+ moments in a macroscopic spurious phase would result in a fraction of the ZF asymmetry spectrum with oscillations or rapid relaxation. This is not seen at the level of a few percent. The resolution of these issues is not clear, and more work will be required to elucidate the impact of the present results on the QSL debate.
IV.2 Characterization of sample inhomogeneity, consequences for ZF results
Our SR results suggest reinterpretation of some of the previous work. The observation of two equal-amplitude lines in the TF-SR data is evidence for the two stopping sites in the two inequivalent O2- lattice planes. This, rather than, for example, Mg2+/Ga3+ site mixing Li et al. (2017a), is the main source of inhomogeneity in the dynamic relaxation, and strongly suggests a two-exponential analysis of LF- and ZF-SR data [Eqs. (5) and (6)] rather than a stretched-exponential analysis.
The fact that good fits can be obtained with either two-exponential or stretched-exponential functions is not surprising. In general, the relaxation function associated with a spatially inhomogeneous distribution of rates is given by the Laplace transform
| (9) |
Two-exponential and stretched-exponential functions are effectively two choices of .
Solving Eq. (9) for is a mathematically ill-posed problem Press et al. (1992); is not sensitive to the form of . The difficulty is greater when the range of the independent variable is limited, as it is for SR asymmetry spectra by the muon lifetime 444This is the problem in the present case. At late enough times, the sum of two exponentials with very different rates differs significantly from a stretched exponential. We also note that for , the relation of to depends on ; is not simply an average rate, and one should not compare values of for different values of Johnston (2006).
The temperature dependence of in fits to ZF data is also consistent with the two-exponential scenario. (Quasi)static relaxation in ZF and weak LF by nuclear dipolar fields should not be ignored, although the lack of structure in the asymmetry spectra and the limitation imposed by the muon lifetime make the analysis difficult. We argue that the reported increase of with increasing temperature in ZF stretched-exponential fits is not a temperature-dependent effect of the spin dynamics Li et al. (2016a). Instead, the decrease of ZF dynamic relaxation with increasing temperature (Fig. 8) increases the importance of the temperature-independent “super-exponential” (Gaussian) nuclear dipolar field distribution. This renders the overall ZF relaxation function less sub-exponential at high temperatures, leading to at 10 K Li et al. (2016a).
V CONCLUSIONS
We have carried out SR experiments on single-crystalline samples of the candidate spin liquid YbMgGaO4, which complement and extend earlier work Li et al. (2016a). The spatial inhomogeneity that gives rise to sub-exponential spin relaxation is attributed to two distinct stopping sites in the unit cell, rather than Mg2+/Ga3+ site mixing or other local disorder. With an upper bound of /Yb ion, no static magnetism, ordered or disordered, is observed down to 22 mK, a factor of two lower in temperature than previous measurements. The field dependence of the spin relaxation is the same in functional form and relaxation rate at 22 mK and 0.20 K up to at least 1 kOe. These results indicate persistent (i.e.,temperature-independent) spin dynamics with no spin freezing for this field and temperature range, thus extending the previous ZF results Li et al. (2016a) over a substantial region of the - phase diagram.
Acknowledgements.
We wish to thank Z. Ma for providing single crystals of YbMgGaO4, and S. Y. Li for fruitful discussions. We are very grateful to the TRIUMF CMMS SR support staff for their help during the experiments. This research was supported by the National Key Research and Development Program of China (Nos. 2016YFA0300503 and 2017YFA0303104), the National Natural Science Foundation of China under Grant No. 11774061, and Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01). Research at the University of California, Riverside (UCR) was supported by the UCR Academic Senate.Appendix A Dipolar lattice sums
The dipolar lattice-sum calculation is straightforward. The software sets up a general orthorhombic lattice (with a non-primitive unit cell for a triangular structure such as that of YbMgGaO4). 1- local moments are placed at lattice sites in the magnetic structure (with or without a net moment in the unit cell) and candidate stopping sites in the unit cell are designated. For each site, dipolar fields from the local moments are summed between an inner cutoff radius (if desired) and an outer Lorentz sphere radius . The value of is chosen so that larger values have negligible effect; typically Å, containing – moments, is sufficient. For a paramagnet the moments are all in the same direction, induced by the applied field, and the shift is given by the resultant field in that direction. Mean-square fields, which are involved in fluctuation-induced dynamic relaxation, are calculated by summing the squared magnitudes of the individual moment fields. The calculated fields are in units of [field] per local moment. No Lorentz or demagnetizing corrections are made.
Appendix B Two-exponential fits
Figure 9
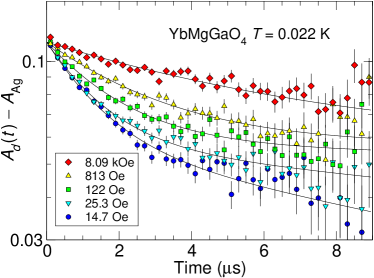
shows log-linear plots of representative LF asymmetry spectra at 22 mK, kOe. Upward curvature is clearly visible. The curves are two-exponential fits to Eq. (5) with the slowly-relaxing fraction fixed at 0.52 (see main text). The fits are good at all fields, but for Oe the upward curvature is reduced. As discussed in Secs. III.2.1 and IV, this is expected at low enough LF to permit static relaxation by nuclear dipolar fields. For kOe, the overall relaxation has slowed enough so that the late-time slow exponential is no longer visible in the experimental time window.
References
- Anderson (1973) P. W. Anderson, Resonating valence bonds: A new kind of insulator?, Mater. Res. Bull. 8, 153 (1973).
- Anderson (1987) P. W. Anderson, The Resonating Valence Bond State in La2CuO4 and Superconductivity, Science 235, 1196 (1987).
- Lee (2008) P. A. Lee, An End to the Drought of Quantum Spin Liquids, Science 321, 1306 (2008).
- Balents (2010) L. Balents, Spin liquids in frustrated magnets, Nature 464, 199 (2010).
- Savary and Balents (2017) L. Savary and L. Balents, Quantum spin liquids: a review, Rep. Prog. Phys. 80, 016502 (2017).
- Zhou et al. (2017) Y. Zhou, K. Kanoda, and T.-K. Ng, Quantum spin liquid states, Rev. Mod. Phys. 89, 025003 (2017).
- Uemura et al. (1994) Y. J. Uemura, A. Keren, K. Kojima, L. P. Le, G. M. Luke, W. D. Wu, Y. Ajiro, T. Asano, Y. Kuriyama, M. Mekata, H. Kikuchi, and K. Kakurai, Spin Fluctuations in Frustrated Kagomé Lattice System SrCr8Ga4O19 Studied by Muon Spin Relaxation, Phys. Rev. Lett. 73, 3306 (1994).
- Shimizu et al. (2003) Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato, and G. Saito, Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice, Phys. Rev. Lett. 91, 107001 (2003).
- Nakatsuji et al. (2006) S. Nakatsuji, Y. Machida, Y. Maeno, T. Tayama, T. Sakakibara, J. v. Duijn, L. Balicas, J. N. Millican, R. T. Macaluso, and J. Y. Chan, Metallic Spin-Liquid Behavior of the Geometrically Frustrated Kondo Lattice Pr2Ir2O7, Phys. Rev. Lett. 96, 087204 (2006).
- Helton et al. (2007) J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J.-H. Chung, D. G. Nocera, and Y. S. Lee, Spin Dynamics of the Spin- Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2, Phys. Rev. Lett. 98, 107204 (2007).
- Okamoto et al. (2007) Y. Okamoto, M. Nohara, H. Aruga-Katori, and H. Takagi, Spin-Liquid State in the Hyperkagome Antiferromagnet Na4Ir3O8, Phys. Rev. Lett. 99, 137207 (2007).
- Itou et al. (2008) T. Itou, A. Oyamada, S. Maegawa, M. Tamura, and R. Kato, Quantum spin liquid in the spin- triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2, Phys. Rev. B 77, 104413 (2008).
- Li et al. (2015a) Y. Li, H. Liao, Z. Zhang, S. Li, F. Jin, L. Ling, L. Zhang, Y. Zou, L. Pi, Z. Yang, J. Wang, Z. Wu, and Q. Zhang, Gapless quantum spin liquid ground state in the two-dimensional spin-1/2 triangular antiferromagnet YbMgGaO4, Sci. Rep. 5, 16419 (2015a).
- Li et al. (2015b) Y. Li, G. Chen, W. Tong, L. Pi, J. Liu, Z. Yang, X. Wang, and Q. Zhang, Rare-Earth Triangular Lattice Spin Liquid: A Single-Crystal Study of YbMgGaO4, Phys. Rev. Lett. 115, 167203 (2015b).
- Li et al. (2016a) Y. Li, D. Adroja, P. K. Biswas, P. J. Baker, Q. Zhang, J. Liu, A. A. Tsirlin, P. Gegenwart, and Q. Zhang, Muon Spin Relaxation Evidence for the U(1) Quantum Spin-Liquid Ground State in the Triangular Antiferromagnet YbMgGaO4, Phys. Rev. Lett. 117, 097201 (2016a).
- Xu et al. (2016) Y. Xu, J. Zhang, Y. S. Li, Y. J. Yu, X. C. Hong, Q. M. Zhang, and S. Y. Li, Absence of Magnetic Thermal Conductivity in the Quantum Spin-Liquid Candidate YbMgGaO4, Phys. Rev. Lett. 117, 267202 (2016).
- Shen et al. (2016) Y. Shen, Y.-D. Li, H. Wo, Y. Li, S. Shen, B. Pan, Q. Wang, H. C. Walker, P. Steffens, M. Boehm, Y. Hao, D. L. Quintero-Castro, L. W. Harriger, M. D. Frontzek, L. Hao, S. Meng, Q. Zhang, G. Chen, and J. Zhao, Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate, Nature 540, 559 (2016).
- Paddison et al. (2017) J. A. M. Paddison, M. Daum, Z. Dun, G. Ehlers, Y. Liu, M. B. Stone, H. Zhou, and M. Mourigal, Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4, Nat. Phys. 13, 117 (2017).
- Li et al. (2017a) Y. Li, D. Adroja, R. I. Bewley, D. Voneshen, A. A. Tsirlin, P. Gegenwart, and Q. Zhang, Crystalline Electric-Field Randomness in the Triangular Lattice Spin-Liquid YbMgGaO4, Phys. Rev. Lett. 118, 107202 (2017a).
- Li et al. (2017b) Y. Li, D. Adroja, D. Voneshen, R. I. Bewley, Q. Zhang, A. A. Tsirlin, and P. Gegenwart, Nearest-neighbour resonating valence bonds in YbMgGaO4, Nat. Commun. 8, 15814 (2017b).
- Shen et al. (2018) Y. Shen, Y. Li, H. Walker, P. Steffens, M. Boehm, X. Zhang, S. Shen, H. Wo, G. Chen, and J. Zhao, Fractionalized excitations in the partially magnetized spin liquid candidate YbMgGaO4, Nat. Commun. 9, 4138 (2018).
- Zhang et al. (2018) X. Zhang, F. Mahmood, M. Daum, Z. Dun, J. A. M. Paddison, N. J. Laurita, T. Hong, H. Zhou, N. P. Armitage, and M. Mourigal, Hierarchy of exchange interactions in the triangular-lattice spin liquid YbMgGaO4, Phys. Rev. X 8, 031001 (2018).
- Ma et al. (2018) Z. Ma, J. Wang, Z.-Y. Dong, J. Zhang, S. Li, S.-H. Zheng, Y. Yu, W. Wang, L. Che, K. Ran, S. Bao, Z. Cai, P. Čermák, A. Schneidewind, S. Yano, J. S. Gardner, X. Lu, S.-L. Yu, J.-M. Liu, S. Li, J.-X. Li, and J. Wen, Spin-Glass Ground State in a Triangular-Lattice Compound YbZnGaO4, Phys. Rev. Lett. 120, 087201 (2018).
- Li et al. (2019) Y. Li, S. Bachus, B. Liu, I. Radelytskyi, A. Bertin, A. Schneidewind, Y. Tokiwa, A. A. Tsirlin, and P. Gegenwart, Rearrangement of Uncorrelated Valence Bonds Evidenced by Low-Energy Spin Excitations in , Phys. Rev. Lett. 122, 137201 (2019).
- Li et al. (2016b) Y.-D. Li, X. Wang, and G. Chen, Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets, Phys. Rev. B 94, 035107 (2016b).
- Li et al. (2017c) Y.-D. Li, Y.-M. Lu, and G. Chen, Spinon Fermi surface spin liquid in the spin-orbit-coupled triangular-lattice Mott insulator YbMgGaO4, Phys. Rev. B 96, 054445 (2017c).
- Li and Chen (2017) Y.-D. Li and G. Chen, Detecting spin fractionalization in a spinon Fermi surface spin liquid, Phys. Rev. B 96, 075105 (2017).
- Luo et al. (2017) Q. Luo, S. Hu, B. Xi, J. Zhao, and X. Wang, Ground-state phase diagram of an anisotropic spin- model on the triangular lattice, Phys. Rev. B 95, 165110 (2017).
- Zhu et al. (2017) Z. Zhu, P. A. Maksimov, S. R. White, and A. L. Chernyshev, Disorder-Induced Mimicry of a Spin Liquid in YbMgGaO4, Phys. Rev. Lett. 119, 157201 (2017).
- Parker and Balents (2018) E. Parker and L. Balents, Finite-temperature behavior of a classical spin-orbit-coupled model for with and without bond disorder, Phys. Rev. B 97, 184413 (2018).
- Kimchi et al. (2018) I. Kimchi, A. Nahum, and T. Senthil, Valence Bonds in Random Quantum Magnets: Theory and Application to , Phys. Rev. X 8, 031028 (2018).
- Schenck (1985) A. Schenck, Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics (A. Hilger, Bristol & Boston, 1985).
- Blundell (1999) S. J. Blundell, Spin-polarized muons in condensed matter physics, Contemp. Phys. 40, 175 (1999).
- Brewer (2003) J. H. Brewer, in Digital Encyclopedia of Applied Physics, edited by G. L. Trigg, E. S. Vera, and W. Greulich (Wiley-VCH Verlag GmbH & Co KGaA, Weinheim, 2003).
- Yaouanc and Dalmas de Réotier (2011) A. Yaouanc and P. Dalmas de Réotier, Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter, International Series of Monographs on Physics (Oxford University Press, New York, 2011).
- Bert et al. (2009) F. Bert, A. Olariu, A. Zorko, P. Mendels, J. C. Trombe, F. Duc, M. A. d. Vries, A. Harrison, A. D. Hillier, J. Lord, A. Amato, and C. Baines, Frustrated magnetism in the quantum Kagome Herbertsmithite ZnCu3(OH)6Cl2 antiferromagnet, J. Phys. Conf. Ser. 145, 012004 (2009).
- Pratt et al. (2011) F. L. Pratt, P. J. Baker, S. J. Blundell, T. Lancaster, S. Ohira-Kawamura, C. Baines, Y. Shimizu, K. Kanoda, I. Watanabe, and G. Saito, Magnetic and non-magnetic phases of a quantum spin liquid, Nature 471, 612 (2011).
- Clark et al. (2013) L. Clark, J. C. Orain, F. Bert, M. A. De Vries, F. H. Aidoudi, R. E. Morris, P. Lightfoot, J. S. Lord, M. T. F. Telling, P. Bonville, J. P. Attfield, P. Mendels, and A. Harrison, Gapless Spin Liquid Ground State in the Vanadium Oxyfluoride Kagome Antiferromagnet , Phys. Rev. Lett. 110, 207208 (2013).
- Khuntia et al. (2016) P. Khuntia, F. Bert, P. Mendels, B. Koteswararao, A. V. Mahajan, M. Baenitz, F. C. Chou, C. Baines, A. Amato, and Y. Furukawa, Spin Liquid State in the 3D Frustrated Antiferromagnet PbCuTe2O6: NMR and Muon Spin Relaxation Studies, Phys. Rev. Lett. 116, 107203 (2016).
- Pratt (2018) F. L. Pratt, Probing Quantum Critical Spin Liquids with SR, JPSJ Conf. Proc. 21, 011002 (2018), Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (SR2017).
- Johnston (2006) D. C. Johnston, Stretched exponential relaxation arising from a continuous sum of exponential decays, Phys. Rev. B 74, 184430 (2006).
- Bonfà and De Renzi (2016) P. Bonfà and R. De Renzi, Toward the Computational Prediction of Muon Sites and Interaction Parameters, J. Phys. Soc. Jpn. 85, 091014 (2016).
- Knight (1949) W. D. Knight, Nuclear Magnetic Resonance Shift in Metals, Phys. Rev. 76, 1259 (1949).
- Hayano et al. (1979) R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki, and R. Kubo, Zero-and low-field spin relaxation studied by positive muons, Phys. Rev. B 20, 850 (1979).
- Morris and Heffner (2003) G. D. Morris and R. H. Heffner, A method of achieving accurate zero-field conditions using muonium, Physica B 326, 252 (2003).
- Suter and Wojek (2012) A. Suter and B. Wojek, Musrfit: A free platform-independent framework for SR data analysis, Phys. Procedia 30, 69 (2012), 12th International Conference on Muon Spin Rotation, Relaxation and Resonance (SR2011).
- Note (1) http://computing.triumf.ca/legacy/physica/.
- Carter et al. (1977) G. C. Carter, L. H. Bennett, and D. J. Kahan, Metallic shifts in NMR, in Progress in Materials Science, Vol. 20 (Pergamon Press, Oxford & New York, 1977) pp. 58–59.
- Akishin and Gaganov (1992) P. Akishin and I. Gaganov, The macroscopic demagnetizing effects in cylindrical and rectangular box samples, J. Magn. Magn. Mater. 110, 175 (1992).
- Clogston and Jaccarino (1961) A. M. Clogston and V. Jaccarino, Susceptibilities and Negative Knight Shifts of Intermetallic Compounds, Phys. Rev. 121, 1357 (1961).
- Miao et al. (2016) X. F. Miao, L. Caron, J. Cedervall, P. C. M. Gubbens, P. Dalmas de Réotier, A. Yaouanc, F. Qian, A. R. Wildes, H. Luetkens, A. Amato, N. H. van Dijk, and E. Brück, Short-range magnetic correlations and spin dynamics in the paramagnetic regime of , Phys. Rev. B 94, 014426 (2016).
- Keren and Bazalitsky (2000) A. Keren and G. Bazalitsky, Muon polarization in the presence of exotic spin correlations, Physica B 289-290, 205 (2000).
- Moriya (1956) T. Moriya, Nuclear magnetic relaxation in antiferromagnetics, Progr. Theoret. Phys. (Kyoto) 16, 23 (1956).
- Uemura et al. (1985) Y. J. Uemura, T. Yamazaki, D. R. Harshman, M. Senba, and E. J. Ansaldo, Muon-spin relaxation in AuFe and CuMn spin glasses, Phys. Rev. B 31, 546 (1985).
- Note (2) Long-range magnetic order gives rise to oscillation, which for low frequency varies quadratically with time and cannot be distinguished from a slow Gaussian. The disordered estimate therefore also applies to this case.
- Keren (2004) A. Keren, Muons as probes of dynamical spin fluctuations: some new aspects, J. Phys. Condens. Matter 16, S4603 (2004).
- Press et al. (1992) W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C (Cambridge University Press, Cambridge, New York, 1992) Chap. 18, 2nd ed.
- Note (3) This is the problem in the present case. At late enough times, the sum of two exponentials with very different rates differs significantly from a stretched exponential.