Phonon renormalization effects accompanying the 6 K anomaly in the Quantum Spin Liquid Candidate $\kappa$-(BEDT-TTF)₂Cu₂(CN)₃

Quantum spin liquids (QSLs) have been at the center of scientific attention in the field of magnetism as a novel quantum state. The organic charge-transfer salt $\kappa$-(BEDT-TTF)₂Cu₂(CN)₃ ($\kappa$-CN), where BEDT-TTF is bis-(ethylenedithio)tetrathiafulvalene C₆S₈[(CH₂)₂]₂ (ET), has attracted attention in this area as a promising QSL candidate: the system is a weak dimer-Mott (DM) insulator forming a nearly isotropic two-dimensional triangular spin lattice which lacks long-range magnetic order down to low temperatures despite its large exchange coupling of $J\sim 250$ K [1]. Despite the absence of a magnetic phase transition, anomalous behavior at low temperatures around $T^{*}\sim 6$ K has been observed in various quantities probing either spin- [1, 2, 3, 4, 5, 6], charge- [7], lattice- [8, 9, 10], or composite properties thereof [11, 12], see also Ref. [13].

Recently, the discussion has taken a new twist by results of an electron spin resonance (ESR) study, reporting the formation of a spin-singlet state below about 6 K, consistent with a valence bond solid (VBS) ground state [4], but contradicting with the QSL scenarios discussed so far. Arguments in favor of a glassy VBS state have been proposed by Riedl et al. [14] based on their analysis of magnetic data [6]. In addition to the signatures in the magnetic response, which are of moderate strength and prone to extrinsic factors [4], clear evidence for the strong involvement of the lattice in the 6 K anomaly was revealed by measurements of thermal expansion [9], ⁶³Cu-NQR, [8], and ultrasound velocity [10]. Since both the proposed QSL and VBS scenarios emerge through the 6 K anomaly, a clarification of its origin is key for understanding the ground state in this material.

Besides the spin- and lattice degrees of freedom, indications for the presence of charge degrees of freedom within the dimers in $\kappa$-CN and various other related DM molecular conductors were pointed out. In $\kappa$-CN, a relaxor-type anomaly was observed in the dielectric constant below about 40 K, suggesting a charge disproportionation within the dimers and a freezing of these fluctuations on cooling towards 6 K [7, 15, 16]. As for the origin of these observations, conflicting results were reported based on measurements of charge-sensitive molecular vibrational modes. Whereas infrared optical spectroscopy failed to detect any clear line splitting, suggesting the absence of charge disproportionation [17], Raman scattering reveals a noticeable line broadening [18]. A similar relaxor-type dielectric behavior was observed for the DM insulator $\beta$’-(ET)₂ICl₂ [19], in which an intra-dimer charge disproportionation was reported. In addition, clear evidence for a first-order ferroelectric transition, accompanied by intra-dimer charge order [20], was revealed for $\kappa$-(ET)₂Hg(SCN)₂Cl [21]. Moreover, for the closely related DM system $\kappa$-(ET)₂Cu[N(CN)₂]Cl ($\kappa$-Cl), indications for long-range ferroelectric order coinciding with antiferromagnetic ordering below $T_{N}=27$ K were observed [22, 23]. In a recent inelastic neutron scattering (INS) study on this $\kappa$-Cl system it was found that the dynamics of a low-lying breathing/shearing mode of the ET dimers reacts sensitively to the charge- and spin degrees of freedom once the $\pi$-electrons become localized on the dimer site [24]. Motivated by these findings, we report here an INS study of low-energy intra-dimer vibrational modes on $\kappa$-CN for probing lattice effects and their coupling to charge- and spin fluctuations associated with the 6 K anomaly.

Deuterated single crystals of $\kappa$-CN were grown by utilizing an electrochemical method [25]. The as-grown single crystals are thin plates (thickness of $\sim 0.1$ mm) with a flat and large crystal surface (a few mm²) parallel to the $bc$ plane [see Figs. S1(a), (b) in the supplemental material (SM)]. Overall, forty-seven crystals (total mass of $\sim 26$ mg) were co-aligned within 10 degree (Fig. S2 in SM) according to their shape, i.e., the crystal edges including characteristic angles [Fig. S1 (b) in SM]. The $b$- and $c$-axes were also confirmed using polarized micro infrared reflectance spectroscopy measurements for all the single crystals. In neutron scattering, the phonon scattering intensity is proportional to ($\mbox{\boldmath$Q$}\cdot\mbox{\boldmath$\xi$}$)² where $Q$ is the momentum transfer between the initial and final states of the neutron, and $\xi$ is the polarization vector of the phonon mode. In order to detect the breathing mode of the ET dimers ($\mbox{\boldmath$\xi$}\parallel$ [011] or [01$\bar{1}$]), we measured phonon signals at $Q$ = (060) [Figs. 1 (f) and (g)]. INS experiments were performed using the triple-axis spectrometer IN8 at the Institut Laue Langevin [26]. The momentum transfers in this report are represented in units of reciprocal lattice vectors $b^{*}=0.733$ Å^-1 in the monoclinic notation. The initial and final neutron energies were selected using a doubly focused Cu (200) monochromator and analyzer, which resulted in an energy resolution of 0.62 meV at $\mbox{\boldmath$Q$}=(060)$ and $E=0$. A pyrolytic graphite filter was placed in front of the analyzer to suppress higher-order neutrons.

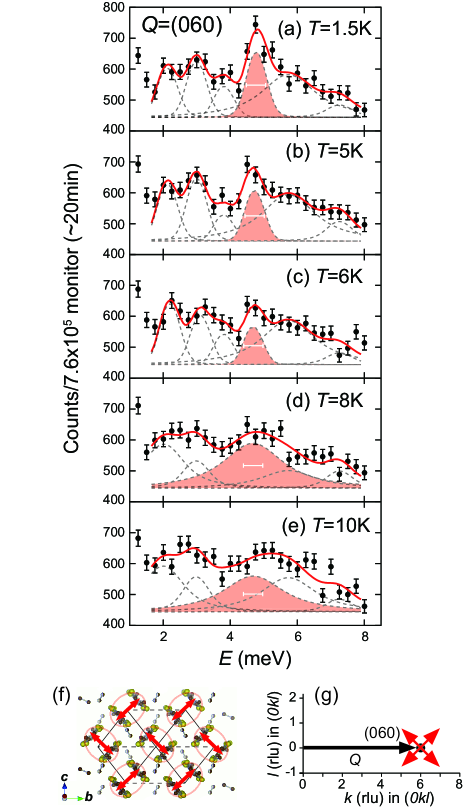
Figure 1 shows the temperature dependence of the phonon spectra measured at $Q=$(060) and $T=1.5$ - 10 K. At $T=1.5$ K, phonon peaks were observed at $E=2.0$, 2.9, 3.7, 4.7, 5.7, and 7.2 meV, consistent with results of optical conductivity measurements on $\kappa$-CN [27]. According to density-functional-theory calculations [27], the peak at 4.7 meV can be assigned to an intra-dimer breathing mode. As the temperature rises, the intensity of this mode reduces, and all peaks become broad above 6 K. Since the linewidth of the peak is inversely proportional to the phonon lifetime, the broadening of these peaks indicates that the phonon lifetime becomes substantially reduced above 6 K.

The broadened phonon peaks were fitted using the damped harmonic-oscillator (DHO) function [28]:

where $\Gamma_{i}$ and $\hbar\omega_{i}$ denote the damping factor and phonon energy of the $i$-th mode, respectively. The phonon spectra were fitted to a constant background BG and the sum of the DHO functions convolved with the resolution function $R(\mbox{\boldmath$Q$},\omega)$ using the RESTRAX simulation package [29]: $\sum_{i}\mathrm{DHO}_{i}(\mbox{\boldmath$Q$},\omega)\otimes R(\mbox{\boldmath$Q$},\omega)+BG$, where $\otimes$ denotes the convolution operator.

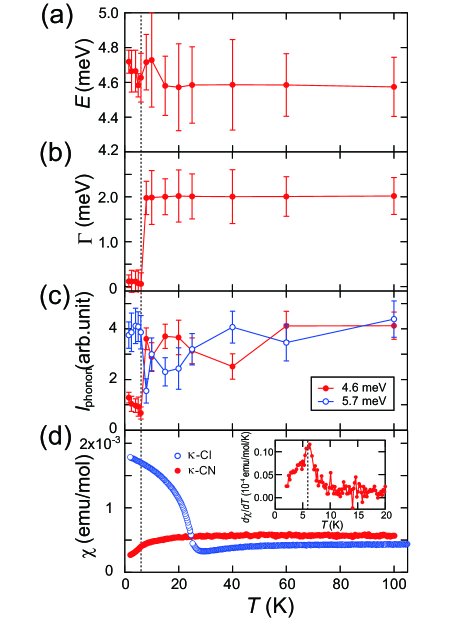
Figures 2 (a)-(c) show the temperature dependence of the DHO fitting parameters for the intra-dimer breathing mode. The peak energy remains constant within the error bars except for a slight hardening below $T^{*}\sim 6$ K [Fig. 2(a)]. Note that a similar small change ($\Delta E\sim 0.2$ meV) in the phonon energy was observed also for the organic superconductor $\kappa$-(ET)₂Cu(NCS)₂ [30] upon cooling through the superconducting transition temperature, indicating a significant electron-phonon interaction in these soft organic compounds. The most prominent phonon anomaly in $\kappa$-CN is the change in the peak width at $T^{*}$ as observed in the phonon spectra (Fig. 1) and the corresponding reduction in the damping factor $\Gamma$ [Fig. 2(b)]. Whereas the large damping factor above $T^{*}$ reflects an anharmonic lattice due to scattering processes, the small $\Gamma$ below $T^{*}$ suggests a freezing of these processes as the width becomes comparable to the instrumental resolution. In addition to the narrowing of the phonon linewidth for $T\leq T^{*}$, the integrated intensity ($I_{\mathrm{phonon}}$) of the breathing mode at $E=4.7$ meV decreases significantly, whereas $I_{\mathrm{phonon}}$ is enhanced for the $E=5.7$ meV mode [Fig. 2(c)]. The intensity of the mode at $E=3.7$ meV also grows below $T^{*}$ (Fig. 1). These changes in the phonon intensities at $T^{*}$ indicate the transfer of spectral weight from the breathing modes to other vibration modes of the ET dimers.

For a deeper understanding of the scattering processes involved in the phonon renormalization effects revealed here for $\kappa$-CN, it is instructive to compare the results with those of the previously reported phonon study on the DM insulator $\kappa$-Cl. Despite some structural differences to $\kappa$-CN (Fig. S1 in SM), in $\kappa$-Cl, a similar increase in the damping of a phonon peak at $E=2.6$ meV was observed below $T_{ins}\sim$ 50 - 60 K where the rapid increase in the resistivity reflects the opening of the charge gap [24]. These observations suggest a close coupling of low-energy intra-dimer breathing/shearing modes to the $\pi$-electrons as a characteristic feature of these DM organic compounds.

In fact, following the phonon modes to higher temperatures points to a correlation between the onset of phonon damping and the localization of the $\pi$-electrons on the dimer sites, cf. Figs. S4 and S5 in SM. Upon warming to $T=100$ K, where $\kappa$-CN is still in its insulating, i.e., high-resistance DM state, the phonon modes remain broad. In contrast, for $\kappa$-Cl at this temperature, where the $\pi$-electrons have regained a considerable degree of itineracy, as revealed in the resistivity, reflecting the closure of the charge gap, the spectrum exhibits well-defined phonon peaks (Figs. S4 and S5 in SM).

These observations on $\kappa$-CN and $\kappa$-Cl suggest that it is the $\pi$-electrons and their localization on the dimer site which cause the observed phonon damping. According to the pseudospin-coupling model [31], we expect the characteristic energy of the electrons’ fluctuations in their charge- or spin components to be of the same size as the energies of the low-lying optical phonon modes, i.e., $2-4$ meV. Once the fluctuations become frozen due to ordering in the charge- and/or spin channel, the phonon lifetime recovers. In fact, such a reduction in $\Gamma$ was observed for $\kappa$-Cl upon cooling below $T_{\mathrm{N}}=27$ K [24] where magnetic order coinciding with ferroelectric order was observed [22].

Similar to $\kappa$-Cl, the bulk of experimental findings on $\kappa$-CN indicate fluctuations and ordering phenomena in both the charge- [7] and spin [4] sectors. A minimal model that describes the coupling between the spin- and charge degrees of freedom within the dimers has been proposed based on the following Kügel-Khomskii-type Hamiltonian [32, 15, 16]:

where $\langle ij\rangle$ denotes the nearest-neighbor bonds; $\mbox{\boldmath$S$}_{i}$ and $Q_{i}$ are the spin and charge pseudo-spin operators at the $i$-th dimer unit, respectively. The $x$ component in the pseudo-spin, $Q^{x}=\pm 1/2$, represents the polarized states of a hole on the dimer (cf. insets in Fig. 3), and the $z$ component, $Q^{z}=1/2(-1/2)$, represents a bonding (antibonding) state, where a hole is equally distributed on the two molecules. $J_{ij}$($>0$) is the inter-dimer exchange interaction, $V_{ij}$ is the inter-dimer Coulomb interaction, $t_{\mathrm{dim}}$ ($>0$) is the intra-dimer hopping integral, and $K_{ij}$ ($>0$) is the coupling between spins and dimer dipoles. Owing to the spin-charge coupling $K_{ij}$, the interaction between the neighboring $Q^{x}$ is modulated by the spin-spin correlation as $V_{\rm eff}=V_{ij}+K{\bm{S}}_{i}\cdot{\bm{S}}_{j}$.

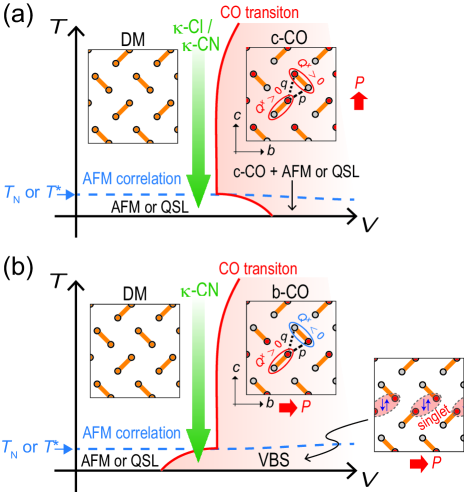
Figure 3 shows schematic phase diagrams in the $V$-$T$ plane, deduced using the mean-field analysis of Eq. (2) [32] where the DM ($\langle Q^{x}\rangle=0$) and charge order (CO) ($\langle Q^{x}\rangle>0$) phases compete. In DM insulators, two patterns of CO are possible: $b$-CO and $c$-CO types, in which polarization occurs along the $b$- and $c$-axes, respectively. The direction of the electric polarization strongly depends on the sign of $V_{ij}=V_{p}-V_{q}$ on the diagonal bonds, termed $p$ and $q$ in Fig. 3. In several $\kappa$-type ET compounds, $V_{p}>V_{q}$ is obtained assuming a $1/r$-type dependence of $V_{ij}$, which prefers the $c$-CO state [15, 16, 33]. However, since the magnitudes of $V_{p}$ and $V_{q}$ are almost identical, it is quite possible that other effects, e.g., due to electron-lattice coupling, make the $V_{ij}$ effectively negative, resulting in the $b$-CO state. When AFM correlations develop (${\bm{S}}_{i}\cdot{\bm{S}}_{j}<0$), $|V_{\rm eff}|$ becomes smaller for the $c$-CO ($V_{ij}>0$), whereas $|V_{\rm eff}|$ is enhanced for the $b$-CO ($V_{ij}<0$). Thus, due to the effects of AFM correlations, the $c$-CO is suppressed [Fig. 3(a)], while the $b$-CO is enhanced [Fig. 3(b)], resulting in a VBS phase, i.e., a spin-singlet state. Therefore, depending on the type of CO, different $V$-$T$ phase diagrams are obtained below $T^{*}$.

In what follows, we discuss our experimental findings on phonon damping and its suppression below $T^{*}\sim 6$ K for the two scenarios shown in Fig. 3. In the QSL scenario ($c$-CO) [Fig. 3(a)], these charge fluctuations become harder at low temperatures, resulting in a decoupling between the lattice- and charge degrees of freedom. For the VBS scenario ($b$-CO) [Fig. 3(b)], spin singlets form via a spin-Peierls-like transition at $T^{*}$. In this case, a spin gap is opening and a hardening of charge fluctuations is expected as well. Thus, a phonon anomaly at $T^{*}$ is expected through the decoupling of the lattice degrees of freedom from either the charge- or the charge- and spin degrees of freedom, corresponding to the QSL or VBS scenarios, respectively. Then, the key difference between these scenarios is whether the system undergoes a distinct phase transition at $T^{*}$ [Fig. 3(b)] or a crossover [Fig. 3(a)]. The present finding of an abrupt change in the phonon linewidths at $T^{*}$ is considered a strong indication for a phase transition, supporting the VBS scenario.

For temperatures above $T^{*}$, the system is situated in the DM phase near the CO phase, cf. Fig. 3. Upon cooling $\kappa$-CN comes closer to the CO phase boundary, corresponding to a softening of the intra-dimer charge fluctuations [34] (see Fig. S6 in SM). This is consistent with the growth of charge fluctuations observed in the optical conductivity upon cooling towards $T^{*}$ [35]. The distinct $c$-axis polarization of the fluctuations revealed in these experiments would be in support of the QSL scenario. On the other hand, arguments in favor of a VBS scenario can be derived from the observation of a spin gap [4, 13] in combination with findings from thermal expansion measurements where well-pronounced signatures were observed at $T^{*}$ [9, 36]. In particular, these latter data provide strong evidence for a second-order phase transition at $T^{*}\sim 6$ K, rather than a crossover, albeit with significant sample-to-sample variations in the shape of the anomaly [36]. Moreover, for those crystals were the effects are most strongly pronounced, the phase transition anomaly shows striking similarities to that revealed for the spin-Peierls transition in (TMTTF)₂AsF₆ [37]. A phase transition into a VBS state, suggested by these results, would also be consistent with the abrupt change in the phonon linewidth, and the sharp feature observed in d$\chi$/d$T$ at $T^{*}$ [cf. inset of Fig. 2(d)].

In conclusion, by studying the spectra of selected low-energy optical phonons of the quantum spin liquid candidate $\kappa$-(ET)₂Cu₂(CN)₃ as a function of temperature, we observe an abrupt change in the phonon linewidth at $T^{*}\sim 6$ K. We argue that the recovery of long-lived (underdamped) breathing modes of ET-dimers below 6 K can be attributed to a cooperative phenomenon involving the lattice and its coupling to the charge- and spin degrees of freedom around 6 K. Our data are consistent with the formation of a VBS state below 6 K.

We thank N. Sato and S. Sugiura for their help in preparating the experiments. The neutron experiments were performed with the approval of ILL (7-01-513). This study was financially supported by Grants-in-Aid for Scientific Research (19H01833, 19K03723, 20H05144, and 22H04459) from the Japan Society for the Promotion of Science. Work at Goethe University, Frankfurt, was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding through TRR 288 - 422213477 (project A06 and B02).