Photoassociation spectroscopy of weakly bound ${}^{87}Rb_{2}$ molecules near $5P_{1/2}+5S_{1/2}$ threshold by optical Bragg scattering in Bose-Einstein condensates

The photoassociation (PA) process of cold atoms Stallway1999 ; Jones2006 has become one of the most precise techniques for spectroscopy of long range molecular states, which is very important for studies of cold molecules, atom-atom collisions, atom-molecule collisions, etc. The desire to achieve quantum degeneracy in molecules was a natural consequence after the first observation of the BEC in alkali atoms Anderson1995 ; Davis1995 ; Bradley1995 . One of the approaches is the indirect production of ultracold molecules by associating atoms to form molecules from cooled atoms Ni2008 ; Danzl2008 ; Molony2014 ; Park2015 ; Guo2016 ; elberg2018 . The PA process is the first step of this excitation-deexcitation scheme Ni2008 ; Danzl2008 ; Molony2014 ; Park2015 ; Guo2016 ; elberg2018 . Due to this reason, PA spectroscopy in ultracold atoms must be studied first, which provides accurate and useful data that could determine or predict new routes in cold-molecule formation. Moreover, the PA process has become an important tool for tuning interatomic interactions Fedichev1996 ; Bohn1999 ; Enomoto2008 ; Yamazaki2010 ; Blatt2011 ; Yan2013 ; Junker2008 ; Bauer2009 ; Fu2013 ; Peng2018 , called optical Feshbach resonance, in which free atom pairs are coupled to an excited molecular state by laser field near a PA resonance.

The PA spectroscopy usually employs the trap loss detection technique Wang1996 ; Gerton2001 ; McKenzie2002 or two-photon ionization Gabbanini2000 . The trap loss detection consists of recording the trap fluorescence (proportional to the atom number) for cold atoms in magneto-optical trap (MOT) Wang1996 or measuring the remaining atoms for quantum degenerate atoms in the trap Gerton2001 ; McKenzie2002 while the PA laser is frequency scanned. If the laser wavelength is resonant with a molecular state, the PA will create long-range excited molecules. These excited molecules, having a very short lifetime will rapidly decay, inducing atom loss from the MOT or trap. In this paper, we develop a method of optical Bragg scattering in ${}^{87}Rb$ BEC to measure PA spectrum, which is especially suitable for near the dissociation limit (near the atomic resonant transition). Optical Bragg scattering from optical lattice is a widely used method for observing and analyzing periodic structures, in which light is incident on the atomic layers confined by optical standing wave at well defined angle and is Bragg reflected (scattered). It has been studied experimentally in cold atomic gases Birkl1995 ; Weidemuller1996 ; Slama2005 ; Hart2015 ; Chen2018 . The signal of optical Bragg scattering in BEC is strong when the probe light is near the atomic resonant transition. Therefore, we obtain the high resolution photoassociation spectrum of excited molecular states in the range of $\pm 1$ GHz near the dissociation limit of $5P_{1/2}+5S_{1/2}$ of ${}^{87}Rb$ atoms.

The PA spectra of ⁸⁷Rb₂ $5P+5S$ excited molecular bound states have been studied and analysed in great detail in Hoffmann1992 ; Hoffinann1994 ; Peters1994 ; Cline1994 ; Fioretti2001 ; Gutterres2002 ; Kemmann2004 ; Jelassi2006 ; Jelassi2006-1 ; Hamley2009 ; Tsai2013 ; Jelassi2014 . In this paper we study the ⁸⁷Rb₂ weakly bound excited dimers formation in an ⁸⁷Rb BEC using PA within $\pm 1$ GHz of the D1 hyperfine asymptotes, which is never reported before. Previous studies in this region could not detect the quantized losses of PA for atoms in MOT and only a continuous loss was observed Peters1994 . The quantum degenerate gases bring several advantages for PA spectroscopy, such as the PA rate is enhanced since it increases proportionally with phase space density and the spectroscopic precision is increased since the energy spread of atoms at low temperature is low. We also compare the PA spectra with the conventional method of trap atom loss and show the mutual agreement. Many interesting phenomena of excited molecular states are observed, such as light-induced frequency red shift, the simple ordered molecular lines, and the anomalously strong bound molecular lines at the atomic transition from $|F=1\rangle$ to $|F^{\prime}=2\rangle$.

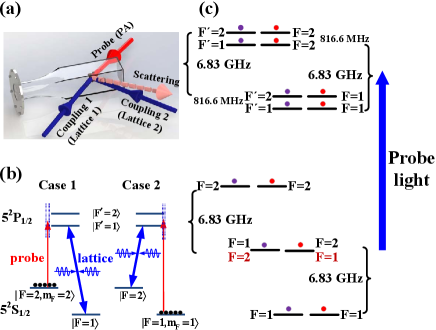
The experimental setup and energy levels are shown in Fig. 1. The starting point for our experiments is an essentially pure BEC with typically $5\times 10^{5}$ ${}^{87}Rb$ atoms in the $|F=2,m_{F}=2\rangle$ hyperfine ground state sublevel confined in a cross-beam dipole trap at a wavelength near 1064 nm Chen2018 . The geometric mean of trapping frequencies $\overline{\omega}\simeq 2\pi\times 80$ Hz in our system. The atoms can be transferred to the $|F=1,m_{F}=1\rangle$ state via a rapid adiabatic passage induced by a microwave frequency field at 2 G of the bias magnetic field.

The optical Bragg scattering technique uses a weak probe (PA) laser and a pair of strong coupling laser beams forming one-dimensional optical lattice as shown in Fig. 1(a). Both of the coupling beams are derived from the same laser and they intersect at an angle of $48^{0}$. The coupling laser beams have a waist ($1/e^{2}$ radius) of about 280 $\mu m$ at the position of the BEC. The weak probe laser acting as PA light has a waist of about 600 $\mu m$. The relative frequencies of the lattice and probe laser are locked by the optical phase locked loop (OPLL). The probe (PA) laser frequency is changed by setting the frequency of local oscillator of the OPLL. The intersecting angle between the probe light and the optical Bragg emission is about $132^{0}$, which satisfy the phase matching condition as discussed in our previous work Chen2018 ; wang2020 . In order to obtain the dark background and high signal-noise ratio for detecting the Bragg emission, the intersecting angle between the plane of the two coupling beams and the plane of the probe-Bragg beams is kept at $11^{0}$.

When atoms are prepared in the $|F=2,m_{F}=2\rangle$ state, the frequency of the coupling laser beams is locked at transition from $|F=1\rangle$ to $|F^{\prime}=1\rangle$ as shown in Fig. 1(b). At the same time, the frequency of the probe (PA) laser is scanned to near the transition between $|F=2,m_{F}=2\rangle$ and the excited state $|F^{\prime}=2\rangle$. In this configuration, the coupling beams form a far detuning optical lattice that mainly modulate the initial state $|F=2,m_{F}=2\rangle$, such that the refractive index of the probe beam is periodically modulated and a structure similar to a photonic crystal is formed. Therefore, the directional emission generated in this configuration corresponds to the ordinary optical Bragg scattering. The spectrum of optical Bragg scattering can be obtained by scanning the frequency of the probe (PA) laser and fixing the frequency of the coupling beams. However, when the probe (PA) laser drive atoms from the transition from $|F=2,m_{F}=2\rangle$ and the excited state $|F^{\prime}=1\rangle$, a pair of the coupling laser beams together with the probe laser form standing wave-coupled electromagnetically induced transparency (EIT) configuration. This case becomes the special form of optical Bragg scattering, called superradiance scattering Wang2015 . The lineshape of the ordinary optical Bragg scattering spectra is different from that of superradiance scattering Chen2018 . Here we study two cases as shown in Fig. 1(b). Case 1: Atoms are prepared in the $|F=2,m_{F}=2\rangle$ state, the frequency of the coupling laser beams is locked at transition from $|F=1\rangle$ to $|F^{\prime}=1\rangle$ (or $|F^{\prime}=2\rangle$); Case 2: Atoms are prepared in the $|F=1,m_{F}=1\rangle$ state, the frequency of the coupling laser beams is locked at transition from $|F=2\rangle$ to $|F^{\prime}=1\rangle$ (or $|F^{\prime}=2\rangle$). In the optical Bragg scattering spectra, the strength of Bragg scattering will be reduced when the probe laser is resonant with an excited molecular state due to atom losses of BEC. By this process, we obtain the spectrum of excited molecular states.

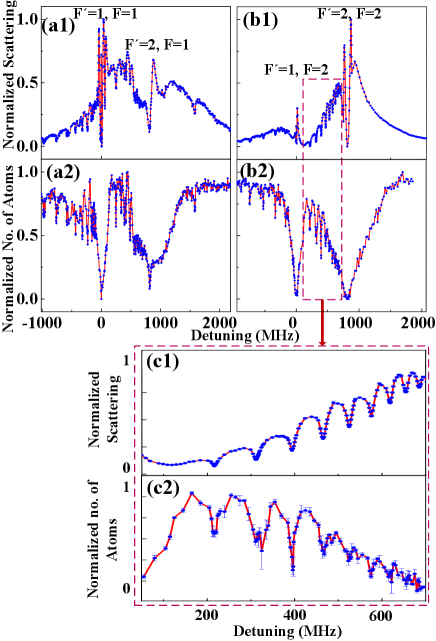
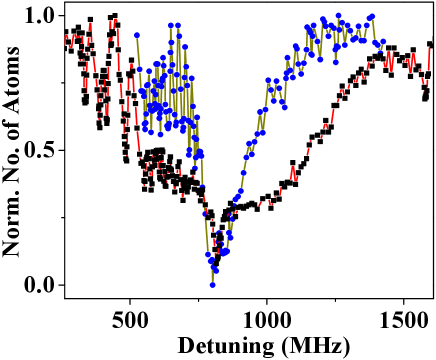
To get the Bragg scattering spectra, all the optical fields, including the coupling and probe (PA) lasers, illuminate BEC in the optical dipole trap simultaneously for 20 $\mu$s, and simultaneously the resulting Bragg emission is detected by EMCCD. We also obtain PA spectra by trap loss, in which the remaining atoms are measured by the time of flight absorption imaging after exposing the BEC to this single probe (PA) laser for 20 $\mu$s. The difference between the two techniques is that in the Bragg scattering two coupling laser beams makes a density modulated lattice in the BEC and the probe (PA) laser scattered from this lattice, is recorded live by the EMCCD while in the trap loss method, only the probe (PA) laser interacts with the BEC and then the BEC is left to expand for 30 ms after which an image is taken by imaging laser to count the number of remaining atoms. Fig. 2 shows the optical Bragg scattering and trap loss spectra of the ⁸⁷Rb atoms prepared in the $|F=1,m_{F}=1\rangle$ and $|F=2,m_{F}=2\rangle$ states respectively, when the frequencies of the probe (PA) laser are scanned below or above the lower $|F^{\prime}=1\rangle$ and upper excited hyperfine level $|F^{\prime}=2\rangle$ of the D1 line. Here, the frequency of the coupling laser beams is locked at transition from $|F=2\rangle$ to $|F^{\prime}=1\rangle$ (Fig. 2(a1)) when atoms are initially prepared in $|F=1,m_{F}=1\rangle$ and from $|F=1\rangle$ to $|F^{\prime}=2\rangle$ (Fig. 2(b1)) when atoms are prepared in $|F=2,m_{F}=2\rangle$. The spectrum of optical Bragg scattering presents the broader peaks on both sides of the atomic resonance (marked by the respective atomic hyperfine quantum numbers) and several narrower and shallower dips with the reduced scattering corresponding to the weak bound molecular states due to atomic loss by PA. As a comparison, Fig. 2(a2) and (b2) show PA spectra measured by trap loss without the coupling laser beams (no lattice, only BEC+probe (PA) laser), when BEC is prepared in the $|F=1,m_{F}=1\rangle$ and $|F=2,m_{F}=2\rangle$ state respectively. The lineshape of trap loss spectrum shows broader Lorentzian dip near the atomic resonance and several narrower and shallower dips corresponding to the weakly bound molecular states. Fig. 2(c1) and (c2) show the enlarged plots of Fig. 2(b1) and (b2). From the error bars, PA spectrum by optical Bragg scattering detection present the high signal-noise ratio compared with that of trap loss especially in the region of near dissociation threshold. One reason is that the spectrum of optical Bragg scattering presents the broad M lineshape (dip at the resonance) Schilke2015 , in contrast, the lineshape of trap loss presents broad Lorentzian dip near the atomic resonance. The other is that the spectrum for trap loss is prone to more noise compared to the spectrum for optical Bragg scattering. The trap loss technique employs the absorption images to count the number of remaining atoms. The absorption images have several technical noise sources, such as the interference fringes and the change in imaging laser power between recording of the absorption and the reference image Kristensen2019 , while the Bragg sattering technique measures the scattered light live from the dark background during the scattering process and avoid these extra steps. Our results demonstrate that the two methods compliment each other, however, the Bragg scattering technique has a high signal to noise ratio near atomic resonance.

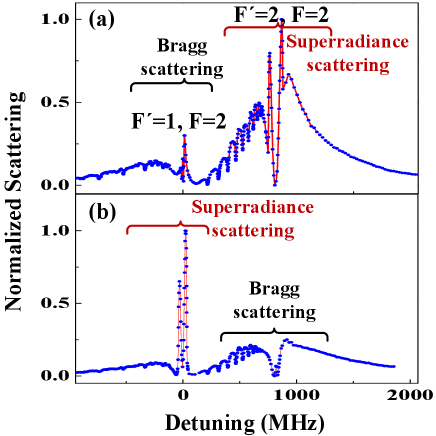
The spectral lineshapes of optical Bragg scattering and superradiance scattering have been studied in our previous work Chen2018 . In the case of Bragg scattering, the coupling beams forms a far detuned lattice which modulate the ground state BEC to generate a periodic structure in the ground state atoms, which induce a directional optical scattering. The spectrum of optical Bragg scattering presents a broader M lineshape, which is clearly shown in the Bragg scattering part of Fig. 3(b) when the frequencies of the probe laser are scanned cross an atomic transition. For the superradiance scattering, the coupling laser and the probe (PA) laser couple the same excited state to different ground states to induce alternate periodic structures of atoms in the excited state and ground state Chen2018 ; wang2020 . The superradiance scattering spectrum present two narrow and intense peaks at the two side of resonance (the superradiance scattering part of Fig. 3(a)) due to the density of state of the periodic structure in the excited state. We can see that the spectral lineshapes in Fig. 3 are different for the probe transitions near the $|F\rangle\rightarrow|F^{\prime}=F-1\rangle$, $|F\rangle\rightarrow|F^{\prime}=F\rangle$, and $|F\rangle\rightarrow|F^{\prime}=F+1\rangle$. Here, both cases have the same broad wings. Therefore, the lineshape of superradiance and Bragg scattering are quite different near the atomic resonance, however, this lineshape does not influence the weak bound molecular states since the PA loss is measured using these broad wings.

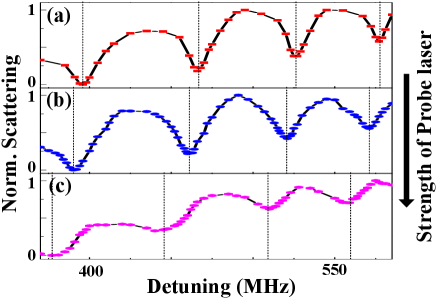
PA light-induced frequency red shift is a typical characteristic of PA spectra Gerton2001 ; McKenzie2002 . We also observe this phenomenon in the PA spectra where the lines shift to the red with increasing PA laser power as shown in Fig. 4. This phenomenon arises from coupling of the various ground-state threshold scattering states to the excited-state bound molecular levels by PA light. The density of ground continuum states always increases versus energy and therefore, the bound states shift in frequency with the addition of new ground states from the continuum.

We present the observed PA lines in tabular form as shown in Table I. Those PA lines are presented which are observable in both of the techniques. The lines are recorded for a probe (PA) laser power of 25 $\mu$W. We use the same probe power for the two techniques in order to avoid PA light-induced frequency red shift. Thus, we obtain mutually consistent molecular dips using the two techniques for a large number of peaks with an uncertainty of $\pm$0.2 MHz.

Now we analyze the weak bound molecular states near the dissociation limit, which we have divided into several regions in Table I, as follows. Region A: There are no weakly bound molecular states due to being higher than the last dissociation limit ($F^{\prime}=2,F=2$). Here, the $5P_{3/2}+5S_{1/2}$ molecular threshold is not considered due to far blue detuning of 15 nm. Region B: The spectrum of the weakly bound molecular states represent the simple ordered lines of the vibrational levels of single molecular potential curve. Here, the rotational energy is neglected due to the huge internuclear separation (the rotational constant has a magnitude on the order of only several MHz) Kemmann2004 . So the rotational structure is unresolved in our work. Regime C: The bound molecular lines are not very regular, since there are two molecular potential energy curves (one terminating at $F^{\prime}=1$ and the other at $F^{\prime}=2$) and thus two vibrational series are overlapped together. Region D: There should be no the bound molecular states in this regime due to blue detuning of the dissociation limit ($F^{\prime}=2,F=1$). However, one bound molecular line is observed, which originate from the molecular potentials of the higher dissociation limit ($F^{\prime}=1,F=2$) and ($F^{\prime}=2,F=2$). The reason is explained as follow in Region E. Region E: The coupling strength (Franck-Condon factor) between the ground continuum state and the excited-state bound molecular state in this region are anomalously stronger than that of other regions at the same power of PA laser. The width of each bound molecular line is determined by the coupling strength between the ground continuum state and to the excited-state bound molecular state. Therefore, the power broadening of the bound molecular lines in this region causes the lineshape of the atomic transition from $|F=1\rangle$ to $|F^{\prime}=2\rangle$ to deviate from a standard Lorentzian shape, as shown in Fig. 5. Upon reducing the power of PA laser, we can see that many narrow bound molecular lines appear in red detuning side at the atomic resonant transition (from $|F=1\rangle$ to $|F^{\prime}=2\rangle$) and the whole lineshape of the atomic transition recovers to the broad Lorentzian shape. This anomalous feature may be explained in terms of an additional broadening of the resonance due to the strong coupling with the deep bound molecular channels of ($F^{\prime}=1,F=2$) and ($F^{\prime}=2,F=2$). Region F: The bound molecular lines are not very regular, which is similar to Regime III.

In conclusion, we demonstrate high resolution PA spectroscopy of weakly bound ${}^{87}Rb_{2}$ molecular near $5P_{1/2}+5S_{1/2}$ threshold by optical Bragg scattering in Bose-Einstein condensates. Optical Bragg scattering provides a useful tool to measure the PA spectra near the atomic resonant transition. We present the high resolution PA spectrum of excited molecular states in the range of $\pm 1$ GHz near the dissociation limit of $5P_{1/2}+5S_{1/2}$ of ${}^{87}Rb$ atoms, which is never studied in this region before. For comparison, we also perform the measurement with the traditional method of trap atom loss and the strong consistency between the two methods provides confirmation for its validity. The last few bound molecular states from the dissociation limit are of great interest as this can improve the long range molecular potential curves. In the future, combined with the theoretical calculations about long range molecular potential curves near $5P_{1/2}+5S_{1/2}$ threshold, we can further supplement and improve the data of PA spectra including the finer and smaller molecular transition lines. Moreover due to anomalous strong bound molecular lines at the atomic transition from $|F=1\rangle$ to $|F^{\prime}=2\rangle$, the contribution of bound excited molecular states to the lineshape of the atomic resonant transition will play some role, when using this atomic resonant transition spectrum to study precise spectroscopic phenomena, such as EIT phenomena.

^∗ chenlchao@gmail.com. ^† jzhang74@sxu.edu.cn, jzhang74@yahoo.com.