Photoproduction and detection of decays in ultra-peripheral collisions and at an electron-ion collider
Abstract
Vector meson photoproduction is an important probe of nuclear structure. Light vector mesons are most sensitive to low structure, as long as they are not too light for perturbative QCD calculations. The is of interest as an intermediate mass state (between the and ) that is easier to detect than the .
Using HERA data on proton targets, we make projections for lead/gold targets in UPCs at the Large Hadron Collider and RHIC, and for and collisions at a future Electron-Ion Collider (EIC). These projections for ion targets depend on the largely-unknown branching ratio, and use existing data to constrain that branching ratio. Current data points to a relatively low branching ratio, less than 50%. The HERA and ALICE UPC Pb data exhibit very similar mass spectra, indicating that, if the system is composed of two resonances, the products of their photon couplings with their four-pion branching ratios are similar.
The predicted rates are high for both UPCs and the EIC. The decay can be observed at the EIC with high efficiency. In collisions at the highest energy, the forward B0 detector is needed to observe this channel down to the lowest achievable Bjorken values.
I Introduction
Vector meson photoproduction has been studied extensively at fixed-target accelerators Bauer et al. (1978), the HERA collider Ivanov et al. (2006), and with ultra-peripheral collisions (UPCs) at heavy-ion colliders Klein and Steinberg (2020). It will also be an important probe of nucleons and nuclei at a future electron-ion collider (EIC) Accardi et al. (2016); Abdul Khalek et al. (2021); Adam et al. (2022). Through the Good-Walker paradigm, coherent vector meson production is sensitive to the average nuclear configuration, while incoherent vector meson photoproduction is related to fluctuations in the nuclear configuration, including gluonic hotspots Miettinen and Pumplin (1978); Mäntysaari and Schenke (2016); Klein and Mäntysaari (2019).
The dependence of exclusive production is an important signature of saturation Mäntysaari and Venugopalan (2018). Definitive conclusions about saturation will require studies of different mesons, with different wave functions and masses.
The is straightforward to reconstruct Adler et al. (2002), but from the theory perspective is rather light, limiting the applicability of perturbative QCD (pQCD) based calculations. The is heavy enough that saturation phenomena are greatly reduced Mäntysaari and Venugopalan (2018). The is attractive because it has an intermediate mass (between the and the ).
Early plans for exclusive vector meson production at a U. S. EIC focused on the and Accardi et al. (2016). However, production at low is hard to reconstruct Abdul Khalek et al. (2021); Arrington et al. (2021) because the main channel, , suffers from a low value, with the daughter kaons having a momentum of only 127 MeV/c in the rest frame. Other final states have either low branching ratios or include a long-lived . For UPCs, the situation is similar, with coherent photoproduction on ion targets difficult to observe Acharya et al. (2024a); Chekhovsky et al. (2025).
The states are attractive alternatives to the , as they also have intermediate masses, between the and . However, these states have a more complex wave function and a more complex phenomenology. There are likely two overlapping resonances, the and the Workman et al. (2022). These resonances can decay to many different final states, but both have a significant branching ratio to . Since the final state is easy to reconstruct, we will focus on it. Most photoproduction analyses have fit the mass spectrum to a single resonance, so we will perforce do the same here.
The final state has been studied at fixed-target accelerators, using collisions at HERA and in ultra-peripheral collisions (UPCs) of gold ions at RHIC and lead ions at the LHC. Using HERA and fixed-target data on proton targets as input, we will use a Glauber calculation to predict the RHIC and LHC cross sections for ion targets. These predictions depend significantly on the branching ratio, giving us some sensitivity to that quantity.
We also make predictions about the the cross sections in and collisions at the EIC, and estimate the reconstruction efficiency using a simple model of the proposed ePIC detector. As with UPCs, the cross sections depend on the branching ratio.
II Modeling of photoproduction
are radial excitations of the , with the same quantum numbers. These states are most visible in the final state, which has been studied at a variety of fixed-target photoproduction experiments and in collisions Navas et al. (2024). The photoproduced final state is observed as a single broad resonance, which has usually not been separated into two different states.
The first studies of photoproduction were done in fixed-target experiments at photon energies from 3 GeV to 70 GeVBingham et al. (1972); Schacht et al. (1974); Alexander et al. (1975); Barber et al. (1980); Aston et al. (1981a); Atkinson et al. (1985); Atiya et al. (1979). Four pion photoproduction was first studied at collider energies by the Solenoidal Tracker at RHIC (STAR) collaboration Abelev et al. (2010), and later by the ALICE detector at the LHC Acharya et al. (2024b). We use the mass and width that STAR measured: mass MeV and width MeV.
The H1 collaboration has also studied 4-pion photoproduction, and observed a resonance with similar parameters to STAR, also well fit by a single resonance Schmitt (2018); H1 Collaboration (2918). We will use this HERA cross-section data as input to make predictions for ion targets in UPCs and at the EIC.
II.1 Proton targets
We make a fit to as a function the center of mass energy . Since the branching ratios are unknown, the data are for the cross sections times branching ratio. The H1 and fixed-target cross-section data are fit to a two-component Reggeon Pomeron model Klein and Nystrand (1999); Klein et al. (2017):
| (1) |
The first term represents Pomeron exchange (with strength and power-law exponent ), while the second is for Reggeon exchange (with strength and power-law exponent ). Br is the branching ratio for the specified decay. Figure 1 shows the data, with both statistical and systematic errors. The H1 systematic uncertainties include point-to-point correlations. Also shown are three fits to the data, with the parameters given in Tab. 1. These parameters are for a 100% branching ratio for . For smaller branching ratios, and should be scaled up by dividing by the branching ratio.
In Model I, all four parameters in Eq. 1 were allowed to float. This led to a fairly large value of of 0.87, considerably above expectations for Pomeron exchange. In this fit, the Pomeron contribution was generally small, with the cross section dominated by the Reggeon component, even at H1 energies.
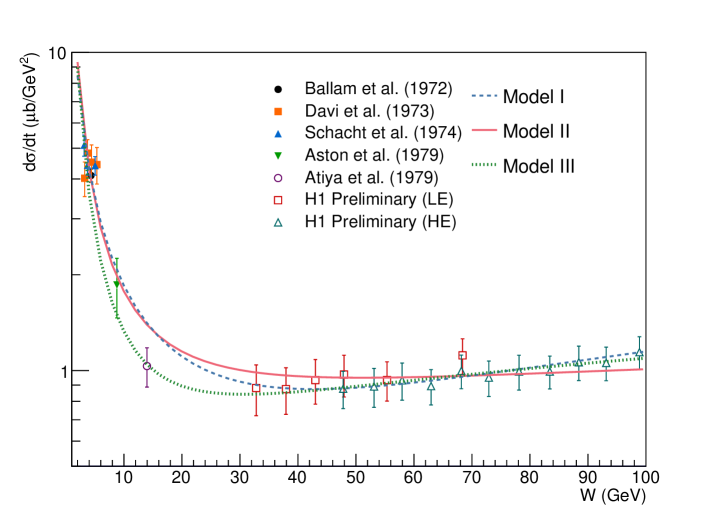
The second fit, Model II, added a nuisance term, based on the value for found by H1. A term was added to the in the fit, where and are taken from the fit in Fig. 4 of Ref. H1 Collaboration (2918). The rationale for this was that was dominated by systematic errors; the H1 fit correctly accounted for the correlated systematic errors in their analysis, so was more precise than if we just used their data points and errors. This fit pulled to 0.28, similar to that found by H1, and to many other studies of light mesons Szuba (2009). The downside is that this approach uses the H1 data twice - in the H1 and in our fit. This decreases the importance of the fixed-target data. Since that data is far away in energy from the region of interest, this should not cause problems.
The third fit, Model III, is from a previous work Klusek-Gawenda and Tapia Takaki (2020). It differs from our fit in that it includes a slightly larger selection of fixed-target data, especially at very low energies. It found an intermediate between Model I and Model II.
The remainder of the paper uses the Model II fit. The differences in predictions between the three fits in the energy range of current interest are generally moderate.
| Model I | 0.02 | 0.87 | 16.61 | 0.99 |
|---|---|---|---|---|
| Model II | 0.26 | 0.28 | 20.78 | 1.21 |
| Model III | 0.16 | 0.41 | 23.0 | 1.4 |
The branching ratio in Eq. 1 converts the cross section into the cross section. The branching fraction is important when considering ion targets, since a Glauber calculation, discussed below, maps into , the cross section on an ion target. The ion-target cross section does not scale linearly with the proton-target cross section, so it is necessary to remove the branching ratio before doing this mapping. However, the branching ratio to the final state is poorly known.
One estimate comes from Ref. Frankfurt et al. (2003a), which suggests a rough branching ratio of approximately 30%. This estimate is based on the inferred cross-section for decaying into in gold-gold collisions at RHIC, which is about one-third of that for the . Another study, by H1, estimated a branching ratio of about 40% (summing nonresonant and ) Andreev et al. (2020).
Here, we consider branching ratios between 10% and 100%. 100% is the obvious maximum, while a branching ratio below 10% would require that the cross section is larger than that for the , which seems unlikely. In Ref. Frankfurt et al. (2003a), the cross-section to produce a decaying to in gold-gold collisions at RHIC is estimated to be about 1/3 of that for the , roughly consistent with a 30% branching ratio.
II.2 Production on ion targets
The cross section for photoproduction on nuclear targets is found through a quantum Glauber calculation 111This differs from Ref. Klusek-Gawenda and Tapia Takaki (2020) which used a classical Glauber calculation. The cross section for forward production, is equal to , where is the slope of at small . This forward cross section has two parts: the probability for a photon to fluctuate into the , and the -nucleon elastic scattering cross section:
| (2) |
Here, we use the slope GeV-2 222Taken from the softer (coherent) exponent in Fig. 6 of Ref. H1 Collaboration (2918) to convert from the total cross section to .
The vector-meson photon coupling can be determined from the meson coupling to :
| (3) |
where is the vector meson mass, is the partial width for that meson to decay to and is the fine structure constant. The coupling is unmeasured for the . Ref. Klusek-Gawenda and Tapia Takaki (2020) estimated keV and for the . Alternately, Generalized Vector Meson Dominance (GVDM) predicts that Frankfurt et al. (1998)
| (4) |
This leads to an estimate of and keV, or about four times greater than the previous estimate. This GVDM treatment lacks off-diagonal elements (which couple different mesons), which may be important for Bronstein (1977). The GVDM estimate of also leads to a cross section that seems too small, as will be discussed below. The use of two resonances, each with the GVDM coupling, would not reduce these discrepancies. For these reasons, we use the coupling from Ref. Klusek-Gawenda and Tapia Takaki (2020) as our baseline.
The uncertainty on the coupling is the largest single uncertainty in the calculation. Its use in the and equations does not completely cancel out because of the Glauber calculation; any change in this coupling will corresponding alter the best-fit branching ratio.
The optical theorem is then used to find the total cross section.
| (5) |
At GeV, the total cross-section is 18 mb, assuming a 100% branching ratio, and 57 mb for a 10% branching ratio. In comparison, the cross sections for the and are 24 and 26 mb respectively Klein and Nystrand (1999). It seems unlikely that the cross section is twice that of the . This disfavors scenarios with low branching ratios.
The cross section is then found using a quantum Glauber calculation Frankfurt et al. (2003a):
| (6) |
where is the nuclear thickness function.
The optical theorem can be used again, to convert into . Then, we use the nuclear form factor from Ref. Klein and Nystrand (2000) to get the total cross-section.
| (7) |
III production in ultra-peripheral collisions
The cross section for photoproduction in UPCs is given by combining the (Eq. 1) or cross sections (Eq. 7) with the appropriate photon flux for protons Klein and Nystrand (2004) or ions Klein and Nystrand (2000). This code is now implemented in the STARlight Monte Carlo code Klein et al. (2017).
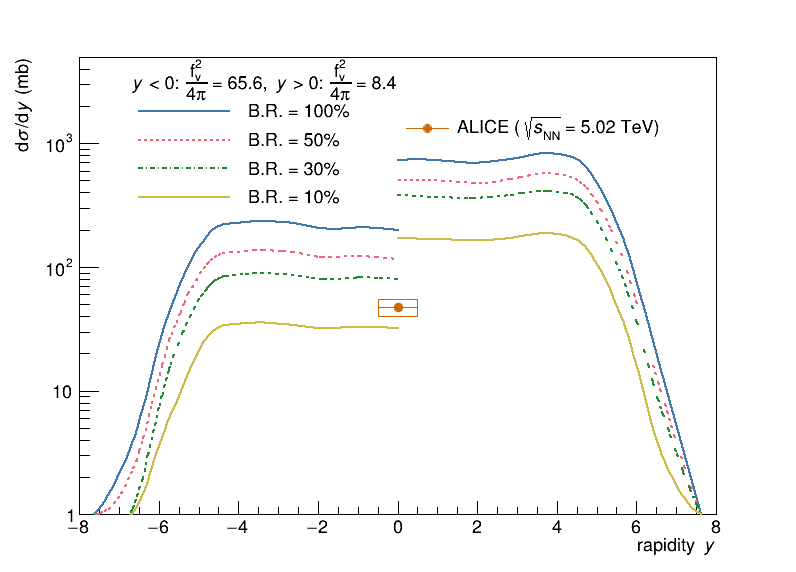
Figure 2 shows the calculated for the for four assumptions about the branching ratio between 10% and 100% and for the two different possible s. The calculations are compared with ALICE data on 5.02 TeV lead-lead collisions Acharya et al. (2024b). For the Ref. Klusek-Gawenda and Tapia Takaki (2020) coupling, the data matches the cross section with about a 30% branching ratio. Including the estimated 17% error on from Ref. Klusek-Gawenda and Tapia Takaki (2020) does not introduce large uncertainties into this estimate.
For the GVDM-predicted coupling, the best-fit branching ratio is unreasonably low, requiring a very large total cross section. The GVDM prediction in Eq. 4 must be too high. A GVDM calculation that included off-diagonal elements might do better, though. Alternately, a calculation that included inelastic shadowing (cross-section fluctuations) might improve the match between UPC data and a quantum Glauber calculation Frankfurt et al. (2016).
The poorly-known nature of the introduces another uncertainty. If, as seems likely, the is composed of two resonances, then there is no reason that the two resonances should have the same branching ratio or . With these caveats, in the single-resonance model, branching ratios near 100% are disfavored.
Unfortunately, the STAR data on the final state suffers from large experimental uncertainty Abelev et al. (2010) so it cannot contribute to the comparison.
Another uncertainty involves the resonance substructure of the final state, which can impact the experimental acceptance, and, with it, the comparison with data. Here, we modeled the final state using phase space and use the resulting events to determine the acceptance, using simple models for three different LHC detectors. The assumed detector parameters are given in Table 2, along with the determined detector efficiencies. For all four detectors, the efficiency is limited because the signal is spread over a much wider rapidity range than the detector acceptance. Figure 3 shows the expected acceptance for the different detectors. If there are two resonances, then there is no reason they should have the same resonant substructure; this would further complicate the picture.
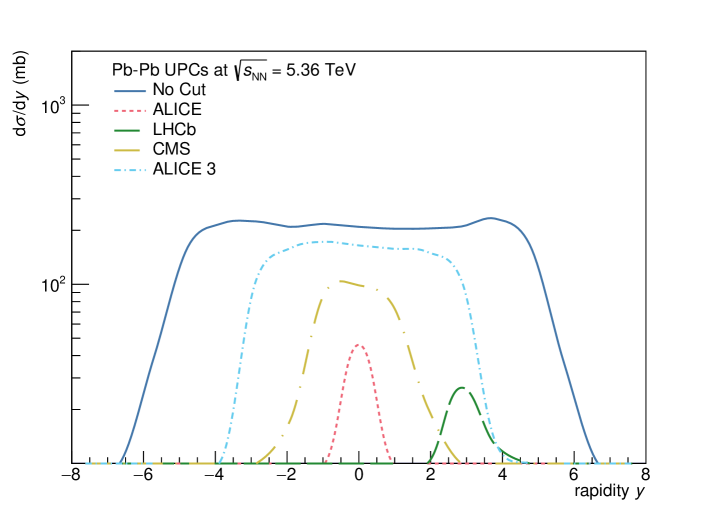
| Experiment | Kinematic coverage | Acceptance |
|---|---|---|
| ALICE | 2.2% | |
| LHCb | 1.8% | |
| CMS | 12% | |
| ALICE 3 | 43% |
IV photoproduction in collisions
Photoproduction in collisions adds another dimension: the photon . There is no data on cross sections for virtual photons, so we assume that the evolution of the cross-section is the same as for the Aaron et al. (2010); Lomnitz and Klein (2019):
| (8) |
where .
production is assumed to follow vector meson dominance, with the final state being linearly polarized transverse to the beam direction at , but with an increasing longitudinal polarization as rises. The rate of this increase is not known for the , but we use the approach described in Ref. Lomnitz and Klein (2019) here, assuming that the spin matrix for the is the same as for the . The decays are assumed to follow a 4-pion phase space distribution; assuming a final state Abelev et al. (2010) would lead to some changes in efficiency, but would not alter the conclusions here.
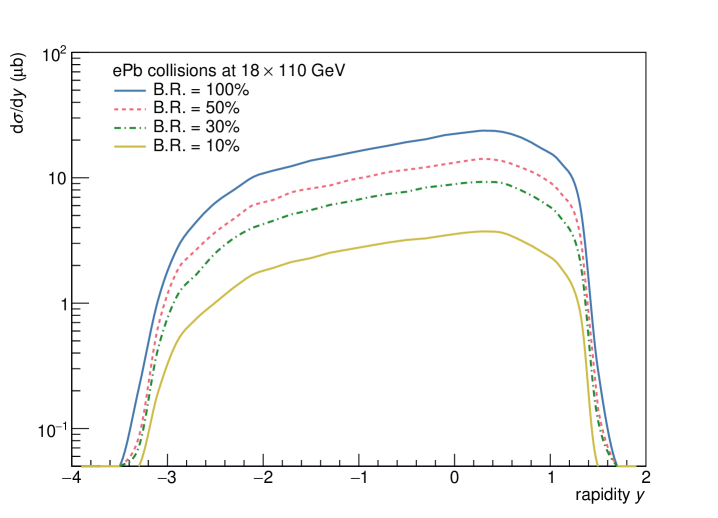
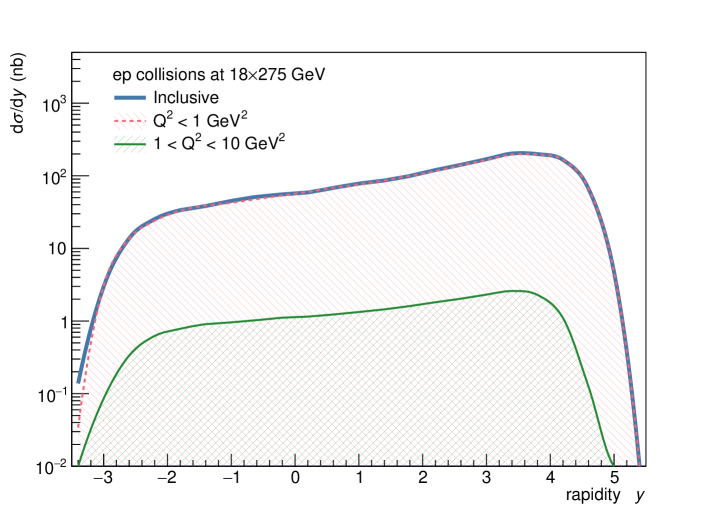
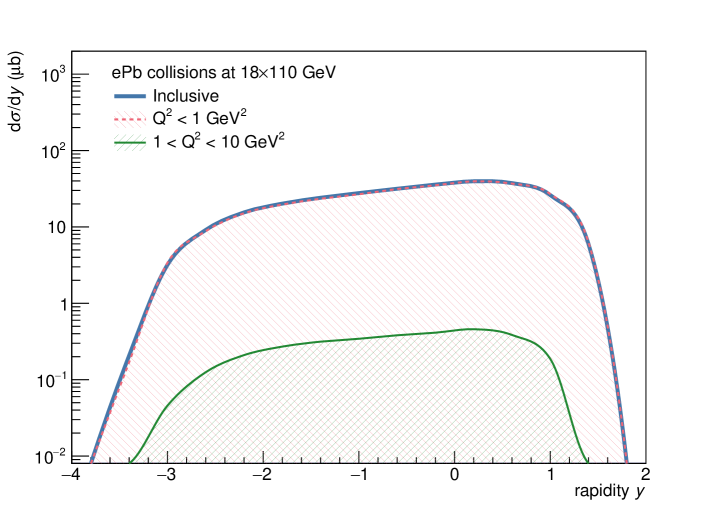
Simulations were performed in the eSTARlight framework Lomnitz and Klein (2019). Calculations were done for the top EIC energies: 18 GeV electrons colliding with either 275 GeV protons or 110 GeV/nucleon lead ions. Table 3 shows the calculated cross sections. In addition to the total (integrated over all ) cross section, cross sections are given for photoproduction ( and electroproduction ). The total cross section is dominated by photoproduction, as expected.
The cross section for production in Pb collisions is about 45 times that for collisions. This is a smaller ratio than for the or , but is similar to the ratio found for A and collisions in Ref. Klusek-Gawenda and Tapia Takaki (2020). For collisions, the cross-section is about 1/7 of the cross section, and about 1/3 of the cross section. For Pb collisions, the ratios are lower, with the cross section 1/30 of the cross section, and half that for the . In both cases, the rates are high enough (7 or 1.5 billion events per 10 fb of integrated luminosity) to allow high-precision differential measurements. Measurements of final states with small branching ratios, including , should also be possible, to accurately measure the photon- coupling. If there are two resonances, then it should be possible to measure separate branching ratios for different final states.
| Collision System | Range () | Total Cross Section | Events for () | Acceptance | Acceptance with |
|---|---|---|---|---|---|
| at GeV | Inclusive | 0.39 | 0.41 | ||
| 0.39 | 0.41 | ||||
| 0.52 | 0.53 | ||||
| Pb at GeV | Inclusive | 0.73 | 0.73 | ||
| 0.73 | 0.73 | ||||
| 0.76 | 0.76 |
The corresponding are shown in the two top panels in Fig. 4. Also shown is the acceptance of the ePIC detector. ePIC is modeled with two components: a central barrel tracker sensitive to and the B0 detector, which covers . For both detectors, we required track MeV/c, but this cut had little effect on the efficiency. The bottom panels of Fig. 4 show the detection efficiency for the photoproduction events. The efficiency is high for , but falls off at larger , as expected. The B0 detector plays an important role for collisions in the region ; otherwise the efficiency would be near zero for . Even though the efficiency is fairly low in this region, the rates are high enough that high statistics data should be achievable.
The rapidity is closely related to the target Bjorken
| (9) |
where is the proton mass and is the Lorentz boost of the proton beam at maximum EIC energy. The central detector cutoff, , corresponds roughly to (as can be seen in Fig. 4), or . For collisions, covering the full range of Bjorken requires acceptance out to rapidity , corresponding to . Although this is beyond the range of the central tracker, Fig. 4 shows that the B0 tracker does cover this region, albeit with low total efficiency. Nuclear shadowing (beyond that present in the Glauber calculation) or saturation would most clearly manifest itself as a reduction in cross-section with decreasing , i. e. with increasing rapidity at low/moderate Mäntysaari and Venugopalan (2018). There would also be changes in Accardi et al. (2016). The rates are high enough that statistics will not limit these measurements, even at the lowest .
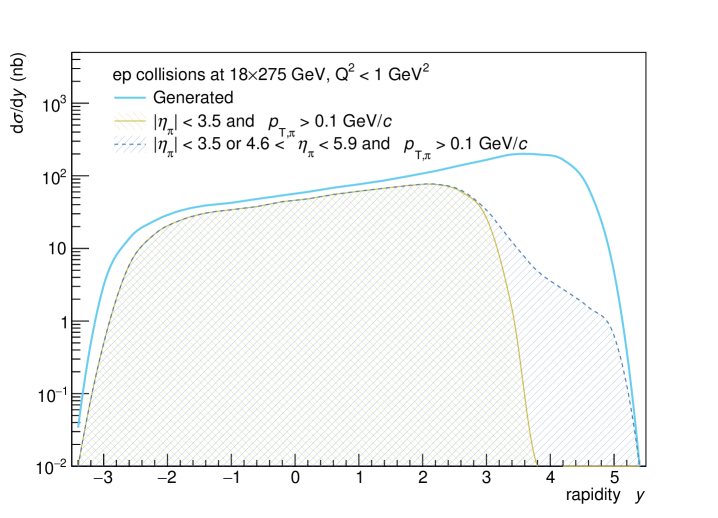
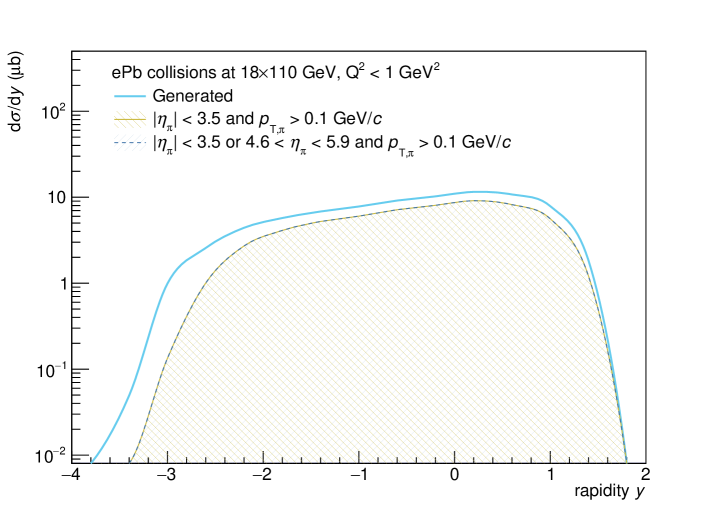
In short, the is copiously produced and relatively easy to reconstruct, showing promise for use in saturation studies. The largest uncertainties in the rates are due to the photon-meson coupling constant and to the uncertainty as to whether this is one meson or two. Fortunately, the coupling to can be determined experimentally, by measuring that final state, while the number of resonances can be determined by detailed studies of the resonance line shape and substructure. The remaining uncertainties are much smaller, making the an excellent medium-mass candidate for mapping out shadowing as a function of .
V Discussion and conclusions
We have calculated the cross section for on ion targets, using fixed-target and HERA data for photoproduction on proton targets as input. The resulting ion-target cross sections depend on the photon-meson couplings and the branching ratio for the to decay to . The couplings predicted using a GVDM model lead ion-target cross-sections that are high enough to require implausibly small branching ratios. Using the coupling from Ref. Klusek-Gawenda and Tapia Takaki (2020), ALICE data on , prefers branching ratios in the 30% to 50% range. This estimate relies on the validity of a Glauber calculation approach, but small deviations will not have a large effect on this conclusion.
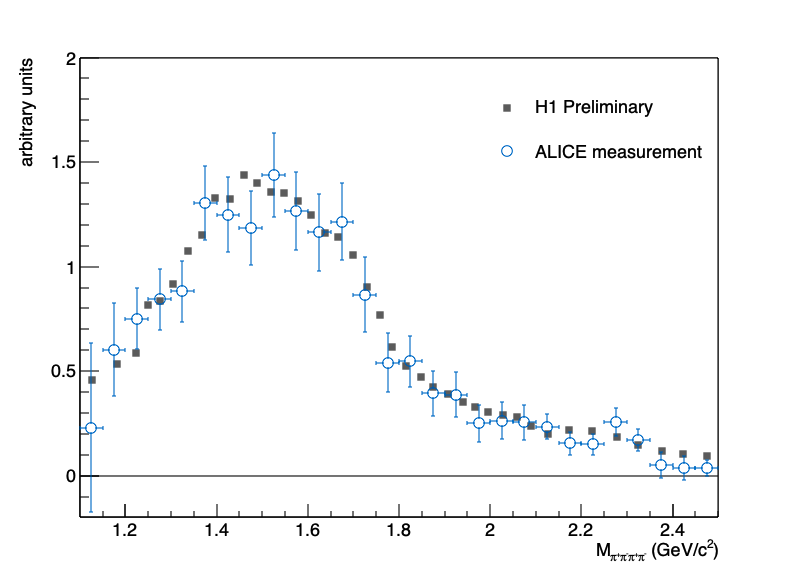
As previously noted, the is likely a composite of two mesons, the and . The ALICE data is well fit by a two meson model, but the mass spectrum does not fit a single meson by itself. However, as Fig. 5 shows, the two mass spectra for the two targets look very similar. This indicates that the photon-meson couplings times the branching ratio to are similar for the two mesons. Otherwise, the Glauber approach would distort the mass spectra for ion targets. More detailed comparisons of the resonance shape and substructure should clearly show if there is one resonance or two. High-statistics data from LHC Runs 3 and 4 Citron et al. (2019) should allow for a definitive comparison.
With this LHC data, it should also be possible to measure the coupling to . This might be easiest using higher pairs from incoherent photoproduction, to avoid backgrounds from . It would also be possible to investigate whether a GVDM model with off-diagonal intermediate states might better predict the photon-meson couplings Kobayashi (1973); Fraas and Kuroda (1977); Frankfurt et al. (2003b).
We have also made predictions for at the proposed U. S. EIC. The production rates are high, and the meson is an easy-to-reconstruct probe of nuclear structure. It is intermediate in mass between the and the , so it should show significant saturation, but also be amenable to pQCD calculations. These features should also hold at the proposed Chinese electron-ion collider, EiCC Chen et al. (2020) or the proposed LHeC collider Agostini et al. (2021). For the LHeC, excellent forward instrumentation is critical to be able to observe photoproduction and electroproduction at the highest energies, corresponding to the lowest Bjorken. For the LHeC, though, the rate differences between the three cross-section fits will be larger.
The approach developed here, comparing and A collisions may also be applicable for determining absolute branching ratios for some other mesons, as long as the photon-meson coupling is known.
This work is supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under contract numbers DE-AC02-05CH11231 and DE-FG02-96ER40991.
References
- Bauer et al. (1978) T. H. Bauer, R. D. Spital, D. R. Yennie, and F. M. Pipkin, Rev. Mod. Phys. 50, 261 (1978), [Erratum: Rev.Mod.Phys. 51, 407 (1979)].
- Ivanov et al. (2006) I. P. Ivanov, N. N. Nikolaev, and A. A. Savin, Phys. Part. Nucl. 37, 1 (2006), arXiv:hep-ph/0501034 .
- Klein and Steinberg (2020) S. Klein and P. Steinberg, Ann. Rev. Nucl. Part. Sci. 70, 323 (2020), arXiv:2005.01872 [nucl-ex] .
- Accardi et al. (2016) A. Accardi et al., Eur. Phys. J. A 52, 268 (2016), arXiv:1212.1701 [nucl-ex] .
- Abdul Khalek et al. (2021) R. Abdul Khalek et al., (2021), arXiv:2103.05419 [physics.ins-det] .
- Adam et al. (2022) J. Adam et al. (ATHENA), JINST 17, P10019 (2022), arXiv:2210.09048 [physics.ins-det] .
- Miettinen and Pumplin (1978) H. I. Miettinen and J. Pumplin, Phys. Rev. D 18, 1696 (1978).
- Mäntysaari and Schenke (2016) H. Mäntysaari and B. Schenke, Phys. Rev. Lett. 117, 052301 (2016), arXiv:1603.04349 [hep-ph] .
- Klein and Mäntysaari (2019) S. R. Klein and H. Mäntysaari, Nature Rev. Phys. 1, 662 (2019), arXiv:1910.10858 [hep-ex] .
- Mäntysaari and Venugopalan (2018) H. Mäntysaari and R. Venugopalan, Phys. Lett. B 781, 664 (2018), arXiv:1712.02508 [nucl-th] .
- Adler et al. (2002) C. Adler et al. (STAR), Phys. Rev. Lett. 89, 272302 (2002), arXiv:nucl-ex/0206004 .
- Arrington et al. (2021) J. Arrington et al., (2021), arXiv:2102.08337 [nucl-ex] .
- Acharya et al. (2024a) S. Acharya et al. (ALICE), Phys. Rev. Lett. 132, 222303 (2024a), arXiv:2311.11792 [nucl-ex] .
- Chekhovsky et al. (2025) V. Chekhovsky et al. (CMS), (2025), arXiv:2504.05193 [nucl-ex] .
- Workman et al. (2022) R. L. Workman et al. (Particle Data Group), PTEP 2022, 083C01 (2022).
- Navas et al. (2024) S. Navas et al. (Particle Data Group), Phys. Rev. D 110, 030001 (2024).
- Bingham et al. (1972) H. H. Bingham et al., Phys. Lett. B 41, 635 (1972).
- Schacht et al. (1974) P. Schacht, I. Derado, D. C. Fries, J. Park, and D. Yount, Nucl. Phys. B 81, 205 (1974).
- Alexander et al. (1975) G. Alexander, O. Benary, J. Gandsman, D. Lissauer, A. Levy, Y. Oren, and L. M. Rosenstein, Phys. Lett. B 57, 487 (1975).
- Barber et al. (1980) D. P. Barber et al. (LAMP2 Group), Z. Phys. C 4, 169 (1980).
- Aston et al. (1981a) D. Aston et al. (Bonn-CERN-Ecole Poly-Glasgow-Lancaster-Manchester-Orsay-Paris-Rutherford-Sheffield), Nucl. Phys. B 189, 15 (1981a).
- Atkinson et al. (1985) M. Atkinson et al. (Omega Photon), Z. Phys. C 26, 499 (1985).
- Atiya et al. (1979) M. S. Atiya et al., Phys. Rev. Lett. 43, 1691 (1979).
- Abelev et al. (2010) B. I. Abelev et al. (STAR), Phys. Rev. C 81, 044901 (2010), arXiv:0912.0604 [nucl-ex] .
- Acharya et al. (2024b) S. Acharya et al. (ALICE), (2024b), arXiv:2404.07542 [nucl-ex] .
- Schmitt (2018) S. Schmitt (Presented at Deep Inelastic Scattering, 2018).
- H1 Collaboration (2918) H1 Collaboration, “Exclusive photoproduction of final state at her,” (2918), H1 prelim 18-211.
- Klein and Nystrand (1999) S. Klein and J. Nystrand, Phys. Rev. C 60, 014903 (1999), arXiv:hep-ph/9902259 .
- Klein et al. (2017) S. R. Klein, J. Nystrand, J. Seger, Y. Gorbunov, and J. Butterworth, Comput. Phys. Commun. 212, 258 (2017), arXiv:1607.03838 [hep-ph] .
- Davier et al. (1973) M. Davier, I. Derado, D. Fries, F. Liu, and R. Mozley, Nuclear Physics B 58, 31 (1973).
- Aston et al. (1981b) D. Aston, M. Atkinson, R. Bailey, A. Ball, and B. Bouquet, Nuclear Physics B 189, 15 (1981b).
- Klusek-Gawenda and Tapia Takaki (2020) M. Klusek-Gawenda and J. D. Tapia Takaki, Acta Phys. Polon. B 51, 1393 (2020), arXiv:2005.13624 [hep-ph] .
- Szuba (2009) D. Szuba (H1, ZEUS), PoS EPS-HEP2009, 333 (2009).
- Frankfurt et al. (2003a) L. Frankfurt, M. Strikman, and M. Zhalov, Phys. Rev. C 67, 034901 (2003a), arXiv:hep-ph/0210303 .
- Andreev et al. (2020) V. Andreev et al. (H1), Eur. Phys. J. C 80, 1189 (2020), arXiv:2005.14471 [hep-ex] .
- Note (1) This differs from Ref. Klusek-Gawenda and Tapia Takaki (2020) which used a classical Glauber calculation.
- Note (2) Taken from the softer (coherent) exponent in Fig. 6 of Ref. H1 Collaboration (2918).
- Frankfurt et al. (1998) L. Frankfurt, V. Guzey, and M. Strikman, Phys. Rev. D 58, 094039 (1998), arXiv:hep-ph/9712339 .
- Bronstein (1977) J. M. Bronstein, High-Energy Photoproduction of the and Vector Mesons, Ph.D. thesis, Illinois U., Urbana (1977).
- Klein and Nystrand (2000) S. R. Klein and J. Nystrand, Phys. Rev. Lett. 84, 2330 (2000), arXiv:hep-ph/9909237 .
- Lomnitz and Klein (2019) M. Lomnitz and S. Klein, Phys. Rev. C 99, 015203 (2019), arXiv:1803.06420 [nucl-ex] .
- Klein and Nystrand (2004) S. R. Klein and J. Nystrand, Phys. Rev. Lett. 92, 142003 (2004), arXiv:hep-ph/0311164 .
- Frankfurt et al. (2016) L. Frankfurt, V. Guzey, M. Strikman, and M. Zhalov, Phys. Lett. B 752, 51 (2016), arXiv:1506.07150 [hep-ph] .
- (44) LHCb-PAPER-2024-042.
- (45) CMS-DP-2024-011.
- arX (2022) Letter of intent for ALICE 3: A next generation heavy-ion experiment at the LHC, Tech. Rep. (CERN, Geneva, 2022) arXiv:2211.02491 .
- Aaron et al. (2010) F. D. Aaron et al. (H1), JHEP 05, 032 (2010), arXiv:0910.5831 [hep-ex] .
- Citron et al. (2019) Z. Citron et al., CERN Yellow Rep. Monogr. 7, 1159 (2019), arXiv:1812.06772 [hep-ph] .
- Kobayashi (1973) T. Kobayashi, Prog. Theor. Phys. 49, 282 (1973).
- Fraas and Kuroda (1977) H. Fraas and M. Kuroda, Phys. Rev. D 16, 2778 (1977).
- Frankfurt et al. (2003b) L. Frankfurt, M. Strikman, and M. Zhalov, Acta Phys. Polon. B 34, 3215 (2003b), arXiv:hep-ph/0304301 .
- Chen et al. (2020) X. Chen, F.-K. Guo, C. D. Roberts, and R. Wang, Few Body Syst. 61, 43 (2020), arXiv:2008.00102 [hep-ph] .
- Agostini et al. (2021) P. Agostini et al. (LHeC, FCC-he Study Group), J. Phys. G 48, 110501 (2021), arXiv:2007.14491 [hep-ex] .