Photoproduction of $\omega$ mesons on nuclei near the production threshold

Modifications of hadron properties in a strongly interacting environment have attracted a lot of attention and have been intensively studied both theoretically and experimentally. These studies were motivated by the expectation that chiral symmetry, a fundamental symmetry of Quantum Chromodynamics (QCD) in the limit of vanishing quark masses, may be restored in a nuclear medium at high temperatures or

densities. In vacuum this symmetry is broken as visible in the low mass part of the hadronic spectrum: chiral partners - hadronic states with the same spin but opposite parity - like the $\rho$ and $a_{1}$ meson are different in mass while they should be mass degenerate if chiral symmetry were to hold. It turns out, however, (for details see LMM ) that a connection between chiral symmetry restoration and hadronic in-medium spectral functions is much more involved. QCD sum rules provide a link between the quark-gluon sector and hadronic descriptions but do not fix the properties of hadrons in the strongly interacting medium. They only provide constraints for hadronic models which are still needed for calculating the in-medium self-energies of hadrons and their spectral functions.

Experimentally this field has been addressed in heavy ion collisions and reactions with proton and photon beams. Light vector mesons are particularly suited for these investigations since - after production in a nuclear reaction - they decay in the nuclear medium with sizable probability because of their short lifetimes. Experimental results are summarized and critically evaluated in recent reviews LMM ; Hayano_Hatsuda . Almost all experiments report a softening of the spectral functions of the light vector mesons $\rho,\omega$ and $\phi$. Increases in width are observed depending on the density and temperature of the hadronic environment. Mass shifts are only reported by the KEK group Naruki ; Muto who studied $\rho,\omega$ and $\phi$ production in proton nucleus reactions at 12 GeV. The claim of a mass shift of the $\omega$ meson in photoproduction on $Nb$ Trnka has not been confirmed in a re-analysis of the data Nanova .

In the latter experiment incident photon energies covered the range from 900 - 2200 MeV. Because of the increase of the production cross section with photon energy most of the observed $\omega$ mesons are produced with photons of energy larger than 1500 MeV. For the energy range of 1500 - 2200 MeV transport calculations Gallmeister ; Muehlich_PhD have shown that the $\omega$ lineshape is rather insensitive to different in-medium modification scenarios like broadening or broadening and mass shift since most of the $\omega$ decays occur outside of the nuclear medium, even despite of a cut on the $\omega$ momentum ($p_{\omega}\leq 500$ MeV/c). Furthermore, due to the experimentally observed strong absorption of $\omega$ mesons in the nuclear medium Kotulla $\omega$ mesons produced in the interior of the nucleus are largely removed by inelastic reactions and do not reach the detector; information on possible in-medium mass shifts thereby gets lost. The limited sensitivity of the $\omega$ lineshape to in-medium modifications has been confirmed experimentally in Nanova .

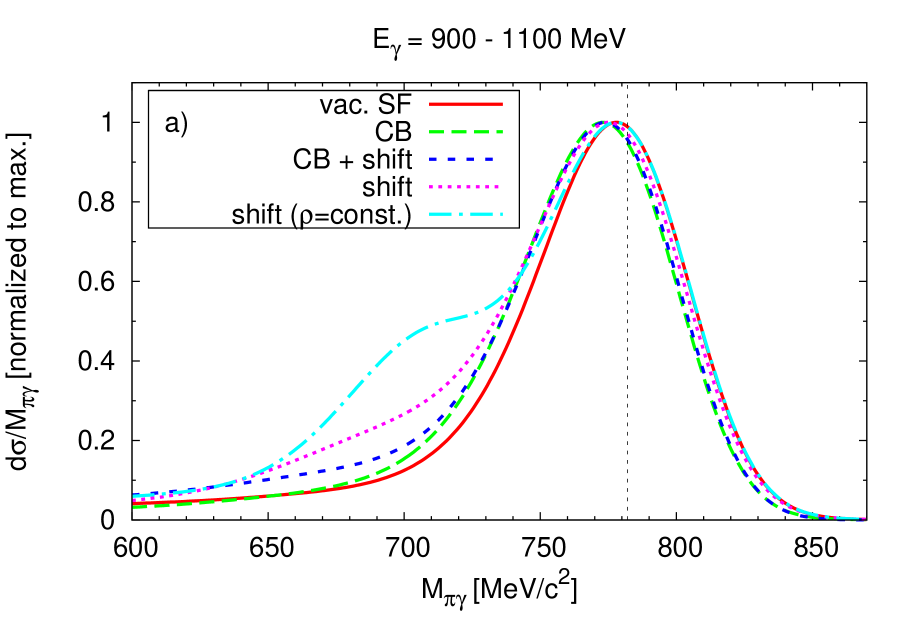
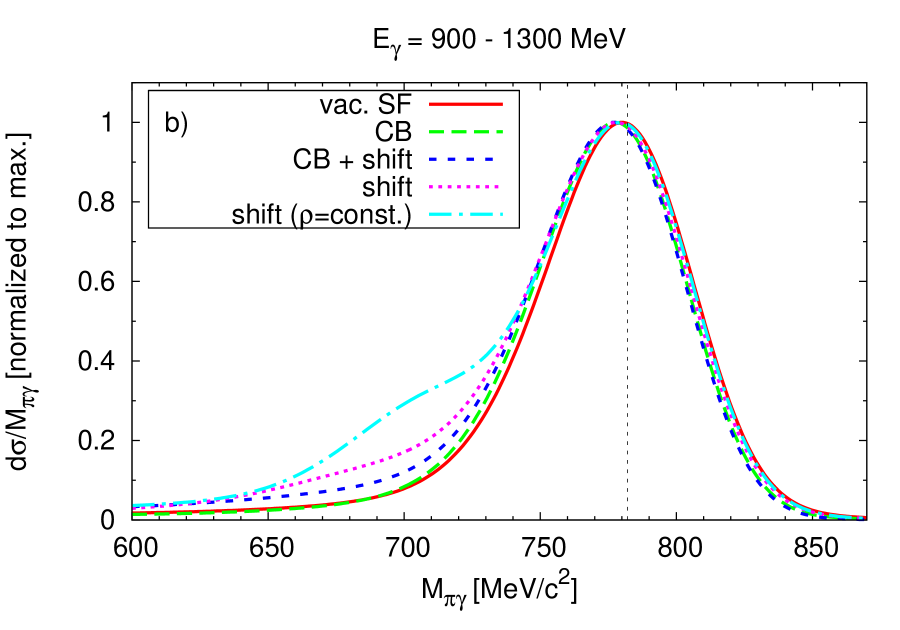
Gallmeister et al. Gallmeister argue that a search for medium effects would be much more promising for incident photon energies below or near the photoproduction threshold on a free nucleon of $E_{\gamma}^{lab}=1109$ MeV. New calculations along these lines illustrate in Fig.1 the expected sensitivity of the $\omega$ signal to various in-medium changes, such as mass shift with and without collisional broadening for two different energy ranges. It is seen that the lower-energy window indeed leads to a more pronounced – though not dramatic – sensitivity than the higher-energy one. This relatively weak sensitivity is to a large extent simply a consequence of the density profile of the nucleus that spans all densities from 0 to $\rho_{0}$ and thus smears any density-dependent signal. Assuming for the sake of the argument a density profile with a constant density of $0.6\rho_{0}$ - roughly corresponding to the average density in nuclei - and a sharp fall off at the surface the dash-dotted line in Fig.1 is obtained; here the in-medium signal is significantly stronger. For a realistic nuclear density profile contributions to the spectral function from the surface dominate, suppressing contributions from higher density regions Mosel:2010mp .

In both energy windows a tail towards lower masses is predicted for the scenario of a dropping $\omega$ mass. This tail is due to $\omega$ mesons which are produced off-shell within the nucleus. In Gallmeister ; Muehlich_PhD an even stronger enhancement in the low mass tail region was obtained. This calculation used a phenomenological method for the off-shell propagation while the present results are based on the theoretical framework provided by Leupold Leupold and Juchem and Cassing Juchem who have derived equations of motion for the testparticles that represent the spectral function in the transport simulation starting from the general Kadanoff-Baym equations KB . While the Leupold and Juchem-Cassing method has a firm theoretical basis it is nevertheless useful to remember that it relies on the assumption of adiabaticity, i.e. small gradients in space and time of all physical properties (potential, density, spectral function). Non-adiabatic effects such as those at level-crossings are not taken into account.

The experiment was performed at the ELSA electron accelerator facility Husmann_Schwille ; Hillert at the University of Bonn, using the Crystal Barrel/TAPS detector set up which provides an almost complete coverage of the full solid angle. The

features of this calorimeter system and its capability for the detection of multi-photon final states have been described in detail elsewhere Aker ; Novotny ; Gabler . Tagged photon beams of 900 - 1300 MeV were generated by bremsstrahlung and impinged in subsequent runs on $LH_{2}$, $C$ and $Nb$ targets with thicknesses of 53 mm, 20 mm and 1 mm (30 mm diameter), respectively. The running conditions were the same as described in Nanova .

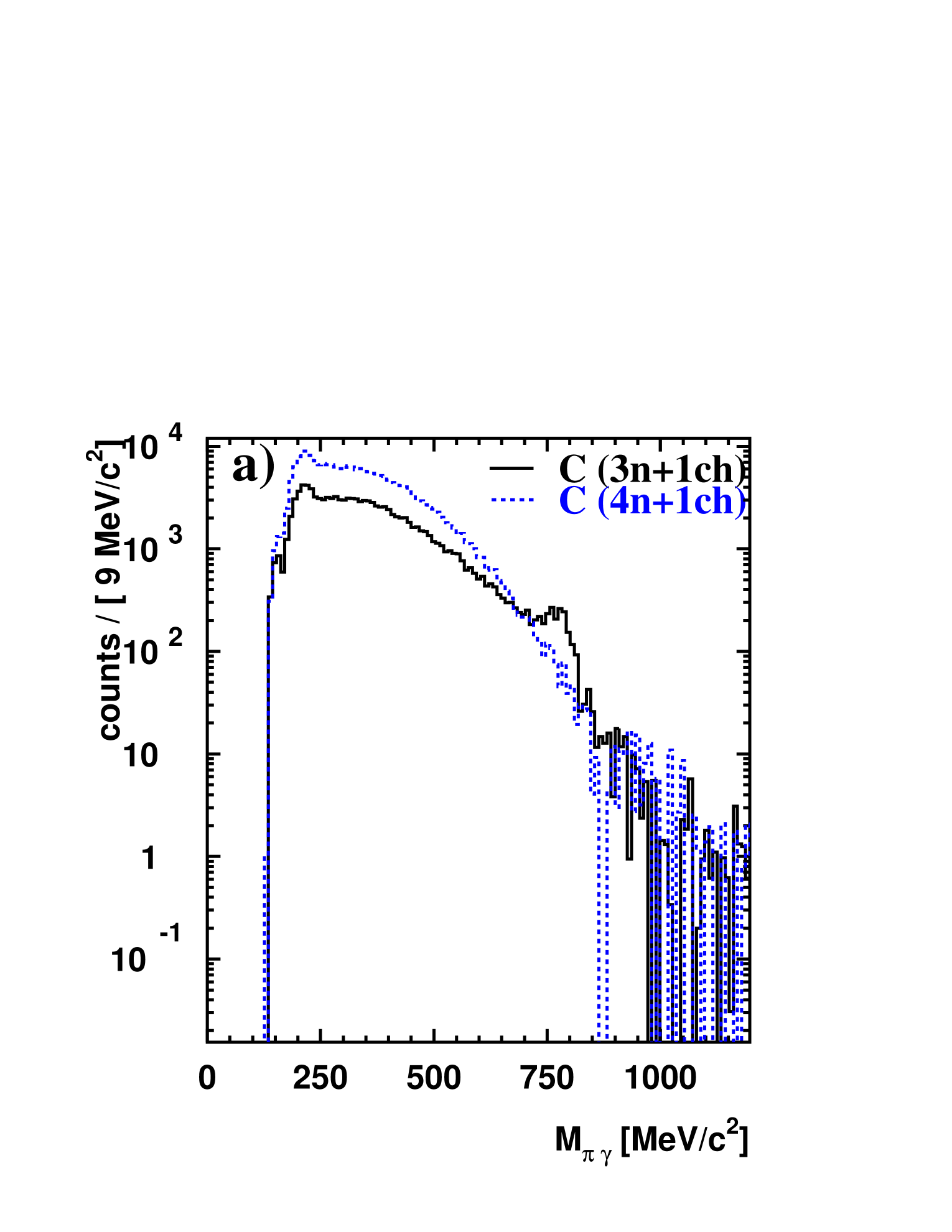
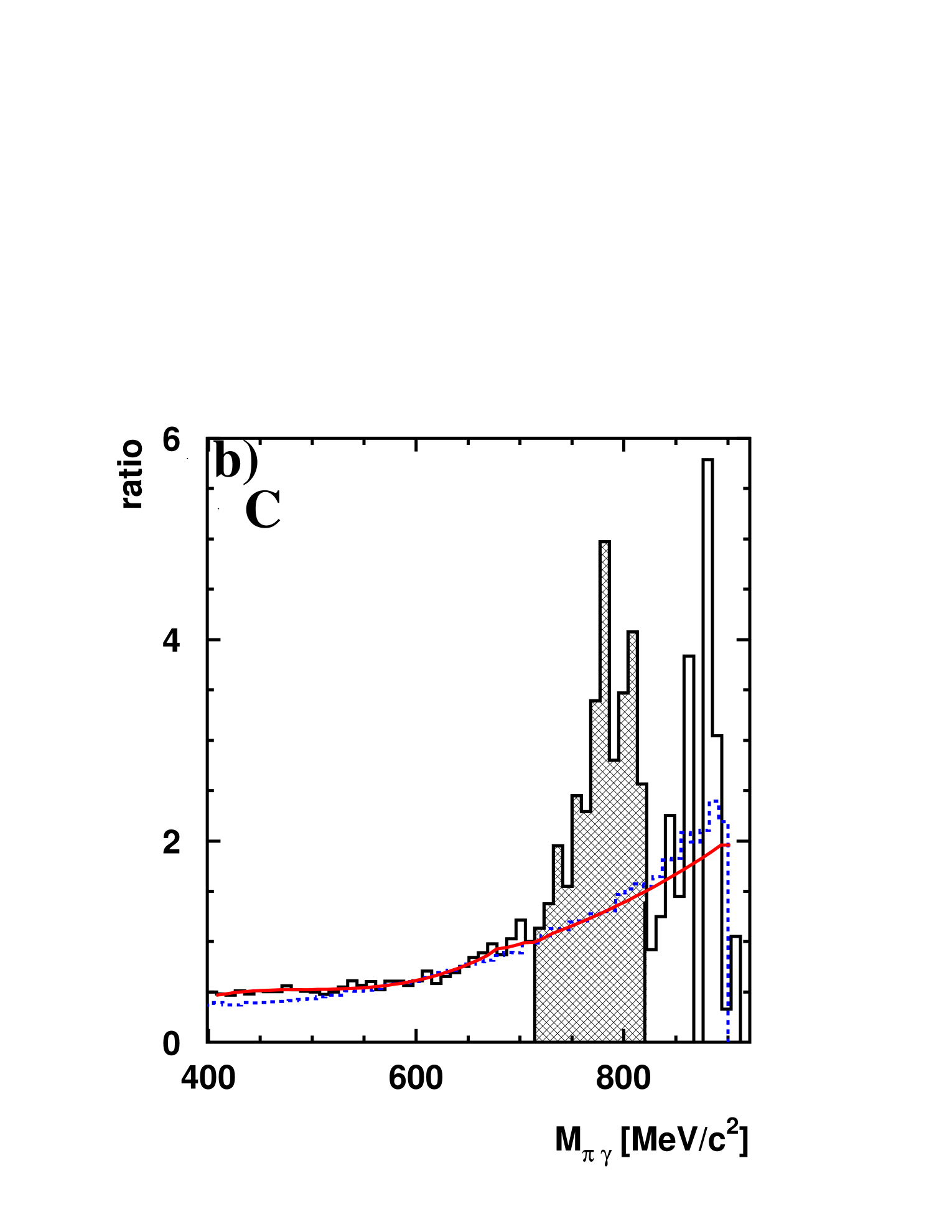
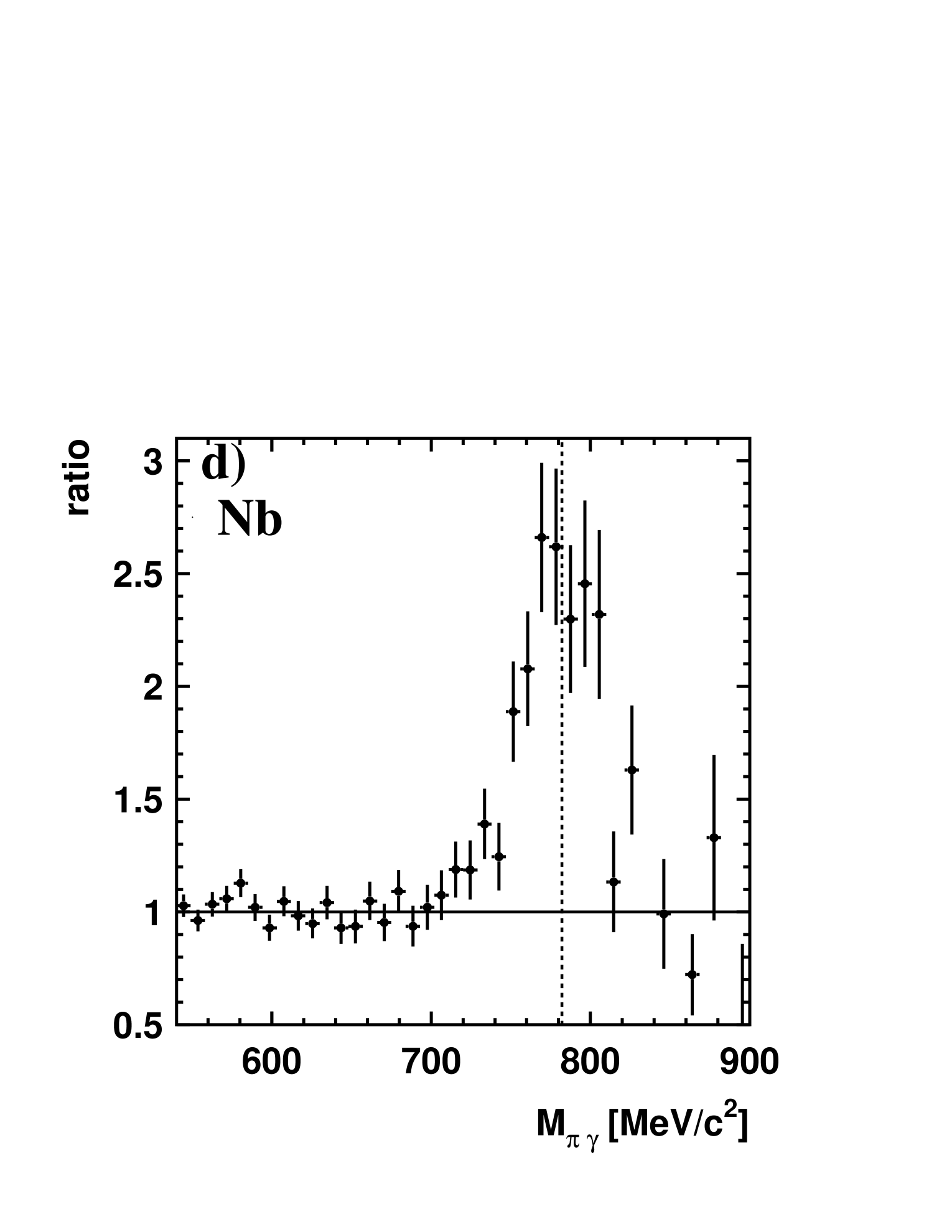
The analysis of the data follows exactly the scheme described in detail in Nanova . In fact, the data discussed here represent a subset of the data published in Nanova . $\omega$ mesons were reconstructed in the reaction $\gamma A\rightarrow(A-1)p\omega\rightarrow(A-1)p\pi^{0}\gamma\rightarrow(A-1)p\gamma\gamma\gamma$ from events with 3 photons and 1 proton in the final state. Fig. 2a shows the $\pi^{0}\gamma$ invariant mass spectrum for the carbon target for events with 1 charged and 3 neutral hits in the system. An $\omega$ signal is observed on a steeply falling background. As discussed in Nanova this background stems dominantly from $\pi^{0}\pi^{0}$ and also $\pi^{0}\eta\rightarrow 4\gamma$ final states where due to shower overlap in the detector or detector inefficiencies 1 out of the 4 photons escapes detection. Fig. 2a also shows the $\pi^{0}\gamma$ invariant mass spectrum for events with 1 charged and 4 neutral hits where 1 neutral hit has been arbitrarily omitted to simulate the background in the 3 neutral and 1 charged spectrum. The slopes of the two spectra are different, reflecting the energy dependence of the probability to register only 3 out of 4 photons relative to detecting all 4 photons. The ratio of the two spectra in Fig. 2a is given in Fig. 2b. This ratio is a smooth function of the invariant mass as verified by Monte Carlo simulations, also shown in Fig. 2b. Since no strong in-medium effects are expected for a light nucleus like carbon this ratio can be applied to correct the $\pi^{0}\gamma$ background spectrum derived from events with 1 charged and 4 neutral hits measured for the $Nb$ target. Fig. 2c shows the $\pi^{0}\gamma$ invariant mass spectrum for $Nb$ together with this background distribution after applying this correction. The normalization of the background spectrum is done by requesting the same number of events in the mass range from 400 - 900 MeV, excluding the counts in the $\omega$ peak which account for only 2 $\%$ of the total yield in this mass range. It is important to note that this determination of the background in magnitude and shape does not pay any attention to the $\omega$ signal region. The background in the (3 neutral +1 charged) signal spectrum is well reproduced by the corrected (4 neutral + 1 charged) spectrum. This is demonstrated by the ratio of the two spectra shown in Fig. 2d. In the mass range from 400 - 700 MeV the average deviation from unity is 5 $\%$. This uncertainty determines the systematic error in the background subtraction.

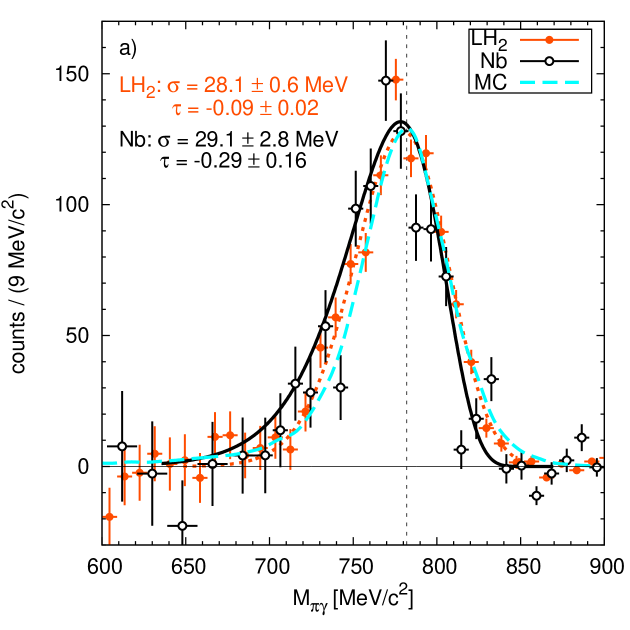
After subtraction of the background spectrum from the $\pi^{0}\gamma$ signal spectrum the $\omega$ lineshape shown in Fig. 3a is obtained for the $Nb$ target. The experimental distribution has been fitted using the Novosibirsk function Novosibirsk :

where

Here $A$ is the amplitude of the signal, $x_{0}$ is the peak position, $\sigma$ is FWHM/2.35 and $\tau$ is the asymmetry parameter. This function takes into account the tail in the region of lower invariant masses resulting from the energy response of the calorimeters. The fit in the mass range 700 to 820 MeV is compared with the $\omega$ signal measured on the $LH_{2}$ target and with a Monte Carlo simulation of the $\omega$ signal in Fig. 3a. It should be noted that the 53 mm length of the $LH_{2}$ target leads to an increase in $\omega$-signal width by less than 10 $\%$. The agreement between the $\omega$ signal on the $LH_{2}$ target with the Monte Carlo simulation demonstrates that the detector response is under control. The fit parameters are $\sigma$ = (29.1 $\pm$ 2.8) MeV, $\tau$ = -0.29 $\pm$ 0.16 for $Nb$ and $\sigma$ = (28.1 $\pm$ 0.6) MeV, $\tau$ = -0.09 $\pm$ 0.02 for $LH_{2}$, respectively. The fit of the data with the function of eqs.(1),(2) yields a $\chi^{2}$/DoF = 18.95/12 with a $\chi^{2}$- probability of 9.0$\%$ while a fit of the data with the $\omega$ line shape measured on the $LH_{2}$ target gives a $\chi^{2}$/DoF = 32.8/15, corresponding to a $\chi^{2}$-probability of 0.5$\%$. Nevertheless, in view of the systematic and statistical uncertainties no significant deviation from the reference signals is claimed. Higher statistics will be needed to draw any conclusion. Corresponding data have been taken at MAMI-C using the Crystal Ball/TAPS set up. The analysis is ongoing.

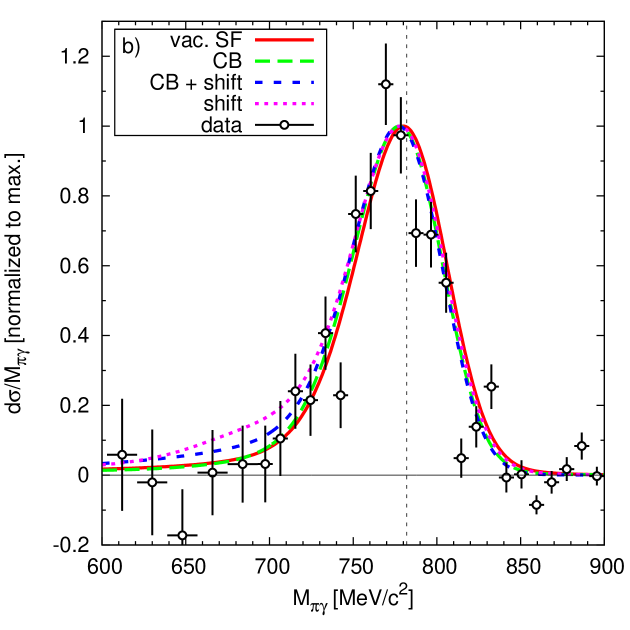
In Fig. 3b the measured $\omega$ signal is compared to predictions of transport calculations using the GiBUU model GiBUU for the same scenarios as in Fig. 1. While all the curves seem to underestimate the data slightly on the low mass side of the $\omega$ peak, the experimental data obviously do not allow to distinguish between the various theoretical scenarios, in contrast to initial expectations.

The photoproduction of $\omega$ mesons on $LH_{2}$, $C$ and $Nb$ targets has been measured for incident photon energies from 900 - 1300 MeV, i.e. near the photoproduction threshold on a free nucleon of $E_{\gamma}^{lab}$ = 1109 MeV. The experimentally observed $\omega$ signal does not allow to distinguish between various in-medium scenarios which - also near threshold - lead all to only a weak tail at low invariant masses. Access to the in-medium spectral function of vector mesons is thus very limited, mainly due to the dependence of the in-medium properties such as mass and width on the nuclear density Mosel:2010mp ; Lehr and the inherent density-smearing caused by the density profile of nuclei. On the other hand, transparency measurements Kaskulov ; Muehlich can give at least access to the imaginary part of the in-medium self energy of the hadron. Another promising tool could be the measurement of excitation functions Om-ex . Such experiments are presently being analyzed.

We thank the scientific and technical staff at ELSA and the collaborating institutions for their important contribution to the success of the experiment. We gratefully acknowledge detailed discussions with S. Leupold and P. Mühlich. This work was supported financially by the Deutsche Forschungs Gemeinschaft through SFB/TR16, by the Schweizerischer Nationalfond and by the Stichting voor Fundamenteel Onderzoek der Materie (FOM) and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO).