Planar graphs having no cycle of length $4$ , $6$ or $8$ are DP-3-colorable

Ligang Jin¹¹1School of Mathematical Sciences, Zhejiang Normal University, Yingbin Road 688, 321004 Jinhua, China; ligang.jin@zjnu.cn (Ligang Jin), xdzhu@zjnu.edu.cn (Xuding Zhu) , Yingli Kang²²2Department of Mathematics, Jinhua University of Vocational Technology, Western Haitang Road 888, 321017 Jinhua, China; ylk8mandy@126.com (Yingli Kang) , Xuding Zhu¹¹footnotemark: 1

Abstract

The concept of DP-coloring of graphs was introduced by Dvořák and Postle, and was used to prove that planar graphs without cycles of length from $4$ to $8$ are $3$ -choosable. In the same paper, they proposed a more natural and stronger claim that such graphs are DP- $3$ -colorable. This paper confirms that claim by proving a stronger result that planar graphs having no cycle of length $4$ , $6$ or $8$ are DP-3-colorable.

Keywords: DP-coloring; Erdős problem; $S_{3}$ -signed graphs; reducible configurations; discharging

1 Introduction

Steinberg [7] conjectured in 1976 that every planar graph without cycles of length 4 or 5 is 3-colorable. This conjecture received considerable attention and was finally disproved in 2017 by Cohen-Addad, Hebdige, Král, Li, and Salgado [4].

Motivated by Steinberg’s conjecture, Erdős asked whether there exists a constant $k$ such that every planar graph without cycles of length from 4 to $k$ is 3-colorable? If so, what is the smallest constant $k$ ? It was proved by Abbott and Zhou [1] that such an integer exists and $k\leq 11$ . The upper bound on the smallest constant $k$ was improved in a sequence of papers, and the current known best upper bound is $k\leq 7$ , obtained by Borodin, Glebov, Raspaud, and Salavatipour [3]. It remains open whether $k=6$ or $k=7$ .

Erdős’ problem has a natural list coloring version, that has also been studied extensively in the literature. Abbott and Zhou [1] actually showed that planar graphs without cycles of length $4$ to $11$ are $3$ -choosable, and the question is to find the smallest integer $k^{\prime}$ such that planar graphs without cycles of length from $4$ to $k^{\prime}$ are 3-choosable. It was proved by Voigt [8] that $k^{\prime}\geq 6$ and the following result of Dvořák and Postle gives the current known best upper bound for $k^{\prime}$ .

Theorem 1.1 ([5]).

Every planar graph without cycles of length from 4 to 8 is 3-choosable.

Theorem 1.1 answers a question posed by Borodin [2] in 1996. Nevertheless, it turns out that the more important impact of the work of Dvořák and Postle is the concept of DP-coloring introduced in [5], which has attracted considerable attention and has motivated a lot of research.

Definition 1.2.

A cover of a graph $G$ is a pair $(L,M)$ , where $L=\{L(v)\colon v\in V(G)\}$ is a family of disjoint sets, and $M=\{M_{e}\colon e\in E(G)\}$ , where for each edge $e=uv$ , $M_{e}$ is a matching between $L(u)$ and $L(v)$ . For $f\in\mathbb{N}^{G}$ , we say $(L,M)$ is an $f$ -cover of $G$ if $|L(v)|\geq f(v)$ for each vertex $v\in V(G)$ .

Definition 1.3.

Given a cover $(L,M)$ of a graph $G$ , an $(L,M)$ -coloring of $G$ is a mapping $\phi\colon V(G)\to\bigcup_{v\in V(G)}L(v)$ such that for each vertex $v\in V(G)$ , $\phi(v)\in L(v)$ , and for each edge $e=uv\in E(G)$ , $\phi(u)\phi(v)\notin E(M_{e})$ . We say $G$ is $(L,M)$ -colorable if it has an $(L,M)$ -coloring. We say $G$ is DP- $f$ -colorable, where $f\in\mathbb{N}^{G}$ , if for every $f$ -cover $(L,M)$ , $G$ has an $(L,M)$ -coloring. The DP-chromatic number of $G$ is defined as

\chi_{DP}(G)=\min\{k\colon G\text{ is DP-$k$-colorable}\}.

Given an $f$ -list assignment $L^{\prime}$ of a graph $G$ , let $(L,M)$ be the $f$ -cover of $G$ , where $L(v)=\{(i,v)\colon i\in L^{\prime}(v)\}$ and $M=\{M_{uv}\colon uv\in E(G)\}$ , where for each edge $uv$ of $G$ ,

M_{uv}=\{\{(i,u),(i,v)\}\colon i\in L^{\prime}(u)\cap L^{\prime}(v)\}.

It is obvious that $G$ is $L^{\prime}$ -colorable if and only if $G$ is $(L,M)$ -colorable. Therefore if $G$ is DP- $f$ -colorable, then it is $f$ -choosable, and hence $ch(G)\leq\chi_{DP}(G)$ .

The advantage of transforming a list coloring problem to a DP-coloring problem is that the information of the lists are encoded in the matchings $M_{e}$ for edges $e\in E(G)$ . There are tools one can use in the study of DP-coloring of graphs that are not applicable in the setting of list coloring. For example, one can identify non-adjacent vertices in the study of DP-coloring, that is not applicable in the study of list coloring. It is by using such tools that Dvořák and Postle were able to prove that planar graphs without cycles of length from $4$ to $8$ are 3-choosable.

As DP-3-colorable graphs are 3-choosable, and DP-coloring technique is used to prove that planar graphs without cycles of length from 4 to 8 are 3-choosable, it seems more natural to prove that these planar graphs are DP-3-colorable. However, in the proof in [5], the family of matchings $M_{e}$ are restricted to be consistent on closed walks of length 3. This is enough to conclude that the graphs in concern are 3-choosable, but not enough to conclude that they are DP-3-colorable. It was proved in [6] that every planar graph without cycles of length from $\{4,5,6,9\}$ is DP-3-colorable. The problem whether all planar graphs without cycles of length from 4 to 8 are DP-3-colorable is proposed in [5] and remains open.

In this paper, we solve this problem and prove the following result.

Theorem 1.4.

Every planar graph having no cycle of length 4, 6 or 8 is DP-3-colorable.

2 $S_{3}$ -signed graphs and configurations

We denote by $\mathcal{G}$ the family of connected plane graphs having no cycle of length $4$ , $6$ or $8$ . We shall prove the following result that implies Theorem 1.4.

Theorem 2.1.

Assume $G\in\mathcal{G}$ with infinite face $f_{0}$ , and $(L,M)$ is a 3-cover of $G$ . If the boundary of $f_{0}$ has length at most 12, then every $(L,M)$ -3-coloring of $G[V(f_{0})]$ extends to an $(L,M)$ -3-coloring of $G$ .

We may assume that $L(v)=\{1,2,3\}\times\{v\}$ for each vertex $v$ , and assume that for each edge $uv$ of $G$ , $M_{uv}$ is a perfect matching between $L(u)$ and $L(v)$ . For each edge $uv$ , the matching $M_{uv}$ can be represented by a permutation $\sigma_{(u,v)}$ of $\{1,2,3\}$ , defined as $\sigma_{(u,v)}(i)=j$ if $(i,u)(j,v)\in M_{uv}$ . Instead of a family $M=\{M_{uv}\colon uv\in E(G)\}$ of matchings, we have a family $\sigma=\{\sigma_{(u,v)}\colon uv\in E(G)\}$ of permutations of $\{1,2,3\}$ , satisfying $\sigma_{(v,u)}=\sigma_{(u,v)}^{-1}$ . An $(L,M)$ -coloring of $G$ is equivalent to a mapping $\phi\colon V(G)\to\{1,2,3\}$ such that for each edge $uv$ , $\phi(v)\neq\sigma_{(u,v)}(\phi(u))$ . We call the pair $(G,\sigma)$ an $S_{3}$ -signed graph (where $\sigma_{(u,v)}$ is viewed as a sign of the arc $(u,v)$ ), and call the mapping $\phi$ a proper 3-coloring of $(G,\sigma)$ .

The following theorem is an equivalent formulation of Theorem 2.1.

Theorem 2.2.

Let $(G,\sigma)$ be an $S_{3}$ -signed graph with $G\in\mathcal{G}$ . If the boundary of the infinite face $f_{0}$ has length at most 12, then every 3-coloring of $(G[V(f_{0})],\sigma)$ extends to a 3-coloring of $(G,\sigma)$ .

The proof of Theorem 2.2 is by induction. Assume $(G,\sigma)$ is a counterexample, with $|V(G)|$ minimum. We first prove that a family of configurations are reducible, i.e., none of them can be contained in $G$ . In the next section, by using discharging method, we derive a contradiction.

In the remainder of the paper, we consider proper 3-colorings of $S_{3}$ -signed graphs $(G,\sigma)$ for $G\in\mathcal{G}$ (which is equivalent to DP-3-colorings of graphs $G\in\mathcal{G}$ ). For convenience, we may denote an $S_{3}$ -signed graphs $(G,\sigma)$ by $G$ . The signs $\sigma(e)$ of edges in $G$ are specified when needed.

By a switching at a vertex $v$ , we mean choose a permutation $\tau$ of $\{1,2,3\}$ , and for each edge $uv$ incident to $v$ , replace $\sigma_{(u,v)}$ with $\tau\circ\sigma_{(u,v)}$ (and hence replace $\sigma_{(v,u)}$ with $\sigma_{(v,u)}\circ\tau^{-1}$ ). Switching at a vertex $v$ just changes the names of colors for $v$ , and does not change the colorability of $G$ .

An edge $uv$ is called straight if $\sigma_{(u,v)}=id$ , where $id$ is the identity permutation.

Remark 2.3.

For any set $E^{\prime}$ of edges that induces an acyclic subgraph of $G$ , by applying some switchings, if needed, we may assume that all edges in $E^{\prime}$ are straight.

A cycle $C$ is called positive if there exist a sequence of switchings that make all edges in $C$ straight. Otherwise, $C$ is negative.

A vertex on the boundary of $f_{0}$ is an external vertex, and other vertices are internal. Denote by $|P|$ the length of a path $P$ (which is the number of edges of $P$ ), $|C|$ the length of a cycle $C$ , and $d(f)$ the size of a face $f$ . A $k$ -vertex (resp., $k^{+}$ -vertex and $k^{-}$ -vertex) is a vertex $v$ with $d(v)=k$ (resp., $d(v)\geq k$ and $d(v)\leq k$ ). The notations of $k$ -path, $k$ -cycle, $k$ -face etc. are defined similarly. A $k$ -cycle with vertices $v_{1},\ldots,v_{k}$ in cyclic order is denoted by $[v_{1}\ldots v_{k}]$ . Let $d_{1},d_{2},d_{3}$ be three integers with $3\leq d_{1}\leq d_{2}\leq d_{3}$ . A $(d_{1},d_{2},d_{3})$ -face is a 3-face $[v_{1}v_{2}v_{3}]$ such that $v_{i}$ is an internal $d_{i}$ -vertex for $i\in\{1,2,3\}$ .

•

A bad vertex is a vertex incident with a positive $(3,3,3)$ -face.
•

A $3_{\Delta}$ -vertex is an internal 3-vertex incident with a 3-face.
•

A $4_{\bowtie}$ -vertex is an internal 4-vertex incident with two non-adjacent 3-faces.
•

A $C$ -vertex is a vertex which is neither a 2-vertex nor a $3_{\Delta}$ -vertex nor a $4_{\bowtie}$ -vertex.

Assume $u$ is a $3_{\Delta}$ -vertex on a 3-face $f$ . The neighbor of $u$ not on $f$ is called the outer neighbor of $u$ (also of $f$ ). We say $u$ is

1.

a $3_{\Delta^{+}}$ -vertex if $f$ is positive and contains at least two $3_{\Delta}$ -vertices;
2.

a $3_{\Delta^{-}}$ -vertex if $f$ is negative and contains at least two $3_{\Delta}$ -vertices;
3.

a $3_{\Delta^{\circ}}$ -vertex if $u$ is the only $3_{\Delta}$ -vertex on $f$ .

A $3_{\Delta^{\star}}$ -vertex is a $3_{\Delta^{\circ}}$ -vertex whose outer neighbor is not a bad vertex.

Two vertices $u$ and $v$ are $\bowtie$ -connected if there exists a $u$ - $v$ -path whose interior vertices are all $4_{\bowtie}$ -vertices.

Let $f_{1},\dots,f_{k}$ be internal 3-faces. The union $S=\bigcup_{i=1}^{k}f_{i}$ is called a snowflake if the following hold:

(1)

For each $4_{\bowtie}$ -vertex $w$ of $S$ , both 3-faces containing $w$ belong to $S$ ;
(2)

Any two nonadjacent vertices of $S$ are $\bowtie$ -connected.

Note that two snowflakes of $G$ may share vertices but they are edge-disjoint. For each snowflake $S$ , denote by $3_{\Delta^{+}}(S)$ the set of $3_{\Delta^{+}}$ -vertices of $S$ and similarly, we define $3_{\Delta^{-}}(S)$ , $3_{\Delta^{\circ}}(S)$ , $3_{\Delta^{\star}}(S)$ , $3_{\Delta}(S)$ , $4_{\bowtie}(S)$ , and $C(S)$ . Let $T(S)$ be the set of 3-faces of $S$ , and for $u\in C(S)$ , let $t(S,u)$ denote the number of 3-faces of $S$ containing $u$ . Let

•

$C_{1}(S)=\{v\in C:v\text{ is an external $3$-vertex or an external $4$-vertex incident with two}\\ \text{non-adjacent 3-faces}\}.$
•

$C_{2}(S)=C(S)\setminus C_{1}(S)$ .
•

For $i\in\{1,2\}$ , $t_{i}(S)=\sum_{u\in C_{i}(S)}t(S,u)$ .

Definition 2.4.

A configuration is a 4-tuple $\mathcal{H}=(H,\tau,\theta,Z)$ such that $(H,\tau)$ is an $S_{3}$ -signed plane graph, $\theta$ is a mapping $V(H)\to\mathbb{N}\cup\{\star\}$ , and $Z$ is a subset of $V(H)$ . We say an $S_{3}$ -signed plane graph $(G,\sigma)$ contains $(H,\tau,\theta,Z)$ as a configuration if $(H,\tau)$ is an induced $S_{3}$ -signed subgraph (with the same plane embedding), vertices in $Z$ are internal vertices, and for $v\in V(H)$ , $d_{G}(v)=\theta(v)$ if $\theta(v)$ is an integer. If $\theta(v)=\star$ , then there is no restriction on $d_{G}(v)$ .

A configuration $(H,\tau,\theta,Z)$ is called reducible if any minimal counterexample $(G,\sigma)$ does not contain configuration $(H,\tau,\theta,Z)$ .

Note that vertices of $H$ not in $Z$ can be either internal or external vertices.

If $(G,\sigma)$ contains a configuration $(H,\tau,\theta,Z)$ , we say $(G,\sigma)$ is the host signed graph of $(H,\tau,\theta,Z)$ . A vertex $v$ in a configuration $(H,\tau,\theta,Z)$ is called a $k$ -vertex if $\theta(v)=k$ , i.e., $v$ has degree $k$ in the host graph.

We shall often represent a configuration by a figure, and the value $\theta(v)$ and the set $Z$ is indicated by the “shape” of the vertex $v$ : a solid triangle, a solid square, and a solid circle stands for an internal 3-vertex, an internal 4-vertex, and an arbitrary vertex, respectively. There will be no other type of vertices. The signs $\tau$ on a set of acyclic edges is irrelevant, as by switching we may assume all the edges are straight. The sign of a cycle (usually a triangle) is labelled by P, if all edges can be made straight by a switching, or N otherwise. An unlabelled triangle means that it can be either positive or negative. So the signature $\tau$ is omitted and only some triangles are labelled by P or N. The embedding of a configuration is also important (it matters if a path is on the boundary of a face or not), which will be indicated in the figure.

If the mappings $\tau$ , $\theta$ and $Z$ are clear from the context, we simply call $H$ a configuration.

Definition 2.5.

For $k\geq 1$ ,

(1)

$I_{k}$ is the configuration consisting of $k$ negative triangles $T_{i}=[u_{i-1}u_{i}w_{i}]$ ( $i=1,2,\ldots,k$ ), where $w_{1},w_{2},\ldots,w_{k},u_{k}$ are internal 3-vertices and $u_{1},u_{2},\ldots,u_{k-1}$ are internal 4-vertices. The vertex $u_{0}$ is an arbitrary vertex, and is called the port of $I_{k}$ .
(2)

$J_{k}$ is the configuration consisting of $2k$ triangles $T_{i}=[u_{i-1}u_{i}w_{i}]$ and $T^{\prime}_{i}=[x_{i}y_{i}z_{i}]$ ( $i=1,2,\ldots,k$ ), where each $T^{\prime}_{i}$ is positive, $w_{i}$ is adjacent to $z_{i}$ , vertices $w_{i},x_{i},y_{i},z_{i}$ are internal 3-vertices, and $u_{1},u_{2},\ldots,u_{k-1}$ are internal 4-vertices. The vertices $u_{0}$ and $u_{k}$ are arbitrary vertices, and are called the two ports of $J_{k}$ .

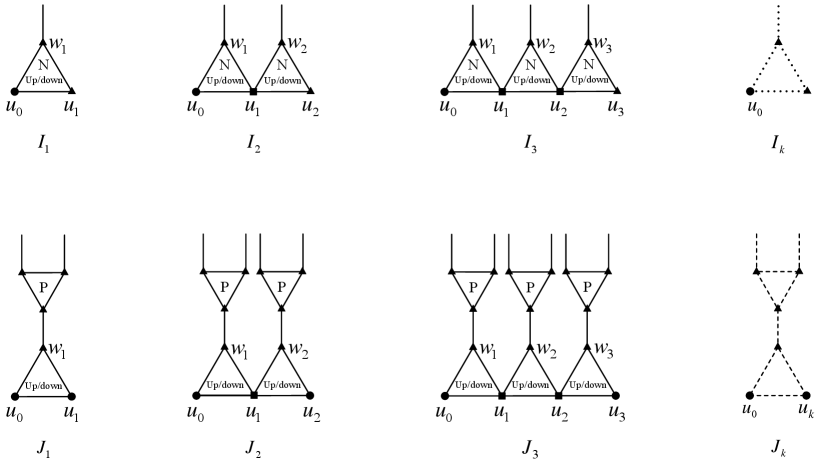
Refer to caption — Figure 1: Configurations $I_{k}$ and $J_{k}$ . “Up/down” indicates that in the plane, the triangle may locate in either side of the path $u_{0}u_{1}\ldots u_{k}$ .

Figure 1 are Configurations $I_{1},I_{2},I_{3},J_{1},J_{2},J_{3}$ and drawings of general $I_{k},J_{k}$ .

Assume $(H,\tau,\theta,Z)$ is a configuration and $v\in V(H)$ with $\theta(v)=d_{H}(v)+1$ (i.e., $v$ has one neighbor in $V(G)\setminus V(H)$ ). Let $H^{\prime}$ be obtained from the disjoint union of $H$ and $I_{k}$ by identifying $v$ with the port of $I_{k}$ , and let $\theta^{\prime}(v)=\theta(v)+1=d_{H^{\prime}}(v)$ . For other vertices $u$ of $H^{\prime}$ and edges $e$ , $\tau^{\prime}(e)$ and $\theta^{\prime}(u)$ and status of $u$ are inherited from $H$ or $I_{k}$ . Then the configuration $(H^{\prime},\tau^{\prime},\theta^{\prime},Z^{\prime})$ is called the $I_{k}$ -extension of $H$ at $v$ , and is denoted as $H_{v,I_{k}}$ .

Assume $(H,\tau,\theta,Z)$ is a configuration and $v\in V(H)$ with $\theta(v)=d_{H}(v)=4$ and $v$ is incident with two non-adjacent triangles, say $T_{1}$ and $T_{2}$ . Let $H^{\prime}$ be obtained from the disjoint union of $H$ and $J_{k}$ by splitting $v$ into two vertices $v_{1}$ and $v_{2}$ so that each $v_{i}$ is incident with $T_{i}$ and identifying each $v_{i}$ with a port of $J_{k}$ , and let $\theta^{\prime}(v_{1})=\theta^{\prime}(v_{2})=4$ . For other vertices $u$ of $H^{\prime}$ and edges $e$ , $\tau^{\prime}(e)$ and $\theta^{\prime}(u)$ and status of $u$ are inherited from $H$ or $J_{k}$ . Then the configuration $(H^{\prime},\tau^{\prime},\theta^{\prime},Z^{\prime})$ is called the $J_{k}$ -extension of $H$ at $v$ , and is denoted as $H_{v,J_{k}}$ .

Definition 2.6.

Assume $f=[v_{1}v_{2}\ldots v_{9}]$ is a 9-face of $G$ , and $x$ is a vertex of $f$ . We say $f$ is a nice $9$ -face and $x$ is a nice vertex of $f$ if one of the following holds:

(1)

$v_{2},v_{3},v_{4},v_{5}$ are $4_{\bowtie}$ -vertices, $v_{1}$ and $v_{6}$ are $3_{\Delta}$ -vertices, and either $x=v_{8}$ is a $5^{+}$ -vertex or $x\in\{v_{7},v_{9}\}$ is a $4^{+}$ -vertex or an external 3-vertex;
(2)

$v_{4}$ is a $4_{\bowtie}$ -vertex, $v_{3}$ and $v_{5}$ are $3_{\Delta}$ -vertices, $v_{1},v_{2},v_{6},v_{7}$ are bad vertices, and $x\in\{v_{8},v_{9}\}$ is a $4^{+}$ -vertex or an external 3-vertex;
(3)

$v_{4}$ and $v_{5}$ are $4_{\bowtie}$ -vertices, $v_{3}$ and $v_{6}$ are $3_{\Delta}$ -vertices, $v_{1},v_{2},v_{7},v_{8}$ are bad vertices, and $x=v_{9}$ is a $4^{+}$ -vertex or an external 3-vertex.

The snowflake containing $v_{4}$ is called the related snowflake of $f$ . We further call $x$ a 2-nice vertex of $f$ if $f$ satisfies (1) above, a 1-nice vertex of $f$ otherwise.

It is easy to see that a nice 9-face is related to precisely one snowflake.

Consider a plane graph $G$ . For $Y\subseteq V(G)$ or $Y\subseteq E(G)$ , denote by $G[Y]$ the subgraph of $G$ induced by $Y$ . For a subgraph $H$ of $G$ , denote by $N_{G}(H)$ (shortly, $N(H)$ ) the set of vertices of $G-V(H)$ which has a neighbor in $H$ . For a cycle $C$ , ${\rm int}(C)$ and ${\rm ext}(C)$ are the set of vertices in the interior and exterior of $C$ , respectively. Denote by ${\rm int}[C]$ (resp., ${\rm ext}[C]$ ) the subgraph of $G$ induced by ${\rm int}(C)\cup V(C)$ (resp., ${\rm ext}(C)\cup V(C)$ ). A cycle $C$ is separating if both ${\rm int}(C)$ and ${\rm ext}(C)$ are nonempty. A path $P$ and a vertex $v$ are adjacent if $v\notin V(P)$ and $v$ is adjacent to a vertex of $P$ . A path on $k$ 2-vertices is called a $k$ -string if it is adjacent to no 2-vertices. Note that if a vertex $v$ is adjacent to a string, then it is adjacent to an end vertex of the string, as vertices in a string are 2-vertices in $G$ .

3 The proof of Theorem 2.2

To see that Theorem 1.4 follows from Theorem 2.2, take any $S_{3}$ -signed graph $(G,\sigma)$ . If $G$ has no triangles, then it has girth at least 5 and is known to be DP- $3$ -colorable [5]. We may next assume that $G$ has a triangle $T$ . Any 3-coloring of $(T,\sigma)$ can be extended to both $({\rm ext}[T],\sigma)$ and $({\rm int}[T],\sigma)$ by Theorem 2.2, which together result in a 3-coloring of $(G,\sigma)$ .

The remainder of this paper is devoted to the proof of Theorem 2.2.

Assume to the contrary that Theorem 2.2 is false. Let $(G,\sigma)$ be a counterexample with minimum $|V(G)|$ . Thus the infinite face $f_{0}$ is a $12^{-}$ -face, and there exists a 3-coloring $\phi_{0}$ of $(G[V(f_{0})],\sigma)$ that cannot extend to $(G,\sigma)$ .

Denote by $D$ the boundary of $f_{0}$ . By the minimality of $(G,\sigma)$ , $D$ has no chords.

3.1 Reducible configurations

Lemma 3.1.

$G$ has no separating $12^{-}$ -cycles.

Proof.

If $C$ is a separating $12^{-}$ -cycle of $G$ , then by the minimality of $(G,\sigma)$ , we can extend $\phi_{0}$ to $({\rm ext}[C],\sigma)$ and then extend the resulting coloring of $C$ to $({\rm int}[C],\sigma)$ . ∎

Lemma 3.2.

$G$ is 2-connected. Consequently, the boundary of each face is a cycle.

Proof.

Otherwise, we may assume that $G$ has a block $B$ and a cut vertex $v\in V(B)$ with $V(D)\cap V(B-v)=\emptyset$ . Let $H=G-(B-v).$ By the minimality of $(G,\sigma)$ , we can extend $\phi_{0}$ to $(H,\sigma)$ . Let $C$ be a cycle of $B$ of minimum length that contains $v$ . If $|C|\leq 12$ , then $C$ is a facial cycle, since $C$ has no chords by its minimality and $C$ is not separating by Lemma 3.1. We can extend the coloring of $v$ to a 3-coloring of $(C,\sigma)$ and further to $(B,\sigma)$ by the minimality of $(G,\sigma)$ . If $|C|>12$ , then insert an edge with an arbitrary sign between any two consecutive neighbors (say $x$ and $y$ ) of $v$ in $B$ . Note that $B+xy\in\mathcal{G}$ . We can extend the coloring of $v$ to a 3-coloring of $([vxy],\sigma)$ and further to $(B+xy,\sigma)$ . In either case, the resulting coloring of $(G,\sigma)$ is an extension of $\phi_{0}$ , a contradiction. ∎

Since $G\in\mathcal{G}$ , the following corollary is a consequence of Lemmas 3.1 and 3.2.

Corollary 3.3.

Every $k$ -cycle of $G$ with $k\in\{3,5,7,9\}$ is facial.

Lemma 3.4.

Every internal vertex of $G$ has degree at least 3.

Proof.

If $v$ is an internal vertex with $d(v)\leq 2$ , then we can extend $\phi_{0}$ to $(G-v,\sigma)$ , and then extend to $(G,\sigma)$ by coloring $v$ with a color not matched to the colors of its two neighbors. ∎

Lemma 3.5.

If $f\neq f_{0}$ is a $k$ -face of $G$ and $P$ is a $t$ -string contained in the boundary of $f$ , then $t<\lfloor\frac{k-1}{2}\rfloor$ .

Proof.

By Lemma 3.4, $P$ is contained in the boundary of $f_{0}$ . Assume $t\geq\lfloor\frac{k-1}{2}\rfloor$ . Let $G^{\prime}=G-V(P)$ and $f_{0}^{\prime}$ be the infinite face of $G^{\prime}$ . Then $d(f_{0}^{\prime})=d(f_{0})+k-2(t+1)\leq d(f_{0})$ . We can first extend $\phi_{0}$ to $(f_{0}\cup f_{0}^{\prime},\sigma)$ and then extend the coloring of $f^{\prime}_{0}$ to $(G^{\prime},\sigma)$ . ∎

Lemma 3.6.

Let $[uvw]$ be a 3-face such that $d(u)=d(v)=3$ . We may assume that edges of $u^{\prime}uwvv^{\prime}$ are all straight, where $u^{\prime}$ and $v^{\prime}$ are the other neighbor of $u$ and $v$ , respectively. Let $\phi$ be a 3-coloring of $u^{\prime},v^{\prime}$ .

(1)

If $uv$ is straight and $\phi(u^{\prime})\neq\phi(v^{\prime})$ , then for any $c\in[3]$ , $\phi$ can be extended to $[uvw]$ with $\phi(w)=c$ .
(2)

If $uv$ is not straight, then for at least two colors $c\in[3]$ , $\phi$ can be extended to $[uvw]$ with $\phi(w)=c$ .

The proof of Lemma 3.6 is a straightforward verification and hence omitted.

Lemma 3.6 (2) says that if $uv$ is not straight, then any $3$ -coloring of $u^{\prime},v^{\prime}$ forbids at most one color for $w$ . Thus pre-coloring $u^{\prime}$ and $v^{\prime}$ has the same effect as pre-coloring one neighbor of $w$ . This property is used in the proof of Lemma 3.7 below and also in some later arguments.

Lemma 3.7.

Let $u_{0}$ be the port of $I_{k}$ . For any 3-coloring $\phi$ of $N(I_{k})\setminus N(u_{0})$ , there exist at least two colors $c\in[3]$ such that $\phi$ can be extended to $I_{k}$ so that $\phi(u_{0})=c$ .

Proof.

If $k=1$ , then this is Lemma 3.6 (2). Assume $k\geq 2$ and the lemma holds for $I_{k-1}$ . Let the vertices of $I_{k}$ be labelled as in Figure 1. Let $w^{\prime}_{k}$ and $u^{\prime}_{k}$ be the other neighbor of $w_{k}$ and $u_{k}$ , respectively. Apply Lemma 3.6 to $G[\{u_{k-1},u_{k},w_{k},w^{\prime}_{k},u^{\prime}_{k}\}]$ , we conclude that there are two colors $c^{\prime}\in[3]$ such that $\phi$ can be extended to $u_{k-1},u_{k},w_{k}$ so that $\phi(u_{k-1})=c^{\prime}$ . Thus $u_{k-1}$ can be treated as a 3-vertex with one pre-colored neighbor. By induction hypothesis, there are two colors $c\in[3]$ such that $\phi$ can be extended to $I_{k}$ so that $\phi(u_{0})=c$ . ∎

Figure 2: Configuration a-1

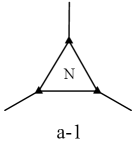
Lemma 3.8.

If $I_{k}$ is contained in $G$ , then the port vertex $u_{0}$ has degree at least $4$ . In particular, $G$ has no Configuration a-1, see Figure 2.

Proof.

Assume to the contrary that $I_{k}\subseteq G$ and $d_{G}(u_{0})=3$ . By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G-I_{k},\sigma)$ , say the resulting coloring $\phi$ . Let $u^{\prime}_{0}$ be the neighbor of $u_{0}$ in $G-I_{k}$ . By Lemma 3.7, there are at least two colors $c\in[3]$ such that $\phi(G-I_{k}-u^{\prime}_{0})$ can be extended to $I_{k}$ so that $\phi(u_{0})=c$ . The coloring of $u^{\prime}_{0}$ forbids one color for $u_{0}$ . Hence, there is at least one color $c\in[3]$ such that $\phi$ can be extended to $I_{k}$ so that $\phi(u_{0})=c$ . ∎

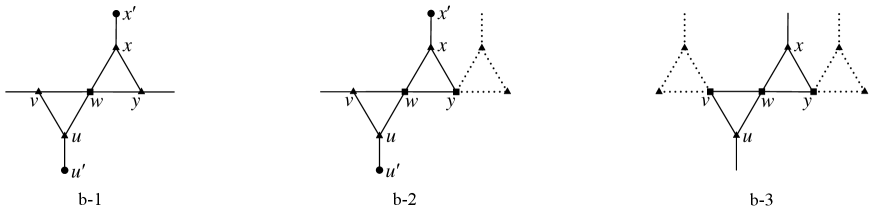
Lemma 3.9.

$G$ has none of Configurations b-1, b-2, b-3, see Figure 3.

Proof.

(1) Suppose to the contrary that $G$ has Configuration b-1, say $H$ . By Remark 2.3, we may assume that edges of the path $u^{\prime}uwxx^{\prime}$ are all straight. Remove $V(H)$ from $(G,\sigma)$ and identify $u^{\prime}$ with $x^{\prime}$ . Denote by $(G^{\prime},\sigma^{\prime})$ the resulting $S_{3}$ -signed graph.

We shall show that $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ and $\phi_{0}$ is still proper in $G^{\prime}$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, this new cycle corresponds to an $8^{-}$ -path in $G$ connecting $u^{\prime}$ and $x^{\prime}$ , which together with $u^{\prime}uwxx^{\prime}$ forms a $12^{-}$ -cycle, say $C$ . As one of $v$ and $y$ lies inside $C$ and the other lies outside, $C$ is a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1.

Also the operation does not identify an external vertex with another vertex which is either external or adjacent to an external vertex. Otherwise, the operation creates a cycle $C$ formed by a path of $D$ and possibly one more edge with $|C|\leq\frac{|D|}{2}+1$ . Since $|D|\leq 12$ , we have $|C|\leq 7$ , contradicting the conclusion above that the operation creates no $8^{-}$ -cycles.

Therefore, $\phi_{0}$ is still proper in $G^{\prime}$ , and by the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: color $w$ the same as $u^{\prime}$ and consequently, $v$ and $u$ (as well as $y$ and $x$ ) can be properly colored in turn.

(2) Suppose to the contrary that $G$ has Configuration b-2, say $H$ . Note that $H$ is an $I_{k}$ -extension of Configuration b-1 at $y$ . So, we can apply a similar proof as for (1), deriving a contradiction. Note that the graph operation here removes $V(I_{k})$ instead of $y$ . For the coloring $\phi$ extended from $(G^{\prime},\sigma^{\prime})$ to $(G,\sigma)$ : by Lemma 3.7, there are two colors $c\in[3]$ such that $\phi$ can be extended to $I_{k}$ so that $\phi(y)=c$ . This has the same effect as $y$ is a 3-vertex and has a pre-colored neighbor. Hence, following the proof for (1), color $w$ the same as $u^{\prime}$ and consequently, $v$ and $u$ (as well as $y$ and $x$ ) can be properly colored in turn.

(3) Suppose to the contrary that $G$ has Configuration b-3, say $H$ . Note that $H$ is an $I_{k}$ -extension of Configuration b-1 at both $y$ and $v$ . We can also apply similar argument as for (1), deriving a contradiction. Note that $v$ is also the port of an $I_{k}$ , and so it will be treated the same as $y$ for both the graph operation and the coloring extension. ∎

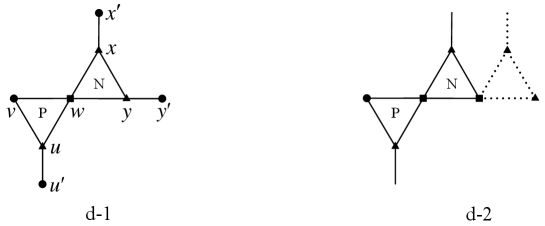
Lemma 3.10.

$G$ has none of Configurations d-1 and d-2, see Figure 4.

Proof.

(1) Suppose to the contrary that $G$ has Configuration d-1, say $H$ . By Remark 2.3, we may assume edges of $x^{\prime}xwuu^{\prime}$ and $uvw$ are all straight. Remove $u,w,x,y$ from $(G,\sigma)$ and identify $u^{\prime}$ with $x^{\prime}$ , obtaining a new $S_{3}$ -signed graph $(G^{\prime},\sigma^{\prime})$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, this new cycle corresponds to an $8^{-}$ -path in $G$ , which together with $u^{\prime}uwxx^{\prime}$ forms a $12^{-}$ -cycle, say $C$ . Then either one of $v$ and $y$ lies inside $C$ and the other lies outside or $v\in V(C)$ . In the former case, $C$ is a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1. In the latter case, $uv$ and $vw$ divide $C$ into a 3-cycle and two $9^{+}$ -cycles, contradicting the fact that $|C|\leq 12$ .

Similarly as the proof of Lemma 3.9, we can show that $\phi_{0}$ is still proper in $G^{\prime}$ . Hence, by the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: let $\alpha$ and $\beta$ be the colors of $u^{\prime}$ and $v$ , respectively. If $\alpha\neq\beta$ , then color $w$ with $\alpha$ , which obviously extends to $u,y,x$ , since $x^{\prime},w,u^{\prime}$ are of the same color. Assume $\alpha=\beta$ . Note that $w$ has a pre-colored neighbor $v$ . By Lemma 3.6, there exists an available color for $w$ such that the resulting coloring is extendable to $x$ and $y$ . As $v$ and $u^{\prime}$ are of the same color, $u$ can be properly colored.

(2) Note that Configuration d-2 is an $I_{k}$ -extension of Configuration d-1 at $y$ . By similar argument as for (1), we can show that $G$ has no Configuration d-2. ∎

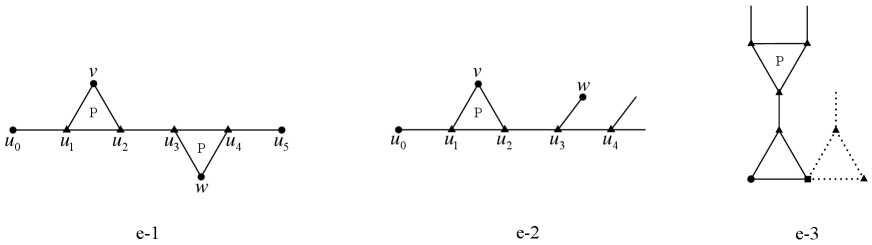
Lemma 3.11.

$G$ contains none of Configurations e-1, e-2, e-3, see Figure 5. In particular, the outer neighbor of a $3_{\Delta^{+}}$ -vertex is not a $3_{\Delta^{+}}$ -vertex, and the outer neighbor of a bad vertex is neither a $3_{\Delta^{+}}$ -vertex nor a $3_{\Delta^{-}}$ -vertex.

Proof.

(1) Suppose to the contrary that $G$ has Configuration e-1. By Remark 2.3, we may assume edges incident with $u_{1}$ , $u_{2}$ , $u_{3}$ , or $u_{4}$ are all straight. Remove $u_{1},u_{2},u_{3},u_{4}$ from $(G,\sigma)$ and add a straight edge between $u_{0}$ and $u_{5}$ , obtaining a new $S_{3}$ -signed graph $(G^{\prime},\sigma^{\prime})$ .

We shall show that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . If not, a $12^{-}$ -cycle $C$ of $G$ can be obtained from this $8^{-}$ -cycle by substituting $u_{0}u_{1}\cdots u_{5}$ for $u_{0}u_{5}$ . If $v\in V(C)$ , then $vu_{1}$ and $vu_{2}$ divide $C$ into a 3-cycle and two $9^{+}$ -cycles, contradicting the fact that $|C|\leq 12$ . Thus $v\notin V(C)$ and similarly, $w\notin V(C)$ . Now $C$ is a separating $12^{-}$ -cycle, contradicting Lemma 3.1.

We shall show that the operation does not add an edge between two external vertices and consequently, $\phi_{0}$ is still proper in $G^{\prime}$ . If not, the operation creates a cycle $C$ formed by a path of $D$ and $u_{0}u_{5}$ with $|C|\leq\frac{|D|}{2}+1\leq 7$ , a contradiction.

By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: Let $\phi$ be the resulting coloring of $(G^{\prime},\sigma^{\prime})$ . If $\phi(u_{0})=\phi(v)$ or $\phi(u_{5})=\phi(w)$ , then obviously $\phi$ can be extended to $(G,\sigma)$ in the order $u_{4}\rightarrow u_{3}\rightarrow u_{2}\rightarrow u_{1}$ or $u_{1}\rightarrow u_{2}\rightarrow u_{3}\rightarrow u_{4}$ , respectively; otherwise, color $u_{2}$ same as $u_{0}$ , and $u_{3}$ same as $u_{5}$ and consequently, we can properly color $u_{1}$ and $u_{4}$ .

(2) Suppose to the contrary that $G$ has Configuration e-2. By Remark 2.3, we may assume edges incident with $u_{1}$ , $u_{2}$ , or $u_{3}$ are all straight. Remove $u_{1},u_{2},u_{3},u_{4}$ from $(G,\sigma)$ and identify $u_{0}$ with $w$ . We thereby obtain a new $S_{3}$ -signed graph $(G^{\prime},\sigma^{\prime})$ . Similarly as the proof of Lemma 3.10, we can show that $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ and $\phi_{0}$ is still proper in $G^{\prime}$ . Therefore, by the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: properly color $u_{4}$ and $u_{3}$ in turn. Since $u_{0}$ and $u_{3}$ receive different colors, the resulting coloring can be extended to $u_{1}$ and $u_{2}$ by Lemma 3.6.

(3) Note that Configuration e-3 is an $I_{k}$ -extension of Configuration e-2 at $u_{4}$ for which $u_{4}w\in E(G)$ and $v$ is an internal 3-vertex in $G$ . By similar argument as for (2), we can show that $G$ has no Configuration e-3. ∎

Lemma 3.12.

Let $H=J_{2}\subseteq G$ . Then the unique 4-vertex of $H$ which is not a port is incident with two 9-faces.

Proof.

Let $f$ and $g$ be the two faces (other than triangles) incident with $u_{2}$ . Assume to the contrary that at least one of $f,g$ is not a $9$ -face. Then $d(f)+d(g)\geq 19$ . We distinguish two cases, see Figure 6.

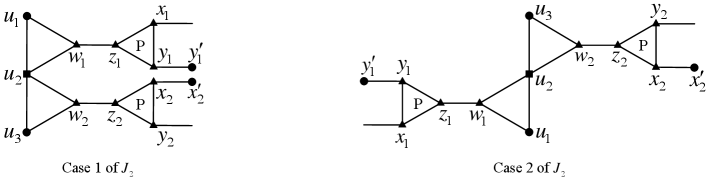
Case 1: $[u_{1}w_{1}u_{2}]$ and $[u_{2}w_{2}u_{3}]$ locate on the same side of $u_{1}u_{2}u_{3}$ .

By Remark 2.3, we may assume that edges of paths $u_{1}w_{1}z_{1}y_{1}y_{1}^{\prime}$ and $u_{3}w_{2}z_{2}x_{2}x_{2}^{\prime}$ are all straight. Remove all the vertices of $H$ except $u_{1}$ and $u_{3}$ , and identify $u_{1}$ with $y_{1}^{\prime}$ , and $u_{3}$ with $x_{2}^{\prime}$ . We thereby obtain from $(G,\sigma)$ a new $S_{3}$ -signed graph, say $(G^{\prime},\sigma^{\prime})$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, this new cycle contains either one path (say $P$ ) between $u_{1}$ and $y^{\prime}_{1}$ or between $u_{3}$ and $x^{\prime}_{2}$ , or two paths such that one (say $P_{1}$ ) between $u_{1}$ and $u_{3}$ and the other (say $P_{2}$ ) between $y_{1}^{\prime}$ and $x_{2}^{\prime}$ in $G$ . In the former case, $P$ together with $u_{1}w_{1}z_{1}y_{1}y_{1}^{\prime}$ or $u_{3}w_{2}z_{2}x_{2}x_{2}^{\prime}$ forms a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1. In the latter case, it follows that $d(f)+d(g)=|P_{1}|+|P_{2}|+10\leq 18$ , contradicting the assumption that $d(f)+d(g)\geq 19$ .

Similarly as the proof of Lemma 3.9, we can show that $\phi_{0}$ is still proper in $G^{\prime}$ .

Therefore, by the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: properly color $u_{2}$ and then $w_{1}$ and $w_{2}$ . Properly color $x_{1}$ and $y_{2}$ . By Lemma 3.6, the resulting coloring is extendable to $y_{1}$ and $z_{1}$ , and to $x_{2}$ and $z_{2}$ as well.

Case 2: $[u_{1}w_{1}u_{2}]$ and $[u_{2}w_{2}u_{3}]$ locate on distinct sides of $u_{1}u_{2}u_{3}$ .

Note that $x_{2},y_{2},z_{2}$ locate in anti-clockwise order around the incident 3-face while $x_{1},y_{1},z_{1}$ do in clockwise order. By the same argument as for Case 1, a contradiction can be derived. ∎

Lemma 3.13.

Let $H=J_{k}\subseteq G$ with $k\geq 4$ . Then among all the 9-faces containing a 4-vertex of $H$ which is not a port, there exist at least $k-2$ nice 9-faces.

Proof.

Denote by $P=u_{1}u_{2}\ldots u_{k+1}$ the unique path of $H$ with $u_{1}$ and $u_{k+1}$ being ports of $H$ and $u_{2},u_{3},\ldots,u_{k}$ being $4_{\bowtie}$ -vertices. Let $T_{i}=[u_{i}w_{i}u_{i+1}]$ for $i\in\{1,2,\ldots,k\}$ . For any $1\leq i<j\leq k$ such that $T_{i}$ and $T_{j}$ locate on one side of $P$ and $T_{i+1},\ldots,T_{j-1}$ locate on the other side, let the face $f_{ij}=[y_{i}z_{i}w_{i}u_{i+1}u_{i+2}\ldots u_{j}w_{j}z_{j}x_{j}o_{1}o_{2}\ldots]$ . See Figure 7 for an example of $J_{4}$ and $f_{ij}$ .

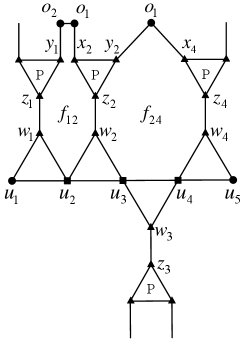
We claim that each $f_{ij}$ is a nice 9-face and $1\leq j-i\leq 2$ . By Lemma 3.12, $d(f_{ij})=9$ . This implies that $1\leq j-i\leq 3$ . Since $G$ has no Configuration e-2, we can deduce that: (1) $y_{i}x_{j}\notin E(G)$ , i.e., $j-i\neq 3$ ; (2) if $j-i=2$ , then $o_{1}$ is not an internal 3-vertex; (3) if $j-i=1$ , then at least one of $o_{1}$ and $o_{2}$ is not an internal 3-vertex. By definition, $f_{ij}$ is a nice 9-face.

Let $F$ be the set of all such faces $f_{ij}$ . By the claim above, $|F|\geq k-2$ . ∎

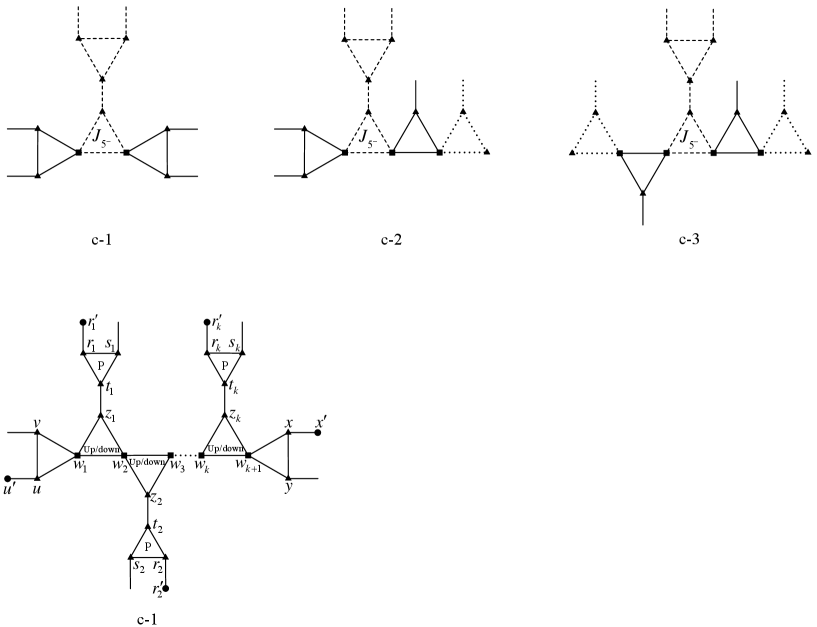
Lemma 3.14.

$G$ has none of Configurations c-1, c-2, c-3, see Figure 8.

Proof.

(1) Suppose to the contrary that $G$ has Configuration c-1, say $H$ . Note that for each $i\in\{1,2,\ldots,k\}$ , the vertices $r_{i},s_{i},t_{i}$ are labelled in clockwise order around their incident triangle no matter on which side of the path $w_{1}w_{2}\ldots w_{k+1}$ this triangle is located. By Remark 2.3, we may assume that edges of $u^{\prime}uw_{1}$ , $z_{1}t_{1}r_{1}r_{1}^{\prime}$ , $z_{2}t_{2}r_{2}r_{2}^{\prime}$ , $\ldots$ , $z_{k}t_{k}r_{k}r_{k}^{\prime}$ , $w_{k+1}xx^{\prime}$ are all straight. Let $Q=[w_{1}z_{1}w_{2}]\cup[w_{2}z_{2}w_{3}]\cup\cdots\cup[w_{k}z_{k}w_{k+1}]$ . Remove $V(H)\setminus V(Q)$ from $(G,\sigma)$ , identify $u^{\prime}$ with $w_{1}$ into a new vertex $w^{*}_{1}$ , and $w_{k+1}$ with $x^{\prime}$ into a new vertex $w^{*}_{k+1}$ , and insert a new straight edge $e_{i}$ between $r_{i}^{\prime}$ and $z_{i}$ for each $i\in\{1,2,\ldots,k\}$ . Denote by $(G^{\prime},\sigma^{\prime})$ the resulting $S_{3}$ -signed graph. We shall show that $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ and $\phi_{0}$ is still proper in $G^{\prime}$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, denote by $C^{\prime}$ this new $8^{-}$ -cycle. A segment of $C^{\prime}$ is a subpath $P^{\prime}$ of $C^{\prime}$ such that each of its two ends is either a new vertex $w^{*}_{1}$ or $w^{*}_{k+1}$ , or a new edge $e_{j}=z_{j}r^{\prime}_{j}$ , and whose interior vertices are in $Q$ . Let $P^{\prime}_{1},P^{\prime}_{2},\ldots,P^{\prime}_{l}$ be the segments of $C^{\prime}$ . For $1\leq i\leq l$ , construct a path $P_{i}$ from $P^{\prime}_{i}$ as follows: if $e_{j}=z_{j}r^{\prime}_{j}$ is an edge of $P^{\prime}_{i}$ , then replace $e_{j}$ by $z_{j}t_{j}r_{j}r_{j}^{\prime}$ ; if $w^{*}_{1}$ (resp., $w^{*}_{k+1}$ ) is an end vertex of $P^{\prime}_{i}$ , then replace $w^{*}_{1}$ by $w_{1}uu^{\prime}$ (resp., replace $w^{*}_{k+1}$ by $w_{k+1}xx^{\prime}$ ). Denote by $C$ the cycle obtained from $C^{\prime}$ by replacing $P^{\prime}_{i}$ by $P_{i}$ for $i=1,2,\ldots,l$ .

Note that if the two ends of $P^{\prime}_{i}$ are new edges, then $P^{\prime}_{i}$ contains at least two edges of $Q$ , and hence $|P^{\prime}_{i}|\geq 4$ ; and $|P^{\prime}_{i}|\geq 2$ if one end of $P^{\prime}_{i}$ is a new vertex and the other end is a new edge. As there are only two new vertices, $8\geq|C^{\prime}|\geq\sum_{i=1}^{l}|P^{\prime}_{i}|\geq 4l-4$ and hence $1\leq l\leq 3$ .

It follows from the construction that $|P_{i}|=|P^{\prime}_{i}|+4$ and $|C|=|C^{\prime}|+4l$ .

If $l=1$ , then $C$ is a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1. If $l\in\{2,3\}$ , then $C-\bigcup_{i=1}^{l}E(P_{i})\cap E(Q)$ consists of $l$ paths $R_{1},R_{2},\ldots,R_{l}$ in $G-Q$ , each $R_{i}$ together with the shortest path $R^{\prime}_{i}$ of $Q$ connecting the two end vertices of $R_{i}$ forms a cycle $C_{i}$ of $G$ . Note that each $R^{\prime}_{i}$ has length at most $k\leq 5$ . Moreover, each path $E(P_{i})\cap E(Q)$ has length at least $2$ , except that there are at most two such paths that has one end vertex in $\{w_{1},w_{k+1}\}$ , and has length at least 1. So $8+4l\geq|C^{\prime}|+4l=|C|\geq\sum_{i=1}^{l}|R_{i}|+2l-2$ and hence, $\sum_{i=1}^{l}|C_{i}|=\sum_{i=1}^{l}(|R_{i}|+|R^{\prime}_{i}|)\leq\sum_{i=1}^{l}|R_{i}|+5l\leq(10+2l)+5l=10+7l$ . So one of the $C_{i}$ is a separating $12^{-}$ -cycle of $G$ , a contradiction.

Note that all the vertices of $Q$ are internal. The operation makes $\phi_{0}$ still proper in $G^{\prime}$ .

By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: since $u^{\prime}$ and $w_{1}$ receive the same color, we can properly color $v$ and $u$ in turn, and so do $y$ and $x$ . For $1\leq i\leq k$ , properly color $s_{i}$ . Since $z_{i}$ and $r_{i}^{\prime}$ receive distinct colors, the resulting coloring can be extended to $r_{i}$ and $t_{i}$ by Lemma 3.6.

(2) By definition, Configuration c-2 (resp., c-3) is an $I_{k}$ -extension of Configuration c-1 at $y$ (resp., at $y$ and $v$ ). So by a similar proof as for (1), we can show that $G$ has neither c-2 nor c-3. ∎

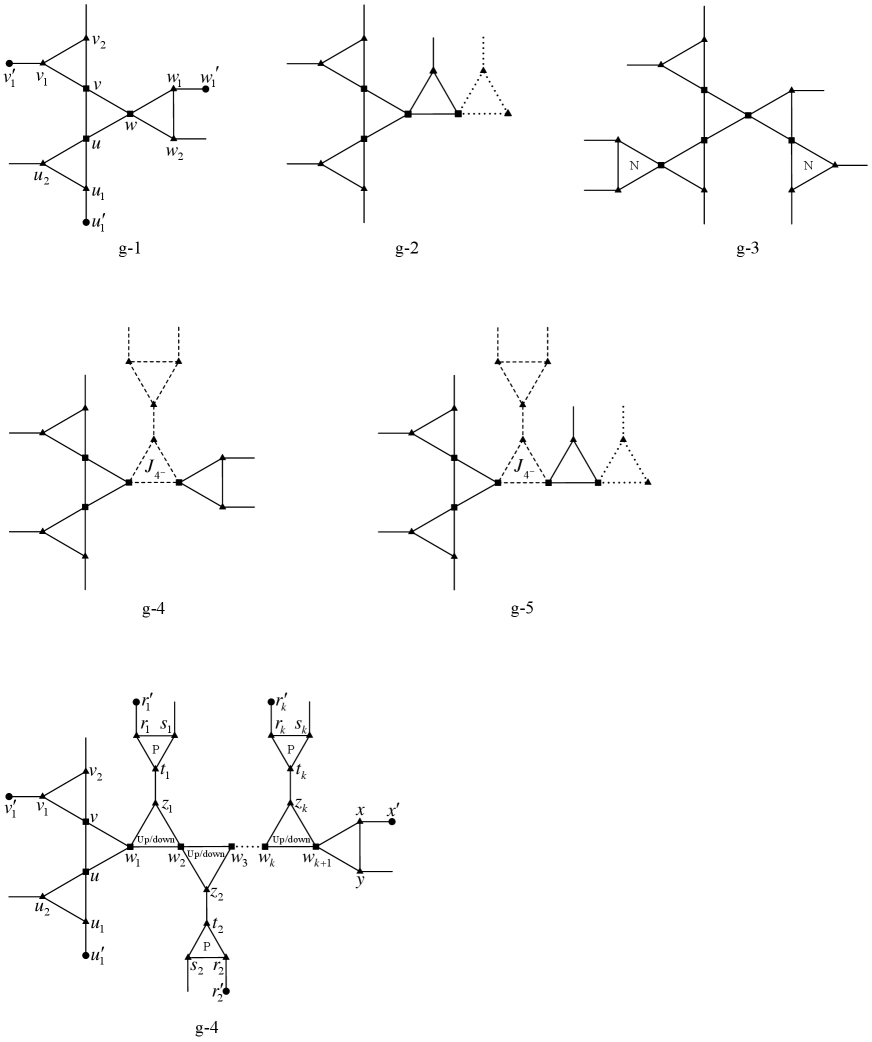
Lemma 3.15.

$G$ has none of Configurations g-1, g-2, g-3, g-4, g-5, see Figure 9.

Proof.

(1) Suppose to the contrary that $G$ has Configuration g-1, say $H$ . By Remark 2.3, we may assume edges of $u_{1}^{\prime}u_{1}u,v_{1}^{\prime}v_{1}v,w_{1}^{\prime}w_{1}w$ are all straight. Remove $u_{1},u_{2},v_{1},v_{2},w_{1},w_{2}$ from $(G,\sigma)$ and identify $u$ with $u_{1}^{\prime}$ , $v$ with $v_{1}^{\prime}$ , and $w$ with $w_{1}^{\prime}$ , obtaining a new $S_{3}$ -signed graph $(G^{\prime},\sigma^{\prime})$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, denote by $C$ this new $8^{-}$ -cycle. Clearly, $C$ contains precisely one path of $[uvw]$ (that is either an edge or a 2-path). W.l.o.g., let $u$ and $v$ be ends of this path. So, $C$ corresponds to two paths of $G$ , which together with $u_{1}^{\prime}u_{1}u$ and $vv_{1}v_{1}^{\prime}$ forms a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1.

We claim that $\phi_{0}$ is still proper in $G^{\prime}$ . Otherwise, there exist at least two external vertices among $u^{\prime}_{1}$ , $v^{\prime}_{1}$ , and $w^{\prime}_{1}$ , w.l.o.g., say $u^{\prime}_{1}$ and $v^{\prime}_{1}$ . So, the operation creates a cycle $C^{\prime}$ formed by $uv$ and a path of $D$ with $|C^{\prime}|\leq\frac{|D|}{2}+1\leq 7$ , a contradiction.

By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: since $u$ and $u_{1}^{\prime}$ receive the same color, $u_{2}$ and $u_{1}$ can be properly colored in turn. So do $v_{2}$ and $v_{1}$ , as well as $w_{2}$ and $w_{1}$ .

(2) Note that Configuration g-2 is an $I_{k}$ -extension of Configuration g-1 at $w_{2}$ , and Configuration g-3 is an $I_{1}$ -extension of Configuration g-1 at both $w_{2}$ and $u_{2}$ . Therefore, by a similar argument as for (1), we can show that $G$ has neither g-2 nor g-3.

(3) Suppose to the contrary that $G$ has Configuration g-4, say $H$ . Note that $H$ is a $J_{k}$ -extension of Configuration g-1 at $w$ for some $k\leq 4$ . We will follow the proof for the reducibility of both c-1 and g-1.

By Remark 2.3, we may assume that edges of $u_{1}^{\prime}u_{1}u$ , $v_{1}^{\prime}v_{1}v$ , $z_{1}t_{1}r_{1}r_{1}^{\prime}$ , $z_{2}t_{2}r_{2}r_{2}^{\prime}$ , $\ldots$ , $z_{k}t_{k}r_{k}r_{k}^{\prime}$ , and $w_{k+1}xx^{\prime}$ are all straight. Let $Q=[uvw_{1}]\cup[w_{1}z_{1}w_{2}]\cup\cdots\cup[w_{k}z_{k}w_{k+1}]\cup[w_{k+1}xy]$ . Remove $V(H)\setminus V(Q)$ from $(G,\sigma)$ , identify $u_{1}^{\prime}$ with $u$ , $v^{\prime}$ with $v$ , and $x^{\prime}$ with $w_{k+1}$ , and insert a straight edge $e_{i}$ between $r_{i}^{\prime}$ and $z_{i}$ for each $i\in\{1,2,\ldots,k\}$ . Denote by $(G^{\prime},\sigma^{\prime})$ the resulting $S_{3}$ -signed graph.

By similar proof as for the reducibility of Configuration c-1, we can show that $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ and $\phi_{0}$ is still proper in $G^{\prime}$ . Note that here the distance of any two vertices of $Q$ is at most $k+1$ , which is still no more than $5$ , since $k\leq 4$ . So, the similar proof still works. Finally, $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ in a similar way.

(4) Note that Configuration g-5 is an $I_{k}$ -extension of Configuration g-4 at $y$ . By similar argument as for (3), we can show that $G$ has no g-5. ∎

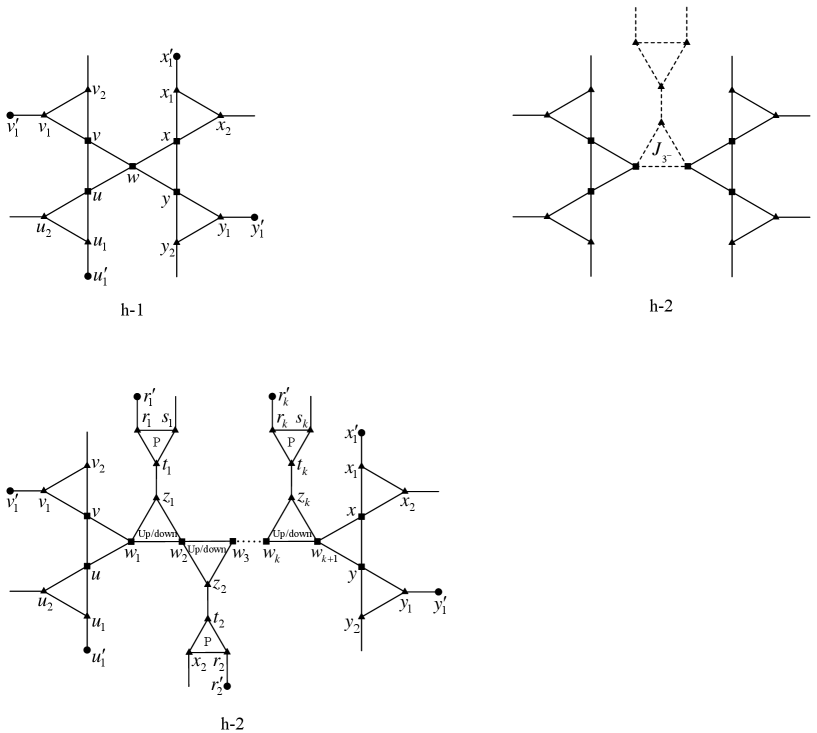
Lemma 3.16.

$G$ has none of Configurations h-1 and h-2, see Figure 10.

Proof.

(1) Suppose to the contrary that $G$ has Configuration h-1, say $H$ . By Remark 2.3, we may assume that edges of $u_{1}^{\prime}u_{1}u$ , $v_{1}^{\prime}v_{1}v$ , $x_{1}^{\prime}x_{1}x$ , and $y_{1}^{\prime}y_{1}y$ are all straight. Let $Q=[uvw]\cup[wxy]$ . Remove $V(H)\setminus V(Q)$ from $(G,\sigma)$ and identify $u$ with $u_{1}^{\prime}$ , $v$ with $v_{1}^{\prime}$ , $x$ with $x_{1}^{\prime}$ , and $y$ with $y_{1}^{\prime}$ (resulting in four new vertices $u^{*},v^{*},x^{*},y^{*}$ , respectively). We thereby obtain a new $S_{3}$ -signed graph $(G^{\prime},\sigma^{\prime})$ .

We claim that the operation creates no $8^{-}$ -cycles and consequently, $(D^{\prime},\sigma^{\prime})\in\mathcal{G}$ . Otherwise, denote by $C^{\prime}$ this new $8^{-}$ -cycle. A segment of $C^{\prime}$ is a subpath $P^{\prime}$ of $C^{\prime}$ such that both of its two ends are in $\{u^{*},v^{*},x^{*},y^{*}\}$ , and whose interior vertices are in $Q$ . Let $P^{\prime}_{1},P^{\prime}_{2},\ldots,P^{\prime}_{l}$ be the segments of $C^{\prime}$ . By the structure of $Q$ , $1\leq l\leq 2$ . For $1\leq i\leq l$ , construct a path $P_{i}$ from $P^{\prime}_{i}$ as follows: if $u^{*}$ (resp., $v^{*},x^{*},y^{*}$ ) is an end vertex of $P^{\prime}_{i}$ , then replace $u^{*}$ by $uu_{1}u^{\prime}_{1}$ (resp., replace $v^{*}$ by $vv_{1}v^{\prime}_{1}$ , replace $x^{*}$ by $xx_{1}x^{\prime}_{1}$ , replace $y^{*}$ by $yy_{1}y^{\prime}_{1}$ ). Denote by $C$ the cycle obtained from $C^{\prime}$ by replacing $P^{\prime}_{i}$ by $P_{i}$ for $i=1,2,\ldots,l$ . Clearly, $|C|=|C^{\prime}|+4l$ . For $l=1$ , $C$ is a separating $12^{-}$ -cycle of $G$ , contradicting Lemma 3.1. For $l=2$ , one of $P^{\prime}_{1}$ and $P^{\prime}_{2}$ connects $u^{*}$ with $v^{*}$ and the other connects $x^{*}$ with $y^{*}$ . So, by replacing $P_{1}\cup P_{2}$ by $v^{\prime}_{1}v_{1}vwxx_{1}x^{\prime}_{1}\cup u^{\prime}_{1}u_{1}uwyy_{1}y^{\prime}_{1}$ , we can obtain from $C$ two cycles of $G$ , say $C_{1}$ and $C_{2}$ , with $w$ as their only common vertex. Clearly, $|C_{1}|+|C_{2}|\leq|C|+2\leq 18$ . So, at least one of $C_{1}$ and $C_{2}$ is a separating $9^{-}$ -cycle, contradicting Lemma 3.1.

We claim that $\phi_{0}$ is still proper in $G^{\prime}$ . Otherwise, either both $u_{1}^{\prime}$ and $v_{1}^{\prime}$ are external or both $x_{1}^{\prime}$ and $y_{1}^{\prime}$ are external. W.l.o.g., say the former case. Then the operation creates a cycle $C^{\prime\prime}$ formed by $u^{*}v^{*}$ and a path of $D$ with $|C^{\prime\prime}|\leq\frac{|D|}{2}+1\leq 7$ , a contradiction.

By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ as follows: since $u$ and $u_{1}^{\prime}$ receive the same color, $u_{2}$ and $u_{1}$ can be properly colored in turn. So do pairs $v_{2}$ and $v_{1}$ , $x_{2}$ and $x_{1}$ , $y_{2}$ and $y_{1}$ .

(2) Suppose to the contrary that $G$ has Configuration h-2, say $H$ . Note that $H$ is a $J_{k}$ -extension of Configuration h-1 at $w$ for $k\leq 3$ . By Remark 2.3, we may assume that edges of $uu_{1}u_{1}^{\prime}$ , $vv_{1}v_{1}^{\prime}$ , $z_{1}t_{1}r_{1}s_{1}^{\prime}$ , $z_{2}t_{2}r_{2}s_{2}^{\prime}$ , $\ldots$ , $z_{k}t_{k}r_{k}s_{k}^{\prime}$ , $xx_{1}x_{1}^{\prime}$ , $yy_{1}y_{1}^{\prime}$ are all straight. Let $Q=[uvw_{1}]\cup[w_{1}z_{1}w_{2}]\cup\cdots\cup[w_{k}z_{k}w_{k+1}]\cup[w_{k+1}xy]$ . Remove $V(H)\setminus V(Q)$ from $(G,\sigma)$ , identify $u^{\prime}$ with $u$ , $v^{\prime}$ with $v$ , $x^{\prime}$ with $x$ , and $y^{\prime}$ with $y$ , and insert a straight edge $e_{i}$ between $r_{i}^{\prime}$ and $z_{i}$ for each $i\in\{1,2,\ldots,k\}$ . Denote by $(G^{\prime},\sigma^{\prime})$ the resulting $S_{3}$ -signed graph.

By similar proof as for the reducibility of Configuration c-1, we can show that $(G^{\prime},\sigma^{\prime})\in\mathcal{G}$ and $\phi_{0}$ is still proper in $G^{\prime}$ . Note that here the distance between any two vertices of $Q$ is at most $k+2$ , which is still no more than $5$ , since $k\leq 3$ . So, the similar proof still works. Finally, $\phi_{0}$ can be extended to $(G^{\prime},\sigma^{\prime})$ and further to $(G,\sigma)$ in a similar way. ∎

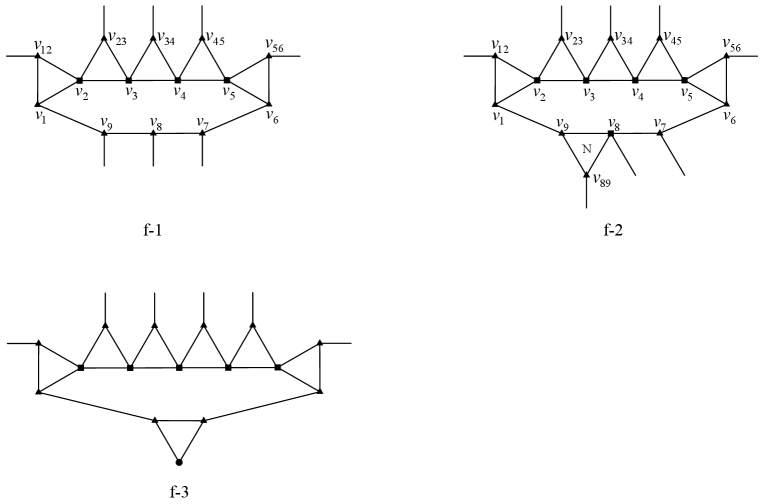
Lemma 3.17.

$G$ has none of Configurations f-1, f-2, f-3, see Figure 11.

Proof.

(1) Suppose to the contrary that $G$ has Configuration f-1, say $H$ . By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G-V(H),\sigma)$ and further to $(G,\sigma)$ as follows: Note that the vertex $v_{6}$ has three permissible color, and $v_{7}$ has at least two permissible colors. Choose a color for $v_{6}$ so that after $v_{6}$ is colored, $v_{7}$ still has at least two permissible colors. Then properly color all the remaining uncolored vertices in the order $v_{56}$ , $v_{5}$ , $v_{45}$ , $v_{4}$ , $v_{34}$ , $v_{3}$ , $v_{23}$ , $v_{2}$ , $v_{12}$ , $v_{1}$ , $v_{9}$ , $v_{8}$ , $v_{7}$ .

(2) Suppose to the contrary that $G$ has Configuration f-2, say $H$ . By the minimality of $(G,\sigma)$ , $\phi_{0}$ can be extended to $(G-V(H),\sigma)$ and further to $(G,\sigma)$ as follows: Similarly as in (1), we can choose a color for $v_{6}$ so that after $v_{6}$ is colored, $v_{7}$ still has at least two permissible colors. Then properly color vertices $v_{56}$ , $v_{5}$ , $v_{45}$ , $v_{4}$ , $v_{34}$ , $v_{3}$ , $v_{23}$ , $v_{2}$ , $v_{12}$ , $v_{1}$ in order. Note that $v_{8}$ has one pre-colored neighbor. Since the triangle $[v_{8}v_{9}v_{89}]$ is negative, by Lemma 3.6, the resulting coloring can be extended to $[v_{8}v_{9}v_{89}]$ . Finally, properly color $v_{7}$ .

(3) By similar argument as for (1), we can also show that $G$ has no Configuration f-3. ∎

3.2 Discharging in $G$

In what follows, let $V$ , $E$ , and $F$ be the set of vertices, edges, and faces of $G$ , respectively. For each $x\in V\cup F$ , the initial charge $ch(x)$ of $x$ is defined as

ch(x)=\begin{cases}d(x)+4,\text{~{}if~{}}x=f_{0};\\ d(x)-4,\text{~{}otherwise}.\end{cases}

Move charge among elements of $V\cup F$ according to the following rules:

$R1.$

$f_{0}$ sends to each incident vertex charge $\frac{4}{3}$ .
$R2.$

A $C$ -vertex $u$ sends to each incident 3-face $f$ with $f\neq f_{0}$ charge $\frac{5}{9}$ if $u$ is either an external 3-vertex or an external 4-vertex incident with two 3-faces; charge $1$ otherwise.
$R3.$

Every $5^{+}$ -face $f$ with $f\neq f_{0}$ sends charge $\frac{d(f)-4}{d(f)}$ to each of its incident vertices.
$R4.$
Let $u$ be a $3_{\Delta}$ -vertex of a snowflake $S$ such that the outer neighbor $u^{\prime}$ of $u$ is not a vertex of $S$ .
1. $(1)$
  
  If $u$ is a bad vertex and $u^{\prime}$ is a $3_{\Delta^{\circ}}$ - or $C$ -vertex, then $u^{\prime}$ sends charge $\frac{2}{9}$ to $u$ ;
2. $(2)$
  
  If $u$ is a $3_{\Delta^{+}}$ -vertex but not bad, and $u^{\prime}$ is a $3_{\Delta^{-}}$ -, $3_{\Delta^{\circ}}$ -, or $C$ -vertex, then $u^{\prime}$ sends charge $\frac{2}{27}$ to $u$ ;
3. $(3)$
  
  If $u$ is a $3_{\Delta^{-}}$ -vertex, and $u^{\prime}$ is a $3_{\Delta^{\circ}}$ - or $C$ -vertex, then $u^{\prime}$ sends charge $\frac{2}{27}$ to $u$ .
$R5.$
Let $f$ be a nice 9-face related to a snowflake $S$ , and $u$ be a nice vertex of $f$ .
1. $(1)$
  
  If $u$ is a 1-nice vertex of $f$ , then $u$ sends charge $\frac{2}{27}$ to $S$ through $f$ .
2. $(2)$
  
  If $u$ is a 2-nice vertex of $f$ , then $u$ sends charge $\frac{4}{27}$ to $S$ through $f$ .
$R6.$

Let $L$ be a string on the boundary of an $11^{-}$ -face $f$ with $f\neq f_{0}$ . If $u$ is a vertex adjacent to $L$ , then $u$ sends to each vertex of $L$ charge $\frac{12-d(f)}{6d(f)}$ .

Let $ch^{*}(x)$ denote the final charge of an element $x$ of $V\cup F$ after the discharging procedure. By Euler’s formula $|V|-|E|+|F|=2$ together with Handshaking Theorem $2|E|=\sum\limits_{v\in V}d(v)=\sum\limits_{f\in F}d(f)$ , we can deduce from the definition of $ch(x)$ that

	$\displaystyle\sum\limits_{x\in V\cup F}ch(x)$	$\displaystyle=\sum\limits_{v\in V}(d(v)-4)+\sum\limits_{f\in F}(d(f)-4)+8$
		$\displaystyle=\sum\limits_{v\in V}d(v)-4\|V\|+\sum\limits_{f\in F}d(f)-4\|F\|+8$
		$\displaystyle=4(\|E\|-\|V\|-\|F\|)+8$
		$\displaystyle=0.$

As $\sum\limits_{x\in V\cup F}ch^{*}(x)=\sum\limits_{x\in V\cup F}ch(x)$ , to complete the proof of Theorem 2.1 by deriving a contradiction, it suffices to show that $\sum\limits_{x\in V\cup F}ch^{*}(x)>0$ .

The initial charge $ch(S)$ and the final charge $ch^{*}(S)$ of a snowflake $S$ are defined as follows:

ch(S)=\sum_{v\in 3_{\Delta}(S)\cup 4_{\bowtie}(S)}ch(v)+\sum_{f\in T(S)}ch(f)=-|3_{\Delta}(S)|-|T(S)|.

(1)

ch^{*}(S)=\sum_{v\in 3_{\Delta}(S)\cup 4_{\bowtie}(S)}ch^{*}(v)+\sum_{f\in T(S)}ch^{*}(f).

Claim 3.18.

$ch^{*}(S)\geq 0$ for each snowflake $S$ of $G$ .

Proof.

First assume that $S$ is a positive $(3,3,3)$ -face. We can calculate from Formula 1 that $ch(S)=-4$ . For each vertex $u$ of $S$ , let $u^{\prime}$ be the outer neighbor of $u$ . By Lemma 3.11, $u^{\prime}$ is not a $3_{\Delta^{+}}$ -vertex or a $3_{\Delta^{-}}$ -vertex. Clearly, $u^{\prime}$ is neither a $4_{\bowtie}$ -vertex nor a 2-vertex. So, $u^{\prime}$ is a $3_{\Delta^{\circ}}$ -vertex or a $C$ -vertex. By $R\ref{rule-A1-vertex}(1)$ , $u$ receives charge $\frac{2}{9}$ from $u^{\prime}$ . Moreover, since $G\in\mathcal{G}$ , $u$ is incident with two $9^{+}$ -faces. By $R\ref{rule-face}$ , $u$ receives charge at least $\frac{5}{9}$ from each of them. Therefore, $ch^{*}(S)\geq ch(S)+\frac{2}{9}\times 3+\frac{5}{9}\times 6=0.$

Assume $S$ is not a positive $(3,3,3)$ -face. By Lemma 3.5, $S$ contains no 2-vertices. By $R\ref{rule-face}$ , each vertex of $3_{\Delta}(S)\cup 4_{\bowtie}(S)$ receives a total charge at least $\frac{5}{9}\times 2$ from its two incident $9^{+}$ -faces. For each $v\in 3_{\Delta}(S)$ , let $v^{\prime}$ be the outer neighbor of $v$ . If $v$ is a $3_{\Delta^{+}}$ -vertex, then $v^{\prime}$ is not by Lemma 3.11. So, $v^{\prime}$ is a $3_{\Delta^{-}}$ -vertex or a $3_{\Delta^{\circ}}$ -vertex or a $C$ -vertex. By $R\ref{rule-A1-vertex}(2)$ , $v$ receives charge $\frac{2}{27}$ from $v^{\prime}$ . If $v$ is a $3_{\Delta^{-}}$ -vertex, then $v^{\prime}$ might be a $3_{\Delta^{+}}$ -vertex, for which case $v$ sends charge $\frac{2}{27}$ to $v^{\prime}$ . If $v$ is a $3_{\Delta^{\circ}}$ -vertex, then by $R\ref{rule-A1-vertex}$ , $v$ sends to $v^{\prime}$ charge $\frac{2}{9}$ if $v^{\prime}$ is bad, and charge at most $\frac{2}{27}$ otherwise. Finally, the 3-faces of $S$ receive a total charge $\frac{5}{9}t_{1}(S)+t_{2}(S)$ from incident $C$ -vertices by $R\ref{rule-C-vertex}$ . Therefore,

\begin{split}ch^{*}(S)\geq~{}&ch(S)+\frac{5}{9}\times 2\times(|3_{\Delta}(S)|+|4_{\bowtie}(S)|)+\frac{2}{27}\times|3_{\Delta^{+}}(S)|-\frac{2}{27}\times|3_{\Delta^{-}}(S)|\\ &-\frac{2}{9}\times(|3_{\Delta^{\circ}}(S)|-|3_{\Delta^{\star}}(S)|)-\frac{2}{27}\times|3_{\Delta^{\star}}(S)|+\frac{5}{9}t_{1}(S)+t_{2}(S).\end{split}

(2)

Let $H$ be a graph whose vertex set $V(H)=T(S)$ and edge set $E(H)$ is given by: for any $f,g\in V(H)$ , $fg\in E(H)$ if and only if $f$ and $g$ are intersecting at a $4_{\bowtie}$ -vertex in $G$ . Clearly, $H$ is a connected subcubic plane graph.

Notice that the number of 3-faces of $S$ containing $v$ is one if $v\in 3_{\Delta}(S)$ , two if $v\in 4_{\bowtie}(S)$ , and $t_{i}(S,v)$ if $v\in C_{i}(S)$ for $i\in\{1,2\}$ . Hence,

3|T(S)|=|3_{\Delta}(S)|+2|4_{\bowtie}(S)|+t_{1}(S)+t_{2}(S).

(3)

Combining Formulas 1, 2, 3 gives

ch^{*}(S)\geq-\frac{4}{27}|3_{\Delta^{+}}(S)|-\frac{8}{27}|3_{\Delta^{-}}(S)|-\frac{4}{9}|3_{\Delta^{\circ}}(S)|+\frac{4}{27}|3_{\Delta^{\star}}(S)|+\frac{4}{9}|4_{\bowtie}(S)|+\frac{2}{9}t_{1}(S)+\frac{2}{3}t_{2}(S).

(4)

Moreover, since $H$ is a connected graph, $E(H)\geq V(H)-1$ , i.e.,

|4_{\bowtie}(S)|\geq|T(S)|-1.

(5)

If $H$ is not a tree, then Formula 5 can be strengthened as $|4_{\bowtie}(S)|\geq|T(S)|$ , which together with Formula 3 gives $|4_{\bowtie}(S)|\geq|3_{\Delta}(S)|+t_{1}(S)+t_{2}(S)$ . Hence, we can deduce from Formula 4 that $ch^{*}(S)\geq\frac{8}{27}|3_{\Delta^{+}}(S)|+\frac{4}{27}|3_{\Delta^{-}}(S)|+\frac{4}{27}|3_{\Delta^{\star}}(S)|+\frac{2}{3}t_{1}(S)+\frac{10}{9}t_{2}(S)\geq 0$ . Therefore, we may next assume that $H$ is a tree.

We will first show that the following inequality holds:

|3_{\Delta^{+}}(S)|+|3_{\Delta^{-}}(S)|+2t_{1}(S)+2t_{2}(S)\geq 4.

(6)

Note that each leaf of $H$ corresponds to a 3-face of $S$ which contains a $C$ -vertex or at least two $3_{\Delta^{+}}$ - or $3_{\Delta^{-}}$ -vertices. Formula 6 follows when $H$ is not an isolated vertex. Next, let $H$ be an isolated vertex, i.e., $S$ is a 3-face. By Lemma 3.8 and the assumption that $S$ is not a positive $(3,3,3)$ -face, $S$ contains a $C$ -vertex. It follows that $S$ contains either another $C$ -vertex or two $3_{\Delta^{+}}$ - or $3_{\Delta^{-}}$ -vertices, yielding Formula 6 as well.

Combining Formulas 3 and 5 gives $|4_{\bowtie}(S)|\geq|3_{\Delta}(S)|+t_{1}(S)+t_{2}(S)-3.$ Hence, we can deduce from Formula 4 that

ch^{*}(S)\geq\frac{8}{27}|3_{\Delta^{+}}(S)|+\frac{4}{27}|3_{\Delta^{-}}(S)|+\frac{4}{27}|3_{\Delta^{\star}}(S)|+\frac{2}{3}t_{1}(S)+\frac{10}{9}t_{2}(S)-\frac{4}{3}.

(7)

Clearly, both $3_{\Delta^{+}}(S)$ and $3_{\Delta^{-}}(S)$ are even integers, and if $t_{1}(S)=1$ then $t_{2}(S)\geq 1$ . So by applying Formula 6, we can deduce from Formula 7 that $ch^{*}(S)\geq 0$ except the following six cases:

(a)

$|3_{\Delta^{+}}(S)|=0$ , $|3_{\Delta^{-}}(S)|=4$ , $|3_{\Delta^{\star}}(S)|\leq 4$ , $t_{1}(S)=t_{2}(S)=0$ ;
(b)

$|3_{\Delta^{+}}(S)|=2$ , $|3_{\Delta^{-}}(S)|=2$ , $|3_{\Delta^{\star}}(S)|\leq 2$ , $t_{1}(S)=t_{2}(S)=0$ ;
(c)

$|3_{\Delta^{+}}(S)|=4$ , $|3_{\Delta^{-}}(S)|=0$ , $|3_{\Delta^{\star}}(S)|=0$ , $t_{1}(S)=t_{2}(S)=0$ ;
(d)

$|3_{\Delta^{+}}(S)|=0$ , $|3_{\Delta^{-}}(S)|=6$ , $|3_{\Delta^{\star}}(S)|\leq 2$ , $t_{1}(S)=t_{2}(S)=0$ ;
(e)

$|3_{\Delta^{+}}(S)|=0$ , $|3_{\Delta^{-}}(S)|=8$ , $|3_{\Delta^{\star}}(S)|=0$ , $t_{1}(S)=t_{2}(S)=0$ ;
(f)

$|3_{\Delta^{+}}(S)|=2$ , $|3_{\Delta^{-}}(S)|=4$ , $|3_{\Delta^{\star}}(S)|=0$ , $t_{1}(S)=t_{2}(S)=0$ .

Next we consider these exceptional cases, for which the calculation of $ch^{*}(S)$ will always be based on Formula 7. Since $t_{1}(S)=t_{2}(S)=0$ , $S$ has no $C$ -vertices. Recall that $H$ is a subcubic planar tree. So, $H$ contains two less vertices of degree 3 (in $H$ ) than leaves. Correspondingly, $S$ contains two less $(4,4,4)$ -faces than $(3,3,4)$ -faces. Moreover, the remaining 3-faces of $S$ must be $(3,4,4)$ -faces.

For Cases a, b, and c: Since $|3_{\Delta^{+}}(S)|+|3_{\Delta^{-}}(S)|=4$ , $H$ is a path. Denote by $k$ the length of $H$ . If $k=1$ (i.e., $H$ is an edge), then $S$ is Configuration b-1, which however is reducible by Lemma 3.9. So, $k\geq 2$ . The snowflake $S$ can be labelled as follows: let $T_{0}=[uvw_{1}]$ and $T_{k}=[w_{k}xy]$ be two $(3,3,4)$ -faces, and $T_{i}=[w_{i}z_{i}w_{i+1}]$ be a $(3,4,4)$ -face for $1\leq i\leq k-1$ so that $T_{j}$ intersects with $T_{j+1}$ at the 4-vertex $w_{j+1}$ for $0\leq j\leq k-1$ . Let $t_{j}$ be the outer neighbor of $z_{j}$ .

Case c: Since $G$ has no Configuration c-1 by Lemma 3.14, $k\geq 7$ . By Lemma 3.13, the snowflake $S$ is related to at least four nice 9-faces, whose nice vertices send to $S$ a total charge at least $\frac{2}{27}\times 4$ by $R\ref{rule_nice face}$ . Therefore, it follows from Formula 7 that $ch^{*}(S)\geq\frac{8}{27}\times 4-\frac{4}{3}+\frac{2}{27}\times 4>0.$

Case b: W.l.o.g., let $T_{0}$ be negative. Since $G$ has no Configuration d-1 by Lemma 3.10, $T_{1}$ is negative. Since $G$ has no Configuration b-2 by Lemma 3.9, $k\notin\{2,3\}$ . Hence, $k\geq 4$ . Since $G$ has no Configuration e-3 by Lemma 3.11, neither $t_{1}$ nor $t_{2}$ is a bad vertex. So, $|3_{\Delta^{\star}}(S)|=2$ , i.e., all of $t_{3},t_{4},\ldots,t_{k-1}$ are bad vertices. Since $G$ has no Configuration c-2 by Lemma 3.14, $k\geq 9$ . By Lemma 3.13, $S$ is related to at least four nice 9-faces, strengthening Formula 7 as $ch^{*}(S)\geq\frac{8}{27}\times 2+\frac{4}{27}\times 2+\frac{4}{27}\times 2-\frac{4}{3}+\frac{2}{27}\times 4>0$ by $R\ref{rule_nice face}$ .

Case a: Similar to Case b, we can show that $k\geq 4$ , both $T_{1}$ and $T_{k-1}$ are negative, and none of $t_{1},t_{2},t_{k-2},t_{k-1}$ are bad vertices. Let $P=w_{1}w_{2}\ldots w_{k}$ .

Case a.1: assume that $T_{1},T_{2},\ldots,T_{k-1}$ locate on the same side of $P$ . So, $P$ belongs to the boundary of some face, say $f=[uw_{1}w_{2}\ldots w_{k}ys_{1}s_{2}\ldots s_{n}]$ .

Case a.1.1: let $k\geq 5$ . In this case, $|3_{\Delta^{\star}}(S)|=4$ , i.e., $t_{3},t_{4},\ldots,t_{k-3}$ (if exist) are all bad vertices. If $d(f)\geq 10$ , then $f$ sends to each vertex of $uw_{1}w_{2}\ldots w_{k}y$ charge at least $\frac{6}{10}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+(\frac{6}{10}-\frac{5}{9})\times(2+k)>0.$ Next, let $d(f)=9$ . Then $k\in\{5,6,7\}$ . For $k=5$ , since $G$ has no Configuration f-3 by Lemma 3.17, at least one of $s_{1}$ and $s_{2}$ (w.l.o.g., say $s_{1}$ ) is not a $3_{\Delta}$ -vertex. Then $y$ sends no charge to $s_{1}$ and instead, it receives charge $\frac{2}{27}$ from $s_{1}$ , giving $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+(\frac{2}{27}+\frac{2}{27})=0.$ For $k\in\{6,7\}$ , it is obvious that neither the outer neighbor of $u$ nor that of $y$ is a $3_{\Delta^{+}}$ -vertex. So, both $u$ and $y$ send no charge to their outer neighbor, yielding $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+\frac{2}{27}\times 2=0$ .

Case a.1.2: let $k=4$ . In this case, $t_{2}$ coincides with $t_{k-2}$ , and thus $|3_{\Delta^{\star}}(S)|=3$ .

If $d(f)\geq 11$ , then $f$ sends to each vertex of $uw_{1}w_{2}w_{3}w_{4}y$ charge at least $\frac{7}{11}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 3-\frac{4}{3}+(\frac{7}{11}-\frac{5}{9})\times 6>0.$

Let $d(f)=10$ . If both $s_{1}$ and $s_{4}$ are $3_{\Delta^{+}}$ -vertices, say 3-faces $[s_{1}r_{12}s_{2}]$ and $[s_{3}r_{34}s_{4}]$ , then at least one of $xys_{1}r_{12}$ , $s_{1}s_{2}s_{3}s_{4}$ , and $r_{34}s_{4}uv$ is Configuration e-2, contradicting Lemma 3.11. Hence, at least one of $s_{1}$ and $s_{4}$ is not a $3_{\Delta^{+}}$ -vertex and correspondingly, at least one of $u$ and $y$ sends no charge to its outer neighbor. Moreover, $f$ sends to each vertex of $uw_{1}w_{2}w_{3}w_{4}y$ charge $\frac{6}{10}$ by $R\ref{rule-face}$ . Therefore, $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 3-\frac{4}{3}+\frac{2}{27}+(\frac{6}{10}-\frac{5}{9})\times 6>0.$

It remains to assume that $d(f)=9$ . If $s_{1}$ is a $4^{+}$ -vertex or an external 3-vertex, i.e., $s_{1}$ is a 2-nice vertex of $f$ , then $s_{1}$ sends charge $\frac{4}{27}$ to $S$ and $\frac{2}{27}$ to $y$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 3-\frac{4}{3}+\frac{4}{27}+(\frac{2}{27}+\frac{2}{27})=0.$ Hence, we may next assume that $s_{1}$ is an internal 3-vertex and similarly, so does $s_{3}$ . Since $G$ has no Configuration f-1 by Lemma 3.17, $d(s_{2})\geq 4$ . Then $s_{1}$ cannot be a $3_{\Delta^{+}}$ -vertex, since otherwise $xys_{1}r_{12}$ is Configuration e-2. Similarly, neither does $s_{3}$ . So, both $u$ and $y$ send no charge to their outer neighbors. If $d(s_{2})\neq 4$ , i.e., $s_{2}$ is a 2-nice vertex of $f$ , then $s_{2}$ sends charge $\frac{4}{27}$ to $S$ , giving $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 3-\frac{4}{3}+\frac{2}{27}\times 2+\frac{4}{27}=0.$ Next, let $d(s_{2})=4$ . Since $G$ has no Configuration f-2 by Lemma 3.17, neither $s_{1}$ nor $s_{3}$ is a $3_{\Delta^{-}}$ -vertex. So, both $u$ and $y$ receive charge $\frac{2}{27}$ from their outer neighbors, giving $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 3-\frac{4}{3}+(\frac{2}{27}+\frac{2}{27})\times 2=0.$

Case a.2: assume that not all of $T_{1},T_{2},\ldots,T_{k-1}$ locate on the same side of $P$ . Recall that both $T_{1}$ and $T_{k-1}$ are negative. If $k=4$ , then either $S$ is Configuration b-2 or $S$ contains Configuration d-2, contradicting Lemma 3.9 or 3.10, respectively. Hence, $k\geq 5$ . It follows that $|3_{\Delta^{\star}}(S)|=4$ , and thus $t_{3},t_{4},\ldots,t_{k-3}$ (if exist) are all bad vertices.

Case a.2.1: let $k=5$ . Since $G$ has none of Configurations b-2, b-3 and d-1, we can deduce that precisely one of $T_{2}$ and $T_{3}$ (w.l.o.g., say $T_{3}$ ) is positive, and $T_{1}$ locates on one side of $P$ while $T_{2},T_{3},T_{4}$ locate on the other side. So, $t_{1}z_{1}w_{2}w_{3}w_{4}w_{5}$ belongs to the boundary of some face, say $f=[t_{1}z_{1}w_{2}w_{3}w_{4}w_{5}ys_{1}s_{2}\ldots]$ . If $d(f)\geq 10$ , then $f$ sends to each vertex of $z_{1}w_{2}w_{3}w_{4}w_{5}y$ charge at least $\frac{6}{10}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+(\frac{6}{10}-\frac{5}{9})\times 6>0.$ Next, let $d(f)=9$ . If $s_{1}$ is not a $3_{\Delta^{+}}$ - or $3_{\Delta^{-}}$ -vertex, then $y$ receives charge $\frac{2}{27}$ from $s_{1}$ by $R\ref{rule-A1-vertex}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+(\frac{2}{27}+\frac{2}{27})=0.$ Next, let $s_{1}$ be a $3_{\Delta^{+}}$ - or $3_{\Delta^{-}}$ -vertex. Moreover, if at least one of $t_{1}$ and $s_{2}$ is a nice vertex of $f$ , then it is a 2-nice vertex and sends charge $\frac{4}{27}$ to $S$ , giving $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+\frac{4}{27}=0.$ Next, let $t_{1}$ be an internal 3-vertex and let $d(s_{2})\leq 4$ . Since $G$ has no Configuration b-1, we can deduce that $t_{1}$ is not a $3_{\Delta^{+}}$ - or $3_{\Delta^{-}}$ -vertex. Moreover, since $G$ has no Configuration e-2, we can deduce that $s_{1}$ cannot be a $3_{\Delta^{+}}$ -vertex. Now, both $y$ and $z_{1}$ send no charge to their outer neighbors, giving $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+\frac{2}{27}\times 2=0.$

Case a.2.2: let $k\geq 6$ . Since $G$ has no Configuration e-3 by Lemma 3.11, both $T_{2}$ and $T_{k-2}$ are positive. Since $G$ has neither Configuration d-2 nor Configuration c-3 by Lemma 3.10 or 3.14, $T_{1},T_{2},T_{k-2},T_{k-1}$ locate on the same side of $P$ . Denote by $i$ the minimum index such that $T_{i}$ and $T_{1}$ locate on different sides of $P$ , and $j$ the maximum one. W.l.o.g., let $uw_{1}w_{2}\dots w_{i}z_{i}t_{i}$ belong to the boundary of a face $f_{1}$ , and $t_{j}z_{j}w_{j+1}w_{j+2}\ldots w_{k}y$ belong to the boundary of a face $f_{2}$ . If $d(f_{1})\geq 10$ , then $f_{1}$ sends to each vertex of $uw_{1}w_{2}\dots w_{i}z_{i}$ charge at least $\frac{6}{10}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+(\frac{6}{10}-\frac{5}{9})\times(2+i)>0$ . We may next assume that $d(f_{1})=9$ and similarly, $d(f_{2})=9$ . Notice that $3\leq i\leq j\leq k-3$ . Since $G$ has no Configuration e-2, we can deduce that the outer neighbor of $u$ (resp., $y$ ) cannot be a $3_{\Delta^{+}}$ -vertex and so it receives no charge from $u$ (resp., $y$ ), strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 4+\frac{4}{27}\times 4-\frac{4}{3}+\frac{2}{27}\times 2=0$ .

Case d: Clearly, $H$ is a subdivision of a claw. Denote by $k_{1},k_{2},k_{3}$ ( $1\leq k_{1}\leq k_{2}\leq k_{3}$ ) the length of paths between a leaf and the 3-vertex in $H$ . So, the snowflake $S$ can be labelled as follows: let $T_{0}=[w_{11}w_{21}w_{31}]$ be a $(4,4,4)$ -face, $T_{ik_{i}}=[w_{ik_{i}}x_{i}y_{i}]$ be a $(3,3,4)$ -face, $T_{ij}=[w_{ij}z_{ij}w_{i,j+1}]$ be a $(3,4,4)$ -face, $t_{ij}$ be the outer neighbor of $z_{ij}$ so that $T_{i,l-1}$ intersects with $T_{il}$ at the 4-vertex $w_{il}$ for $1\leq i\leq 3$ , $1\leq j\leq k_{i}-1$ , and $1\leq l\leq k_{i}$ . W.l.o.g., let $w_{11},w_{21},w_{31}$ locate in clockwise order around $T_{0}$ , and so do $x_{1},y_{1},x_{2},y_{2},x_{3},y_{3}$ .

For $1\leq i\leq 3$ , if $k_{i}\geq 2$ , then the face $T_{i,k_{i}-1}$ is negative (since $G$ has no Configuration d-1 by Lemma 3.10) and $t_{i,k_{i}-1}$ is not a bad vertex (since $G$ has no Configuration e-3 by Lemma 3.11). Furthermore, if $k_{i}\geq 3$ , then $t_{i,k_{i}-2}$ is not a bad vertex (again since $G$ has no Configuration e-3). Since $|3_{\Delta^{\star}}(S)|\leq 2$ , it suffices to consider two cases: either $(k_{1},k_{2},k_{3})=(1,1,k_{3})$ or $(k_{1},k_{2},k_{3})=(1,2,2)$ .

Case d.1: assume that $(k_{1},k_{2},k_{3})=(1,1,k_{3})$ . Since $G$ has neither Configuration g-1 nor Configuration g-2 by Lemma 3.15, $k_{3}\geq 4$ . So, $t_{3,1},t_{3,2},\ldots,t_{3,k_{3}-3}$ are all bad vertices. Since $G$ has no Configuration g-5 by Lemma 3.15, $k_{3}\geq 8$ . By Lemma 3.13, the snowflake $S$ is related to at least three nice 9-faces, whose nice vertices send to $S$ a total charge at least $\frac{2}{27}\times 3$ by $R\ref{rule_nice face}$ . Therefore, $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+\frac{2}{27}\times 3>0.$

Case d.2: assume that $(k_{1},k_{2},k_{3})=(1,2,2)$ . Since $G$ has no Configuration g-3 by Lemma 3.15, $T_{21}$ and $T_{31}$ must locate on the same side of $w_{22}w_{21}w_{31}w_{32}$ . We distinguish two cases depending on which side.

Case d.2.1: let $y_{2}w_{22}w_{21}w_{31}w_{32}x_{3}$ belong to the boundary of some face $f_{23}$ . If $d(f_{23})\geq 10$ , then $f_{23}$ sends to each vertex of $y_{2}w_{22}w_{21}w_{31}w_{32}x_{3}$ charge at least $\frac{6}{10}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+(\frac{6}{10}-\frac{5}{9})\times 6>0.$ We may next assume that $d(f_{23})=9$ . Let $f_{23}=[y_{2}w_{22}w_{21}w_{31}w_{32}x_{3}s_{1}s_{2}s_{3}]$ . If neither $s_{1}$ nor $s_{3}$ is a $3_{\Delta^{+}}$ -vertex, then both $x_{3}$ and $y_{2}$ send no charge to their outer neighbors, strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+\frac{2}{27}\times 2=0.$ W.l.o.g., next let $s_{1}$ be a $3_{\Delta^{+}}$ -vertex. Since $G$ has no Configuration e-2, $s_{2}$ must be a $3_{\Delta^{+}}$ -vertex and hence, $s_{3}$ cannot be an internal 3-vertex. So, $y_{2}$ receives charge $\frac{2}{27}$ from $s_{3}$ , giving $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+(\frac{2}{27}+\frac{2}{27})=0.$

Case d.2.2: let $y_{1}w_{11}w_{21}w_{22}x_{2}$ (resp., $y_{3}w_{32}w_{31}w_{11}x_{1}$ ) belong to the boundary of some face $f_{12}$ (resp., $f_{13}$ ). If $d(f_{12})\geq 10$ , then $f_{12}$ sends to each vertex of $y_{1}w_{11}w_{21}w_{22}x_{2}$ charge at least $\frac{6}{10}$ by $R\ref{rule-face}$ , strengthening Formula 7 as $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+(\frac{6}{10}-\frac{5}{9})\times 5>0.$ We may next assume that $d(f_{12})=9$ and similarly, $d(f_{13})=9$ . Let $f_{12}=[y_{1}w_{11}w_{21}w_{22}x_{2}s_{1}s_{2}s_{3}s_{4}]$ . If both $s_{1}$ and $s_{4}$ are $3_{\Delta^{+}}$ -vertices, say 3-faces $[s_{1}r_{12}s_{2}]$ and $[s_{3}r_{34}s_{4}]$ . It is easy to see that at least one of $y_{2}x_{2}s_{1}r_{12}$ , $s_{1}s_{2}s_{3}s_{4}$ , and $r_{34}s_{4}y_{1}x_{1}$ is Configuration e-2, contradicting Lemma 3.11. So, at least one of $s_{1}$ and $s_{4}$ is not a $3_{\Delta^{+}}$ -vertex and consequently, at least one of $y_{1}$ and $x_{2}$ sends no charge to its outer neighbor. Similarly, at least one of $x_{1}$ and $y_{3}$ sends no charge to its outer neighbor. Therefore, Formula 7 can be strengthened as $ch^{*}(S)\geq\frac{4}{27}\times 6+\frac{4}{27}\times 2-\frac{4}{3}+\frac{2}{27}\times 2=0.$

Case e: Clearly, $S$ consists of two $(4,4,4)$ -faces, four negative $(3,3,4)$ -faces, and $(3,4,4)$ -faces. Recall that $|3_{\Delta^{\star}}(S)|=0$ . Since $G$ has no Configuration e-3 by Lemma 3.11, each $(4,4,4)$ -face of $S$ must intersect with two negative $(3,3,4)$ -faces. Since $G$ has neither Configuration h-1 nor Configuration h-2 by Lemma 3.16, $S$ must be a $J$ -extension of Configuration h-1 for some $k\geq 4$ . By Lemma 3.13, $S$ is related to at least two nice 9-faces, whose nice vertices send to $S$ a total charge at least $\frac{2}{27}\times 2$ by $R\ref{rule_nice face}$ . Therefore, $ch^{*}(S)\geq\frac{4}{27}\times 8-\frac{4}{3}+\frac{2}{27}\times 2=0.$

Case f: We apply a similar argument as Case e. Clearly, $S$ consists of one $(4,4,4)$ -face, one positive $(3,3,4)$ -face, two negative $(3,3,4)$ -faces, and $(3,4,4)$ -faces. Since $G$ has no Configuration e-3 by Lemma 3.11, the $(4,4,4)$ -face of $S$ intersects with two negative $(3,3,4)$ -faces. Since $G$ has neither Configuration g-1 nor Configuration g-4 by Lemmas 3.15, $S$ must be a $J_{k}$ -extension of Configuration g-1 for some $k\geq 5$ . By Lemma 3.13, the snowflake $S$ is related to at least three nice 9-faces, whose nice vertices send to $S$ a total charge at least $\frac{2}{27}\times 3$ by $R\ref{rule_nice face}$ . Therefore, $ch^{*}(S)\geq\frac{8}{27}\times 2+\frac{4}{27}\times 4-\frac{4}{3}+\frac{2}{27}\times 3>0.$ ∎

Claim 3.19.

$ch^{*}(v)\geq 0$ for each internal $C$ -vertex $v$ of $G$ .

Proof.

Since $v$ is internal, $v$ is adjacent to no strings of $G$ . So, $R\ref{rule-string}$ is not applicable to $v$ . Denote by $n_{3}(v)$ and $n_{9}(v)$ the number of 3-faces and $9^{+}$ -faces containing $v$ , respectively. Let $n(v)$ be the number of $3_{\Delta}$ -vertices whose outer neighbor is $v$ . Since $G\in\mathcal{G}$ ,

\begin{split}n_{9}(v)&\geq n(v)+n_{3}(v),\\ d(v)&\geq n(v)+2n_{3}(v).\end{split}

(8)

The vertex $v$ sends charge 1 to each incident 3-face by $R$ 2, and charge at most $\frac{2}{9}$ to each $3_{\Delta}$ -vertex whose outer neighbor is $v$ by $R$ 4. Moreover, $v$ receives charge at least $\frac{5}{9}$ from each incident $9^{+}$ -face by $R$ 3. Finally, recall that a nice 9-face is related to precisely one snowflake. If $v$ is a nice vertex of a nice 9-face $f$ , then $v$ sends to the related snowflake of $f$ charge at most $\frac{4}{27}$ by $R\ref{rule_nice face}$ . Therefore, we can conclude from above that

\begin{split}ch^{*}(v)&\geq d(v)-4-n_{3}(v)-\frac{2}{9}n(v)+(\frac{5}{9}-\frac{4}{27})n_{9}(v)\\ &=d(v)-4+\frac{2}{27}n(v)+\frac{11}{27}(n_{9}(v)-n_{3}(v))-\frac{8}{27}(n(v)+2n_{3}(v))\\ &\geq d(v)-4+\frac{2}{27}n(v)+\frac{11}{27}n(v)-\frac{8}{27}d(v)\\ &=\frac{19}{27}d(v)-4+\frac{13}{27}n(v),\end{split}

(9)

where the second inequality uses Formula 8. By Lemma 3.4, $d(v)\geq 3$ . We distinguish the following three cases.

Case 1: assume that $d(v)\geq 5$ . The last line of Formula 9 gives $ch^{*}(v)\geq 0$ directly except when $d(v)=5$ and $n(v)=0$ . For this exceptional case, $n_{3}(v)\leq 2$ , and $n_{3}(v)=2$ implies $n_{9}(v)=3$ . So, the first line of Formula 9 yields $ch^{*}(v)\geq 1-n_{3}(v)+\frac{11}{27}n_{9}(v)\geq 0$ .

Case 2: assume that $d(v)=4$ . Since $n(v)\leq n_{9}(v)$ by Formula 8, if $n_{3}(v)=0$ , then the first line of Formula 9 gives $ch^{*}(v)\geq-\frac{2}{9}n(v)+\frac{11}{27}n_{9}(v)\geq 0$ . Since $v$ is not a $4_{\bowtie}$ -vertex, it remains to assume that $n_{3}(v)=1$ . Denote by $f_{1},f_{2},f_{3},f_{4}$ the faces containing $v$ , and $w,x,y,z$ the neighbors of $v$ , in the same cyclic order with $f_{4}=[vwx]$ . Clearly, both $f_{1}$ and $f_{3}$ are $9^{+}$ -faces. If $n(v)=0$ , then $v$ cannot be a nice vertex by definition, strengthening the first line of Formula 9 as $ch^{*}(v)\geq-1+\frac{5}{9}\times 2>0$ . Next, let $n(v)\in\{1,2\}$ . Then $f_{2}$ is also a $9^{+}$ -face. Note that if $y$ (resp., $z$ ) is a bad vertex, then $v$ cannot be a 2-nice vertex of $f_{1}$ (resp., $f_{3}$ ). Also note that if both $y$ and $z$ are bad vertices, then $v$ cannot be a 2-nice vertex of $f_{2}$ . Considering charges $v$ receives from incident $9^{+}$ -faces and charges $v$ sends to $f_{4}$ , to $y$ and $z$ , and to snowflakes related to $f_{1}$ , $f_{2}$ or $f_{3}$ , we have $ch^{*}(v)\geq\frac{5}{9}\times 3-1-\max\{\frac{2}{9}\times 2+\frac{2}{27}\times 3,(\frac{2}{9}+\frac{2}{27})+(\frac{4}{27}\times 2+\frac{2}{27}),\frac{2}{27}\times 2+\frac{4}{27}\times 3\}=0$ .

Case 3: assume that $d(v)=3$ . In this case, $n_{3}(v)=0$ and $v$ cannot be a nice vertex. Clearly, the faces incident with $v$ are one $5^{+}$ -face and two $7^{+}$ -faces if $n(v)=0$ , one $5^{+}$ -face and two $9^{+}$ -faces if $n(v)=1$ , and three $9^{+}$ -faces if $n(v)\geq 2$ . Therefore, $ch^{*}(v)\geq-1+\min\{\frac{1}{5}+\frac{3}{7}\times 2,-\frac{2}{9}+\frac{1}{5}+\frac{5}{9}\times 2,-\frac{2}{9}\times 3+\frac{5}{9}\times 3\}=0$ by $R\ref{rule-C-vertex}$ and $R\ref{rule-face}$ . ∎

Claim 3.20.

$ch^{*}(v)>0$ for each external $C$ -vertex $v$ of $G$ .

Proof.

By Lemma 3.5 and the rule $R$ 6, $v$ sends to the vertices of each adjacent string a total charge at most

\begin{split}\frac{12-d(f)}{6d(f)}\times(\lfloor\frac{d(f)-1}{2}\rfloor-1)&\leq\frac{(12-d(f))(d(f)-3)}{12d(f)}=\frac{5}{4}-(\frac{d(f)}{12}+\frac{3}{d(f)})\\ &\leq\frac{5}{4}-2\sqrt{\frac{d(f)}{12}\times\frac{3}{d(f)}}=\frac{1}{4},\end{split}

(10)

where $f$ is the face (other than $f_{0}$ ) containing this string.

Take the notation $n_{3}(v)$ , $n_{9}(v)$ , and $n(v)$ for the same meaning as in the proof of Claim 3.19. So, Formula 8 still holds. However, Formula 9 should be changed to

\begin{split}ch^{*}(v)&\geq d(v)-4-n_{3}(v)-\frac{2}{9}n(v)+(\frac{5}{9}-\frac{4}{27})(n_{9}(v)-1)+\frac{4}{3}-\frac{1}{4}\times 2\\ &\geq d(v)-4-\frac{16}{27}n_{3}(v)+\frac{5}{27}n(v)+\frac{23}{54}\quad\quad\text{(by using $n_{9}(v)\geq n(v)+n_{3}(v)$)}\\ &\geq\frac{19}{27}d(v)-4+\frac{13}{27}n(v)+\frac{23}{54}.\quad\quad\text{(by using $n_{3}(v)\leq\frac{d(v)-n(v)}{2}$)}\end{split}

(11)

This is because $v$ receives from $f_{0}$ charge $\frac{4}{3}$ and additionally, $v$ sends a total charge at most $\frac{1}{4}\times 2$ to the vertices of adjacent strings by Formula 10.

Therefore, the conclusion $\mathrm{ch}^{*}(v)\geq 0$ follows directly from the last line of Formula 11 when either $d(v)\geq 6$ or $d(v)=5$ and $n(v)\geq 1$ , follows from the second line of Formula 11 when either $(d(v),n(v))=(5,0)$ (since $n_{3}(v)\leq 2$ in this case) or $(d(v),n_{3}(v))=(4,0)$ , and follows from the first line of Formula 11 when $(d(v),n_{3}(v))=(4,1)$ (since $n_{9}(v)\geq\min\{2+n(v),3\}$ in this case). So, it remains to consider the following two cases:

Firstly, assume that $(d(v),n_{3}(v))=(4,2)$ . In this case, $v$ cannot be a nice vertex by definition. If $d(f_{0})=3$ , then $v$ receives charge $\frac{4}{3}$ from $f_{0}$ and charge $\frac{5}{9}$ from each incident $9^{+}$ -face, and $v$ sends charge $1$ to the other incident 3-face and charge at most $\frac{1}{4}$ to each adjacent string, giving $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{5}{9}\times 2-1-\frac{1}{4}\times 2>0$ . We may next assume that $d(f_{0})\neq 3$ , i.e., $f_{0}$ is one of the $9^{+}$ -faces containing $v$ . So, $v$ receives charge $\frac{4}{3}$ from $f_{0}$ and charge $\frac{5}{9}$ from the other incident $9^{+}$ -face, and $v$ sends to each incident 3-face charge $\frac{5}{9}$ by $R\ref{rule-C-vertex}$ , giving $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{5}{9}-\frac{5}{9}\times 2>0$ .

Secondly, assume that $d(v)=3$ . Denote by $f_{1}$ and $f_{2}$ the two faces (besides $f_{0}$ ) containing $v$ with $d(f_{1})\leq d(f_{2})$ . First let $d(f_{1})=3$ . Then $d(f_{2})\geq 9$ and $v$ is not a nice vertex. Note that $v$ receives charge $\frac{4}{3}$ from $f_{0}$ by $R\ref{rule-ext-face}$ and charge at least $\frac{5}{9}$ from $f_{2}$ by $R\ref{rule-face}$ , and $v$ sends charge $\frac{5}{9}$ to $f_{1}$ by $R\ref{rule-C-vertex}$ and charge at most $\frac{1}{4}$ to one adjacent string (if exists) by $R$ 6, giving $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{5}{9}-\frac{5}{9}-\frac{1}{4}>0$ . Next let $d(f_{1})\geq 5$ . Since $G\in\mathcal{G}$ , $f_{2}$ is a $7^{+}$ -face. So, $v$ receives a total charge at least $\frac{4}{3}+\frac{1}{5}+\frac{3}{7}$ from incident faces. Moreover, $v$ sends to adjacent strings (if exist) a total charge at most $\frac{1}{4}\times 2$ . If the internal neighbor of $v$ is not a $3_{\Delta}$ -vertex, then $v$ sends no charge to this neighbor and $v$ is not a nice vertex of $f_{1}$ or $f_{2}$ , yielding $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{1}{5}+\frac{3}{7}-\frac{1}{4}\times 2>0$ ; otherwise, both $f_{1}$ and $f_{2}$ are $9^{+}$ -faces, yielding $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{5}{9}+\frac{5}{9}-\frac{1}{4}\times 2-\frac{2}{9}-\frac{4}{27}\times 2>0$ . ∎

Claim 3.21.

$ch^{*}(v)\geq 0$ for each 2-vertex $v$ of $G$ .

Proof.

Let $f$ be the face containing $v$ other than $f_{0}$ . Clearly, $v$ receives charge $\frac{4}{3}$ from $f_{0}$ by $R$ 1 and charge $\frac{d(f)-4}{d(f)}$ from $f$ by $R$ 3, which gives $ch^{*}(v)\geq d(v)-4+\frac{4}{3}+\frac{d(f)-4}{d(f)}=\frac{d(f)-12}{3d(f)}\geq 0$ , provided by $d(f)\geq 12$ . Next, let $d(f)\leq 11$ . Denote by $L$ the string containing $v$ . Lemma 3.5 implies that the two vertices adjacent to $L$ do not coincide, and they send to $v$ a total charge $\frac{12-d(f)}{6d(f)}\times 2$ by $R$ 6. So, $ch^{*}(v)\geq\frac{d(f)-12}{3d(f)}+\frac{12-d(f)}{6d(f)}\times 2=0.$ ∎

Claim 3.22.

$ch^{*}(f_{0})\geq 0$ .

Proof.

Since $R$ 1 is the only rule making $f_{0}$ move charge out, we have $ch^{*}(f_{0})=d(f_{0})+4-\frac{4}{3}\times d(f_{0})=4-\frac{d(f_{0})}{3}\geq 0$ , since $d(f_{0})\leq 12$ . ∎

Claim 3.23.

$ch^{*}(f)\geq 0$ for each $5^{+}$ -face $f$ of $G$ with $f\neq f_{0}$ .

Proof.

Since $R$ 3 is the only rule making $f$ move charge out, we have $ch^{*}(f)=d(f)-4-\frac{d(f)-4}{d(f)}\times d(f)=0.$ ∎

As a counterexample to Theorem 2.2, $(G,\sigma)$ must contain an external $C$ -vertex. So by Claims 3.18–3.23, we have $\sum_{x\in V\cup F}ch^{*}(x)>0$ , completing the proof of Theorem 2.2.

4 Acknowledgement

Ligang Jin is supported by NSFC 11801522, U20A2068. Yingli Kang is supported by NSFC 11901258 and ZJNSF LY22A010016. Xuding Zhu is supported by NSFC 12371359, U20A2068.

References

[1] H. L. Abbott and B. Zhou, On small faces in 4-critical graphs, Ars Combin. 32 (1991) 203-207.
[2] O. V. Borodin, Colorings of plane graphs: a survey, Discrete Math. 313 (2013) 517–539.
[3] O. V. Borodin, A. N. Glebov, A. Raspaud, and M. R. Salavatipour, Planar graphs without cycles of length from 4 to 7 are 3-colorable, J. Combin. Theory Ser. B 93 (2005) 303-311.
[4] V. Cohen-Addad, M. Hebdige, D. Král, Z. Li, and E. Salgado, Steinberg’s Conjecture is false, J. Combin. Theory Ser. B 122 (2017) 452-456.
[5] Z. Dvořák and L. Postle, Correspondence coloring and its application to list-coloring planar graphs without cycles of lengths 4 to 8, J. Combin. Theory Ser. B 129 (2018) 38-54.
[6] R. Liu, S. Loeb, Y. Lin, and G. Yu, DP-3-coloring of some planar graphs, Discrete Math. 342 (1) (2019) 178-189.
[7] R. Steinberg, The state of the three color problem, in: J. Gimbel, J. W. Kennedy & L. V. Quintas (eds.), Quo Vadis, Graph Theory? Ann Discrete Math 55 (1993) 211-248.
[8] M. Voigt, A non-3-choosable planar graph without cycles of length 4 and 5, Discrete Math. 307 (2007) 1013-1015.

Planar graphs having no cycle of length 44, 66 or 88 are DP-3-colorable

Abstract

1 Introduction

Theorem 1.1 ([5]).

Definition 1.2.

Definition 1.3.

Theorem 1.4.

2 S3S_{3}-signed graphs and configurations

Theorem 2.1.

Theorem 2.2.

Remark 2.3.

Definition 2.4.

Definition 2.5.

Definition 2.6.

3 The proof of Theorem 2.2

3.1 Reducible configurations

Lemma 3.1.

Proof.

Lemma 3.2.

Proof.

Corollary 3.3.

Lemma 3.4.

Proof.

Lemma 3.5.

Proof.

Lemma 3.6.

Lemma 3.7.

Proof.

Lemma 3.8.

Proof.

Lemma 3.9.

Proof.

Lemma 3.10.

Proof.

Lemma 3.11.

Proof.

Lemma 3.12.

Proof.

Lemma 3.13.

Proof.

Lemma 3.14.

Proof.

Lemma 3.15.

Proof.

Lemma 3.16.

Proof.

Lemma 3.17.

Proof.

3.2 Discharging in GG

Claim 3.18.

Proof.

Claim 3.19.

Proof.

Claim 3.20.

Proof.

Claim 3.21.

Proof.

Claim 3.22.

Proof.

Claim 3.23.

Proof.

4 Acknowledgement

References

Planar graphs having no cycle of length $4$ , $6$ or $8$ are DP-3-colorable

2 $S_{3}$ -signed graphs and configurations

3.2 Discharging in $G$