Planar Voronoi Diagrams for Sums of Convex Functions,
Smoothed Distance, and Dilation

Any bivariate function $f$ and finite set of point sites $p_{i}$ in the plane give rise to a minimization diagram in which the cell for site $p_{i}$ consists of points $q$ such that the value of the translated function $f(q-p_{i})$ is less than or equal to the value of any of the other translates of $f$. A familiar example is given by Euclidean Voronoi diagrams, the minimization diagrams of translates of the convex functions $f(x,y)=\sqrt{x^{2}+y^{2}}$ (or, equivalently, $f(x,y)=x^{2}+y^{2}$) that measure the (squared) distance of $(x,y)$ from the origin.

Minimization diagrams have many applications, and typically have quadratic complexity [9], but in some important cases their complexity is much smaller. In a Euclidean Voronoi diagram, each cell is a convex polygon, so the Voronoi diagram for $n$ sites partitions the plane into $n$ connected regions and has $O(n)$ vertices and edges. These combinatorial facts form the basis of efficient algorithms for constructing Euclidean Voronoi diagrams and using them in other geometric algorithms. It is natural, therefore, to ask: Which other minimization diagrams have connected cells and a linear number of number of features?

A partial answer was provided by Chew and Drysdale [1]: Voronoi diagrams for convex distance functions have connected cells and linear complexity. A convex function $f$ is a convex distance function if, for any positive scalar $\alpha$ and any point $p$, $f(\alpha p)=\alpha\,f(p)$. Not every convex function has this property: it implies that the level sets $\{p\mid f(p)=k\}$ are all similar, and that the function is linear on rays from the origin, neither of which are true for all convex functions. Another answer is given by the abstract Voronoi diagrams [14] defined by a family of bisector curves that are required to intersect each other finitely many times and form simply connected cells. Bregman Voronoi diagrams [20] fall into this class: they have linear bisectors and convex-polygon cells. Abstract Voronoi diagrams may be constructed efficiently [14, 15, 19] but it is unclear how to tell whether a given convex function has minimization diagrams that form abstract Voronoi diagrams.

In this paper we study minimization diagrams for another class of convex functions, different from the convex distance functions. The functions we study take the form $f(x,y)=g(x)+h(y)$, where $g$ and $h$ are triply-differentiable and $g^{\prime}(x)g^{\prime\prime\prime}(x)<g^{\prime\prime}(x)^{2}$ and $h^{\prime}(y)h^{\prime\prime\prime}(y)<h^{\prime\prime}(y)^{2}$ for all $x$ and $y$. For example, squared Euclidean distance has this form with $g(x)=x^{2}$ and $h(y)=y^{2}$. More generally, $f(x,y)=|x|^{c}+|y|^{c}$ (for $c>1$) satisfies these requirements,¹¹1The divergence of the double derivative of $|x|^{c}$ at the origin when $c<2$, and its non-differentiability there when $2<c<3$, do not present any serious difficulties to our theory. and its minimization diagrams are the Voronoi diagrams for $L_{c}$ distance, known to have linear complexity [1]. We show in Section III that the minimization diagrams of arbitrary functions in this class have analogous properties:

• •

  Any two level sets $S_{r}(p)=\{q\mid f(q-p)=r\}$ are simple closed curves that intersect in at most two points; if they intersect at two points, they cross properly at these points. That is, these sets, which are defined analogously to Euclidean circles, form a family of pseudocircles [13, 16].

• •

  Any bisector $B(p,q)=\{s\mid f(s-p)=f(s-q)\}$ forms either an axis-parallel line or a simple curve that is both $x$-monotone and $y$-monotone; $f(s-p)$ and $f(s-q)$ vary unimodally along the bisector $B(p,q)$.

• •

  Any two bisectors $B(p,q)$ and $B(p,q^{\prime})$ intersect in at most one point; if they intersect, they do so at a proper crossing. That is, if we fix $p$ and let $q$ vary, the bisectors $B(p,q)$ form a weak pseudoline arrangement [6, 7, 3], and the correspondence between $q$ and $B(p,q)$ can be viewed as a form of duality for these pseudolines.

• •

  Each cell of the minimization diagram is simply connected, as it is a single cell in a pseudoline arrangement. Thus, the minimization diagram has linear complexity and, like Voronoi diagrams for convex distance functions and abstract Voronoi diagrams,²²2We do not show that these diagrams satisfy all requirements of an abstract Voronoi diagram, as we do not bound the number of crossings between bisectors for unrelated pairs of points. can be constructed in randomized expected time $O(n\log n)$ (Theorem 8).

In Section IV we provide examples showing that our restrictions are necessary: minimization diagrams for more general convex functions do not in general have these properties.

Our motivation for studying this type of minimization diagram comes from smoothed distance. Given a fixed point $o$ in the plane, the smoothed distance or biotope transform metric $d_{o}(p,q)=2d(p,q)/(d(p,o)+d(q,o)+d(p,q))$ [2, DezDez-09] is a geometric analogue of the Jaccard similarity measure for clustering binary data. A maximal set of points with a given minimum smoothed distance will be distributed around $o$ with exponentially decreasing density [2], but as we show in Section VI, the point spacing may be improved by using smoothed distance in Lloyd’s algorithm [DuFabGun-SR-99, 17], a continuous variant of $K$-means clustering that repeatedly moves each site to the centroid of its Voronoi cell.

Smoothed distance is a monotonic function of the dilation $(d(p,o)+d(o,q))/d(p,q)$, a measure of the quality of a star network as an approximation to the Euclidean distances among a set of points. For the maximum dilation pair of points $(p,q)$ from a set $P$ for a fixed center $o$, $q$ is among the $O(1)$ nearest neighbors to $p$ either in Euclidean distance or in the sequence of points sorted by distance from $o$, and this result forms the basis of an efficient algorithm for finding the center $o$ that minimizes the maximum dilation [8] . However, this can be simplified using smoothed distance: the maximum-dilation pair must be neighbors in the smoothed distance Voronoi diagram (Proposition 1).

Neither smoothed distance nor dilation are translates of convex functions. However, in Section II we use complex logarithms to transform the plane and we perform a suitable monotonic transformation of smoothed distance, showing that Voronoi diagrams for smoothed distance are equivalent to minimization diagrams for the convex function

As we require, this function is the sum of univariate functions $g(x)$ and $h(y)$, with $g^{\prime}g^{\prime\prime\prime}<(g^{\prime\prime})^{2}$. It is not true that $h^{\prime}h^{\prime\prime\prime}<(h^{\prime\prime})^{2}$ for all $y$, but it is true for $-\pi/2<y<\pi/2$, so smoothed distance Voronoi diagrams are well behaved whenever each Voronoi cell spans an angle of at most $\pi/2$ on each side of its site with respect to $o$ (Theorem 9).

Two important measures of similarity between sets $A$ and $B$ are the Hamming distance $d_{H}(A,B)=|A\mathbin{\triangle}B|$ (where $\mathbin{\triangle}$ denotes the symmetric difference of sets) and the Jaccard distance [12], which weights the Hamming distance by the size of the union of the sets:

A monotone transformation of this distance lies in the interval $[0,1]$:

The same formula defining the (modified) Jaccard distance in terms of the Hamming distance can be used to derive a new metric from any given metric space $(X,d)$ and fixed point $o\in X$. Define the $o$-smoothed distance or biotope transform metric by the formula

This is a metric on $X\setminus\{o\}$, as can be shown using the tight span [11, 4], the minimal $L_{\infty}$-like metric completion of a metric space. Any four points $\{o,p,q,r\}\subset(X,d)$ may be embedded isometrically into a metric space formed by an axis-aligned rectangle of the $L_{1}$ plane (possibly a degenerate rectangle), together with four line segments (possibly of length zero) connecting the corners of this rectangle to the four points. When the four line segments all have length zero, the four points are in cyclic order ($o$, $p$, $r$, $q$) on the rectangle’s corners, and the rectangle has aspect ratio $a$, then the triangle inequality for $d_{o}$ is satisfied exactly: $d_{o}(p,q)=1=\frac{1}{a+1}+\frac{a}{a+1}=d_{o}(p,r)+d_{o}(q,r)$. Increasing the length of the line segments connecting the four points to the rectangle or placing the points in a different cyclic order only strengthens the triangle inequality.

For the points within a $d$-ball of radius $\epsilon\,d(o,c)$ around a point $c$, the factor $d(p,o)+d(q,o)+d(p,q)$ in the definition of $d_{o}$ ranges from $(1-\epsilon)2d(o,c)$ to $(1+2\epsilon)2d(o,c)$, varying by a factor of approximately $1+3\epsilon$ within this range as $\epsilon$ approaches zero. Thus, closely spaced sets of points in the smoothed distance have distances that are approximately similar to their unsmoothed distances. As a metric space on $X\setminus\{o\}$, the smoothed distance $d_{o}$ is topologically equivalent to the metric induced by $d$ on the same space: both distances have the same open sets and neighborhood structures.

Smoothed distance $d_{o}$ for the Euclidean plane is invariant with respect to rotations and scaling centered at $o$. These transformations may be expressed by representing point $(x,y)$ as the complex number $x+iy$, with $o=0$: if $z$ is any complex number, then the product $zp$ may be interpreted geometrically as rotating the point $p$ by the angle $\angle z01$ and scaling the rotated point by $|z|$. With this interpretation,

$d_{o}(zp,zq)=d_{o}(p,q)$.

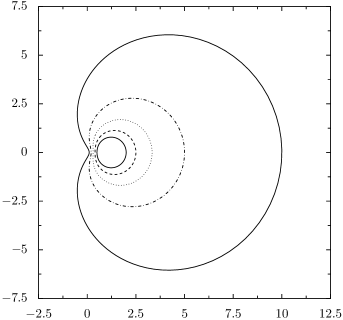
As Figure 1 shows, smoothed-distance circles with smaller radius closely resemble Euclidean circles, while larger-radius smoothed-distance circles are not even convex.

Smoothed distance is closely related to dilation, a measure of the quality of a graph as an approximation to a metric space [5]. The dilation of vertices $p$ and $q$ is the ratio of their distances in the graph and in the ambient space; the dilation of the graph is the largest dilation of any pair of vertices. For a star graph $G$ with center $o$ and all other vertices as leaves [8], the dilation of pair $(p,q)$ is

and the dilation of the whole star graph is

Because dilation is a monotonic transformation of smoothed distance, the point $p$ that is nearest to a query point $q$ in terms of smoothed distance is also the point that has the greatest dilation with $q$. The Voronoi diagram for smoothed distance partitions the plane into regions such that the region containing a query point $q$ corresponds to the point $p$ for which a path from $q$ will have to make the greatest detour by passing through $o$ instead of connecting directly. The adjacency relations between cells in this Voronoi diagram are also meaningful for dilation:

Thus, we would like to understand and compute Voronoi diagrams for smoothed distance. Smoothed distance is neither convex nor translation-invariant, but we can transform it into an equivalent distance that is, by interpreting polar coordinates in the plane for which we are computing smoothed distance as Cartesian coordinates in a transformed plane. Equivalently, using complex numbers (with $o=0$), if complex number $z$ has polar coordinates $(r,\theta)$, then $\ln z$ has Cartesian coordinates $(\ln r,\theta)$. Define a distance $\delta$ on the transformed complex number plane by the formula

This logarithmic transformation replaces the invariance of $d_{o}$ under complex multiplication by invariance of $\delta$ under complex addition (that is, translation of the plane):

Figure 2 shows concentric circles for $\delta$.

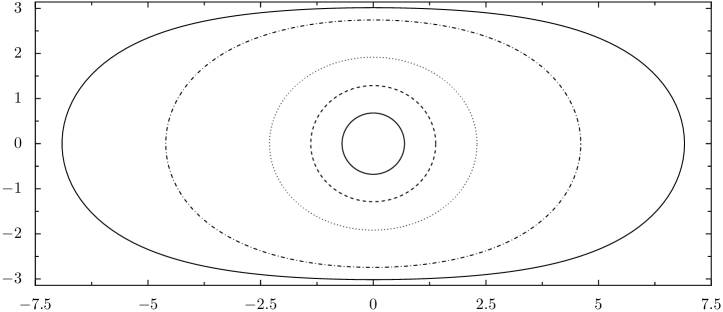
We may calculate $\delta((x,y),(0,0))$ directly as a formula of $x$ and $y$: it equals $d_{o}(p,q)$, where $o=(0,0)$, $p=(e^{x}\cos y,e^{x}\sin y)$, and $q=(1,0)$. Thus, $d(p,o)=e^{x}$, $d(q,o)=1$, and

Therefore, the smoothed distance is

It is convenient to monotonically transform this formula:

and

Therefore, if we define

it follows that

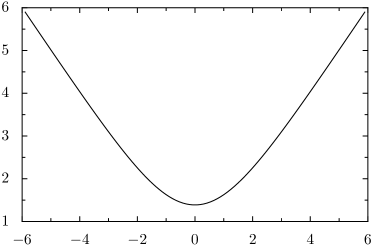
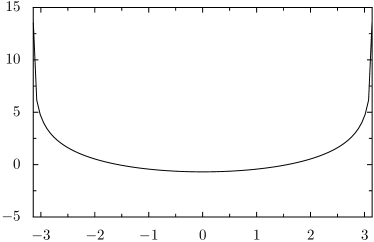
Thus, we have represented smoothed distance as a monotonic transform of translates of $f(x,y)=g(x)+h(y)$, where

Graphs of these two functions are depicted in Figure 3.

The transformation in Section II from a Voronoi diagram of smoothed distance to a minimization diagram of translates of $f(x,y)=g(x)+h(y)$ motivates the more general study of minimization diagrams of this type of function. A univariate function $f:\mathbb{R}\mapsto\mathbb{R}$ is convex if the set of points

on or above $f(x)$ is a convex subset of the plane. In higher dimensions, a multivariate function $f:\mathbb{R}^{d}\mapsto\mathbb{R}$ is convex if the set

is a convex subset of $\mathbb{R}^{d+1}$. A convex univariate function is strictly convex if there is no interval within which it is linear. For a doubly-differentiable univariate function $g(x)$, convexity is equivalent to the inequality $g^{\prime\prime}\geq 0$ and strict convexity is equivalent to the inequality $g^{\prime\prime}>0$. A curve in the $(x,y)$-plane is $x$-monotone if every line parallel to the $y$ axis intersects it in at most one point; intuitively, these curves are the graphs of functions from $x$ to $y$. Symmetrically, a curve is $y$-monotone if every line parallel to the $x$ axis intersects it in at most one point. These concepts should be distinguished from that of a function being monotonically increasing or strictly monotonically increasing: if $x_{1}>x_{0}$, and $\phi(x)$ is monotonically increasing, then $\phi(x_{1})\geq\phi(x_{0})$; if $\phi(x)$ is strictly monotonically increasing, then $\phi(x_{1})>\phi(x_{0})$. In a minimization diagram of translates of a function $f(x,y)$, a bisector $B(p,q)$ of two distinct points $p$ and $q$ is the locus of points with equal values of $f_{p}$ and $f_{q}$: $B(p,q)=\{r\mid f_{p}(r)=f_{q}(r)\}$. The minimization diagram of the points $\{p,q\}$ is formed by partitioning the plane into two cells along the bisector.

In particular, each bisector must be a pseudoline (the image of a line under a homeomorphism of the plane³³3This definition is from [21]; see [7] for a comparison with other common definitions of pseudolines.), because it is either itself a line or a monotonic curve that partitions the plane into two cells. In the next sequence of lemmas, we show that the level sets of the translates of $f$ are pseudocircles (simple closed curves that cross each other at most twice) by comparing their curvatures at tangent points of the same slope. For convenience, when the argument of the functions $g(x)$ and $h(y)$ is specified in the context, the notations $g$, $h$, $g^{\prime}$, $h^{\prime}$, etc., refer to the values $g(x)$, $h(y)$, $\frac{d}{dx}g(x)$, $\frac{d}{dy}h(y)$, etc.

Next, suppose we move $\epsilon$ units along the curve $S_{r}$ from $p$; to within first order, the point we move to is found by adding $(\epsilon\frac{-h^{\prime}}{\sqrt{h^{\prime 2}+g^{\prime 2}}},\epsilon\frac{g^{\prime}}{\sqrt{g^{\prime 2}+h^{\prime 2}}})$ to $p$. When we do so, $g^{\prime}$ changes by a factor of $1-\epsilon\frac{g^{\prime\prime}h^{\prime}}{g^{\prime}\sqrt{g^{\prime 2}+h^{\prime 2}}}+O(\epsilon^{2})$, and $h^{\prime}$ changes by a factor of $1+\epsilon\frac{g^{\prime}h^{\prime\prime}}{h^{\prime}\sqrt{g^{\prime 2}+h^{\prime 2}}}+O(\epsilon^{2})$, so the slope $h^{\prime}/g^{\prime}$ changes by a factor of $1+\epsilon\frac{g^{\prime}h^{\prime\prime}/h^{\prime}+h^{\prime}g^{\prime\prime}/g^{\prime}}{\sqrt{g^{\prime 2}+h^{\prime 2}}}+O(\epsilon^{2})$. We may view the term $\frac{g^{\prime}h^{\prime\prime}/h^{\prime}+h^{\prime}g^{\prime\prime}/g^{\prime}}{\sqrt{g^{\prime 2}+h^{\prime 2}}}$ appearing in this expression as a local measure of the curvature of $S_{r}$; it is not rotation-invariant but can be used to compare the curvatures of two curves at points of equal tangent slope. Larger values of this term mean a smaller radius of curvature and lower values mean a greater radius. To show that the radius of curvature at a given slope increases as $r$ increases, we will examine the behavior of this function as we increase $r$ by a small quantity $\epsilon$ while moving $p$ along a curve that keeps the slope of the tangent to $S_{r}$ fixed.

Due to the convexity of $f$, and the strict convexity of $g$ and $h$, the level sets $S_{r}(p)=\{q\mid f_{p}(q)=r\}$ are themselves convex; in particular, they are simple closed curves in the plane and, as the following proposition shows, they form a family of pseudocircles in the plane.

The next proposition states that (with the same assumptions as Lemma 5 and Proposition 6) the bisectors $B(p,q)$ and $B(p,s)$ act like pseudolines: they meet in at most one point, and if they meet they cross properly.

In other words, if we fix $p$ and let $q$ vary, the family of bisectors $B(p,q)$ forms a weak pseudoline arrangement. However, the proposition applies only to pairs of bisectors that share one of their defining points. These results are not quite enough to show that minimization diagrams for $f$ are abstract Voronoi diagrams in the sense of Klein [14], because abstract Voronoi diagrams require all bisectors to have a constant number of intersection points. However, the same general results as for abstract Voronoi diagrams follow in this case.

The assumptions that we make on the form of $f(x,y)=g(x)+h(y)$ as a sum of two univariate convex functions, and on the triple derivatives of these functions, may seem technical and unnecessary. However, in this section we provide examples showing that without the assumption on the form of $f$ beyond convexity, its minimization diagrams may have quadratic complexity, and without assumption on the triple derivatives of $g$ and $h$, the level sets for $f$ may not be pseudocircles.

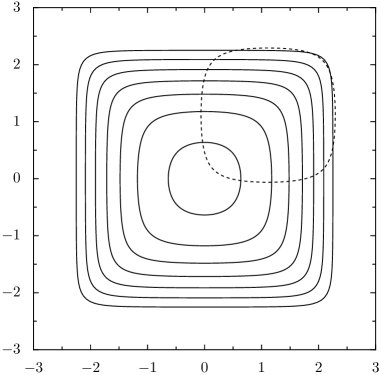
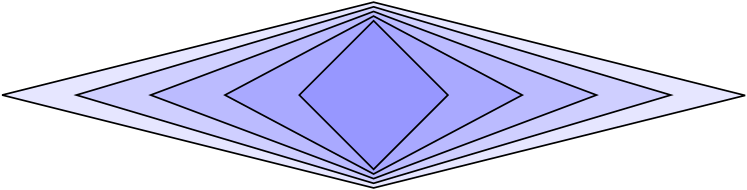
Figure 4 shows an example in which $g(x)$ and $h(y)$ grow so quickly that $g^{\prime\prime\prime}g^{\prime}>(g^{\prime\prime})^{2}$ and $h^{\prime\prime\prime}h^{\prime}>(h^{\prime\prime})^{2}$ for sufficiently large $x$. Specifically, $g^{\prime\prime\prime}g^{\prime}=(16x^{4}+24x^{2})e^{2x^{2}}$, while $(g^{\prime\prime})^{2}=(16x^{4}+16x^{2}+4)e^{2x^{2}}$; it follows that $g^{\prime\prime\prime}g^{\prime}>(g^{\prime\prime})^{2}$ for $x>1/\sqrt{2}$. One level set has been translated so that it crosses the outer level set four times, so these level sets are not pseudocircles. More generally, whenever $g^{\prime\prime\prime}g^{\prime}>(g^{\prime\prime})^{2}$ over some interval of values of $x$, the level sets of $f(x,y)=g(x)+g(y)$ do not form pseudocircles: the radius of curvature at one of the tangents with slope $-1$ shrinks rather than growing for increasing values of $f$.

Figures 5 and 6 provide a sketch of a construction for a convex function that has minimization diagrams with quadratically growing complexity. The function grows most slowly on a horizontal line through the origin, and more quickly along any other horizontal line, so that for any sites $p$ and $q$ that are not on a horizontal line, the Voronoi cell for $p$ dominates that for $q$ for points far enough away from both sites on a horizontal line through $p$. In particular the vertical line of cells to the right of the figure generates a sequence of cells with horizontal boundaries that extends, despite interruptions, through the whole figure. A more widely spaced sequence of sites at the bottom of the figure interrupts these cells, splitting them into linearly many pieces.

So, now that we’ve transformed the smoothed distance Voronoi diagram into the form of a minimization diagram for a function $f(x,y)=g(x)+h(y)$, and now that we know conditions on $g$ and $h$ that ensure that the minimization diagram to have linear complexity and be constructable efficiently, do the specific $g$ and $h$ arising in this application meet these conditions? The answer is: it depends.

First, consider the function $g(x)=\ln(e^{x}+2+e^{-x})$, with derivatives $g^{\prime}(x)=(e^{x}-1)/(e^{x}+1)$, $g^{\prime\prime}(x)={2e^{x}}/{(1+e^{x})^{2}}$, and $g^{\prime\prime\prime}(x)=-{2e^{x}(e^{x}-1)}/{(e^{x}+1)^{3}}$. For positive $x$, $g^{\prime\prime\prime}$ and therefore $g^{\prime\prime\prime}g^{\prime}$ are negative while $(g^{\prime\prime})^{2}$ is positive, so $g^{\prime\prime\prime}g^{\prime}<(g^{\prime\prime})^{2}$. Because the function is symmetric ($g(-x)=g(x)$) the same holds for negative $x$. And at zero, $g^{\prime\prime\prime}g^{\prime}=0$ while $(g^{\prime\prime})^{2}$ is nonzero. Therefore, $g$ meets the conditions of Theorem 8.

Next, consider the function $h(y)=-\ln(1+\cos y)$. Its derivatives are $h^{\prime}(y)=\tan(y/2)=\sin y/(1+\cos y)$, $h^{\prime\prime}(y)=1/(1+\cos y)$, and $h^{\prime\prime\prime}(y)=\sin y/(1+\cos y)^{2}$. Then $h^{\prime\prime\prime}h^{\prime}=\sin^{2}y/(1+\cos y)^{3}$, while $(h^{\prime\prime})^{2}=1/(1+\cos y)^{2}$. The ratio of these two values, $\sin^{2}y/(1+\cos y)^{2}=\tan^{2}(y/2)$, is less than one when $|y|<\pi/2$ and greater than one when $|y|>\pi/2$. Thus, $h$ satisfies the requirement that $h^{\prime\prime\prime}h^{\prime}<(h^{\prime\prime})^{2}$ only for $y$ in the interval $(-\pi/2,\pi/2)$. This implies that we may only apply Theorem 8 to smoothed distance when each Voronoi cell consists of points spanning at most a right angle with $o$ and the cell’s site.