Polarized Charge Dynamics of a Novel Charge Density Wave in Kagome FeGe

The kagome lattice, a hexagonal network of corner-sharing triangles, has been studied for over 70 years [1]. Its unique band structure features the coexistence of flat bands (FBs), Dirac crossings, and van Hove singularities (VHSs), making it an excellent platform for studying the variety of emergent quantum phases resulting from the complex interplay between geometry, topology, and electronic correlations. In the early days, research mainly focused on the geometric spin frustration, showing its great potential to realize quantum spin liquid states [2, 3, 4, 5]. Subsequently, a range of topological quantum states have been explored, such as Weyl fermions in Co₃Sn₂S₂ [6, 7, 8], Dirac fermions and flat bands in CoSn [9], and Chern gapped Dirac fermions in TbMn₆Sn₆ [10]. More recently, charge density wave (CDW) and unconventional superconductivity [11, 12, 13, 14], as well as other exotic quantum phenomena, including electronic nematicity [15], roton pair density wave [16], and giant anomalous Hall effect [17], have been reported in the non-magnetic kagome metals AV₃Sb₅ ($A=$ Cs, K, Rb).

Generally, the discovered kagome materials can only host either magnetism or charge orders, owing to the large energy separation between the FBs and the vHSs. However, lately, a CDW order ($T_{\mathrm{CDW}}\simeq$ 100 K) has been found inside the antiferromagnetic (AFM) phase of kagome FeGe ($T_{N}\simeq$ 410 K) [18]. This CDW transition is associated with an increase of ordered magnetic moments [19], which demonstrates an intertwined nature of magnetism and charge order (CO) in FeGe, thus offering a unique opportunity to explore a novel CDW with magnetism. Currently, the origin of CDW in FeGe is still full of controversy [18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 26, 29, 30, 31, 32]. The nesting of VHSs at the M point and electron-phonon coupling were initially proposed to explain the formation of CDW [18, 19, 20], similar to AV₃Sb₅ [33, 34, 35, 36, 37, 38, 39, 40, 41]. However, Wu et al. found that the maximum nesting function of FeGe is at the K point instead of the M point, and suggested the key role of electronic correlations for CDW [21]. Additionally, electronic correlations induces a softening effect along the L-H direction in the calculated phonon spectrum of FeGe [29, 30, 31]. Furthermore, recent theoretical calculations and angle-resolved photoemission spectroscopy (ARPES) measurements in annealed samples support a new mechanism, in which the large dimerization partial Ge1-dimerization reduces the magnetic energy and leads to a stable $2\times 2\times 2$ CDW ground state [22, 23], in sharp contrast to AV₃Sb₅. Therefore, to clarify the origin of CDW in FeGe, a systematic study of charge dynamics across various electronic states or phases is essential.

In this letter, we utilize polarized optical spectroscopy and density functional theory (DFT) calculations to systematically study the charge dynamics of FeGe spanning from paramagnetic (PM) to AFM and to CDW phases. Our study reveals significant optical anisotropy and a variety of intraband and interband excitations associated with VHSs and FBs. Particularly noteworthy is the magnetization-induced shift of FBs and the CDW transition, which result in two distinct types of spectral weight (SW) redistributions. Furthermore, we observe that the CDW response lacks a gap feature and exhibits characteristics of a first-order transition, contrasting with observations in AV₃Sb₅. Our results thus are consistent with the novel CDW mechanism based on a first-order structural transition involving large partial Ge1-dimerization.

Sample synthesis, experimental methods, and details of Drude-Lorentz analysis and DFT calculations are provided in the Supplemental Material.

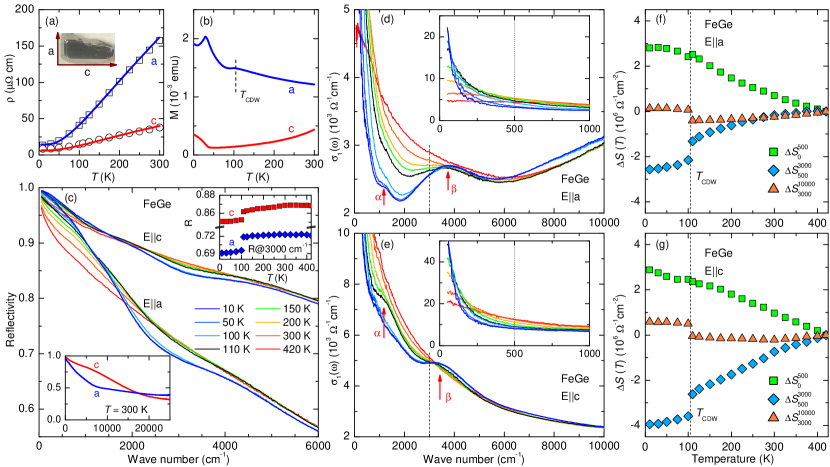
Figure 1(a) displays the temperature ($T$) dependence of the resistivity for kagome FeGe along the $a$-axis and $c$-axis. Both directions exhibit typical metallic behavior and manifest strong electronic anisotropy with lower resistivity along the $c$-axis. In Fig. 1(b), the $T$-dependent magnetizations, $M_{a}(T)$ and $M_{c}(T)$, show notable magnetic anisotropy. Upon cooling, $M_{a}(T)$ gradually increases and shows an anomaly at the CDW transition ($T_{\mathrm{CDW}}\simeq 105$ K). In contrast, $M_{c}(T)$ decreases and then turns upward below $T_{\mathrm{Cant}}\simeq 60$ K, attributed to spin canting. These observations are consistent with previous studies [18].

Due to the electronic and magnetic anisotropies, we measured the polarized reflectivity $R(\omega)$ of FeGe. In Fig. 1(c), $R(\omega)$ is presented up to 6 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$ from 420 to 10 K for $\textbf{E}\parallel a$ and $\textbf{E}\parallel c$. The bottom inset compares $R_{a}(\omega)$ and $R_{c}(\omega)$ at $T=300$ K up to 25 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$. In the infrared region, $R_{c}(\omega)$ is much higher than $R_{a}(\omega)$, indicating an optical anisotropy consistent with the lower resistivity along the $c$-axis. In the low-frequency limit, both $R_{a}(\omega)$ and $R_{c}(\omega)$ approach unity and increase with decreasing $T$, reflecting the metallic nature of FeGe. Furthermore, there is no clear anomalous change across the AFM transition ($T_{\mathrm{N}}\simeq 410$ K) for both polarizations. However, below $T_{\mathrm{CDW}}$, $R(\omega)$ shows a sudden drop in the range of 2 000 – 5 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$. Such a sudden change, as highlighted by the $T$-evolution of $R(\omega=3000\leavevmode\nobreak\ \textrm{cm}^{-1})$ in the top inset, provides an initial spectroscopic indication of a first-order CDW transition in FeGe, which is consistent with the neutron [18], x-ray scattering [29], and Raman experiments [24].

The optical conductivity $\sigma_{1}(\omega)$ provides direct information about the charge dynamics. Fig. 1(d) and Fig. 1(e) display the $T$-dependent $\sigma_{1a}(\omega)$ and $\sigma_{1c}(\omega)$ for $\textbf{E}\parallel a$ and $\textbf{E}\parallel c$, respectively. In the far-infrared region, $\sigma_{1}(\omega)$ is dominated by a Drude-like peak, and $\sigma_{1c}(\omega)$ is about twice higher than $\sigma_{1a}(\omega)$, indicating a strong three-dimensional (3D) metallic response. With decreasing $T$, the Drude peak narrows and exhibits coherent behavior at low temperatures, as emphasized in the insets. In the mid-infrared region (500 – 3 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$), $\sigma_{1}(\omega)$ decreases and transfers the SW to lower frequencies. Meanwhile, an absorption peak (labeled as $\beta$) gradually appears around 4 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$. Across the CDW transition, $\sigma_{1}(\omega)$ below 3 000$\leavevmode\nobreak\ \textrm{cm}^{-1}$ is further suppressed, while its associated SW is transferred to the $\beta$ peak and other high-energy interband transitions. Both $\sigma_{1a}(\omega)$ and $\sigma_{1c}(\omega)$ exhibit similar features, particularly in their responses to the CDW transition, providing strong evidence for the formation of a 3D CDW state in FeGe, consistent with the $2\times 2\times 2$ CDW order observed from other experiments [25, 26]. Additionally, with the narrowing of the Drude peak or the CDW transition, a low-energy peak (labeled as $\alpha$) emerges around 1 200$\leavevmode\nobreak\ \textrm{cm}^{-1}$.

The $T$-dependent spectral changes have been further analyzed in terms of the partial SW, $S_{\omega_{a}}^{\omega_{b}}(T)=\int_{\omega_{a}}^{\omega_{b}}\sigma_{1}(\omega,T)d\omega$, restricted by the cutoff frequencies $\omega_{a}$ and $\omega_{b}$. This approach allows us to specify the SW changes of different electronic excitations by choosing suitable $\omega_{a}$ and $\omega_{b}$. Fig. 1(f) and Fig. 1(g) detail the SW changes, $\Delta S(T)=S(T)-S(420\leavevmode\nobreak\ \mathrm{K})$, at various restricted frequency ranges for $\textbf{E}\parallel a$ and $\textbf{E}\parallel c$, respectively. For $\Delta S_{0}^{500}$ and $\Delta S_{500}^{3000}$, that are governed by the coherent and incoherent excitations, respectively, the transfer of incoherent to coherent excitations leads to an increase in $\Delta S_{0}^{500}$ and a corresponding decrease in $\Delta S_{500}^{3000}$ at $T>T_{\mathrm{CDW}}$. For $\Delta S_{3000}^{10000}$, dominated by the $\beta$ peak and other high-energy excitations, it remains nearly $T$-independent. As $T<T_{\mathrm{CDW}}$, $\Delta S_{0}^{500}$ undergoes a slight suppression and $\Delta S_{500}^{3000}$ is suddenly reduced, while $\Delta S_{3000}^{10000}$ is enhanced, indicating an abrupt SW transfer from low to high frequencies due to the CDW transition. Additionally, $\Delta S_{500}^{3000}$ and $\Delta S_{3000}^{10000}$ exhibit more significant anomalies compared to $\Delta S_{0}^{500}$, implying a more pronounced impact of CDW on incoherent excitations than on coherent ones.

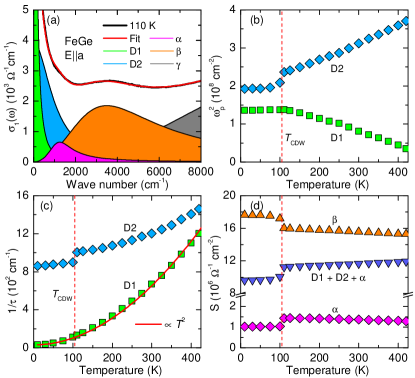
To perform a quantitative analysis of various intra- and interband excitations, we employed the Drude-Lorentz model to fit the measured $\sigma_{1}(\omega)$ spectra. Fig. 2(a) shows the decomposition of $\sigma_{1a}(\omega)$ at $T=$ 110 K. A similar decomposition of $\sigma_{1c}(\omega)$ is available in the Supplemental Materials. The fitting curve consists of two Drude terms (labeled as D1 and D2), along with three Lorentz terms (labeled as $\alpha$, $\beta$, and $\gamma$) that account for interband transitions at higher energies. The two-Drude fit suggests two types of charge carriers with different scattering rates. Specifically, the scattering rate ($1/\tau$) of D1 is quite smaller compared to that of D2, e.g., $1/\tau_{D1}=130\leavevmode\nobreak\ \textrm{cm}^{-1}$ and $1/\tau_{D2}=1\,000\leavevmode\nobreak\ \textrm{cm}^{-1}$ at 110 K. The Drude fit also enables the extraction of the dc resistivity, $\rho\equiv 1/\sigma_{1}(\omega\rightarrow 0)$, as shown by open symbols in Fig. 1(a), which aligns well with the results from the dc transport measurement. With decreasing $T$, D1 exhibits a Fermi-liquid behavior with $1/\tau\propto T^{2}$ and a substantial increase in weight (proportional to $\omega^{2}_{p}$), while D2 shows a slight decrease in $1/\tau$ and a corresponding loss in weight, as shown in Figs. 2(b–c). The compensated changes of weights for D1 and D2 imply a $T$-induced shift of bands near the Fermi energy ($E_{\mathrm{F}}$). Notably, the CDW transition only has a strong impact on D2 (i.e., the incoherent excitations), where $\omega^{2}_{p}$ and $1/\tau$ for D2 show an abrupt suppression at $T<T_{\mathrm{CDW}}$, whereas those for D1 show no anomalies. In Fig. 2(d), we revealed a sudden decrease (increase) in the SW of the $\alpha$ ($\beta$) band at $T_{\mathrm{CDW}}$. Overall, the CDW results in a sudden SW redistribution between the low-energy (two Drude and $\alpha$ bands) and high-energy components ($\beta$ and other high-energy bands).

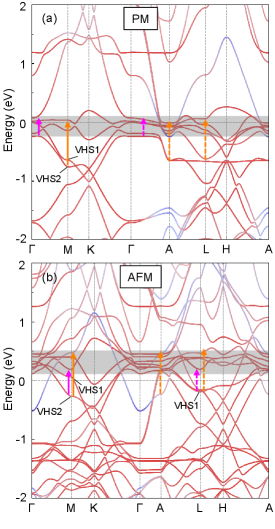
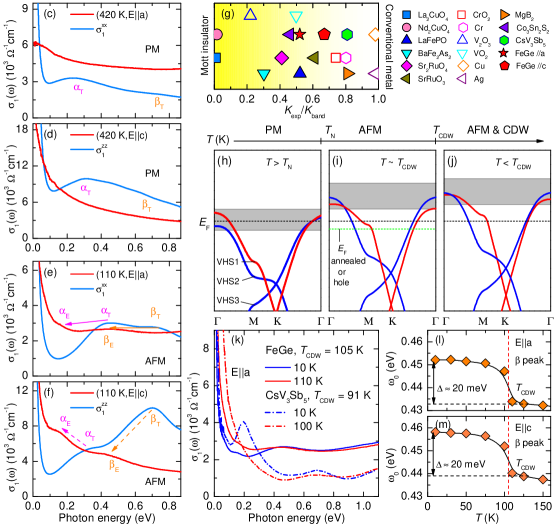
Next, to unravel the origin of each component in $\sigma_{1}(\omega)$, we calculated the band structure of FeGe in both the PM and AFM phases. In the PM phase, as shown in Fig. 3(a), the band structure features a pair of typical kagome bands along the $\Gamma$-M-K-$\Gamma$ direction, where the FBs (marked by a grey bar) are situated around $E_{\mathrm{F}}$, VHSs (VHS1 and VHS2) are below $E_{\mathrm{F}}$ at the M point and Dirac crossings are present at the K point. As shown in Fig. 3(b), the AFM order shifts the FBs upward above $E_{\rm F}$ and brings the VHSs closer to $E_{\rm F}$, particularly for VSH1. Additionally, a highly dispersive band emerges around the $\Gamma$ point and intersects with $E_{\rm F}$. In Figs. 3(c–f), we compared the calculated and experimental $\sigma_{1}(\omega)$ spectra. In the PM phase, the calculated $\sigma^{xx}_{1}(\omega)$ displays three features: a Drude response of intraband transitions of FBs, an $\alpha$ peak of interband transitions between the bottom and top FBs at $\sim$ 0.25 eV (magenta arrows), and a $\beta$ peak of interband transitions between VHSs and top FBs at $\sim$ 0.75 eV (orange arrows). The $\sigma^{zz}_{1}(\omega)$ exhibits similar features, but with almost twice the strength of the response. In the experimental $\sigma_{1}(\omega)$ spectra above $T_{N}$, these features are smeared out due to the strong thermal broadening effect at $T=420$ K. In the AFM phase, the calculated $\alpha_{\rm T}$ peak loses SW, while the $\beta_{\rm T}$ peak gains SW, due to all FBs are elevated above $E_{\rm F}$, resulting in the $\alpha$ peak being replaced by the interband transitions between VHSs and the bottom FBs. Compared to theoretical results, the experimental $\alpha_{\rm E}$ and $\beta_{\rm E}$ peaks shift significantly to lower energies, with $\omega^{\alpha}_{0}=$ 0.43 $\rightarrow$ 0.17 eV and $\omega^{\beta}_{0}=$ 0.75 $\rightarrow$ 0.45 eV for $\textbf{E}\parallel a$, and $\omega^{\alpha}_{0}=$ 0.32 $\rightarrow$ 0.17 eV and $\omega^{\beta}_{0}=$ 0.70 $\rightarrow$ 0.46 eV for $\textbf{E}\parallel c$.

The significant position shift of interband transitions between the experimental and theoretical results suggests a strong renormalization of band structure caused by electronic correlations. Since the $\beta$ peak is mainly dominated by the interband transitions within the kagome bands (i.e., between VHSs and FBs), the ratio $\omega^{\beta,\rm T}_{0}/\omega^{\beta,\rm E}_{0}$ can serve as a reliable estimation for the strength of electronic correlations. Here, $\omega^{\beta,\rm T}_{0}/\omega^{\beta,\rm E}_{0}=$ 1.67 and 1.52 for $\textbf{E}\parallel a$ and $\textbf{E}\parallel c$, respectively, which agrees well with the renormalization factor of 1.6 observed in ARPES measurements [19] and dynamical mean-field theory calculations [44, 29]. Furthermore, the ratio of the experimental kinetic energy $K_{\mathrm{exp}}$ to that from band theory $K_{\mathrm{band}}$ also provides crucial information about electronic correlations, where $K_{\mathrm{exp}}$ or $K_{\mathrm{band}}$ is proportional to the SW of the Drude component. Fig. 3(g) summarizes $K_{\mathrm{exp}}/K_{\mathrm{band}}$ for FeGe and several other representative materials. Details about the determination of $K_{\mathrm{exp}}/K_{\mathrm{band}}$ are included in the Supplemental Materials. In FeGe, $K_{\mathrm{exp}}/K_{\mathrm{band}}$ is $0.52\pm 0.05$ and $0.67\pm 0.05$ for $\textbf{E}\parallel a$ and $\textbf{E}\parallel c$, respectively, suggesting a moderate strength of electronic correlations, which falls between Co₃Sn₂S₂ and CsV₃Sb₅.

Electronic correlations and, in particular, magnetism, have pronounced effects on the band structure in kagome materials. For instance, in Co₃Sn₂S₂ the magnetic splitting of bands shifts the FBs and Weyl points toward $E_{\rm F}$, making electrons possess the properties of both correlation and topology. Similarly, as summarized in Figs. 3(h)–(j), the magnetic splitting in FeGe, which is proportional to the ordered magnetic moment [19], elevates the VHSs close to $E_{\rm F}$, improving the activity of electronic states and thus the possibility of CDW instability. However, unlike the nesting mechanism of VHSs in AV₃Sb₅, our experimental observations suggest a different origin of CDW in FeGe. As compared in Fig. 3(k), CsV₃Sb₅ and FeGe exhibit distinct charge responses to the CDW transition. The former shows a clear gap feature of CDW due to the nesting of VHSs around the M-point [38], whereas these features are absent in the latter. Recent theoretical calculations and ARPES measurements in FeGe provide a novel CDW mechanism, where the CDW is primarily driven by saving magnetic energies via a first-order structural transition involving large partial Ge1-dimerization [22, 23]. ARPES experiments on annealed samples did not detect the CDW gap but instead a sudden jump of bands originating from the enhanced spin-polarization in the CDW phase [23]. Our findings of charge dynamics are fully consistent with these above theoretical and experimental facts, thus supporting such a novel CDW mechanism.

Accordingly, the sudden SW changes at the CDW transition can be explained by the jump of VHS1 relative to $E_{\rm F}$. Specifically, as illustrated in Figs. 3(i–j), VHS1 lies slightly below $E_{\rm F}$ at $T\sim T_{\mathrm{CDW}}$ and then abruptly shifts above $E_{\rm F}$ at $T<T_{\mathrm{CDW}}$ for our sample. This band jump is also evident in the shift of the $\beta$ peak. As demonstrated in the Figs. 3(l–m), the $\beta$ peak shows an increase of about 20 meV after the CDW transition, which is consistent with the results of the ARPES experiments [23]. Note that, in annealed or hole-doped samples, since VHS1 is already positioned above $E_{\rm F}$ at $T\sim T_{\mathrm{CDW}}$ (marked by green dashed line) due to stronger magnetic moment [23, 45] or hole doping, the further upward shift of VHS1 at $T<T_{\mathrm{CDW}}$ may not result in obvious changes in SW. This may clarify why another recent optical study on FeGe did not find strong SW redistributions under the CDW transition [46].

In summary, our optical conductivity measurements revealed rich information about the charge dynamics in FeGe, including a remarkable optical anisotropy, moderate electronic correlations, unconventional SW redistributions associated with magnetization-induced band shift and CDW transition, as well as a first-order transition and 3D character of CDW. These findings contrast with the conventional CDW mechanism observed in other kagome metals, and instead highlight a novel mechanism involving the intricate interplay among structure, magnetism, electronic correlations, and charge order in FeGe.