ifaamas \acmConference[AAMAS ’22]Proc. of the 21st International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2022)May 9–13, 2022 Auckland, New ZealandP. Faliszewski, V. Mascardi, C. Pelachaud, M.E. Taylor (eds.) \copyrightyear2022 \acmYear2022 \acmDOI \acmPrice \acmISBN \acmSubmissionID??? \affiliation \institutionPeking University \cityBeijing \countryChina \affiliation \institutionPeking University \cityBeijing \countryChina \affiliation \institutionPeking University \cityBeijing \countryChina \affiliation \institutionPeking University \cityBeijing \countryChina
PooL: Pheromone-inspired Communication Framework for Large Scale Multi-Agent Reinforcement Learning
Abstract.
Being difficult to scale poses great problems in multi-agent coordination. Multi-agent Reinforcement Learning (MARL) algorithms applied in small-scale multi-agent systems are hard to extend to large-scale ones because the latter is far more dynamic and the number of interactions increases exponentially with the growing number of agents. Some swarm intelligence algorithms simulate the release and utilization mechanism of pheromones to control large-scale agent coordination. Inspired by such algorithms, PooL, an pheromone-based indirect communication framework applied to large scale multi-agent reinforcement learning is proposed in order to solve the large-scale multi-agent coordination problem. Pheromones released by agents of PooL are defined as outputs of most reinforcement learning algorithms, which reflect agents’ views of the current environment. The pheromone update mechanism can efficiently organize the information of all agents and simplify the complex interactions among agents into low-dimensional representations. Pheromones perceived by agents can be regarded as a summary of the views of nearby agents which can better reflect the real situation of the environment. Q-Learning is taken as our base model to implement PooL and PooL is evaluated in various large-scale cooperative environments. Experiments show agents can capture effective information through PooL and achieve higher rewards than other state-of-arts methods with lower communication costs.
Key words and phrases:
multi-agent communication, swarm intelligence, reinforcement learning, pheromones1. Introduction
MARL focuses on developing algorithms to optimize behaviors of different agents which share a common environment Buşoniu et al. (2010). Agents’ behaviors in MARL settings are usually modeled as Partially Observable Markov Decision Process (POMDP), in which agents only have a partial observation of the global state. MARL faces two major problems. First, partial observations from different agents as input features cause a curse of dimensionality. Second, it is difficult to consider all possible interactions among agents because the number of possible interactions grows exponentially. With the increase of agents’ scale, these two problems will become more and more serious. In MARL, there are various methods to solve the two problems. These methods can be roughly divided into two categories, Centralized Training Decentralized Execution (CTDE) Oliehoek et al. (2008) and multi-agent communication. In the CTDE framework, agents can access global information while training, and agents select actions based on partial observations while execution. But CTDE algorithms are still unable to deal with large-scale agents for the reason that the dimension of global information is still too high to handle even at the training step. Multi-agent communication is another promising approach to coordinate the behaviors of large-scale agents. Agents can choose actions by their partial observations and information received from other agents. But designing an effective communication mechanism is not a trivial task. For an agent, the message representation, message sender selection, and message utilization all need to be carefully designed. In addition, agents’ communication is limited by bandwidth in reality. This bandwidth limitation also affects the scale of multi-agent communication.
Swarm Intelligence refers to solving problems by the interactions of simple information-processing units Kennedy (2006). One of the key concepts of Swarm Intelligence is Stigmergy which is proposed in the 1950s by Pierre-Paul Grassé Heylighen (2015). Summarizing from behaviors of insects, Stigmergy refers to a mechanism of indirect coordination between agents by the trace left in the environment. A representative algorithm inspired by Stigmergy is Ant Colony Optimization (ACO) algorithm. It takes inspiration from the foraging behavior of some ant species and uses a mechanism similar to pheromones for solving optimization problems Dorigo et al. (2006). ACO is widely used in various path-finding problems in the real world Konatowski and Pawłowski (2018); Dai et al. (2019). The effectiveness of such ACO algorithms depends on the exploration of a large number of units (e.g. robots) and pheromone-based indirect communication among them. However, in ACO’s settings, units’ behaviors are confined by predefined rules, which is unsuitable in MARL environments.
In this paper, inspired by the pheromone mechanism introduced in ACO, an indirect communication framework for MARL is developed by introducing pheromones into Deep Reinforcement Learning (DRL). The output of reinforcement learning algorithms is usually the scoring of actions or the probabilities of selecting a certain action. These values can be used not only to select actions but also to reflect the agents’ views of the environment. These values output by different agents can be organized by a pheromone update mechanism similar to ACO. Therefore, the pheromone information perceived by agents combines the views and knowledge of other agents around them, and can better reflect the real situation of the current agent.
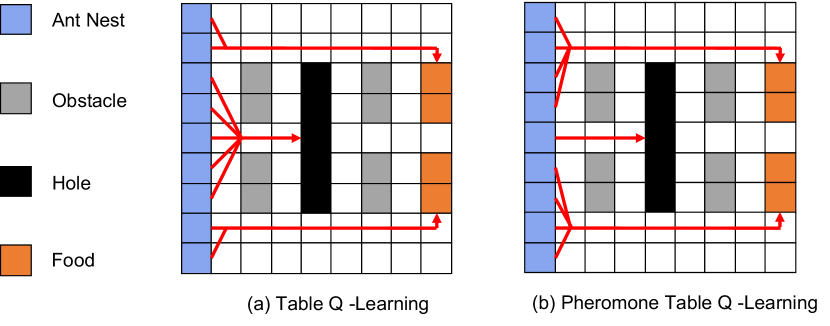
Intuition behind PooL (a) Most agents trained by Table Q-Learning without any communication fall into holes. (b) More than half agents find food with the guidance of pheromones by pheromone based Table Q-Learning.
The intuition behind our framework is shown in Figure 1. In a simple grid maze environment, there are ant nests (blue grids), obstacles (grey grids), holes (black grids), and food (orange grids). Agents (i.e. ants) get negative rewards at every time step. Agents will exit from the environment if they fall into holes or find food. Agents who find food get extra positive rewards. If agents take actions dependently, they are very easy to fall into local optimization (fall into holes). But if agents communicate through pheromones, those agents who find the optimal solution will transfer the information of the optimal solution to other agents. As a result, more agents find the optimal solution with the guidance of pheromones. More details about this motivation example will be discussed in Section 6.
Following the intuition above, the pheromone mechanism is extended to the field of DRL. PooL simulates the process of ant colonies releasing pheromone, feeling the pheromone and the surrounding environment, and making decisions. A pheromone receptor is designed to convert pheromone information to a fixed dimension feature. For each agent, the original reinforcement learning component receives information from the real world and the pheromone receptor to choose actions and release pheromones. In this way, PooL realizes indirect agent communication and distributed training and execution in MARL. We combine PooL with Deep Q-Learning and evaluate PooL in a variety of settings of MAgent Zheng et al. (2018) which is further capsuled by PettingZoo Terry et al. (2020). Experiments show that PooL can achieve effective communication of local information and get higher rewards.
The contributions of our paper can be summarized as follows:
-
(1)
We propose a pheromone-based indirect communication framework that combines MARL with swarm intelligence algorithms.
-
(2)
PooL realizes more effective large-scale multi-agent coordination and achieves better performance than the existing methods when there are hundreds of agents in the environment.
-
(3)
PooL can be combined with any reinforcement learning algorithms, and the additional cost is very small, which makes it easier to apply to real-world scenes.
Our paper is organized as follows. Section 2 introduces work that is closely related to our proposed framework. Section 3 introduces the background knowledge related to our problem to be solved. In Section 4, we give a detailed description of PooL. In section 5, we show the performance of PooL in a variety of settings. Section 6 summarizes our paper.
2. Related Work
Our paper is closely related to two branches of study: Multi-agent Reinforcement Learning (MARL) and control algorithms that are based on Swarm Intelligence.
2.1. Multi-agent Reinforcement Learning
DRL methods like Deep Q-Learning (DQN) Mnih et al. (2013) promote the application of reinforcement learning in many fields such as Atari Games Mnih et al. (2015) and Go Silver et al. (2016). But most existing methods of DRL focus on the control of a single agent. As in real life, many scenes contain multi-agent interactions and cooperation. MARL attracts more and more attention. Lowe et al. (2020); Wei et al. (2018); Foerster et al. (2018) are classic MARL algorithms following the framework of CTDE Oliehoek et al. (2008). These algorithms apply modified single-agent reinforcement learning algorithms such as DDPG lillicrap et al. (2016) and Soft Q-Learning Haarnoja et al. (2017) in MARL settings. However, such methods still suffer from the curse of dimensionality because the method still needs to handle all agents’ features while training. Communication is an effective way to solve such problems. CommNet Sukhbaatar et al. (2016) designs a channel for all agents to communicate and extract information from all agents by average pooling. In order to better handle the situation with more agents, Zhao and Ma (2019) uses an information filtering network to select useful information. VAIN Hoshen (2018), ATOC Jiang and Lu (2018) and TarMAC Das et al. (2019) use attention mechanism to select communication targets and information more reasonably. But these methods still assume a centralized controller that can access all communication needed information while training. DGN Jiang et al. (2020) models agents’ interactions with graph structures by Graph Neural Networks (GNN) Zhou et al. (2020). In DGN, agents’ communication is achieved by the convolution of graph nodes(e.g. agents nearby). Graph convolution is able to express more complex agent interactions. But its performance and convergence speed are still confined by the number of agents.
In order to make algorithms scale to many agents, MFQ Luo* et al. (2018) accepts the average action value of nearby agents as extra network input. Zhou et al. (2019) proposes to approximate Q-function with factorized pairwise interactions. Wang et al. (2020) provides another idea that trains agents from few to more with transfer mechanisms.
2.2. Control Algorithms Based on Swarm Intelligence
Swarm Intelligence is widely used in group control problems. Di Caro and Dorigo (1998); Maru et al. (2016) discusses the use of swarm intelligence in adaptive learning of routing tables and network-failure-detection. Bourenane et al. (2007); Xu et al. (2019) utilize pheromones to achieve multi-agent coordination. However, Swarm Intelligence algorithms like Bird Swarm Algorithm and Ant Colony Optimization are rule-based, as a result, they can not learn from environments. Phe-Q Monekosso and Remagnino (2001) first introduces the idea of pheromone mechanisms to reinforcement learning. Matta et al. (2019); Meerza et al. (2019) follow similar ideas and improve the convergence speed of Q-Learning in different environments. Xu et al. (2021) proposes to release the pheromone according to the distance between the agent and the target, and apply the pheromone information to Deep Reinforcement Learning.
Learning-based methods are more and more popular with the success of deep learning in many fields. Most methods mentioned above can not take advantage of deep neural networks. DRL is applied in Xu et al. (2021), but the way Xu et al. (2021) obtains pheromones is artificially designed based on the specific environment. It will be more appropriate if pheromones are generated based on learning algorithms.
3. Background
3.1. Problem Formulation
The problem for multi-agent coordination in this paper can be considered as a Dec-POMDP game Hansen et al. (2004). It can be well defined by a tuple , where is a set of agents, is the state space, is the action space for agent , is the observation space for agent , is the time horizon for the game and is the discount factor for individual rewards . When agents took actions in state , the probability of the environment transitioning to state is and the probability of agents seeing observations is .
For agents in the problem above, their goal is to maximize their own expected return . The achievement of this goal requires the cooperation of agents belonging to the same team.
3.2. Table Q-Learning and Deep Q-Learning
Q-Learning is a popular method in single agent reinforcement learning. For agent , Q-Learning uses an action-value function for policy as . Table Q-Learning maintains a Q-table and update Q-values by the following equation:
| (1) |
For every step, the agent selects its action based on the max value of these actions with an epsilon-greedy exploration strategy.
As Q-Table can not handle high dimensional states, Deep Q-Learning (DQN) uses neural network to approximate Q-function. DQN tries to optimize with back propagation by minimizing the follwing loss function:
| (2) | ||||
In DQN Mnih et al. (2015), there is a replay buffer to store agent information. Data is randomly extracted from the replay buffer to train the model. Target Q-network has the same architecture with . copies parameters from frequently. In this way, DQN disrupts the temporal correlation and makes the training of the model more stable.
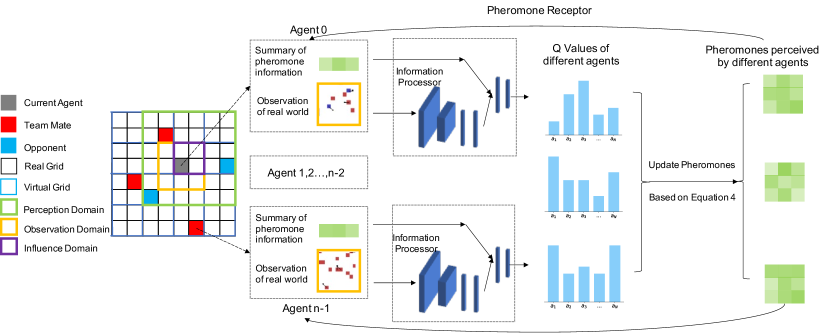
Overview of our framework
4. Methodology
In this section, we discuss how our pheromone-based framework is realized. Firstly, a general view of PooL is described. Then, implementation details will be introduced step by step. We choose Q-Learning as a base model for PooL in the following sections but our framework is able to combine with most existing reinforcement learning algorithms.
4.1. Communication Framework Overview
Figure 2 gives a whole picture of PooL. In the left of Figure 2, a simple grid world is built as a demonstration. From the view of the grey agent, the black-bordered squares represent the real grids of our environment. They are the smallest units to express information in our environment. In order to realize indirect communication based on pheromones, we need to set up a virtual medium, which is represented by the blue-bordered squares. The area near the current agent is divided into three regions from small to large: Influence Domain, Observation Domain, and Perception Domain. Agents handle these three regions with different behaviors. The meanings of the three regions are as follows.
-
•
Influence Domain: the influence range of pheromones released by agents.
-
•
Observation Domain: the partial observation of the agent in the environment.
-
•
Perception Domain: the range of pheromones that agents can perceive.
In nature, generally, animals perceive a much larger range of pheromones than they observe their surrounding environment by eyes. Therefore, in our settings, the Perception Domain is larger than the Observation Domain.
The right part of Figure 2 shows how PooL processes received information and updates pheromones. PooL consists of three components. The first is the information processor (composed of convolution layers and fully connected layers). Its input feature consists of two parts: real-world observations and a summary of pheromone information. Its output is Q-values, which can be transformed into pheromones. The second is the pheromone update mechanism realized through a virtual medium. Thirdly, a pheromone receptor is used to sense the pheromone information from the surrounding by convolution layers and transform the information into the representation features of the current environment. With the increase of the number of agents, the pheromone information extracted by agents can more accurately reflect the situation of the local environment.
In the following sections, we introduce the realization of our framework in three steps. First, a virtual medium is defined to allow the propagation of pheromones. Then, when agents release their pheromones, an update mechanism updates the values of pheromones stored in the virtual medium. Finally, pheromone information is processed by the pheromone receptor and serves as extra input for our reinforcement learning algorithms such as DQN.
4.2. Virtual Medium Settings
In order to achieve pheromone-based indirect communication in the environment, a virtual medium to simulate the mechanism of pheromones in nature needs to be built first. A virtual map can be constructed by dividing the real environment map into virtual grids. denotes a mapping function that can return agent ’s current position like . represents the pheromone value stored in the virtual medium whose shape is ( is denoted as the number of actions). represents the current number of agents in . The pheromone released by agent is denoted as . is a vector with dimensions.
4.3. Pheromone Update Rule
Following Q-Learning’s idea, pheromones are defined based on the Q-function. As the range of the Q-function’s estimated values changes while training, Q-values are standardized as pheromones. For agent ’s Q-values , they are transformed by a standardization function . After standardization, values of pheromones obey the standard normal distribution with the mean of and the standard deviation of .
| (3) | ||||
At the beginning of each time step, each agent calculates their Q-values and releases their pheromones on their Influence Domain. We take the mean value of all released pheromones in each grid, and update the value of pheromones in each grid according to the evaporation coefficient . For a virtual grid, whose position is , its pheromone value is updated by the following equation:
| (4) | ||||
is a set of agents where for every , there is .
4.4. Pheromone Based Deep Q-Learning
The main difference between our proposed pheromone-based deep Q-Learning and DQN is that our information processor receives inputs from two sources. Except for the partial observation of the current environment, our processor also receives the information processed by the pheromone receptor. For agent , the summary of pheromone information processed by agent is denoted as . The optimization goal for Q-learning can be updated to:
| (5) | ||||
The complete algorithm is described in Algorithm 1. The algorithm can be divided into two parts: calculate and update pheromones released by different agents and choose actions based on information observed by agents.
4.5. Algorithm Cost Analysis
Compared with DQN, the extra cost of PooL lies in the pheromone update mechanism and pheromone receptor. For pheromone update, it can be done in time. For the pheromone receptor, the complexity of its network structure depends on the size of the Perception Domain, and the size of the Perception Domain is generally much smaller than the Observation Domain. As a result, the extra cost of PooL is relatively small compared with DQN.
4.6. Implementation Details
As shown in Figure 2, we use the structure of multi-layer convolution and multi-layer fully connected layers as our information processor to process observations and summary of pheromone information. The receptor is also a convolution structure and processes pheromone information from the virtual medium. The size of the Influence Domain is and the size of the Perception Domain is . The selection of hyperparameters such as the virtual map size , and the evaporation coefficient will be discussed in Section 5.
5. Experiment
In this section, we describe the settings of our experiment environments and show the performance of PooL. We first discuss the motivation example mentioned in Section 1. Then, main results compared with other methods is shown in various settings of MAgent. Finally, Battle environment is taken as an example to discuss details about our framework.
5.1. Motivation Experiment
5.1.1. Detailed Settings of Motivation Environment
In our motivation environment, agents get rewards of at every time step and get rewards of if they find food. For each agent, they will exit from the environment if they fall into holes or find food. The game ends when there are no agents in the environment. In order to set up a multi-agent environment, several agents are placed in each ant nest. This problem is solved by two methods: Table Q-Learning and PooL motivated Table Q-Learning. Agents using Table Q-Learning will update their Q-functions by Equation 1. For agents with pheromones, expect for Equation 1, we also maintain pheromone information by Equation 3. At every time step, agents fuse their Q-values of the current state with pheromone information according to a certain weight. In this way, we pass information from other agents to the current agent’s Q-table.
5.1.2. Motivation Result
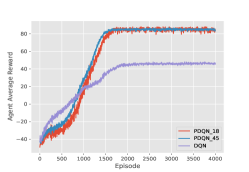
Figure 3 shows results of Table Q-Learning and PooL with different numbers of agents. Although Table Q-Learning achieves higher rewards at the beginning, more agents of PooL find the optimal solution at the end, which leads to higher average rewards for PooL. Our framework’s rewards will be smoother if there are more agents in the environment, which indicates that our framework is more advantageous when there are more agents.
5.2. Main Experiments
PooL is mainly evaluated in six multi-agent environments. We first introduce the settings of these six environments, and then show performance of different methods in these six environments.
5.2.1. Environment Description


Our environment settings are based on MAgentZheng et al. (2018) encapsulated by PettingzooTerry et al. (2020). Pettingzoo implements a variety of large-scale multi-agent environments based on MAgent. Agents in MAgent settings can get the location of obstacles and the location and HP (Health Points) of other agents within their view range. In our experiment, we use Battle, Battlefield, Combined Arms, Tiger-Deer, Adversarial Pursuit, and Gather as our running multi-agent environments. In the following experiments, the evaporation coefficient is and the virtual map size is for Gather with real-world map size and for other environments with smaller real-world map sizes.
-
•
Battle: In Battle, there are two teams: Red and Blue. At each time step, agents from the two teams decide their actions: move or attack. Agents will get rewards if they attack or kill their opponents.
-
•
Battlefield: The settings of Battlefield are similar to Battle except that there are indestructible obstacles in Battlefield.
-
•
Combined Arms: The settings of Combined Arms are also similar to Battle except that for each team there are two kinds of agents: ranged units and melee units. Ranged units have a longer attack range and are easier to be killed, while melee units have a shorter attack range and are harder to be killed.
-
•
Tiger-Deer: Tiger-Deer is an environment that simulates hunting in nature. Tigers try to attack and kill deer to get food. Deer will die if they are attacked too many times and tigers will starve to death if they can’t kill deer for a few time steps.
-
•
Adversarial Pursuit:Adversarial Pursuit settings are similar to Tiger-Deer without death. There are two teams in this environment: Red and Blue. Red agents are slower and larger than blue agents. Red agents will get rewards by tagging blue agents and blue agents try to avoid being tagged.
-
•
Gather: There are hundreds of agents and thousands of pieces of food in this environment. Agents should work together to break the food into pieces and eat them. Agents can attach each other to snatch food. It is an environment where competition and cooperation coexist. But in this paper, we focus more on cooperation. We limit the number of time steps in the game. In the case of sufficient food, agents can reduce competition and focus on cooperation.
| Environment | Agents to be trained | Agents of opponents | ||||
|---|---|---|---|---|---|---|
| Observation Space | Amount | Role | Observation Space | Amount | Role | |
| Battle,Battle Field | (5,7,7) | 80 | Red or Blue | (5,7,7) | 100 | Red or Blue |
| Tiger and Deer | (5,3,3) | 101 | Deer | (5,9,9) | 20 | Tiger |
| Pursuit | (5,5,5) | 100 | Blue | (5,6,6) | 25 | Red |
| Gather | (5,7,7) | 495 | Predator | - | 1636 | Food |
| Combined Arms | (7,7,7) | 66,55 | Melee, Ranged | (7,7,7) | 66,55 | Melee, Ranged |
Details of our environments are shown in Table 1. Observation Space describes the shape of the features from the environment received by agents. Amount describes the initial value of the number of agents in the environment. For Battle, Battle Field, and Combined Arms which are symmetrical, there is no difference between our agents and opponents in roles they play. In particular, in Combined Arms, each team has two kinds of heterogeneous agents. More detailed information can refer to Zheng et al. (2018); Terry et al. (2020).
PooL is compared with DQN Mnih et al. (2015), MFQ Yang et al. (2018), DGN Jiang et al. (2020). DGN is applied in Battle, Battlefield, Adversarial Pursuit, Tiger-Deer environments. In these four environments, We use the same settings as DGN —— the number of agents remains unchanged during the game. But for Combined Arms and Gather, the previous setting goes against the original intention of these two environments. Therefore, we only compare PooL with MFQ and DQN in these two environments.
5.2.2. Main Result
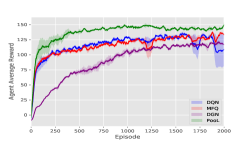
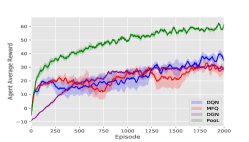
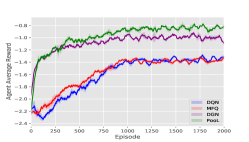
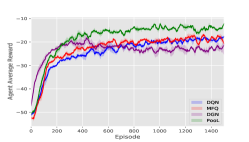
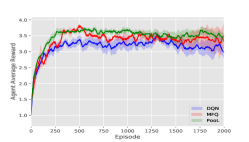
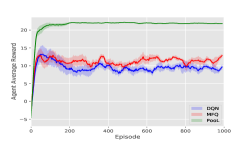
DQN models are trained by self-play as our opponents. Then our models are trained against those opponents. In the following experiments, for PooL, the Influence Domain is virtual grid, The Perception Domain is virtual grids. The Observation Domain for different environments is shown in Table 1. Our experimental results are shown in Figure 5.
-
•
Battle: In Battle, to improve the difficulty of our game, the team to be trained controls 80 agents and the team of opponents controls 100 agents respectively. The agents based on PooL learn the local coordination strategy faster, so as to obtain higher rewards with fewer games.
-
•
Battlefield: In Battlefield, the obstacles in the environment separate different agents, so for agents with only partial observations, communication is more important. As a result, PooL performs better than in Battle. With pheromones, agents based on our proposed framework obtain effective information on a larger scale and learn the coordination strategy faster.
-
•
Tiger-Deer: We control deer to avoid being attacked by tigers. Tiger-Deer is a simulated hunting environment in nature, which is very consistent with our pheromone-based indirect communication mechanism. As a result, through pheromones, deer in the environment can quickly know which direction there is a tiger and where other deer are fleeing.
-
•
Adversarial Pursuit: We control the smaller blue agents to avoid being tagged by red agents. Experiments show that blue agents can communicate through pheromones to escape from red agents.
-
•
Combined Arms: As there are two kinds of agents (ranged and melee) in one team. In this experiment, our channel of is the sum of the number of actions of the two. Experiments show that PooL and MFQ perform better than DQN.
-
•
Gather: In such an agent-intensive environment, experiments show that our framework can greatly promote cooperation among agents. The average reward of agents trained by PooL is about twice that of other methods.
It can be seen from Figure 5 that our method has a higher reward and faster convergence speed under various environmental settings. In Table 2, we choose the best model in the training step for each method and do a final evaluation. In most environments, rewards achieved by PooL are far more higher than other methods.
In summary, MFQ pays more attention to the coordination of global information. As a result, when the starting position of the agent is random, the performance of MFQ is similar to DQN. DGN is powerful to utilize information from its neighborhood. But as it regards agents as a graph, the convergence speed of agent training is much slower than other methods. In order to make DGN perform better in the scene of large-scale agents, we improve the update frequency of DGN parameters, which makes the time cost of DGN much higher than other methods. PooL effectively simplifies complex information in the environment, so that the agent trained by PooL can not only converge quickly but also use additional information to find better policies. PooL also has its limitation. The results in Combined Arms show that the current framework can not obtain significant advantages compared with other algorithms when there are heterogeneous agents in the same team.
| Environment | Average Cumulated Reward | |||
|---|---|---|---|---|
| DQN | MFQ | DGN | PooL | |
| Battle | ||||
| Battlefield | ||||
| Tiger-Deer | ||||
| Pursuit | ||||
| Combined Arms:Melee | - | |||
| Combined Arms:Ranged | - | |||
| Gather | - | |||
In order to further demonstrate the advantages of our proposed framework, we use our model trained by PooL against models trained by other methods. Because only Battle and BattleField are completely symmetrical in settings, our comparison experiment is only carried out in these two environments.
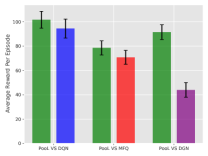
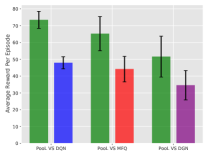
Figure 6 indicates that PooL not only has better convergence and cumulative reward in the training process but also has advantages against other methods. In the comparison, the overall worst performing method is DGN, which is based on graph convolution. This may be due to DGN overfitting the opponent’s strategy in environments with large-scale agents. PooL not only achieves higher rewards when fighting against the baseline but also learns more general strategies than other methods.
5.3. Detailed Experiments in Battle
In this section, we take Battle as an example to discuss the details of our proposed method.
5.3.1. Effectiveness
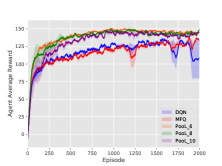
In order to show the effectiveness of our method, we compare our model with DQN with global information and MFQ with neighbor information. In MAgent, the density information of agents in the environment is available. This global information is added as an extra input to DQN. MFQ method uses information from surrounding agents. In section 6.3, we follow the settings of the original source code of MFQ which averages the actions of all agents. To promote local coordination of MFQ, we divide the environment into different grids like our framework. The area of the grid is close to the area of the Perception Domain of our framework. This modified MFQ denoted as MFQ_N receives information from its current grid.
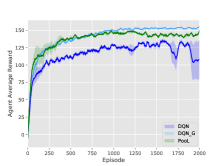
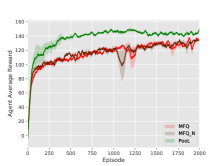
Performance of PooL compared with DQN with global information and MFQ with neighborhood information.
Figure 7 shows that our proposed framework still outperforms MFQ_N, and achieve similar results of DQN_G. This former result indicates that PooL not only receives signals from a wider range around but also contains more useful information than MFQ. The latter result shows that PooL is powerful to utilize local pheromone information to approximate the global situation.
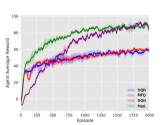
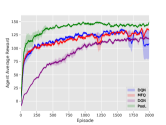
5.3.2. Scale Influence
Figure 8 shows how the number of agents from different teams affects our experimental result. Experimental results show that PooL is scalable and can give full play to its advantages when the number of agents in the environment is different. DQN, however, fails to learn a good policy when the number of agents becomes larger. MFQ suffers from unstable training procedures when there are more agents.

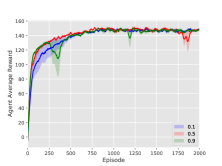
5.3.3. Hyper Parameters Selection
In our proposed method, there are two key hyperparameters to choose: the size of our virtual map and the evaporation coefficient of pheromones. In Figure 9(a), models are trained with virtual map sizes 6, 8 and 10 respectively. The result indicates that PooL is not sensitive to this parameter. Figure 9(b) indicates that when the evaporation coefficient is between 0.1-0.9, the average reward after model convergence is almost the same. A value of 0.1 or 0.9 may slightly reduce the convergence speed of the model. Therefore, we recommend a value of about 0.5 according to the actual environment. If the evaporation coefficient is too large, the model can not effectively extract historical information. If the evaporation coefficient is too small, the information reflected by pheromone will lag.
6. Conclusion
In this paper, we propose PooL, a pheromone-based indirect communication framework applied to MARL cooperation task. Inspired by swarm intelligence algorithms like ACO, PooL inherits the advantage of swarm intelligence algorithms that can be applied to large-scale agent coordination. Unlike ACO, pheromones released by agents are the output of DRL algorithms. Q-Learning is taken as an example to realize our framework, but other reinforcement learning algorithms can be applied to PooL in the same way. In our proposed framework, the information of agents in the environment is organized and dimensionally reduced by the pheromone update mechanism. Therefore, the cost of communication between agents is also very small. PooL is evaluated with different MARL algorithms in various environments proposed by Pettingzoo which contains hundreds of agents. Experimental results show that PooL converges faster and has higher rewards than other methods. Its superior performance with low cost in game environments shows that it has the potential to be applied in more complex real-world scenes with a bandwidth limit. PooL’s success indicates that rule-based swarm intelligence control algorithms are promising to combine with learning-based models for large-scale agents’ coordination.
This work was supported by NSF China under grand xxxxxxxx.
References
- (1)
- Bourenane et al. (2007) Malika Bourenane, Abdelhamid Mellouk, and Djilali Benhamamouch. 2007. Reinforcement learning in multi-agent environment and ant colony for packet scheduling in routers. In Proceedings of the 5th ACM international workshop on Mobility management and wireless access. 137–143.
- Buşoniu et al. (2010) Lucian Buşoniu, Robert Babuška, and Bart De Schutter. 2010. Multi-agent reinforcement learning: An overview. Innovations in multi-agent systems and applications-1 (2010), 183–221.
- Dai et al. (2019) Xiaolin Dai, Shuai Long, Zhiwen Zhang, and Dawei Gong. 2019. Mobile robot path planning based on ant colony algorithm with A* heuristic method. Frontiers in neurorobotics 13 (2019), 15.
- Das et al. (2019) Abhishek Das, Théophile Gervet, Joshua Romoff, Dhruv Batra, Devi Parikh, Mike Rabbat, and Joelle Pineau. 2019. Tarmac: Targeted multi-agent communication. In International Conference on Machine Learning. PMLR, 1538–1546.
- Di Caro and Dorigo (1998) Gianni Di Caro and Marco Dorigo. 1998. AntNet: Distributed stigmergetic control for communications networks. Journal of Artificial Intelligence Research 9 (1998), 317–365.
- Dorigo et al. (2006) Marco Dorigo, Mauro Birattari, and Thomas Stutzle. 2006. Ant colony optimization. IEEE computational intelligence magazine 1, 4 (2006), 28–39.
- Foerster et al. (2018) Jakob Foerster, Gregory Farquhar, Triantafyllos Afouras, Nantas Nardelli, and Shimon Whiteson. 2018. Counterfactual multi-agent policy gradients. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 32.
- Haarnoja et al. (2017) Tuomas Haarnoja, Haoran Tang, Pieter Abbeel, and Sergey Levine. 2017. Reinforcement learning with deep energy-based policies. In International Conference on Machine Learning. PMLR, 1352–1361.
- Hansen et al. (2004) Eric A Hansen, Daniel S Bernstein, and Shlomo Zilberstein. 2004. Dynamic programming for partially observable stochastic games. In AAAI, Vol. 4. 709–715.
- Heylighen (2015) Francis Heylighen. 2015. Stigmergy as a Universal Coordination Mechanism: components, varieties and applications. Human Stigmergy: Theoretical Developments and New Applications; Springer: New York, NY, USA (2015).
- Hoshen (2018) Yedid Hoshen. 2018. VAIN: Attentional Multi-agent Predictive Modeling. ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 30 (NIPS 2017) (2018), 2701–2711.
- Jiang et al. (2020) Jiechuan Jiang, Chen Dun, Tiejun Huang, and Zongqing Lu. 2020. Graph Convolutional Reinforcement Learning. ICLR (2020).
- Jiang and Lu (2018) Jiechuan Jiang and Zongqing Lu. 2018. Learning Attentional Communication for Multi-Agent Cooperation. ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 31 (NIPS 2018) (2018), 7254–7264.
- Kennedy (2006) James Kennedy. 2006. Swarm intelligence. In Handbook of nature-inspired and innovative computing. Springer, 187–219.
- Konatowski and Pawłowski (2018) Stanisław Konatowski and Piotr Pawłowski. 2018. Ant colony optimization algorithm for UAV path planning. In 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET). IEEE, 177–182.
- lillicrap et al. (2016) p timothy lillicrap, j jonathan hunt, alexander pritzel, nicolas heess, tom erez, yuval tassa, david silver, and daan wierstra. 2016. Continuous control with deep reinforcement learning. CoRR (2016).
- Lowe et al. (2020) Ryan Lowe, Yi Wu, Aviv Tamar, Jean Harb, Pieter Abbeel, and Igor Mordatch. 2020. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 30 (NIPS 2017) (2020), 6379–6390.
- Luo* et al. (2018) Rui Luo*, Yaodong Yang*, Minne Li, Ming Zhou, Weinan Zhang, and Jun Wang. 2018. Mean Field Multi Agent Reinforcement Learning. The 35th International Conference on Machine Learning (ICML’18), PMLR (2018), 5567–5576.
- Maru et al. (2016) Chihiro Maru, Miki Enoki, Akihiro Nakao, Shu Yamamoto, Saneyasu Yamaguchi, and Masato Oguchi. 2016. QoE Control of Network Using Collective Intelligence of SNS in Large-Scale Disasters. In 2016 IEEE International Conference on Computer and Information Technology (CIT). IEEE, 57–64.
- Matta et al. (2019) Marco Matta, Gian Carlo Cardarilli, Luca Di Nunzio, Rocco Fazzolari, Daniele Giardino, M Re, F Silvestri, and S Spanò. 2019. Q-RTS: a real-time swarm intelligence based on multi-agent Q-learning. Electronics Letters 55, 10 (2019), 589–591.
- Meerza et al. (2019) Syed Irfan Ali Meerza, Moinul Islam, and Md Mohiuddin Uzzal. 2019. Q-Learning Based Particle Swarm Optimization Algorithm for Optimal Path Planning of Swarm of Mobile Robots. In 2019 1st International Conference on Advances in Science, Engineering and Robotics Technology (ICASERT). IEEE, 1–5.
- Mnih et al. (2013) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. 2013. Playing Atari with Deep Reinforcement Learning. CoRR (2013).
- Mnih et al. (2015) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. 2015. Human-level control through deep reinforcement learning. nature 518, 7540 (2015), 529–533.
- Monekosso and Remagnino (2001) Ndedi Monekosso and Paolo Remagnino. 2001. Phe-Q: A pheromone based Q-learning. In Australian Joint Conference on Artificial Intelligence. Springer, 345–355.
- Oliehoek et al. (2008) Frans A Oliehoek, Matthijs TJ Spaan, and Nikos Vlassis. 2008. Optimal and approximate Q-value functions for decentralized POMDPs. Journal of Artificial Intelligence Research 32 (2008), 289–353.
- Silver et al. (2016) David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. 2016. Mastering the game of Go with deep neural networks and tree search. nature 529, 7587 (2016), 484–489.
- Sukhbaatar et al. (2016) Sainbayar Sukhbaatar, Arthur Szlam, and Rob Fergus. 2016. Learning Multiagent Communication with Backpropagation. ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 29 (NIPS 2016) (2016), 2252–2260.
- Terry et al. (2020) J. K Terry, Benjamin Black, Nathaniel Grammel, Mario Jayakumar, Ananth Hari, Ryan Sulivan, Luis Santos, Rodrigo Perez, Caroline Horsch, Clemens Dieffendahl, Niall L Williams, Yashas Lokesh, Ryan Sullivan, and Praveen Ravi. 2020. PettingZoo: Gym for Multi-Agent Reinforcement Learning. arXiv preprint arXiv:2009.14471 (2020).
- Wang et al. (2020) Weixun Wang, Tianpei Yang, Yong Liu, Jianye Hao, Xiaotian Hao, Yujing Hu, Yingfeng Chen, Changjie Fan, and Yang Gao. 2020. From few to more: Large-scale dynamic multiagent curriculum learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 34. 7293–7300.
- Wei et al. (2018) Ermo Wei, Drew Wicke, David Freelan, and Sean Luke. 2018. Multiagent soft q-learning. In 2018 AAAI Spring Symposium Series.
- Xu et al. (2021) Xing Xu, Rongpeng Li, Zhifeng Zhao, and Honggang Zhang. 2021. Stigmergic Independent Reinforcement Learning for Multiagent Collaboration. IEEE Transactions on Neural Networks and Learning Systems (2021).
- Xu et al. (2019) Xing Xu, Zhifeng Zhao, Rongpeng Li, and Honggang Zhang. 2019. Brain-inspired stigmergy learning. IEEE Access 7 (2019), 54410–54424.
- Yang et al. (2018) Yaodong Yang, Rui Luo, Minne Li, Ming Zhou, Weinan Zhang, and Jun Wang. 2018. Mean field multi-agent reinforcement learning. In International Conference on Machine Learning. PMLR, 5571–5580.
- Zhao and Ma (2019) Yuhang Zhao and Xiujun Ma. 2019. Learning Efficient Communication in Cooperative Multi-Agent Environment.. In AAMAS. 2321–2323.
- Zheng et al. (2018) Lianmin Zheng, Jiacheng Yang, Han Cai, Ming Zhou, Weinan Zhang, Jun Wang, and Yong Yu. 2018. Magent: A many-agent reinforcement learning platform for artificial collective intelligence. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 32.
- Zhou et al. (2020) Jie Zhou, Ganqu Cui, Shengding Hu, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, and Maosong Sun. 2020. Graph neural networks: A review of methods and applications. AI Open 1 (2020), 57–81.
- Zhou et al. (2019) Ming Zhou, Yong Chen, Ying Wen, Yaodong Yang, Yufeng Su, Weinan Zhang, Dell Zhang, and Jun Wang. 2019. Factorized q-learning for large-scale multi-agent systems. In Proceedings of the First International Conference on Distributed Artificial Intelligence. 1–7.