Portfolio Optimization with Relative Tail Risk
Abstract
This paper proposes analytic forms of portfolio CoVaR and CoCVaR on the normal tempered stable market model.
Since CoCVaR captures the relative risk of the portfolio with respect to a benchmark return,
we apply it to the relative portfolio optimization.
Moreover, we derive analytic forms for the marginal contribution to CoVaR and the marginal contribution to CoCVaR.
We discuss the Monte-Carlo simulation method to calculate CoCVaR and the marginal contributions of CoVaR and CoCVaR.
As the empirical illustration, we show relative portfolio optimization with thirty stocks under the distress condition of the Dow Jones Industrial Average. Finally, we perform the risk budgeting method to reduce the CoVaR and CoCVaR of the portfolio based on the marginal contributions to CoVaR and CoCVaR.
Key words:
Portfolio Optimization Relative Risk Normal Tempered Stable Model CoVaR CoCVaR
Marginal Contribution to Risk
1 Introduction
Harry Markowitz’s mean-variance portfolio optimization technique (Markowitz (1952)) has made a remarkable impact on portfolio theory in finance. This innovative method has been extensively utilized successfully in portfolio selection, allocation, and risk management practices. The adoption of Markowitz’s mean-variance model has resulted in significant improvements in investment outcomes and become a cornerstone of modern portfolio theory. Many investors have utilized Markowitz’s method to determine an efficient portfolio weight vector. Still, constructing a portfolio that surpasses the market index (e.g., S&P 500 index or DJIA) is not easy to be achieved. For that reason, some investors use relative portfolio optimization, that is, relaxing the assumption of the portfolio variance as the tracking error, which is a variance of the relative return. Here, the relative return is the difference between the portfolio return and a benchmark return, such as the market index return
This paper presents how to improve relative portfolio optimization based on two aspects. First, we loosen the Gaussian assumption of Markowitz’s model, which was empirically rejected in literature including Fama (1963), Mandelbrot (1963a, b), and Cont and Tankov (2004). Non-Gaussian multivariate distributions have been introduced to capture stylized facts, such as fat-tails and asymmetric dependence, that are not accounted for by the Gaussian model. This paper proposes the normal tempered stable (NTS) distribution as an alternative distribution to the Gaussian distribution. The NTS is defined by the tempered stable subordinated Gaussian distribution (Barndorff-Nielsen (1978), Barndorff-Nielsen and Levendorskii (2001) and Barndorff-Nielsen and Shephard (2001)). The NTS distribution has been popularly applied in finance by capturing the fat-tails of the asset return distribution and describing asymmetric dependence (See Kim and Volkmann (2013)). For example, it is applied to financial risk management in Anand et al. (2017) and Kurosaki and Kim (2018), and portfolio management in Eberlein and Madan (2010), Anand et al. (2016), and Kim (2022). In addition, Kim et al. (2015) applies a Lévy process generated by the two-dimensional NTS distribution to Quanto option pricing, and its extension to capture stochastic dependence is further discussed in Kim et al. (2023). Recently, the NTS distribution was applied to cryptocurrency portfolio optimization in Kurosaki and Kim (2022).
Second, we enhance the portfolio theory by replacing CoVaR and CoCVaR instead of the variance of the relative return as the risk measure. Traditionally, portfolio variance, value at risk (VaR), and conditional value at risk (CVaR) have been employed as the portfolio risk measure, but those are absolute risk measures. Relative traders prefer to use tracking errors such as the variance of relative return with respect to the benchmark return instead of the absolute risk measures. In this paper, we take CoVaR (Adrian and Brunnermeier (2016)) and CoCVaR (Huang and Uryasev (2018)) as the risk measures of relative portfolio optimization. CoVaR is proposed as a measure of systemic risk, which is the VaR of the financial system under the condition of a distressed market. Girardi and Tolga Ergün (2013) calculate CoVaR on the multivariate GARCH model and Reboredo and Ugolini (2015) use the copula method. CoCVaR (or CoES by Adrian and Brunnermeier (2016)) is an expected downturn of the financial system under the condition of a distressed market. Huang and Uryasev (2018) define the mathematical formula of CoCVaR and apply it to measure the risk of the ten largest publicly traded banks in the United States under a distressed condition of market factors222VIX, liquidity spread, three-month treasury change, term spread change, credit spread change, equity market return, and real estate sector excess return.. Recently, Liu et al. (2021) discuss CoVaR and CoCVaR on the GARCH model with two-dimensional NTS innovations and do the back-testing.
The paper discusses portfolio optimization minimizing the portfolio CoVaR and CoCVaR concerning the market index and derives the marginal contributions to risk for the portfolio CoVaR and CoCVaR. The marginal contribution to risk is the rate of change in risk with respect to a small percentage change in proportion to a member’s asset. Mathematically it is defined by the first derivative of CoVaR or CoCVaR with respect to the marginal weight. In the context of absolute optimization, the marginal contributions to VaR and CVaR are employed to identify assets with high and low levels of risk. The general form of marginal risk contributions for the VaR and CVaR are provided in Gourieroux et al. (2000). The analytic forms of the marginal contributions for VaR and CVaR are discussed under the skewed- distribution in Stoyanov et al. (2013), and under the NTS distribution in Kim et al. (2012) and Kim (2022). Since we focus on relative optimization in this paper, we provide analytic formulas for the marginal contributions to CoVaR and CoCVaR under the NTS market model instead of VaR and CVaR. Those marginal contributions to CoVaR and CoCVaR help relative traders to make decisions in portfolio rebalancing. However, the multiple integrals involved in these formulas can present technical difficulties for numerical calculations. To solve this problem, we use Monte-Carlo simulation (MCS) methods. Furthermore, we perform the risk budgeting based on the marginal contributions to CoVaR and CVaR empirically.
The remainder of this paper is organized as follows. The definition of portfolio CoVaR and portfolio CoCVaR are presented in Section 2. Section 3 reviews the NTS market model. Section 4 presents the portfolio CoVaR and CoCVaR on the NTS market model, along with a detailed analysis of the marginal contributions to CoVaR and CoCVaR. Empirical illustrations are given in section 5. In this section, we exhibit MCS method to calculate CoCVaR on the NTS market model and do the portfolio CoCVaR minimizing portfolio optimization with the estimated parameters. We also discuss portfolio budgeting using the marginal CoVaR and the marginal CoCVaR. Finally, Section 6 concludes. Proofs and mathematical details are presented in Appendix.
2 CoVaR and CoCVaR
Let be a random variable for a market factor, for instance, the market index returns, and be a random variable for asset or portfolio returns. We consider a random vector following a joint distribution. The CoVaR and CoCVaR of at a significant level under a condition of the event are defined by
and
respectively333See Adrian and Brunnermeier (2016),Huang and Uryasev (2018), and Liu et al. (2021) for more details, where is the Value-at-Risk (VaR) of for a significant level given as
If the joint distribution of is continuous, then where is the cumulative distribution function (cdf) for the marginal distribution of and is the inverse function of . Moreover, we have
for the joint cdf of .
Consider number of stocks and a market index and an -dimensional random vector , , , , where is the index return and is the return of the th stock for , , , . Let , , , be an -dimensional vector satisfying for . The th element of is the proportion of capital invested in the th stock for . In this case, be referred to as the capital allocation weight vector for the stocks in the market444In this paper, we consider the long-only portfolio.. Then we have the random variable of the portfolio return as .
Suppose that follows -dimensional normal distribution with a mean vector , , , and a covariance matrix , that is . Let be the -th element of for . Then the bivariate random vector follows the bivariated normal distribution, with
where , , . We can calculate VaR of as , where is -quantile value of the standard normal distribution. Suppose the value satisfies
where is the probability density function of . Then . Moreover,
3 Standard NTS distribution and NTS Market model
In this section, we define the multivariate standard NTS distribution and construct the market model based on the distribution.
3.1 Standard NTS Distribution
Let be a finite positive integer and be a multivariate random variable given by
where
-
•
is the tempered stable subordinator with parameters , and is independent of for all .
-
•
with for all .
-
•
with for all and .
-
•
is -dimensional standard normal distribution with a covariance matrix . That is, for and -th element of is given by for . Note that .
In this case, is referred to as the -dimensional standard NTS random variable with parameters , , , and we denote it by , , , (See more details in Kim and Volkmann (2013) and Kim (2022).).
-
•
The probability density function (pdf) of is , where is the characteristic function (ch.f) of given by
-
•
The cdf of the stdNTS vector is given by
(1) where is the pdf of -dimensional normal distribution with mean and covariance .
-
•
The pdf if the vector is given by
(2) where is the pdf of the -dimensional normal distribution with mean and covariance .
-
•
By Gil-Pelaez (1951), the marginal cdf of for is equal to
(3) where is the ch.f of given by
Moreover, the marginal pdf of is obtained by the inverse Fourier transform for the characteristic function as
-
•
Covariance between and for is equal to
(4)
3.2 NTS Market Model
Consider a portfolio having assets for a positive integer . The return of the assets in the portfolio is given by a random vector , , , . We suppose that the return follows
| (5) |
where , and . Then, we have and for all . This market model is referred to as the NTS market model.
Let be the capital allocation weight vector. Then the portfolio return for is equal to . The distribution of is presented in the following proposition from Kim (2022).
4 Portfolio CoVaR and CoCVaR with respect to a Market Index
Consider number of stocks and a market index for a given market as follows:
-
•
is the market index return.
-
•
for is the individual stock return of a stock portfolio consisting of stocks.
Suppose follows a ()-dimensional NTS market model, that is, we have
| (7) |
where
-
•
, and ,
-
•
, , with for ,
-
•
is the covariance matrix and is the -th element of for .
Based on the assumption, we obtain the following proposition whose proof is in Appendix.
Proposition 4.1.
Suppose follows a ()-dimensional NTS market model as (7). Let be a capital allocation weight vector and . The bivariate random vector follows 2-dimensional NTS model such as
for
where
and
| (8) |
for .
Remark Let , , and . Then
for and .
With the positive homogeneity and translation invariance properties of VaR and CoVaR, we have
and
Since marginal distributions of , and are continuous, we have , where and are the cdf and inverse cdf of , respectively. Moreover, is the value satisfying
i.e.
| (9) |
where is the cdf of . By (1), is given as
where , and is the pdf of the bivariate standard normal distribution with covariance .
By the same arguments, we have CoCVaR as
| (10) |
and
where
and
by (2). By the change of variables, we have
| (11) |
or
| (12) |
where , , , is the bivariate standard normal random vector with covariance , and is the tempered stable subordinator with parameters independent of .
4.1 Marginal Contribution to CoVaR and CoCVaR
In this section, we discuss the marginal contributions to CoVaR and CoCVaR under the -dimensional NTS market model with the market index defined in the previous section. Let be the th element of the capital allocation vector , , for , , , . Let , and , where , , and . Let be the bivariate standard normal pdf with covariance , that is
Define
Then if by (9).
Proposition 4.2.
The marginal contribution to CoVaR for the th element of the portfolio capital allocation weight vector is
| (13) |
with
| (14) |
and
| (15) | |||
where
Proposition 4.3.
The marginal contribution to CoCVaR for the -th element of the portfolio capital allocation weight vector is
| (16) | ||||
where
-
•
,
-
•
,
- •
-
•
is the bivariate standard normal distributed random vector with covariance ,
-
•
and is the tempered stable subordinator with parameters independent of .
We deduce the marginal contribution to CoVaR as follows:
or
| (17) | ||||
where is given as (13) in Proposition 4.2. By the same arguments, we obtain the marginal contribution to CoCVaR as follows
| (18) | ||||
| Company | Symbol | Company | Symbol |
|---|---|---|---|
| 3M | MMM | American Express | AXP |
| Amgen | AMGN | Apple Inc. | AAPL |
| Boeing | BA | Caterpillar Inc. | CAT |
| Chevron Corporation | CVX | Cisco Systems | CSCO |
| The Coca-Cola Company | KO | DuPont de Nemours Inc. | DD |
| Goldman Sachs | GS | The Home Depot | HD |
| Honeywell | HON IBM | IBM | |
| Intel | INTC | Johnson & Johnson | JNJ |
| JPMorgan Chase | JPM | McDonald’s | MCD |
| Merck & Co. | MRK | Microsoft | MSFT |
| Nike | NKE | Procter & Gamble | PG |
| Salesforce | CRM | The Travelers Companies | TRV |
| United Health Group | UNH | Verizon | VZ |
| Visa Inc. | V | Walmart | WMT |
| Walgreens Boots Alliance | WBA | The Walt Disney Company | DIS |
5 Empirical Illustration
We fit the parameters of the NTS market model to Dow Johns Industrial Average (DJIA) index and 30 major stocks555The selected 30 stocks are the components of the DJIA index as of 2022. Since Dow Inc.(DOW) in the components does not have enough history, it is replaced by DuPont de Nemours Inc.(DD). in the U.S. stock market. The company names and symbols of those 30 stocks are listed in Table 1.
The parameter estimation method in this section is similar as the method in Kim (2022). We take the set of daily log returns for the DJIA index and each stock from 11/27/2018 to 11/15/2022 and calculate sample means and sample standard deviations for each stock and the index. The residuals are extracted by the z-score, and then fit the stdNTS parameters to the residuals of each stock (or index) return. The curve fit method is used between the cdf of the stdNTS distribution obtained by (3) and the empirical cdf obtained by the kernel density estimation. The same as Kim (2022), we use the index-based method with DJIA index data in order to find and and then estimate the vector and matrix. That is, we find the 30-dimensional stdNTS parameters as the following two-step method:
-
Step 1 Find using the curve fit method between the empirical cdf and stdNTS cdf for the residual of DJIA index. The parameters are considered the parameters of the tempered stable subordinator.
-
Step 2 Taking estimated at Step 1, find by applying the curve fit method with the fixed and for each -th stock returns .
-
Step 3 Find sample covariance matrix using the standardized residual. Here the index is assigned to the DJIA index. Find using (4).
The parameters of the tempered stable subordinator in this investigation are and . The other estimated parameters are presented in Table 2 with Kolmogorov-Smirnov (KS) p-values present in the table for the goodness of fit test.
5.1 Calculating CoCVaR, MCT-CoVaR and MCT-CoCVaR with MCS
In this section, we discuss MCS to find portfolio CoCVaR, MCT-CoVaR and MCT-CoCVaR using the parameters in Table 2 on the NTS market model. Here, we use R language version 4.2.2 running on MS-Windows 10 operating system with the processor Intel Core i7-4790, 3.60GHz. To calculate CVaR of the portfolio, we use equation (10) and is obtained by a multiple-integral form (11) or an expectation form (12).
Assume that we have an equally weighted portfolio with the 30 stocks in Table 2, i.e. for . We apply Proposition 4.1 to find , , , , and . Let be the sample size of the simulation and generate two sets of independent pairs of standard normal random numbers, with and generate one set of tempered stable subordinators, , which are independent of . Considering the correlation , we set .
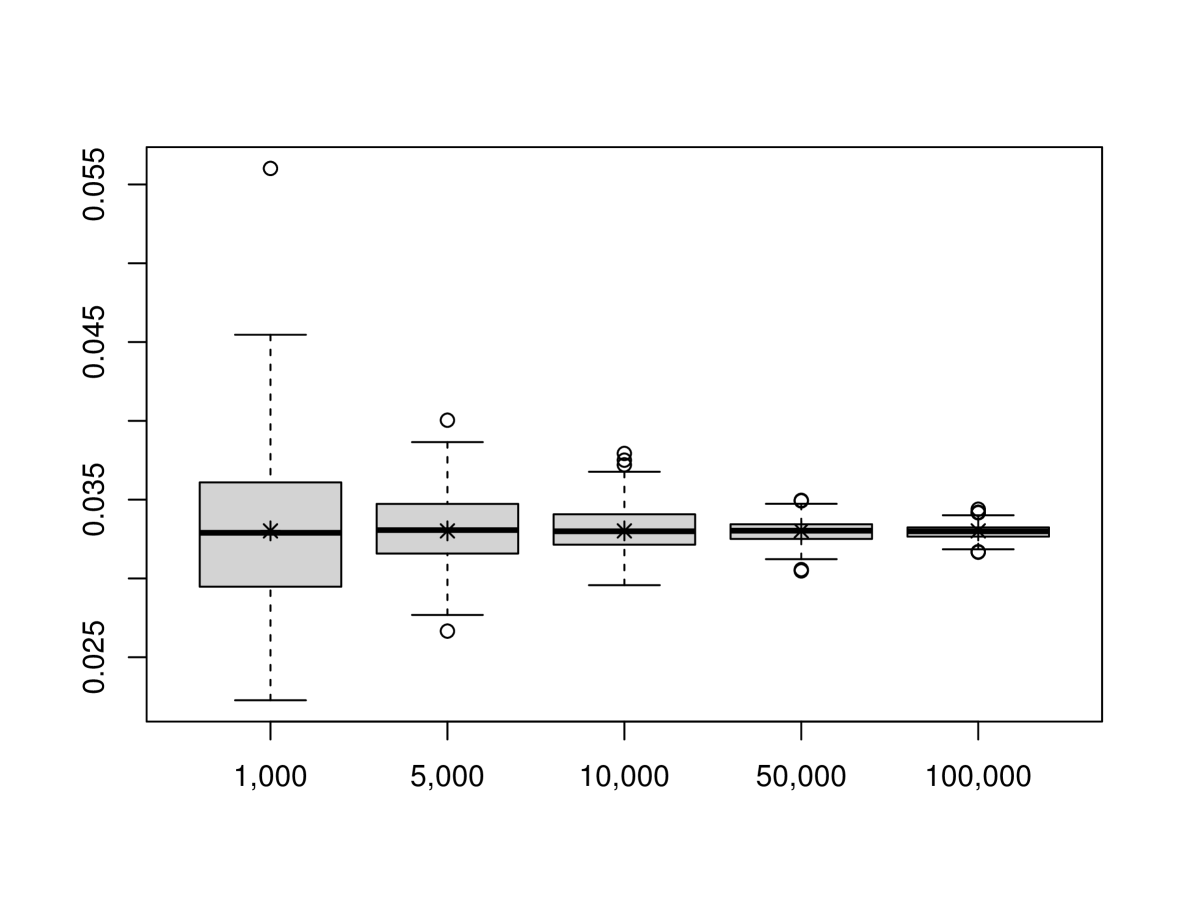
We obtain as
| (19) |
for and , by MCS and (10). We check the convergence of MCS using bootstrapping. We draw the first boxplot from the left by repeating the MCS 100 times using (19) for a given sample size in Figure 1. In addition, we draw the other boxplots for each sample size , which are presented sequentially after the first box plot in the figure. We also show (by the symbol ‘*’) the CoCVaR computed by numerical integration based on (11). We observe that, as the sample size increases, the interquartile distance of MCS CoCVaR narrows, and dispersions are reduced. All box plots contain the CoCVaR computed by the numerical integration in the interquartile range. The multiple-integral form (11) takes a relatively longer numerical calculation time of 18.13 seconds, while the MCS takes 7.57 seconds for a 100,000 sample size.
Using the same arguments, we can calculate MCT-CoVaR and MCT-CoCVaR using MCS. We calculate the expectations in equations in Proposition 4.2 and 4.3 use the random numbers in , and , and substitute those MCS expectations into (14), (15), and (16) to obtain and . Finally, we obtain and by substituting and into (17), and (18), respectively.
The result of MCT-CoVaR and MCT-CoCVaR values using MCS for each individual stocks of the equally weighted portfolio are exhibited in Table 2 with the rank of the values for the ascending order. For example, MCT-CoVaR and MCT-CoCVaR values for MRK rank 1st and those values of AXP rank 30th, respectively. DD ranks 2nd for MCT-CoVaR but 4th for MCT-CoCVaR and so on. We can see that AXP is largest CoVaR and CoCVaR contributor, and is recommended to reduce the proportion of the capital allocation. This idea will be discussed in the Risk Budgeting, below.
5.2 Portfolio Optimization
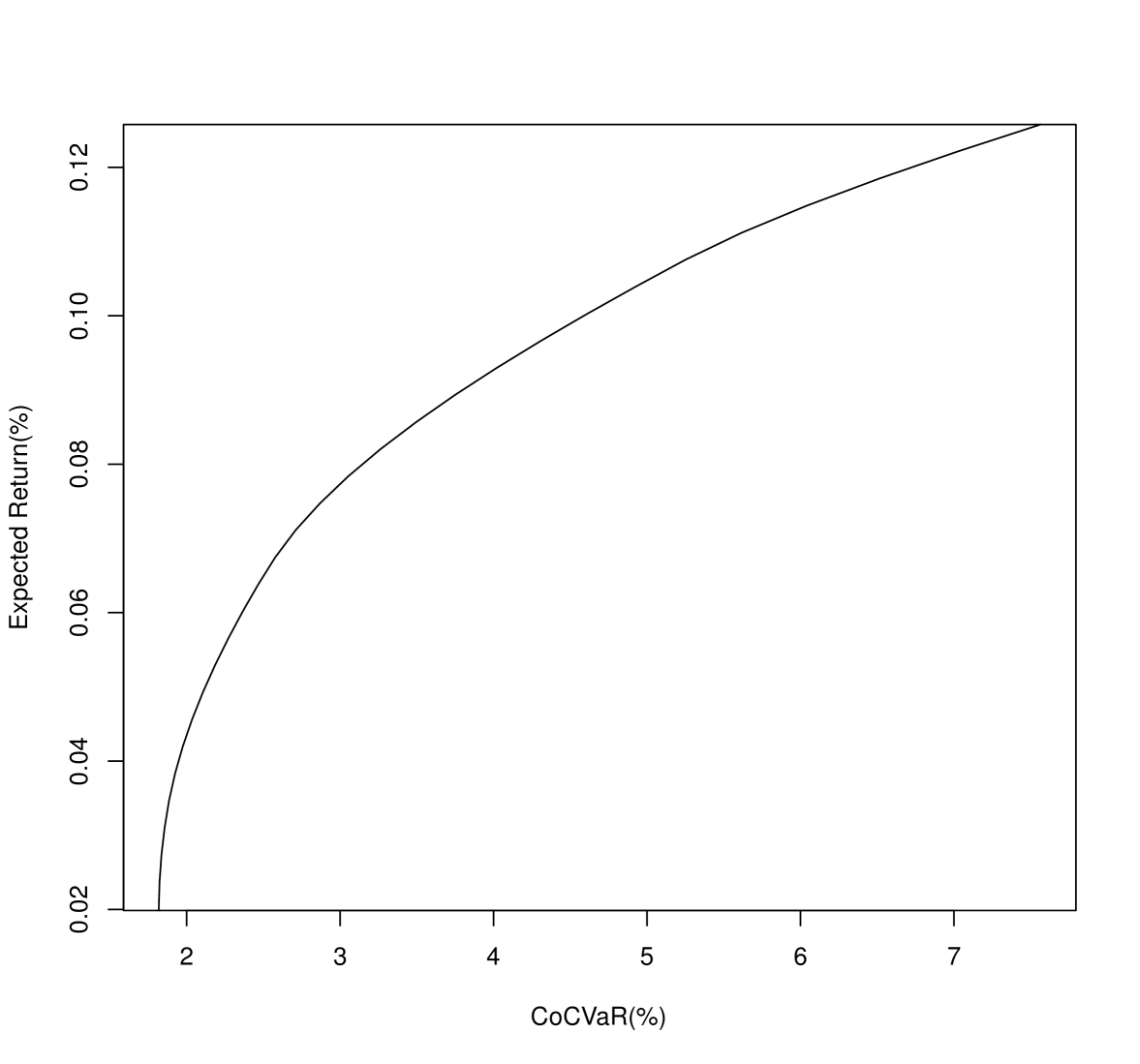
Since CoVaR and CoCVaR can capture the relative tail risk under the condition of distressed condition of a benchmark asset or index, we can use those two risk measures for relative portfolio optimization. In this section, we show an empirical example of CoCVaR minimizing portfolio optimization for the 30 stocks with respect to the DJIA index on the NTS market model.
We set a nonlinear programming problem for the portfolio optimization as
| subject to | |||
where the benchmark values for the portfolio expected return is . Using the parameters in Table 2, we perform the portfolio optimization for 51 points of in . We finally obtain the efficient frontier in Figure 2.
| Symbol | KS | |||||||
|---|---|---|---|---|---|---|---|---|
| DJIA | 0.0310 | 1.4575 | 3.7939 | 0.0100 | MCT-CoVaR(%) | Rank | MCT-CoCVaR(%) | Rank |
| AAPL | 0.1258 | 2.1977 | 1.2679 | 0.0587 | 1.6529 | 17 | 3.5957 | 19 |
| AMGN | 0.0490 | 1.6810 | 1.8704 | 0.0416 | 3.2980 | 22 | 2.1241 | 7 |
| AXP | 0.0395 | 2.5245 | 0.5258 | 0.0241 | 7.4288 | 30 | 6.6507 | 30 |
| BA | 0.0564 | 3.4757 | 3.7589 | 0.0168 | 1.7783 | 18 | 6.3659 | 29 |
| CAT | 0.0733 | 2.1609 | 0.3824 | 0.0502 | 5.5670 | 26 | 4.8958 | 22 |
| CRM | 0.0284 | 2.5370 | 1.0588 | 0.0514 | 5.1597 | 23 | 5.3903 | 27 |
| CSCO | 0.0117 | 1.9311 | 1.3543 | 0.0323 | 1.5658 | 15 | 2.2187 | 8 |
| CVX | 0.0678 | 2.4216 | 1.5941 | 0.0176 | 5.6102 | 27 | 4.9429 | 23 |
| DD | 0.0096 | 2.4072 | 0.3164 | 0.0593 | 0.1376 | 2 | 1.4762 | 4 |
| DIS | 0.0140 | 2.1879 | 4.1225 | 0.0337 | 0.3701 | 10 | 3.4376 | 18 |
| GS | 0.0791 | 2.2039 | 2.0020 | 0.0485 | 6.0133 | 29 | 5.4714 | 28 |
| HD | 0.0709 | 1.9351 | 3.9629 | 0.0261 | 5.3208 | 25 | 4.9610 | 24 |
| HON | 0.0483 | 1.8365 | 2.3242 | 0.0341 | 1.5242 | 14 | 2.6857 | 13 |
| IBM | 0.0437 | 1.8054 | 1.5555 | 0.0287 | 0.5364 | 11 | 3.1157 | 16 |
| INTC | 0.0314 | 2.4868 | 2.8086 | 0.0295 | 0.2124 | 8 | 2.6130 | 11 |
| JNJ | 0.0260 | 1.3628 | 0.5663 | 0.0285 | 0.8420 | 12 | 1.5451 | 5 |
| JPM | 0.0333 | 2.1622 | 2.5850 | 0.0357 | 5.6910 | 28 | 5.1918 | 26 |
| KO | 0.0324 | 1.4671 | 3.6931 | 0.0249 | 0.3419 | 9 | 2.6197 | 12 |
| MCD | 0.0476 | 1.5731 | 1.2955 | 0.0162 | 0.2091 | 7 | 2.3540 | 9 |
| MMM | 0.0286 | 1.7824 | 2.1382 | 0.0420 | 0.0681 | 6 | 2.7091 | 14 |
| MRK | 0.0461 | 1.5310 | 0.0218 | 0.0463 | 0.7418 | 1 | 0.2360 | 1 |
| MSFT | 0.0879 | 2.0241 | 2.1377 | 0.0469 | 2.4863 | 20 | 3.9390 | 20 |
| NKE | 0.0424 | 2.1704 | 0.2999 | 0.0418 | 2.4980 | 21 | 4.5851 | 21 |
| PG | 0.0511 | 1.4348 | 3.0200 | 0.0322 | 0.1305 | 3 | 0.7501 | 3 |
| TRV | 0.0444 | 1.9422 | 2.8043 | 0.0255 | 1.1151 | 13 | 3.3984 | 17 |
| UNH | 0.0714 | 1.9919 | 1.6187 | 0.0288 | 0.0165 | 5 | 2.5646 | 10 |
| V | 0.0472 | 1.9411 | 2.5133 | 0.0423 | 5.2771 | 24 | 5.1686 | 25 |
| VZ | 0.0226 | 1.2645 | 2.5648 | 0.0357 | 0.1084 | 4 | 0.3166 | 2 |
| WBA | 0.0539 | 2.2096 | 1.4927 | 0.0360 | 1.6265 | 16 | 2.7307 | 15 |
| WMT | 0.0508 | 1.4940 | 1.0659 | 0.0263 | 2.4613 | 19 | 1.7390 | 6 |
5.3 Risk Budgeting
The MCT-CoVaR and MCT-CoCVaR allow portfolio managers to decide to rebalance their capital allocation weights. Managers can reduce portfolio risk by decreasing the weight of high-risk contributors and increasing the weight of low-risk contributors. The high-risk contributors are assets having high MCT-CoVaR (or MCT-CoCVaR), while the low-risk contributors are assets having low MCT-CoVaR (or MCT-CoCVaR).
Consider a capital allocation vector for a portfolio with member stocks. Let , , , where is a zero neighborhood in , and let
and
The optimal portfolios with respect to CoVaR and CoCVaR are obtained by solving the following problem:
| (20) | |||
and
| (21) | |||
Since we have
we can find the optimal portfolio on the local domain with respect to CoVaR and CoCVaR, respectively, as follows:
| (22) | ||||
and
| (23) | ||||
We perform the risk budgeting for CoVaR and CoCVaR using the 30 stocks in Table 1, i.e. , with the estimated parameters in Table 2, iteratively, as the following algorithm:
-
Step 1. Generate a set of independent pairs of standard normal random numbers , and a set of tempered stable subordinators, , which are independent of , as we discussed in Section 5.1. Here, the sample size is .
-
Step 2. Select an initial capital allocation weight vector .
-
Step 3. Find , , , and by Proposition 4.1.
-
Step 4. Regenerate a set of bivariate standard normal random vectors with correlation .
-
Step 5. Calculate MCT-CoVaR or MCT-CoCVaR for using the MCS method we discussed in Section 5.1.
-
Step 7. Change to and go to Step 3. Repeat [Step 2 - Step 7] times.
Let the initial capital allocation weight vector be equally weighted. We perform the iterative risk budgeting times for the local domain be
The results are exhibited in Figure 3. For each iteration, we show the values of CoVaR, and CoCVaR with the MCS method in the left and right plate, respectively. The figure shows that the portfolio CoVaR and CoCVaR with respect to the DJIA index decreases as increasing the number of iterations. That is using risk budgeting of CoVaR and CoCVaR on the NTS market model, we obtain a portfolio having the same expected return but less relative tail risk.
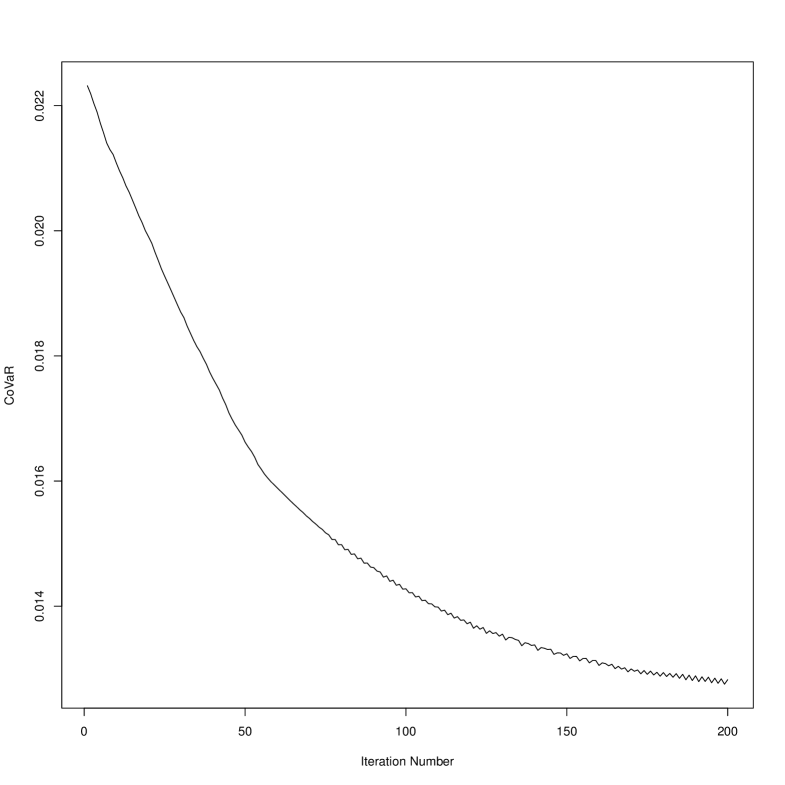
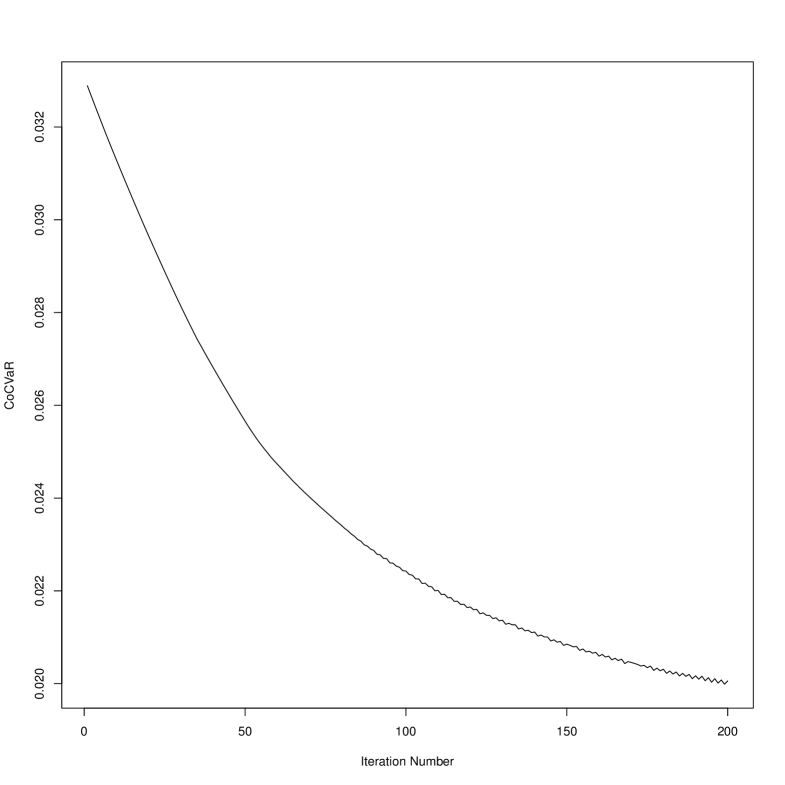
6 conclusion
This paper presents portfolio CoVaR and portfolio CoCVaR on the NTS market model. We develop an MCS method to calculate portfolio CoVaR and CoCVaR, and apply it to portfolio optimization. As an empirical illustration, we consider a portfolio consisting of 30 stocks and measure the CoCVaR of the portfolio with respect to the DJIA index, and then find the efficient frontiers of the portfolio, maximizing the portfolio’s expected return and minimizing the relative tail risk captured by the CoCVaR. In addition, we find an analytic formula for the marginal contributions to CoVaR and CoCVaR, which we calculate using the MCS method to overcome numerical difficulties. We also perform portfolio risk budgeting methods using the marginal contributions to CoVaR and CoCVaR on the NTS market model. We empirically show that the portfolio CoVaR and CoCVaR are decreased by using portfolio budgeting iteratively.
7 Appendix
Proof of Proposition 4.1.
By Proposition 3.1, the stock portfolio return is equal to
where
and
| (24) |
Since we have
with . Note that we have
and
For the Gaussian property, we get
where . Hence, we have
where . Therefore, we have
| (25) |
On the other hand, we have
Since we have
we obtain
| (26) |
or
| (27) |
Using the definition , we obtain
| (28) |
Lemma 7.1.
Based on the setting in Section 4.1, we have
(i)
| (29) |
(ii)
| (30) |
and
| (31) |
(iii)
| (32) | ||||
(iv) Let
Then
| (33) | ||||
(v)
| (34) |
Proof.
(i)
(ii)
and
(v)
∎
Lemma 7.2.
Let be the pdf of the bivariate standard normal distribution with covariance , then we have
| (36) |
Moreover, if we put and let be the -th element of then we have
| (37) |
Proof.
Proof of Proposition 4.2.
Since , we get
By applying implicit differentiation, we have
and hence
We have
By (36), we have
Proof of Proposition 4.3.
(i) Calculating
We have
Let
and
Then .
Let’s simplify . Note that by the definition of . By (36), we have
where is the tempered stable subordinator with parameters .
Consider the integral . We have
Hence, we obtain
Let
and
Then we have
We get by (11). Assume is the bivariate standard normal distributed random vector with covariance , and is the tempered stable subordinator with parameters independent of . Then
and
where . Substituting , , , into
we obtain
| (39) | ||||
(ii) Calculating
Since we have
we get
Using the same arguments in the proof of Proposition 4.2, we obtain
| (40) | ||||
By substituting (39), (40), and into (38), we get
Hence we obtain (16).
∎
References
- Adrian and Brunnermeier (2016) Adrian, T. and Brunnermeier, M. K. (2016). Covar. American Economic Review, 106(7), 1705–41. URL https://www.aeaweb.org/articles?id=10.1257/aer.20120555.
- Anand et al. (2016) Anand, A., Li, T., Kurosaki, T., and Kim, Y. S. (2016). Foster-Hart optimal portfolios. Journal of Banking and Finance, 68, 117–130.
- Anand et al. (2017) Anand, A., Li, T., Kurosaki, T., and Kim, Y. S. (2017). The equity risk posed by the too-big-to-fail banks: A foster-hart estimation. Annals of Operations Research, 253(1), 21–41.
- Barndorff-Nielsen (1978) Barndorff-Nielsen, O. (1978). Hyperbolic distributions and distributions on hyperbolae. Scandinavian Journal of Statistics, 5(3), 151–157.
- Barndorff-Nielsen and Levendorskii (2001) Barndorff-Nielsen, O. E. and Levendorskii, S. (2001). Feller processes of normal inverse Gaussian type. Quantitative Finance, 1, 318 – 331.
- Barndorff-Nielsen and Shephard (2001) Barndorff-Nielsen, O. E. and Shephard, N. (2001). Normal modified stable processes. Economics Series Working Papers from University of Oxford, Department of Economics, 72.
- Cont and Tankov (2004) Cont, R. and Tankov, P. (2004). Financial Modelling with Jump Processes. Chapman & Hall / CRC.
- Eberlein and Madan (2010) Eberlein, E. and Madan, D. B. (2010). On correlating Lévy processes. Journal of Risk, 13(1), 3–16.
- Fama (1963) Fama, E. (1963). Mandelbrot and the stable Paretian hypothesis. Journal of Business, 36, 420–429.
- Gil-Pelaez (1951) Gil-Pelaez, J. (1951). Note on the inversion theorem. Biometrika, 38(3-4).
- Girardi and Tolga Ergün (2013) Girardi, G. and Tolga Ergün, A. (2013). Systemic risk measurement: Multivariate garch estimation of covar. Journal of Banking & Finance, 37(8), 3169–3180. URL https://www.sciencedirect.com/science/article/pii/S0378426613001155.
- Gourieroux et al. (2000) Gourieroux, C., Laurent, J., and Scaillet, O. (2000). Sensitivity analysis of values at risk. Journal of Empirical Finance, 7, 225–245.
- Huang and Uryasev (2018) Huang, W.-Q. and Uryasev, S. P. (2018). The cocvar approach: systemic risk contribution measurement. Journal of Risk, 20, 75–93.
- Kim (2005) Kim, Y. (2005). The Modified Tempered Stable Processes with Applications to Finance. Ph.D. thesis, Sogang University.
- Kim (2022) Kim, Y. S. (2022). Portfolio optimization and marginal contribution to risk on multivariate normal tempered stable model. Annals of Operations Research, 1–29.
- Kim et al. (2012) Kim, Y. S., Giacometti, R., Rachev, S. T., Fabozzi, F. J., and Mignacca, D. (2012). Measuring financial risk and portfolio optimization with a non-Gaussian multivariate model. Annals of Operations Research, 201(1), 325–343.
- Kim et al. (2023) Kim, Y. S., Kim, H., Choi, J., and Fabozzi, F. J. (2023). Multi-asset option pricing using normal tempered stable processes with stochastic correlation. The Journal of Derivatives, 30(3), 42–64.
- Kim et al. (2015) Kim, Y. S., Lee, J., Mittnik, S., and Park, J. (2015). Quanto option pricing in the presence of fat tails and asymmetric dependence. Journal of Econometrics, 187(2), 512 – 520.
- Kim and Volkmann (2013) Kim, Y. S. and Volkmann, D. (2013). NTS copula and finance. Applied Mathematics Letters, 26, 676–680.
- Kurosaki and Kim (2018) Kurosaki, T. and Kim, Y. S. (2018). Foster-Hart optimization for currency portfolio. Studies in Nonlinear Dynamics & Econometrics, 23(2), Published Online.
- Kurosaki and Kim (2022) Kurosaki, T. and Kim, Y. S. (2022). Cryptocurrency portfolio optimization with multivariate normal tempered stable processes and foster-hart risk. Finance Research Letters, 45, 102143.
- Liu et al. (2021) Liu, Y., Djurić, P. M., Kim, Y. S., Rachev, S. T., and Glimm, J. (2021). Systemic risk modeling with Lévy copulas. Journal of Risk and Financial Management, 14(6), 251.
- Mandelbrot (1963a) Mandelbrot, B. B. (1963a). New methods in statistical economics. Journal of Political Economy, 71, 421–440.
- Mandelbrot (1963b) Mandelbrot, B. B. (1963b). The variation of certain speculative prices. Journal of Business, 36, 394–419.
- Markowitz (1952) Markowitz, H. (1952). Portfolio selection. Journal of Finance, 7(1), 77–91.
- Reboredo and Ugolini (2015) Reboredo, J. C. and Ugolini, A. (2015). Systemic risk in european sovereign debt markets: A covar-copula approach. Journal of International Money and Finance, 51, 214–244. URL https://www.sciencedirect.com/science/article/pii/S0261560614002162.
- Stoyanov et al. (2013) Stoyanov, S. V., Rachev, S. T., and Fabozzi, F. J. (2013). Sensitivity of portfolio VaR and CVaR to portfolio return characteristics. Annals of Operations Research, 205, 169–187.