PPCU: Proportional Per-packet Consistent Updates for Software Defined Networks - A Technical Report
Abstract
In Software Defined Networks, where the network control plane can be programmed by updating switch rules, consistently updating switches is a challenging problem. In a per-packet consistent update (PPC), a packet either matches the new rules added or the old rules to be deleted, throughout the network, but not a combination of both. PPC must be preserved during an update to prevent packet drops and loops, provide waypoint invariance and to apply policies consistently. No algorithm exists today that confines changes required during an update to only the affected switches, yet preserves PPC and does not restrict applicable scenarios. We propose a general update algorithm called PPCU that preserves PPC, is concurrent and provides an all-or-nothing semantics for an update, irrespective of the execution speeds of switches and links, while confining changes to only the affected switches and affected rules. We use data plane time stamps to identify when the switches must move from the old rules to the new rules. For this, we use the powerful programming features provided to the data plane by the emerging programmable switches, which also guarantee line rate. We prove the algorithm, identify its significant parameters and analyze the parameters with respect to other algorithms in the literature.
I Introduction
A network is composed of a data plane, which examines packet headers and takes a forwarding decision by matching the forwarding tables in switches, and a control plane, which builds the forwarding tables. A Software Defined Network (SDN) simplifies network management by separating the data and control planes and providing a programmatic interface to the control plane.
SDN applications running on one or more controllers can program the network control plane dynamically by updating the rules of the forwarding tables of switches to alter the behaviour of the network. Every Rules Update consists of a set of updates in a subset of the switches in a network. Every update in switch consists of two sets of rules and . Rule set is to be deleted and rule set is to be inserted. One of or may be NULL. The rules are denoted by . Every switch , , is called an affected switch. All other switches are unaffected switches. The set of rules that is neither inserted nor deleted is an unaffected set of rules and is denoted by .
Packets that traverse the network during the course of an update must not be dropped (drop-freedom) and must not loop (loop-freedom) on account of the update. In Figure 1(a), when switches are updated to change a route from the old path (solid lines), to the new path (dotted lines), if is updated first, packets arriving at will get dropped, while if is updated first, packets arriving at will loop. Flows in a network may need to pass through a number of waypoints in a certain order at all times (waypoint invariance). In Figure 1(b), , and are the waypoints to be traversed in that order and this cannot be achieved by sequencing the updates in any order[1]. While the above three properties can be preserved in many update scenarios by finding a suitable order of updates [1, 2, 3, 4], the example in Figure 1(c) cannot be solved by suitably sequencing updates, in any scenario. Initially the network has a policy which requires an ingress switch to drop packets whose ports are in the range and , an egress switch, to drop packets whose destination addresses are in the range to . Policies may be distributed over various switches in an SDN to reduce load on middleboxes or on links to them [5] or due to lack of rule space on a switch [6]. When the policy is changed to , the network administrator desires either or to be applied to any packet and not, for example, at and at . We call this property pure per-packet consistency (pure PPC).
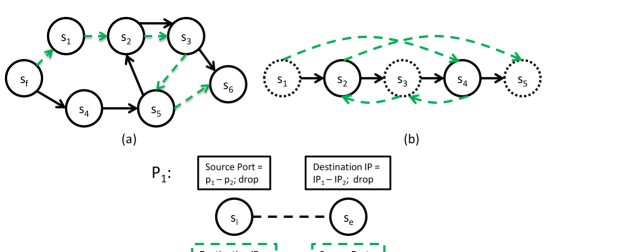
In order to preserve all the properties for all scenarios, every Rules Update must be per-packet consistent [7] (PPC): every packet travelling through the network must use either rule in every affected switch or rule in every affected switch , and never a combination of both, during a Rules Update. Other rules in the switches are to be used if they match. The number of packets that get subjected to any of the inconsistencies can be quite large because the time to update a few rules at a switch, which is of the order of milliseconds [8], is far greater than the time to switch a packet out of a switch, which is of the order of nanoseconds, given that the line rate of switches is 10-100 Gbits/s on 10-100 ports [9] and assuming an average packet size of 850 bytes [10].
The basic algorithm that preserves PPC is a two-phase update (2PU) [7]: All the rules in all the switches check for version numbers. All the incoming packets are labelled with the appropriate version number by all the ingresses. To update a set of rules from to , first the new rules and a copy of the unaffected rules are installed to check for , in every internal ( non-ingress) switch. Now all the ingresses start labelling all the packets as . All packets match only the new rules and the packets in the network match only the old rules, preserving PPC. After all the packets exit the network, the controller deletes the old rules on all the switches. 2PU affects all the switches in the network.
We propose an update algorithm called Proportional Per-packet Consistent Updates, PPCU, that is general, preserves PPC, confines changes to only the affected switches and rules and provides an all-or-nothing semantics for a Rules Update, regardless of the execution speeds of switches and links.
The summary of PPCU is as follows: Let the latest time at which all the switches in install the new rules be . Each affected switch examines the time stamp, set to the current time by the ingresses, in each data packet. If its value is less than , it is switched according to the old rules while if it is greater than or equal to , it is switched according to the new rules.
II Motivation and related work
Why preserving PPC is important: Proper installation of policies require preservation of PPC and no less. Middle box deployment in SDN [5] [11] rely on packets traversing middle boxes in a certain order [12] [13]. Languages [14] that enable SDN application developers to specify and use states, also require the order of traversal of switches that store those states to be preserved during an update. These examples emphasize the importance of preserving waypoint invariance for all scenarios and therefore of PPC. For many algorithms that preserve more relaxed properties, a PPC preserving update is a fall-back option, for example, if they cannot find an order of updates that preserve waypoint invariance [1] or if their Integer Linear Programming algorithms do not converge [15].
Why the number of switches involved in the update must be less: Algorithms that perform a Rules Update while preserving PPC either 1) need to update all the switches in the network [7] [16] or 2) identify paths affected by and update all the switches along those paths [1] [17] or 3) update only and all the ingresses [18] [19], regardless of the number of elements in and regardless of the number of rules to be updated.
If paths affected by a Rules Update are identified (category 2), every switch in the path, which may be across the network, needs to be changed, even to modify one rule on one switch. If one rule affects a large number of paths, such as “if TCP port=80, forward to port 1”, computing the paths affected is time consuming [1]. In update methods of categories 1 and 2, the number of rules used in every switch modified during the update doubles, as the new and old rules co-exist for some time. Hence the update time is disproportionately large, even if the number of rules updated is small.
If rules can be proactively installed on switches to prevent a control message being sent to a central controller for every missing rule [20], one controller can manage an entire data centre. In a data centre with a Fat Tree topology with a k-ary tree [21] where the number of ports , the number of ingress switches is about of the total number of switches. Even to modify one rule in a switch, all of the ingresses will need to be modified, for algorithms of category 3.
Updating only switches in instead of and other switches in will reduce the number of controller-switch messages and the number of individual switch updates that need to be successful for the Rules Update to be successful. We wish to characterize this need as footprint proportionality (FP), which is the ratio of the number of affected switches for a Rules Update to the number of switches actually modified for the update. In the best case the FP is 1, and there is no general update algorithm that achieves this while maintaining PPC, as far as we know.
Why using rules with wildcards is important: Installing wildcarded rules for selected flows or rule compression in TCAM for flows or policies [22] reduces both space occupancy in TCAM [23] and prevents sending a message to the controller for every new flow in the network [20]. [24] provides solutions for the tradeoff between visibility of rules and space occupancy. Thus in a real network, using wildcarded rules is inevitable. Many of the existing solutions do not address rules that cater to more than one flow [8] [1]. A Rules Update may require only removing rules and not adding any rule or vice versa, on one or more switches in a network. Though [19] addresses this, it needs changes to all the ingresses for all the rules for any update and limits concurrency. We wish to have for all the update scenarios possible.
Why concurrent updates must be supported: Support of multiple tenants on data center networks require updating switches for virtual to physical network mapping [25, 26]. Applications that control the network [27], [28], [29] and VM and virtual network migration[30] will require frequent updates to the network, making large concurrent updates common to SDNs. Existing algorithms that preserve PPC and allow concurrent updates limit the maximum number of concurrent updates [18] [19] [1], with the last one becoming impractical if the number of paths affected by the update is large. 2PU [7] does not support concurrency.
Why algorithms that use data plane time stamping are inadequate: Update algorithms that use data plane time stamping either cater to only certain update scenarios or require very accurate and synchronous time stamping [31] or do not guarantee an all-or-nothing semantics for Rules Updates as they depend on an estimate for the time at which the update must take place [32] [33], thus relying on the execution speeds on switches and links to be predictable.
Our contributions in this paper are:
1) We specify and prove an update algorithm PPCU that: a) requires modifications
to only the affected switches and affected rules, while preserving PPC.
b) allows practically unlimited concurrent non-conflicting updates.
c) allows all update scenarios:
this includes Rules Updates that involve only deletion of rules or only insertion
of rules or a combination of both and Rules Updates that involve forwarding
rules that match more than one flow.
d) expects the switches to be synchronized to a global
clock but tolerates inaccuracies.
e) updates all of or none at
all, irrespective of the execution speeds of the switches or links.
2) We prove the algorithm, analyze its significant parameters and find
them to be better than comparable algorithms.
3) We illustrate that the algorithm can be implemented at line
rate.
III Using data plane programmability:
With the advent of line rate switches whose parsers, match fields and actions can be programmed in the field using languages such as P4 [34] and Domino [9], it has become possible to write algorithms for the data plane in software. Programmable switch architectures such as Banzai [9], RMT[35], FlexPipe[36] (used in Intel FM6000 chip set[37]) and XPliant[38] aid this and languages to develop SDN applications leveraging these abilities [39][14] and P4 applications [40] [41] indicate acceptability.
Data plane programmability is important to PPCU for several reasons: 1) It is easier to change protocols to add and remove headers to and from packets 2) It is possible to process packet headers in the data plane, still maintaining line rate 3) Once the packet processing algorithm is specified in a language, the language compiler finds the best arrangement of rules on the physical switch [42]. It is possible that rules that require a ternary match may be stored in TCAM and exact match rules in SRAM [35] or the former in a Frame Forwarding Unit and the latter in a hash table [36]. 4) The actual match-field values in the rules, the actions, the parameters associated with actions and the variables associated with rules can be populated and modified at run time. How to do this is a part of the control plane and is proposed to be “Openflow 2.0” [34]. Specifications such as SAI[43] or Thrift [44] or the run-time API generated by the P4 compiler [45] [41] may be used at present. We assume that switches support data plane programmability and can be programmed in P4.
IV Model Description
Description of a programmable switch model: The abstract forwarding model advocated by protocol independent programmable switches [45] consists of a parser that parses the packet headers, sends them to a pipeline of ingress match-action tables (the ingress pipeline) that in turn consist of a set of match-fields and associated actions, then a queue or a buffer, followed by a pipeline of egress match-action tables (the egress pipeline). In this section, we describe only the features of P4 that are relevant to PPCU.
A P4 program consists of definitions of 1) packet header fields 2) parser functions for the packet headers 3) a series of match-action tables 4) compound actions, made of a series of primitive actions and 5) a control flow, which imperatively specifies the order in which tables must be applied to a packet. Each match-action table specifies the input fields to match against; the input fields may contain packet headers and metadata. The match-action table also contains the actions to apply, which may use metadata and registers. Metadata is memory that is specific to each packet, which may be set by the switch on its own (example: value of ingress port) or by the actions. It may be used in the match field to match packets or it may be read in the actions. Upon entering the switch for the first time, the metadata associated with a packet is initialised to by default. A register is a stateful resource and it may be associated with each entry in a table (not with a packet). A register may be written to and read in actions.
P4 provides a set of primitive actions such as and and allows passing parameters to these actions, that may be metadata, packet headers, registers etc. When the primitive action is applied to the ingress pipeline, a packet completes its ingress pipeline and then resubmits the original packet header and the possibly modified metadata associated with the packet, to the parser; the metadata is available for matching. If there are multiple actions, the metadata associated with each of them must be made available to the parser when the packet is resubmitted. Similarly, when is applied to a packet in the egress pipeline, the packet, with its header modifications and metadata modifications, if any, is posted to the parser. Conditional operators are available for use in compound actions to process expressions (we use if statements in the paper to improve readability).
While this specifies the definition of the programmable regions of the switch, actual rules (table entries) and the parameters to be passed to actions need to be specified and is described below. These need to be populated by an entity external to this model - the controller, through the switch CPU. This is facilitated by a run-time API.
Description of Rules and packets: A switch has an ordered set of rules , consisting of rules . Each rule has three parts: a priority , a match field and an action field and is represented as . Let and . if . must be as per the match field defined in the table and must be one of the actions associated with the table. A packet only has match fields. An incoming packet is matched with the match fields of the rules in the first table specified in the control flow of the switch and the action associated with the highest priority rule that matches it is executed. The packet is then forwarded to the next match-action table, as specified in the control flow.
In , some rules may be dependent on the other. For example, in Figure 2, the rules , , and depend on each other. The solid arrows show the existing dependencies among rules and the dotted arrows, the dependencies after a Rules Update.
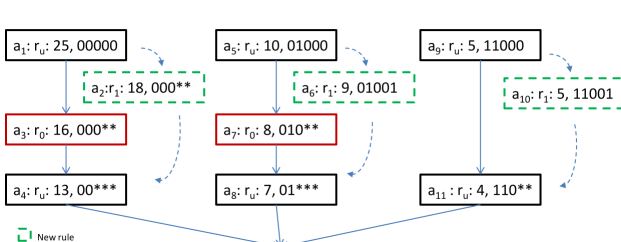
with suitable subscripts or superscripts denotes an individual rule, while with suitable subscripts or superscripts denotes a set of rules, with , and , throughout the paper. A packet that matches any in any is called a new packet. A packet that matches any in any is called an old packet and all old and new packets are called affected packets. The first affected switch containing at least one of or that a packet matches is denoted as .
Disjoint Rules Updates: Let be the set of all packets that match at least one of or of a Rules Update and let be the set of all packets that match at least one of or of another Rules Update . and are said to be disjoint or non-conflicting if and are disjoint. If and are disjoint, they can occur concurrently and every packet in the network will be affected by at most one of the updates or . For example, let . Let be the only update in . Let . Let be the only update of . and conflict. Let . Let be the only update in . and are disjoint. One Rules Update can consist of one or more disjoint updates. In Figure 2, and need to be deleted and , and need to be installed. They can all be part of the same Rules Update.
Relationship between the old and the new rules: Two ordered sets of rules and are said to be match-field equivalent if the total set of packets that they are capable of matching are identical. Thus and are match-field equivalent.
The set of rules in for which no match-field equivalent rules of priority equal to or lower than exists in is called the special difference of and , denoted . If = and =, where , . The set of rules in for which no match-field equivalent rules of priority equal to or greater than exists in is called the inverse special difference of and , denoted . If = and , where , .
V Challenges in a Rules Update
Providing an FP of 1 is difficult because multiple disjoint updates may be combined into one Rules Update and a switch rule may belong to more than one flow, due to usage of wild carded rules. Thus for packets belonging to different flows the first affected switch may be different - that is, there may be more than one belonging to a Rules Update. Neither the controller nor the switches know the paths that are affected by the update or the for each path. Due to these reasons, firstly, the controller cannot instruct a specific switch to relabel packets to switch to the new version of rules, as is done in some of the update algorithms [1]. Secondly, all switches must have the same algorithm, regardless of their position in a flow. Moreover, the rules to be deleted and installed and the unaffected rules depend on each other in complex ways, as discussed in 2, causing difficulty in maintaining PPC. The key insight is that all the affected switches must know if the rest of the affected switches and itself are ready to move to the next version, and after that, if a packet crosses its , it must store that fact in its header ; the switch examines , the time stamped at the ingress on every packet, to understand the readiness and stores the result in two one-bit fields and in the packet.
Since the controller-switch network is asynchronous, when a controller sends messages to switches, all switches will not receive them at the same time, or complete processing them and respond to the controller at the same time or they may not respond at all. Solving race conditions arising out of these scenarios is possible if the values of and which are set by determine whether they match or or , regardless of what the states of the switches in its path are. Also, the clocks at the switches may be out of sync to the extent the time synchronising protocol would permit. In the next section, we shall state the algorithm first and then describe the measures taken in them to address the above challenges.
VI Algorithm for concurrent consistent updates
Data plane changes at the ingress and egress switches: Each packet entering the network has a time stamp field and two one bit fields and added to it and removed from it programmatically, at the ingress and the egress, respectively. All ingresses set to the current time at the switch and and to for all the packets entering it from outside the network. Altering the value of , wherever required in the update algorithm, occurs only after it is thus set.
Notations used: indicates if the rule is new (), old () or unaffected (). , when set to , indicates that the packet must be switched only according to rules, where they exist and , when set to indicates that the packet must be switched only according to rules, where they exist. The metadata bit when set to for a packet indicates that this packet must not be matched by a rule. The metadata bit when set to for a packet indicates that this packet must not be matched by an rule.
Algorithm at the control plane: This section first specifies the algorithm for the control plane, at the controller (Algorithm 1) and at each (Algorithm 2) and later for the data plane, in Algorithm 3. The message exchanges below are the same as in [16] and [18]; the parameters in them and actions upon receiving them have been modified to suit PPCU.
-
1.
The Controller receives an Update Request from the application, with the list of affected switches , and , for every switch . The actions of all rules are as in Algorithm 3. An update identifier is associated with each update. The controller sends a “Commit” message to every switch (line 5 of Algorithm 1) with , and as its parameters.111It is assumed that the controller and the switch maintain all parameters related to an update in a store and check whether each message received is appropriate; we omit these details and the error handling required for an all-or-nothing semantics to improve clarity.
-
2.
A switch receives the “Commit” message, extracts , and . The switch 1) changes the match part of the installed rules to check if and 2) installs the rules and 3) sets for the rules and for the rules. The above actions must be atomic, as indicated in the algorithm. Now it sends “Ready to Commit” with the current time of the switch as a parameter (lines 3 to 16 in Algorithm 2).
- 3.
- 4.
-
5.
The controller receives “Ack Commit OK” from all the switches. Let the largest value of time received in “Ack Commit OK” be . It sends “Discard Old” to all the switches with .
-
6.
Let the time at which a switch receives “Discard Old” be . The switch sends “Discard Old Ack” to the controller. The switch starts a timer whose value is , where is the maximum lifetime of a packet within the network and the time received in “Discard Old”. (line 33 in Algorithm 2). When the timer expires, all the packets that were switched using the rules are no longer in the network. Therefore the switch deletes . It sets for every rule and modifies its , , and to check for , as shown in lines 35 to 40, in Algorithm 2. With this, the update at the switch is complete.
- 7.
Note: After units after timer expiry at the last affected switch, the last of packets tagged will exit the network. Now the next update not disjoint with the current one may begin.
Algorithm at the data plane - actions at switches:
Algorithm 3 specifies the template for a compound action associated with every rule in a match-action table in a switch. Each rule has two metadata fields of bit each, and , associated with it, initialised to by default, indicating that the packet is entering that table in that switch for the first time (If other tables in the same switch has rule updates, a separate set of two bits need to be used for each of those tables. For ease of exposition, we describe only one table being updated). Each rule has two registers, , initialised to , which is less than the maximum value that can have, and , which decides if the rule is old (), new () or unaffected (), initialised to . Unaffected rules have , , and set to in their match-fields and do not check for the value of . A new rule is always installed with a priority higher than that of an old rule. In P4, rules with ternary matches have priorities associated with them as such rules can have overlapping entries.
A rule may execute any of its own actions, which is what is referred to in 7, 18 and 31 in Algorithm 3. The parameters that are passed to the compound action are in turn passed to the actions associated with the rule. For example, a new rule may require a packet to be forwarded to port , instead of port . Then, the table entry for the new rule would pass as a parameter from its rule, while the old rule would pass .
Suppose , the first affected switch of affected packet in Rules Update , receives “Commit”. of and let for . will match in , get its set to and get resubmitted (line 12). Now it will not match and instead match , get its set to (line 17) and get switched by in subsequent affected switches and , if no exists. After receives “Commit OK” and sets its , when a packet whose arrives at , it gets switched by the new rule, gets its set to (line 6) and gets switched by rules in all the subsequent affected switches and if no exists. Suppose in Rules Update , has and receives “Commit”. Now a packet entering it with gets its set to , and then resubmitted(line 12). The resubmitted packet matches another rule and gets its set to (line 27), making the packet use rules in subsequent switches and , where no exists. After receives “Commit OK”, a packet whose matches , gets its set to and gets switched in subsequent switches by or , if does not exist. The case for an update where has is similar.
Specific scenarios: We shall use a list (inexhaustive) of scenarios to illustrate that each step in Algorithm 3 is necessary: Consider two switches and , in Figures 3 and 4, far apart from each other in the network. In all the cases, the lower priority rule forwards a packet to a port while a higher priority rule forwards a packet to the same port and increments a field in the packet. The value of and the rest of the packet header are shown in boxes with dotted lines, before and after crossing . The numbers , and against the boxes indicate the sequence of occurrence of events.
VI-1 Case 1, new rules must not be immediately applied
After receiving “Commit”, if any installs earlier than others, as packets will immediately begin to match the new rules, PPC will be violated. Therefore, each rule must check if where before it executes the actions associated with (line 5).
VI-2 Case 2, when to switch to the new rules
must not be for packets to ever start using . That time must be after all the affected switches have installed the new rules and is now ready to use them, which is . Therefore after receiving “Commit OK”, each affected switch will set by using the run time API and start using the new rules if of an incoming packet. However, this is insufficient to guarantee PPC.
VI-3 Case 3, receives “Commit OK” first
See Figure 3. Suppose a packet whose arrives at the first affected switch . Since has received “Commit OK”, it switches the packet using rules. Now the next affected switch has not received “Commit OK” yet. Therefore in checks if , and since that is not so, gets switched using rules, thus violating PPC. To solve this problem, of must set of all incoming packets that match and whose . must check if in the action (lines 5 and 6).
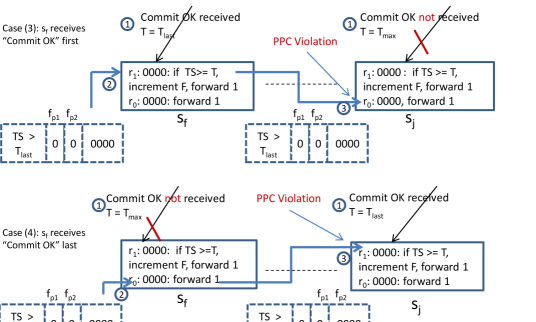
VI-4 Case 4, receives “Commit OK” last
VI-5 Case 5, for and
To solve this issue, illustrated in Figure 4, the switch must set for packets whose and matching (lines 9 to 12, line 27). For this, the switch first sets and then resubmits the packet. Since checks for , the packet does not match . No exists for this packet. Therefore the packet matches , as intended. In , if , is set to .
VI-6 Case 6, for
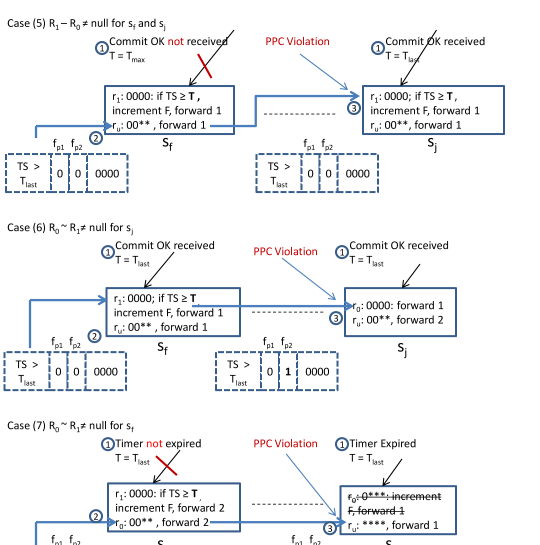
VI-7 Case 7, for
See Figure 4. gets deleted from after its timer expires (line 35 in Algorithm 2). The solution for the issue here is to set of packets that match as well, if their (lines 21 to 23 and line 29). Packets with will use rules if they match and unaffected rules if they do not, as unaffected rules do not check for or . Similar to the explanation in section VI-5, such a packet needs to be resubmitted after setting and must check for . Subsequently, in , the packet has its set to . Since metadata instances are always intialised to [45], unaffected rules need not set and to 0.
On resubmitting packets: It must be noted that packets need to be resubmitted 1) only at and 2) only after receiving “Commit OK” and until the timer expires, if has for an update. In all other cases, packets need to be resubmitted 1) only at and 2) only after receiving “Commit” and until the switch receives “Commit OK”. The action must be used instead of , if the change is to a table in the egress pipeline.
Impact of multiple tables: The algorithm requires no changes to support updates to more than one ingress or egress table in a switch. The update to each table must be atomic with respect to the update to another table within the same switch. For example, when a switch receives “Commit OK”, it must set to the affected rules in all the tables, for that Rules Update, atomically. How a switch implementation addresses this is outside the scope of this paper. [46] is a line of work in this direction.
VII Concurrent Updates
Each disjoint Rules Update requires a unique update identifier for the duration of the update, to track the update states at the affected switches and the controller. The number of disjoint Rule Updates that can be simultaneously executed is limited only by the size of . is exchanged only between the controller and the switches and hence is not dependent on the size of a field in any data packet. Therefore as many disjoint updates as the size of the update identifier or the processing power of switches would allow can be executed concurrently.
VIII Using time stamps
Feasibility of adding at the ingress: We assume that all switches have their clocks synchronized and the maximum time drift of switches from each other is known. If the network supports Precision Time Protocol, [31]. Intel FM6000, a programmable SDN capable switch, supports PTP, its and the time stamp is accessible in software [37]. The size of the register used to store a packet timestamp in FM6000 is bits. P4 supports a feature called “intrinsic metadata”, that has target specific semantics and that may be used to access the packet timestamp. Using the and actions and intrinsic metadata, the field may be added at the ingress and removed at the egress for every packet, for targets that support protocols such as PTP.
Asynchronous time at each switch: Since a single rule update in a TCAM is of the order of milliseconds, a time stamp granularity of milliseconds is sufficient for Rules Updates. Let us assume that the timestamp value is in milliseconds and that an ingress is faster than an affected internal switch (at the most by ). Let be the time stamp of a packet in the network that is stamped by , even before the Rules Update begins. After the Rules Update begins, let the (temporally) last affected switch send its current time stamp in “Ready To Commit”. Let , since the ingress is faster. Now a switch , which is not an , will switch with the new rules, violating PPC. To prevent this, each switch may set , instead of . If an ingress clock is slow, there will be no PPC violations. Thus PPCU tolerates known inaccuracies in time synchronisation. To reduce packet transmission times, the size of may be reduced, thus reducing the granularity. will need to wait longer to receive packets whose , thus lengthening the Rules Update time. Since the size of is programmable in the field, the operator may be choose it according to the nature of the network.
IX Proof
We need to prove that the algorithms 1, 2 and 3 together provide PPC updates. denotes an affected packet with match-field and fields and . denotes a rule whose match-field is (in both, excludes , and ). By definition of , for a packet , any has either a rule or or both.
Let us assume that the individual algorithms 1, 2 and 3 are correct. Let us assume that switches are synchronized, to make descriptions easier. In the description below, when we refer to a packet, we mean a packet affected by the update. The update duration is split into three intervals: before receiving “Commit”, from receiving “Commit” to the timer expiring, and after the timer expiry.
Property 1: After the Rules Update begins and before receives “Commit”, PPC is preserved: (and all that have not received “Commit”) switches all packets using a rule that will be marked on receiving “Commit” or (if no rule is to be deleted on that switch). The first that receives “Commit” switches using or (the latter if the switch does not have but has only ) and sets for all received packets. Subsequent s will not use as and use if it exists (or if no exists) . Thus packets follow if it exists or if does not exist, preserving PPC.
Property 2: Between receiving “Commit” at and its timer expires PPC is preserved: Property 2.1: As per Algorithm 3, if has received “Commit”, will exit as either or , until its timer expires.
Property 2.2: will receive any of the types of packets ) with its or ) or ) and no other type of packet, until its timer expires. Proof: Packets of type may reach as it may have crossed before received “Commit” and will always be less than of such packets, as is the time at which the last switch has received “Commit”. If a packet of type other than these three reaches , it means it has not crossed , by Property 2.1. In that case, the only possibility is that is the first switch, which is not true by defintion.
By Algorithm 3, packets of types and referred to in Property 2.2 can use only rules (or if does not exist) on all switches . By the same algorithm, packets of type match only rules (or if does not exist) on all switches . In , packets match . can change the value of or of a packet only if or for that packet is set, which occurs only on an affected switch. Therefore, PPC is preserved.
Property 3: When the timer expires at any switch , all packets that were switched using at least at one have left the network: Let us consider two cases: 1) All packets whose get switched by using rules, by Algorithm 3. Such packets exit the network by time . However, . 2) All packets whose that arrive at get switched using , until that receives its “Commit OK”, by Algorithm 3. At time , the last of s have received “Commit OK” and have started switching packets using . Hence at time , all the packets (whether due to case 1 or 2) that were switched using have left the network. The current time at a switch is and the switch receives an instruction to start a timer that expires at . The elapsed time, that is, must be subtracted from , giving the timer a value of . Therefore when this timer expires, all the old packets have left the network.
Property 4: After timer expiry at : All packets in the network have their after timer expiry at , as all packets whose have left the network by the timer expiry at any switch, by Property 3. Therefore all packets leaving are of the form . Therefore all switches will use if it exists (or if does not exist), if the timer has not expired on . If the timer has expired on , it will only cause it to not check for , , or , which makes no difference to matching the rule that the packet matches. Since packets have only to match (or where it does not exist), PPC is preserved.
Thus due to Properties 1 to 4, PPC is preserved during and after the update.
X Analysis of the Algorithm
The symbols used in the analysis are: : the propagation time between the controller and a switch, : the time taken to insert rules in a switch TCAM, : the time taken to delete rules from the TCAM, : the time taken to modify rules in the TCAM, : the time taken to modify registers associated with a rule, : the time for which a switch waits after it receives “Discard Old” and before it deletes rules, : the number of old rules that need to be removed, : the number of new rules that need to be added, : the maximum number of rules in a switch, : the number of affected switches, : the number of ingresses, : the total number of switches, : The time between the switch receiving “Commit” and sending “Ready To Commit”, : The time between the switch receiving “Commit OK” and sending “Ack Commit OK” and : The time between the switch receiving “Discard Old” and the switch performing its functions after timer expiry. It is assumed that the value of is uniform for all switches and all rounds, the values of time are the worst for that round, the number of rules, the highest for that round and that the processing time at the controller is negligible. Since unaffected rules have ternary matches for and , we assume that all the match fields are stored in TCAM and the corresponding actions in SRAM [35] [42], for PPCU, and for other algorithms.
| Parameter | PPCU | E2PU[16] | [19] |
|---|---|---|---|
| Message complexity | |||
| FP | 1 | ||
| Round 1 (R1) | |||
| Round 2 (R2) | |||
| Round 3 (R3) | |||
| Round 4 | Not applicable | Not applicable | |
| Propagation Time P | |||
| Time Complexity | |||
| Concurrency | Unlimited | Number of bits in version field |
We add to and evaluate using the parameters of interest identified for a PPC in [16]: 1) Overlap: Duration for which the old and new rules exist at each type of switch 2) Transition time: Duration within which new rules become usable from the beginning of the update at the controller 3) Message complexity: the number of messages required to complete the protocol 4) Time complexity: the total update time222Excludes the time for current packets to be removed from the network at the end of the update, where applicable. 5) Footprint Proportionality 6) Concurrency: Number of disjoint concurrent updates.
The purpose of the analysis is to understand what the above depend upon and to compare with a single update in E2PU (using rule updates in TCAMs) [16], which updates switches using 2PU with 3 rounds of message exchanges, and with the algorithm in [19]. We assume that [19] uses acknowledgements for each message sent. Since all three have similar rounds, it is meaningful to compare the time taken by each round as given in table I. The Overlap is and Transition time is for all the algorithms under consideration.
Since the values associated with the action part of a rule ( and ) are stored in SRAM, we assume that update times of these values (in ) will be negligible compared to TCAM update times and ignore the terms that involve . We find in table I that 1) PPCU has lower message complexity, assuming and better FP 2) PPCU and [19] have comparable times for Rounds 1 and 3. For Round 2, PPCU fares better. Therefore, PPCU fares better for Overlap, Transition time and Time complexity. 3) PPCU has better concurrency. From VI-7 it may be inferred that for PPCU, packets need to be resubmitted either for a duration of or at only . Since is an action supported by line rate switches, we assume that the delay due to a resubmission at for this time frame during an update is tolerable.
Feasibility of implementation at line rate: Adding and removing headers such as , and are feasible at line rate; so are setting and checking metadata, such as and and header fields and in actions, as per table in RMT [35]. While compiling the action part, Domino [9] checks if operations on stateful variables in actions can run at line rate by mapping those operations to its instruction set - PPCU requires only reading the state variables and and this can be achieved using the “Read/Write atom” (name of instruction) in Domino. This demonstrates the feasibility of PPCU running at line rate.
XI Conclusions
PPCU is able to provide non-conflicting per-packet consistent updates with an all-or-nothing semantics, with updates confined to the affected switches and rules, with no restrictions on the scenarios supported and no limits to concurrency. The algorithm fares better than other algorithms that preserve PPC, in a theoretical evaluation of significant parameters. PPCU uses only existing programming features for the data plane, are implementable with the machine instruction sets supported and therefore must work at line rate. Available programmable switches support timing protocols such as PTP and time stamping packets is possible at line rate, as required by the algorithm. It accomodates time asynchrony, as long as the maximum time drift of switches from each other is known, which is the case with PTP.
References
- [1] W. Zhou, D. Jin, J. Croft, M. Caesar, and B. P. Godfrey, “Enforcing customizable consistency properties in software-defined networks,” in NSDI 2015, May.
- [2] A. Ludwig, M. Rost, D. Foucard, and S. Schmid, “Good network updates for bad packets: Waypoint enforcement beyond destination-based routing policies,” in Proceedings of the 13th ACM Workshop on Hot Topics in Networks. ACM, 2014.
- [3] S. Dudycz, A. Ludwig, and S. Schmid, “Can’t touch this: Consistent network updates for multiple policies,” in Proc. 46th IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), 2016.
- [4] D. M. F. Mattos, O. C. M. B. Duarte, and G. Pujolle, “Reverse update: A consistent policy update scheme for software defined networking,” Communications Letters, IEEE, vol. 20, no. 5, May 2016.
- [5] Y. Ben-Itzhak, K. Barabash, R. Cohen, A. Levin, and E. Raichstein, “EnforSDN: Network policies enforcement with SDN,” in 2015 IFIP/IEEE International Symposium on Integrated Network Management (IM).
- [6] X.-N. Nguyen, D. Saucez, C. Barakat, and T. Turletti, “Rules placement problem in openflow networks: a survey,” IEEE Communications Surveys & Tutorials, 2016, to appear.
- [7] M. Reitblatt, N. Foster, J. Rexford, C. Schlesinger, and D. Walker, “Abstractions for network update,” in SIGCOMM 2012.
- [8] X. Jin, H. H. Liu, R. Gandhi, S. Kandula, R. Mahajan, M. Zhang, J. Rexford, and R. Wattenhofer, “Dynamic scheduling of network updates,” in SIGCOMM 2014.
- [9] A. Sivaraman, M. Budiu, A. Cheung, C. Kim, S. Licking, G. Varghese, H. Balakrishnan, M. Alizadeh, and N. McKeown, “Packet transactions: High-level programming for line-rate switches,” in SIGCOMM 2016, to appear.
- [10] T. Benson, A. Anand, A. Akella, and M. Zhang, “Understanding data center traffic characteristics,” ACM SIGCOMM Computer Communication Review, vol. 40, no. 1, 2010.
- [11] A. Gember-Jacobson, R. Viswanathan, C. Prakash, R. Grandl, J. Khalid, S. Das, and A. Akella, “OpenNF: Enabling innovation in network function control,” ACM SIGCOMM Computer Communication Review, vol. 44, no. 4, 2015.
- [12] D. A. Joseph, A. Tavakoli, and I. Stoica, “A policy-aware switching layer for data centers,” ACM SIGCOMM Computer Communication Review, vol. 38, no. 4, 2008.
- [13] S. K. Fayazbakhsh, V. Sekar, M. Yu, and J. C. Mogul, “Flowtags: Enforcing network-wide policies in the presence of dynamic middlebox actions,” in Proceedings of the second ACM SIGCOMM workshop on Hot topics in software defined networking, 2013.
- [14] M. T. Arashloo, Y. Koral, M. Greenberg, J. Rexford, and D. Walker, “SNAP: Stateful network-wide abstractions for packet processing,” SIGCOMM 2016, to appear.
- [15] L. C. Stefano Vissicchio, “FLIP the (flow) table: Fast lightweight policy-preserving SDN updates,” in INFOCOM 2016. IEEE.
- [16] R. Sukapuram and G. Barua, “Enhanced algorithms for consistent network updates,” in IEEE Conference on Network Function Virtualization and Software Defined Network (NFV-SDN). IEEE, 2015.
- [17] N. P. Katta, J. Rexford, and D. Walker, “Incremental consistent updates,” in Proceedings of the second ACM SIGCOMM workshop on Hot topics in Software Defined Networking 2013. ACM.
- [18] R. Sukapuram and G. Barua, “CCU: Algorithm for Concurrent Consistent Updates for a Software Defined Network,” in Twenty Second National Conference on Communications : NCC. IEEE, 2016.
- [19] S. Luo, H. Yu, and L. Li, “Consistency is not easy: How to use two-phase update for wildcard rules?” Communications Letters, IEEE, vol. 19, no. 3, 2015.
- [20] S. H. Yeganeh, A. Tootoonchian, and Y. Ganjali, “On scalability of software-defined networking,” Communications magazine, IEEE, vol. 51, no. 2, 2013.
- [21] M. Al-Fares, A. Loukissas, and A. Vahdat, “A scalable, commodity data center network architecture,” SIGCOMM Comput. Commun. Rev., vol. 38, no. 4, Aug. 2008.
- [22] S. Zhang, F. Ivancic, C. Lumezanu, Y. Yuan, A. Gupta, and S. Malik, “An adaptable rule placement for software-defined networks,” in 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN). IEEE.
- [23] S. Luo, H. Yu et al., “Fast incremental flow table aggregation in SDN,” in 2014 23rd International Conference on Computer Communication and Networks (ICCCN). IEEE, 2014.
- [24] A. S. Iyer, V. Mann, and N. R. Samineni, “Switchreduce: Reducing switch state and controller involvement in openflow networks,” in IFIP Networking Conference, 2013. IEEE.
- [25] M. Banikazemi, D. Olshefski, A. Shaikh, J. Tracey, and G. Wang, “Meridian: an SDN platform for cloud network services,” Communications Magazine, IEEE, vol. 51, no. 2, 2013.
- [26] A. Al-Shabibi, M. De Leenheer, M. Gerola, A. Koshibe, G. Parulkar, E. Salvadori, and B. Snow, “OpenVirtex: Make your virtual SDNs programmable,” in Proceedings of the third workshop on Hot topics in software defined networking. ACM, 2014.
- [27] T. Benson, A. Anand, A. Akella, and M. Zhang, “MicroTE: Fine grained traffic engineering for data centers,” in CoNEXT. ACM, 2011.
- [28] M. Al-Fares, S. Radhakrishnan, B. Raghavan, N. Huang, and A. Vahdat, “Hedera: Dynamic flow scheduling for data center networks.” in NSDI, vol. 10, 2010.
- [29] B. Heller, S. Seetharaman, P. Mahadevan, Y. Yiakoumis, P. Sharma, S. Banerjee, and N. McKeown, “ElasticTree: Saving energy in data center networks.” in NSDI, vol. 10, 2010.
- [30] S. Ghorbani, C. Schlesinger, M. Monaco, E. Keller, M. Caesar, J. Rexford, and D. Walker, “Transparent, live migration of a software-defined network,” in Proceedings of the ACM Symposium on Cloud Computing. ACM, 2014.
- [31] T. Mizrahi and Y. Moses, “Software defined networks: It’s about time,” in IEEE INFOCOM, 2016.
- [32] T. Mizrahi, E. Saat, and Y. Moses, “Timed consistent network updates,” in SOSR, 2015.
- [33] “Openflow switch specification version 1.5.0,” 2014.
- [34] P. Bosshart, D. Daly, G. Gibb, M. Izzard, N. McKeown, J. Rexford, C. Schlesinger, D. Talayco, A. Vahdat, G. Varghese et al., “P4: Programming protocol-independent packet processors,” ACM SIGCOMM Computer Communication Review, vol. 44, no. 3, 2014.
- [35] P. Bosshart, G. Gibb, H.-S. Kim, G. Varghese, N. McKeown, M. Izzard, F. Mujica, and M. Horowitz, “Forwarding metamorphosis: Fast programmable match-action processing in hardware for SDN,” in ACM SIGCOMM Computer Communication Review, vol. 43, no. 4, 2013.
- [36] R. Ozdag, “White paper:intel® Ethernet Switch FM6000 Series-Software Defined Networking,” 2012.
- [37] [Online]. Available: http://www.intel.com/content/dam/www/public/us/en/documents/datasheets/ethernet-switch-fm5000-fm6000-datasheet.pdf
- [38] “XPliant ethernet switch family.” [Online]. Available: http://www.cavium.com/XPliant-Ethernet-Switch-Product-Family.html
- [39] C. Schlesinger, M. Greenberg, and D. Walker, “Concurrent NetCore: From policies to pipelines,” ACM SIGPLAN Notices, vol. 49, no. 9, 2014.
- [40] N. Katta, M. Hira, C. Kim, A. Sivaraman, and J. Rexford, “HULA: Scalable load balancing using programmable data planes,” in SOSR, 2016.
- [41] A. Sivaraman, C. Kim, R. Krishnamoorthy, A. Dixit, and M. Budiu, “DC.p4: programming the forwarding plane of a data-center switch,” in SOSR, 2015.
- [42] L. Jose, L. Yan, G. Varghese, and N. McKeown, “Compiling packet programs to reconfigurable switches,” in NSDI, 2015.
- [43] [Online]. Available: http://www.opencompute.org/wiki/Networking/SpecsAndDesigns#Switch_Abstraction_Interface
- [44] “Apache thrift.” [Online]. Available: https://thrift.apache.org/
- [45] “The P4 language specification, version 1.1.0, January 27, 2016.”
- [46] J. H. Han, P. Mundkur, C. Rotsos, G. Antichi, N. H. Dave, A. W. Moore, and P. G. Neumann, “Blueswitch: Enabling provably consistent configuration of network switches,” in Proceedings of the Eleventh ACM/IEEE Symposium on Architectures for networking and communications systems. IEEE Computer Society, 2015, pp. 17–27.