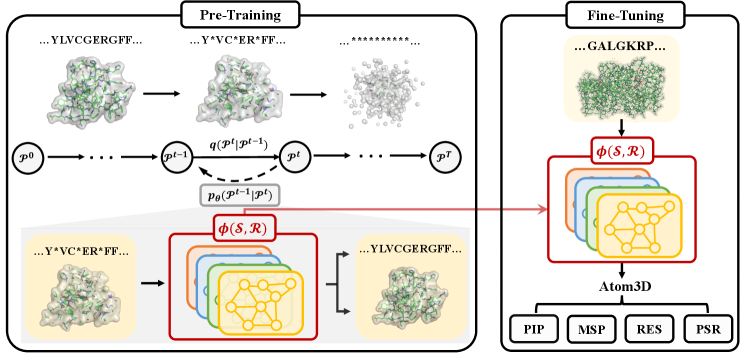
Pre-Training Protein Encoder via Siamese Sequence-Structure Diffusion Trajectory Prediction
Abstract
Self-supervised pre-training methods on proteins have recently gained attention, with most approaches focusing on either protein sequences or structures, neglecting the exploration of their joint distribution, which is crucial for a comprehensive understanding of protein functions by integrating co-evolutionary information and structural characteristics. In this work, inspired by the success of denoising diffusion models in generative tasks, we propose the DiffPreT approach to pre-train a protein encoder by sequence-structure joint diffusion modeling. DiffPreT guides the encoder to recover the native protein sequences and structures from the perturbed ones along the joint diffusion trajectory, which acquires the joint distribution of sequences and structures. Considering the essential protein conformational variations, we enhance DiffPreT by a method called Siamese Diffusion Trajectory Prediction (SiamDiff) to capture the correlation between different conformers of a protein. SiamDiff attains this goal by maximizing the mutual information between representations of diffusion trajectories of structurally-correlated conformers. We study the effectiveness of DiffPreT and SiamDiff on both atom- and residue-level structure-based protein understanding tasks. Experimental results show that the performance of DiffPreT is consistently competitive on all tasks, and SiamDiff achieves new state-of-the-art performance, considering the mean ranks on all tasks. Our implementation is available at https://github.com/DeepGraphLearning/SiamDiff.
1 Introduction
Machine learning-based methods have made remarkable strides in predicting protein structures [43, 5, 49] and functionality [54, 23]. Among them, self-supervised (unsupervised) pre-training approaches [19, 60, 86] have been successful in learning effective protein representations from available protein sequences or from their experimental/predicted structures. These pre-training approaches are based on the rationale that modeling the input distribution of proteins provides favorable initialization of model parameters and serves as effective regularization for downstream tasks [24]. Previous methods have primarily focused on modeling the marginal distribution of either protein sequences to acquire co-evolutionary information [19, 60], or protein structures to capture essential characteristics for tasks such as function prediction and fold classification [86, 32]. Nevertheless, both these forms of information hold significance in revealing the underlying functions of proteins and offer complementary perspectives that are still not extensively explored. To address this gap, a more promising approach for pre-training could involve modeling the joint distribution of protein sequences and structures, surpassing the limitations of unimodal pre-training methods.
To model this joint distribution, denoising diffusion models [36, 64] have recently emerged as one of the most effective methods due to their simple training objective and high sampling quality and diversity [2, 53, 39, 73]. However, the application of diffusion models has predominantly been explored in the context of generative tasks, rather than within pre-training and fine-tuning frameworks that aim to learn effective representations for downstream tasks. In this work, we present a novel approach that adapts denoising diffusion models to pre-train structure-informed protein encoders111It is important to note that protein structure encoders in this context take both sequences and structures as input, distinguishing them from protein sequence encoders as established in previous works.. Our proposed approach, called DiffPreT, gradually adds noise to both protein sequence and structure to transform them towards random distribution, and then denoises the corrupted protein structure and sequence using a noise prediction network parameterized with the output of the protein encoder. This approach enables the encoder to learn informative representations that capture the inter-atomic interactions within the protein structure, the residue type dependencies along the protein sequence, and the joint effect of sequence and structure variations.
In spite of these advantages, DiffPreT ignores the fact that any protein structure exists as a population of interconverting conformers, and elucidating this conformational heterogeneity is essential for predicting protein function and ligand binding [26]. In both DiffPreT and previous studies, no explicit constraints are added to acquire the structural correlation between different conformers of a specific protein or between structural homologs, which prohibits capturing the conformational energy landscape of a protein [55]. Therefore, to consider the physics underlying the conformational change, we propose Siamese Diffusion Trajectory Prediction (SiamDiff) to augment the DiffPreT by maximizing the mutual information between representations of diffusion trajectories of structurally-correlated conformers (i.e., siamese diffusion trajectories). We first adopt a torsional perturbation scheme on the side chain to generate randomly simulated conformers [35]. Then, for each protein, we generate diffusion trajectories for a pair of its conformers. We theoretically prove that the problem can be transformed to the mutual prediction of the trajectories using representations from their counterparts. In this way, the model can keep the advantages of DiffPreT and inject conformer-related information into representations as well.
Both DiffPreT and SiamDiff can be flexibly applied to atom-level and residue-level structures to pre-train protein representations. To thoroughly assess their capabilities, we conduct extensive evaluations of the pre-trained models on a wide range of downstream protein understanding tasks. These tasks encompass protein function annotation, protein-protein interaction prediction, mutational effect prediction, residue structural contributions, and protein structure ranking. In comparison to existing pre-training methods that typically excel in only a subset of the considered tasks, DiffPreT consistently delivers competitive performance across all tasks and at both the atomic and residue-level resolutions. Moreover, SiamDiff further enhances model performance, surpassing previous state-of-the-art results in terms of mean ranks across all evaluated tasks.
2 Related Work
Pre-training Methods on Proteins. Self-supervised pre-training methods have been widely used to acquire co-evolutionary information from large-scale protein sequence corpus, inducing performant protein language models (PLMs) [19, 52, 60, 49]. Typical sequence pre-training methods include masked protein modeling [19, 60, 49] and contrastive learning [52]. The pre-trained PLMs have achieved impressive performance on a variety of downstream tasks for structure and function prediction [58, 80]. Recent works have also studied pre-training on unlabeled protein structures for generalizable representations, covering contrastive learning [86, 32], self-prediction of geometric quantities [86, 10] and denoising score matching [28, 75]. Compared with existing works, our methods model the joint distribution of sequences and structures via diffusion models, which captures both co-evolutionary information and detailed structural characteristics.
Diffusion Probabilistic Models (DPMs). DPM was first proposed in Sohl-Dickstein et al. [62] and has been recently rekindled for its strong performance on image and waveform generation [36, 11]. While DPMs are commonly used for modeling continuous data, there has also been research exploring discrete DPMs that have achieved remarkable results on generating texts [4, 48], graphs [70] and images [37]. Inspired by these progresses, DPMs have been adopted to solve problems in chemistry and biology domain, including molecule generation [81, 38, 77, 42], molecular representation learning [51], protein structure prediction [76], protein-ligand binding [15], protein design [2, 53, 39, 73] and motif-scaffolding [68]. In alignment with recent research efforts focused on diffusion-based image representation learning [1], this work presents a novel investigation into how DPMs can contribute to protein representation learning.
3 DiffPreT: Diffusion Models for Pre-Training
Recently, there have been promising progress on applying denoising diffusion models for protein structure-sequence co-design [53, 2]. The effectiveness of the joint diffusion model on modeling the distribution of proteins suggests that the process may reflect physical and chemical principles underlying protein formation [3, 17], which could be beneficial for learning informative representations. Based on this intuition, in this section, we explore the application of joint diffusion models on pre-training protein encoders in a pre-training and fine-tuning framework.
3.1 Preliminary
Notation. A protein with residues (amino acids) and atoms can be represented as a sequence-structure tuple . We use to denote its sequence with as the type of the -th residue, while denotes its structure with as the Cartesian coordinates of the -th atom. To model the structure, we construct a graph for each protein with edges connecting atoms whose Euclidean distance below a certain threshold.
Equivariance. Equivariance is ubiquitous in machine learning for modeling the symmetry in physical systems [66, 74] and is shown to be critical for successful design and better generalization of 3D networks [45]. Formally, a function is equivariant w.r.t. a group if , where and are transformations corresponding to an element acting on the space and , respectively. The function is invariant w.r.t if the transformations is identity. In this paper, we consider SE(3) group, i.e., rotations and translations in 3D space.
Problem Definition. Given a set of unlabeled proteins , our goal is to train a protein encoder to extract informative -dimensional residue representations and atom representations that are SE(3)-invariant w.r.t. protein structures .
3.2 Diffusion Models on Proteins
Diffusion models are a class of deep generative models with latent variables encoded by a forward diffusion process and decoded by a reverse generative process [62]. We use to denote the ground-truth protein and for to be the latent variables over diffusion steps. Modeling the protein as an evolving thermodynamic system, the forward process gradually injects small noise to the data until reaching a random noise distribution at time . The reverse process learns to denoise the latent variable towards the data distribution. Both processes are defined as Markov chains:
| (1) |
where defines the forward process at step and with learnable parameters defines the reverse process at step . We decompose the forward process into diffusion on protein structures and sequences, respectively. The decomposition is represented as follows:
| (2) |
where the reverse processes use representations and learned by the protein encoder .
Forward diffusion process . For diffusion on protein structures, we introduce random Gaussian noises to the 3D coordinates of the structure. For diffusion on sequences, we utilize a Markov chain approach with an absorbing state [MASK], where each residue either remains the same or transitions to [MASK] with a certain probability at each time step [4]. Specifically, we have:
| (3) |
Here, and are a series of fixed variances and masking ratios, respectively. denotes the random masking operation, where each residue in is masked with a probability of at time step .
Reverse process on structures . The reverse process on structures is parameterized as a Gaussian with a learnable mean and user-defined variance . Given the availability of as an input, we reparameterize the mean following Ho et al. [36]:
| (4) |
where , and the network learns to decorrupt the data and should be translation-invariant and rotation-equivariant w.r.t. the structure .
To define our noise prediction network, we utilize the atom representations (which is guaranteed to be SE(3)-invariant w.r.t. by the encoder) and atom coordinates (which is SE(3)-equivariant w.r.t. ). We build an equivariant output based on normalized directional vectors between adjacent atom pairs. Each edge is encoded by its length and the representations of two end nodes , , and the encoded score will be used for aggregating directional vectors. Specifically,
| (5) |
where denotes the neighbors of the atom in the corresponding graph of . Note that achieves the equivariance requirement, as is SE(3)-invariant w.r.t. while is translation-invariant and rotation-equivariant w.r.t. .
Reverse process on sequences . For the reverse process , we adopt the parameterization proposed in [4]. The diffusion trajectory is characterized by the probability , and we employ a network to predict the probability of :
| (6) |
We define the predictor with residue representations . For each masked residue in , we feed its representation to an MLP and predict the type of the corresponding residue type in :
| (7) |
where the softmax function is applied over all residue types.
3.3 Pre-Training Objective
Now we derive the pre-training objective of DiffPreT by optimizing the diffusion model above with the ELBO loss [36]:
| (8) |
Under the assumptions in (2), it can be shown that the objective can be decomposed into a structure loss and a sequence loss (see proof in App. C.2):
| (9) |
Both loss functions can be simplified as follows.
Structure loss . It has been shown in Ho et al. [36] that the loss function can be simplified under our parameterization by calculating KL divergence between Gaussians as weighted L2 distances between means and (see details in App. C.3):
| (10) |
where the coefficients are determined by the variances . In practice, we follow Ho et al. [36] to set all weights for the simplified loss .
Since is designed to be rotation-equivariant w.r.t. , to make the loss function invariant w.r.t. , the supervision is also supposed to achieve such equivariance. Therefore, we adopt the chain-rule approach proposed in Xu et al. [81], which decomposes the noise on pairwise distances to obtain the modified noise vector as supervision. We refer readers to Xu et al. [81] for more details.
Sequence loss . Since we parameterize with and as in (6), it can be proven that the -th KL divergence term in reaches zero when assigns all mass on the ground truth (see proof in App. C.4). Therefore, for pre-training, we can simplify the KL divergence to the cross-entropy between the correct residue type and the prediction:
| (11) |
where CE denotes the cross-entropy loss.
The ultimate training objective is the sum of simplified structure and sequence diffusion losses:
| (12) |
3.4 Two-Stage Noise Scheduling
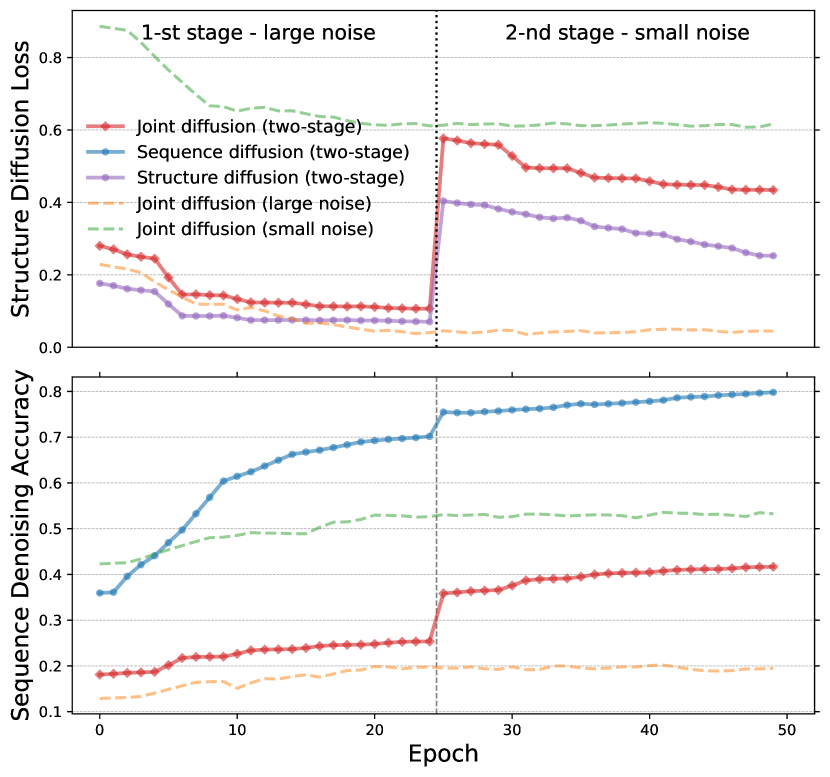
Previous studies on scheduled denoising autoencoders on images [22] have shown that large noise levels encourage the learning of coarse-grained features, while small noise levels require the model to learn fine-grained features. We observe a similar phenomenon in structure diffusion, as depicted in Fig. 2. The diffusion loss with large noise at a fixed scale (orange) is smaller than that with small noise at a fixed scale (green), indicating the higher difficulty of structure diffusion with small noises. Interestingly, the opposite is observed in sequence diffusion, where the denoising accuracy with small noise (green) is higher than that with large noise (orange). This can be attributed to the joint diffusion effects on protein sequences and structures. The addition of large noise during joint diffusion significantly disrupts protein structures, making it more challenging to infer the correct protein sequences. For validation, we compare the loss of sequence-only diffusion pre-training (blue) with joint diffusion pre-training (red) in Fig. 2. Sequence diffusion achieves higher denoising accuracy than joint diffusion when using uncorrupted structures, supporting our hypothesis.
Unlike recent denoising pre-training methods that rely on a fixed noise scale as a hyperparameter [84], DiffPreT incorporates a denoising objective at various noise levels to capture both coarse- and fine-grained features and consider the joint diffusion effect explained earlier. Both granularities of features are crucial for downstream tasks, as they capture both small modifications for assessing protein structure quality and large changes leading to structural instability. In our implementation, we perform diffusion pre-training using noise levels (time steps). Following the intuition of learning coarse-grained features before fine-grained ones in curriculum learning [8], we divide the pre-training process into two stages: the first stage focuses on large noise levels (), while the second stage targets small noise levels (). As observed in Fig. 2, structure diffusion becomes more challenging and sequence diffusion becomes easier during the second stage, as we discussed earlier. However, even with this two-stage diffusion strategy, there remains a significant gap between the accuracy of sequence diffusion and joint diffusion. We hypothesize that employing protein encoders with larger capacities could help narrow this gap, which is left as our future works.
4 SiamDiff: Siamese Diffusion Trajectory Prediction
Through diffusion models on both protein sequences and structures, the pre-training approach proposed in Sec. 3 tries to make representations capture (1) the atom- and residue-level spatial interactions and (2) the statistical dependencies of residue types within a single protein. Nevertheless, no constraints or supervision have been added for modeling relations between different protein structures, especially different conformers of the same protein. Generated under different environmental factors, these conformers typically share the same protein sequence but different structures due to side chain rotation driving conformational variations. These conformers’ properties are highly correlated [57], and their representations should reflect this correlation.
In this section, we introduce Siamese Diffusion Trajectory Prediction (SiamDiff), which incorporates conformer-related information into DiffPreT by maximizing mutual information (MI) between diffusion trajectory representations of correlated conformers. We propose a scheme to generate simulated conformers (Sec. 4.1), generate joint diffusion trajectories (Sec. 4.2), and transform MI maximization into mutual denoising between trajectories (Sec. 4.3), sharing similar loss with DiffPreT.
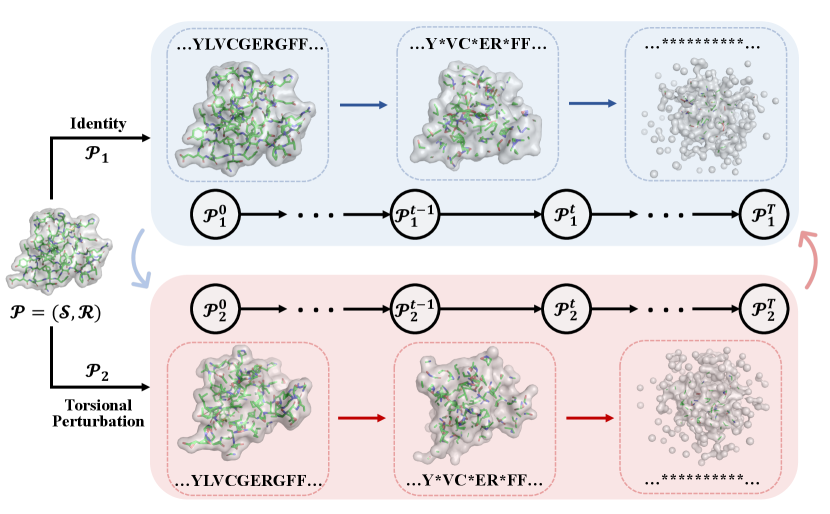
4.1 Conformer Simulation Scheme
Our method begins by generating different conformers of a given protein. However, direct sampling requires an accurate characterization of the energy landscape of protein conformations, which can be difficult and time-consuming. To address this issue, we adopt a commonly used scheme for sampling randomly simulated conformers by adding torsional perturbations to the side chains [35].
Specifically, given the original protein , we consider it as the native state and generate a correlated conformer by randomly perturbing the protein structure. That is, we set to be the same as , and is obtained by applying a perturbation function to the original residue structure, where is a noise vector drawn from a wrapped normal distribution [15]. The function rotates the side-chain of each residue according to the sampled torsional noises. To avoid atom clashes, we adjust the variance of the added noise and regenerate any conformers that violate physical constraints. It should be noted that the scheme can be adapted flexibly when considering different granularities of structures. For example, instead of considering side chain rotation on a fixed backbone, we can also consider a flexible backbone by rotating backbone angles, thereby generating approximate conformers.
4.2 Siamese Diffusion Trajectory Generation
To maintain the information-rich joint diffusion trajectories from DiffPreT, we generate trajectories for pairs of conformers, a.k.a., siamese trajectories. We first sample the diffusion trajectories and for conformers and , respectively, using the joint diffusion process outlined in Sec. 3. For example, starting from , we use the joint diffusion on structures and sequences to define the diffusion process . We derive trajectories on structures using the Gaussian noise in (3) and derive the sequence diffusion process using the random masking in (6). In this way, we define the trajectory for and can derive the siamese trajectory similarly.
4.3 Mutual Information Maximization between Representations of Siamese Trajectories
We aim to maximize the mutual information (MI) between representations of siamese trajectories constructed in a way that reflects the correlation between different conformers of the same protein. Direct optimization of MI is intractable, so we instead maximize a lower bound. In App. C.1, we show that this problem can be transformed into the minimization of a loss function for mutual denoising between two trajectories: , where
| (13) |
with being either or and being representations of the trajectory .
The two terms share the similar formula as the ELBO loss in (8). Take for example. Here is a posterior analytically tractable with our definition of each diffusion step in (3) and (6). The reverse process is learnt to generate a less noisy state given the current state and representations of the siamese trajectory , which are extracted by the protein encoder to be pre-trained. The parameterization of the reverse process is similar as in Sec. 3.2, with the representations replaced by those of (see App. B for details).
Our approach involves mutual prediction between two siamese trajectories, which is similar to the idea of mutual representation reconstruction in [27, 14]. However, since and share information about the same protein, the whole trajectory of could provide too many clues for denoising towards , making the pre-training task trivial. To address this issue, we parameterize with . For diffusion on sequences, we further guarantee that the same set of residues are masked in and to avoid leakage of ground-truth residue types across correlated trajectories.
Final pre-training objective. Given the similarity between the one-side objective and the ELBO loss in (8), we can use a similar way to decompose the objective into structure and sequence losses and then derive simplified loss functions for each side. To summarize, the ultimate training objective for our method is
| (14) |
where is the loss term defined by predicting from (see App. B for derivation).
4.4 Discussion
Now we discuss the relationship between our method and previous works.
Advantages of joint denoising. Compared with previous diffusion models focusing on either protein sequences [82] or structures [28] or cross-modal contrastive learning [12, 83], in this work, we perform joint diffusion on both modalities. Note that given a sequence and a structure that exist in the nature with high probability, the sequence-structure tuple may not be a valid state of this protein. Consequently, instead of modeling the marginal or conditional distribution, we model the joint distribution of protein sequences and structures.
Connection with diffusion models. Diffusion models excel in image and text generation [16, 48] and have been applied to unsupervised representation learning [1]. Previous works explored denoising objectives [22, 9] but lacked explicit supervision for different conformers, while our method incorporates mutual prediction between siamese diffusion trajectories to capture conformer correlation and regularize protein structure manifold.
Difference with denoising distance matching. While previous works rely on perturbing distance matrices [51, 28], which can violate the triangular inequality and produce negative values, our approach directly adds noise at atom coordinates, as demonstrated in Xu et al. [81]. This distinction allows us to address the limitations associated with denoising distance matching algorithms used in molecule and protein generation and pre-training.
Comparison with other deep generative models. Self-supervised learning essentially learns an Energy-Based Model (EBM) for modeling data distribution [47], making VAE [44], GAN [25], and normalizing flow [59] applicable for pre-training. However, these models limit flexibility or fail to acquire high sampling quality and diversity compared to diffusion models [53]. Therefore, we focus on using diffusion models for pre-training and leave other generative models for future work.
5 Experiments
Method PIP MSP RES PSR Mean Rank AUROC AUROC Accuracy Global Mean GearNet-Edge 0.8680.002 0.6330.067 0.4410.001 0.7820.021 0.488 0.012 7.6 w/ pre-training Denoising Score Matching 0.8770.002 0.6290.040 0.4480.001 0.8130.003 0.5180.020 5.2 Residue Type Prediction 0.8790.004 0.6200.027 0.4490.001 0.8260.020 0.5180.018 4.4 Distance Prediction 0.8720.001 0.6770.020 0.4220.001 0.8400.020 0.5220.004 4.0 Angle Prediction 0.8780.001 0.6420.013 0.4190.001 0.8130.007 0.5030.012 6.2 Dihedral Prediction 0.8780.004 0.5910.008 0.4140.001 0.8210.002 0.4970.004 6.8 Multiview Contrast 0.8710.003 0.6460.006 0.3680.001 0.8050.005 0.5020.009 7.2 DiffPreT 0.8800.005 0.6800.018 0.4520.001 0.8210.007 0.5330.006 2.4 SiamDiff 0.8840.003 0.6980.020 0.4600.001 0.8290.012 0.5460.018 1.2
Method EC MSP PSR Mean Rank AUPR Fmax AUROC Global Mean GearNet-Edge 0.8370.002 0.8110.001 0.6440.023 0.7630.012 0.3730.021 7.8 w/ pre-training Denoising Score Matching 0.8590.003 0.8400.001 0.6450.028 0.7950.027 0.4290.017 5.0 Residue Type Prediction 0.8510.002 0.8260.005 0.6360.003 0.8280.005 0.4800.031 5.4 Distance Prediction 0.8580.003 0.8360.001 0.6230.007 0.7960.017 0.4160.021 6.4 Angle Prediction 0.8730.003 0.8490.001 0.6310.041 0.8020.015 0.4460.009 4.2 Dihedral Prediction 0.8580.001 0.8400.001 0.5680.022 0.7320.021 0.3980.022 7.2 Multiview Contrast 0.8750.003 0.8570.003 0.7130.036 0.7520.012 0.3880.015 4.0 DiffPreT 0.8640.002 0.8440.001 0.6730.042 0.8150.008 0.5050.007 3.2 SiamDiff 0.8780.003 0.8570.003 0.7000.043 0.8560.007 0.5210.016 1.2
5.1 Experimental Setups
Pre-training datasets. Following Zhang et al. [86], we pre-train our models with the AlphaFold protein structure database v1 [43, 69], including 365K proteome-wide predicted structures.
Downstream benchmark tasks. In our evaluation, we assess EC prediction task [23] for catalysis behavior of proteins and four ATOM3D tasks [67]. The EC task involves 538 binary classification problems for Enzyme Commission (EC) numbers. We use dataset splits from Gligorijević et al. [23] with a 95% sequence identity cutoff. The ATOM3D tasks include Protein Interface Prediction (PIP), Mutation Stability Prediction (MSP), Residue Identity (RES), and Protein Structure Ranking (PSR) with different dataset splits based on sequence identity or competition year. Details are in App. D.
Baseline methods. In our evaluation, we utilize GearNet-Edge as the underlying model for both atom- and residue-level structures. GearNet-Edge incorporates various types of edges and edge-type-specific convolutions, along with message passing between edges, to model protein structures effectively. We compare our proposed methods with several previous protein structural pre-training algorithms, including multiview contrastive learning [86], denoising score matching [28], and four self-prediction methods (residue type, distance, angle, and dihedral prediction) [86]. For residue-level tasks, we include EC, MSP, and PSR in our evaluation, while PIP and RES tasks are specifically designed for atom-level models. Besides, we exclude EC from the atom-level evaluation due to the limited presence of side-chain atoms in the downloaded PDB dataset.
Training and evaluation. We pre-train our model for 50 epochs on the AlphaFold protein structure database following Zhang et al. [86] and fine-tune it for 50 epochs on EC, MSP, and PSR. However, due to time constraints, we only fine-tune the models for 10 epochs on the RES and PIP datasets. Results are reported as mean and standard deviation across three seeds (0, 1, and 2). Evaluation metrics include Fmax and AUPR for EC, AUROC for PIP and MSP, Spearman’s for PSR, and micro-averaged accuracy for RES. More details about experimental setup can be found in App. D.
5.2 Experimental Results
Tables 1 and 2 provide a comprehensive overview of the results obtained by GearNet-Edge on both atom- and residue-level benchmark tasks. The tables clearly demonstrate that both DiffPreT and SiamDiff exhibit significant improvements over GearNet-Edge without pre-training on both levels, underscoring the effectiveness of our pre-training methods.
An interesting observation from the tables is that previous pre-training methods tend to excel in specific tasks while showing limitations in others. For instance, Multiview Contrast, designed for capturing similar functional motifs [86], struggles with structural intricacies and local atomic interactions, resulting in lower performance on tasks like Protein Interface Prediction (PIP), Protein Structure Ranking (PSR), and Residue Identity (RES). Self-prediction methods excel at capturing structural details or residue type dependencies but show limitations in function prediction tasks, such as Enzyme Commission (EC) number prediction and Mutation Stability Prediction (MSP), and do not consistently improve performance on both atom and residue levels.
In contrast, our DiffPreT approach achieves top-3 performance in nearly all considered tasks, showcasing its versatility and effectiveness across different evaluation criteria. Moreover, SiamDiff surpasses all other pre-training methods, achieving the best results in 6 out of 7 tasks, establishing it as the state-of-the-art pre-training approach. These results provide compelling evidence that our joint diffusion pre-training strategy successfully captures the intricate interactions between different proteins (PIP), captures local structural details (RES) and global structural characteristics (PSR), and extracts informative features crucial for accurate function prediction (EC) across various tasks.
5.3 Ablation Study
Method PIP MSP RES PSR AUROC AUROC Accuracy Global GearNet-Edge 0.8680.002 0.6330.067 0.4410.001 0.7820.021 SiamDiff 0.8840.003 0.6980.020 0.4600.001 0.8290.008 w/o seq. diff. 0.8730.004 0.6950.002 0.4430.001 0.8030.010 w/o struct. diff. 0.8780.003 0.6520.021 0.4560.001 0.8050.005 w/o MI max. 0.8800.005 0.6800.018 0.4520.001 0.8210.007 w/ small noise 0.8750.002 0.6460.031 0.4440.001 0.8280.005 w/ large noise 0.8670.003 0.6830.020 0.4430.001 0.8190.011
To analyze the effect of different components of SiamDiff, we perform ablation study on atom-level tasks and present results in Table 3. We first examine two degenerate settings of joint diffusion, i.e., "w/o sequence diffusion" and "w/o structure diffusion". These settings lead to a deterioration in performance across all benchmark tasks, highlighting the importance of both sequence diffusion for residue type identification in RES and structure diffusion for capturing the structural stability of mutation effects in MSP. Next, we compare SiamDiff with DiffPreT, which lacks mutual information maximization between correlated conformers. The consistent improvements observed across all tasks indicate the robustness and effectiveness of our proposed mutual information maximization scheme.
Besides, we compare our method to baselines with fixed small () and large () noise levels to demonstrate the benefits of multi-scale denoising in diffusion pre-training. Interestingly, we observe that denoising with large noise enhances performance on MSP by capturing significant structural changes that lead to structural instability, while denoising with small noise improves performance in PSR by capturing fine-grained details for protein structure assessment. By incorporating multi-scale noise, we eliminate the need for manual tuning of the noise level as a hyperparameter and leverage the advantages of both large- and small-scale noise, as evidenced in the table.
5.4 Combine with Protein Language Models
Method EC MSP PSR AUPR Fmax AUROC Global Mean GearNet-Edge 0.8370.002 0.8110.001 0.6640.023 0.7640.012 0.3730.021 w/ SiamDiff 0.8780.003 0.8570.003 0.7000.043 0.8560.007 0.5210.016 ESM-GearNet 0.9040.002 0.8900.002 0.6850.027 0.8290.013 0.5950.010 w/ SiamDiff 0.9070.001 0.8970.001 0.6920.010 0.8630.009 0.6560.011
Protein language models (PLMs) have recently become a standard method for extracting representations from protein sequences, such as ESM [49]. However, these methods are unable to directly handle structure-related tasks in Atom3D without using protein structures as input. A recent solution addresses this by feeding residue representations outputted by ESM into the protein structure encoder GearNet [85]. To showcase the potential of SiamDiff on PLM-based encoders, we pre-trained the ESM-GearNet encoder using SiamDiff and evaluated its performance on residue-level tasks. Considering the model capacity and computational budget, we selected ESM-2-650M as the base PLM. The results in Table 4 demonstrate the performance improvements obtained by introducing the PLM component in ESM-GearNet. Furthermore, after pre-training with SiamDiff, ESM-GearNet achieves even better performance on all tasks, especially on PSR where ESM-only representations are not indicative for structure ranking. This highlights the benefits of our method for PLM-based encoders.
6 Conclusions
In this work, we propose the DiffPreT approach to pre-train a protein encoder by sequence-structure joint diffusion modeling, which captures the inter-atomic interactions within structure and the residue type dependencies along sequence. We further propose the SiamDiff method to enhance DiffPreT by additionally modeling the correlation between different conformers of one protein. Extensive experiments on diverse types of tasks and on both atom- and residue-level structures verify the competitive performance of DiffPreT and the superior performance of SiamDiff.
Acknowledgments
The authors would like to thank Meng Qu, Zhaocheng Zhu, Shengchao Liu, Chence Shi, Jiarui Lu, Huiyu Cai, Xinyu Yuan and Bozitao Zhong for their helpful discussions and comments.
This project is supported by AIHN IBM-MILA partnership program, the Natural Sciences and Engineering Research Council (NSERC) Discovery Grant, the Canada CIFAR AI Chair Program, collaboration grants between Microsoft Research and Mila, Samsung Electronics Co., Ltd., Amazon Faculty Research Award, Tencent AI Lab Rhino-Bird Gift Fund, a NRC Collaborative R&D Project (AI4D-CORE-06) as well as the IVADO Fundamental Research Project grant PRF-2019-3583139727.
References
- Abstreiter et al. [2021] Korbinian Abstreiter, Stefan Bauer, Bernhard Schölkopf, and Arash Mehrjou. Diffusion-based representation learning. arXiv preprint arXiv:2105.14257, 2021.
- Anand and Achim [2022] Namrata Anand and Tudor Achim. Protein structure and sequence generation with equivariant denoising diffusion probabilistic models. arXiv preprint arXiv:2205.15019, 2022.
- Anfinsen [1972] Christian B Anfinsen. The formation and stabilization of protein structure. Biochemical Journal, 128(4):737, 1972.
- Austin et al. [2021] Jacob Austin, Daniel D Johnson, Jonathan Ho, Daniel Tarlow, and Rianne van den Berg. Structured denoising diffusion models in discrete state-spaces. Advances in Neural Information Processing Systems, 34:17981–17993, 2021.
- Baek et al. [2021] Minkyung Baek, Frank DiMaio, Ivan Anishchenko, Justas Dauparas, Sergey Ovchinnikov, Gyu Rie Lee, Jue Wang, Qian Cong, Lisa N Kinch, R Dustin Schaeffer, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science, 373(6557):871–876, 2021.
- Barrio-Hernandez et al. [2023] Inigo Barrio-Hernandez, Jingi Yeo, Jürgen Jänes, Tanita Wein, Mihaly Varadi, Sameer Velankar, Pedro Beltrao, and Martin Steinegger. Clustering predicted structures at the scale of the known protein universe. bioRxiv, pages 2023–03, 2023.
- Belghazi et al. [2018] Mohamed Ishmael Belghazi, Aristide Baratin, Sai Rajeshwar, Sherjil Ozair, Yoshua Bengio, Aaron Courville, and Devon Hjelm. Mutual information neural estimation. In International conference on machine learning, pages 531–540. PMLR, 2018.
- Bengio et al. [2009] Yoshua Bengio, Jérôme Louradour, Ronan Collobert, and Jason Weston. Curriculum learning. In International Conference on Machine Learning, 2009.
- Chandra and Sharma [2014] B Chandra and Rajesh Kumar Sharma. Adaptive noise schedule for denoising autoencoder. In International conference on neural information processing, pages 535–542. Springer, 2014.
- Chen et al. [2022] Can Chen, Jingbo Zhou, Fan Wang, Xue Liu, and Dejing Dou. Structure-aware protein self-supervised learning. arXiv preprint arXiv:2204.04213, 2022.
- Chen et al. [2020a] Nanxin Chen, Yu Zhang, Heiga Zen, Ron J Weiss, Mohammad Norouzi, and William Chan. Wavegrad: Estimating gradients for waveform generation. arXiv preprint arXiv:2009.00713, 2020a.
- Chen et al. [2023] Tianlong Chen, Chengyue Gong, Daniel Jesus Diaz, Xuxi Chen, Jordan Tyler Wells, qiang liu, Zhangyang Wang, Andrew Ellington, Alex Dimakis, and Adam Klivans. Hotprotein: A novel framework for protein thermostability prediction and editing. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=YDJRFWBMNby.
- Chen et al. [2020b] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pages 1597–1607. PMLR, 2020b.
- Chen and He [2021] Xinlei Chen and Kaiming He. Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 15750–15758, 2021.
- Corso et al. [2023] Gabriele Corso, Hannes Stärk, Bowen Jing, Regina Barzilay, and Tommi Jaakkola. Diffdock: Diffusion steps, twists, and turns for molecular docking. International Conference on Learning Representations (ICLR), 2023.
- Dhariwal and Nichol [2021] Prafulla Dhariwal and Alexander Nichol. Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems, 34:8780–8794, 2021.
- Dill and MacCallum [2012] Ken A Dill and Justin L MacCallum. The protein-folding problem, 50 years on. science, 338(6110):1042–1046, 2012.
- Donsker and Varadhan [1983] Monroe D Donsker and SR Srinivasa Varadhan. Asymptotic evaluation of certain markov process expectations for large time. iv. Communications on Pure and Applied Mathematics, 36(2):183–212, 1983.
- Elnaggar et al. [2021] Ahmed Elnaggar, Michael Heinzinger, Christian Dallago, Ghalia Rehawi, Wang Yu, Llion Jones, Tom Gibbs, Tamas Feher, Christoph Angerer, Martin Steinegger, Debsindhu Bhowmik, and Burkhard Rost. Prottrans: Towards cracking the language of lifes code through self-supervised deep learning and high performance computing. IEEE Transactions on Pattern Analysis and Machine Intelligence, pages 1–1, 2021. doi: 10.1109/TPAMI.2021.3095381.
- Fuglede and Topsoe [2004] Bent Fuglede and Flemming Topsoe. Jensen-shannon divergence and hilbert space embedding. In International Symposium onInformation Theory, 2004. ISIT 2004. Proceedings., page 31. IEEE, 2004.
- Gainza et al. [2020] Pablo Gainza, Freyr Sverrisson, Frederico Monti, Emanuele Rodola, D Boscaini, MM Bronstein, and BE Correia. Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning. Nature Methods, 17(2):184–192, 2020.
- Geras and Sutton [2014] Krzysztof J Geras and Charles Sutton. Scheduled denoising autoencoders. arXiv preprint arXiv:1406.3269, 2014.
- Gligorijević et al. [2021] Vladimir Gligorijević, P Douglas Renfrew, Tomasz Kosciolek, Julia Koehler Leman, Daniel Berenberg, Tommi Vatanen, Chris Chandler, Bryn C Taylor, Ian M Fisk, Hera Vlamakis, et al. Structure-based protein function prediction using graph convolutional networks. Nature communications, 12(1):1–14, 2021.
- Goodfellow et al. [2016] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.
- Goodfellow et al. [2014] Ian J Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 2, pages 2672–2680, 2014.
- Grant et al. [2010] Barry J Grant, Alemayehu A Gorfe, and J Andrew McCammon. Large conformational changes in proteins: signaling and other functions. Current opinion in structural biology, 20(2):142–147, 2010.
- Grill et al. [2020] Jean-Bastien Grill, Florian Strub, Florent Altché, Corentin Tallec, Pierre Richemond, Elena Buchatskaya, Carl Doersch, Bernardo Avila Pires, Zhaohan Guo, Mohammad Gheshlaghi Azar, et al. Bootstrap your own latent-a new approach to self-supervised learning. Advances in neural information processing systems, 33:21271–21284, 2020.
- Guo et al. [2022] Yuzhi Guo, Jiaxiang Wu, Hehuan Ma, and Junzhou Huang. Self-supervised pre-training for protein embeddings using tertiary structures. In AAAI, 2022.
- Gutmann and Hyvärinen [2010] Michael Gutmann and Aapo Hyvärinen. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pages 297–304. JMLR Workshop and Conference Proceedings, 2010.
- Gutmann and Hyvärinen [2012] Michael U Gutmann and Aapo Hyvärinen. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics. Journal of machine learning research, 13(2), 2012.
- Hassani and Khasahmadi [2020] Kaveh Hassani and Amir Hosein Khasahmadi. Contrastive multi-view representation learning on graphs. In International Conference on Machine Learning, pages 4116–4126. PMLR, 2020.
- Hermosilla and Ropinski [2022] Pedro Hermosilla and Timo Ropinski. Contrastive representation learning for 3d protein structures. arXiv preprint arXiv:2205.15675, 2022.
- Hermosilla et al. [2021] Pedro Hermosilla, Marco Schäfer, Matěj Lang, Gloria Fackelmann, Pere Pau Vázquez, Barbora Kozlíková, Michael Krone, Tobias Ritschel, and Timo Ropinski. Intrinsic-extrinsic convolution and pooling for learning on 3d protein structures. International Conference on Learning Representations, 2021.
- Hjelm et al. [2018] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, and Yoshua Bengio. Learning deep representations by mutual information estimation and maximization. arXiv preprint arXiv:1808.06670, 2018.
- Ho and Agard [2009] Bosco K Ho and David A Agard. Probing the flexibility of large conformational changes in protein structures through local perturbations. PLoS computational biology, 5(4):e1000343, 2009.
- Ho et al. [2020] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33:6840–6851, 2020.
- Hoogeboom et al. [2021] Emiel Hoogeboom, Didrik Nielsen, Priyank Jaini, Patrick Forré, and Max Welling. Argmax flows and multinomial diffusion: Learning categorical distributions. Advances in Neural Information Processing Systems, 34:12454–12465, 2021.
- Hoogeboom et al. [2022] Emiel Hoogeboom, Vıctor Garcia Satorras, Clément Vignac, and Max Welling. Equivariant diffusion for molecule generation in 3d. In International Conference on Machine Learning, pages 8867–8887, 2022.
- Ingraham et al. [2022] John Ingraham, Max Baranov, Zak Costello, Vincent Frappier, Ahmed Ismail, Shan Tie, Wujie Wang, Vincent Xue, Fritz Obermeyer, Andrew Beam, et al. Illuminating protein space with a programmable generative model. bioRxiv, 2022.
- Jing et al. [2021a] Bowen Jing, Stephan Eismann, Pratham N. Soni, and Ron O. Dror. Learning from protein structure with geometric vector perceptrons. In International Conference on Learning Representations, 2021a. URL https://openreview.net/forum?id=1YLJDvSx6J4.
- Jing et al. [2021b] Bowen Jing, Stephan Eismann, Pratham N Soni, and Ron O Dror. Equivariant graph neural networks for 3d macromolecular structure. arXiv preprint arXiv:2106.03843, 2021b.
- Jing et al. [2022] Bowen Jing, Gabriele Corso, Jeffrey Chang, Regina Barzilay, and Tommi S. Jaakkola. Torsional diffusion for molecular conformer generation. In Alice H. Oh, Alekh Agarwal, Danielle Belgrave, and Kyunghyun Cho, editors, Advances in Neural Information Processing Systems, 2022. URL https://openreview.net/forum?id=w6fj2r62r_H.
- Jumper et al. [2021] John Jumper, Richard Evans, Alexander Pritzel, Tim Green, Michael Figurnov, Olaf Ronneberger, Kathryn Tunyasuvunakool, Russ Bates, Augustin Žídek, Anna Potapenko, et al. Highly accurate protein structure prediction with alphafold. Nature, 596(7873):583–589, 2021.
- Kingma and Welling [2013] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
- Köhler et al. [2020] Jonas Köhler, Leon Klein, and Frank Noé. Equivariant flows: exact likelihood generative learning for symmetric densities. In International conference on machine learning, pages 5361–5370. PMLR, 2020.
- Kryshtafovych et al. [2019] Andriy Kryshtafovych, Torsten Schwede, Maya Topf, Krzysztof Fidelis, and John Moult. Critical assessment of methods of protein structure prediction (casp)—round xiii. Proteins: Structure, Function, and Bioinformatics, 87(12):1011–1020, 2019.
- LeCun and Misra [2021] Yann LeCun and Ishan Misra. Self-supervised learning: The dark matter of intelligence, 2021. URL https://ai.facebook.com/blog/self-supervised-learning-the-dark-matter-of-intelligence/.
- Li et al. [2022] Xiang Lisa Li, John Thickstun, Ishaan Gulrajani, Percy Liang, and Tatsunori B Hashimoto. Diffusion-lm improves controllable text generation. arXiv preprint arXiv:2205.14217, 2022.
- Lin et al. [2022] Zeming Lin, Halil Akin, Roshan Rao, Brian Hie, Zhongkai Zhu, Wenting Lu, Nikita Smetanin, Allan dos Santos Costa, Maryam Fazel-Zarandi, Tom Sercu, Sal Candido, et al. Language models of protein sequences at the scale of evolution enable accurate structure prediction. bioRxiv, 2022.
- Liu et al. [2021] Shengchao Liu, Hanchen Wang, Weiyang Liu, Joan Lasenby, Hongyu Guo, and Jian Tang. Pre-training molecular graph representation with 3d geometry. In International Conference on Learning Representations, 2021.
- Liu et al. [2023] Shengchao Liu, Hongyu Guo, and Jian Tang. Molecular geometry pretraining with SE(3)-invariant denoising distance matching. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=CjTHVo1dvR.
- Lu et al. [2020] Amy X Lu, Haoran Zhang, Marzyeh Ghassemi, and Alan M Moses. Self-supervised contrastive learning of protein representations by mutual information maximization. BioRxiv, 2020.
- Luo et al. [2022] Shitong Luo, Yufeng Su, Xingang Peng, Sheng Wang, Jian Peng, and Jianzhu Ma. Antigen-specific antibody design and optimization with diffusion-based generative models for protein structures. 2022. URL https://openreview.net/forum?id=jSorGn2Tjg.
- Meier et al. [2021] Joshua Meier, Roshan Rao, Robert Verkuil, Jason Liu, Tom Sercu, and Alexander Rives. Language models enable zero-shot prediction of the effects of mutations on protein function. bioRxiv, 2021. doi: 10.1101/2021.07.09.450648. URL https://www.biorxiv.org/content/10.1101/2021.07.09.450648v1.
- Nienhaus et al. [1997] G Ulrich Nienhaus, Joachim D Müller, Ben H McMahon, and Hans Frauenfelder. Exploring the conformational energy landscape of proteins. Physica D: Nonlinear Phenomena, 107(2-4):297–311, 1997.
- Oord et al. [2018] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.
- O’Connor et al. [2010] Clare M O’Connor, Jill U Adams, and Jennifer Fairman. Essentials of cell biology. Cambridge, MA: NPG Education, 1:54, 2010.
- Rao et al. [2019] Roshan Rao, Nicholas Bhattacharya, Neil Thomas, Yan Duan, Peter Chen, John Canny, Pieter Abbeel, and Yun Song. Evaluating protein transfer learning with tape. Advances in neural information processing systems, 32, 2019.
- Rezende and Mohamed [2015] Danilo Rezende and Shakir Mohamed. Variational inference with normalizing flows. In International conference on machine learning, pages 1530–1538. PMLR, 2015.
- Rives et al. [2021] Alexander Rives, Joshua Meier, Tom Sercu, Siddharth Goyal, Zeming Lin, Jason Liu, Demi Guo, Myle Ott, C Lawrence Zitnick, Jerry Ma, et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proceedings of the National Academy of Sciences, 118(15), 2021.
- Shapovalov and Dunbrack Jr [2011] Maxim V Shapovalov and Roland L Dunbrack Jr. A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions. Structure, 19(6):844–858, 2011.
- Sohl-Dickstein et al. [2015] Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning, pages 2256–2265, 2015.
- Somnath et al. [2021] Vignesh Ram Somnath, Charlotte Bunne, and Andreas Krause. Multi-scale representation learning on proteins. Advances in Neural Information Processing Systems, 34, 2021.
- Song et al. [2020] Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456, 2020.
- Sverrisson et al. [2021] Freyr Sverrisson, Jean Feydy, Bruno E Correia, and Michael M Bronstein. Fast end-to-end learning on protein surfaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 15272–15281, 2021.
- Thomas et al. [2018] Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, and Patrick Riley. Tensor field networks: Rotation-and translation-equivariant neural networks for 3d point clouds. arXiv preprint arXiv:1802.08219, 2018.
- Townshend et al. [2020] Raphael JL Townshend, Martin Vögele, Patricia Suriana, Alexander Derry, Alexander Powers, Yianni Laloudakis, Sidhika Balachandar, Bowen Jing, Brandon Anderson, Stephan Eismann, et al. Atom3d: Tasks on molecules in three dimensions. arXiv preprint arXiv:2012.04035, 2020.
- Trippe et al. [2023] Brian L. Trippe, Jason Yim, Doug Tischer, David Baker, Tamara Broderick, Regina Barzilay, and Tommi S. Jaakkola. Diffusion probabilistic modeling of protein backbones in 3d for the motif-scaffolding problem. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=6TxBxqNME1Y.
- Varadi et al. [2021] Mihaly Varadi, Stephen Anyango, Mandar Deshpande, Sreenath Nair, Cindy Natassia, Galabina Yordanova, David Yuan, Oana Stroe, Gemma Wood, Agata Laydon, et al. Alphafold protein structure database: massively expanding the structural coverage of protein-sequence space with high-accuracy models. Nucleic acids research, 2021.
- Vignac et al. [2022] Clement Vignac, Igor Krawczuk, Antoine Siraudin, Bohan Wang, Volkan Cevher, and Pascal Frossard. Digress: Discrete denoising diffusion for graph generation. arXiv preprint arXiv:2209.14734, 2022.
- Wang et al. [2004] Junmei Wang, Romain M Wolf, James W Caldwell, Peter A Kollman, and David A Case. Development and testing of a general amber force field. Journal of computational chemistry, 25(9):1157–1174, 2004.
- Wang et al. [2022] Limei Wang, Haoran Liu, Yi Liu, Jerry Kurtin, and Shuiwang Ji. Learning protein representations via complete 3d graph networks. arXiv preprint arXiv:2207.12600, 2022.
- Watson et al. [2022] Joseph L Watson, David Juergens, Nathaniel R Bennett, Brian L Trippe, Jason Yim, Helen E Eisenach, Woody Ahern, Andrew J Borst, Robert J Ragotte, Lukas F Milles, et al. Broadly applicable and accurate protein design by integrating structure prediction networks and diffusion generative models. bioRxiv, 2022.
- Weiler et al. [2018] Maurice Weiler, Mario Geiger, Max Welling, Wouter Boomsma, and Taco S Cohen. 3d steerable cnns: Learning rotationally equivariant features in volumetric data. Advances in Neural Information Processing Systems, 31, 2018.
- Wu et al. [2022a] Fang Wu, Qiang Zhang, Dragomir Radev, Yuyang Wang, Xurui Jin, Yinghui Jiang, Zhangming Niu, and Stan Z Li. Pre-training of deep protein models with molecular dynamics simulations for drug binding. arXiv preprint arXiv:2204.08663, 2022a.
- Wu et al. [2022b] Kevin E Wu, Kevin K Yang, Rianne van den Berg, James Y Zou, Alex X Lu, and Ava P Amini. Protein structure generation via folding diffusion. arXiv preprint arXiv:2209.15611, 2022b.
- Wu et al. [2022c] Lemeng Wu, Chengyue Gong, Xingchao Liu, Mao Ye, and Qiang Liu. Diffusion-based molecule generation with informative prior bridges. arXiv preprint arXiv:2209.00865, 2022c.
- Xu et al. [2021] Minghao Xu, Hang Wang, Bingbing Ni, Hongyu Guo, and Jian Tang. Self-supervised graph-level representation learning with local and global structure. In International Conference on Machine Learning, pages 11548–11558. PMLR, 2021.
- Xu et al. [2022a] Minghao Xu, Yuanfan Guo, Yi Xu, Jian Tang, Xinlei Chen, and Yuandong Tian. Eurnet: Efficient multi-range relational modeling of spatial multi-relational data. arXiv preprint arXiv:2211.12941, 2022a.
- Xu et al. [2022b] Minghao Xu, Zuobai Zhang, Jiarui Lu, Zhaocheng Zhu, Yangtian Zhang, Chang Ma, Runcheng Liu, and Jian Tang. Peer: A comprehensive and multi-task benchmark for protein sequence understanding. arXiv preprint arXiv:2206.02096, 2022b.
- Xu et al. [2022c] Minkai Xu, Lantao Yu, Yang Song, Chence Shi, Stefano Ermon, and Jian Tang. Geodiff: A geometric diffusion model for molecular conformation generation. In International Conference on Learning Representations, 2022c. URL https://openreview.net/forum?id=PzcvxEMzvQC.
- Yang et al. [2022] Kevin K Yang, Niccolò Zanichelli, and Hugh Yeh. Masked inverse folding with sequence transfer for protein representation learning. bioRxiv, 2022.
- You and Shen [2022] Yuning You and Yang Shen. Cross-modality and self-supervised protein embedding for compound–protein affinity and contact prediction. Bioinformatics, 38(Supplement_2):ii68–ii74, 2022.
- Zaidi et al. [2023] Sheheryar Zaidi, Michael Schaarschmidt, James Martens, Hyunjik Kim, Yee Whye Teh, Alvaro Sanchez-Gonzalez, Peter Battaglia, Razvan Pascanu, and Jonathan Godwin. Pre-training via denoising for molecular property prediction. In The Eleventh International Conference on Learning Representations, 2023. URL https://openreview.net/forum?id=tYIMtogyee.
- [85] Zuobai Zhang, Minghao Xu, Aurelie Lozano, Vijil Chenthamarakshan, Payel Das, and Jian Tang. Enhancing protein language model with structure-based encoder and pre-training. In ICLR 2023-Machine Learning for Drug Discovery workshop.
- Zhang et al. [2022] Zuobai Zhang, Minghao Xu, Arian Jamasb, Vijil Chenthamarakshan, Aurelie Lozano, Payel Das, and Jian Tang. Protein representation learning by geometric structure pretraining. arXiv preprint arXiv:2203.06125, 2022.
- Zhu et al. [2022] Zhaocheng Zhu, Chence Shi, Zuobai Zhang, Shengchao Liu, Minghao Xu, Xinyu Yuan, Yangtian Zhang, Junkun Chen, Huiyu Cai, Jiarui Lu, et al. Torchdrug: A powerful and flexible machine learning platform for drug discovery. arXiv preprint arXiv:2202.08320, 2022.
Appendix A More Related Works
Protein Structure Encoder. The community witnessed a surge of research interests in learning informative protein structure representations using structure-based encoders. The encoders are designed to capture protein structural information on different granularity, including residue-level structures [23, 86, 79], atom-level structures [33, 40, 72] and protein surfaces [21, 65, 63]. In this work, we focus on pre-training a typical residue-level structure encoder, i.e., GearNet-Edge [86], and a typical atom-level structure encoder, i.e., GVP [40].
Mutual Information (MI) Estimation and Maximization. MI can measure both the linear and non-linear dependency between random variables. Some previous works [7, 34] try to use neural networks to estimate the lower bound of MI, including Donsker-Varadhan representation [18], Jensen-Shannon divergence [20] and Noise-Contrastive Estimation (NCE) [29, 30]. The optimization with InfoNCE loss [56] maximizes a lower bound of MI and is broadly shown to be a superior representation learning strategy [13, 31, 78, 50, 86]. In this work, we adopt the MI lower bound proposed by Liu et al. [51] with two conditional log-likelihoods, and we formulate the learning objective by mutually denoising the multimodal diffusion processes of two correlated proteins.
A.1 Broader Impacts and Limitations
The main objective of this research project is to enhance protein representations by utilizing joint pre-training using a vast collection of unlabeled protein structures. Unlike traditional unimodel pre-training methods, our approach takes advantage of both sequential and structural information, resulting in superior representations. This advantage allows for more comprehensive analysis of protein research and holds potential benefits for various real-world applications, including protein function prediction and sequence design.
Limitations.
In this paper, we limit our pre-training dataset to less than 1M protein structures. However, considering the vast coverage of the AlphaFold Protein Structure Database, which includes over 200 million proteins, it becomes feasible to train more advanced and extensive protein encoders on larger datasets in the future. Furthermore, an avenue for future exploration is the incorporation of conformer-related information during pre-training and the development of improved noise schedules for multi-scale denoising pre-training. It is important to acknowledge that powerful pretrained models can potentially be misused for harmful purposes, such as the design of dangerous drugs. We anticipate that future studies will address and mitigate these concerns.
Appendix B Details of SiamDiff
In this section, we discuss details of our SiamDiff method. We first describe the parameterization of the generation process in Sec. B.1, derive the pre-training objective in Sec. B.2, and discuss some modifications when applied on residue-level models in Sec. B.3.
B.1 Parameterization of Generation Process
Remember that we use and to denote the representation of the siamese trajectories and , respectively. Different from the generation process in traditional diffusion models, the parameterization of should inject information from . Therefore, we use the extracted residue and atom representations (denoted as and ) of for this denoising step. Given the conditional independence in (2), this generation process can be decomposed into that on protein structures and sequences similarly in Sec. 3.3.
Input: training dataset , learning rate
Output: trained encoder
Generation process on protein structures. As in (4), modeling the generation process of protein structures is to model the noise on and gradually decorrupt the noisy structure. This can be parameterized with a noise prediction network that is translation-invariant and rotation-equivariant w.r.t. . Besides, the noise applied on should not change with transformations on , so should be SE(3)-invariant w.r.t. .
To achieve these goals, we build our noise prediction network with atom representations (which is SE(3)-invariant w.r.t. ) and atom coordinates (which is SE(3)-equivariant w.r.t. ). We define an equivariant output similarly as in DiffPreT. Specifically, we have
where denotes the neighbors of the atom in the corresponding graph of . Note that achieves the equivariance requirement, as is SE(3)-invariant w.r.t. and while is translation-invariant and rotation-equivariant w.r.t. .
Generation process on protein sequences. As in (7), the generation process on sequences aims to predict masked residue types in with a predictor . In our setting of mutual prediction, we define the predictor based on representations of the same residues in , which are also masked. Hence, for each masked residue in , we feed its representation to an MLP and predict the type of the corresponding residue type in :
where the softmax function is applied over all residue types.
B.2 Pre-Training Objective
Given the defined forward and reverse process on two trajectories, we now derive the pre-training objective based on the mutual diffusion loss in (13).We take the term for example and its counterpart can be derived in the same way. The objective can be decomposed into a structure loss and a sequence loss :
| (15) | ||||
| (16) |
B.3 Residue-level model
Residue-level protein graphs can be seen as a concise version of atom graphs that enable efficient message passing between nodes and edges. As in Zhang et al. [86], we only keep the alpha carbon atom of each residue and add sequential, radius and K-nearest neighbor edges as different types of edges. For SiamDiff, the residue-level model cannot discriminate conformers generated by rotating side chains, since we only keep CA atoms. To solve this problem, we directly add Gaussian noises to the coordinates instead to generate approximate conformers. Specifically, the correlated conformer is defined by , where is the noise drawn from a normal distribution.
Appendix C Proofs
In this section, we provide proofs for propositions in Sec. 3 and Sec. 4. Due to the similarity between the two methods, all propositions are restated for SiamDiff. DiffPreT can be seen as a special case that two siamese trajectories collapse into one.
C.1 Proof of Proposition 1
For notations, we use the bold symbol to denote the representation of an object and use and to denote the corresponding random variables of representations of the siamese trajectories and .
Proposition 1
With some approximations, the mutual information between representations of two siamese trajectories is lower bounded by:
where is a constant independent of our encoder and the term from trajectory to is defined as
with being either or .
Proof. First, the mutual information between representations of two trajectories is defined as:
| (19) |
where the joint distribution is defined as . Next, we can derive a lower bound with this definition:
However, since the distribution of representations are intractable to sample for optimization, we instead sample the trajectories and from our defined diffusion process, i.e., . Besides, instead of predicting representations, we use the representations from one trajectory to recover the other trajectory, which reflects more information than its representation. With these approximations, the lower bound above can be further written as:
We now show the first term on the right hand side can be written as the loss defined in Proposition 1. The derivation is very similar with the proof of Proposition 3 in Xu et al. [81]. We include it here for completeness:
where we merge the term into the sum of KL divergences for brevity and use to denote the constant independent of our encoder. Note that the counterpart can be derived in the same way. Adding these two terms together finishes the proof of Proposition 1.
C.2 Proof of Pre-Training Loss Decomposition
We restate the proposition of pre-training loss decomposition rigorously as below.
Proposition 2
Given the assumptions 1) the separation of the diffusion process on protein structures and sequences
| (20) |
and 2) the conditional independence of the generation process
| (21) |
it can be proved that
| (22) |
where the three loss terms are defined as
with referring to the term from trajectory to .
C.3 Proof of Simplified Structure Loss
For completeness, we show how to derive the simplified structure loss. The proof is directly adapted from [81].
Proposition 3
Given the definition of the forward process
| (23) |
and the reverse process
| (24) | |||
| (25) |
the structure loss function
| (26) |
can be simplified to
| (27) |
where with , and is either or .
Proof. First, we prove . Let be the standard Gaussian random variable at time step . Then, we have
which suggests that the mean of is and the variance matrix is .
Next, we derive the posterior distribution as:
Let , then the -th KL divergence term can be written as:
which completes the proof.
C.4 Proof of Simplified Sequence Loss
Now we show the equivalence of optimizing sequence loss and the masked residue type prediction problem on .
Proposition 4
Given the definition of reverse process on protein sequences
| (28) |
the sequence loss reaches zero when puts all mass on the ground truth .
Proof. The loss function can be written as:
where is the normalization constant. Hence, when puts all mass on the ground truth , the distribution will be identical with , which makes the KL divergence become zero.
Appendix D Experimental Details
In this section, we introduce the details of our experiments. All these methods are developed based on PyTorch and TorchDrug [87].
Downstream benchmark tasks. For downstream evaluation, we adopt the EC prediction task [23] and four ATOM3D tasks [67].
-
1.
Enzyme Commission (EC) number prediction task aims to predict EC numbers of proteins which describe their catalysis behavior in biochemical reactions. This task is formalized as 538 binary classification problems. We adopt the dataset splits from Gligorijević et al. [23] and use the test split with 95% sequence identity cutoff following Zhang et al. [86].
-
2.
Protein Interface Prediction (PIP) requires the model to predict whether two amino acids from two proteins come into contact when the proteins bind (binary classification). The protein complexes of this benchmark are split with 30% sequence identity cutoff.
-
3.
Mutation Stability Prediction (MSP) task seeks to predict whether a mutation will increase the stability of a protein complex or not (binary classification). The benchmark dataset is split upon a 30% sequence identity cutoff among different splits.
-
4.
Residue Identity (RES) task studies the structural role of an amino acid under its local environment. A model predicts the type of the center amino acid based on its surrounding atomic structure. The environments in different splits are with different protein topology classes.
-
5.
Protein Structure Ranking (PSR) predicts global distance test scores of structure predictions submitted to the Critical Assessment of Structure Prediction (CASP) [46] competition. This dataset is split according to the competition year.
Graph construction.
For atom graphs, we connect atoms with Euclidean distance lower than a distance threshold. For PSR and MSP tasks, we remove all hydrogen atoms following Jing et al. [41]. For residue graphs, we discard all non-alpha-carbon atoms and add three different types of directed edges: sequential edges, radius edges and K-nearest neighbor edges. For sequential edges, two atoms are connected if their sequential distance is below a threshold and these edges are divided into different types according to these distances. For two kinds of spatial edges, we connect atoms according to Euclidean distance and k-nearest neighbors. We further apply a long range interaction filter that removes edges with low sequential distances. We refer readers to Zhang et al. [86] for more details.
Atom-level backbone models.
To adapt GearNet-Edge to atom-level structures with moderate computational cost, we construct the atom graph by using only the spatial edge with the radius . We concatenate one-hot features of atom types and residue types as node features and concatenate (1) one-hot features of residue types of end nodes, (2) one-hot features of edge types, (3) one-hot features of sequential distance, (4) spatial distance as edge features. The whole model is composed of 6 message passing layers with 128 hidden dimensions and ReLU activation function. For edge message passing, we employ the discretized angles to determine the edge types on the line graph. The final prediction is performed upon the hidden representation concatenated across all layers.
Residue-level backbone models.
We directly borrow the best hyperparameters reported in the original paper of GearNet-Edge [86]. We adopt the same configuration of relational graph construction, i.e., the sequential distance threshold , the radius , the number of neighbors and the long range interaction cutoff . We use one-hot features of residue types as node features and concatenate (1) features of end nodes, (2) one-hot features of edge types, (3) one-hot features of sequential distance, (4) spatial distance as edge features. Then we use 6 message passing layers with 512 hidden dimensions and ReLU as the activation function. For edge message passing, the edge types on the line graph are determined by the discretized angles. The hidden representations in each layer of GearNet will be concatenated for the final prediction.
Baseline pre-training methods.
Here we briefly introduce the considered baselines. Multiview Contrast aims to maximize the mutual information between correlated views, which are extracted by randomly chosen augmentation functions to capture protein sub-structures. Residue type, distance, angle and dihedral prediction masks single residues, single edges, edge pairs and edge triplets, respectively, and then predict the corresponding properties. Denoising score matching performs denoising on noised pairwise distance matrices based on the learnt representations.
For all baselines in [86], we adopt the original configurations. For Multiview Contrast, we use subsequence cropping that randomly extracts protein subsequences with no more than 50 residues and space cropping that takes all residues within a Euclidean ball with a random center residue. Then, either an identity function or a random edge masking function with mask rate equal to 0.15 is applied for constructing views. The temperature in the InfoNCE loss function is set as 0.07. We set the number of sampled items in each protein as 256 for Distance Prediction and as 512 for Angle and Dihedral Prediction. The mask rate for Residue Type Prediction is set as 0.15. When masking a residue on atom graphs, we discard all non-backbone atoms and set the residue features as zero. Since the backbone models and tasks in our paper are quite different with those in Guo et al. [28], we re-implement the method on our codebase. We consider 50 different noise levels log-linearly ranging from 0.01 to 10.0.
In DiffPreT, for structure diffusion, we use a sigmoid schedule for variances with the lowest variance and the highest variance . For sequence diffusion, we simply set the cumulative transition probability to [MASK] over time steps as a linear interpolation between minimum mask rate 0.15 and maximum mask rate 1.0. The number of diffusion steps is set as 100. In SiamDiff, we adopt the same hyperparameters for multimodal diffusion models. We set the variance of torsional perturbation noises as on the atom level and that of Gaussian perturbation noises as on the residue level when constructing the correlated conformer.
All other optimization configurations for these pre-training methods are reported in Table 5. All methods are pre-trained on 4 Tesla A100 GPUs and Table 5 reports the batch sizes on each GPU.
Method Max length Batch size Optimizer lr residue atom residue atom Residue Type Prediction 100 100 96 64 Adam 1e-3 Distance Prediction 100 100 128 64 Adam 1e-3 Angle Prediction 100 100 96 64 Adam 1e-3 Dihedral Prediction 100 100 96 64 Adam 1e-3 Multiview Contrast - - 96 64 Adam 1e-3 Denoising Score Matching 200 200 12 12 Adam 1e-4 DiffPreT 150 100 16 64 Adam 1e-4 SiamDiff 150 100 16 32 Adam 1e-4
Fine-tuning on downstream tasks.
For all models on all downstream tasks, we apply a three-layer MLP head for prediction, the hidden dimension of which is set to the dimension of model outputs. The number of used gpus and batch sizes for each model are chosen according the memory limit. All residue-level tasks are run on 4 V100 GPUs while all atom-level tasks are run on A100 GPUs.
Task # GPUS Batch size Optimizer lr residue atom residue atom EC 4 N/A 2 N/A Adam 1e-4 PIP N/A 1 N/A 8 Adam 1e-4 MSP 4 1 1 8 Adam 1e-4 RES N/A 4 N/A 64 Adam 1e-4 PSR 4 1 8 8 Adam 1e-4
Evaluation metrics.
We clarify the definitions of Fmax (used in EC), global Spearman’s (used in PSR) and mean Spearman’s (used in PSR) as below:
-
•
Fmax denotes the protein-centric maximum F-score. It first computes the precision and recall for each protein at a decision threshold :
(29) where denotes a functional term in the ontology, is the set of experimentally determined functions for protein , is the set of predicted functions for protein whose scores are greater or equal to , and represents the indicator function. After that, the precision and recall are averaged over all proteins:
(30) where denotes the total number of proteins, and denotes the number of proteins which contain at least one prediction above the threshold , i.e., .
Based on these two metrics, the Fmax score is defined as the maximum value of F-measure over all thresholds:
(31) -
•
Global Spearman’s for PSR measures the correlation between the predicted global distance test (GDT_TS) score and the ground truth. It computes the Spearman’s between the prediction and the ground truth over all test proteins without considering the different biopolymers that these proteins lie in.
-
•
Mean Spearman’s for PSR also measures the correlation between GDT_TS predictions and the ground truth. However, it first splits all test proteins into multiple groups based on their corresponding biopolymers, then computes the Spearman’s within each group, and finally reports the mean Spearman’s over all groups.
Appendix E Results of Pre-Training on Different Sizes of Datasets
Pre-training Dataset Size PSR MSP PIP RES Global Mean AUROC AUROC Acc. AlphaFold DB v1 365K 0.829 0.546 0.698 0.884 0.460 Clustered AlphaFold DB 10K 0.816 0.501 0.586 0.880 0.444 Clustered AlphaFold DB 50K 0.797 0.498 0.648 0.879 0.450 Clustered AlphaFold DB 100K 0.805 0.540 0.685 0.882 0.454 Clustered AlphaFold DB 500K 0.848 0.537 0.599 0.880 0.459 Clustered AlphaFold DB 2.2M 0.840 0.560 0.700 0.882 0.460
In the main paper, we followed the setting in Zhang et al. [86] and used AlphaFold Database v1 as our pre-training dataset for fair comparison. Here, we investigate the impact of pre-training on different dataset sizes. Since previous work by Zhang et al. [86] showed minimal differences between using experimental or predicted structures, we conduct experiments on the AlphaFold Database in this section and do not use PDB as our pre-training dataset. We utilize the preprocessed clustered AlphaFold Database provided in [6], which includes 2.2M non-singleton clusters with an average of 13.2 proteins per cluster and an average pLDDT of 71.59. For each cluster, we use the representative structure from [6]. To explore the effects of dataset size, we pre-train our encoder using 10K, 50K, 100K, 500K, and 2.2M clusters in the database. The results, shown in Table 7, reveal a general trend of increased performance with larger datasets. However, for certain tasks like MSP, the performance does not consistently improve, possibly due to the limited size and variability of the downstream datasets. Overall, scaling the model to the entire AlphaFold Database holds promise for achieving performance gains.
Appendix F Results of Multimodal Pre-Training Baselines
Method PSR MSP PIP RES Global Mean AUROC AUROC Acc. GearNet-Edge 0.782 0.488 0.633 0.868 0.441 w/ pre-training Residue Type Prediction 0.826 0.518 0.620 0.879 0.449 Residue Type & Distance Prediction 0.817 0.518 0.665 0.873 0.402 Residue Type & Angle Prediction 0.837 0.524 0.642 0.878 0.415 Residue Type & Dihedral Prediction 0.823 0.494 0.597 0.871 0.414 DiffPreT 0.821 0.533 0.680 0.880 0.452 SiamDiff 0.829 0.546 0.698 0.884 0.460
In Sec. 5, we include all pre-training baselines from existing works, which solely focus on unimodal pre-training objectives and overlook the joint distribution of sequences and structures. In this section, we introduce three additional pre-training baselines that leverage both sequence and structure information. These baselines combine residue type prediction with distance/angle/dihedral prediction objectives. Following established settings, we pre-train the encoder and present the results in Table 8. While the Residue Type & Angle Prediction method achieves higher performance on PSR, there are still substantial gaps compared to our DiffPreT and SiamDiff across other tasks. Notably, the introduction of geometric property prediction tasks leads to a drop in performance on RES, indicating that a simple combination of pre-training objectives diminishes the benefits of each individual objective. Once again, these findings underscore the effectiveness of our methods in modeling the joint distribution of protein sequences and structures.
Appendix G Results of Different Diffusion Models for Pre-Training
Method PIP RES PSR AUROC Accuracy Global Mean GearNet-Edge 0.868 0.441 0.782 0.488 w/ pre-training DiffPreT 0.880 0.452 0.821 0.533 SiamDiff 0.884 0.460 0.829 0.546 Sequence Diffusion 0.879 0.456 0.802 0.508 Structure Diffusion 0.877 0.448 0.813 0.518 Torsional Diffusion 0.877 0.442 0.819 0.505
In Sec. 3, we consider joint diffusion models on protein sequences and structures for pre-training. In this section, we explore the performance of different diffusion models when applied for pre-training. The results are shown in Table 9.
First, we simply run diffusion models on protein sequences and structures for pre-training, both of which achieve improvement compared with the baseline GearNet-Edge. By combining two diffusion models, DiffPreT can achieve better performance on PIP and PSR. This advantage will be further increased after using siamese diffusion trajectory prediction as shown in Table 3. It can be observed that sequence diffusion achieves better performance than DiffPreT due to the consistency of objectives between pre-training and RES tasks.
Besides, we also consider diffusion models on torsional angles of protein side chains for pre-training. This method has shown its potential in the protein-ligand docking task [15]. For each residue, we randomly select one side-chain torsional angle and add some noises drawn from wrapped Gaussian distribution during the diffusion process. Then, we predict the added noises with the extracted atom representations corresponding to the torsional angle. In Table 9, we can see clear improvements on PIP and PSR tasks compared with GearNet-Edge. This suggests that it would be a promising direction to explore more different diffusion models for pre-training, e.g., diffusion models on backbone dihedral angles.
Appendix H Results of Pre-Training GVP
Method PSR MSP PIP RES Mean Rank Global Mean AUROC AUROC Acc. GVP 0.809 0.486 0.610 0.846 0.481 8.6 w/ pre-training Denoising Score Matching 0.849 0.535 0.625 0.851 0.529 5.4 Residue Type Prediction 0.845 0.527 0.652 0.847 0.518 5.8 Distance Prediction 0.825 0.513 0.632 0.836 0.483 7.6 Angle Prediction 0.872 0.545 0.637 0.881 0.557 2.0 Dihedral Prediction 0.852 0.538 0.677 0.881 0.555 2.2 Multiview Contrast 0.848 0.518 0.656 0.833 0.490 6.4 DiffPreT 0.850 0.540 0.631 0.851 0.542 4.4 SiamDiff 0.854 0.548 0.673 0.863 0.554 2.2
To study the effect of our proposed pre-training methods on different backbone models, we show the pre-training results on GVP [40, 41] in this section.
Setup. GVP constructs atom graphs and adds vector channels for modeling equivariant features. The original design only includes atom types as node features, which makes pre-training tasks with residue type prediction very difficult to learn. To address this issue, we slightly modify its architecture to add the embedding of atom and corresponding residue types as atom features. Then, the default configurations in Jing et al. [41] are adopted. We construct an atom graph for each protein by drawing edges between atoms closer than . Each edge is featured with a 16-dimensional Gaussian RBF encoding of its Euclidean distance. We use five GVP layers and hidden representations with 16 vector and 100 scalar channels and use ReLU and identity for scalar and vector activation functions, respectively. The dropout rate is set as 0.1. The final atom representations are followed by two mean pooling layers to obtain residue and protein representations, respectively. All other hyperparameters for pre-training and downstream tasks are the same as those in App. D.
Experimental results. The results are shown in Table 10. Among all pre-training methods, SiamDiff, angle prediction and dihedral prediction are the top three. This is different from what we observe in Table 1, where residue type and distance prediction are more competitive baselines. We hypothesize that this is because GearNet-Edge includes angle information in the encoder while GVP does not. Therefore, GVP will benefit more from pre-training methods with supervision on angles. Nevertheless, we find that SiamDiff is the only method that performs well on different backbone models.