Preconditioning for a Variational Quantum Linear Solver
Abstract
We apply preconditioning, which is widely used in classical solvers for linear systems , to the variational quantum linear solver. By utilizing incomplete LU factorization as a preconditioner for linear equations formed by random sparse matrices, we numerically demonstrate a notable reduction in the required ansatz depth, demonstrating that preconditioning is useful for quantum algorithms. This reduction in circuit depth is crucial to improving the efficiency and accuracy of Noisy Intermediate-Scale Quantum (NISQ) algorithms. Our findings suggest that combining classical computing techniques, such as preconditioning, with quantum algorithms can significantly enhance the performance of NISQ algorithms.
I Introduction
Recently, Variational Quantum Linear Solvers (VQLS) have emerged as promising quantum algorithms for solving sparse linear systems of equations [1, 2] on Noisy Intermediate-Scale Quantum (NISQ) machines [3], with potential applications across various domains, including computational fluid dynamics simulation [4, 5], finite difference time domain method [6, 7], and machine learning [8, 9, 10]. VQLS leverages the power of NISQ machines by employing parameterized quantum circuits, known as ansatz, to represent and approximate solutions to linear equations. However, the effectiveness of VQLS depends heavily on the ability of the ansatz to express the optimal solution within its parameterized space [11, 12, 13, 14].
One significant challenge in employing ansatz for VQLS is that these parameterized quantum circuits with a certain circuit depth do not inherently span the entire space of the unitary matrices [12]. Although increasing the circuit depth can enhance the expressiveness of the ansatz, it leads to longer optimization times of the circuit’s parameters and the potential emergence of ‘barren plateaus,’ where gradients vanish during optimization, making it challenging [15, 16, 17, 18, 19]. Consequently, there is no guarantee that the ansatz will always converge to the optimal solution and its performance can be limited by these factors.
To address this limitation, we introduce a novel approach in this study, wherein we incorporate preconditioning strategies as a crucial step in VQLS. Preconditioning, a technique commonly used in iterative Krylov subspace methods, aims to modify a system to improve its numerical properties [20, 21, 22, 23]. This tailored modification results in a matrix with enhanced spectral properties or a closer approximation to a diagonal matrix, leading to improved convergence.
In our study, we aim to leverage this aspect of preconditioning to reduce the required circuit depth for the ansatz in VQLS. Specifically, we focused on employing incomplete LU (ILU) factorization as a preconditioning method for linear equations [24, 25, 26, 27, 28]. ILU factorization is a technique that approximates the LU factorization of a matrix, which is the process of factorizing a matrix into a lower triangular matrix (L) and an upper triangular matrix (U). This approximation is particularly useful in sparse matrix scenarios, where it reduces computational complexity while capturing the essential features of the matrix. By enhancing the spectral properties of the matrix involved in the linear equations with ILU factorization, we hypothesize that the depth of the circuit necessary for the ansatz can be reduced. This potential reduction in the circuit depth could lead to more efficient implementations of VQLS, making it a practical and powerful tool for applications in NISQ computing.
II Preconditioning with ILU factorization
Here, we discuss the use of ILU factorization as a preconditioning technique for classical iterative Krylov subspace methods. ILU plays a crucial role in solving linear equations of the form , where is a given matrix; x and b are vectors. The essence of ILU lies in approximating the exact LU factorization of matrix . In LU factorization, matrix is factored into two matrices, and , where is a lower triangular matrix and is an upper triangular matrix, and the factorization can be expressed as .
However, in the case of ILU, the goal is to create an approximation of and that is computationally less expensive and particularly beneficial for large sparse matrices. The ILU factorization is represented as
| (1) |
where and are the incomplete lower and upper triangular matrices, respectively. The approximation involves dropping certain elements in and , typically based on a threshold or pattern-based strategy, to maintain sparsity and manage computational complexity.
In the context of sparse matrices, ILU factorization aims to approximate LU factorization by filling only the positions in and , where has non-zero elements. This was performed to control computational complexity by focusing only on the significant elements of . This can be expressed using the set notation as follows: Let be the set of indices where has nonzero elements. Then, the elements of and are filled only for those indices in . Mathematically, this can be represented as
| (2) |
where and are the elements in the -th row and -th column of matrices and , respectively. To apply this to preconditioning, we consider the product as the preconditioning matrix , and its inverse is applied to the left side of the linear equation. The preconditioned system using ILU can then be expressed as
| (3) |
where . This transformation of the system aims to improve the condition number of matrix , thereby enhancing the convergence properties of the classical iterative methods used for solving the linear equation.
III Preconditioning for VQLS
In this section, we discuss the theoretical underpinnings of the VQLS and explore the application of preconditioning techniques. Our focus is on elucidating the fundamental principles governing the VQLS and examining how classical preconditioning methods can be integrated to enhance the efficiency of the algorithm in solving linear equations.
VQLS is a quantum algorithm designed to solve linear equations of the form , where is a given matrix and x and b are vectors. The goal is to determine the vector x that satisfies this equation.
The key idea behind VQLS is to represent the solution x as a quantum state and minimize a cost function that quantifies the difference between and . The cost function is defined as
| (4) |
This cost function is designed to be minimized when is proportional to . The VQLS algorithm iteratively adjusts the parameters of a variational quantum circuit to prepare the state such that it minimizes the cost function .
The variational quantum circuit used in VQLS is parameterized by a set of angles , and state is prepared as . Initially, does not necessarily represent the solution to the linear equation; however, it is iteratively adjusted through the classical optimization process to approximate the solution of . This transformation is expressed as follows:
| (5) |
Similarly, the unitary operation is used to transform the initial state into state , which represents the known vector b in the linear equation. This transformation is essential for evaluating the cost function and is represented as
| (6) |
The efficient implementation of unitary operations , , and is crucial in the VQLS. If is Hermitian, matrix can be decomposed into a sum of unitary matrices as . Even if is not Hermitian, it can be Hermitianized by either setting or using an ancillary qubit to construct . This decomposition enables the embedding of into a quantum circuit. Notably, the efficiency of this embedding is significantly enhanced when is a sparse matrix. Sparse matrices allow for a more streamlined and resource-efficient implementation of the unitary matrices in the quantum circuit.
Furthermore, it is typically challenging to efficiently embed classical data b as a quantum state using [29]. Several techniques have been proposed in recent years [30, 31, 32, 33, 34, 35], primarily within the field of quantum machine learning [36, 37].
In our approach to optimizing in VQLS, we focus on reducing the necessary circuit depth of the ansatz through classical preconditioning. Instead of directly solving the linear system , we solve the preconditioned system defined by Eq. (3). In this transformation, the original matrix and vector are preconditioned using ILU factorization, resulting in a new system , where and .
A typical ansatz is shown in Fig. 1(a), known as a hardware-efficient ansatz corresponding to in conventional VQLS. This ansatz structure comprises local phase rotation gates with independently adjustable parameters and CNOT gates between adjacent qubits, repeated for cycles.
Fig. 1(b) illustrates the effect of preconditioning on reducing the required depth of the ansatz in VQLS. By applying preconditioning, the space of quantum states that needs to be explored by the ansatz can be narrowed, potentially reducing the necessary circuit depth .
Fig. 1(c) depicts the impact of preconditioning on the search space in the Krylov subspace method for classical iterative linear solvers. Preconditioning can help to focus the iterative search within a smaller subspace, thereby improving the efficiency of the classical solver.
To reduce the search space required, as shown in Fig. 1(b), the required for obtaining the optimal solution must evolve from ‘complex’ to ‘simpler’ by preconditioning. In conventional VQLS, is typically defined as the operator that transforms state into . However, in our approach, we redefine as the operator that transforms the preconditioned state into as
| (7) |
where .
Based on this definition, the cost function in Eq. (4) can be rewritten as
| (8) |
can be embedded into a quantum circuit as a sum of unitary matrices, expressed as . Following this formulation and Eq. (8), the cost function can be computed on a quantum computer using the Hadamard tests for and for .
In Ref. [1], the authors proposed a definition of the cost function given by local measurements to mitigate the barren plateau. However, in this study, we focused on exploring the ability of preconditioning to reduce the necessary depth of the ansatz. Therefore, for numerical demonstrations , we adopted the cost function defined in Eq. (8).
IV Numerical demonstration
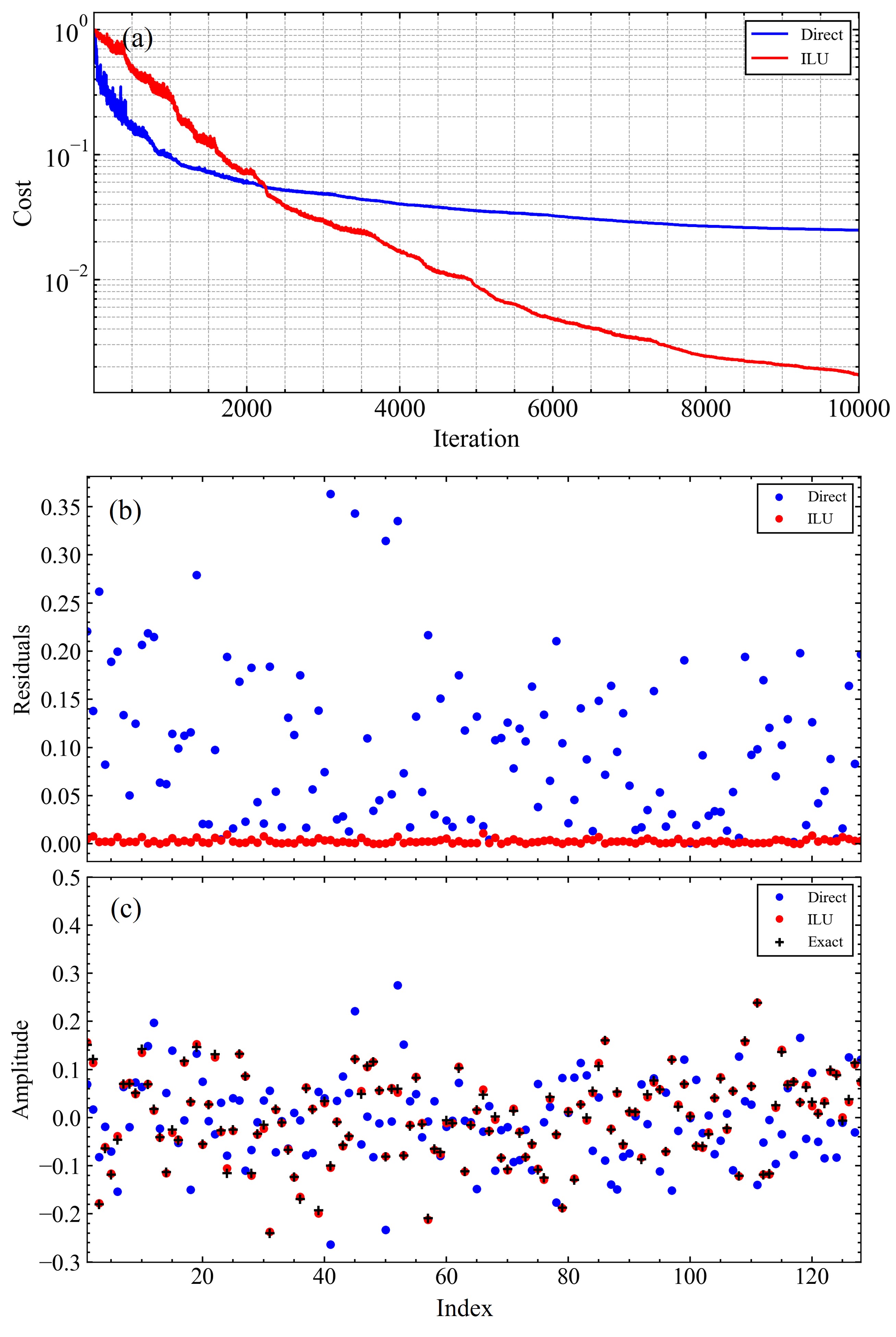
We applied ILU factorization as a preconditioning to a linear equation defined by a sparse matrix and numerically investigated the effects of this preconditioning. A variational quantum circuit of this size can be described using an 8-qubit quantum circuit because seven qubits are used to represent the Hilbert space, and an ancilla qubit is used to convert to the Hermite matrix. In the tested linear equation, both the matrix and vector comprised entirely real numbers; thus, we adopted a hardware-efficient ansatz consisting of RY and CNOT gates, as depicted in Fig. 1(a). This configuration ensures that all amplitudes remain real. The density of matrix was set to 0.2, and the elements of and were generated using uniform random numbers ranging from to . The number of iterations was set to 10,000, and the Adam optimizer with a learning rate of 0.001 was used to optimize the ansatz parameters.
The results demonstrating the effects of preconditioning under the condition of a circuit depth of 20 are presented in Fig. 2. After 10,000 iterations, the VQLS with preconditioning exhibited improved cost convergence and residuals compared to those without preconditioning, with respect to the exact solution. The results presented in Fig. 2 pertain to a particular involving a randomly generated sparse matrix. We observed similar improvements in solution convergence owing to the preconditioning of the other linear equations generated using the same procedure.
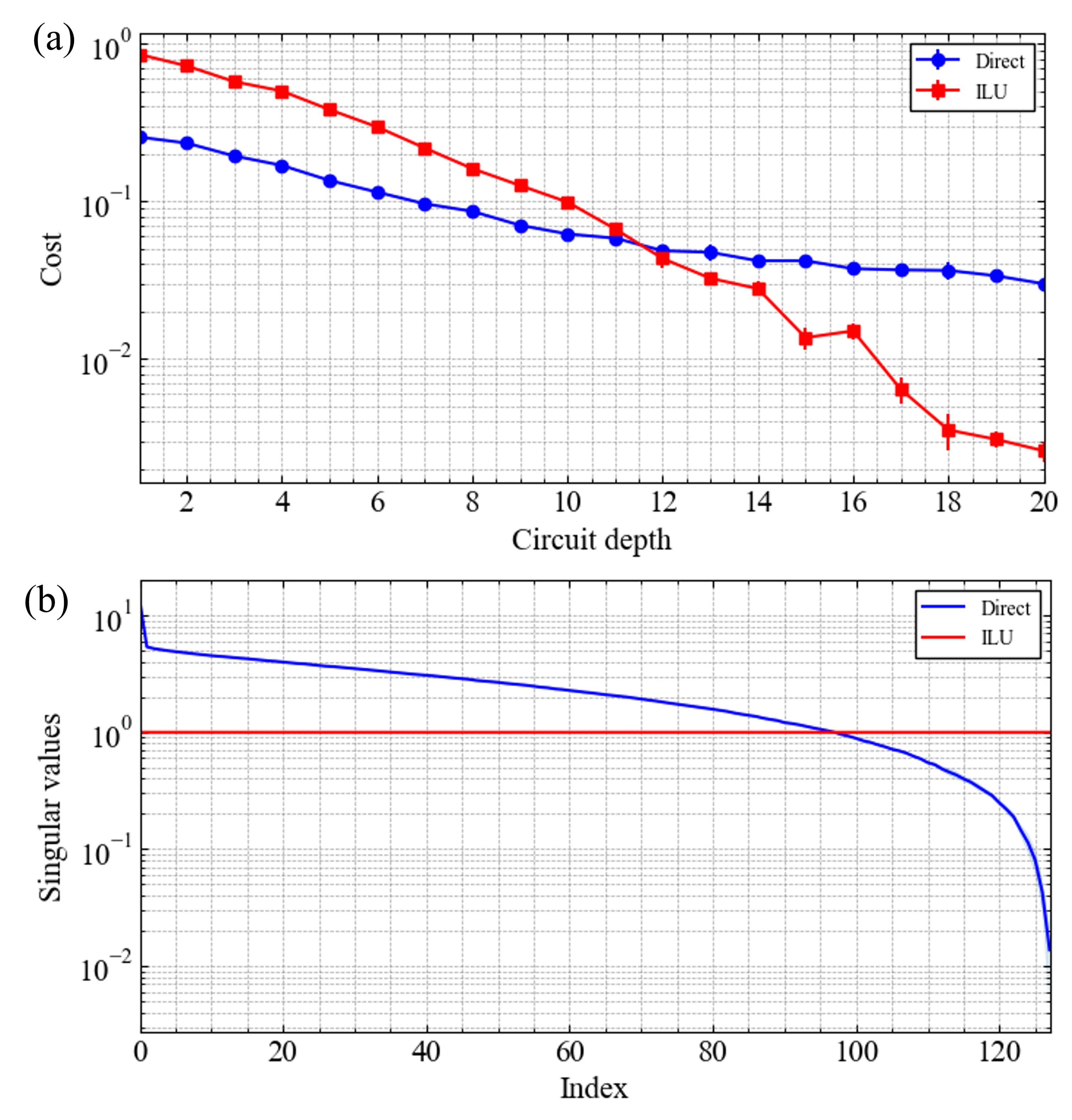
To demonstrate the reduction in the required depth of the ansatz owing to preconditioning, Fig. 3(a) presents the average cost obtained after 10,000 iterations for linear equations defined by 10 different random sparse matrices, with the ansatz’s circuit depth varying from 1 to 20. As shown in the figure, preconditioning reduces the complexity of the unitary operations that the ansatz must represent, leading to an improved convergence of the solution with respect to the circuit depth.
To investigate the reason for the improved solution convergence, the average spectra of the singular values before and after preconditioning for the 10 random sparse matrices are presented in Fig. 3(b). Although the original matrices exhibited a skew in singular values, preconditioning led to a uniform distribution in the spectrum. This implies that the preconditioning brought matrix closer to the identity matrix, enabling the ansatz to generate solutions with less entanglement.
V Application to Real-World Problems
The solution of linear equations is a crucial task that appears in real-world scenarios. Here, as an example of the linear equations that emerge in real-world contexts, we solve the steady-state solution of a one-dimensional heat diffusion equation.
We benchmark the effectiveness of the preconditioned VQLS by solving the simplest example of heat diffusion found in standard textbooks. Both ends of the rod are subject to boundary conditions with constant temperatures, and assuming that the conductor uniformly generates heat at a constant rate , the differential equation representing this problem is given as follows:
| (9) |
By discretizing this equation, it can be converted into a linear equation. Considering is sufficiently small in the interval to , we have . Furthermore, the boundary conditions are and . When . From these relations, the coefficients of the linear equation can be determined.
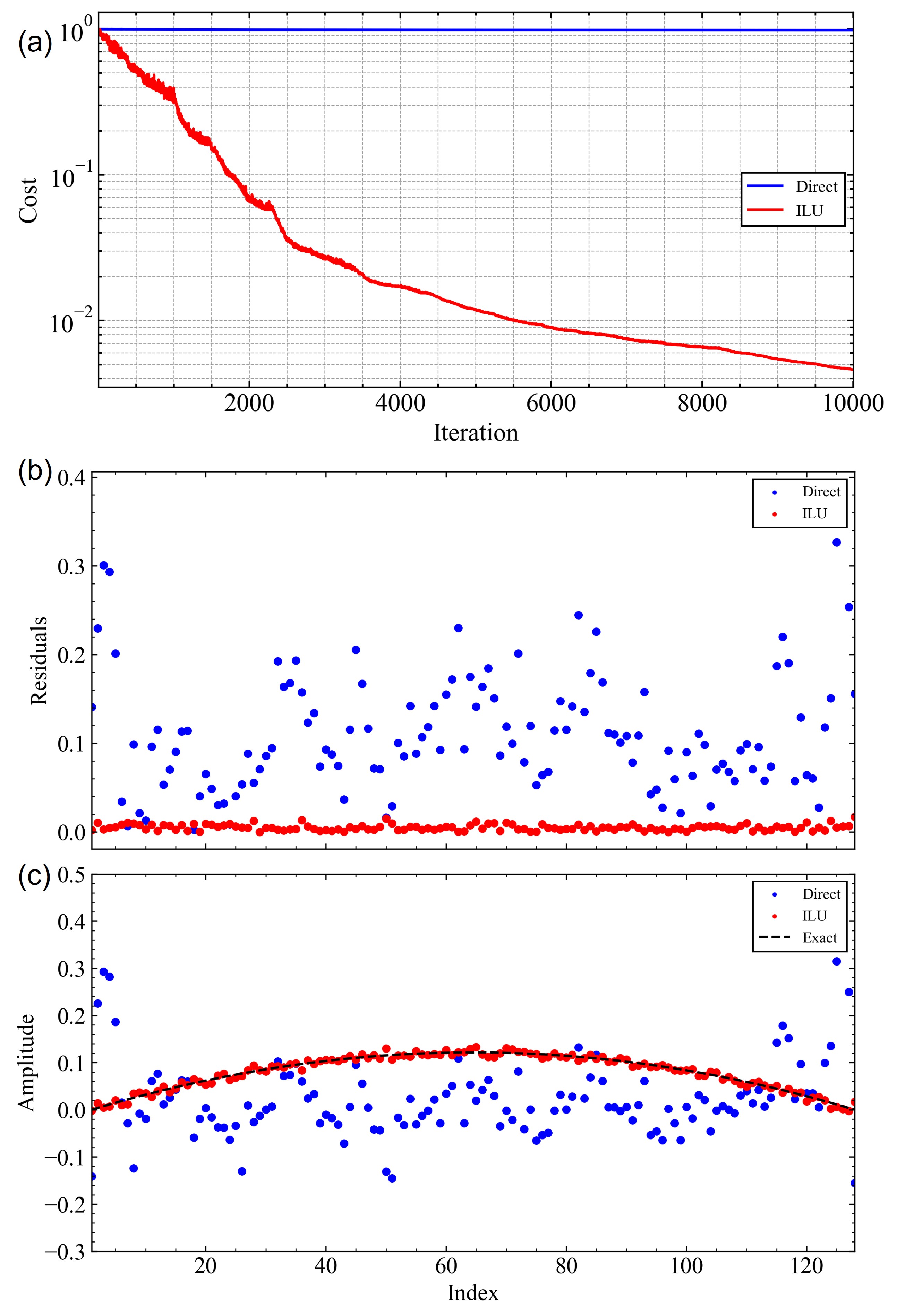
Figure 4 illustrates the application of preconditioning to the solution of the steady-state heat- diffusion equation. In this example, we have discretized the 1D rod into segments. The linear equation resulting from the discretization of the differential equation was solved using VQLS, both with and without preconditioning.
Figure 4(a) shows the convergence of the cost function in both cases. The blue line represents the cost function without preconditioning, whereas the red line represents the cost function with preconditioning. Notably, in this example, vector contains only low-frequency components, as opposed to a more general case in which can contain a mixture of low- and high-frequency components. In such scenarios, where is dominated by low-frequency components, the convergence of the VQLS algorithm without preconditioning can become particularly challenging. This is because ansatz might struggle to efficiently represent solutions that are predominantly low frequency, leading to slower convergence rates. Conversely, the application of preconditioning can significantly improve the convergence by effectively transforming the problem into a form that is easier for the ansatz to represent, thereby enhancing the overall performance of the VQLS algorithm.
Figure 4(b) shows the absolute values of the residuals between the solution obtained from VQLS and the exact solution calculated using classical matrix inversion techniques. The residuals are lower for the preconditioned case (red line) than for the non-preconditioned case (blue line), demonstrating that preconditioning accelerates the convergence and enhances the accuracy of the solution obtained from VQLS.
Finally, Figure 4(c) presents a comparison between the solution obtained from the VQLS (both with and without preconditioning) and the exact solution. The blue dots represent the solution obtained without preconditioning, the red dots represent the solution obtained with preconditioning, and the black line represents the exact solution. The plot illustrates that the solution obtained with preconditioning is closer to the exact solution, further validating the effectiveness of preconditioning in improving the performance of the VQLS for real-world problems such as the heat diffusion equation.
VI Discussion
Preconditioning using classical computers can reduce the amount of entanglement required for the VQLS. However, this preconditioning might increase the amount of entanglement needed to generate . Typically, generating any arbitrary requires gates [29]; however, for some linear equations, can be represented with fewer gates. However, the application of preconditioning may complicate the problems that were previously advantageous for efficiently generating , potentially increasing the number of gates required to generate .
However, adding preconditioning could potentially reduce the number of gates required to generate , and the best strategy is to choose a preconditioner that improves the properties of while reducing the number of gates required to generate .
In our numerical demonstration, we adopted ILU as the preconditioner, several methods are known as preconditioners. When choosing a preconditioner, it is necessary to consider the balance between three costs: the number of gates required to generate , the depth of the ansatz required to obtain the solution, and the additional computational cost required for preconditioning on a classical computer.
VII Conclusion
We applied preconditioning, commonly used in Krylov subspace methods, to variational quantum circuits and demonstrated its effectiveness numerically. By applying ILU to 10 instances of linear equations given by random sparse matrices, we observed a reduction in the required depth of the ansatz in all cases owing to preconditioning.
Reducing the depth of the ansatz is important for decreasing the number of iterations needed for optimization in variational quantum algorithms and crucial for increasing noise resilience and avoiding barren plateaus in NISQ machines. By incorporating classical computing assistance, such as preconditioning, it is conjectured that the calculation costs of quantum computers can be reduced, and more accurate computational results can be obtained with NISQ machines.
References
- Bravo-Prieto et al. [2023] C. Bravo-Prieto, R. LaRose, M. Cerezo, Y. Subasi, L. Cincio, and P. J. Coles, Quantum 7, 1188 (2023).
- Xu et al. [2021] X. Xu, J. Sun, S. Endo, Y. Li, S. C. Benjamin, and X. Yuan, Sci. Bull. 66, 2181 (2021).
- Preskill [2018] J. Preskill, Quantum 2, 79 (2018).
- Bharadwaj and Sreenivasan [2023] S. S. Bharadwaj and K. R. Sreenivasan, Proc. Natl. Acad. Sci. USA 120, e2311014120 (2023).
- Liu et al. [2022] Y. Liu, Z. Chen, C. Shu, S.-C. Chew, B. C. Khoo, X. Zhao, and Y. Cui, Phys. Fluids 34 (2022).
- Novak [2023] R. Novak, IEEE Access 11, 111545 (2023).
- Trahan et al. [2023] C. J. Trahan, M. Loveland, N. Davis, and E. Ellison, Entropy 25, 580 (2023).
- Duan et al. [2020] B. Duan, J. Yuan, C.-H. Yu, J. Huang, and C.-Y. Hsieh, Phys. Lett. A 384, 126595 (2020).
- Yoshikura et al. [2023] T. Yoshikura, S. L. Ten-no, and T. Tsuchimochi, J. Phys. Chem. A 127, 6577 (2023).
- Demirdjian et al. [2022] R. Demirdjian, D. Gunlycke, C. A. Reynolds, J. D. Doyle, and S. Tafur, Quantum Inf. Process. 21, 322 (2022).
- Patil et al. [2022] H. Patil, Y. Wang, and P. S. Krsti’c, Phys. Rev. A 105, 012423 (2022).
- Du et al. [2022] Y. Du, Z. Tu, X. Yuan, and D. Tao, Phys. Rev. Lett. 128, 080506 (2022).
- Funcke et al. [2021] L. Funcke, T. Hartung, K. Jansen, S. K”uhn, and P. Stornati, Quantum 5, 422 (2021).
- Tangpanitanon et al. [2020] J. Tangpanitanon, S. Thanasilp, N. Dangniam, M.-A. Lemonde, and D. G. Angelakis, Phys. Rev. Res. 2, 043364 (2020).
- Holmes et al. [2022] Z. Holmes, K. Sharma, M. Cerezo, and P. J. Coles, PRX Quantum 3, 010313 (2022).
- Wang et al. [2021] S. Wang, E. Fontana, M. Cerezo, K. Sharma, A. Sone, L. Cincio, and P. J. Coles, Nat. Commun. 12, 6961 (2021).
- Cerezo et al. [2021] M. Cerezo, A. Sone, T. Volkoff, L. Cincio, and P. J. Coles, Nat. Commun. 12, 1791 (2021).
- Uvarov and Biamonte [2021] A. Uvarov and J. D. Biamonte, J. Phys. A 54, 245301 (2021).
- Tilly et al. [2022] J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth, et al., Phys. Rep. 986, 1 (2022).
- Ghai et al. [2019] A. Ghai, C. Lu, and X. Jiao, Numer. Linear Algebra Appl. 26, e2215 (2019).
- Saad [1989] Y. Saad, SIAM J. Sci. Stat. Comput. 10, 1200 (1989).
- Knyazev [1998] A. V. Knyazev, Electron. Trans. Numer. Anal. 7, 104 (1998).
- Brown et al. [1994] P. N. Brown, A. C. Hindmarsh, and L. R. Petzold, SIAM J. Sci. Comput. 15, 1467 (1994).
- Elman [1986] H. C. Elman, Math. Comput. pp. 191–217 (1986).
- Chow and Saad [1997] E. Chow and Y. Saad, J. Comput. Appl. Math. 86, 387 (1997).
- Benzi [2002] M. Benzi, J. Comput. Phys. 182, 418 (2002).
- Chow and Saad [1998] E. Chow and Y. Saad, SIAM J. Sci. Comput. 19, 995 (1998).
- Li and Saad [2013] R. Li and Y. Saad, J. Supercomput. 63, 443 (2013).
- Plesch and Brukner [2011] M. Plesch and i. c. v. Brukner, Phys. Rev. A 83, 032302 (2011).
- Park et al. [2019] D. K. Park, F. Petruccione, and J.-K. K. Rhee, Sci. Rep. 9, 3949 (2019).
- LaRose and Coyle [2020] R. LaRose and B. Coyle, Phys. Rev. A 102, 032420 (2020).
- Mitarai et al. [2019] K. Mitarai, M. Kitagawa, and K. Fujii, Phys. Rev. A 99, 012301 (2019).
- Nakaji et al. [2022] K. Nakaji, S. Uno, Y. Suzuki, R. Raymond, T. Onodera, T. Tanaka, H. Tezuka, N. Mitsuda, and N. Yamamoto, Phys. Rev. Res. 4, 023136 (2022).
- Ashhab et al. [2022] S. Ashhab, N. Yamamoto, F. Yoshihara, and K. Semba, Phys. Rev. A 106, 022426 (2022).
- Zhang et al. [2022] X.-M. Zhang, T. Li, and X. Yuan, Phys. Rev. Lett. 129, 230504 (2022).
- Abbas et al. [2021] A. Abbas, D. Sutter, C. Zoufal, A. Lucchi, A. Figalli, and S. Woerner, Nat. Comput. Sci. 1, 403 (2021).
- Schuld et al. [2021] M. Schuld, R. Sweke, and J. J. Meyer, Phys. Rev. A 103, 032430 (2021).