Predicting Coupled Electron and Phonon Transport Using the Steepest-Entropy-Ascent Quantum Thermodynamics Framework
Abstract
The principal paradigm for determining the thermoelectric properties of materials is based on the Boltzmann transport equations (BTEs) or Landauer equivalent. These equations depend on the electron and phonon density of states (e-DOS and p-DOS) derived from ab initio calculations performed using density functional theory and density functional perturbation theory. Recent computational advances have enabled consideration of phonon-phonon and electron-phonon interactions in these calculations. Leveraging these DOS, the single species BTE or Landauer equivalent can ascertain key thermoelectric properties but overlooks the intrinsic coupling between the e-DOS and p-DOS. To account for this, the multispecies BTE paradigm has, despite its substantial computational burden, been utilized, yielding excellent results in agreement with experiment. To alleviate this computational burden, the steepest-entropy-ascent quantum thermodynamic (SEAQT) equation of motion (EOM), which inherently satisfies both the postulates of quantum mechanics and thermodynamics and predicts the evolution of non-equilibrium states, can be used. Employing the e-DOS and p-DOS as input as well as calculated SEAQT electron and phonon relaxation parameter values that are based on ab initio values of relaxation times, group velocities, and effective masses found in the literature, the EOM accurately computes material transport properties, accounting for the e-DOS and p-DOS coupling. It does so at a significantly reduced computational cost across multiple spatial and temporal scales in a single analysis. A succinct overview of the SEAQT framework and its EOM with comparisons of its predictions to measured data for the transport properties of Si, doped Si, and Bi2Te3 is given.
1 Introduction
Predicting the thermal and electrical transport properties through ab initio calculations is crucial to understanding the fundamental physics and thermodynamics governing materials. However, modeling non-equilibrium phenomena, especially in complex material systems with coupled phenomena such as electron-electron, phonon-phonon and electron-phonon coupling poses significant challenges due to the complicated theoretical and heavy computational burdens. Nonetheless, it is precisely these systems that often hold the greatest interest for material applications.
To make such predictions, one needs the densities of states of a material’s electrons (e-DOS) and phonons (p-DOS). These can be determined through calculations using density functional theory (DFT)[24, 25, 13, 19, 23] and density functional perturbation theory (DFPT) [67, 68, 2], respectively. In addition, new codes have emerged enabling the computational assessment of phonon-phonon [36, 38, 37, 69] and electron-phonon interactions [69, 50, 76, 49] on the e-DOS and p-DOS. Leveraging these density of states, the phonon (lattice) thermal conductivity and electron electrical conductivity can be determined from a complete solution of the single-species Boltzmann transport equation (BTE) or equivalent Landauer formalism in combination with Fourier-based Shankland-Koelling-Wood interpolation [36, 38, 37], Wannier function interpolation [50, 76, 49, 51], or Landauer distribution modes [69]. However, such single-species approaches disregard the impact of the coupling between the electron and phonon densities of states on these transport properties. Incorporating this coupling, which involves the non-equilibrium effect of electron drag on phonons and phonon drag on electrons, is essential for attaining a thorough understanding of the underlying physics and thermodynamics.
To tackle this challenge, Protik and Broido [52] successfully developed a fully coupled electron–phonon solution using a set of coupled BTEs to analyze the transport properties of GaAs. Subsequent enhancements by Protik and Kozinsky [53], incorporating fully electron–phonon coupling, were applied to investigate the transport properties of SiC. Further refinements to this methodology were introduced by Protik [54] with their advancements integrated into the code assessible through [55]. In their study [54], the authors detail that the computational effort, including determining the e-DOS and p-DOS and various types of electron and phonon scattering and solving the fully coupled electron–phonon BTEs for Si with an n-type doping concentration of 2.75 x 1014 cm-3 at 300 K, requires approximately 3000 CPU-hr using four nodes each equipped with 28 Intel(R) Xeon(R) CPU E5-2680 v4 2.40 GHz cores. The solution domain for the BTEs encompasses 5050 50 q-meshes and 150150150 k-meshes with a relative convergence threshold set at eV. Comparative analysis against experimental data demonstrates very good agreement [54].
An alternative to this Boltzmann or Landauer paradigm, which addresses the complex theoretical and heavy computational burdens, is that provided by the steepest-entropy-ascent quantum thermodynamic (SEAQT) framework [4, 3, 5, 7, 32, 34, 61]. This framework is based on a unification of quantum mechanics and thermodynamics [15, 16, 17, 18] and the development of a nonlinear equation of motion (EOM) [4, 3, 5, 7, 6] that extends the time-dependent Schrödinger (or von Neumann) EOM into the realm of irreversible thermodynamic phenomena. The SEAQT EOM, which is based on a gradient dynamic of entropy in state space constrained by the energy, particle number, etc., is guided by the principle of SEA at each instant of time and, therefore, obviates the need for an assumption of the kinetic mechanisms involved. This aspect contributes to the generality and versatility of this approach. In fact, the SEA principle has recently been proposed by Beretta as a fourth law of thermodynamics [8]. In addition, based on the foundational work of Beretta [4, 3, 5, 7] and Li and von Spakovsky [4, 29, 31], the SEAQT EOM has been validated and practically applied across multiple spatial and temporal scales to model the non-equilibrium behavior of a variety of quantum and classical systems [9, 44, 11, 43, 46, 64, 65, 57, 56, 45, 40, 42, 41, 75, 39, 14, 73, 72, 74, 26, 71, 35, 27, 33, 62].
By leveraging the e-DOS and p-DOS obtained through calculations for a given material, the SEAQT EOM accounts for the coupled electron-phonon non-equilibrium behavior, enabling predictions of both thermal and electrical transport properties. To scale these results, SEAQT electron and phonon relaxation parameters are calculated based on ab initio values for the eigenenergies, effective masses, group velocities, and relaxation times. Experimental instead of ab initio values could also be used. Further details of the theoretical basis for the SEAQT relaxation parameters can be found in [34] and in Section 2.3 below.
As demonstrated in the following sections, these predictions align well with experimental observations. One key advantage of this method is that the EOM, rooted in the SEA principle and satisfying the postulates of both quantum mechanics and thermodynamics, consists of first-order ordinary differential equations in time, which require minimal computational overhead. Detailed analysis reveals (see Table 1) that determining the e-DOS and p-DOS and solving the SEAQT EOM for undoped Si at 300 K takes approximately 36.5 CPU-hr on a single node equipped with an AMD EPYC 7702 chip and 128 cores. Nearly all of this time (98.6%) is devoted to determining the density of states via DFT and DFPT. Furthermore, predicting the transport properties for 16 different temperatures requires only about 44 CPU-hr since the established DOS need not be recalculated for each temperature.
| e-DOS | p-DOS |
|---|---|
| 32 CPU hr | 4 CPU hr |
| SEAQT with e-p coupling at 300 K | SEAQT with e-p coupling for 16 T’s between 250 K and 1000 K |
| 30 CPU min | 8 CPU hr |
The SEAQT EOM also offers a versatile tool for studying the dynamics of a network of local non-equilibrium systems. This enables the modeling of intricate material structures, including defects and interfaces across various spatial and temporal scales within a single analysis. Coupled with the hypoequilibrium concept [32, 29, 31, 30, 28], the SEAQT framework facilitates the generalization of the Onsager relations and the extension of the thermodynamic equilibrium descriptions of intensive properties (such as temperature, pressure, and chemical potential), the Gibbs relation, etc. to the entire non-equilibrium realm.
The subsequent sections offer a concise introduction to the SEAQT framework and its EOM. This is followed by a description of its implementation in our SEAMater code [60] and its application to predicting the transport properties of Si and doped Si in time and with temperature. Comprehensive comparisons with experimental data are presented, along with an examination of the outcomes. The discussion concludes with some closing reflections.
2 SEAQT Framework
The following section details the background of the SEAQT framework, covering the equation of motion and energy eigenstructure, which consists of the the desnity of states of the material, i.e., the discrete eigenenergy spectrum and the degeneracies associated with each of the energy eigenlevels. The development presented here is based on that given in [7, 32, 34, 15, 16].
2.1 SEAQT Equation of Motion
The equation of motion of the SEAQT framework moves through thermodynamic state space (e.g., Hilbert space) where there are single-particle energy eigenlevels that can be occupied by particles. A system eigenstate is denoted by nanb…nm⟩ where nk is the occupation number and the energy of the single particle energy eigenlevel. For fermions, has a value of 0 or 1, and for bosons, a value between 0 and . A system thermodynamic state is selected from the Hilbert space spanned by the system eigenstates and can be represented by a -dimensional vector where represents the probability that particles are observed at the single-particle energy eigenlevel. The system thermodynamic state can alternatively be denoted by , which is the square root of the probability vector given by:
| (1) |
-space is then defined as a manifold in Hilbert space whose elements are all of the vectors of the real finite numbers and with an inner product expressed as
| (2) |
Each system property is then defined by a functional and its functional derivative by .
The time evolution of the thermodynamic state obeys the following -vector form of the equation of motion:
| (3) |
where is an element of the manifold used to describe the local production densities associated with the balance equations for the entropy and the conserved quantities and is derived from the SEA principle subject to a set of conservation laws denoted by . In this particular development, these include the conservation of energy, , and of particle number, , as well as probability normalization conditions . Using Eq. (2), the time evolution of the system entropy and the conserved system properties must satisfy the following set of equations:
| (4) |
with and
| (5) |
with where and are functional derivatives of the system properties defined by Eqs. (A1) to (A4) of Appendix A of Li, von Spakovsky, and Hin [34].
The time evolution of a system state is a unique trajectory in thermodynamic state space that obeys the SEA principle. This corresponds to a variational problem that finds the instantaneous “direction” of that maximizes the rate of entropy production consistent with the conservation constraints . This requires the state space to have a metric field with which to determine the norm of and the distance traveled during the evolution of state. The differential of this distance is then expressed as
| (6) |
where is a real, symmetric, positive-definite operator on the manifold [7, 32, 34, 29, 31] that is chosen here to be the identity operator. This choice corresponds to the Fisher-Rao metric. The SEA variational problem then consists of maximizing subject to the conservation constraints and the additional constraint , which ensures that the norm of remains constant. Here, is some small constant. To find the solution, the method of Lagrange multipliers is used such that
| (7) |
where the and are the Lagrange multipliers. The variational derivative of with respect to is now set equal to zero so that
| (8) |
Solving this last equation for yields the SEA equation of motion, i.e.,
| (9) |
In this last expression, is assumed to be a diagonal operator. The diagonal terms of for fermions and for bosons} are associated with the relaxation parameters of the system single-particle eigenlevels such that
| (10) |
The values of the Lagrange multipliers are determined by substituting Eq. (9) into Eq. (5) yielding
| (11) |
where the are proportional to the measurements of non-equilibrium system intensive properties such as temperature, pressure, and chemical potential [31].
Now, substituting the functional derivatives of the system properties as defined in Appendix A of Li, von Spakovsky, and Hin [34], the equations of motion for the and the of the single-particle energy eigenlevels are expressed as
| (12) | |||||
| (13) | |||||
where , , and are the Lagrange multipliers corresponding, respectively, to the generators of the motion , , and , while is the single-particle eigenlevel index and the occupation number at that level.
2.2 Hypoequilibrium concept
In [32, 29, 31], Li and von Spakovsky introduce the hypoequilibrium concept to simplify the presentation of the equation of motion and facilitate physically interpreting the state evolution. Without significant loss in generality, the assumption is made that the particles in the same single-particle energy eigenlevel initially are in mutual stable equilibrium relative to the temperature and the chemical potential . As a result, the initial probability distribution of the occupation states is Maxwelliam, i.e.,
| (14) |
where , , and
| (15) |
Such an initial state is an -order hypoequilibrium state where is the total number of eigenlevels.
An additional assumption made is that the different occupation states of the same single-particle eigenlevel have the same relaxation parameter so that
| (16) |
This makes each relaxation parameter a property of a particular single-particle eigenlevel.
As is proven in [34], with these two assumptions, the equation of motion, Eq. (13), maintains the state of the system in a hypoequilibrium state throughout the entire time evolution. As a result, the evolution can be found from the motion of the state of a single-particle eigenlevel using the following equation of motion found by substituting Eq. (14) into (13):
| (17) |
where
| (18) |
Now, multiplying Eq. (13) by the extensive value of the particle number, , and integrating over and doing likewise with the extensive values for the energy, , and the entropy, , the following equations capture the contributions to these properties from a single-particle energy eigenlevel:
| (19) |
| (20) |
| (21) |
where , which is the particle number fluctuation of the single-particle energy eigenlevel, is given by
| (22) | |||||
Here, fermions are represented with the plus sign and bosons with the negative.
2.3 Electron transport equation
For the transport of electrons between two locations (subsystems) and , the single-particle energy eigenlevels involved are those of , , and , . Integrating Eq. (19) over the eigenlevels at location results in
| (23) | |||||
In this last expression, is the volume of subsystem and the DOS per unit volume of . In the near-equilibrium region, both subsystems and are approximately in stable equilibrium and as a result, and so that Eq. (23) can be rewritten as
| (24) |
A similar development holds for .
This near-equilibrium assumption allows use of the zeroth-order approximation of the terms inside the integrals, leaving only the first-order approximation of . Thus, it is assumed that and have the same energy eigenstructure and DOS so that
| (25) |
| (26) |
and the fluctuations of subsystems and are approximately equal to their mutual equilibrium value at , i.e.,
| (27) |
Now, using these last three conditions and particle conservation, the flow from to is given by
Furthermore, defining where , the total particle flux to , , can be written as
| (29) |
where is the interface cross-sectional area between subsystems and . Introducing the following variational relation for every energy eigenlevel:
| (30) |
where is the distance between locations and , the total flux can be reformulated as
| (31) |
If initially the system is in a hypoequilibrium state, the fluctuation can be related to the Fermi distribution by
| (32) |
and as a result, the particle flux becomes
where , is the electric charge, the electric field potential, the fermi level without an external field, the differential chemical potential, and the external field.
As shown in Ref [34], Eq. (LABEL:eq:33), which results from the SEAQT equation of motion, recovers the Boltzmann transport equation (BTE) [70] in the low-field region even though the former operates in state space and the latter in phase space. As a result, the SEAQT and BTE relaxation parameters and , respectively, can be related via the following relation:
| (34) |
Here, is the particle mass and a group or particle velocity.
2.4 Phonon transport equation
The derivation of the SEAQT equation for phonon transport is similar to that for electron transport except that there is no particle number operator. Thus, the conservation laws only involve the energy and the probabilities such that . As was the case for the electrons, the hypoequilibrium concept is used for the initial states so that the time evolution of the energy at location (subsystem) is given by
| (35) |
Again, as before, in the near-equilibrium region, and and Eqs. (25) to (27) hold so that the energy flow from to is written as

The fluctuation in this case is based on the boson distribution so that in terms of the Fermi distribution,
| (37) |
and the energy flux is expressed as
| (38) | |||||
where it is noted that for convenience the argument of the integral has been converted from the energy to the frequency domain. The relaxation parameter is again chosen based on Eq. (34).
2.5 Electron-Phonon Coupling
As indicated earlier and shown in [34], the BTE in the low-field limit can be recovered from the SEAQT framework via Eq. (LABEL:eq:33). In a similar fashion, the two-temperature model (TTM) of electron-phonon coupling given, for example, in [70] can be derived from the SEAQT framework as a special case as shown in [31]. Although that development is not presented here, the result is given by the following two equations of motion for and , which are inversely proportional to the electron and phonon temperatures, respectively:
| (39) |
| (40) |
Here and are the relaxation parameters for the electrons and phonons, respectively, and (see [34]) is a function of the energy, entropy, and particle fluctuations in the local electron and phonon subsystems that make up a network of such subsystems as shown in Fig. 1. The first term on the right of the equals in each expression is the heat diffusion, while the second accounts for the phonon-electron coupling.
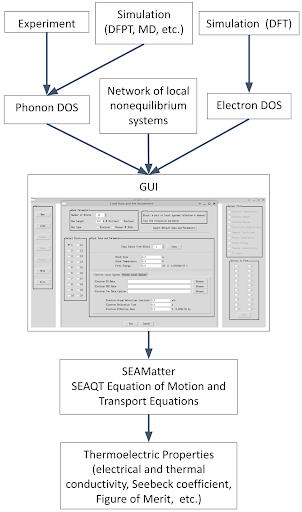
Clearly, these equations, as was the case with the BTE, are limited to the near-equilibrium region. To cover the entire non-equilibrium region, even that far from equilibrium, one must return to the equations of motion, Eqs. (12) and (13), from which the TTM and BTE are derived. It is, in fact, these more general equations, which are used with the network of local subsystems seen in Fig. 1 to determine the electrical and thermal transport properties of the semiconductor materials modeled here. However, before discussing this, we define in the next sections our transport properties and briefly describe the methods used to obtain our energy eigenstructures.
2.6 Transport Properties
The electrical conductivity is defined based on Eq. (LABEL:eq:33) as
| (41) |
where the BTE relaxation parameter, , is related to the SEAQT relaxation parameter, , via Eq. (34), , and the Fermi distribution is that for fermions given in Eq. (32).
The thermal conductivity is expressed as
| (42) |
where the specific heat per unit frequency, , is given by
| (43) |
and is Planck’s modified constant. To determine the electron contribution, the Fermi distribution for fermions (Eq. (32)) is used, while for the phonon contribution, the distribution for bosons (Eq. (37)) is employed. Note that the temperature is either the electron or the phonon temperature.
As to the Seebeck coefficient, it is given by
| (44) |
Here is the chemical potential and the average of the electron and phonon temperatures.
a
)
 b)
b)
Finally, the figure of merit, , which is used to define the performance of semiconductors for thermoelectric applications, is written as
| (45) |
3 SEAQT Implementation and Input Data
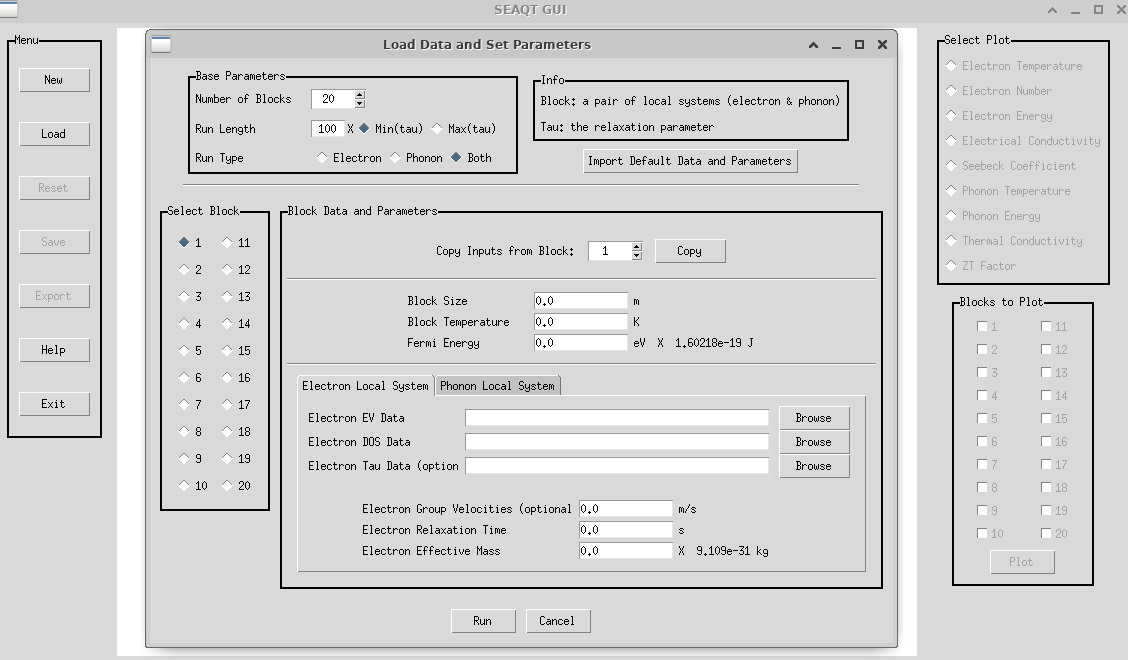
The SEAMatter code, implemented in MATLAB R2021a and Python 3.6, utilizes MATLAB as the primary backend for solving the SEAQT equation of motion with the ODE45 solver [21]. The workflow of the SEAQT concept and SEAMater code are depicted in Fig. 2. The energy eigenstructures for both phonons and electrons can be obtained via experimental or simulation methods. In addition, accurate determination of the phonon relaxation parameter and phonon velocity is essential for reliable results.
In this work, the electron energy eigenstructure, represented by the e-DOS, is determined using density functional theory (DFT) with VASP. The Local Density Approximation (LDA) pseudo-potential for cell relaxation and the additional hybrid functional HSE06 for static band structure calculations is employed. The hybrid functional is utilized to account for the common small band gap problem observed in semiconductor materials using DFT methods. The phonon energy eigenstructure is calculated using DFPT along with the post-processing phonon calculation code phonopy [68]. The input data for the Si e-DOS and p-DOS along with the relaxation parameters is provided in .
Additional necessary inputs come from the network of local non-equilibrium subsystems, shown in Fig. 1, that describes the number of such subsystems and their respective sizes. These inputs are then fed into the SEAMater code via the GUI after which the thermoelectric property predictions are made. Although the most optimized approach involves utilizing both the e-DOS and p-DOS, calculations using only one type of DOS can still be made, providing inherent material properties specific to either electrons or phonons only.
To compute the total rate of change of energy and mass within a given local subsystem, the energy and mass exchanges with neighboring local subsystems at each instant of time must be determined. For example (see Fig. 1), Electron-2 interfaces with three neighbors: Electron-1, Electron-3, and Phonon-2. Calculating the mass and energy transfers from Electron-1 to Electron-2 involves applying the SEAQT equations of motion, Eqs. (19) and (20), to a composite system comprised of the Electron-1 and Electron-2 subsystems under specific constraints. This composite system constitutes a hypo-equilibrium description of -order, where represents the number of eigenlevels in Electron-1 and the number in Electron-2. The mass and energy transfers result from the relaxation of this non-equilibrium composite system. Electron-electron transport is resolved subject to the constraints on , phonon-phonon transport to the constraints on , and phonon-electron transport to the constraints on . In the latter case, represents the contributions from both the electrons and phonons. This process is repeated for other pairings with Electron-3 and Phonon-2, resulting in the total rate of energy and mass change of Electron-2. By employing this method, the energy and mass exchanges in all local subsystems are determined.
4 Results
Results are presented for the electrical and thermal conductivities, the Seebeck coefficient, and the figure of merit for both Si and doped Si. The calculated SEAQT electron and phonon relaxation parameter values used for these results are provided in Supplementary Materials. In addition, supplementary materials demonstrate SEAQT’s ability to predict the properties of anisotropic materials, as evidenced by the results obtained for Bi2Te3 given in the Supplementary Materials.
4.1 Semiconductor Investigation
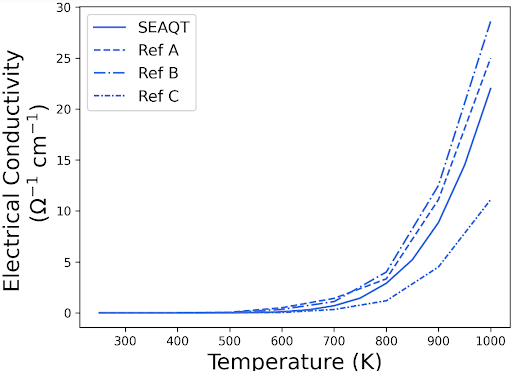
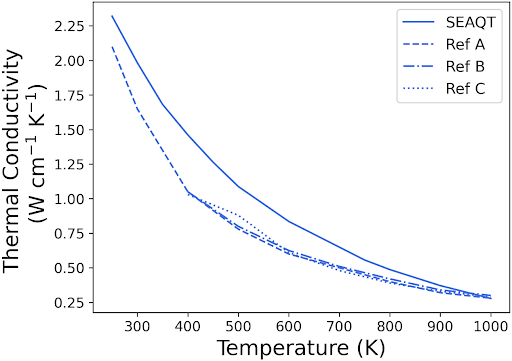
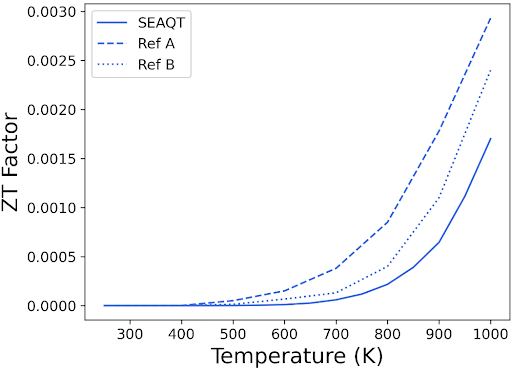
Figure 3 demonstrates that the SEAQT predictions closely match the values and trends observed in various experimental studies [10, 12, 58] for the electrical and thermal conductivities, Seebeck coefficient, and figure of merit of Si. While there are some discrepancies, particularly in thermal conductivity and factor, these differences potentially stem from crystal defects inherent in the fabrication process, affecting phonon velocities and lifetimes and, consequently, reducing the thermal conductivity. Since the SEAQT simulations are based on a perfect Si crystal structure, the calculated thermal conductivity tends to be higher than the experimental values. However, such point and extended defects can be accommodated by the SEAQT framework by obtaining the e-DOS and p-DOS and modified relaxation parameters and group velocities of the specific materials with said defects via experimental methods or DFT, DFPT or molecular dynamics. This will be described in a followup paper.
a)
 b)
b)
 c)
c)
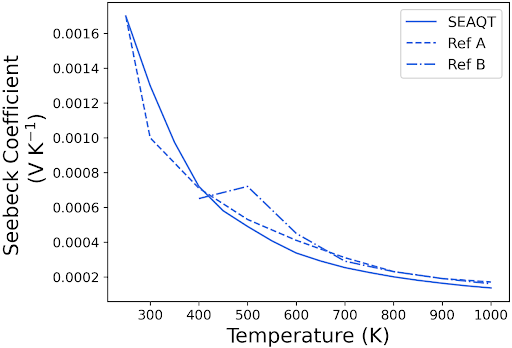 d)
d)
4.2 Doped Si
Extrinsic Si semiconductors are investigated within the SEAQT framework with either Boron (p-type) or Phosphorous (n-type) doping elements. Doping can also emanate from charged vacancies, although their concentration typically has minimal impact on semiconductor electrical properties compared to doping elements [20]. Doping elements are employed to boost electrical conductivity at lower temperatures, which is achieved either by augmenting the electron concentration in the conduction band (n-type doping), leading to a rise in the Fermi level, or by introducing holes in the valence band (p-type doping), resulting in a decrease in the Fermi level [20]. It is posited here that Si doping levels insignificantly affect the electron DOS but can be taken into account by altering the Fermi level, a crucial step in modeling the modified transport properties of doped Si within the SEAQT framework. This is done using the techniques outlined in Refs. [37, 59]. The chosen doping levels are informed by experimental n- and p-type doping levels for comparative analysis with predicted outcomes [48]. The principal alteration in phonon transport properties arises from variations in phonon relaxation due to additional scattering by impurities, free electrons/holes, and bound electrons/holes. This can be taken into account without substantial adjustments to the phonon DOS [1]. Calculated phonon relaxation parameters are tabulated and provided in the Supplementary Materials in Table S1 [1].
a)
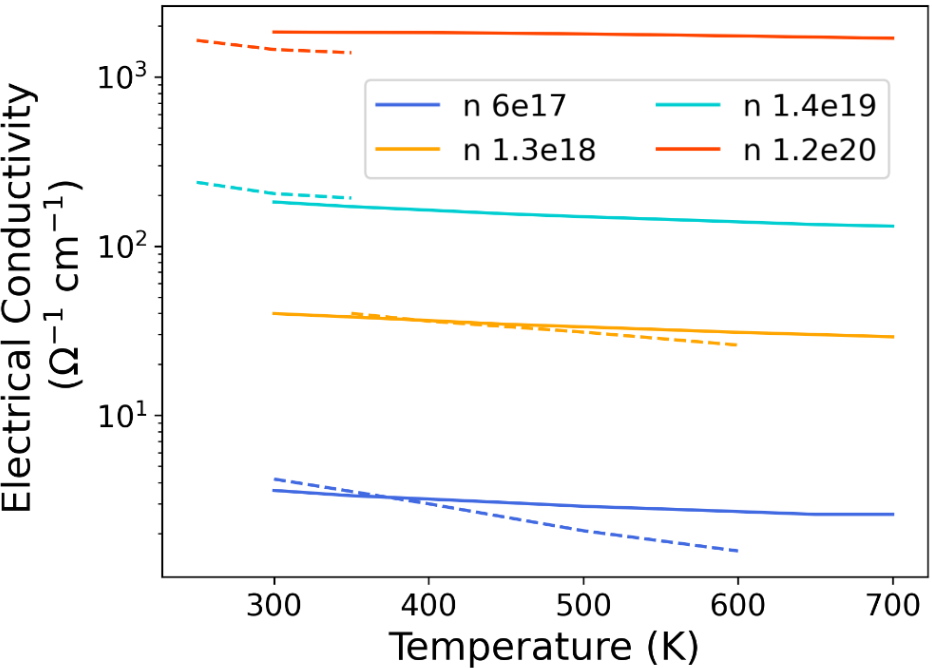 b)
b)
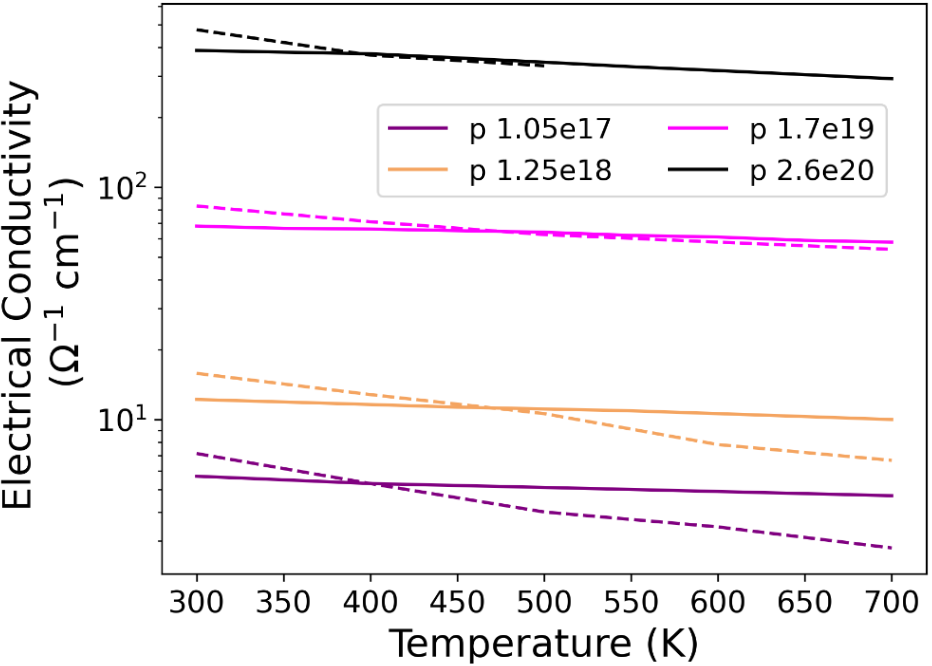
c)
 d)
d)
e)
 f)
f)
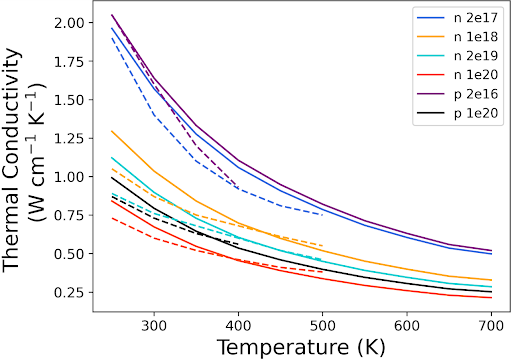
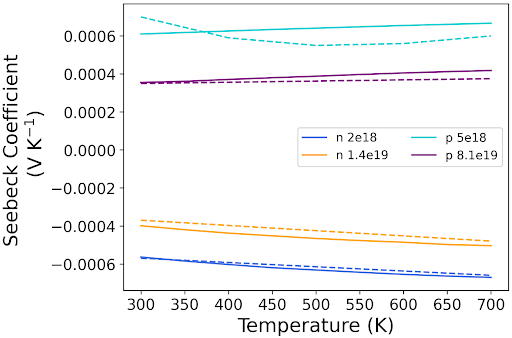
As depicted in Figs. 4a), b), and d), the predicted SEAQT values for the electrical conductivity and Seebeck coefficient align well with experimental results, demonstrating an increase in electrical conductivity with increased doping, a decrease in the absolute Seebeck coefficient with increased doping, and the expected trends for increasing temperature. SEAQT predictions for thermal conductivity, encompassing contributions from both electrons and phonons, are illustrated in Fig. 4c. The SEAQT results for n-doping with Phosphorus and p-doping with Boron closely mirror experimental values, with the most notable deviation occurring for the case of the smallest n-doping. The thermal conductivity for the doped Si consists of a phonon contribution, and an electron contribution, such that the total thermal conductivity . is proportional to the electrical conductivity, , via the Lorentz number such that
| (46) |
where T is the temperature and L the Lorentz number that ranges approximately from 2.4×10-8 for degenerate semiconductors to 1.5×10-8 for non-degenerate semiconductors [22, 66].
As is evident from this last equation, at lower electrical conductivities, the electron contribution to the total thermal conductivity remains minimal but escalates with higher doping levels corresponding to increased electrical conductivity. Fig. 5 illustrates that while higher doping leads to enhanced electrical conductivity, the increment is insufficient to significantly influence the total thermal conductivity of doped Si.
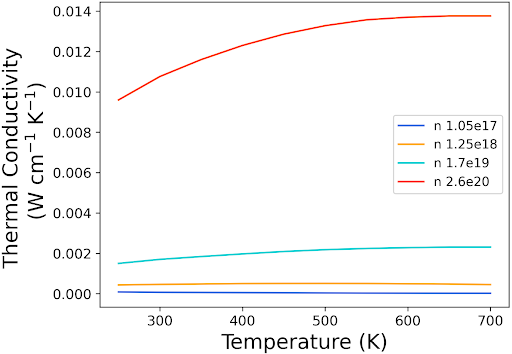
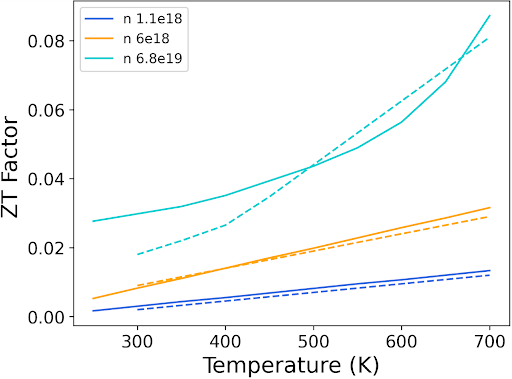
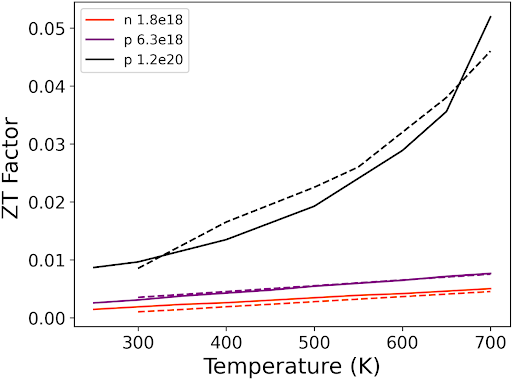
Finally, there are minor disparities between the thermal conductivity results obtained from SEAQT and the experimental data, with the SEAQT values being slightly higher. This could potentially stem from adjustments in the relaxation parameter or the exclusion of other defects such as dislocations in the experimental samples, which would impact the thermal conductivity. Despite these slight differences, the SEAQT ZT factor closely matches experimental data across all doping levels. Moreover, the electron contribution to the total thermal conductivity of a conventional semiconductor like Si is small. This is not the case for narrow-bandgap semiconductors like Bi2Te3. The SEAQT results obtained for Bi2Te3 given in the Supplementary Materials clearly demonstrate this.
5 Conclusions
The SEAQT framework is an effective approach for accurately predicting the transport properties of semiconductor materials. SEAQT takes into account electron and phonon energy eigenstructures to determine material transport properties. Furthermore, this framework inherently satisfies the laws of quantum mechanics and thermodynamics, utilizing an equation of motion to determine unique non-equilibrium thermodynamic paths through Hilbert space and is able to cross several spatial and temporal scales in a single analysis.
The SEAQT framework, which has been used to accurately determine the transport properties of Si and doped Si (as well as Bi2Te3 in the Supplementary Materials), provides results similar to those found with current computational methods but does so with a significantly reduced computational burden. The robustness of the SEAQT framework is such that it can be applied to a multitude of systems and can be used to analyze the effect of defect structures and thermoelectric breakdown. This is left for future work.
Acknowledgements
The authors would like to thank Virginia Tech’s Advanced Research Computing Center (ARC) for the use of its high-performance supercomputing clusters. The lead author would also like to thank the Nuclear Regulatory Commission (NRC) for its financial support (grant number 31310019M0045) and the support with internal funds provided by the second author and by the Virginia Tech College of Engineering.
Data Availability
The underlying code for this study is not publicly available but may be made available to qualified researchers on reasonable request from the corresponding author.
References
- [1] M. Asheghi, K. Kurabayashi, R. Kasnavi and K.. Goodson “Thermal conduction in doped single-crystal silicon films” In Journal of Applied Physics 91.8, 2002, pp. 5079–5088 DOI: 10.1063/1.1458057
- [2] Stefano Baroni, Stefano Gironcoli, Andrea Dal Corso and Paolo Giannozzi “Phonons and related crystal properties from density-functional perturbation theory” Publisher: American Physical Society In Reviews of Modern Physics 73.2, 2001, pp. 515–562 DOI: 10.1103/RevModPhys.73.515
- [3] G.. Beretta, E.. Gyftopoulos and J.. Park “Quantum thermodynamics. A new equation of motion for a general quantum system” Number: 1 In Il Nuovo Cimento B Series 11 87.1, 1985, pp. 77–97 DOI: 10.1007/BF02729244
- [4] G.. Beretta, E.. Gyftopoulos, J.. Park and G.. Hatsopoulos “Quantum thermodynamics. A new equation of motion for a single constituent of matter” In Il Nuovo Cimento B Series 11 82.2, 1984, pp. 169–191 DOI: 10.1007/BF02732871
- [5] Gian Paolo Beretta “Nonlinear quantum evolution equations to model irreversible adiabatic relaxation with maximal entropy production and other nonunitary processes” In Reports on Mathematical Physics 64.1-2, 2009, pp. 139–168 DOI: 10.1016/S0034-4877(09)90024-6
- [6] Gian Paolo Beretta “On the general equation of motion of quantum thermodynamics and the distinction between quantal and nonquantal uncertainties” PhD Thesis. Massachusetts Institute of Technology, 1981
- [7] Gian Paolo Beretta “Steepest entropy ascent model for far-nonequilibrium thermodynamics: Unified implementation of the maximum entropy production principle” Number: 4 In Physical Review E 90.4, 2014, pp. 042113 DOI: 10.1103/PhysRevE.90.042113
- [8] Gian Paolo Beretta “The fourth law of thermodynamics: steepest entropy ascent” In Philos. Trans. R. Soc. A 378.2170, 2020, pp. 20190168 DOI: 10.1098/rsta.2019.0168
- [9] Sergio Cano-Andrade, Gian Paolo Beretta and Michael R. Spakovsky “Steepest-entropy-ascent quantum thermodynamic modeling of decoherence in two different microscopic composite systems” Number: 1 In Physical Review A 91.1, 2015, pp. 013848 DOI: 10.1103/PhysRevA.91.013848
- [10] Lois D’abbadie “Enhancement of the figure of merit of silicon germanium thin films for thermoelectric applications” PhD Thesis. UNSW Sydney, 2013
- [11] Cesar Damian, Robert Holladay, Adriana Saldana and Michael Spakovsky “Modeling the effects of perturbations and steepest entropy ascent on the time evolution of entanglement” Version Number: 2, 2024 DOI: 10.48550/ARXIV.2404.05473
- [12] W. Fulkerson et al. “Thermal Conductivity, Electrical Resistivity, and Seebeck Coefficient of Silicon from 100 to 1300°K” In Physical Review 167.3, 1968, pp. 765–782 DOI: 10.1103/PhysRev.167.765
- [13] M. Gajdoš et al. “Linear optical properties in the projector-augmented wave methodology” Publisher: American Physical Society In Physical Review B 73.4, 2006, pp. 045112 DOI: 10.1103/PhysRevB.73.045112
- [14] Ishan Goswami, Robert Bielitz, Scott S. Verbridge and Michael R. Spakovsky “A thermodynamic scaling law for electrically perturbed lipid membranes: Validation with steepest entropy ascent framework” In Bioelectrochemistry (Amsterdam, Netherlands) 140, 2021, pp. 107800 DOI: 10.1016/j.bioelechem.2021.107800
- [15] George N. Hatsopoulos and Elias P. Gyftopoulos “A unified quantum theory of mechanics and thermodynamics. Part I. Postulates” In Foundations of Physics 6.1, 1976, pp. 15–31 DOI: 10.1007/BF00708660
- [16] George N. Hatsopoulos and Elias P. Gyftopoulos “A unified quantum theory of mechanics and thermodynamics. Part IIa. Available energy” In Foundations of Physics 6.2, 1976, pp. 127–141 DOI: 10.1007/BF00708955
- [17] George N. Hatsopoulos and Elias P. Gyftopoulos “A unified quantum theory of mechanics and thermodynamics. Part IIb. Stable equilibrium states” In Foundations of Physics 6.4, 1976, pp. 439–455 DOI: 10.1007/BF00715033
- [18] George N. Hatsopoulos and Elias P. Gyftopoulos “A unified quantum theory of mechanics and thermodynamics. Part III. Irreducible quantal dispersions” In Foundations of Physics 6.5, 1976, pp. 561–570 DOI: 10.1007/BF00715108
- [19] P. Hohenberg and W. Kohn “Inhomogeneous Electron Gas” Publisher: American Physical Society In Physical Review 136.3B, 1964, pp. B864–B871 DOI: 10.1103/PhysRev.136.B864
- [20] Wm.G. Hoover “Nonequilibrium molecular dynamics” In Nuclear Physics A 545.1-2, 1992, pp. 523–536 DOI: 10.1016/0375-9474(92)90490-B
- [21] The MathWorks Inc. “MATLAB version: (R2021a)” The MathWorks Inc., 2021 URL: https://www.mathworks.com
- [22] Hyun-Sik Kim et al. “Characterization of Lorenz number with Seebeck coefficient measurement” In APL Materials 3.4, 2015, pp. 041506 DOI: 10.1063/1.4908244
- [23] W. Kohn and L.. Sham “Self-Consistent Equations Including Exchange and Correlation Effects” Publisher: American Physical Society In Physical Review 140.4A, 1965, pp. A1133–A1138 DOI: 10.1103/PhysRev.140.A1133
- [24] G. Kresse and J. Furthmüller “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set” In Computational Materials Science 6.1, 1996, pp. 15–50 DOI: 10.1016/0927-0256(96)00008-0
- [25] G. Kresse and D. Joubert “From ultrasoft pseudopotentials to the projector augmented-wave method” Publisher: American Physical Society In Physical Review B 59.3, 1999, pp. 1758–1775 DOI: 10.1103/PhysRevB.59.1758
- [26] Akira Kusaba et al. “CH4 Adsorption Probability on GaN(0001) and (000-1) during Metalorganic Vapor Phase Epitaxy and Its Relationship to Carbon Contamination in the Films” Number: 6 In Materials 12.6, 2019, pp. 972 DOI: 10.3390/ma12060972
- [27] Akira Kusaba et al. “Modeling the Non-Equilibrium Process of the Chemical Adsorption of Ammonia on GaN(0001) Reconstructed Surfaces Based on Steepest-Entropy-Ascent Quantum Thermodynamics” Number: 8 In Materials 10.8, 2017, pp. 948 DOI: 10.3390/ma10080948
- [28] Guanchen Li, Omar Al-Abbasi and Michael R Spakovsky “Atomistic-level non-equilibrium model for chemically reactive systems based on steepest-entropy-ascent quantum thermodynamics” In Journal of Physics: Conference Series 538, 2014, pp. 012013 DOI: 10.1088/1742-6596/538/1/012013
- [29] Guanchen Li and Michael R. Spakovsky “Generalized thermodynamic relations for a system experiencing heat and mass diffusion in the far-from-equilibrium realm based on steepest entropy ascent” Number: 3 In Physical Review E 94.3, 2016, pp. 032117 DOI: 10.1103/PhysRevE.94.032117
- [30] Guanchen Li and Michael R. Spakovsky “Modeling the nonequilibrium effects in a nonquasi-equilibrium thermodynamic cycle based on steepest entropy ascent and an isothermal-isobaric ensemble” In Energy 115, 2016, pp. 498–512 DOI: 10.1016/j.energy.2016.09.010
- [31] Guanchen Li and Michael R. Spakovsky “Steepest-entropy-ascent model of mesoscopic quantum systems far from equilibrium along with generalized thermodynamic definitions of measurement and reservoir” In Physical Review E 98.4, 2018, pp. 042113 DOI: 10.1103/PhysRevE.98.042113
- [32] Guanchen Li and Michael R. Spakovsky “Steepest-entropy-ascent quantum thermodynamic modeling of the relaxation process of isolated chemically reactive systems using density of states and the concept of hypoequilibrium state” In Physical Review E 93.1, 2016, pp. 012137 DOI: 10.1103/PhysRevE.93.012137
- [33] Guanchen Li and Michael R. Spakovsky “Study of Nonequilibrium Size and Concentration Effects on the Heat and Mass Diffusion of Indistinguishable Particles Using Steepest-Entropy-Ascent Quantum Thermodynamics” Number: 12 In Journal of Heat Transfer 139.12, 2017, pp. 122003 DOI: 10.1115/1.4036735
- [34] Guanchen Li, Michael R. Spakovsky and Celine Hin “Steepest entropy ascent quantum thermodynamic model of electron and phonon transport” Number: 2 In Physical Review B 97.2, 2018, pp. 024308 DOI: 10.1103/PhysRevB.97.024308
- [35] Guanchen Li, Michael R. Spakovsky, Fengyu Shen and Kathy Lu “Multiscale Transient and Steady-State Study of the Influence of Microstructure Degradation and Chromium Oxide Poisoning on Solid Oxide Fuel Cell Cathode Performance” Number: 1 In Journal of Non-Equilibrium Thermodynamics 43.1, 2018, pp. 21–42 DOI: 10.1515/jnet-2017-0013
- [36] Wu Li, Jesús Carrete, Nebil A. and Natalio Mingo “ShengBTE: A solver of the Boltzmann transport equation for phonons” In Computer Physics Communications 185.6, 2014, pp. 1747–1758 DOI: 10.1016/j.cpc.2014.02.015
- [37] Georg K.H. Madsen, Jesús Carrete and Matthieu J. Verstraete “BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients” In Computer Physics Communications 231, 2018, pp. 140–145 DOI: 10.1016/j.cpc.2018.05.010
- [38] Georg K.H. Madsen and David J. Singh “BoltzTraP. A code for calculating band-structure dependent quantities” In Computer Physics Communications 175.1, 2006, pp. 67–71 DOI: 10.1016/j.cpc.2006.03.007
- [39] Jared McDonald, Michael R. Spakovsky and William T. Reynolds “Entropy-driven microstructure evolution predicted with the steepest-entropy-ascent quantum thermodynamic framework” In Acta Materialia 237, 2022, pp. 118163 DOI: 10.1016/j.actamat.2022.118163
- [40] Jared McDonald, Michael R. Spakovsky and William T. Reynolds “Predicting Ion Sequestration in Charged Polymers with the Steepest-Entropy-Ascent Quantum Thermodynamic Framework” Number: 5 Publisher: Multidisciplinary Digital Publishing Institute In Nanomaterials 14.5, 2024, pp. 458 DOI: 10.3390/nano14050458
- [41] Jared McDonald, Michael R. Spakovsky and William T. Reynolds “Predicting non-equilibrium folding behavior of polymer chains using the steepest-entropy-ascent quantum thermodynamic framework” Number: 10 Publisher: American Institute of Physics In The Journal of Chemical Physics 158.10, 2023, pp. 104904 DOI: 10.1063/5.0137444
- [42] Jared McDonald, Michael R. Spakovsky and William T. Reynolds “Predicting Polymer Brush Behavior in Solvents Using the Steepest-Entropy-Ascent Quantum Thermodynamic Framework” In The Journal of Physical Chemistry B 127.48, 2023, pp. 10370–10391 DOI: 10.1021/acs.jpcb.3c02713
- [43] J.. Montañez-Barrera, Michael R. Spakovsky, Cesar E. Damian Ascencio and Sergio Cano-Andrade “Decoherence predictions in a superconducting quantum processor using the steepest-entropy-ascent quantum thermodynamics framework” Number: 3 In Physical Review A 106.3, 2022, pp. 032426 DOI: 10.1103/PhysRevA.106.032426
- [44] J.. Montañez-Barrera, Cesar E. Damian-Ascencio, Michael R. Spakovsky and Sergio Cano-Andrade “Loss-of-entanglement prediction of a controlled-phase gate in the framework of steepest-entropy-ascent quantum thermodynamics” Number: 5 In Physical Review A 101.5, 2020, pp. 052336 DOI: 10.1103/PhysRevA.101.052336
- [45] Tenpei Morishita, Kiyoshi Kobayashi and Akira Ishikawa “Quantum Nano-system Dynamics Based on the Steepest-Entropy-Ascent Quantum Thermodynamics” Publisher: The Physical Society of Japan In Journal of the Physical Society of Japan 92.2, 2023, pp. 024001 DOI: 10.7566/JPSJ.92.024001
- [46] Tenpei Morishita, Kiyoshi Kobayashi and Akira Ishikawa “Relaxation dynamics of nonresonant excitation transfer processes assisted by coherent phonon environment” Publisher: IOP Publishing In Japanese Journal of Applied Physics 62.10, 2023, pp. 102005 DOI: 10.35848/1347-4065/acfcfa
- [47] Yuji Ohishi et al. “Thermoelectric properties of heavily boron- and phosphorus-doped silicon” Publisher: IOP Publishing In Japanese Journal of Applied Physics 54.7, 2015, pp. 071301 DOI: 10.7567/JJAP.54.071301
- [48] G.. Pearson and J. Bardeen “Electrical Properties of Pure Silicon and Silicon Alloys Containing Boron and Phosphorus” In Physical Review 75.5, 1949, pp. 865–883 DOI: 10.1103/PhysRev.75.865
- [49] Giovanni Pizzi et al. “BoltzWann: A code for the evaluation of thermoelectric and electronic transport properties with a maximally-localized Wannier functions basis” In Computer Physics Communications 185.1, 2014, pp. 422–429 DOI: 10.1016/j.cpc.2013.09.015
- [50] S. Poncé, E.. Margine, C. Verdi and F. Giustino “EPW: Electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions” In Computer Physics Communications 209, 2016, pp. 116–133 DOI: 10.1016/j.cpc.2016.07.028
- [51] Samuel Poncé, Elena R. Margine and Feliciano Giustino “Towards predictive many-body calculations of phonon-limited carrier mobilities in semiconductors” Publisher: American Physical Society In Physical Review B 97.12, 2018, pp. 121201 DOI: 10.1103/PhysRevB.97.121201
- [52] Nakib H. Protik and David A. Broido “Coupled transport of phonons and carriers in semiconductors: A case study of n-doped GaAs” Publisher: American Physical Society In Physical Review B 101.7, 2020, pp. 075202 DOI: 10.1103/PhysRevB.101.075202
- [53] Nakib H. Protik and Boris Kozinsky “Electron-phonon drag enhancement of transport properties from a fully coupled ab initio Boltzmann formalism” Publisher: American Physical Society In Physical Review B 102.24, 2020, pp. 245202 DOI: 10.1103/PhysRevB.102.245202
- [54] Nakib H. Protik et al. “The elphbolt ab initio solver for the coupled electron-phonon Boltzmann transport equations” Number: 1 Publisher: Nature Publishing Group In npj Computational Materials 8.1, 2022, pp. 1–9 DOI: 10.1038/s41524-022-00710-0
- [55] Nakib Haider Protik “elphbolt. https://github.com/nakib/elphbolt”, 2021 URL: https://github.com/nakib/elphbolt
- [56] Rohit Kishan Ray “Steepest entropy ascent solution for a continuous-time quantum walker” In Physical Review E 106.2, 2022, pp. 024115 DOI: 10.1103/PhysRevE.106.024115
- [57] Rohit Kishan Ray and Gian Paolo Beretta “No-signaling in Nonlinear Extensions of Quantum Mechanics” Version Number: 2, 2023 DOI: 10.48550/ARXIV.2301.11548
- [58] H.. Shanks, P.. Maycock, P.. Sidles and G.. Danielson “Thermal Conductivity of Silicon from 300 to 1400°K” In Physical Review 130.5, 1963, pp. 1743–1748 DOI: 10.1103/PhysRev.130.1743
- [59] Arno Hendrikus Marie Smets et al. “Solar energy: the physics and engineering of photovoltaic conversion, technologies and systems” sbn: 978-1-906860-32-5 (UIT Cambridge, Cambridge, England Cambridge, England: UIT Cambridge, 2016
- [60] M.. Spakovsky, Celine Hin, C Li and Jarod Worden “SEAMater. https://github.com/azsprague/seaqt-gui”, 2024
- [61] Michael Spakovsky and Jochen Gemmer “Some Trends in Quantum Thermodynamics” Number: 6 In Entropy 16.6, 2014, pp. 3434–3470 DOI: 10.3390/e16063434
- [62] Michael R. Spakovsky, Charles Schlosser, Joseph B. Martin and Eswar Josyula “Predicting the Chemical Kinetics of Air at High Temperatures Using Steepest-Entropy-Ascent Quantum Thermodynamics” AIAA AVIATION 2020 FORUM, American Institute of Aeronautics and Astronautics American Institute of AeronauticsAstronautics, 2020 DOI: 10.2514/6.2020-3274
- [63] A. Stranz, J. Kähler, A. Waag and E. Peiner “Thermoelectric Properties of High-Doped Silicon from Room Temperature to 900 K” Num Pages: 2381-2387 Place: Warrendale, Netherlands Publisher: Springer Nature B.V. In Journal of Electronic Materials 42.7, 2013, pp. 2381–2387 DOI: 10.1007/s11664-013-2508-0
- [64] Frank Tabakin “Local model dynamics for two qubits” In Annals of Physics 457, 2023, pp. 169408 DOI: 10.1016/j.aop.2023.169408
- [65] Frank Tabakin “Model dynamics for quantum computing” In Annals of Physics 383, 2017, pp. 33–78 DOI: 10.1016/j.aop.2017.04.013
- [66] Mischa Thesberg, Hans Kosina and Neophytos Neophytou “On the Lorenz number of multiband materials” In Physical Review B 95.12, 2017, pp. 125206 DOI: 10.1103/PhysRevB.95.125206
- [67] Atsushi Togo and Isao Tanaka “First principles phonon calculations in materials science” In Scripta Materialia 108, 2015, pp. 1–5 DOI: 10.1016/j.scriptamat.2015.07.021
- [68] Atsushi Togo, Laurent Chaput, Terumasa Tadano and Isao Tanaka “Implementation strategies in phonopy and phono3py” arXiv:2301.05784 arXiv, 2023 URL: http://arxiv.org/abs/2301.05784
- [69] Xufeng Wang, Evan Witkoske, Jesse Maassen and Mark Lundstrom “LanTraP: A code for calculating thermoelectric transport properties with the Landauer formalism” arXiv:1806.08888 arXiv, 2020 URL: http://arxiv.org/abs/1806.08888
- [70] Yan Wang, Xiulin Ruan and Ajit K. Roy “Two-temperature nonequilibrium molecular dynamics simulation of thermal transport across metal-nonmetal interfaces” In Physical Review B 85.20, 2012, pp. 205311 DOI: 10.1103/PhysRevB.85.205311
- [71] Ryo Yamada, Michael R Spakovsky and William T Reynolds “A method for predicting non-equilibrium thermal expansion using steepest-entropy-ascent quantum thermodynamics” Number: 32 In Journal of Physics: Condensed Matter 30.32, 2018, pp. 325901 DOI: 10.1088/1361-648X/aad072
- [72] Ryo Yamada, Michael R Spakovsky and William T Reynolds “Low-temperature atomistic spin relaxation and non-equilibrium intensive properties using steepest-entropy-ascent quantum-inspired thermodynamics modeling” Number: 50 In Journal of Physics: Condensed Matter 31.50, 2019, pp. 505901 DOI: 10.1088/1361-648X/ab4014
- [73] Ryo Yamada, Michael R. Spakovsky and William T. Reynolds “Kinetic pathways of ordering and phase separation using classical solid state models within the steepest-entropy-ascent quantum thermodynamic framework” In Acta Materialia 182, 2020, pp. 87–99 DOI: 10.1016/j.actamat.2019.10.002
- [74] Ryo Yamada, Michael R. Spakovsky and William T. Reynolds “Predicting continuous and discontinuous phase decompositions using steepest-entropy-ascent quantum thermodynamics” Number: 5 In Physical Review E 99.5, 2019, pp. 052121 DOI: 10.1103/PhysRevE.99.052121
- [75] Aimen Younis, Fazel Baniasadi, Michael R Spakovsky and William T Reynolds Jr “Predicting defect stability and annealing kinetics in two-dimensional PtSe using steepest entropy ascent quantum thermodynamics” Number: 7 In Journal of Physics: Condensed Matter 35.7, 2023, pp. 075703 DOI: 10.1088/1361-648X/aca3f1
- [76] Jin-Jian Zhou et al. “Perturbo: A software package for ab initio electron–phonon interactions, charge transport and ultrafast dynamics” In Computer Physics Communications 264, 2021, pp. 107970 DOI: 10.1016/j.cpc.2021.107970