Pretrained equivariant features improve unsupervised landmark discovery
Abstract
Locating semantically meaningful landmark points is a crucial component of a large number of computer vision pipelines. Because of the small number of available datasets with ground truth landmark annotations, it is important to design robust unsupervised and semi-supervised methods for landmark detection. Many of the recent unsupervised learning methods rely on the equivariance properties of landmarks to synthetic image deformations. Our work focuses on such widely used methods and sheds light on its core problem, its inability to produce equivariant intermediate convolutional features. This finding leads us to formulate a two-step unsupervised approach that overcomes this challenge by first learning powerful pixel-based features and then use the pre-trained features to learn a landmark detector by the traditional equivariance method. Our method produces state-of-the-art results in several challenging landmark detection datasets such as the BBC Pose dataset and the Cat-Head dataset. It performs comparably on a range of other benchmarks.
1 Introduction
Producing models that learn with minimal human supervision is crucial for tasks that are otherwise expensive to solve with manual supervision. Discovering landmarks within natural images falls into this category since manually annotating landmark points at the pixel level scales poorly with the number of annotations and the size of the dataset. Recent advancements in Deep Learning have brought significant performance improvements to various computer vision tasks. This work focuses on using deep-learning models for unsupervised discovery of landmarks, as adopted in several recent articles (Thewlis et al., 2017b; Jakab et al., 2018; Thewlis et al., 2019; Zhang et al., 2018).
Equivariance, the fundamental concept most modern unsupervised landmark discovery approaches are based upon, formalizes the intuitive property that, when an image is deformed through the action of a geometric transformation, semantically meaningful landmarks associated with that image should also be deformed through the action of the same deformation.
Most recent approaches for unsupervised landmark discovery leverage this equivariance property of landmark points.
The tasks of discovering and detecting semantically meaningful landmarks have been extensively studied. Developed before the advent of more recent deep-learning techniques and among the large number of proposed methods for solving these problems, it is worth mentioning the supervised and weakly-supervised learning approaches based on templates (Zhu and Ramanan, 2012; Pedersoli et al., 2014), active appearance (Cootes et al., 1998; Matthews and Baker, 2004; Cristinacce and Cootes, 2008), as well as the regression-based models (Valstar et al., 2010; Dantone et al., 2012; Cao et al., 2014; Ren et al., 2014).
Most of the recently proposed methodologies such as Cascade CNN (Sun et al., 2013), CFAN (Zhang et al., 2014a), coordinate regression (Nibali et al., 2018) and several variants (Zhang et al., 2014b, 2015; Yu et al., 2016; Xiao et al., 2016; Wu et al., 2017; Xiao et al., 2017) leverage deep-convolutional feature extractors for solving the task of supervised landmark detection.
In contrast, the approach described in this text is fully unsupervised and yet can perform more robustly than several supervised approaches.
Among other unsupervised landmark discovery pipelines, the approach of Thewlis et al. (2017b) was one of the first ones to leverage the equivariance property of landmarks. Equivariance was also used to discover 3D landmarks in the work of Suwajanakorn et al. (2018). Several other approaches are based on the creation of representations that disentangle geometric structures from appearance. Such approaches can be seen in the work of Rocco et al. (2017), Warpnet (Kanazawa et al., 2016), as well as Shu et al. (2018). In the work of Thewlis et al. (2017a), objects are mapped to labels for capturing structures in the image. Similar ideas can also be found (Thewlis et al., 2019).
Several approaches attempt to disentangle the latent representation of images into visual and structural content by comparing representation between related images. These related images can be obtained through synthetic image deformations, or by exploiting the temporal continuity of video streams. Jakab et al. (2018) reconstructs images by combining the visual and the structural content to discover landmarks. Simultaneous image generation and landmark discovery can also be seen in (Zhang et al., 2018; Reed et al., 2016, 2017). Although this set of methods has proven to be successful in some situations, the reliance on reconstructing high-resolution images is problematic in several aspects: these methods require high-capacity models, are often slow to train, and perform sub-optimally in situations where images are corrupted by a high level of noise or in the presence of artifact, as is, for example, common in medical applications. The proposed approach does not rely on image reconstruction and the numerical experiments presented in Section 5 demonstrate that it can still perform competitively on challenging tasks involving human-pose estimations, a task generally solved by leveraging the temporal continuity of adjacent video frames.
Contributions. In this article, we take a closer look at the equivariance property of intermediate representations within deep learning models for landmark discovery.
-
•
We empirically demonstrate that standard landmark discovery approaches are not efficient at enforcing that the intermediate representations satisfy the equivariance property. To this end, we define a metric similar to cumulative error distribution curves that we use to quantify the equivariance of convolutional features.
-
•
We propose a two-step approach for landmark discovery. In the first step, powerful equivariant features are learned through a contrastive learning method. In a second step, these equivariant features are leveraged within more standard unsupervised landmark discovery pipelines. Our method is able to find semantically meaningful and consistent landmarks, even in challenging datasets with high inter-class variations.
-
•
Our numerical studies indicate that the proposed methodology outperforms previously proposed approaches in the difficult task of finding human body landmarks in the BBC Pose dataset, facial landmarks in the Cat-head dataset. Our method performs comparably to other unsupervised methods in the CelebA-MAFL facial landmark dataset.
2 Background
Landmarks can be defined as a finite set of points that define the structure of an object. A particular class of objects is expected to have the same set of landmarks across different instances.
In many scenarios, the variations in the locations of the landmarks across different instances of the same object can be used for downstream tasks (e.g., facial recognition, shape analysis, tracking).
Consider an image represented as a tensor with height , width and number of channels . This image can also be thought of as (the discretization of) a mapping from to . We are interested in designing a landmark extraction function that associates to the image a set of landmarks where for . In this work, the mapping is parametrized by a neural network, although it is not a requirement. Occasionally, in order to avoid notational clutter, we omit the dependence of on the input image .
Consider a bijective mapping that describes a geometric deformation within of the domain . Examples include translations, rotations, elastic deformations, with a proper treatment of the boundary conditions. To any function can be associated the function defined as for all . Since images can be thought of as discretizations of functions from to , the function also defines, with a slight abuse of notation, a deformation mapping on the set of images. With these notations, the function describes the transformation of coordinates (i.e. elements of ), while the function describes the action of the transformation when applied to all pixels of a given image. A landmark extraction function is said to satisfy the equivariance property if the condition
| (1) |
holds for all images . Equation (1) translate the intuitive property that, when an image is deformed under the action of a deformation mapping , the associated landmarks are deformed through the action of the same deformation.
In this article, we follow the standard approach (Jakab et al., 2018; Thewlis et al., 2017b) of implementing the landmark extraction mapping as a differentiable function by expressing it as the composition of a heatmap function with the standard spatial soft-argmax (Chapelle and Wu, 2010) function ,
so that . In order to train a landmark extraction model, it is consequently a natural choice to try to minimize the equivariance loss
| (2) |
This formulation was first used by Thewlis et al. (2017b), and then subsequently adopted by several other articles (Thewlis et al., 2019; Zhang et al., 2018). Unfortunately, minimizing the equivariance loss alone generally leads to a trivial solution: all landmarks coincide. In practice, it is consequently necessary to consider an additional diversity loss
| (3) |
where is the usual spatial softmax function, although other choices are certainly possible. The notation denotes the spatial softmax evaluated at the coordinate . The loss (3) was first proposed in Thewlis et al. (2017b) in conjunction with the equivariance loss to penalize the concentration of different heatmaps at the same coordinate. The diversity loss is often computed for small image patches rather than individual coordinates. Landmarks can be learned by directly minimizing the total loss on a dataset on unlabeled images and randomly generated deformation mappings .
3 Equivariance of intermediate representations
this section defines a measure of equivariance for convolutional features. This allows us to
measure the equivariance of intermediate convolutional features learned by the set of methods described in Section 2.
Equivariant features.
Fully Convolutional Neural Networks (FCNN) are leveraged in most modern deep learning based landmark discovery methods (Jakab et al., 2018; Thewlis et al., 2017b, 2019). Let be an image and be a convolutional feature obtained from by passing it through a fully convolutional network . One can always assume, using a spatial change of resolution if necessary, that the convolutional features have the same dimensions as the input image and can thus be parametrized by . For any 2D coordinate , the vector can be thought of as a -dimensional representation of a small region (i.e. receptive field) of the input image centred at . This remark motivates a natural extension of the notion of equivariance for convolutional features. Consider two images and related by a geometric deformation in the sense that , as well as the associated convolutional features defined as and . The convolutional feature extractor would be perfectly equivariant if the extracted features and were such that for any location . A landmark extraction function, as described in
Section 2, that exploits equivariant convolutional features would directly inherit the equivariance properties of these features.
Note, though, that training a landmark extractor through the loss function described in Equation (2) only attempts to enforce the equivariance property of the final landmarks. Consequently, it is natural to investigate whether (i) this equivariance property naturally percolates through the convolutional neural network and leads to the creation of equivariant convolutional features (ii) there are more efficient training methodologies for enforcing the equivariance property throughout the neural network model.
Measure of equivariance: Let be the convolutional features associated to two images and related through the deformation function . As described previously, one can always assume that the convolutional features and the images themselves have the same dimension and can, consequently, be parametrized by . To quantify the equivariance of the convolutional features, it is computationally impractical to require the property to hold for all . Furthermore, it is desirable to focus on the equivariance property of a few well chosen locations.
To this end, in our study of the equivariance properties of intermediate convolutional features, we exploit a labelled dataset whose images have been annotated with semantically meaningful landmark points: to each image is associated landmarks. For such an image and a geometric deformation , consider the deformed image as well as the associated convolutional features and . For each landmark associated to , we consider the location in the deformed image whose representation is the most similar to ,
| (4) |
In (4) we have used the cosine similarity,
| (5) |
although other choices are indeed possible. For discriminative and equivariant convolutional features, we expect the Euclidean distance between and to be small. Consequently, for a distance threshold , the accuracy at threshold is defined as
| (6) |
where and denote the -th landmark quantities associated to image .
In the sequel, the curve will be referred to as the accuracy curve. An example is depicted in Figure 1.
Features learned from landmark equivariance. The accuracy metric (6) can be used to investigate whether the intermediate convolutional features learned by directly minimizing the equivariance loss (2) combined to the diversity regularization (3), i.e. , also exhibit good equivariance properties. The approach consisting in directly minimizing the combined loss is referred to as the end-to-end learning approach, in contrast to our proposed two-step approach, described in Section 4. Furthermore, we use standard so-called hourglass convolutional neural architectures as recommended by most recent work on landmark discovery (Jakab et al., 2018; Thewlis et al., 2019; Zhang et al., 2018). Such a model architecture can be described as the composition of a convolutional feature extractor that produces -dimensional spatial features followed by another convolutional network that transforms these features into heatmaps where . As described in Section 2, these heatmaps are finally transformed into landmark points through a spatial soft-argmax operation. For our experiments, we chose landmark points and convolutional features of dimension . We trained in an end-to-end manner the hourglass network on the BBC Pose dataset (Charles et al., 2013a) training dataset for landmark discovery. The accuracy metric (6) was then computed on the BBC Pose dataset’s test set (i.e. not used during training). To this end, we chose a set of manually annotated human body landmarks: head, two shoulders, two elbows, and two wrists. The images were resized to a resolution pixels.
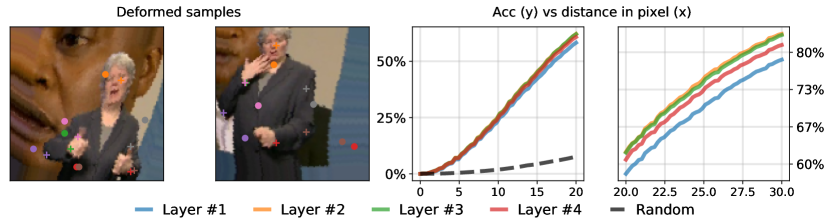
Figure 1 presents examples from the BBC Pose test dataset where random rotations and random elastic deformations were applied. The circles denote the locations estimated through Equation (4) and the crosses indicate the ground truth locations ; these locations were obtained by training a landmark extractor in an end-to-end manner. The right-most plots of Figure 1 report the accuracy curves estimated from a set of annotated landmarks. Each of the four accuracy curves is associated to one of four intermediate convolutional features coined Layer 1 to Layer 4. Here, Layer 1 is the output of the feature extractor while Layer (2, 3, 4) are representation situated in between Layer 1 and the final heatmaps generated through the complete network . For comparison, the black dashed line shows the performance associated with locations generated uniformly at random within . The results indicate that, even though the intermediate convolutional features do possess some degree of equivariance (i.e. better than random), the performance is relatively poor with an accuracy for a distance threshold of pixels.
4 Method
The previous section demonstrates that the direct minimization of the combined loss is not efficient at inducing equivariance properties to the intermediate convolutional features. In contrast, the first step of the methodology described in this section aims at directly enforcing that the intermediate features enjoy enhanced equivariance properties. In a second step, these pre-trained features are leveraged within more standard landmark discovery pipelines. Although we can choose to pre-train any of the convolutional features of the complete landmark extractor , our experiments indicate that it is most efficient to concentrate on the final convolutional features (i.e. layer 1 with the terminology of the previous section) generated by the feature extractor network . As depicted in the right-most plot of Figure 1, when end-to-end training is used, the layer 1 is the worst in terms of equivariance among the four layers considered in the previous section. At a heuristic level, this can be explained by the fact that the layer 1 is the further “away" from the training signal among the four layers considered.
Our proposed methodology proceeds in two steps.
Step 1: train the feature extractor convolutional network with the contrastive learning approach described in the remainder of this section.
Step 2: freeze the parameters of the feature extractor network and train the complete network with a standard landmark discovery approach, i.e. minimize the combined objective .
Step 1: training the feature extractor . We employ a contrastive learning framework similar to simCLR (Chen et al., 2020) to train the features extractor. To this end, we leverage (1) random geometric deformations that only change the locations of the pixels (eg. rotations, dilatations, elastic deformations) (2) random appearance changes denoted by that do not change the locations of the pixels (eg. noise addition, intensity change, contrast perturbation). For a batch of images , we consider augmented versions defined as augmented by random generated geometric and appearance augmentations and . Furthermore, for each image in the batch, we also consider randomly selected spatial locations : the location is transform to under the action of the geometric deformation . Finally, these pairs of images are passed through the feature extractor and -dimensional features are extracted at the locations and for and . We have and . The feature extractor is trained by minimizing the contrastive loss defined as
| (7) |
where the quantities and are defined as
and is the exponential similarity between scaled by temperature . The similarity is defined in Equation (5).
Minimizing the contrastive loss not only ensures equivariance, it also encourages dissimilarity between features belonging to different parts of the image. The landmark detector trained in the second step described below benefits from both the consistency and contrast of these features.
Step 2: training the landmark detector. After training the feature extractor as described in the previous section, its parameters are frozen. The entire network is then unsupervisedly trained in a standard fashion for landmark discovery. In this text, we follow the approach of Thewlis et al. (2017b) although other approaches are possibles. We use a fully convolutional architecture with residual connections and minimize the combined loss . Furthermore, to encourage the heatmaps to be more concentrated, we also penalize the variance of the heatmaps. In other words, we consider an additional regularization term expressed as
In the above Equation, denotes the spatial softmax operation that transforms a heatmap on into a probability measure on . The notation designates the covariance matrix. We defer additional details of implementation to the supplementary.
4.1 Implementation Details
We choose the network to be an hourglass encoder-decoder network. The encoder contains four convolution-maxpool blocks, each of which halves the spatial dimension of its input. Symmetrically, the decoder block expands the spatial dimension to produce final features of the same spatial dimension as that of the original input image. We use skip-connections to join the encoder and decoder. Each of the convolution blocks contains two convolution units separated by non-linear activation ReLU and one max-pool/up-sample unit. The final channel dimension of the features is . The landmark network is fully convolutional with the same intermediate spatial dimension as that of the image. For contrastive learning, we used a temperature of .
We first train the network with the contrastive loss described in equation 6 of the main draft on all the datasets. The image deformation set includes random affine transformations, random crop and zoom operations, image augmentations related to intensity and contrast, as well as elastic deformations. Next, we freeze the parameters of the network and train the landmark detector. For this, we use the combined loss with the image deformation as random rotation and elastic deformation. Note that this combined loss was also used to train the end-to-end network presented in ablation.
For the diversity loss, we choose image patches of size for images of size and patches for images. We use the Adam optimizer with a learning rate of and LR decay of every epoch for both training steps. For both steps, we train our model for 20 epochs. We also use regularization of strength . To check the performance of unsupervisedly discovered landmarks, we use a linear regressor without bias to predict the ground truth annotations. The regressor is always trained on the training set and then evaluated on the test dataset. We keep the training and test split the same as previous works. We use Ridge regression as our choice of regressor with regularization .
5 Experiments
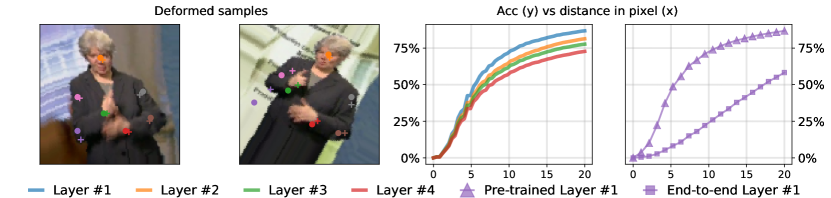
In this section, we illustrate the performance gains in terms of equivariance of the intermediate features when adopting our proposed two-step method. Figure 2 shows some examples of deformed images from the BBC Pose dataset with the ground truth and predicted locations of landmarks: the setting is similar to the one of Figure 1. The predicted locations were estimated through maximizing the similarity, as described in Equation (4). The third plot shows the accuracy of the four intermediate representations layers (1,2,3,4) previously described at the end of Section 4: note that all layers benefited in terms of equivariance from the two-step approach, even though only layer 1 was pre-trained with contrastive learning. The right-most plot compares the equivariance accuracy curve associated to Layer 1 when the model is trained in an end-to-end fashion and when trained with our proposed approach: there is a considerable boost in equivariance accuracy (6). At a distance threshold of pixels, the end-to-end method leads to an accuracy of while the proposed two-step approach leads to an equivariance accuracy of .
5.1 Human body landmarks.
Learning human body landmarks in an unsupervised manner poses some unique challenges. Unlike rigid and semi-rigid structures such as the human face, vehicles, or other non-deformable objects, the human body allows flexibility around different body joints. The BBC Pose dataset is comprised of videos of sign language interpreters. The positional variability of the different upper body parts during sign language communication leads to unique challenges. Following the setup of Jakab et al. (2018), loose crops around the interpreters were resized to and used for our experiments.

Qualitative results. We used the training part (ten videos) of the BBC Pose dataset to learn in an unsupervised manner landmarks with our proposed two-step method. After training, the discovered landmarks were computed on the validation dataset (five videos) and were used as features to train a linear regressor (without bias) to predict the actual location of the seven annotated landmarks. This regression model is then evaluated on the test dataset (five videos). Figure 3 shows some example of the test dataset with predicted (o) and ground truth (+) locations of the landmarks.
| Proportion (%) within pixels | |||||
| Supervised | Head | Wrst | Elbw | Shldr | Avg. |
| Pfister et al. (2015) | |||||
| Charles et al. (2013b) | |||||
| Chen and Yuille (2014) | |||||
| Pfister et al. (2014) | |||||
| Yang and Ramanan (2011) | |||||
| Unsupervised | |||||
| Jakab et al. (2018) | |||||
| Ours | |||||
| Overall accuracy % | ||
| Training Samples | Jakab et al. (2018) | Ours |
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| (full dataset) | ||
Quantitative results.
In table 1 we present our numerical results on the unsupervised landmark detection. The first few methods are fully supervised, and most of these methods leverage temporal continuity to track landmarks reliably across video frames. In contrast, Jakab et al. (2018) and ours are unsupervised and only use the ground truth annotations of the validation dataset to predict the locations of the annotated landmarks on the test dataset.
Following the evaluation procedure of Jakab et al. (2018), we report the proportion of landmarks predicted within a Euclidian distance of pixels from the ground truth in an image of size .
Table 1 shows the prediction score for different classes of upper-body joints, as well as the overall score. When averaged all the landmarks, our method outperforms three of the supervised methods and outperforms the unsupervised method of Jakab et al. (2018). Furthermore, except for the wrists, our method outperforms all the supervised methods for predicting individual landmarks. The relatively poor performance for detecting the location of the wrists stems from the fact that our method uses elastic deformations of the same image frame to learn equivariance. In contrast, most of the supervised methods exploit implicit temporal continuity while the method of Jakab et al. (2018) uses a different frame from the same video to obtain original and deformed image pair. Our methodology could certainly leverage recent image key-point matching methods in order to leverage more efficiently video modalities. Finally, table 2 reports the performance of our method as a function of the number of supervised samples from the validation dataset (total 1000 samples) used to fit the regression model. We can see that with just 100 supervised annotations, our method outperforms the approach of Jakab et al. (2018).
5.2 Facial landmarks
For the task of learning facial landmarks, we implement our methodologies on the CelebA (Liu et al., 2015) dataset (200k human face images of 10k celebrity) as well as the Cat Head (Zhang et al., 2008) dataset (9k images of cat faces). The celebA dataset contains annotated facial landmarks (two eyes, nose, two corners of mouth) whereas the cat dataset has annotated landmark points (six points in ears, two eyes, one mouth). The cat head dataset features more holistic variations than human face images and contains a considerable amount of occlusions. Similar to human body landmarks, we train our two-step landmark detection network on a training set, fit a linear regressor on a validation set and finally evaluate the performance of the regressor on a test dataset. In all our experiments related to facial landmarks, we adopt the popular metric inter-ocular distance normalized MSE,
| (8) |
where denotes the test dataset, is the set of manually annotated landmarks, and are respectively the predicted and ground truth location of the landmark in image , and denotes the distance between the ground truth eyes in an image .
| Performance on Cat head dataset | ||
|---|---|---|
| Landmark count | ||
| Thewlis et al. (2017b) | ||
| Zhang et al. (2018) | ||
| Ours ( Training Samples) | ||
| (full dataset) | ||
Cat head dataset. We keep the size of the cat images to their original resolution and maintain the same train/test split as Zhang et al. (2018). Furthermore, we discard the two annotations corresponding to the end of the ears (Zhang et al., 2018; Thewlis et al., 2017b).
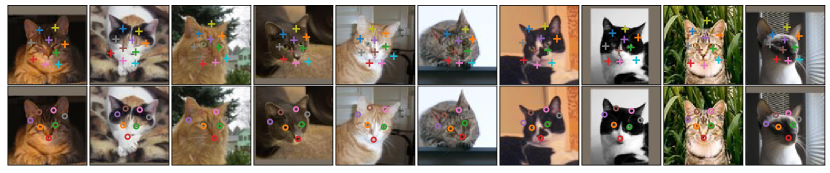
Qualitative results. Figure 4 shows some examples of cat head test dataset. The top row shows images annotated with the ten unsupervised landmark locations discovered by our model. The bottom row shows the result of predicting ground truth landmark locations of seven facial landmark points. It is worth noting that the inter-example variation in this dataset is more than any human face dataset as the images vary in pose, color, cat breed, occlusion.
| Performance on MAFL dataset | |||
|---|---|---|---|
| Landmark count | NA | ||
| Supervised | |||
| CFAN (Zhang et al., 2014a) | - | - | |
| Cascaded CNN (Sun et al., 2013) | - | - | |
| TCDCN (Zhang et al., 2015) | - | - | |
| MTCNN (Zhang et al., 2014b) | - | - | |
| Un/Self-supervised | - | - | - |
| Thewlis et al. (2017b) | - | ||
| Thewlis et al. (2017a) | - | - | |
| Shu et al. (2018) | - | - | |
| Sanchez and Tzimiropoulos (2019) | - | - | |
| Zhang et al. (2018) | - | - | |
| Thewlis et al. (2019) | - | - | |
| Jakab et al. (2018) | - | ||
| Ours | - | ||
| No. sample | Jakab et al. (2018) | Ours |
|---|---|---|
| 1 | ||
| 5 | ||
| 10 | ||
| full data |
Quantitative results. Table 3 shows performance of our method. The performances of two unsupervised methods are listed at the top of the table. The bottom part of the table reports the performance of our proposed approach as a function of the number of supervised samples. We report both the mean and standard deviation in order to account for the variability in the regression training set. Our method can outperform previous unsupervised methods when only supervised samples out of the total available training samples are utilized.
CelebA dataset. The CelebA images were resized to as done by most works (Jakab et al., 2018). The MAFL dataset, a subset of the CelebA dataset, has a training set of 19k images and a test set of 1k images. Like previous works, we take our unsupervised model trained on CelebA and then train a linear regressor to predict the MAFL training set’s manual annotations.

Qualitative results. Some predictions generated by our approach are depicted in Figure 5. The top row shows ten unsupervised landmarks learned for each image. The bottom row shows five landmarks as predicted by the unsupervised landmarks through a linear regressor without bias.
Quantitative results. Table 4 reports the performance of several supervised, unsupervised, and semi-supervised methods. Although our performance is not better than the previous state-of-the-art in terms of iod-mse%, for an image size of , the difference in actual MSE in terms of pixel distance is marginal. Table 5 presents the performance of the proposed approach as a function of the number of supervised samples utilized to train the regressor: our model performs comparably with the SOTA.
| BBC Pose Accuracy (%) | MAFL mse (%) | Cat head mse (%) | |||||||
| Method | Head | Wrst | Elbw | Shldr | Avg. | 30 | 50 | 10 | 20 |
| Thewlis et al. (2017b) | – | – | – | – | – | ||||
| End-to-end | |||||||||
| Pre-training | |||||||||
5.3 Ablation study
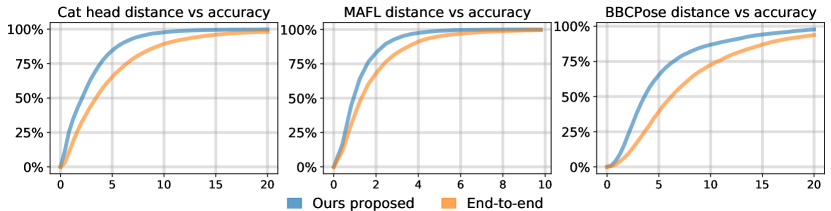
We perform our ablation table 6 that lists three methods. We compare our proposed method to the one of Thewlis et al. (2017b) since it is the most similar. The second row reports the performance of the end-to-end learning framework of Thewlis et al. (2017b) when the architecture is replaced by ours: the only difference when compared to the first row is solely due to the effect of our architecture. In the third row, we present our proposed two-step method. The improvement in performance from the second to the third row is only due to our pre-training method approach: we emphasize that the neural architectures and landmark losses are exactly the same. Our approach consistently leads to significantly improved performances. In figure 6 we plot the final accuracy curves of our pre-training method vs the end-to-end training method. As discussed before, we fit a linear regressor that predicts the location of the ground truth annotations by taking the unsupervised landmark locations as input. The regressor is fitted on a training dataset and then used on a separate test dataset. The accuracy curves in figure 6 are obtained from the test data predicted vs ground truth manual annotations of the three datasets BBCPose, Cat head, and MAFL.
6 Conclusions
Our study shows that the intermediate neural representations learned by standard end-to-end approach leveraging equivariance losses enjoy poor equivariance properties. Instead, for unsupervised landmark discovery, we proposed to use contrastive learning for pre-training equivariant intermediate neural representations. The numerical experiments demonstrate that this simple strategy, which can naturally be used within several other pipelines and tasks, can lead to a significant performance boost even in challenging situations such as the one described in Section 5.
References
- Cao et al. [2014] Xudong Cao, Yichen Wei, Fang Wen, and Jian Sun. Face alignment by explicit shape regression. International Journal of Computer Vision, 107(2):177–190, 2014.
- Chapelle and Wu [2010] Olivier Chapelle and Mingrui Wu. Gradient descent optimization of smoothed information retrieval metrics. Information retrieval, 13(3):216–235, 2010.
- Charles et al. [2013a] J. Charles, T. Pfister, M. Everingham, and A. Zisserman. Automatic and efficient human pose estimation for sign language videos. International Journal of Computer Vision, 2013a.
- Charles et al. [2013b] J. Charles, T. Pfister, D. Magee, D. Hogg, and A. Zisserman. Domain adaptation for upper body pose tracking in signed TV broadcasts. In British Machine Vision Conference, 2013b.
- Chen et al. [2020] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A Simple Framework for Contrastive Learning of Visual Representations. 2020. URL http://arxiv.org/abs/2002.05709.
- Chen and Yuille [2014] Xianjie Chen and Alan L. Yuille. Articulated pose estimation by a graphical model with image dependent pairwise relations. CoRR, abs/1407.3399, 2014. URL http://arxiv.org/abs/1407.3399.
- Cootes et al. [1998] TF Cootes, GJ Edwards, and CJ Taylor. Active appearance models. eccv’98: Proceedings of the 5th european conference on computer vision-volume ii (pp. 484–498), 1998.
- Cristinacce and Cootes [2008] David Cristinacce and Tim Cootes. Automatic feature localisation with constrained local models. Pattern Recognition, 41(10):3054–3067, 2008.
- Dantone et al. [2012] Matthias Dantone, Juergen Gall, Gabriele Fanelli, and Luc Van Gool. Real-time facial feature detection using conditional regression forests. In 2012 IEEE Conference on Computer Vision and Pattern Recognition, pages 2578–2585. IEEE, 2012.
- Jakab et al. [2018] Tomas Jakab, Ankush Gupta, Hakan Bilen, and Andrea Vedaldi. Unsupervised learning of object landmarks through conditional image generation. Advances in Neural Information Processing Systems, (NeurIPS), 2018. ISSN 10495258.
- Kanazawa et al. [2016] Angjoo Kanazawa, David W Jacobs, and Manmohan Chandraker. Warpnet: Weakly supervised matching for single-view reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3253–3261, 2016.
- Liu et al. [2015] Ziwei Liu, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision (ICCV), December 2015.
- Matthews and Baker [2004] Iain Matthews and Simon Baker. Active appearance models revisited. International journal of computer vision, 60(2):135–164, 2004.
- Nibali et al. [2018] Aiden Nibali, Zhen He, Stuart Morgan, and Luke Prendergast. Numerical Coordinate Regression with Convolutional Neural Networks. 2018. URL http://arxiv.org/abs/1801.07372.
- Pedersoli et al. [2014] Marco Pedersoli, Tinne Tuytelaars, and Luc Van Gool. Using a deformation field model for localizing faces and facial points under weak supervision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3694–3701, 2014.
- Pfister et al. [2014] T. Pfister, K. Simonyan, J. Charles, and A. Zisserman. Deep convolutional neural networks for efficient pose estimation in gesture videos. In Asian Conference on Computer Vision, 2014.
- Pfister et al. [2015] T. Pfister, J. Charles, and A. Zisserman. Flowing convnets for human pose estimation in videos. In IEEE International Conference on Computer Vision, 2015.
- Reed et al. [2017] Scott Reed, Aäron van den Oord, Nal Kalchbrenner, Sergio Gómez Colmenarejo, Ziyu Wang, Dan Belov, and Nando De Freitas. Parallel multiscale autoregressive density estimation. arXiv preprint arXiv:1703.03664, 2017.
- Reed et al. [2016] Scott E Reed, Zeynep Akata, Santosh Mohan, Samuel Tenka, Bernt Schiele, and Honglak Lee. Learning what and where to draw. In Advances in neural information processing systems, pages 217–225, 2016.
- Ren et al. [2014] Shaoqing Ren, Xudong Cao, Yichen Wei, and Jian Sun. Face alignment at 3000 fps via regressing local binary features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1685–1692, 2014.
- Rocco et al. [2017] Ignacio Rocco, Relja Arandjelovic, and Josef Sivic. Convolutional neural network architecture for geometric matching. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 6148–6157, 2017.
- Sanchez and Tzimiropoulos [2019] Enrique Sanchez and Georgios Tzimiropoulos. Object landmark discovery through unsupervised adaptation. CoRR, abs/1910.09469, 2019. URL http://arxiv.org/abs/1910.09469.
- Shu et al. [2018] Zhixin Shu, Mihir Sahasrabudhe, Rıza Alp Güler, Dimitris Samaras, Nikos Paragios, and Iasonas Kokkinos. Deforming autoencoders: Unsupervised disentangling of shape and appearance. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 11214 LNCS:664–680, 2018. ISSN 16113349. doi: 10.1007/978-3-030-01249-6_40.
- Sun et al. [2013] Yi Sun, Xiaogang Wang, and Xiaoou Tang. Deep convolutional network cascade for facial point detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3476–3483, 2013.
- Suwajanakorn et al. [2018] Supasorn Suwajanakorn, Noah Snavely, Jonathan Tompson, and Mohammad Norouzi. Discovery of latent 3d keypoints via end-to-end geometric reasoning. CoRR, abs/1807.03146, 2018. URL http://arxiv.org/abs/1807.03146.
- Thewlis et al. [2017a] James Thewlis, Hakan Bilen, and Andrea Vedaldi. Unsupervised object learning from dense equivariant image labelling. CoRR, abs/1706.02932, 2017a. URL http://arxiv.org/abs/1706.02932.
- Thewlis et al. [2017b] James Thewlis, Hakan Bilen, and Andrea Vedaldi. Unsupervised Learning of Object Landmarks by Factorized Spatial Embeddings. Proceedings of the IEEE International Conference on Computer Vision, 2017-October:3229–3238, 2017b. ISSN 15505499. doi: 10.1109/ICCV.2017.348.
- Thewlis et al. [2019] James Thewlis, Samuel Albanie, Hakan Bilen, and Andrea Vedaldi. Unsupervised learning of landmarks by descriptor vector exchange. Proceedings of the IEEE International Conference on Computer Vision, 2019. ISSN 15505499. doi: 10.1109/ICCV.2019.00646.
- Valstar et al. [2010] Michel Valstar, Brais Martinez, Xavier Binefa, and Maja Pantic. Facial point detection using boosted regression and graph models. In 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 2729–2736. IEEE, 2010.
- Wu et al. [2017] Yue Wu, Chao Gou, and Qiang Ji. Simultaneous facial landmark detection, pose and deformation estimation under facial occlusion. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3471–3480, 2017.
- Xiao et al. [2016] Shengtao Xiao, Jiashi Feng, Junliang Xing, Hanjiang Lai, Shuicheng Yan, and Ashraf Kassim. Robust facial landmark detection via recurrent attentive-refinement networks. In European conference on computer vision, pages 57–72. Springer, 2016.
- Xiao et al. [2017] Shengtao Xiao, Jiashi Feng, Luoqi Liu, Xuecheng Nie, Wei Wang, Shuicheng Yan, and Ashraf Kassim. Recurrent 3d-2d dual learning for large-pose facial landmark detection. In Proceedings of the IEEE International Conference on Computer Vision, pages 1633–1642, 2017.
- Yang and Ramanan [2011] Y. Yang and D. Ramanan. Articulated pose estimation with flexible mixtures-of-parts. In CVPR 2011, pages 1385–1392, 2011. doi: 10.1109/CVPR.2011.5995741.
- Yu et al. [2016] Xiang Yu, Feng Zhou, and Manmohan Chandraker. Deep deformation network for object landmark localization. In European Conference on Computer Vision, pages 52–70. Springer, 2016.
- Zhang et al. [2014a] Jie Zhang, Shiguang Shan, Meina Kan, and Xilin Chen. Coarse-to-fine auto-encoder networks (cfan) for real-time face alignment. In European conference on computer vision, pages 1–16. Springer, 2014a.
- Zhang et al. [2008] Weiwei Zhang, Jian Sun, and Xiaoou Tang. Cat head detection - how to effectively exploit shape and texture features. volume 5305, pages 802–816, 10 2008. doi: 10.1007/978-3-540-88693-8_59.
- Zhang et al. [2018] Yuting Zhang, Yijie Guo, Yixin Jin, Yijun Luo, Zhiyuan He, and Honglak Lee. Unsupervised Discovery of Object Landmarks as Structural Representations. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 2694–2703, 2018. ISSN 10636919. doi: 10.1109/CVPR.2018.00285.
- Zhang et al. [2014b] Zhanpeng Zhang, Ping Luo, Chen Change Loy, and Xiaoou Tang. Facial landmark detection by deep multi-task learning. In European conference on computer vision, pages 94–108. Springer, 2014b.
- Zhang et al. [2015] Zhanpeng Zhang, Ping Luo, Chen Change Loy, and Xiaoou Tang. Learning deep representation for face alignment with auxiliary attributes. IEEE transactions on pattern analysis and machine intelligence, 38(5):918–930, 2015.
- Zhu and Ramanan [2012] Xiangxin Zhu and Deva Ramanan. Face detection, pose estimation, and landmark localization in the wild. In 2012 IEEE conference on computer vision and pattern recognition, pages 2879–2886. IEEE, 2012.