This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Preventing Exceptions to Robins InEquality

Thomas Schwabhäuser schwabts@googlemail.com
Abstract

For sufficiently large nn Ramanujan gave a sufficient condition for the truth Robin’s InEquality X​(n):=σ​(n)n​ln⁡ln⁡n<eγX(n):=\frac{\sigma(n)}{n\ln\ln n}<e^{\gamma} (RIE). The largest known violation of RIE is n8=5040n_{8}=5040. In this paper Robin’s multipliers are split into logarithmic terms ℒ\mathcal{L} and relative divisor sums 𝒢\mathcal{G}. A violation of RIE above n8n_{8} is proposed to imply oscillations that cause 𝒢\mathcal{G} to exceed ℒ\mathcal{L}. To this aim Alaoglu and Erdős’s conjecture for the CA numbers algorithm is used and the paper could almost be reduced to section 4.3 on pages 4.3 to 5.

1 Introduction

1.1 Outline

Robin’s Inequality σ​(n)n​ln⁡ln⁡n<eγ\frac{\sigma(n)}{n\ln\ln n}<e^{\gamma} (RIE) for sufficiently large nn can be derived from Ramanujan’s Lost Notebook as necessary condition for RH. Unfortunately his work was not published until 1997. The inequality can be derived from an asymptotic expression that emerged from the study of generalised highly composite and generalised superior highly composite numbers. Alaoglu and Erdős coined the terms superabundant (SA) and colossally abundant (CA) in 1944 and mentioned the role of transcendental number theory in the process of finding CA numbers.

Proposition.

(Ramanujan [40, (382)])

If RH is true, [40, §56], it follows that

∑−1(N)=eγ​(ln⁡ln⁡N−2​(2−1)ln⁡n+S1​(ln⁡N)+O​(1)ln⁡N​ln⁡ln⁡N).{\textstyle\sum_{-1}}\left(N\right)=e^{\gamma}\left(\ln\ln N-\frac{2\left(\sqrt{2}-1\right)}{\sqrt{\ln n}}+S_{1}\left(\ln N\right)+\frac{O\left(1\right)}{\sqrt{\ln N}\ln\ln N}\right).
Conclusion.

There is an n0n_{0} such that σ​(n)n<eγ​ln⁡ln⁡n\frac{\sigma\left(n\right)}{n}<e^{\gamma}\ln\ln n for all n>n0n>n_{0}.

[Rf. notes at the end of [40].]

Robin clarified the meaning of “sufficiently large” in 1984 by finding

  1. 1.

    that the function X​(n):=σ​(n)n​ln⁡ln⁡nX\left(n\right):=\frac{\sigma(n)}{n\ln\ln n} takes maximal values on CA numbers.

  2. 2.

    It is sufficient for RH that RIE holds true for sufficiently large nn, i.e. for n>5040n>5040.

  3. 3.

    The oscillation theorem X​(n)=eγ⋅(1+Ω±​((ln⁡n)−b))X\left(n\right)=e^{\gamma}\cdot\left(1+\Omega_{\pm}\left(\left(\ln n\right)^{-b}\right)\right) in CA numbers if RH is false.

  4. 4.

    X​(n)X\left(n\right) has an unconditional bound B​(n)B\left(n\right) for some B​(n)=eγ+o​(1)B\left(n\right)=e^{\gamma}+o\left(1\right).

The major tool were estimations with Chebyshev’s functions ψ\psi and ϑ\vartheta using the results of Rosser and Schoenfeld. In order to show that XX takes maximal values on CA numbers Robin used a multiplier consisting of ratios of relative divisor sums σ−1​(n)\sigma_{-1}(n) of consecutive CA numbers and iterated logarithms. The argument is iterated in this report which proves that XX takes a greater value on a subsequent CA number if the product of ratios of relative divisor sums of intermediate CA numbers exceeds the respective product of ratios of iterated logarithms. But the CA numbers algorithm relies on the quotient of consecutive CA numbers to be prime which is not guaranteed unless Alaoglu and Erdős’ special case of the Four Exponentials Conjecture is true.

The point of this investigation has been to find out if the minimal oscillations in case RH is false will force the products of ratios of relative divisor sums to become greater than the corresponding products of ratios of iterated logarithms. This has been achieved by finding a template for the quotient of maximal and minimal values of X​(n)X\left(n\right) as nn proceeds in CA numbers and analysing the template with polar coordinates.

The paper is primarily organised as a chain of reductions that is summarised in the final Conclusion 4.32. Section 1.2 establishes the need to find multiples of every natural nn on which XX takes a greater value than it takes on nn. Such multiples prevent nn from being an exception. Section 2 demonstrates how the multipliers used by Robin work and how they can be split. This method is iterated in Section 3 to show the sufficiency of testing 𝒢>ℒ\mathcal{G}>\mathcal{L} for 𝒢=σ−1​(n​x)σ−1​(n)\mathcal{G}=\frac{\sigma_{-1}(nx)}{\sigma_{-1}(n)} and ℒ=ln⁡ln⁡n​xln⁡ln⁡n\mathcal{L}=\frac{\ln\ln nx}{\ln\ln n}. Similar conditions were found in [33, 35, 34] during the course of my investigation. The setup of the latter two reports is summarised using the present setup as a part of section 4 after presenting some numerical data. Then Mertens’ theorem motivates expecting the truth of 𝒢>ℒ\mathcal{G}>\mathcal{L} before Robin’s oscillation theorem is used in section 4.3 to propose an indirect proof.

1.2 Preparation

Notation.

Let X​(n):=σ​(n)n​ln⁡ln⁡nX(n):=\frac{\sigma(n)}{n\ln\ln n} with the sum of divisors σ\sigma, write RIE​(n)\textrm{RIE}\left(n\right) short for Robin’s InEquality X​(n)<eγX(n)<e^{\gamma},[46], and denote the set of primes {pn}n=1∞=2,3,5,…\left\{p_{n}\right\}_{n=1}^{\infty}=2,3,5,\ldots by ℙ\mathbb{P}. The kkth largest prime factor of an integer nn is denoted by Pk​(n)P_{k}\left(n\right), [42, 5.17]. Also let [a,b]ℕ:=[a,b]∩ℕ\left[a,b\right]_{\mathbb{N}}:=\left[a,b\right]\cap\mathbb{N}.

Grönwall [17] mentioned that the asymptotic behaviour of the function Y​(n):=φ​(n)n⋅ln⁡ln⁡nY(n):=\frac{\varphi(n)}{n}\cdot\ln\ln n had been studied by Landau, [25]. Then he proved Theorem 1.3 below. Rf. [36, 13] for Nicolas’ inequality and [52, 53] for approaches with the Dedekind ψ\psi function. Suppose

Condition 1.1.

For every n>5040n>5040 there is a number xx such that X​(n​x)>X​(n)X(nx)>X(n).

Note.

This section establishes

Claim 1.2.

RIE​(n)\textrm{RIE}\left(n\right) is true for all n>5040n>5040.

If the opposite of Condition 1.1 was true for some n>5040n>5040 the number nn may be said to be exceptional since no such nn is known so far. Without requiring n>5040n>5040 this is called GA2 in [8, p. 2]. Known GA2 numbers are 3, 4, 5, 6, 8, 10, 12, 18, 24, 36, 48, 60, 72, 120, 180, 240, 360, 2520, and 5040. Recall

Theorem 1.3.

(Grönwall)         lim supn→∞X​(n)=eγ.\limsup\limits_{n\to\infty}X(n)=e^{\gamma}.

This is easily extended.

Theorem 1.4.

lim supx→∞X​(n⋅x)=eγ=1.78107 24179 90197​….\limsup\limits_{x\to\infty}X(n\cdot x)=e^{\gamma}=1.78107\,24179\,90197....

Proof.

An adaption of [20, §22.9]. Rf. [24, App. A] for the numerical value.∎

Definition 1.5.

C:=(73−eγ⋅ln⁡ln⁡12)⋅ln⁡ln⁡12≈0.64821365C:=\left(\frac{7}{3}-e^{\gamma}\cdot\ln\ln 12\right)\cdot\ln\ln 12\approx 0.64821365, rf. [7, Theorem 1.1], [35, Eq. (1.4)], or [49, Lemma 13] and [50, Theorem 7].

Theorem 1.6.

([46, Théorème 2])

X​(n)≤B​(n):=eγ+C⋅(ln⁡ln⁡n)−2X(n)\leq B\left(n\right):=e^{\gamma}+C\cdot\left(\ln\ln n\right)^{-2} for all n∈ℕ∖{1,2,12}n\in\mathbb{N}\setminus\left\{1,2,12\right\}.

Thus, assuming Condition 1.1 it is easily seen that a minimal counterexample of RIE above 5040 contradicts Theorem 1.6 since for any number nn Condition 1.1 implies the existence of a non-decreasing sequence of values of XX that starts at X​(n)X(n). If X​(n)>eγX(n)>e^{\gamma} choose x1⋅⋯⋅xkx_{1}\cdot\cdots\cdot x_{k} such that

  1. 1.

    X​(n⋅yi+1)>X​(n⋅yi)X(n\cdot y_{i+1})>X(n\cdot y_{i}) for all i∈[0,k−1]ℕi\in\left[0,k-1\right]_{\mathbb{N}} where yi:=∏{xj;j∈[1,i]ℕ}y_{i}:=\prod\left\{x_{j};j\in\left[1,i\right]_{\mathbb{N}}\right\} and

  2. 2.

    C⋅lnln(n⋅yk)−2<X(n)−eγC\cdot\ln\ln\left(n\cdot y_{k}\right)^{-2}<X(n)-e^{\gamma}, i.e. n⋅yk>exp⁡(exp⁡(CX​(n)−eγ))=B−1​(X​(n))n\cdot y_{k}>\exp\left(\exp\left(\sqrt{\frac{C}{X(n)-e^{\gamma}}}\right)\right)=B^{-1}\left(X(n)\right).

The contradiction X(n⋅yk)>eγ+C⋅lnln(n⋅yk)−2X(n\cdot y_{k})>e^{\gamma}+C\cdot\ln\ln(n\cdot y_{k})^{-2} to Theorem 1.6 follows. Thus

Theorem 1.7.

Claim 1.2 follows from Condition 1.1.

Assuming Condition 1.1 a consequence of [8, Thm 5] is

Corollary 1.8.

There is no GA2 number n>5040n>5040. In other words there is no exceptional number.

Proving the absence of exceptional numbers seems to be just as difficult as proving Condition 1.1. This is no surprise because a one is an indirect proof of the other.

2 Colosally Abundant Numbers

Definition 2.1.

Rf. [62, Superabundant and colossally abundant number]

  1. 1.

    nn is SA if it meets σ−1​(n)≥σ−1​(k)\sigma_{-1}(n)\geq\sigma_{-1}(k) for all k<nk<n, rf. [64, p. 839], [51, A004394].

  2. 2.

    nn is CA if σ−1​(n)⋅n−ε≥σ−1​(k)⋅k−ε\sigma_{-1}(n)\cdot n^{-\varepsilon}\geq\sigma_{-1}(k)\cdot k^{-\varepsilon} for all kk and an ε>0\varepsilon>0, rf. [51, A004490].

By Theorem 1.3 there are infinitely many SA numbers but they are only mentioned here because the SA property suffices to determine the asymptotic behaviour of P1​(n)P_{1}\left(n\right).

Fact 2.2.
  1. 1.

    By [16, p. 68] CA numbers are SA.

  2. 2.

    If nn is SA and pp the largest prime factor in nn then p∼ln⁡np\sim\ln n by [3, Theorem 7].

Rf. [37, 38] for more information.

“A superparticular number is when a great number contains a lesser number, to which it is compared, and at the same time one part of it.” Rf. [57, p.III.6.12,n.7].

Notation 2.3.

Let F​(x,v):=1ln⁡x​ln⁡(G​(x,v))F\left(x,v\right):=\frac{1}{\ln x}\ln\left(G\left(x,v\right)\right) with G​(x,v):=1+1g​(x,v)G\left(x,v\right):=1+\frac{1}{g\left(x,v\right)}; g​(x,v):=σ​(xv)−1g\left(x,v\right):=\sigma\left(x^{v}\right)-1. In virtue of assumption 2.9 below the parameters ε\varepsilon of CA numbers belong to the set ℰ:=⋃p∈ℙ{F​(p,v);v∈ℕ}\mathcal{E}:=\bigcup\limits_{p\in\mathbb{P}}\left\{F\left(p,v\right);v\in\mathbb{N}\right\}. Write EE as decreasing sequence ℰ=(εi)i=1∞\mathcal{E}=\left(\varepsilon_{i}\right)_{i=1}^{\infty} allowing for the definition ni:=n​(εi)n_{i}:=n\left(\varepsilon_{i}\right), rf. [40, 3, 16, 7]. Additionally put qi+1:=ni+1niq_{i+1}:=\frac{n_{i+1}}{n_{i}} and gi:=G​(qi,vqi​(ni))g_{i}:=G\left(q_{i},v_{q_{i}}\left(n_{i}\right)\right) such that εi=F​(qi,vqi​(ni))=logqi⁡(gi)\varepsilon_{i}=F\left(q_{i},v_{q_{i}}\left(n_{i}\right)\right)=\log_{q_{i}}\left(g_{i}\right) and qiεi=gi=σ−1​(ni)σ−1​(ni−1)q_{i}^{\varepsilon_{i}}=g_{i}=\frac{\sigma_{-1}\left(n_{i}\right)}{\sigma_{-1}\left(n_{i-1}\right)} is superparticular. Let q0:=1=:n0q_{0}:=1=:n_{0}, ε0=1\varepsilon_{0}=1, and Li​(n):=ln⁡(ln⁡(n))ln⁡(ln⁡(ni))L_{i}\left(n\right):=\frac{\ln\left(\ln\left(n\right)\right)}{\ln\left(\ln\left(n_{i}\right)\right)}, too.

Definition 2.4.

Let fεf_{\varepsilon} denote the function x↦ε⋅x−ln⁡(ln⁡(x))x\ {\mapsto}\ \varepsilon\cdot x-\ln\left(\ln\left(x\right)\right) and Robin’s multiplier be Rj​(n,ε):=exp⁡(fε​(ln⁡n)−fε​(ln⁡nj))=(nnj)ε⋅(Lj​(n))−1R_{j}\left(n,\varepsilon\right):=\exp\left(f_{\varepsilon}\left(\ln n\right)-f_{\varepsilon}\left(\ln n_{j}\right)\right)=\left(\frac{n}{n_{j}}\right)^{\varepsilon}\cdot\left(L_{j}\left(n\right)\right)^{-1}.

Note 2.5.
  1. 1.

    The derivatives of fεf_{\varepsilon} are given by

    fε′​(x)=ε−1x⋅ln⁡(x)andfε′′​(x)=1x2​ln⁡(x)+1(x⋅ln⁡(x))2>0f_{\varepsilon}^{\prime}(x)=\varepsilon-\frac{1}{x\cdot\ln\left(x\right)}\quad\text{{and}}\quad f_{\varepsilon}^{\prime\prime}(x)=\frac{1}{x^{2}\ln\left(x\right)}+\frac{1}{\left(x\cdot\ln\left(x\right)\right)^{2}}>0

    which implies that fε∈C2​(1,∞)f_{\varepsilon}\in C^{2}\left(1,\infty\right) is convex for every ε>0\varepsilon>0.

  2. 2.

    fε​(x)→∞f_{\varepsilon}\left(x\right)\rightarrow\infty as x→1x\rightarrow 1 or as x→∞x\rightarrow\infty since logs grow slower than any power of xx.

  3. 3.

    If ε1<ε2\varepsilon_{1}<\varepsilon_{2} then fε1​(x)<fε2​(x)f_{\varepsilon_{1}}\left(x\right)<f_{\varepsilon_{2}}\left(x\right) for all xx because fε2​(x)−fε1​(x)=(ε2−ε1)⋅x>0f_{\varepsilon_{2}}\left(x\right)-f_{\varepsilon_{1}}\left(x\right)=\left(\varepsilon_{2}-\varepsilon_{1}\right)\cdot x>0. In particular fε1f_{\varepsilon_{1}} and fε2f_{\varepsilon_{2}} do not intersect if ε1≠ε2\varepsilon_{1}\neq\varepsilon_{2}.

  4. 4.

    Ri​(ni+1,εi+1)⋅Li​(ni+1)=gi+1R_{i}\left(n_{i+1},\varepsilon_{i+1}\right)\cdot L_{i}\left(n_{i+1}\right)=g_{i+1} and X​(ni)⋅Ri​(ni+1,εi+1)=X​(ni+1)X\left(n_{i}\right)\cdot R_{i}\left(n_{i+1},\varepsilon_{i+1}\right)=X\left(n_{i+1}\right).

  5. 5.

    ε=εi+1\varepsilon=\varepsilon_{i+1} if σ−1​(ni)⋅ni−ε=σ−1​(ni+1)⋅ni+1−ε\sigma_{-1}(n_{i})\cdot n_{i}^{-\varepsilon}=\sigma_{-1}(n_{i+1})\cdot n_{i+1}^{-\varepsilon}.

Proposition 2.6.

([46, §3, Prop 1], [44, p. 237])

Colosally abundant numbers maximise XX, i.e. X​(n)≤max⁡(X​(ni),X​(ni+1))X(n)\leq\max\left(X(n_{i}),X(n_{i+1})\right) if n∈[ni,ni+1]ℕn\in\left[n_{i},n_{i+1}\right]_{\mathbb{N}}.

Proof.

X​(n)≤X​(nj)X(n)\leq X(n_{j}) follows from Rj​(n,ε)≤1R_{j}\left(n,\varepsilon\right)\leq 1 since X​(n)≤X​(nj)​Rj​(n,ε)X\left(n\right)\leq X\left(n_{j}\right)R_{j}\left(n,\varepsilon\right) follows from σ−1​(n)⋅n−ε≤σ−1​(nj)⋅nj−ε\sigma_{-1}(n)\cdot n^{-\varepsilon}\leq\sigma_{-1}(n_{j})\cdot n_{j}^{-\varepsilon} with Note 2.5, #4/5 if n∈[ni,ni+1]ℕn\in\left[n_{i},n_{i+1}\right]_{\mathbb{N}}, ε=εi+1\varepsilon=\varepsilon_{i+1}, and j∈{i,i+1}j\in\left\{i,i+1\right\}. For nεln⁡ln⁡n≤njεln⁡ln⁡nj\frac{n^{\varepsilon}}{\ln\ln n}\leq\frac{n_{j}^{\varepsilon}}{\ln\ln n_{j}} it is sufficient to show the consequence fε​(ln⁡n)≤max⁡(fε​(ln⁡ni),fε​(ln⁡ni+1))f_{\varepsilon}\left(\ln n\right)\leq\max\left(f_{\varepsilon}\left(\ln n_{i}\right),f_{\varepsilon}\left(\ln n_{i+1}\right)\right) of Note 2.5, #1. ∎

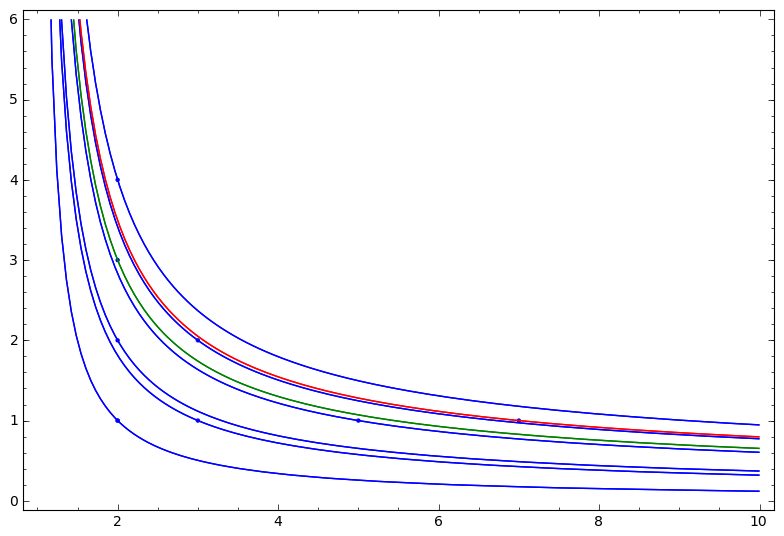
Refer to caption
Refer to caption
Figure 2.1: The surface ε=F​(x,v)\varepsilon=F\left(x,v\right)

Based on this setup the algorithm computing the sequence (ni)i\left(n_{i}\right)_{i} of CA numbers seems to be well-understood, [39, 3, 16, 46, 40, 37, 7, 38, 13, 8, 9, 51]. Nevertheless there is the open

Question 2.7.
  1. 1.

    Can the algorithm find a new violation of RIE? (Does one exist?)

  2. 2.

    Do two consecutive CA numbers exist whose quotient qiq_{i} is semiprime?

Item 2. has been given a negative answer under the following Conjecture, rf. [3, p. 455].

Conjecture 2.8.

(Four Exponentials)

If x1x_{1}, x2x_{2} and y1y_{1}, y2y_{2} are two pairs of complex numbers, with each pair being linearly independent over the rational numbers, then at least one of the following four numbers is transcendental:

ex1​y1,ex1​y2,ex2​y1,ex2​y2,e^{x_{1}y_{1}},e^{x_{1}y_{2}},e^{x_{2}y_{1}},e^{x_{2}y_{2}}\,,

rf. [16, p. 71], [27, ch. 2], [60, ch. 2], [61, Section 1.3].

Semiprime quotients cause unexpected difficulties. Therefore I assume a special case of Conjecture 2.8.

Assumption 2.9.

(Alaoglu and Erdős)

For any two distinct prime numbers pp and qq, the only real numbers tt for which both ptp^{t} and qtq^{t} are rational are the positive integers.

Conclusion 2.10.

qiq_{i} is prime for all ii, rf. [62, Colossally abundant number].

3 Subsequent Maximisers

3.1 Extending Robin’s Method

Robin’s crucial argument was Proposition 2.6. A Transfer to Condition 1.1 follows.

Definition 3.1.

Let 𝒬i,k:=∏j=1kqi+j\mathcal{Q}_{i,k}:=\prod\limits_{j=1}^{k}q_{i+j}, ℛi,k:=∏j=1kRi+j−1​(ni+j,εi+j)\mathcal{R}_{i,k}:=\prod\limits_{j=1}^{k}R_{i+j-1}\left(n_{i+j},\varepsilon_{i+j}\right), ℒi,k:=∏j=1kLi+j−1​(ni+j)=ln⁡ln⁡ni+kln⁡ln⁡ni\mathcal{L}_{i,k}:=\prod\limits_{j=1}^{k}L_{i+j-1}\left(n_{i+j}\right)=\frac{\ln\ln n_{i+k}}{\ln\ln n_{i}}, and 𝒢i,k:=∏j=1kgi+j=σ−1​(ni+k)σ−1​(ni)\mathcal{G}_{i,k}:=\prod\limits_{j=1}^{k}g_{i+j}=\frac{\sigma_{-1}\left(n_{i+k}\right)}{\sigma_{-1}\left(n_{i}\right)}. Contextually write 𝒳i,⋅\mathcal{X}_{i,\cdot} for (𝒳i,j)j∈ℕ\left(\mathcal{X}_{i,j}\right)_{j\in\mathbb{N}} or {𝒳i,j}j∈ℕ\left\{\mathcal{X}_{i,j}\right\}_{j\in\mathbb{N}} if 𝒳∈{ℛ,𝒢,ℒ,𝒬,𝒟}\mathcal{X}\in\left\{\mathcal{R},\mathcal{G},\mathcal{L},\mathcal{Q},\mathcal{D}\right\} where 𝒟i,k:=𝒢i,k−ℒi,k\mathcal{D}_{i,k}:=\mathcal{G}_{i,k}-\mathcal{L}_{i,k}. Put ki:=inf{k∈ℕ;ℛi,k≥1}k_{i}:=\inf\left\{k\in\mathbb{N};\mathcal{R}_{i,k}\geq 1\right\}.

Fact.

𝒢i,kℒi,k=σ−1​(ni+k)ln⁡ln⁡ni+k⋅ln⁡ln⁡niσ−1​(ni)=X​(ni+k)X​(ni)\frac{\mathcal{G}_{i,k}}{\mathcal{L}_{i,k}}=\frac{\sigma_{-1}\left(n_{i+k}\right)}{\ln\ln n_{i+k}}\cdot\frac{\ln\ln n_{i}}{\sigma_{-1}\left(n_{i}\right)}=\frac{X\left(n_{i+k}\right)}{X\left(n_{i}\right)}.

Lemma 3.2.

ℛi,k⋅ℒi,k=𝒢i,k\mathcal{R}_{i,k}\cdot\mathcal{L}_{i,k}=\mathcal{G}_{i,k} and X​(ni)⋅ℛi,k=X​(ni+k)X\left(n_{i}\right)\cdot\mathcal{R}_{i,k}=X\left(n_{i+k}\right).

Proof.

By induction on kk using Lemma 2.5, #4.∎

Corollary 3.3.

If ki<∞k_{i}<\infty then 𝒢i,ki≥ℒi,ki\mathcal{G}_{i,k_{i}}\geq\mathcal{L}_{i,k_{i}} so 𝒢i,k<ℒi,k\mathcal{G}_{i,k}<\mathcal{L}_{i,k} for all kk if ki=∞k_{i}=\infty but k≥kik\geq k_{i} if 𝒟i,k≥0\mathcal{D}_{i,k}\geq 0.

Theorem 3.4.

nin_{i} is exceptional if and only if ki=∞k_{i}=\infty and i>8i>8.

Proof.

X​(ni)>X​(ni+k)X\left(n_{i}\right)>X\left(n_{i+k}\right) for all kk iff nin_{i} is exceptional. On the the other hand ℛi,k<1\mathcal{R}_{i,k}<1 for all kk iff ki=∞k_{i}=\infty and the claim follows with Lemma 3.2.∎

Condition 3.5.

ki<∞k_{i}<\infty for all i>8i>8.

Theorem 3.6.

Conditions 3.5 and 3.7 are equivalent to Condition 1.1 with n=nin=n_{i} and x=𝒬i,kix=\mathcal{Q}_{i,k_{i}}.

Proof.

For the bounds on ii consider n8=5040n_{8}=5040 and section 3.2.

All other statements follow from Lemma 3.2.∎

Condition 3.7.

For every nin_{i} with i>143215i>143215 there is some kk such that 𝒟i,k≥0\mathcal{D}_{i,k}\geq 0.

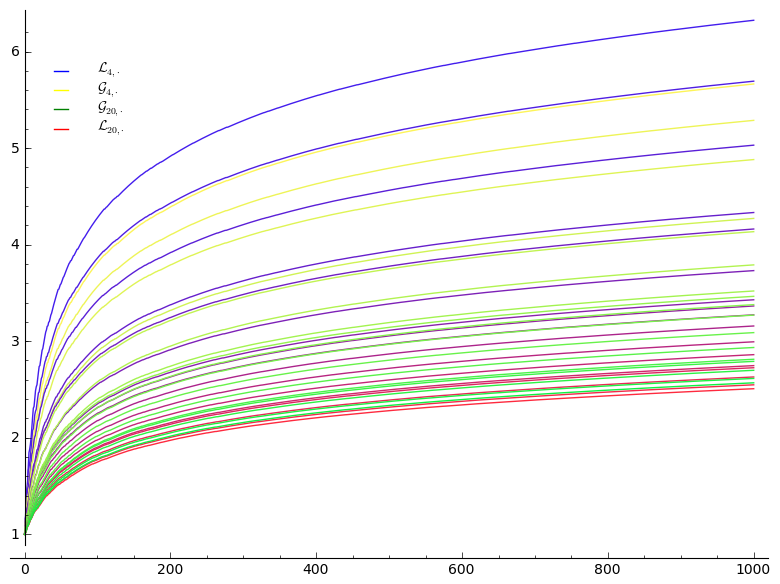
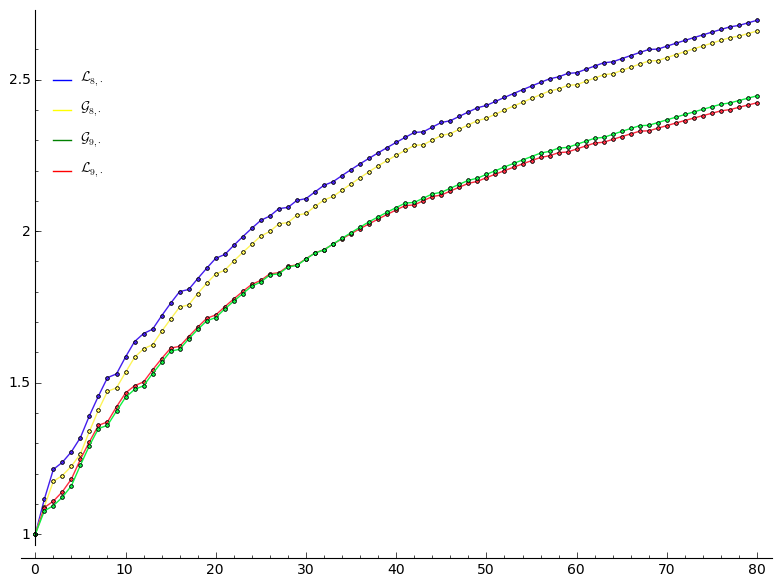
Refer to caption
Refer to caption
Figure 3.1: “The 𝒢i,⋅\mathcal{G}_{i,\cdot}’s are enclosed by the ℒi,⋅\mathcal{L}_{i,\cdot}’s”

3.2 Number Crunching

  • 1.

    Sage led me to my first results, [55]. My algorithm passed the CA numbers in table 3.2. According to [37, 38] T.D.Noe’s form (αv)v=1n\left(\alpha_{v}\right)_{v=1}^{n} represents ∏v=1n∏j=π​(αv+1)+1π​(αv)pjv\prod\limits_{v=1}^{n}\prod\limits_{j=\pi(\alpha_{v+1})+1}^{\pi(\alpha_{v})}p_{j}^{v} if α\alpha contains no zeros and αn+1=0∧p0=1\alpha_{n+1}=0\wedge p_{0}=1. Thus n8=(7,3,0,2)\qquad n_{8}=\left(7,3,0,2\right), n508=(3257,73,19,7,5,02,3,05,2)n_{508}=\left(3257,73,19,7,5,0^{2},3,0^{5},2\right),
    n9=(11,3,0,2)n_{9}=(11,3,0,2), n42=(101,13,5,0,3,02,2)n_{42}=(101,13,5,0,3,0^{2},2), n2386=(20359,193,37,13,7,0,5,02,3,06,2)n_{2386}=\left(20359,193,37,13,7,0,5,0^{2},3,0^{6},2\right),
    n143215=(1911373,1907,173,47,23,13,0,7,0,5,04,3,08,2)n_{143215}=(1911373,1907,173,47,23,13,0,7,0,5,0^{4},3,0^{8},2), and n13=(13,5,3,0,2)n_{13}=\left(13,5,3,0,2\right).

n8n_{8} n508n_{508} n9n_{9} n13n_{13} n42n_{42} n2386n_{2386} n143215n_{143215}
v2​(⋅)v_{2}(\cdot)\quad 4 14 4 5 8 17 24
ln\ln\quad 8.5251 3274.0 10.9230 16.889 107.7176 20432.8 1912150.6
ln⁡(P1​(⋅))\ln(P_{1}\left(\cdot\right))\quad 1.9459 8.0885 2.3978 2.5649 4.6151 9.9212 14.4633
ln⁡(−1ε​ln⁡(ε))\ln\left(-\frac{1}{\varepsilon\ln\left(\varepsilon\right)}\right)\quad 1.9356 7.8588 2.1174 2.5342 4.3330 9.7132 14.2938
ln⁡ln\ln\ln\quad 2.1430 8.0937 2.3908 2.8266 4.6795 9.9249 14.4637
kik_{i} ∞\infty 1 33 1 1 1 1
lg\lg\quad 3.7024 1421.9 4.7438 7.335 46.7811 8873.60 830436.46
lg⁡lg\lg\lg\quad 0.5684 3.1528 0.6761 0.8654 1.6700 3.9480 5.9193
σ−1\sigma_{-1}\quad 3.8380 14.3887 4.1870 4.8559 8.1962 17.6663 25.7599
XX\quad 1.79097 1.7777 1.7512 1.7179 1.7515 1.7800001 1.7810000003
BB\quad 1.9047 1.79096 1.8944 1.8621 1.8106 1.7877 1.7842
ln⁡ln⁡B−1∘X\ln\ln B^{-1}\circ X\quad 8.0913                                                            undefined since X​(n)<eγ=1.7811X\left(n\right)<e^{\gamma}=1.7811
Table 1: Statistics of some CA numbers
Theorem 3.8.

For every CA nin_{i} if i≤143215i\leq 143215 there is a subsequent CA ni+jn_{i+j} such that X​(ni)<X​(ni+j)X(n_{i})<X(n_{i+j}).

Proof.

RIE​(n)\textrm{RIE}\left(n\right) was confirmed in every loop. (Not shown in Appendix A.) ∎

  • 2.

    Keith Briggs reported to me: "E.g. the following is a CA number:

    n=241⋅325⋅517⋅714⋅1111⋅1310⋅179​⋯​238​⋯​377​⋯​536​⋯​1015​⋯⋯​2394​⋯​8873​⋯​77892​⋯​5623991​⋯​1622163421870\begin{array}[]{l}n=2^{41}\cdot 3^{25}\cdot 5^{17}\cdot 7^{14}\cdot 11^{11}\cdot 13^{10}\cdot 17^{9}\cdots 23^{8}\cdots 37^{7}\cdots 53^{6}\cdots 101^{5}\cdots\\ \hphantom{n_{\textrm{Br}}=\cdots 101^{5}}\cdots 239^{4}\cdots 887^{3}\cdots 7789^{2}\cdots 562399^{1}\cdots 162216342187^{0}\end{array}

    with loglog nn about 26." Denote it by nBrn_{\textrm{Br}} and call the tuple (2, 0150^{15}, 3, 070^{7}, 5, 020^{2}, 7, 020^{2}, 11, 13, 17, 23, 37, 53, 101, 239, 887, 7789, 562399, 162216342187) bottom-up form. Since he reached about 10101010^{10^{10}} according to [7, §3]

    lg⁡lg⁡nBr≈lg⁡(lg⁡(exp⁡(exp⁡(26))))=lg⁡(exp⁡(26)ln⁡10)=1ln⁡10​(26−ln⁡ln⁡10)≈10.9294\lg\lg n_{\textrm{Br}}\approx\lg\left(\lg\left(\exp\left(\exp\left(26\right)\right)\right)\right)=\lg\left(\frac{\exp\left(26\right)}{\ln 10}\right)=\frac{1}{\ln 10}\left(26-\ln\ln 10\right)\approx 10.9294

    reveals ln⁡ln⁡nBr≈26\ln\ln n_{\textrm{Br}}\approx 26 in compliance with [56, Section 10.1.2] and Fact 2.2. This was significantly more than the theoretically obtained bound 108576<e1974710^{8576}<e^{19747} from [8, Corollary 1] which my rather short calculation capped, too. Noe’s top-down representation is

    (162216342179,562361,7759,883,233,97,47,31,19,13,11,02,7,02,5,07,3,015,2).\left(162216342179,562361,7759,883,233,97,47,31,19,13,11,0^{2},7,0^{2},5,0^{7},3,0^{15},2\right).
    Theorem 3.9.

    For every CA nin_{i} such that ln⁡ln⁡ni≤25<26\ln\ln n_{i}\leq 25<26 there is a subsequent CA ni+jn_{i+j} such that X​(ni)<X​(ni+j)X(n_{i})<X(n_{i+j}).

i+ji+j v2v_{2} qi+jq_{i+j} pp ln\ln vi,jv_{i,j} gi+jg_{i+j} 𝒢8,j\mathcal{G}_{8,j} εi+j\varepsilon_{i+j} l​lll ℒ8,j\mathcal{L}_{8,j} −𝒟9,j-\mathcal{D}_{9,j}
8 4 2 7 8.5 4 31:30 1 4.73d2d^{2} 2.143 1
9 4 11 11 10.9 1 12:11 1.090 3.62d2d^{2} 2.390 1.115 1
10 4 13 13 13.4 1 14:13 1.174 2.88d2d^{2} 2.601 1.214 1.13d2d^{2}
11 5 2 13 14.1 5 63:62 1.193 2.31d2d^{2} 2.651 1.237 1.48d2d^{2}
12 5 3 13 15.2 3 40:39 1.224 2.30d2d^{2} 2.726 1.272 1.80d2d^{2}
13 5 5 13 16.8 2 31:30 1.265 2.03d2d^{2} 2.826 1.319 2.25d2d^{2}
14 5 17 17 19.7 1 18:17 1.339 2.01d2d^{2} 2.981 1.391 1.91d2d^{2}
15 5 19 19 22.6 1 20:19 1.410 1.74d2d^{2} 3.120 1.456 1.27d2d^{2}
16 5 23 23 25.8 1 24:23 1.471 1.35d2d^{2} 3.250 1.516 1.07d2d^{2}
17 6 2 23 26.4 6 127:126 1.483 1.12d2d^{2} 3.276 1.529 1.11d2d^{2}
18 6 29 29 29.8 1 30:29 1.534 1.00d2d^{2} 3.396 1.584 1.42d2d^{2}
19 6 31 31 33.2 1 32:31 1.583 9.24d3d^{3} 3.505 1.635 1.44d2d^{2}
20 6 7 31 35.2 2 57:56 1.612 9.09d3d^{3} 3.562 1.662 1.22d2d^{2}
21 6 3 31 36.3 4 121:120 1.625 7.55d3d^{3} 3.592 1.676 1.27d2d^{2}
22 6 37 37 39.9 1 38:37 1.669 7.38d3d^{3} 3.687 1.720 1.21d2d^{2}
23 6 41 41 43.6 1 42:41 1.710 6.48d3d^{3} 3.776 1.762 1.19d2d^{2}
24 6 43 43 47.4 1 44:43 1.749 6.11d3d^{3} 3.859 1.800 1.00d2d^{2}
25 7 2 43 48.1 7 255:254 1.756 5.66d3d^{3} 3.873 1.807 9.82d3d^{3}
26 7 47 47 51.9 1 48:47 1.794 5.46d3d^{3} 3.950 1.843 7.75d3d^{3}
27 7 53 53 55.9 1 54:53 1.828 4.70d3d^{3} 4.024 1.877 7.51d3d^{3}
28 7 59 59 60.0 1 60:59 1.858 4.12d3d^{3} 4.094 1.910 8.54d3d^{3}
29 7 5 59 61.6 3 156:155 1.870 3.99d3d^{3} 4.121 1.923 8.61d3d^{3}
30 7 61 61 65.7 1 62:61 1.901 3.95d3d^{3} 4.185 1.953 7.51d3d^{3}
31 7 67 67 69.9 1 68:67 1.930 3.52d3d^{3} 4.247 1.982 7.42d3d^{3}
32 7 71 71 74.2 1 72:71 1.957 3.28d3d^{3} 4.306 2.009 7.25d3d^{3}
33 7 73 73 78.4 1 74:73 1.984 3.17d3d^{3} 4.363 2.035 6.18d3d^{3}
34 7 11 73 80.8 2 133:132 1.999 3.14d3d^{3} 4.393 2.049 4.99d3d^{3}
35 7 79 79 85.2 1 80:79 2.024 2.87d3d^{3} 4.445 2.074 3.79d3d^{3}
36 8 2 79 85.9 8 511:510 2.028 2.82d3d^{3} 4.453 2.078 3.54d3d^{3}
37 8 83 83 90.3 1 84:83 2.052 2.71d3d^{3} 4.503 2.101 2.11d3d^{3}
38 8 3 83 91.4 5 364:363 2.058 2.50d3d^{3} 4.516 2.107 1.98d3d^{3}
39 8 89 89 95.9 1 90:89 2.081 2.48d3d^{3} 4.563 2.129 8.18d4d^{4}
40 8 97 97 100 1 98:97 2.103 2.24d3d^{3} 4.610 2.151 6.26d4d^{4}
41 8 13 97 103 2 183:182 2.114 2.13d3d^{3} 4.635 2.163 5.70d4d^{4}
42 8 101 101 107 1 102:101 2.135 2.13d3d^{3} 4.679 2.183 -3.05d4d^{4}
⋮\vdots ⋮\vdots ⋮\vdots
507 14 3253 3253 3265 1 3254:3253 3.747 3.80d5d^{5} 8,091 3.775 -5.12d2d^{2}
508 14 3257 3257 3274 1 3258:3257 3.748 3.79d5d^{5} 8.093 3.776 -5.12d2d^{2}
Table 3: Quotients qi+jq_{i+j} of CA numbers, note k9=33k_{9}=33, [51, A073751] and abbreviate p=P1​(ni+j)p=P_{1}\left(n_{i+j}\right), l​l=ln⁡ln⁡ni+jll=\ln\ln n_{i+j}, vi,j=vqi+j​(ni+j)v_{i,j}=v_{q_{i+j}}\left(n_{i+j}\right) and d=10−1d=10^{-1}.

4 The Question of Life

The next Lemma has a long track in my notes since the preprint of [13, Lemma 6.1] was not hard to complement in the present setup.

Proposition 4.1.

ki=1k_{i}=1 if

(∑l=1vi,1qi+1l)​ln⁡qi+1≤ln⁡ni⋅ln⁡ln⁡ni.\left(\sum\limits_{l=1}^{v_{i,1}}q_{i+1}^{l}\right)\ln q_{i+1}\leq\ln n_{i}\cdot\ln\ln n_{i}\,.
Proof.

𝒢i,1=1+(∑l=1vi,1qi+1l)−1≥1+ln⁡𝒬i,1ln⁡ni⋅ln⁡ln⁡ni\mathcal{G}_{i,1}=1+\left(\sum\limits_{l=1}^{v_{i,1}}q_{i+1}^{l}\right)^{-1}\geq 1+\frac{\ln\mathcal{Q}_{i,1}}{\ln n_{i}\cdot\ln\ln n_{i}} by assumption. A Taylor approximation of logln⁡ni⁡(ln⁡ni+h)\log_{\ln n_{i}}\left(\ln n_{i}+h\right) for h=ln⁡(𝒬i,k)h=\ln\left(\mathcal{Q}_{i,k}\right) has remainder term −12⋅(ln⁡𝒬i,kln⁡ni+ϑ​ln⁡𝒬i,k)2⋅1ln⁡ln⁡ni<0-\frac{1}{2}\cdot\left(\frac{\ln\mathcal{Q}_{i,k}}{\ln n_{i}+\vartheta\ln\mathcal{Q}_{i,k}}\right)^{2}\cdot\frac{1}{\ln\ln n_{i}}<0. Therefore the case k=1k=1 yields 𝒟i,1≥0\mathcal{D}_{i,1}\geq 0. ∎

Most recently, Morkotun demonstrated in [33, Theorem 2] how to include all prime factors of nin_{i} without requiring the CA or SA property of nin_{i}. The existence of a sequence on which XX increases follows from Grönwall’s theorem if exceptional numbers do not exist. But if there are exceptional numbers XX will stop to take larger values because of Robin’s unconditional bound. [33, (4)] is often met but once in a while abundant numbers have prime factors larger than ln⁡n\ln n in which case it would have been possible to argue with Lemma 4.2 below. Likewise it is very possible that the sequence of ii’s with ki>1k_{i}>1 is infinite although the gaps between regions with ki>1k_{i}>1 may be large.

Lemma 4.2.

[13, Lemma 6.1]: If ln⁡n<P1​(n)\ln n<P_{1}\left(n\right) for a tt-free nn with t≥2t\geq 2 then R​I​E​(n)RIE\left(n\right).

However, applying either the Proposition above or Morkotun’s condition of RIE it is sufficient to consider the greatest primes pp with vp​(n)=vv_{p}\left(n\right)=v for each valuation vv between 1=vP1​(ni)​(ni)1=v_{P_{1}\left(n_{i}\right)}\left(n_{i}\right) and v2​(ni)v_{2}\left(n_{i}\right). This is reflected by Noe’s representation of SA numbers in section 3.2. In each loop the CA numbers algorithm chooses the qiq_{i} for which εi+1=1ln⁡qi+1​ln⁡gi+1\varepsilon_{i+1}=\frac{1}{\ln q_{i+1}}\ln g_{i+1} is maximal when qi+1q_{i+1} varies over the primes pp for which n=ni​pn=n_{i}p meets vq​(n)<vp​(n)v_{q}\left(n\right)<v_{p}\left(n\right) if q>pq>p.

4.1 Extremely Abundant Numbers

The recent papers [35, 34] will be summarised in the context of the present one. After some quotations from the follow-up paper this section employs the numbers of the text modules in [35].

Definition.

(2.1): [34, Def. 1.2, 1.3, and 1.8]

  1. 1.

    n∈X​An\in XA iff X​(n)>X​(m)X\left(n\right)>X\left(m\right) for m∈[10080,n]ℕm\in\left[10080,n\right]_{\mathbb{N}},

  2. 2.

    n∈X​A′n\in XA^{\prime} iff σ−1​(n)σ−1​(m)>1+ln⁡n−ln⁡mln⁡n⋅ln⁡ln⁡m\frac{\sigma_{-1}(n)}{\sigma_{-1}(m)}>1+\frac{\ln n-\ln m}{\ln n\cdot\ln\ln m} for m=max⁡{k∈X​A′;k<n}m=\max\left\{k\in XA^{\prime};k<n\right\}, and

  3. 3.

    n∈X​A′′n\in XA^{\prime\prime} iff σ−1​(n)σ−1​(m)>1+2​ln⁡n−ln⁡m(ln⁡n+ln⁡m)⋅ln⁡ln⁡m\frac{\sigma_{-1}(n)}{\sigma_{-1}(m)}>1+2\frac{\ln n-\ln m}{\left(\ln n+\ln m\right)\cdot\ln\ln m} for m=max⁡{k∈X​A′′;k<n}m=\max\left\{k\in XA^{\prime\prime};k<n\right\}.

Conclusion.

[34, (6)] X​A⊆X​A′⊆S​AXA\subseteq XA^{\prime}\subseteq SA.

Lemma.

[34, Lemma 1.4] X​A′XA^{\prime} is well-defined.

Theorem.

[34, Theorem 1.7] |X​A′|=∞\left|XA^{\prime}\right|=\infty.

Theorem.

(2.3): The least n>5040n>5040 such that R​I​E​(n)RIE\left(n\right) is false is in XA.

Theorem.

(2.4): R​H⟺|X​A|=∞RH\Longleftrightarrow\left|XA\right|=\infty.

Theorem.

(4.28): R​H⟹|C​A∩X​A|=∞RH\Longrightarrow\left|CA\cap XA\right|=\infty.

Theorem.

(4.31): |n∈CA;lnn<P1(n)|=∞\left|n\in CA;\ln n<P_{1}\left(n\right)\right|=\infty.

Theorem.

(4.32): n∈X​A⟹P1​(n)<ln⁡nn\in XA\Longrightarrow P_{1}\left(n\right)<\ln n.

Theorem.

(4.34): |C​A∖X​A|=∞\left|CA\setminus XA\right|=\infty.

Essentially Theorem (2.4) asserts the necessity and sufficiency of Condition 1.1 for RH. Theorem (4.28) provides a necessary condition by restriction to CA numbers without mentioning the obvious reverse implication in virtue of Theorem (2.4). In particular, |C​A∖X​A|=∞\left|CA\setminus XA\right|=\infty and |C​A∩X​A|=∞\left|CA\cap XA\right|=\infty in case of RH make this case delicate. The advantage is the minimality condition of Theorem (2.3) at the cost of loosing the availability of an algorithm that computes the sequence of hypothetic counterexamples of RIE.

4.2 Stronger Ingredients

The goal of this section is to show that Condition 3.7 is true. The subsection’s title insinuates Assumption 4.5. The easiest step towards it was quoting Lemma 4.2.

Thus RIE is not violated unless the prime divisors of nin_{i} cumulate too densely and n9n_{9} is the only CA number in section 3.2 with P1​(n)>ln⁡nP_{1}(n)>\ln n. On the other hand by [3, Thm 2] there must not be too many small prime divisors for RIE.

Theorem 4.3.

(Mertens, [32], [20, Thm 427-429]) The Meissel–Mertens constant is given by

B1=limn→∞(∑p≤n1p−ln⁡ln⁡n)=γ+∑p(ln⁡(1−1p)+1p)=0.26149 72128 47642​….B_{1}=\lim_{n\to\infty}\left(\sum_{p\leq n}\frac{1}{p}-\ln\ln n\right)=\gamma+\sum_{p}\left(\ln\left(1-\frac{1}{p}\right)+\frac{1}{p}\right)=0.26149\,72128\,47642....
Note.

Interesting additional references are [58] and [29, §1 (1)].

It can be considered reasonable to assume that 𝒢i,⋅\mathcal{G}_{i,\cdot} grows at least as fast as ℒi,⋅\mathcal{L}_{i,\cdot} for increasing kk. This conjecture is based on Theorem 4.3 and the culmination of the work on the asymptotics of pkp_{k}, [48, 47, 45, 31] in P. Dusart’s statement pk≥k​(ln⁡k+ln⁡ln⁡k−1)p_{k}\geq k\left(\ln k+\ln\ln k-1\right), [15] after pn≥n​(ln⁡n+ln⁡ln⁡n−1+o​(ln⁡ln⁡nln⁡n))+kp_{n}\geq n\left(\ln n+\ln\ln n-1+o\left(\frac{\ln\ln n}{\ln n}\right)\right)+k had become available in [41] without guaranteeing Dusart’s lower bound, yet.

Lemma 4.4.

𝒢i,k→∞\mathcal{G}_{i,k}\rightarrow\infty and ℒi,k→∞\mathcal{L}_{i,k}\rightarrow\infty as k→∞k\rightarrow\infty and 𝒟i,1>0\mathcal{D}_{i,1}>0 if and only i

gi+1−1>2​a​r​t​a​n​h​(ln⁡qi+12​ln⁡ni+ln⁡qi+1)g_{i+1}-1>2\mathrm{artanh}\left(\frac{\ln q_{i+1}}{2\ln n_{i}+\ln q_{i+1}}\right).

Proof.

For every prime p>P1​(ni)p>P_{1}\left(n_{i}\right) there is some kk such that vp​(ni+k)=1v_{p}\left(n_{i+k}\right)=1. Therefore 1p\frac{1}{p} occurs as a summand when expanding 𝒢i,k:=∏j=1k(1+1gvi,j​(x))\mathcal{G}_{i,k}:=\prod\limits_{j=1}^{k}\left(1+\frac{1}{g_{v_{i,j}}\left(x\right)}\right) which must be a bound for the summed reciprocals of subsequent primes, i.e. Ri,k:=∑{p−1;P1​(ni)<p<P1​(ni+k)}<𝒢i,kR_{i,k}:=\sum\left\{p^{-1};P_{1}\left(n_{i}\right)<p<P_{1}\left(n_{i+k}\right)\right\}<\mathcal{G}_{i,k}. But Ri,k→∞R_{i,k}\rightarrow\infty as k→∞k\rightarrow\infty by Theorem 4.3. With y=1+x1−xy=\frac{1+x}{1-x} iff x=y−1y+1x=\frac{y-1}{y+1} and ln⁡(y)=2​artanh⁡(x)\ln(y)=2\operatorname{artanh}\left(x\right)

ℒi,k=logln⁡ni⁡(ln⁡ni+k)=1+logln⁡ni⁡(1+ln⁡𝒬i,kln⁡ni)\mathcal{L}_{i,k}=\log_{\ln n_{i}}\left(\ln n_{i+k}\right)=1+\log_{\ln n_{i}}\left(1+\frac{\ln\mathcal{Q}_{i,k}}{\ln n_{i}}\right)

can be expanded to

loga⁡(a+z)−1=2ln⁡a​(z2​a+z+13​(z2​a+z)3+15​(z2​a+z)5+⋯)\log_{a}\left(a+z\right)-1=\frac{2}{\ln a}\left(\frac{z}{2a+z}+\frac{1}{3}\left(\frac{z}{2a+z}\right)^{3}+\frac{1}{5}\left(\frac{z}{2a+z}\right)^{5}+\cdots\right)

for a=ln⁡ni>0a=\ln n_{i}>0 and z=ln⁡𝒬i,k≥−az=\ln\mathcal{Q}_{i,k}\geq-a, rf. [1, 4.1.29]. The conclusion can be drawn by using 𝒢i,1−1=gi+1−1\mathcal{G}_{i,1}-1=g_{i+1}-1. (I came across the last formula in some book dealing with elliptic functions, too. Unfortunately I seem to be unable to find it again.)∎

Assumption 4.5.

𝒟i,⋅\mathcal{D}_{i,\cdot} has at most one change of sign.

This is quite a strong assumtion. Given Littlewood’s theorem on the difference π​(x)−Li⁡(x)\pi(x)-\operatorname{Li}(x), [30] and Robin’s theorem on ∑{p−1;n≥p∈ℙ}−ln⁡ln⁡n−B1\sum\left\{p^{-1};n\geq p\in\mathbb{P}\right\}-\ln\ln n-B_{1}, [44, Théorème 2] it makes sense to assume the opposite. Viewing B1B_{1} as safty buffer between ∑{p−1;n≥p∈ℙ}\sum\left\{p^{-1};n\geq p\in\mathbb{P}\right\} and ln⁡ln⁡n\ln\ln n may render Assumption 4.5 reasonable and it could probably be deduced from [35, Thm 4.21] if its implied constant is not too large.

In virtue of Theorem 3.6 it is easy to derive Condition 1.1 from Assumption 4.5. For this the key is to derive

∀k≥ki:ln⁡qi+k+1>(ln⁡ni+1)𝒢i+1,k−(ln⁡ni)𝒢i,k>(ln⁡qi+1)𝒢i+1,k+(ln⁡ni)𝒢i+1,k−(ln⁡ni)𝒢i,k\begin{array}[]{rl}\forall k\geq k_{i}:\;\ln q_{i+k+1}&>\left(\ln n_{i+1}\right)^{\mathcal{G}_{i+1,k}}-\left(\ln n_{i}\right)^{\mathcal{G}_{i,k}}\\ &>\left(\ln q_{i+1}\right)^{\mathcal{G}_{i+1,k}}+\left(\ln n_{i}\right)^{\mathcal{G}_{i+1,k}}-\left(\ln n_{i}\right)^{\mathcal{G}_{i,k}}\end{array}

from ki<∞k_{i}<\infty and ki+1=∞k_{i+1}=\infty. This in turn can be done with the equivalence of 𝒟i,k>0\mathcal{D}_{i,k}>0 and ln⁡𝒬i,k<(ln⁡ni)G​(qi+1,vi,1)⋅⋯⋅G​(qi+k,vi,k)−ln⁡ni\ln\mathcal{Q}_{i,k}<\left(\ln n_{i}\right)^{G\left(q_{i+1},v_{i,1}\right)\cdot\cdots\cdot G\left(q_{i+k},v_{i,k}\right)}-\ln n_{i}. Therefore if ki+1=∞k_{i+1}=\infty then small primes could occur only finitely often in the sequence (qi)i=1∞\left(q_{i}\right)_{i=1}^{\infty} which contradicts the CA numbers algorithm. It should have been possible to reduce Assumption 4.5 to requiring that 𝒟i,⋅\mathcal{D}_{i,\cdot} has only finitely many changes of sign the last of which being from - to +. However, Assumption 4.5 remains undecided.

The idea that ℒi,k\mathcal{L}_{i,k} converges faster to 1 than 𝒢i,k\mathcal{G}_{i,k} as i→∞i\rightarrow\infty - or equivalently 𝒢i,⋅\mathcal{G}_{i,\cdot} does not grow slower than ℒi,⋅\mathcal{L}_{i,\cdot} - was motivated by Figure 3.1 which covers a much too small part for a reasonable confidence level. Another way to express the higher speed of convergence is the next claim which is equivalent to Claim 1.2.

Claim 4.6.

i>8i>8 and ki+1<∞k_{i+1}<\infty if ki<∞k_{i}<\infty for some i>2i>2.

By Theorem 3.6 this claim is sufficient for Claim 1.2. Conversely it is necessary as can be seen with Condition 3.5 and section 3.2, too.

4.3 Oscillation Theorems

Clearly, everything works fine if RH is true. An indirect proof with osciallation theorems like [36, Corollaire 1], [44, Sec. 4], or [18, 4] will be proposed by showing that the minimal oscillations force 𝒢i,k\mathcal{G}_{i,k} above ℒi,k\mathcal{L}_{i,k} for kk sufficiently large. After all, Voros reported in [59, Ch. 11] that the amplitude of Keiper’s sequence (λn)n\left(\lambda_{n}\right)_{n} grows exponentially, [22, 28, 6].

Definition 4.7.

[19, 26]

  1. 1.

    f​(x)=Ω±​(g​(x))f(x)=\Omega_{\pm}(g(x)) (x→∞)\left(x\to\infty\right) means that both f​(x)=Ω+​(g​(x))f(x)=\Omega_{+}(g(x)) and f​(x)=Ω−​(g​(x))f(x)=\Omega_{-}(g(x))(x→∞)\left(x\to\infty\right) are valid where

    • •

      f​(x)=Ω+​(g​(x))​(x→∞)⇌lim supx→∞f​(x)g​(x)>0​andf(x)=\Omega_{+}(g(x))\;\left(x\to\infty\right)\quad\rightleftharpoons\quad\limsup\limits_{x\to\infty}\frac{f\left(x\right)}{g\left(x\right)}>0\;\textrm{and}

    • •

      f​(x)=Ω−​(g​(x))​(x→∞)⇌lim infx→∞f​(x)g​(x)<0.f\left(x\right)=\Omega_{-}(g(x))\;\left(x\to\infty\right)\quad\rightleftharpoons\quad\liminf\limits_{x\to\infty}\frac{f\left(x\right)}{g\left(x\right)}<0\,.

  2. 2.

    For θ:=sup{ℜ(z);z∈ℂ,ζ(z)=0}\theta:=\sup\left\{\Re\left(z\right);z\in\mathbb{C},\,\zeta\left(z\right)=0\right\} the set [1−θ,θ]+i​ℝ\left[1-\theta,\theta\right]+i\mathbb{R} will be called very critical strip.

Obviously RH is true if and only if the very critical strip coincides with the critical line.

Note 4.8.
  1. 1.

    By definition f​(x)=Ω+​(g​(x))f(x)=\Omega_{+}(g(x)) and f​(x)=Ω−​(g​(x))f(x)=\Omega_{-}(g(x)) holf if and only if f​(x)<o​(g​(x))f\left(x\right)<o\left(g\left(x\right)\right) and f​(x)>o​(g​(x))f\left(x\right)>o\left(g\left(x\right)\right) are respectively false whereas f​(x)=Ω​(g​(x))f(x)=\Omega(g(x)) means that f​(x)≠o​(g​(x))f(x)\neq o(g(x)) is false, i.e. on some sequence of xx’s ff is at least of order gg.

  2. 2.

    D. E. Knuth preferred f​(x)=Ω​(g​(x))⇌g​(x)=O​(f​(x))f(x)=\Omega(g(x))\rightleftharpoons g(x)=O(f(x)) which is not quite the same, [23].

Assumption 4.9.

For the rest of the section let b<12b<\frac{1}{2} be in the very critical strip and nin_{i} the least exceptional number which fixes an index ii for the remaining section.

Theorem 4.10.

[46, §4, Proposition]

Under Assumption 4.9 the following holds true for CA numbers nn.

X​(n)=eγ⋅(1+Ω±​((ln⁡n)−b))X\left(n\right)=e^{\gamma}\cdot\left(1+\Omega_{\pm}\left(\left(\ln n\right)^{-b}\right)\right)
Corollary 4.11.

X​(n)eγ−1<o​((ln⁡n)−b)\frac{X\left(n\right)}{e^{\gamma}}-1<o\left(\left(\ln n\right)^{-b}\right) and X​(n)eγ−1>o​((ln⁡n)−b)\frac{X\left(n\right)}{e^{\gamma}}-1>o\left(\left(\ln n\right)^{-b}\right) are false, i.e. there are ε1,ε2>0\varepsilon_{1},\varepsilon_{2}>0 such that for every natural NN there are CA numbers n1,n2>Nn_{1},n_{2}>N for which (σ​(n1)eγ⋅n1⋅ln⁡ln⁡n1−1)⋅(ln⁡n1)b>ε1\left(\frac{\sigma\left(n_{1}\right)}{e^{\gamma}\cdot n_{1}\cdot\ln\ln n_{1}}-1\right)\cdot\left(\ln n_{1}\right)^{b}>\varepsilon_{1} and (σ−1​(n2)ln⁡ln⁡n2−eγ)​(ln⁡n2)beγ<−ε2\left(\frac{\sigma_{-1}\left(n_{2}\right)}{\ln\ln n_{2}}-e^{\gamma}\right)\frac{\left(\ln n_{2}\right)^{b}}{e^{\gamma}}<-\varepsilon_{2} are true.

Definition 4.12.

Let δi:=12⋅min⁡(−βi,αi)>0\delta_{i}:=\frac{1}{2}\cdot\min\left(-\beta_{i},\alpha_{i}\right)>0 for

αi:=lim supk→∞((σ−1​(ni+k)λi​(k)−eγ)⋅(ln⁡ni+k)beγ)>0,βi:=lim infk→∞((σ−1​(ni+k)λi​(k)−eγ)⋅(ln⁡ni+k)beγ)<0.\begin{array}[]{rl}\alpha_{i}&:=\limsup_{k\to\infty}\left(\left(\frac{\sigma_{-1}\left(n_{i+k}\right)}{\lambda_{i}\left(k\right)}-e^{\gamma}\right)\cdot\frac{\left(\ln n_{i+k}\right)^{b}}{e^{\gamma}}\right)>0\,,\\ \beta_{i}&:=\liminf_{k\to\infty}\left(\left(\frac{\sigma_{-1}\left(n_{i+k}\right)}{\lambda_{i}\left(k\right)}-e^{\gamma}\right)\cdot\frac{\left(\ln n_{i+k}\right)^{b}}{e^{\gamma}}\right)<0\,.\end{array}

The oscillation quotient is fi​(c,d):=λi​(c)​(1+δi​e−b​λi​(c))λi​(d)​(1−δi​e−b​λi​(d))f_{i}\left(c,d\right):=\frac{\lambda_{i}\left(c\right)\left(1+\delta_{i}e^{-b\lambda_{i}\left(c\right)}\right)}{\lambda_{i}\left(d\right)\left(1-\delta_{i}e^{-b\lambda_{i}\left(d\right)}\right)} for λi​(k):=ln⁡ln⁡ni+k\lambda_{i}\left(k\right):=\ln\ln n_{i+k} .

Note 4.13.

Under Assumption 4.9 infinitely many changes of sign of (σ−1​(n)ln⁡ln⁡n−eγ)⋅eb​ln⁡ln⁡n−γ\left(\frac{\sigma_{-1}\left(n\right)}{\ln\ln n}-e^{\gamma}\right)\cdot e^{b\ln\ln n-\gamma} were established by Robin referring to the contributions of Nicolas, Landau, and Grönwall.

Condition 4.14.

There are indices cc and dd with c<dc<d and fi​(c,d)>1f_{i}\left(c,d\right)>1.

Theorem 4.15.

There is no exceptional number under Condition 4.14.

Proof.

(σ​(n1)eγ⋅n1⋅ln⁡ln⁡n1−1)⋅(ln⁡n1)b>ε1\left(\frac{\sigma\left(n_{1}\right)}{e^{\gamma}\cdot n_{1}\cdot\ln\ln n_{1}}-1\right)\cdot\left(\ln n_{1}\right)^{b}>\varepsilon_{1} and (σ−1​(n2)ln⁡ln⁡n2−eγ)​(ln⁡n2)beγ<−ε2\left(\frac{\sigma_{-1}\left(n_{2}\right)}{\ln\ln n_{2}}-e^{\gamma}\right)\frac{\left(\ln n_{2}\right)^{b}}{e^{\gamma}}<-\varepsilon_{2} for some indices cc and dd follow from Corollary 4.11. Therefore

σ−1​(ni+c)>eγ​(1+δi​e−b​λi​(c))​λi​(c)andσ−1​(ni+d)<eγ​(1+δi​e−b​λi​(d))​λi​(d)\begin{array}[]{rl}\sigma_{-1}\left(n_{i+c}\right)&>e^{\gamma}\left(1+\delta_{i}e^{-b\lambda_{i}\left(c\right)}\right)\lambda_{i}\left(c\right)\quad\textrm{and}\\ \sigma_{-1}\left(n_{i+d}\right)&<e^{\gamma}\left(1+\delta_{i}e^{-b\lambda_{i}\left(d\right)}\right)\lambda_{i}\left(d\right)\end{array}

contradict c<dc<d as claimed by Condition 4.14 because a consequence after dividing the two inequalitites is

1<fi​(c,d)≤σ−1​(ni+c)σ−1​(ni+d)={(𝒢i+c,d)−1<1;c<d,𝒢i+d,c>1;d<c.1<f_{i}\left(c,d\right)\leq\frac{\sigma_{-1}\left(n_{i+c}\right)}{\sigma_{-1}\left(n_{i+d}\right)}=\begin{cases}\left(\mathcal{G}_{i+c,d}\right)^{-1}&<1\quad;\,c<d\>,\\ \mathcal{G}_{i+d,c}&>1\quad;\,d<c\>.\end{cases}

∎

Lemma 4.16.

The oscillation quotient can be written as fi​(c,d)=g​(λi​(c),λi​(d))f_{i}\left(c,d\right)=g\left(\lambda_{i}\left(c\right),\lambda_{i}\left(d\right)\right) for

g​(μ,ν):=μ​(eb⋅(μ+ν)+δi​eb⋅ν)ν​(eb⋅(μ+ν)−δi​eb⋅μ)=μν⋅(1+δi​e−b​μ)⋅eb​νeb​ν−δi.g\left(\mu,\nu\right):=\frac{\mu\left(e^{b\cdot\left(\mu+\nu\right)}+\delta_{i}e^{b\cdot\nu}\right)}{\nu\left(e^{b\cdot\left(\mu+\nu\right)}-\delta_{i}e^{b\cdot\mu}\right)}=\frac{\mu}{\nu}\cdot\left(1+\delta_{i}e^{-b\mu}\right)\cdot\frac{e^{b\nu}}{e^{b\nu}-\delta_{i}}\,. (4.1)
Proof.

Verify the factorisation by expanding the product on RHS. What remains follows from

fi​(c,d)=λi​(c)​(1+δi​e−b​λi​(c))λi​(d)​(1−δi​e−b​λi​(d))=λi​(c)​((eλi​(c)⋅eλi​(d))b+δi​eb​λi​(d))λi​(d)​((eλi​(c)⋅eλi​(d))b−δi​eb​λi​(c))=g​(λi​(c),λi​(d)).\begin{array}[]{rl}f_{i}\left(c,d\right)&=\frac{\lambda_{i}\left(c\right)\left(1+\delta_{i}e^{-b\lambda_{i}\left(c\right)}\right)}{\lambda_{i}\left(d\right)\left(1-\delta_{i}e^{-b\lambda_{i}\left(d\right)}\right)}\\ &=\frac{\lambda_{i}\left(c\right)\left(\left(e^{\lambda_{i}\left(c\right)}\cdot e^{\lambda_{i}\left(d\right)}\right)^{b}+\delta_{i}e^{b\lambda_{i}\left(d\right)}\right)}{\lambda_{i}\left(d\right)\left(\left(e^{\lambda_{i}\left(c\right)}\cdot e^{\lambda_{i}\left(d\right)}\right)^{b}-\delta_{i}e^{b\lambda_{i}\left(c\right)}\right)}=g\left(\lambda_{i}\left(c\right),\lambda_{i}\left(d\right)\right)\,.\end{array}

∎

Definition 4.17.

Define three sets of points (μ,ν)∈ℝ2\left(\mu,\nu\right)\in\mathbb{R}^{2}:

  1. 1.

    Eligible points (μ,ν)∈Ei\left(\mu,\nu\right)\in E_{i} meet μ=λi​(c)\mu=\lambda_{i}\left(c\right) and ν=λi​(d)\nu=\lambda_{i}\left(d\right) for some (c,d)∈K1×K2\left(c,d\right)\in K_{1}\times K_{2},

  2. 2.

    the upper part is U={ν>μ}U=\left\{\nu>\mu\right\}, and

  3. 3.

    the big points are those in B={g>1}B=\left\{g>1\right\}.

Claim 4.18.

The margin M:=U∩BM:=U\cap B contains at least one eligible point.

Theorem 4.19.

Condition 4.14 follows from Claim 4.18.

Proof.

By Claim 4.18 there is at least one (μ,ν)∈M∩Ei\left(\mu,\nu\right)\in M\cap E_{i}. Then there are indices cc and dd with μ=λi​(c)\mu=\lambda_{i}\left(c\right), ν=λi​(d)\nu=\lambda_{i}\left(d\right) because of (μ,ν)∈Ei\left(\mu,\nu\right)\in E_{i} and (μ,ν)∈U\left(\mu,\nu\right)\in U implies ν>μ\nu>\mu. Lemma 4.16 is invoked to obtain fi​(c,d)=g​(μ,ν)f_{i}\left(c,d\right)=g\left(\mu,\nu\right) which is greater than 1 because of (μ,ν)∈B\left(\mu,\nu\right)\in B.∎

Definition 4.20.

Let

  1. 1.

    φ0:=arctan⁡(eϵ∞)\varphi_{0}:=\arctan\left(e^{\epsilon_{\infty}}\right) for ϵ∞:=ln⁡(1+δi1−δi)\epsilon_{\infty}:=\ln\left(\frac{1+\delta_{i}}{1-\delta_{i}}\right),

  2. 2.

    ϵμ,ν:=ln⁡(1+δi​e−b​μ1−δi​e−b​ν)\epsilon_{\mu,\nu}:=\ln\left(\frac{1+\delta_{i}e^{-b\mu}}{1-\delta_{i}e^{-b\nu}}\right) and ϵr,φ:=ln⁡(1+δi​e−b​r​cos⁡φ1−δi​e−b​r​sin⁡φ)\epsilon_{r,\varphi}:=\ln\left(\frac{1+\delta_{i}e^{-br\cos\varphi}}{1-\delta_{i}e^{-br\sin\varphi}}\right), a context-sensitive notation.

Fact 4.21.

If μ=r​cos⁡φ\mu=r\cos\varphi and ν=r​sin⁡φ\nu=r\sin\varphi then ϵr,φ=ϵμ,ν\epsilon_{r,\varphi}=\epsilon_{\mu,\nu} is positive because eb​r​cos⁡φ+δieb​r​sin⁡φ−δi>eb​r​cos⁡φeb​r​sin⁡φ\frac{e^{br\cos\varphi}+\delta_{i}}{e^{br\sin\varphi}-\delta_{i}}>\frac{e^{br\cos\varphi}}{e^{br\sin\varphi}}. With dd​r​eϵr,φ=−(11−δi​e−b​ν​b​δi​e−b​μ​cos⁡φ+(1+δi​e−b​μ)(1−δi​e−b​ν)2​b​δi​e−b​ν​sin⁡φ)<0\frac{d}{dr}e^{\epsilon_{r,\varphi}}=-\left(\frac{1}{1-\delta_{i}e^{-b\nu}}b\delta_{i}e^{-b\mu}\cos\varphi+\frac{\left(1+\delta_{i}e^{-b\mu}\right)}{\left(1-\delta_{i}e^{-b\nu}\right)^{2}}b\delta_{i}e^{-b\nu}\sin\varphi\right)<0 it turns out ϵr,φ\epsilon_{r,\varphi} is decreasing in rr for all φ\varphi such that ϵ∞<ϵr,φ\epsilon_{\infty}<\epsilon_{r,\varphi} and ϵr,φ→ϵ∞\epsilon_{r,\varphi}\rightarrow\epsilon_{\infty} as r→∞r\rightarrow\infty. Note ϵ∞=2​a​r​t​a​n​h​δi>2​δi>0\epsilon_{\infty}=2\mathrm{artanh}\delta_{i}>2\delta_{i}>0, rf. [21, §0.7 16.] or [1, 4.6.22].

Lemma 4.22.
  1. 1.

    g​(μ,μ)=eb​μ+δieb​μ−δi=eϵr,φg\left(\mu,\mu\right)=\frac{e^{b\mu}+\delta_{i}}{e^{b\mu}-\delta_{i}}=e^{\epsilon_{r,\varphi}} if r=μ​2r=\mu\sqrt{2} and φ=π4\varphi=\frac{\pi}{4}.

  2. 2.

    If μ=r​cos⁡φ\mu=r\cos\varphi and ν=r​sin⁡φ\nu=r\sin\varphi and r→∞r\rightarrow\infty for constant φ\varphi then

    g​(μ,ν)=eϵμ,ν⋅cot⁡(atan2​(μ,ν))↘eϵ∞⋅cot⁡φ>cot⁡φ.g\left(\mu,\nu\right)=e^{\epsilon_{\mu,\nu}}\cdot\cot\left(\mathrm{atan2}\left(\mu,\nu\right)\right)\searrow e^{\epsilon_{\infty}}\cdot\cot\varphi>\cot\varphi\,.
  3. 3.

    ∇g​(μ,ν)=1ν⋅eb​νeb​ν−δi⋅(1+(1−μ​b)⋅δi​e−b​μ,−μ⋅(1ν+b⋅δieb​ν−δi)⋅(1+δi​e−b​μ))\nabla g\left(\mu,\nu\right)=\frac{1}{\nu}\cdot\frac{e^{b\nu}}{e^{b\nu}-\delta_{i}}\cdot\left(1+(1-\mu b)\cdot\delta_{i}e^{-b\mu}\;,\;-\mu\cdot\left(\frac{1}{\nu}+\frac{b\cdot\delta_{i}}{e^{b\nu}-\delta_{i}}\right)\cdot\left(1+\delta_{i}e^{-b\mu}\right)\right).

Proof.

For g​(μ,ν)=μν⋅(1+δi​e−b​μ)⋅eb​νeb​ν−δig\left(\mu,\nu\right)=\frac{\mu}{\nu}\cdot\left(1+\delta_{i}e^{-b\mu}\right)\cdot\frac{e^{b\nu}}{e^{b\nu}-\delta_{i}} from Lemma 4.16 it holds true that

  1. 1.

    Both sides are equal to μμ⋅eb​μ+δieb​μ⋅eb​μeb​μ−δi\frac{\mu}{\mu}\cdot\frac{e^{b\mu}+\delta_{i}}{e^{b\mu}}\cdot\frac{e^{b\mu}}{e^{b\mu}-\delta_{i}}, and

  2. 2.

    g​(μ,ν)=r​cos⁡φr​sin⁡φ⋅eb​r​cos⁡φ+δieb​r​cos⁡φ⋅eb​r​sin⁡φeb​r​sin⁡φ−δig\left(\mu,\nu\right)=\frac{r\cos\varphi}{r\sin\varphi}\cdot\frac{e^{br\cos\varphi}+\delta_{i}}{e^{br\cos\varphi}}\cdot\frac{e^{br\sin\varphi}}{e^{br\sin\varphi}-\delta_{i}} such that eϵr,φ​eb​r​(cos⁡φ−sin⁡φ)=eb​r​cos⁡φ+δieb​r​sin⁡φ−δie^{\epsilon_{r,\varphi}}e^{br\left(\cos\varphi-\sin\varphi\right)}=\frac{e^{br\cos\varphi}+\delta_{i}}{e^{br\sin\varphi}-\delta_{i}} causes

    g​(μ,ν)=cot⁡φ⋅eb​r​(sin⁡φ−cos⁡φ)⋅eb​r​cos⁡φ+δieb​r​sin⁡φ−δi=cot⁡φ⋅eb​r​(sin⁡φ−cos⁡φ)⋅eϵr,φ​eb​r​(cos⁡φ−sin⁡φ)=eϵr,φ⋅cot⁡φ.\begin{array}[]{rl}g\left(\mu,\nu\right)&=\cot\varphi\cdot e^{br\left(\sin\varphi-\cos\varphi\right)}\cdot\frac{e^{br\cos\varphi}+\delta_{i}}{e^{br\sin\varphi}-\delta_{i}}=\cot\varphi\cdot e^{br\left(\sin\varphi-\cos\varphi\right)}\cdot e^{\epsilon_{r,\varphi}}e^{br\left(\cos\varphi-\sin\varphi\right)}\\ &=e^{\epsilon_{r,\varphi}}\cdot\cot\varphi\,.\end{array}
  3. 3.

∂∂ν​g​(μ,ν)=μ⋅(1+δi​e−b​μ)⋅(−1ν2⋅eb​νeb​ν−δi+1ν⋅(b​eb​ν⋅(eb​ν−δi)−eb​ν⋅b​eb​ν(eb​ν−δi)2))=−μν⋅(1ν+b⋅δieb​ν−δi)⋅eb​νeb​ν−δi⋅(1+δi​e−b​μ)<0.\begin{array}[t]{rl}\frac{\partial}{\partial\nu}g\left(\mu,\nu\right)&=\mu\cdot\left(1+\delta_{i}e^{-b\mu}\right)\cdot\left(-\frac{1}{\nu^{2}}\cdot\frac{e^{b\nu}}{e^{b\nu}-\delta_{i}}+\frac{1}{\nu}\cdot\left(\frac{be^{b\nu}\cdot\left(e^{b\nu}-\delta_{i}\right)-e^{b\nu}\cdot be^{b\nu}}{\left(e^{b\nu}-\delta_{i}\right)^{2}}\right)\right)\\ &=-\frac{\mu}{\nu}\cdot\left(\frac{1}{\nu}+\frac{b\cdot\delta_{i}}{e^{b\nu}-\delta_{i}}\right)\cdot\frac{e^{b\nu}}{e^{b\nu}-\delta_{i}}\cdot\left(1+\delta_{i}e^{-b\mu}\right)<0\,.\end{array}

∎

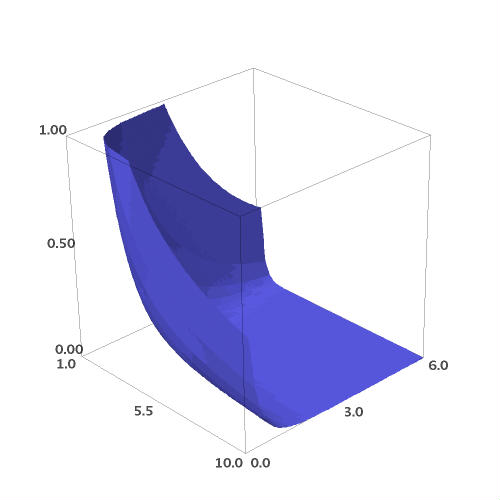
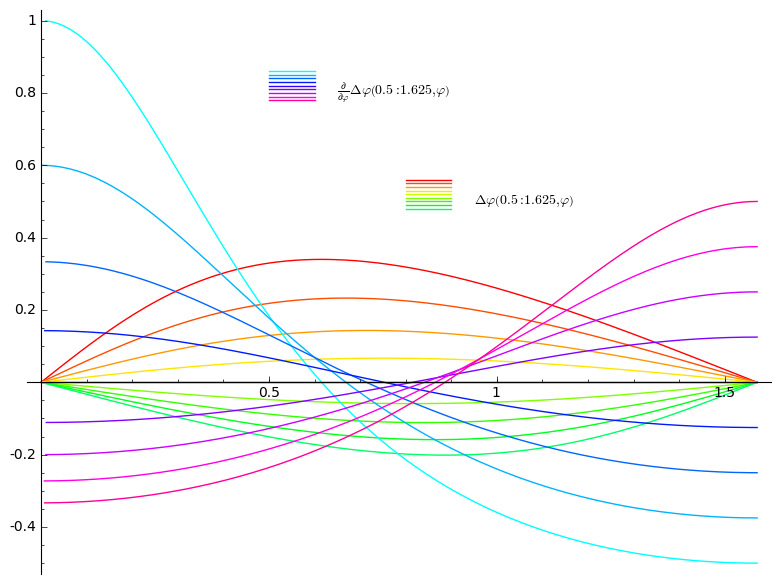
Figure 4.1: Contour Plot of gg and Cartesian Plots of Δ​φ​(x,φ)\Delta\varphi\left(x,\varphi\right), rf. Appendix

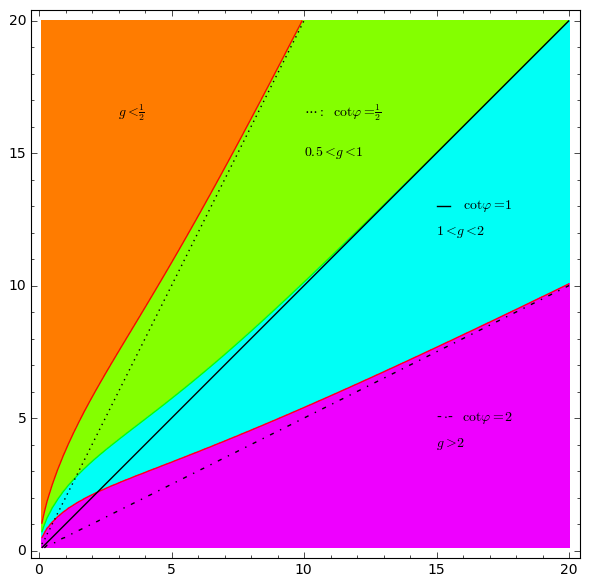
Refer to caption
(a) gg if (b,δi)=(0.5,1)\left(b,\delta_{i}\right)=\left(0.5,1\right)
Refer to caption
(b) Δ​φ​(x,φ)\Delta\varphi\left(x,\varphi\right) and ∂∂φ​Δ​φ​(x,φ)\frac{\partial}{\partial\varphi}\Delta\varphi\left(x,\varphi\right)

Multiplying cot⁡φ\cot\varphi by eϵr,φe^{\epsilon_{r,\varphi}} can be realised by adding Δ​φ​(x,φ):=arccot​(x⋅cot⁡φ)−φ\Delta\varphi\left(x,\varphi\right):=\mathrm{arccot}\left(x\cdot\cot\varphi\right)-\varphi to φ\varphi presuming x=eϵr,φ>0x=e^{\epsilon_{r,\varphi}}>0 and φ∈(0,π2)\varphi\in\left(0,\frac{\pi}{2}\right) s.t. Δ​φ​(x,φ)<0\Delta\varphi\left(x,\varphi\right)<0 iff x>1x>1. With arccot\mathrm{arccot} Δ​φ​(x,φ)\Delta\varphi\left(x,\varphi\right) is decreasing in xx and φ↦∂∂φ​Δ​φ​(x,φ)=x⋅csc(φ)2x2cot(φ)2+1−1\varphi\mapsto\frac{\partial}{\partial\varphi}\Delta\varphi\left(x,\varphi\right)=\frac{x\cdot\csc\left(\varphi\right)^{2}}{x^{2}\cot\left(\varphi\right)^{2}+1}-1 has one change of sign. So Δ​φ​(x,φ)\Delta\varphi\left(x,\varphi\right) as a function of φ\varphi has one minimal and one maximal turning point for x>1x>1 and for x<1x<1, resp.

Corollary.

cot⁡(φ+Δ​φ​(x,φ))=cot⁡(φ+arccot​(x⋅cot⁡φ)−φ)=x⋅cot⁡(φ)\cot\left(\varphi+\Delta\varphi\left(x,\varphi\right)\right)=\cot\left(\varphi+\mathrm{arccot}\left(x\cdot\cot\varphi\right)-\varphi\right)=x\cdot\cot\left(\varphi\right) and if μ=r​cos⁡φ\mu=r\cos\varphi and ν=r​sin⁡φ\nu=r\sin\varphi then g​(μ,ν)=cot⁡(φ+Δ​φ​(eϵr,φ,φ))g\left(\mu,\nu\right)=\cot\left(\varphi+\Delta\varphi\left(e^{\epsilon_{r,\varphi}},\varphi\right)\right).

Proposition 4.23.

g​(μ,ν)=1g\left(\mu,\nu\right)=1 for μ=r​cos⁡φ\mu=r\cos\varphi and ν=r​sin⁡φ\nu=r\sin\varphi iff tan⁡φ=1+δi​e−b​r​cos⁡φ1−δi​e−b​r​sin⁡φ\tan\varphi=\frac{1+\delta_{i}e^{-br\cos\varphi}}{1-\delta_{i}e^{-br\sin\varphi}}. Moreover g​(μ,ν)>1g\left(\mu,\nu\right)>1 iff tan⁡φ<eϵr,φ\tan\varphi<e^{\epsilon_{r,\varphi}} such that eϵr,φ>1e^{\epsilon_{r,\varphi}}>1 for φ=14​π\varphi=\frac{1}{4}\pi.

Proof.

1=g​(μ,ν)=cot⁡(φ+Δ​φ​(eϵr,φ,φ))1=g\left(\mu,\nu\right)=\cot\left(\varphi+\Delta\varphi\left(e^{\epsilon_{r,\varphi}},\varphi\right)\right) holds if and only if π4=arccot​(eϵr,φ⋅cot⁡φ)\frac{\pi}{4}=\mathrm{arccot}\left(e^{\epsilon_{r,\varphi}}\cdot\cot\varphi\right) which is true if and impossible unless tan⁡φ=eϵr,φ\tan\varphi=e^{\epsilon_{r,\varphi}}. Likewise π4>arccot​(eϵr,φ⋅cot⁡φ)\frac{\pi}{4}>\mathrm{arccot}\left(e^{\epsilon_{r,\varphi}}\cdot\cot\varphi\right) holds if and only if tan⁡φ<eϵr,φ\tan\varphi<e^{\epsilon_{r,\varphi}}. A special case is tan⁡φ=1<eb​r​2/2+δieb​r​2/2−δi\tan\varphi=1<\frac{e^{br\sqrt{2}/2}+\delta_{i}}{e^{br\sqrt{2}/2}-\delta_{i}} for φ=14​π\varphi=\frac{1}{4}\pi. ∎

Proposition 4.24.

Let (an)n\left(a_{n}\right)_{n} be a sequence in ℝ\mathbb{R} with H<∞H<\infty for H:=lim infn→∞an+1−anH:=\liminf\limits_{n\rightarrow\infty}a_{n+1}-a_{n} and an→∞a_{n}\rightarrow\infty. Then arctan⁡a1+nkank→π4\arctan\frac{a_{1+n_{k}}}{a_{n_{k}}}\rightarrow\frac{\pi}{4} as k→∞k\to\infty for the indices (nk)k\left(n_{k}\right)_{k} of a suitable subsequence. Moreover ank<a1+nka_{n_{k}}<a_{1+n_{k}} and arctan⁡a1+nkank>π4\arctan\frac{a_{1+n_{k}}}{a_{n_{k}}}>\frac{\pi}{4} for all natural kk.

Proof.

A sequence (nk)k\left(n_{k}\right)_{k} of indices with a1+nk−ank→Ha_{1+n_{k}}-a_{n_{k}}\rightarrow H and ank→∞a_{n_{k}}\rightarrow\infty can be chosen. (ank,a1+nk)∈ℝ2\left(a_{n_{k}},a_{1+n_{k}}\right)\in\mathbb{R}^{2} in polar coordinates has the angle φk\varphi_{k} with tan⁡φk=1+a1+nk−ankank≤1+H+ϵank→1\tan\varphi_{k}=1+\frac{a_{1+n_{k}}-a_{n_{k}}}{a_{n_{k}}}\leq 1+\frac{H+\epsilon}{a_{n_{k}}}\rightarrow 1 for an arbitrarily fixed ϵ>0\epsilon>0 if kk is sufficiently large. (ank)k\left(a_{n_{k}}\right)_{k} has infinitely many members with ank<a1+nka_{n_{k}}<a_{1+n_{k}} since ank→∞a_{n_{k}}\rightarrow\infty. Other members are not suitable.∎

Proposition 4.25.

If (an)n\left(a_{n}\right)_{n} is an increasing sequence in ℝ\mathbb{R} with φn+1:=arctan⁡a1+nan→π4\varphi_{n+1}:=\arctan\frac{a_{1+n}}{a_{n}}\rightarrow\frac{\pi}{4} as n→∞n\rightarrow\infty then there is an index nn with (an,a1+n)∈M\left(a_{n},a_{1+n}\right)\in M.

Proof.

If (an,a1+n)∉M\left(a_{n},a_{1+n}\right)\notin M was true for all nn then each nn would meet either an≥a1+na_{n}\geq a_{1+n} or g​(an,a1+n)≤1g\left(a_{n},a_{1+n}\right)\leq 1. Therefore tan⁡φn≥eϵrn,φn>eϵ∞>1\tan\varphi_{n}\geq e^{\epsilon_{r_{n},\varphi_{n}}}>e^{\epsilon_{\infty}}>1 follows from Proposition 4.23 for all nn where an=rn​sin⁡φna_{n}=r_{n}\sin\varphi_{n} and a1+n=rn​sin⁡φna_{1+n}=r_{n}\sin\varphi_{n}. But this contradicts the assumption tan⁡φn→1\tan\varphi_{n}\rightarrow 1 as n→∞n\rightarrow\infty.∎

Theorem 4.26.

[65]: lim infn→∞pn+1−pn≤H\liminf\limits_{n\rightarrow\infty}p_{n+1}-p_{n}\leq H for H=70⋅106H=70\cdot 10^{6}.

Proposition.

Polymath8:

The last theorem holds true with H=5414H=5414.

Corollary 4.27.

MM contains infinitely many pairs (pnk,p1+nk)\left(p_{n_{k}},p_{1+n_{k}}\right) of consecutive primes.

Proof.

φk:=arctan⁡p1+nkpnk→π4\varphi_{k}:=\arctan\frac{p_{1+n_{k}}}{p_{n_{k}}}\rightarrow\frac{\pi}{4} with φk>π4\varphi_{k}>\frac{\pi}{4} and p1+nkpnk→1\frac{p_{1+n_{k}}}{p_{n_{k}}}\rightarrow 1 for a suitable sequence of indices nkn_{k} follow from Proposition 4.24 because its requirements are fulfilled by Theorem 4.26. Proposition 4.25 shows that there is a pair (pn,p1+n)∈M\left(p_{n},p_{1+n}\right)\in M for some index nn. The argument can be applied to the sequence of primes above p1+np_{1+n}, too. ∎

Figure 4.1a seems to show that the margin MM is essentially a bulge that only allows eligible points with small coordinates. But the so-called bulge depends on the choice of δi\delta_{i} and disappears as δi\delta_{i} approaches zero. The factor eϵr,φe^{\epsilon_{r,\varphi}} has a positive lower limit because of which the contour g=1g=1 diverges away from the bisecting line. Because of the convergence ϵr,φ↘ϵ∞\epsilon_{r,\varphi}\searrow\epsilon_{\infty} the asymptote is given by atan2​(μ,ν)=π4+Δ​φ​(e−ϵ∞,π4)>π4\mathrm{atan2}\left(\mu,\nu\right)=\frac{\pi}{4}+\Delta\varphi\left(e^{-\epsilon_{\infty}},\frac{\pi}{4}\right)>\frac{\pi}{4}.

Lemma 4.28.

ln⁡ln⁡n​xln⁡ln⁡n→1\frac{\ln\ln nx}{\ln\ln n}\rightarrow 1 as n→∞n\rightarrow\infty for every fixed real number xx.

Proof.

Put an:=ln⁡n+ln⁡xa_{n}:=\ln n+\ln x. Since ln⁡ln⁡n​x→∞←ln⁡ln⁡n\ln\ln nx\rightarrow\infty\leftarrow\ln\ln n as n→∞n\rightarrow\infty l’Hôspital’s rule implies

ln⁡ln⁡n​xln⁡ln⁡n∼n​ln⁡nn​ln⁡n​x=1−ln⁡xan→1(n→∞).\frac{\ln\ln nx}{\ln\ln n}\sim\frac{n\ln n}{n\ln nx}=1-\frac{\ln x}{a_{n}}\rightarrow 1\quad(n\rightarrow\infty)\,.

∎

Corollary 4.29.

If Assumption 2.9 is true then lim infc→∞ℒi+c,1=1\liminf\limits_{c\rightarrow\infty}\mathcal{L}_{i+c,1}=1 and λi​(k)→∞\lambda_{i}\left(k\right)\rightarrow\infty as k→∞k\rightarrow\infty.

Proof.

Requiring εi+ck+1=F​(p,v)\varepsilon_{i+c_{k}+1}=F\left(p,v\right) for a fixed prime pp and v>vp​(ni)v>v_{p}\left(n_{i}\right) determines a sequence (ck)k\left(c_{k}\right)_{k} such that qi+ck+1=pq_{i+c_{k}+1}=p for all kk. Then lim infk→∞ℒi+ck,1=1≥lim infc→∞ℒi+c,1≥1\liminf\limits_{k\rightarrow\infty}\mathcal{L}_{i+c_{k},1}=1\geq\liminf\limits_{c\rightarrow\infty}\mathcal{L}_{i+c,1}\geq 1 follows with Lemma 4.28. λi​(k)=ln⁡ln⁡ni+k→∞\lambda_{i}\left(k\right)=\ln\ln n_{i+k}\rightarrow\infty as k→∞k\rightarrow\infty follows from Theorem 1.3.∎

Proposition 4.30.

Let (an)n\left(a_{n}\right)_{n} be an increasing sequence in ℝ\mathbb{R} with lim infn→∞an+1an=1\liminf\limits_{n\rightarrow\infty}\frac{a_{n+1}}{a_{n}}=1. Then arctan⁡a1+nkank→π4\arctan\frac{a_{1+n_{k}}}{a_{n_{k}}}\rightarrow\frac{\pi}{4} as k→∞k\to\infty for the indices (nk)k\left(n_{k}\right)_{k} of a suitable subsequence. Moreover ank<a1+nka_{n_{k}}<a_{1+n_{k}} and arctan⁡a1+nkank>π4\arctan\frac{a_{1+n_{k}}}{a_{n_{k}}}>\frac{\pi}{4} for all natural kk.

Proof.

A sequence (nk)k\left(n_{k}\right)_{k} of indices with an+1an→1\frac{a_{n+1}}{a_{n}}\rightarrow 1 can be chosen. ank<a1+nka_{n_{k}}<a_{1+n_{k}} holds for infinitely many members of (ank)k\left(a_{n_{k}}\right)_{k} because an→∞a_{n}\rightarrow\infty. In polar coordinates the points (ank,a1+nk)∈ℝ2\left(a_{n_{k}},a_{1+n_{k}}\right)\in\mathbb{R}^{2} have the angle φk\varphi_{k} with tan⁡φk=a1+nkank≤1+ϵ\tan\varphi_{k}=\frac{a_{1+n_{k}}}{a_{n_{k}}}\leq 1+\epsilon for an arbitrarily fixed ϵ>0\epsilon>0 if kk is sufficiently large. Members with ank≥a1+nka_{n_{k}}\geq a_{1+n_{k}} are not suitable.∎

Corollary 4.31.

MM contains eligible points.

Proof.

φk:=arctan⁡λi​(1+nk)λi​(nk)→π4\varphi_{k}:=\arctan\frac{\lambda_{i}\left(1+n_{k}\right)}{\lambda_{i}\left(n_{k}\right)}\rightarrow\frac{\pi}{4} as k→∞k\rightarrow\infty is true with φk>π4\varphi_{k}>\frac{\pi}{4} for a suitable sequence of indices nkn_{k} as Proposition 4.30 can be applied because of Corollary 4.29. Proposition 4.25 shows that there is a pair (λi​(k),λi​(1+k))∈M\left(\lambda_{i}\left(k\right),\lambda_{i}\left(1+k\right)\right)\in M for some index kk. It should also be possible to apply the argument to the sequence of CA numbers above ni+kn_{i+k} but one eligible point is sufficient.∎

Conclusion 4.32.

Claim 1.2 follows from Assumption 2.9.

Proof.

A chain of reductions:

  1. 1.

    Claim 1.2 is reduced to Condition 1.1 by Theorem 1.7,

  2. 2.

    which is reduced to Condition 3.7 by Theorem 3.6,

  3. 3.

    which is reduced to Condition 4.14. The contradiction to Assumption 4.9 in Theorem 4.15 is achieved with Assumption 2.9 and the methods of section 3.

  4. 4.

    Condition 4.14 is reduced to Claim 4.18 by Theorem 4.19 and

  5. 5.

    Claim 4.18 is established by Corollary 4.31 for which Assumption 2.9 has been used in Corollary 4.29, too.

∎

5 Final Remarks

Recently it has already been pointed out in [12, 10, 11] that RIE holds for all n>5040n>5040 without requiring Assumption 2.9. Independently of this approach Conclusion 4.32 will have many consequences once Assumption 2.9 is established. A few of them are metioned.

  1. 1.

    RH follows with the original papers [44, 46] while GRH remains undecided.

  2. 2.

    The weakened version M​(x)=O​(x12+ε)M(x)=O(x^{\frac{1}{2}+\varepsilon}) of the disproved Mertens conjecture.

  3. 3.

    The only extraordinary number is 4, [8, 9].

  4. 4.

    There are infinitely many extremely abundant numbers, [35, Thm 2.4].

  5. 5.

    The status of Cramér’s conjecture is still undecided but with Cramér’s work O​(p⋅ln⁡p)O\left(\sqrt{p}\cdot\ln p\right) can be deduced for every gap.

  6. 6.

    A recent result is Hypothesis P in [14] according to Proposition 40 in that paper.

  7. 7.

    The Riesz criterion, Nicolas’ inequality for φ\varphi, Weil’s and Li’s criterions, and Speiser’s statement on ζ′\zeta^{\prime}, [43, 36, 5, 63, 28, 54].

Approaches related to the present one are [35, 34] as well as [33, 2]. The former led to [34, Thm 1.7] and a sequence of increasing values of XX whose existence follows from Grönwall’s theorem with Robin’s Oscillation theorems. The latter pointed out that increasing values of σ​(n)n⋅ln⁡ln⁡n\frac{\sigma\left(n\right)}{n\cdot\ln\ln n} on superabundant numbers are sufficient. CA numbers do not allow for the minimality condition. Exceptional numbers cause oscillations whereas the explicit formulas are more precise under RH. If oscillations prevent exceptional numbers RH could be said to be hoist by its own petard.

Acknowledgements

Unfortunately I never received the support I would have liked to thank for at this place for which there is a variety of reasons. However, I want to thank Dr. Thomas Severin for recommending to me to investigate RIE when I worked for the Allianz insurance company in 1997. Likewise I thank Alexander Rueff for his suggestion to study Ramanujan’s lost notebook during my first year at university. Thanks for helpful feedback from an anonymous referee. I appreciate many fruitful discussions with Sebastian Spang while I worked with him, again for the Allianz. I thank Keith Briggs for our conversation, too. Last not least I thank my cousin Benedict Scholl for an additional pair of eyes as it might have been difficult for him to provide the strictly non-mathematical review I asked for.

Appendix A Implementation

Results have already been mentioned above. Sage code follows below. My first version computed for two weeks last year on a MacBook Air until X​(n)>1.781X\left(n\right)>1.781, i.e. n143215n_{143215} was reached. A revised implementation did the job in a bit more than half an hour (without standby phases). There are two reasons for the difference:

  1. 1.

    Pre-Computation of a list of primes,

  2. 2.

    Consequent exploitation of the factorisation of CA numbers.

Because of assumption 2.9 it is only necessary to select the next prime in every loop, determine new primes that may follow next, and to compute the values of ε\varepsilon associated with the (in virtue of [40, §59] and [3, Thm 1] at most 2) additional new primes.

The following functions compute CA numbers as they were represented in section 3.2. Noe’s top-down form of primes triggering the next valuation is used to store nin_{i}. When nin_{i} has been computed the primes pp such that ni​pn_{i}p does not violate the basic SA condition are called candidates for qi+1q_{i+1}, rf. [3, Theorem 2]. It is convenient that the candidates for qi+1q_{i+1} are the primes that occur in the bottom-up form of nin_{i}.

TODO: in triggers and candidates store indices in sieve instead of elements of sieve, endow sieve with logs of primes, in addSievedPrimeToTriggers() avoid searching newprime in sieve.

Compute CA Numbers in top-down form, a potentially not so big CA number is to be given, e.g. counter = 4 and triggers = [5, 2], seems not to work with the known smaller CA numbers

  • sieve = prime_range(2, 50000000)

    def getSubsequentCAnumber(counter, triggers, number, sieve):

    k = 0

    candidates = getBottomUpTriggers(triggers)

    epsilons = map(lambda i: getCAparameter(candidates[i], i+1),

    range(len(candidates)))

    while k < number:

    k = k + 1

    vmax = selectNextTrigger(epsilons)

    triggers = addSievedPrimeToTriggers(candidates[vmax], triggers,

    candidates, epsilons, sieve)

    return triggers

Convert CA Numbers to bottom-up form

  • def getBottomUpTriggers(triggers):

    l = len(triggers); i = 0

    result = []

    while i<l:

    p = triggers[i]; j = 1

    if p!=0:

    result.append(next_prime(p))

    else:

    p = triggers[i+j]

    while p==0:

    j=j+1

    p = triggers[i+j]

    result.append(next_prime(p))

    result.extend([0 for dummy in range(j)])

    j=j+1

    i=i+j

    result.append(2)

    return result

Choose the next candidate

  • def selectNextTrigger(E):

    emax = max(E)

    vmax = [v for v in range(len(E)) if E[v] >= emax]

    if len(vmax) > 1:

    print "FOUR EXPONENTIALS DISPROVED!"

    else:

    return vmax[0]

Enter the next candidate in the list of triggering primes and update candidates and epsilons

  • def addSievedPrimeToTriggers(newprime, triggers, candidates, epsilons, sieve):

    vmax = candidates.index(newprime)+1

    npi = sieve.index(newprime)

    i = vmax-1

    l = len(triggers)

    if i < l:

    triggers[i] = newprime

    if candidates[i+1] == 0:

    candidates[i+1] = newprime

    epsilons[i+1] = getCAparameter(newprime, vmax+1)

    if triggers[i-1] == newprime:

    triggers[i-1] = 0

    candidates[i] = 0

    epsilons[i] = 0

    else:

    candidates[i] = sieve[npi+1]

    epsilons[i] = getCAparameter(candidates[i], vmax)

    else:

    triggers.append(newprime)

    candidates.append(newprime)

    vmax = vmax + 1

    epsilons.append(getCAparameter(newprime, vmax))

    if triggers[i-1] > 0:

    triggers[i-1] = 0

    candidates[i] = 0

    epsilons[i] = 0

    return triggers

Plotting Δ​φ​(x,φ)\Delta\varphi\left(x,\>\varphi\right) and ∂∂φ​Δ​φ​(x,φ)\frac{\partial}{\partial\varphi}\Delta\varphi\left(x,\>\varphi\right) in Figure 4.1b.

  • DeltaPhi(x, phi) = arccot(x*cot(phi))-phi

    P = sum([plot(DeltaPhi(i/8,phi), (phi, 0, pi/2),

    rgbcolor = hue(((i+16)%20)/20)) for i in range(4, 13)])

    P = P + sum([line([(0.8, 0.6-i/100), (0.9, 0.6-i/100)],

    rgbcolor = hue(((i+16)%20)/20)) for i in range(4, 13)])

    P = P + text(’$\\Delta\\varphi\\left(0.5:1.625,\\varphi\\right)$’,

    (0.95, 0.5), color="black", horizontal_alignment=’left’)

    P = P + sum([plot(DeltaPhi.diff(phi)(i/8,phi), (phi, 0, pi/2),

    rgbcolor = hue(((i+6)%20)/20)) for i in range(4, 13)])

    P = P + sum([line([(0.5, 0.9-i/100), (0.6, 0.9-i/100)],

    rgbcolor = hue(((i+6)%20)/20)) for i in range(4, 13)])

    (P+text(’$\\frac{\\partial}{\\partial\\varphi}

    \\Delta\\varphi\\left(0.5:1.625,\\varphi\\right)$’,

    (0.65, 0.8), color="black", horizontal_alignment=’left’)).show()

Compute ε=F​(x,v)\varepsilon=F\left(x,v\right)

  • def getCAparameter(x, v):

    if x == 0:

    return 0

    else:

    if v == 0:

    return log(1+1/x)/log(x)

    else:

    return log((1-x^(v+1))/(x-x^(v+1))) / log(x)

References

  • [1] Milton Abramowitz and Irene Stegun. Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (Dover Books on Mathematics). Dover Publications, 1964.
  • [2] Amir Akbary and Zachary Friggstad. Superabundant numbers and the riemann hypothesis. AMER MATH MON, 116(3):273–275, 2009.
  • [3] Leonidas Alaoglu and Paul Erdős. On highly composite and similar numbers. Transactions of the American Mathematical Society, 56 (3):448–469, 1944.
  • [4] R. J. Anderson and H. M. Stark. Oscillation theorems. In Marvin Isadore Knopp, editor, Analytic Number Theory: proceedings of a conference held at Temple University, Philadelphia, May 12-15, 1980, volume 899 of Lecture Notes in Mathematics, pages 79–106. University of Michigan, Springer, 1981.
  • [5] Moree Nevans Banks, Hart. The nicolas and robin inequalities with sums of two squares. MONATSH MATH, 157(4):303–322, 2009.
  • [6] Enrico Bombieri and Jeffrey C. Lagarias. Complements to li’s criterion for the riemann hypothesis. J. Number Theory, 77:274–287, 1999.
  • [7] Keith Briggs. Abundant numbers and the riemann hypothesis. Experimental Mathematics, 15, 2006.
  • [8] Nicolas Jean-Louis Caveney, Geoffrey and Jonathan Sondow. On sa, ca, and ga numbers. arXiv:1112.6010v1, 2011.
  • [9] Nicolas Jean-Louis Caveney, Geoffrey and Jonathan Sondow. Robin’s theorem, primes, and a new elementary reformulation of the riemann hypothesis. arXiv:1110.5078v2, 2012.
  • [10] Wang Juping Cheng, Yuanyou and Sergio Albeverio. Proof of the lindelöf hypothesis. arXiv:1010.3374, 2013.
  • [11] Yuanyou Cheng. From the density and lindelöf hypotheses to prove the riemann hypothesis via a power sum method. arXiv:0810.2102, 2013.
  • [12] Yuanyou Cheng and Sergio Albeverio. Proof of the density hypothesis. arXiv:0810.2103, 12 2008-2012.
  • [13] Lichiardopol-N. Moree P. Choie, Y.-J. and P. Solé. On robin’s criterion for the riemann hypothesis. J. Théor. Nombres Bordeaux, 19(2):357–372, 2007.
  • [14] Juan Arias de Reyna and Jan van de Lune. On the exact location of the non-trivial zeros of riemann’s zeta function. arXiv, 1305.3844:28, 2013.
  • [15] Pierre Dusart. The kkth prime is greater than k​(ln⁡k+ln⁡ln⁡k−1)k(\ln k+\ln\ln k-1) for k≥2k\geq 2. MATHEMATICS OF COMPUTATION, 68(225):411–415, 1999.
  • [16] Paul Erdős and Jean-Louis Nicolas. Répartition des nombres superabondants. Bull. Soc. Math. France, 103:65–90, 1975.
  • [17] Thomas H. Grönwall. Some asymptotic expressions in the theory of numbers. Trans. Amer. Math. Soc., 14:113 – 122, 1913.
  • [18] Emil Grosswald. Oscillation theorems of arithmetical functions. Trans. Amer. Math. Soc., 126:1–28, 1967.
  • [19] Geoffrey H. Hardy and John E. Littlewood. Some problems of diophantine approximation. Acta Mathematica, 37:225, 1914.
  • [20] Geoffrey H. Hardy and Edward M. Wright. An Introduction to the Theory of Numbers. Oxford University Press, Oxford, England, 5 edition, 1979.
  • [21] Alan Jeffrey. Handbook of Mathematical Formulas and Integrals, Third Edition. Academic Press, 2003.
  • [22] J. B. Keiper. Power series expansions of riemann’s ξ\xi function. Math. Comput., 58:765–773, 1992.
  • [23] Donald E. Knuth. Big omicron and big omega and big theta. In SIGACT News, pages 18–24, Apr.-June 1976.
  • [24] Donald E. Knuth. The Art Of Computer Programming - Fundamental Algorithms. Addison-Wesley, 1997.
  • [25] Edmund Landau. Handbuch der Lehre von der Verteilung der Primzahlen. Teubner, Leipzig, 1909.
  • [26] Edmund Landau. Über die anzahl der gitterpunkte in gewissen bereichen. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1924:137–150, 1924.
  • [27] Serge Lang. Introduction to Transcendental Numbers. Number 4178 in Addison-Wesley series in mathematics. Addison-Wesley, Reading, Mass., 1966.
  • [28] Xian-Jin Li. The positivity of a sequence of numbers and the riemann hypothesis. Journal of Number Theory, 65(2):325–333, 1997.
  • [29] Peter Lindqvist and Jaak Peetre. On the remainder in a series of mertens. Expositiones Mathematicae, 15:467–478, 1997.
  • [30] John E. Littlewood. Sur la distribution des nombres premiers. Comptes rendus hebdomadaires des séances de l’Académie des sciences, 1914:1869–1872, 158.
  • [31] Jean-Pierre Massias and Guy Robin. Bornes effectives pour certaines fonctions concernant les nombres premiers. J. Théor. Nombres Bordeaux, 8(1):215–242, 1996.
  • [32] Franz Mertens. Ein beitrag zur analytischen zahlentheorie. Journal für die reine und angewandte Mathematik, 78:46–62, 1874.
  • [33] Aleksandr Morkotun. On the increase of grönwall function value at the multiplication of its argument by a prime. arXiv, 1307.0083, July 2013.
  • [34] Sadegh Nazardonyavi and Semyon Yakubovich. Delicacy of the riemann hypothesis and certain subsequences of superabundant numbers. arXiv, 1306.3434, June 2013.
  • [35] Sadegh Nazardonyavi and Semyon Yakubovich. Superabundant numbers, their subsequences and the riemann hypothesis. arXiv, 1211.2147v3, February 2013.
  • [36] Jean-Louis Nicolas. Petites valeurs de la fonction d’euler. Journal of Number Theory, 17(3):375 – 388, 1983.
  • [37] T. D. Noe. First 500 superabundant numbers. 2005.
  • [38] T. D. Noe. First 1000000 superabundant numbers. 2009.
  • [39] Srinivasa Ramanujan. Highly composite numbers. Proc. London Math. Soc., 14:347–407, 1915.
  • [40] Srinivasa Ramanujan. Highly composite numbers. The Ramanujan Journal, 1:119–153, 1997.
  • [41] Paulo Ribenboim. The little book of big primes. Springer Verlag, 1991.
  • [42] Hans Riesel. Prime Numbers and Computer Methods for Factorization. Modern Birkhäuser Classics. Springer, 2 edition, November 2011.
  • [43] Marcel Riesz. Sur l’hypothèse de riemann. Acta Arith., 40:185 – 190, 1916.
  • [44] Guy Robin. Sur l’ordre maximum de la fonction somme des diviseurs. Séminaire de théorie des nombres, Paris - Birkhauser, pages 233 – 244, 1981-82, 1983.
  • [45] Guy Robin. Estimation de la fonction de tchebychef θ\theta sur le k-ième nombre premier et grandes valeurs de la fonction ω​(n)\omega(n) nombre de diviseurs premiers de nn. Acta Arithmetica, 42(4):367 – 389, 1983.
  • [46] Guy Robin. Grandes valeurs de la fonction somme des diviseurs et hypothèse de riemann. Journal de Mathématiques Pures et Appliquées. Neuvième Série, 63 (2):187 – 213, 1984.
  • [47] Rosser and Schoenfeld. Sharper bounds for the chebyshev functions θ​(x)\theta(x) and ψ​(x)\psi(x) (part i). Math. Comput., 29(129):243–269, JANUARY 1975.
  • [48] Barkley Rosser. The nn-th prime is greater than n​log⁡nn\log n. Proceedings of the London Mathematical Society, 2(1):21–44, 1939.
  • [49] I. B. Rosser and L. Schoenfeld. Approximate formulas for some functions of prime numbers. Illinois J. Math., 6:64–94, 1962.
  • [50] Lowell Schoenfeld. Sharper bounds for the chebyshev functions θ​(x)\theta(x) and ψ​(x)\psi(x), part ii. Math. Comput., 30(134):337–360, Aptil 1976.
  • [51] Neil J. A. Sloane. The on-line encyclopedia of integer sequences® (oeis®).
  • [52] Michel Solé, Patrick; Planat. Extreme values of the dedekind ψ\psi function. arXiv, 1011.1825, January 2011.
  • [53] Michel Solé, Patrick; Planat. Robin inequality for 7-free integers. Electronic Journal of Combinatorial Number Theory, 11(11), December 2011.
  • [54] Andreas Speiser. Geometrisches zur riemannschen zetafunktion. Math. Ann., 110:514 – 521, 1934. Mathematische Annalen.
  • [55] The Sage Development Team. Sage reference. 5.2, 2005–2011.
  • [56] Ambler Thompson and Barry N. Taylor. Guide for the use of the international system of units (si), March 2008.
  • [57] Priscilla Throop. Isidore of Seville’s Etymologies: Complete English Translation, volume I of Isidore of Seville’s Etymologies: The Complete English Translation of Isidori Hispalensis Episcopi Etymologiarum Sive Originum Libri XX. Lulu.Com, paperback edition, 2006.
  • [58] Mark B. Villarino. Mertens’ proof of mertens’ theorem. 2005.
  • [59] André Voros. Zeta Functions over Zeros of Zeta Functions, volume 8 of Lecture Notes of the Unione Matematica Italiana. Springer, 2010. ISBN 978-3-642-05202-6.
  • [60] Michel Waldschmidt. Nombres transcendants. Lecture notes in mathematics. Springer, Berlin, 1974.
  • [61] Michel Waldschmidt. Diophantine approximation on linear algebraic groups. Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. Springer, Berlin, 2000.
  • [62] Jimmy Wales and Larry Sanger. Wikipedia, the free encyclopedia.
  • [63] André Weil. Sur les ’formules explicites’ de la théorie des nombres premiers. Comm. Lund, vol. dédié a Marcel Riesz:252–265, 1952. Collected Papers II.
  • [64] Eric W. Weisstein. CRC Concise Encyclopedia of Mathematics. CRC Press, 1999.
  • [65] Yitang Zhang. Bounded gaps between primes. Annals of Mathematics, 2013. to appear.