Principal component analysis balancing prediction and approximation accuracy for spatial data
2Department of Environmental & Occupational Health Sciences, University of Washington
3Department of Civil & Environmental Engineering, University of Washington )
Abstract
Dimension reduction is often the first step in statistical modeling or prediction of multivariate spatial data. However, most existing dimension reduction techniques do not account for the spatial correlation between observations and do not take the downstream modeling task into consideration when finding the lower-dimensional representation. We formalize the closeness of approximation to the original data and the utility of lower-dimensional scores for downstream modeling as two complementary, sometimes conflicting, metrics for dimension reduction. We illustrate how existing methodologies fall into this framework and propose a flexible dimension reduction algorithm that achieves the optimal trade-off. We derive a computationally simple form for our algorithm and illustrate its performance through simulation studies, as well as two applications in air pollution modeling and spatial transcriptomics.
Keywords: dimension reduction, principal component analysis, spatial prediction, air pollution, spatial transcriptomics
1 Introduction
Statistical modeling of multivariate data is a common task in many areas of research. Environmental epidemiologists often seek to learn the relationship between some health outcome and a complex mixture of multiple air pollutants, where the health effects of such mixture could vary depending on its chemical composition rather than the overall quantity alone (Goldberg, 2007; Lippmann et al., 2013; Dai et al., 2014; Achilleos et al., 2017). Spatial transcriptomics is another area involving the analysis of multivariate, and most often, high-dimensional measurements, where researchers analyze gene expressions on tissues with spatial localization information (Hu et al., 2021; Zhao et al., 2021).
Despite the different domain areas, there are several common challenges for such tasks: First, the (potential) high dimensionality and strong autocorrelation of the multivariate measurements would require additional exploratory data analysis, such as dimension reduction, as a preliminary step; see e.g., Dominici et al. (2003) for epidemiological and Kiselev et al. (2017); Sun et al. (2019) for genomics studies. The spatial characteristics of the measurements should be accounted for in such dimension reduction.
The second complexity is that dimension reduction is often executed independently from the subsequent modeling steps, which would cause the dimension-reduced data to be uninterpretable, or of sub-optimal utility, for downstream analyses. One example is the study of health effects of air pollution, where there is often spatial misalignment between the air pollution monitoring sites and locations where health outcomes are available (Özkaynak et al., 2013; Bergen et al., 2013; Chan et al., 2015). Therefore, after lower-dimensional scores are obtained, they still need to be extrapolated to the latter locations; but these lower-dimensional scores may be noisy and not spatially predictable. This problem is also present in spatial gene expression analyses, where the reduced-dimensional gene expression matrix may not preserve all biologically meaningful patterns. When the processed gene expression data further undergo spatial imputation due to incomplete profiling (Pierson and Yau, 2015; Prabhakaran et al., 2016; Li et al., 2021), or are clustered into spatial domains based on spatial and other biological information (commonly termed spatial domain detection in spatial transcriptomics) (Zhao et al., 2021; Long et al., 2023), the statistical performance may be affected by loss of information that seems unimportant in dimension reduction, but is significant for downstream modeling (Liu et al., 2022).
Principal component analysis (PCA) is a classical dimension-reduction technique. It leads to independent and lower-dimensional scores, called principal component scores, or PC scores, that approximate the multivariate measurements (Jolliffe, 2002). Existing methodologies that tackle some of the aforementioned challenges are often based on extensions of PCA. Jandarov et al. (2017) proposed a spatially predictive PCA algorithm, where the PC scores were constrained to be linear combinations of covariates and spatial basis, so they can be more accurately predicted at new locations. Bose et al. (2018) extended this predictive PCA approach and enabled adaptive selection of covariates to be included for each PC. Vu et al. (2020, 2022) proposed a probabilistic version of predictive PCA along with a low-rank matrix completion algorithm, which offers improved performance when there is spatially informative missing data. Keller et al. (2017) developed a predictive -means algorithm where dimension reduction was conducted by clustering.
In spatial transcriptomics applications such as domain detection (see detailed discussion in Section 5.2), Zhao et al. (2021) processed gene expression information using PCA and conducted downstream clustering via a Bayesian approach, where the spatial arrangement of the measured spots were modeled using the PC scores. Shang and Zhou (2022) proposed a probabilistic PCA algorithm, where spatial information was incorporated into a latent factor model for gene expression. Liu et al. (2022) developed a joint approach that simultaneously performs dimension reduction and clustering, and uses a latent hidden Markov random field model to enforce spatial structures of the clusters.
When dimension reduction is used as an initial step before downstream analyses such as prediction, statistical inference and clustering, there are two key considerations for the quality of dimension reduction. The first is representability, which is how well the lower dimensional components approximate the original measurements. The second, often conflicting, goal is predictability of the resulting components, so that they preserve meaningful scientific and spatial information when extrapolated to locations without measurements; such predictability ensures that the extrapolations are of high quality for subsequent modeling. Even in analytical tasks that do not primarily focus on prediction (e.g., domain detection in spatial transcriptomics), the predictability of the PC scores is still desirable and implicitly considered, since it enforces the interpretability and spatial structure of the PCs; see Section 5.2 for further illustration.
Among existing methodologies, classical PCA solely focuses on representability, while predictive PCA (Jandarov et al., 2017) and its variants (Bose et al., 2018) prioritize predictability and optimize representability only after the former is guaranteed. Probabilistic approaches, such as Shang and Zhou (2022), Liu et al. (2022) and Vu et al. (2020), implicitly incorporate both tasks into the latent factor models, though their performance depends on the validity of the parametric model assumptions, and there is no explicit interpretation or optimality guarantee on either property or the trade-off between them.
In this work, we propose a flexible dimension reduction algorithm, termed representative and predictive PCA (RapPCA), that explicitly minimizes a combination of representation and prediction errors and finds the optimal balance between them. We further allow the underlying lower-dimensional scores to have complex spatial structure and non-linear relationships with external covariates (if any). We show that the optimization problem involved can be solved by eigendecomposition of transformed data, enabling simple and efficient computation.
We start in Section 2 by briefly reviewing related methods, introducing notations, and defining various performance metrics of dimension reduction. Section 3 describes our proposed approach, and establishes the optimality of the proposed solution. We compare the performance of our method with existing variants of PCA via simulation studies in Section 4, and demonstrate its application in epidemiological exposure assessment as well as spatial transcriptomics in Section 5. Section 6 concludes the manuscript with a discussion of our methodology and related alternatives.
2 Setting
2.1 Classical and Predictive PCA
Let represent -dimensional spatially-structured variables of interest measured at locations. Examples include the concentrations of a mixture of pollutants at monitoring sites, or the expression of genes at spots on tissues. In addition, we observe the spatial coordinates of the locations, along with (potential) observations of covariates, . These could be, for example, population density and land use information for air pollution studies, or histology information from images for spatial transcriptomics.
The ultimate goal is to conduct prediction, clustering or other modeling tasks on based on the spatial coordinates and covariates. Since the columns of may be strongly correlated and/or noisy (Rao et al., 2021), dimension reduction can be used to to extract scientifically meaningful signals from the original data. The classical PCA achieves this by maximizing the proportion of variability in that is explained by the lower dimensional PCs. We briefly introduce the classical PCA algorithm under the formulation of Shen and Huang (2008) to highlight its connection with related techniques.
Suppose the columns of are centered and scaled. To find an -dimensional representation of , classical PCA can be expressed as a sequence of rank-1 optimization problems for (Shen and Huang, 2008):
| (1) |
where the 1-dimensional PC score is an -vector, the loading is , and and represent Frobenius norm for matrices and norm for vectors, respectively. is the residual from approximation after each iteration: denoting as the solution to (1), we define for and .
While each of the ’s explain the greatest variability in , there is no guarantee that they are scientifically interpretable, and they do not explicitly account for the spatial structures underlying . Recognizing this, predictive PCA (Jandarov et al., 2017) builds upon the expression in (1), but constrains each PC score to be in a model space of the spatial coordinates and covariates , leading to the optimiztion problem,
| (2) |
for each . Here, , contains thin-plate regression spline basis functions capturing the spatial effects, and in contrast to (1), normalization is done on the term instead of . As before, is the residual after approximation, i.e. for and . Note that the quantity corresponds to in the expression of PCA. Compared with (1), this formulation restricts each PC score to fall within the space spanned by the columns of . This ensures the spatial smoothness and the inclusion of information from covariates in the PC score , and thus enforces predictability.
After solving either (1) or (2) for all PCs, the loadings are -normalized () if not already done, and then concatenated as . The PC scores are then defined as .
As noted earlier, classical PCA aims to achieve optimal representability of the PC scores , but these ’s may not retain meaningful signals in or important spatial patterns to be well predictable. In contrast, predictive PCA and its variants (Jandarov et al., 2017; Bose et al., 2018) minimize the approximation gap, which will be formally defined in Section 2.2, after constraining each to lie within a specific model space; but when these PC scores are predicted at new locations and transformed back to the higher dimensional space of , closeness in the space of may not necessarily translate to the original space of observations due to reduced approximation accuracy. Our proposed method, introduced in Section 3, is based on an interpolation between classical and predictive PCA, and encourages to be close to, but not exactly within, the specified model space while balancing the quality of representation.
2.2 Evaluation Metrics for Dimension Reduction
Before introducing our proposal, it is helpful to formalize different aspects of dimension reduction performances, such as representability and predictability, and to characterize the overall balance between them.
Suppose the PC scores and loadings are obtained on a set of training data with size , and are then predicted at test locations with a user-specified spatial prediction model as . We define the mean-squared prediction error (MSPE) of this procedure as
where . Thus, is what the actual PC scores on the test set would be according to the loadings , if were known. Consequently, MSPE characterizes the gap between the predicted and true PC scores and reflects the predictability of the PCs.
The mean-squared representation error (MSRE) is defined as
which measures the gap between the true data, , and the closest approximation possible based on . Since the quality of representation alone, without considering predictive performance, is of more interest for the training than the test data, we instead examine MSRE-trn as the metric for representation: . It can be seen that MSRE-trn exactly matches the objective function for PCA in (1).
Given any outcome data , loadings from a dimension reduction procedure and predicted PC scores , we define the total mean-squared error (TMSE) resulting from both dimension reduction and prediction as . This quantity measures the discrepancy between the true data and the predicted scores that are transformed back to the original, higher-dimensional space. In the specific training-test setting, the expression of TMSE becomes
MSPE and MSRE can be viewed informally as a decomposition of the overall TMSE, where the prediction and approximation gaps, i.e., and , are components of the overall error .
3 Representative and Predictive PCA (RapPCA)
Predictive PCA restricts the PC scores within some model space — specifically, — to enforce predictability while trading off representability to some extent. A natural idea, with more flexibility, would be relaxing this constraint, and instead using a penalty term to force to be close to, but not exactly within, the model space. By choosing the magnitude of such a penalty term data-adaptively, we aim to achieve the optimal balance between representation and prediction leading to the smallest overall error.
Noting that the model space can be generalized from the linear span in (2) to incorporate more flexible mechanisms underlying each PC , we adopt kernel methods (Evgeniou et al., 2000; Hastie et al., 2009) to capture non-linear covariate effects; additionally, we use smoothing splines (Wahba, 1990; Wood, 2003) rather than unpenalized regression splines to enforce spatial structures.
More conceretely, we propose to solve the following sequence of optimization problems, for , to extract PCs from :
| (3) |
As in Section 2, denotes the residual for , and is set to the original data when . Moreover, is a kernel matrix such that for some kernel function , with being the th observation (row) of . The kernel function maps the covariates into a higher-dimensional space, and the kernel matrix encodes the pairwise similarities between each entry in this transformed space. Linear operations in the high-dimensional space effectively captures non-linear relationships in the original input space of . This enables more flexibility than most existing predictive variants of PCA which specify linear relationships (e.g., Jandarov et al., 2017; Bose et al., 2018; Vu et al., 2020; Shang and Zhou, 2022). Common choices of kernel functions include linear kernel, , and Gaussian kernel, (Hofmann et al., 2008; Murphy, 2012). The columns of are evaluations of spline basis functions, e.g., thin-plate regression splines as in predictive PCA, at the spatial coordinates , and is the penalty matrix induced by the choice of smoothing splines. For example, the penalty corresponding to the thin-plate regression splines is the wiggliness penalty defined in Wood (2003); for P-splines, the penalty term depends on the differences between consecutive entries of , i.e., (Wood, 2017).
In (3), the first term measures the approximation gap of the score and loading , similar to the objective of minimization for classical PCA. The second term reflects the distance between the score and the model space specified by and , and encourages to be predictable based on the covariates and spatial coordinates. The constraint ensures a similar relationship between the PC scores and loadings as in classical PCA.
The computation of the optimization problem in (3) could suffer when or is near-singular. Therefore in practice, we replace and with and for a small, data-independent constant , and identity matrices and in the penalty terms to avoid near-singularity; see also Li et al. (2019) for similar handling. This leads to
| (4) |
Here, , and are tuning parameters, among which is of most interest as it controls the trade-off between predictability and representability, with larger imposing higher penalty on unpredictable scores . The third and fourth terms in (4) are penalties that enforce the identifiability of the model parameters and help to avoid overfitting the data.
Though optimizing iteratively via coordinate descent is straightforward to implement, the optimization problem (4) is non-convex due to the joint optimization of and , as well as the non-convex feasible set of . Consequently, iterative algorithms, including coordinate descent are not guaranteed to converge to the global minimizer. Instead, we propose an analytical solution to (4) that attains the global miminum despite the non-convexity of the objective function and/or the constraints. We describe our proposed procedure in Algorithm 1, and refer to the proposed method as representative and predictivePCA, or RapPCA. Theorem 1, proved in Appendix A, establishes the optimality of and . Numerical examples in Appendix B.1 empirically verify the optimality.
Theorem 1.
The computational complexity of the procedure described above is , where we recall that is the sample size, is the dimensionality of , and is the number of spline basis functions included in . This algorithm is computationally simple in that it obtains the optimal solution with an explicit expression, as opposed to iterative numerical optimization procedures. This algorithm depends on the specification of several quantities. For the hyper-parameters , one could adopt cross-validation and choose the combination that minimizes TMSE or other metrics (e.g., MSPE/MSRE) depending on the targeted use case, sequentially for each PC. Taking TMSE as an example, for the th PC and for each combination of , we calculate on the training set, predict on the validation set, and then examine to choose the optimal combination minimizing . Specification of the dimension of is not critical due to the inclusion of penalty on (Wood, 2017). One can start with a large (e.g., close to the sample size ) and the degree of freedom of will be controlled data-adaptively via .
4 Simulations
In this section, we compare the performance of RapPCA on simulated data with classical and predictive PCA. In particular, we investigate three scenarios with different trade-offs between predictability and representability resulting from different data generating mechanisms.
In all settings, we randomly generate locations within . For each location, we generate covariates ( and ) from independent Uniform distributions and calculate 6 independently distributed PCs as
| (5) |
where with controlling the signal-to-noise ratio and hence the predictability of each PC; is a specified mean function, and the covariance matrix has an exponential structure with . The outcome represents concentrations of pollutants, and is given by
where is adjusted differently in each scenario to control the contribution from different PCs, and the entries of the noise terms are drawn from independent Normal distributions.
We examine metrics including TMSE, MSPE and MSRE-trn for 100 replicates of data, in terms of their overall magnitudes, as well as the breakdown by each PC and/or (the tuning parameter). We also report the individual prediction MSEs for each PC, which is , recalling from Section 2.2 that . We extract PCs sequentially with each of the three candidate algorithms, PCA, predictive PCA and RapPCA. The optimal combination of , and is selected by minimizing TMSE via 10-fold cross-validation. For each PC score , test set predictions are obtained via a two-step procedure (see, e.g., Wai et al., 2020), where we first train a random forest model, and then conduct spatial smoothing on the residuals with thin-plate regression splines (TPRS) (Wood, 2003). We discuss the role played by the primary tuning parameter in this section. Figure S3 for RapPCA in Appendix B.2 provides further details about the impact of on the solution.
4.1 Scenario 1: PCs with Equal Contribution
We first consider the setting with 3 well-predictable PCs and 3 PCs mainly consisting of structured and unstructured Gaussian errors. More specifically, for the mean model in (5), we let where the entries of are drawn independently from Uniform, and , for ; we let and for . is set to be , where is diagonal with and the entries of are independent Uniform. In other words, we first scale the 6 PCs to have equal variability, and then assign random but overall comparable weights to them.
Comparing the two existing methods, it is expected that in this scenario predictive PCA would outperform classical PCA in prediction without severely compromising approximation accuracy, since the predictable PCs explain a similar amount of variability compared to the unpredictable ones. Consequently, predictive PCA would achieve better overall performance as reflected by TMSE. RapPCA flexibly interpolates between classical and predictive PCA, and is expected to have comparable or better performance than predictive PCA.
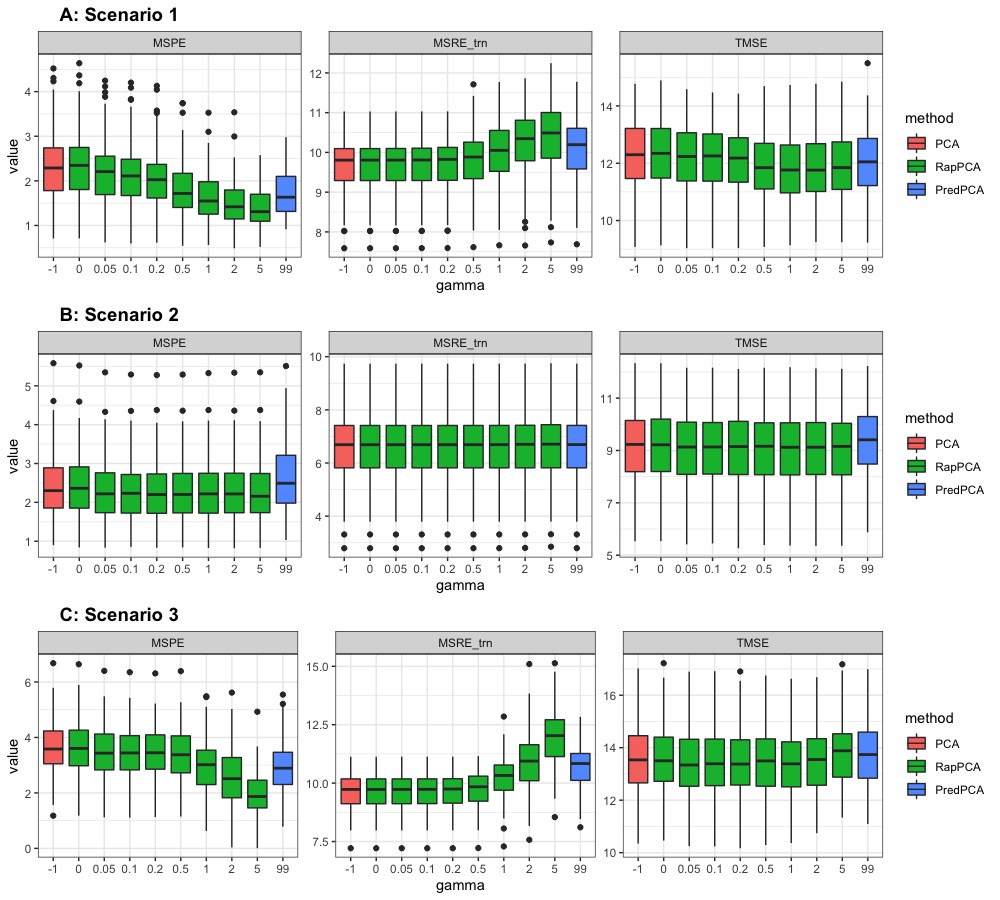
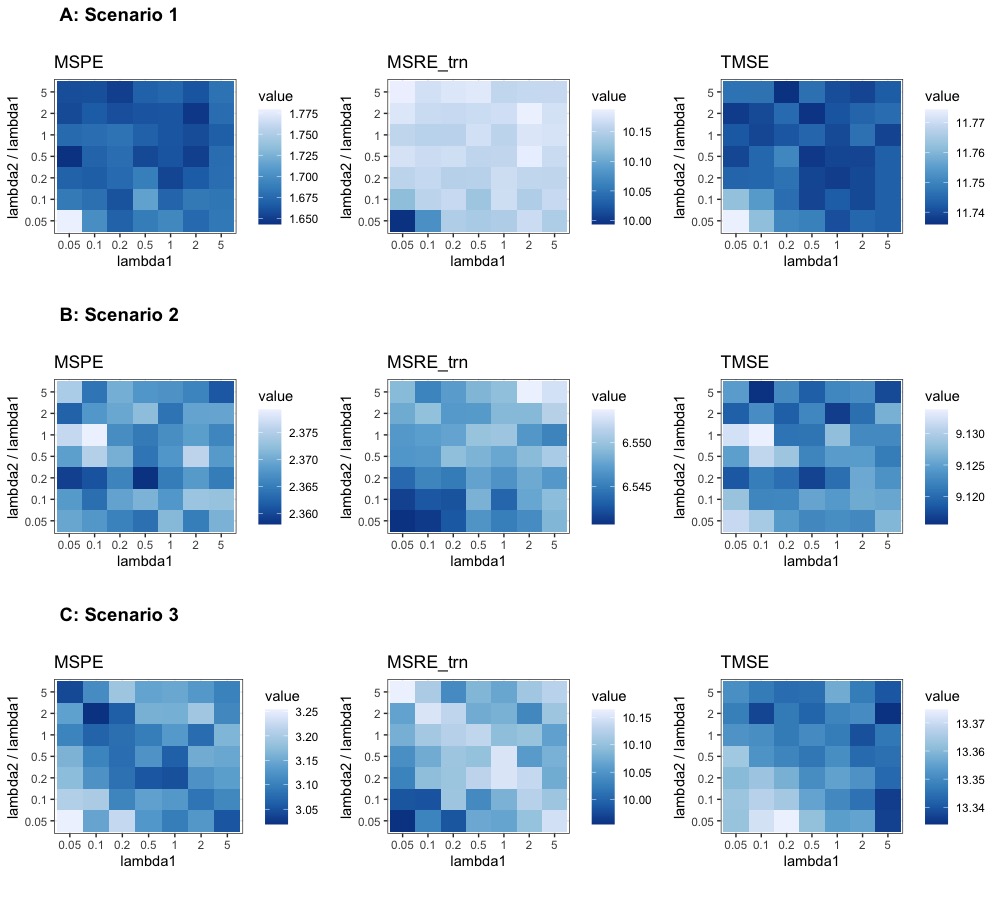
Panel A in Figure 1 presents the breakdown of MSPE, MSRE-trn and TMSE for the first PC by , in comparison to PCA and predictive PCA for this scenario. We only present this breakdown for the first PC but not the subsequent ones because starting from the second PC, different PCA algorithms will have different residuals (recall Equations 1, 2 and 4), and the PC-specific breakdown of metrics is consequently no longer comparable. We observe that MSPE decreases and training MSRE increases as we increase for RapPCA, since this imposes a greater penalty on prediction errors in optimization.
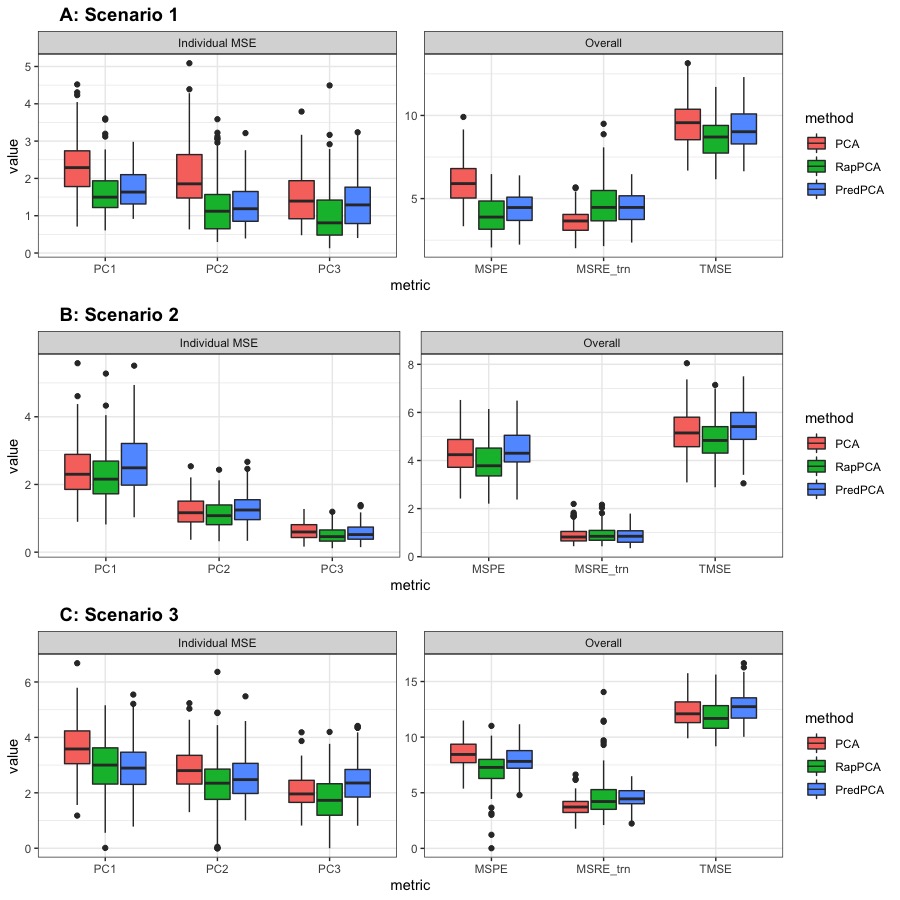
Figure 2 compares the prediction MSEs for each PC, as well as the overall TMSE, MSPE and MSRE-trn for different methods. As expected for this scenario, we observe in Panel A that predictive PCA achieves lower prediction errors than PCA for each PC, as well as lower overall MSPE. This advantage does not cost a higher approximation gap (MSRE), since the predictable components in the outcome explain a similar amount of variability as the unpredictable ones. RapPCA is able to adjust the penalties on the covariate versus spatial effect terms adaptively, especially when there are a large number of spatial basis terms (recall the separate tuning parameters and in Equation 4), as opposed to predictive PCA which is restricted to a low-dimensional combination of covariates and spatial basis functions (recall the term in Equation 2). Consequently, predictive PCA achieves better overall performance (reflected by smaller TMSE) than PCA, while RapPCA further improves the prediction and overall performance due to its flexibility to data-adaptively capture the covariate and spatial effects.
4.2 Scenario 2: PCs with Unequal Contribution
We now consider a scenario where the predictable PCs explain a higher proportion of variability than the unpredictable PCs. In particular, the simulation setting is similar to Scenario 1, except that the entries of are first drawn from independent Uniform distributions, and then the rows are scaled to have decaying norm (recall that the first 3 PCs are more predictable than the last 3 PCs). We expect in this case that PCA and predictive PCA would have comparable prediction, approximation and overall accuracy, since the well-predictable components of coincide with those that explain the greatest amount of variance.
For the same reason, adjusting in this case would not lead to steep changes in MSPE, MSRE or TMSE for RapPCA, as reflected by the flat curves of each metric in Panel B of Figure 1. Despite the similar behaviors of PCA and predictive PCA, Panel B of Figure 2 reveals that RapPCA is still able to improve the prediction and overall performance by more flexibly exploiting the covariate and spatial information when identifying the PCs.
4.3 Scenario 3: PCs with Non-Linear Mean
In our last simulation, we investigate the setting where the relationship between the true PCs and the covariates is non-linear. We modify the setting in Scenario 1 so that
for , where and denote element-wise multiplication and square, and denotes the largest integer not exceeding . In other words, we specify the mean function to be a combination of squared and interaction terms of the covariates, where interactions exist between pairs of consecutive covariates ( and ; and , etc).
Panel C of Figure 1 indicates that by flexibly handling non-linear effects, RapPCA gains a clear advantage in prediction accuracy compared to both predictive and classical PCA in this scenario, when we impose a large enough penalty on prediction errors in optimization. It is not surprising that putting an emphasis on prediction leads to some loss in approximation accuracy; however, we observe from Panel C of Figure 2 that by balancing the two objectives data-adaptively, RapPCA achieves meaningful improvement in MSPE while maintaining comparable, if not superior, overall performance.
5 Applications
We illustrate the utility of RapPCA using real datasets in two different domain areas — environmental epidemiology and spatial transcriptomics. The first application of dimension reduction in Section 5.1 () represents the case where practitioners seek to improve predictability (MSPE) and the overall performance (TMSE), and hence RapPCA is able to explicitly optimize these metrics as desired. The second example in Section 5.2 () includes the scenario where tasks other than spatial prediction (e.g., clustering) are of interest; we demonstrate that RapPCA, though not directly incorporating the ultimate goal into its optimization, is able to capture meaningful biological and spatial information in the extracted PCs by enforcing predictability, leading to desirable model performance.
5.1 Analysis of Seattle Traffic-Related Air Pollution Data
The performance of RapPCA in comparison with common existing methods, including classical and predictive PCA, is first illustrated with the multivariate traffic-related air pollution (TRAP) data in Seattle (Blanco et al., 2022). The study leverages a mobile monitoring campaign where a vehicle equipped with air monitors repeatedly collected two-minute samples at stationary roadside sites in the greater Seattle area. Repeated samples for the concentrations of 6 types of pollutants were obtained, including ultrafine particles (UFP), black carbon (BC), nitrogen dioxide (NO2), carbon monoxide (CO), carbon dioxide (CO2) and fine particulate matter (PM2.5). Following Blanco et al. (2022), we focus on UFP, BC and NO2 in our analysis due to data quality considerations. For UFP and BC, the concentrations were measured with multiple instruments corresponding to different measurement ranges or units. In particular, NanoScan instrument with 13 different bin sizes, as well as DiSCmini and PTRAK 8525 (with and without diffusion screen) instruments measured the concentration of UFP in terms of the counts of particles with different size ranges, along with the median size and overall count of particles. Black carbon was assessed by micro-aethalometer (MA200), which measures the concentration of particles with different light absorbing properties, corresponding to 5 different ranges of wavelengths.
The median 2-minute visit concentrations were winsorized at the site level such that concentrations below the 5th and above the 95th quantile for a given site were set to those thresholds, respectively. This was done to reduce the influence of outliers in the measurements. These winsorized medians were then averaged for each site, leading to annual average measurements of pollutant concentrations in total, including 17 for UFP, 5 for BC, and one for NO2. We use the concentration of NO2 to normalize all other variables except the median size measurements for UFP from the DiSCmini. All variables are centered and scaled before running each PCA algorithm.
We are interested in extrapolating the pollutant measurements to unobserved locations in the same study region. Because of the autocorrelation between these measurements, predicting each of them separately might not always lead to sensible results; instead, dimension reduction is needed before building spatial prediction models. Dimension reduction also allows us to understand the health effects of pollutant mixtures rather than separate pollutants alone. As in Section 4, we compare the performance of RapPCA with classical and predictive PCA, each extracting the top 3 PCs from the 23 measurements of air pollutants. Due to the high dimensionality of geographical covariates, we first ran PCA on these 189 covariates and used the top 15 PCs as predictors for predictive PCA. PCA and RapPCA were applied without this additional step. We examine the overall metrics as well as the individual prediction MSEs for each PC via 10-fold cross-validation following the same spatial prediction approach as Section 4, namely, a random forest model followed by spatial smoothing via TPRS on the residuals (Wai et al., 2020).
Table 1 compares each dimension reduction algorithm in terms of cross-validated TMSE, MSPE and MSRE-trn as well as prediction MSEs for each PC. Consistent with the findings from simulation studies, RapPCA achieves the lowest prediction and overall errors, while PCA has the smallest approximation gap on the training data. The advantage in predictability of RapPCA is reflected in both the overall MSPE and the individual MSEs for each PC. In this particular data analysis task, predictive PCA has good predictive performance for the second PC but is otherwise similar to or outperformed by both classical PCA and RapPCA. More generally, in settings with high-dimensional predictors (covariates and/or spatial basis), predictive PCA is not guaranteed to show an advantage in predictability since it requires a separate processing step on these predictors instead of selecting the information to use for prediction data-adaptively as RapPCA does.
| Overall Metrics | Individual MSEs | |||||
|---|---|---|---|---|---|---|
| TMSE | MSPE | MSRE-trn | PC1 | PC2 | PC3 | |
| PCA | 14.79 | 7.93 | 6.38 | 3.93 | 2.86 | 1.14 |
| PredPCA | 14.81 | 7.16 | 7.28 | 3.41 | 2.53 | 1.22 |
| RapPCA | 13.92 | 6.66 | 6.75 | 2.62 | 2.92 | 1.12 |
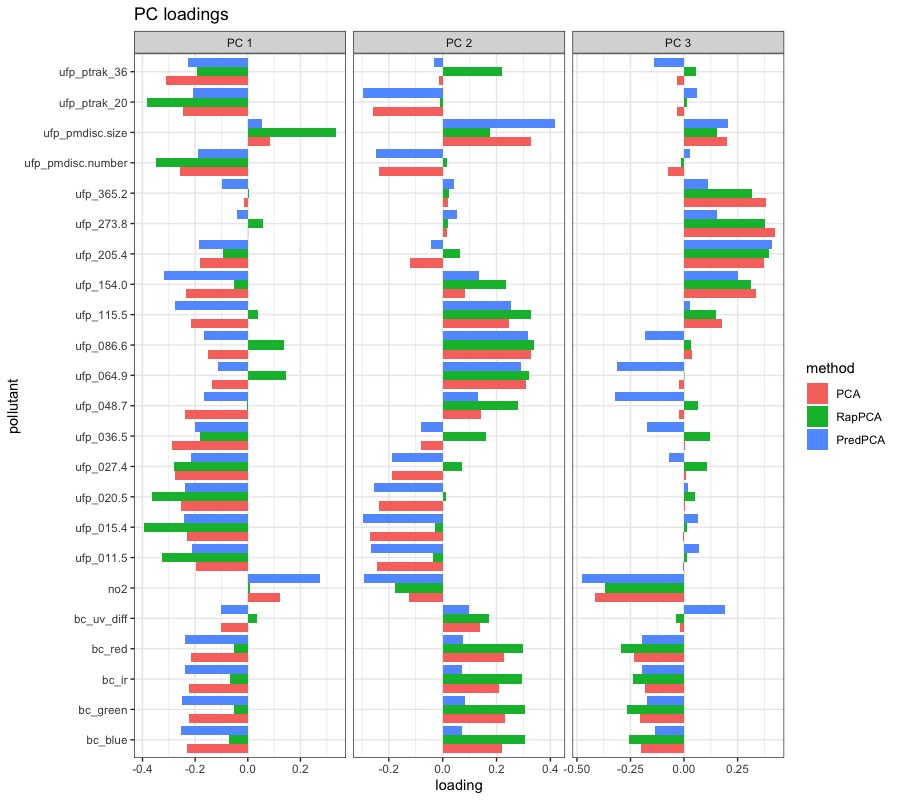
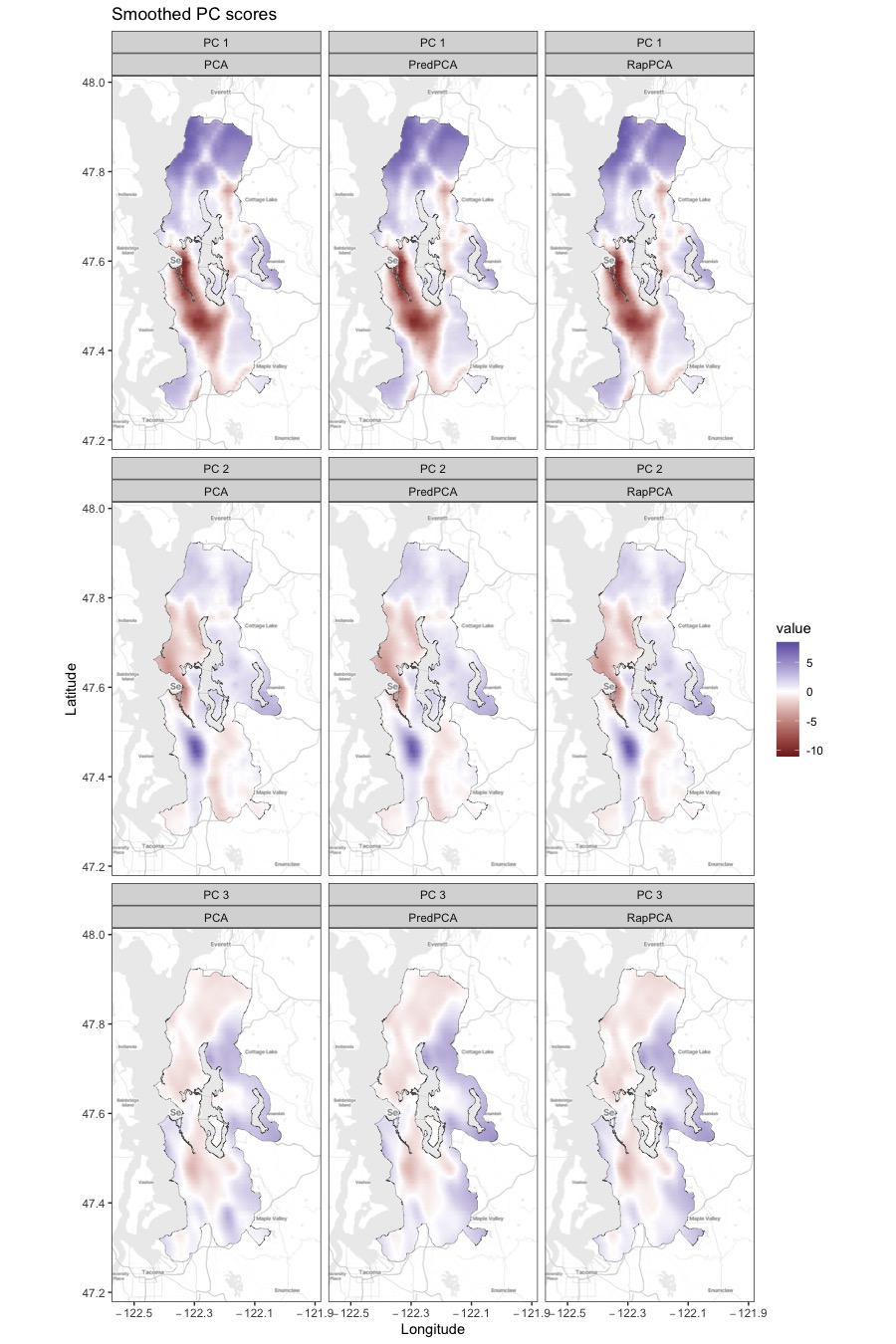
We then run dimension reduction with each of the PCA algorithms on the whole dataset to assess the spatial distribution of top 3 PC scores, where for RapPCA we select the tuning parameters and that lead to the optimal TMSE. Next, we train spatial prediction models for each of the PC scores, and evaluate these models on a finer grid of 5,040 locations over the study region to obtain smoothed plots of each PC score. Figure S4 in Appendix B.3 visualizes the smoothed, finer-grain PC scores obtained by each method across the study region. Figure 3 presents the PC loadings reflecting the contribution of each pollutant on the PC scores. Roughly categorizing various UFP particle sizes into small, moderate and large groups, one key difference we observe from Figure 3 between RapPCA and the two benchmark algorithms is that RapPCA identifies one size group to be the main contributor to each of the 3 PCs, while the other two groups have negligible loadings: small particles contributing to the top PC, moderately-sized particles to the second PC, and large ones to the third PC. In addition, BC is mainly contributing to the second PC according to RapPCA. This observation is consistent with findings from other studies, where aircraft emissions (primarily composed of small UFPs) and road traffic, especially diesel exhaust (comprising moderately-sized UFPs and BC), were identified as two key sources of traffic-related air pollution (Austin et al., 2021; Nie et al., 2022). These findings reflect the benefits in downstream model interpretability brought by dimension reduction that well preserves scientific and spatial information. In contrast, neither predictive nor classical PCA effectively distinguishes the contributions of UFPs with different sizes or the contribution of BC.
5.2 Analysis of HER2-Positive Breast Tumor Spatial Transcriptomics
In this section, we present another use case of RapPCA by analyzing spatial transcriptomics data. While dimension reduction is also a common data handling step in these applications, there are a variety of downstream modeling tasks where spatial prediction, as in the Seattle TRAP study, may not be the primary focus. We will nevertheless illustrate that optimizing the balance between predictability and representability with RapPCA still leads to desirable performance in these tasks.
We analyze the human epidermal growth factor receptor 2 positive (HER2+) breast tumor data, which includes expression measures of genes in HER2+ tumors from eight individuals (Andersson et al., 2021). We focus on the first tumor section of the last individual, coded as sample H1 in Andersson et al. (2021), where the data consists of expression counts of genes on tissue locations. Following the same filtering steps as in Shang and Zhou (2022), we removed genes with non-zero expression at less than 20 locations and those confounded by technical artifacts (Andersson et al., 2021), as well as locations with non-zero expressions for less than 20 genes. The filtered set of data contains genes measured on spots, which is then normalized via regularized negative binomial regression as implemented by the Seurat R package (Hafemeister and Satija, 2019).
Due to the large number of genes along with the noise present in the expression measurements (Rao et al., 2021), dimension reduction is commonly performed before the main analytic tasks on genomic data to extract biologically meaningful signals as well as to facilitate computation; see Sun et al. (2019); Zhao et al. (2021); Shang and Zhou (2022) for related examples. We focus on two modeling tasks: spatial extrapolation and domain detection. In addition to the three PCA methods (PCA, predictive PCA, RapPCA) that were investigated in previous sections, we also include spatial PCA in our comparison. Spatial PCA is a probabilistic PCA algorithm for spatial transcriptomics data which incorporates spatial proximity information when modeling PC scores (Shang and Zhou, 2022).
The first application is more similar to the analysis in Section 5.1, where we are interested in predicting the gene expression PC scores at tissue locations with no measurements. This prediction problem is involved, for example, in the reconstruction of high-resolution spatial maps of gene expression (Gryglewski et al., 2018; Shang and Zhou, 2022). For each dimension reduction method, we extract the top 20 PCs from the expression of all genes, and conduct 10-fold cross-validation to assess TMSE, MSPE and MSRE-trn, where spatial prediction is done by random forest followed by TPRS smoothing as in previous sections. For spatial PCA, we also include results from its built-in spatial prediction function (using the SpatialPCA R package) for completeness. Table 2 summarizes the overall metrics along with individual prediction MSEs for the top 3 PCs. RapPCA demonstrates significant advantage in overall prediction accuracy (MSPE) compared to all other methods, followed by predictive PCA which also has the lowest per-PC MSEs for the top 3 PCs. Also, consistent with findings from previous sections, RapPCA achieves the optimal trade-off between prediction and approximation gaps, as reflected by TMSE.
| Overall Metrics | Individual MSEs | |||||
|---|---|---|---|---|---|---|
| TMSE | MSPE | MSRE-trn | PC1 | PC2 | PC3 | |
| PCA | 272.21 | 32.24 | 239.97 | 6.64 | 5.09 | 3.18 |
| PredPCA | 278.08 | 31.85 | 246.15 | 3.93 | 4.12 | 2.26 |
| SpatialPCA | 292.78 | 46.09 | 246.70 | 6.84 | 5.89 | 3.69 |
| SpatialPCA: built-in | 296.59 | 49.90 | 246.70 | 6.81 | 5.96 | 3.81 |
| RapPCA | 271.35 | 20.56 | 250.80 | 5.59 | 4.86 | 3.79 |
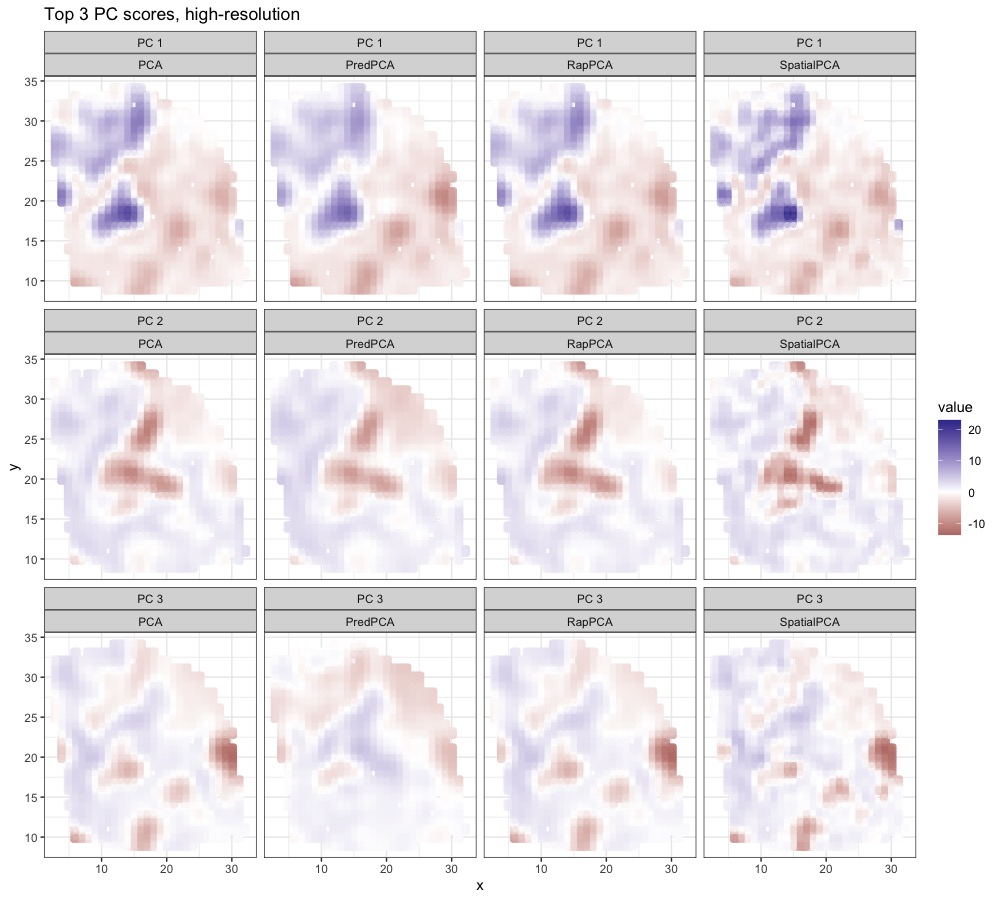
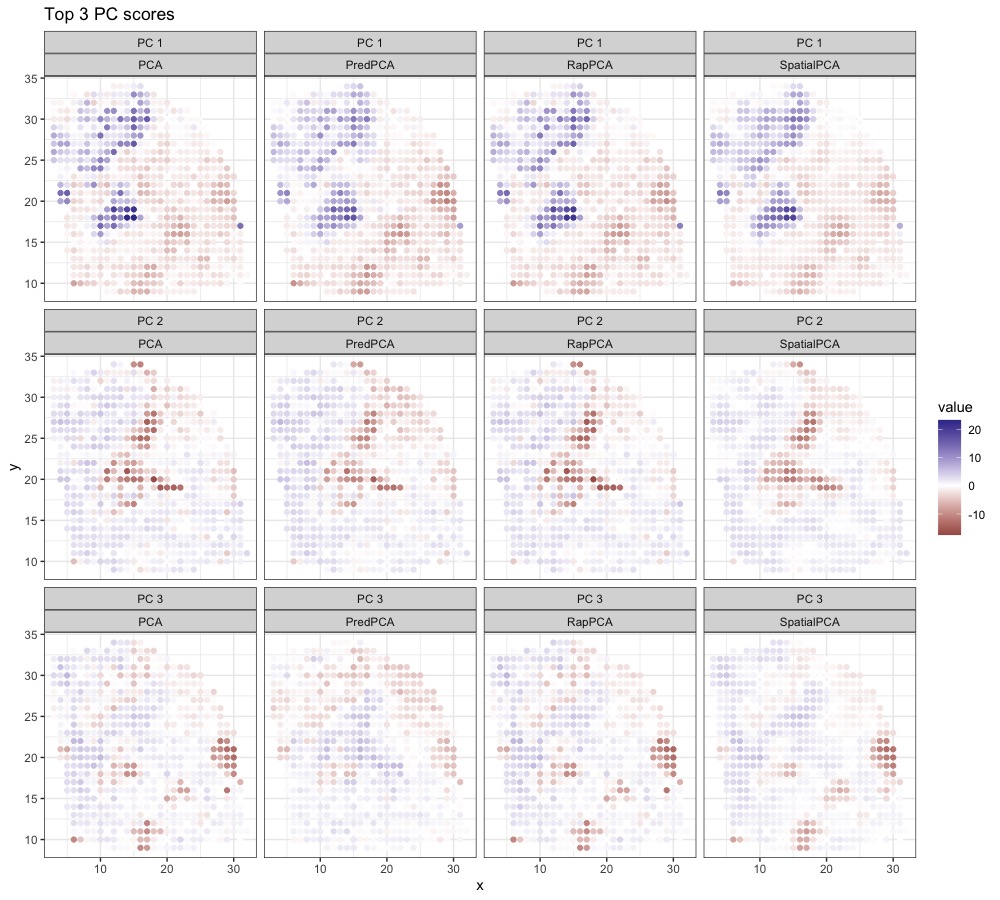
Figure 4 visualizes the top 3 PC scores from the expressions of all genes. We observe that spatial PCA and predictive PCA produce spatially smoother surfaces of PC scores compared to the other two methods. This is natural for predictive PCA since it prioritizes spatial predictability of the PC scores, which results in stronger spatial smoothing; for spatial PCA, the prediction-representation balance is implicit and less straightforward to interpret. The gap in the prediction performance of spatial or predictive PCA compared with RapPCA may be the consequence of over-smoothing, which also indicates the effectiveness of explicit optimization for the prediction-representation balance achieved by (4). Figure S5 in Appendix B.3 visualizes the smoothed high-resolution maps of PC scores based on predictions at unmeasured locations.
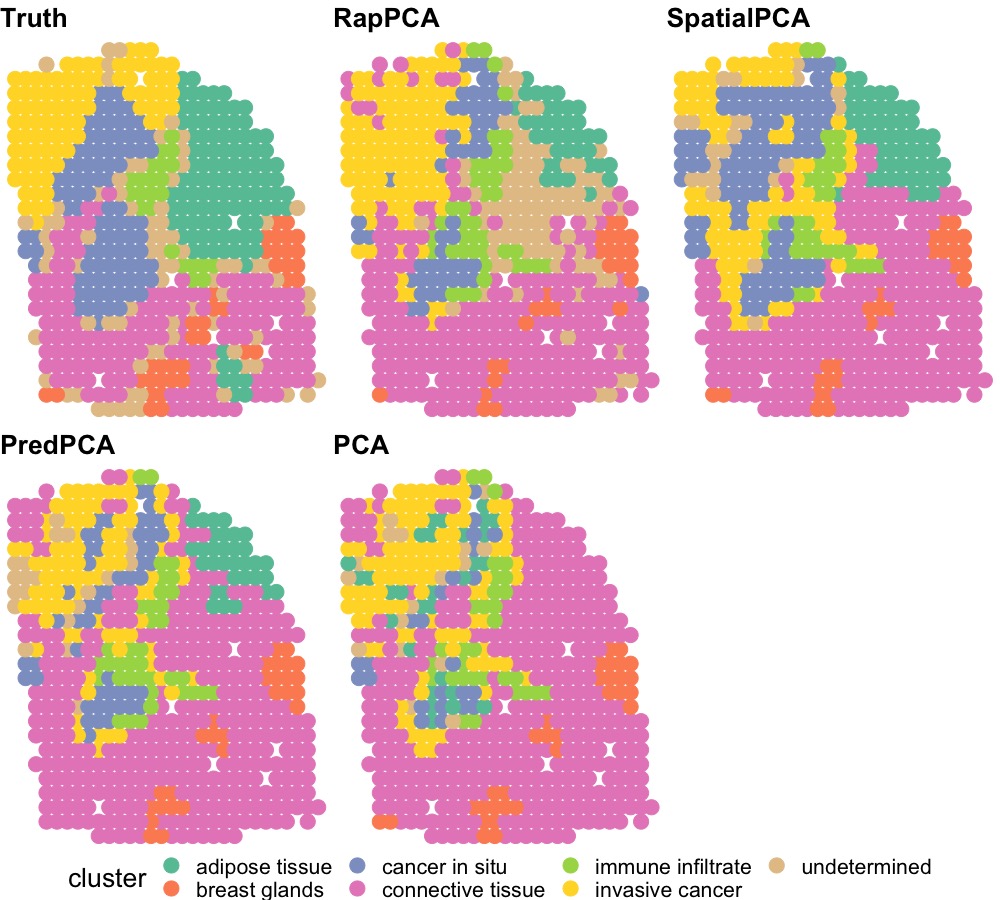
In the second application, we investigate the problem of domain detection following the dimension reduction step. In domain detection, different sections of tissues are identified as various spatially coherent and functionally distinct regions (Dong and Zhang, 2022; Shang and Zhou, 2022), providing helpful insights into the biological function of tissues. To this end, we conduct domain detection via the walktrap clustering algorithm (Pons and Latapy, 2005) using the top 20 PCs extracted by each algorithm. The number of clusters is set to align with the “ground truth” labels based on pathologist annotations of tissue regions in the original study (Andersson et al., 2021). The hyperparameters are chosen based on silhouette value measuring the difference between nearest-cluster versus intra-cluster distances (Rousseeuw, 1987).
Figure 5 visualizes the detected spatial domains based on PCs extracted from different dimension reduction procedures, compared to the ground truth labels. In general, the relative performance of each algorithm differs across spatial domains. For example, PCA fails to detect the adipose tissue region and produces noisier results for regions surrounding invasive cancer cells. Predictive PCA and RapPCA both mis-classify part of the cancer in situ region as invasive cancer, where predictive PCA results are noisier for the top left region, and RapPCA shows larger uncertainty regarding adipose tissue. Spatial PCA, on the other hand, infers part of the connective tissue to be cancerous.
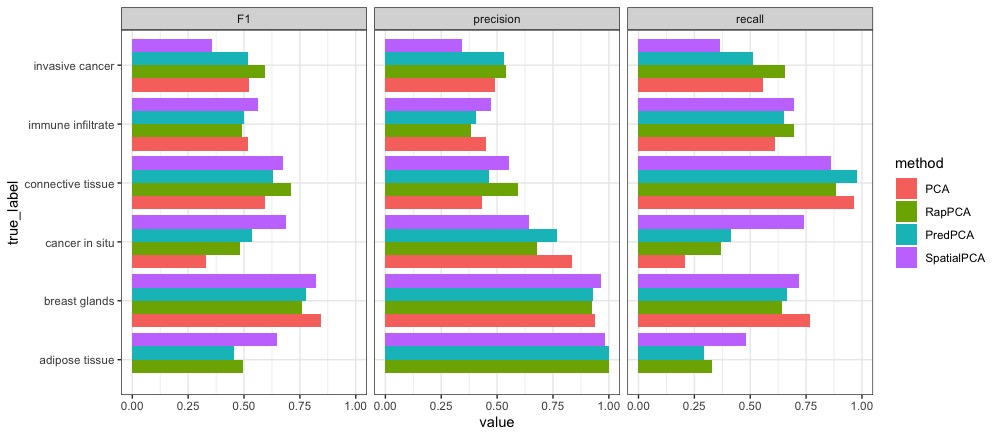
To make a more in-depth comparison, we examine the breakdown of clustering accuracy by ground truth labels; that is, whether or not each approach correctly classifies the spots belonging to each spatial domain, with the undetermined cluster removed from comparison. Figure 6 presents this breakdown for each method in terms of precision, recall and F1 score. As observed from the spatial domain plots, the relative accuracy for each method differs by region, and in particular, RapPCA has the best performance in both precision and recall on the identification of invasive cancer regions, whereas spatial PCA shows an advantage in recall for cancer in situ.
6 Discussion
When dimension reduction is conducted as an intermediate step before a spatial modeling task of interest, there are two typically conflicting considerations guiding the choice of approaches. The more obvious one is how closely the lower dimensional score represents the original variables, which we refer to as representability. Another important aspect is the predictability of the resulting scores, i.e., how well they could be expressed or predicted by available covariates and/or spatial effects.
We discussed how existing dimension reduction algorithms fit into this general framework of optimizing either criterion, and proposed a flexible interpolation between them that achieves the optimal representability-predictability trade-off. Our proposal, called RapPCA, can also handle high-dimensional predictors (including covariates and spatial basis) and non-linear relationships between covariates and PC scores. Simulation studies under different scenarios illustrate the gain in downstream prediction accuracy by our method, which also achieves smaller overall errors when both predictability and representability are taken into account. Applications to real datasets in different scientific domains further demonstrate the utility of our proposed method, even in analytic tasks that do not explicitly involve prediction.
The balance between prediction and representation performance can be viewed as a generalized form of bias-variance trade-off. While methods such as classical PCA minimize the representation gap specifically for the training data at hand, such representation may capture excessive noise if it explains a large amount of variability in the data. In contrast, the formulation of predictive PCA restricts the PC scores to fall within a certain model space, the linear span of the covariates, which is a form of regularization enforcing the smoothness of the PCs. Many probabilistic dimension reduction approaches implicitly address both aspects, while our proposal seeks the optimal balance in an explicit and interpretable way.
While we used TMSE to guide the choice of tuning parameters in most of our examples, in practice tuning parameter selection could be driven by the specific analytic goal. For example, we used silhouette value reflecting the goodness of clustering for the domain detection task in Section 5.2; while for the health effect analysis of air pollution in Jandarov et al. (2017), the main focus was spatial extrapolation accuracy and hence prediction error is of primary interest. Researchers could examine the trend of prediction, representation and total errors by each tuning parameter, and in particular in (4), on a set of test data, and choose the combination leading to the desired trade-off. Our empirical evaluations suggest that striking such balance with our proposed method would most often improve, or at least maintain similar, overall errors compared to the existing alternatives.
The procedure described in Algorithm 1 depends on a specified number of PCs. Since increasing will reduce the total MSRE and increase the total MSPE, one could examine the trajectory of MSPE and MSRE with respect to , and identify the ‘elbow’ of these curves as a practical choice of ; this reflects the threshold beyond which adding more PCs would not alter either the prediction or representation meaningfully. Practitioners may also be interested in estimating the variability of evaluation metrics such as TMSE, MSPE and MSRE to better understand the trade-off between them. While our method does not directly provide uncertainty estimates, one could conduct bootstrap to assess this, with the potential caveat of sample splitting on correlated data.
References
- Achilleos et al. (2017) Achilleos, S., Kioumourtzoglou, M.-A., Wu, C.-D., Schwartz, J. D., Koutrakis, P. and Papatheodorou, S. I. (2017) Acute effects of fine particulate matter constituents on mortality: A systematic review and meta-regression analysis. Environment International, 109, 89–100.
- Andersson et al. (2021) Andersson, A., Larsson, L., Stenbeck, L., Salmén, F., Ehinger, A., Wu, S. Z., Al-Eryani, G., Roden, D., Swarbrick, A., Borg, Å. et al. (2021) Spatial deconvolution of HER2-positive breast cancer delineates tumor-associated cell type interactions. Nature Communications, 12, 6012.
- Austin et al. (2021) Austin, E., Xiang, J., Gould, T. R., Shirai, J. H., Yun, S., Yost, M. G., Larson, T. V. and Seto, E. (2021) Distinct ultrafine particle profiles associated with aircraft and roadway traffic. Environmental Science & Technology, 55, 2847–2858.
- Bendtsen et al. (2021) Bendtsen, K. M., Bengtsen, E., Saber, A. T. and Vogel, U. (2021) A review of health effects associated with exposure to jet engine emissions in and around airports. Environmental Health, 20, 1–21.
- Bergen et al. (2013) Bergen, S., Sheppard, L., Sampson, P. D., Kim, S.-Y., Richards, M., Vedal, S., Kaufman, J. D. and Szpiro, A. A. (2013) A national prediction model for PM2.5 component exposures and measurement error-corrected health effect inference. Environmental Health Perspectives, 121, 1017–1025.
- Blanco et al. (2022) Blanco, M. N., Gassett, A., Gould, T., Doubleday, A., Slager, D. L., Austin, E., Seto, E., Larson, T. V., Marshall, J. D. and Sheppard, L. (2022) Characterization of annual average traffic-related air pollution concentrations in the Greater Seattle Area from a year-long mobile monitoring campaign. Environmental Science & Technology, 56, 11460–11472.
- Bose et al. (2018) Bose, M., Larson, T. and Szpiro, A. A. (2018) Adaptive predictive principal components for modeling multivariate air pollution. Environmetrics, 29, e2525.
- Chan et al. (2015) Chan, S. H., Van Hee, V. C., Bergen, S., Szpiro, A. A., DeRoo, L. A., London, S. J., Marshall, J. D., Kaufman, J. D. and Sandler, D. P. (2015) Long-term air pollution exposure and blood pressure in the sister study. Environmental Health Perspectives, 123, 951–958.
- Dai et al. (2014) Dai, L., Zanobetti, A., Koutrakis, P. and Schwartz, J. D. (2014) Associations of fine particulate matter species with mortality in the United States: a multicity time-series analysis. Environmental Health Perspectives, 122, 837–842.
- Dominici et al. (2003) Dominici, F., Sheppard, L. and Clyde, M. (2003) Health effects of air pollution: a statistical review. International Statistical Review, 71, 243–276.
- Dong and Zhang (2022) Dong, K. and Zhang, S. (2022) Deciphering spatial domains from spatially resolved transcriptomics with an adaptive graph attention auto-encoder. Nature Communications, 13, 1739.
- Evgeniou et al. (2000) Evgeniou, T., Pontil, M. and Poggio, T. (2000) Regularization networks and support vector machines. Advances in Computational Mathematics, 13, 1–50.
- Goldberg (2007) Goldberg, M. S. (2007) On the interpretation of epidemiological studies of ambient air pollution. Journal of Exposure Science & Environmental Epidemiology, 17, S66–S70.
- Gryglewski et al. (2018) Gryglewski, G., Seiger, R., James, G. M., Godbersen, G. M., Komorowski, A., Unterholzner, J., Michenthaler, P., Hahn, A., Wadsak, W., Mitterhauser, M. et al. (2018) Spatial analysis and high resolution mapping of the human whole-brain transcriptome for integrative analysis in neuroimaging. Neuroimage, 176, 259–267.
- Hafemeister and Satija (2019) Hafemeister, C. and Satija, R. (2019) Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biology, 20, 296.
- Hastie et al. (2009) Hastie, T., Tibshirani, R., Friedman, J. H. and Friedman, J. H. (2009) The elements of statistical learning: data mining, inference, and prediction, vol. 2. Springer.
- Hofmann et al. (2008) Hofmann, T., Schölkopf, B. and Smola, A. J. (2008) Kernel methods in machine learning. The Annals of Statistics, 36, 1171–1220.
- Hu et al. (2021) Hu, J., Li, X., Coleman, K., Schroeder, A., Ma, N., Irwin, D. J., Lee, E. B., Shinohara, R. T. and Li, M. (2021) SpaGCN: Integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nature Methods, 18, 1342–1351.
- Jandarov et al. (2017) Jandarov, R. A., Sheppard, L. A., Sampson, P. D. and Szpiro, A. A. (2017) A novel principal component analysis for spatially misaligned multivariate air pollution data. Journal of the Royal Statistical Society. Series C, Applied statistics, 66, 3.
- Jolliffe (2002) Jolliffe, I. T. (2002) Principal component analysis for special types of data. Springer.
- Keller et al. (2017) Keller, J. P., Drton, M., Larson, T., Kaufman, J. D., Sandler, D. P. and Szpiro, A. A. (2017) Covariate-adaptive clustering of exposures for air pollution epidemiology cohorts. The Annals of Applied Statistics, 11, 93.
- Kiselev et al. (2017) Kiselev, V. Y., Kirschner, K., Schaub, M. T., Andrews, T., Yiu, A., Chandra, T., Natarajan, K. N., Reik, W., Barahona, M. and Green, A. R. (2017) SC3: consensus clustering of single-cell RNA-seq data. Nature Methods, 14, 483–486.
- Li et al. (2019) Li, T., Levina, E. and Zhu, J. (2019) Prediction models for network-linked data. The Annals of Applied Statistics, 13, 132–164.
- Li et al. (2021) Li, Z., Song, T., Yong, J. and Kuang, R. (2021) Imputation of spatially-resolved transcriptomes by graph-regularized tensor completion. PLoS Computational Biology, 17, e1008218.
- Lippmann et al. (2013) Lippmann, M., Chen, L. C., Gordon, T., Ito, K. and Thurston, G. D. (2013) National Particle Component Toxicity (NPACT) Initiative: integrated epidemiologic and toxicologic studies of the health effects of particulate matter components. Research Report (Health Effects Institute), 177, 5–13.
- Liu et al. (2022) Liu, W., Liao, X., Yang, Y., Lin, H., Yeong, J., Zhou, X., Shi, X. and Liu, J. (2022) Joint dimension reduction and clustering analysis of single-cell RNA-seq and spatial transcriptomics data. Nucleic Acids Research, 50, e72–e72.
- Long et al. (2023) Long, Y., Ang, K. S., Li, M., Chong, K. L. K., Sethi, R., Zhong, C., Xu, H., Ong, Z., Sachaphibulkij, K., Chen, A. et al. (2023) Spatially informed clustering, integration, and deconvolution of spatial transcriptomics with GraphST. Nature Communications, 14, 1155.
- Murphy (2012) Murphy, K. (2012) Machine Learning–A probabilistic Perspective. The MIT Press.
- Nie et al. (2022) Nie, D., Qiu, Z., Wang, X. and Liu, Z. (2022) Characterizing the source apportionment of black carbon and ultrafine particles near urban roads in Xi’an, china. Environmental Research, 215, 114209.
- Özkaynak et al. (2013) Özkaynak, H., Baxter, L. K., Dionisio, K. L. and Burke, J. (2013) Air pollution exposure prediction approaches used in air pollution epidemiology studies. Journal of Exposure Science & Environmental Epidemiology, 23, 566–572.
- Pierson and Yau (2015) Pierson, E. and Yau, C. (2015) ZIFA: Dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biology, 16, 1–10.
- Pons and Latapy (2005) Pons, P. and Latapy, M. (2005) Computing communities in large networks using random walks. In Computer and Information Sciences - ISCIS 2005: 20th International Symposium, Istanbul, Turkey, October 26-28, 2005. Proceedings 20, 284–293. Springer.
- Prabhakaran et al. (2016) Prabhakaran, S., Azizi, E., Carr, A. and Pe’er, D. (2016) Dirichlet process mixture model for correcting technical variation in single-cell gene expression data. In International Conference on Machine Learning, 1070–1079. PMLR.
- Rao et al. (2021) Rao, A., Barkley, D., França, G. S. and Yanai, I. (2021) Exploring tissue architecture using spatial transcriptomics. Nature, 596, 211–220.
- Rousseeuw (1987) Rousseeuw, P. J. (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53–65.
- Shang and Zhou (2022) Shang, L. and Zhou, X. (2022) Spatially aware dimension reduction for spatial transcriptomics. Nature Communications, 13, 7203.
- Shen and Huang (2008) Shen, H. and Huang, J. Z. (2008) Sparse principal component analysis via regularized low rank matrix approximation. Journal of Multivariate Analysis, 99, 1015–1034.
- Sun et al. (2019) Sun, S., Zhu, J., Ma, Y. and Zhou, X. (2019) Accuracy, robustness and scalability of dimensionality reduction methods for single-cell RNA-seq analysis. Genome Biology, 20, 1–21.
- Vu et al. (2020) Vu, P. T., Larson, T. V. and Szpiro, A. A. (2020) Probabilistic predictive principal component analysis for spatially misaligned and high-dimensional air pollution data with missing observations. Environmetrics, 31, e2614.
- Vu et al. (2022) Vu, P. T., Szpiro, A. A. and Simon, N. (2022) Spatial matrix completion for spatially misaligned and high-dimensional air pollution data. Environmetrics, 33, e2713.
- Wahba (1990) Wahba, G. (1990) Spline models for observational data. SIAM.
- Wai et al. (2020) Wai, T. H., Young, M. T. and Szpiro, A. A. (2020) Random spatial forests. arXiv preprint arXiv:2006.00150.
- Wood (2003) Wood, S. N. (2003) Thin plate regression splines. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 65, 95–114.
- Wood (2017) — (2017) Generalized additive models: an introduction with R. Chapman and Hall/CRC.
- Zhang et al. (2019) Zhang, X., Chen, X. and Wang, J. (2019) A number-based inventory of size-resolved black carbon particle emissions by global civil aviation. Nature Communications, 10, 534.
- Zhao et al. (2021) Zhao, E., Stone, M. R., Ren, X., Guenthoer, J., Smythe, K. S., Pulliam, T., Williams, S. R., Uytingco, C. R., Taylor, S. E., Nghiem, P. et al. (2021) Spatial transcriptomics at subspot resolution with BayesSpace. Nature Biotechnology, 39, 1375–1384.
APPENDIX
Appendix A Proof
Proof of Theorem 1.
For the th component, denote the singular value decomposition of as . Let , , and let the combined penalty matrix be
We verify that the optimization problem (4) has a unique global minimizer given by
by doing so, we establish the optimality of our solution given by Algorithm 1.
Recall the form of the optimization problem given in (4):
Suppressing the superscript for simplicity, we denote and start by examining the first term in the objective function, which can be expressed as
| (6) |
where denotes the trace of a matrix, means equal up to a constant not depending on or , and we have made use of the cyclic property of trace. Since and , denoting , (6) can be written as
Under the reparametrization in Theorem 1, namely, and , the objective function becomes
which is a quadratic function of for fixed , with
Since the Hessian is positive semidefinite, we can profile out by setting it to the minimizer . The objective function can thus be rearranged as
| (7) |
where .
It then follows that the original optimization problem (4) is equivalent to
for which the optimal solution is the normalized first eigenvector of (i.e., the one corresponding to the largest eigenvalue). By construction and the properties of eigendecomposition, such is guaranteed to be the global minimizer of . Recalling the form of and the fact that the untransformed optimal solution satisfies and completes the proof. ∎
Appendix B Additional Numerical Results
B.1 Optimality of Proposed Solution
We use the first replicate (out of 100 total) of data in Simulation Scenario 1 (Section 4.1) to numerically verify our claim in Theorem 1, i.e., the optimality of the derived solution.
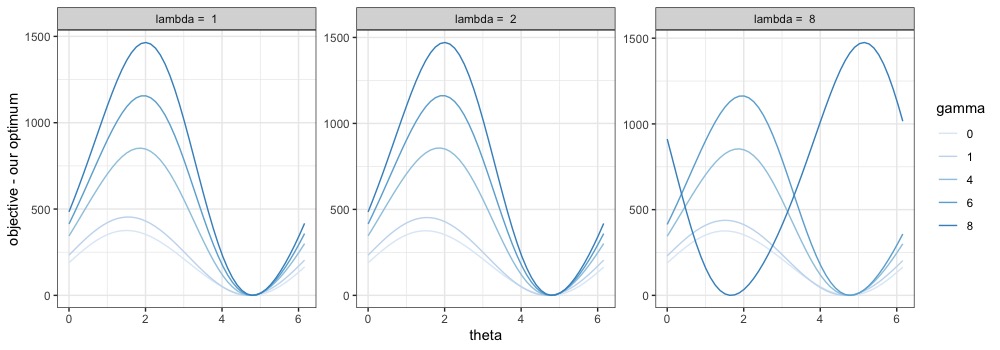
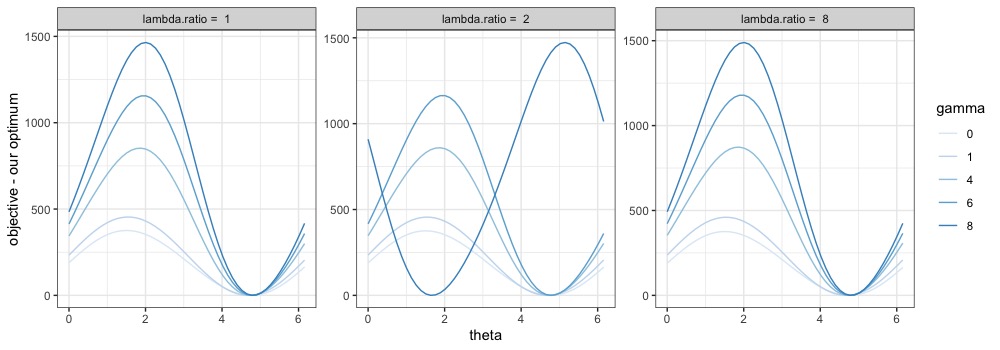
Specifically, we solve the optimization problem (4) to extract the first PC score, and vary the first two entries of the optimal loadings while keeping everything else (including the PC scores and coefficients ) intact, and ensuring that the constraint is still satisfied. This is done under polar coordinates: letting , we write as the modified loading vector, where the entries for . We let and where . Then, as varies within , the two entries take all possible combinations that satisfy the constraint.
We explore different values of tuning parameters and compare the objective function evaluated at the optimal solution versus the modified solution for . We plot their differences against for various values of tuning parameters in Figures S1 and S2. Note that the optimal , i.e., the value leading to the optimal loading , may differ with different sets of tuning parameters and . The fact that each curve is always above or equal to zero, and reaches zero exactly once, verifies the uniqueness of the optimal solution, as well as the optimality of the proposed form of , at least for fixed and .
B.2 Additional Simulation Results
Figure S3 is an analog of Figure 1 presented in our simulation studies, which visualizes the variation of TMSE, MSPE and MSRE-trn for the first PC with respect to the combination of and , instead of . For each combination, the additional tuning parameter is chosen such that it leads to the lowest TMSE. In Scenarios 1 through 3, the median values of the selected parameters via cross-validation are (0.5, 1), (1, 0.75) and (0.5, 0.25) respectively, all of which are reasonably close to near-optimal region(s) in Figure S3. This reflects the effectiveness of the cross-validation procedure to control the degree of freedom of coefficients and in (4).
B.3 Additional Data Analysis Results
For the TRAP data analysis presented in Section 5.1, Figure S4 presents the smoothed, finer-grain PC scores obtained by each method across the study region. We observe similar spatial patterns in the distribution of the PC scores across different methods, except for the south end of the study region for the third PC where PCA identifies a stronger signal than RapPCA and predictive PCA. In particular, all methods highlight regions near the airport and/or around major roads (the dark red area) for the first PC, indicating aircraft and road traffic emissions as a major source of overall pollution level. This is consistent with the large contributions of BC as well as UFP with small or moderate sizes (Zhang et al., 2019; Bendtsen et al., 2021), as reflected by the loadings of UFP (with relatively small particle sizes) and BC in Figure 3.
For the spatial transcriptomics application in Section 5.2, Figure S5 presents the smoothed high-resolution maps of predicted PC scores, obtained by spatial prediction following each dimension reduction approach. We observe that predictive PCA produces the smoothest predicted map due to its emphasis on the predictability of PC scores; however, it could over-smooth and omit meaningful spatial variations in gene expression, as can be seen in the high-resolution map for the third PC. For spatial PCA, while the extracted low-resolution PCs also demonstrate smoothness as predictive PCA (see Figure 4), they are not guaranteed to be well predictable and the extrapolated high-resolution map appears noisier. RapPCA achieves a reasonable balance among all algorithms.