This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Principle of Helical & Nonhelical Dynamo and α\alpha effect in Field Structure model

Kiwan Park,1
1Center for Astronomy, Institute for Theoretical Astrophysics at University of Heidelberg 69120 Heidelberg, Germany E-mail: oz150@uni-heidelberg.de, pkiwan@gmail.com
(Accepted XXX. Received YYY; in original form ZZZ)
Abstract

We explain the (non)helical dynamo process using a field-structure model based on magnetic induction equation in an intuitive way. We show how nonhelical kinetic energy converts into magnetic energy and cascades toward smaller eddies in a mechanically forced plasma system. Also, we show how helical magnetic energy is inversely cascaded (α\alpha effect) toward large scale magnetic eddies in a mechanically or magnetically forced system. We, then, compare the simulation results with the model qualitatively for the verification of the model. In addition to these intuitive and numerical approaches, we show how to get α\alpha and β\beta coefficient semi-analytically from the temporally evolving large scale magnetic energy and magnetic helicity.

keywords:
Magnetic field – MHD turbulence – Dynamo
††pubyear: 2018††pagerange: Principle of Helical & Nonhelical Dynamo and α\alpha effect in Field Structure model–Principle of Helical & Nonhelical Dynamo and α\alpha effect in Field Structure model

1 Introduction

Although the various scales of magnetic field 𝐁{\mathbf{B}} and conducting fluids (plasma) are ubiquitous in space, it is not yet clearly understood how the magnetic fields and plasmas exchange energy through their mutual interactions (Moffatt, 1978; Krause & Rädler, 1980; Brandenburg & Subramanian, 2005). The energy transferred from the conducting fluid to the magnetic field generates various scales of magnetic fields and amplifies them (dynamo). Briefly, the dynamo phenomena are classified as a large-scale dynamo (LSD) and a small-scale dynamo (SSD) depending on the direction of energy transfer. In particular, since many physical turbulent phenomena e.g. transport of momentum or material are mostly controlled by large scale motions, the evolution and role of large scale magnetic field (B¯\overline{B}) in a turbulent plasma system are fundamental and practical problems that cannot be limited only to academic interests.

Large scale dynamo theory shows how the small scale magnetic energy with helicity (α\alpha effect, (Park & Blackman, 2012a, b)), differential rotation (Ω\Omega effect, Balbus & Hawley (1991)), or shear current (Rogachevskii & Kleeorin (2003)) can be (inversely) cascaded toward 𝐁¯{\overline{\mathbf{B}}}. Out of them, the α\alpha effect is indispensable to the self consistent dynamo process, or inverse cascade of magnetic energy EME_{M} in the helical large scale dynamo. Moreover, since the properties of the helicity provide a relatively clear mathematical advantage in the theoretical description of the LSD phenomena, many LSD theories aim to represent electromotive force (EMF, ξ≡⟨𝐮×𝐛⟩\xi\equiv\langle\mathbf{u}\times\mathbf{b}\rangle), which is a source of 𝐁¯\overline{\mathbf{B}}, with (pseudo) tensors and 𝐁¯\overline{\mathbf{B}}.

Analytically α\alpha effect can be derived with a scale-divided function feedback method which is also a basic principle of numerical calculation. The representative theories like first order smoothing approximation (FOSA, or second order correlation approximation, SOCA, Moffatt (1978); Krause & Rädler (1980); Brandenburg & Subramanian (2005)), minimal tau approximation (MTA, Blackman & Field (2002)), or Quasi Normalized approximation (QN, Frisch et al. (1975)) are actually based on the method in a dynamic or stationary state. However, since the α\alpha effect is not a strict mathematical concept, some ambiguities are inevitable for the analytical derivation, which does not depreciate the importance of α\alpha effect in the helical dynamo. Numerically, α\alpha, β\beta coefficient in the α\alpha effect can be found applying an external magnetic field 𝐁e​x\mathbf{B}_{ex} to the system (Schrinner et al. (2005)). However, since 𝐁e​x\mathbf{B}_{ex} affects the dynamo process (Cattaneo & Hughes (1996)), well-designed numerical results without 𝐁e​x\mathbf{B}_{ex} would be used to derive the coefficients (test field method, Schrinner et al. (2005)).

Conventional dynamo theories show what happen over the statistical number of realizations of magnetohydrodynamic (MHD) system. The analytical theories give a qualitative and more or less quantitative description of the evolution of magnetic fields in the plasma, but they do not tell us how the actual plasma and magnetic field interact physically within the system. To explain the physical processes of evolving 𝐁\mathbf{B}, a cartoon model of stretching of 𝐁\mathbf{B} field ‘(𝐁⋅∇)𝐮\mathbf{B}\cdot\nabla)\mathbf{u}’ has been used in analogy to stretching vorticity (ω⋅∇𝐮\mathbf{\omega}\cdot\nabla\mathbf{u}, ω=∇×𝐮\mathbf{\omega}=\nabla\times\mathbf{u}) neglecting tilting effect (Zeldovich, 1983; Schekochihin et al., 2002). However, 𝐁\mathbf{B} is essentially not so directly related to 𝐮\mathbf{u} as ω\mathbf{\omega} is. Moreover, the concept of ‘stretching, twist, folding’ is not relevant to any physics law or fluidal equation. Furthermore, the model implying the co-stretching of 𝐁\mathbf{B} and 𝐮\mathbf{u} needs to explain the nontrivial EMF (∼⟨𝐮×𝐁⟩≠0\sim\langle\mathbf{u}\times\mathbf{B}\rangle\neq 0). This large gap between the dynamo model and the dynamo mechanism makes it more difficult to derive a more accurate dynamo theory.

Here, we introduce an improved field structure model (Park, 2017b) based on magnetic induction equation for the physical mechanisms of a helical large scale dynamo (LSD) and nonhelical small scale dynamo (SSD). The dynamo processes shown in the model are in line with the theory and consistent with the simulation results. Also, we show how to get α\alpha coefficients in the helical LSD from large scale magnetic energy E¯M​(⟨B¯2⟩/2)\overline{E}_{M}\,(\langle\overline{B}^{2}\rangle/2) and magnetic helicity H¯M​(⟨𝐀¯⋅𝐁¯⟩)\overline{H}_{M}\,(\langle\overline{\mathbf{A}}\cdot\overline{\mathbf{B}}\rangle) which can be measured in observation and simulation.

2 Simulation

For the numerical investigation we used the PENCIL\mathrm{PENCIL} CODE\mathrm{CODE}. We used PENCIL\mathrm{PENCIL} CODE\mathrm{CODE}, which solves the coupled fluid equations for the compressible conducting fluids in a periodic box (Brandenburg, 2001).

D​ρD​t\displaystyle\frac{D\rho}{Dt} =\displaystyle= −ρ​∇⋅𝐔,\displaystyle-\rho{\bf\nabla}\cdot{\bf U}, (1)
D​𝐔D​t\displaystyle\frac{D{\bf U}}{Dt} =\displaystyle= −∇ln​ρ+1ρ​(∇×𝐁)×𝐁\displaystyle-{\bf\nabla}\mathrm{ln}\,\rho+\frac{1}{\rho}(\nabla\times{\bf B})\times{\bf B} (2)
+ν​(∇2𝐔+13​∇∇⋅𝐔)​(+𝐟k​i​n)\displaystyle+\nu\big{(}{\bf\nabla}^{2}{\bf U}+\frac{1}{3}{\bf\nabla}{\bf\nabla}\cdot{\bf U}\big{)}\,\,(+\mathbf{f}_{kin})
∂𝐀∂t\displaystyle\frac{\partial{\bf A}}{\partial t} =\displaystyle= 𝐔×𝐁−η​∇×𝐁​(+𝐟m​a​g).\displaystyle{\bf U}{\bf\times}{\bf B}-\eta\,{\bf\nabla}{\bf\times}{\bf B}\,\,(+\mathbf{f}_{mag}). (3)

Here, ρ\rho and D/Dt(=∂/∂t+𝐔⋅∇D/Dt(=\partial/\partial t+{\bf U}\cdot{\bf\nabla}) indicate the density and Lagrangian time derivative. ν\nu and η\eta are kinematic viscosity and magnetic diffusivity respectively. The velocity is in unit of the sound speed, and the magnetic field is normalized by (ρ0​μ0)1/2​cs(\rho_{0}\,\mu_{0})^{1/2}c_{s}, where μ0\mu_{0} and csc_{s} are magnetic permeability and sound speed, respectively. The forcing function 𝐟​(x,t){\bf f}(x,t) in Fourier space is N​𝐟k​(t)​e​x​p​[i​𝐤f​(t)⋅𝐱+i​ϕ​(t)]N\,{\bf f}_{k}(t)\,exp\,[i\,{\bf k}_{f}(t)\cdot{\bf x}+i\phi(t)]:

𝐟k​i​n,o​r​m​a​g​(t)=i​𝐤​(t)×(𝐤​(t)×𝐞)−ξ​|k​(t)|​(𝐤​(t)×𝐞)k​(t)2​1+ξ2​1−(𝐤​(t)⋅𝐞)2/k​(t)2.\displaystyle{\bf f}_{kin,\,ormag}(t)=\frac{i\mathbf{k}(t)\times(\mathbf{k}(t)\times\mathbf{e})-\xi|k(t)|(\mathbf{k}(t)\times\mathbf{e})}{k(t)^{2}\sqrt{1+\xi^{2}}\sqrt{1-(\mathbf{k}(t)\cdot\mathbf{e})^{2}/k(t)^{2}}}.

Here ‘𝐞\mathbf{e}’ is an arbitrary unit vector, ‘ξ\xi’ denotes the helicity ratio, and ‘ϕ​(t)\phi(t)’ is a random phase (|ϕ​(t)|≤π|\phi(t)|\leq\pi). For example if ‘ξ\xi’ is ‘±1\pm 1’, i​𝐤×𝐟k=±k​𝐟ki\mathbf{k}\times\mathbf{f}_{k}=\pm k\mathbf{f}_{k} (fully helical). If ‘ξ\xi’ is ‘0’, i​𝐤×𝐟ki\mathbf{k}\times\mathbf{f}_{k} is not proportional to 𝐟k\mathbf{f}_{k}. The calculated forcing function in Fourier space at k=kfk=k_{f} is again inversely Fourier transformed and applied to Eq. (2) or (3).

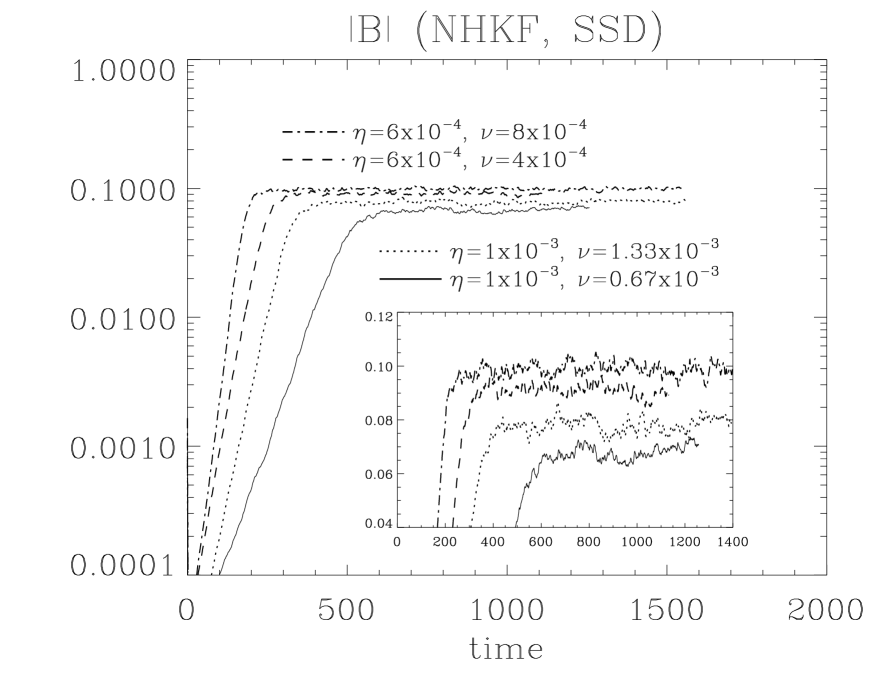
We simulated MHD systems forced with a helical kinetic forcing dynamo (HKFD), helical magnetic forcing dynamo (HMFD), and nonhelical kinetic forcing dynamo (NHKFD) with an isothermal environment (π3\pi^{3}, a periodic boundary condition). For the HKFD, a fully helical energy (∇×𝐟k​i​n=kf​𝐟k​i​n\nabla\times\mathbf{f}_{kin}=k_{f}\mathbf{f}_{kin}, kf=5k_{f}=5) is given to Eq. (2). For the HKFD, a fully helical energy (∇×𝐟m​a​g=kf​𝐟m​a​g\nabla\times\mathbf{f}_{mag}=k_{f}\mathbf{f}_{mag}) is given to Eq. (3), but |𝐟m​a​g|=|𝐟k​i​n|/kf|\mathbf{f}_{mag}|=|\mathbf{f}_{kin}|/k_{f}. For NHKFD, the forcing method is the same as that of HKFD except the helicity ratio: ∇×𝐟≁𝐟\nabla\times\mathbf{f}\nsim\mathbf{f}.

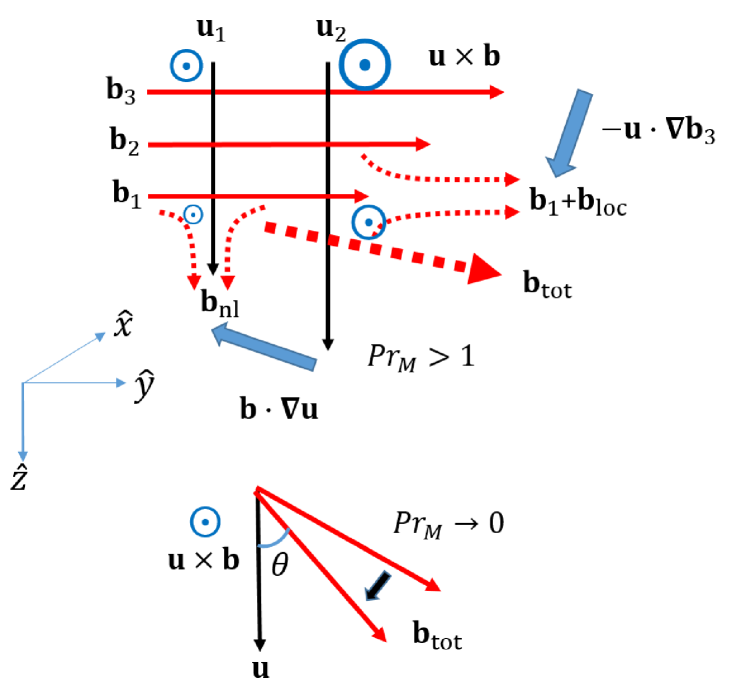
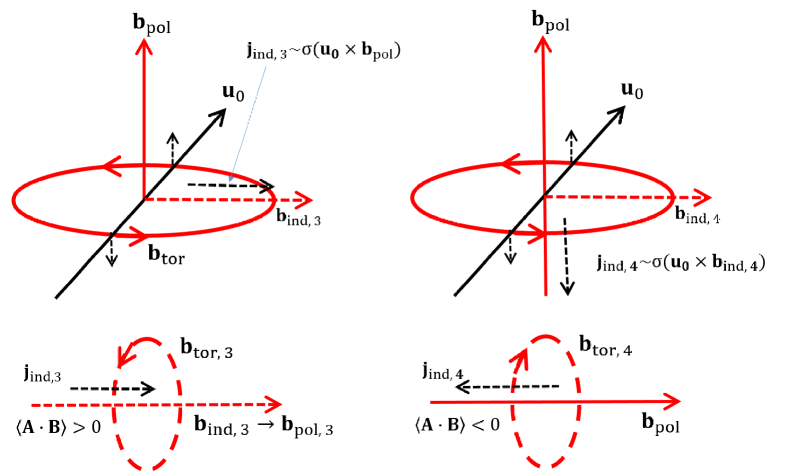
Refer to caption
Figure 1: Field structure from 𝐛i⋅∇𝐮i−𝐮i⋅∇𝐛i(∼∇×⟨𝐮i×𝐛i⟩)\mathbf{b}_{i}\cdot\nabla\mathbf{u}_{i}-\mathbf{u}_{i}\cdot\nabla\mathbf{b}_{i}\,(\sim\nabla\times\langle\mathbf{u}_{i}\times\mathbf{b}_{i}\rangle) shows how nonhelical magnetic energy migrates along 𝐮i\mathbf{u}_{i} and 𝐛i\mathbf{b}_{i}.
Refer to caption
Refer to caption
Figure 2: (a) 𝐛t​o​r\mathbf{b}_{tor} and 𝐛p​o​l\mathbf{b}_{pol} form a left handed (negative) magnetic helicity, and 𝐮t​o​r\mathbf{u}_{tor} and 𝐮p​o​l\mathbf{u}_{pol} form a right handed (positive) kinetic helicity. (b) Magnetic energy at 𝐛1\mathbf{b}_{1} diffuses toward 𝐛3\mathbf{b}_{3} through −𝐮⋅∇𝐛-\mathbf{u}\cdot\nabla\mathbf{b}.
Refer to caption
((a))  HKF
Refer to caption
((b))  HMF
Figure 3: In principle, a helically forced system (HKF or HMF) can generate both a positive and negative helical magnetic helicity.
Refer to caption
Refer to caption
Refer to caption
Figure 4: Evolving EME_{M} and HMH_{M} at k=1, 5 in a system forced with the positive kinetic helicity. As P​rMPr_{M} increases, the forced eddy kfk_{f} is relatively more influenced by the kinetic helicity than the magnetic diffusion from the large scale magnetic field.
Refer to caption
((a))   HKF & HMF of fh=+1f_{h}=+1
Refer to caption
((b))   HKF & HMF of fh=−1f_{h}=-1
Figure 5: (a), (b) Large scale magnetic energy E¯M​(⟨B¯2⟩/2)\overline{E}_{M}(\langle\overline{B}^{2}\rangle/2) and its helical component k​⟨𝐀¯⋅𝐁¯⟩/2​(k=1)k\langle\overline{\mathbf{A}}\cdot\overline{\mathbf{B}}\rangle/2\,(k=1) for HKFD and HMFD. The evolution of EME_{M} and HMH_{M} can be explained by Eq. (9), (10) according to α>0\alpha>0 or α<0\alpha<0.
Refer to caption
((a))   NHKF (fh=0f_{h}=0)
Figure 6: SSD forced with the nonhelical kinetic energy at kk=5. |B||B| is (inversely) proportional to (η)​ν(\eta)\,\nu or magnetic Prandtl number P​rMPr_{M}.

Dynamo process shown in Fig. 1 is mathematically straightforward. The interaction between 𝐮i\mathbf{u}_{i} and 𝐛i\mathbf{b}_{i} yields EMF (ξi∼⟨𝐮i×𝐛i⟩\xi_{i}\sim\langle\mathbf{u}_{i}\times\mathbf{b}_{i}\rangle(−x^-\hat{x})), which is the weakest at 𝐮1\mathbf{u}_{1} & 𝐛1\mathbf{b}_{1} and strongest at 𝐮2\mathbf{u}_{2} & 𝐛3\mathbf{b}_{3}. This inhomogeneous EMF arouses a nontrivial curl effect, i.e., growth rate of magnetic field: ∇×⟨𝐮i×𝐛i⟩∼∂𝐛i/∂t\nabla\times\langle\mathbf{u}_{i}\times\mathbf{b}_{i}\rangle\sim\partial\mathbf{b}_{i}/\partial\,t. The growth rate is the weakest at 𝐮2\mathbf{u}_{2} & 𝐛3\mathbf{b}_{3} and strongest at 𝐮1\mathbf{u}_{1} & 𝐛1\mathbf{b}_{1}. This indicates energy transfer from 𝐛3\mathbf{b}_{3} (𝐮2\mathbf{u}_{2}) to 𝐛1\mathbf{b}_{1} (𝐮1\mathbf{u}_{1}). Essentially the transport of magnetic energy occurs in a bimodal way. A transferred magnetic field from 𝐮2\mathbf{u}_{2} to 𝐮1\mathbf{u}_{1} through 𝐛⋅∇𝐮\mathbf{b}\cdot\nabla\mathbf{u}111Here, a bold letter 𝐮\mathbf{u} or 𝐛\mathbf{b} indicates a vector field. is represented by 𝐛n​l\mathbf{b}_{nl} (𝐛n​l​(t)=∫t𝐛⋅∇𝐮​d​τ\mathbf{b}_{nl}(t)=\int^{t}\mathbf{b}\cdot\nabla\mathbf{u}\,d\tau), which is parallel to the velocity field. Similarly, a transferred magnetic field from 𝐛3\mathbf{b}_{3} to 𝐛1\mathbf{b}_{1} through −𝐮⋅∇𝐛-\mathbf{u}\cdot\nabla\mathbf{b} is represented by 𝐛l​o​c\mathbf{b}_{loc} (𝐛l​o​c​(t)=−∫t𝐮⋅∇𝐛​d​τ\mathbf{b}_{loc}(t)=-\int^{t}\mathbf{u}\cdot\nabla\mathbf{b}\,d\tau), which is parallel to the magnetic field. Net magnetic field 𝐛t​o​t\mathbf{b}_{tot} from these two transferred magnetic fields again interacts with 𝐮\mathbf{u} at the next dynamo process.

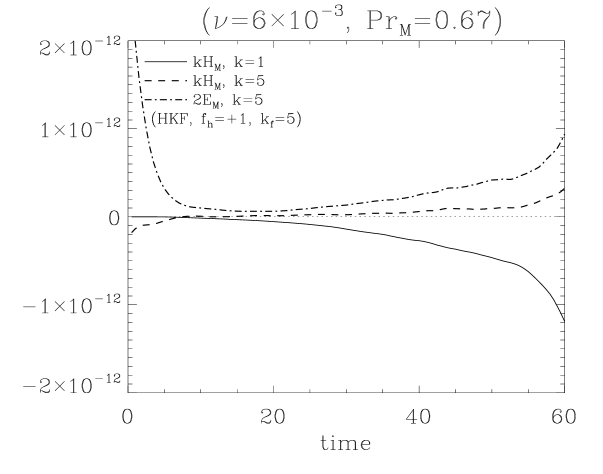
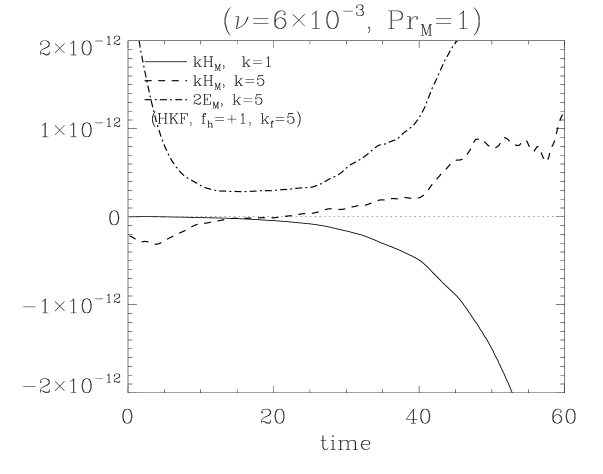
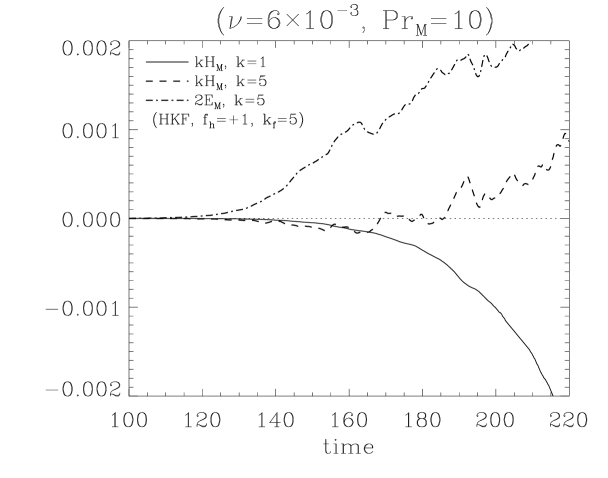
In addition to the strength of 𝐮\mathbf{u} and 𝐛\mathbf{b}, the angle θ\theta between 𝐛n​l\mathbf{b}_{nl} and 𝐛1+𝐛l​o​c\mathbf{b}_{1}+\mathbf{b}_{loc} plays a crucial role in EMF. If 𝐛n​l\mathbf{b}_{nl} grow faster than 𝐛l​o​c\mathbf{b}_{loc}, θ\theta and EMF decrease. Several factors can affect their relative ratio, but magnetic Prandtl number P​rM=ν/ηPr_{M}=\nu/\eta has a paradoxical effect. Both ν\nu and η\eta are related to the dissipation of energy; but, their roles work in the opposite way. Decreasing η\eta increases 𝐛l​o​c\mathbf{b}_{loc} and EMF. However, with small ν\nu more kinetic energy is transported to a smaller eddy. Then, more magnetic energy is transferred to the smaller eddy leading to the growth of 𝐛n​l\mathbf{b}_{nl}, which disturbs dynamo (see Fig. 6(a)).

In the model 𝐛1\mathbf{b}_{1} (or 𝐮1\mathbf{u}_{1}) can be considered as a large or small scale field. However, as ∂𝐛/∂t∼∇×⟨𝐮×𝐛⟩∼l−1​⟨𝐮×𝐛⟩\partial\mathbf{b}/\partial t\sim\nabla\times\langle\mathbf{u}\times\mathbf{b}\rangle\sim l^{-1}\langle\mathbf{u}\times\mathbf{b}\rangle implies, if 𝐮1\mathbf{u}_{1} and 𝐛1\mathbf{b}_{1} are the small scale eddies, the magnetic energy transfer from 𝐛3\mathbf{b}_{3} (𝐮3\mathbf{u}_{3}) to 𝐛1\mathbf{b}_{1} (𝐮1\mathbf{u}_{1}) occurs more easily due to the small characteristic length. In contrast, if 𝐛1\mathbf{b}_{1} and 𝐮1\mathbf{u}_{1} are large scale eddies, additional process is required to overcome the large characteristic length l1l_{1}. Nonetheless, the energy transport is essentially bidirectional, which appears clearly in a decaying MHD system (Park, 2017a, b).

2.1 Amplification of the helical BB field for LSD

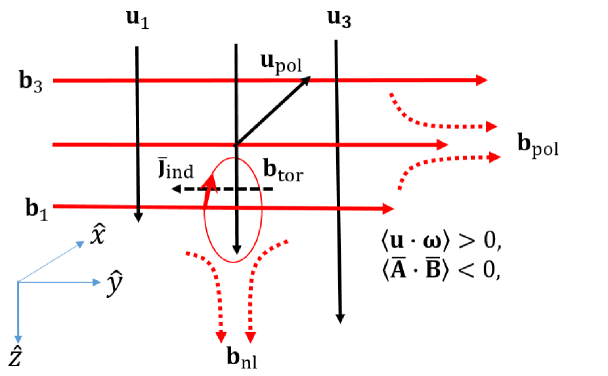
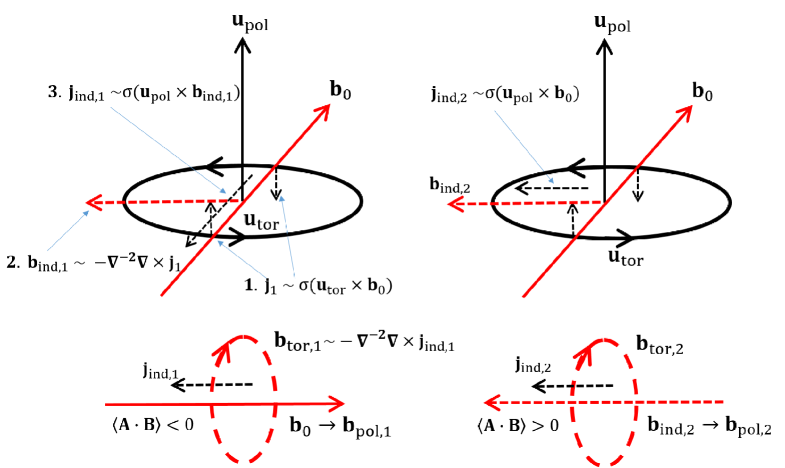
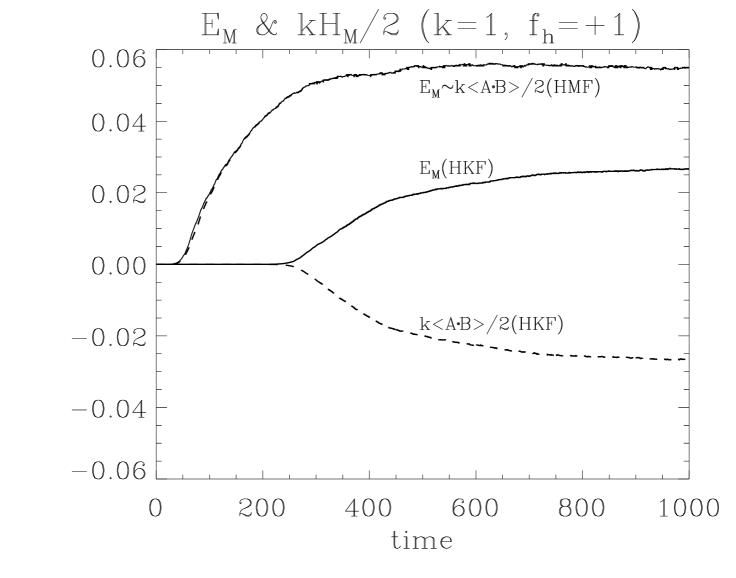
Fig. 2 shows a dynamo system forced by the right handed helical kinetic energy (HKF) composed of a toroidal field 𝐮t​o​r\mathbf{u}_{tor} and poloidal one 𝐮p​o​l​(x^)\mathbf{u}_{pol}(\hat{x}) (⟨𝐮⋅ω⟩>0,ω=∇×𝐮)\langle\mathbf{u}\cdot\mathbf{\omega}\rangle>0,\,\omega=\nabla\times\mathbf{u}). 222In Fig. 2 only a representative 𝐮p​o​l\mathbf{u}_{pol} is considered to synchronize the two-scale dynamo theory. 𝐣i​n​d\mathbf{j}_{ind}, 𝐛t​o​r\mathbf{b}_{tor}, and the resultant left handed magnetic helicity exist in the whole scales. The interaction between 𝐮p​o​l​(x^)\mathbf{u}_{pol}(\hat{x}) and 𝐛n​l​(z^)\mathbf{b}_{nl}(\hat{z}) induces a current density 𝐣i​n​d=σ​(𝐮p​o​l×𝐛n​l)​(−y^)\mathbf{j}_{ind}=\sigma(\mathbf{u}_{pol}\times\mathbf{b}_{nl})(-\hat{y}), which generates a toroidal magnetic field 𝐛t​o​r(=−∇−2∇×𝐣i​n​d)\mathbf{b}_{tor}(=-\nabla^{-2}\nabla\times\mathbf{j}_{ind}) around 𝐛1\mathbf{b}_{1}(=𝐛p​o​l\mathbf{b}_{pol}) forming a left handed magnetic helicity (⟨𝐚⋅𝐛⟩<0)(\langle\mathbf{a}\cdot\mathbf{b}\rangle<0). 𝐛t​o​r\mathbf{b}_{tor} interacts with 𝐮\mathbf{u} to induce another circular current density 𝐣c​i​r​c\mathbf{j}_{circ} antiparallel to 𝐛t​o​r\mathbf{b}_{tor}. 𝐣c​i​r​c\mathbf{j}_{circ} amplifies 𝐛p​o​l\mathbf{b}_{pol}, which amplifies 𝐛t​o​r\mathbf{b}_{tor} back through the α2\alpha^{2} dynamo process (Park, 2017a, b). This compound process makes possible |𝐛1||\mathbf{b}_{1}| surpasses |𝐛2||\mathbf{b}_{2}| and |𝐛3||\mathbf{b}_{3}|. As |𝐛i||\mathbf{b}_{i}| grows, dissipation effect plays a decisive role. So if 𝐛1\mathbf{b}_{1} is a small scale field, its dissipation ∼k12​b1\sim k_{1}^{2}b_{1} (k1≫1k_{1}\gg 1) becomes larger than that of other eddies. Therefore 𝐛1\mathbf{b}_{1} should be a large scale field for the continuous dynamo process.

As 𝐛1\mathbf{b}_{1} increases, the energy diffuses toward 𝐛3\mathbf{b}_{3} through −𝐮⋅∇𝐛1-\mathbf{u}\cdot\nabla\mathbf{b}_{1} (Fig. 2). However, the direction of curl effect is opposite so the induced field heads for −y^-\hat{y}. 𝐛3​(y^)\mathbf{b}_{3}(\hat{y}) can be inferred to approach to z​e​r​ozero and regrow to be 𝐛3′​(−y^)\mathbf{b}^{\prime}_{3}(-\hat{y}). Also, the toroidal field 𝐛t​o​r′\mathbf{b}^{\prime}_{tor} around 𝐛3′\mathbf{b}^{\prime}_{3} is induced due to 𝐣¯i​n​d\overline{\mathbf{j}}_{ind}. The direction of 𝐛t​o​r′\mathbf{b}^{\prime}_{tor} does not change. Subsequently, 𝐛3′\mathbf{b}^{\prime}_{3} and 𝐛t​o​r′\mathbf{b}^{\prime}_{tor} make the right handed magnetic helicity in small scale regime. This is supported by the changing sign of HMH_{M} at minimum of 𝐛3\mathbf{b}_{3} (see Fig. 4). Simultaneously, 𝐛3′\mathbf{b}^{\prime}_{3} can be suppressed by the interaction between 𝐛t​o​r′\mathbf{b}^{\prime}_{tor} and 𝐮i\mathbf{u}_{i}. Also, the growth of 𝐛1\mathbf{b}_{1} modifies the curvature radius of magnetic fields so that Lorentz force suppresses 𝐮i\mathbf{u}_{i}. All of these effects explain the conservation of magnetic helicity in HKFD.

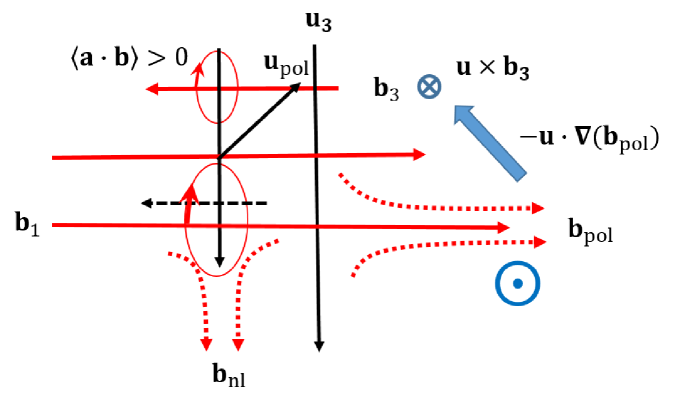
Left panel in Fig. 3(a) shows the dynamo process discussed above. However, right panel shows a different possibility that 𝐮p​o​l×𝐛0\mathbf{u}_{pol}\times\mathbf{b}_{0} can generate 𝐣i​n​d, 2​(−y^)\mathbf{j}_{ind,\,2}(-\hat{y}) which is parallel to the 𝐛i​n​d, 2(=𝐛i​n​d, 1)\mathbf{b}_{ind,\,2}\,(=\mathbf{b}_{ind,\,1}). 𝐣i​n​d, 2\mathbf{j}_{ind,\,2} induces 𝐛t​o​r, 2\mathbf{b}_{tor,\,2}, and 𝐛t​o​r, 2\mathbf{b}_{tor,\,2} forms the right handed magnetic helicity with 𝐛i​n​d, 2\mathbf{b}_{ind,\,2}. These two dynamo processes seem to result in z​e​r​ozero net helicity. However, a careful look shows an essential difference between these two processes. The amplified 𝐛i​n​d, 1\mathbf{b}_{ind,\,1} due to the enhanced 𝐛0\mathbf{b}_{0} yields stronger 𝐣i​n​d, 1\mathbf{j}_{ind,\,1}, which amplifies 𝐛t​o​r, 1\mathbf{b}_{tor,\,1}. This toroidal field fortifies 𝐛0\mathbf{b}_{0} again, which produces the enhanced 𝐛i​n​d, 1\mathbf{b}_{ind,\,1}. In contrast, 𝐛i​n​d, 2\mathbf{b}_{ind,\,2} and 𝐛t​o​r, 2\mathbf{b}_{tor,\,2} do not have such a mutual interaction, rather evolve passively. This essential difference decides the dominant magnetic helicity in the system.

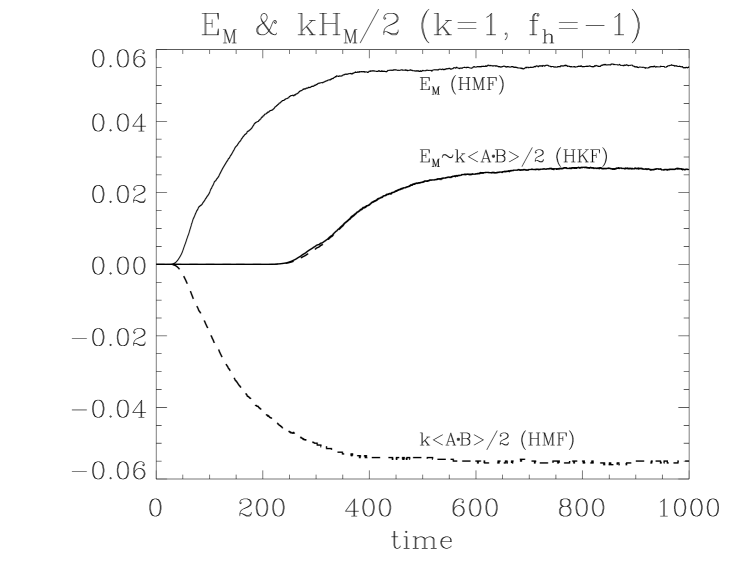
The principle of helical magnetic forcing dynamo (HMFD) in Fig. 3(b) is similar to that of HKFD except some slight but essential differences. In the system forced by the right handed (positive) helical magnetic energy, 𝐛i​n​d, 3​(y^)\mathbf{b}_{ind,\,3}(\hat{y}) is generated from 𝐮0×𝐛t​o​r\mathbf{u}_{0}\times\mathbf{b}_{tor}. But, 𝐮0\mathbf{u}_{0} can induce two different current densities: 𝐣i​n​d, 3​(y^)\mathbf{j}_{ind,\,3}(\hat{y}) from 𝐮0×𝐛p​o​l\mathbf{u}_{0}\times\mathbf{b}_{pol} and 𝐣i​n​d, 4​(z^)\mathbf{j}_{ind,\,4}(\hat{z}) from 𝐮0×𝐛i​n​d, 4​(𝐛i​n​d, 3=𝐛i​n​d, 4)\mathbf{u}_{0}\times\mathbf{b}_{ind,\,4}\,(\mathbf{b}_{ind,\,3}=\mathbf{b}_{ind,\,4}). 𝐣i​n​d, 3​(y^)\mathbf{j}_{ind,\,3}(\hat{y}) generates 𝐛t​o​r, 3\mathbf{b}_{tor,\,3} around 𝐛i​n​d, 3\mathbf{b}_{ind,\,3} leading to the right handed magnetic helicity. But, 𝐣i​n​d, 4\mathbf{j}_{ind,\,4} generates 𝐛t​o​r, 4\mathbf{b}_{tor,\,4} around 𝐛i​n​d, 4\mathbf{b}_{ind,\,4} to generate the left handed magnetic helicity. However, since 𝐛t​o​r, 4\mathbf{b}_{tor,\,4} is antiparallel to 𝐛t​o​r\mathbf{b}_{tor}, the left handed magnetic helicity cancels with the injected right handed one. This is why the magnetic helicity generated in HMFD has the same sign of a forcing magnetic helicity.

2.2 Derivation of α\alpha coefficients

Thus far, we have shown the physical mechanisms of LSD and SSD in the field structure. Being different from SSD, LSD requires an additional amplifying process of the 𝐁\mathbf{B} field, α\alpha effect. The model implies that the growth of 𝐁¯\overline{\mathbf{B}} field (𝐛1\mathbf{b}_{1}) is related to the (helical) motion of 𝐮i\mathbf{u}_{i}, 𝐛i\mathbf{b}_{i} in small scale and 𝐁¯\overline{\mathbf{B}} field itself. Therefore, if the characteristic length ll and time scale τ\tau of turbulent eddies are smaller than those of 𝐁¯\overline{\mathbf{B}}, EMF may be expanded like:

⟨𝐮×𝐛⟩i∼αi​j​B¯j+βi​l​m​∂B¯l∂xm+γi​l​m​n​∂2B¯l∂xm​∂xn​…\displaystyle\langle\mathbf{u}\times\mathbf{b}\rangle_{i}\sim\alpha_{ij}\overline{B}_{j}+\beta_{ilm}\frac{\partial\,\overline{B}_{l}}{\partial\,x_{m}}+\gamma_{ilmn}\frac{\partial^{2}\overline{B}_{l}}{\partial x_{m}\partial x_{n}}... (4)

Moreover, if a smaller quantity out of R​eM≡u​l/ηRe_{M}\equiv ul/\eta and S≡u​τ/lS\equiv u\tau/l is much smaller than ‘1’ (min(R​eM,S)≪1(Re_{M},\,S)\ll 1), triple correlation terms and GG (≡(𝐮×𝐛−⟨𝐮×𝐛⟩)(\equiv(\mathbf{u}\times\mathbf{b}-\langle\mathbf{u}\times\mathbf{b}\rangle) in the magnetic induction equation in the small scale regime can be neglected. Then, ξ\xi can be calculated from 𝐮×∫τ∂𝐛/∂t​d​t\mathbf{u}\times\int^{\tau}\partial\mathbf{b}/\partial t\,dt (Moffatt, 1978) or from ∫τ∂𝐮/∂t​d​t×𝐛\int^{\tau}\partial\mathbf{u}/\partial t\,dt\times\mathbf{b} (Keinigs, 1983). However, these anticommutative FOSAs are not generally valid besides the considerable GG in space. In MTA, the third order moment terms, neglected in FOSA, are replaced by ξ/τ\xi/\tau without further calculation. It starts from the differentiation of a multi-variable function ξ​(𝐮,𝐛)\mathbf{\xi}(\mathbf{u},\,\mathbf{b}).

∂∂t​∇×⟨𝐮×𝐛⟩=∇×⟨∂𝐮∂t×𝐛⟩+∇×⟨𝐮×∂𝐛∂t⟩.\displaystyle\frac{\partial}{\partial\,t}\nabla\times\langle\mathbf{u}\times\mathbf{b}\rangle=\nabla\times\big{\langle}\frac{\partial\mathbf{u}}{\partial\,t}\times\mathbf{b}\big{\rangle}+\nabla\times\big{\langle}\mathbf{u}\times\frac{\partial\mathbf{b}}{\partial\,t}\big{\rangle}. (5)

After some analytical calculations, we can derive the simple forms of α=1/3​∫τ(⟨𝐣⋅𝐛⟩−⟨𝐮⋅ω⟩)​𝑑t\alpha=1/3\int^{\tau}(\langle\mathbf{j}\cdot\mathbf{b}\rangle-\langle\mathbf{u}\cdot\mathbf{\omega}\rangle)dt and β=1/3​∫τ⟨u2⟩​𝑑t\beta=1/3\int^{\tau}\langle u^{2}\rangle dt. Mathematically, the quenching effect of 𝐣⋅𝐛\mathbf{j}\cdot\mathbf{b} in the α\alpha coefficient is from the definition of a vector product and differentiation of a multi variable function. Physically, it is caused by the interaction between the current density and magnetic field in different scales.

Additional differentiation of Eq. (5) produces the fourth order moments which can be decomposed into the combination of second order ones: ⟨X1​X2​X3​X4⟩∼∑i​j​l​m⟨Xi​Xj⟩​⟨Xl​Xm⟩\langle X_{1}X_{2}X_{3}X_{4}\rangle\sim\sum_{ijlm}\langle X_{i}X_{j}\rangle\langle X_{l}X_{m}\rangle (QN, Kraichnan & Nagarajan (1967)). With the assumption of isotropy without reflection symmetry, the second order moment can be replaced by

⟨Xl​(k)​Xm​(−k)⟩\displaystyle\langle X_{l}(k)X_{m}(-k)\rangle =\displaystyle= Pl​m​(k)​E​(k)+i2​knk2​ϵl​m​n​H​(k),\displaystyle P_{lm}(k)E(k)+\frac{i}{2}\frac{k_{n}}{k^{2}}\epsilon_{lmn}H(k), (6)

where Pl​m​(k)=δl​m−kl​km/k2P_{lm}(k)=\delta_{lm}-k_{l}k_{m}/k^{2}, ⟨X2/2⟩=∫E​(k)​𝑑𝐤\langle X^{2}/2\rangle=\int E(k)\,d\mathbf{k}, and ⟨𝐗⋅∇×𝐗⟩=∫H​(k)​𝑑𝐤\langle\mathbf{X}\cdot\nabla\times\mathbf{X}\rangle=\int H(k)\,d\mathbf{k}. With some calculations, α\alpha, β\beta coefficient similar to those of MTA can be derived (Frisch et al., 1975).

All these methods are essentially to solve a closure issue in the MHD equations approximately without the exact solution of anisotropy and energy cascade time τ\tau affected by the magnetic field. Therefore, if there is a practical method to find the exact α\alpha, β\beta coefficient from observation and simulation, it will be helpful to infer a better closing method leading to a more exact helical dynamo theory.

2.3 Derivation of ‘α\alpha’ and ‘β\beta’ coefficients using semi-analytic method

In principle, α\alpha and β\beta coefficients can be found from ∂𝐁¯/∂t∼∇×α​𝐁¯+(η+β)​∇2𝐁¯\partial\overline{\mathbf{B}}/\partial t\sim\nabla\times\alpha\overline{\mathbf{B}}+(\eta+\beta)\nabla^{2}\overline{\mathbf{B}}. However, this vector equation is not so useful to the practical calculation. Instead, the scalar equations for E¯M\overline{E}_{M} and H¯M\overline{H}_{M} are more useful. We can get them like (Park, 2017b)

∂∂t​⟨𝐀¯⋅𝐁¯⟩\displaystyle\frac{\partial}{\partial t}\langle{\bf\overline{A}}\cdot{\bf\overline{B}}\rangle =\displaystyle= 2​⟨ξ¯⋅𝐁¯⟩−2​η​⟨𝐁¯⋅∇×𝐁¯⟩\displaystyle 2\langle{\bf\overline{\xi}}\cdot{\bf\overline{B}}\rangle-2\eta\langle{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{B}}\rangle
=\displaystyle= 2​α​⟨𝐁¯⋅𝐁¯⟩−2​(β+η)​⟨𝐁¯⋅∇×𝐁¯⟩\displaystyle 2\alpha\langle{\bf\overline{B}}\cdot{\bf\overline{B}}\rangle-2(\beta+\eta)\langle{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{B}}\rangle
→∂∂t​H¯M\displaystyle\rightarrow\frac{\partial}{\partial t}\overline{H}_{M} =\displaystyle= 4​α​E¯M−2​(β+η)​H¯M,\displaystyle 4\alpha\overline{E}_{M}-2(\beta+\eta)\overline{H}_{M}, (7)
∂∂t​12​⟨B¯2⟩\displaystyle\frac{\partial}{\partial t}\frac{1}{2}\langle\overline{B}^{2}\rangle =\displaystyle= ⟨𝐁¯⋅∇×ξ¯⟩−cσ​⟨𝐁¯⋅∇×𝐉¯⟩\displaystyle\langle{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}\overline{{\bf\xi}}\rangle-\frac{c}{\sigma}\langle{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{J}}\rangle
=\displaystyle= ⟨α​𝐁¯⋅∇×𝐁¯⟩−⟨β​∇×𝐁¯⋅∇×𝐁¯⟩−cσ​⟨𝐉¯⋅∇×𝐁¯⟩.\displaystyle\langle\alpha{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{B}}\rangle-\langle\beta{\bf\nabla}{\bf\times}{\bf\overline{B}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{B}}\rangle-\frac{c}{\sigma}\langle{\bf\overline{J}}\cdot{\bf\nabla}{\bf\times}{\bf\overline{B}}\rangle.
→∂∂t​E¯M\displaystyle\rightarrow\frac{\partial}{\partial t}\overline{E}_{M} =\displaystyle= α​H¯M−2​(β+η)​E¯M.\displaystyle\alpha\overline{H}_{M}-2\big{(}\beta+\eta\big{)}\overline{E}_{M}. (8)

The solutions of coupled Eqs. (7), (8) are333E¯M(∼⟨B¯2⟩\overline{E}_{M}(\sim\langle\overline{B}^{2}\rangle) includes the helical and nonhelical components of B¯\overline{B}. However, the nonhelical component of 𝐁\mathbf{B} is dropped when 𝐀¯⋅𝐁¯\overline{\mathbf{A}}\cdot\overline{\mathbf{B}} is averaged over the large scale.,

2​H¯M​(t)\displaystyle 2\overline{H}_{M}(t) =\displaystyle= (H¯M​(0)+2​E¯M​(0))​e2​∫0t(α−β−η)​𝑑τ\displaystyle(\overline{H}_{M}(0)+2\overline{E}_{M}(0))e^{2\int^{t}_{0}(\alpha-\beta-\eta)d\tau} (9)
+\displaystyle+ (H¯M​(0)−2​E¯M​(0))​e−2​∫0t(α+β+η)​𝑑τ,\displaystyle(\overline{H}_{M}(0)-2\overline{E}_{M}(0))e^{-2\int^{t}_{0}(\alpha+\beta+\eta)d\tau},
4​E¯M​(t)\displaystyle 4\overline{E}_{M}(t) =\displaystyle= (H¯M​(0)+2​E¯M​(0))​e2​∫0t(α−β−η)​𝑑τ\displaystyle(\overline{H}_{M}(0)+2\overline{E}_{M}(0))e^{2\int^{t}_{0}(\alpha-\beta-\eta)d\tau} (10)
−\displaystyle- (H¯M​(0)−2​E¯M​(0))​e−2​∫0t(α+β+η)​𝑑τ.\displaystyle(\overline{H}_{M}(0)-2\overline{E}_{M}(0))e^{-2\int^{t}_{0}(\alpha+\beta+\eta)d\tau}.

Eqs. (9), (10) are consistent with the field structure (Fig. 3(a), 3(b)) and the simulation results (Fig. 5(a), 5(b)). If α<0\alpha<0 (positive HKF or negative HMF), the second term in the right-hand side of Eqs. (9), (10) become dominant with increasing time. Since 2​E¯M​(0)≥H¯M​(0)2\overline{E}_{M}(0)\geq\overline{H}_{M}(0), H¯M​(t)\overline{H}_{M}(t) becomes negative. In contrast, if α>0\alpha>0 (negative HKF or positive HMF), H¯M​(t)\overline{H}_{M}(t) becomes positive and converges to 2​E¯M​(t)2\overline{E}_{M}(t) eventually. But E¯M​(t)\overline{E}_{M}(t) is positive in any case. When making these theoretical predictions, we referred to the simplest definitions of α\alpha and β\beta coefficients. However, these coefficients can be derived from

2​∫t(α−β−η)​𝑑τ\displaystyle 2\int^{t}(\alpha-\beta-\eta)\,d\tau =\displaystyle= l​n​(H¯M​(t)+2​E¯M​(t)H¯M​(0)+2​E¯M​(0)),\displaystyle ln\bigg{(}\frac{\overline{H}_{M}(t)+2\overline{E}_{M}(t)}{\overline{H}_{M}(0)+2\overline{E}_{M}(0)}\bigg{)}, (11)
2​∫t(−α−β−η)​𝑑τ\displaystyle 2\int^{t}(-\alpha-\beta-\eta)d\,\tau =\displaystyle= l​n​(H¯M​(t)−2​E¯M​(t)H¯M​(0)−2​E¯M​(0))\displaystyle ln\bigg{(}\frac{\overline{H}_{M}(t)-2\overline{E}_{M}(t)}{\overline{H}_{M}(0)-2\overline{E}_{M}(0)}\bigg{)} (12)

With C​(t)≡H¯M​(t)+2​E¯M​(t)C(t)\equiv\overline{H}_{M}(t)+2\overline{E}_{M}(t) and D​(t)≡H¯M​(t)−2​E¯M​(t)D(t)\equiv\overline{H}_{M}(t)-2\overline{E}_{M}(t), we can further obtain the separate coefficients like

α​(t)\displaystyle\alpha(t) =\displaystyle= 14​(1C​(t)​∂C​(t)∂t−1D​(t)​∂D​(t)∂t),\displaystyle\frac{1}{4}\bigg{(}\frac{1}{C(t)}\frac{\partial C(t)}{\partial t}-\frac{1}{D(t)}\frac{\partial D(t)}{\partial t}\bigg{)}, (13)
β​(t)\displaystyle\beta(t) =\displaystyle= −14​(1C​(t)​∂C​(t)∂t+1D​(t)​∂D​(t)∂t)−η.\displaystyle-\frac{1}{4}\bigg{(}\frac{1}{C(t)}\frac{\partial C(t)}{\partial t}+\frac{1}{D(t)}\frac{\partial D(t)}{\partial t}\bigg{)}-\eta. (14)

As the results show, if we know the temporal changes of large scale magnetic helicity H¯M​(t)\overline{H}_{M}(t) and large scale magnetic energy E¯M​(t)\overline{E}_{M}(t), α​(t)\alpha(t) and β​(t)\beta(t) coefficients can be found. Considering that other theoretical and numerical methods to find these coefficients require considerable analytic calculations and elaborate simulations, which are not yet accurate, these results give us quite a clear method to find α​(t)\alpha(t) and β​(t)\beta(t) coefficients. Additional differentiation over time leads to the integrand of each coefficients: d​α​(t)/d​t=d​∫t⟨⋅⟩​𝑑τ/𝑑td\alpha(t)/dt=d\int^{t}\langle\cdot\rangle d\tau/dt, d​β​(t)/d​t=d​∫t⟨⋅⟩​𝑑τ/𝑑td\beta(t)/dt=d\int^{t}\langle\cdot\rangle d\tau/dt. They can give us a chance to test the classical analytic results of FOSA or MTA d​α​(t)/d​t∼⟨𝐣⋅𝐛⟩−⟨𝐮⋅ω⟩d\alpha(t)/dt\sim\langle\mathbf{j}\cdot\mathbf{b}\rangle-\langle\mathbf{u}\cdot\mathbf{\omega}\rangle or d​β​(t)/d​t∼⟨u2⟩d\beta(t)/dt\sim\langle u^{2}\rangle. For a decaying MHD system, these classical results with Eq. (9), (10) reproduce the simulation results quite well (Park, 2017b). But still more numerical test is necessary for a forced system. There may be additional effects which are excluded in MTA and FOSA. Since the results Eq. (13), (14), which are mathematically derived with a statistical assumption and algebra, are exact as long as ⟨𝐮×𝐛⟩∼α​𝐁¯−β​∇×𝐁¯\langle\mathbf{u}\times\mathbf{b}\rangle\sim\alpha\overline{\mathbf{B}}-\beta\nabla\times\overline{\mathbf{B}} is valid, we will be able to see which other terms play a role in the α\alpha effect.

3 Summary

Thus far, we have seen how the field structure model explains the amplification process of the magnetic field in the plasma. Magnetic field 𝐛n​l\mathbf{b}_{nl} parallel to 𝐮\mathbf{u} is transferred through 𝐛⋅∇𝐮\mathbf{b}\cdot\nabla\mathbf{u}, and magnetic field 𝐛l​o​c\mathbf{b}_{loc} parallel to 𝐛\mathbf{b} is transferred through −𝐮⋅∇𝐛-\mathbf{u}\cdot\nabla\mathbf{b}. The net magnetic field 𝐛n​e​t\mathbf{b}_{net} from 𝐛n​l\mathbf{b}_{nl} and 𝐛l​o​c\mathbf{b}_{loc} is used as a seed magnetic field for the next dynamo step. As the field structure shows, growing 𝐛n​l\mathbf{b}_{nl} parallel to 𝐮\mathbf{u} suppresses the dynamo process, whereas growing 𝐛l​o​c\mathbf{b}_{loc} perpendicular to 𝐮\mathbf{u} boosts the dynamo action. This result explains the dependence of dynamo on the magnetic Prandtl number (P​rM≡ν/ηPr_{M}\equiv\nu/\eta). With less magnetic diffusion (decreasing η\eta) and more kinetic dissipation (increasing ν\nu, or increasing P​rMPr_{M}), the dynamo effect elevates. In contrast, the decreasing mechanical dissipation decreases the dynamo effect. These relations imply that the saturation of the magnetic field in an ideal system is related to the field structure between 𝐮\mathbf{u} and 𝐛\mathbf{b} (angle θ\theta) rather than the dissipation effect. We also explained the mechanism of the helical dynamo (α\alpha effect) using vector field analysis. HKFD and HMFD can generate both of the positive and negative magnetic helicity in principle. However, as we discussed, only opposite (same) sign of magnetic helicity is left in a forced HKFD (HMFD) system. Finally, we derived α\alpha, β\beta coefficients from the large-scale magnetic energy and magnetic helicity. The exact coefficients are useful to understanding more accurate internal dynamo processes in a MHD system, which leads to a more general dynamo theory. At present, the field structure model with various physical conditions such as rotation, shear, or 𝐁e​x\mathbf{B}_{ex} remains to be done. Before doing that, we will test the method with the simulation results and observation data.

Acknowledgements

KWP appreciates the support from ERC Advanced Grant STARLIGHT: Formation of the First Stars (339177) and the support from bwForCluster for numerical simulation.

References