PriRoAgg: Achieving Robust Model Aggregation with Minimum Privacy Leakage for Federated Learning
Abstract
Federated learning (FL) has recently gained significant momentum due to its potential to leverage large-scale distributed user data while preserving user privacy. However, the typical paradigm of FL faces challenges of both privacy and robustness: the transmitted model updates can potentially leak sensitive user information, and the lack of central control of the local training process leaves the global model susceptible to malicious manipulations on model updates. Current solutions attempting to address both problems under the one-server FL setting fall short in the following aspects: 1) designed for simple validity checks that are insufficient against advanced attacks (e.g., checking norm of individual update); and 2) partial privacy leakage for more complicated robust aggregation algorithms (e.g., distances between model updates are leaked for multi-Krum). In this work, we formalize a novel security notion of aggregated privacy that characterizes the minimum amount of user information, in the form of some aggregated statistics of users’ updates, that is necessary to be revealed to accomplish more advanced robust aggregation. We develop a general framework PriRoAgg, utilizing Lagrange coded computing and distributed zero-knowledge proof, to execute a wide range of robust aggregation algorithms while satisfying aggregated privacy. As concrete instantiations of PriRoAgg, we construct two secure and robust protocols based on state-of-the-art robust algorithms, for which we provide full theoretical analyses on security and complexity. Extensive experiments are conducted for these protocols, demonstrating their robustness against various model integrity attacks, and their efficiency advantages over baselines.
Index Terms:
Federated Learning, Privacy Preservation, Byzantine Resilience, Secure and Robust Aggregation.I Introduction
Federated learning (FL) is a trending collaborative machine learning (ML) paradigm, where numerous devices collaboratively train a model on their local datasets [1]. FL was designed to protect user data privacy, as the local model training is performed on each user’s private data, and only the model updates are uploaded to the server for aggregation, hence, the server does not directly access users’ data. However, some recent research works have revealed that the uploaded model updates may leak users’ data via attacks such as gradient inversion [2, 3, 4, 5]. On the other hand, due to FL’s distributed nature, the global model’s integrity may also be compromised by malicious users manipulating their local models. A variety of works have proposed attacks that can degenerate global model performance, or implement backdoors to cause misclassifications [6, 7, 8].
Most of the existing works focus on developing protocols that solve either the privacy problem or the model integrity problem, whereas there is a scarcity of studies that simultaneously address both problems. The main reason for that is the conflicting nature of the two goals: robust aggregation protocols for model integrity require the central server to aggregate based on the distribution of user updates [9, 10, 11, 12, 13, 14, 15, 16, 17], while secure aggregation protocols encrypt or mask the user updates so that they are indistinguishable statistically [18, 19, 20, 21, 22, 23, 24]. To compatibly provide security in robust aggregation protocols, commonly used techniques in secure aggregation face many limitations that hinder the combination of secure techniques and robust protocols. For example, homomorphic encryption suffers from high complexity [25, 26, 27, 28] that results in impractical implementations. Differential privacy is inherently imprecise and its masking renders direct computation of privacy data statistics infeasible [29, 22] . A few works provide robustness and security simultaneously, but they are designed for rather simple defensive mechanisms, such as cosine similarity [30] and norm bounding [31]. More importantly, their detection of malicious behaviors relies on single user’s self-check instead of finding overall statistics. In works like [32, 33] that attempt to conceal the local updates from the server, there is additional privacy leakage from the intermediate computation results. Some other privacy-preserving protocols enable the execution of robust algorithms but assume stronger settings, such as non-colluding multi-server scenarios [34, 35, 36]. Therefore, it remains a challenging problem to strengthen powerful robust algorithms with provable privacy under the typical single-server FL paradigm.
To this end, this paper aims to develop a secure aggregation framework, with minimal privacy leakage, for a general class of robust model aggregation algorithms. To rigorously define information leakage including the final model aggregation revealed to the server, we first introduce a new notion of privacy called aggregated privacy which allows certain aggregation of user statistics to be revealed to the server (but not individual ones), enabling robust computations. We formulate the problem as a secure multiparty computation (MPC) problem, and construct PriRoAgg, an FL framework that achieves robust aggregations against a wide range of user-launched attacks, while satisfying aggregated privacy. As concrete instantiations of the proposed PriRoAgg framework, we develop aggregated private protocols that are robust to two specific model poisoning and backdoor attacks; we provide detailed security analyses and experimental evaluations on these two protocols, demonstrating their performance and efficiency advantages over multiple baselines.
At the core of PriRoAgg are three key components: (1) Robust algorithms; (2) Secret sharing with Lagrange coded computing (LCC) [37]; and (3) Zero-knowledge proof (zk-proof). This framework is designed to incorporate robust algorithms that can compute a reliable final aggregation against potential malicious updates. Users’ private data remains in perfect secrecy within a certain number of colluding users since it is secret shared via LCC. In the presence of Byzantine users who may arbitrarily deviate from the protocol, PriRoAgg further leverages SNIP [38], a secret sharing-based zk-proof, to ensure the consistency of local executions. Users generate proofs that are verifiable by the collaboration of all other users and the server. The server can orchestrate the users to perform the final model aggregation securely and robustly.
The contributions of this work are summarized as follows:
-
•
We define a novel privacy notion of Aggregated Privacy for secure aggregation, particularly in FL settings. This definition prevents any user’s individual data from leakage while allowing certain aggregated statistics revealed.
-
•
We propose PriRoAgg, a secure FL framework for robust aggregation that satisfies aggregated privacy, against the collusion of semi-honest server and Byzantine users. It guarantees honest users to keep local data private while receiving a reliable global model resilient to various model integrity attacks.
- •
-
•
PriRoAgg is instantiated into two secure and robust protocols. We provide theoretical analyses for their privacy and efficiency, and perform extensive experiments to demonstrate the protocols’ advantages in terms of robustness and computational overheads.
II Background and Motivation
II-A Vanilla Federated Learning
In a vanilla federated learning protocol, the early concept involves conducting model training locally to ensure the privacy of users’ datasets. [1, 40]. Training is concurrently performed across all the users through an iterative process in which the users interact with the center server to jointly update the global model. A standard FL pipeline operates as follows: at -th iteration, the server shares the current state of the global model with all the users. Upon receiving the global model, each user trains a local model on its dataset, where the corresponding local update is . This is typically done by employing a minibatch stochastic gradient descent rule [41] to minimize the local objective function . Each user then uploads the local update to the server. After receiving the model updates, the server aggregates them to update the global model as follows.
| (1) |
where is the learning rate. The updated global model is distributed to all the users to start the next iteration.
II-B Privacy-preserving Model Aggregation
Contradicting the early concept, studies have revealed that conventional federated learning poses risks of leaking users’ privacy. Works such as [2, 4, 42, 5] have shown that by launching model inversion attacks, it is possible to reveal information about the local training data of individual users from their local updates or gradients. To address this issue, secure aggregation is introduced to resolve the aggregation problem without leaking any information except for the final aggregation result [43, 30, 19, 20, 18, 21, 22, 23, 24].
The main approaches in secure aggregation include Secret sharing (SS) [32, 33, 30, 31], Differential privacy (DP) [43, 18, 21, 22] and Homomorphic encryption (HE) [25, 26, 27]. Secret sharing enables a user to split its local update (secret) into multiple secret shares, where the secret remains theoretically private as long as no entity holds more shares than a specified threshold. Shareholders (other users) can collectively aggregate these secret shares to compute the aggregated secret. The server collects the aggregation of shares and reconstructs the actual aggregation of local updates. The differential privacy technique is to add controlled noise or randomness to updates before aggregation. This ensures that the aggregated results do not disclose sensitive information about local training data. Homomorphic encryption is a powerful cryptographic technique that allows computations to be performed on encrypted data without decrypting it. The server can exploit such a feature to perform a secure aggregation and decrypt the real aggregation without privacy leakage.
II-C Robust Model Aggregation
Aside from concerns for privacy, the issue of model robustness has been pervasively discussed in FL. The defense strategies and attack methods have been competitively growing in recent years. Generally, there are two types of attacks of interest. Some malicious users can launch untargeted attack, during which they upload arbitrary false models to impede the server from completing the model aggregation correctly [44, 45, 5]. There are also omniscient untargeted attacks where the adversary is aware of other benign updates, so it can design the update to launch stronger attacks [46]. The other type is targeted attack, where the malicious users deliberately implant the global model with a backdoor without affecting the main learning task [47, 48, 49, 50, 51, 52, 53].
To detect such fraudulent model updates, robust FL aggregation has been introduced by many studies. At the onset of the introduction of model poisoning, a few noise-filtering-based algorithms are put forward to select honest ones across users [9, 10, 11, 12, 13]. The statistical traits of local updates are exploited to capture the malformed ones and compute a final aggregation without them. However, malicious users can manipulate the updates to bypass the defense so that get selected for the final aggregation [54, 46]. Competitively, Some recent robust aggregation protocols against poisoning attacks have been proposed to address this issue [14, 15, 16, 17].
In addition, various backdoor defense methods have been proposed to counter deliberate manipulations on local updates, as evidenced by studies such as [55, 56, 57, 52, 58, 59, 60, 61, 62, 63, 59, 64]. In [62], the coordinate-wise median and trimmed mean techniques are employed to achieve promising performance in robust aggregation. Several studies also investigate the impact of the sign of updated gradients [63, 59, 64]. Particularly, [63] is the first to utilize majority voting on gradient signs during final aggregation to enhance robustness and convergence. Subsequent works investigate how to use the coordinate-wise sign information to guide the final aggregation; for instance, [59] uses the sign to adjust the learning rate in each round to defend against backdoor attacks, while SignGuard [64] clusters the signs to filter malicious gradients.
II-D Robust and Privacy-preserving Model Aggregation
Recent works attempt to simultaneously address both aspects of privacy and robustness [32, 43, 21, 33, 30, 65, 35, 31]. BREA [32] is the first FL protocol known to consider privacy-preserving and robustness simultaneously. It employs the statistical algorithm multi-Krum [14] to protect the final aggregation from Byzantine local updates, and uses secret sharing to hide the updates from the adversary. A state-of-the-art protocol, EIFFeL [30], provides an exemplary solution that addresses robustness and privacy simultaneously. It significantly improves the privacy guarantees to the privacy using new cryptography preliminaries. Regarding robustness, EIFFeL shows that users can use any function to validate the integrity of their individual updates. EIFFeL does not require users to upload the local updates for integrity validation, instead, a zk-proof for correctly performing the evaluation on updates. RoFL [31] further extends the norm bounding validation in EIFFeL and demonstrates different norm constraints also mitigate the effect of backdoor attacks. It also boosts the efficiency of the protocol in addition. A recent work, ByITFL, proposes a theoretically secure protocol [28] that provides robustness in update aggregation. It builds upon the Byzantine-resilient protocol FLTrust [66] to further provide privacy, especially in scenarios involving colluding users alongside a curious server. Other protocols have also been proposed to offer privacy and robustness by exploiting multiple-server architectures, such as [34, 35, 36].
II-E Challenges and Motivation
Current robust and secure protocols face limitations in either privacy-preserving or robust aggregation performance. The primary issue of BREA [32] is the incomplete privacy left with security breaches. The multi-Krum algorithm [14] used in the protocol reveals the pairwise distances between the local updates to the server. Such pairwise distances potentially provide information to a curious server to reconstruct users’ local updates. On the other hand, for works that provide provable privacy, the defensive measurements are insufficient to advance adversary attacks. EIFFeL [30] and RoFL [31] perform the validation function on user updates individually; hence, their defense cannot leverage the overall statistical information across users. For example, malicious users can easily bypass detection by keeping their updates below the norm threshold while still implanting a backdoor.
For general robust aggregations, cryptography techniques mentioned in Section II-B have limitations in different aspects. Though HE provably addresses privacy concerns, a critical limitation is its impractical complexity [25, 26, 27, 34, 28]. In practice, the computational cost is to times higher than the non-encrypted vanilla FL, even when the models used are as simple as logistic regression and multi-layer perceptron. Hence, many HE protocols suffer from high complexity and become highly impractical when sophisticated models are involved. DP alleviates the high complexity associated with HE, providing better efficiency along with provably secure solution [43, 18, 21, 22]. However, a major issue with DP is that its random masking hinders the detection of malicious updates. A malicious update potentially becomes indistinguishable to many robust algorithms by masquerading as a benign one using a masked update. How to evaluate and provide robustness against deliberately manipulated updates still remains an open problem in DP [29, 22].
To overcome these limitations, we are motivated to introduce a framework for general robust algorithms while minimizing information leakage with provable security. Specifically, we consider the strongest threat model used in single-server FL protocols, where Byzantine users can collude with the server to compromise the privacy of the victim users. Under this threat model, for a general class of robust algorithms against various attacks, we envision that the best scenario of privacy guarantee is the same as the secure aggregation, where only the final model aggregation is revealed to the server. To this end, we ask: For the colluding threat model, what is the minimum amount of information that can be revealed, to accomplish a robust and secure aggregation protocol? To answer this question, we first characterize the minimum privacy leakage through formalizing a novel privacy notion called aggregated privacy, which allows nothing but the aggregation of certain statistics of users’ updates (including the aggregated update) to be revealed. Then, we develop PriRoAgg, a general privacy-preserving framework for robust aggregation that satisfies aggregated privacy.
III Problem Formulation
Consider a federated learning (FL) network, with users who can directly communicate with the server. Users communicate with each other via relaying of the server, such as by the TLS protocol [67] so that the relayed messages are kept confidential from the server [68, 40]. As shown in (1), iterating the global model can be viewed as computing a vector of dimension , , which is flattened from the global model. A user trains a local model from the global model, and uploads local model difference , or local update, to the server. The server collects and aggregates the received updates to compute the global model for the next iteration.
Threat Model. The adversary simultaneously corrupts a set of up to users and the server, and gains full access to their local states. We consider Byzantine users who may arbitrarily deviate from the protocol for multiple purposes; and also a semi-honest server who faithfully follows the protocol, but tries to infer victim users’ private datasets from its received messages. We assume that the set of malicious users is static in a single global iteration.
We note that the semi-honest (honest-but-curious) server setting is pervasively considered in previous works on secure and robust federated learning [32, 43, 23, 69, 34, 70, 36]. In comparison with works [32, 33, 71, 69, 34, 36] which consider the coexistence of semi-honest server(s) and malicious users but acting separately, we also consider the possibility of server-user collusion. For example, an adversary can manipulate the messages sent from a portion of users, such that the aggregated model update, observed at the curious server, reveals more information about the other victim users’ private data. Also, for the single-server setting considered in this work, dealing with a Byzantine server who can arbitrarily deviate from the protocol is extremely challenging. Even for the protocols in [30] and [31] that claim to be secure against a malicious server actively inferring users’ private data, they are vulnerable to recently developed active attacks for data leakage (see, e.g., [72]). Hence, these protocols are essentially secure against a semi-honest server.
For a set of user updates , we denote a robust algorithm by and its output by , i.e., . For example, [14] computes by minimizing the distances between and s; and [73] computes by taking the geometric median of s. Given an aggregation algorithm, the goal is to compute with the minimum information leakage to the adversary. For secure aggregation, where represents summation, protocols are designed to compute the sum of s as the final result such that nothing else is exposed to the adversary. However, for more complicated (e.g., [14, 74, 75]), additional information is often leaked to the curious server and users to accomplish the aggregation. To formalize the minimal possible amount of information leaked to the adversary, we generalize the privacy guarantee to a notion called aggregated privacy, which requires that no additional information is exposed except the summation of some function of . Specifically, to compute in a privacy-preserving manner, we slightly relax the security requirement compared with secure aggregation, by allowing the adversary to know nothing but some aggregated statistics of local updates. We make this notion more concrete in the following definition:
Definition 1 (Aggregated Privacy).
Given users’ local updates , a robust aggregation algorithm , and some function on an individual update, an aggregation protocol satisfies aggregated privacy if nothing other than the aggregation is revealed to the adversary.
Remark: As a special instance, when stands for summation, is the identity function, i.e., , then the aggregated privacy reduces to the same privacy constraint as in concventional secure aggregation. Achieving aggregated privacy for general is highly non-trivial. For example, BREA [32] and ByzSecAgg [33] utilize the Krum algorithm, where the pairwise distances between and are revealed to the curious server, hence violating the aggregated privacy. Also, in EIFFeL [30] and RoFL [31], a valid predicate is applied on updates, where the validity of is revealed to all parties, which also violates the aggregated privacy.
To design provably secure robust protocols with aggregated privacy, we formulate a secure multi-party computation (MPC) problem with input updates from FL users, denoted as (short for secure and robust aggregation with ). The adversary gains full control over a subset of corrupted users and can access the local state of the server; it runs any next-message algorithm denoted by .
Definition 2 ().
Given a robust aggregation algorithm and inputs , a protocol securely computes with aggregated privacy if it satisfies:
-
•
Integrity. Consider the output of the protocol execution , and . Then, there always exists a proper security parameter , such that the following holds:
(2) for any small constant .
-
•
Privacy. For any adversary running who controls a subset of malicious users and a semi-honest server, and denotes the rest of honest users, there exists a probabilistic polynomial-time (P.P.T.) simulator , such that
(3) where represents the joint view of executing ; is a pre-defined function applied to updates; “” denotes computational indistinguishability.
The Proposed Solution. We propose a secure computing framework PriRoAgg to construct protocols. The key idea of PriRoAgg is to choose an appropriate function , such that the robust aggregation can be accomplished via computing aggregation of s. To ensure privacy and integrity for the aggregation operation against malicious adversaries, PriRoAgg mainly relies on the following techniques:
-
1.
Lagrange coded computing [37] enables efficient message encoding with perfect secrecy, while supporting linear computations on the ciphertext. We exploit this technique to create secret shares of the updates and their functions, as well as the aggregation of the updates and functions, such that they are kept private during the aggregation process.
-
2.
Secret-shared non-interactive proof [38] provides a distributed zk-proof for the authenticity of the users’ operations. We use this technique to guarantee that the users have honestly performed the function evaluations on their shares.
IV Building Blocks of PriRoAgg
IV-A Key Agreement (KA)
We use the standard Key agreement (KA) and Authenticated encryption (AE) for user communications’ privacy and integrity. KA involves three algorithms and AE involves two algorithms.
-
•
KA.param(). It generates public parameters from security parameter .
-
•
KA.gen(). The key generation algorithm creates a public-secret key pair.
-
•
KA.agree(). User combines two keys to generate a symmetric session key .
-
•
AE.enc(). The encryption algorithm uses a message with key and returns the ciphertext .
-
•
AE.dec(). The decryption algorithm takes a ciphertext with key and returns the original text , or error symbol when decryption fails.
IV-B Secret Sharing with Lagrange Encoding
The proposed protocol relies on a secret sharing scheme with encoding, which is known as Lagrange coded computation (LCC) [37]. We extend it to the verifiable LCC with constant-size commitment in the next subsection.
Initially, the server and all users agree on distinct elements from in advance. User holds a vector , where is the dimension of the vector. Then, user partitions its message into equal-size pieces, labeled by . To provide -colluding privacy protection, the user independently and uniformly generates random noises from . These random noises are used for masking the partitioned pieces, which are achieved by creating a polynomial of degree such that111Unless otherwise specified, all operations are taken modulo .
| (6) |
The Lagrange interpolation rules and the degree restriction guarantee the existence and uniqueness of the polynomial , which has the form of
| (7) |
Next, user evaluates at point to obtain an encoded piece for user , by
| (8) |
We use to distinguish the original data and its encoded shares 222When user indices appear on both sides of , it indicates the user ’s secret share sent to user . We abuse to present vectors without such indices.. Taking in (8) for an example, is the user ’s secret, and stands for the share holder’s index, therefore, is what user holds for secret . Here, we allow for protocol simplicity. Finally, we wrap LCC as a primitive module that includes two algorithms:
- •
-
•
LCC.recon(). The LCC generates a Reed-Solomon code. It can be decoded by the Gao’s decoding algorithm [76].
IV-C Verifiable LCC with Constant-Size Commitments
We combine LCC and constant-size commitments [33, 39] to leverage threshold privacy and encoding efficiency, which further reduces the communication overhead.
Let be a generator of the cyclic group of order , where should be some enough large prime such that divides . To verify that the piece is correctly constructed by using the Lagrange polynomial from (7), user broadcasts the commitments to all other parties, by
| (9) |
where is the -th entry of . A trusted third party generates and computes , where is public to all users.
Upon receiving the share (8) and the public commitments (9) from user , the user can verify the share by checking
| (10) |
The equality ensures that share is generated correctly by the polynomial in (7). Moreover, assuming the intractability of computing the discrete logarithm for all users and the server, i.e., they cannot compute the discrete logarithm for any , therefore, there is no information leakage about the user’s message. Following (9) and (10), we define two more algorithms for verifiability of LCC:
- •
-
•
LCC.verify(). This algorithm allows user to verify whether the received share is consistent with the commitments opened by user , as defined in (10). The function returns a Boolean value of to indicate success in verification, or the error symbol if verification fails.
IV-D Secret-shared Non-interactive Proof (SNIP)
We introduce the secret-shared non-interactive proof (SNIP) as a primitive [38]. In the FL setting, SNIP can be used to prove that an arithmetic circuit is evaluated on certain local data that is secret shared. SNIP is originally proposed in additive secret sharing, EIFFeL extends it to the Shamir secret sharing [30] and we further extend it to LCC for PriRoAgg.
SNIP follows the LCC module’s setting. Given an arithmetic circuit agreed by all parties, denoted by , the goal is for a user (prover) to prove it has faithfully performed without revealing its inputs and outputs , Without loss of generality, we take a user to act as the prover while all the other users act as verifiers. Assume that the arithmetic circuit of has multiplication gates, where each gate has two input wires and one output wire. The topological order of the multiplication gates is given by and agreed upon by all users. The SNIP works in the following steps.
-
1.
A prover (user ) evaluates function , . For the circuit multiplication gates, denote two input wires for gates to as and . Use each side of input wires to interpolate polynomials, resulting in two polynomials of degree-, and , such that . The product of two polynomials is exactly the output wire of the -th gate at the evaluation . Denote the coefficients of polynomial by . The prover then generates secret shares for by LCC.share() with , which is equivalent to Shamir’s secret sharing, where shares are denoted by .
-
2.
A verifier (user ) recovers the computation of the function by the shares and generates a share for the Schwartz-Zippel polynomial test [77, 78]. Specifically, with , the verifier interpolates a polynomial up to the degree of , , which corresponds to all output wires. Thus, the share of the circuit output, , can be evaluated on the polynomial. Next, with and , it can recover all intermediate results for input wires of all gates as additions and scalar multiplications can be directly applied. Since they are all computed from the share of polynomials, we denote the input wire values by . SNIP interpolates two polynomials for two ways of input wires from to , , . Beaver’s protocol [79] is used to compute from and . All verifiers agree on one or multiple random for the Schwartz-Zippel polynomial test. Recall that the output wire’s polynomial is given by . Given an , a share of polynomial test is generated by computing .
-
3.
The server collects verifiers’ to reconstruct the result of the polynomial identity test. For a prover (user ), the server decodes from by LCC.recon. If the user honestly performs the circuit, the reconstruction is . Otherwise, user fails in the proof.
We summarize the described scheme as a module SNIP with two functions for prover and verifier correspondingly.
-
•
SNIP.prove. is the given arithmetic circuit a prover (user ) wants to prove with input and output . 333The Beaver’s triplet is generated and broadcast by each user insetup phase. Algorithm output is the coefficients given at the end of step 1.
-
•
SNIP.recon(). This algorithm constructs the share of the polynomial test and the share of the circuit output as in step 2.
V Detailed Description of PriRoAgg
We first describe the general PriRoAgg framework and then provide two concrete instantiations for robust aggregation against backdoor attacks and model poisoning attacks, respectively. For a given robust algorithm , to compute aggregation in a privacy-preserving and fault-tolerant manner, PriRoAgg exploits LCC to secret share individual updates across users and chooses an appropriate such that can be computed from . To guarantee the correctness in the presence of Byzantine users, PriRoAgg utilizes SNIP to verify the computations of the arithmetic circuit induced from function . PriRoAgg proceeds in three main rounds: in the first round, the users perform local training to acquire updates, then they secret share updates and SNIP proofs; in the second round, the users perform local computations on the acquired shares and send results to the server; in the last round, the server processes the received results and compute the final robust aggregation. A full pipeline of PriRoAgg is presented in Fig.1
V-A General PriRoAgg Framework
PriRoAgg starts with a setup phase to prepare all parties with some public parameters, which includes the security parameter for key initializations, the finite field with sufficiently large and amplifier for update computations, threshold for the maximum number of malicious users, partitioning parameter for LCC, vector for constant-size commitment scheme, a set of points for LCC evaluations.
Round 1 (Users Training and Secret Sharing). After acquiring the update from local model training, user first maps the float local update vector to a finite-field vector following a standard quantize technique as in [32, 80] with amplifier . User uses LCC.share to slice and encode each into shares . To ensure the authenticity of the shared information, user commits to its shares through the constant-size commitment scheme and generates commitment . Next, a user needs to prove that it has faithfully evaluated an arithmetic circuit , where is defined based on . Using SNIP.prove, the user generates its proof for the equality , then encodes to and commits to it by . At the end of the round, each user sends AE.enc() to user encrypted by secret session key, and broadcasts commitments .
Round 2 (Users Local Computation). Using the broadcast commitments, user can verify the received shares from any user . If user ’s message does not pass the verification, user adds user to the local malicious user set . Next, user uses SNIP.recon to construct a share of the polynomial identity check for user , denoted by . User combines the update shares over all users as the aggregation of the shares. Then, the user submits the following four messages to the server: : the local malicious user set ; : the shares of polynomial identity check ; : summation of output’s shares ; and : the aggregation of updates’ shares .
Round 3 (Server’s Computation and Aggregation). The server collects users’ messages and performs consistency checks to construct a global malicious user set . Specifically, for message , the server looks for user who satisfies any of two cases to add into . The first case is when a user is tagged more than times, then it must have been tagged by at least one honest user. The second case is when a user tags more than other users, then it must have tagged at least one honest user as malicious. For message , the server decodes each and checks the reconstructed value. If is zero, it means that the circuit is correctly executed by user . If it is not, the circuit computations fail in at least one multiplication gate for user , so will be added to . With the message , the server reconstructs the aggregation of outputs . It is used as the guidance for robust aggregation of updates. How the aggregated information guides the final robust aggregation is expanded in the next section. After the server computes , it uses dequantize()444dequantize is the inverse function of quantize that maps values in to . to map the aggregation back to the real domain for the global model updating as in (1). Before releasing the final aggregation, the server checks the global malicious user set . It concludes the current iteration if , or aborts the current iteration if . However, if , the server will invoke an additional execution of round by sending its global malicious set to all users, so that users should recalculate each message with respect to set instead of . Then, the server normally proceeds round with the malicious users removed.
V-B Two Instantiations
Leveraging the proposed framework PriRoAgg, we construct two concrete protocols for two specific robust aggregation algorithms. One is Robust Learning Rate (RLR) for backdoor attack, and the other is Robust Federated Aggregation (RFA) for model poisoning attack. For each robust aggregation algorithm, we first explain how the robust algorithms operate in plaintext, and then present how the robust algorithms apply to PriRoAgg to achieve the protocols. Additionally, a special feature of repeated pattern circuits is used in both instantiations to reduce SNIP’s computational overhead. Detail is provided in Appendix A.
PriRoAgg with RLR. In RLR [59], it is shown to be effective to use the sign information of updates to avoid the backdoor behaviors. For each coordinate of final aggregation, the positive/negative sign is decided on the number of positive/negative signs of all user updates. The users’ majority vote of signs generates a binary mask with values in . The final aggregation’s coordinate signs are determined by applying this binary mask to eliminate the malicious updates. Specifically, for and the -th entry , RLR assigns to a binary vector if , or assigns otherwise, where the threshold is and returns or for positive or negative inputs, respectively. The final aggregation result is , where is the element-wise multiplication.
Applying PriRoAgg with RLR, we let be:
| (11) |
In this case, the evaluation circuit to prove is simply . As a result, the server reconstructs and in the last round, with no additional information revealed. Next, it recovers the binary mask from to correctly compute final robust aggregation as in RLR.

PriRoAgg with RFA. RFA [73] exploits the Weiszfeld algorithms [81] to compute the geometric median for the user updates. Specifically, we utilize the one-step smoothed Weiszfeld algorithm (Algorithm 3 in [73]) to compute the approximation of the geometric median. RFA computes and uses as the weight for the final robust aggregation. More precisely, .
In RFA instantiation, we choose to be :
| (12) |
where . Since the arithmetic circuit does not allow division, the circuit to be verified is designed as , where . In round , user computes from and by the Beaver’s protocol [79]. At the end of round 2, user substitutes by concatenating and as message . In the final round, the server reconstructs and checks if . Together with the fact check of polynomial identity , the server ensures the circuit is faithfully evaluated. For the final aggregation, the server reconstructs and decomposes to compute the weighted average as in RFA.
VI Theoretical Analysis
VI-A Security analysis
In this subsection, we provide the security proofs for the privacy guarantees of two protocols in PriRoAgg.
| PriRoAgg | EIFFeL | |
|---|---|---|
| User computation | ||
| Server computation | ||
| User communication | ||
| Server communication |
Theorem 1.
() For a protocol that securely implements a , assuming an adversary who controls a subset of malicious users and gains full access to the local state of the server, and denoting as the subset of honest users, there exists a probabilistic polynomial-time (P.P.T.) simulator , such that
| (13) |
where represents the joint view of executing ; is defined as (11).
Proof.
The proof uses a hybrid argument to demonstrate the indistinguishability between the real execution and the simulator’s output.
-
•
: This random variable represents the joint view of in the real world execution.
-
•
: In this hybrid, for any honest user , instead of using for key generation, the simulator generates the uniformly random key in the Diffie-Hellman key exchange protocol [82] for the set-up phase. The Diffie-Hellman assumption guarantees that this hybrid is indistinguishable from the previous one.
-
•
: In this hybrid, the only difference from is that the simulator substitutes , and with generated , and for any honest user in round 1. The simulator first randomly samples such that
Then, the signs of the entries in are constrained. The simulator samples by the uniform distribution such that
The shares and commitments are generated accordingly to . The is generated, shared and committed by protocol. Because , in the joint view, the adversary cannot know anything about the secret as long as the commitments are consistent with the shares. The indistinguishability is guaranteed by the property of LCC.
-
•
: In this hybrid, the only difference from is that substitutes the ’s messages sent to the server with the generated messages in round 2. The does not record any honest users and the rest of the users are processed by protocol. The messages , and are computed by the protocol after substituting , and with , and respectively. As they are computed in the form of secret shares, the indistinguishability is guaranteed by the property of LCC.
∎
Theorem 2.
() For a protocol that securely implements a , assuming an adversary who controls a subset of malicious users and gains full access to the local state of the server, and denoting as the subset of honest users, there exists a probabilistic polynomial-time (P.P.T.) simulator , such that
| (14) |
where represents the joint view of executing ; is defined as (12).
Proof.
Here, we only present since the other hybrids are identical to the proof of in Theorem 1.
-
•
: In this hybrid, the only difference with is substituting by randomly generated for in round 1. generates weight parameters , by a uniform distribution such that
According to (12), the norm of is constrained by . samples with a fixed -norm, such that
The shares and commitments are generated accordingly for the to the . The is generated, shared and committed by protocol. Because , in the joint view, the adversary cannot know anything about the secret as long as the commitments are consistent with the shares. The indistinguishability is guaranteed by the property of LCC.
∎
VI-B Complexity Analysis
The computational overhead and communication overhead per iteration are summarized in Table I, and the comparison with EIFFeL is presented. Recall that there are users with up to malicious users; the update dimension is ; is the partitioning parameter for LCC satisfying ; the number of circuit ’s multiplication gates is .
Computational overhead. In round 1, the user generates secret shares for the update and commits to them by the complexity of 555Pre-compute the Lagrange coefficients.. The user also performs SNIP by the complexity of since the repeat-pattern circuit is used to reduce the overhead. Each circuit’s proof and commitment takes [83] with a total number of circuits. Shares and commitments of constant are generated in , which is absorbed by the first term. The total complexity for each user in round 1 is . In round 2, the user constructs shares for the polynomial identity test with complexity for each prover. The secure computations are of the complexity . If each user computes the others’ shares in a linear sequence, the total complexity for each user in round 2 is . In round 3, the server decodes the proof by the complexity of and the aggregation by the complexity of [76]. The other operations are of the complexity that is absorbed by the other terms. Then, the total complexity for the server in round 3 is .
Communication overhead. In round 1, sharing the update and sharing the proof takes and . All commitments are constant-size and, hence, absorbed by the first term. In round 2, the messages are shares of constant-size objects except the aggregations of . ’s output dimension is and in RFA and RLR correspondingly. Therefore, round 2 complexity is at maximum. Complexity of round 3 is simply .
Comparison with EIFFeL. In experiments, the model dimension significantly exceeds the number of users, i.e., , with both being of order . The usage of LCC reduces the overhead in terms of to . Therefore, PriRoAgg’s user and server computational overheads are and , respectively, compared to EIFFeL’s and , respectively. For communication overhead, the server communication remains consistent, while the user communication is substantially reduced from to through the constant-size commitment scheme.
VII Experiments
We conduct experiments to demonstrate robust performance and computational overhead of PriRoAgg instantiations. We consider several targeted and untargeted attacks on two datasets. All experiments are simulated on a single machine using Intel(R) Xeon(R) Gold 5118 CPU @ 2.30GHz and four NVIDIA GeForce RTX 4090 GPUs.
VII-A Setup
The untargeted and targeted attacks. For different types of attacks, we choose two attack strategies for each of trivial update poisoning, omniscient update poisoning, and backdoor attacks. For trivial update poisoning, the malicious update is manipulated by adding Gaussian noise [73] or scaling by constants [84]. For omniscient update poisoning, Min-Max and Min-Sum attack [46] are considered, where the attacker knows all benign updates to design its malformed update. For backdoor attacks, we consider image trojan attacks [85] with two different pattern types. We use the validation accuracy to demonstrate comparisons against other privacy-preserving protocols, and present the protocol’s overhead with different parameter settings.
Baselines. We consider protocols with both robustness and privacy guarantees. BREA [32] and ByzSecAgg [33] ensure robustness using the Byzantine-resilient algorithm, multi-Krum [14], but both reveal pairwise distances to the server, thus violating aggregated privacy notion in our context. RoFL [31] and EIFFeL [30] provide theoretical guarantees for privacy in the same FL settings. They utilize the validation functions to ensure the updates’ robustness, with and norm bounding used as the baselines. We additionally use cosine similarity for EIFFeL’s implementation to present the effect of different choices of validation. Note that RoFL and EIFFeL’s validation functions rely on a public dataset and a given threshold; nevertheless, we compare PriRoAgg with them without any additional advantage. We also consider a two-server privacy-preserving protocol, EPPRFL, for backdoor attacks [36]. It uses the F&C algorithm adopted from [86] to filter malicious updates based on historical updating information.
Datasets. We use Fashion-MNIST [87], CIFAR-10 [88] to evaluate performance and test the end-to-end execution time. We assume the data is independent and identically distributed (i.i.d.) unless otherwise specified.
We choose for all Fashion-MNIST experiments and for all CIFAR-10 experiments, with malicious users. The security threshold is set to and to maximize efficiency while ensuring compliance with privacy guarantee. Each experiment is run for times and the average results are reported.
VII-B Results
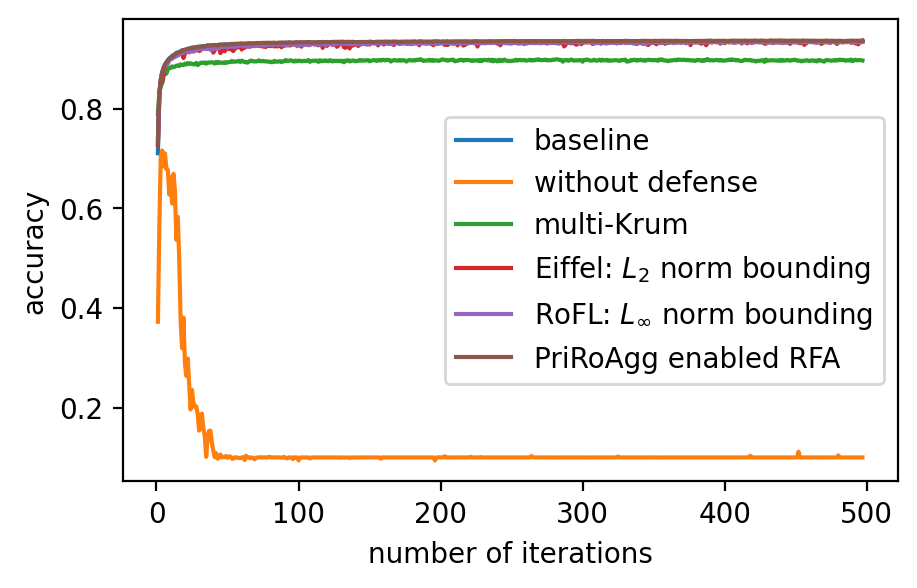
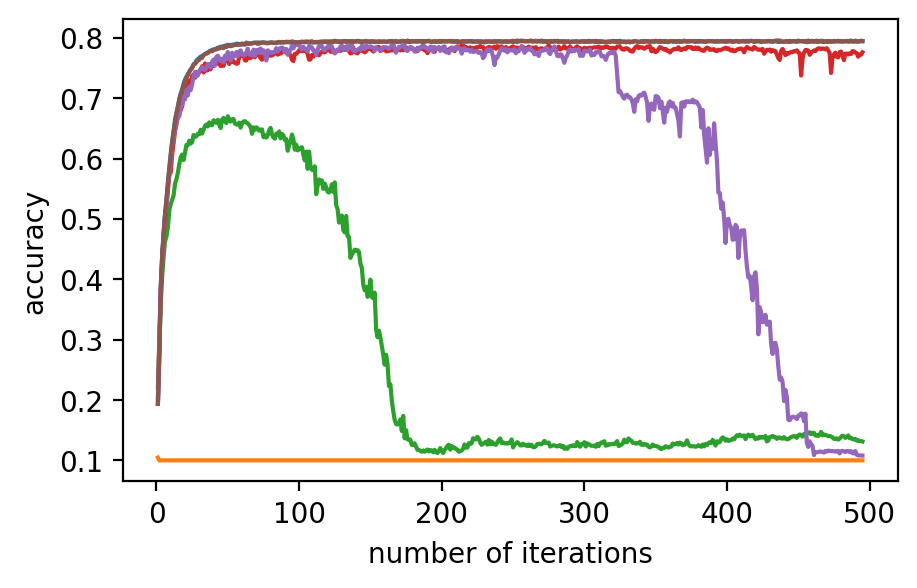
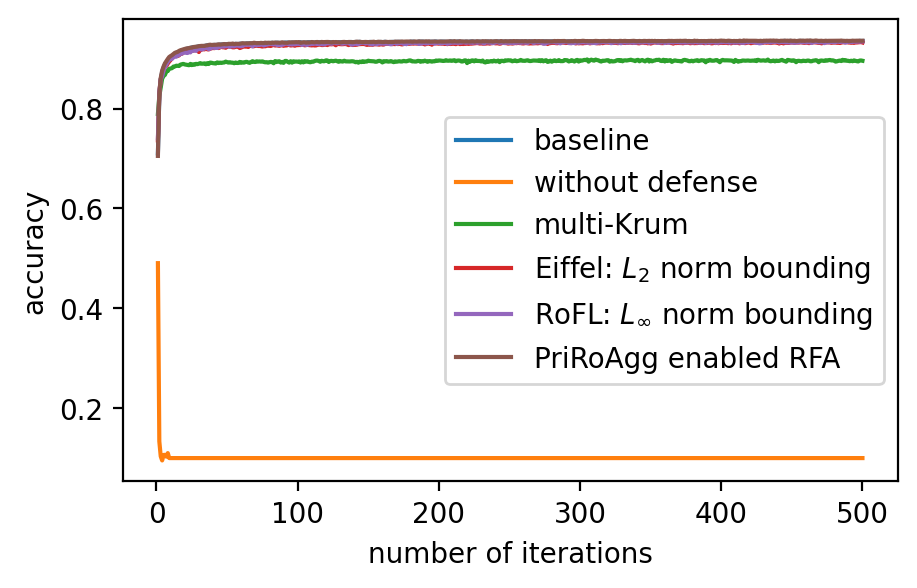
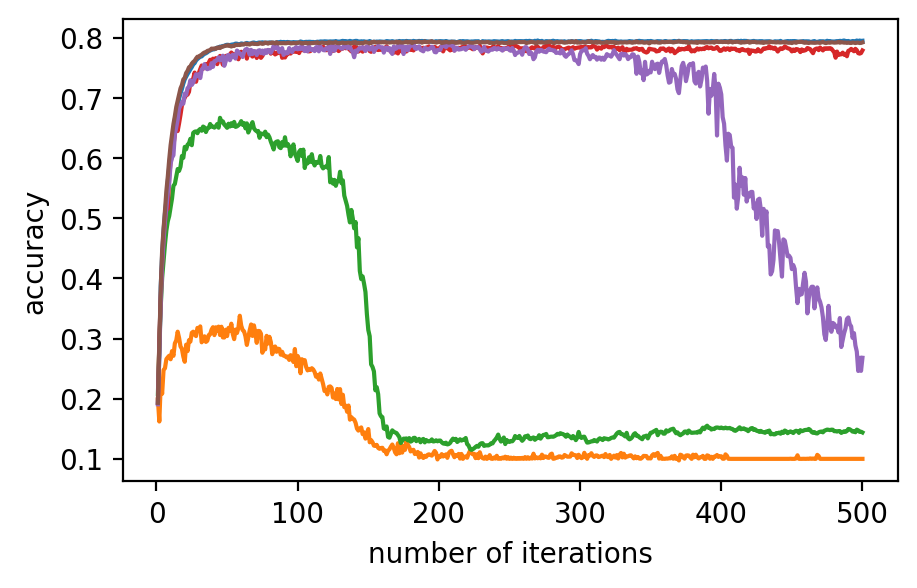
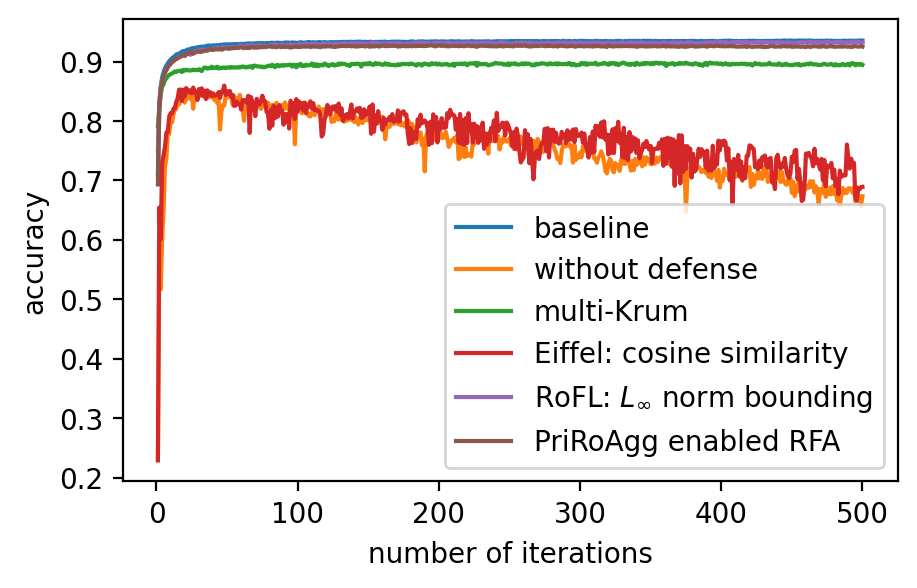
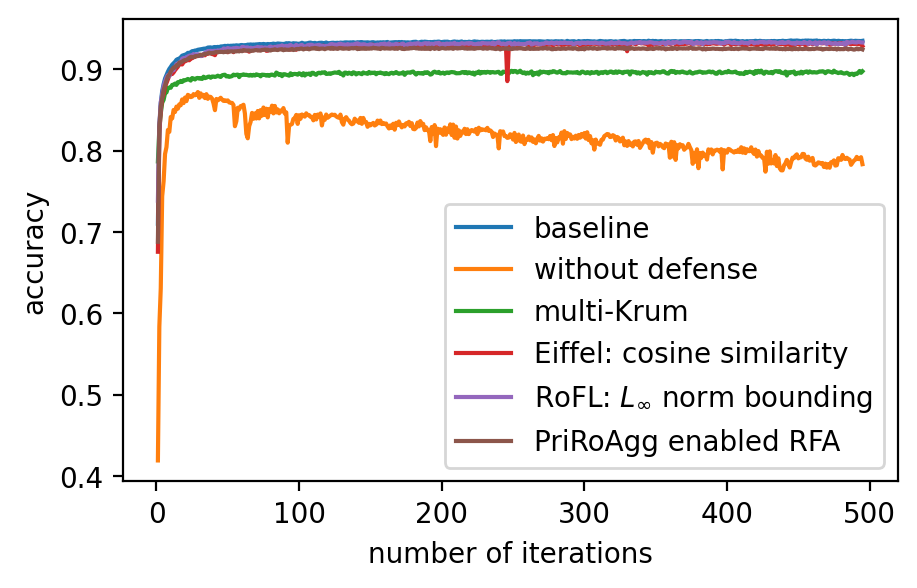
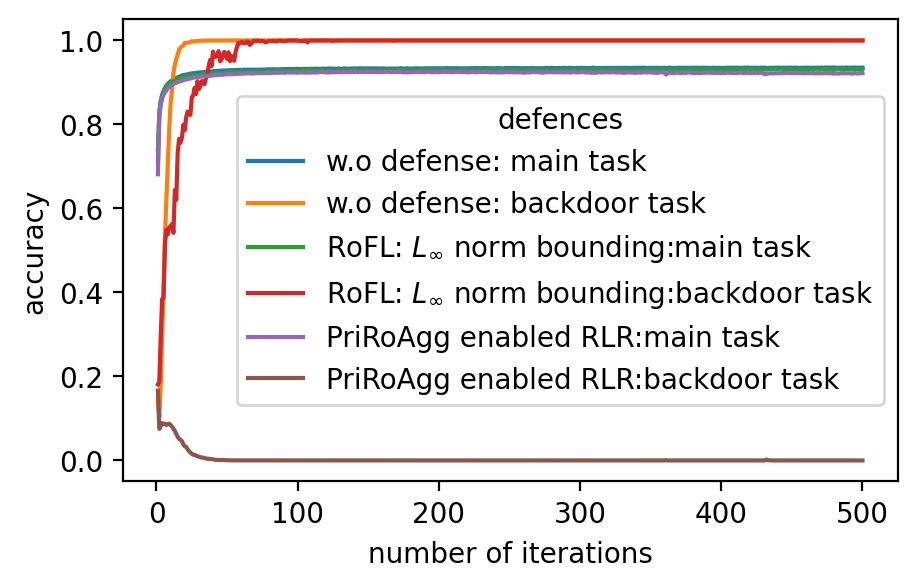
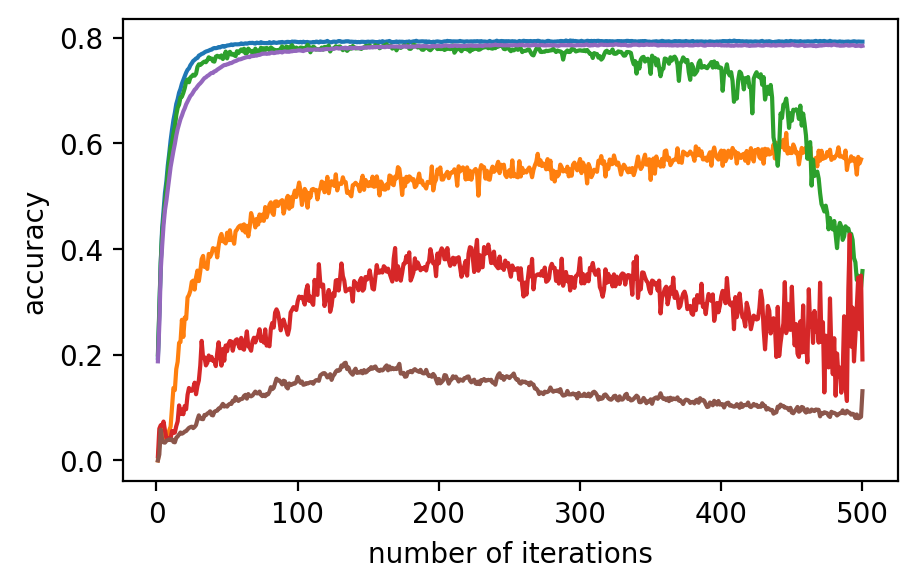
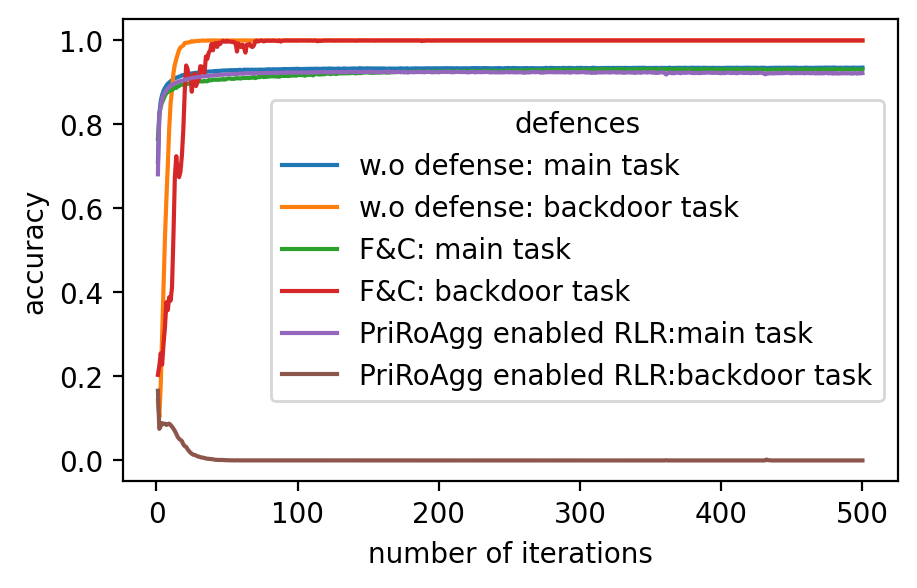
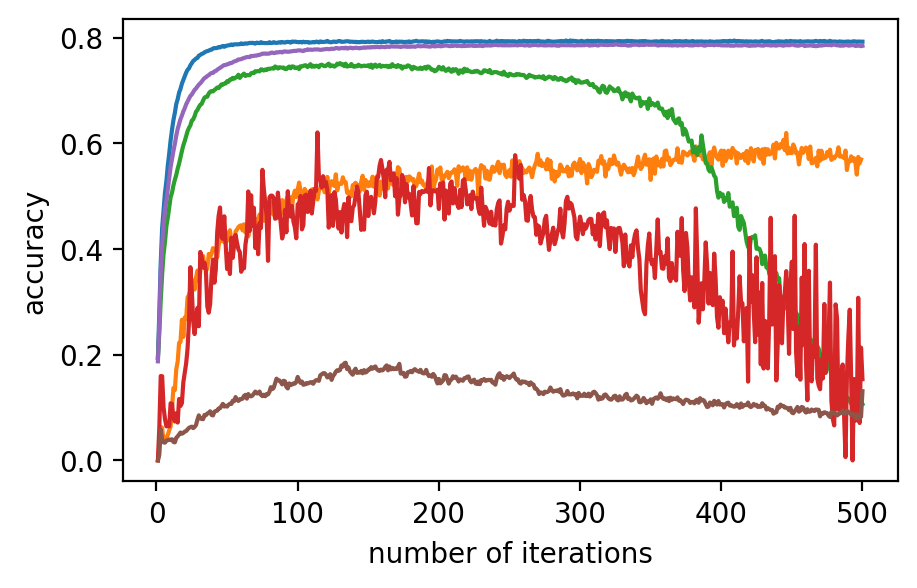
Performance. In Fig. 2 (a)-(f), the performance of the global model, which is measured by accuracy on the validation dataset, after applying different model poisoning attacks, is shown. PriRoAgg is consistently robust against model poisoning attacks. The multi-Krum algorithm demonstrates convergence in each scenario on Fashion-MNIST, but its accuracy is not as high as the other convergent baselines. For EIFFeL, its performance depends on the chosen validation predicate. For instance, EIFFeL with cosine similarity defends poorly against the Min-Max attack shown in (e) but succeeds in the Min-Sum attack in (f). RoFL performs well on Fashion-MNIST; however, it is no longer robust when CIFAR-10 is used. As CIFAR-10 serves as a more complex dataset, these baseline protocols become less effective. The multi-Krum algorithm diverges eventually, while RoFL experiences a drastic decrease around the th iteration. EIFFeL exhibits relatively better performance with a different choice of validation, but it falls short in terms of accuracy and stability when compared to PriRoAgg.
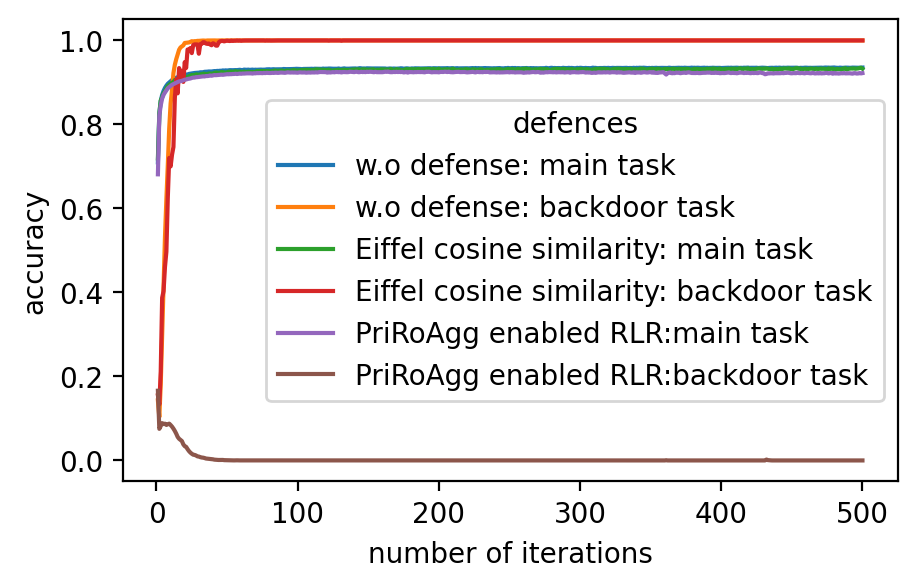
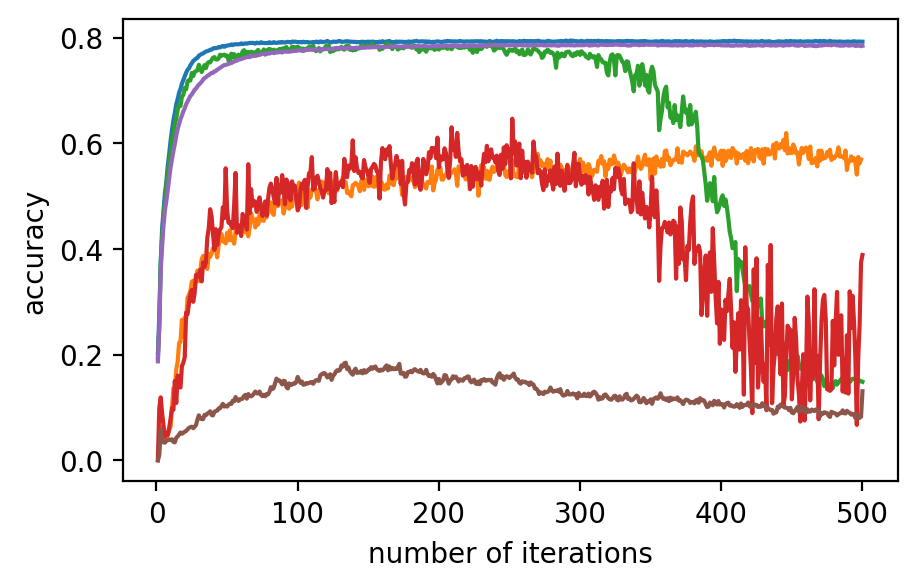
For backdoor attacks in (g)-(l) on Fig. 2, we evaluate the main task on the validation dataset and test the backdoor task on the poisoned validation dataset. As shown in (i) and (k), although RoFL and F&C manage to slow down the implantation process on Fashion-MNIST, both ultimately succumb to the backdoor. Compared to them, PriRoAgg with RLR performs significantly well against backdoor implantation on both datasets. It greatly supports the discussion in Section II-E about validation on the sole update not sufficiently supporting sophisticated model aggregation. The EIFFeL with cosine similarity has nearly no defensive capability against backdoor attacks, while RoFL with norm bounding performs slightly better. We consider multiple parameter settings for EPPRFL with F&C and find that F&C highly relies on its early-stage updates’ history; that is, if it cannot detect the malicious users in the first several rounds, it fails in the backdoor attack. Hence, F&C exhibits notable instability. As PriRoAgg allows the overall statistics of the updates, PriRoAgg with RLR robustly defends against the backdoor in both datasets, as well as achieving the best performance in the main task.
Complexity results. We present the end-to-end runtime of PriRoAgg with the instantiations of RLR and RFA. The instantiation with RFA is presented with the default setting of and . To provide a comprehensive and fair comparison, we implement EIFFeL and use identical encoding and proving algorithms across protocols.
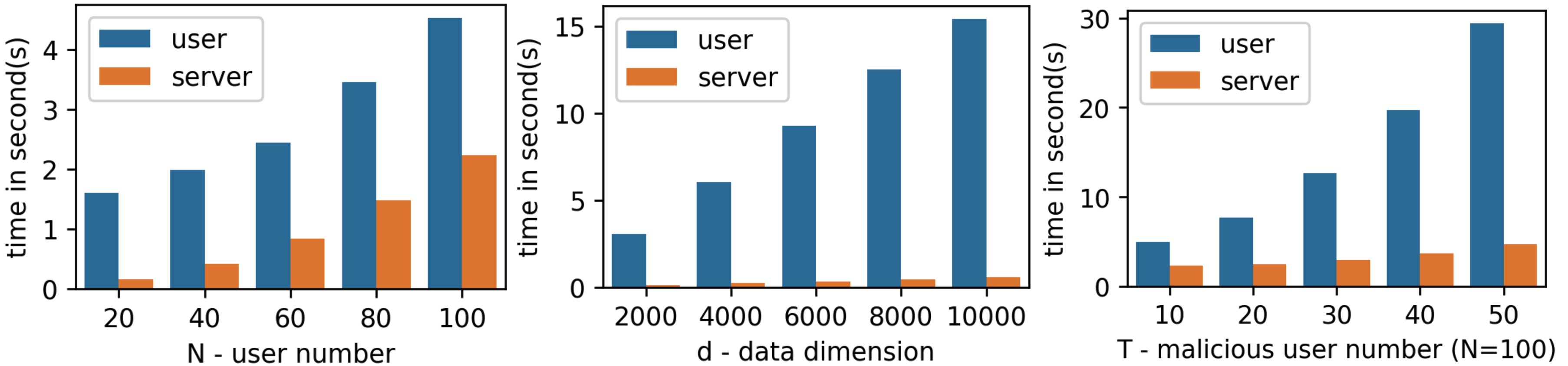
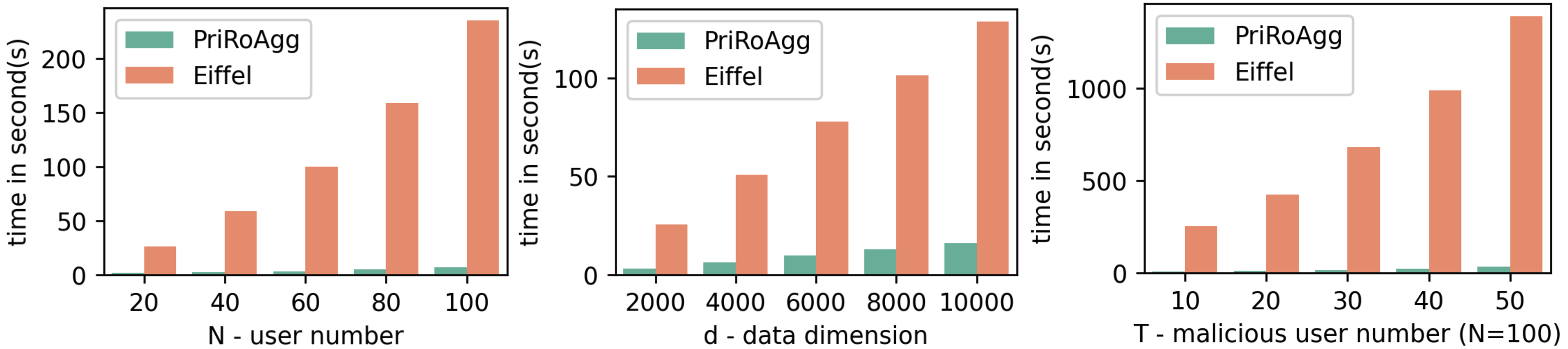
As shown in Fig. 3, the time against the number of users and the dimension of update follows the complexity analysis in Table I. The time cost increases almost linearly as it is primarily dominated by variables and . For time against with fixed , the LCC parameter is chosen as the maximum, , inducing a quadratic relation between time and . In Fig.4, compared with EIFFeL, PriRoAgg benefits from higher encoding efficiency of LCC and repeated pattern circuit in SNIP. Consequently, PriRoAgg is superior in end-to-end efficiency, especially when is large since it allows for a larger for LCC. This advantage is particularly evident in Fig.4.
VIII Conclusion
Under realistic consideration, FL requires protocols to provide both robustness and security at the same time. In this paper, we introduce a new notion of security for users’ data privacy called aggregated privacy, and propose a novel framework PriRoAgg to provide aggregated privacy to participants, while utilizing powerful robust algorithms to defend against both targeted and untargeted attacks. Two concrete protocols are proposed as instantiations of PriRoAgg, with each addressing model poisoning and backdoor attacks. Security proofs and experiments are presented to demonstrate PriRoAgg’s superiority compared with previous works.
References
- [1] B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Artificial intelligence and statistics. PMLR, 2017, pp. 1273–1282.
- [2] L. Zhu, Z. Liu, and S. Han, “Deep leakage from gradients,” Advances in neural information processing systems, vol. 32, 2019.
- [3] J. Geiping, H. Bauermeister, H. Dröge, and M. Moeller, “Inverting gradients-how easy is it to break privacy in federated learning?” Advances in neural information processing systems, vol. 33, pp. 16 937–16 947, 2020.
- [4] H. Yin, A. Mallya, A. Vahdat, J. M. Alvarez, J. Kautz, and P. Molchanov, “See through gradients: Image batch recovery via gradinversion,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 16 337–16 346.
- [5] L. Lyu, H. Yu, and Q. Yang, “Threats to federated learning: A survey,” arXiv preprint arXiv:2003.02133, 2020.
- [6] M. Rigaki and S. Garcia, “A survey of privacy attacks in machine learning,” ACM Computing Surveys, vol. 56, no. 4, pp. 1–34, 2023.
- [7] M. Barreno, B. Nelson, A. D. Joseph, and J. D. Tygar, “The security of machine learning,” Machine Learning, vol. 81, pp. 121–148, 2010.
- [8] M. Xue, C. Yuan, H. Wu, Y. Zhang, and W. Liu, “Machine learning security: Threats, countermeasures, and evaluations,” IEEE Access, vol. 8, pp. 74 720–74 742, 2020.
- [9] A. Ghosh, R. K. Maity, S. Kadhe, A. Mazumdar, and K. Ramchandran, “Communication-efficient and byzantine-robust distributed learning,” in 2020 Information Theory and Applications Workshop (ITA). IEEE, 2020, pp. 1–28.
- [10] S. P. Karimireddy, L. He, and M. Jaggi, “Byzantine-robust learning on heterogeneous datasets via bucketing,” arXiv preprint arXiv:2006.09365, 2020.
- [11] R. K. Velicheti, D. Xia, and O. Koyejo, “Secure byzantine-robust distributed learning via clustering,” arXiv preprint arXiv:2110.02940, 2021.
- [12] T. Orekondy, B. Schiele, and M. Fritz, “Prediction poisoning: Towards defenses against dnn model stealing attacks,” arXiv preprint arXiv:1906.10908, 2019.
- [13] Z. Sun, P. Kairouz, A. T. Suresh, and H. B. McMahan, “Can you really backdoor federated learning?” arXiv preprint arXiv:1911.07963, 2019.
- [14] P. Blanchard, E. M. El Mhamdi, R. Guerraoui, and J. Stainer, “Machine learning with adversaries: Byzantine tolerant gradient descent,” Advances in Neural Information Processing Systems, vol. 30, 2017.
- [15] R. Guerraoui, S. Rouault et al., “The hidden vulnerability of distributed learning in byzantium,” in International Conference on Machine Learning. PMLR, 2018, pp. 3521–3530.
- [16] J. Chen, X. Zhang, R. Zhang, C. Wang, and L. Liu, “De-pois: An attack-agnostic defense against data poisoning attacks,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 3412–3425, 2021.
- [17] Y. Zhao, J. Chen, J. Zhang, D. Wu, J. Teng, and S. Yu, “Pdgan: A novel poisoning defense method in federated learning using generative adversarial network,” in Algorithms and Architectures for Parallel Processing: 19th International Conference, ICA3PP 2019, Melbourne, VIC, Australia, December 9–11, 2019, Proceedings, Part I 19. Springer, 2020, pp. 595–609.
- [18] K. Wei, J. Li, M. Ding, C. Ma, H. H. Yang, F. Farokhi, S. Jin, T. Q. Quek, and H. V. Poor, “Federated learning with differential privacy: Algorithms and performance analysis,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 3454–3469, 2020.
- [19] J. H. Bell, K. A. Bonawitz, A. Gascón, T. Lepoint, and M. Raykova, “Secure single-server aggregation with (poly) logarithmic overhead,” in Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, 2020, pp. 1253–1269.
- [20] S. Truex, L. Liu, K.-H. Chow, M. E. Gursoy, and W. Wei, “Ldp-fed: Federated learning with local differential privacy,” in Proceedings of the Third ACM International Workshop on Edge Systems, Analytics and Networking, 2020, pp. 61–66.
- [21] M. Naseri, J. Hayes, and E. De Cristofaro, “Local and central differential privacy for robustness and privacy in federated learning,” arXiv preprint arXiv:2009.03561, 2020.
- [22] A. El Ouadrhiri and A. Abdelhadi, “Differential privacy for deep and federated learning: A survey,” IEEE access, vol. 10, pp. 22 359–22 380, 2022.
- [23] J. So, C. He, C.-S. Yang, S. Li, Q. Yu, R. E Ali, B. Guler, and S. Avestimehr, “Lightsecagg: a lightweight and versatile design for secure aggregation in federated learning,” Proceedings of Machine Learning and Systems, vol. 4, pp. 694–720, 2022.
- [24] T. Jahani-Nezhad, M. A. Maddah-Ali, S. Li, and G. Caire, “Swiftagg+: Achieving asymptotically optimal communication loads in secure aggregation for federated learning,” IEEE Journal on Selected Areas in Communications, vol. 41, no. 4, pp. 977–989, 2023.
- [25] H. Fang and Q. Qian, “Privacy preserving machine learning with homomorphic encryption and federated learning,” Future Internet, vol. 13, no. 4, p. 94, 2021.
- [26] C. Chen, J. Zhou, L. Wang, X. Wu, W. Fang, J. Tan, L. Wang, A. X. Liu, H. Wang, and C. Hong, “When homomorphic encryption marries secret sharing: Secure large-scale sparse logistic regression and applications in risk control,” in Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, 2021, pp. 2652–2662.
- [27] J. Ma, S.-A. Naas, S. Sigg, and X. Lyu, “Privacy-preserving federated learning based on multi-key homomorphic encryption,” International Journal of Intelligent Systems, vol. 37, no. 9, pp. 5880–5901, 2022.
- [28] Y. Xia, C. Hofmeister, M. Egger, and R. Bitar, “Byzantine-resilient secure aggregation for federated learning without privacy compromises,” arXiv preprint arXiv:2405.08698, 2024.
- [29] L. Lyu, H. Yu, X. Ma, C. Chen, L. Sun, J. Zhao, Q. Yang, and S. Y. Philip, “Privacy and robustness in federated learning: Attacks and defenses,” IEEE transactions on neural networks and learning systems, 2022.
- [30] A. Roy Chowdhury, C. Guo, S. Jha, and L. van der Maaten, “Eiffel: Ensuring integrity for federated learning,” in Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, 2022, pp. 2535–2549.
- [31] H. Lycklama, L. Burkhalter, A. Viand, N. Küchler, and A. Hithnawi, “Rofl: Robustness of secure federated learning,” in 2023 IEEE Symposium on Security and Privacy (SP). IEEE, 2023, pp. 453–476.
- [32] J. So, B. Güler, and A. S. Avestimehr, “Byzantine-resilient secure federated learning,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 7, pp. 2168–2181, 2020.
- [33] T. Jahani-Nezhad, M. A. Maddah-Ali, and G. Caire, “Byzantine-resistant secure aggregation for federated learning based on coded computing and vector commitment,” arXiv preprint arXiv:2302.09913, 2023.
- [34] Z. Ma, J. Ma, Y. Miao, Y. Li, and R. H. Deng, “Shieldfl: Mitigating model poisoning attacks in privacy-preserving federated learning,” IEEE Transactions on Information Forensics and Security, vol. 17, pp. 1639–1654, 2022.
- [35] M. Rathee, C. Shen, S. Wagh, and R. A. Popa, “Elsa: Secure aggregation for federated learning with malicious actors,” in 2023 IEEE Symposium on Security and Privacy (SP). IEEE, 2023, pp. 1961–1979.
- [36] X. Li, X. Yang, Z. Zhou, and R. Lu, “Efficiently achieving privacy preservation and poisoning attack resistance in federated learning,” IEEE Transactions on Information Forensics and Security, 2024.
- [37] Q. Yu, S. Li, N. Raviv, S. M. M. Kalan, M. Soltanolkotabi, and S. A. Avestimehr, “Lagrange coded computing: Optimal design for resiliency, security, and privacy,” in The 22nd International Conference on Artificial Intelligence and Statistics. PMLR, 2019, pp. 1215–1225.
- [38] H. Corrigan-Gibbs and D. Boneh, “Prio: Private, robust, and scalable computation of aggregate statistics,” in 14th USENIX symposium on networked systems design and implementation (NSDI 17), 2017, pp. 259–282.
- [39] K. Nazirkhanova, J. Neu, and D. Tse, “Information dispersal with provable retrievability for rollups,” in Proceedings of the 4th ACM Conference on Advances in Financial Technologies, 2022, pp. 180–197.
- [40] C. Zhang, Y. Xie, H. Bai, B. Yu, W. Li, and Y. Gao, “A survey on federated learning,” Knowledge-Based Systems, vol. 216, p. 106775, 2021.
- [41] L. Bottou, “Large-scale machine learning with stochastic gradient descent,” in Proceedings of COMPSTAT’2010: 19th International Conference on Computational StatisticsParis France, August 22-27, 2010 Keynote, Invited and Contributed Papers. Springer, 2010, pp. 177–186.
- [42] W. Wei and L. Liu, “Gradient leakage attack resilient deep learning,” IEEE Transactions on Information Forensics and Security, vol. 17, pp. 303–316, 2021.
- [43] K. Bonawitz, V. Ivanov, B. Kreuter, A. Marcedone, H. B. McMahan, S. Patel, D. Ramage, A. Segal, and K. Seth, “Practical secure aggregation for privacy-preserving machine learning,” in proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017, pp. 1175–1191.
- [44] Z. Sun, P. Kairouz, A. T. Suresh, and H. B. McMahan, “Can you really backdoor federated learning?” arXiv preprint arXiv:1911.07963, 2019.
- [45] H. Wang, K. Sreenivasan, S. Rajput, H. Vishwakarma, S. Agarwal, J.-y. Sohn, K. Lee, and D. Papailiopoulos, “Attack of the tails: Yes, you really can backdoor federated learning,” Advances in Neural Information Processing Systems, vol. 33, pp. 16 070–16 084, 2020.
- [46] V. Shejwalkar and A. Houmansadr, “Manipulating the byzantine: Optimizing model poisoning attacks and defenses for federated learning,” in NDSS, 2021.
- [47] T. Gu, B. Dolan-Gavitt, and S. Garg, “Badnets: Identifying vulnerabilities in the machine learning model supply chain,” arXiv preprint arXiv:1708.06733, 2017.
- [48] X. Chen, C. Liu, B. Li, K. Lu, and D. Song, “Targeted backdoor attacks on deep learning systems using data poisoning,” arXiv preprint arXiv:1712.05526, 2017.
- [49] M. Barni, K. Kallas, and B. Tondi, “A new backdoor attack in cnns by training set corruption without label poisoning,” in 2019 IEEE International Conference on Image Processing (ICIP). IEEE, 2019, pp. 101–105.
- [50] T. A. Nguyen and A. Tran, “Input-aware dynamic backdoor attack,” Advances in Neural Information Processing Systems, vol. 33, pp. 3454–3464, 2020.
- [51] Y. Li, Y. Li, B. Wu, L. Li, R. He, and S. Lyu, “Invisible backdoor attack with sample-specific triggers,” in Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 16 463–16 472.
- [52] Y. Zeng, W. Park, Z. M. Mao, and R. Jia, “Rethinking the backdoor attacks’ triggers: A frequency perspective,” in Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 16 473–16 481.
- [53] Y. Li, Y. Jiang, Z. Li, and S.-T. Xia, “Backdoor learning: A survey,” IEEE Transactions on Neural Networks and Learning Systems, 2022.
- [54] M. Fang, X. Cao, J. Jia, and N. Gong, “Local model poisoning attacks to Byzantine-Robust federated learning,” in 29th USENIX security symposium (USENIX Security 20), 2020, pp. 1605–1622.
- [55] E. Bagdasaryan, A. Veit, Y. Hua, D. Estrin, and V. Shmatikov, “How to backdoor federated learning,” in International conference on artificial intelligence and statistics. PMLR, 2020, pp. 2938–2948.
- [56] C. Fung, C. J. Yoon, and I. Beschastnikh, “Mitigating sybils in federated learning poisoning,” arXiv preprint arXiv:1808.04866, 2018.
- [57] Y. Li, X. Lyu, N. Koren, L. Lyu, B. Li, and X. Ma, “Neural attention distillation: Erasing backdoor triggers from deep neural networks,” arXiv preprint arXiv:2101.05930, 2021.
- [58] ——, “Anti-backdoor learning: Training clean models on poisoned data,” Advances in Neural Information Processing Systems, vol. 34, pp. 14 900–14 912, 2021.
- [59] M. S. Ozdayi, M. Kantarcioglu, and Y. R. Gel, “Defending against backdoors in federated learning with robust learning rate,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 10, 2021, pp. 9268–9276.
- [60] W. Chen, B. Wu, and H. Wang, “Effective backdoor defense by exploiting sensitivity of poisoned samples,” Advances in Neural Information Processing Systems, vol. 35, pp. 9727–9737, 2022.
- [61] X. Qi, T. Xie, J. T. Wang, T. Wu, S. Mahloujifar, and P. Mittal, “Towards a proactive ML approach for detecting backdoor poison samples,” in 32nd USENIX Security Symposium (USENIX Security 23), 2023, pp. 1685–1702.
- [62] D. Yin, Y. Chen, R. Kannan, and P. Bartlett, “Byzantine-robust distributed learning: Towards optimal statistical rates,” in International Conference on Machine Learning. PMLR, 2018, pp. 5650–5659.
- [63] J. Bernstein, J. Zhao, K. Azizzadenesheli, and A. Anandkumar, “signsgd with majority vote is communication efficient and fault tolerant,” arXiv preprint arXiv:1810.05291, 2018.
- [64] J. Xu, S.-L. Huang, L. Song, and T. Lan, “Signguard: Byzantine-robust federated learning through collaborative malicious gradient filtering,” arXiv preprint arXiv:2109.05872, 2021.
- [65] D. N. Yaldiz, T. Zhang, and S. Avestimehr, “Secure federated learning against model poisoning attacks via client filtering,” arXiv preprint arXiv:2304.00160, 2023.
- [66] X. Cao, M. Fang, J. Liu, and N. Z. Gong, “Fltrust: Byzantine-robust federated learning via trust bootstrapping,” arXiv preprint arXiv:2012.13995, 2020.
- [67] T. Dierks and C. Allen, “The tls protocol version 1.0,” Tech. Rep., 1999.
- [68] L. Li, Y. Fan, M. Tse, and K.-Y. Lin, “A review of applications in federated learning,” Computers & Industrial Engineering, vol. 149, p. 106854, 2020.
- [69] X. Liu, H. Li, G. Xu, Z. Chen, X. Huang, and R. Lu, “Privacy-enhanced federated learning against poisoning adversaries,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 4574–4588, 2021.
- [70] J. Le, D. Zhang, X. Lei, L. Jiao, K. Zeng, and X. Liao, “Privacy-preserving federated learning with malicious clients and honest-but-curious servers,” IEEE Transactions on Information Forensics and Security, 2023.
- [71] J. Shao, Y. Sun, S. Li, and J. Zhang, “Dres-fl: Dropout-resilient secure federated learning for non-iid clients via secret data sharing,” Advances in Neural Information Processing Systems, vol. 35, pp. 10 533–10 545, 2022.
- [72] D. Pasquini, D. Francati, and G. Ateniese, “Eluding secure aggregation in federated learning via model inconsistency,” in Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, 2022, pp. 2429–2443.
- [73] K. Pillutla, S. M. Kakade, and Z. Harchaoui, “Robust aggregation for federated learning,” IEEE Transactions on Signal Processing, vol. 70, pp. 1142–1154, 2022.
- [74] J. Liu, J. Z. Huang, J. Luo, and L. Xiong, “Privacy preserving distributed DBSCAN clustering,” in Proceedings of the 2012 Joint EDBT/ICDT Workshops, 2012, pp. 177–185.
- [75] B. Bozdemir, S. Canard, O. Ermis, H. Möllering, M. Önen, and T. Schneider, “Privacy-preserving density-based clustering,” in Proceedings of the 2021 ACM Asia Conference on Computer and Communications Security, 2021, pp. 658–671.
- [76] S. Gao, “A new algorithm for decoding reed-solomon codes,” Communications, information and network security, pp. 55–68, 2003.
- [77] J. T. Schwartz, “Fast probabilistic algorithms for verification of polynomial identities,” Journal of the ACM (JACM), vol. 27, no. 4, pp. 701–717, 1980.
- [78] R. Zippel, “Probabilistic algorithms for sparse polynomials,” in International symposium on symbolic and algebraic manipulation. Springer, 1979, pp. 216–226.
- [79] D. Beaver, “Efficient multiparty protocols using circuit randomization,” in Advances in Cryptology—CRYPTO’91: Proceedings 11. Springer, 1992, pp. 420–432.
- [80] S. Li, D. Yao, and J. Liu, “Fedvs: Straggler-resilient and privacy-preserving vertical federated learning for split models,” in International Conference on Machine Learning. PMLR, 2023, pp. 20 296–20 311.
- [81] E. Weiszfeld and F. Plastria, “On the point for which the sum of the distances to n given points is minimum,” Annals of Operations Research, vol. 167, pp. 7–41, 2009.
- [82] W. Diffie and M. E. Hellman, “New directions in cryptography,” in Democratizing Cryptography: The Work of Whitfield Diffie and Martin Hellman, 2022, pp. 365–390.
- [83] J. Von Zur Gathen and J. Gerhard, Modern computer algebra. Cambridge university press, 2003.
- [84] A. N. Bhagoji, S. Chakraborty, P. Mittal, and S. Calo, “Analyzing federated learning through an adversarial lens,” in International Conference on Machine Learning. PMLR, 2019, pp. 634–643.
- [85] Y. Liu, S. Ma, Y. Aafer, W.-C. Lee, J. Zhai, W. Wang, and X. Zhang, “Trojaning attack on neural networks,” in 25th Annual Network And Distributed System Security Symposium (NDSS 2018). Internet Soc, 2018.
- [86] S. P. Karimireddy, L. He, and M. Jaggi, “Learning from history for byzantine robust optimization,” in International Conference on Machine Learning. PMLR, 2021, pp. 5311–5319.
- [87] H. Xiao, K. Rasul, and R. Vollgraf. (2017) Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms.
- [88] A. Krizhevsky, G. Hinton et al., “Learning multiple layers of features from tiny images,” 2009.
Appendix A Extension for SNIP
We introduce an extension of SNIP for repeated pattern circuits using LCC to reduce a term in the computational cost from to . It is effective when and is of order , the term in PriRoAgg becomes . In both instantiations of PriRoAgg, a special trait is that the users compute each entry of in the same way. Specifically, RLR computes the function for all entries of and RFA computes the square for those. Utilizing such a trait, we split the repeated computations of to computations of each coordinate of . All notations are directly inherited from Section.IV-D.
For demonstration, say we split arithmetic circuits from with the same topology structures. Each is applied on input and outputs . For each , step 1 is executed in the same manner and results in . Then, is viewed as the partitioned pieces from as in (6), on which LCC.share is applied with partitioning parameter instead of . Therefore, the shares of are still . The rest of steps are performed identically except when the server reconstructs by LCC.recon, it should decode ’s many if the prover honestly executes the evaluation.
Appendix B Quantization technique
In PriRoAgg, we follow the same stochastic quantization method as [32], which presents the theoretical guarantees of convergence. Given a real variable in range , it computes a probabilistic rounding ,
| (17) |
where denotes the largest integer no more than , and is an integer that controls the quantization loss. Next, it maps the rounding to the finite field domain by ,
| (20) |
Then, we define the element-wise quantization function for PriRoAgg to be: . dequantize() is defined to be the inverse function that maps values in to . In the experiment, is chosen between to achieve indistinguishable performance as real-domain execution.