compat=1.1.0
Probing Long-Range Forces in Neutrino Oscillations at the ESSnuSB Experiment
(ESSnuSB Collaboration)
Abstract
Neutrino oscillations constitute an excellent tool to probe physics beyond the Standard Model. In this paper, we investigate the potential of the ESSnuSB experiment to constrain the effects of flavour-dependent long-range forces (LRFs) in neutrino oscillations, which may arise due to the extension of the Standard Model gauge group by introducing new symmetries. Focusing on three specific symmetries—, , and , we demonstrate that ESSnuSB offers a favourable environment to search for LRF effects. Our analyses reveal that ESSnuSB can set 90% confidence level bounds of , , and , which are competitive to the upcoming Deep Underground Neutrino Experiment (DUNE). It is also observed that reducing the systematic uncertainties from to improves the ESSnuSB limits on . Interestingly, we find limited correlations between LRF parameters and the less constrained lepton mixing parameters and , preserving the robustness of ESSnuSB’s sensitivity to CP violation. Even under extreme LRF potentials (), the CP-violation sensitivity and precision remain largely unaffected. These results establish ESSnuSB as a competitive experimental setup for probing LRF effects, complementing constraints from other neutrino sources and offering critical insights into the physics of long-range forces.
1 Introduction
The discovery of neutrino oscillations Super-Kamiokande:1998kpq ; SNO:2002tuh ; Kajita:2016cak ; McDonald:2016ixn has provided compelling evidence for physics beyond the Standard Model (SM), opening new avenues to explore new fundamental interactions and forces. The unique properties of neutrinos, including their elusive nature and tiny masses, make them an excellent probe to detect even the most subtle signatures of new physics. The neutrino experiments with their increasing precision are now sensitive to sub-leading effects due to potential non-standard interactions (NSIs), offering an indirect hint of new particles and forces not predicted by the SM.
In the standard scenario, the interaction of neutrinos with matter is described by the so-called Mikheyev–Smirnov–Wolfenstein (MSW) mechanism, which results from coherent forward scattering of neutrinos with ambient matter Wolfenstein:1977ue . In this seminal paper, Wolfenstein also proposed the possibility of NSIs111In this manuscript, we will focus on new interactions mediated by vector bosons. There exists other forms of such interactions with different Lorentz structures Kopp:2007ne ; Du:2020dwr ; Gupta:2023wct ; ESSnuSB:2023lbg ; Denton:2024upc , which physics signatures are however different from the ones discussed here., which have been extensively studied in the literature Ohlsson:2012kf ; Miranda:2015dra ; Farzan:2017xzy ; 10.21468/SciPostPhysProc.2.001 ; Huitu:2016bmb ; Chaves:2021kxe .
In this work, we focus on another kind of such a new leptonic neutrino-matter interaction known as the long-range force (LRF), which may be flavour-dependent and mediated by light vector mediators He:1990pn ; Foot:1990mn ; He:1991qd ; Foot:1994vd ; Dolgov:1999gk . This is particularly intriguing since their effects can accumulate over astronomical distances, making them distinct from other NSIs. For instance, the matter content within astrophysical objects (Sun, Earth, Milky Way, etc.) can act as a source of LRF potential. These interactions significantly modify the probabilities of neutrino oscillations by introducing new potential terms in the Hamiltonian for neutrino propagation Smirnov:2019cae . Such interactions originate by extending the SM gauge group with additional anomaly-free symmetries associated with lepton numbers and the baryon number . We consider the three possible combinations of lepton flavours of symmetries Pontecorvo:1967fh ; Gribov:1968kq ; Cirigliano:2005ck ; Altarelli:2010gt , for example, , , . These symmetries are also important for generating neutrino masses Asai:2017ryy ; Asai:2018ocx ; Lou:2024fvw . The constraints on the LRF parameters have already been obtained from solar Grifols:2003gy ; Bandyopadhyay:2006uh ; Gonzalez-Garcia:2006vic , atmospheric Joshipura:2003jh and astrophysical neutrinos Bustamante:2018mzu ; Agarwalla:2023sng 222Most works on LRFs in neutrino oscillations take into account specific models or mediator mass ranges. The only model-independent constraints on the LRF potentials from existing experiments come from high-energetic neutrinos observed at IceCube Agarwalla:2023sng and of . These bounds are much tighter than the ones expected at terrestrial experiments due to energy-enhanced effects of LRFs. However, it is still worth exploring the bounds of accelerator experiments that employ a well-known and controlled neutrino beam.. In Ref. Coloma:2020gfv , a global analysis of three-flavour oscillation data has been performed in the presence of flavour-dependent long-range interactions. Furthermore, the effect of LRFs on long-baseline (LBL) neutrino experiments has been explored in Refs. Chatterjee:2015gta ; Khatun:2018lzs ; Singh:2023nek ; Mishra:2024riq .
A key objective of present and future neutrino oscillation experiments T2K:2017hed ; T2K:2019bcf ; NOvA:2019cyt ; DUNE:2020jqi is the precise determination of the leptonic CP-violating phase . The European Spallation Source (ESS) neutrino Super-Beam ESSnuSB ESSnuSB:2021azq is a next-to-next-generation long-baseline neutrino oscillation experiment designed to achieve this goal. Located in Sweden, ESSnuSB will produce a high-intensity muon neutrino beam using a 5 MW proton beam from the upgraded ESS facility in Lund Abele:2022iml ; Alekou:2022emd . The neutrinos will be detected by a water-Cherenkov detector situated 360 km away from Lund at the mine in Zinkgruvan. By focusing on the second oscillation maximum in the appearance probability , ESSnuSB is uniquely positioned to provide a precise measurement of . Currently, ESSnuSB is at the stage of preparation of a second conceptual design report to be followed by the development of a technical design report. This will help to plan the construction and data collection at a later stage ESSnuSB:2023ogw ; ESSnuSB:2024tmn . In the present work, we perform the first comprehensive study of the impact of long-range forces on the physics sensitivities of the ESSnuSB experiment. We derive bounds on the LRF potentials and the associated coupling parameters, comparing them with those achievable in the next-generation LBL experiments DUNE and T2HK. In addition, we investigate the effects of LRFs on the measurement of by ESSnuSB. Our analysis demonstrates that ESSnuSB’s long baseline and high precision make it an ideal facility for probing the subtle effects of LRFs, offering sensitivity that surpasses those of some existing experiments.
This paper is organized as follows. In Section 2, we provide a brief overview of the theoretical framework of LRFs in neutrino oscillations, focusing on the three symmetries under consideration. Then, in Section 3, the description of the ESSnuSB experiment and other simulation details are provided. Next, in Section 4, we compute the transition probabilities and generate the event plots in the presence of LRFs for ESSnuSB. In Section 5, the sensitivity of the ESSnuSB experiment to constrain the LRF potentials and new coupling parameters are presented. Especially, Subsection 5.1 deals with some interesting correlations of LRF potentials with and . Furthermore, in Section 6, the impact of LRFs on the measurement of is discussed, which is followed by a precision study of CP violation (CPV) in Section 7. Finally, in Section 8, we summarize our findings and conclusions.
2 Theoretical formalism
Neutrino flavour transitions are significantly influenced by the interactions between neutrinos and the ambient matter as they propagate from the source to the detector. These interactions induce an effective potential in the Hamiltonian interaction Wolfenstein:1977ue . In standard scenario, neutrino-matter interactions occur through Charged Current (CC) and Neutral Current (NC) mechanisms. While standard NC interactions are flavour-universal and do not impact neutrino oscillations, possible Beyond Standard Model (BSM) neutrino-matter interactions could introduce new potential terms that significantly alter neutrino propagation. Long-range forces are one such case, which may affect the measurements of neutrino oscillations in long-baseline experiments.
2.1 Long-range forces from new symmetries
This can be envisaged by the extension of the SM gauge group with the minimal particle content by introducing the anomaly-free combination of the symmetries and associated with the corresponding lepton numbers and baryon numbers. There are three possible lepton flavour combinations, for instance, , , , which can be gauged anomaly-free with the particles already present in the SM333In addition to these combinations, LRFs can also arise from other new U(1) symmetries, as discussed in Ref. Agarwalla:2024ylc . The corresponding ESSnuSB constraints on certain textures are provided in Appendix A.. In principle, these extra symmetries cannot reproduce the neutrino observables Choubey:2024krp ; Ibe:2025rwk ; however, with the addition of Higgs-like particles Asai:2017ryy ; Asai:2018ocx ; Lou:2024fvw , neutrino mixing and mass prediction can be reconciled. In addition, they induce a new flavour-dependent neutrino-matter interactions mediated by a new neutral gauge boson , and if the mediator is extremely light, the resulting forces might become significant over very large distances. The magnitude of the LRFs depends upon the matter contained within the radius which acts as a source of new potential.
The Lagrangian corresponding to the new interactions between a neutrino field and a charged lepton field mediated by a new gauge boson , for the combination of symmetry , is given by
| (1) |
where denote the dimensionless new gauge couplings and PL is the left-handed projection operator. It is to be noted that the (radiative) mixing Babu:1997st ; Joshipura:2019qxz between and can also induce such long-range interactions, whose strengths are proportional to the couplings Babu:1997st , where the quantity is the kinetic mixing parameter between and Holdom:1985ag ; Babu:1997st , the quantity is the rotation angle between mass and flavour bases of the gauge bosons and is the Weinberg angle. In Fig. 1, we show the NC-like neutrino interactions mediated by boson which can modify the oscillation probabilities; the left (right) diagram refers to the () case, see the following section for details.
2.2 Modified Hamiltonian due to long-range interaction potential
Assuming the three new gauge symmetries , and that induce new neutrino-matter interactions, the effective Hamiltonian for neutrino propagation in the flavour basis is
| (2) |
In the above expression, is the standard Pontecorvo-Maki-Nakagawa-Sakata (PMNS) mixing matrix in vacuum, and is the usual matter potential term due to the CC interactions of neutrinos with matter444NC interactions in neutrino propagation do not contribute to the oscillation probabilities in the usual three active neutrino framework. It is worth to mention that, in presence of sterile neutrinos or other forms of new physics, they could affect the matter-induced modifications of the vacuum neutrino oscillation probabilities Ghoshal:2020hyo ; Gehrlein:2024vwz ; Denton:2022pxt ; Agarwalla:2021owd ; Coloma:2017ptb ; Giarnetti:2021wur ; Giarnetti:2024mdt ; Berryman:2016szd .. The signs of and are positive (negative) in the case of neutrino (antineutrino) oscillations. The neutrino energy is denoted by , and is the electron number density. The contribution due to the long-range interaction is given by the new potential which, for the three different symmetries, can be written as
| (3) |
The specific form of the LRF Lagrangian generates a Yukawa-like potential with an interaction length inversely proportional to the mediator mass Bustamante:2018mzu ; Wise:2018rnb . Under transformations of the symmetry , where , this potential will be sourced by a population of electrons located at a distance from the neutrinos on Earth and is given as Bustamante:2018mzu ; Singh:2023nek
| (4) |
where is the effective coupling (which corresponds to in Eq. (1), is the mass of new mediating gauge boson . For , the LRF is originated from the mixing between new gauge boson and the SM gauge boson Heeck:2010pg ; Joshipura:2019qxz . In this case, assuming the Universe to be electrically neutral, the new potential experienced by neutrinos is only due to its interaction with number of neutrons which is given by Heeck:2010pg
| (5) |
where is the electric charge. For the symmetry, the effective coupling is related to the coupling as Babu:1997st .
It is worth mentioning that the structure of the new interaction potential is very similar to the standard matter potential except for the fact that in the former case, the mediator is extremely light (), while in the latter case, the mediator is very heavy (the SM boson). For this reason, LRFs can introduce new resonances in the transition probabilities at lower energies than the usual MSW resonance Wolfenstein:1977ue such as Chatterjee:2015gta ; Khatun:2018lzs
| (6) |
for the case. No resonances are expected in the scenario Agarwalla:2024ylc ; Agarwalla:2021zfr . However, deriving expressions for neutrino oscillation probabilities in the presence of LRFs is cumbersome and not very enlightening. In some works, the “effective” mixing angles and mass-squared differences are computed using particular approximations and assumptions Chatterjee:2015gta ; Singh:2023nek ; Mishra:2024riq . It should be noted that, at the Hamiltonian level, the effect of long-range forces is the same as the effect of flavour conserving vector NSIs Mishra:2024riq ; Wise:2018rnb ; Agarwalla:2021zfr ; Giarnetti:2024mdt . As it can be noted from analytical expansions presented in Refs. Kopp:2007ne ; Kikuchi:2008vq , the flavour conserving vector NSI parameters appear in the oscillation probabilities as sub-leading effects in the channel and at the first order in the channel. However, given the presence of the new resonance in Eq. (6) in the appearance probability and since to be sensitive to LRF parameters we need of the order of the standard matter effect, the overall effects of LRFs cannot be fully understood from analytical expansions in small new physics parameters. In this work, we discuss the LRF effects on the probabilities only numerically in Sec. 4.1.
3 Simulation details of the ESSnuSB experiment
To generate the probability spectrum, analyze event rates, and perform sensitivity studies of ESSnuSB in the presence of LRFs, we employed the GLoBES software Huber:2004ka ; Huber:2007ji . We introduced modifications to the probability engine to incorporate new potential terms due to the LRF as a new physics effect and then carried out numerical computations to obtain event rates and values. The experimental configuration and parameters for ESSnuSB used in our study are based on the ESSnuSB Conceptual Design Report Alekou:2022emd and were therefore implemented in GLoBES.
In particular, we considered a water Cherenkov far detector with a fiducial volume of 538 kt, positioned in the mine at Zinkgruvan, 360 km away from the neutrino source at ESS in Lund. A powerful linear accelerator (linac) will deliver protons on target per year, with a beam power of 5 MW and a proton kinetic energy of 2.5 GeV. We adopted updated neutrino fluxes, peaking at approximately 0.25 GeV, and applied updated migration matrices for event selection, as outlined in Refs. Alekou:2022emd ; ESSnuSB:2024yji . The energy spectrum in the [0, 2.5] GeV range was divided into 50 bins for event calculations.
Our analyses included both the appearance () and disappearance () channels and their CP-conjugate transitions, and accounted for all the relevant backgrounds. We assumed systematic errors of for signals and for backgrounds unless otherwise stated. The total exposure time assumed for the far detector is 10 years, equally divided between 5 years of running the neutrino beam and 5 years for the antineutrino beam.
4 Investigating LRFs at probability and event levels
In this section, we first examine how the appearance and disappearance oscillations probabilities of muon neutrinos are influenced by the presence of a new interaction potential, , sourcing the LRF at the ESSnuSB energies. Subsequently, we analyze the expected total event rates under the inclusion of LRFs in the theoretical framework. Unless stated otherwise, we adopt the best-fit values for the standard oscillation parameters from NuFIT 5.2 Esteban:2020cvm ; NuFIT5.2 , which incorporate Super-Kamiokande atmospheric data and these parameters are summarized in Table 1. For this analysis, we focus solely on the normal mass ordering (NO) for neutrinos, in line with the global fit preference for NO Capozzi:2017ipn ; Esteban:2018azc ; deSalas:2020pgw ; Capozzi:2021fjo ; Gonzalez-Garcia:2021dve , which might also be suggested by recent DESI-BAO cosmological results Jiang:2024viw .
| Oscillation parameters () | Normal ordering (NO) |
| (eV2) | |
| (eV2) |
4.1 The and oscillation probabilities
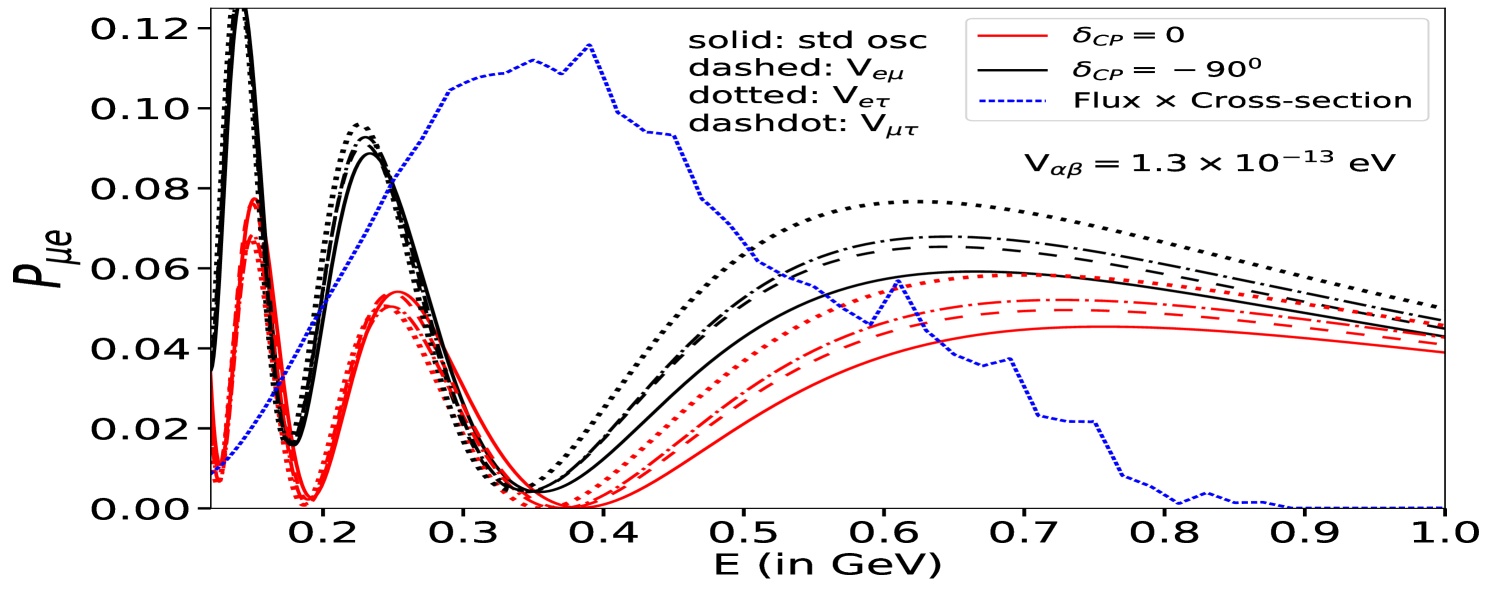
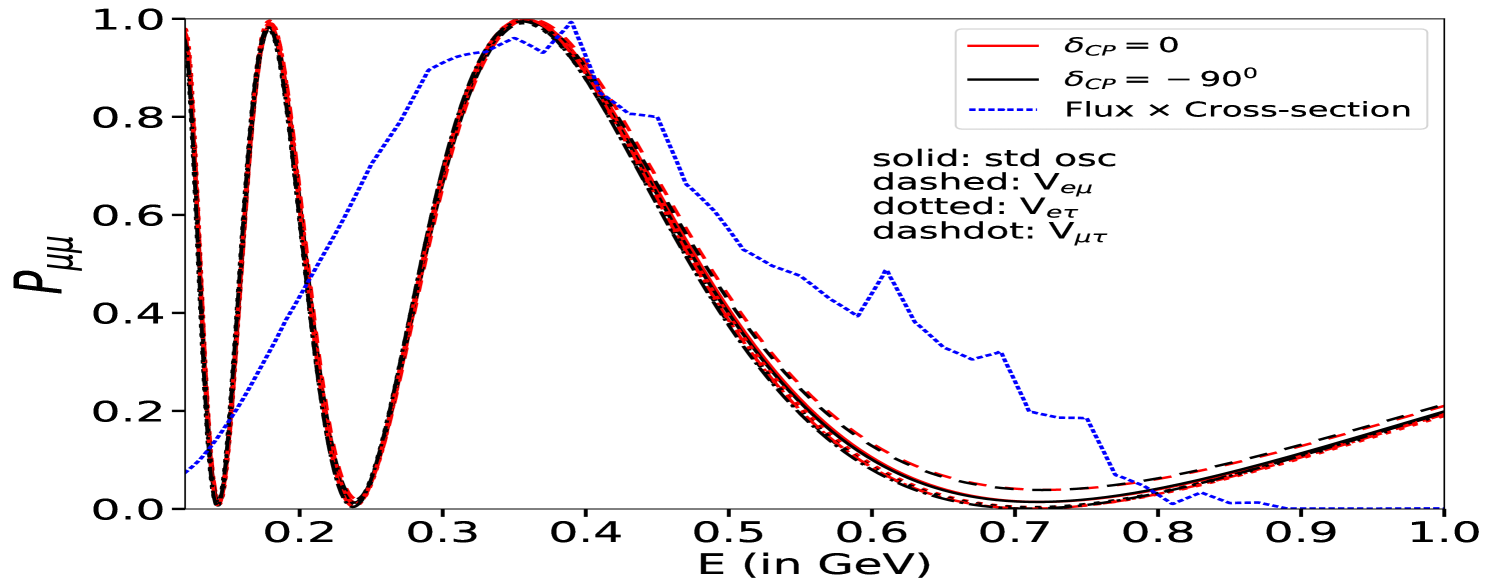
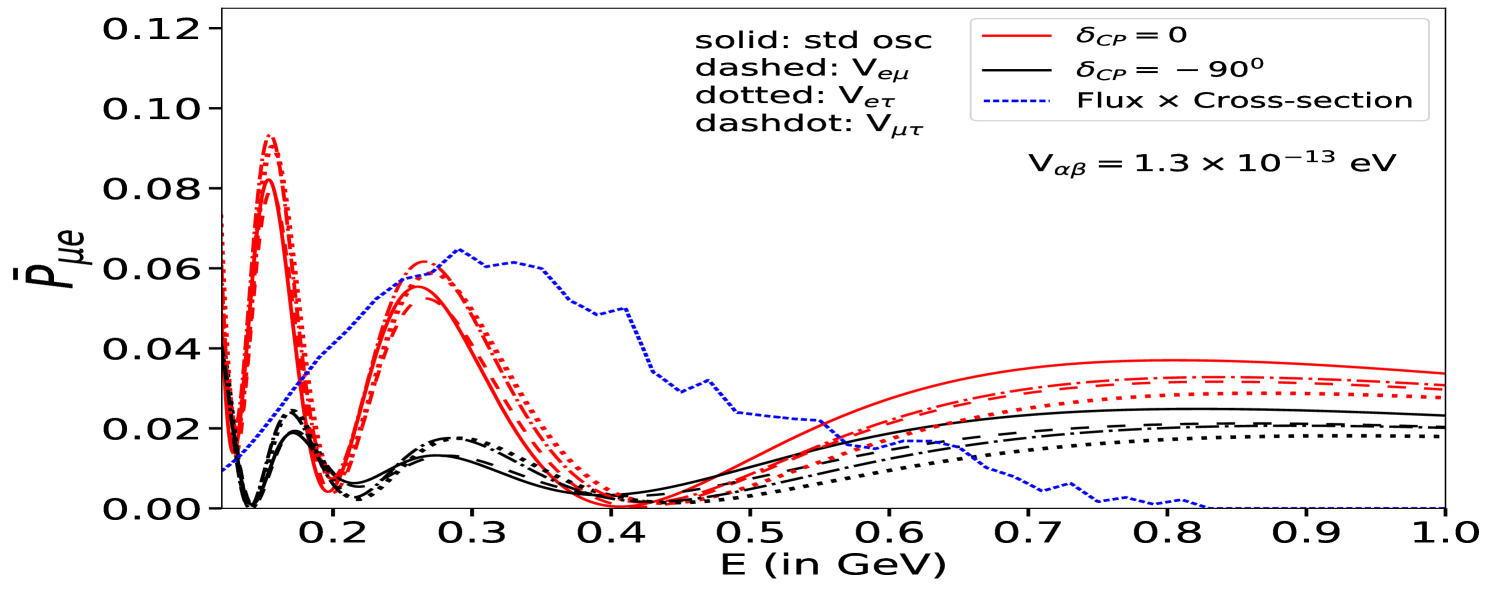
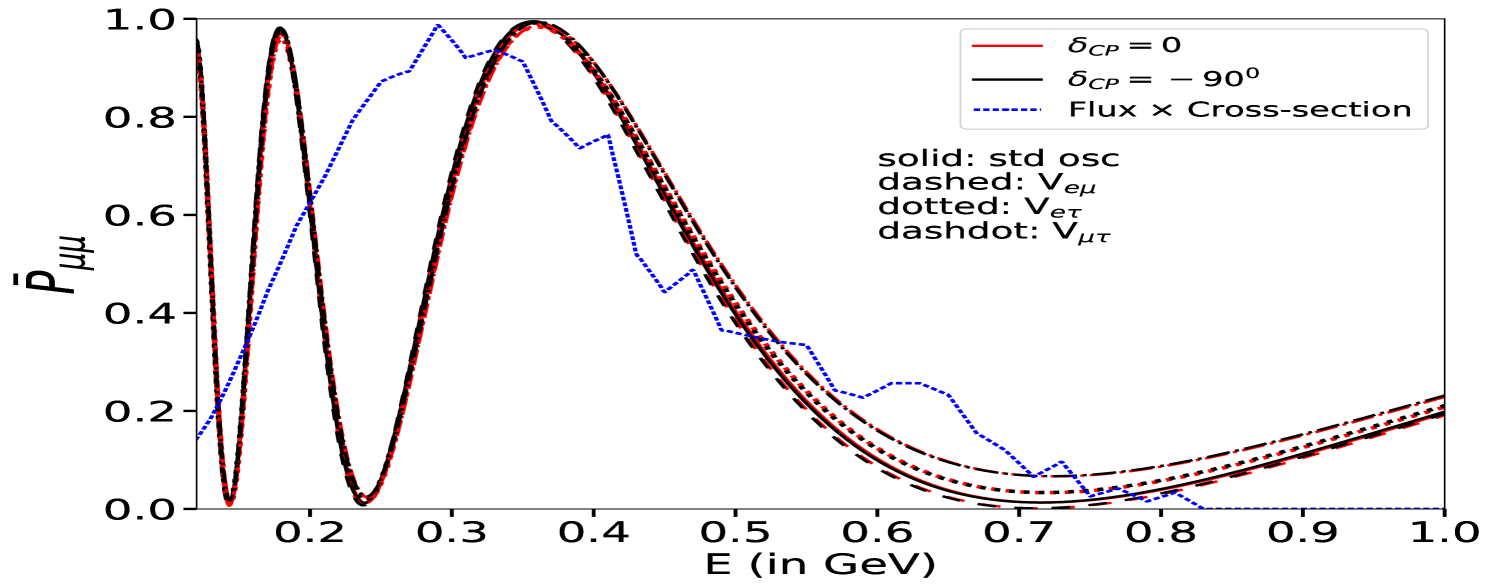
In Fig. 2, we display the plots for neutrino oscillation probabilities, computed numerically in the presence of LRF potentials, , as a function of neutrino energy relevant for the ESSnuSB experiment. To show the impact of LRF potentials, we set their values, eV, which is of the same order of magnitude as the standard matter potential Giarnetti:2024mdt ; Singh:2023nek . The top (bottom) panel is presented for the neutrino (antineutrino) oscillation probability. The left (right) panel depicts the effect of on the appearance (disappearance) channel. In each panel, the solid curves denote the standard probabilities without , while the dashed, dotted and dash-dotted curves refer to potentials, , corresponding to the three different symmetries, , and , respectively. Moreover, two extreme values for have been chosen, corresponding to the case of maximal CP violation (, black curve) and vanishing CP violation (, red curve). To show the energy region relevant for the ESSnuSB experiment in each figure, we also superimpose the ESSnuSB flux multiplied by the charged current (CC) neutrino cross-section.
From Fig. 2 (top left), we observe that the neutrino appearance probability, , is enhanced around the first oscillation maximum in all three cases due to the presence of LRF potentials, whereas for antineutrino case, the appearance probability (bottom left), , is suppressed. This is because the sign of LRF potential is flipped () for the antineutrino case, similar to the standard matter potential. However, around the second oscillation maximum, the appearance probability increases for both the neutrino and antineutrino cases. For the neutrino appearance probability, , the first oscillation maximum also shifts towards lower energies for all three cases of LRF potentials, . We also notice that the effects are more significant for the LRF potential (dotted curve), whereas (dashed curve) affects mildly. The disappearance channel, on the other hand, is less affected by compared to the appearance one for all three cases. In particular, at the first oscillation minimum, the effect of is larger for neutrinos (top right), while for antineutrinos (bottom right), the effect is more visible for and cases. However, given the much larger expected number of events at the far detector, the small disappearance probability modifications due to LRFs are crucial in constraining LRF potentials, .
4.2 Event rates in the presence of LRFs
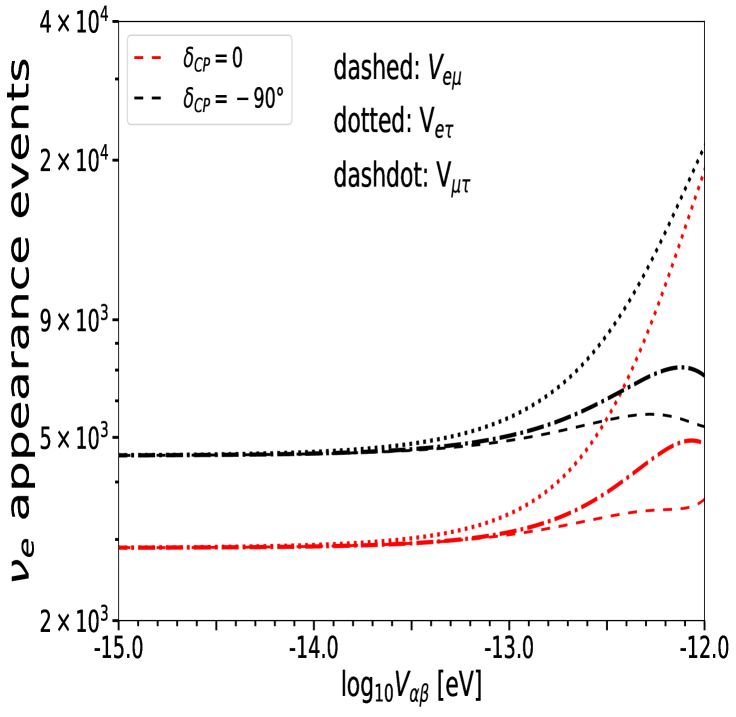
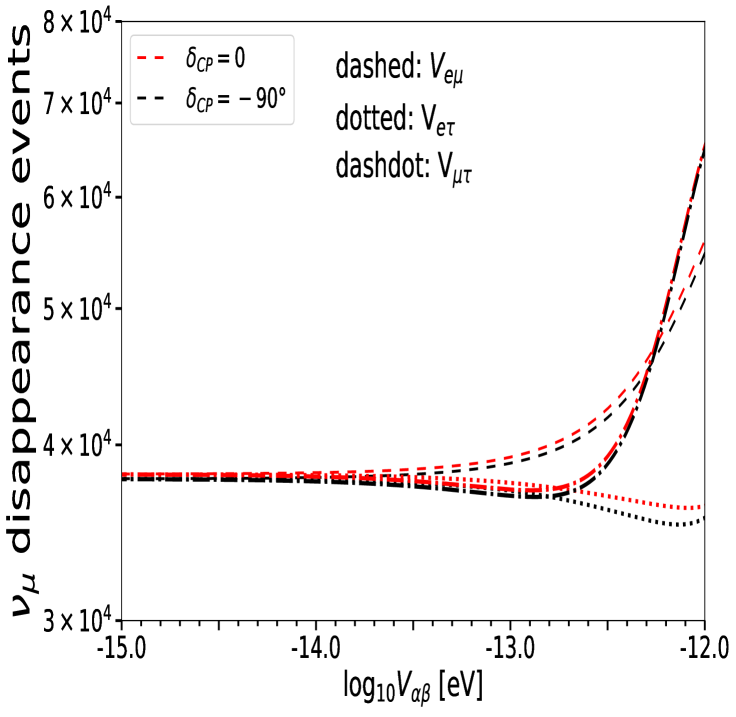
In order to make an initial guess about the limits that ESSnuSB would set on LRF parameters, , we plot the total number of neutrino appearance (and disappearance) events as a function of the LRF parameter for 10 years of running, 5 in neutrino and 5 in antineutrino mode. The potential, , is varied from eV to eV. The results are presented in Fig. 3, where the left panel is for the appearance of electron neutrino events and the right one refers to events corresponding to the disappearance of muon neutrinos. The black curves in each plot depict the case of maximal CP violation (), while red curves refer to the case of CP conservation (). The features observed in the discussion of the probabilities can be directly translated into these plots. Indeed, in each case, we can observe a transition from the standard case (without LRFs) to the LRF-dominated case. The transition begins for values of LRF potentials, , for which the correction in the standard probability due to the presence of LRFs overcomes the standard matter probability. A rough estimate of the constraint on that is obtainable from the ESSnuSB experiment can be derived directly from Fig. 3, eV; indeed, for larger potentials the expected number of events is much larger than the one expected in the case . However, the detailed analysis illustrated in the following section reveals stronger and more precise bounds on the LRF potentials. It can be observed from Fig. 3 that for in the appearance case and in the disappearance one, the number of events increases for both values of . The disappearance events, however, decrease in the range eV, with under transformations of the and symmetries.
5 Constraint plots for ESSnuSB
In this section, we explore the capability of the ESSnuSB experiment to constrain the parameters of LRFs. The statistical analysis has been performed using a Poissonian function, defined as
| (7) |
where represents the set of oscillation parameters needed to compute the rates, is the normalization error, is the number of energy bins, are the observed rates and are the expected rates used for the fit. Systematic uncertainties are incorporated using the pull method Huber:2002mx ; Fogli:2002pt , implemented in GLoBES with the nuisance parameter . The significance of our results in terms of standard deviations () has been obtained assuming the Wilk’s theorem Wilks:1938dza ; for instance, for 1 d.o.f .
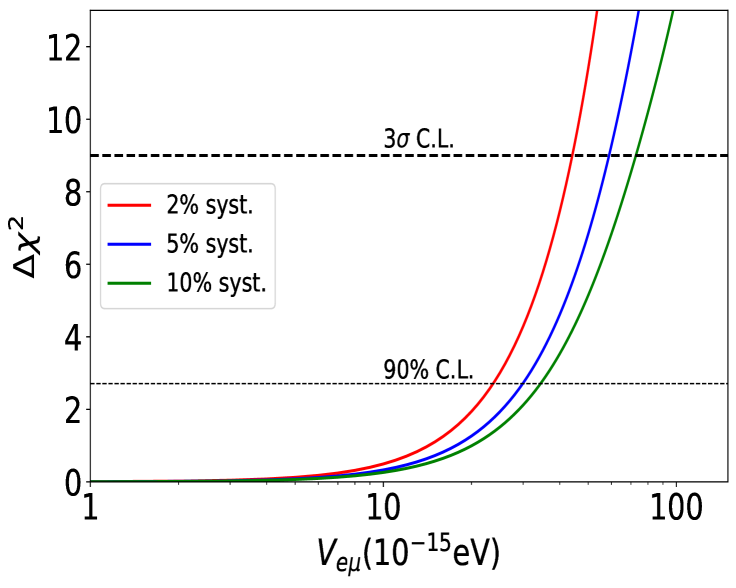
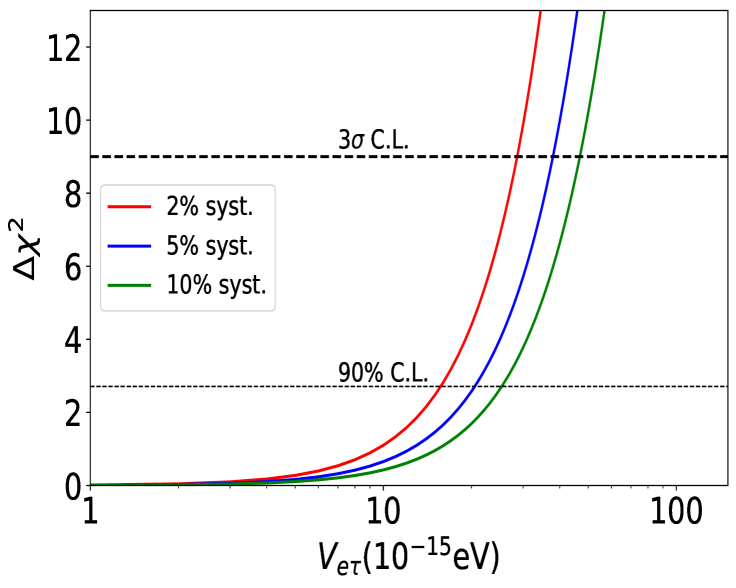
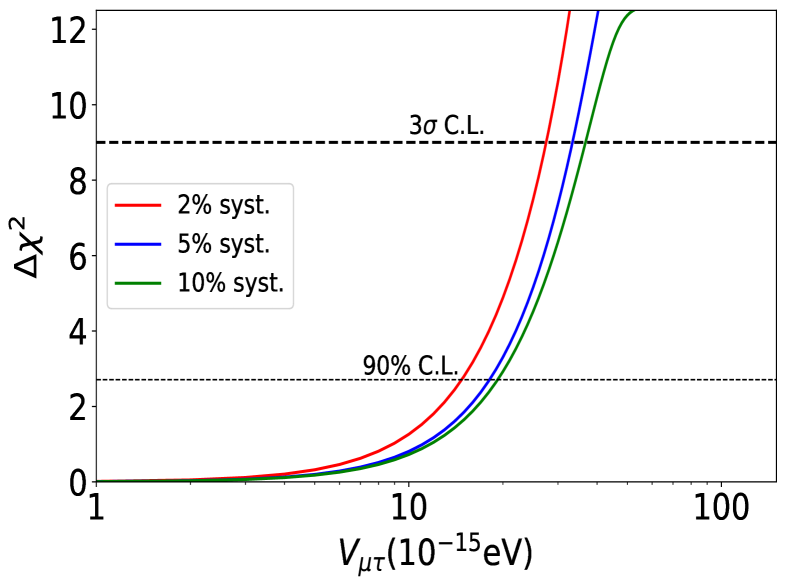
In order to compute the bounds on , we generate the true event spectrum using the hypothesis of no LRFs (i.e. (true) = 0) corresponding to standard three-flavour neutrino oscillations and fit the true data using the probabilities in the presence of LRFs. It should be noted that, while fitting the true data, only one LRF parameter is considered at a time in the test. This approach is justified as different potentials stem from distinct symmetries, independently affecting the oscillations. In all three cases of symmetries, we vary the potentials, from eV to eV in the test. The marginalization has been performed over and by varying them within the uncertainty ranges reported in Table 1, while is scanned over its full range. We keep the two oscillation parameters, and , fixed at their best-fit values Esteban:2020cvm . The results are displayed in Fig. 4 where the one-dimensional is plotted as a function of LRF potentials . The upper left (right) plot of Fig. 4 gives the bound on the LRF parameter while the lower plot displays the constraint on . We also show the results for different values of the normalization systematic uncertainty, namely 2% (red curves), 5% (blue curves) and 10% (green curves). The 3 and 90% C.L. bounds are summarized in Table 2 for the standard 5% systematics case along with the 2% and 10% systematics cases. The main results are that ESSnuSB in the nominal conditions (i.e. 5% systematics) may be able to set the 90% limits on eV, eV and eV. Notably, a change between and in the bounds can also be observed by variations in systematic uncertainties, particularly when and are considered. The effect of systematics on is, on the other hand, less prominent.
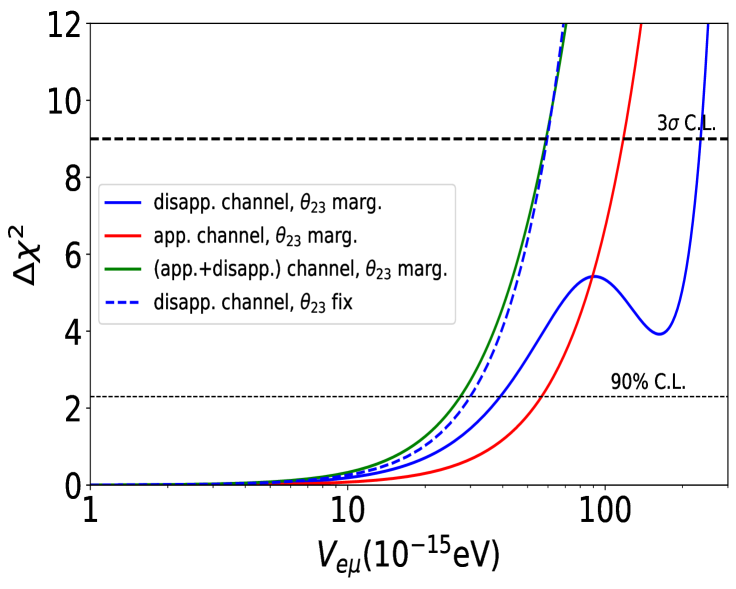
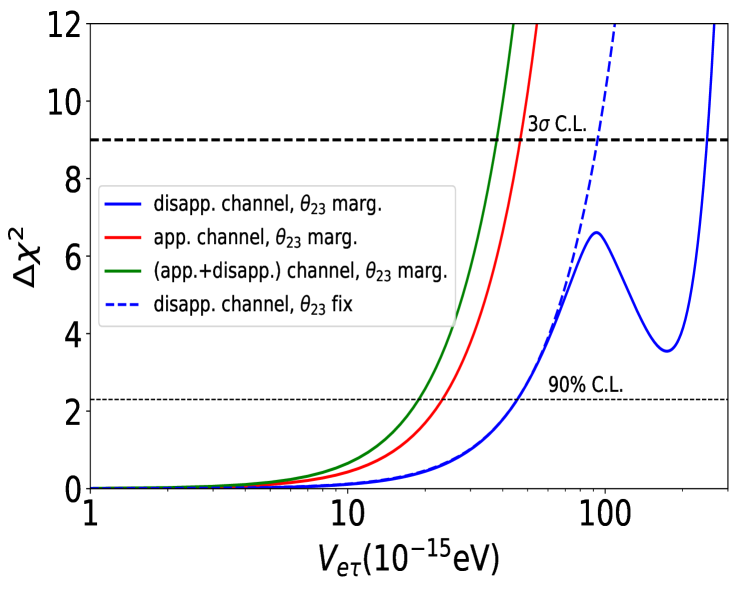
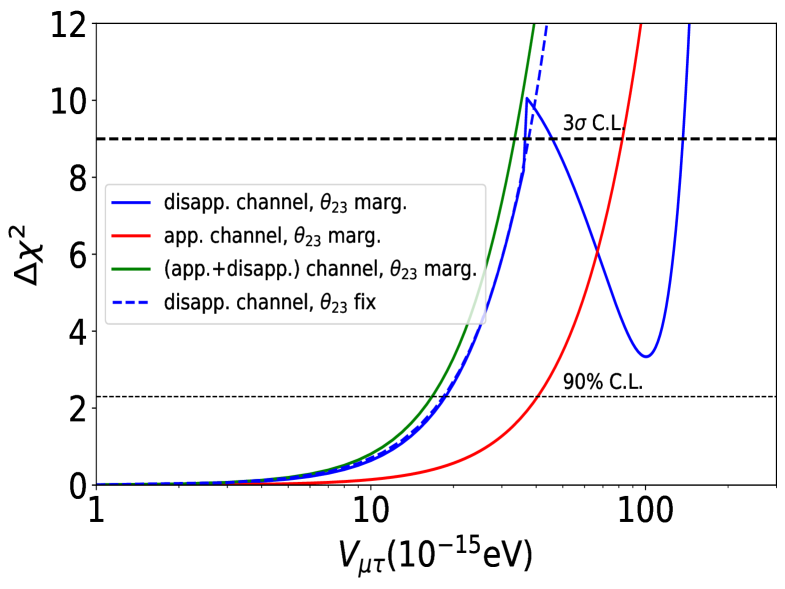
Before comparing the ESSnuSB limits on LRF potentials with other experimental bounds, let us try to understand the role of appearance and disappearance channels in constraining . In Fig. 5, we demonstrate how individual probability channels contribute for the ESSnuSB sensitivity towards LRF potentials, . It is evident that for the and symmetries the major sensitivity comes from the disappearance () probability, whereas the appearance probability () plays a major role to place a bound on the potential corresponding to the symmetry. This is also clear from the probability plots presented in Fig. 2, where the effect of the sector is more visible in the appearance probability (). Although from Fig. 2, it seems that the and sectors affect both and , however, due to the high statistics of the disappearance event numbers at the far detector, disappearance channel plays an important role in constraining and . This explains why different oscillation channels are sensitive to different LRF potentials. In Fig. 5, we notice a dip corresponding to the disappearance-only sensitivity curves (blue solid curves) for all three cases of the LRF potentials when a marginalization over is performed. Similar features are also observed in other works Singh:2023nek ; Mishra:2024riq . This is because, in the disappearance probability, the octant of develops a degeneracy with the potential picking up the wrong solution in the minimum calculation when marginalization is performed over . The dip vanishes for the disappearance only case if we fix to its best-fit value while computing the . Also, the dip disappears when we combine both the appearance and disappearance channels (green solid curves), while marginalizing over , highlighting the importance of the appearance channel, which is less affected by the octant degeneracy.
In the context of LBL experiments, the most stringent foreseen C.L. limits on LRF potentials have been derived by simulating the future experiment P2SO Mishra:2024riq due to its longer baseline, whereas the bounds (at C.L.) from the simulations of “upcoming” DUNE and T2HK experiments with the standard neutrino flux are given by Singh:2023nek :
| (8) |
It is worth mentioning that with a high-energy neutrino flux, the DUNE bounds on might become weaker as shown in Ref. Giarnetti:2024mdt .
| LRF Potential (in eV) | C.L. | C.L. | ||||
| syst. | syst. | syst. | syst. | syst. | syst. | |
Comparing the ESSnuSB results with other expected limits from upcoming LBL experiments in Eq. (5), we find that assuming nominal conditions ( systematics), ESSnuSB bounds are less stringent than the DUNE ones by about a factor of 2. This is due to the higher energy and longer baseline for DUNE, so the effect of LRFs is more pronounced. However, ESSnuSB outperforms T2HK by approximately . As mentioned earlier, systematic uncertainties play a noticeable role in placing bounds on the LRF potential by ESSnuSB, i.e., achieving a normalization uncertainty could improve the and constraints, making them comparable to future DUNE bounds. Overall, ESSnuSB is projected to set bounds on LRF parameters that are competitive with those from future LBL experiments such as DUNE and T2HK. Importantly, the complementarity of constraints from various neutrino sources, including accelerator, atmospheric, and solar neutrino data, provides a unique opportunity to significantly narrow the allowed parameter space for LRFs. By combining these results, the interplay between different datasets may uncover synergies that enhance sensitivity to LRF parameters and help elucidate the underlying physics of these new interactions.
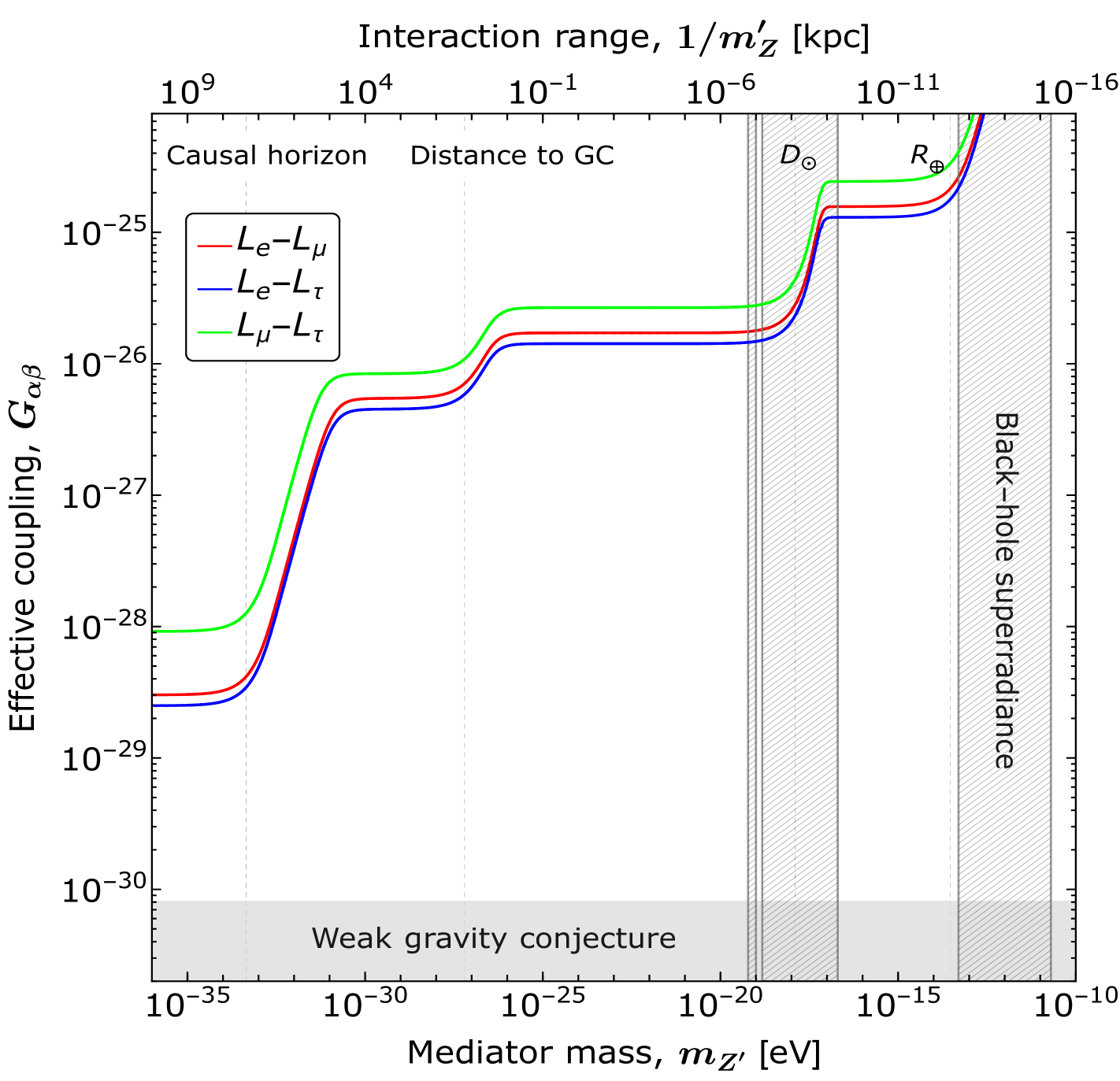
In addition to the LRF potentials, , we also put constraints on the actual parameters of the new neutrino-matter interaction, namely, the mass of the new gauge boson and the effective gauge couplings . Following the methodology presented in refs. Bustamante:2018mzu ; Singh:2023nek ; Giarnetti:2024mdt , we use Eqs. (4) and (5) to derive the limits on and . In order to take into account all the matter content present in the Universe, we consider neutrinos from different sources ranging at distances up to Gp away from the Earth. This corresponds to the mediator mass, in the range eV and the LRF potentials originating from all the matter content of the Universe can be rewritten in terms of the contributions from effective potentials relevant at different distances, i.e.,
| (9) |
To find the electron and neutron numbers for the LRF potentials from the Earth, an average density of a continuous distribution is modeled for the Earth such that we get . The Moon and the Sun are assumed to be point-like electron and neutron sources which correspond to the number of electrons and neutrons as given by and Singh:2023nek . In case of the Milky Way, the total matter content can be assumed to be distributed in the form of a thin and a thick disk, a central bulge and a diffuse gas Dehnen:1996fa ; Miller:2013nza ; Bustamante:2018mzu , yielding . For the cosmological matter content, we use adopted from refs. Bustamante:2018mzu ; Singh:2023nek . Utilizing these values of electron and neutron numbers and using Eqs. (4) and (5), the contributing terms of LRF potentials from all sources can be computed provided that the values of and are known. To constrain and , we use the C.L. limits on obtained in Table 2 and vary the free parameters. The results are presented in Fig. 6 where red, blue and green curves correspond to the , and symmetries, respectively. We also show the interaction range on the upper axis of the plot. It is worthwhile to mention that some astrophysical and cosmological phenomena, such as black-hole superradiance Baryakhtar:2017ngi and weak gravity conjecture Arkani-Hamed:2006emk may also exclude some parameter space of the LRFs, providing the non-oscillation exclusion limits. These regions are displayed by the grey bands in Fig. 6. From this figure, one can observe that the most stringent limit comes from the location of the causal horizon, which contains the highest number of electrons and neutrons. Therefore, the LRF potentials experienced by neutrinos from this location will be the largest.
5.1 Correlations
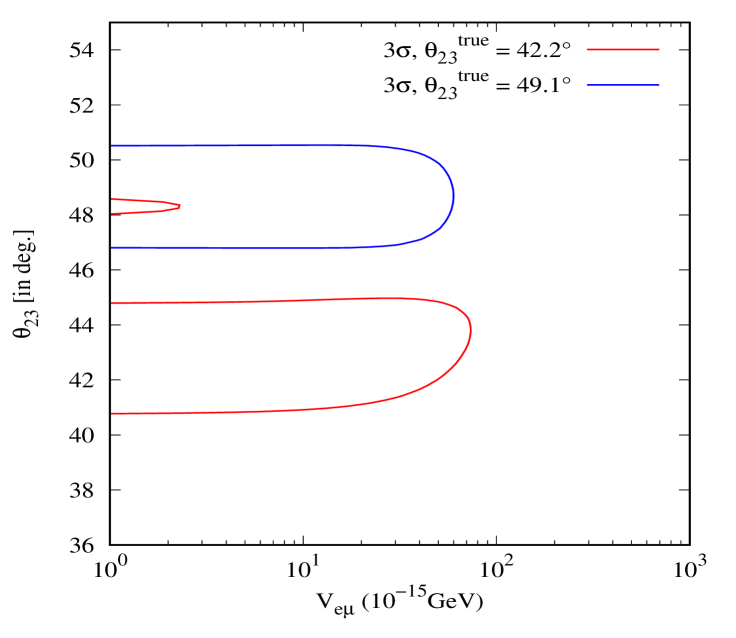
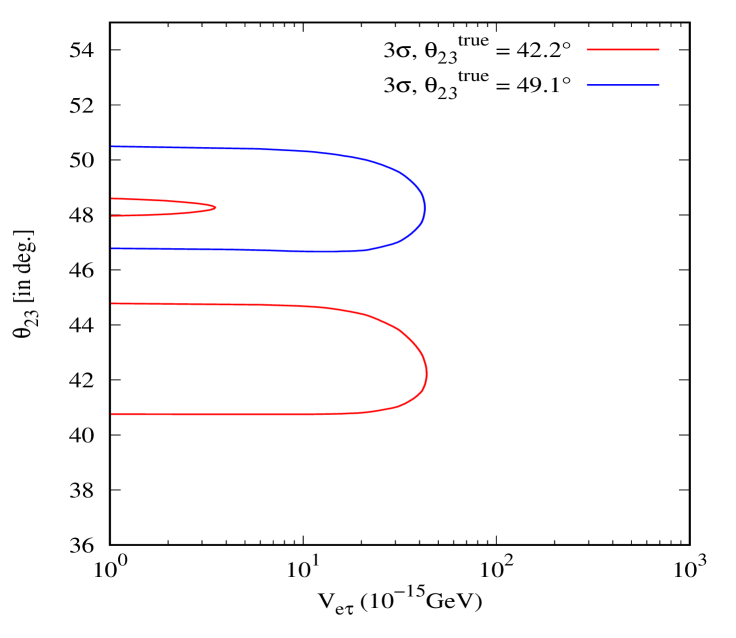
In this subsection, we want to explore the correlations between the LRF potentials, and the two poorly constrained standard neutrino oscillation parameters for ESSnuSB, namely and . To conduct this analysis, the true event spectra were generated under the assumption of no LRFs, using the best-fit values for the standard oscillation parameters listed in Table 1. The fit was obtained by marginalizing over all standard oscillation parameters not explicitly shown, except for and . Figure 7 displays the 3 allowed regions in the plane. The upper-left and upper-right panels illustrate the correlations between and whereas the lower panels represent the correlation in the plane. We present the results for two different choices of true values of the mixing angle , one in the lower octant () and one in the upper octant (). These values correspond to the best-fits from Ref. Esteban:2020cvm , with and without the inclusion of the Super-Kamiokande atmospheric data. We see that, in the absence of LRFs, the ESSnuSB results suggest that the octant degeneracy might not be resolved if the true value is . In this case, allowed values in the upper octant persist. However, in the presence of LRFs, this degeneracy appears to be resolved as the LRF potentials and tend to increase (see the upper left and right panels of Fig. 7). A similar trend is observed for (lower panel), although at relatively larger values of the potential. On the other hand, for and , the octant degeneracy appears to be already broken. Even in the presence of LRFs, we do not see any octant ambiguity when the true value of . As discussed in the previous section, we remark that the octant degeneracy breaking is mainly due to the appearance channel. Indeed, if we only consider the disappearance channel, the octant ambiguity plays a major role in the analysis.

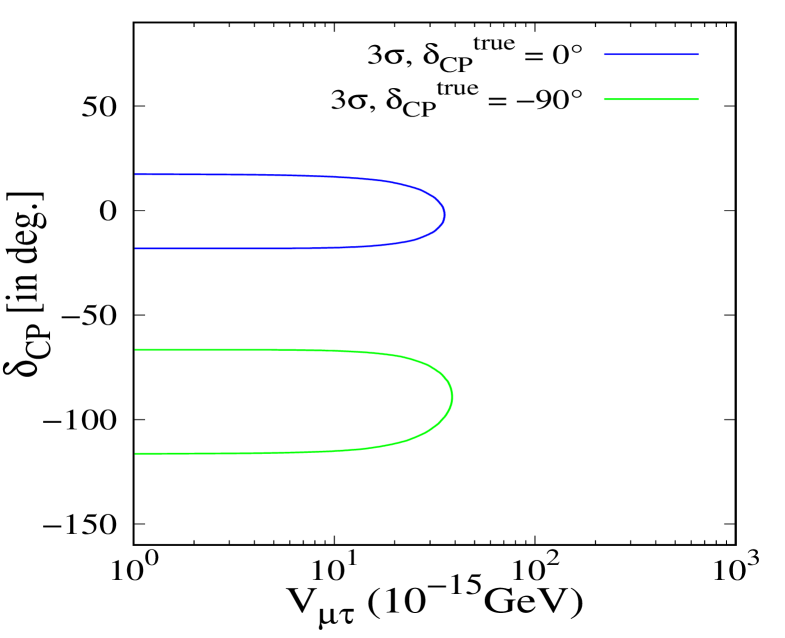
In Fig. 8, we present the results in the (upper-left panel), (upper-right panel) and (lower panel) planes for two true values of corresponding to maximal CPV () and no CPV (). The marginalization scheme used in this analysis follows the same procedure as previously described, where all other oscillation parameters, except and , are marginalized. In this case, we observe no significant correlations between and any of the LRF potentials, , and . However, it is worth noting that the effects of on the determination of could become significant if the LRF strengths are large enough to achieve the sensitivity of the ESSnuSB experiment. In such a scenario, those values might become measurable, introducing a potential influence on determination. We will delve deeper into this possibility and its implications in the next section.


6 CPV sensitivity of ESSnuSB in the presence of LRFs
In this section, we examine how the LRF potentials influence the CP-violation sensitivity of the ESSnuSB experiment. This analysis is crucial, as the primary aim of ESSnuSB is to achieve precise measurements of . It is worth noting that, in the case of maximal CP violation ( ), the sensitivity of ESSnuSB can reach up to 12.5 and it can also achieve at least 5 sensitivity for approximately 75% of the other possible values of Alekou:2022emd ; ESSnuSB:2023lbg . This surpasses the sensitivity of all upcoming next-generation LBL neutrino oscillation experiments Agarwalla:2022xdo . It is, therefore, vital to determine whether the presence of new physics, such as long-range interactions of neutrinos with matter, could jeopardize this capability or not. To do this, we generate the true event spectrum by varying (true) over the full range and compare this with or in the test. The same value of LRF potentials is considered in both true and test event spectra. The CPV-sensitivity plots are displayed in Fig. 9 in units of , where
| (10) |
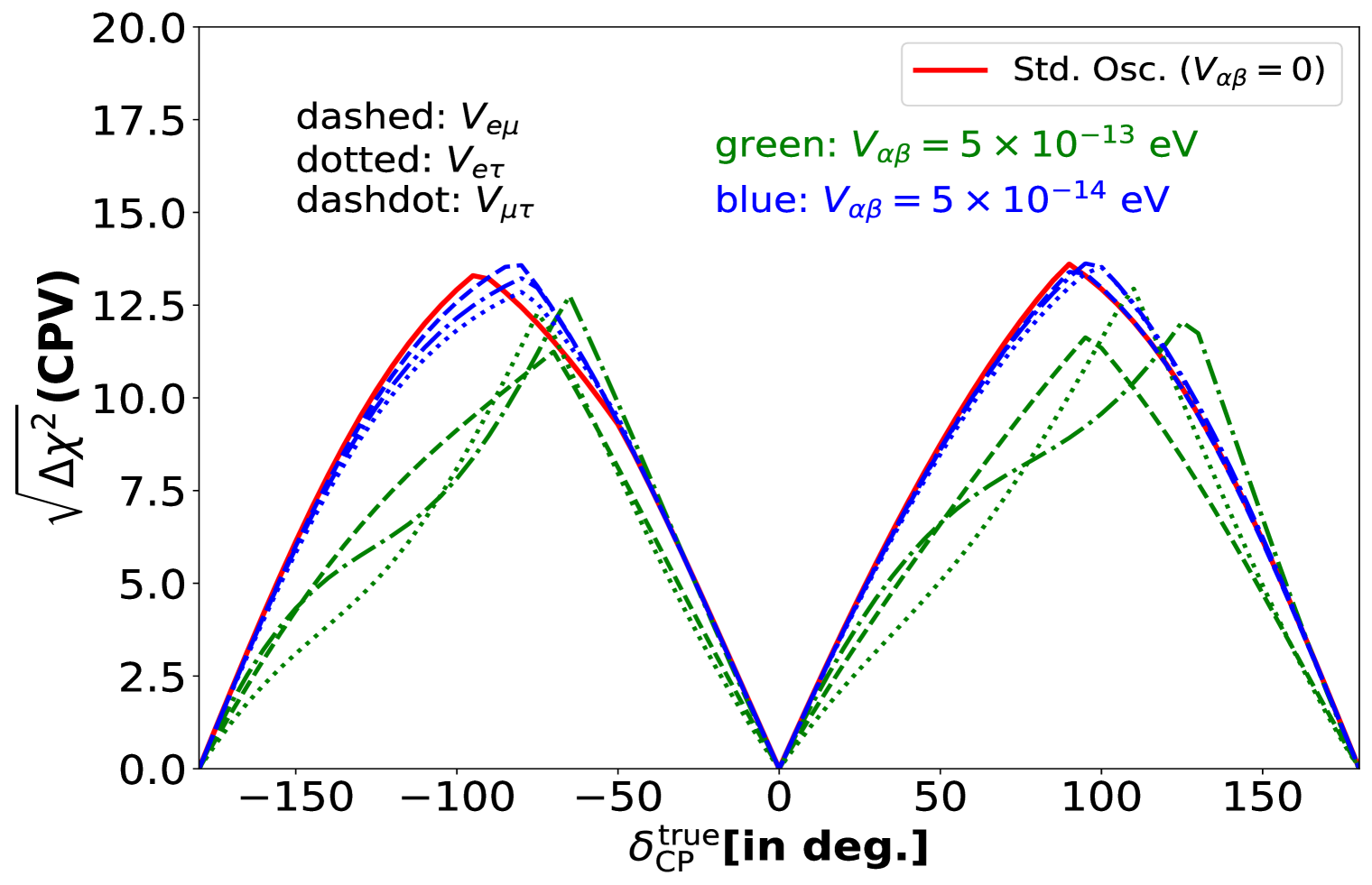
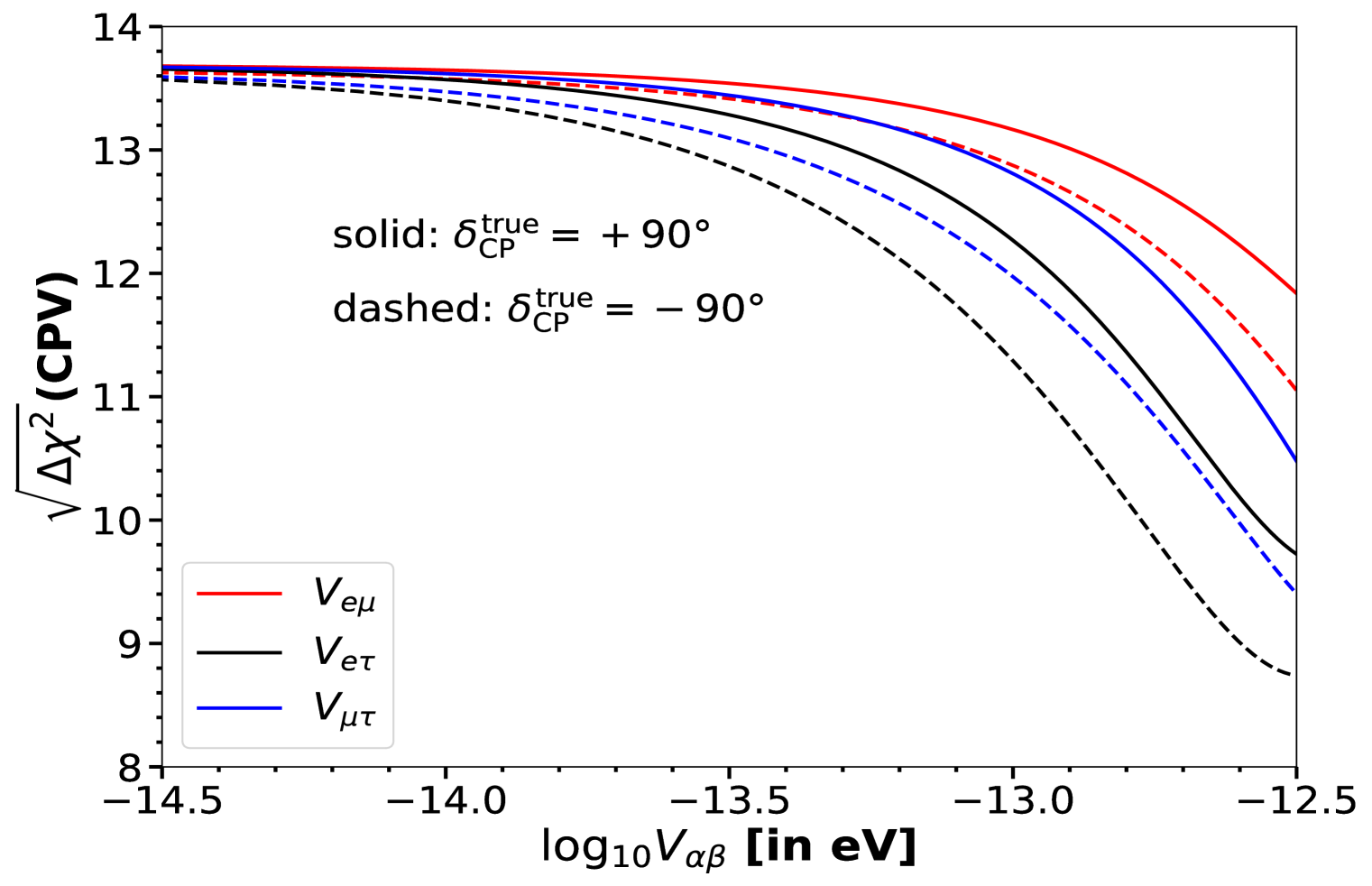
In this figure, the red curve represents the sensitivity in the standard oscillation scenario ( . The dashed, dotted and dashdot curves are for the potentials , and , respectively. The sensitivity curves plotted in blue colour correspond to the value of = eV, which is comparable to the ESSnuSB constraints, while the curves in green are computed for the LRF potentials, = eV, a much larger potential value than the ESSnuSB bounds. We notice that for small values of the new potentials, the ESSnuSB CP-violation sensitivity remains intact with some negligible impact on its sensitivity around . However, for large values of the LRF potentials, the changes and the positions of the sensitivity maxima are also slightly shifted. To understand this in more detail, we compute the CPV sensitivity as a function of the LRF potentials, . The results are displayed in Fig. 10 for two choices of , i.e. (solid curves) and (dashed curves). We can observe that, for small values of ( eV), the sensitivity of ESSnuSB more or less does not change for all three cases of . However, with increasing , the sensitivity decreases, especially for the potential corresponding to the symmetry. The reason is that when are small, they appear as a correction to the standard probability and mildly affect the sensitivity, whereas, for large values of , new resonances might appear, causing a significant drop in the CPV sensitivity of ESSnuSB.
7 CP precision of ESSnuSB in the presence of LRFs
In this section, we will try to understand the impact of LRF potentials on the uncertainty of measurement by the ESSnuSB experiment. Since the primary objective of ESSnuSB is to perform a precision measurement of in addition to discovering it (if next-generation LBL experiments fall short), it is imperative to see how new physics affects this capability of ESSnuSB. In Ref. Alekou:2022emd ; ESSnuSB:2023lbg , it has been shown that the optimal baseline of 360 km allows the ESSnuSB experiment to measure with a 1 uncertainty of less than for all possible values of . Remarkably, the experiment achieves its best precision, , for CP-conserving values. Such a level of accuracy is unparalleled, as it surpasses the capabilities of next-generation LBL experiments, emphasizing the transformative potential of ESSnuSB in this area of research.
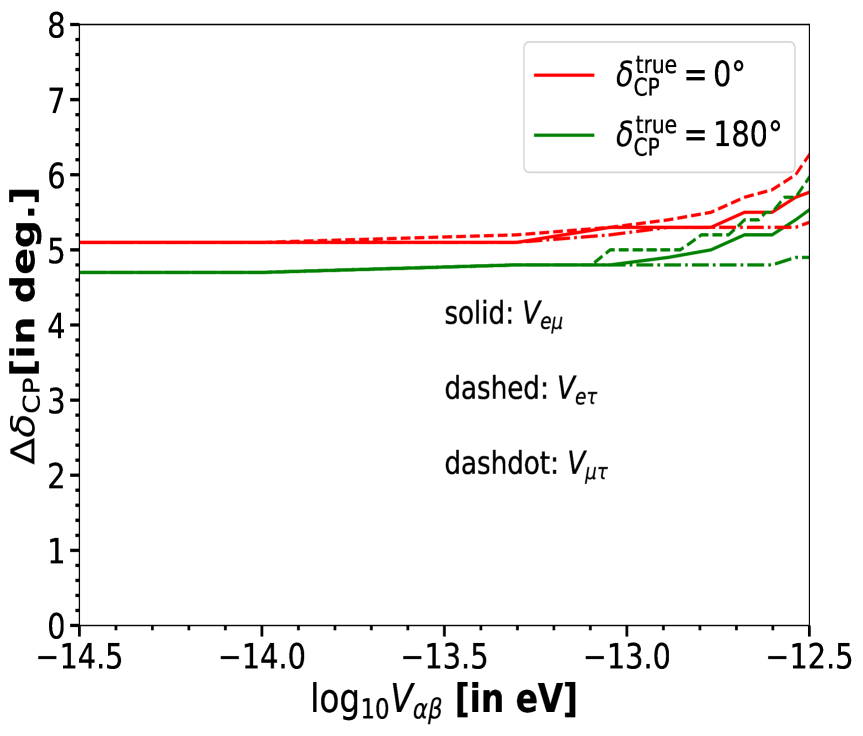
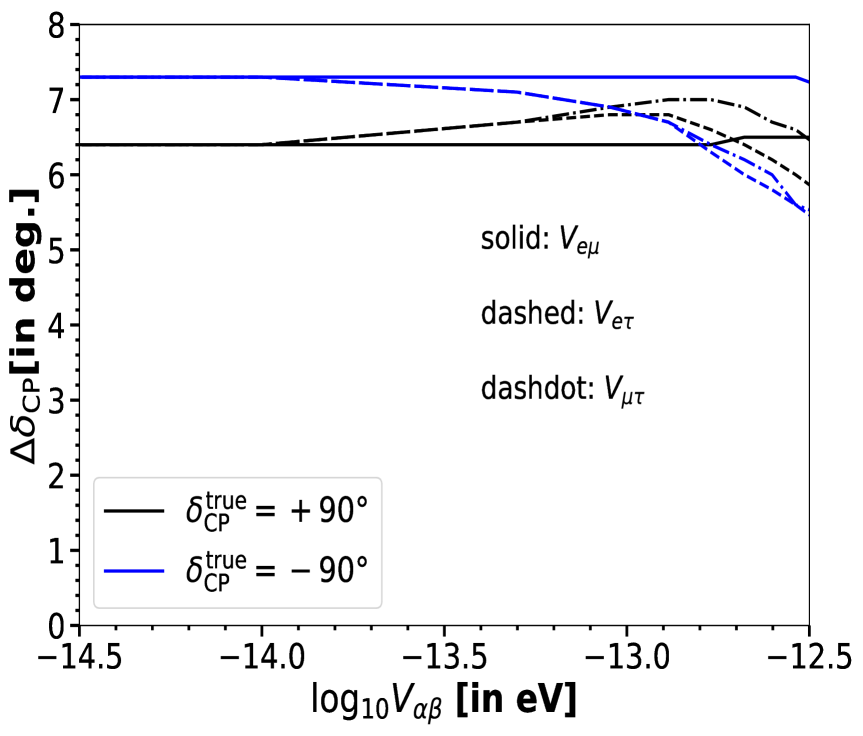
In Fig. 11, we present the projected 1 uncertainty in the measurement of for two scenarios: the CP-conserving values ( and , shown in the left panel) and the maximally CP-violating values (, shown in the right panel), as functions of the LRF potentials, . In both panels, solid, dashed and dashdot curves represent LRF potentials, namely, , and , respectively. From Fig. 11 it is evident that the effects of LRF potentials on the precision of ESSnuSB are negligible. Even when the values of all three potentials are large enough (almost an order of magnitude larger than the ESSnuSB bounds), the effects of are not significant enough to meaningfully degrade the performance of ESSnuSB. Specifically, for the maximally CP-violating values (), illustrated in the right panel of Fig. 11, the experiment can achieve a robust precision of , as long as remain below eV. For the CP-conserving values ( and ), illustrated in the left panel of Fig. 11, the precision is even better, with across the entire range of LRF potentials, .
These results highlight the resilience of ESSnuSB in maintaining high precision in measurements, even in the presence of LRFs, further demonstrating its capability to probe CP violation with unprecedented accuracy.
8 Summary and conclusions
In this paper, we explored the capabilities of the ESSnuSB experiment to set bounds on the effects of LRFs in neutrino oscillations. In the presence of additional gauge symmetries in the particle physics Lagrangian, a new vector mediator might be responsible for new interactions between SM particles. In the case of a very light mediator, such interactions might occur at very long distances and feebly interacting particles like neutrinos could provide valuable information about them. For instance, in neutrino oscillation experiments, LRFs modify matter effects in the neutrino oscillation probabilities introducing new terms in the Hamiltonian. We considered three different symmetries, namely , and . We demonstrated how the ESSnuSB setup could provide a good environment to search for LRFs. In particular, using nominal conditions (5% systematics), we observed that ESSnuSB could be able to set 90% C.L. limits on eV, eV and eV. The bounds on such parameters have been obtained by means of a standard analysis performed using the GloBES software. Among the upcoming next-generation LBL experiments, only DUNE is expected to outperform ESSnuSB, while T2HK will set weaker limits Singh:2023nek ; Giarnetti:2024mdt . The ESSnuSB bounds might become comparable to the DUNE ones if systematic uncertainties in both the appearance and disappearance channels are reduced for the ESSnuSB experiment. We explored the correlations between the LRF parameters and the most unknown oscillation parameters, namely and . We found that the octant degeneracy of is broken in the presence of LRFs when . We also could not observe any strong correlation between and the LRF potentials .
Finally, we addressed another crucial point in the context of the ESSnuSB experiment: the robustness of its most important measurement, namely the determination. We observed that, even in the presence of LRFs, both the CPV sensitivity and the precision remain unaltered except in the case of extremely large LRF potentials ().
Acknowledgements
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.
We acknowledge further support provided by the following research funding agencies: Centre National de la Recherche Scientifique, France; Deutsche Forschungsgemeinschaft, Germany, Projektnummer 423761110; Ministry of Science and Education of Republic of Croatia grant No. KK.01.1.1.01.0001; the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 860881-HIDDeN; the European Union NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project No. BG-RRP-2.004-0008-C01; as well as support provided by the universities and laboratories to which the authors of this report are affiliated, see the author list on the first page.
Appendix A LRF induced by other symmetries
In Ref. Agarwalla:2024ylc , other possibilities for the symmetries, which might generate new interactions modifying the neutrino oscillation probabilities, have been explored for the first time. In the context of neutrino oscillation, the different anomaly-free combinations of baryon number and lepton numbers Coloma:2020gfv ; Davoudiasl:2011sz ; Araki:2012ip ; delaVega:2021wpx ; Farzan:2016wym ; Joshipura:2019qxz ; Almumin:2022rml can only modify the diagonal entries of the matter potential part of the oscillation Hamiltonian (see Table 3 for a list of the symmetries and Ref. Agarwalla:2024ylc for details). Thus, regardless of the specific combination of the charges of the particles under the specific symmetries, the only textures of the LRF matrix in the Hamiltonian not discussed in our previous analyses are Agarwalla:2024ylc
| (11) |
To quantitatively discuss the effects of the LRF mediated by the symmetries generating the matrices in the oscillation Hamiltonian, we show in Fig. 12 the (panels a and c) and (panels b and d) oscillation probabilities in the energy range interesting for ESSnuSB. In the appearance probability, the textures and have the same effect, enhancing (reducing) the neutrino (antineutrino) probability at oscillation maximum by roughly the same amount. The texture, on the other hand, has approximately the same but opposite effect of the texture. The texture does not significantly affect the oscillations. This behaviour also explains why the symmetry modifies the probabilities more than and ; indeed in this specific case, the effects of the and texture are summed, enhancing the probabilities more. The disappearance probabilities, on the other hand, are almost unaffected by the textures and for the neutrino case, is enhanced (reduced) at the minimum by the () textures. The antineutrino disappearance probability exhibits opposite behaviour compared to the neutrino case when textures and are considered.
We finally study the sensitivity of the ESSnuSB experiment to the parameters in the four studied cases in Fig. 13. We summarize in Table 3 the bounds for the four textures obtained using the same procedure described in Sec. 5 with 5% systematics. The bounds in these cases are, in general, less stringent than in the symmetries cases. In particular, the texture gives the tightest bound on , while the texture is the looser. It is interesting to notice that since texture does not affect significantly the appearance channel but only the disappearance one, the octant degeneracy causes a reduction of the sensitivity for .
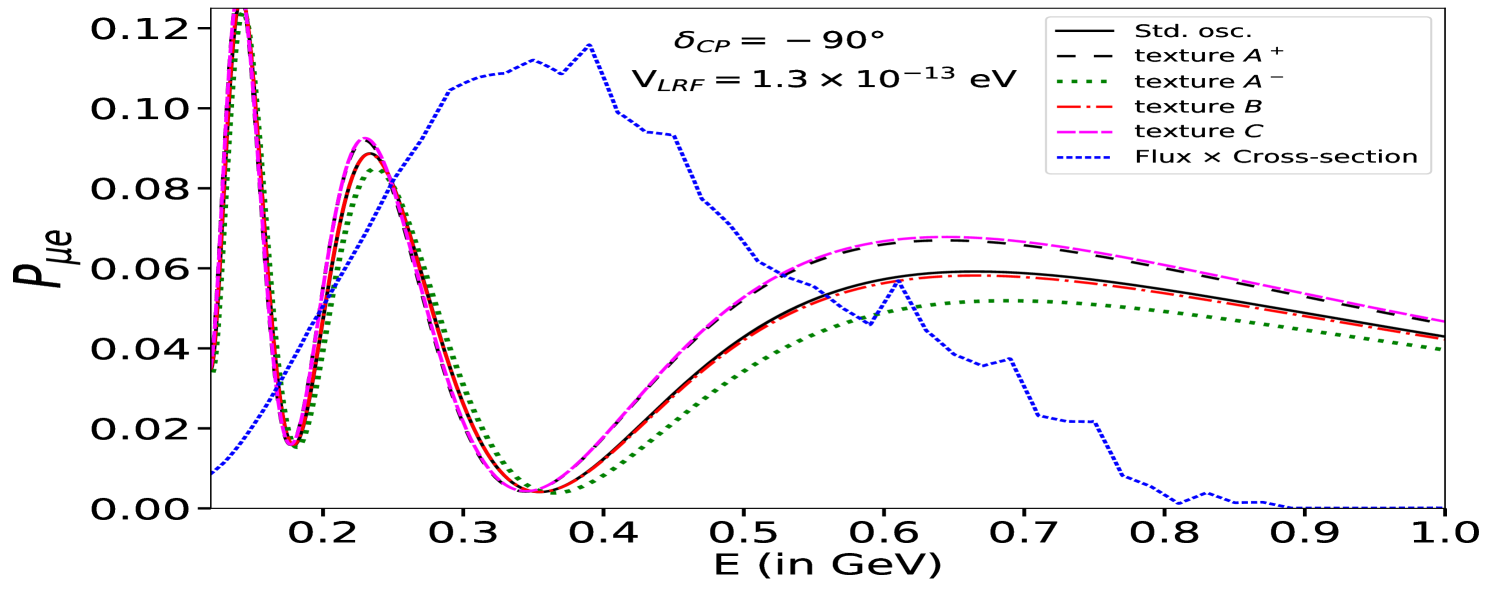
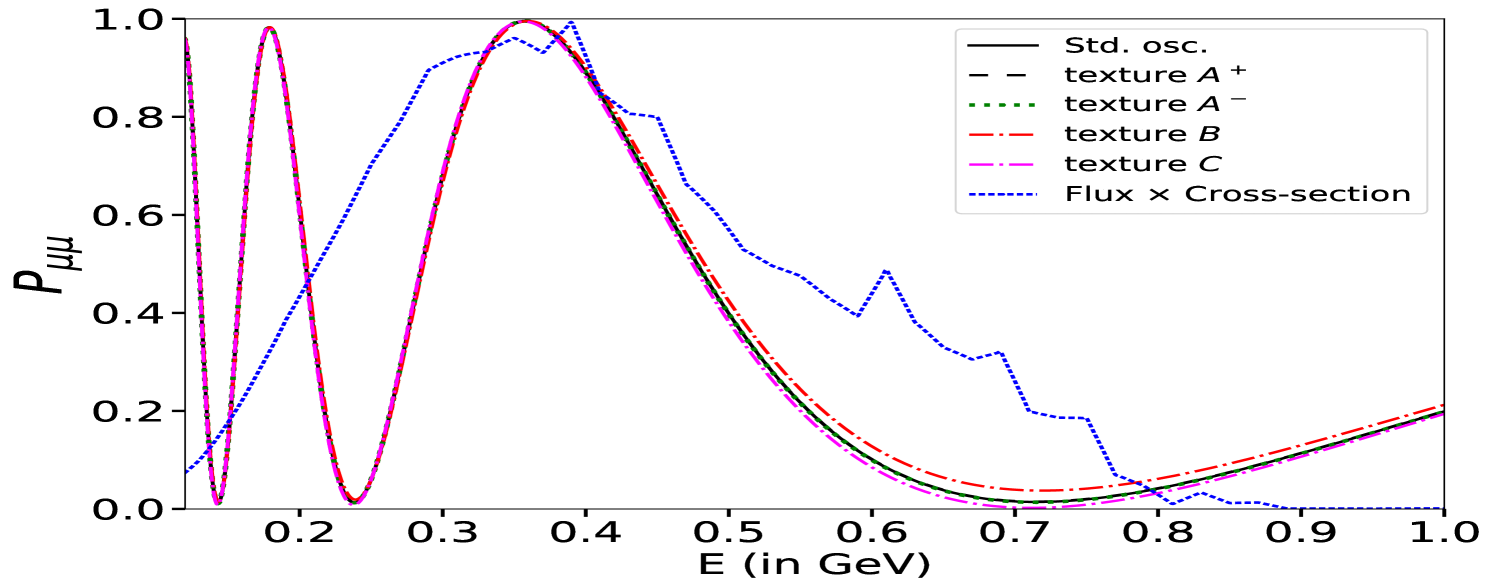
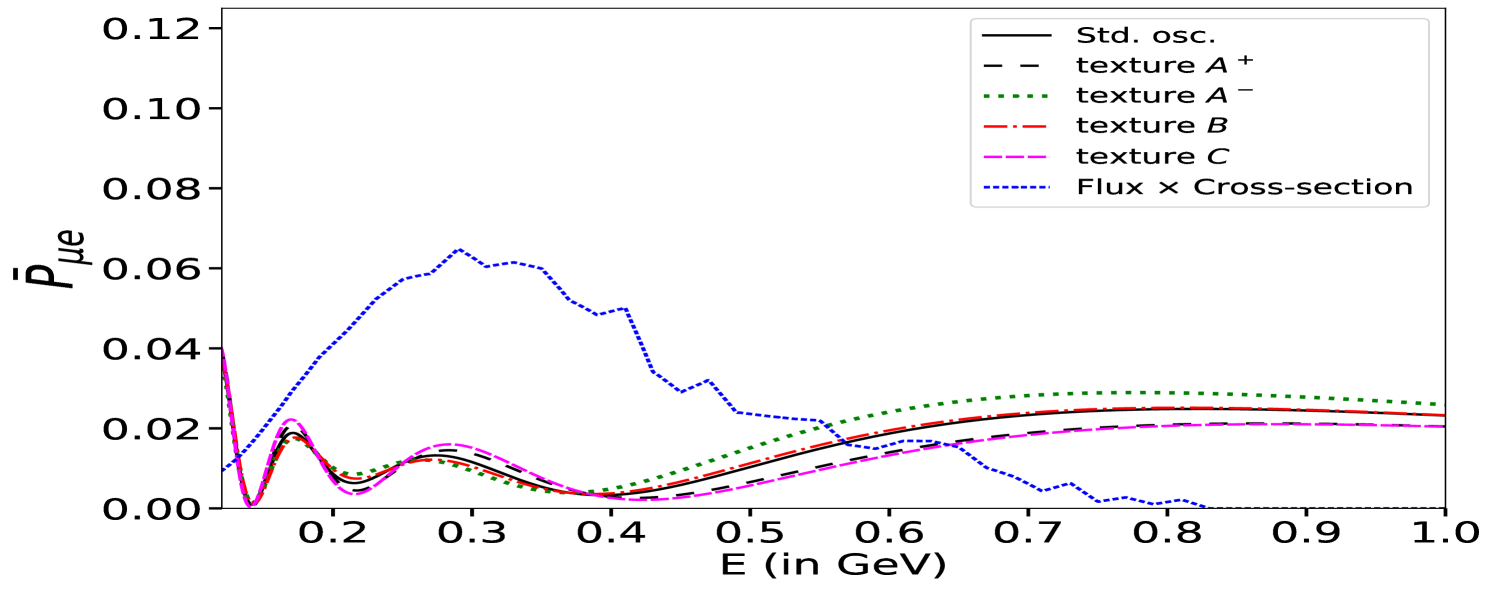
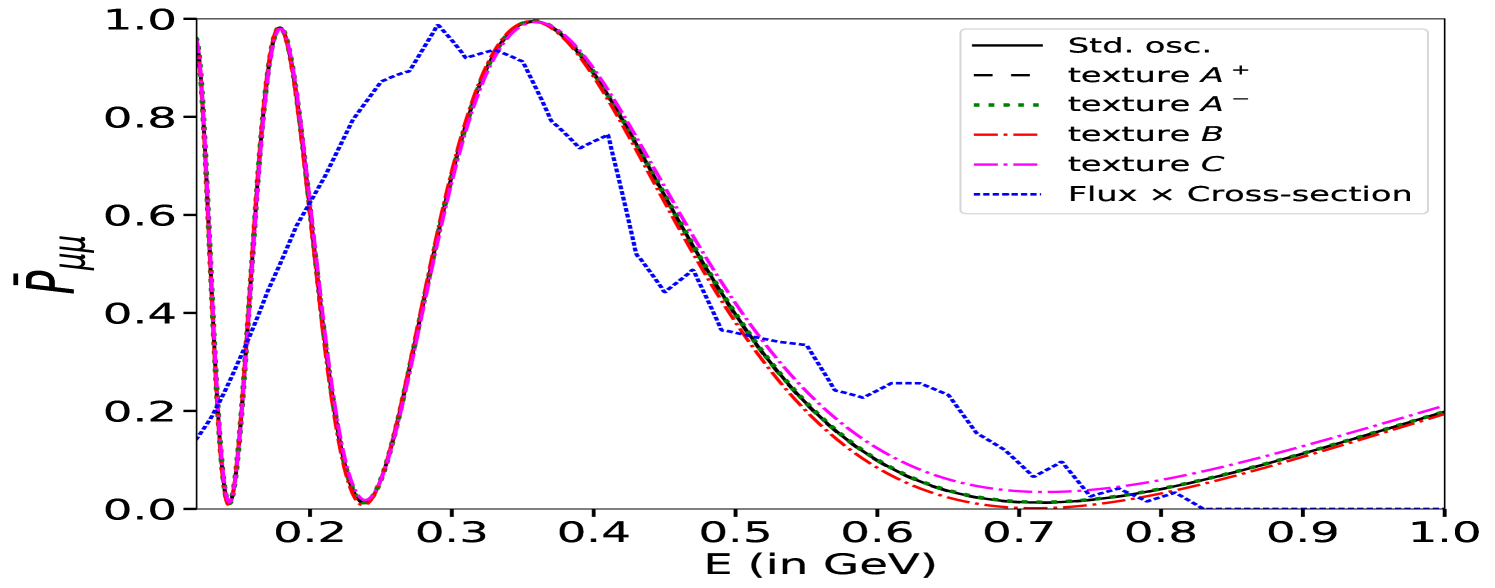
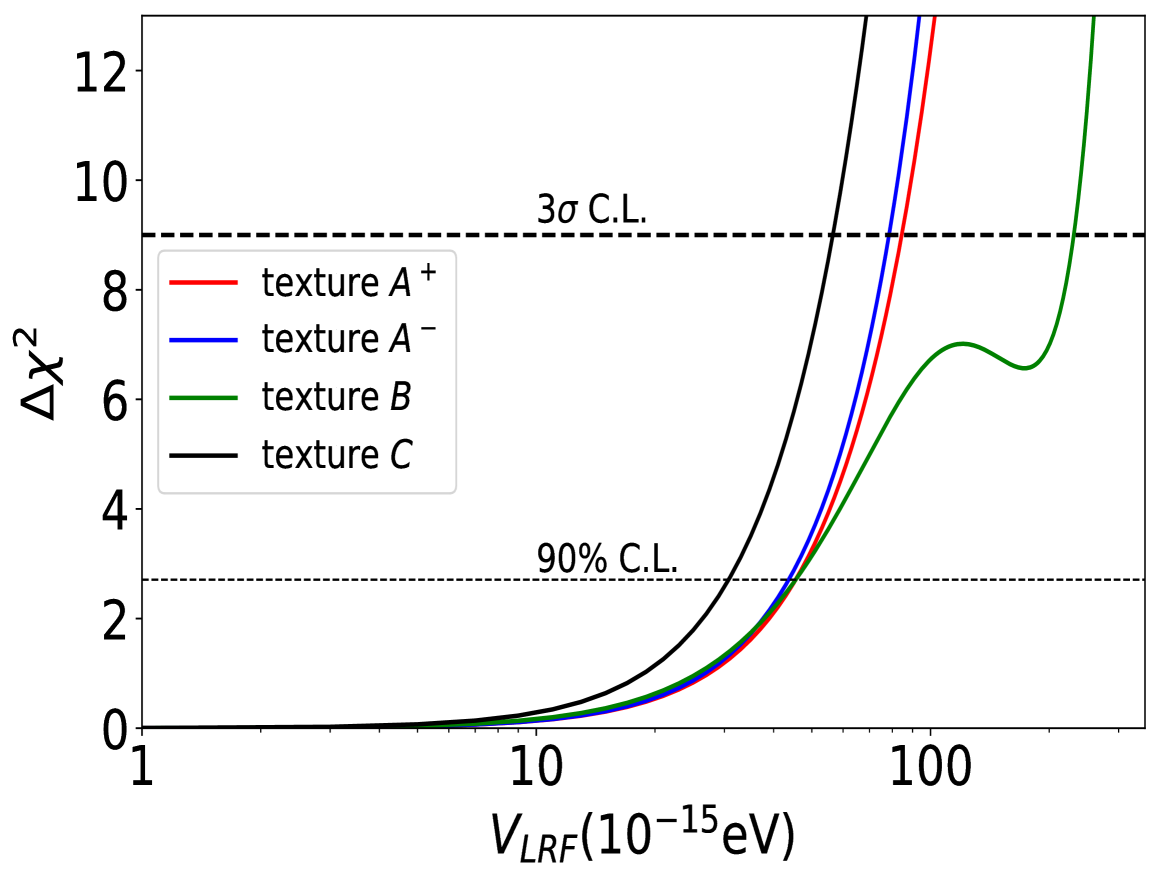
| LRF Potential Textures | C.L. eV | C.L. eV | symmetries from Ref. Agarwalla:2024ylc | ||||
| 8.45 | 4.55 |
|
|||||
| 7.85 | 4.37 |
|
|||||
| 23.09 | 4.55 |
|
|||||
| 5.65 | 3.08 |
|
References
- (1) Super-Kamiokande Collaboration, Y. Fukuda et al., Evidence for oscillation of atmospheric neutrinos, Phys. Rev. Lett. 81 (1998) 1562–1567, [hep-ex/9807003].
- (2) SNO Collaboration, Q. R. Ahmad et al., Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory, Phys. Rev. Lett. 89 (2002) 011301, [nucl-ex/0204008].
- (3) T. Kajita, Nobel Lecture: Discovery of atmospheric neutrino oscillations, Rev. Mod. Phys. 88 (2016) 030501.
- (4) A. B. McDonald, Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos, Rev. Mod. Phys. 88 (2016) 030502.
- (5) L. Wolfenstein, Neutrino Oscillations in Matter, Phys. Rev. D 17 (1978) 2369–2374.
- (6) J. Kopp, M. Lindner, T. Ota, and J. Sato, Non-standard neutrino interactions in reactor and superbeam experiments, Phys. Rev. D 77 (2008) 013007, [arXiv:0708.0152].
- (7) Y. Du, H.-L. Li, J. Tang, S. Vihonen, and J.-H. Yu, Non-standard interactions in SMEFT confronted with terrestrial neutrino experiments, JHEP 03 (2021) 019, [arXiv:2011.14292].
- (8) A. Gupta, D. Majumdar, and S. Prakash, Neutrino oscillation measurements with KamLAND and JUNO in the presence of scalar NSI, arXiv:2306.07343.
- (9) ESSnuSB Collaboration, J. Aguilar et al., Study of nonstandard interactions mediated by a scalar field at the ESSnuSB experiment, Phys. Rev. D 109 (2024), no. 11 115010, [arXiv:2310.10749].
- (10) P. B. Denton, A. Giarnetti, and D. Meloni, Solar neutrinos and the strongest oscillation constraints on scalar NSI, JHEP 01 (2025) 097, [arXiv:2409.15411].
- (11) T. Ohlsson, Status of non-standard neutrino interactions, Rept. Prog. Phys. 76 (2013) 044201, [arXiv:1209.2710].
- (12) O. G. Miranda and H. Nunokawa, Non standard neutrino interactions: current status and future prospects, New J. Phys. 17 (2015), no. 9 095002, [arXiv:1505.06254].
- (13) Y. Farzan and M. Tortola, Neutrino oscillations and Non-Standard Interactions, Front. in Phys. 6 (2018) 10, [arXiv:1710.09360].
- (14) P. S. Bhupal Dev et al., Neutrino Non-Standard Interactions: A Status Report, SciPost Phys. Proc. 2 (2019) 001, [arXiv:1907.00991].
- (15) K. Huitu, T. J. Kärkkäinen, J. Maalampi, and S. Vihonen, Constraining the nonstandard interaction parameters in long baseline neutrino experiments, Phys. Rev. D 93 (2016), no. 5 053016, [arXiv:1601.07730].
- (16) M. E. Chaves, P. C. de Holanda, and O. L. G. Peres, Testing non-standard neutrino interactions in (anti)-electron neutrino disappearance experiments, JHEP 03 (2023) 180, [arXiv:2106.15725].
- (17) X. G. He, G. C. Joshi, H. Lew, and R. R. Volkas, NEW Z-prime PHENOMENOLOGY, Phys. Rev. D 43 (1991) 22–24.
- (18) R. Foot, New Physics From Electric Charge Quantization?, Mod. Phys. Lett. A 6 (1991) 527–530.
- (19) X.-G. He, G. C. Joshi, H. Lew, and R. R. Volkas, Simplest Z-prime model, Phys. Rev. D 44 (1991) 2118–2132.
- (20) R. Foot, X. G. He, H. Lew, and R. R. Volkas, Model for a light Z-prime boson, Phys. Rev. D 50 (1994) 4571–4580, [hep-ph/9401250].
- (21) A. D. Dolgov, Long range forces in the universe, Phys. Rept. 320 (1999) 1–15.
- (22) A. Y. Smirnov and X.-J. Xu, Wolfenstein potentials for neutrinos induced by ultra-light mediators, JHEP 12 (2019) 046, [arXiv:1909.07505].
- (23) B. Pontecorvo, Neutrino Experiments and the Problem of Conservation of Leptonic Charge, Zh. Eksp. Teor. Fiz. 53 (1967) 1717–1725.
- (24) V. N. Gribov and B. Pontecorvo, Neutrino astronomy and lepton charge, Phys. Lett. B 28 (1969) 493.
- (25) V. Cirigliano, B. Grinstein, G. Isidori, and M. B. Wise, Minimal flavor violation in the lepton sector, Nucl. Phys. B 728 (2005) 121–134, [hep-ph/0507001].
- (26) G. Altarelli and F. Feruglio, Discrete Flavor Symmetries and Models of Neutrino Mixing, Rev. Mod. Phys. 82 (2010) 2701–2729, [arXiv:1002.0211].
- (27) K. Asai, K. Hamaguchi, and N. Nagata, Predictions for the neutrino parameters in the minimal gauged U(1) model, Eur. Phys. J. C 77 (2017) 763, [arXiv:1705.00419].
- (28) K. Asai, K. Hamaguchi, N. Nagata, S.-Y. Tseng, and K. Tsumura, Minimal Gauged U(1) Models Driven into a Corner, Phys. Rev. D 99 (2019) 055029, [arXiv:1811.07571].
- (29) Y. Lou and T. Nomura, Neutrino observables in gauged models with two Higgs doublet and one singlet scalars, arXiv:2406.01030.
- (30) J. A. Grifols and E. Masso, Neutrino oscillations in the sun probe long range leptonic forces, Phys. Lett. B 579 (2004) 123–126, [hep-ph/0311141].
- (31) A. Bandyopadhyay, A. Dighe, and A. S. Joshipura, Constraints on flavor-dependent long range forces from solar neutrinos and KamLAND, Phys. Rev. D 75 (2007) 093005, [hep-ph/0610263].
- (32) M. C. Gonzalez-Garcia, P. C. de Holanda, E. Masso, and R. Zukanovich Funchal, Probing long-range leptonic forces with solar and reactor neutrinos, JCAP 01 (2007) 005, [hep-ph/0609094].
- (33) A. S. Joshipura and S. Mohanty, Constraints on flavor dependent long range forces from atmospheric neutrino observations at super-Kamiokande, Phys. Lett. B 584 (2004) 103–108, [hep-ph/0310210].
- (34) M. Bustamante and S. K. Agarwalla, Universe’s Worth of Electrons to Probe Long-Range Interactions of High-Energy Astrophysical Neutrinos, Phys. Rev. Lett. 122 (2019) 061103, [arXiv:1808.02042].
- (35) S. K. Agarwalla, M. Bustamante, S. Das, and A. Narang, Present and future constraints on flavor-dependent long-range interactions of high-energy astrophysical neutrinos, JHEP 08 (2023) 113, [arXiv:2305.03675].
- (36) P. Coloma, M. C. Gonzalez-Garcia, and M. Maltoni, Neutrino oscillation constraints on U(1)’ models: from non-standard interactions to long-range forces, JHEP 01 (2021) 114, [arXiv:2009.14220]. [Erratum: JHEP 11 (2022) 115].
- (37) S. S. Chatterjee, A. Dasgupta, and S. K. Agarwalla, Exploring Flavor-Dependent Long-Range Forces in Long-Baseline Neutrino Oscillation Experiments, JHEP 12 (2015) 167, [arXiv:1509.03517].
- (38) A. Khatun, T. Thakore, and S. Kumar Agarwalla, Can INO be Sensitive to Flavor-Dependent Long-Range Forces?, JHEP 04 (2018) 023, [arXiv:1801.00949].
- (39) M. Singh, M. Bustamante, and S. K. Agarwalla, Flavor-dependent long-range neutrino interactions in DUNE & T2HK: alone they constrain, together they discover, JHEP 08 (2023) 101, [arXiv:2305.05184].
- (40) P. Mishra, R. Majhi, S. K. Pusty, M. Ghosh, and R. Mohanta, Study of long range force in P2SO and T2HKK, JHEP 09 (2024) 100, [arXiv:2402.19178].
- (41) T2K Collaboration, K. Abe et al., Combined Analysis of Neutrino and Antineutrino Oscillations at T2K, Phys. Rev. Lett. 118 (2017) 151801, [arXiv:1701.00432].
- (42) T2K Collaboration, K. Abe et al., Constraint on the matter–antimatter symmetry-violating phase in neutrino oscillations, Nature 580 (2020) 339–344, [arXiv:1910.03887]. [Erratum: Nature 583 (2020) E16].
- (43) NOvA Collaboration, M. A. Acero et al., First Measurement of Neutrino Oscillation Parameters using Neutrinos and Antineutrinos by NOvA, Phys. Rev. Lett. 123 (2019), no. 15 151803, [arXiv:1906.04907].
- (44) DUNE Collaboration, B. Abi et al., Long-baseline neutrino oscillation physics potential of the DUNE experiment, Eur. Phys. J. C 80 (2020) 978, [arXiv:2006.16043].
- (45) ESSnuSB Collaboration, A. Alekou et al., Updated physics performance of the ESSnuSB experiment: ESSnuSB collaboration, Eur. Phys. J. C 81 (2021) 1130, [arXiv:2107.07585].
- (46) H. Abele et al., Particle Physics at the European Spallation Source, Phys. Rept. 1023 (2023) 1–84, [arXiv:2211.10396].
- (47) A. Alekou et al., The European Spallation Source neutrino super-beam conceptual design report, Eur. Phys. J. ST 231 (2022) 3779–3955, [arXiv:2206.01208]. [Erratum: Eur. Phys. J. ST 232 (2023) 15–16].
- (48) ESSnuSB Collaboration, A. Alekou et al., The ESSnuSB Design Study: Overview and Future Prospects, Universe 9 (2023), no. 8 347, [arXiv:2303.17356].
- (49) ESSnuSB Collaboration, J. Aguilar et al., Search for Leptonic CP Violation with the ESSnuSBplus Project, LHEP 2024 (2024) 517.
- (50) S. K. Agarwalla, M. Bustamante, M. Singh, and P. Swain, A plethora of long-range neutrino interactions probed by DUNE and T2HK, JHEP 09 (2024) 055, [arXiv:2404.02775].
- (51) S. Choubey, S. Khan, M. Merchand, and S. Vihonen, Constraining dark matter from strong phase transitions in a model: implications for neutrino masses and muon g 2, JHEP 10 (2024) 186, [arXiv:2406.16460].
- (52) M. Ibe, S. Shirai, and K. Watanabe, Global Neutrino Constraints on the Minimal U(1) Model, arXiv:2503.01399.
- (53) K. S. Babu, C. F. Kolda, and J. March-Russell, Implications of generalized Z - Z-prime mixing, Phys. Rev. D 57 (1998) 6788–6792, [hep-ph/9710441].
- (54) A. S. Joshipura, N. Mahajan, and K. M. Patel, Generalised - symmetries and calculable gauge kinetic and mass mixing in models, JHEP 03 (2020) 001, [arXiv:1909.02331].
- (55) B. Holdom, Two U(1)’s and Epsilon Charge Shifts, Phys. Lett. B 166 (1986) 196–198.
- (56) A. Ghoshal, A. Giarnetti, and D. Meloni, Neutrino Invisible Decay at DUNE: a multi-channel analysis, J. Phys. G 48 (2021), no. 5 055004, [arXiv:2003.09012].
- (57) J. Gehrlein, P. A. N. Machado, and J. a. P. Pinheiro, Constraining non-standard neutrino interactions with neutral current events at long-baseline oscillation experiments, JHEP 05 (2025) 065, [arXiv:2412.08712].
- (58) P. B. Denton, A. Giarnetti, and D. Meloni, How to identify different new neutrino oscillation physics scenarios at DUNE, JHEP 02 (2023) 210, [arXiv:2210.00109].
- (59) S. K. Agarwalla, S. Das, A. Giarnetti, and D. Meloni, Model-independent constraints on non-unitary neutrino mixing from high-precision long-baseline experiments, JHEP 07 (2022) 121, [arXiv:2111.00329].
- (60) P. Coloma, D. V. Forero, and S. J. Parke, DUNE Sensitivities to the Mixing between Sterile and Tau Neutrinos, JHEP 07 (2018) 079, [arXiv:1707.05348].
- (61) A. Giarnetti and D. Meloni, New Sources of Leptonic CP Violation at the DUNE Neutrino Experiment, Universe 7 (2021), no. 7 240, [arXiv:2106.00030].
- (62) A. Giarnetti, S. Marciano, and D. Meloni, Exploring New Physics with Deep Underground Neutrino Experiment High-Energy Flux: The Case of Lorentz Invariance Violation, Large Extra Dimensions and Long-Range Forces, Universe 10 (2024) 357, [arXiv:2407.17247].
- (63) J. M. Berryman, A. de Gouvêa, K. J. Kelly, O. L. G. Peres, and Z. Tabrizi, Large, Extra Dimensions at the Deep Underground Neutrino Experiment, Phys. Rev. D 94 (2016), no. 3 033006, [arXiv:1603.00018].
- (64) M. B. Wise and Y. Zhang, Lepton Flavorful Fifth Force and Depth-dependent Neutrino Matter Interactions, JHEP 06 (2018) 053, [arXiv:1803.00591].
- (65) J. Heeck and W. Rodejohann, Gauged and different Muon Neutrino and Anti-Neutrino Oscillations: MINOS and beyond, J. Phys. G 38 (2011) 085005, [arXiv:1007.2655].
- (66) S. K. Agarwalla, S. Das, M. Masud, and P. Swain, Evolution of neutrino mass-mixing parameters in matter with non-standard interactions, JHEP 11 (2021) 094, [arXiv:2103.13431].
- (67) T. Kikuchi, H. Minakata, and S. Uchinami, Perturbation Theory of Neutrino Oscillation with Nonstandard Neutrino Interactions, JHEP 03 (2009) 114, [arXiv:0809.3312].
- (68) P. Huber, M. Lindner, and W. Winter, Simulation of long-baseline neutrino oscillation experiments with GLoBES (General Long Baseline Experiment Simulator), Comput. Phys. Commun. 167 (2005) 195, [hep-ph/0407333].
- (69) P. Huber, J. Kopp, M. Lindner, M. Rolinec, and W. Winter, New features in the simulation of neutrino oscillation experiments with GLoBES 3.0: General Long Baseline Experiment Simulator, Comput. Phys. Commun. 177 (2007) 432–438, [hep-ph/0701187].
- (70) ESSnuSB Collaboration, J. Aguilar et al., Decoherence in neutrino oscillation at the ESSnuSB experiment, JHEP 08 (2024) 063, [arXiv:2404.17559].
- (71) I. Esteban, M. C. Gonzalez-Garcia, M. Maltoni, T. Schwetz, and A. Zhou, The fate of hints: updated global analysis of three-flavor neutrino oscillations, JHEP 09 (2020) 178, [arXiv:2007.14792].
- (72) NuFIT 5.2, (2022), http://www.nu-fit.org/.
- (73) F. Capozzi, E. Di Valentino, E. Lisi, A. Marrone, A. Melchiorri, and A. Palazzo, Global constraints on absolute neutrino masses and their ordering, Phys. Rev. D 95 (2017) 096014, [arXiv:2003.08511]. [Addendum: Phys. Rev. D 101 (2020) 116013].
- (74) I. Esteban, M. C. Gonzalez-Garcia, A. Hernandez-Cabezudo, M. Maltoni, and T. Schwetz, Global analysis of three-flavour neutrino oscillations: synergies and tensions in the determination of , , and the mass ordering, JHEP 01 (2019) 106, [arXiv:1811.05487].
- (75) P. F. de Salas, D. V. Forero, S. Gariazzo, P. Martínez-Miravé, O. Mena, C. A. Ternes, M. Tórtola, and J. W. F. Valle, 2020 global reassessment of the neutrino oscillation picture, JHEP 02 (2021) 071, [arXiv:2006.11237].
- (76) F. Capozzi, E. Di Valentino, E. Lisi, A. Marrone, A. Melchiorri, and A. Palazzo, Unfinished fabric of the three neutrino paradigm, Phys. Rev. D 104 (2021) 083031, [arXiv:2107.00532].
- (77) M. C. Gonzalez-Garcia, M. Maltoni, and T. Schwetz, NuFIT: Three-Flavour Global Analyses of Neutrino Oscillation Experiments, Universe 7 (2021) 459, [arXiv:2111.03086].
- (78) J.-Q. Jiang, W. Giarè, S. Gariazzo, M. G. Dainotti, E. Di Valentino, O. Mena, D. Pedrotti, S. S. da Costa, and S. Vagnozzi, Neutrino cosmology after DESI: tightest mass upper limits, preference for the normal ordering, and tension with terrestrial observations, arXiv:2407.18047.
- (79) P. Huber, M. Lindner, and W. Winter, Superbeams versus neutrino factories, Nucl. Phys. B 645 (2002) 3–48, [hep-ph/0204352].
- (80) G. L. Fogli, E. Lisi, A. Marrone, D. Montanino, and A. Palazzo, Getting the most from the statistical analysis of solar neutrino oscillations, Phys. Rev. D 66 (2002) 053010, [hep-ph/0206162].
- (81) S. S. Wilks, The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses, Annals Math. Statist. 9 (1938), no. 1 60–62.
- (82) W. Dehnen and J. Binney, Mass models of the Milky Way, Mon. Not. Roy. Astron. Soc. 294 (1998) 429, [astro-ph/9612059].
- (83) M. J. Miller and J. N. Bregman, The Structure of the Milky Way’s Hot Gas Halo, Astrophys. J. 770 (2013) 118, [arXiv:1305.2430].
- (84) M. Baryakhtar, R. Lasenby, and M. Teo, Black Hole Superradiance Signatures of Ultralight Vectors, Phys. Rev. D 96 (2017) 035019, [arXiv:1704.05081].
- (85) N. Arkani-Hamed, L. Motl, A. Nicolis, and C. Vafa, The String landscape, black holes and gravity as the weakest force, JHEP 06 (2007) 060, [hep-th/0601001].
- (86) S. K. Agarwalla, S. Das, A. Giarnetti, D. Meloni, and M. Singh, Enhancing sensitivity to leptonic CP violation using complementarity among DUNE, T2HK, and T2HKK, Eur. Phys. J. C 83 (2023) 694, [arXiv:2211.10620].
- (87) H. Davoudiasl, H.-S. Lee, and W. J. Marciano, Long-Range Lepton Flavor Interactions and Neutrino Oscillations, Phys. Rev. D 84 (2011) 013009, [arXiv:1102.5352].
- (88) T. Araki, J. Heeck, and J. Kubo, Vanishing Minors in the Neutrino Mass Matrix from Abelian Gauge Symmetries, JHEP 07 (2012) 083, [arXiv:1203.4951].
- (89) L. M. G. de la Vega, L. J. Flores, N. Nath, and E. Peinado, Complementarity between dark matter direct searches and CENS experiments in U(1)’ models, JHEP 09 (2021) 146, [arXiv:2107.04037].
- (90) Y. Farzan and J. Heeck, Neutrinophilic nonstandard interactions, Phys. Rev. D 94 (2016) 053010, [arXiv:1607.07616].
- (91) Y. Almumin, M.-C. Chen, M. Cheng, V. Knapp-Perez, Y. Li, A. Mondol, S. Ramos-Sanchez, M. Ratz, and S. Shukla, Neutrino Flavor Model Building and the Origins of Flavor and CP Violation, Universe 9 (2023) 512, [arXiv:2204.08668].