Progress in Solar Cycle Predictions: Sunspot Cycles 24–25 in Perspective

Dibyendu Nandy Center of Excellence in Space Sciences India, Indian Institute of Science Education and Research Kolkata, Mohanpur 741246, West Bengal, India Department of Physical Sciences, Indian Institute of Science Education and Research Kolkata, Mohanpur 741246, West Bengal, India

keywords:

Solar Activity; Sunspots; Solar Cycle Prediction; Magnetohydrodynamics; Solar Dynamo

\setlastpage\inarticletrue

{opening}

1 The Case for Solar Cycle Predictions

The space environment in the solar system is governed by the variable activity of the Sun. This variability is manifested in changing flux of solar radiation, solar energetic particles, solar magnetic fields and a variable solar wind output. Occasionally, energetic events such as flares and coronal mass ejections (CMEs) introduce extreme perturbations in our space environment. These phenomena are collectively referred to as space weather. Severe space weather can impact the health of satellites and astronauts in outer space, disrupt satellite-based communications and navigational networks, high frequency radio communications, electric power grids, oil pipelines and air-traffic on polar routes. Understanding, assessing and predicting space weather is therefore critical to protection of modern day technologies and is considered a high priority research area (National Research Council, 1997, 2013; National Science and Technology Council, 2019; Krausmann et al., 2016; UNOOSA Space Weather, 2017; Schrijver et al., 2015).

Slower, longer term modulation in the solar activity output over time scales ranging from decades to centuries to millennia (Solanki et al., 2004; Usoskin, 2017) define what is known as space climate (Versteegh, 2005). Space climate plays a role in the forcing of planetary atmospheres, e.g., in the heating of the upper atmosphere and its expansion which is relevant for satellite drag and mission life-time estimates. While magnetically modulated variations in the solar irradiance provide a link to planetary climate systems (Solanki and Krivova, 2003), solar open flux variations determine the flux of galactic cosmic rays at Earth (Usoskin et al., 2002). Secular variations in the Sun, solar wind and interplanetary magnetic flux also impacts planetary magnetospheres with consequences for geomagnetic activity (Mursula, Zieger, and Vilppola, 2003) and atmospheric evolution (Das et al., 2019). Indeed, the intimate relationship between solar-stellar activity and the planets that they host can extend over their coupled lifetimes and is based on causal connections between physical processes in stellar interiors and planetary atmospheres (Nandy and Martens, 2007).

Stripped bare to its roots, space weather and space climate are fundamentally products of the solar magnetic cycle and its diverse manifestations – which are consequences of the emergence, evolution and dynamics of solar magnetic fields or sunspots and their impact on the heliospheric environment. Thus, the quest to assess and forecast our space environment in intimately related to, and contingent upon understanding the physics of the solar magnetic cycle, and develop predictive capabilities based on this understanding.

Solar magnetic fields are generated by a magnetohydrodynamic (MHD) dynamo mechanism that is sustained by complex interactions between plasma flows and magnetic fields in the Sun’s convection zone (Parker, 1955a; Babcock, 1961; Leighton, 1969; Charbonneau, 2020). The toroidal component of the dynamo generated magnetic field buoyantly emerges through the solar surface creating sunspots – strongly magnetized, and relatively darker regions on the solar surface. Sunspots have been monitored for over four centuries starting with the pioneering observations of Galileo Galilei. Their magnetic nature was discovered in the early $20^{th}$ century (Hale, 1908). Development of the magnetograph instrument (Babcock and Babcock, 1955) allowed observations of the large-scale (relatively weaker) magnetic field that exists outside of sunspots and which plays a crucial role in the build up of the polar flux leading to the reversal of the global dipolar field (i.e., the poloidal component of the dynamo generated magnetic field).

These long term observations illuminate various facets of the sunspot cycle on the one hand (Hathaway, 2015) and on the other hand, provide important constraints on the solar dynamo mechanism (Nandy and Choudhuri, 2002) and motivate various approaches for solar cycle predictions (Petrovay, 2020).

2 Sunspot Cycle Observations: The Prediction Challenge

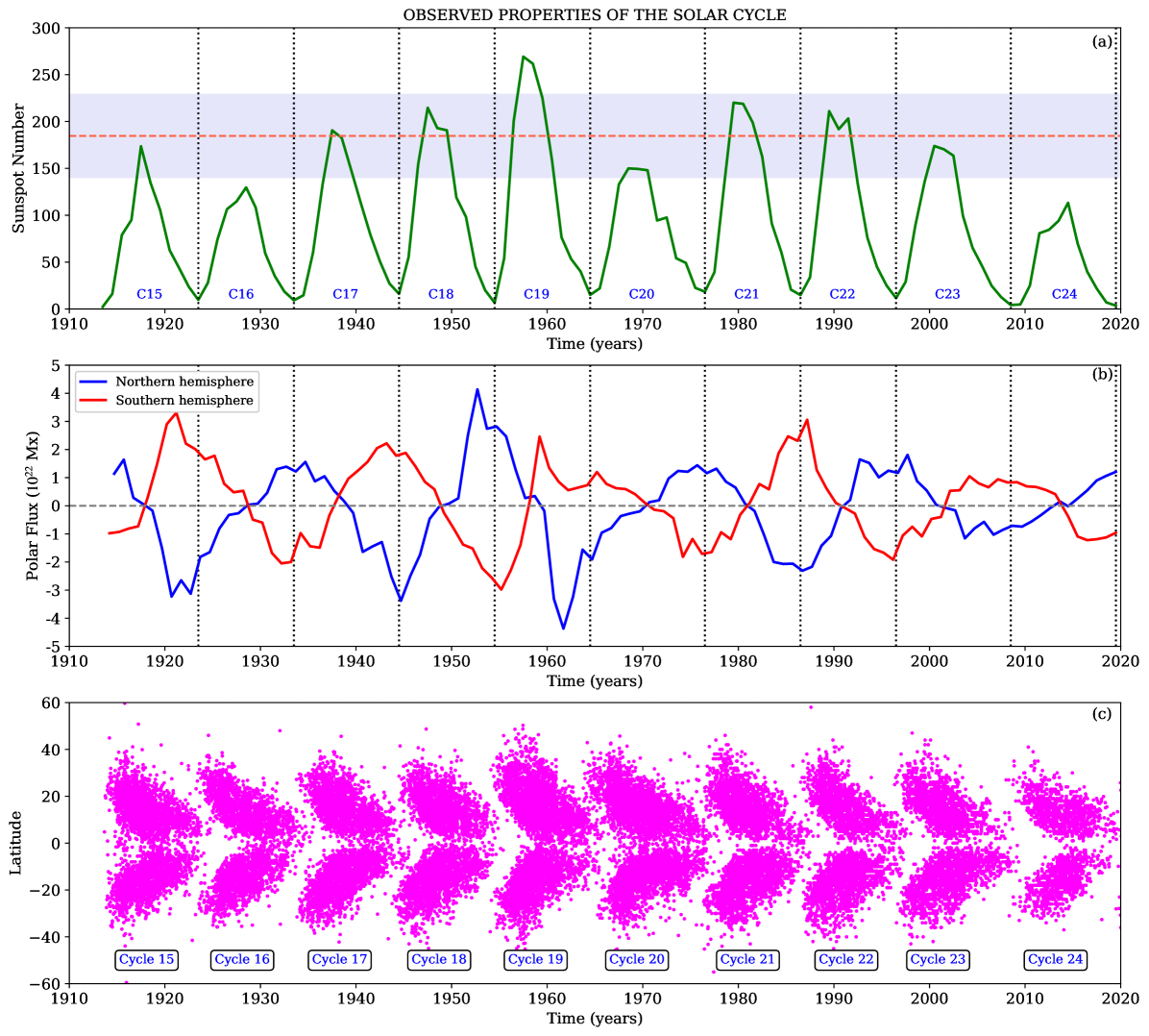
Long term observations indicate that the number of sunspots on the solar surface (which is a proxy for the toroidal component of the solar magnetic field) increases and decreases in a cyclic fashion with an average periodicity of 11 years. Barring episodes of grand minima in activity, e.g., the Maunder minimum, this trend has been maintained over the last four centuries. In Figure \ireffig:1 we present an overview of solar cycle observations over the last 100 years and establish century-scale solar cycle climatological trends of relevance to cycle predictions. Figure \ireffig:1a presents the (revised) sunspot number time series covering cycles 15–24. It is evident that while the solar cycle period varies only slightly from cycle to cycle, there is significant variability in its amplitude – quantified by the (annual averaged) peak sunspot number. From these observations we establish a century-scale mean sunspot cycle amplitude 184.630 $\pm$ 44.282 ( $\sigma$ , i.e., standard deviation). The climatological mean is indicated by the red-dashed line, while the range (mean $\pm$ 1 $\sigma$ ) is indicated by the shaded region in Figure \ireffig:1a. We define cycles whose peak lies within the shaded region (mean $\pm$ 1 $\sigma$ ) as moderate solar cycles; cycles which lie within this region but are higher than the mean may be further sub-classified in to moderate-strong cycles and which lie below the mean may be sub-classified in to moderate-weak cycles. Extreme solar cycles which lie over this region (greater than mean $+$ 1 $\sigma$ ) are classified as strong cycles and cycles which lie below this range (mean $-$ 1 $\sigma$ ) are classified as weak cycles. We note that only one cycle (19) has been extremely strong, while two cycles (16 and 24) have been extremely weak. In fact the recently concluded solar cycle 24 has been the weakest cycle of the past century. There is no discernible pattern in amplitude variability from one cycle to another in the sunspot time series which makes their prediction a challenging task.

The variation of the Sun’s polar flux, which is a proxy for the poloidal component of the solar magnetic cycle, is depicted in Figure \ireffig:1b. The (radial) polar flux in the solar north and south poles are found to be opposite to each other indicative of a global dipole field configuration near solar minima. The polar fields also undergo cyclic reversals. They are the weakest and reverse their sign (polarity) during sunspot maxima and they are the strongest during sunspot cycle minima; the polar field lags the sunspot cycle (i.e., the toroidal field component) with a phase difference of $90^{\circ}$ . In fact, although not evident here, the relative orientation of bipolar sunspot pairs reverse orientation from one cycle to another, indicating that the toroidal component of the solar magnetic field also reverses from one sunspot cycle to another.

A pattern emerges when one compares the amplitude of the polar field (Figure \ireffig:1b) at sunspot cycle minima with the strength of the following sunspot cycle (Figure \ireffig:1a). A stronger polar field at solar minimum is indicative of a stronger (upcoming) sunspot cycle. There is a causal basis for this connection, as the solar polar field acts as the seed which is further amplified by the Sun’s differential rotation to produce the next sunspot cycle. This causal connection is the basis of one of the more successful empirical prediction techniques – the precursor method.

Figure \ireffig:1c depicts the solar butterfly diagram, which indicates that there is also a spatio-temporal pattern in the sunspot cycle. Cycles begin with sunspots appearing at mid-latitudes, with more and more spots appearing at lower and lower latitudes as the cycle progresses. This pattern is followed in both the hemispheres with the cycle eventually ending with sunspots appearing only close to the equator. This pattern repeats from one cycle to another.

Ideally, one would expect that advances in understanding the solar dynamo mechanism and advances in methodologies for accurate solar cycle predictions would be commensurate with each other. This expectation would imply that attempts at solar cycle predictions must also imbibe many of the constraints available from solar cycle observations, and be able to explain most, if not all, features of the spatio-temporal variability in the sunspot cycle. This is the rather restrictive view that is taken in categorizing physics- or model-based predictions in this review with the additional consideration that this class of predictions must also be based on MHD models of solar magnetic field evolution. Nevertheless, several other techniques – ranging from some which have no connection with the underlying physics whatsoever to some which draw inspiration from the underlying physics – have been utilized for forecasting the solar cycle. In the next section we revisit such predictions for solar cycle 24 and summarize predictions made until now for solar cycle 25. These predictions are further analyzed and compared to ascertain any apparent progress over the last decade in efforts at predicting the sunspot cycle.

3 Predictions of Solar Cycle 24

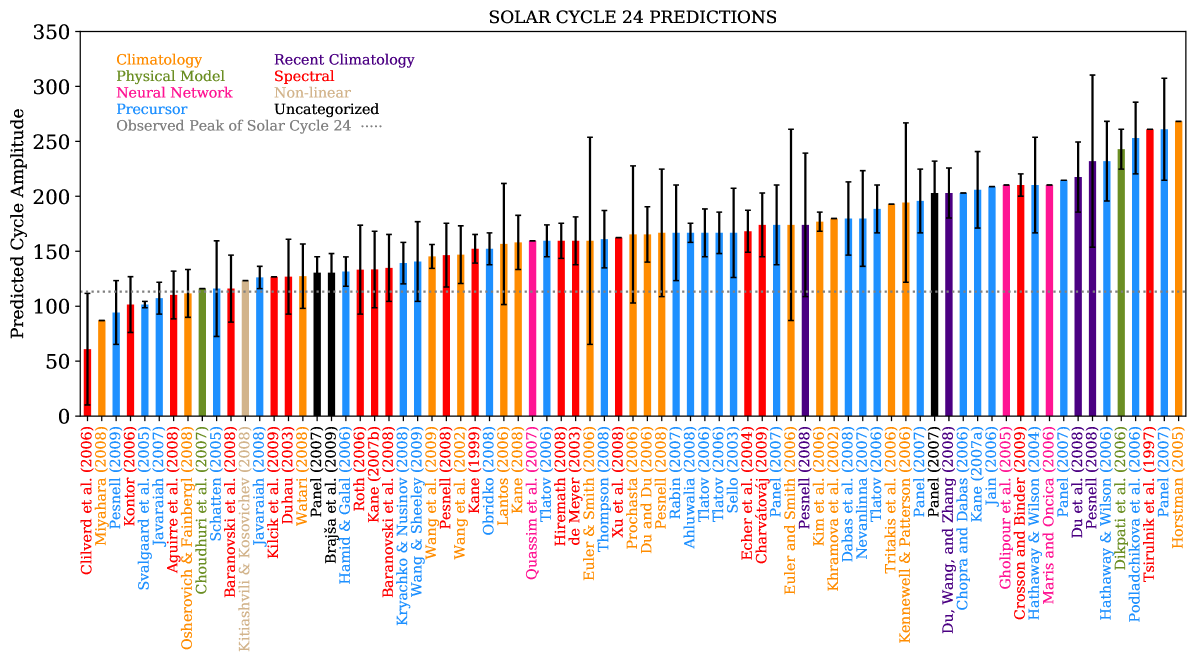
Solar cycle 24 commenced following a series of sequentially weaker solar cycles and an unusually extended minimum of sunspot cycle 23 (Nandy, Muñoz-Jaramillo, and Martens, 2011). Multiple predictions were made for solar cycle 24. Following (Pesnell, 2008, 2012a) in Figure \ireffig:2, we summarize the predictions of cycle 24. In this figure, predictions have been categorized based on the underlying methodology utilized for making the forecast for the peak cycle amplitude. Note that the numbers for the predicted cycle amplitude in Figure 2 have been scaled to conform to the new, revised sunspot time series (Clette et al., 2015) for ease of comparative analysis (and thus numbers are different from those in (Pesnell, 2008, 2012a). The observed peak amplitude of solar cycle 24 is depicted in Figure \ireffig:2 with a gray-dashed line.

An analysis of solar cycle 24 predictions in Figure \ireffig:2 reveal that a majority of the forecasts predicted a much higher cycle than what was observed. The mean ( $\pm$ $1\sigma$ ) of all the cycle 24 predictions is 165.390 $\pm$ 42.762 in units of sunspot number (SSN). The observed peak (113.3 SSN) was outside the range of these predictions! Clearly, there was no convergence in predictions utilizing the diverse techniques.

Evidently, there is no physical meaning in arriving at a mean or an average forecast) from such diverging predictions employing unrelated and disparate techniques; any solar cycle prediction panel should keep this in mind. Nonetheless, as we shall see, the mean and standard deviation of different cycle predictions across different cycles may provide a purely pragmatic method to assess relative consensus among techniques.

The two physical (dynamo) model based predictions by Dikpati, de Toma, and Gilman (2006) and Choudhuri, Chatterjee, and Jiang (2007) predicted very strong and very weak cycles, respectively. Although the latter prediction for a weak cycle turned out to match observations, it was not immediately obvious why, and the non-convergence in physics-based forecasts led to massive heartburn and controversies that shook the field. To make matters worse – if that were possible – the NOAA-NASA Solar Cycle Prediction Panel made an early declaration of a strong cycle and subsequently had to revise the forecast to a weak cycle after the cycle had already started! Perhaps the early panel statement was motivated from the perspective of achieving a consensus based on the many strong-cycle-forecasts and it may have been particularly influenced by the Dikpati, de Toma, and Gilman (2006) prediction.

It is natural that anyone looking at the “confusogram” of forecasts for solar cycle 24, their non-convergence and disagreement with the eventually observed cycle 24 peak would conclude that the understanding of solar cycle predictability was at a very immature stage at this juncture. In hindsight of solar cycle 24 and now armed with recent predictions for sunspot cycle 25 at the intervening cycle minimum, one is tempted to pose the question, are we any better off a decade down the line one solar minimum later? To assess the current scenario, we present predictions for solar cycle 25 in the next section and analyze them.

4 Predictions of Solar Cycle 25

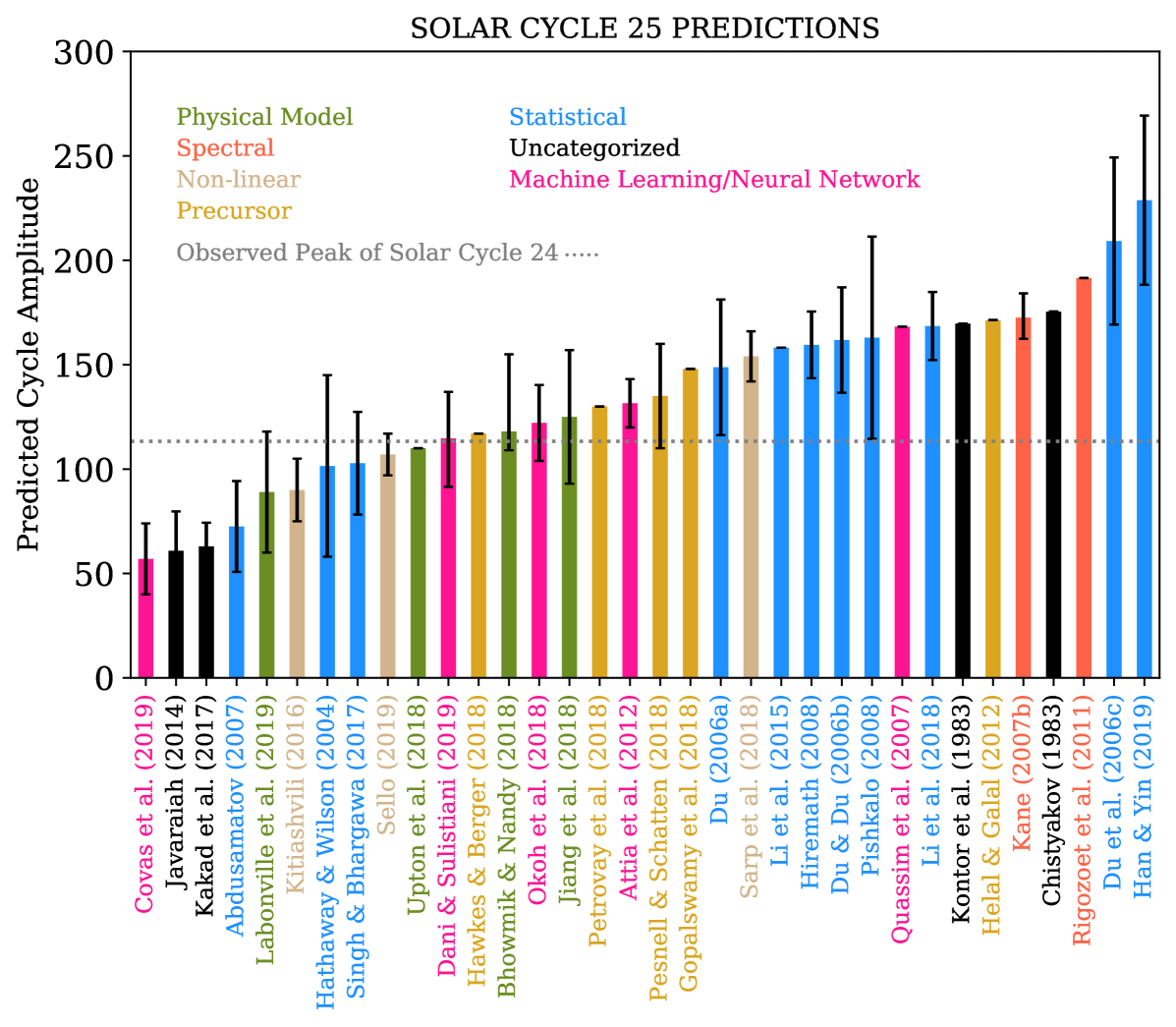
In Figure \ireffig:3 we present predictions of the peak amplitude of sunspot cycle 25 from various groups using a diversity of techniques. For predictions made before the year 2016, we have scaled the predicted amplitude to conform to the revised sunspot time series but have left the numbers unchanged for predictions published in the year 2016 or thereafter; i.e., we have assumed that predictions published in the year 2016 and thereafter have been calibrated with the new sunspot time series released in 2015 (Clette et al., 2015). First, we categorize solar cycle 25 predictions based on the utilized methodology and provide a brief narrative summary of each of the predictions.

4.1 Physical Model Based Forecasts

i)

Bhowmik and Nandy (2018) utilized a observational data assimilated, century-scale calibrated SFT model whose output was coupled to a solar internal dynamo model to predict that sunspot cycle 25 would be similar or slightly stronger than solar cycle 24 with a peak SSN of 118 and a range from 109 - 155. They also predicted that the peak of solar cycle 25 would occur in 2025 ( $\pm$ 1 year).
ii)

Jiang et al. (2018) predicted solar cycle 25 utilizing a solar Surface Flux Transport (SFT) model. They used the correlation between the axial dipole moment at cycle minimum and the subsequent cycle strength and the other empirical properties of solar cycles to predict the possible behaviours of the succeeding cycle. Their predicted peak SSN is 125 $\pm$ 32.
iii)

Upton and Hathaway (2018) used their Advective Flux Transport (AFT) model and the empirical (precursor) relationship between the polar field and the subsequent cycle amplitude to predict the SSN. According to them solar cycle 25 would be slightly weaker than solar cycle 24. They have predicted a maximum sunspot number (SSN) of 110.
iv)

Labonville, Charbonneau, and Lemerle (2019) used a data-driven hybrid 2 $\times$ 2D flux transport dynamo (FTD) model to forecast properties of the upcoming sunspot Cycle 25. They predicted that the maximum sunspot number SSN for solar cycle 25 would be between $89-14$ to $89+29$ . The peak is predicted to occur between 2025.3+0.89 to 2025.3-1.05.

4.2 Precursor Technique Based Forecasts

i)

Helal and Galal (2013) used a solar activity precursor technique of spotless events to predict maximum SSN of solar cycle 25 which would be 118.2. According to this study the upcoming cycle will peak between 2022-2023.
ii)

Pesnell and Schatten (2018) utilized Solar Dynamo (SODA) index that combines values of the solar polar magnetic field and the solar spectral irradiance at 10.7 cm to create a precursor of future solar activity. They predict a maximum SSN of 135 $\pm$ 25 occurring in 2025.2 $\pm$ 1.5.
iii)

Hawkes and Berger (2018) calculated the helicity flux through both the hemispheres using a model that takes account of the Omega effect, using the magnetic field data from Wilcox Solar Observatory (WSO) covering a total of 60 years. Using various correlation analysis between helicity flux and the sunspot time series they predict the amplitude of solar cycle 25 to be 117 which is slightly higher than that of cycle 24.
iv)

Petrovay et al. (2018) used Rush To The Poles phenomenon (RTTP) in coronal green line emission to predict the peak SSN for solar cycle 25. Based on the correlation between the rate of the RTTP and the time delay until the maximum of the next solar cycle and the known internal regularities of the sunspot number series, they predicted that the peak amplitude to be 130 occurring in late 2024.
v)

Gopalswamy et al. (2018) used the polar and low-latitude brightness temperatures as proxies for the polar magnetic field to predict cycle 25. The polar microwave brightness temperature is found to be correlated with the polar magnetic field strength and the fast solar wind speed. These correlations are used to predict a maximum SSN of 89 in the south and 59 in in the northern hemisphere (unsmoothed SSN), 116 in South and 97 in north (smoothed SSN).

4.3 Non-linear Model Based Forecasts

i)

Sarp et al. (2018) implemented a non-linear prediction algorithm based on delay-time and phase space reconstruction to forecast a maximum SSN of 154 $\pm$ 12 occurring in 2023.2 $\pm$ 1.1.
ii)

Sello (2019) used revised Non Linear Dynamics methods to predict the maximum SSN for solar cycle 25 to be 107 $\pm$ 10 occurring in July 2023 $\pm$ 1 year.
iii)

Kitiashvili (2016) applied an ensemble Kalman filter method to predict solar cycles using a low-order, nonlinear dynamo model. They used data assimilation approach to predict a maximum SSN of 90 $\pm$ 15 occurring in 2024 $\pm$ 1 year.

4.4 Statistical Forecasts

i)

Li, Feng, and Li (2015) found that the ascent duration (AD) of a solar cycle is statistically related to the descent duration (DD) of the Cycle. Statistical relations among feature parameters of the solar cycle are used to predict the behaviour of solar cycle 25. The maximum SSN is predicted to be 109.1 occurring around October 2023.
ii)

Pishkalo (2008) used the correlation between cycle parameters to predict SSN for solar cycle 25. According to this study the peak SSN would occur on 2023.4 $\pm$ 0.7 with an amplitude of 112.37 $\pm$ 33.4.
iii)

Li et al. (2018) utilised relations among the feature parameters of solar cycles under the bimodal distribution for the modern era cycles (10–23). These relations are utilized to predict that the solar cycle 25 would initiate in October 2020 and reach its maximum amplitude of 168.5 $\pm$ 16.3 in October 2024.
iv)

Singh and Bhargawa (2017) performed a statistical test for persistence of solar activity based on the value of Hurst exponent (H). They predict that the maximum SSN would occur on June 2024 with a value of 102.8 $\pm$ 24.6.
v)

Han and Yin (2019) implemented Vondrak smoothing method to produce a series of smoothed SSN (denoted SSN-VS) – which closely mimics the 13-month running mean SSN. Applying these techniques to the descending phase of cycle 24 they make predictions for cycle 25 whose peak is estimated to be 228.8 $\pm$ 40.5 occurring in 2023.918 $\pm$ 1.64 year.
vi)

Du (2006a) used the maximum–maximum cycle length as one of the indicators to predict the amplitude of solar cycle 25. This study found that the maximum SSN amplitude will be 102.6 $\pm$ 22.4.
vii)

Du and Du (2006b), based on their analysis, claims that the amplitude of a solar activity cycle is correlated with the descending time of the [ $n-3$ ] cycle. Based on this correlation they predict a peak SSN of 111.6 $\pm$ 17.4.
viii)

Hiremath (2008) modeled solar cycles considering a forced and damped harmonic oscillator. They obtain long-term amplitudes, frequencies, phases and decay factors from 22 cycles (1755–1996). Using these parameters and employing a autoregressive model they predict a maximum SSN of 110 $\pm$ 11 occurring in 2023.
ix)

Du, Wang, and He (2006c) claim that the maximum amplitude of solar activity cycles are anti-correlated with the newly defined solar cycle lengths three cycles before. They use this correlation to predict a peak SSN of 144.3 $\pm$ 27.6.
x)

Abdusamatov (2007) analyzed the long-term cyclic variations of solar activity, radius, and solar constant claiming them to be correlated in both phase and amplitude. Based on this they predict a very low cycle 25 peak of 50 $\pm$ 15.

4.5 Spectral Methods Based Forecasts

i)

Kane (2007b) used spectral analysis of the sunspot time series to detect periodicities by the maximum entropy method (MEM). The periodicities obtained are further utilized in a multiple regression analysis (MRA) to estimate the amplitude of cycle 25 to be between 112-127 with a mean value 119 occurring around 2022-2023.
ii)

Rigozo et al. (2011) decomposed monthly sunspot number data during the 1850-2007 interval (solar cycles 9–23) into several levels and searched for periodicities by iterative regression at each level. Their prediction is based on extrapolation of SSN time series spectral components. They estimate a maximum SSN of 132.1 occurring in April 2023.

4.6 Machine Learning and Neural Network Based Forecasts

i)

Dani and Sulistiani (2019) used machine learning method of Linear Regression (LR), Random Forest (RF), Radial Basis Function (RBF) and Support Vector Machine (SVM) to predict the peak SSN for solar cycle 25. Predicted peak amplitudes are 159.4 $\pm$ 22.3, 110.2 $\pm$ 12.8, 95.5 $\pm$ 21.9 and 93.7 $\pm$ 23.2 occurring in September 2023, December 2024, December 2024 and July 2024, respectively. The predicted peak values are $114.7-23.2$ and $114.7+22.3$ .
ii)

Quassim, Attia, and Elminir (2007) used neuro fuzzy approach to predict solar cycle 25. According to their study the cycle maximum would have an amplitude of 116 around 2020.
iii)

Okoh et al. (2018) used a method known as Hybrid Regression-Neural Network that combines regression analysis and neural network learning (Ap index is used for prediction) to forecast the amplitude of solar cycle 25. They predict a peak amplitude of 122.1 $\pm$ 18.2 occurring on January 2025 $\pm$ 6.
iv)

Attia, Ismail, and Basurah (2013) used neural network model and found a suitable number of network inputs for the sunspot data series based on sequential forward search for the Neuro-Fuzzy model. This study predicts a peak SSN of 90.7 $\pm$ 15.
v)

Covas, Peixinho, and Fernandes (2019) used neural network technique to perform a spatio-temporal analysis of solar cycle data and estimates the maximum SSN for cycle 25 to be 57 $\pm$ 17 occurring on 2022-2023.

4.7 Uncategorized Forecasts

i)

Javaraiah (2015) studied the combined Greenwich and Solar Optical Observing Network (SOON) sunspot group data during 1874-2013. They analysed and studied the relatively long-term variations in the annual sums of the areas of sunspot groups in 0–10, 10–20, and 20–30 latitude intervals of the Sun’s northern and southern hemispheres. Long-term variations in the north–south asymmetry of solar activity is used to predict a SSN of 42 $\pm$ 13.
ii)

Kakad, Kakad, and Ramesh (2017) estimated the Shannon entropy related to the declining phase of the preceding Solar Cycle which is used to predict SSN. Two SSN maximum for two different values of entropy are estimate at 63 $\pm$ 11.3 and 116 $\pm$ 11.3.
iii)

Chistyakov (1983) used regularities of secular and 22-year variations for their forecast. The predict a peak SSN of 121 occurring in 2028.5.
iv)

Kontor et al. (1984) utilized a hypothesis that the cycle peak envelop oscillates between the time dependent high and low levels to predict the nature of the solar cycle 25. They estimate a peak SSN of 117 around 2024.

4.8 Analysis of Solar Cycle 25 Forecasts

In Figure \ireffig:3 we summarize the various predictions for solar cycle 25. For reference, the gray-dashed line indicates the observed peak amplitude of solar cycle 24 (113.3 SSN). We find that forecasts for cycle 25 based on different techniques still diverge widely, and a majority of the forecasts indicate a cycle 25 stronger than cycle 24. The mean ( $\pm$ $1\sigma$ ) of the different predictions is 134.012 $\pm$ 39.053 which nonetheless conforms to a climatological weak cycle keeping in mind the definition of cycle strengths based on observed cycle amplitudes over the past 100 years (with reference to Figure \ireffig:1). We note that there are far fewer forecasts for solar cycle 25 – approximately half – than there were for cycle 24; this in itself is encouraging and perhaps indicative of the realization that playing Russian roulette with solar cycle forecasting is perhaps not the best of ideas.

On a more serious note, it is important to delve deeper in to physics-based forecasts for solar cycle 25 to ascertain whether any meaningful progress has occurred in this front. While these are part of the “confusogram” of solar cycle 25 forecasts based on diverse techniques (Figure \ireffig:3), we extract them out and analyze them separately in the next section.

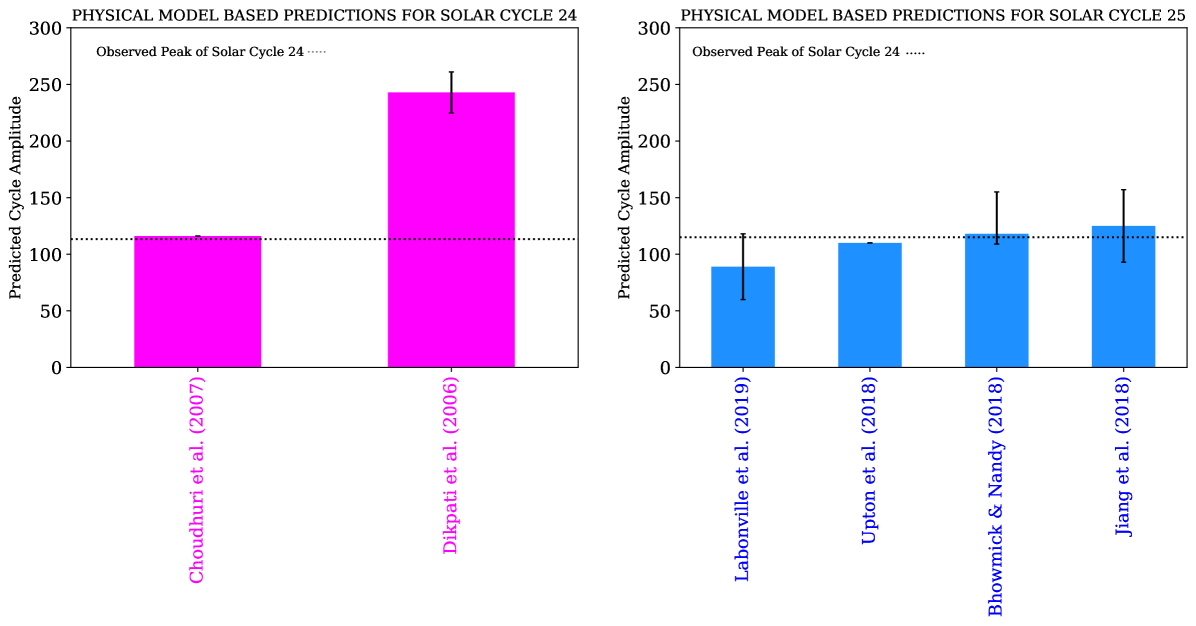
4.9 Comparative Assessment of Physics-based Predictions of Solar Cycles 24-25

In Figure \ireffig:4, we compare those physical model based predictions of solar cycles 24 and 25 which explicitly predicted peak SSNs (as opposed to qualitative forecasts such as weak or moderate or strong cycles). We estimate the mean ( $\pm$ $1\sigma$ ) of the physics-based predictions for cycle 24 to be 179.438 $\pm$ 63.438 (SSN). This mean is much larger than what was observed (113.3 SSN) and the standard deviation is indicative of a large divergence.

There were four distinct physical model based forecasts for cycle 25. Two of these models (Upton and Hathaway, 2018; Jiang et al., 2018) utilized different methodologies for simulating the evolution of the Sun’s surface radial fields and were driven by assimilating the observed emergence profiles of bipolar active regions. They predicted the polar field expected at the end of cycle 24 and utilized the observed relationship between the polar field and the subsequent cycle amplitude (i.e., a calibrated precursor method) to forecast the peak of cycle 25.

Bhowmik and Nandy (2018) utilized a surface flux transport model calibrated over a century by assimilating the observed statistics of emergence of bipolar sunspot pairs to simulate the evolution of the Sun’s surface radial field and polar flux. This was coupled to a solar dynamo model which assimilated the data from the surface flux transport model at every solar minima. Using this methodology they first predicted the polar field expected at the minimum of cycle 24 (in effect 4 years in advance) and subsequently utilized the century-scale dynamo simulation to forecast cycle 25. The Bhowmik and Nandy (2018) century-scale data driven solar dynamo simulation (the first such attempt) reasonably matched past solar cycles (except the extreme cycle 19) and predicted a weak cycle 25 similar or slightly stronger than cycle 24. (Labonville, Charbonneau, and Lemerle, 2019) used a slightly different methodology of coupling a surface flux transport and dynamo model more intimately. In this approach the two models communicated more frequently with each-other. (Labonville, Charbonneau, and Lemerle, 2019) predicted a solar cycle 25 which is much weaker than cycle 24.

For the four physics-based predictions of solar cycle 25 the mean predicted amplitude ( $\pm$ $1\sigma$ ) is 110.5 $\pm$ 13.5 (SSN), i.e., very similar to the observed peak of the recently concluded solar cycle 24.

Independently, the four physics-based forecasts for solar cycle 25 are not too distinct from each other in the sense all predict a climatogically weak sunspot cycle. More importantly, there is a small range over which the predicted uncertainties (or range of forecasts) agree. Taken together, and compared to the physics-based forecasts for cycle 24, the physics-based cycle 25 forecasts indicate significant progress towards a convergence (or a “consensus forecast”). Is this accidental or is this convergence of predicted numbers for solar cycle 25 indicative of a convergence of fundamental ideas related to the solar dynamo mechanism? We tackle this question in the next section.

5 Advances in Understanding Solar Cycle Predictability

The solar dynamo mechanism is believed to operate throughout the Sun’s convection zone (and up to its surface layers) wherein, differential rotation, turbulent convection and large-scale plasma flows such as meridional circulation, turbulent flux pumping play important roles in induction and transport of magnetic fields (see, e.g., Figure 5). Following the pioneering work of Parker (1955a), there has been a community wide consensus that the toroidal component of the Sun’s magnetic field is generated by the stretching of poloidal field lines by the solar differential rotation in the solar convection zone (SCZ). We note that observations and simulations of magnetic activity in other stars also bear out the importance of stellar differential rotation in sustenance of magnetic cycles (Brun et al., 2015).

The toroidal flux tubes rise up due to magnetic buoyancy (Parker, 1955b) during which they are twisted by helical turbulent convective motions which is thought to sustain a mean-field $\alpha$ -effect that can reproduce the Sun’s poloidal field (Parker, 1955a). This process remains unobserved and unconstrained till date. Simulations of the dynamic rise of magnetic flux tubes through the SCZ show that the Coriolis force can impart a systematic tilt to bipolar sunspot pairs (D’Silva and Choudhuri, 1993; Fan, Fisher, and Deluca, 1993) which explains the observed Joy’s law for active region tilt angles (Hale et al., 1919). Babcock (1961) and Leighton (1969) suggested that the decay and dispersal of these tilted bipolar sunspot pairs can regenerate the Sun’s large-scale poloidal (dipolar) field (Figure 5) mediated via flux transport processes providing an alternative formulation to the mean-field $\alpha$ effect. This alternative formulation came to be known as the Babcock-Leighton (hereafter BL) dynamo mechanism – a process in which near-surface flux transport processes play a critical role in the build-up and reversal of the Sun’s large-scale dipolar field (of which the observed surface radial field is a proxy). This process is observed in action on the Sun’s surface. Numerous flux transport dynamo models have been built based on the Babcock-Leighton mechanism with different levels of complexity (Durney, De Young, and Roxburgh, 1993; Durney, 1995; Choudhuri, Schussler, and Dikpati, 1995; Dikpati and Charbonneau, 1999; Nandy and Choudhuri, 2001, 2002; Muñoz-Jaramillo et al., 2010; Kumar, Jouve, and Nandy, 2019) which reasonably match various solar cycle properties. Nevertheless, for long there has been no consensus on which of this two mechanisms for poloidal field generation plays an predominant role in the dynamo mechanism. The resolution to this dilemma is fundamental because the dominant poloidal source is also likely to be the primary source of variability in the solar magnetic cycle and the ability to adequately model this variability is fundamental to predictive models of the sunspot cycle.

Careful analysis of long-term solar cycle observations relating the tilt and flux content of solar active regions (i.e. the BL source term) to the strength of the next sunspot cycle clearly implicates the BL mechanism as the primary determinant of solar cycle amplitudes (Dasi-Espuig et al., 2010). Fundamental theoretical analysis without recourse to parameterizations suggests that the surface magnetic field distribution which is a byproduct of the BL mechanism must be the primary source to the internal induction of the toroidal field (Cameron and Schüssler, 2015). Surface flux transport simulations imbibing the BL mechanism is able to reproduce the observed evolution of the Sun’s large scale polar fields (Jiang et al., 2014). Coupled models of magnetic field evolution on the solar surface and in the convection zone (i.e., surface flux transport and dynamo models) successfully explain a century of solar cycle observations (Bhowmik and Nandy, 2018). These observations and theoretical simulations leave little doubt that the primary source for the Sun’s poloidal field and the basis of cycle to cycle variability is the Babcock-Leighton solar dynamo mechanism driven by the emergence and dispersal of tilted bipolar sunspot pairs mediated via near-surface flows; anyone who believes otherwise is ignoring evidence – a fundamental tenet of the scientific process.

However, both the dynamo models that were utilized for predictions of solar cycle 24 – and whose predictions diverged widely – were based on the BL mechanism. Does this go against the emergent understanding that the BL dynamo mechanism is the major source of variability in the solar magnetic cycle? Yeates, Nandy, and Mackay (2008) and Karak and Nandy (2012) demonstrated that the BL dynamo model behaves very differently under different assumed flux transport scenarios and that the relative efficacy of turbulent diffusion, meridional circulation and turbulent pumping determines the dynamical memory of the dynamo which is fundamental to predictability. Yeates, Nandy, and Mackay (2008) argued that differing assumptions related to the dominant flux transport mechanisms in the Dikpati, de Toma, and Gilman (2006) and Choudhuri, Chatterjee, and Jiang (2007) predictive models resulted in the discrepancy in their predictions.

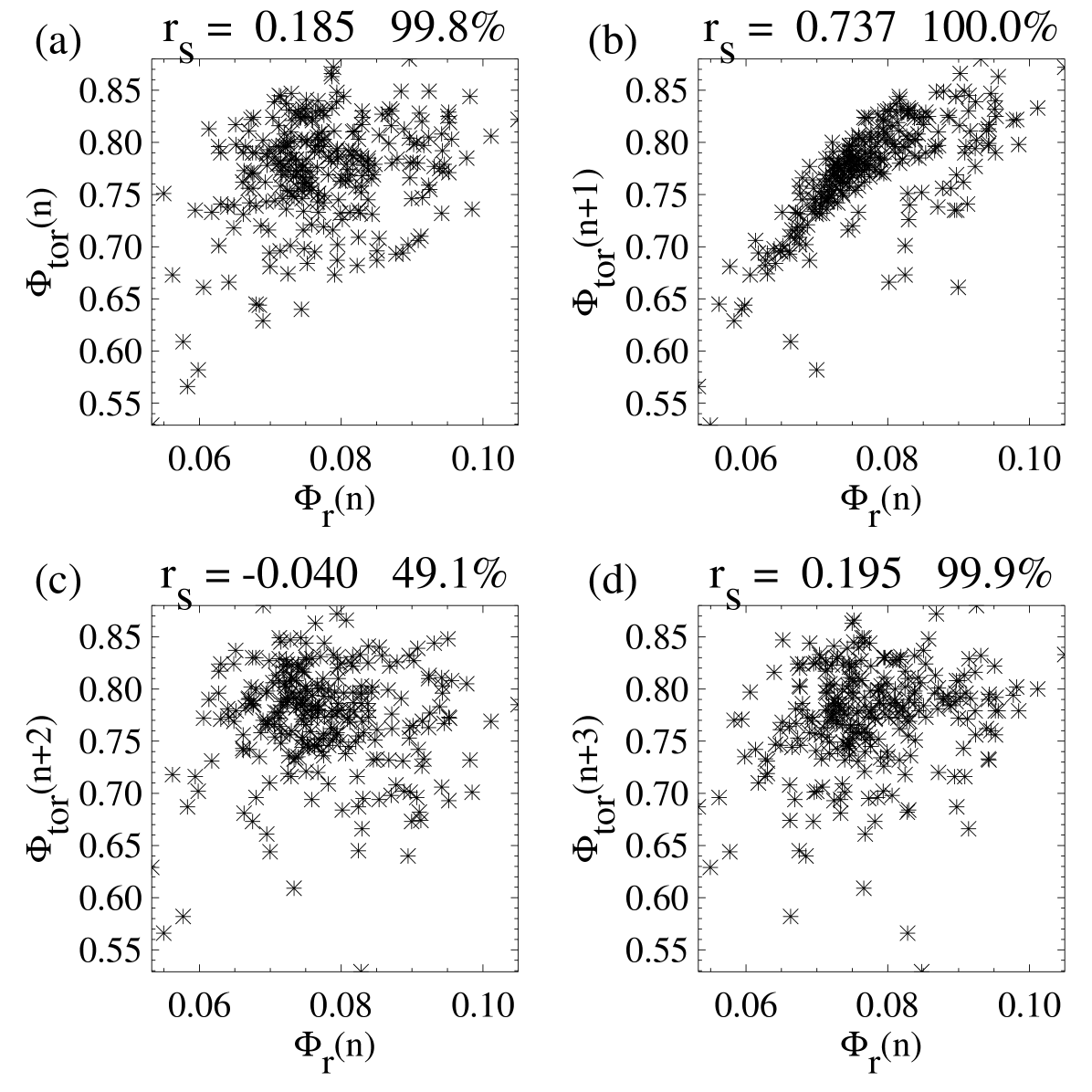
Furthermore, Yeates, Nandy, and Mackay (2008) and Karak and Nandy (2012) utilized stochastically fluctuating source terms in a non-linear BL dynamo model to estimate correlations between the polar field at cycle minima and subsequent cycle strengths and established that efficient transport of magnetic flux by turbulent diffusion and pumping in the SCZ reduces the dynamical memory of the sunspot cycle to only one cycle (see Figure \ireffig:6). This implies that solar cycle predictions are only possible one cycle in advance, and that the polar field at cycle minima contributes only to the strength of the next sunspot cycle.

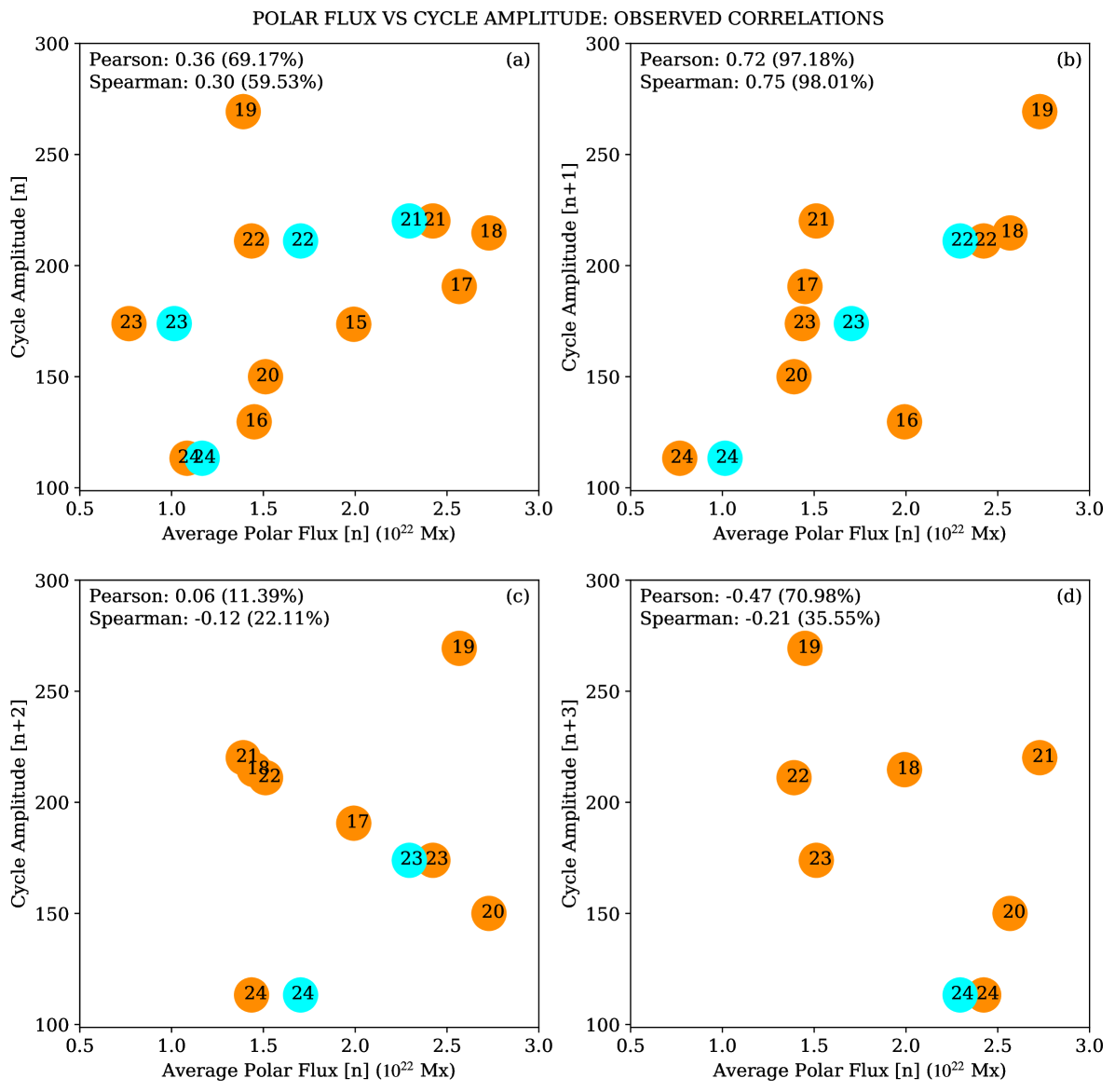
The theoretical hypothesis of this short one cycle memory in the dynamo mechanism was soon confirmed in an analysis of the relationship between polar flux and the amplitude of different cycles by Muñoz-Jaramillo et al. (2012). Following their approach, we perform an analysis of the relationship between polar flux (estimated from flux calibrated faculae count) and the peak sunspot number of different cycles. This analysis, based on the revised sunspot time series is presented in Figure \ireffig:7. In both theoretical dynamo simulations based on the BL mechanism with fluctuating poloidal source term (Figure 6) and observed solar cycle correlations (Figure \ireffig:7), we see that the toroidal flux of a cycle is not correlated with the poloidal flux measured near the poles at the end of that cycle. This indicates the the poloidal field source is stochastic (imbibing random variations) and the link of predictability is broken from the toroidal field to the poloidal field conversion process in the dynamo cycle. However, we find that these long-term statistically significant observations confirm the existence of a correlation between the polar field at the minima of a cycle [ $n$ ] and the cycle amplitude of the next cycle [ $n+1$ ]. This relationship is causally explained on the basis of dynamo theory, which we have established earlier, and provides the basis for predictive solar dynamo models and precursor prediction techniques – explaining why the latter tend to be more accurate than other solar cycle prediction methods.

5.1 Resolution of Outstanding Questions in Solar Cycle Predictions

Finally, we summarize below resolutions to some outstanding questions in solar cycle predictions that were a challenge to the community about a decade back. These resolutions reflect the advances in our understanding of the physics of solar cycle predictability in the intervening period from the minimum of solar cycle 23 to the minimum of solar cycle 24 and lays the basis for future efforts in forecasting solar cycles.

i)

Is it possible to predict the sunspot cycle?
Based on numerical simulations with stochastic and deterministic non-linear dynamo models Bushby and Tobias (2007) argued that the solar cycle is not predictable. Their conclusion was based on solutions to the non-linear system of equations diverging over large time-scales when slightly different initial conditions were assumed. That solutions in a non-linear dynamical systems would diverge over large timescales was well known, however, in the weather community and was demonstrated about half a century back in the pioneering work by Lorenz (1963). However, it is our considered view that Bushby and Tobias (2007) over-interpreted their results (or erred on the side-of-caution) to generalize their conclusion that short-term predictions are not possible. Numerous simulations with stochastically forced, non-linear dynamo models and observational analysis have since indicated that short term predictions of the upcoming solar cycle are possible (based on a causal relationship between the Sun’s polar field and the toroidal field of the next sunspot cycle) (Yeates, Nandy, and Mackay, 2008; Dasi-Espuig et al., 2010; Karak and Nandy, 2012; Muñoz-Jaramillo et al., 2012; Bhowmik and Nandy, 2018) have demonstrated that reasonably accurate (not exact) predictions of multiple solar cycles over a century is possible based on the current understanding. Thus, we reiterate that short-term, one cycle forecasts (at least of climatological relevance) is possible.
ii)

What is the best proxy for solar cycle predictions?
Theory of the solar dynamo mechanism Cameron and Schüssler (2015), numerical dynamo simulations (Yeates, Nandy, and Mackay, 2008; Karak and Nandy, 2012; Bhowmik and Nandy, 2018), and analysis of long-term observations Dasi-Espuig et al. (2010); Muñoz-Jaramillo et al. (2012) indicate that the best proxy for solar cycle predictions is the polar field (flux) at the minimum of the previous cycle. There is a causal relationship between the polar flux at cycle minima (which is a measure of the poloidal field strength) and the sunspot cycle amplitude (which is a measure of the underlying toroidal field) as the former acts as the source of the latter. Thus precursor technique based predictions that use direct polar field measurements or its proxy to predict the sunspot cycle are physically well founded.
iii)

How early can we predict the sunspot cycle?
A good idea of the polar field at sunspot cycle minima is necessary to predict the next sunspot cycle. Typically, therefore, predictions made with accurate knowledge of the polar field strength at minima are likely to be more accurate. However, solar surface flux transport models can be used with synthetic input profiles of the declining phase of a cycle to predict in advance the polar field strength at the minimum of that cycle (Upton and Hathaway, 2018); this predicted polar field can be utilized in precursor methods (Jiang et al., 2018) or dynamo models of the solar cycle (Bhowmik and Nandy, 2018) to predict the next sunspot cycle. Such methodologies therefore can extend the prediction window of a cycle, say cycle [ $n+1$ ], to a few years before the minima of cycle [ $n$ ].
iv)

How many cycles in to the future can we predict?
Theoretical simulations exploring the memory of the sunspot cycle based on solar dynamo simulations show that the polar field at the minima of cycle [ $n$ ] is causally related to the toroidal field of the next, i.e., [ $n+1$ ] cycle only (Yeates, Nandy, and Mackay, 2008; Karak and Nandy, 2012) when turbulent flux transport processes dominate in the solar convection zone (see Figure 6). Long-term observations (Muñoz-Jaramillo et al., 2012) of solar activity correlations confirm this (see Figure 7). Therefore, we postulate that the dynamical memory of the solar cycle – as far as cycle to cycle variations are concerned – is short. Reasonably accurate predictions are possible only for the next sunspot cycle, and not beyond.
v)

What properties of the solar cycle can we predict?
The strength of the sunspot cycle as well as its timing can be approximately predicted. For example, Bhowmik and Nandy (2018) predicted the complete profile of sunspot cycle 25 based on a combination of a solar surface flux transport model and a solar dynamo model. Because the strength of a sunspot cycle is related to its rate of rise, the latter can also in fact be a byproduct of solar cycle predictions.
vi)

What physical dynamo model of the solar cycle is best suited for predictive purposes?
Recent progress in solar dynamo theory and modeling and observational evidence together indicate that the Babcock-Leighton mechanism for poloidal field generation is the primary source of variability in the solar cycle (Dasi-Espuig et al., 2010; Cameron and Schüssler, 2015; Bhowmik and Nandy, 2018). These models can also be constrained by observations and driven by data assimilation. Philosophically and logically therefore, solar dynamo models based on the Babcock-Leighton framework should be utilized for predictive purposes.
vii)

Has convergence been achieved in physics-based solar cycle predictions for sunspot cycle 25?
Yes, based on our analysis we conclude that physics-based forecasts for solar cycle 24 have converged and agree with each other with minor differences (Figure 4). These differences may result from disparate modeling techniques and (or) data assimilation methodologies. Our analysis reveals all the physics-based predictions of solar cycle 25 – based on the Babcock-Leighton framework – predict a climatologically weak cycle. Considering the range of uncertainty in these forecasts, it is safe to say that sunspot cycle 25 would be a weak to a moderately weak cycle that will peak around 2024 ( $\pm 1$ ).
viii)

With what accuracy can we predict the solar cycle?
Some uncertainties in prediction are bound to result from the many uncertainties and parameterizations involved in modeling. Models that make early predictions are perhaps prone to larger uncertainties because of the higher probability of statistically extreme fluctuations, e.g., appearance of anomalous active regions (Nagy et al., 2017) in the intervening prediction window. However, many of the physical model-based predictions can account for reasonable uncertainties through ensemble forecasts that provide a range of values for the predicted amplitude of the solar cycle (Bhowmik and Nandy, 2018; Jiang et al., 2018; Labonville, Charbonneau, and Lemerle, 2019).
ix)

What is the best approach to achieving a consensus forecast in any Solar Cycle Prediction Panel?
A large number of solar cycle forecasts utilizing a large number of techniques resulting in greater divergence indicates a statistical reality rather than a great scientific debate of equally viable ideas. This is well proven in our comparative analysis of predictions for solar cycles 24 and 25. The path towards consensus prediction from any solar cycle prediction panels such as the NOAA-NASA Prediction Panel is then well defined. Such panels must consider the underlying physics of solar cycle predictability and seriously assess only those methods – and their agreements or disagreements – which are rooted in firm physical foundations. It is clear from our analysis that while predictions for solar cycle 25 (Figure 3) utilizing diverse techniques still suffer from non-convergence just like cycle 24 (Figure 2), physically well founded model-based predictions for sunspot cycle 25 have converged (Figure 4). The basis of the consensus and any disagreements must be clearly declared for the community to understand and appreciate the subtleties involved in the prediction. Finally, the research manuscripts that have contributed to the consensus prediction must be disclosed. On the one hand, this allows independent scrutiny and analysis by the community, and on the other hand this provides due credit to the researchers whose work inform and contribute to a consensus prediction.

6 Concluding Remarks

\ilabel

s:3

In summary, here we review predictions of sunspot cycles 24-25 from different groups based on diverse techniques and perform a comparative analysis of these predictions.

Our analysis reveals that while predictions based on diverse techniques continue to disagree across sunspot cycles 24-25, physical model based forecasts for solar cycle 25 have converged. This convergence indicates a weak to moderately weak sunspot cycle 25. We argue that this convergence in physics-based predictions is a consequence of the convergence of ideas and new insights in to the physics of solar cycle predictability. In particular, we note there is now overwhelming evidence that the Babcock-Leighton mechanism is the dominant driver of solar cycle variability and that the dynamical memory of the solar cycle is short, allowing for predictions of only the next cycle.

Following the early disagreements and controversies related to solar cycle 24 predictions, significant progress has been achieved in the intervening decade, between the minimum of solar cycle 23 and solar cycle 24. This progress is presented and discussed in the light of resolutions to many outstanding questions related to solar cycle predictability. It is our hope that this progress will lay the foundations of more accurate, physics-based predictive models of the sunspot cycle on the one hand, and on the other hand, will more usefully constrain the fundamental physics of solar and stellar magnetic cycles.

Acknowledgments

This review is dedicated to the memory of Bernard Durney who passed away last year somewhere in the South of France, his last years spent in relative obscurity far away from the solar physics community. Bernard made fundamental contributions to the development of Babcock-Leighton models of the solar cycle, including elucidating the role of meridional circulation in the near-surface evolution of the Sun’s large-scale dipolar magnetic fields. I first started corresponding with him as a PhD student from India and I am indebted to him for his generosity in sharing his knowledge and debating ideas with someone he had never met. In fact, although we corresponded for many years, I never got a chance to meet him in person. I am grateful to Soumyaranjan Dash and Shaonwita Pal for assistance with literature survey and preparation of some of the figures. I acknowledge utilization of data from the NASA/SDO HMI instrument maintained by the HMI team, the Royal Greenwich Observatory/USAF-NOAA active region database compiled by David H. Hathaway and MWO calibrated polar faculae data from the solar dynamo database maintained by Andrés Muñoz-Jaramillo. I acknowledge utilization of the hemispheric polar field data obtained by J. Todd Hoeksema and many dedicated graduate students at Stanford University’s Wilcox Solar Observatory . The Wilcox Solar Observatory is currently supported by NASA. I acknowledge usage of the yearly mean sunspot number data from the Solar Influences Data Analysis Centre (SIDC) at the Royal Observatory of Belgium. Much of the understanding related to the solar magnetic cycle and its predictability has resulted from confronting theoretical dynamo models with these long-term solar activity databases and the continued sustenance of these databases cannot be overemphasized. The Center of Excellence in Space Sciences India (CESSI) is funded by the Ministry of Human Resource Development, Government of India, under the Frontier Areas of Science and Technology (FAST) scheme. Finally, I am grateful to the solar physicists of Argentina, and its wonderful people, for an inspiring time during my sabbatical visit to that country in connection to the 2019 total solar eclipse – during which the idea and early work for this review was initiated.

References

Abdusamatov (2007) Abdusamatov, K.I.: 2007, Optimal prediction of the peak of the next 11-year activity cycle and of the peaks of several succeeding cycles on the basis of long-term variations in the solar radius or solar constant. Kinemat. Phys. Celest. Bodies 23, 97. DOI.
Aguirre, Letellier, and Maquet (2008) Aguirre, L.A., Letellier, C., Maquet, J.: 2008, Forecasting the Time Series of Sunspot Numbers. Sol. Phys. 249(1), 103. DOI. ADS.
Ahluwalia (2008) Ahluwalia, H.S.: 2008, Development of Solar Activity Cycle 24: Some Comments. In: 37th COSPAR Scientific Assembly 37, 36. ADS.
Attia, Ismail, and Basurah (2013) Attia, A.-F., Ismail, H.A., Basurah, H.M.: 2013, A Neuro-Fuzzy modeling for prediction of solar cycles 24 and 25. Ap&SS 344(1), 5. DOI. ADS.
Babcock (1961) Babcock, H.W.: 1961, The Topology of the Sun’s Magnetic Field and the 22-YEAR Cycle. ApJ 133, 572. DOI. ADS.
Babcock and Babcock (1955) Babcock, H.W., Babcock, H.D.: 1955, The Sun’s Magnetic Field, 1952-1954. ApJ 121, 349. DOI. ADS.
Baranovski, Clette, and Nollau (2008) Baranovski, A.L., Clette, F., Nollau, V.: 2008, Nonlinear solar cycle forecasting: theory and perspectives. Annales Geophysicae 26(2), 231. DOI. ADS.
Bhowmik and Nandy (2018) Bhowmik, P., Nandy, D.: 2018, Prediction of the strength and timing of sunspot cycle 25 reveal decadal-scale space environmental conditions. Nature Communications 9, 5209. DOI. ADS.
(9) Biesecker, D.: the solar cycle 24 prediction panel: 2007, consensus statement of the solar cycle 24 prediction panel, released march 2007. http://www.swpc.noaa.gov/SolarCycle/SC24/.
Brajša et al. (2009) Brajša, R., Wöhl, H., Hanslmeier, A., Verbanac, G., Ruždjak, D., Cliver, E., Svalgaard, L., Roth, M.: 2009, On solar cycle predictions and reconstructions. A&A 496(3), 855. DOI. ADS.
Brun et al. (2015) Brun, A.S., García, R.A., Houdek, G., Nandy, D., Pinsonneault, M.: 2015, The Solar-Stellar Connection. Space Sci. Rev. 196(1-4), 303. DOI. ADS.
Bushby and Tobias (2007) Bushby, P.J., Tobias, S.M.: 2007, On Predicting the Solar Cycle Using Mean-Field Models. ApJ 661(2), 1289. DOI. ADS.
Cameron and Schüssler (2015) Cameron, R., Schüssler, M.: 2015, The crucial role of surface magnetic fields for the solar dynamo. Science 347(6228), 1333. DOI. ADS.
Cameron, Jiang, and Schüssler (2016) Cameron, R.H., Jiang, J., Schüssler, M.: 2016, Solar Cycle 25: Another Moderate Cycle? ApJ 823(2), L22. DOI. ADS.
Charbonneau (2020) Charbonneau, P.: 2020, Dynamo models of the solar cycle. Living Reviews in Solar Physics 17(1), 4. DOI. ADS.
Charvátová (2009) Charvátová, I.: 2009, Long-term predictive assessments of solar and geomagnetic activities made on the basis of the close similarity between the solar inertial motions in the intervals 1840 1905 and 1980 2045. New A 14(1), 25. DOI. ADS.
Chistyakov (1983) Chistyakov, V.F.: 1983, A forecast of solar activity till the year 2030. Byulletin Solnechnye Dannye Akademie Nauk SSSR 1983, 97. ADS.
Chopra and Dabas (2006) Chopra, P., Dabas, R.S.: 2006, Prediction of maximum amplitude of the next Solar Cycle 24 using modified Precursor Method. In: 36th COSPAR Scientific Assembly 36, 909. ADS.
Choudhuri, Chatterjee, and Jiang (2007) Choudhuri, A.R., Chatterjee, P., Jiang, J.: 2007, Predicting Solar Cycle 24 With a Solar Dynamo Model. Phys. Rev. Lett. 98(13), 131103. DOI. ADS.
Choudhuri, Schussler, and Dikpati (1995) Choudhuri, A.R., Schussler, M., Dikpati, M.: 1995, The solar dynamo with meridional circulation. A&A 303, L29. ADS.
Clette et al. (2015) Clette, F., Svalgaard, L., Vaquero, J.M., Cliver, E.W.: 2015, In: Balogh, A., Hudson, H., Petrovay, K., von Steiger, R. (eds.) Revisiting the Sunspot Number, Springer, New York, NY, 35. ISBN 978-1-4939-2584-1. DOI. https://doi.org/10.1007/978-1-4939-2584-1˙3.
Clilverd et al. (2006) Clilverd, M.A., Clarke, E., Ulich, T., Rishbeth, H., Jarvis, M.J.: 2006, Predicting solar cycle 24 and beyond. Space Weather 4(9). DOI. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2005SW000207.
Covas, Peixinho, and Fernandes (2019) Covas, E., Peixinho, N., Fernandes, J.: 2019, Neural Network Forecast of the Sunspot Butterfly Diagram. Sol. Phys. 294(3), 24. DOI. ADS.
Crosson and Binder (2009) Crosson, I.J., Binder, P.-M.: 2009, Chaos-based forecast of sunspot cycle 24. JOURNAL OF GEOPHYSICAL RESEARCH 114(A01108). DOI. ADS.
Dabas et al. (2008) Dabas, R.S., Sharma, K., Das, R.M., Pillai, K.G.M., Chopra, P., Sethi, N.K.: 2008, A Prediction of Solar Cycle 24 Using a Modified Precursor Method. Sol. Phys. 250(1), 171. DOI. ADS.
Dani and Sulistiani (2019) Dani, T., Sulistiani, S.: 2019, Prediction of maximum amplitude of solar cycle 25 using machine learning. In: Journal of Physics Conference Series, Journal of Physics Conference Series 1231, 012022. DOI. ADS.
Das et al. (2019) Das, S.B., Basak, A., Nandy, D., Vaidya, B.: 2019, Modeling Star-Planet Interactions in Far-out Planetary and Exoplanetary Systems. ApJ 877(2), 80. DOI. ADS.
Dasi-Espuig et al. (2010) Dasi-Espuig, M., Solanki, S.K., Krivova, N.A., Cameron, R., Peñuela, T.: 2010, Sunspot group tilt angles and the strength of the solar cycle. A&A 518, A7. DOI. ADS.
de Meyer (2003) de Meyer, F.: 2003, A Transfer Function Model for the Sunspot Cycle. Sol. Phys. 217(2), 349. DOI. ADS.
Dikpati and Charbonneau (1999) Dikpati, M., Charbonneau, P.: 1999, A Babcock-Leighton Flux Transport Dynamo with Solar-like Differential Rotation. ApJ 518(1), 508. DOI. ADS.
Dikpati, de Toma, and Gilman (2006) Dikpati, M., de Toma, G., Gilman, P.A.: 2006, Predicting the strength of solar cycle 24 using a flux-transport dynamo-based tool. Geophys. Res. Lett. 33(5), L05102. DOI. ADS.
D’Silva and Choudhuri (1993) D’Silva, S., Choudhuri, A.R.: 1993, A theoretical model for tilts of bipolar magnetic regions. A&A 272, 621. ADS.
Du (2006a) Du, Z.L.: 2006a, Relation between solar maximum amplitude and max-max cycle length. ApJ 132(1), 1485.
Du and Du (2006b) Du, Z., Du, S.: 2006b, The Relationship Between the Amplitude and Descending Time of a Solar Activity Cycle. Sol. Phys. 238(2), 431. DOI. ADS.
Du, Wang, and He (2006c) Du, Z., Wang, H., He, X.-T.: 2006c, The relation between the amplitude and the period of solar cycles. Chin. J. Astron. Astrophys 6, 489. DOI.
Du, Wang, and Zhang (2008) Du, Z.-L., Wang, H.-N., Zhang, L.-Y.: 2008, A Running Average Method for Predicting the Size and Length of a Solar Cycle. Chinese J. Astron. Astrophys. 8(4), 477. DOI. ADS.
Du et al. (2008) Du, Z.L., Wang, H.N., He, H., Zhang, L.Y., Li, R., Cui, Y.M.: 2008, A summary of the applications of a weighted average method determining times of solar cycle extrema. Advances in Space Research 42(9), 1457. DOI. ADS.
Duhau (2003) Duhau, S.: 2003, An Early Prediction of Maximum Sunspot Number in Solar Cycle 24. Sol. Phys. 213(1), 203. DOI. ADS.
Durney (1995) Durney, B.R.: 1995, On a Babcock-Leighton dynamo model with a deep-seated generating layer for the toroidal magnetic field. Sol. Phys. 160(2), 213. DOI. ADS.
Durney, De Young, and Roxburgh (1993) Durney, B.R., De Young, D.S., Roxburgh, I.W.: 1993, On the Generation of the Largescale and Turbulent Magnetic Fields in the Solar Type Stars. Sol. Phys. 145(2), 207. DOI. ADS.
Echer et al. (2004) Echer, E., Rigozo, N., Nordemann, D., Vieira, L.: 2004, Prediction of solar activity on the basis of spectral characteristics of sunspot number. Annales Geophysicae 22(6), 2239. DOI. ADS.
Euler and Smith (2006) Euler, H.J., Smith, S.: 2006, Future solar activity estimates for use in prediction of space environmental effects on spacecraft orbital lifetime and performance. technical report, nasa, marshall space flight center, quoted in pesnell (2008). http://sail.msfc.nasa.gov/current˙solar˙report/CurRpt.pdf.
Fan, Fisher, and Deluca (1993) Fan, Y., Fisher, G.H., Deluca, E.E.: 1993, The Origin of Morphological Asymmetries in Bipolar Active Regions. ApJ 405, 390. DOI. ADS.
Gholipour et al. (2005) Gholipour, A., Lucas, C., Araabi, B.N., Shafiee, M.: 2005, Solar activity forecast: Spectral analysis and neurofuzzy prediction. Journal of Atmospheric and Solar-Terrestrial Physics 67(6), 595. DOI. ADS.
Gopalswamy et al. (2018) Gopalswamy, N., Mäkelä, P., Yashiro, S., Akiyama, S.: 2018, Long-term solar activity studies using microwave imaging observations and prediction for cycle 25. Journal of Atmospheric and Solar-Terrestrial Physics 176, 26. DOI. ADS.
Hale (1908) Hale, G.E.: 1908, On the Probable Existence of a Magnetic Field in Sun-Spots. ApJ 28, 315. DOI. ADS.
Hale et al. (1919) Hale, G.E., Ellerman, F., Nicholson, S.B., Joy, A.H.: 1919, The Magnetic Polarity of Sun-Spots. ApJ 49, 153. DOI. ADS.
Hamid and Galal (2006) Hamid, R.H., Galal, A.A.: 2006, Preliminary Prediction of the Strength of the 24th 11-Year Solar Cycle. In: Bothmer, V., Hady, A.A. (eds.) Solar Activity and its Magnetic Origin, IAU Symposium 233, 413. DOI. ADS.
Han and Yin (2019) Han, Y.B., Yin, Z.Q.: 2019, A Decline Phase Modeling for the Prediction of Solar Cycle 25. Sol. Phys. 294(8), 107. DOI. ADS.
Hathaway (2015) Hathaway, D.H.: 2015, The Solar Cycle. Living Reviews in Solar Physics 12(1), 4. DOI. ADS.
Hathaway and Wilson (2004) Hathaway, D.H., Wilson, R.M.: 2004, What the Sunspot Record Tells Us About Space Climate. Sol. Phys. 224(1-2), 5. DOI. ADS.
Hathaway and Wilson (2006) Hathaway, D.H., Wilson, R.M.: 2006, Geomagnetic activity indicates large amplitude for sunspot cycle 24. Geophys. Res. Lett. 33(18), L18101. DOI. ADS.
Hawkes and Berger (2018) Hawkes, G., Berger, M.A.: 2018, Magnetic Helicity as a Predictor of the Solar Cycle. Sol. Phys. 293(7), 109. DOI. ADS.
Helal and Galal (2013) Helal, H.R., Galal, A.A.: 2013, An early prediction of the maximum amplitude of the solar cycle 25. Journal of Advanced Research 4(3), 275 . DOI. http://www.sciencedirect.com/science/article/pii/S2090123212000975.
Hiremath (2008) Hiremath, K.M.: 2008, Prediction of solar cycle 24 and beyond. Ap&SS 314(1-3), 45. DOI. ADS.
Horstman (2005) Horstman, M.: 2005, Varying solar flux models and their effect on the future debris environment projections. Orbital Debris Q. News 9, 4.
Jain (2006) Jain, R.: 2006, Prediction of the Amplitude in Sunspot Cycle 24. In: 36th COSPAR Scientific Assembly 36, 642. ADS.
Javaraiah (2007) Javaraiah, J.: 2007, North–south asymmetry in solar activity: predicting the amplitude of the next solar cycle. Monthly Notices of the Royal Astronomical Society: Letters 377(1), L34. DOI. https://doi.org/10.1111/j.1745-3933.2007.00298.x.
Javaraiah (2008) Javaraiah, J.: 2008, Predicting the Amplitude of a Solar Cycle Using the North - South Asymmetry in the Previous Cycle: II. An Improved Prediction for Solar Cycle 24. Sol. Phys. 252(2), 419. DOI. ADS.
Javaraiah (2015) Javaraiah, J.: 2015, Long-term variations in the north-south asymmetry of solar activity and solar cycle prediction, III: Prediction for the amplitude of solar cycle 25. New A 34, 54. DOI. ADS.
Jiang et al. (2014) Jiang, J., Hathaway, D.H., Cameron, R.H., Solanki, S.K., Gizon, L., Upton, L.: 2014, Magnetic Flux Transport at the Solar Surface. Space Sci. Rev. 186(1-4), 491. DOI. ADS.
Jiang et al. (2018) Jiang, J., Wang, J.-X., Jiao, Q.-R., Cao, J.-B.: 2018, Predictability of the Solar Cycle Over One Cycle. ApJ 863(2), 159. DOI. ADS.
Kakad, Kakad, and Ramesh (2017) Kakad, B., Kakad, A., Ramesh, D.S.: 2017, Shannon Entropy-Based Prediction of Solar Cycle 25. Sol. Phys. 292(7), 95. DOI. ADS.
Kane (1999) Kane, R.P.: 1999, Prediction of the sunspot maximum of solar cycle 23 by extrapolation of spectral components. Sol. Phys. 189(1), 217. DOI. ADS.
Kane (2007a) Kane, R.P.: 2007a, A Preliminary Estimate of the Size of the Coming Solar Cycle 24, based on Ohl’s Precursor Method. Sol. Phys. 243(2), 205. DOI. ADS.
Kane (2007b) Kane, R.P.: 2007b, Solar Cycle Predictions Based on Extrapolation of Spectral Components: An Update. Sol. Phys. 246(2), 487. DOI. ADS.
Kane (2008) Kane, R.P.: 2008, How useful is the Waldmeier effect for prediction of a sunspot cycle? Journal of Atmospheric and Solar-Terrestrial Physics 70(11-12), 1533. DOI. ADS.
Karak and Nandy (2012) Karak, B.B., Nandy, D.: 2012, Turbulent Pumping of Magnetic Flux Reduces Solar Cycle Memory and thus Impacts Predictability of the Sun’s Activity. ApJ 761(1), L13. DOI. ADS.
Kennewell and Patterson (2006) Kennewell, J., Patterson, G.: 2006, Prediction, quoted in pesnell (2008).
Khramova, Krasotkin, and Kononovich (2002) Khramova, M.N., Krasotkin, S.A., Kononovich, E.V.: 2002, New aspects of solar activity forecast. In: Sawaya-Lacoste, H. (ed.) Solspa 2001, Proceedings of the Second Solar Cycle and Space Weather Euroconference, ESA Special Publication 477, 229. ADS.
Kilcik et al. (2009) Kilcik, A., Anderson, C.N.K., Rozelot, J.P., Ye, H., Sugihara, G., Ozguc, A.: 2009, Nonlinear Prediction of Solar Cycle 24. ApJ 693(2), 1173. DOI. ADS.
Kim, Wilson, and Cucinotta (2006) Kim, M.Y., Wilson, J.W., Cucinotta, F.A.: 2006, A solar cycle statistical model for the projection of space radiation environment. Advances in Space Research 37(9), 1741. DOI. ADS.
Kitiashvili and Kosovichev (2008) Kitiashvili, I., Kosovichev, A.G.: 2008, Application of data assimilation method for predicting solar cycles. The Astrophysical Journal 688(1), L49–L52. DOI. http://dx.doi.org/10.1086/594999.
Kitiashvili (2016) Kitiashvili, I.N.: 2016, Data Assimilation Approach for Forecast of Solar Activity Cycles. ApJ 831(1), 15. DOI. ADS.
Kontor (2006) Kontor, N.N.: 2006, Statistics-based regular extrapolation, quoted in pesnell (2008).
Kontor et al. (1984) Kontor, N.N., Lyubimov, G.P., Pereslegina, N.V., Khotilovskaya, T.G.: 1984, A prediction of the sunspot maxima for solar cycles NN 22-44. Byulletin Solnechnye Dannye Akademie Nauk SSSR 1983, 74. ADS.
Krausmann et al. (2016) Krausmann, E., Andersson, E., Murtagh, W., Gibbs, M.: 2016, Space weather & critical infrastructures: Findings and outlook, European Union, ??? ISBN 978-92-79-63903-6. DOI. https://op.europa.eu/en/publication-detail/-/publication/c06e62fb-03d0-11e7-8a35-01aa75ed71a1/language-en#.
Kryachko and Nusinov (2008) Kryachko, A.V., Nusinov, A.A.: 2008, Standard prediction of solar cycles. Geomagnetism and Aeronomy 48(2), 145. DOI. ADS.
Kumar, Jouve, and Nandy (2019) Kumar, R., Jouve, L., Nandy, D.: 2019, A 3D kinematic Babcock Leighton solar dynamo model sustained by dynamic magnetic buoyancy and flux transport processes. A&A 623, A54. DOI. ADS.
Labonville, Charbonneau, and Lemerle (2019) Labonville, F., Charbonneau, P., Lemerle, A.: 2019, A Dynamo-based Forecast of Solar Cycle 25. Sol. Phys. 294(6), 82. DOI. ADS.
Lantos (2005) Lantos, P.: 2005, Predictions of Galactic Cosmic Ray Intensity Deduced from that of Sunspot Number. Sol. Phys. 229(2), 373. DOI. ADS.
Leighton (1969) Leighton, R.B.: 1969, A Magneto-Kinematic Model of the Solar Cycle. ApJ 156, 1. DOI. ADS.
Lemerle and Charbonneau (2017) Lemerle, A., Charbonneau, P.: 2017, A Coupled 2 $\times$ 2D Babcock-Leighton Solar Dynamo Model. II. Reference Dynamo Solutions. ApJ 834(2), 133. DOI. ADS.
Li et al. (2018) Li, F.Y., Kong, D.F., Xie, J.L., Xiang, N.B., Xu, J.C.: 2018, Solar cycle characteristics and their application in the prediction of cycle 25. Journal of Atmospheric and Solar-Terrestrial Physics 181, 110 . DOI. http://www.sciencedirect.com/science/article/pii/S1364682617306612.
Li, Feng, and Li (2015) Li, K.J., Feng, W., Li, F.Y.: 2015, Predicting the maximum amplitude of solar cycle 25 and its timing. Journal of Atmospheric and Solar-Terrestrial Physics 135, 72 . DOI. http://www.sciencedirect.com/science/article/pii/S1364682615300511.
Lorenz (1963) Lorenz, E.N.: 1963, Deterministic Nonperiodic Flow. Journal of Atmospheric Sciences 20(2), 130. DOI. ADS.
Maris and Oncica (2006) Maris, G., Oncica, A.: 2006, Solar cycle 24 forecasts. Sun and Geosphere 1.
Miyahara (2008) Miyahara, V.: 2008, Prediction based on radiocarbon record, quoted in pesnell (2008).
Muñoz-Jaramillo et al. (2012) Muñoz-Jaramillo, A., Sheeley, N.R., Zhang, J., DeLuca, E.E.: 2012, Calibrating 100 Years of Polar Faculae Measurements: Implications for the Evolution of the Heliospheric Magnetic Field. ApJ 753(2), 146. DOI. ADS.
Muñoz-Jaramillo et al. (2010) Muñoz-Jaramillo, A., Nandy, D., Martens, P.C.H., Yeates, A.R.: 2010, A DOUBLE-RING ALGORITHM FOR MODELING SOLAR ACTIVE REGIONS: UNIFYING KINEMATIC DYNAMO MODELS AND SURFACE FLUX-TRANSPORT SIMULATIONS. The Astrophysical Journal 720(1), L20. DOI. https://doi.org/10.1088%2F2041-8205%2F720%2F1%2Fl20.
Mursula, Zieger, and Vilppola (2003) Mursula, K., Zieger, B., Vilppola, J.H.: 2003, Mid-term quasi-periodicities in geomagnetic activity during the last 15 solar cycles: Connection to solar dynamo strength To the memory of Karolen I. Paularena (1957-2001). Sol. Phys. 212(1), 201. DOI. ADS.
Nagy et al. (2017) Nagy, M., Lemerle, A., Labonville, F., Petrovay, K., Charbonneau, P.: 2017, The Effect of “Rogue” Active Regions on the Solar Cycle. Sol. Phys. 292(11), 167. DOI. ADS.
Nandy and Choudhuri (2001) Nandy, D., Choudhuri, A.R.: 2001, Toward a mean field formulation of the babcock-leighton type solar dynamo. i. $\alpha$ -coefficient versus durney’s double-ring approach. The Astrophysical Journal 551(1), 576. DOI. https://doi.org/10.1086%2F320057.
Nandy and Choudhuri (2002) Nandy, D., Choudhuri, A.R.: 2002, Explaining the Latitudinal Distribution of Sunspots with Deep Meridional Flow. Science 296(5573), 1671. DOI. ADS.
Nandy and Martens (2007) Nandy, D., Martens, P.C.H.: 2007, Space Climate and the Solar Stellar connection: What can we learn from the stars about long-term solar variability? Advances in Space Research 40(7), 891. DOI. ADS.
Nandy, Muñoz-Jaramillo, and Martens (2011) Nandy, D., Muñoz-Jaramillo, A., Martens, P.C.H.: 2011, The unusual minimum of sunspot cycle 23 caused by meridional plasma flow variations. Nature 471(7336), 80. DOI. ADS.
National Research Council (1997) National Research Council: 1997, Space weather: A research perspective, The National Academies Press, Washington, DC. DOI. https://www.nap.edu/catalog/12272/space-weather-a-research-perspective.
National Research Council (2013) National Research Council: 2013, Solar and space physics: A science for a technological society, The National Academies Press, Washington, DC. ISBN 978-0-309-16428-3. DOI. https://www.nap.edu/catalog/13060/solar-and-space-physics-a-science-for-a-technological-society.
National Science and Technology Council (2019) National Science and Technology Council: 2019, National space weather strategy and action plan, THE WHITE HOUSE OFFICE OF SCIENCE AND TECHNOLOGY, Washington, DC. https://www.whitehouse.gov/wp-content/uploads/2019/03/National-Space-Weather-Strategy-and-Action-Plan-2019.pdf.
Nevanlinna (2007) Nevanlinna, H.: 2007, Geomagnetic precursor based on aa, quoted in pesnell (2008).
Obridko (2008) Obridko, V.: 2008, Average of four separate precursor predictions, quoted in pesnell (2008).
Okoh et al. (2018) Okoh, D.I., Seemala, G.K., Rabiu, A.B., Uwamahoro, J., Habarulema, J.B., Aggarwal, M.: 2018, A Hybrid Regression-Neural Network (HR-NN) Method for Forecasting the Solar Activity. Space Weather 16(9), 1424. DOI. ADS.
Osherovich and Fainberg (2008) Osherovich, V., Fainberg, J.: 2008, New Method of Solar Maximum Prediction With Application to the Next Solar Cycle. In: AGU Fall Meeting Abstracts 2008, SH13A. ADS.
Parker (1955a) Parker, E.N.: 1955a, Hydromagnetic Dynamo Models. ApJ 122, 293. DOI. ADS.
Parker (1955b) Parker, E.N.: 1955b, The Formation of Sunspots from the Solar Toroidal Field. ApJ 121, 491. DOI. ADS.
Pesnell (2008) Pesnell, W.D.: 2008, Predictions of Solar Cycle 24. Sol. Phys. 252(1), 209. DOI. ADS.
Pesnell (2009) Pesnell, W.D.: 2009, Predicting Solar Cycle 24 With Geomagnetic Precursors. In: AAS/Solar Physics Division Meeting #40, AAS/Solar Physics Division Meeting, 11.05. ADS.
Pesnell (2012a) Pesnell, W.D.: 2012a, Solar Cycle Predictions (Invited Review). Sol. Phys. 281(1), 507. DOI. ADS.
Pesnell and Schatten (2018) Pesnell, W.D., Schatten, K.H.: 2018, An Early Prediction of the Amplitude of Solar Cycle 25. Sol. Phys. 293(7), 112. DOI. ADS.
Pesnell, Thompson, and Chamberlin (2012b) Pesnell, W.D., Thompson, B.J., Chamberlin, P.C.: 2012b, The Solar Dynamics Observatory (SDO). Sol. Phys. 275, 3. DOI. ADS.
Petrovay (2020) Petrovay, K.: 2020, Solar cycle prediction. Living Reviews in Solar Physics 17(1), 2. DOI. ADS.
Petrovay et al. (2018) Petrovay, K., Nagy, M., Gerják, T., Juhász, L.: 2018, Precursors of an upcoming solar cycle at high latitudes from coronal green line data. Journal of Atmospheric and Solar-Terrestrial Physics 176, 15. DOI. ADS.
Pishkalo (2008) Pishkalo, M.I.: 2008, Preliminary prediction of solar cycles 24 and 25 based on the correlation between cycle parameters. Kinematics and Physics of Celestial Bodies 24(5), 242. DOI. ADS.
Podladchikova, Lefebvre, and Van der Linden (2008) Podladchikova, T., Lefebvre, B., Van der Linden, R.: 2008, Peak sunspot number for solar cycle 24, quoted in pesnell (2008).
Prochasta (2006) Prochasta, R.: 2006, Climatological prediction submitted to panel, quoted in pesnell (2008).
Quassim, Attia, and Elminir (2007) Quassim, M.S., Attia, A.-F., Elminir, H.K.: 2007, Forecasting the Peak Amplitude of the 24th and 25th Sunspot Cycles and Accompanying Geomagnetic Activity. Sol. Phys. 243(2), 253. DOI. ADS.
Rabin (2007) Rabin, D.M.: 2007, Forecast of the Amplitude of Solar Cycle 24 Based on the Disturbed Days Precursor. In: American Astronomical Society Meeting Abstracts #210, American Astronomical Society Meeting Abstracts 210, 92.05. ADS.
Rigozo et al. (2011) Rigozo, N.R., Souza Echer, M.P., Evangelista, H., Nordemann, D.J.R., Echer, E.: 2011, Prediction of sunspot number amplitude and solar cycle length for cycles 24 and 25. Journal of Atmospheric and Solar-Terrestrial Physics 73(11-12), 1294. DOI. ADS.
Roth (2006) Roth, M.: 2006, Arma prediction of solar cycle 24, quoted in pesnell (2008).
Sarp et al. (2018) Sarp, V., Kilcik, A., Yurchyshyn, V., Rozelot, J.P., Ozguc, A.: 2018, Prediction of solar cycle 25: a non-linear approach. MNRAS 481(3), 2981. DOI. ADS.
Schatten (2005) Schatten, K.: 2005, Fair space weather for solar cycle 24. Geophys. Res. Lett. 32(21), L21106. DOI. ADS.
Scherrer et al. (2012) Scherrer, P.H., Schou, J., Bush, R.I., Kosovichev, A.G., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall, T.L., Zhao, J., Title, A.M., Schrijver, C.J., Tarbell, T.D., Tomczyk, S.: 2012, The Helioseismic and Magnetic Imager (HMI) Investigation for the Solar Dynamics Observatory (SDO). Sol. Phys. 275, 207. DOI. ADS.
Schrijver et al. (2015) Schrijver, C.J., Kauristie, K., Aylward, A.D., Denardini, C.M., Gibson, S.E., Glover, A., Gopalswamy, N., Grande, M., Hapgood, M., Heynderickx, D., Jakowski, N., Kalegaev, V.V., Lapenta, G., Linker, J.A., Liu, S., Mandrini, C.H., Mann, I.R., Nagatsuma, T., Nandy, D., Obara, T., Paul O’Brien, T., Onsager, T., Opgenoorth, H.J., Terkildsen, M., Valladares, C.E., Vilmer, N.: 2015, Understanding space weather to shield society: A global road map for 2015-2025 commissioned by COSPAR and ILWS. Advances in Space Research 55(12), 2745. DOI. ADS.
Sello (2003) Sello, S.: 2003, Solar cycle activity: A preliminary prediction for cycle #24. A&A 410, 691. DOI. ADS.
Sello (2019) Sello, S.: 2019, Solar cycle activity: an early prediction for cycle 25.
Singh and Bhargawa (2017) Singh, A.K., Bhargawa, A.: 2017, An early prediction of 25th solar cycle using Hurst exponent. Ap&SS 362(11), 199. DOI. ADS.
Solanki and Krivova (2003) Solanki, S.K., Krivova, N.A.: 2003, Can solar variability explain global warming since 1970? Journal of Geophysical Research (Space Physics) 108(A5), 1200. DOI. ADS.
Solanki et al. (2004) Solanki, S.K., Usoskin, I.G., Kromer, B., Schüssler, M., Beer, J.: 2004, Unusual activity of the Sun during recent decades compared to the previous 11,000 years. Nature 431(7012), 1084. DOI. ADS.
Svalgaard, Cliver, and Kamide (2005) Svalgaard, L., Cliver, E.W., Kamide, Y.: 2005, Sunspot cycle 24: Smallest cycle in 100 years? Geophysical Research Letters 32(1). DOI. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2004GL021664.
Thompson (2008) Thompson, R.J.: 2008, Prediction for cycle 24 using minimum value of ap (12-month average), quoted in pesnell (2008).
Tlatov (2006) Tlatov, A.: 2006, Indices of solar activity minimum of sunspot cycles and prediction solar cycle 24, quoted in pesnell (2008).
Tritakis, Mavromichalaki, and Giouvanellis (2006) Tritakis, V., Mavromichalaki, H., Giouvanellis, G.: 2006, Prediction of basic elements of the forthcoming solar cycles 24 and 25 (years 2005-2027). , American Institute of Physics Conference Series 848. ADS.
Tsirulnik, Kuznetsova, and Oraevsky (1997) Tsirulnik, L.B., Kuznetsova, T.V., Oraevsky, V.N.: 1997, Forecasting the 23^rd and 24^th solar cycles on the basis of MGM spectrum. Advances in Space Research 20(12), 2369. DOI. ADS.
UNOOSA Space Weather (2017) UNOOSA Space Weather: 2017, Special report of the inter-agency meeting on outer space activities on developments within the united nations system related to space weather. http://www.unoosa.org/oosa/oosadoc/data/documents/2017/aac.105/aac.1051146˙0.html.
Upton and Hathaway (2018) Upton, L.A., Hathaway, D.H.: 2018, An Updated Solar Cycle 25 Prediction With AFT: The Modern Minimum. Geophys. Res. Lett. 45(16), 8091. DOI. ADS.
Usoskin (2017) Usoskin, I.G.: 2017, A history of solar activity over millennia. Living Reviews in Solar Physics 14(1), 3. DOI. ADS.
Usoskin et al. (2002) Usoskin, I.G., Mursula, K., Solanki, S.K., Schüssler, M., Kovaltsov, G.A.: 2002, A physical reconstruction of cosmic ray intensity since 1610. Journal of Geophysical Research (Space Physics) 107(A11), 1374. DOI. ADS.
Versteegh (2005) Versteegh, G.J.M.: 2005, Solar Forcing of Climate. 2: Evidence from the Past. Space Sci. Rev. 120(3-4), 243. DOI. ADS.
Wang et al. (2002) Wang, J.-L., Gong, J.-C., Liu, S.-Q., Le, G.-M., Sun, J.-L.: 2002, The Prediction of Maximum Amplitudes of Solar Cycles and the Maximum Amplitude of Solar Cycle 24. Chinese J. Astron. Astrophys. 2, 557. DOI. ADS.
Wang et al. (2009) Wang, J.-L., Zong, W.-G., Le, G.-M., Zhao, H.-J., Tang, Y.-Q., Zhang, Y.: 2009, Predicting the start and maximum amplitude of solar cycle 24 using similar phases and a cycle grouping. Research in Astronomy and Astrophysics 9(2), 133. DOI. ADS.
Wang and Sheeley (2009) Wang, Y.-M., Sheeley, N.R.: 2009, Understanding the Geomagnetic Precursor of the Solar Cycle. ApJ 694(1), L11. DOI. ADS.
Watari (2008) Watari, S.: 2008, Forecasting Solar Cycle 24 using the relationship between cycle length and maximum sunspot number. Space Weather 6(12), S12003. DOI. ADS.
Xu et al. (2008) Xu, T., Wu, J., Wu, Z.-S., Li, Q.: 2008, Long-Term Sunspot Number Prediction based on EMD Analysis and AR Model. Chinese J. Astron. Astrophys. 8(3), 337. DOI. ADS.
Yeates, Nandy, and Mackay (2008) Yeates, A.R., Nandy, D., Mackay, D.H.: 2008, Exploring the Physical Basis of Solar Cycle Predictions: Flux Transport Dynamics and Persistence of Memory in Advection- versus Diffusion-dominated Solar Convection Zones. ApJ 673(1), 544. DOI. ADS.

Refer to caption — Figure 1.: Solar cycle observations. The solid green curve in Figure 1a depicts the sunspot time series from 1914.5 to 2019.5. This time series is generated utilizing the revised version of the annually averaged new sunspot number data (Clette et al., 2015) acquired from the World Data Center SILSO, Royal Observatory of Belgium. The red-dashed line denotes the mean (184.630) of all cycle amplitudes during this period and the shaded portion indicates 1 $\sigma$ (44.282) variation around the mean. In Figure 1b, we show the evolution of the polar hemispheric flux derived from Mount Wilson Observatory calibrated polar faculae data (Muñoz-Jaramillo et al., 2012) covering 1914 to 2014. This data is acquired from the solar dynamo database maintained by Andrés Muñoz-Jaramillo. We extend this plot with the calibrated Wilcox Solar Observatory polar field data till 2019.5. The blue (red) curve represents the polar flux in northern (southern) hemisphere. In Figure 1c we plot the sunspot butterfly diagram. The data for the butterfly diagram is acquired from the Royal Greenwich Observatory/USAF-NOAA active region database compiled by David H. Hathaway for the period 1914 to 2016. The subsequent data until 2019 is acquired from the Helioseismic and Magnetic Imager (HMI) instrument (Scherrer et al., 2012) on board the Solar Dynamics Observatory (SDO; Pesnell, Thompson, and Chamberlin (2012b)). Solar cycle numbers are indicated in the top and bottom panels.\ilabelfig:1

Table 1.: A list of predictions for the solar cycle 25 by different groups using diverse methods.\ilabelT-complex

Authors	Predicted SSN	Time	Category\tabnoteS: Statistical/Correlation analysis; P: Precursor technique; MB: Model Based; N: Non-linear techniques; ML/NN: Machine Learning or Neural Network method; SP: SPectral method.
Chistyakov (1983)	121	2028.5	–
Kontor et al. (1984)	117	2024	–
Quassim, Attia, and Elminir (2007)	116	2020	ML/NN
Javaraiah (2015)	42 $\pm$ 13	–	–
Li, Feng, and Li (2015)	109.1	Oct 2023	S
Pishkalo (2008)	112.37 $\pm$ 33.4	2023.4 $\pm$ 0.7	S
Li et al. (2018)	168.5 $\pm$ 16.3	Oct 2024	S
Singh and Bhargawa (2017)	102.8 $\pm$ 24.6	June 2024	S
Gopalswamy et al. (2018)	148	–	–
Helal and Galal (2013)	118.2	2022-2023	P
Pesnell and Schatten (2018)	135 $\pm$ 25	2025.2 $\pm$ 1.5	P
Bhowmik and Nandy (2018)	118	2024 $\pm$ 1	MB
Labonville, Charbonneau, and Lemerle (2019)	89-14/89+29	2025.3+0.89/2025.3-1.05	MB
Upton and Hathaway (2018)	110	–	MB
Sarp et al. (2018)	154 $\pm$ 12	2023.2 $\pm$ 1.1	N
Han and Yin (2019)	228.8 $\pm$ 40.5	2023.918 $\pm$ 1.64	S
Kakad, Kakad, and Ramesh (2017)	63 $\pm$ 11.3 or 116 $\pm$ 11.3	–	–
Sello (2019)	107 $\pm$ 10	July 2023 $\pm$ 1	N
Okoh et al. (2018)	122.1 $\pm$ 18.2	January 2025 $\pm$ 6	ML/NN
Du (2006a)	102.6 $\pm$ 22.4	–	S
Kane (2007b)	112 to 127 (mean 119)	2022-2023	SP
Du and Du (2006b)	111.6 $\pm$ 17.4	–	S
Attia, Ismail, and Basurah (2013)	90.7 $\pm$ 8	2022	ML/NN
Jiang et al. (2018)	125 $\pm$ 32	–	MB
Covas, Peixinho, and Fernandes (2019))	57 $\pm$ 17	2022-2023	ML/NN
Rigozo et al. (2011)	132.1	April 2023	SP
Hawkes and Berger (2018)	117	–	P
Petrovay et al. (2018)	130	Late 2024	P
Kitiashvili (2016)	90 $\pm$ 15	2024 $\pm$ 1	N
Hiremath (2008)	110 $\pm$ 11	2023	S
Dani and Sulistiani (2019)\tabnoteThe predicted SSN is the mean of their four predictions using different machine learning classifiers. The errorbar is chosen to include the maximum range of the predictions.	114.7-23.2/114.7+22.3	Sep 2023	ML/NN
Hathaway and Wilson (2004)	70 $\pm$ 30	2023	S
Du, Wang, and He (2006c)	144.3 $\pm$ 27.6	–	S
Abdusamatov (2007)	50 $\pm$ 15	–	S

\make@ao\writelastpage

\lastpagegivenfalse

\inarticlefalse