Progressive Random Convolutions for Single Domain Generalization
Abstract
Single domain generalization aims to train a generalizable model with only one source domain to perform well on arbitrary unseen target domains. Image augmentation based on Random Convolutions (RandConv), consisting of one convolution layer randomly initialized for each mini-batch, enables the model to learn generalizable visual representations by distorting local textures despite its simple and lightweight structure. However, RandConv has structural limitations in that the generated image easily loses semantics as the kernel size increases, and lacks the inherent diversity of a single convolution operation. To solve the problem, we propose a Progressive Random Convolution (Pro-RandConv) method that recursively stacks random convolution layers with a small kernel size instead of increasing the kernel size. This progressive approach can not only mitigate semantic distortions by reducing the influence of pixels away from the center in the theoretical receptive field, but also create more effective virtual domains by gradually increasing the style diversity. In addition, we develop a basic random convolution layer into a random convolution block including deformable offsets and affine transformation to support texture and contrast diversification, both of which are also randomly initialized. Without complex generators or adversarial learning, we demonstrate that our simple yet effective augmentation strategy outperforms state-of-the-art methods on single domain generalization benchmarks.
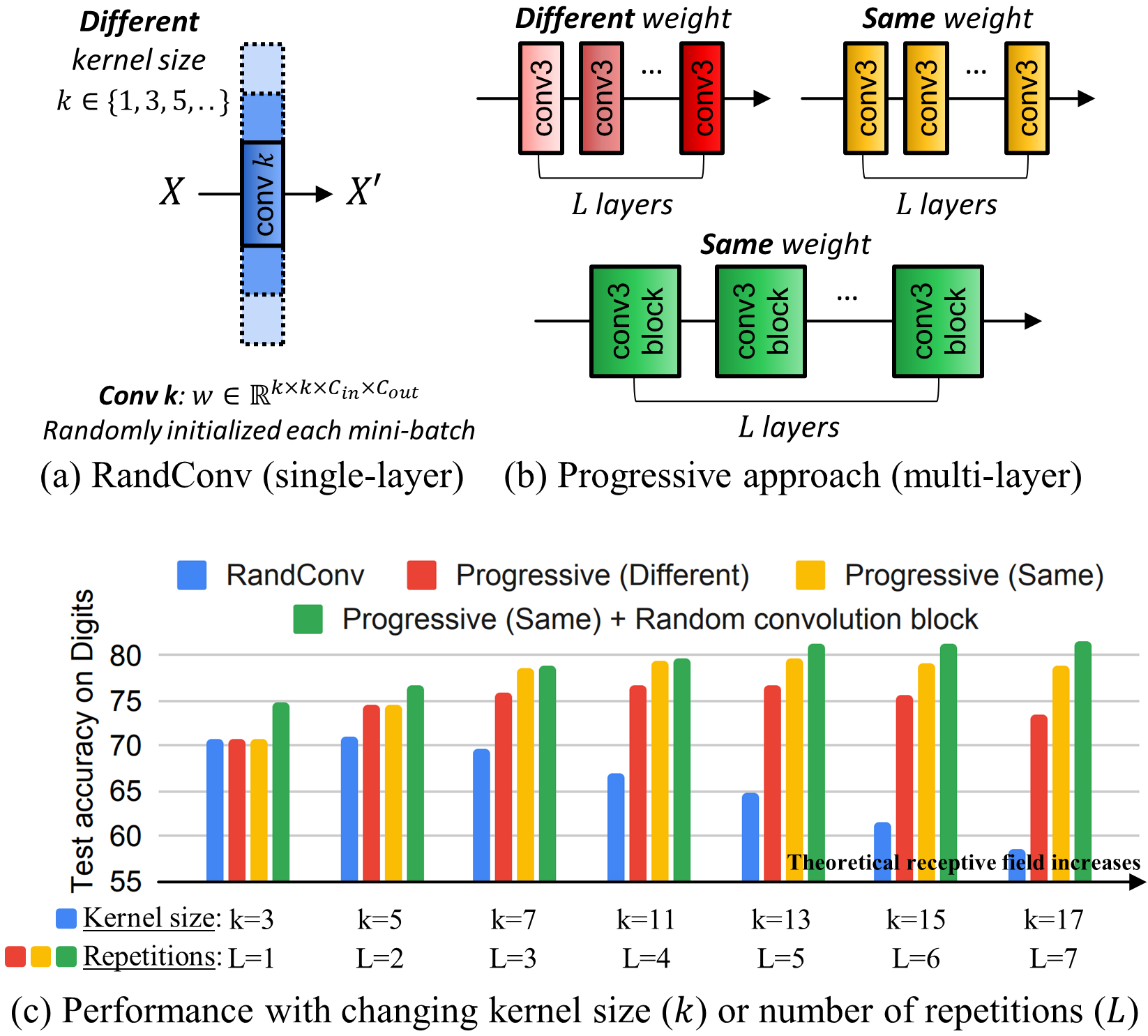
1 Introduction
††footnotetext: Qualcomm AI Research is an initiative of Qualcomm Technologies, Inc.
In recent years, deep neural networks have achieved remarkable performance in a wide range of applications [30, 31]. However, this success is built on the assumption that the test data (i.e. target) should share the same distribution as the training data (i.e. source), and they often fail to generalize to out-of-distribution data [56, 12, 24]. In practice, this domain discrepancy problem between source and target domains is commonly encountered in real-world scenarios. Especially, a catastrophic safety issue may occur in medical imaging [74, 37] and autonomous driving [71, 78] applications. To tackle this problem, one line of work focuses on domain adaptation (DA) to transfer knowledge from a source domain to a specific target domain [17, 25, 29, 6]. This approach usually takes into account the availability of labeled or unlabeled target domain data. Another line of work deals with a more realistic setting known as domain generalization (DG), which aims to learn a domain-agnostic feature representation with only data from source domains without access to target domain data. Thanks to its practicality, the task of domain generalization has been extensively studied.
In general, the paradigm of domain generalization depends on the availability of using multi-source domains [66]. Previously, many studies [45, 19, 34, 20, 5] have focused on using multi-source domains, and the distribution shift can be alleviated by simply aggregating data from multiple training domains [34, 35]. However, this approach faces practical limitations due to data collection budgets [51]. As an alternative, the single domain generalization problem has recently received attention [38, 66], which learns robust representation using only a single source domain. A common solution to this challenging problem is to generate diverse samples in order to expand the coverage of the source domain through an adversarial data augmentation scheme [79, 63]. However, most of these methods share a complicated training pipeline with multiple objective functions.
In contrast, Xu et al. suggested Random Convolution (RandConv) [70] that consists of a single convolution layer whose weights are randomly initialized for each mini-batch, as described in Fig. 1(a). When RandConv is applied to an input image, it tends to modify the texture of the input image depending on the kernel size of the convolution layer. This is a simple and lightweight image augmentation technique compared to complex generators or adversarial data augmentation. Despite these advantages, this method has structural limitations. Firstly, the image augmented by RandConv easily loses its semantics while increasing the kernel size, which is shown in Fig. 2(a). As a result, the ability to generalize in the test domain is greatly reduced as shown in Fig. 1(c). Secondly, RandConv lacks the inherent diversity of a single convolution operation.
To solve these limitations, we propose a progressive approach based on random convolutions, named Progressive Random Convolutions (Pro-RandConv). Figure 1(b) describes the progressive approach consisting of multiple convolution layers with a small kernel size. Our progressive approach has two main properties. The first is that the multi-layer structure can alleviate the semantic distortion issues by reducing the impact on pixels away from the center in the theoretical receptive field, as revealed in [41]. Therefore, the progressive approach does not degrade the performance much even if the receptive field increases, as shown in Fig. 1(c). The second property is that stacking random convolution layers of the same weights can generate more effective virtual domains rather than using different weights. This is an interesting observation that can be interpreted as gradually increasing the distortion magnitude of a single transformation to the central pixels. This approach enables more fine-grained control in image transformation than a single layer with a large kernel, which has the effect of incrementally improving style diversity.
In addition, we propose a random convolution block including deformable offsets and affine transformation to support texture and contrast diversification. It is noteworthy that all weights are also sampled from a Gaussian distribution, so our convolution block is an entirely stochastic process. Finally, we can maximize the diversity of styles while maintaining the semantics of newly generated images through the progressive method of this random convolution block, as described in Fig. 2(b). We argue that the proposed Pro-RandConv could be a strong baseline because it surpasses recent single DG methods only by image augmentation without an additional loss function or complex training pipelines. To summarize, our main contributions are as follows:
-
•
We propose a progressive approach of recursively stacking small-scale random convolutions to improve the style diversity while preserving object semantics.
-
•
We develop a random convolution layer with deformable offsets and affine transformation to promote texture and contrast diversity for augmented images.
-
•
We perform comprehensive evaluation and analyses of our method on single and multi DG benchmarks on which we produce significant improvement in recognition performance compared to other methods.
2 Related work
2.1 Domain generalization
Domain generalization aims to learn a model from source domains and generalize it to unseen target domains without access to any of the target domain data. Domain generalization is classified into single-source or multi-source depending on the number of source domains. Multi domain generalization methods tackle domain shift mostly by alignment [45, 43, 36, 13] or ensembling [42]. We note that these alignment and ensembling methods assume the existence of multiple source domains and cannot be trivially extended to the single domain generalization setup.
Single domain generalization methods rely on generating more diverse samples to expand the coverage of the source domain [63, 51, 58, 79, 38, 66]. These fictitious domains are generally created through an adversarial data augmentation scheme [63, 51]. More recently, PDEN [38] uses a progressive approach to generate novel domains by optimizing a contrastive loss function based on adversaries. In L2D [66], the authors propose to alternatively learn the stylization module and the task network by optimizing mutual information. Recently, Liu et al. [40] proposed to reduce the domain gap through geometric and textural augmentation by sampling from the distribution of augmentations for an object class. In MetaCNN [64], the authors propose to decompose convolutional features into meta features which are further processed to remove irrelevant components for better generalization. However, most of these methods have complex and dedicated training pipelines with multiple objective functions compared to our method which can generate new domains through simple augmentation.
2.2 Data augmentation
Data augmentation commonly uses manual methods for vision tasks including photometric transformations (e.g. color jitter and grayscale) and geometric transformations (e.g. translation, rotation, and shearing). To address challenges of manual data augmentation design, automatic augmentation methods [77, 62, 8, 9, 73, 72] have been proposed. AutoAugment [8] uses a reinforcement learning agent to optimize an augmentation policy while RandAugment [9] decreases the search space of AutoAugment by randomly choosing a subset of augmentation type. However, these methods are not specialized enough to deal with large domain shifts present in the single domain generalization setting.
2.3 Domain randomization
Domain randomization, normally used for robotics and autonomous vehicles, varies the scene parameters in a simulation environment to expand the training data and produce better generalization. Tobin et al. [57] pioneered domain randomization by varying different configurations of the simulated environment for robot manipulation. Yue et al. [76] extended domain randomization to semantic segmentation and proposed a pyramid consistency loss. Style randomization can also simulate novel source domains through random convolutions [70] or normalization layer modulation [27]. In our work, we also create new styles based on random convolutions [70], but we point out that there are inherent problems with the previous work. To solve these, we propose a progressive approach with a random convolution block, which can improve style diversity while maintaining semantics.
3 Background
3.1 Problem formulation
We first define the problem setting and notations. We assume that the source data is observed from a single domain , where and are the -th image and class label, and is the number of samples in the source domain. The goal of single domain generalization is to learn a domain-agnostic model with only to correctly classify the images from unseen target domains. In this case, as the training objective, we use the empirical risk minimization (ERM) [60] as follows:
| (1) |
where is the base network, including a feature extractor and a classifier, is the set of the parameters of the base network, and is a loss function measuring prediction error. Although ERM showed significant achievements on domain generalization datasets for multiple source domains [21], unfortunately, using the vanilla empirical risk minimization only with the single source domain could be sub-optimal [63, 15] and is prone to overfitting. To derive domain-agnostic feature representations, we concentrate on generating novel styles based on random convolutions.
3.2 Revisiting random convolutions
In the subsection, we briefly discuss about RandConv [70], which forms the basis of our proposed framework. This is an image augmentation technique that applies a convolution layer with random weights on the input image, as shown in Fig. 1(a). When RandConv is applied to an input image, it tends to modify the texture of the input image while keeping the shape of objects intact. Essentially, this layer is initialized differently for each mini-batch during training, making the network robust to different textures and removing the texture bias inherently present in CNNs. Mathematically, the convolution weights are sampled from a Gaussian distribution , where and are the number of image channels in the input and output, and is the kernel size of the convolution layer. The kernel size is uniformly sampled from a pool to produce multiple-scale data augmentation. Finally, we can obtain the augmented image as , where is the convolution operation. The advantage of RandConv is simple and lightweight compared to complex generators or adversarial data augmentation.
However, RandConv suffers from structural limitations. Firstly, a large-sized kernel can become an ineffective data augmentation type that interferes with learning generalizable visual representations due to excessively increased randomness and semantic distortions. In particular, this issue occurs more frequently as a larger range of pixels is affected as the kernel size increases. Figure 2(a) shows that artificial patterns can be easily created from large-sized kernels. As a result, as the kernel size increases, the generalization ability in the test domain cannot be prevented from dropping sharply, as shown in Fig. 1(c). Secondly, RandConv lacks the inherent diversity of a single convolution operation. In this paper, we strive to address these limitations of RandConv through a progressive augmentation scheme and an advanced design that can create more diverse styles.
4 Proposed method
4.1 Progressive random convolutions
We aim to improve the style diversity while maintaining class-specific semantic information, which is a common goal of most data augmentation methods [63, 79, 51, 66, 38] in domain generalization. To this end, we propose a progressive approach that repeatedly applies a convolution layer with a small kernel to the image. The structure of our method is described in Fig. 1(b). Our progressive approach has two main properties. The first property is that pixels at the center of a theoretical receptive field have a much larger impact on output like a Gaussian, which is discussed in [41]. As a result, it tends to relax semantic distortions by reducing the influence of pixels away from the center. The second property is that stacking random convolution layers of the same weights can create more effective virtual domains by gradually increasing the style diversity. This approach enables more fine-grained control in image transformation. Especially, using multiple kernels with the same weight enables a more balanced and consistent application of a single transformation, whereas using different weights for each layer can result in overexposure to various transformation sets, leading to semantic distortion easily. As shown in Fig. 1(c), our innovative change from a large kernel size to a progressive approach contributes to substantial performance improvement.
4.2 Random convolution block
To create more diverse styles, we introduce an advanced design in which a single convolution layer is replaced with a random convolution block while preserving the progressive structure, which is depicted in Fig. 3. In addition to a convolution layer, our convolution block consists of a sequence of deformable convolution, standardization, affine transform, and hyperbolic tangent function to support texture and contrast diversification. We emphasize that all parameters in the convolution block are sampled differently for each mini-batch, but are used the same in the progressive process without additional initialization as with the second property in the previous subsection.
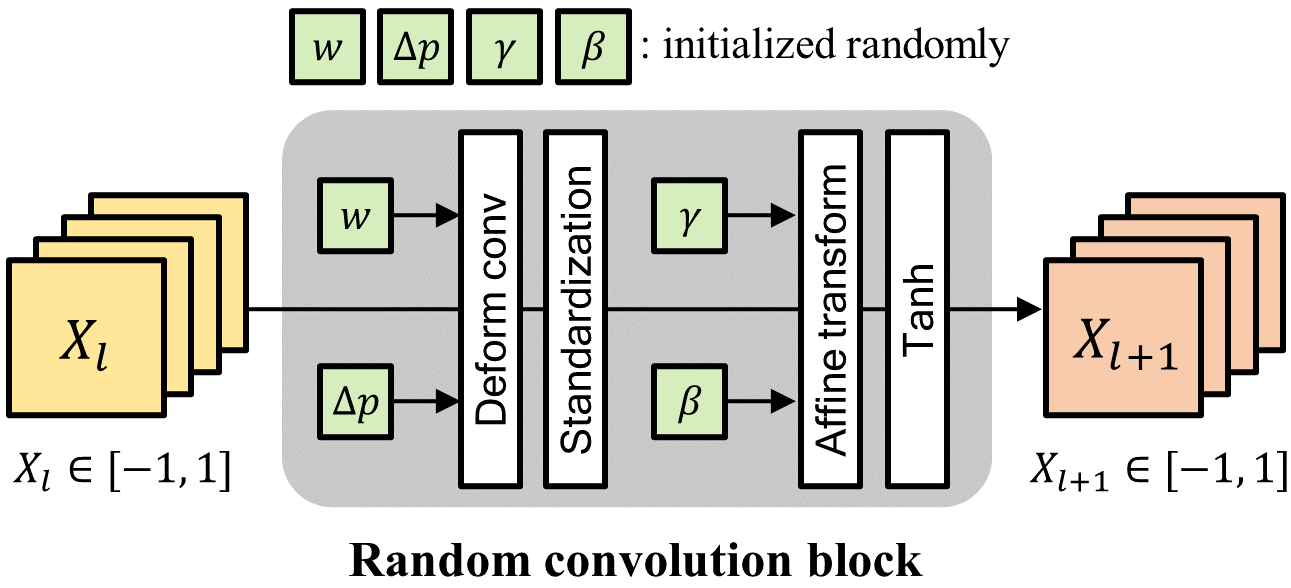
Texture diversification
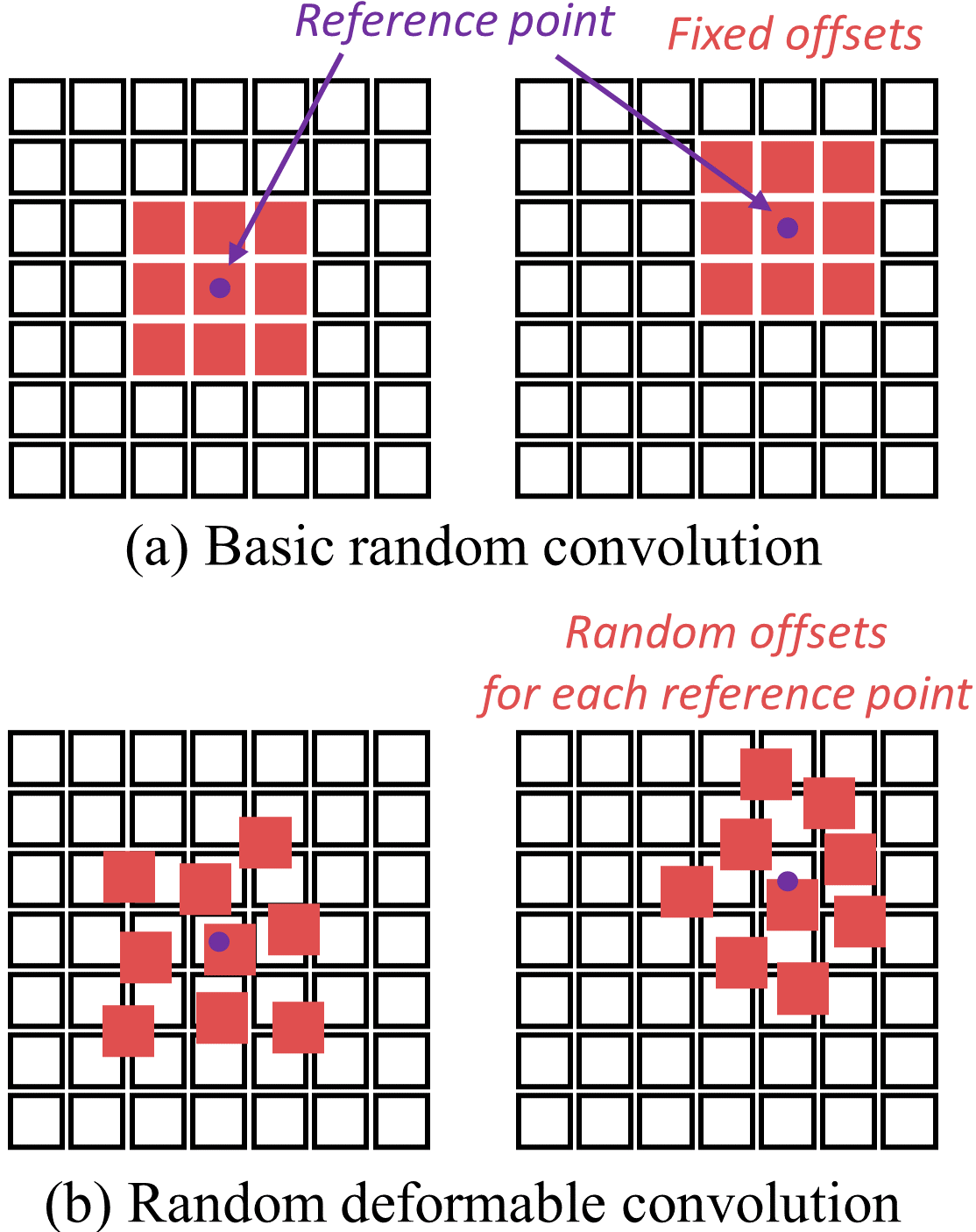
Given the randomized convolution weights, the conventional convolution is applied equally to each position in the image, as shown in Fig. 4(a). We develop the random convolution operation by relaxing the constraints on the fixed grid, which can further increase the diversity of texture modifications. We adopt a deformable convolution layer [10] with randomly initialized offsets, which is a generalized version of the random convolution layer [70]. We assume the 2D deformable convolution with a regular grid . For example, means a 33 kernel with dilation 1. The operation of deformable convolution can be expressed as
| (2) |
where , indicate the locations in the regular grid, is weights of the 2D convolution kernel, and , are random offsets of deformable convolution. For clarity, input and output channels are omitted. Each location on the output image is transformed by the weighted summation of weights and the pixel values on irregular locations of the input image , which is described in Fig. 4(b). When all offsets , are allocated to zero-values, this equation is equivalent to the original random convolution layer [70]. The offsets in deformable convolution can be considered as an extremely lightweight spatial transformer (STN) [28], encouraging the generation of more diverse samples that include geometric transformations. For example, when kernel size is 1, our deformable convolution covers translation as well, while the original random convolution layer changes only color.
Contrast diversification
According to [70], assuming that the input pixel values follow the standard normal distribution, the output passed through a random convolution layer should follow the same distribution. However, when the input or convolution weights do not have an ideal distribution, the output distribution may be gradually saturated during the progressive process. To avoid this issue and diversify global style, we propose a contrast diversification method that intentionally changes the distribution of the output randomly. Given an image augmented by random convolution, we standardize the image to have zero mean and unit variance. Then, we apply an affine transformation using the randomly initialized affine parameters and as follows:
| (3) |
| (4) |
where , are the per-channel mean and variance, respectively, and , are height and width of the image. Finally, the hyperbolic tangent function transforms the image into a range between and . This entire modeling can be interpreted as a process of random gamma correction.
Initialization
Finally, we introduce initialization strategies. All parameters in the random convolution block are sampled from a Gaussian distribution , as shown in Algorithm 1. However, we apply practical techniques for convolution weights and deformable offsets to control excessive texture deformation and induce realistic transformations. For convolution weights, we multiply the convolution kernel element-wise with a Gaussian filter , where . Specifically, is randomly sampled per mini-batch, so the smoothing effect is different each time. This technique can be used to alleviate the problem of severely distorted object semantics when the random offset of the deformation convolution is too irregular. Next, we use a Gaussian Random Field111https://github.com/bsciolla/gaussian-random-fields (GRF) as an initialization method for deformable offsets to induce natural geometric changes. All values of GRF basically follow a Gaussian distribution, but spatial correlation can be controlled by coefficients of the power spectrum.
Input: Source domain
Output: Trained network
4.3 Training pipeline
For each mini-batch, we initialize a random convolution block , and then progressively augment a set of images by the selected number of repetitions . In the end, we train a network by minimizing the empirical risk in Eq. 1 realized as the cross-entropy loss of the original and augmented images.222Besides using both original and augmented images, other strategies for choosing images to augment are explored in the supplementary Section 3. Algorithm 1 shows the entire training process, which is simple and easy to implement. Note that it does not require additional loss functions or complex training pipelines.
5 Experiments
5.1 Datasets and settings
Digits dataset consists of five sub-datasets: MNIST [33], SVHN [47], MNIST-M [17], SYN [17], and USPS [11]. Each sub-dataset is regarded as a different domain containing 10-digit handwritten images in a different style. PACS [34] contains four domains (Art, Cartoon, Photo, and Sketch), and each domain shares seven object categories (dog, elephant, giraffe, guitar, house, horse, and person). This dataset includes 9,991 images. OfficeHome [61] is an object recognition benchmark consisting of four domains (Art, Clipart, Product, and Real-World). The whole dataset consists of 15,500 images across 65 classes. VLCS [59] is an image classification dataset that contains 10,729 images aggregated from four datasets (PASCAL VOC 2007 [14], LabelMe [54], Caltech101 [16], and Sun09 [67]) across five shared categories (bird, car, chair, dog, and person). In addition, we extend our work to the task of semantic segmentation.333Segmentation results are covered in the supplementary Section 2.
Implementation details
In Digits, we utilize LeNet [32] as a base network. We train the network using SGD with batch size 64, momentum 0.9, initial learning rate 0.01, and cosine learning rate scheduling for 500 epochs. All images are resized to 3232 pixels. In PACS, OfficeHome, and VLCS, we employ AlexNet [30], ResNet18 [23], and ResNet50 [23], respectively. We train the network using SGD with batch size 64, momentum 0.9, initial learning rate 0.001, and cosine learning rate scheduling for 50 epochs and 150 epochs in single DG and multi DG experiments, respectively. All images are resized to 224224. For a fair comparison, we follow the experimental protocol as in [82, 40]. We used in-domain validation sets to choose the best model from multiple saved checkpoints during training, as Training-Domain Validation in DomainBed [21].
Unlike RandConv [70], we fix the kernel size of the convolution to 3 and set the maximum number of repetitions to 10, which means that for each mini-batch, the convolution block is recursively stacked a different number of times chosen between 1 and 10. For initialization, we set to , known as He-initialization [22]. Furthermore, we re-weight the convolution weights once more by Gaussian smoothing , where the scale is sampled from , where indicates a small value. We sample the deformable offsets from , where the scale is sampled from uniform distribution as . We use of 0.2 for Digits and 0.5 for other datasets because the deformation scale is affected by the size of the image. In contrast diversification, we set both and to 0.5. Please refer to the supplementary Section 6 for more details.
5.2 Evaluation of single domain generalization
| Methods | SVHN | MNIST-M | SYN | USPS | Avg. |
| CCSA [44] | 25.89 | 49.29 | 37.31 | 83.72 | 49.05 |
| d-SNE [69] | 26.22 | 50.98 | 37.83 | 93.16 | 52.05 |
| JiGen [2] | 33.80 | 57.80 | 43.79 | 77.15 | 53.14 |
| ADA [63] | 35.51 | 60.41 | 45.32 | 77.26 | 54.62 |
| M-ADA [51] | 42.55 | 67.94 | 48.95 | 78.53 | 59.49 |
| ME-ADA [79] | 42.56 | 63.27 | 50.39 | 81.04 | 59.32 |
| L2D [66] | 62.86 | 87.30 | 63.72 | 83.97 | 74.46 |
| PDEN [38] | 62.21 | 82.20 | 69.39 | 85.26 | 74.77 |
| MetaCNN [64] | 66.50 | 88.27 | 70.66 | 89.64 | 78.76 |
| Baseline (ERM) | 32.52 | 54.92 | 42.34 | 78.21 | 52.00 |
| RandConv* [70] | 61.66 | 84.53 | 67.87 | 85.31 | 74.84 |
| Progressive (Diff) | 60.73 | 78.47 | 71.46 | 88.20 | 74.72 |
| Progressive (Same) | 65.67 | 76.26 | 77.13 | 93.98 | 78.26 |
| Pro-RandConv | 69.67 | 82.30 | 79.77 | 93.67 | 81.35 |
| Methods | Art | Cartoon | Photo | Sketch | Avg. |
| JiGen [2] | 67.70 | 72.23 | 41.70 | 36.83 | 54.60 |
| ADA [63] | 72.43 | 71.97 | 44.63 | 45.73 | 58.70 |
| SagNet [46] | 73.20 | 75.67 | 48.53 | 50.07 | 61.90 |
| GeoTexAug [40] | 72.07 | 78.70 | 49.07 | 59.97 | 65.00 |
| L2D [66] | 76.91 | 77.88 | 52.29 | 53.66 | 65.18 |
| Baseline (ERM) | 74.64 | 73.36 | 56.31 | 48.27 | 63.15 |
| RandConv* [70] | 76.93 | 76.47 | 62.46 | 54.13 | 67.50 |
| Progressive (Diff) | 75.46 | 75.39 | 60.02 | 55.02 | 66.47 |
| Progressive (Same) | 76.81 | 78.27 | 62.38 | 56.08 | 68.39 |
| Pro-RandConv | 76.98 | 78.54 | 62.89 | 57.11 | 68.88 |
Results on Digits
In Table 1, we compare our proposed method in the Digits benchmark. We use MNIST as the source domain and train the model with the first 10,000 samples from 60,000 training images. The remaining four sub-datasets are employed as the target domains. We observed that our method has the following properties: 1) Our method outperforms data augmentation methods444Policy-based image augmentation methods (i.e. AutoAugment and RandAugment) are discussed in the supplementary Section 5. based on adversarial learning (ADA [63], ME-ADA [79], M-ADA [51], L2D [66], and PDEN [38]) only by image augmentation without a complicated training pipeline or multiple objective functions. 2) Compared with the PDEN method that progressively expands the domain using a learning-based generator, our method shows that the domain can be expanded through a simple random convolution block without learning. 3) The SVHN, SYN, and USPS datasets have a large domain gap with MNIST in terms of font shapes. Our Pro-RandConv method produces significantly improved recognition performance compared to RandConv [70] on these domains due to the progressive approach.
Results on PACS
We also compare our method on the challenging PACS benchmark, as shown in Table 2. Our method outperforms all of the competitors by a large margin. It is noteworthy that generalizable representations can be learned with a simple image augmentation by random convolutions, unlike a geometric and textural augmentation method [40] that borrows elaborate sub-modules (e.g. an arbitrary neural artistic stylization network [18] and a geometric warping network [39]) to generate novel styles. Compared to the existing RandConv [70], the performance improvement on cartoon and sketch domains is remarkable.
5.3 Evaluation of multi domain generalization
To further validate the performance of our method, we conducted multi DG experiments on PACS. In multi DG experiments, we use a leave-one-domain-out protocol, where we choose one domain as the test domain and use the remaining three as source domains for model training. Table 3 shows that our method outperforms other DG methods except for Fourier Augmented Co-Teacher (FACT) [68] and Geometric and Textural Augmentation (GeoTexAug) [40]. It is meaningful that the performance is much more competitive than the traditional RandConv [70]. This proves that the progressive approach and diversification techniques are highly effective.
| Methods | Art | Cartoon | Photo | Sketch | Avg. |
| ResNet-18 | |||||
| Jigen [2] | 79.42 | 75.25 | 96.03 | 71.35 | 80.51 |
| MASF [13] | 80.29 | 77.17 | 94.99 | 71.68 | 81.03 |
| ADA [63] | 78.32 | 77.65 | 95.61 | 74.21 | 81.44 |
| Epi-FCR [35] | 82.10 | 77.00 | 93.90 | 73.00 | 81.50 |
| MetaReg [1] | 83.70 | 77.20 | 95.50 | 70.30 | 81.70 |
| ME-ADA [79] | 78.61 | 78.65 | 95.57 | 75.59 | 82.10 |
| EISNet [65] | 81.89 | 76.44 | 95.93 | 74.33 | 82.15 |
| InfoDrop [55] | 80.27 | 76.54 | 96.11 | 76.38 | 82.33 |
| L2A-OT [81] | 83.30 | 78.20 | 96.20 | 73.60 | 82.80 |
| DDAIG [80] | 84.20 | 78.10 | 95.30 | 74.70 | 83.10 |
| SagNet [46] | 83.58 | 77.66 | 95.47 | 76.30 | 83.25 |
| MixStyle [82] | 84.10 | 78.80 | 96.10 | 75.90 | 83.70 |
| L2D [66] | 81.44 | 79.56 | 95.51 | 80.58 | 84.27 |
| FACT [68] | 85.37 | 78.38 | 95.15 | 79.15 | 84.51 |
| Baseline (ERM) | 81.54 | 80.06 | 95.80 | 68.40 | 81.45 |
| RandConv* [70] | 80.15 | 78.04 | 93.65 | 77.88 | 82.43 |
| Pro-RandConv | 83.15 | 81.07 | 96.24 | 76.71 | 84.29 |
| ResNet-50 | |||||
| MASF [13] | 82.89 | 80.49 | 95.01 | 72.29 | 82.67 |
| MetaReg [1] | 87.20 | 79.20 | 97.60 | 70.30 | 83.60 |
| EISNet [65] | 86.64 | 81.53 | 97.11 | 78.07 | 85.84 |
| FACT [68] | 89.63 | 81.77 | 96.75 | 84.46 | 88.15 |
| GeoTexAug [40] | 89.98 | 83.84 | 98.10 | 84.75 | 89.17 |
| Baseline (ERM) | 87.15 | 83.82 | 97.77 | 73.71 | 85.61 |
| RandConv* [70] | 86.13 | 82.00 | 96.65 | 81.72 | 86.63 |
| Pro-RandConv | 89.28 | 84.13 | 97.83 | 81.85 | 88.27 |
5.4 Discussion
| Dataset | Model | Single DG | Multi DG | ||||
| RC [70] | P-RC | RC [70] | P-RC | ||||
| Alex | 60.71 | 62.59 | 1.88 | 72.49 | 74.91 | 2.42 | |
| PACS | Res18 | 67.50 | 68.88 | 1.38 | 82.43 | 84.29 | 1.86 |
| Res50 | 72.33 | 73.26 | 0.93 | 86.63 | 88.27 | 1.64 | |
| Office Home | Alex | 42.04 | 43.25 | 1.21 | 53.92 | 55.71 | 1.79 |
| Res18 | 50.61 | 51.32 | 0.71 | 63.08 | 64.59 | 1.51 | |
| Res50 | 58.57 | 59.20 | 0.63 | 68.83 | 69.89 | 1.06 | |
| Alex | 56.80 | 60.70 | 3.90 | 69.74 | 71.30 | 1.56 | |
| VLCS | Res18 | 53.05 | 53.35 | 0.30 | 67.83 | 69.55 | 1.72 |
| Res50 | 53.57 | 54.23 | 0.66 | 70.26 | 71.68 | 1.42 | |
Comparative analysis with RandConv
In Table. 4, we compare RandConv [70] and Pro-RandConv using AlexNet [30], ResNet18 [23] and ResNet50 [23] models on PACS, OfficeHome, and VLCS datasets. We emphasize that the proposed Pro-RandConv outperforms RandConv in all datasets and all models. In addition, this performance improvement is more pronounced in multi DG experiments. Through these results, we show that our progressive approach using a random convolution block significantly contributes to the improvement of generalization capability by generating more effective virtual domains.
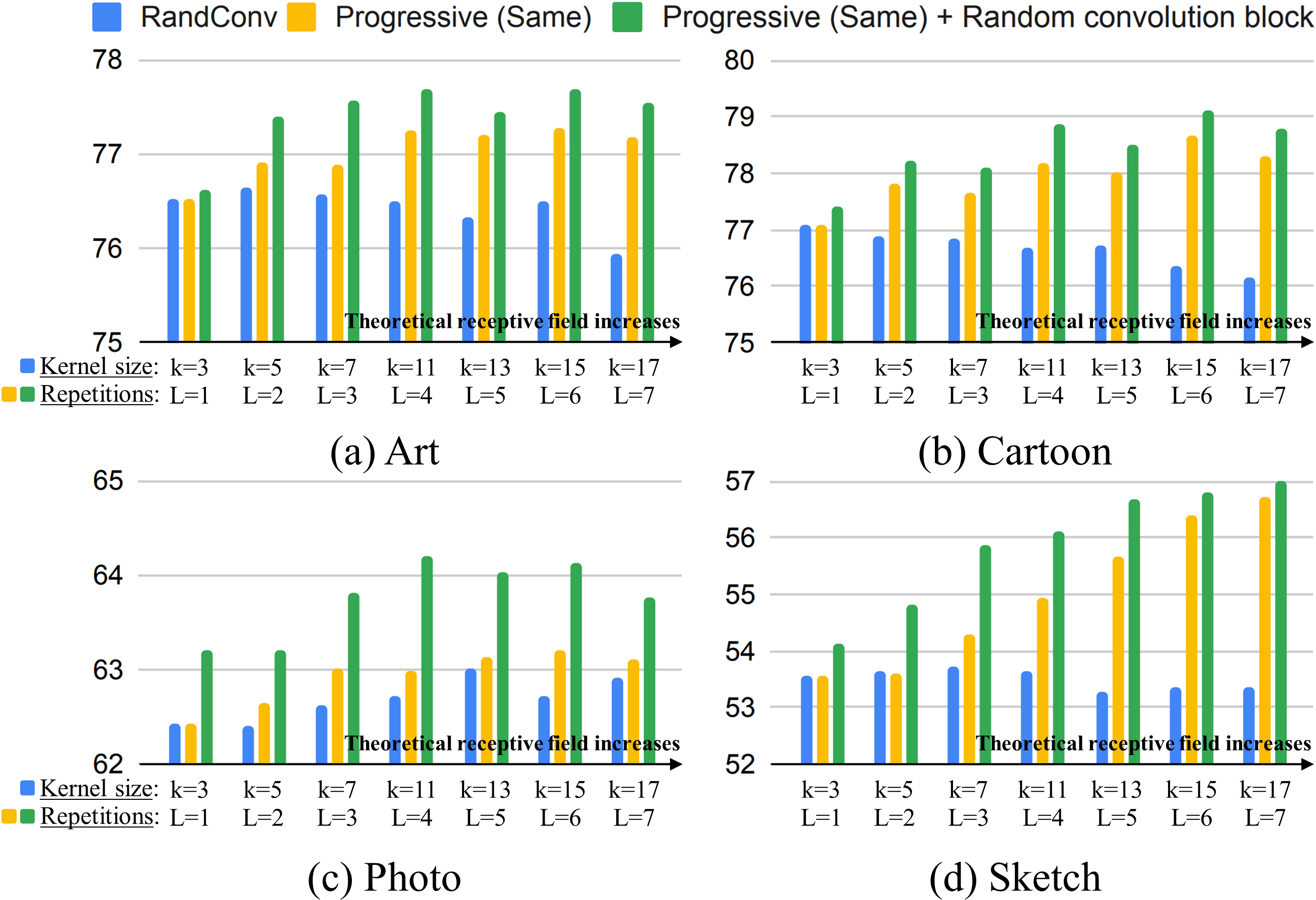
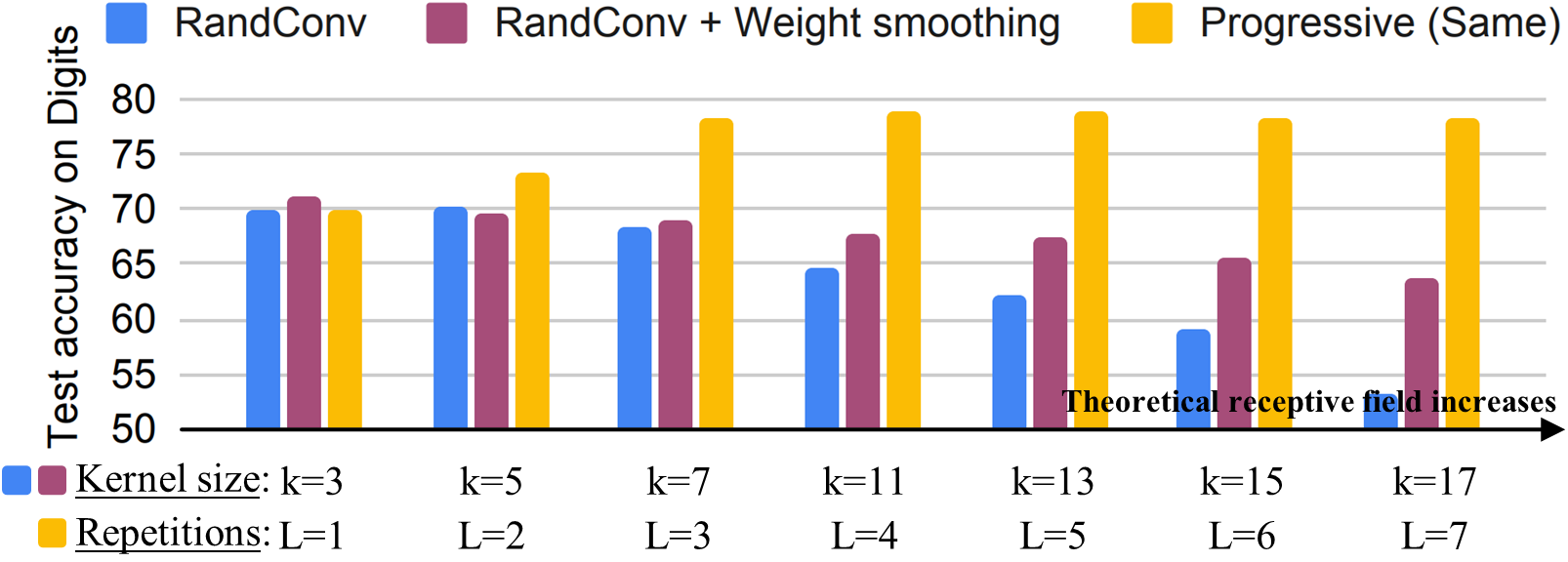
In Fig. 5, we compare RandConv with our progressive models on PACS. Since the image size of PACS is larger than that of digits, the performance does not drop sharply as the kernel size of RandConv increases. However, the ability of RandConv to create novel styles for learning domain generalizable representations is significantly different from that of the progressive model with the same weight (blueyellow). In other words, using a large-sized kernel is a less effective data augmentation technique compared to the repeated use of a small-sized kernel. This can be considered an inherent problem of the single convolution operation in RandConv. In addition, the performance gap between the presence and absence of random convolution blocks is the largest in the photo domain, which is a meaningful observation that diversification techniques work well on realistic images (yellowgreen).
We hypothesized that the progressive approach with equal weights works well for two reasons: The first is to mitigate semantic distortion by reducing the influence of pixels away from the center, and the second is to create effective virtual domains by gradually increasing the distortion magnitude to the central pixels. To indirectly validate the first assumption, we applied Gaussian smoothing to a convolution kernel of RandConv. Figure 6 shows that the performance decreases less compared to the conventional RandConv as the size of the kernel increases. In other words, the Gaussian-like effective receptive field [41] can help mitigate semantic distortion. Beyond that, the reason why the progressive approach performs much better is that even if the effective receptive field is similar, our progressive approach enables more fine-grained control in image transformation than a single layer with randomly initialized.
Analysis on texture and contrast diversification
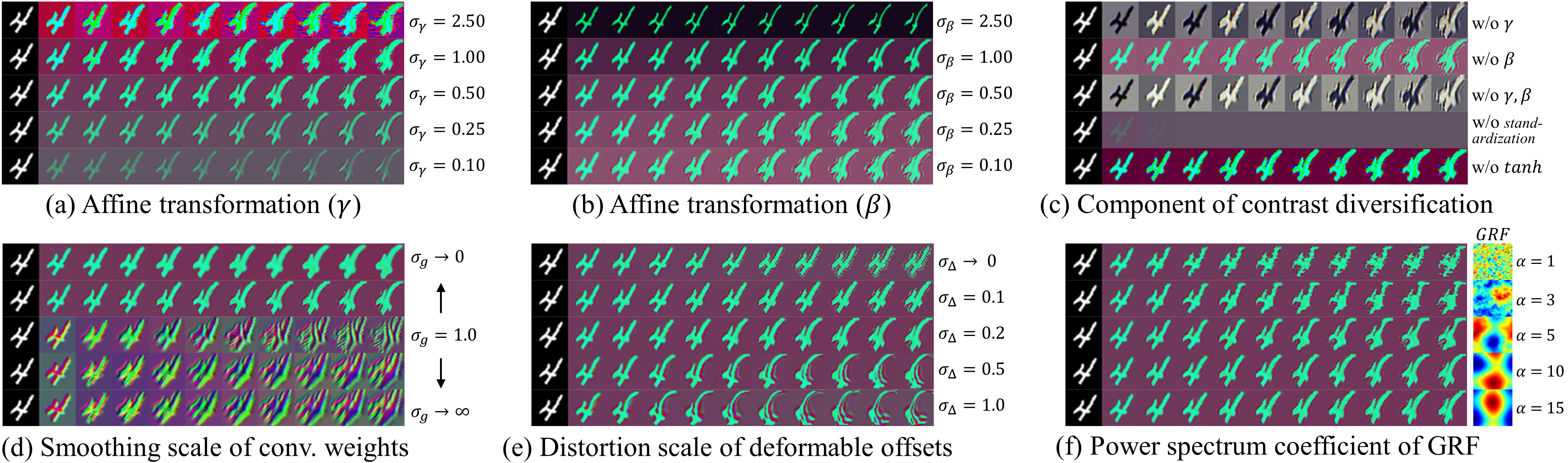
We introduce the effects of contrast diversification and texture diversification through qualitative results. First, contrast diversification consists of affine transformation, standardization, and hyperbolic tangent function, as shown in Fig. 3. Figure 7(a) and (b) show that gamma correction is differently performed according to and in affine transformation. If the standard deviation for affine transformation is too large or too small, erroneous distortion or saturation can occur in the image. In Fig. 7(c), we check the qualitative results by disabling individual components one by one. If there is no affine transformation, the contrast diversity is limited because the texture or color of the image is just determined by the input distribution and the convolution weight. When a standardization layer is removed, a saturation problem occurs. Finally, the hyperbolic tangent function reduces the image saturation and stabilizes the distribution.
Next, Fig. 7(d) shows the result of applying Gaussian smoothing to the 33 convolution kernel of Pro-RandConv. When approaches 0. it simulates a 11 kernel. When approaches infinity, it simulates a normal 33 kernel ignoring smoothing. This implies that we can suppress excessive deformation of texture through this smoothing function. We sample it from a uniform distribution as to reduce the sensitivity of the hyperparameter. Figure 7(e) shows the distortion scale of deformable offsets. This parameter is related to image size, so we use different values considering the image size. Figure 7(f) shows the coefficients of the power spectrum in a Gaussian Random Field. The lower the coefficient, the more similar the shape of the white noise. We use reasonably high values to induce natural transformations. Please refer to supplementary Sections 4 and 6 for component analysis of Pro-RandConv and hyperparameter selection.
| Digits | Size:[3,32,32] | Training | Inference | Acc | |||
| Methods | Versions | Memory | Time | MACs | Time | (%) |
| ERM | - | 2.11GB | 3.30ms | 28.77M | 0.53ms | 52.00 |
| PDEN [38] | - | 2.39GB | 31.8ms | 73.89 | ||
| RandConv [70] | w/o KLD | 2.11GB | 4.67ms | 73.74 | ||
| w/ KLD (default) | 2.22GB | 13.0ms | 74.84 | |||
| Ours | Progressive (Same) | 2.17GB | 6.47ms | 78.26 | ||
| + RC Block | 2.17GB | 12.0ms | 81.35 | |||
Computational complexity and inference time
In the training process, the computational complexity (MACs) is increased by 0.45M in RandConv and 0.92M in Pro-RandConv, representing a relatively small increase of 2-3% compared to the base model (28.77M MACs). And the training time also increases, primarily caused by the Kullback-Leibler (KL) divergence loss in RandConv and the initialization process of the deformable operator in Pro-RandConv. However, we note that the training efficiency of Pro-RandConv is comparable to that of competitors (RandConv and PDEN [38]), as shown in Table 5. Moreover, image augmentation is not utilized during inference, so it does not affect complexity or time in inference.
6 Conclusion
We proposed Pro-RandConv as an effective image augmentation technique to enhance generalization performance in domain generalization tasks. Our approach involves progressively applying small-scale random convolutions instead of a single large-scale convolution. Furthermore, we allow deformable offsets and affine transformations to promote texture and contrast diversity. We evaluated the effectiveness of our method on both single and multi-domain generalization benchmarks and found that it outperformed recent competitors significantly. We also conducted a comprehensive analysis to show that Pro-RandConv produces qualitative and quantitative improvements over the RandConv method. In the future, we look forward to seeing its impact on improving generalization performance in real-world scenarios.
References
- [1] Yogesh Balaji, Swami Sankaranarayanan, and Rama Chellappa. Metareg: Towards domain generalization using meta-regularization. Advances in neural information processing systems, 31, 2018.
- [2] Fabio M Carlucci, Antonio D’Innocente, Silvia Bucci, Barbara Caputo, and Tatiana Tommasi. Domain generalization by solving jigsaw puzzles. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2229–2238, 2019.
- [3] Liang-Chieh Chen, Yukun Zhu, George Papandreou, Florian Schroff, and Hartwig Adam. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European conference on computer vision (ECCV), pages 801–818, 2018.
- [4] Sungha Choi, Sanghun Jung, Huiwon Yun, Joanne T Kim, Seungryong Kim, and Jaegul Choo. Robustnet: Improving domain generalization in urban-scene segmentation via instance selective whitening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11580–11590, 2021.
- [5] Seokeon Choi, Taekyung Kim, Minki Jeong, Hyoungseob Park, and Changick Kim. Meta batch-instance normalization for generalizable person re-identification. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, pages 3425–3435, 2021.
- [6] Sungha Choi, Seunghan Yang, Seokeon Choi, and Sungrack Yun. Improving test-time adaptation via shift-agnostic weight regularization and nearest source prototypes. In Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part XXXIII, pages 440–458. Springer, 2022.
- [7] Marius Cordts, Mohamed Omran, Sebastian Ramos, Timo Rehfeld, Markus Enzweiler, Rodrigo Benenson, Uwe Franke, Stefan Roth, and Bernt Schiele. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3213–3223, 2016.
- [8] Ekin D. Cubuk, Barret Zoph, Dandelion Mane, Vijay Vasudevan, and Quoc V. Le. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.
- [9] Ekin D Cubuk, Barret Zoph, Jonathon Shlens, and Quoc V Le. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pages 702–703, 2020.
- [10] Jifeng Dai, Haozhi Qi, Yuwen Xiong, Yi Li, Guodong Zhang, Han Hu, and Yichen Wei. Deformable convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 764–773, 2017.
- [11] JS Denker, WR Gardner, HP Graf, D Henderson, RE Howard, W Hubbard, LD Jackel, HS Baird, and I Guyon. Advances in neural information processing systems 1. chapter neural network recognizer for hand-written zip code digits. 1989.
- [12] Josip Djolonga, Jessica Yung, Michael Tschannen, Rob Romijnders, Lucas Beyer, Alexander Kolesnikov, Joan Puigcerver, Matthias Minderer, Alexander D’Amour, Dan Moldovan, et al. On robustness and transferability of convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 16458–16468, 2021.
- [13] Qi Dou, Daniel Coelho de Castro, Konstantinos Kamnitsas, and Ben Glocker. Domain generalization via model-agnostic learning of semantic features. Advances in Neural Information Processing Systems, 32:6450–6461, 2019.
- [14] Mark Everingham and John Winn. The pascal visual object classes challenge 2007 (voc2007) development kit. University of Leeds, Tech. Rep, 2007.
- [15] Xinjie Fan, Qifei Wang, Junjie Ke, Feng Yang, Boqing Gong, and Mingyuan Zhou. Adversarially adaptive normalization for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8208–8217, 2021.
- [16] Li Fei-Fei, Rob Fergus, and Pietro Perona. Learning generative visual models from few training examples: An incremental bayesian approach tested on 101 object categories. In 2004 conference on computer vision and pattern recognition workshop, pages 178–178. IEEE, 2004.
- [17] Yaroslav Ganin and Victor Lempitsky. Unsupervised domain adaptation by backpropagation. In International conference on machine learning, pages 1180–1189. PMLR, 2015.
- [18] Golnaz Ghiasi, Honglak Lee, Manjunath Kudlur, Vincent Dumoulin, and Jonathon Shlens. Exploring the structure of a real-time, arbitrary neural artistic stylization network. arXiv preprint arXiv:1705.06830, 2017.
- [19] Muhammad Ghifary, W Bastiaan Kleijn, Mengjie Zhang, and David Balduzzi. Domain generalization for object recognition with multi-task autoencoders. In Proceedings of the IEEE international conference on computer vision, pages 2551–2559, 2015.
- [20] Thomas Grubinger, Adriana Birlutiu, Holger Schöner, Thomas Natschläger, and Tom Heskes. Multi-domain transfer component analysis for domain generalization. Neural processing letters, 46(3):845–855, 2017.
- [21] Ishaan Gulrajani and David Lopez-Paz. In search of lost domain generalization. arXiv preprint arXiv:2007.01434, 2020.
- [22] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision, pages 1026–1034, 2015.
- [23] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- [24] Dan Hendrycks, Steven Basart, Norman Mu, Saurav Kadavath, Frank Wang, Evan Dorundo, Rahul Desai, Tyler Zhu, Samyak Parajuli, Mike Guo, et al. The many faces of robustness: A critical analysis of out-of-distribution generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 8340–8349, 2021.
- [25] Judy Hoffman, Eric Tzeng, Taesung Park, Jun-Yan Zhu, Phillip Isola, Kate Saenko, Alexei Efros, and Trevor Darrell. Cycada: Cycle-consistent adversarial domain adaptation. In International conference on machine learning, pages 1989–1998. PMLR, 2018.
- [26] Lei Huang, Yi Zhou, Fan Zhu, Li Liu, and Ling Shao. Iterative normalization: Beyond standardization towards efficient whitening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4874–4883, 2019.
- [27] Philip TG Jackson, Amir Atapour Abarghouei, Stephen Bonner, Toby P Breckon, and Boguslaw Obara. Style augmentation: data augmentation via style randomization. In CVPR Workshops, volume 6, pages 10–11, 2019.
- [28] Max Jaderberg, Karen Simonyan, Andrew Zisserman, et al. Spatial transformer networks. Advances in neural information processing systems, 28, 2015.
- [29] Taekyung Kim, Minki Jeong, Seunghyeon Kim, Seokeon Choi, and Changick Kim. Diversify and match: A domain adaptive representation learning paradigm for object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12456–12465, 2019.
- [30] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems, 25, 2012.
- [31] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. nature, 521(7553):436–444, 2015.
- [32] Yann LeCun, Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, and Lawrence D Jackel. Backpropagation applied to handwritten zip code recognition. Neural computation, 1(4):541–551, 1989.
- [33] Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- [34] Da Li, Yongxin Yang, Yi-Zhe Song, and Timothy M Hospedales. Deeper, broader and artier domain generalization. In Proceedings of the IEEE international conference on computer vision, pages 5542–5550, 2017.
- [35] Da Li, Jianshu Zhang, Yongxin Yang, Cong Liu, Yi-Zhe Song, and Timothy M Hospedales. Episodic training for domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1446–1455, 2019.
- [36] Haoliang Li, Sinno Jialin Pan, Shiqi Wang, and Alex C Kot. Domain generalization with adversarial feature learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5400–5409, 2018.
- [37] Haoliang Li, YuFei Wang, Renjie Wan, Shiqi Wang, Tie-Qiang Li, and Alex Kot. Domain generalization for medical imaging classification with linear-dependency regularization. Advances in Neural Information Processing Systems, 33:3118–3129, 2020.
- [38] Lei Li, Ke Gao, Juan Cao, Ziyao Huang, Yepeng Weng, Xiaoyue Mi, Zhengze Yu, Xiaoya Li, and Boyang Xia. Progressive domain expansion network for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 224–233, 2021.
- [39] Xiao-Chang Liu, Yong-Liang Yang, and Peter Hall. Learning to warp for style transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 3702–3711, 2021.
- [40] Xiao-Chang Liu, Yong-Liang Yang, and Peter Hall. Geometric and textural augmentation for domain gap reduction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14340–14350, 2022.
- [41] Wenjie Luo, Yujia Li, Raquel Urtasun, and Richard Zemel. Understanding the effective receptive field in deep convolutional neural networks. Advances in neural information processing systems, 29, 2016.
- [42] Massimiliano Mancini, Samuel Rota Bulo, Barbara Caputo, and Elisa Ricci. Best sources forward: domain generalization through source-specific nets. In 2018 25th IEEE International Conference on Image Processing (ICIP), pages 1353–1357. IEEE, 2018.
- [43] Saeid Motiian, Quinn Jones, Seyed Iranmanesh, and Gianfranco Doretto. Few-shot adversarial domain adaptation. In Advances in Neural Information Processing Systems, pages 6670–6680, 2017.
- [44] Saeid Motiian, Marco Piccirilli, Donald A Adjeroh, and Gianfranco Doretto. Unified deep supervised domain adaptation and generalization. In Proceedings of the IEEE International Conference on Computer Vision, pages 5715–5725, 2017.
- [45] Krikamol Muandet, David Balduzzi, and Bernhard Schölkopf. Domain generalization via invariant feature representation. In International Conference on Machine Learning, pages 10–18, 2013.
- [46] Hyeonseob Nam, HyunJae Lee, Jongchan Park, Wonjun Yoon, and Donggeun Yoo. Reducing domain gap by reducing style bias. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8690–8699, 2021.
- [47] Yuval Netzer, Tao Wang, Adam Coates, Alessandro Bissacco, Bo Wu, and Andrew Y Ng. Reading digits in natural images with unsupervised feature learning. 2011.
- [48] Gerhard Neuhold, Tobias Ollmann, Samuel Rota Bulo, and Peter Kontschieder. The mapillary vistas dataset for semantic understanding of street scenes. In Proceedings of the IEEE international conference on computer vision, pages 4990–4999, 2017.
- [49] Xingang Pan, Ping Luo, Jianping Shi, and Xiaoou Tang. Two at once: Enhancing learning and generalization capacities via ibn-net. In Proceedings of the European Conference on Computer Vision (ECCV), pages 464–479, 2018.
- [50] Xingang Pan, Xiaohang Zhan, Jianping Shi, Xiaoou Tang, and Ping Luo. Switchable whitening for deep representation learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1863–1871, 2019.
- [51] Fengchun Qiao, Long Zhao, and Xi Peng. Learning to learn single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 12556–12565, 2020.
- [52] Stephan R Richter, Vibhav Vineet, Stefan Roth, and Vladlen Koltun. Playing for data: Ground truth from computer games. In European conference on computer vision, pages 102–118. Springer, 2016.
- [53] German Ros, Laura Sellart, Joanna Materzynska, David Vazquez, and Antonio M Lopez. The synthia dataset: A large collection of synthetic images for semantic segmentation of urban scenes. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3234–3243, 2016.
- [54] Bryan C Russell, Antonio Torralba, Kevin P Murphy, and William T Freeman. Labelme: a database and web-based tool for image annotation. International journal of computer vision, 77(1):157–173, 2008.
- [55] Baifeng Shi, Dinghuai Zhang, Qi Dai, Zhanxing Zhu, Yadong Mu, and Jingdong Wang. Informative dropout for robust representation learning: A shape-bias perspective. In International Conference on Machine Learning, pages 8828–8839. PMLR, 2020.
- [56] Rohan Taori, Achal Dave, Vaishaal Shankar, Nicholas Carlini, Benjamin Recht, and Ludwig Schmidt. Measuring robustness to natural distribution shifts in image classification. Advances in Neural Information Processing Systems, 33:18583–18599, 2020.
- [57] Josh Tobin, Rachel Fong, Alex Ray, Jonas Schneider, Wojciech Zaremba, and Pieter Abbeel. Domain randomization for transferring deep neural networks from simulation to the real world. In 2017 IEEE/RSJ international conference on intelligent robots and systems (IROS), pages 23–30. IEEE, 2017.
- [58] I Tolstikhin, O Bousquet, S Gelly, and B Schölkopf. Wasserstein auto-encoders. In International Conference on Learning Representations (ICLR), 2018.
- [59] Antonio Torralba and Alexei A Efros. Unbiased look at dataset bias. In CVPR 2011, pages 1521–1528. IEEE, 2011.
- [60] Vladimir Vapnik. The nature of statistical learning theory. Springer science & business media, 1999.
- [61] Hemanth Venkateswara, Jose Eusebio, Shayok Chakraborty, and Sethuraman Panchanathan. Deep hashing network for unsupervised domain adaptation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 5018–5027, 2017.
- [62] Riccardo Volpi and Vittorio Murino. Addressing model vulnerability to distributional shifts over image transformation sets. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 7980–7989, 2019.
- [63] Riccardo Volpi, Hongseok Namkoong, Ozan Sener, John C Duchi, Vittorio Murino, and Silvio Savarese. Generalizing to unseen domains via adversarial data augmentation. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, editors, Advances in Neural Information Processing Systems 31, pages 5334–5344. Curran Associates, Inc., 2018.
- [64] Chaoqun Wan, Xu Shen, Yonggang Zhang, Zhiheng Yin, Xinmei Tian, Feng Gao, Jianqiang Huang, and Xian-Sheng Hua. Meta convolutional neural networks for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4682–4691, 2022.
- [65] Shujun Wang, Lequan Yu, Caizi Li, Chi-Wing Fu, and Pheng-Ann Heng. Learning from extrinsic and intrinsic supervisions for domain generalization. In European Conference on Computer Vision, pages 159–176. Springer, 2020.
- [66] Zijian Wang, Yadan Luo, Ruihong Qiu, Zi Huang, and Mahsa Baktashmotlagh. Learning to diversify for single domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 834–843, 2021.
- [67] Jianxiong Xiao, James Hays, Krista A Ehinger, Aude Oliva, and Antonio Torralba. Sun database: Large-scale scene recognition from abbey to zoo. In 2010 IEEE computer society conference on computer vision and pattern recognition, pages 3485–3492. IEEE, 2010.
- [68] Qinwei Xu, Ruipeng Zhang, Ya Zhang, Yanfeng Wang, and Qi Tian. A fourier-based framework for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14383–14392, 2021.
- [69] Xiang Xu, Xiong Zhou, Ragav Venkatesan, Gurumurthy Swaminathan, and Orchid Majumder. d-sne: Domain adaptation using stochastic neighborhood embedding. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2497–2506, 2019.
- [70] Zhenlin Xu, Deyi Liu, Junlin Yang, Colin Raffel, and Marc Niethammer. Robust and generalizable visual representation learning via random convolutions. In International Conference on Learning Representations, 2021.
- [71] Luona Yang, Xiaodan Liang, Tairui Wang, and Eric Xing. Real-to-virtual domain unification for end-to-end autonomous driving. In Proceedings of the European conference on computer vision (ECCV), pages 530–545, 2018.
- [72] Seunghan Yang, Debasmit Das, Simyung Chang, Sungrack Yun, and Fatih Porikli. Distribution estimation to automate transformation policies for self-supervision. NeurIPS Workshops, 2021.
- [73] Seunghan Yang, Debasmit Das, Janghoon Cho, Hyoungwoo Park, and Sungrack Yun. Domain agnostic few-shot learning for speaker verification. INTERSPEECH, 2022.
- [74] Li Yao, Jordan Prosky, Ben Covington, and Kevin Lyman. A strong baseline for domain adaptation and generalization in medical imaging. arXiv preprint arXiv:1904.01638, 2019.
- [75] Fisher Yu, Haofeng Chen, Xin Wang, Wenqi Xian, Yingying Chen, Fangchen Liu, Vashisht Madhavan, and Trevor Darrell. Bdd100k: A diverse driving dataset for heterogeneous multitask learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 2636–2645, 2020.
- [76] Xiangyu Yue, Yang Zhang, Sicheng Zhao, Alberto Sangiovanni-Vincentelli, Kurt Keutzer, and Boqing Gong. Domain randomization and pyramid consistency: Simulation-to-real generalization without accessing target domain data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 2100–2110, 2019.
- [77] Ling Zhang, Xiaosong Wang, Dong Yang, Thomas Sanford, Stephanie Harmon, Baris Turkbey, Bradford J Wood, Holger Roth, Andriy Myronenko, Daguang Xu, et al. Generalizing deep learning for medical image segmentation to unseen domains via deep stacked transformation. IEEE transactions on medical imaging, 39(7):2531–2540, 2020.
- [78] Yang Zhang, Philip David, and Boqing Gong. Curriculum domain adaptation for semantic segmentation of urban scenes. In Proceedings of the IEEE international conference on computer vision, pages 2020–2030, 2017.
- [79] Long Zhao, Ting Liu, Xi Peng, and Dimitris Metaxas. Maximum-entropy adversarial data augmentation for improved generalization and robustness. In Advances in Neural Information Processing Systems (NeurIPS), 2020.
- [80] Kaiyang Zhou, Yongxin Yang, Timothy Hospedales, and Tao Xiang. Deep domain-adversarial image generation for domain generalisation. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 13025–13032, 2020.
- [81] Kaiyang Zhou, Yongxin Yang, Timothy Hospedales, and Tao Xiang. Learning to generate novel domains for domain generalization. In European conference on computer vision, pages 561–578. Springer, 2020.
- [82] Kaiyang Zhou, Yongxin Yang, Yu Qiao, and Tao Xiang. Domain adaptive ensemble learning. IEEE Transactions on Image Processing, 30:8008–8018, 2021.
Supplementary Materials

Appendix 1 Reproducibility
We have provided implementation details and pseudocode in the main paper for reproducibility. Note that all the experiments have been performed eight times and averaged.
Appendix 2 Domain generalized semantic segmentation
To show the applicability of Pro-RandConv, we conducted semantic segmentation experiments in addition to the object recognition experiments provided in the main paper. We use the experimental protocol used in RobustNet [4] for a fair comparison. We adopt a DeepLabV3+ [3] architecture with ResNet50 [23] as a baseline. We use the GTAV [52] dataset as the training domain and measure the generalization capability on the Cityscapes [7], BDD-100K [75], SYNTHIA [53], and Mapillary [48] datasets. Mean Intersection over Union (mIoU) is used to quantitatively evaluate semantic segmentation performance. We use a batch size of 8 for experiments on a single GPU, which is different from the experimental protocol in [4] using a batch size of 16 for GTAV. Except for the batch size, all environments are the same as the official experimental protocol, refer to [4] for more details. In our augmentation settings, we use all of the same hyperparameters for object recognition without additional tuning. We also randomly select only half of the images for each batch and perform augmentation.
Tabel 6 shows a comparison of generalization performance in semantic segmentation. To prove the superiority of Pro-RandConv, we compare the performance not only with RandConv [70] but also with RobustNet [4], a domain generalization method for semantic segmentation. Besides that, we compare the performance with various competitors (e.g. Switchable Whitening (SW) [50], IBN-Net [49], and IterNorm [26]) provided by [4]. Our method outperforms all of the competitors including RandConv and RobustNet by a big margin. In particular, we note that our method shows a great performance improvement on real-world datasets (i.e. Cityscapes, BDD-100K, and Mapillary). We also provide experimental results with various versions to observe the importance of each component. All components except the deformable offset improve the generalization performance, which can be interpreted as the geometrical change of the object shape from the deformable offset causing a negative effect on the pixel-level classification. We expect to get better generalization performance if we change the ground truth to accommodate geometric changes. Figure 8 describes the semantic segmentation results on Cityscapes. Ours-C version of the model with removed deformable offsets is used for visualization.
| Methods | C | B | S | M | Avg. |
| Baseline [4] | 28.95 | 25.14 | 26.23 | 28.18 | 27.13 |
| SW [50] | 29.91 | 27.48 | 27.61 | 29.71 | 28.68 |
| IterNorm [26] | 31.81 | 32.70 | 27.07 | 33.88 | 31.37 |
| IBN-Net [49] | 33.85 | 32.30 | 27.90 | 37.75 | 32.95 |
| RobustNet [4] | 36.58 | 35.20 | 28.30 | 40.33 | 35.11 |
| Baseline* | 35.10 | 27.18 | 26.71 | 30.63 | 29.91 |
| RandConv* [70] | 35.38 | 30.92 | 24.45 | 32.43 | 30.80 |
| RobustNet* [4] | 39.72 | 35.61 | 26.87 | 39.50 | 35.43 |
| Ours-A | 39.53 | 34.14 | 26.30 | 36.74 | 34.18 |
| Ours-B | 41.60 | 34.95 | 26.18 | 41.31 | 36.01 |
| Ours-C | 42.36 | 37.03 | 25.52 | 41.63 | 36.64 |
| Ours-D | 40.48 | 36.68 | 26.82 | 40.76 | 36.19 |
| Methods | Selection strategies | Digits | PACS | ||
| In- domain | Out-of- domain | In- domain | Out-of- domain | ||
| RC* [70] | or | 98.90 | 74.84 | 92.75 | 67.50 |
| Ours (batch) | only (baseline) | 98.64 | 52.00 | 95.37 | 63.15 |
| only | 99.25 | 80.99 | 94.66 | 68.10 | |
| or | 99.25 | 81.08 | 95.59 | 67.65 | |
| Ours (instance) | , | 99.28 | 81.20 | 95.18 | 68.43 |
| , | 99.31 | 81.13 | 95.65 | 68.20 | |
| , | 99.25 | 80.22 | 95.73 | 67.26 | |
| , | 99.27 | 80.66 | 96.00 | 69.11 | |
| Ours ( and ) | 99.29 | 81.35 | 95.51 | 68.88 | |
Appendix 3 Strategies for selecting images to augment
In the main paper, we provided a performance on a basic learning strategy using both original images and augmented images . Table 7 shows various data fraction methods to effectively use augmented data for training. RandConv [70] applied augmentation with half probability for every mini-batch. That is, sometimes the original images are used and at other times the augmented images are used for training. We call this a batch-level image augmentation strategy. We first compare these batch-level augmentation strategies using only the original images, using only the augmented images, and using both sets with half probability. Using only original images significantly degrades out-of-domain performance. On the other hand, using only augmented images degrades in-domain performance, especially in PACS. Therefore, it is important to properly combine the two types of images to balance in-domain and out-of-domain performance.
Next, we provide experiments on an instance-level augmentation strategy to learn both original and augmented images within a mini-batch. indicates this strategy, where is the data fraction of the original images. The larger , the higher the proportion of the original images in the mini-batch. Generally, a high value of tends to improve in-domain performance and decrease out-of-domain performance. The most appropriate solution is to set to a value of 0.5 or to sample from . In particular, the random sampling strategy achieves satisfactory values for both in-domain performance and out-of-domain performance, and obtains comparable performance to the basic strategy using both original and augmented images. It is noteworthy that RandConv degrades the in-domain performance on PACS from 95.37% to 92.75% compared to the baseline, whereas our method improves both in-domain and out-of-domain performance.
| Model | Conv. smooth | Contrast | Offsets | Digits | PACS | |
| SDG | SDG | MDG | ||||
| Baseline | - | - | - | 52.00 | 63.13 | 81.45 |
| Single | - | - | - | 74.84 | 67.50 | 82.43 |
| ✓ | - | - | 74.34 | 67.95 | 82.53 | |
| - | ✓ | - | 77.14 | 67.81 | 83.16 | |
| - | - | ✓ | 75.73 | 67.24 | 82.38 | |
| 76.59 | 67.46 | 82.53 | ||||
| 75.80 | 67.99 | 82.50 | ||||
| Multi (D) | - | - | - | 74.72 | 66.47 | 82.49 |
| Multi (S) | - | - | - | 78.26 | 67.89 | 83.72 |
| - | ✓ | - | 77.09 | 68.73 | 84.17 | |
| - | - | ✓ | 77.41 | 68.25 | 84.04 | |
| - | ✓ | ✓ | 77.08 | 69.01 | 84.24 | |
| ✓ | - | - | 80.03 | 68.3 | 83.79 | |
| ✓ | ✓ | - | 80.02 | 68.55 | 84.22 | |
| ✓ | - | ✓ | 81.06 | 67.98 | 83.77 | |
| ✓ | ✓ | ✓ | 81.35 | 68.88 | 84.29 | |
Appendix 4 Component analysis
Table 8 shows a detailed performance comparison for each component of Pro-RandConv. First, we analyze whether we can improve performance by adding our components to the single-layer approach used in RandConv [70]. Gaussian smoothing of convolution weights does not have a significant effect in a single-layer approach, whereas contrast diversification and deformable offsets help to improve performance. However, it does not contribute to a significant performance improvement, because of the limitation of style diversity and the problem of excessive semantic distortion in the single-layer approach. In addition, the method of variously adjusting the variance of the Gaussian distribution without fixing the convolution weight to He-initialization [22] shows some performance improvement on Digits.
Second, we analyze the influence of components in detail under our progressive approach. The key to the progressive approach is to initialize one layer and keep the remaining layers with the same parameters, which leads to a significant performance improvement. Next, we compare the performance with and without Gaussian smoothing of the convolution layer. In Digits, since the size of the object is relatively small, the multi-layer structure of the convolution layer has excessive diversity. Thus, increasing the contrast and texture diversity without Gaussian smoothing has the effect of inducing semantic distortion. In other words, it is more effective to secure the contrast and texture diversity while controlling the deformation scale of texture with Gaussian smoothing. Conversely, in PACS, since the resolution of the image is large, the multi-layer structure of the convolution layer is inefficient in diversity. Therefore, even if Gaussian smoothing is not applied, the generalization capability can be improved by contrast diversification and deformable offsets.
Appendix 5 Additional performance analysis
5.1 Comparison with traditional augmentation
In this section, we compare the traditional augmentation methods with our Pro-RandConv. Table 9 and Table 10 provide performance comparisons on Digits and PACS, respectively. In both datasets, color jitter and grayscale are more effective than perspective and rotate in terms of improving generalization ability. Also, AutoAugment [8] and RandAugment [9], which apply various augmentation types simultaneously, enhance domain generalization capability more than single augmentation methods. Furthermore, the proposed Pro-RandConv outperforms all these augmentation methods with a simple random network structure. Thanks to its effective generalization capability, we argue that the proposed Pro-RandConv could be a strong baseline for various tasks.
| Methods | SVHN | MNIST-M | SYN | USPS | Avg. |
| Baseline | 32.52 | 54.92 | 42.34 | 78.21 | 52.00 |
| Color jitter* | 36.04 | 57.56 | 43.94 | 77.76 | 53.83 |
| Grayscale* | 32.92 | 55.44 | 42.38 | 78.22 | 52.24 |
| Pespective* | 33.63 | 43.86 | 40.92 | 69.12 | 46.88 |
| Rotate* | 31.99 | 54.86 | 38.22 | 69.54 | 48.65 |
| AutoAugment [8] | 45.23 | 60.53 | 64.52 | 80.62 | 62.72 |
| RandAugment [9] | 54.77 | 74.05 | 59.60 | 77.33 | 66.44 |
| Ours | 69.67 | 82.30 | 79.77 | 93.67 | 81.35 |
| Methods | Art | Cartoon | Photo | Sketch | Avg. |
| Baseline | 74.64 | 73.36 | 56.31 | 48.27 | 63.15 |
| Color jitter* | 75.94 | 76.56 | 59.27 | 50.24 | 65.50 |
| Grayscale* | 74.29 | 75.75 | 58.96 | 47.67 | 64.17 |
| Pespective* | 72.29 | 70.17 | 59.99 | 43.79 | 61.31 |
| Rotate* | 73.47 | 71.06 | 56.95 | 46.61 | 62.02 |
| AutoAugment* [8] | 76.48 | 77.09 | 60.99 | 52.46 | 66.76 |
| RandAugment* [9] | 76.76 | 78.00 | 62.09 | 56.40 | 68.31 |
| Ours | 76.98 | 78.54 | 62.89 | 57.11 | 68.88 |
| Methods | SVHN | MNIST-M (A/B) | SYN | USPS | Average (A/B) |
| RC [70] | 57.52 | - / 87.76 | 62.88 | 83.36 | - / 72.88 |
| Ours-T | 62.76 | 74.52 / 81.91 | 78.07 | 93.01 | 77.09 / 78.94 |
| Ours-C | 70.35 | 82.98 / 88.34 | 77.40 | 93.52 | 81.06 / 82.40 |
| Ours | 69.67 | 82.30 / 87.72 | 79.77 | 93.67 | 81.35 / 82.72 |
5.2 Fair comparison on MNIST-M
We confirmed that RandConv uses the test set of MNIST-M [17] differently from the existing methods (e.g. PDEN [38], M-ADA [51], and ME-ADA [79]). Existing methods use MNIST-M consisting of 9,001 images, which we refer to as set A. RandConv uses MNIST-M which consists of 10,000 images, which we refer to as set B. For a fair comparison, we compare the performance of both MNIST-M sets. Table 11 shows that performance comparison on two sets of MNIST-M. We emphasize that our Pro-RandConv method has higher generalization capability than RandConv [70] in all domains including MNIST-M.
Appendix 6 Hyperparameter selection
6.1 Hyperparameters of the progressive approach
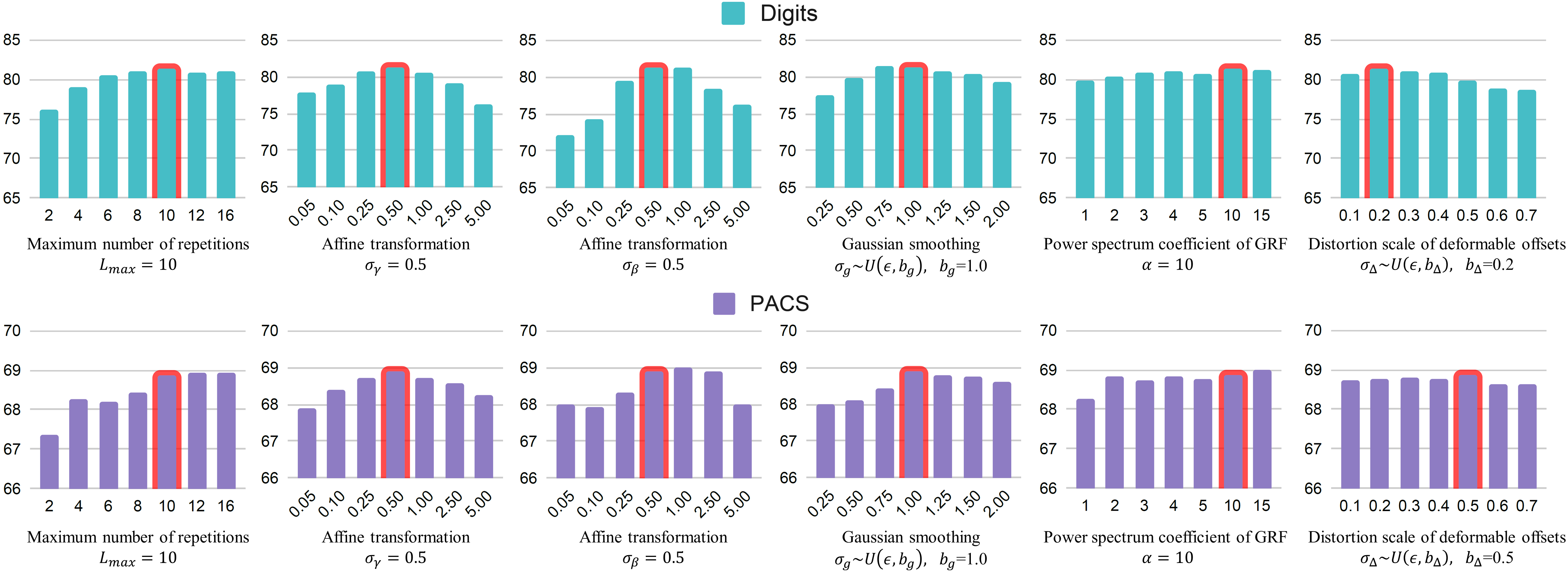
The core idea of this paper is a progressive method that initializes a random convolution layer once and then stacks it multiple times with the same structure. Eventually, from a hyperparameter selection perspective, RandConv’s traditional approach of choosing the kernel size changes to choosing the number of repetitions of the convolution layers. For example, RandConv generates random-style images based on a kernel size randomly selected from for each mini-batch. In a similar way, we choose a different number of repetitions with uniform sampling from 1 to for each mini-batch. Figure 1(c) and 2(a) in the main paper show that as the kernel size increases, images augmented by RandConv easily lose their semantics and eventually the performance degrades rapidly. The progressive approach, on the other hand, is less sensitive to increasing , since the performance does not degrade significantly as the receptive field increases, as shown in Fig 9. However, the computational cost increases proportionally to the number of repetitions, so we chose a reasonable value of 10 to account for the tradeoff.
6.2 Hyperparameters of convolution blocks
We further provide a performance comparison for all hyperparameters in the random convolution block, as shown in Fig. 9. We first analyze the hyperparameters for contrast diversification. We chose and to be 0.5, as they show the highest performance on both Digits and PACS datasets. This means that the affine transformation parameters, and , are sampled from . Figure 7(a) and (b) in the main paper show that and can cause false distortion or saturation if they are smaller or larger than 0.5, so we recommend keeping them at 0.5 regardless of the dataset.
Next, we analyze the hyperparameters for the convolution weights. The convolution weights are initialized by [22] as in RandConv (i.e., ). We further apply Gaussian smoothing to this kernel. For Gaussian smoothing , the smoothing scale is sampled from , where indicates a small value. This means that is randomly sampled for each mini-batch, so the smoothing effect is different each time. This technique can be used to mitigate the problem of severely distorted object semantics when the random offset of the deformation convolution is too irregular and large in scale. We chose to be 1.0 because it performs best on both Digits and PACS datasets. As with the hyperparameter selection for contrast diversification, we set the same value for all datasets.
Finally, we introduce hyperparameters for deformable convolution that further enhance texture diversity. The tensor for deformable offsets consists of , where is the kernel size of the convolution layer, and and are the height and weight of an image, respectively. That is, there are a total of offsets per pixel in the image of , where 2 means the values of and . To induce natural geometric variation, we consider spatial correlation by generating a total of Gaussian Random Fields (GRF) with a size of . We refer to this code555https://github.com/bsciolla/gaussian-random-fields for the GRF implementation, where spatial correlation can be controlled by varying the coefficient of the power spectrum. As shown in Fig. 7(f) of the main paper, the larger the coefficient , the higher the spatial correlation. We scaled the Gaussian random field (GRF) by choosing a coefficient of 10 for the power spectrum. Another hyperparameter is the distortion scale of the deformable offset. In particular, geometric information such as rotation is an important attribute for digits recognition, so severe deformation impairs class-specific semantic information. Figure 7(e) in the main paper shows that the shape of the object becomes unrecognizable as the scale increases. This hyperparameter is also related to the size of the image, so we choose different hyperparameters according to image size. For Digits, a small scale of 0.2 is used, while for PACS, OfficeHome, and VLCS, a scale of 0.5 is used. As with the other hyperparameters, uniform sampling is performed as to make it less sensitive to hyperparameter selection.