Prompt-SAW: Leveraging Relation-Aware Graphs for Textual Prompt Compression
Abstract
Large Language Models (LLMs) have shown exceptional abilities for multiple different natural language processing tasks. While prompting is a crucial tool for LLM inference, we observe that there is a significant cost associated with exceedingly lengthy prompts. Existing attempts to compress lengthy prompts lead to sub-standard results in terms of readability/interpretability of the compressed prompt, with a detrimental impact on prompt utility. To address this, we propose Prompt-SAW: Prompt compresSion via Relation AWare graphs, an effective strategy for prompt compression over task-agnostic and task-aware prompts. Prompt-SAW uses the prompt’s textual information to build a graph, later extracts key information elements in the graph to come up with the compressed prompt. We also propose GSM8K-aug, i.e., an extended version of the existing GSM8K benchmark for task-agnostic prompts in order to provide a comprehensive evaluation platform. Experimental evaluation using benchmark datasets shows that prompts compressed by Prompt-SAW are not only better in terms of readability, but they also outperform the best-performing baseline models by up to 10.1% and 77.1% respectively for task-agnostic and task-aware settings while compressing the original prompt text by 34.9% and 56.7%.
1 Introduction
LLMs have attracted considerable attention for their superior performance across a wide range of applications. For this, instructions (aka. prompts) play a crucial role in extending the capabilities of LLMs for multiple different tasks. The prompts provide the provision to guide the model to elucidate desired model behavior without perturbing the model parameters. This is also highlighted in recent studies that show well-designed prompts and the integration of external knowledge are significant to enhance the effectiveness of LLMs’ (Sahoo et al., 2024). Different LLMs-related techniques directly benefiting from prompts include but are not limited to: In-Context Learning (Dong et al., 2022), Chain-of-Thought (Wei et al., 2022), Retrieval Augmented Generation (Lewis et al., 2020), and Agents (Park et al., 2023) etc. Generally, prompts may be sub-divided into two types: task-aware and task-agnostic prompts, a quick overview is given in Appendix A.2 and Appendix A.3 respectively.
At the same time, the abilities of LLMs are significantly compromised/constrained by increasingly lengthy prompts, even comprising thousands of tokens. Lengthy prompts not only obscure requisite information but also increase computational costs and incur inference latency. To tackle this challenge, prompt compression techniques, e.g., Li (2023), have garnered significant interest. These approaches are based on the fact that natural language is inherently redundant (Shannon, 1951). Thus, it is possible to substantially compress the length of original textual prompts by preserving requisite information in small segments.
Existing prompt compression approaches focus on compressing text at the token level, i.e., they verify whether compression is applicable to each individual token. For instance, Li (2023) proposed Selective-Context that uses a compact language model to evaluate context’s lexical units, enabling compression by eliminating units with minimal information. Also, LLMLingua (Jiang et al., 2023a) and LongLLMLingua (Jiang et al., 2023b) developed budget control mechanisms to compresses prompts based on their perplexity.
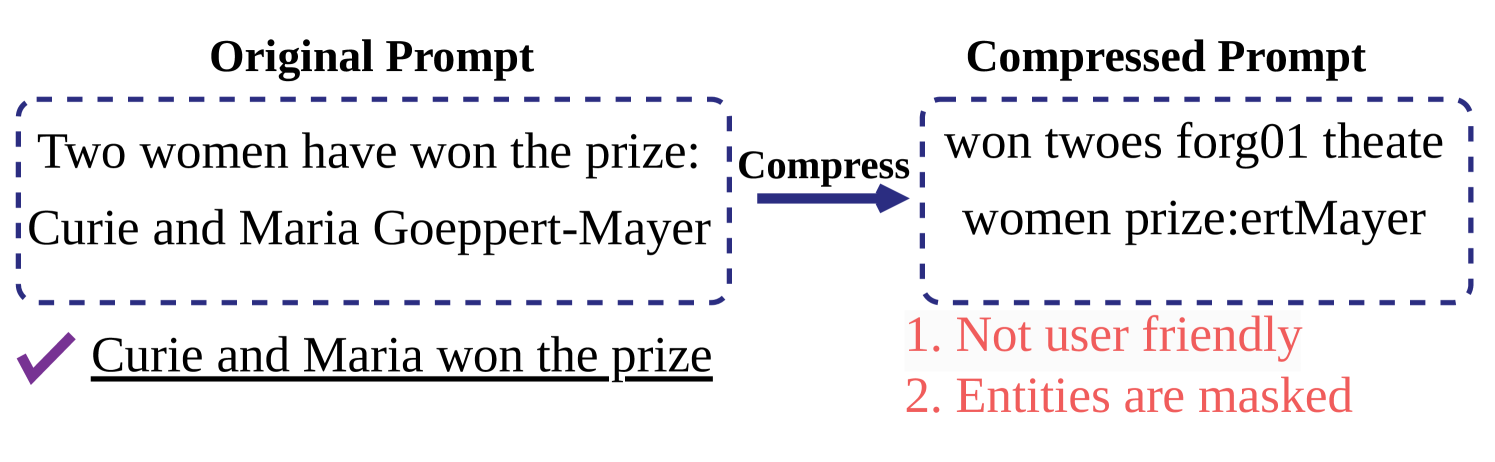
While existing approaches could enhance the ability to deal with lengthy prompts for LLMs, they lack grammatical coherence, i.e., existing approaches neglect the syntactic and semantic structure of the compressed prompt. This is because contemporary prompt compression methods primarily focus on quantifying token-level information, neglecting the overall grammatical structure of the compressed prompt. Such ignorance not only increases the risk of semantic loss within the compressed prompt but also hampers its readability for human readers. An example in this regard is shown in Figure 1, where the original prompt text: ”Two women have won the prize: Curie and Maria Goeppert-Mayer” is compressed to: ”won twoes forg01 theate women prize:ertMayer” by LongLLMlingua (Jiang et al., 2023b).
To fill in the gap, in this paper, we propose Prompt-SAW, i.e., Prompt compresSion via Relation AWare graphs, a novel method designed to cut down unnecessary information in the prompt text by using Knowledge Graph (KG) structures to exploit the small-scale information elements (Section 3.1) in the prompts, i.e., information units comprising entities and their underlying relations.
Prompt-SAW first extracts all entities and their relations in the prompt to formulate the graph. Later, (i) for task-aware prompts, Prompt-SAW looks for small-scale information elements in the graph to only retain task-specific information as a sub-graph, (ii) for task-agnostic prompts, Prompt-SAW measures similarity scores between successive information elements in the graph to remove the redundant elements to obtain required sub-graph. To retain the syntactic and semantics of the prompt structure, Prompt-SAW finally reinstates the information contained in the sub-graph resulting in an optimized and compressed prompt.
We conducted extensive experimental analysis of Prompt-SAW under both task-agnostic and task-aware settings against existing best-performing models as baselines. For evaluation, we used: (i) GSM8K-aug, i.e., an extended experimental setting proposed by us for GSM8K (Cobbe et al., 2021), (ii) NaturalQuestions (Liu et al., 2023), and (iii) ShareGPT111https://sharegpt.com/. Experimental results show that Prompt-SAW significantly outperforms other baseline models. We summarize the key contributions of this work as follows:
-
•
We propose Prompt-SAW, a novel framework crafted for compressing prompts by exploiting graph structures to infer key information elements in the prompt that are helpful for compression.
-
•
As current benchmarks for task-agnostic prompts lack comprehensive evaluation, we propose GSM8K-aug, an extended version of the existing GSM8K benchmark for an intensive evaluation of Prompt-SAW.
-
•
We demonstrate the effectiveness of Prompt-SAW by comprehensive experiments, showing Prompt-SAW attained state-of-the-art performance outperforming baseline models by up to 10.1% and 77.1% respectively for task-agnostic and task-aware settings while compressing the original prompt text by 34.9% and 56.7%.
2 Related Work
Prompt Compression. Prompt compression techniques are used to reduce the inference cost of LLMs across a wide range of applications. Existing work can be categorized into soft prompt compression and discrete prompt compression.
Soft prompts were introduced by Lester et al. (2021). A soft prompt integrates additional trainable parameters at the model’s input stage. Wingate et al. (2022) emphasized that soft prompt compression effectively retains crucial abstract information with a reduced parameter count. Xu et al. (2023) emphasized that carefully crafted prompts are helpful in augmenting the end-performance of compressed LLMs, also the compressed LLMs are helpful in the prompt learning phase.
Compared to soft prompt compression, discrete prompt compression seeks to optimize the effectiveness of prompts via token-level search strategies. Jung and Kim (2023) employed policy networks to eliminate unnecessary tokens for prompt compression. Li (2023) utilized self-information metrics to identify and remove superfluous information in prompts. Capitalizing on these advancements, Jiang et al. (2023a) and Jiang et al. (2023b) formulated algorithms for dynamically adjusting compression rates across different prompt sections, giving precedence to tokens with higher perplexity.
Despite the significant advancements achieved by these studies, their primary focus lies on token-level compression, neglecting the comprehensive graph structure information inherent in the prompt.
Knowledge Graphs (KGs) for LLM. KGs organize information as structured units, i.e., relational triplets (explained in Appendix A.1), that encapsulate a wide variety of entities/concepts along with underlying relations (Ji et al., 2020). Pan et al. (2023) illustrated multiple different scenarios for integration of KGs with LLM for knowledge and data-driven bi-directional reasoning. Luo et al. (2023) combined LLMs with KGs for interpretable reasoning over KG Question Answering tasks. Kim et al. (2023) introduced an innovative framework that leverages LLM’s reasoning capabilities for executing KG-based tasks. To the best of our knowledge, Prompt-SAW is the first to make an attempt to leverage knowledge graph structure for prompt compression.
3 Preliminaries
In this section, we first introduce mathematical notations and formulate our problem. Background on the core concepts required for the design and development of Prompt-SAW is provided in Appendix A.
3.1 Notations.
We use and to represent the original and compressed prompt respectively. Likewise, we use and to represent the length of the original and compressed prompt. We use to represent the compression rate and as the compression ratio. is used to represent the target compression rate. The graph is represented by , where , and represent the subject entity, relation and object entity in the graph respectively; and denote the set of entities and relations in . is used to represent small-scale information elements in , equivalent to graph triplet. represents auxiliary models used for graph construction. is used to represent the encoder network. represents the similarity threshold used for sub-graph construction.
3.2 Problem Setting
In this work, we aim to design and develop an effective prompt compression strategy that can cut down the prompt text by only preserving the requisite information content while at the same time maintaining the semantics and end performance of the prompt to the best possible extent.
Formally, we aim to generate a compressed prompt given the original prompt , where , , and , denote the prompt instruction, information and question, respectively; , , and represent the number of tokens in , , , and respectively. We denote + + as the length of the original prompt.
4 Prompt-SAW
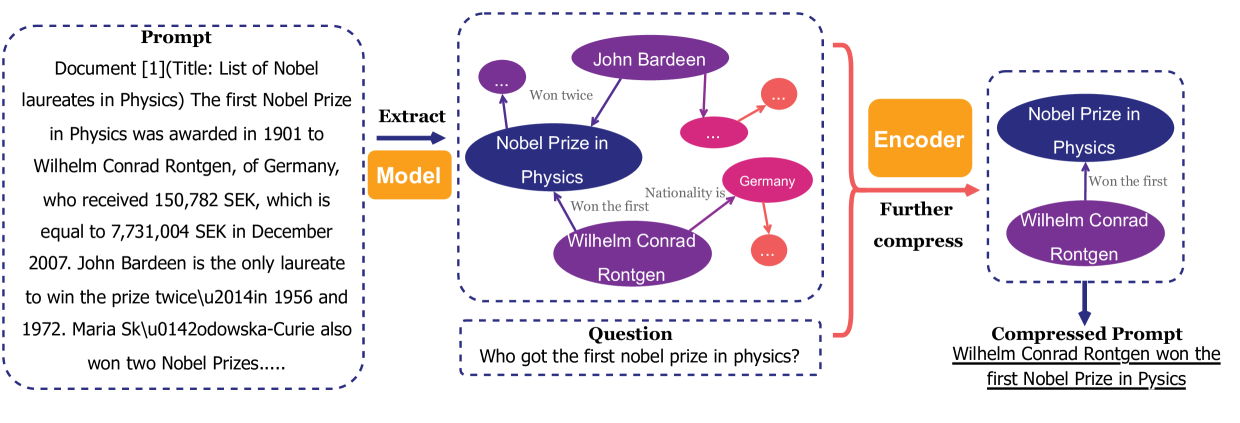
In this section, we provide details of Prompt-SAW. The workflow is shown in Figure 2. As shown in the figure, Prompt-SAW takes the original prompt text as input and generates the compressed prompt as the output.
In contrast to the existing token-level compression methods, in Prompt-SAW we use a graph structure to effectively represent the textual information in the prompt, which is helpful to analyze the key aspects of the prompt. Later, we can refine the information in the graph structure to come up with a compressed prompt in a way that: (i) The semantic consistency of the compressed prompt is preserved; (ii) The end performance and/or utility of the prompt is not distorted. Below, we first introduce the motivation of Prompt-SAW, followed by the prompt compression process.
4.1 Motivation of Prompt-SAW
Prompt-SAW is motivated by the observation that the key information within the prompt text could be inferred as a set of entities and relations, which can also be organized into a graph structure, commonly known as a knowledge graph in literature.
Formally, given a prompt text , we claim it encompasses a set of entities , i.e., names of persons, locations, organizations, miscellaneous elements, etc., (Ali et al., 2020). These entities serve as the key elements of the prompt structure. In addition to the entities, we can also infer some relations in that may be used to describe the connections between the entities. Prompt-SAW re-organizes these key elements of the prompt (i.e., entities and their relations) in a graph structure, represented by . We use to represent the -th information element of , i.e., a fact stating that has - relation with .
We argue this transformation of text information to graph is a more reasonable and natural approach as: (i) It helps in highlighting the key information elements in the prompt. (ii) Later, analyzing these key entities in combination with underlying relations helps in filtering/digging out the salient content within the prompt to come up with a compressed prompt.
4.2 Workflow of Prompt-SAW
The workflow of Prompt-SAW consists of two parts. First, it uses the information in prompt to construct a graph . Then, based on the specific scenario, we proceed as follows:
(a) Task-aware scenario. For this scenario,
we traverse the graph in a way to preserve
only the information elements that are relevant to the task as
task-specific subgraphs, indicative of information useful
for the compressed prompt.
(b) Task-agnostic scenario. For this scenario, we no longer have access to task-specific information. Thus, we use similarity scores between the information elements in to identify and remove the redundant elements to obtain subgraphs that are helpful for compression.
Further details about the model components of Prompt-SAW are provided in the following subsections.
4.2.1 Graph Construction.
For graph construction from the text data, we primarily rely traditional knowledge extraction approaches, i.e., OpenIE (Kolluru et al., 2020), to construct a graph , as follows
| (1) |
where is the prompt text, and is an information extraction module that takes as input and return graph as output. For the cases not addressed by the above equation, we use an in-context learning prompt as our auxiliary method that prompts the language model to construct the graph from the original prompt text as follows:
| (2) |
where is the prompt text and is the prompt template (explained in Appendix B.1) used to guide the LLM to extract the graph . Note, for Equation 2, we typically prefer a small-scale open-source LLM in order to avoid higher computational costs incurred by large models.
4.2.2 Task-aware Prompts
Task-aware scenarios refer to the settings when the information within the prompt is helpful and/or is related to the end-task, e.g., question answering. For such cases, Prompt-SAW aims to retain only the task-specific information in , while filtering out the redundant/useless information. For this, it first uses an encoder function to get the embeddings for the prompt question, as follows.
| (3) |
where is the embedding for prompt question , and is the encoder network. Then, it computes the pair-wise similarity between the and information elements in , as shown below.
| (4) |
where corresponds to the - information element in , is used to encode the information in , is the set of the similarity scores between information element in and the question embeddings . Later, it ranks the scores in in order to retain only the elements in showing a higher degree of similarity with , as shown below.
| (5) |
where is used to sort the similarity scores in and return corresponding high-ranked information elements as . We then use the information in to iterate over to extract the sub-graph not surpassing the targeted compression ratio . Its process-flow is illustrated in Algorithm 1.
Workflow of Algorithm 1. The workflow of Algorithm 1 is explained as follows: (i) initialize as an empty set (line-1); (ii) for each element in repeatedly add in until the compression rate surpasses the target compression rate (lines 2-7); (iii) return final graph as output (line-10).
Finally, we restore/reconstruct the information elements in to come up with our compressed prompt , as shown below.
| (6) |
where is the concatenation operator used to combine the entities and relations within the information elements in the extracted subgraph , and is the delimiter used to separate different information elements in .
4.2.3 Task-agnostic Prompts
A task-agnostic scenario implies that it is almost impossible to filter useful and/or task-specific information within the original prompt text . In such cases, Prompt-SAW looks for recurring information elements in for probable prompt compression. We assume two main sources of recurring elements in , i.e., (i) the verbose expression of the prompt itself and (ii) the repeated element generated by auxiliary models. Note that these assumptions are based on empirical observation illustrating that large models’ re-reading phenomenon leads to the repeated generation of the extracted knowledge (Yan et al., 2023).
For compression over task-agnostic scenarios, we sequentially traverse the information elements in and select only the elements exhibiting a lower similarity with priorly selected information elements. Our underlying intuition is that highly similar information elements will carry repeated information. Thus, we could avoid redundant information in by selecting only dissimilar elements.
For this, we use a threshold as a selection criteria for Prompt-SAW. The value of the is determined using a binary search algorithm (shown in Algorithm 2) that computes an appropriate value of threshold required to meet the targeted compression rate .
Workflow of Algorithm 2. The process-flow of Algorithm 2 is explained as follows: (i) firstly, we initialize an interval for the threshold (line-1); (ii) at each step, we partition the interval into two parts and via the midpoint (line-3); (iii) we will compute the graph subset, i.e., via function (explained below) with the value of as threshold, shown in line-4; (iv) compute the compression rate for the and accordingly update the values of and (lines 6-9). Specifically, if the compression rate is smaller than , then the current threshold is too stringent thus we judge is in , otherwise it is in ; (v) depending upon the interval threshold (line-2), we compute the value as the final similarity threshold (line-11); (vi) finally, use the value of to return the final graph subset (line-13).
Compress Function. The workflow of the is shown in Algorithm 3 and explained as follows: (i) start with an empty graph (line-1); (ii) iterate the information elements in the graph to compute the similarity score of with the elements in to look for maximal similarity, i.e., (lines 2-3); (iii) compare against the compression threshold to insert in (lines 4-5); (iv) finally, return as the final subset of the graph. The end-goal of Algorithm 2 is to select highly dis-similar information elements by neglecting cases with . For such cases, we assume that the corresponding information element, i.e., is redundant because there is already an element in that is very similar to .
5 GSM8K-AUG
As a benchmark dataset, GSM8K (Cobbe et al., 2021) encompasses high-quality, linguistically diverse grade math word problems. However, we find that the original dataset poses some limitations for evaluating the prompt compression methods. Specifically, it only allows compressing prompts under one fix setting, i.e., 8-shot. This is inadequate for rigorously evaluating the abilities of the prompt compression systems. For instance, it makes it harder to analyze and answer the questions: (i) Whether prompt compression methods destroy connections between individual shots? (ii) Also, what impact will these connections have on the end-performance for in-context-learning tasks?
To address these limitations, we propose GSM8K-aug, an extended and more comprehensive experimental setting for original GSM8K data. GSM8K-aug extends the original data set to -shot setting (), with -shot meaning example demonstrations in the prompt. Note, GSM8K-aug has a broader coverage, as it encompasses the experimental settings of the current GSM8K data settings (i.e., 8-shot). We argue GSM8K-aug helps in overcoming the limitations mentioned above, as it provides us with the provision to find correlations between different shots. For instance, it can help us to quickly answer the above questions by analyzing the models’ performance by compressing two prompts at the same time, i.e., 2-shot settings compared against compressing them independently, i.e., 1-shot settings.
6 Experiments
In this section, we conduct comprehensive experiments for the performance evaluation for Prompt-SAW compared against different baseline models.
6.1 Experiment Settings
Datasets. To comprehensively evaluate the effectiveness of compressed prompts, we evaluate their performance under both task-agnostic and task-aware data settings. For task-agnostic data sets, we consider GSM8K-aug, i.e., an extended variant of the original GSM8K (Cobbe et al., 2021) devised by us to report the model performance under -shot settings with (details in Section 5). For the task-aware dataset, we use NaturalQuestions (Liu et al., 2023), and ShareGPT222https://sharegpt.com/. The statistics of dataset is given in Table 5, and further details are provided in Appendix C.1.
Baselines. We compare the performance of Prompt-SAW against following models as baselines: (i) Selective-Context (Li, 2023), (ii) LLMLingua (Jiang et al., 2023a), (iii) LongLLMlingua (Jiang et al., 2023b), and (iv) GPT4 (Achiam et al., 2023). Details about the baselines are provided in Appendix C.2. Note, in order to setup a fair platform for comparative evaluation, we re-compute the results for the baseline models as per our data settings.
Evaluation Metrics. For GSM8K-aug, we use Exact Match (EM) as the evaluation metric. This metric is also employed by Cobbe et al. (2021) and Jiang et al. (2023a). For the evaluation of NaturalQuestions, we used Span Accuracy (Span-Acc) as a metric. This is similar to previous work by Liu et al. (2023) and Jiang et al. (2023b). For the evaluation of ShareGPT, we used Rouge as the evaluation metric (Lin, 2004). Apart from these, we also use fluency (FL) (Meng et al., 2022) to measure the readability and grammatical coherence of the compressed prompt. Further details and mathematical formulation of these metrics are given in Appendix C.3.
| Method | GSM8K-aug(1-shot) | GSM8K-aug(2-shot) | GSM8K-aug(4-shot) | GSM8K-aug(8shot) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EM | Tokens | 1/ | EM | Tokens | 1/ | EM | Tokens | 1/ | EM | Tokens | 1/ | |
| Original | 73.33 | 306 | 1.00 | 78.17 | 612 | 1.00 | 78.92 | 1224 | 1.00 | 82.53 | 2365 | 1.00 |
| Selective-Context | 55.55 | 228 | 1.34 | 58.01 | 449 | 1.36 | 58.13 | 881 | 1.39 | 61.47 | 1752 | 1.35 |
| LLMLLingua | 63.25(7.3%) | 232 | 1.32 | 65.70 | 428 | 1.43 | 67.41(5.5%) | 906 | 1.35 | 73.02(4.2%) | 1799 | 1.31 |
| GPT4-Generation | 60.51 | 215 | 1.42 | 66.44(10.1%) | 411 | 1.49 | 66.39 | 956 | 1.28 | 71.41 | 1273 | 1.86 |
| Prompt-SAW | 67.84 | 207 | 1.48 | 73.17 | 399 | 1.53 | 71.14 | 820 | 1.49 | 76.13 | 1586 | 1.49 |
Large Models. To demonstrate the generalization of our algorithm on different LLMs, we use GPT3.5-turbo and LLaMA2-7B-chat as our target LLMs.
Experimental Setup. Following the setting of LLMLingua (Jiang et al., 2023a), we employ greedy decoding with the temperature set to 0. The max number of tokens generated by LLMs are limited to 400. For graph construction, we use Open-IE tooklit (Kolluru et al., 2020) as the primary tool and Phi-3-mini 333https://ollama.com/library/phi3 as our auxiliary solution. Note, on average 90-% graphs were constructed using the Open-IE toolkit. We use OpenAI embedding API 444https://openai.com/ as the embedding encoder . The value for is set to {0.1, 0.3, 0.5} for both ShareGPT and NaturalQuestions, while = 0.7 for GSM8K-aug. In Algorithm 2, we use = 0.001. All the results reported in this paper are averaged over five runs. All experiments were performed using PyTorch 2.1.0 with Nvidia RTX 4090 24GB GPU.
6.2 Experimental Results
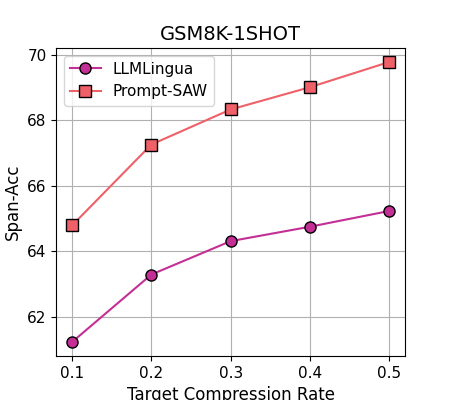
Results for Task-agnostic Settings. For task-agnostic settings, we report the results of Prompt-SAW for GSM8K-aug in Table 1. Note, unlike existing research that reports their performance for one fixed setting, we report these results for -shot settings, where indicates the number of prompts have been employed by Prompt-SAW, i.e., {1, 2, 4 and 8}-shots.
Comparing these results against the baseline models, we can observe that Prompt-SAW outperforms the previous state-of-the-art by a significant margin. For instance, compared to the best performing baselines, Prompt-SAW improves the EM score by up to 7.3%, 10.1%, 5.5% and 4.2% under 1-shot, 2-shot, 4-shot and 8-shot settings, respectively. Correspondingly reduction in the prompt size is 32.3%, 34.9%, 33.0% and 32.9%. We attribute such drastic performance improvement to the following factors: (1) Prompt-SAW retains the logical integrity of the prompts by sub-dividing the original prompts into smaller comprehensive information elements; (2)Prompt-SAW benefits from the workflow that allows selecting and omitting individual information elements for prompt compression without destroying the overall information structure of the compressed prompt. These help Prompt-SAW to ensure the utility of the compressed prompt for the end task.
| Target LLM | Method | NaturalQuestions | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| = 0.5 | = 0.3 | = 0.1 | ||||||||
| Acc | Tokens | 1/ | Acc | Tokens | 1/ | Acc | Tokens | 1/ | ||
| GPT3.5-turbo | Original | 92.18 | 524 | 1.00 | 92.18 | 524 | 1.00 | 92.18 | 524 | 1.00 |
| Selective-Context | 49.23 | 283 | 1.85 | 45.71 | 173 | 3.03 | 31.12 | 68 | 7.69 | |
| LongLLMlingua | 59.65(39.0%) | 270 | 1.94 | 52.02(40.8%) | 161 | 3.25 | 47.14(14.7%) | 57 | 9.21 | |
| Prompt-SAW | 82.93 | 227 | 2.31 | 73.22 | 136 | 3.86 | 54.07 | 33 | 16.08 | |
| LLaMA2-7B-chat | Original | 71.25 | 524 | 1.00 | 71.25 | 524 | 1.00 | 71.25 | 524 | 1.00 |
| Selective-Context | 40.87 | 283 | 1.85 | 34.26 | 173 | 3.03 | 21.37 | 68 | 7.69 | |
| LongLLMlingua | 43.56(77.1%) | 270 | 1.94 | 38.87(71.2%) | 161 | 3.25 | 26.12(72.7%) | 57 | 9.21 | |
| Prompt-SAW | 77.14 | 227 | 2.31 | 66.53 | 136 | 3.86 | 45.11 | 33 | 16.08 | |
| Target LLM | Method | ShareGPT | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = 0.5 | = 0.3 | = 0.1 | ||||||||||||||
| Rouge-1 | Rouge-2 | Rouge-L | Tokens | 1/ | Rouge-1 | Rouge-2 | Rouge-L | Tokens | 1/ | Rouge-1 | Rouge-2 | Rouge-L | Tokens | 1/ | ||
| GPT3.5-turbo | Selective-Context | 36.41 | 16.48 | 23.17 | 312 | 1.80 | 34.41 | 14.81 | 22.04 | 217 | 2.59 | 33.32 | 11.87 | 19.66 | 95 | 5.92 |
| LongLLMlingua | 38.13(29.3%) | 17.07(52.6%) | 25.22(29.1%) | 305 | 1.84 | 36.13(34.9%) | 15.61(70.9%) | 23.17(38.3%) | 202 | 2.78 | 34.23(38.6%) | 12.64(87.6%) | 21.16(32.0%) | 90 | 6.24 | |
| Prompt-SAW | 49.31 | 26.04 | 32.57 | 176 | 3.19 | 48.75 | 26.68 | 32.04 | 146 | 3.85 | 47.44 | 23.71 | 27.93 | 61 | 9.21 | |
| LLaMA2-7B-chat | Selective-Context | 32.24 | 13.42 | 23.74 | 312 | 1.80 | 30.78 | 10.95 | 22.96 | 217 | 2.59 | 30.15 | 10.32 | 19.13 | 95 | 5.92 |
| LongLLMlingua | 34.51(0.8%) | 15.18 | 27.73 | 305 | 1.84 | 32.97(1.1%) | 13.78 | 26.01 | 202 | 2.78 | 31.26(2.8%) | 12.11 | 23.08 | 90 | 6.24 | |
| Prompt-SAW | 34.81 | 14.03(8.2%) | 24.88(11.4%) | 176 | 3.19 | 33.34 | 12.19(13.0%) | 24.08(8.0%) | 146 | 3.85 | 32.15 | 11.34(6.8%) | 20.35(13.4%) | 61 | 9.21 | |
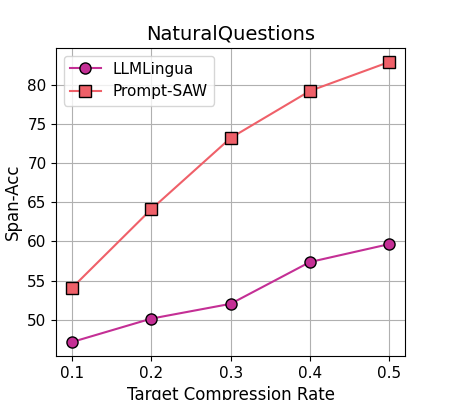
Results for Task-aware Settings. Table 2 reports the performance of Prompt-SAW under task-aware settings on NaturalQuestions using GPT3.5-turbo and LLaMA2-7B-chat as target LLMs. These results show that, Prompt-SAW improves the Span Accuracy by 39.0%, 40.8% and 14.7% for GPT3.5-turbo, and 77.1%, 71.2%, 72.7% for LLaMA2-7B-chat, respectively, for different values of the target compression rates , against the best-performing baseline (LongLLMLingua). Correspondingly, the reduction in the prompt size is 56.7%, 74.0%, and 93.7% respectively.
The results of Prompt-SAW on ShareGPT (in Table 3) show for GPT3.5-turbo as target LLM, Prompt-SAW improves the Rouge-1 score by up to 29.3%, 34.9% and 38.6%. The performance for Rouge-2 and Rouge-L exhibit a similar behavior. For these results, we also observe for LLaMA2-7B-chat, the improvement in performance is relatively lower compared to that of GPT3.5-turbo. A probable justification in this regard is the fact that LLaMA2-7B-chat is more influenced by the change in context for the compressed prompt. Whereas, higher performance on GPT3.5-turbo indicates that Prompt-SAW preserves the critical information in the prompt.
Correlating the results for both settings, we observe that compared to the task-agnostic scenarios, Prompt-SAW yields better performance for task-aware settings, especially for NaturalQuestions. This is due to the fact that it is more difficult to dig out the latent correlation between information elements within the prompt’s internal structure rather than explicit task-aware correlation extraction.
From Table 2 and Figure 3 we can also find that the performance of Prompt-SAW drops when the value for the target compression rate decreases from 0.5 to 0.1. A probable justification that the actual compression ratio of Prompt-SAW is significantly higher than the target compression ratio when the target compression ratio is 10, i.e., . This is owing to the fact that Prompt-SAW only retains the information elements in as the key/basic information units for the compression process. It will delete some entities and relations that may be highly similar to the problem but their overall structure is too long, leading to relatively poor performance for a higher compression ratio.
6.3 Further Analysis
In this section, we perform an in-depth analysis of the performance of Prompt-SAW.
Different Target LLMs. We also analyze the performance of Prompt-SAW using different target LLMs. Comparing the results in Table 2 and Table 3, we can find that GPT3.5-turbo performs better than LLaMA2-7B-chat.
For NaturalQuestions, GPT3.5-turbo achieves up to 19.8% higher Acc scores compared to that of LLaMA2-7B-chat. Likewise for ShareGPT, it achieve up to 47.55% higher value for Rouge-1. We attribute this result to GPT3.5’s stronger ability to understand and comprehend context, resulting in generating higher quality response for the prompts compressed by Prompt-SAW.
| Selective-Context | LLMLingua | Prompt-SAW | |
| FL | 5.61 | 5.74 | 6.30 |
Readability of Compressed Prompts. As explained in the introduction (also highlighted in Figure 1), a key limitation of existing prompt compression approaches is the limited readability of the compressed prompt. In order to validate the results of Prompt-SAW in terms of human readability and/or interpretability, we report some example prompts along with prompt compressed using Prompt-SAW and LLMLingua (Jiang et al., 2023a) in Appendix D.1, for a quick comparison. These examples clearly indicate that the prompt compressed by Prompt-SAW exhibit better readability and/or interpretability compared to compressed using LLMLingua.
For instance, as shown in Example D.1 (Appendix D.1), the prompt compressed by LLMLingua encompasses grammatical incoherent text, such as: {“List of Nobelates in The first Prize1 Wilhelmrad, of who received82 in en prize”}. Lack of grammatical coherence significantly undermines the readability and/or interpretability of the compressed prompt, thus impacting its end-utility. Whereas, the prompt compressed by Prompt-SAW, relying on knowledge graph triples exhibits a consistent grammatical sentence structure, as shown in the lower half of Example D.1.
 |
 |
To further support our claims, we also conducted a quantitative comparison. Specifically, we assess the fluency of the compressed prompts through the computation of a weighted mean of bi-gram and tri-gram entropies (Meng et al., 2022). Its computational details are given in Appendix C.3, and result is reported in Table 4. These results show that Prompt-SAW yields relatively higher fluency scores than the baseline models. A lower score for baseline models, e.g., LLMLingua, is attributable to loss of intrinsic semantic relationship between the tokens for the compressed prompt.
Computational Overhead. One of the key objectives of prompt compression is to efficiently reduce the overall computational and corresponding fiscal cost associated with the proprietary LLMs, while at the same time preserving the end-utility of the prompt.
In order to compute the computational overhead of Prompt-SAW, we assume embedding and computing similarity takes a constant amount of time and its cost may be ignored because it is much smaller than that of LLM. Specifically, we use the following formulation to study the computational efficiency of Prompt-SAW:
| (7) |
where represents the per-token computation load to generate knowledge triples and is per-token computation for target LLMs to generate final output respectively. represents length of the original prompt, is the target compress rate, and represents the total computational overhead for compression.
Following the assumption of Jiang et al. (2023a), we estimate and based on model parameters, as: using OpenIE toolkit as the knowledge extraction approach. When , we have . This means we can achieve nearly 5x savings in terms of computational resources. For the cases employing a small LLM for graph construction, , the computational overhead is , which is only slightly higher than the first case.
Overall, these results show the computation efficiency of our model is comparable with that of Jiang et al. (2023a). On the other hand, Prompt-SAW offers much higher benefits, i.e., compressing prompts without distorting their readability for end-users, while at the same time preserving their end-utility to the best possible extent.
7 Conclusion
In this work, we proposed Prompt-SAW that leverages graph structures to infer key information in the prompt in order to come up with a compressed prompt. Experimental evaluation showed that Prompt-SAW outperforms the existing research on by a significant margin. Moreover, Prompt-SAW addressed a key limitation of existing prompt compression approaches, i.e., the compressed prompts are easy to read and understand for end-readers.
8 Limitations
Some of the limitations of the Prompt-SAW are as follows:
-
1.
Currently our work is focused on compressing prompts that may be reformulated into structured elements, i.e., knowledge graph triplets . We consider its generalization to text segments that may not be organized as graph triplets as a future research direction.
-
2.
The performance of Prompt-SAW relies on the quality of the knowledge graph constructed. We use OpenIE toolkit as our primary graph construction tool. The errors in the graph are propagated in the compressed prompt and may impact the end utility of the compressed prompt.
Ethics Statement
This work fully complies with the ACL Ethics Policy. We declare that there are no ethical issues in this paper, to the best of our knowledge.
References
- Achiam et al. (2023) Josh Achiam, Steven Adler, Sandhini Agarwal, Lama Ahmad, Ilge Akkaya, Florencia Leoni Aleman, Diogo Almeida, Janko Altenschmidt, Sam Altman, Shyamal Anadkat, et al. 2023. Gpt-4 technical report. arXiv preprint arXiv:2303.08774.
- Ali et al. (2020) Muhammad Asif Ali, Yifang Sun, Bing Li, and Wei Wang. 2020. Fine-grained named entity typing over distantly supervised data based on refined representations. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34(05), pages 7391–7398.
- Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021. Training verifiers to solve math word problems. ArXiv, abs/2110.14168.
- Dong et al. (2022) Qingxiu Dong, Lei Li, Damai Dai, Ce Zheng, Zhiyong Wu, Baobao Chang, Xu Sun, Jingjing Xu, and Zhifang Sui. 2022. A survey on in-context learning. arXiv preprint arXiv:2301.00234.
- Ji et al. (2020) Shaoxiong Ji, Shirui Pan, E. Cambria, Pekka Marttinen, and Philip S. Yu. 2020. A survey on knowledge graphs: Representation, acquisition, and applications. IEEE Transactions on Neural Networks and Learning Systems, 33:494–514.
- Jiang et al. (2023a) Huiqiang Jiang, Qianhui Wu, Chin-Yew Lin, Yuqing Yang, and Lili Qiu. 2023a. Llmlingua: Compressing prompts for accelerated inference of large language models. In Conference on Empirical Methods in Natural Language Processing.
- Jiang et al. (2023b) Huiqiang Jiang, Qianhui Wu, Xufang Luo, Dongsheng Li, Chin-Yew Lin, Yuqing Yang, and Lili Qiu. 2023b. Longllmlingua: Accelerating and enhancing llms in long context scenarios via prompt compression. ArXiv, abs/2310.06839.
- Jung and Kim (2023) Hoyoun Jung and Kyung-Joong Kim. 2023. Discrete prompt compression with reinforcement learning. ArXiv, abs/2308.08758.
- Kim et al. (2023) Jiho Kim, Yeonsu Kwon, Yohan Jo, and Edward Choi. 2023. Kg-gpt: A general framework for reasoning on knowledge graphs using large language models. ArXiv, abs/2310.11220.
- Kolluru et al. (2020) Keshav Kolluru, Vaibhav Adlakha, Samarth Aggarwal, Mausam, and Soumen Chakrabarti. 2020. Constrained iterative labeling for open information extraction. In Conference on Empirical Methods in Natural Language Processing.
- Lester et al. (2021) Brian Lester, Rami Al-Rfou, and Noah Constant. 2021. The power of scale for parameter-efficient prompt tuning. In Conference on Empirical Methods in Natural Language Processing.
- Lewis et al. (2020) Patrick Lewis, Ethan Perez, Aleksandara Piktus, Fabio Petroni, Vladimir Karpukhin, Naman Goyal, Heinrich Kuttler, Mike Lewis, Wen tau Yih, Tim Rocktäschel, Sebastian Riedel, and Douwe Kiela. 2020. Retrieval-augmented generation for knowledge-intensive nlp tasks. ArXiv, abs/2005.11401.
- Li (2023) Yucheng Li. 2023. Unlocking context constraints of llms: Enhancing context efficiency of llms with self-information-based content filtering. ArXiv, abs/2304.12102.
- Lin (2004) Chin-Yew Lin. 2004. Rouge: A package for automatic evaluation of summaries. In Annual Meeting of the Association for Computational Linguistics.
- Liu et al. (2023) Nelson F. Liu, Kevin Lin, John Hewitt, Ashwin Paranjape, Michele Bevilacqua, Fabio Petroni, and Percy Liang. 2023. Lost in the middle: How language models use long contexts. Transactions of the Association for Computational Linguistics, 12:157–173.
- Luo et al. (2023) Linhao Luo, Yuan-Fang Li, Gholamreza Haffari, and Shirui Pan. 2023. Reasoning on graphs: Faithful and interpretable large language model reasoning. ArXiv, abs/2310.01061.
- Meng et al. (2022) Kevin Meng, David Bau, Alex Andonian, and Yonatan Belinkov. 2022. Locating and editing factual associations in gpt. In Neural Information Processing Systems.
- Pan et al. (2023) Shirui Pan, Linhao Luo, Yufei Wang, Chen Chen, Jiapu Wang, and Xindong Wu. 2023. Unifying large language models and knowledge graphs: A roadmap. ArXiv, abs/2306.08302.
- Park et al. (2023) Joon Sung Park, Joseph C. O’Brien, Carrie J. Cai, Meredith Ringel Morris, Percy Liang, and Michael S. Bernstein. 2023. Generative agents: Interactive simulacra of human behavior. Proceedings of the 36th Annual ACM Symposium on User Interface Software and Technology.
- Sahoo et al. (2024) Pranab Sahoo, Ayush Kumar Singh, Sriparna Saha, Vinija Jain, Samrat Sohel Mondal, and Aman Chadha. 2024. A systematic survey of prompt engineering in large language models: Techniques and applications. ArXiv, abs/2402.07927.
- Shannon (1951) Claude E. Shannon. 1951. Prediction and entropy of printed english. Bell System Technical Journal, 30:50–64.
- Touvron et al. (2023) Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. 2023. Llama: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971.
- Wei et al. (2022) Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Ed Huai hsin Chi, F. Xia, Quoc Le, and Denny Zhou. 2022. Chain of thought prompting elicits reasoning in large language models. ArXiv, abs/2201.11903.
- Wingate et al. (2022) David Wingate, Mohammad Shoeybi, and Taylor Sorensen. 2022. Prompt compression and contrastive conditioning for controllability and toxicity reduction in language models. In Conference on Empirical Methods in Natural Language Processing.
- Xu et al. (2023) Zhaozhuo Xu, Zirui Liu, Beidi Chen, Yuxin Tang, Jue Wang, Kaixiong Zhou, Xia Hu, and Anshumali Shrivastava. 2023. Compress, then prompt: Improving accuracy-efficiency trade-off of llm inference with transferable prompt. ArXiv, abs/2305.11186.
- Yan et al. (2023) Jianhao Yan, Jin Xu, Chiyu Song, Chenming Wu, Yafu Li, and Yue Zhang. 2023. Understanding in-context learning from repetitions. ArXiv, abs/2310.00297.
Appendix A Background
A.1 Knowledge Graph
Knowledge Graph (KG) can be represented as , where and denote the set of entities and relations. Here entities are represented as nodes in , while relations form up edges between the nodes.
A.2 Task-aware Prompts
Task-aware prompts refer to the ones that are strongly related to the task and need to be re-compressed while changing the question. These prompts usually contain the specific information needed to solve the task, and some redundant parts can be removed. For example, the task can be the question, ”Who are the first people to win the Nobel Prize?” and the prompt may contain a document that includes all the information about people who won the Nobel Prize.
A.3 Task-agnostic Prompts
Opposite to task-aware prompts, task-agnostic prompts are weakly related to the task. This kind of prompt usually just provides LLMs with an example of what to do, such as how to solve the problem step by step. For example, the prompt may be ”The weather is really nice today, emotion: positive.” The model then follows this format and judges the emotion of the input sentence.
A.4 Chain-of-thought Prompt
This is a type of task-agnostic prompt. Chain-of-thought Prompt aims to improve performance on tasks requiring logic and calculation by mimicking human reasoning. That is include several demonstrations with detailed reasoning . We research how to compress chain-of-thought prompts on mathematical reasoning tasks.
A.5 Prompt with external documentation
This is a type of task-aware prompt. Prompt with external documentation implies that the prompt contains some additional information, such as external knowledge, that the model may refer to to answer the question. That external knowledge may include several external documents . Question Answering is a specific scenario for prompts with external knowledge.
A.6 Token-level Prompt compression
In this section, we introduce the previous token-level compression method, e.g., LLMlingua (Jiang et al., 2023a), and LongLLMlingua (Jiang et al., 2023b).
LLMLingua is a token-level prompt compression method that performs compression based on perplexity. It includes a budget controller to calculate the compression ratio of demonstrations and the further compression ratio of each demonstration based on given parameters. LLMLingua uses the LLAMA-2 Touvron et al. (2023) to calculate the perplexity of each token. Finally, LLMLingua compresses the prompt based on the perplexity and compression ratio.
LongLLMlingua is a token-level prompt compression method that aims at task-aware prompt compression. It changes the perplexity measure method and relates it to the specific question.
Appendix B Prompts
B.1 Prompts for Graph Construction
B.2 Instructions used for GPT-4 response Generation
The instructions we used in the GPT-4 Generation are shown below:
Appendix C Experimental Details
C.1 Dataset
We provide a detailed description of the evaluation data sets below. The statistics of the dataset are given in Table 5.
| Statistics | GSM8K-aug | NaturalQuestions | ShareGPT | |||
|---|---|---|---|---|---|---|
| 1shot | 2shot | 4shot | 8shot | |||
| Token number of prompt | 306 | 612 | 1224 | 2365 | 3040 | 562 |
| Number of questions | 1319 | 2654 | 575 | |||
(i) GSM8K-aug. we use GSM8K-aug, an extended version of original GSM8k data set allowing computations for under i-shot settings, i.e., i = {1, 2, 4 and 8}-shots. Its process-flow is explained in Section 5. The statistics of the data set is shown in Table 5.
(ii) NaturalQuestions. It is a QA dataset that is comprised of real-world queries collected by individuals Liu et al. (2023). Each question of this dataset has 20 related documents, one of which contains the correct answer. We select documents containing answers as compression targets to examine better the compression performance of different methods on a single document.
(iii) ShareGPT. It is a conversation dataset encompassing users’ conversation with ChatGPT555ShareGPT.com. Each data sample is a complete conversation between the user and ChatGPT, covering multiple languages across different scenarios. Following Li (2023) and Jiang et al. (2023a), we use a subset of 575 samples provide by Li (2023) for evaluation. We use all dialogues except the final round as the prompt, and the human’s question in the last round as the question.
C.2 Baseline Models
(i) Selective-Context. Selective-Context by Li (2023) uses a small language model to calculate the self-information in the prompt and then filter out on token-level based on the self-information of each token.
(ii) LLMLingua. LLMLingua by Jiang et al. (2023a) perform token-level prompt compression based on the perplexity calculated by the small language model.
(iii) LongLLMLingua. Based on LLMLingua, LongLLMlingua by Jiang et al. (2023b) further adds a coarse-grained filtering module, which is more suitable for long document compression.
We followed their original experimental setting, uses LLMLlingua on GSM8K and LongLLMlingua on NaturalQuestions.
C.3 Evaluation Metrics
Detailed description and mathematical formulation of the evaluation metrics is provided as follows:
Exact Match (EM). In EM, when the model output answer is completely consistent with the golden answer, the answer is considered correct. It is shown below.
| (8) |
Where represents the model used to answer the question, and represent the question, and indicate the answer for question, and indicate the prompt compression method.
Span Accuracy (SAcc). We follow previous work and use SAcc to measure the performance of QA datasets. SAcc determines whether the standard answer is part of the response answer of the GPT model, as shown below.
| (9) |
Rouge. To measure the similarity between the output of the original prompt and the compressed prompt, we apply commonly used overlap metric ROUGE (Lin, 2004). We report uni-gram and bi-gram overlap as the metric of assessing informativeness (Rouge-1 and Rouge-2), and the longest common sub-sequence as the metric of assessing fluency (Rouge-L).
Fluency (FL). We use fluency as a metric to measure the readability and grammatical coherence of the compressed prompt. Following Meng et al. (2022), we use the following formula to compute the fluency.
| (10) |
where means the -gram frequency distribution.
Appendix D Additional Results
D.1 Interpretability of Compressed prompts (Examples)
In this section, we report some examples prompts along with prompts compressed by Prompt-SAW and LLMLingua (Jiang et al., 2023a) for a quick comparison in terms of readability and/or interpretability of the compressed prompt. As an example, for the compressed prompt text compressed using LLMLingua in Table D.1, the text ”won twoes forg01 theate women prize:ertMayer” is hard to interpret for humans. On the contrary, the prompt compressed by Prompt-SAW yields comprehensive information units helpful that are not only easy to interpret but are also highly relevant to the question.