Proof of the $C^{2}$ Mañé’s conjecture on surfaces.

Gonzalo Contreras CIMAT
A.P. 402, 36.000
Guanajuato. GTO
México. gonzalo@cimat.mx

Abstract.

We prove that $C^{2}$ generic hyperbolic Mañé sets contain a periodic periodic orbit. In dimension 2, adding a result in [7] which states that $C^{2}$ generic Mañé sets are hyperbolic we obtain Mañé’s Conjecture for surfaces in the $C^{2}$ topology: Given a Tonelli Lagrangian $L$ on a compact surface $M$ there is a $C^{2}$ open and dense set of functions $f:M\to{\mathbb{R}}$ such that the Mañé set of the Lagrangian $L+f$ is a hyperbolic periodic orbit.

Key words and phrases:

Mañé’s Conjecture, Aubry-Mather Theory, Lagrangian Systems.

1991 Mathematics Subject Classification:

37J51, 37D05

Partially supported by CONACYT, Mexico, grant A1-S-10145.

1. Introduction.

Let $M$ be a closed riemannian manifold. A Tonelli Lagrangian is a $C^{2}$ function $L:TM\to{\mathbb{R}}$ that is

(i)

Convex: $\exists a>0$ $\forall(x,v),(x,w)\in TM$ , $w\cdot\partial^{2}_{vv}L(x,v)\cdot w\geq a|w|_{x}^{2}$ .

The uniform convexity assumption and the compactness of $M$ imply that $L$ is

(ii)

Superlinear: $\forall A>0$ $\exists B>0$ such that $\forall(x,v)\in TM$ : $L(x,v)>A\,|v|_{x}-B$ .

Given $k\in{\mathbb{R}}$ , the Mañé action potential is defined as $\Phi_{k}:M\times M\to{\mathbb{R}}\cup\{-\infty\}$ ,

(1)

\Phi_{k}(x,y):=\inf_{\gamma\in{\mathcal{C}}(x,y)}\int k+L(\gamma,{\dot{\gamma}}),

where

(2)

{\mathcal{C}}(x,y):=\{\gamma:[0,T]\to M\;{\text{absolutely continuous }}|\;T>0,\;\gamma(0)=x,\;\gamma(T)=y\;\}.

The Mañé critical value is

(3)

c(L):=\sup\{\,k\in{\mathbb{R}}\;|\;\exists\,x,y\in M:\;\Phi_{k}(x,y)=-\infty\;\}.

See [13] for several characterizations of $c(L)$ .

A curve $\gamma:{\mathbb{R}}\to M$ is semi-static if

\forall s<t\qquad\int_{s}^{t}c(L)+L(\gamma,{\dot{\gamma}})=\Phi_{c(L)}(\gamma(s),\gamma(t)).

Also $\gamma:{\mathbb{R}}\to M$ is static if

\forall s<t\qquad\int_{s}^{t}c(L)+L(\gamma,{\dot{\gamma}})=-\Phi_{c(L)}(\gamma(t),\gamma(s)).

The Mañé set of $L$ is

{\mathcal{N}}(L):=\{(\gamma(t),{\dot{\gamma}}(t))\in TM\;|\;t\in{\mathbb{R}},\;\gamma:{\mathbb{R}}\to M\text{ is semi-static }\},

and the Aubry set is

{\mathcal{A}}(L):=\{(\gamma(t),{\dot{\gamma}}(t))\in TM\;|\;t\in{\mathbb{R}},\;\gamma:{\mathbb{R}}\to M\text{ is static }\}.

The Euler-Lagrange equation

\tfrac{d}{dt}\,\partial_{v}L=\partial_{x}L

defines the Lagrangian flow $\varphi_{t}$ on $TM$ . The energy function $E_{L}:TM\to{\mathbb{R}}$ ,

E_{L}(x,v):=\partial_{v}L(x,v)\cdot v-L(x,v),

is invariant under the Lagrangian flow. The Mañé set ${\mathcal{N}}(L)$ is invariant under the Lagrangian flow and it is contained in the energy level ${\mathcal{E}}:=E_{L}^{-1}\{c(L)\}$ (see Mañé [24, p. 146] or [13]).

Let ${\mathcal{M}}_{\text{inv}}(L)$ be the set of Borel probabilities in $TM$ which are invariant under the Lagrangian flow. Define the action functional $A_{L}:{\mathcal{M}}_{\text{inv}}(L)\to{\mathbb{R}}\cup\{+\infty\}$ as

A_{L}(\mu):=\int L\,d\mu.

The set of minimizing measures is

{\mathcal{M}}_{\min}(L):=\arg\min_{{\mathcal{M}}_{\text{inv}}(L)}A_{L},

and the Mather set ${\mathcal{M}}(L)$ is the union of the support of minimizing measures:

{\mathcal{M}}(L):=\textstyle\bigcup\limits_{\mu\in{\mathcal{M}}_{\min}(L)}\operatorname{supp}(\mu).

Mañé proves (cf. Mañé [24, Thm. IV] also [11, p. 165]) that an invariant measure is minimizing if and only if it is supported in the Aubry set. Therefore we get the set of inclusions

(4)

{\mathcal{M}}\subseteq{\mathcal{A}}\subseteq{\mathcal{N}}\subseteq{\mathcal{E}}.

1.1 Definition.

We say that ${\mathcal{N}}(L)$ is hyperbolic if there are sub-bundles $E^{s}$ , $E^{u}$ of $T{\mathcal{E}}|_{{\mathcal{N}}(L)}$ and $T_{0}>0$ such that

(i)

$T{\mathcal{E}}|_{{\mathcal{N}}(L)}=E^{s}\oplus\langle\frac{d}{dt}\varphi_{t}\rangle\oplus E^{u}$ .
(ii)

$\left\|D\varphi_{T_{0}}|_{E^{s}}\right\|<1$ , $\left\|D\varphi_{-T_{0}}|_{E^{u}}\right\|<1$ .
(iii)

$\forall t\in{\mathbb{R}}$ $(D\varphi_{t})^{*}(E^{s})=E^{s}$ , $(D\varphi_{t})^{*}(E^{u})=E^{u}$ .

Hyperbolicity for autonomous lagrangian or hamiltonian flows is always understood as hyperbolicity for the flow restricted to the energy level.

Fix a Tonelli Lagrangian ${L}$ . Let

{\mathcal{H}}^{k}({L}):=\{\,\phi\in C^{k}(M,{\mathbb{R}})\;|\;{\mathcal{N}}({L}+\phi)\text{ is hyperbolic }\},

endowed with the $C^{k}$ topology. By [14, lemma 5.2, p. 661] the map $\phi\mapsto{\mathcal{N}}({L}+\phi)$ is upper semi-continuous and $\phi\mapsto c({L}+\phi)$ is continuous [14, lemma 5.1]. This, together with the persistence of hyperbolicity (cf. [17, 5.1.8] or proposition A.1 below) imply that ${\mathcal{H}}^{k}({L})$ is an open set for any $k\geq 2$ .

In [14] theorem C shows that generically ${\mathcal{M}}={\mathcal{A}}={\mathcal{N}}$ is the support of a single minimizing measure. Mañé [23, theorem F] proves that this measure is a strong limit of invariant probabilities supported on periodic orbits.

Let

{\mathcal{P}}^{2}({L}):=\{\,\phi\in C^{2}(M,{\mathbb{R}})\;|\;{\mathcal{N}}({L}+\phi)\text{ contains a periodic orbit or a singularity}\},

and let $\overline{{\mathcal{P}}^{2}({L})}$ be its closure in $C^{2}(M,{\mathbb{R}})$ . We will prove

Theorem A.

${\mathcal{H}}^{2}({L})\subset\overline{{\mathcal{P}}^{2}({L})}$ .

In [12] we proved that if $\Gamma\subset{\mathcal{N}}({L})$ is a periodic orbit, adding a potential $\phi_{0}\geq 0$ which is locally of the form $\phi_{0}(x)=\varepsilon\,d(x,\pi(\Gamma))^{2}$ makes $\Gamma$ a hyperbolic periodic orbit (or hyperbolic singularity) for the Lagrangian flow of ${L}+\phi_{0}$ and also ${\mathcal{N}}({L}+\phi_{0})=\Gamma$ . Moreover [12, p. 934], $\Gamma$ has the locking property meaning that there is a $C^{2}$ neighborhood ${\mathcal{U}}$ of $\phi_{0}$ such that for $\phi\in{\mathcal{U}}$ , ${\mathcal{N}}(L+\phi)=\Gamma_{\phi}$ the continuation $\Gamma_{\phi}$ of the periodic orbit $\Gamma$ in the energy level $E_{L+\phi}^{-1}\{c(L+\phi)\}$ . This follows from the semicontinuity of $\phi\mapsto{\mathcal{N}}(L+\phi)$ and the expansivity of $\Gamma$ . Therefore defining

{\mathcal{H}}{\mathcal{P}}^{2}({L}):=\{\,\phi\in C^{2}(M,{\mathbb{R}})\;|\;{\mathcal{N}}({L}+\phi)\text{ is a hyperbolic periodic orbit or singularity}\}

we get

Corollary B.

The set ${\mathcal{H}}{\mathcal{P}}^{2}({L})$ contains an open and dense set in ${\mathcal{H}}^{2}({L})$ .

With A. Figalli and L. Rifford in [7] we prove

Theorem C.

If $\dim M=2$ then ${\mathcal{H}}^{2}({L})$ is open and dense.

Thus for surfaces in the $C^{2}$ topology we obtain Mañé’s Conjecture [24, p. 143]:

Corollary D.

If $\dim M=2$ then ${\mathcal{H}}{\mathcal{P}}^{2}({L})$ contains an open and dense set in $C^{2}(M,{\mathbb{R}})$ .

Observe that from the inclusions in (4), for potentials $\phi\in{\mathcal{H}}{\mathcal{P}}^{2}({L})$ the lagrangian $L+\phi$ has a unique minimizing measure and it is supported on a hyperbolic periodic orbit or a hyperbolic singularity. The set ${\mathcal{H}}{\mathcal{P}}^{2}({L})$ is open in the $C^{2}$ topology, so we can approximate the lagrangian ${L}$ with a $C^{\infty}$ potential $\phi$ to obtain a periodic minimizing measure, but the approximation is only proved to be $C^{2}$ small.

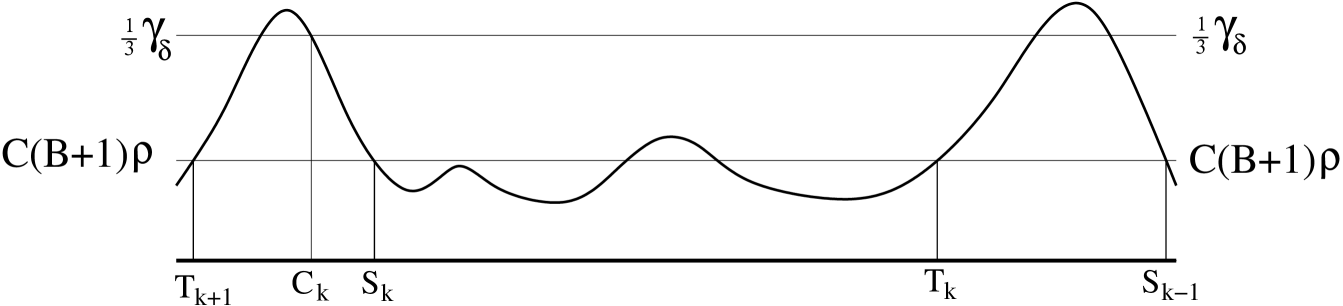
Since in theorem A the Aubry set is hyperbolic, by the shadowing lemma ${\mathcal{A}}({L})$ is accumulated by periodic orbits. The idea of the proof is to choose a special periodic orbit $\Gamma$ nearby ${\mathcal{A}}({L})$ with small action and small period and prove that adding a channel $\phi$ centered at $\Gamma$ , defined in (96) produces that $\Gamma\subset{\mathcal{A}}({L}+\phi)$ .

Theorem A is the same as the main theorem in the manuscript [10] which will remain unpublished. The proof below uses a simplification devised by Huang, Lian, Ma, Xu, Zhang [20], [21], see also Bochi [2]. The proof in [10], [9] is based in the fact that generic hyperbolic Mañé sets have zero topological entropy. The following proof is based on the periodic orbit which is used to prove zero entropy. The point is that the estimates of Bressaud and Quas [6] for the action and period of optimal periodic orbits nearby ${\mathcal{A}}({L})$ are so good that the cutting process in proposition 4.3 stops before the estimates get spoiled.

This proof owes a lot to the people working on ergodic optimization. Ergodic optimization was born as a baby version of Aubry-Mather theory adapted to symbolic dynamics [8]. Now the subject has matured enough to give the main ideas of the proof of an important conjecture in Aubry-Mather theory.

Main differences of lagrangian systems with ergodic optimization besides that the dynamical system depends on the lagrangian, are that perturbations need to be $C^{2}$ instead of Lipschitz and that the perturbations $\phi$ are defined in the configuration space and not in the phase space. These problems are solved by comparing the actions with static orbits and using Fathi’s differentiability estimates for weak KAM solutions, and observing that quasi minimizing objects inherit part of Mather’s graph property.

In section 3 we obtain periodic specifications in ${\mathcal{A}}(L)$ with exponentially small jumps and sub-exponential period. In section 4 proposition 4.3 we obtain periodic orbits $\Gamma$ nearby ${\mathcal{A}}(L)$ with small action compared to their self-approximations, called class I by Yuan-Hunt [31]. In section 5 we prove in proposition 5.3 that adding a channel $\phi$ centered in $\Gamma$ we obtain $\Gamma\subset{\mathcal{A}}(L+\phi)$ , thus proving theorem A. In symbolic dynamics this was known to Yuan-Hunt [31] but here we use the method of Quas-Siefken [29]. In appendix A we prove the refinement of the shadowing lemmas that we need.

2. Preliminars.

Let ${\mathcal{M}}_{\text{inv}}(L)$ be the set of Borel probabilities in $TM$ invariant under the Lagrangian flow. Denote by ${\mathcal{M}}_{\min}(L)$ the set of minimizing measures for the Lagrangian $L$ , i.e.

(5)

{\mathcal{M}}_{\min}(L):=\Big{\{}\,\mu\in{\mathcal{M}}_{\text{inv}}(L)\;\Big{|}\;\int_{TM}L\,d\mu=-c(L)\;\Big{\}}.

Their name is justified (cf. Mañé [24, Theorem II]) by

(6)

-c(L)=\min_{\mu\in{\mathcal{M}}_{\text{inv}}(L)}\int_{TM}L\;d\mu=\min_{\mu\in{\mathcal{C}}(TM)}\int_{TM}L\;d\mu.

Fathi and Siconolfi [16, Theorem 1.6] prove the second equality in (6) where the set of closed measures is defined by

{\mathcal{C}}(TM):=\Big{\{}\,\mu\text{ Borel probability on }TM\;\Big{|}\;\forall\phi\in C^{1}(M,{\mathbb{R}})\;\int_{TM}d\phi\;d\mu=0\,\Big{\}}.

Given a closed curve $\gamma:[0,T]\to M$ , using the closed measure $\int f\,d\mu_{\gamma}:=\frac{1}{T}\int_{0}^{T}f(\gamma,{\dot{\gamma}})\,dt$ in (6) we get

(7)

\gamma\text{ closed curve in $M$}\quad\Longrightarrow\quad A_{L+c(L)}(\gamma)\geq 0.

Recall that a curve $\gamma:{\mathbb{R}}\to M$ is static for a Tonelli Lagrangian $L$ if

(8)

s<t\quad\Longrightarrow\quad\int_{s}^{t}L(\gamma,{\dot{\gamma}})=-\Phi_{c(L)}(\gamma(t),\gamma(s));

equivalently (cf. Mañé [24, pp. 142–143]), if $\gamma$ is semi-static and

(9)

s<t\quad\Longrightarrow\quad\Phi_{c(L)}(\gamma(s),\gamma(t))+\Phi_{c(L)}(\gamma(t),\gamma(s))=0.

The Aubry set is defined as

{\mathcal{A}}(L):=\{\,(\gamma(t),{\dot{\gamma}}(t))\;|\;t\in{\mathbb{R}},\;\gamma\text{ is static}\;\},

its elements are called static vectors. In this section we prove that with this definition ${\mathcal{A}}(L)$ is invariant.

2.1 Lemma (A priori bound).

For $C>0$ there exists $A_{0}=A_{0}(C)>0$ such that if $\gamma:[0,T]\to M$ is a solution of the Euler-Lagrange equation with $A_{L}(\gamma)<C\,T$ , then

\left|{\dot{\gamma}}(t)\right|<A_{0}\qquad\text{ for all }t\in[0,T].

Proof:.

The Euler-Lagrange flow preserves the energy function

(10)

E_{L}:=v\cdot\partial_{v}L-L.

We have that

	$\displaystyle\hskip-19.91684pt\forall s\geq 0\qquad\tfrac{d\,}{ds}E_{L}(x,sv)\big{\|}_{s}$	$\displaystyle=s\,v\cdot\partial_{vv}L(x,v)\cdot v\geq s\,a\|v\|_{x}^{2}.$
	$\displaystyle E_{L}(x,v)$	$\displaystyle=E_{L}(x,0)+\int_{0}^{1}\tfrac{d\,}{ds}E_{L}(x,sv)\,ds$
(11)			$\displaystyle\geq\min_{y\in M}E_{L}(y,0)+\tfrac{1}{2}a\|v\|_{x}^{2}.$

Let

g(r):=\sup\big{\{}w\cdot\partial_{vv}L(x,v)\cdot w\,:\,|v|_{x}\leq r,\,|w|_{x}=1\big{\}}.

Then $g(r)\geq a$ and

(12)

E_{L}(x,v)\leq\max_{z\in M}E_{L}(z,0)+\tfrac{1}{2}\,g(|v|_{x})\,|v|_{x}^{2}.

By the superlinearity there is $B>0$ such that $L(x,v)>|v|_{x}-B$ for all $(x,v)\in TM$ . Since $A_{L}(\gamma)<C\,T$ , the mean value theorem implies that there is $t_{0}\in]0,T[$ such that $|{\dot{\gamma}}(t_{0})|<B+C$ . Then (12) gives an upper bound on the energy of $\gamma$ and (11) bounds the speed of $\gamma$ .

∎

For $x,\,y\in M$ and $T>0$ define

{\mathcal{C}}_{T}(x,y):=\{\,\gamma:[0,T]\to M\,|\,\gamma\text{ is absolutely continuous},\gamma(0)=x,\,\gamma(T)=y\,\}.

2.2 Corollary.

There exists $A_{1}>0$ such that if $x,\,y\in M$ and $\gamma\in{\mathcal{C}}_{T}(x,y)$ is a solution of the Euler-Lagrange equation with

A_{L+c}(\gamma)\leq\Phi_{c}(x,y)+\max\{T,d(x,y)\},

where $c=c(L)$ , then

(a)

$T\,\geq\,\tfrac{1}{A}_{1}\;d(x,y)$ .
(b)

$|{\dot{\gamma}}(t)|\,\leq\,A_{1}$ for all $t\in[0,T]$ .

Proof:.

First suppose that $d(x,y)\leq T$ . Then item (a) holds with $A_{1}=1$ . Let

(13)

\ell(r):=|c|+\sup\{\,L(x,v)\,|\,(x,v)\in TM,\,|v|\leq r\,\}.

Since $d(x,y)\leq T$ , there exists a $C^{1}$ curve $\eta:[0,T]\to M$ joining $x$ to $y$ with $|{\dot{\eta}}|\leq 1$ . We have that

A_{L+c}(\gamma)\leq\Phi_{c}(x,y)+T\leq A_{L+c}(\eta)+T\leq\big{(}\ell(1)+c\big{)}\,T+T.

Then item (b) holds for $A_{1}=A_{0}(|\ell(1)+c+1|)$ where $A_{0}$ is from Lemma 2.1.

Now suppose that $d(x,y)\geq T$ . Let $\eta:[0,d(x,y)]\to M$ be a minimal geodesic with $|{\dot{\eta}}|\equiv 1$ joining $x$ to $y$ . Let $D:=\ell(1)+c+2>0$ . From the superlinearity property there is $B>1$ such that

L(x,v)+c>D\,|v|-B,\qquad\forall(x,v)\in TM.

Then

(14)	$\displaystyle[\ell(1)+c]\;d(x,y)$	$\displaystyle\geq A_{L+c}(\eta)\geq\Phi_{c}(x,y)$
(15)		$\displaystyle\geq A_{L+c}(\gamma)-d(x,y)$
	$\displaystyle\geq\int_{0}^{T}\bigl{(}D\;\|{\dot{\gamma}}\|-B\,\bigr{)}\,dt-d(x,y)$
	$\displaystyle\geq D\;d(x,y)-B\,T-d(x,y).$

Hence

T\geq\tfrac{D-\ell(1)-c-1}{B}\;d(x,y)=\tfrac{1}{B}\;d(x,y).

This implies item (a). From (14) and (15), we get that

	$\displaystyle A_{L}(\gamma)$	$\displaystyle\leq\bigl{[}\,\ell(1)+c+1\,\bigr{]}\;d(x,y)-c\,T,$
		$\displaystyle\leq\bigl{\{}\,B\,[\,\ell(1)+c+1\,]-c\,\bigr{\}}\;T.$

Then Lemma 2.1 completes the proof.

∎

We say that a curve $\gamma:[0,T]\to M$ is a Tonelli minimizer if it minimizes the action functional on ${\mathcal{C}}_{T}(\gamma(0),\gamma(T))$ , i.e. if it is a minimizer with fixed endpoints and fixed time interval.

2.3 Corollary.

There is $A>0$ such that if $x,\,y\in M$ and $\eta_{n}\in{\mathcal{C}}_{T_{n}}(x,y)$ , $n\in{\mathbb{N}}^{+}$ is a Tonelli minimizer with

A_{L+c}(\eta_{n})\leq\Phi_{c}(x,y)+\tfrac{1}{n},

then there is $N_{0}>0$ such that $\forall n>N_{0}$ , $\forall t\in[0,T_{n}]$ , $|{\dot{\eta}}_{n}(t)|<A$ .

Proof:.

If $d(x,y)>0$ then for $n$ large enough $d(x,y)>\tfrac{1}{n}$ . In this case Corollary 2.2 implies the result with the constant $A_{1}$ . If $d(x,y)=0$ let $\xi_{n}:[0,T_{n}]\to\{x\}$ be the constant curve. Since $\eta_{n}$ is a Tonelli minimizer, we have that

A_{L}(\eta_{n})\leq A_{L}(\xi_{n})=\int_{0}^{T_{n}}L(x,0)\,dt\leq|L(x,0)|\,T_{n}.

Lemma 2.1 implies that $|{\dot{\eta}}_{n}|\leq A_{0}(C)$ with $C=\sup_{x\in M}|L(x,0)|$ . Now take $A=\max\{A_{0}(C),A_{1}\}$ .

∎

2.4 Lemma.

If $(x,v)$ is a static vector then $\gamma:{\mathbb{R}}\to M$ , $\gamma(t)=\pi\varphi_{t}(x,v)$ is a static curve, i.e. the Aubry set ${\mathcal{A}}(L)$ is invariant.

Proof:.

Let $\gamma(t)=\pi\,\varphi_{t}(x,v)$ and suppose that $\gamma|_{[a,b]}$ is static. We have to prove that all $\gamma|_{\mathbb{R}}$ is static. Let $\eta_{n}\in{\mathcal{C}}_{T_{n}}(\gamma(b),\gamma(a))$ be a Tonelli minimizer with

A_{L+c}(\eta_{n})<\Phi_{c}(\gamma(b),\gamma(a))+\tfrac{1}{n}.

By Corollary 2.3, for $n$ large enough, $|{\dot{\eta}}_{n}|<A$ . We can assume that ${\dot{\eta}}_{n}(0)\to w$ . Let $\xi(s)=\pi\,\varphi_{s}(w)$ . If $w\neq{\dot{\gamma}}(b)$ then for some $\varepsilon>0$ the curve $\gamma|_{[b-\varepsilon,b]}*\xi|_{[0,\varepsilon]}$ is not $C^{1}$ , and hence it can not be a (Tonelli) minimizer of $A_{L+c}$ in ${\mathcal{C}}_{2\varepsilon}\big{(}\gamma(b-\varepsilon),\xi(\varepsilon)\big{)}$ . Thus

\Phi_{c}(\gamma(b-\varepsilon),\xi(\varepsilon))<A_{L+c}(\gamma|_{[b-\varepsilon,b]})+A_{L+c}(\xi|_{[0,\varepsilon]}).

	$\displaystyle\Phi_{c}(\gamma(a),\gamma(a))\leq\Phi_{c}(\gamma(a),\gamma(b-\varepsilon))+\Phi_{c}(\gamma(b-\varepsilon),\xi(\varepsilon))+\Phi_{c}(\xi(\varepsilon),\gamma(a))$
	$\displaystyle\;<A_{L+c}(\gamma_{[a,b-\varepsilon]})+A_{L+c}(\gamma\|_{[b-\varepsilon,b]})+A_{L+c}(\xi\|_{[0,\varepsilon]})+\liminf_{n}A_{L+c}(\eta_{n}\|_{[\varepsilon,T_{n}]})$
	$\displaystyle\;\leq A_{L+c}(\gamma\|_{[a,b]})+\lim_{n}A_{L+c}\bigl{(}\,\eta_{n}\|_{[0,\varepsilon]}*\eta_{n}\|_{[\varepsilon,T_{n}]}\bigr{)}$
	$\displaystyle\;=-\Phi_{c}(\gamma(b),\gamma(a))+\Phi_{c}(\gamma(b),\gamma(a))=0.$

Thus there is a closed curve, from $\gamma(a)$ to itself, with negative $L+c$ action, and also negative $L+k$ action for some $k>c(L)$ . Concatenating the curve with itself many times shows that $\Phi_{k}(\gamma(a),\gamma(a))=-\infty$ . By (3) this implies that $k\leq c(L)$ , which is a contradiction. Thus $w={\dot{\gamma}}(b)$ and similarly $\lim_{n}{\dot{\eta}}_{n}(T_{n})={\dot{\gamma}}(a)$ .

If $\limsup T_{n}<+\infty$ , we can assume that $\tau=\lim_{n}T_{n}>0$ exists. In this case $\gamma$ is a semi-static periodic orbit of period $\tau+b-a$ and then $\gamma|_{\mathbb{R}}$ is static.

Now suppose that $\lim_{n}T_{n}=+\infty$ . If $s>0$ , we have that

	$\displaystyle A_{L+c}$	$\displaystyle(\gamma\|_{[a-s,b+s]})+\Phi_{c}(\gamma(b+s),\gamma(a-s))\leq$
		$\displaystyle\leq\lim_{n}\big{\{}\,A_{L+c}(\eta_{n}\|_{[T_{n}-s,T_{n}]})+A_{L+c}(\gamma\|_{[a,b]})\begin{aligned} &+A_{L+c}(\eta_{n}\|_{[0,s]})\,\big{\}}\\ &+\Phi_{c}(\gamma(b+s),\gamma(a-s))\end{aligned}$
		$\displaystyle\leq\begin{aligned} &-\Phi_{c}(\gamma(b),\gamma(a))\\ &+\lim_{n}\big{\{}\,A_{L+c}(\eta_{n}\|_{[0,s]})+A_{L+c}(\eta_{n}\|_{[s,T_{n}-s]})+A_{L+c}(\eta_{n}\|_{[T_{n}-s,T_{n}]})\,\big{\}}\end{aligned}$
		$\displaystyle\leq-\Phi_{c}(\gamma(b),\gamma(a))+\Phi_{c}(\gamma(b),\gamma(a))=0.$

Thus $\gamma_{[a-s,b+s]}$ is static for all $s>0$ .

∎

3. Optimal specifications.

Here lemma 3.1 and proposition 3.2 follow arguments by X. Bressaud and A. Quas [6].

Let $A\in\{0,1\}^{M\times M}$ be a $M\times M$ matrix of with entries in $\{0,1\}$ . The subshift of finite type $\Sigma_{A}$ associated to $A$ is the set

\Sigma_{A}=\big{\{}\;(x_{i})_{i\in{\mathbb{Z}}}\in\{0,1\}^{\mathbb{Z}}\;\big{|}\quad\forall i\in{\mathbb{Z}}\quad A(x_{i},x_{i+1})=1\;\big{\}},

endowed with the metric

d(x,y)=2^{-i},\qquad i=\max\{\;k\in{\mathbb{N}}\;|\;x_{i}=y_{i}\;\;\forall|i|\leq k\;\}

and the shift transformation

\sigma:\Sigma_{A}\to\Sigma_{A},\qquad\forall i\in{\mathbb{Z}}\quad\sigma(x)_{i}=x_{i+1}.

3.1 Lemma.

Let $\Sigma_{A}$ be a shift of finite type with $M$ symbols and topological entropy $h$ . Then $\Sigma_{A}$ contains a periodic orbit of period at most $1+M\text{\rm\large e}^{1-h}$ .

Proof:.

Let $k+1$ be the period of the shortest periodic orbit in $\Sigma_{A}$ . We claim that a word of length $k$ in $\Sigma_{A}$ is determined by the set of symbols that it contains. First note that since there are no periodic orbits of period $k$ or less, any allowed $k$ -word must contain $k$ distinct symbols. Now suppose that $u$ and $v$ are two distinct words of length $k$ in $\Sigma_{A}$ containing the same symbols. Then, since the words are different, there is a consecutive pair of symbols, say $a$ and $b$ , in $v$ which occur in the opposite order (not necessarily consecutively) in $u$ . Then the infinite concatenation of the segment of $u$ starting at $b$ and ending at $a$ gives a word in $\Sigma_{A}$ of period at most $k$ , which contradicts the choice of $k$ .

It follows that there are at most $\binom{M}{k}$ words of length $k$ . Using the basic properties of topological entropy [22, 4.1.8]

\displaystyle\text{\rm\large e}^{hk}\leq\binom{M}{k}\leq\frac{M^{k}}{k!}\leq\left(\frac{M\text{\rm\large e}}{k}\right)^{k}.

Taking $k$ -th roots, we see that $k\leq M\text{\rm\large e}^{1-h}$ .

∎

From now on we assume that the Mañé set ${\mathcal{N}}(L)$ is hyperbolic. The definition of a specification or pseudo-orbit appears in A.12 in appendix A.

3.2 Proposition.

There are $C,\lambda>0$ such that for $T>1$ large there is $(\Theta,\mathfrak{T})=(\{\theta_{i}\},\{t_{i}\})$ a periodic T-specification in ${\mathcal{A}}(L)$ , with $P=P_{T}$ jumps $(\theta_{i},t_{i})=(\theta_{i+P},t_{i+P})$ , and period $\leq 4TP_{T}$ such that

(16)		$\displaystyle\lim\nolimits_{T\to\infty}\tfrac{1}{T}\log P_{T}=0,$
(17)		$\displaystyle\forall i\in{\mathbb{Z}}\mod P_{T}\qquad d\big{(}\varphi_{t_{i}}(\theta_{i}),\varphi_{t_{i}}(\theta_{i-1})\big{)}\leq C\,\text{\rm\large e}^{-\lambda T}.$

Proof:.

Given a specification $(\Theta,\mathfrak{T})$ in ${\mathcal{A}}(L)$ write $\xi_{i}:[t_{i},t_{i+1}]\to{\mathcal{A}}(L)$ , $\xi_{i}(s)=\varphi_{s}(\theta_{i})$ ; and $\zeta_{i}:[0,t_{i+1}-t_{i}]\to{\mathcal{A}}(L)$ , $\zeta_{i}(s)=\xi_{i}(s+t_{i})$ . We identify $(\Theta,\mathfrak{T})$ , $\{\xi_{i}\}$ , $\{\zeta_{i}\}$ as the same specification. We will extend the definition of $\xi_{i}$ , $\zeta_{i}$ to larger intervals, with the same formula, as needed.

Let $T>0$ and let $\delta>0$ be smaller than half of an expansivity constant A.8 for ${\mathcal{A}}(L)$ and smaller than $\beta_{0}$ in proposition A.7 applied to ${\mathcal{A}}(L)$ . Let $G=G_{T}$ be a minimal $(2T,\delta)$ -spanning set for ${\mathcal{A}}(L)$ , i.e.

(18)

{\mathcal{A}}(L)\subset\bigcup_{\theta\in G}B(\theta,2T,\delta),

where $B(\theta,2T,\delta)$ is the dynamic ball

B(\theta,2T,\delta)=\{\,\vartheta\in TM\;|\;d(\varphi_{s}(\theta),\varphi_{s}(\vartheta))\leq\delta\;\;\;\forall s\in[0,2T]\;\},

and no proper subset of $G$ satisfies (18). Let $\Sigma\subset G^{\mathbb{Z}}$ be the bi-infinite subshift of finite type with symbols in $G$ and matrix $A\in\{0,1\}^{G\times G}$ defined by

(19)

A(\theta,\vartheta)=1\qquad\Longleftrightarrow\qquad\varphi_{2T}(\theta)\in B(\vartheta,2T,\delta).

Given $N\in{\mathbb{N}}^{+}$ , let $S_{N}$ be a maximal $(2NT,2\delta)$ -separated set in ${\mathcal{A}}(L)$ , i.e.

(20)

\theta,\,\vartheta\in S_{N},\quad\theta\neq\vartheta\quad\Longrightarrow\quad\vartheta\notin B(\theta,2NT,2\delta),

and $S_{N}$ is a maximal subset of ${\mathcal{A}}(L)$ with property (20).

Given $\theta\in S_{N}$ let $I(\theta)$ be an itinerary in $\Sigma$ corresponding to $\theta$ , i.e.

\forall n\in{\mathbb{Z}}\qquad\varphi_{2nT}(\theta)\in B(I(\theta)_{n},2T,\delta),\qquad I(\theta)_{n}\in G_{T}.

If $\theta,\vartheta\in S_{N}$ are different points, then by (20) there are $0\leq n<N$ and $s\in[0,2T]$ such that $d(\varphi_{2nT+s}(\theta),\varphi_{2nT+s}(\vartheta))>2\delta$ . Thus $I(\theta)_{n}\neq I(\vartheta)_{n}$ , i.e. $I(\theta)$ , $I(\vartheta)$ belong to different $N$ -cylinders in $\Sigma$ . Therefore

C_{N}:=\#(\text{$N$-cylinders in $\Sigma$})\geq\#S_{N}.

Since $2\delta$ is smaller than an h-expansivity constant for ${\mathcal{A}}(L)$ , see remark A.9, its topological entropy can be calculated using $(n,2\delta)$ -separated (or $(n,\delta)$ -spanning) sets, $h_{\rm top}(\varphi,{\mathcal{A}}(L))=h(\varphi,{\mathcal{A}}(L),2\delta)$ (c.f. Bowen [3] Thm. 2.4, p. 327), thus

h(\Sigma)\geq\limsup_{N}\frac{\log\#C_{N}}{N}\geq 2T\limsup_{N}\frac{\log\#S_{N}}{2NT}=2T\,h_{top}({\mathcal{A}}(L))=:2Th.

There is $K_{T}$ with sub-exponential growth in $T$ such that $\#G_{T}\leq K_{T}\,\text{\rm\large e}^{2Th}$ . Then Lemma 3.1 gives a periodic orbit $\Theta$ in $\Sigma$ with

(21)

P:={\rm period}(\Theta)\leq 1+K_{T}\,\text{\rm\large e}^{2Th}\;\text{\rm\large e}^{1-2Th}\leq 1+K_{T}\,\text{\rm\large e}.

By Proposition A.7, if $\theta,\,\vartheta\in{\mathcal{A}}(L)$ and $\vartheta\in B(\theta,2T,\delta)$ then there is

(22)

|v|=|v(\vartheta,\theta)|<D\,\delta

such that

(23)

\forall\;|s|\leq T\quad d\big{(}\varphi_{s+v+T}(\vartheta),\varphi_{s+T}(\theta)\big{)}\leq D\,\delta\,\text{\rm\large e}^{-\lambda(T-|s|)}.

Given a sequence $(\theta_{i})_{i\in{\mathbb{Z}}}\in\Sigma$ , define a specification $(\zeta_{i}|_{[0,2T+v_{i}]})_{i\in{\mathbb{Z}}}$ in ${\mathcal{A}}(L)$ by $v_{i}:=v(\varphi_{2T}(\theta_{i}),\theta_{i+1})$ from (22), and $\zeta_{i}(s):=\varphi_{s+T}(\theta_{i})$ . From (19) we have that $\varphi_{2T}(\theta_{i})\in B(\theta_{i+1},2T,\delta)$ . Then by (23), with $\vartheta=\varphi_{2T}(\theta_{i})$ , $\theta=\theta_{i+1}$ and $s=0$

(24)

d(\zeta_{i}(2T+v_{i}),\zeta_{i+1}(0))=d(\varphi_{3T+v_{i}}(\theta_{i}),\varphi_{T}(\theta_{i+1}))\leq D\,\delta\,\text{\rm\large e}^{-\lambda T}.

For the sequence $\Theta\in\Sigma$ in (21) we have that $(\xi_{i})_{i\in{\mathbb{Z}}}$ a periodic $D\delta\,\text{\rm\large e}^{-\lambda T}$ -possible specification with $P$ jumps, and period

(25)

{\rm period}(\{\xi_{i}\})\leq(2T+D\delta)\,(1+K_{T}\,\text{\rm\large e})\leq 4T(1+K_{T}\,\text{\rm\large e}).

∎

4. Optimal periodic orbits.

A dominated function for $L$ is a function $u:M\to{\mathbb{R}}$ such that for any $\gamma:[0,T]\to M$ absolutely continuous and $0\leq s<t\leq T$ we have

(26)

u(\gamma(t))-u(\gamma(s))\leq\int_{s}^{t}\big{[}c(L)+L(\gamma,{\dot{\gamma}})\big{]}.

We say that the curve $\gamma$ calibrates $u$ if the equality holds in (26) for every $0\leq s<t\leq T$ . Dominated functions always exist, for example, by the triangle inequality for Mañé’s potential $\Phi_{c}$ , the functions $u_{p}(x):=\Phi_{c}(p,x)$ are dominated for every $p\in M$ . The definition of the Hamiltonian $H$ associated to $L$ implies that any $C^{1}$ function $u:M\to{\mathbb{R}}$ which satisfies

\forall x\in M,\quad H(x,d_{x}u)\leq c(L)

is dominated.

4.1 Lemma.

If $u$ is a dominated function and $\gamma$ is a static curve then $\gamma$ calibrates $u$ .

Proof:.

Recall from (8), (9) that $\gamma$ is static iff for all $s<t$ we have

(27)

\int_{s}^{t}\big{[}c(L)+L(\gamma,{\dot{\gamma}})\big{]}=-\phi_{c(L)}(\gamma(t),\gamma(s))=\phi_{c(L)}(\gamma(s),\gamma(t)).

If $u$ is dominated, $\gamma$ is static and $s<t$ we have that

\displaystyle u(\gamma(t))\leq u(\gamma(s))+\phi_{c(L)}(\gamma(s),\gamma(t))=u(\gamma(s))-\phi_{c(L)}(\gamma(t),\gamma(s)).

Using again the domination of $u$ and then the previous inequality we get

u(\gamma(s))\leq u(\gamma(t))+\phi_{c(L)}(\gamma(t),\gamma(s))\leq u(\gamma(s)).

Therefore, using (27),

u(\gamma(t))=u(\gamma(s))-\phi_{c(L)}(\gamma(t),\gamma(s))=u(\gamma(s))+\int_{s}^{t}\big{[}c(L)+L(\gamma,{\dot{\gamma}})\big{]}.

∎

4.2 Lemma.

There are $K>0$ and $\delta_{0}>0$ such that if $(z,{\dot{z}})\in{\mathcal{A}}(L)$ is a static vector, $u$ is a dominated function and $d(z,y)<\delta_{0}$ , then in local coordinates

(28)

\big{|}u(y)-u(z)-\partial_{v}L(z,{\dot{z}})(y-z)\big{|}\leq K\,|y-z|^{2},

where $y-z:=(\exp_{z})^{-1}(y)$ .

Proof:.

Let ${\mathbb{E}}\subset TM$ be a compact subset such that $E^{-1}_{L}\{c(L)\}\subset\operatorname{int}{\mathbb{E}}$ . Cover $M$ by a finite set ${\mathcal{O}}$ of charts. Fix $0<\varepsilon<1$ such that if $\gamma:[-\varepsilon,\varepsilon]\to M$ has velocity $(\gamma,{\dot{\gamma}})\in{\mathbb{E}}$ then $\gamma([-\varepsilon,\varepsilon])$ lies inside the domain of a chart in ${\mathcal{O}}$ . There are $\delta_{1}>0$ smaller than the Lebesgue number of the covering ${\mathcal{O}}$ and $A>0$ such that if $(x,v)\in{\mathbb{E}}$ and $\max\{|h|,\,|k|\}\leq\delta_{1}$ then in the charts

(29)

\big{|}L(x+h,v+k)-L(x,v)-DL(x,v)(h,k)\big{|}\leq A(|h|^{2}+|k|^{2}).

Let $u:M\to{\mathbb{R}}$ be dominated and $(z,{\dot{z}})\in{\mathcal{A}}(L)$ . Recall that ${\mathcal{A}}(L)\subset E_{L}^{-1}\{c(L)\}\subset{\mathbb{E}}$ . Write $\gamma(t):=\pi\varphi^{L}_{t}(z,{\dot{z}})$ . By Lemma 2.4 the complete curve $\gamma:{\mathbb{R}}\to M$ is static. By Lemma 4.1, $\gamma$ calibrates $u$ . Let $\delta_{0}:=\varepsilon\,\delta_{1}$ . Let $y\in M$ with $|y-z|<\delta_{0}$ in a local chart. Define $\beta:]-\varepsilon,0]\to M$ by

\beta(t):=\gamma(t)+\left(\tfrac{t+\varepsilon}{\varepsilon}\right)(y-z).

Then $\beta(-\varepsilon)=\gamma(-\varepsilon)$ , $\beta(0)=y$ , ${\dot{\beta}}={\dot{\gamma}}+\tfrac{1}{\varepsilon}(y-z)$ . In particular $|{\dot{\beta}}-{\dot{\gamma}}|\leq\tfrac{1}{\varepsilon}|y-z|\leq\delta_{1}$ and we can apply (29).

\displaystyle\int_{-\varepsilon}^{0}L(\beta,{\dot{\beta}})\leq\int_{-\varepsilon}^{0}L(\gamma,{\dot{\gamma}})+\int_{-\varepsilon}^{0}\Big{\{}L_{x}(\gamma,{\dot{\gamma}})(\beta-\gamma)+L_{v}(\gamma,{\dot{\gamma}})({\dot{\beta}}-{\dot{\gamma}})\Big{\}}+A\varepsilon\big{(}1+\tfrac{1}{\varepsilon^{2}}\big{)}\,|y-z|^{2}.

Using that $\gamma$ is a solution of the Euler-Lagrange equation $\tfrac{d\,}{dt}L_{v}=L_{x}$ and integrating by parts, we get that

	$\displaystyle\int_{-\varepsilon}^{0}L(\beta,{\dot{\beta}})$	$\displaystyle\leq\int_{-\varepsilon}^{0}L(\gamma,{\dot{\gamma}})\,dt+L_{v}(\gamma,{\dot{\gamma}})(\beta-\gamma)\Big{\|}_{-\varepsilon}^{0}+\tfrac{2A}{\varepsilon}\,\|y-z\|^{2},$
(30)			$\displaystyle\leq\int_{-\varepsilon}^{0}L(\gamma,{\dot{\gamma}})\,dt+L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,\|y-z\|^{2}.$

Since $u$ is dominated and calibrated by $\gamma|_{[-\varepsilon,0]}$ we obtain one of the inequalities in (28):

	$\displaystyle u(y)$	$\displaystyle\leq u(\gamma(-\varepsilon))+\int_{-\varepsilon}^{0}c(L)+L(\beta,{\dot{\beta}})$
		$\displaystyle\leq u(\gamma(-\varepsilon))+\int_{-\varepsilon}^{0}\Big{\{}L(\gamma,{\dot{\gamma}})+c(L)\Big{\}}dt+L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,\|y-z\|^{2}$
		$\displaystyle\leq u(z)+L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,\|y-z\|^{2}.$

Now define $\alpha:[0,\varepsilon]\to M$ by

\alpha(t):=\gamma(t)+\left(\tfrac{\varepsilon-t}{\varepsilon}\right)(y-z).

A similar argument to (30) gives

\int_{0}^{\varepsilon}L(\alpha,{\dot{\alpha}})\,dt\leq\int_{0}^{\varepsilon}L(\gamma,{\dot{\gamma}})\,dt-L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,|y-z|^{2}.

Since $u$ is dominated we have that

	$\displaystyle u(\gamma(\varepsilon))$	$\displaystyle\leq u(y)+\int_{0}^{\varepsilon}\Big{\{}L(\alpha,{\dot{\alpha}})+c(L)\Big{\}}$
		$\displaystyle\leq u(y)+\int_{0}^{\varepsilon}\Big{\{}L(\gamma,{\dot{\gamma}})+c(L)\Big{\}}\,dt-L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,\|y-z\|^{2}.$

Since $u$ is calibrated by $\gamma|_{[0,\varepsilon]}$ we have that

u(\gamma(\varepsilon))-\int_{0}^{\varepsilon}\Big{\{}L(\gamma,{\dot{\gamma}})+c(L)\Big{\}}=u(z).

Thus we get the remaining inequality

u(z)\leq u(y)-L_{v}(z,{\dot{z}})(y-z)+\tfrac{2A}{\varepsilon}\,|y-z|^{2}.

∎

The set ${\mathcal{N}}(L)$ is hyperbolic for the Euler-Lagrange flow restricted to the energy level $E_{L}^{-1}\{c(L)\}$ . There is a neighborhood $U$ of ${\mathcal{N}}(L)$ in $E_{L}^{-1}\{c(L)\}$ such that the set

(31)

\Lambda=\textstyle\bigcap_{-\infty}^{+\infty}\varphi_{t}(\overline{U})

is hyperbolic, cf. [17, prop. 5.1.8]. We can assume that ${\mathcal{A}}(L)$ has no periodic orbits. The neighborhood $U$ can be taken so small that any periodic orbit $\Gamma$ in $\Lambda$ has period

(32)

\operatorname{per}(\Gamma)>10.

For $B\subset TM$ write

c(B,{\mathcal{A}}(L)):=\sup\nolimits_{\theta\in B}d(\theta,{\mathcal{A}}(L)).

4.3 Proposition.

For any $\varepsilon>0$ there is a periodic orbit $\Gamma\subset\Lambda\subset E_{L}^{-1}\{c(L)\}$ , such that

(33)

c(\Gamma,{\mathcal{A}}(L))<\varepsilon\,\gamma(\Gamma)\quad\text{and}\quad A_{L+c(L)}(\Gamma)<\varepsilon^{2}\,\gamma(\Gamma)^{2},

where $\gamma(\Gamma):=\min\{d_{TM}(\Gamma(s),\Gamma(t)):|s-t|_{\rm mod\operatorname{per}(\Gamma)}\geq 1\,\}$ .

Proof:.

Let $T>0$ be very large which will be chosen at the end of the proof. Let $\{\xi_{i}\}_{i=0}^{P-1}$ , $\xi_{i}(t)=\varphi_{t-t_{i}}(\theta_{i})$ , $t\in[t_{i},t_{i+1}[$ be the periodic specification from proposition 3.2. Define $(x_{0},{\dot{x}}_{0}):{\mathbb{R}}\to{\mathcal{A}}(L)$ by $x_{0}(t)=\pi(\xi_{i}(t))$ if $t\in[t_{i},t_{i+1}[$ and $x_{0}(s+t_{P}-t_{0})=x_{0}(s)$ .

We will use repeatedly the constants from appendix A applied to the hyperbolic set $\Lambda$ from (31). We will show that if $T$ is chosen sufficiently large then the objects at each step are specifications and periodic orbits inside¹¹1Because they are (segments of) periodic orbits $\Gamma$ with $c(\Gamma,{\mathcal{A}}(L))$ small, and hence $\Gamma\subset U$ . Observe that $\Lambda$ is not necessarily locally maximal, then a priori shadowing objects could be outside $\Lambda$ . $\Lambda$ .

By the shadowing theorem A.13, there is a periodic Euler-Lagrange solution $(y_{0},{\dot{y}}_{0})$ with energy $c(L)$ and a continuous reparametrization $\sigma(t)$ , with $|\sigma(t)-t|\leq EC\,\text{\rm\large e}^{-\lambda T}$ such that

\forall t\qquad d\big{(}[x_{0}(t),{\dot{x}}_{0}(t)],[y_{0}(\sigma(t)),{\dot{y}}_{0}(\sigma(t))]\big{)}<E\cdot C\,\text{\rm\large e}^{-\lambda T}.

Then $Y_{0}(s):=(y_{0}(s),{\dot{y}}_{0}(s))$ is a periodic orbit with a period near $\sigma(t_{P})-\sigma(t_{0})$ . We want a sequence of times $s_{k}$ nearby $\sigma(t_{k})$ such that $s_{P}-s_{0}$ is a period for $Y_{0}(s)$ . Using canonical coordinates from A.3 define $w^{k}\in{\mathbb{R}}$ small by

	$\displaystyle\langle Y_{0}(\sigma(t_{k})),\theta_{k}\rangle$	$\displaystyle=W^{s}_{\gamma}(Y_{0}(\sigma(t_{k})))\cap W^{uu}_{\gamma}(\theta_{k})$
		$\displaystyle=W^{ss}_{\gamma}\big{(}\varphi_{w_{k}}(Y_{0}(\sigma(t_{k})))\big{)}\cap W_{\gamma}^{uu}(\theta_{k})\neq\emptyset.$

Now let $s_{k}:=w_{k}+\sigma(t_{k})$ . Observe that the time shift $w_{k}$ is determined by the sequence $\theta_{k}$ which is periodic. Then the sequence $s_{k}$ is periodic with the period $s_{P}-s_{0}$ of $Y_{0}$ and by proposition 3.2,

(34)

\operatorname{per}(y_{0}):={\rm period}(y_{0})\leq 5TP_{T}.

By proposition A.7 there is $D>0$ such that for $T$ large enough there are $v^{0}_{k}$ such that

(35)		$\displaystyle\|v^{0}_{k}\|\leq DE\cdot C\text{\rm\large e}^{-\lambda T},$
(36)		$\displaystyle\forall s\in[s_{k},s_{k+1}]\quad d\big{(}Y^{0}(s),\varphi_{s-s_{i}+v^{0}_{k}}(\theta_{i})\big{)}\leq DE\cdot C\,\text{\rm\large e}^{-\lambda T}\,\text{\rm\large e}^{-\lambda\min\{s-s_{k},\,s_{k+1}-s\}}.$

Let $z^{0}_{k}(s):=\pi\varphi_{s-s_{i}+v^{0}_{k}}(\theta_{i})$ , $s\in[s_{k},s_{k+1}]$ . Since by 2.4 ${\mathcal{A}}(L)$ is invariant, we also have that $(z_{k}^{0},{\dot{z}}_{k}^{0})\in{\mathcal{A}}(L)$ .

By adding a constant to $L$ we can assume that

(37)

c(L)=0.

On local charts we have that

	$\displaystyle L(y_{0},{\dot{y}}_{0})\leq L(z^{0}_{k},{\dot{z}}^{0}_{k})$	$\displaystyle+\partial_{x}L(z_{k}^{0},{\dot{z}}_{k}^{0})(y_{0}-z^{0}_{k})+\partial_{v}L(z^{0}_{k},{\dot{z}}^{0}_{k})({\dot{y}}_{0}-{\dot{z}}^{0}_{k})$
		$\displaystyle+K_{1}\,d\big{(}[y_{0}(s),{\dot{y}}_{0}(s)],[z^{0}_{k}(s),{\dot{z}}^{0}_{k}(s)]\big{)}^{2}.$

Using that $z^{0}_{k}$ is an Euler-Lagrange solution we obtain

	$\displaystyle\int_{s_{k}}^{s_{k+1}}L(y_{0},{\dot{y}}_{0})$	$\displaystyle\leq\left[\int_{s_{k}}^{s_{k+1}}L(z^{0}_{k},{\dot{z}}^{0}_{k})\right]+\partial_{v}L(z_{k}^{0},{\dot{z}}_{k}^{0})(y_{0}-z_{k}^{0})\Big{\|}_{s_{k}}^{s_{k+1}}+$
(38)			$\displaystyle+K_{1}\int_{s_{k}}^{s_{k+1}}d\big{(}[y_{0}(s),{\dot{y}}_{0}(s)],[z^{0}_{k}(s),{\dot{z}}^{0}_{k}(s)]\big{)}^{2}.$

Write $Z^{0}_{k}:=(z^{0}_{k},{\dot{z}}^{0}_{k})$ . Then

	$\displaystyle A_{L}(y_{0})\leq$	$\displaystyle\sum_{k=0}^{P_{T}-1}A_{L}(z^{0}_{k})\;+$
(39)		$\displaystyle+$	$\displaystyle\sum_{k=0}^{P_{T}-1}\Big{\{}\partial_{v}L(z^{0}_{k},{\dot{z}}^{0}_{k})(y_{0}-z^{0}_{k})\Big{\|}_{s_{k+1}}-\partial_{v}L(z^{0}_{k+1},{\dot{z}}^{0}_{k+1})(y_{0}-z^{0}_{k+1})\Big{\|}_{s_{k+1}}\Big{\}}$
	$\displaystyle+$	$\displaystyle K_{1}\sum_{k=0}^{P_{T}-1}\int_{s_{k}}^{s_{k+1}}d(Y_{0},Z^{0}_{k})^{2}\,ds.$

From (36), for $K_{2}:=K_{1}DEC$ , the last term satisfies

(40)

K_{1}\sum_{k=0}^{P_{T}-1}\int_{s_{k}}^{s_{k+1}}d(Y_{0},Z^{0}_{k})^{2}\,ds\leq P_{T}\,K_{2}\,\text{\rm\large e}^{-2\lambda T}.

Let $u$ be a dominated function. By Lemma 4.2, if $(z,{\dot{z}})\in{\mathcal{A}}(L)$ is a static vector then

(41)

\big{|}u(y)-u(z)-\partial_{v}L(z,{\dot{z}})(y-z)\big{|}\leq K_{3}\,|y-z|^{2}.

By Lemma 4.1, $u$ is necessarily calibrated by static curves. Then using (41),

	$\displaystyle\sum_{k=0}^{P_{T}-1}A_{L}(z^{0}_{k})$	$\displaystyle=\sum_{k}u(z^{0}_{k}(s_{k+1}))-u(z^{0}_{k}(s_{k}))$
		$\displaystyle=\sum_{k}u(z^{0}_{k}(s_{k+1}))-u(z^{0}_{k+1}(s_{k+1}))$
		$\displaystyle=\sum_{k}\big{\{}u(z^{0}_{k})-u(y_{0})+u(y_{0})-u(z^{0}_{k+1})\big{\}}\Big{\|}_{s_{k+1}}$
		$\displaystyle\leq\sum_{k}\Big{\{}\partial_{v}L(z^{0}_{k},{\dot{z}}^{0}_{k})(z^{0}_{k}-y_{0})+\partial_{v}L(z^{0}_{k+1},{\dot{z}}^{0}_{k+1})(y_{0}-z^{0}_{k+1})\Big{\}}\Big{\|}_{s_{k+1}}+$
(42)			$\displaystyle\hskip 56.9055pt+K_{3}\,\Big{\{}\|z^{0}_{k}-y_{0}\|^{2}+\|y_{0}-z^{0}_{k+1}\|^{2}\Big{\}}\Big{\|}_{s_{k+1}}.$

From (36) the last term satisfies

(43)

\sum_{k=0}^{P_{T}-1}K_{3}\,\Big{\{}|z^{0}_{k}-y_{0}|^{2}+|y_{0}-z^{0}_{k+1}|^{2}\Big{\}}\Big{|}_{s_{k+1}}\leq P_{T}\,K_{4}\,\text{\rm\large e}^{-2\lambda T}.

Replacing estimate (42) for $\sum_{k}A_{L}(z_{k}^{0})$ in inequality (4) we obtain

(44)		$\displaystyle A_{L}(y_{0})\leq\sum_{k=0}^{P_{T}-1}\Big{\{}K_{1}\int_{s_{k}}^{s_{k+1}}d(Y_{0},Z^{0}_{k})^{2}\,ds+K_{3}\,\big{(}\|z^{0}_{k}-y_{0}\|^{2}_{s_{k}}+\|z^{0}_{k}-y_{0}\|^{2}_{s_{k}+1}\big{)}\Big{\}}.$
Using (40) and (43) we have that
(45)		$\displaystyle A_{L}(y_{0})\leq\text{sum in \eqref{ALY0int}}\leq K_{5}\,P_{T}\,\text{\rm\large e}^{-2\lambda T}=:A_{1}(T).$

From (36) we get

(46)

c(Y_{0},{\mathcal{A}}(L))<DE\cdot C\,\text{\rm\large e}^{-\lambda T}.

We can choose in (45) $K_{5}>(DEC)^{2}$ , so that

(47)

\max\{A_{L}(y_{0})^{\frac{1}{2}},\,c(Y_{0},{\mathcal{A}}(L))\}<A_{1}(T)^{\frac{1}{2}}.

Also from (35),

(48)

|v^{0}_{k}|\leq A_{1}(T)^{\frac{1}{2}}.

If $\Gamma=Y_{0}$ satisfies (33) then the proof finishes.

If $\Gamma=Y_{0}$ does not satisfy (33) then there are $r_{1},r_{2}$ , $|r_{1}-r_{2}|_{{\rm mod}\,(s_{P}-s_{0})}\geq 1$ such that

(49)		$\displaystyle\varepsilon\,d(Y_{0}(r_{1}),Y_{0}(r_{2}))$	$\displaystyle\leq c(Y_{0},{\mathcal{A}}(L)),\qquad\text{or}$
(49)		$\displaystyle\varepsilon^{2}\,d(Y_{0}(r_{1}),Y_{0}(r_{2}))^{2}$	$\displaystyle\leq A_{L}(y_{0}),$

using (37). Shifting the initial point of $Y_{0}$ , we can assume that $r_{1}<r_{2}$ and $r_{2}-r_{1}\leq\tfrac{1}{2}\operatorname{per}(y_{0})$ . If for some $i,j$ we have that $|r_{j}-s_{i}|\leq 1$ we replace $r_{j}$ by $s_{i}$ and shift the other $r_{k}$ accordingly. By Gronwall’s inequality the distance $d(Y_{0}(r_{1}),Y_{0}(r_{2}))$ increases at most by a multiple, say $B_{0}>1$ . This insures that the times $\{r_{1},r_{2},s_{1},\dots s_{P-1}\}$ are all separated $({\rm mod}\,(s_{P}-s_{0}))$ at least by 1. With this modification we get

(50)

r_{2}-r_{1}\leq\tfrac{1}{2}\operatorname{per}(y_{0})+2.

In the following iteration process we will compare distances of a periodic orbit $Y_{i}(s)$ with a time shifted periodic orbit $Y_{i-1}(s+v^{i})$ . We will ensure in (73) that all the time shifts used are smaller than 1. We will take all the time shifts into account using Gronwall’s inequality by adding a multiple $B_{0}>1$ to the distance estimates. Write

(51)

D_{0}:=B_{0}\cdot DE>1.

Let $Y_{1}=(y_{1},{\dot{y}}_{1})$ be the closed orbit which shadows the periodic specification $Y_{0}|_{[r_{1},r_{2}]}$ . By (46), for $T$ large, $Y_{0}\subset\Lambda$ and hence by (32), $\operatorname{per}(y_{0})>10$ . Then for $R=\frac{5}{4}$ , using (34), we have that

(52)

\operatorname{per}(y_{1})\leq\tfrac{1}{2}\;\operatorname{per}(y_{0})+3\leq R^{-1}\operatorname{per}(y_{0})\leq R^{-1}(5TP_{T}).

By theorem A.13, proposition A.7 and (51), there is $v^{1}$ such that

(53)		$\displaystyle\|v^{1}\|\leq D_{0}\cdot d(Y_{0}(r_{1}),Y_{0}(r_{2})),$
(54)		$\displaystyle\forall s\in[r_{1},r_{2}]\qquad d(Y_{1}(s),Y_{0}(s+v^{1}))\leq D_{0}\,\text{\rm\large e}^{-\lambda\min\{s-r_{1},r_{2}-s\}}\,d(Y_{0}(r_{1}),Y_{0}(r_{2})),$

From (49) and (47),

(55)

d(Y_{0}(r_{1}),Y_{0}(r_{2}))\leq\varepsilon^{-1}\,A_{1}(T)^{\frac{1}{2}}.

Using (54), (55), (49), (47) and $D_{0}\,\varepsilon^{-1}>1$ ,

	$\displaystyle c(Y_{1},{\mathcal{A}}(L))$	$\displaystyle\leq D_{0}\cdot d(Y_{0}(r_{1}),Y_{0}(r_{2}))+c(Y_{0},{\mathcal{A}}(L))$
		$\displaystyle\leq D_{0}\cdot\varepsilon^{-1}c(Y_{0},{\mathcal{A}}(L))+A_{1}(T)^{\frac{1}{2}}$
		$\displaystyle\leq 2D_{0}\,\varepsilon^{-1}\,A_{1}(T)^{\frac{1}{2}}.$
(56)		$\displaystyle c(Y_{1},{\mathcal{A}}(L))$	$\displaystyle\leq B_{4}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{using \eqref{B3}.}$
(57)		$\displaystyle\|v^{1}\|+\|v^{0}_{k}\|$	$\displaystyle\leq B_{4}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{using \eqref{v1}, \eqref{v0k2}.}$

In order to estimate the action of $Y_{1}$ we need to compare it with a specification in ${\mathcal{A}}(L)$ . Write $z^{1}_{k}(s)=z^{0}_{k}(s+v^{1})$ and $Z^{1}_{k}=(z^{1}_{k},{\dot{z}}^{1}_{k})$ . We cut the specification $\{Z^{1}_{k}|_{[s_{k},s_{k+1}]}\}$ at $r_{1}$ and $r_{2}$ and remain with the periodic specification of period $r_{2}-r_{1}\leq\tfrac{1}{2}\operatorname{per}(y_{0})+2$ , and jumps in $r_{1}<s_{i}<s_{i+1}<\ldots<s_{j}<r_{2}$ where $s_{i-1}\leq r_{1}<s_{i}$ and $s_{j}<r_{2}\leq s_{j+1}$ .

For $s\in[s_{k},s_{k+1}]$ we have that

	$\displaystyle d(Y_{1}(s),Z_{k}^{1}(s)))$	$\displaystyle\leq d(Y_{1}(s),Y_{0}(s+v^{1}))+d(Y_{0}(s+v^{1}),Z_{k}^{1}(s)).$
(58)		$\displaystyle d(Y_{1}(\cdot),Z_{k}^{1}(\cdot))^{2}$	$\displaystyle\leq 2\,d(Y_{1}(\cdot),Y_{0}(\cdot))^{2}+2\,d(Y_{0}(\cdot),Z_{k}^{1}(\cdot))^{2},$
(59)			$\displaystyle\leq 2\,(D_{0})^{2}\,\text{\rm\large e}^{-2\lambda\min\{s-r_{1},r_{2}-s\}}\varepsilon^{-2}\,A_{1}(T)\,+\qquad\text{using~{}\eqref{dY0Y1}, \eqref{dy012}, \eqref{A1Tmax} }$
		$\displaystyle\quad+2\,(D_{0}C)^{2}\,\text{\rm\large e}^{-2\lambda T}\,\text{\rm\large e}^{-2\lambda\min\{s-s_{k},\,s_{k+1}-s\}},\qquad\text{using \eqref{dx0y0}, \eqref{D0}.}$

where the omitted arguments in (58) are the same as in the previous inequality.

Repeating the estimates in (38), (4), (42) for the intervals between $r_{1},s_{i},\ldots,s_{j},r_{2}$ , we get

(60)

\displaystyle A_{L}(y_{1})

\displaystyle\leq\sum_{r_{1}\leq s_{k}<r_{2}}\Big{\{}K_{1}\int_{s_{k}}^{s_{k+1}}d(Y_{1},Z_{k}^{1})^{2}\,ds+K_{3}\big{(}|y_{1}-z_{k}^{1}|^{2}_{s_{k}}+|y_{1}-z_{k}|^{2}_{s_{k+1}}\big{)}\Big{\}}.

Using (58) we can separate the sums in (60) into two sums. The sums with terms $2\,d(Y_{0},Z_{k}^{1})^{2}$ or $2\,|y_{0}-z_{k}^{1}|^{2}$ are about half of the terms in (44), with a shift of $v^{1}$ , plus a term for the new jump at $(r_{1},r_{2})$ . The total number of jumps is $\leq\frac{1}{2}P_{T}+1\leq P_{T}$ , then the same estimate (45) gives:

(61)

\displaystyle\sum_{r_{1}\leq s_{k}<r_{2}}\int_{s_{k}}^{s_{k+1}}2K_{1}\,d(Y_{0},Z_{k})^{2}\,ds+2K_{3}\big{(}|y_{0}-z_{k}^{1}|^{2}_{s_{k}}+|y_{0}-z^{1}_{k}|^{2}_{s_{k+1}}\big{)}\leq 2\,A_{1}(T).

The other sum uses terms with $2\,d(Y_{1}(s),Y_{0}(s+v^{1}))^{2}$ which are bounded in (59). Abbreviating the time shift $v^{1}$ , this sum writes

	$\displaystyle\sum_{r_{1}\leq s_{k}<r_{2}}$	$\displaystyle\int_{s_{k}}^{s_{k+1}}2K_{1}\,d(Y_{1},Y_{0})^{2}\,ds+2K_{3}\big{(}\|y_{1}-y_{0}\|^{2}_{s_{k}}+\|y_{1}-y_{0}\|^{2}_{s_{k+1}}\big{)}$
		$\displaystyle\leq\int_{r_{1}}^{r_{2}}2K_{1}\,d(Y_{1},Y_{0})^{2}\,ds+\sum_{r_{1}\leq s_{k}<r_{2}}2K_{3}\big{(}\|y_{1}-y_{0}\|^{2}_{s_{k}}+\|y_{1}-y_{0}\|^{2}_{s_{k+1}}\big{)}$
		$\displaystyle\leq 2K_{1}\,(D_{0})^{2}B_{1}\,\varepsilon^{-2}\,A_{1}(T)+2K_{3}\,(D_{0})^{2}\,2B_{2}\,\varepsilon^{-2}A_{1}(T)$
(62)			$\displaystyle\leq B_{3}\,A_{1}(T),$

using (54), (55), where

	$\displaystyle\textstyle B_{1}:=\int_{-\infty}^{+\infty}\text{\rm\large e}^{-2\lambda\|s\|}ds=\frac{1}{\lambda},\qquad B_{2}:=1+\sum_{n\in{\mathbb{N}}}\text{\rm\large e}^{-2\lambda n},$
(63)		$\displaystyle B_{3}=B_{3}(\varepsilon):=2\,(K_{1}+K_{3})\,(D_{0})^{2}(B_{1}+2B_{2})\,\varepsilon^{-2}.$

Adding (61) and (62) we get

(64)

A_{L}(y_{1})\leq\text{sum in \eqref{aly1k3}}\leq B_{4}\,A_{1}(T),

where

(65)

B_{4}:=\max\{B_{3}+4,2D_{0}\,\varepsilon^{-1}\}>4.

If $Y_{1}=\Gamma$ satisfies (33) the proof finishes. If not there are $r_{3}<r_{4}$ , $r_{4}-r_{3}\leq\tfrac{1}{2}\operatorname{per}(y_{1})+2$ , such that

	$\displaystyle d(Y_{1}(r_{3}),Y_{1}(r_{4}))$	$\displaystyle\leq\varepsilon^{-1}\max\{A_{L}(y_{1})^{\frac{1}{2}},c(Y_{1},{\mathcal{A}}(L))\}$
(66)			$\displaystyle\leq\varepsilon^{-1}B_{4}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{using \eqref{AY1}, \eqref{cY1A}.}$

We shadow the specification $Y_{1}|_{[r_{3},r_{4}]}$ by a periodic orbit $Y_{2}=(y_{2},{\dot{y}}_{2})$ with

(67)		$\displaystyle\|v^{2}\|\leq D_{0}\cdot d(Y_{1}(r_{3}),Y_{1}(r_{4})),$
	$\displaystyle\forall s\in[r_{3},r_{4}]\qquad d(Y_{2}(s),Y_{1}(s+v^{2}))\leq D_{0}\,\text{\rm\large e}^{-\lambda\min\{s-r_{3},r_{4}-s\}}\,d(Y_{1}(r_{3}),Y_{1}(r_{4})),$
	$\displaystyle\operatorname{per}(y_{2})\leq\tfrac{1}{2}\operatorname{per}(y_{1})+3\leq R^{-2}\operatorname{per}(y_{0}).$

Then

	$\displaystyle c(Y_{2},{\mathcal{A}}(L))$	$\displaystyle\leq D_{0}\cdot d(Y_{1}(r_{3}),Y_{1}(r_{4}))+c(Y_{1},{\mathcal{A}}(L))$
		$\displaystyle\leq 2D_{0}\,\varepsilon^{-1}B_{4}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{using \eqref{cr3r4}, \eqref{cY1A}}$
		$\displaystyle\leq(B_{4})^{2}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{using \eqref{B3}.}$
	$\displaystyle\|v^{2}\|+\|v^{1}\|+\|v^{0}_{k}\|$	$\displaystyle\leq(B_{4})^{2}\,A_{1}(T)^{\frac{1}{2}}\qquad\text{similarly, using \eqref{v2}, \eqref{v1v0k}.}$

We need to compare $Y_{2}$ with a specification in ${\mathcal{A}}(L)$ . Write $z_{k}^{2}(s)=z_{k}^{1}(s+v^{2})$ and $Z_{k}^{2}=(z_{k}^{2},{\dot{z}}_{k}^{2})$ . Then

(68)

\displaystyle A_{L}(y_{2})

\displaystyle\leq\sum_{r_{3}\leq k<r_{4}}\int_{s_{k}}^{s_{k+1}}K_{1}\,d(Y_{2},Z_{k}^{2})^{2}\,ds+K_{3}\,\big{(}|y_{2}-z_{k}^{2}|_{s_{k}}^{2}+|y_{2}-z_{k}^{2}|_{s_{k+1}}^{2}\big{)}.

(69)

d(Y_{2},Z^{2}_{k})^{2}\leq 2\,d(Y_{2},Y_{1})^{2}+2\,d(Y_{1},Z^{2}_{k})^{2}.

(70)	$\displaystyle\int_{r_{3}}^{r_{4}}2K_{1}\,d(Y_{2},$	$\displaystyle Y_{1})^{2}\,ds+\sum_{r_{3}\leq s_{k}<r_{4}}2K_{3}\big{(}\|y_{2}-y_{1}\|^{2}_{s_{k}}+\|y_{2}-y_{1}\|^{2}_{s_{k+1}}\big{)}$
	$\displaystyle\leq\big{\{}2K_{1}\,B_{1}\,(D_{0})^{2}+2K_{3}\,(D_{0})^{2}\,2B_{2}\big{\}}\;d(Y_{1}(r_{3}),Y_{1}(r_{4}))^{2}$
	$\displaystyle\leq 2(K_{1}+K_{3})(D_{0})^{2}(B_{1}+2B_{2})\,\varepsilon^{-2}(B_{4})^{2}A_{1}(T)\qquad\text{using~{}\eqref{cr3r4}},$
(71)		$\displaystyle\leq B_{3}\,(B_{4})^{2}\,A_{1}(T)\qquad\text{using~{}\eqref{B2}.}$

From (69) and (68) we have that

	$\displaystyle AL(y_{2})$	$\displaystyle\leq\text{sum in~{}\eqref{sum30}}+2\,\text{sum in~{}\eqref{aly1k3}}$
		$\displaystyle\leq(B_{4})^{3}\,A_{1}(T)\qquad\text{using \eqref{B2B3}, \eqref{AY1}, \eqref{B3},}$
		$\displaystyle\leq(B_{4})^{4}A_{1}(T).$
	$\displaystyle\operatorname{per}(y_{2})$	$\displaystyle\leq R^{-2}\operatorname{per}(y_{0})\leq R^{-2}(5TP_{T}).$

At the $n$ -th iteration we have

	$\displaystyle A_{L}(y_{n})$	$\displaystyle\leq(B_{4})^{2n}\,A_{1}(T),$
(72)		$\displaystyle\operatorname{per}(y_{n})$	$\displaystyle\leq R^{-n}\operatorname{per}(y_{0})\leq R^{-n}(5TP_{T}).$

	$\displaystyle c(Y_{n},{\mathcal{A}}(L))\leq(B_{4})^{n}A_{1}(T)^{\frac{1}{2}}.$
	$\displaystyle\|v^{0}_{k}\|+\operatorname*{{\textstyle\sum}}_{i=1}^{n}\|v^{i}\|\leq(B_{4})^{n}A_{1}(T)^{\frac{1}{2}}.$

Let $\alpha_{2}>0$ be such that $\{\,\theta\in T^{*}M:d(\theta,{\mathcal{A}}(L))<\alpha_{2}\,\}\subset U$ , where $U$ is from (31). This process can be repeated as long as $c(Y_{n},{\mathcal{A}}(L))<\alpha_{2}$ holds and (33) is not satisfied. The resulting periodic $Y_{n}$ is in $\Lambda$ and hence by (32) it has period larger than 10. Thus the process stops at an iterate $N$ where the period in (72) is larger than 1. This is

	$\displaystyle N\leq$	$\displaystyle\log_{R}\operatorname{per}(y_{0})\leq\log_{R}(5TP_{T}),$
	$\displaystyle A_{L}(y_{N})\leq(B_{4})^{2N}A_{1}(T)$	$\displaystyle\leq(5TP_{T})^{2\log_{R}B_{4}}\cdot K_{5}\,P_{T}\,\text{\rm\large e}^{-2\lambda T}\qquad\text{using \eqref{A1T},}$
	$\displaystyle c(Y_{N},{\mathcal{A}}(L))$	$\displaystyle\leq(5TP_{T})^{\log_{R}B_{4}}\sqrt{K_{5}P_{T}}\;\text{\rm\large e}^{-\lambda T},$
(73)		$\displaystyle\|v^{0}_{k}\|+\operatorname*{{\textstyle\sum}}_{i=1}^{n}\|v^{i}\|$	$\displaystyle\leq(5TP_{T})^{\log_{R}B_{4}}\sqrt{K_{5}P_{T}}\;\text{\rm\large e}^{-\lambda T}.$

Since by (16), $P_{T}$ has sub-exponential growth in $T$ , we have that $c(Y_{N},{\mathcal{A}}(L))$ and $A_{L}(y_{N})$ can be made arbitrarily small by choosing $T$ sufficiently large. Then the process stops not because $c(Y_{N},{\mathcal{A}}(L))$ is large, but because (33) holds.

∎

5. The perturbed minimizers.

The following Crossing Lemma is extracted for Mather [25] with the observation that the estimates can be taken uniformly on a $C^{2}$ neighbourhood of $L$ .

5.1 Lemma (Mather [25, p. 186]).

If $K>0$ , then there exist $\varepsilon$ , $\delta$ , $\eta$ , $\zeta>0$ and

(74)

C>1,

such that if $\left\|\phi\right\|_{C^{2}}<\zeta$ , and $\alpha,\gamma:[t_{0}-\varepsilon,t_{0}+\varepsilon]\to M$ are solutions of the Euler-Lagrange equation for $L+\phi$ with $\left\|d\alpha(t_{0})\right\|$ , $\left\|d\gamma(t_{0})\right\|\leq K$ , $d\big{(}\alpha(t_{0}),\gamma(t_{0})\big{)}\leq\delta$ , and

d\big{(}d\alpha(t_{0}),d\gamma(t_{0})\big{)}\geq C\;d\big{(}\alpha(t_{0}),\gamma(t_{0})\big{)},

then there exist $C^{1}$ curves $a,c:[t_{0}-\varepsilon,t_{0}+\varepsilon]\to M$ such that $a(t_{0}-\varepsilon)=\alpha(t_{0}-\varepsilon)$ , $a(t_{0}+\varepsilon)=\gamma(t_{0}+\varepsilon)$ , $c(t_{0}-\varepsilon)=\gamma(t_{0}-\varepsilon)$ , $c(t_{0}+\varepsilon)=\alpha(t_{0}+\varepsilon)$ , and

(75)

A_{L+\phi}(\alpha)+A_{L+\phi}(\gamma)-A_{L+\phi}(a)-A_{L+\phi}(c)>\eta\;d\big{(}d\alpha(t_{0}),d\gamma(t_{0})\big{)}^{2}.

5.2 Lemma.

Given a Tonelli lagrangian $L_{0}$ and a compact subset $\Delta\subset TM$ , there are $\varepsilon>0$ , $K>0$ and $\delta_{1}>0$ such that for any Tonelli lagrangian $L$ with $\left\|(L-L_{0})|_{B_{\varepsilon}(\Delta)}\right\|_{C^{2}}<\varepsilon$ , $B_{\varepsilon}(\Delta):=\{\theta\in TM:d(\theta,\Delta)<\varepsilon\}$ , and any $T>0$ :

(a)

If $x\in C^{1}([0,T],M)$ is a solution of the Euler-Lagrange equation for $L$ with $(x,{\dot{x}})\in\Delta$ and $z\in C^{1}([0,T],M)$ satisfies

d\big{(}[z(t),{\dot{z}}(t)],[x(t),{\dot{x}}(t)]\big{)}\leq 4\rho\leq\delta_{1}\qquad\forall t\in[0,T],

then

(76)

\left|\int_{0}^{T}L(z,{\dot{z}})\,dt-\int_{0}^{T}L(x,{\dot{x}})\,dt-\partial_{v}L(x,{\dot{x}})\cdot(z-x)\Big{|}_{0}^{T}\right|\leq K\,(1+T)\,\rho^{2},

where $z-x:=(\exp_{x})^{-1}(z)$ .

(b)

If $x\in C^{1}([0,T],M)$ is a solution of the Euler-Lagrange equation for $L$ with $(x,{\dot{x}})\in\Delta$ and the curves $w_{1},\,w_{2},\,z\in C^{1}([0,T],M)$ satisfy $w_{1}(0)=x(0)$ , $w_{1}(T)=z(T)$ , $w_{2}(0)=z(0)$ , $w_{2}(T)=x(T)$ , and for all $\xi\in\{z,\,w_{1},\,w_{2}\}$ we have

$d\big{(}[\xi(t),{\dot{\xi}}(t)],[x(t),{\dot{x}}(t)]\big{)}\leq 4\rho\leq\delta_{1}\qquad\forall t\in[0,T],$

then

$\left|A_{L}(x)+A_{L}(z)-A_{L}(w_{1})-A_{L}(w_{2})\right|\leq 3K\rho^{2}(1+T).$

Proof:

(a)

We use a coordinate system on a tubular neighbourhood of $x([0,T])$ with a bound in the $C^{2}$ norm independent of $T$ and of ${\dot{x}}(0)$ . In case $x$ has self-intersections or short returns the coordinate system is an immersion.

We have that

\displaystyle L(z,{\dot{z}})-L(x,{\dot{x}})=\partial_{x}L(x,{\dot{x}})(z-x)+\partial_{v}L(x,{\dot{x}})({\dot{z}}-{\dot{x}})+O(\rho^{2}),

here $O(\rho^{2})\leq K\,\rho^{2}$ where $K$ depends on the second derivatives of $L$ on a small neighbourhood of the compact $\Delta$ and hence it can be taken uniform on a $C^{2}$ neighbourhood of $L$ . Since $x$ satisfies the Euler-Lagrange equation for $L$ ,

\displaystyle L(z,{\dot{z}})-L(x,{\dot{x}})=\tfrac{d}{dt}[\partial_{v}L(x,{\dot{x}})(z-x)]+O(\rho^{2}).

This implies (76).

(b)

By item (a)

	$\displaystyle A_{L}(w_{1})-A_{L}(x)$	$\displaystyle\leq\partial_{v}L(x,{\dot{x}})(w_{1}-x)\Big{\|}_{0}^{T}+K\rho^{2}(1+T)$
		$\displaystyle\leq\partial_{v}L(x(T),{\dot{x}}(T))(z(T)-x(T))+K\rho^{2}(1+T).$
	$\displaystyle A_{L}(w_{2})-A_{L}(x)$	$\displaystyle\leq-\partial_{v}L(x(0),{\dot{x}}(0))(z(0)-x(0))+K\rho^{2}(1+T).$
	$\displaystyle A_{L}(x)-A_{L}(z)$	$\displaystyle\leq-\partial_{v}L(x,{\dot{x}})(z-x)\Big{\|}_{0}^{T}+K\rho^{2}(1+T)$
		$\displaystyle\leq-\partial_{v}L(x(T),{\dot{x}}(T))(z(T)-x(T))$
		$\displaystyle\hskip 10.0pt+\partial_{v}L(x(0),{\dot{x}}(0))(z(0)-x(0))+K\rho^{2}(1+T).$

Adding these inequalities we get

A_{L}(w_{1})+A_{L}(w_{2})-A_{L}(x)-A_{L}(z)\leq 3K\rho^{2}(1+T).

The remaining inequality is obtained similarly. ∎

The following proposition has its origin in Yuan and Hunt [31], the present proof uses some arguments by Quas and Siefken [29]. Proposition 5.3 together with proposition 4.3 imply theorem A.

5.3 Proposition.

Suppose that for every $\delta>0$ there is a periodic orbit $\Gamma\subset\Lambda\subset E_{L}^{-1}\{c(L)\}$ such that

(77)

c(\Gamma,{\mathcal{A}}(L))<\delta\,\gamma(\Gamma)\qquad\text{and}\qquad A_{L+c(L)}(\Gamma)<\delta^{2}\,\gamma(\Gamma)^{2},

where $\gamma(\Gamma):=\min\{d_{TM}(\Gamma(s),\Gamma(t)):|s-t|_{\rm mod(\operatorname{per}{\Gamma})}\geq 1\,\}$ .

Then for any $\varepsilon>0$ there is $\phi\in C^{2}(M,{\mathbb{R}})$ with $\left\|\phi\right\|_{C^{2}}<\varepsilon$ such that $\Gamma\subset{\mathcal{A}}(L+\phi)$ , where $\Gamma$ is one of the periodic orbits in (77).

Idea of the Proof:

We choose $\delta=\delta(\varepsilon)$ sufficiently small and use the periodic orbit $\Gamma$ given by the hypothesis. We perturb the Lagrangian by a potential $\phi$ which is a non-negative channel centered at $\pi(\Gamma)$ defined in (96). The curve $\Gamma$ is a periodic orbit for the flows of $L$ and of $L+\phi$ . We show that $\Gamma$ is contained in the Aubry set ${\mathcal{A}}(L+\phi)$ by proving that any semi-static curve $x:]-\infty,0]\to M$ for $L+\phi$ has

\alpha\text{-limit of }(x,{\dot{x}})=\Gamma;

because by Mañé [24, Theorem V.(c)], $\alpha$ -limits of semi-static orbits are static. This is done by calculating the action of each segment of the semi-static which is spent outside of a small neighbourhood of $\Gamma$ , and proving that it has a uniform positive lower bound. Since the total action of a semi-static is finite, the quantity of those segments is finite. Thus the semi-static eventually stays forever in a small neighbourhood of $\Gamma$ . The expansivity of $\Lambda(L+\phi)\supset{\mathcal{N}}(L+\phi)$ implies that the $\alpha$ -limit of the semi-static is $\Gamma$ .

5.4 Lemma.

If ${\mathcal{A}}(L)$ has no periodic orbits and $\Gamma_{n}$ is a sequence of periodic orbits with

	$\displaystyle c(\Gamma_{n},{\mathcal{A}}(L))<\delta_{n}\cdot\operatorname{diam}({\mathcal{A}}(L)),$
	$\displaystyle\gamma_{n}:=\min\{d(\Gamma_{n}(s),\Gamma_{n}(t)):\|s-t\|_{\rm{mod(per\,}\Gamma_{n})}\geq 1\,\}.$

Then $\lim_{n}\delta_{n}=0$ $\Longrightarrow$ $\lim_{n}\gamma_{n}=0$ .

Proof:.

Let $T_{n}$ be the period of $\Gamma_{n}$ . First we prove that $\lim_{n}T_{n}=\infty$ . If not, we can extract a subsequence where $\theta:=\lim_{n}\Gamma_{n}(0)\in{\mathcal{A}}(L)$ and $S:=\lim_{n}T_{n}$ exist. Then $\theta$ is a periodic point in ${\mathcal{A}}(L)$ which contradicts the hypothesis.

Consider the points $\Gamma_{n}(4m)$ , $0\leq m\leq M_{n}:=[\tfrac{1}{4}T_{n}]$ , $m\in{\mathbb{N}}$ . Since $\lim_{n}T_{n}=\infty$ , the quantity $M_{n}$ of these points tends to infinity. Therefore

\gamma_{n}\leq\min_{m_{1}\neq m_{2}}d(\Gamma_{n}(m_{1}),\Gamma_{n}(m_{2}))\overset{n}{\longrightarrow}0.

∎

Proof of Proposition 5.3:

By adding a constant to $L$ we can assume that

(78)

c(L)=0.

Fix $K_{1}>0$ such that

(79)

[E_{L}\leq c(L)+1]\subset[|v|\leq K_{1}].

Bernard [1] after Fathi and Siconolfi [16] proves that there is a $C^{1+\operatorname{Lip}}$ critical subsolution $u$ of the Hamilton-Jacobi equation for $L$ , $H(x,d_{x}u)\leq c(L)$ . Thus

(80)

L-du\geq 0.

By Gronwall’s inequality and the continuity of Mañé’s critical value $c(L)$ (see [14, Lemma 5.1]) there is $\alpha>0$ and $\gamma_{0}$ such that if $\left\|\phi\right\|_{C^{2}}\leq 1$ , $0<\gamma<\gamma_{0}$ and $\Gamma$ is a periodic orbit for $L+\phi$ with energy smaller than $c(L+\phi)+1$ then

(81)

d(\varphi^{L+\phi}_{s}(\vartheta),\Gamma)\leq\frac{\gamma}{4}\quad\text{ and }\quad d(\varphi^{L+\phi}_{t}(\vartheta),\Gamma)\geq\frac{\gamma}{3}\quad\Longrightarrow\quad|t-s|>\alpha.

The graph property states that the projection $\pi:{\mathcal{A}}(L)\to M$ has a Lipschitz inverse (see Mañé [24]). The Lipschitz constant is the same as $C$ in Mather’s Crossing Lemma 5.1. The Aubry set has energy $c(L)$ and $c(L+\phi)$ is continuous on $\phi$ . Then one can choose

(82)

\varepsilon_{1}<\zeta

and $K$ , $C>1$ in Lemma 5.1 such that if $\left\|\phi\right\|_{C^{2}}<\varepsilon_{1}$ then ${\mathcal{A}}(L+\phi)$ is a graph with Lipschitz constant $C$ .

By the upper semicontinuity of the Mañé set [14, lemma 5.2] we can choose a neighbourhood $U$ of ${\mathcal{N}}(L)$ and $0<\varepsilon_{2}<\varepsilon_{1}$ such that if $\left\|\phi\right\|_{C^{2}}<\varepsilon_{2}$ then the set

\Lambda(\phi):=\bigcap_{t\in{\mathbb{R}}}\varphi_{-t}^{L+\phi}(\overline{U})

is hyperbolic and contains ${\mathcal{N}}(L+\phi)$ . Take $0<\varepsilon_{3}<\varepsilon_{2}$ such that $\Lambda(\phi)$ has uniform constants of hyperbolicity (A.7), expansivity (A.8, A.9) and canonical coordinates (A.3) for all $\left\|\phi\right\|_{C^{2}}<\varepsilon_{3}<\varepsilon_{2}$ .

Write

(83)

{\gamma_{\delta}}:=\gamma(\Gamma).

We can assume that ${\mathcal{A}}(L)$ has no periodic points. By lemma 5.4, $\gamma_{\delta}$ is small when $\delta$ is small. Given $0<\varepsilon<\varepsilon_{3}$ , choose $0<\delta\ll\varepsilon$ and a periodic orbit $\Gamma$ satisfying (77) with $\delta$ and $\gamma_{\delta}$ so small that for all $\left\|\phi\right\|_{C^{2}}<\varepsilon_{3}$ ,

(84)	$\displaystyle{\gamma_{\delta}}$	$\displaystyle<\epsilon_{0}\hskip 6.0pt\text{where $\epsilon_{0}$ is a flow expansivity constant for $\Lambda(\phi)$ as in \ref{dfe} and \ref{rue}. }$
(85)	$\displaystyle 2{\gamma_{\delta}}$	$\displaystyle<\delta_{1}\hskip 5.0pt\text{with }\delta_{1}:=\delta[K_{1}]\text{ from lemma~{}\ref{CL}, where $K_{1}$ is from~{}\eqref{dK1}. }$
(86)	$\displaystyle{\gamma_{\delta}}$	$\displaystyle<\beta_{0}\hskip 4.0pt\text{where $\beta_{0}$ is from proposition~{}\ref{B71} for $\Lambda(\phi)$.}$
(87)	$\displaystyle{\gamma_{\delta}}$	$\displaystyle<\eta_{0}\hskip 9.0pt\text{where $\eta_{0}$ is from the canonical coordinates in \ref{B4} for $\Lambda(\phi)$,}$

and such that writing

(88)

{\overline{\gamma}_{\delta}}:=\frac{{\gamma_{\delta}}}{3C(B+1)}<\tfrac{1}{2}\,{\gamma_{\delta}},

we have that

(89)

\displaystyle{\overline{\gamma}_{\delta}}<\gamma_{0}\hskip 56.9055pt\text{ where $\gamma_{0}$ is from~{}\eqref{tima},}

and there is $\rho$ ,

(90)

\delta\,{\gamma_{\delta}}<\rho<\tfrac{1}{4}{\overline{\gamma}_{\delta}}\ll 1

such that

(91)		$\displaystyle\tfrac{1}{4}\,\varepsilon\,\rho^{2}>\delta^{2}\,({\gamma_{\delta}})^{2},$
(92)		$\displaystyle C\rho>\tfrac{1}{\sqrt{\eta_{1}}}\,{\delta\,\gamma_{\delta}},$
(93)		$\displaystyle\big{(}\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}-\delta^{2}({\gamma_{\delta}})^{2}\big{)}\alpha-6KD^{2}C^{2}(B+1)^{2}\rho^{2}-3\,\delta^{2}({\gamma_{\delta}})^{2}>0,$

where $B$ is from Lemma A.4, $C=C[K_{1}]$ and $\eta_{1}=\eta[K_{1}]$ are from Lemma 5.1 with

(94)

C>1,

$D$ is from Proposition A.7 and $K$ is from Lemma 5.2 applied to the compact $\Delta=[E_{L}\leq c(L)+5]$ . Inequality (93) implies

(95)

\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}>\delta^{2}({\gamma_{\delta}})^{2}.

Let $\phi:M\to[0,1]$ be a $C^{\infty}$ function such that $\left\|\phi\right\|_{C^{2}}<10\,\varepsilon$ and

(96)

0\leq\phi(x)=\begin{cases}0&\text{if }x\in\pi(\Gamma),\\ \geq\tfrac{1}{4}\,\varepsilon\,\rho^{2}&\text{if }d(x,\pi\Gamma)\geq\rho,\\ \tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}&\text{if }d(x,\pi\Gamma)\geq\tfrac{1}{4}{\overline{\gamma}_{\delta}}.\end{cases}

Using $u$ from (80) write

(97)

{\mathbb{L}}:=L+\phi+c(L+\phi)-du.

The Euler-Lagrange flow of ${\mathbb{L}}$ and the sets ${\mathcal{A}}({\mathbb{L}})$ , ${\mathcal{N}}({\mathbb{L}})$ are the same as those of $L+\phi$ . In particular the hyperbolicity constants (84)–(87) and Lipschitz graphs contants (94) remain valid for ${\mathbb{L}}$ .

Claim 5.4.1:

If $\delta$ is small enough then

(1)

We have that

\inf\limits_{d(s,t)_{\text{mod }T}\geq 1}d\big{(}\pi\Gamma(s),\pi\Gamma(t)\big{)}>\tfrac{3}{4}\,{\overline{\gamma}_{\delta}}.

In particular the neighbourhood $B(\pi\Gamma,\tfrac{3}{8}{\overline{\gamma}_{\delta}})$ of $\pi\Gamma$ of radius $\frac{3}{8}{\overline{\gamma}_{\delta}}$ has no self intersections, i.e. it is homeomorphic to $S^{1}\times]0,1[^{\dim M-1}$ .

(2)

If $x:]-\infty,0]\to M$ is a semi-static orbit for ${\mathbb{L}}$ then for all $t\leq-1$

(98)			$\displaystyle\text{either }\quad d\big{(}[x(t),{\dot{x}}(t)],\Gamma\big{)}\leq\tfrac{\delta\,\gamma(\Gamma)}{\sqrt{\eta_{1}}}\quad\text{ or }\quad d\big{(}[x(t),{\dot{x}}(t)],\Gamma\big{)}\leq C\,d\big{(}x(t),\pi\Gamma\big{)},$
(99)			$\displaystyle\text{or }\quad d(x(t),\pi\Gamma)\geq\delta_{1},$

where $\eta_{1}=\eta(K_{1})$ , $C=C(K_{1})$ and $\delta_{1}=\delta_{1}(K_{1})$ are from Lemma 5.1 for $K=K_{1}$ from (79).

Proof:

Let $T=\operatorname{per}(\Gamma)$ be the period of $\Gamma$ .

(1). Given $s,t\in[0,T]$ , by (77) there are $\theta_{s},\theta_{t}\in{\mathcal{A}}(L)$ such that

	$\displaystyle d(\pi\Gamma(s),\pi\theta_{s})$	$\displaystyle\leq d(\Gamma(s),\theta_{s})<\delta\,\gamma(\Gamma),$
	$\displaystyle d(\pi\Gamma(t),\pi\theta_{t})$	$\displaystyle\leq d(\Gamma(t),\theta_{t})<\delta\,\gamma(\Gamma).$

If $d(s,t)_{\text{\rm mod }T}\geq 1$ then

	$\displaystyle d(\theta_{s},\theta_{t})$	$\displaystyle\geq d(\Gamma(s),\Gamma(t))-d(\Gamma(s),\theta_{s})-d(\Gamma(t),\theta_{t})$
		$\displaystyle>\gamma(\Gamma)-2\delta\,\gamma(\Gamma).$

Since $\theta_{s},\theta_{t}\in{\mathcal{A}}(L)$ , by the graph property 5.1 for ${\mathcal{A}}(L)$ and (88), (74) we have that

d(\pi\theta_{s},\pi\theta_{t})\geq\tfrac{1}{C}\,d(\theta_{s},\theta_{t})\geq\frac{\gamma(\Gamma)(1-2\delta)}{C}>{\overline{\gamma}_{\delta}}-2\delta\,{\gamma_{\delta}}.

Then

	$\displaystyle d(\pi\Gamma(s),\pi\Gamma(t))$	$\displaystyle\geq d(\pi\theta_{s},\pi\theta_{t})-d(\pi\Gamma(s),\pi\theta_{s})-d(\pi\Gamma(t),\pi\theta_{t})$
		$\displaystyle>{\overline{\gamma}_{\delta}}-4\delta\,{\gamma_{\delta}}>\tfrac{3}{4}\,{\overline{\gamma}_{\delta}}.$

(2). Suppose by contradiction that there exists $t\leq-1$ such that

(100)		$\displaystyle d(x(t),\pi\Gamma)<\delta_{1}\qquad\text{ and }$
(101)		$\displaystyle d\big{(}[x(t),{\dot{x}}(t)],\Gamma\big{)}^{2}>\frac{\delta^{2}\,\gamma(\Gamma)^{2}}{\eta_{1}}\quad\text{ and }\quad d\big{(}[x(t),{\dot{x}}(t)],\Gamma\big{)}>C\,d\big{(}x(t),\pi\Gamma\big{)}.$

First we check that we can apply the Crossing Lemma 5.1 to ${\mathbb{L}}$ . Given $\gamma:[0,S]\to M$ we have that

\oint_{\gamma}c(L+\phi)-du=S\,c(L+\phi)-u(\gamma(S))+u(\gamma(0))

depends only on the time interval $S$ and the endpoints of $\gamma$ . Thus instead of ${\mathbb{L}}$ in (97), it is enough to apply Lemma 5.1 to $L+\phi$ , for whom it holds if $\left\|\phi\right\|_{C^{2}}<\varepsilon_{1}<\zeta$ by (82).

Now we check the speed hypothesis in Lemma 5.1. Observe that

E_{\mathbb{L}}=v\,{\mathbb{L}}_{v}-{\mathbb{L}}=E_{L+\phi}-c(L+\phi)=E_{L}-\phi-c(L+\phi),

and that by (6)

c({\mathbb{L}})=c\big{(}L+\phi+c(L+\phi)\big{)}=0.

Therefore

{\mathcal{N}}({\mathbb{L}})\subset[E_{\mathbb{L}}=c({\mathbb{L}})]\subset[E_{L}=\phi+c(L+\phi)].

If $\phi$ is small enough

\phi+c(L+\phi)<c(L)+1,

and then ${\dot{x}}(t)\in{\mathcal{N}}({\mathbb{L}})\subset[E_{L}\leq c(L)+1]$ . By hypothesis in 5.3, $\Gamma\subset[E_{L}=c(L)]$ . Therefore by (79),

\forall t\qquad{\dot{x}}(t),\;\Gamma(t)\in[E_{L}\leq c(L)+1]\subset[|v|\leq K_{1}].

Finally we check the distance hypothesis in Lemma 5.1. Let $t_{0}$ be such that $d(x(t),\pi\Gamma)=d(x(t),\pi(\Gamma(t_{0})))$ . By (100) and the definition of $\delta_{1}$ in (85) we can apply Lemma 5.1 for ${\mathbb{L}}$ and $K=K_{1}$ from (79), to $x$ and $\pi\Gamma$ at $x(t)$ and $\pi(\Gamma(t_{0}))$ . Also note that by (101) we have that, as required in Lemma 5.1,

d\big{(}[x(t),{\dot{x}}(t)],\Gamma(t_{0})\big{)}\geq d\big{(}[x(t),{\dot{x}}(t)],\Gamma\big{)}>C\,d\big{(}x(t),\pi\Gamma\big{)}=C\,d\big{(}x(t),\pi\Gamma(t_{0})\big{)}.

Using $0<\varepsilon\leq 1$ from Lemma 5.1 we obtain $C^{1}$ curves $w_{1},\,w_{2}:[-\varepsilon,\varepsilon]\to M$ with $w_{1}(-\varepsilon)=x(t-\varepsilon)$ , $w_{1}(\varepsilon)=\pi\Gamma(t_{0}+\varepsilon)$ , $w_{2}(-\varepsilon)=\pi\Gamma(t_{0}-\varepsilon)$ , $w_{2}(\varepsilon)=x(t+\varepsilon)$ such that

A_{\mathbb{L}}(w_{1})+A_{\mathbb{L}}(w_{2})<A_{\mathbb{L}}(\pi\Gamma|_{[t_{0}-\varepsilon,t_{0}+\varepsilon]})+A_{\mathbb{L}}(x|_{[t-\varepsilon,t+\varepsilon]})-\eta_{1}\,d([x(t),{\dot{x}}(t)],\Gamma(t_{0}))^{2}.

Since $\phi\geq 0$ and (78) we have that

(102)

c(L+\phi)\leq c(L)=0.

Using (77), $\phi|_{\pi\Gamma}\equiv 0$ and that $\pi\Gamma$ is a closed curve we have that

A_{\mathbb{L}}(\pi\Gamma)=A_{L+c(L+\phi)}(\pi\Gamma)\leq A_{L+c(L)}(\pi\Gamma)<\delta^{2}\,\gamma(\Gamma)^{2}.

We compute the action of the curve $w_{1}*\pi\Gamma|_{[t_{0}+\varepsilon,t_{0}+T-\varepsilon]}*w_{2}$ which joins $x(t-\varepsilon)$ to $x(t+\varepsilon)$ .

	$\displaystyle A_{\mathbb{L}}($	$\displaystyle w_{1})+A_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}+\varepsilon,t_{0}+T-\varepsilon]})+A_{\mathbb{L}}(w_{2})<$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]})+A_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}-\varepsilon,t_{0}+\varepsilon]})+{\mathbb{A}}_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}+\varepsilon,t_{0}+T-\varepsilon]})-\eta_{1}\,d([x(t),{\dot{x}}(t)],\Gamma(t_{0}))^{2}$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]})+\delta^{2}\,\gamma(\Gamma)^{2}-\eta_{1}\,d([x(t),{\dot{x}}(t)],\Gamma)^{2}$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]}),\qquad\text{using~{}\eqref{posso3}.}$

This contradicts the assumption that $x$ is semi-static for ${\mathbb{L}}$ .

$\triangle$

Since we can assume that ${\mathcal{A}}(L)$ has no periodic orbits, if $\delta$ is small enough

(103)

T:=\operatorname{per}(\Gamma)>1.

Observe that $\Gamma$ is also a periodic orbit for $L+\phi$ . Let $\mu_{\Gamma}$ be the invariant probability supported on $\Gamma$ . Using (6), (78), (77) we have that

	$\displaystyle c(L+\phi)$	$\displaystyle\geq-\int(L+\phi)\,d\mu_{\Gamma}=-\int L\;d\mu_{\Gamma}$
(104)			$\displaystyle\geq-\tfrac{1}{T}\,\delta^{2}\,\gamma(\Gamma)^{2}.$

We will prove that any semi-static curve $x:]-\infty,0]\to M$ for $L+\phi$ has $\alpha$ -limit $\{(x,{\dot{x}})\}$ $=\Gamma$ . Since $\alpha$ -limits of semi-static orbits are static (Mañé [24, Theorem V.(c)]), this implies that $\Gamma\subset{\mathcal{A}}(L+\phi)$ . Thus finishing the proof of Proposition 5.3.

Since by (84), the number ${\overline{\gamma}_{\delta}}$ is smaller than the flow expansivity constant of ${\mathcal{N}}(L+\phi)$ , it is enough to prove that the tangent $(x,{\dot{x}})$ of any semi-static curve $x:]-\infty,0]\to M$ spends only a bounded time outside the $\tfrac{3}{8}{\overline{\gamma}_{\delta}}$ -neighbourhood of $\Gamma$ .

Let $x:]-\infty,0]\to M$ be a semi-static curve for $L+\phi$ . Let $\theta:=(x(0),{\dot{x}}(0))$ and let $\psi_{t}=\varphi_{t}^{L+\phi}$ be the lagrangian flow of $L+\phi$ . By (85) and (88) we have that

(105)

d(x(t),\pi\Gamma)\geq\delta_{1}\quad\Longrightarrow\quad d(x(t),\pi\Gamma)>\tfrac{1}{4}{\overline{\gamma}_{\delta}}.

By (98)-(99) and (92) we have that

(106)

d(\psi_{t}(\theta),\Gamma)>C\rho\quad\&\quad d(x(t),\pi\Gamma)<\delta_{1}\quad\Longrightarrow\quad d(x(t),\pi\Gamma)\geq\tfrac{1}{C}\,d(\psi_{t}(\theta),\Gamma).

By (90) and (88) we have that $\tfrac{1}{4}\gamma_{\delta}>C\rho$ . And then from (105) and (106) we get

(107)

d(\psi_{t}(\theta),\Gamma)\geq\tfrac{1}{4}{\gamma_{\delta}}\quad\left(>\tfrac{1}{4}C\,{\overline{\gamma}_{\delta}}\right)\quad\Longrightarrow\quad d(x(t),\pi\Gamma)>\tfrac{1}{4}\,{\overline{\gamma}_{\delta}}.

Also, from (105), (106) and (90) we have that

(108)

d(\psi_{t}(\theta),\Gamma)>C\rho\quad\Longrightarrow\quad d(x(t),\pi\Gamma)>\rho.

Then by (108), (96), (104), (103) and (91), we have that

(109)

d(\psi_{t}(\theta),\Gamma)>C\rho\quad\Longrightarrow\quad\phi(x(t))+c(L+\phi)\geq\tfrac{1}{4}\,\varepsilon\rho^{2}-\delta^{2}\,\gamma_{\delta}^{2}=:a_{0}>0.

For $\xi\in\Lambda(\phi)$ consider the local invariant manifolds

	$\displaystyle W^{s}_{\eta}(\xi)$	$\displaystyle:=\{\,\zeta\in E_{\mathbb{L}}^{-1}\{c({\mathbb{L}})\}\;:\;\forall t\geq 0\quad d(\psi_{t}(\zeta),\psi_{t}(\xi))\leq\eta\,\},$
	$\displaystyle W^{ss}_{\eta}(\xi)$	$\displaystyle:=\{\,\zeta\in W^{s}_{\eta}(\xi)\;:\;\lim_{t\to+\infty}d(\psi_{t}(\zeta),\psi_{t}(\xi))=0\,\},$
	$\displaystyle W^{u}_{\eta}(\xi)$	$\displaystyle:=\{\,\zeta\in E_{{\mathbb{L}}}^{-1}\{c({\mathbb{L}})\}\;:\;\forall t\leq 0\quad d(\psi_{t}(\zeta),\psi_{t}(\xi))\leq\eta\,\},$
	$\displaystyle W^{uu}_{\eta}(\xi)$	$\displaystyle:=\{\,\zeta\in W^{u}_{\eta}(\xi)\;:\;\lim_{t\to-\infty}d(\psi_{t}(\zeta),\psi_{t}(\xi))=0\,\}.$

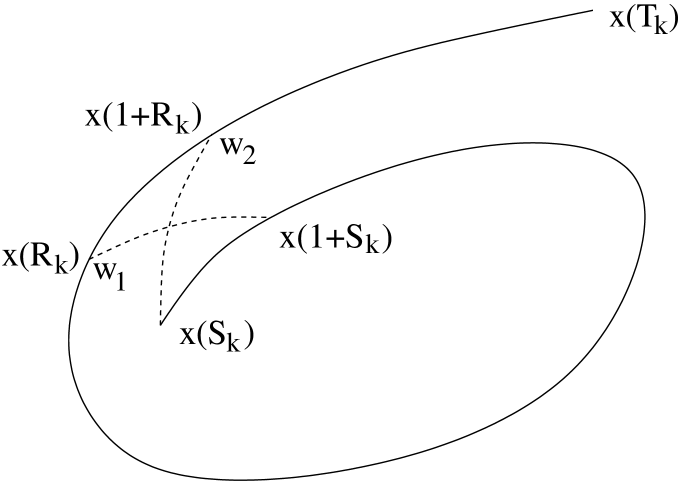
Also consider the canonical coordinates as in A.4 on $\Lambda(\phi)$ , i.e. there are $\eta_{0},\,\eta>0$ such that if $\xi,\,\zeta\in\Lambda(\phi)$ and $d(\xi,\zeta)<\eta_{0}$ then there is $v=v(\xi,\zeta)\in{\mathbb{R}}$ , $|v|\leq\eta$ such that

(110)

\displaystyle\langle\xi,\zeta\rangle:=W^{ss}_{\eta}(\psi_{v}(\xi))\cap W^{uu}_{\eta}(\zeta)\neq\emptyset.

We use the canonical coordinates to parametrize the approaches of $\psi_{t}(\theta)$ to $\Gamma$ in the following way. By (87), ${\gamma_{\delta}}<\eta_{0}$ . The local weak stable manifold of $\Gamma$

W^{s}_{\eta}(\Gamma):=\textstyle\bigcup_{\xi\in\Gamma}W^{s}_{\eta}(\xi)=\bigcup_{\xi\in\Gamma}W^{ss}_{\eta}(\xi)

forms a cylinder homeomorphic to $\Gamma({\mathbb{R}})\times]0,1[^{\dim M-1}$ . When $d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))<{\gamma_{\delta}}$ the strong local unstable manifold $W^{uu}_{\eta}(\psi_{t}(\theta))$ intersects this cylinder transversely and defines a unique time parameter $v(t)$ (mod $T$ ) such that

(111)

W^{ss}_{\eta}(\Gamma(v(t)))\cap W^{uu}_{\eta}(\psi_{t}(\theta))\neq 0.

Since the family of strong invariant manifolds is invariant under each iterate $\psi_{t}$ we have that if $d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))<{\gamma_{\delta}}$ for all $t\in[a,b]$ then

\forall s\in[0,b-a]\qquad v(a+s)=v(a)+s.

Let $B$ be from Lemma A.4. Write $\theta=(x(0),{\dot{x}}(0))$ and define $S_{k}(\theta)$ , $T_{k}(\theta)$ recursively by

(112)		$\displaystyle S_{0}(\theta)$	$\displaystyle:=0,$
	$\displaystyle T_{k}(\theta)$	$\displaystyle:=\sup\,\big{\{}\,t<S_{k-1}(\theta)\;\big{\|}\;d\big{(}\psi_{t}(\theta),\Gamma(v(t))\big{)}\leq C(B+1)\rho\,\big{\}},$
	$\displaystyle C_{k}(\theta)$	$\displaystyle:=\sup\,\big{\{}\,t<T_{k}(\theta)\;\big{\|}\;d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))=\tfrac{1}{3}{\gamma_{\delta}}\,\big{\}},$
	$\displaystyle S_{k}(\theta)$	$\displaystyle:=\inf\big{\{}\,t>C_{k}(\theta)\;\big{\|}\;d\big{(}\psi_{t}(\theta),\Gamma(v(t))\big{)}\leq C(B+1)\rho\,\big{\}}.$

Refer to caption — Figure 1. This figure illustrates the distance of the orbit of $\theta$ to the periodic orbit $\Gamma$ and the choice of $S_{k}$ , $T_{k}$ and $C_{k}$ .

Claim 5.4.2:

(1)

If $S_{k-1}(\theta)>-\infty$ then $T_{k}(\theta)>-\infty$ .
(2)

If $T_{k}(\theta)>-\infty$ then $T_{k+1}(\theta)\leq C_{k}(\theta)$ .
(3)

If $C_{k-1}(\theta)>-\infty$ then $d\big{[}\psi_{T_{k}(\theta)}(\theta),\Gamma(v(T_{k}(\theta)))\big{]}=C(B+1)\rho$ .
(4)

If $C_{k}(\theta)>-\infty$ then $C_{k}(\theta)<S_{k}(\theta)\leq T_{k}(\theta)$ .
(5)

If the sequence $\{T_{k}\}$ is finite, then $\alpha\text{-limit}(x,{\dot{x}})=\Gamma$ .
(6)

If $t\in[S_{k}(\theta),T_{k}(\theta)]$ then $d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))\leq\tfrac{1}{3}{\gamma_{\delta}}$ .

Proof:

(1). Suppose by contradiction that $S_{k-1}(\theta)>-\infty$ but $T_{k}(\theta)=-\infty$ . Let $\Phi^{L}_{k}$ be the action potential (1) for $L$ . Since $\Phi^{L}_{c(L)}$ is Lipschitz, it is bounded on $M\times M$ .

	$\displaystyle\int_{-t}^{S_{k-1}(\theta)}L(x,{\dot{x}})=\int_{-t}^{S_{k-1}(\theta)}\big{\{}c(L)+L(x,{\dot{x}})\big{\}}$	$\displaystyle\geq\Phi^{L}_{c(L)}\big{(}x(-t),x(S_{k-1}(\theta))\big{)}$
(113)			$\displaystyle\geq\inf_{y,z\in M}\Phi^{L}_{c(L)}(y,z)=:b_{0}>-\infty.$

Recall that $\eta$ is from the canonical coordinates A.3 for $\Lambda(\phi)$ as in (110) and satisfies (87). Since $T_{k}(\theta)=-\infty$ we have that for all $t<S_{k-1}(\theta)$ either

(114)

d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))>\eta>{\gamma_{\delta}}\qquad\text{ or }

(115)

d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))\leq\eta\quad\text{ but }\quad d(\psi_{t}(\theta),\Gamma(v(t)))>C(B+1)\rho.

In the case (115) let $s(t)$ be such that $d(\psi_{t}(\theta),\Gamma(s(t)))=d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))\leq\eta$ . We have that

	$\displaystyle\langle\Gamma(s(t)),\psi_{t}(\theta)\rangle$	$\displaystyle=W^{s}_{\eta}(\Gamma(s(t)))\cap W^{uu}_{\eta}(\psi_{t}(\theta))$
		$\displaystyle=W^{s}_{\eta}(\Gamma(v(t)))\cap W^{uu}_{\eta}(\psi_{t}(\theta))=\langle\Gamma(v(t)),\psi_{t}(\theta)\rangle$
(116)			$\displaystyle=W^{ss}_{\eta}(\Gamma(v(t)))\cap W^{uu}_{\eta}(\psi_{t}(\theta)).$

We apply Lemma A.4 with $x:=\Gamma(s(t))$ and $y:=\psi_{t}(\theta)$ . Using (155) we have that

(117)

d(y,\psi_{v}(x))\leq d(y,x)+d(x,\psi_{v}(x))\leq(1+B)\,d(y,x).

Observe that (116) implies that $\psi_{v}(x)=\Gamma(v(t))$ . Replacing $x$ and $y$ in (117) and using (115) we have that

	$\displaystyle d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))$	$\displaystyle=d(\psi_{t}(\theta),\Gamma(s(t)))\geq\tfrac{1}{1+B}\;d(\psi_{t}(\theta),\Gamma(v(t)))$
(118)			$\displaystyle>C\rho.$

Observe that by (90) and (88), in case (114) inequality (118) also holds. Therefore

(119)

\forall t<S_{k-1}(\theta)\qquad d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))>C\rho.

Since $x$ is semi-static for $L+\phi$ we have for all $-t<S_{k-1}(\theta)$ that

	$\displaystyle\infty>\sup_{y,z\in M}\Phi^{L+\phi}_{c(L+\phi)}(y,z)$	$\displaystyle\geq\Phi_{c(L+\phi)}^{L+\phi}\big{(}x(-t),x(S_{k-1}(\theta))\big{)}$
		$\displaystyle=\int_{-t}^{S_{k-1}(\theta)}\big{[}L(x,{\dot{x}})+\phi(x)+c(L+\phi)\big{]}$
		$\displaystyle=\int_{-t}^{S_{k-1}(\theta)}L(x,{\dot{x}})+\int_{-t}^{S_{k-1}(\theta)}\big{[}\phi(x)+c(L+\phi)\big{]}$
(120)			$\displaystyle\geq b_{0}+a_{0}\big{(}t+S_{k-1}(\theta)\big{)}\qquad\text{ by \eqref{intb0} and \eqref{tsk}, \eqref{phirho}.}$

By (109) we have that $a_{0}>0$ . Letting $t\to+\infty$ , inequality (120) gives a contradiction.

(2). Let

(121)

f(t):=d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))\qquad\text{ and }\qquad g(t):=d(\psi_{t}(\theta),\Gamma(v(t))),

when $g$ is defined (in particular by (87) when $f(t)<{\gamma_{\delta}}$ ). Then $f(t)\leq g(t)$ .

Suppose first that $C_{k}(\theta)=-\infty$ . Then $f(t)\neq\tfrac{1}{3}{\gamma_{\delta}}$ for all $t<T_{k}(\theta)$ . By hypothesis $T_{k}(\theta)>-\infty$ , then $f(T_{k}(\theta))\leq g(T_{k}(\theta))\leq C(B+1)\rho$ . By (90), $C(B+1)\rho<\tfrac{1}{3}\gamma_{\delta}$ , and hence $f(t)<\tfrac{1}{3}{\gamma_{\delta}}$ for all $t<T_{k}(\theta)$ . By (86) and Proposition A.7 with $L\to\infty$ we have that $\lim_{t\to-\infty}g(t)=0$ . Then $S_{k}(\theta)=-\infty$ and also $T_{k+1}(\theta)=-\infty$ .

Now suppose that $C_{k}(\theta)>-\infty$ . By the definition of $S_{k}(\theta)$ for all $t\in]C_{k}(\theta),S_{k}(\theta)[$ we have that $g(t)>C(B+1)\rho$ . This implies that $T_{k+1}(\theta)\leq C_{k}(\theta)$ .

(3). Let $f,\,g$ be as in (121). By the hypothesis $C_{k-1}(\theta)>-\infty$ and by the definition of $C_{k-1}(\theta)$ , $C_{k-1}(\theta)\leq T_{k-1}(\theta)$ . Then $f(C_{k-1}(\theta))=\tfrac{1}{3}{\gamma_{\delta}}$ . By (90), $C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}$ and then

(122)

C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}=f(C_{k-1}(\theta))\leq g(C_{k-1}(\theta)).

By the definition of $S_{k-1}(\theta)$ we have that $C_{k-1}(\theta)\leq S_{k-1}(\theta)$ . But by (122), $g(C_{k-1}(\theta))\geq\tfrac{1}{3}{\gamma_{\delta}}$ , and by the definition of $S_{k-1}(\theta)$ , if $S_{k-1}(\theta)<+\infty$ then $g(S_{k-1}(\theta))\leq C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}$ . Therefore $C_{k-1}(\theta)\neq S_{k-1}(\theta)$ and then

(123)

C_{k-1}(\theta)<S_{k-1}(\theta)\leq+\infty.

By (122) and the definition of $S_{k-1}(\theta)$ we have that

\forall t\in]C_{k-1}(\theta),S_{k-1}(\theta)[\qquad g(t)>C(B+1)\rho.

This implies that $T_{k}(\theta)<C_{k-1}(\theta)$ , with strict inequality by (122). By (123) and item (1) we have that $C_{k-1}(\theta)>-\infty$ implies that $T_{k}(\theta)>-\infty$ . Therefore

(124)

-\infty<T_{k}(\theta)<C_{k-1}(\theta)<S_{k-1}(\theta).

The definition of $T_{k}(\theta)$ and the continuity of $g(t)$ on its domain imply that

(125)

g(T_{k}(\theta))\leq C(B+1)\rho.

The domain of definition and continuity of $g$ contains $f^{-1}(]0,{\gamma_{\delta}}[)\supset g^{-1}(]0,{\gamma_{\delta}}[)$ . By the intermediate value theorem for $g$ on connected components of $[g\leq{\gamma_{\delta}}]$ and (124), (125), (122), the image $g([T_{k}(\theta),C_{k-1}(\theta)])$ , and hence also $g(]-\infty,S_{k-1}(\theta)[)$ , contain the closed interval $\big{[}C(B+1)\rho,\tfrac{1}{3}{\gamma_{\delta}}\big{]}$ . Therefore, by the definition of $T_{k}(\theta)$ , we have that $g(T_{k}(\theta))=C(B+1)\rho$ .

(4). Let $f$ , $g$ be from (121). If $C_{k}(\theta)>-\infty$ then by the definition of $C_{k}(\theta)$ ,

(126)

C_{k}(\theta)\leq T_{k}(\theta).

Therefore $T_{k}(\theta)>-\infty$ . Then the definition of $T_{k}(\theta)$ implies that

(127)

g(T_{k}(\theta))\leq C(B+1)\rho.

Since $f(t)$ is continuous,

(128)

f(C_{k}(\theta))=\tfrac{1}{3}{\gamma_{\delta}}.

By (127), (90) and (128) we have that

(129)

g(T_{k}(\theta))\leq C(B+1)\rho<\tfrac{1}{4}\gamma_{\delta}<\tfrac{1}{3}{\gamma_{\delta}}=f(C_{k}(\theta))\leq g(C_{k}(\theta)).

This implies that $C_{k}(\theta)\neq T_{k}(\theta)$ . This together with (126) imply that

(130)

C_{k}(\theta)<T_{k}(\theta).

By (127) and (130) the value $S_{k}(\theta)$ is an infimum of a set which contains $T_{k}(\theta)$ , therefore

(131)

S_{k}(\theta)\leq T_{k}(\theta).

This proves the second inequality in item (4).

The first of the following inequalities follows from the definition of $S_{k}(\theta)$ . The second inequality is (131). The third inequality follows from the definition of $T_{k}(\theta)$ .

(132)

C_{k}(\theta)\leq S_{k}(\theta)\leq T_{k}(\theta)\leq S_{k-1}(\theta).

We get that

-\infty<C_{k}(\theta)\leq S_{k}(\theta)\leq S_{k-1}(\theta)\leq\cdots\leq S_{0}(\theta):=0<+\infty.

From the definition of $S_{k}(\theta)$ and $S_{k}(\theta)<+\infty$ , and then (128), we have that

g(S_{k}(\theta))\leq C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}=f(C_{k}(\theta))\leq g(C_{k}(\theta)).

In particular $C_{k}(\theta)\neq S_{k}(\theta)$ . Thus from (132), $C_{k}(\theta)<S_{k}(\theta)$ .

(5). If the sequence $\{T_{k}\}$ is finite, there is $\ell\in{\mathbb{N}}$ such that $T_{\ell}>-\infty$ and $T_{\ell+1}=-\infty$ . Let $f,\,g$ be from (121). By item (2) we have that $-\infty<T_{\ell}(\theta)\leq C_{\ell-1}(\theta)$ . Then we can apply item (3) and use (90) to obtain

(133)

f(T_{\ell}(\theta))\leq g(T_{\ell}(\theta))=C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}.

Since $T_{\ell+1}(\theta)=-\infty$ , by item (1), $S_{\ell}(\theta)=-\infty$ and by item (4), $C_{\ell}(\theta)=-\infty$ . Since $C_{\ell}(\theta)=-\infty$ we have that $f(t)\neq\tfrac{1}{3}{\gamma_{\delta}}$ for all $t<T_{\ell}(\theta)$ . But by (133), $f(T_{\ell}(\theta))<\tfrac{1}{3}{\gamma_{\delta}}$ . Since $f(t)$ is continuous, using (86) we get that

f(t)<\tfrac{1}{3}{\gamma_{\delta}}<\beta_{0}\qquad\text{ for all }t<T_{\ell}(\theta).

This implies that there is a continuous function $s:]-\infty,T_{\ell}(\theta)]\to{\mathbb{R}}$ such that

\forall t\leq T_{k}(\theta)\qquad d\big{(}\psi_{t}(\theta),\Gamma(s(t))\big{)}\leq\beta_{0}.

By Proposition A.7 there is $v\in{\mathbb{R}}$ and $\lambda>0$ such that

\forall t\leq T_{\ell}(\theta)\qquad d(\psi_{t}(\theta),\Gamma(t+v))\leq D\,\beta_{0}\,\text{\rm\large e}^{-\lambda(T_{\ell}(\theta)-t)}.

This implies that $\lim\limits_{t\to+\infty}d(\psi_{-t}(\theta),\Gamma)=0$ and that $\alpha\text{-limit}(\theta)=\Gamma({\mathbb{R}})$ .

(6). By item (2), $C_{k-1}(\theta)\geq T_{k}(\theta)>-\infty$ . By item (3) we have that $f(T_{k}(\theta))\leq g(T_{k}(\theta))=C(B+1)\rho<\tfrac{1}{3}{\gamma_{\delta}}$ . By the definition of $C_{k}(\theta)$ we have that $\forall t\in]C_{k}(\theta),T_{k}(\theta)]$ $f(t)\neq\tfrac{1}{3}{\gamma_{\delta}}$ . Then by the continuity of $f(t)$ , $\forall t\in]C_{k}(\theta),T_{k}(\theta)]$ $f(t)<\tfrac{1}{3}{\gamma_{\delta}}$ . Now it is enough to see that by item (4), $[S_{k}(\theta),T_{k}(\theta)]\subset]C_{k}(\theta),T_{k}(\theta)]$ .

$\triangle$

Let

B_{k}(\theta):=\sup\big{\{}\;t<C_{k}(\theta)\;\big{|}\;d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))\leq\tfrac{1}{4}{\gamma_{\delta}}\;\big{\}}.

Claim 5.4.3:

[B_{k}(\theta),C_{k}(\theta)]\subset[T_{k+1}(\theta),S_{k}(\theta)].

Proof:

Let $f,\,g$ be as in (121). By the definition of $S_{k}(\theta)$ we have that $S_{k}(\theta)\geq C_{k}(\theta)$ . By the definition of $B_{k}(\theta)$ and (90), we have that

(134)

g|_{]B_{k},C_{k}[}\geq f|_{]B_{k},C_{k}[}>\tfrac{1}{4}{\gamma_{\delta}}>C(B+1)\rho.

By the definition of $S_{k}(\theta)$ we have that

(135)

g|_{]C_{k},S_{k}[}>C(B+1)\rho.

By the definition of $C_{k}(\theta)$ and the continuity of $f(t)$ we have that

(136)

g(C_{k}(\theta))\geq f(C_{k}(\theta))=\tfrac{1}{3}{\gamma_{\delta}}>C(B+1)\rho.

Joining (134), (135) and (136) we get that

g|_{]B_{k},S_{k}[}>C(B+1)\rho.

By the definition of $T_{k+1}(\theta)$ this implies that $T_{k+1}(\theta)\leq B_{k}(\theta)$ .

$\triangle$

If $t\in[B_{k}(\theta),C_{k}(\theta)]$ , by the definition of $B_{k}(\theta)$ we have that

d(\psi_{t}(\theta),\Gamma)\geq\tfrac{1}{4}{\gamma_{\delta}}.

Then by (107),

(137)

t\in[B_{k}(\theta),C_{k}(\theta)]\quad\Longrightarrow\quad d(x(t),\pi\Gamma)>\tfrac{1}{4}{\overline{\gamma}_{\delta}}.

By the definition of $T_{k+1}(\theta)$ we have that

(138)

\forall t\in]T_{k+1}(\theta),S_{k}(\theta)[\qquad\text{either}\qquad d\big{(}\psi_{t}(\theta),\Gamma(v(t))\big{)}>C(B+1)\rho

or $d(\psi_{t}(\theta),\Gamma({\mathbb{R}}))>\eta>C\rho$ (when $v(t)$ does not exist). Here $\eta>C\rho$ follows from (90), (88), (87). The arguments in (117)-(118) apply in the case (138) to obtain

(139)

t\in]T_{k+1}(\theta),S_{k}(\theta)[\quad\Longrightarrow\quad d(\psi_{t}(\theta),\Gamma)>C\rho.

The continuity of $f$ and the definition of $B_{k}$ and $C_{k}$ give

(140)

f(B_{k})\leq\tfrac{1}{4}\,{\gamma_{\delta}},\qquad f(C_{k})=\tfrac{1}{3}{\gamma_{\delta}}.

From Claim 5.4.3, {(137), (96)}, (104), {(89), (140), (81)}, {(95), (103)} and {(139), (109)}, we have that

	$\displaystyle\int_{T_{k+1}(\theta)}^{S_{k}(\theta)}\Big{(}\phi+c(L+\phi)\Big{)}$	$\displaystyle\geq\int_{B_{k}(\theta)}^{C_{k}(\theta)}\Big{(}\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}-\tfrac{1}{T}\,\delta^{2}\,{\gamma_{\delta}}^{2}\Big{)}+\int_{[T_{k+1},S_{k}]\setminus[B_{k},C_{k}]}\Big{(}\phi+c(L+\phi)\Big{)}$
(141)			$\displaystyle\geq\big{(}\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}-\tfrac{1}{T}\,\delta^{2}\,{\gamma_{\delta}}^{2}\big{)}\,\alpha+0.$

Recall from (97) that

{\mathbb{L}}:=L+\phi+c(L+\phi)-du,

where $u$ is from (80). Observe that the lagrangian flow for ${\mathbb{L}}$ is the same as the lagrangian flow $\psi_{t}$ for $L+\phi$ . Also ${\mathcal{N}}({\mathbb{L}})={\mathcal{N}}(L+\phi)$ and ${\mathcal{A}}({\mathbb{L}})={\mathcal{A}}(L+\phi)$ . Using (80) and (141),

	$\displaystyle\int_{T_{k+1}(\theta)}^{S_{k}(\theta)}{\mathbb{L}}(\psi_{t}(\theta))\,dt$	$\displaystyle=\int_{T_{k+1}(\theta)}^{S_{k}(\theta)}(L-du)+\int_{T_{k+1}(\theta)}^{S_{k}(\theta)}\Big{(}\phi+c(L+\phi)\Big{)}$
(142)			$\displaystyle\geq 0+\left(\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}-\tfrac{1}{T}\,\delta^{2}\,{\gamma_{\delta}}^{2}\right)\alpha.$

Case 1: Suppose that $T_{k}(\theta)-S_{k}(\theta)>T+2$ .

Let $m_{k}\in{\mathbb{N}}$ be such that

S_{k}(\theta)+m_{k}T\leq T_{k}(\theta)-1<S_{k}(\theta)+(m_{k}+1)T.

Then $m_{k}\geq 1$ . Let $R_{k}(\theta):=S_{k}(\theta)+m_{k}T$ . Then $1\leq T_{k}(\theta)-R_{k}(\theta)<T+1$ . By Claim 5.4.2.(6), $\Gamma$ is $\tfrac{{\gamma_{\delta}}}{3}$ -shadowed by $\psi_{[S_{k},T_{k}]}(\theta)$ . Therefore by inequality (180) in Proposition A.7 there is $v\in{\mathbb{R}}$ such that $\forall t\in[S_{k},T_{k}]$

(143)

d(\psi_{t}(\theta),\Gamma(t+v))\leq D\,\text{\rm\large e}^{-\lambda\min\{t-S_{k},T_{k}-t\}}[d(\psi_{S_{k}}(\theta),\Gamma(S_{k}+v))+d(\psi_{T_{k}}(\theta),\Gamma(T_{k}+v))].

Also the choice of $v$ in Proposition A.7 is the same as in (111) so that

(144)

t+v=v(t)\qquad\forall t\in[S_{k}(\theta),T_{k}(\theta)].

By the definition of $S_{k}$ and $T_{k}$ in (112) and the continuity of $g(t)$ on its domain we have that

(145)

g(S_{k})\leq C(B+1)\rho,\qquad g(T_{k})\leq C(B+1)\rho.

By (143), (144) and (145) we have for $s\in[0,1]$ that

	$\displaystyle d\big{(}\psi_{s+R_{k}}(\theta)$	$\displaystyle,\Gamma(v(s+R_{k}))\big{)}\leq$
		$\displaystyle\leq D\text{\rm\large e}^{-\lambda\min\{s+R_{k}-S_{k},T_{k}-s-R_{k}\}}\big{[}d(\psi_{S_{k}}(\theta),\Gamma(v(S_{k})))+d(\psi_{T_{k}}(\theta),\Gamma(v(T_{k})))\big{]}$
		$\displaystyle\leq D\,\text{\rm\large e}^{0}\;[g(S_{k})+g(T_{k})]\leq 2DC(B+1)\rho.$
	$\displaystyle d(\Gamma(v(s+$	$\displaystyle S_{k})),\psi_{s+S_{k}}(\theta))\leq 2DC(B+1)\rho.$

From (144) we have that

v(s+R_{k})=s+R_{k}+v=s+S_{k}+v+m_{k}T=v(s+S_{k})+m_{k}T.

So that $\Gamma(v(s+R_{k}))=\Gamma(v(s+S_{k}))$ . Adding the inequalities above we get

(146)

\forall s\in[0,1]\qquad d(\psi_{s+R_{k}}(\theta),\psi_{s+S_{k}}(\theta))\leq 4DC(B+1)\rho.

In local coordinates about $\pi(\Gamma)$ define

	$\displaystyle w_{1}(s+R_{k})$	$\displaystyle=(1-$	$\displaystyle s)\,$	$\displaystyle x(s+R_{k})\;$	$\displaystyle+$		$\displaystyle s\,$	$\displaystyle x(s+S_{k}),\qquad s\in[0,1];$
	$\displaystyle w_{2}(s+S_{k})$	$\displaystyle=$	$\displaystyle s\,$	$\displaystyle x(s+R_{k})$	$\displaystyle+$	$\displaystyle\;(1-$	$\displaystyle s)\,$	$\displaystyle x(s+S_{k}),\qquad s\in[0,1].$

By Lemma 5.2(b) and (146) we have that

A_{L+\phi}(x|_{[S_{k},1+S_{k}]})+A_{L+\phi}(x|_{[R_{k},1+R_{k}]})\geq A_{L+\phi}(w_{1})+A_{L+\phi}(w_{2})-6KD^{2}C^{2}(B+1)^{2}\rho^{2}.

Since the pairs of segments $\{\,x|_{[S_{k},1+S_{k}]},\,x|_{[R_{k},1+R_{k}]}\,\}$ and $\{\,w_{1},\,w_{2}\,\}$ have the same collections of endpoints

\int_{S_{k}}^{1+S_{k}}du({\dot{x}})+\int_{R_{k}}^{1+R_{k}}du({\dot{x}})=\oint_{w_{1}}du+\oint_{w_{2}}du.

Therefore, since $c(L+\phi)$ is constant,

(147)

A_{\mathbb{L}}(x|_{[S_{k},1+S_{k}]})+A_{\mathbb{L}}(x|_{[R_{k},1+R_{k}]})\geq A_{\mathbb{L}}(w_{1})+A_{\mathbb{L}}(w_{2})-6KD^{2}C^{2}(B+1)^{2}\rho^{2}.

The integral of $d_{x}u$ on closed curves is zero. Therefore

(148)

c({\mathbb{L}})=c(L+\phi+c(L+\phi))=0.

Since $w_{1}*x|_{[1+S_{k},R_{k}]}$ is a closed curve and $c({\mathbb{L}})=0$ , using (7),

(149)

A_{\mathbb{L}}(w_{1})+A_{\mathbb{L}}(x|_{[1+S_{k},R_{k}]})\geq 0.

Using (80) and (104),

(150)

{\mathbb{L}}=(L-du)+\phi+c(L+\phi)\geq 0+0-\tfrac{1}{T}\,\delta^{2}({\gamma_{\delta}})^{2}.

Since $T_{k}(\theta)-R_{k}(\theta)\leq T+2$ , using (103), on the curve $w_{2}*x|_{[1+R_{k},T_{k}]}$ we have that

(151)

A_{\mathbb{L}}(w_{2})+A_{\mathbb{L}}(x|_{[1+R_{k},T_{k}]})\geq-\tfrac{T+2}{T}\,\delta^{2}({\gamma_{\delta}})^{2}\geq-3\,\delta^{2}({\gamma_{\delta}})^{2}.

From (147), (149) and (151) we get that

$\displaystyle A_{\mathbb{L}}(x\|_{[S_{k},T_{k}]})$	$\displaystyle\geq A_{\mathbb{L}}(w_{1})$	$\displaystyle+A_{\mathbb{L}}(w_{2})-6KD^{2}C^{2}(B+1)^{2}\rho^{2}$
$\displaystyle+A_{\mathbb{L}}(x\|_{[1+S_{k},R_{k}]})+A_{\mathbb{L}}(x\|_{[1+R_{k},T_{k}]})$
	$\displaystyle\geq-6KD$	${}^{2}C^{2}(B+1)^{2}\rho^{2}-3\,\delta^{2}({\gamma_{\delta}})^{2}.$

Case 2: If $T_{k}-S_{k}\leq T+2$ , from (150) we also have

	$\displaystyle\hskip-56.9055ptA_{\mathbb{L}}(x\|_{[S_{k},T_{k}]})$	$\displaystyle\geq-\tfrac{T+2}{T}\,\delta^{2}({\gamma_{\delta}})^{2}\geq-3\,\delta^{2}({\gamma_{\delta}})^{2}$
		$\displaystyle\geq-6KD^{2}C^{2}(B+1)^{2}\rho^{2}-3\,\delta^{2}({\gamma_{\delta}})^{2}.$

Adding inequality (142) and using (93) we obtain a positive lower bound for the action independent of $k$ :

A_{\mathbb{L}}(x|_{[T_{k+1},T_{k}]})\geq\left(\tfrac{1}{32}\,\varepsilon\,({\overline{\gamma}_{\delta}})^{2}-\delta^{2}\,({\gamma_{\delta}})^{2}\right)\alpha-12KD^{2}C^{2}(B+1)^{2}\rho^{2}-3\,\delta^{2}({\gamma_{\delta}})^{2}>0.

Since $x$ is semi-static for $L+\phi$ , and then also for ${\mathbb{L}}$ , and by (148) $c({\mathbb{L}})=0$ , the total action is finite:

A_{\mathbb{L}}(x|_{]-\infty,0]})\leq\max_{y,z\in M}\Phi^{\mathbb{L}}_{c({\mathbb{L}})}(y,z)<+\infty.

Therefore there must be at most finitely many $T_{k}$ ’s.

By item (5) in claim 5.4.2, we have that $\alpha$ -limit $(x,{\dot{x}})=\Gamma$ . Since $\alpha$ -limits of semi-static orbits are static (Mañé [24, theorem V.(c)]), we obtain that $\Gamma\subset{\mathcal{A}}(L+\phi)$ . This finishes the proof of proposition 5.3.

∎

Appendix A Shadowing

Let $\psi$ be the flow of a $C^{1}$ vector field on a compact manifold $M$ . A compact $\psi$ -invariant subset $\Lambda\subset M$ is hyperbolic for $\psi$ if the tangent bundle restricted to $\Lambda$ is decomposed as the Whitney sum $T_{\Lambda}M=E^{s}\oplus E\oplus E^{u}$ , where $E$ is the 1-dimensional vector bundle tangent to the flow and there are constants $C,\lambda>0$ such that

(a)

$D\psi_{t}(E^{s})=E^{s}$ , $D\psi_{t}(E^{u})=E^{u}$ for all $t\in{\mathbb{R}}$ .
(b)

$|D\psi_{t}(v)|\leq C\,\text{\rm\large e}^{-\lambda t}|v|$ for all $v\in E^{s}$ , $t\geq 0$ .
(c)

$|D\psi_{-t}(u)|\leq C\,\text{\rm\large e}^{-\lambda t}|u|$ for all $u\in E^{u}$ , $t\geq 0$ .

It follows from the definition that the hyperbolic splittig $E^{s}\oplus E\oplus E^{u}$ over $\Lambda$ is continuous.

From now on we shall assume that $\Lambda$ does not contain fixed points for $\psi$ . For $x\in\Lambda$ define the following stable and unstable sets:

	$\displaystyle W^{ss}(x):$	$\displaystyle=\{\,y\in M\;\|\;d(\psi_{t}(x),\psi_{t}(y))\to 0\text{ as }t\to+\infty\,\},$
	$\displaystyle W^{ss}_{\varepsilon}(x):$	$\displaystyle=\{\,y\in W^{ss}(x)\;\|\;d(\psi_{t}(x),\psi_{t}(y))\leq\varepsilon\;\;\forall t\geq 0\,\},$
	$\displaystyle W^{uu}(x):$	$\displaystyle=\{\,y\in M\;\|\;d(\psi_{-t}(x),\psi_{-t}(y))\to 0\text{ as }t\to+\infty\,\},$
(152)		$\displaystyle W^{uu}_{\varepsilon}(x):$	$\displaystyle=\{\,y\in W^{uu}(x)\;\|\;d(\psi_{-t}(x),\psi_{-t}(y))\leq\varepsilon\;\;\forall t\geq 0\,\},$

	$\displaystyle W^{s}_{\varepsilon}(x):$	$\displaystyle=\{\,y\in M\;\|\;d(\psi_{t}(x),\psi_{t}(y))\leq\varepsilon\;\;\forall t\geq 0\,\},$
	$\displaystyle W^{u}_{\varepsilon}(x):$	$\displaystyle=\{\,y\in M\;\|\;d(\psi_{-t}(x),\psi_{-t}(y))\leq\varepsilon\;\;\forall t\geq 0\,\}.$

Conditions {(a),(b),(c)} are equivalent to {(a),(d)}, where

(d)

There exists $T>0$ such that $\left\|D\psi_{T}|_{E^{s}}\right\|<\tfrac{1}{2}$ and $\left\|D\psi_{-T}|_{E^{u}}\right\|<\tfrac{1}{2}$ .

Let ${\mathfrak{X}}^{k}(M)$ be the Banach manifold of the $C^{k}$ vector fields on $M$ , $k\geq 1$ . Let $X=\partial_{t}\psi_{t}$ be the vector field of $\psi_{t}$ . For $Y\in{\mathfrak{X}}^{k}(M)$ denote by $\psi^{Y}_{t}$ the flow of $Y$ .

A.1 Proposition.

There are open sets $X\in{\mathcal{U}}\subset{\mathfrak{X}}^{1}(M)$ and $\Lambda\subset U\subset M$ such that for every $Y\in{\mathcal{U}}$ the set $\Lambda_{Y}:=\bigcap_{t\in{\mathbb{R}}}\psi^{Y}_{t}(\overline{U})$ is hyperbolic for the flow $\psi^{Y}_{t}$ of $Y$ , with uniform constants $C$ , $\lambda$ , $T$ on (b), (c) and (d).

Proposition A.1 can be proven by a characterization of hyperbolicity using cones (cf. Hasselblatt-Katok [18, Proposition 17.4.4]) and obtaining uniform contraction (expansion) for a fixed iterate in $\Lambda_{Y}$ . See Fisher-Hasselblatt [17] prop. 5.1.8 p. 256].

A.2.

Proposition [19, 5.6, p. 63], [4, 1.3], [17, 6.6.1].

There are constants $C,\,\lambda>0$ such that, for small $\varepsilon$ ,

(a)

$d\big{(}\psi_{t}(x),\psi_{t}(y)\big{)}\leq C\,\text{\rm\large e}^{-\lambda t}\,d(x,y)$ when $x\in\Lambda$ , $y\in W_{\varepsilon}^{ss}(x)$ , $t\geq 0$ .
(b)

$d\big{(}\psi_{-t}(x),\psi_{-t}(y)\big{)}\leq C\,\text{\rm\large e}^{-\lambda t}\,d(x,y)$ when $x\in\Lambda$ , $y\in W_{\varepsilon}^{uu}(x)$ , $t\geq 0$ .

A.3.

Canonical Coordinates [28, 3.1], [19, 4.1], [30, 7.4], [4, 1.4], [5, 1.2], [17, 6.2.2]:

There are $\alpha,\,\gamma>0$ for which the following is true: If $x,y\in\Lambda$ and $d(x,y)\leq\alpha$ then there is a unique $v=v(x,y)\in{\mathbb{R}}$ with $|v|\leq\gamma$ such that

(153)

\langle x,y\rangle:=W_{\gamma}^{ss}(\psi_{v}(x))\cap W^{uu}_{\gamma}(y)\neq\emptyset.

This set consists of a single point, which we denote $\langle x,y\rangle\in M$ . The maps $v$ and $\langle\;,\;\rangle$ are continuous on the set $\{\,(x,y)\;|\;d(x,y)\leq\alpha\,\}\subset\Lambda\times\Lambda$ .

A.4 Lemma.

There are $\eta_{0}>0$ , $B>1$ , and open sets $\Lambda\subset U$ , $X\in{\mathcal{U}}\subset{\mathfrak{X}}^{k}(M)$ such that
if $d(x,y)\leq\eta_{0}$ , $Y\in{\mathcal{U}}$ , $x,\,y\in\Lambda^{Y}_{U}$ and $\eta=B\,d(x,y)$ then

(154)		$\displaystyle\langle x,y\rangle\in W^{ss}_{\eta}(\psi^{Y}_{v}(x))\cap W^{uu}_{\eta}(y)\qquad\text{with }\quad\|v(x,y)\|\leq\eta\qquad$
(155)		$\displaystyle\text{and }\qquad d(x,\psi^{Y}_{v}(x))\leq\eta.$

Proof:.

We have that $\langle x,x\rangle=x$ and $v(x,x)=0$ . By uniform continuity, given $\delta>0$ , for $d(x,y)$ small enough

(156)

d(\langle x,y\rangle,x)\leq\delta,\qquad d(\langle x,y\rangle,y)\leq\delta,

and $v=v(x,y)$ is so small that

(157)

d(\psi_{v}(x),x)\leq\delta.

The continuity of the hyperbolic splitting implies that the angles $\measuredangle(E^{s},E^{u})$ , $\measuredangle(Y,E^{s})$ and $\measuredangle(E^{s}\oplus{\mathbb{R}}Y,E^{u})$ are bounded away from zero, uniformly on $\Lambda^{Y}_{V}:=\bigcap_{t\in{\mathbb{R}}}\psi^{Y}_{-t}(\overline{V})$ , for some $V\supset U$ and all $Y$ in an open set ${\mathcal{U}}_{0}\subset{\mathfrak{X}}^{1}(M)$ with $X\in{\mathcal{U}}_{0}$ . There is $\beta_{1}>0$ such that if $x,\,y\in\Lambda^{Y}_{U}$ and $d(x,y)<\beta_{1}$ then

\langle x,y\rangle=W^{s}_{\gamma}(x)\cap W^{uu}_{\gamma}(y)\in V.

The strong local invariant manifolds $W^{ss}_{\gamma}$ , $W^{uu}_{\gamma}$ are tangent to $E^{s}$ , $E^{u}$ at $\Lambda^{Y}_{V}$ and for a fixed $\gamma$ as $C^{1}$ submanifolds they vary continuously on the base point $x\in M$ and on the vector field in the $C^{1}$ topology (cf. [15, Thm. 4.3],[19, Thm. 4.1]). There is a family of small cones $E^{u}_{X}(x)\subset C^{u}(x)\subset T_{x}M$ , $E^{s}_{X}(x)\subset C^{s}(x)\subset T_{x}M$ defined on a neighborhood $W$ of $\Lambda$ invariant under $D\psi^{Y}_{-1}$ and $D\psi^{Y}_{1}$ respectively, for $Y$ in a $C^{1}$ neighborhood ${\mathcal{W}}$ of $X$ . The exponential of these cones contain $W^{uu}_{\gamma}(x)$ and $W^{ss}_{\gamma}(x)$ for $x\in\Lambda^{Y}_{W}$ and $Y\in{\mathcal{W}}$ . The angles between these cones are uniformly bounded away from zero, so for example if $z^{u}\in W^{uu}(x)$ , $z^{s}\in W^{ss}(x)$ and $d(z^{u},x)$ , $d(z^{s},x)$ are small, then $d(z^{u},x)+d(z^{s},x)<A_{0}\,d(z^{u},z^{s})$ for some $A_{0}>0$ . We can construct similiar cones separating $E^{u}$ from $E^{s}\oplus{\mathbb{R}}X$ .

Shrinking $U$ and ${\mathcal{U}}$ if necessary there are $0<\beta_{2}<\beta_{1}$ and $A_{1},\,A_{2},\,A_{3}>0$ such that if $Y\in{\mathcal{U}}$ , $x,\,y\in\Lambda^{Y}_{U}$ and $d(x,y)<\beta_{2}$ , taking $w:=\langle x,y\rangle\in W^{s}_{\gamma}(x)\cap W^{uu}_{\gamma}(y)$ and $v$ such that $w\in W^{ss}_{\gamma}(\psi^{Y}_{v}(x))$ , i.e. $\psi^{Y}_{v}(x)\in\psi^{Y}_{[-1,1]}(x)\cap W^{ss}_{\gamma}(w)$ , then

(158)		$\displaystyle d(x,w)+d(w,y)$	$\displaystyle\leq A_{1}\,d(x,y),$
(159)		$\displaystyle d(x,\psi^{Y}_{v}(x))+d(\psi^{Y}_{v}(x),w)$	$\displaystyle\leq A_{2}\,d(x,w)\leq A_{2}A_{1}\,d(x,y),$
	$\displaystyle\|v\|\leq A_{3}\,d(x,\psi^{Y}_{v}(x))$	$\displaystyle\leq A_{3}A_{2}A_{1}\,d(x,y).$

We can assume that ${\mathcal{U}}_{0}$ and $U$ are so small that the constants $C$ , $\lambda$ , $\varepsilon$ in Proposition A.2 can be taken uniform for all $Y\in{\mathcal{U}}_{0}$ and in $\Lambda^{Y}_{U}$ . By Proposition A.2, since $w:=\langle x,y\rangle\in W^{ss}_{\gamma}(\psi_{v}(x))$ , we have that

	$\displaystyle\forall t\geq 0\qquad d\big{(}\psi^{Y}_{t}(\langle x,y\rangle),\psi^{Y}_{t}(\psi^{Y}_{v}(x))\big{)}$	$\displaystyle\leq C\,\text{\rm\large e}^{-\lambda t}\,d(w,\psi_{v}^{Y}(x))$
		$\displaystyle\leq A_{2}A_{1}C\,\text{\rm\large e}^{-\lambda t}\,d(x,y)\qquad\text{ using~{}\eqref{a2xpw}.}$

Take $B_{1}:=(1+A_{2})A_{1}C$ . Then if $d(x,y)<\beta_{2}$ and $\eta=B_{1}\,d(x,y)$ we obtain that $\langle x,y\rangle\in W^{ss}_{\eta}(\psi^{Y}_{v}(x))$ .

Since $w=\langle x,y\rangle\in W^{uu}_{\gamma}(y)$ we have that

	$\displaystyle\forall t\geq 0\qquad d(\psi^{Y}_{-t}(\langle x,y\rangle),\psi^{Y}_{-t}(y))$	$\displaystyle\leq C\,\text{\rm\large e}^{-\lambda t}\,d(w,y)$
		$\displaystyle\leq A_{1}C\,\text{\rm\large e}^{-\lambda t}d(x,y)\qquad\text{using }\eqref{a1xwy}.$

Thus if $\eta=B_{1}\,d(x,y)$ then $\langle x,y\rangle\in W^{uu}_{\eta}(y)$ .

By (156) and (157) there is $0<\eta_{0}<\beta_{2}$ such that if $d(x,y)\leq\eta_{0}$ then $d(w,x)$ , $d(w,y)$ and $d(\psi_{v}(x),x)$ are small enough to satisfy the above inequalities. Now let

B:=\max\{2,\,B_{1},\,A_{3}A_{2}A_{1},\,A_{2}A_{1}\}.

∎

A.5 Proposition.

There are open sets $X\in{\mathcal{U}}\subset{\mathfrak{X}}^{1}(M)$ and $\Lambda\subset U\subset M$ and $\eta_{0},\gamma>0$ , $B>1$ such that

\forall\eta>0\qquad\exists\beta=\beta(\eta)=\tfrac{1}{B}\,\min\{\eta,\eta_{0}\}\qquad\forall Y\in{\mathcal{U}}

if $\psi_{t}=\psi^{Y}_{t}$ is the flow of $Y$ , $x,y\in\Omega^{Y}_{U}:=\bigcap_{t\in{\mathbb{R}}}\psi_{t}(\overline{U})$ and $s:{\mathbb{R}}\to{\mathbb{R}}$ continuous with $s(0)=0$ satisfy

(160)

d(\psi_{t+s(t)}(y),\psi_{t}(x))\leq\beta\quad\text{ for }|t|\leq L,

then

(161)

|s(t)|\leq 3\eta\quad\text{ for all }|t|\leq L,\qquad|v(x,y)|\leq\eta\quad\text{ and }

	$\displaystyle\forall\|s\|\leq L,\qquad$	$\displaystyle d(\psi_{s}(y),\psi_{s+v}(x))\leq C\,\text{\rm\large e}^{-\lambda(L-\|s\|)}\,\big{[}d(\psi_{L}(w),\psi_{L}(y))+d(\psi_{-L}(w),\psi_{-L+v}(x))\big{]},$
(162)			$\displaystyle\text{where }\qquad w:=\langle x,y\rangle=W^{ss}_{\gamma}(\psi_{v}(x))\cap W^{uu}_{\gamma}(y).$

also

(163)

\forall|s|\leq L,\qquad d(\psi_{s}(y),\psi_{s}\psi_{v}(x))\leq C\,\gamma\,e^{-\lambda(L-|s|)}.

In particular

d(y,\psi_{v}(x))\leq C\,\gamma\,e^{-\lambda L}.

Proof:.

Let $\gamma=B\eta_{0}$ with $\{\eta_{0},B\}$ from A.4. We may assume that $\eta$ is so small that

(164)		$\displaystyle\eta<\tfrac{\gamma}{8},$
(165)		$\displaystyle\sup\{\,d(\psi_{u}(x),x)\;:\;x\in M,\,\|u\|\leq 4\eta\,\}\leq\tfrac{\gamma}{8}.$

Let

(166)

\beta=\beta(\eta):=\tfrac{1}{B}\,\min\{\eta,\eta_{0}\},

where $B>1$ and $\eta_{0}$ are from lemma A.4. Consider $x$ , $y$ and $s(t)$ as in the hypothesis. Since $s(0)=0$ we have that $d(x,y)\leq\beta$ . Using lemma A.4 we can define

(167)

w:=\langle x,y\rangle=W^{ss}_{\eta}(\psi_{v}(x))\cap W^{uu}_{\eta}(y)\neq\emptyset,

we also have

(168)

|v|=|v(x,y)|\leq\eta.

Define the sets

	$\displaystyle A$	$\displaystyle:=\{\,t\in[0,L]\;:\;\|s(t)\|\geq 3\eta\;$	$\displaystyle\text{ or }\;d(\psi_{t}(y),\psi_{t}(w))\geq\tfrac{1}{2}{\gamma}\,\},$
	$\displaystyle B$	$\displaystyle:=\{\,t\in[0,L]\;:\;\|s(-t)\|\geq 3\eta\;$	$\displaystyle\text{ or }\;d(\psi_{-t+v}(x),\psi_{-t}(w))\geq\tfrac{1}{2}\gamma\,\}.$

Suppose that $A\neq\emptyset$ . Let $t_{1}:=\inf A$ . Then $d(\psi_{t}(y),\psi_{t}(w))\leq\tfrac{1}{2}\,\gamma$ , $\forall t\in[0,t_{1}]$ . Since $w\in W^{uu}_{\eta}(y)$ and by (164), $\eta<\tfrac{1}{8}\gamma$ ; from (152) we have that $d(\psi_{t}(y),\psi_{t}(w))\leq\tfrac{1}{8}\gamma$ , $\forall t\leq 0$ . Therefore

(169)

d(\psi_{t_{1}-r}(y),\psi_{t_{1}-r}(w))\leq\tfrac{1}{2}\,\gamma,\qquad\forall r\geq 0.

Since $s$ is continuous, $s(0)=0$ and $t_{1}\in\partial A$ , we have that $|s(t_{1})|\leq 3\eta$ . Using (165) twice with $u=|s(t_{1})|$ , (169) and the triangle inequality we obtain

d(\psi_{t_{1}+s(t_{1})-r}(y),\psi_{t_{1}+s(t_{1})-r}(w))\leq\tfrac{3}{4}\gamma,\qquad\forall r\geq 0.

Hence $\psi_{t_{1}+s(t_{1})}(w)\in W^{uu}_{\gamma}(\psi_{t_{1}+s(t_{1})}(y))$ . From (167), $w\in W^{ss}_{\eta}(\psi_{v}(x))$ , and then

(170)

d(\psi_{r}(w),\psi_{r+v}(x))\leq\eta<\tfrac{\gamma}{8},\qquad\forall r\geq 0.

Since $|s(t_{1})|\leq 3\eta$ , using (165) twice with $u=s(t_{1})$ , and (170) with $r=t_{1}+p\geq 0$ , and the triangle inequality, we get

d(\psi_{t_{1}+s(t_{1})+p}(w),\psi_{t_{1}+s(t_{1})+v+p}(x))\ \leq\tfrac{3\gamma}{8},\qquad\forall p\geq 0.

Hence $\psi_{t_{1}+s(t_{1})}(w)\in W^{ss}_{\gamma}(\psi_{s(t_{1})+v}(\psi_{t_{1}}(x)))$ . We have shown that

(171)

\psi_{t_{1}+s(t_{1})}(w)\in W^{ss}_{\gamma}(\psi_{s(t_{1})+v}(\psi_{t_{1}}(x)))\cap W^{uu}_{\gamma}(\psi_{t_{1}+s(t_{1})}(y)).

Since $|s(t_{1})+v|\leq|s(t_{1})|+|v|\leq 4\eta<\gamma$ and by (160),

(172)

d(\psi_{t_{1}+s(t_{1})}(y),\psi_{t_{1}}(x))\leq\beta,

equation (171) implies that

	$\displaystyle v(\psi_{t_{1}}(x),\psi_{t_{1}+s(t_{1})}(y))=s(t_{1})+v(x,y),$
	$\displaystyle\psi_{t_{1}+s(t_{1})}(w)=\langle\psi_{t_{1}}(x),\psi_{t_{1}+s(t_{1})}(y)\rangle.$

By Lemma A.4, (172) and (166),

(173)		$\displaystyle\|s(t_{1})+v\|\leq\eta\qquad\text{ and }$
	$\displaystyle\psi_{t_{1}+s(t_{1})}(w)\in W^{uu}_{\eta}(\psi_{t_{1}+s(t_{1})}(y)),\;\text{in particular}$
(174)		$\displaystyle d(\psi_{t_{1}+s(t_{1})}(w),\psi_{t_{1}+s(t_{1})}(y))\leq\eta.$

Since $|s(t_{1})|\leq 3\eta$ , from (165), (174) and (164), we get that

d(\psi_{t_{1}}(w),\psi_{t_{1}}(y))\leq\eta+2\left(\tfrac{\gamma}{8}\right)\leq\tfrac{3\gamma}{8}.

From (173) and (168) we have that

|s(t_{1})|\leq|s(t_{1})+v|+|v|\leq 2\eta.

These statements contradict $t_{1}\in A$ . Hence $A=\emptyset$ .

Similarly one shows that $B=\emptyset$ . Since $A=\emptyset$ , inequality (175) holds for all $t\in[0,L]$ . From (167), $w\in W^{uu}_{\eta}(y)$ and by (164), $\eta<\tfrac{\gamma}{8}$ ; thus inequality (175) also holds for $t\leq 0$ .

(175)

\forall t\leq L\qquad d(\psi_{t}(y),\psi_{t}(w))<\tfrac{1}{2}{\gamma}.

Therefore

(176)

\psi_{L}(w)\in W^{uu}_{\frac{1}{2}\gamma}(\psi_{L}(y)).

From Proposition A.2 we get

\forall|s|\leq L\qquad d(\psi_{s}(w),\psi_{s}(y))\leq C\,\text{\rm\large e}^{-\lambda(L-|s|)}\,d(\psi_{L}(w),\psi_{L}(y)).

Similarly, $B=\emptyset$ imples that

(177)

\psi_{-L}(w)\in W^{ss}_{\frac{1}{2}\gamma}(\psi_{-L+v}(x))\qquad\text{ and }

\forall|s|\leq L\qquad d(\psi_{s}(w),\psi_{s+v}(x))\leq C\,\text{\rm\large e}^{-\lambda(L-|s|)}\,d(\psi_{-L}(w),\psi_{-L+v}(x)).

Adding these inequalities we obtain

	$\displaystyle\forall\|s\|\leq L\qquad$	$\displaystyle d(\psi_{s}(y),\psi_{s+v}(x))\leq C\,\text{\rm\large e}^{-\lambda(L-\|s\|)}\,\big{[}d(\psi_{L}(w),\psi_{L}(y))+d(\psi_{-L}(w),\psi_{-L+v}(x))\big{]},$
(178)			$\displaystyle\text{where }\qquad w:=\langle x,y\rangle=W^{ss}_{\gamma}(\psi_{v}(x))\cap W^{uu}_{\gamma}(y).$

This proves inequality (162).

From (168), $|v(x,y)|\leq\eta$ . The fact $A\cup B=\emptyset$ also gives $|s(t)|\leq 3\eta$ for $t\in[-L,L]$ . This proves (161). From (176), (177) and (178) we get inequality (163).

∎

A.6 Proposition.

Let $\gamma$ , $\eta_{0}$ and $\beta=\beta(\eta)$ be from Proposition A.5. Given $\eta<\min\{\eta_{0},\tfrac{1}{2}\gamma\}$

(a)

If $x,\,y\in\Lambda$ and $s:[0,+\infty[\to{\mathbb{R}}$ continuous with $s(0)=0$ satisfy

$d(\psi_{t+s(t)}(y),\psi_{t}(x))\leq\beta\qquad\forall t\geq 0,$

then $|s(t)|\leq 3\eta$ for all $t\geq 0$ and there is $|v(x,y)|\leq\eta$ such that $y\in W^{ss}_{\gamma}(\psi_{v}(x))$ .
(b)

Similarly, if $x,\,y\in\Lambda$ , $s:]-\!\infty,0]\to{\mathbb{R}}$ is continuous with $s(0)=0$ and

$d(\psi_{t+s(t)}(y),\psi_{t}(x))\leq\beta\qquad\forall t\leq 0,$

then $|s(t)|\leq 3\eta$ for all $t\leq 0$ and there is $|v(x,y)|\leq\eta$ such that $y\in W^{uu}_{\gamma}(\psi_{v}(x))$ .

Proof:.

We only prove item (a). The same proof as in Proposition A.5 shows that taking

w:=\langle x,y\rangle=W^{ss}_{\eta}(\psi_{v}(x))\cap W^{uu}_{\eta}(y)\neq\emptyset,

we have that $|v|=|v(x,y)|\leq\eta$ and

\emptyset=A:=\{\,t\in[0,+\infty[\;:\;|s(t)|\geq 3\eta\;\text{ or }\;d(\psi_{t}(y),\psi_{t}(w))\geq\tfrac{1}{2}{\gamma}\,\}.

Therefore $|s(t)|\leq 3\eta$ for all $t\geq 0$ and $w\in W^{ss}_{\frac{1}{2}\gamma}(y)\cap W^{ss}_{\eta}(\psi_{v}(x))$ . Since $\tfrac{1}{2}\gamma+\eta<\gamma$ we get that $y\in W^{ss}_{\gamma}(\psi_{v}(x))$ .

∎

A.7 Proposition.

There are $D>0$ , $\beta_{0}>0$ and open sets $X\in{\mathcal{U}}\subset{\mathfrak{X}}^{1}(M)$ , $\Lambda\subset U\subset M$ , such that

\forall\beta\in]0,\beta_{0}]\qquad\forall Y\in{\mathcal{U}},

if $Y\in{\mathcal{U}}$ , $\psi_{t}=\psi^{Y}_{t}$ is the flow of $Y$ , $x,\,y\in\Lambda^{Y}_{U}:=\bigcap_{t\in{\mathbb{R}}}\psi_{t}(\overline{U})$ and $s:{\mathbb{R}}\to{\mathbb{R}}$ continuous with $s(0)=0$ satisfy

(179)

d(\psi_{t+s(t)}(y),\psi_{t}(x))\leq\beta\quad\text{ for }|t|\leq L,

then $|s(t)|\leq D\beta$ for all $|t|\leq L$ and there is $|v|=|v(x,y)|\leq D\beta$ such that

\displaystyle\forall|s|\leq L,\qquad d(\psi_{s}(y),\psi_{s+v}(x))\leq D\,\beta\,\text{\rm\large e}^{-\lambda(L-|s|)}.

Moreover for all $|s|\leq L$ ,

(180)

d(\psi_{s}(y),\psi_{s+v}(x))\leq D\,\text{\rm\large e}^{-\lambda(L-|s|)}\,\big{[}d(\psi_{L}(y),\psi_{L+v}(x))+d(\psi_{-L}(y),\psi_{-L+v}(x))\big{]},

and $v$ is determined by

\langle x,y\rangle=W^{ss}_{\gamma}(\psi_{v}(x))\cap W^{uu}_{\gamma}(y)\neq\emptyset.

Proof:.

Let $C$ , ${\mathcal{U}}$ , $U$ $\eta_{0}>0$ and $B$ be from Proposition A.5. The continuity of the hyperbolic splitting implies that the angle $\measuredangle(E^{s},E^{u})$ is bounded away from zero. As in the argument after (157), there are invariant families of cones separating $E^{s}$ from $E^{u}$ whose image under the exponential map contain the local invariant manifolds $W^{ss}_{\gamma}$ , $W^{uu}_{\gamma}$ . And hence as in (158) there are $A,\,\beta_{1}>0$ such that if $x,\,y\in\Lambda^{Y}_{U}$ , $d(x,y)<\beta_{1}$ and

w=\langle x,y\rangle=W^{ss}_{\gamma}(\psi_{v}(x))\cap W^{uu}_{\gamma}(y),

then

(181)

d(w,\psi_{v}(x))+d(w,y)\leq A\,d(\psi_{v}(x),y).

Suppose that $0<\beta<\min\{\tfrac{1}{B}\eta_{0},\,\beta_{1}\}$ and $x$ , $y$ , $s(t)$ , $\psi^{Y}_{t}$ , $L$ satisfy (179). Apply Proposition A.5 with $\eta:=B\beta$ .

Then $|s(L)|\leq 3\eta$ , and

	$\displaystyle d(\psi_{L}(y),\psi_{L}(x))$	$\displaystyle\leq d(\psi_{L+s(L)}(y),\psi_{L}(x))+\|s(L)\|\cdot\\|Y\\|_{\sup}$
		$\displaystyle\leq\beta+3\eta\left\\|Y\right\\|_{\sup}<\alpha,$

if $\beta$ is small enough. So that $\langle\psi_{L}(x),\psi_{L}(y)\rangle$ is well defined. Similarly $|s(-L)|\leq 3\eta$ and $d(\psi_{-L}(y),\psi_{-L}(x))<\alpha$ . Since the time $t$ map $\psi_{t}$ preserves the family of strong invariant manifolds, in equation (162) we have that

	$\displaystyle\psi_{L}(w)$	$\displaystyle=\langle\psi_{L}(x),\psi_{L}(y)\rangle=W^{ss}_{\gamma}(\psi_{L+v}(x))\cap W^{uu}_{\gamma}(\psi_{L}(y)),$
	$\displaystyle\psi_{-L}(w)$	$\displaystyle=\langle\psi_{-L}(x),\psi_{-L}(y)\rangle=W^{ss}_{\gamma}(\psi_{-L+v}(x))\cap W^{uu}_{\gamma}(\psi_{-L}(y)).$

Therefore, using (181),

	$\displaystyle d(\psi_{L}(w),\psi_{L}(y))+d$	$\displaystyle(\psi_{-L}(w),\psi_{-L+v}(x))$
(182)			$\displaystyle\leq A\big{[}d(\psi_{L+v}(x),\psi_{L}(y))+d(\psi_{-L+v}(x),\psi_{-L}(y))\big{]},$
	$\displaystyle d(\psi_{L+v}(x),\psi_{L}(y))$	$\displaystyle\leq d(\psi_{L+v}(x),\psi_{L}(x))+d(\psi_{L}(x),\psi_{L+s(L)}(y))+d(\psi_{L+s(L)}(y),\psi_{L}(y))$
		$\displaystyle\leq\|v\|\left\\|Y\right\\|_{\sup}+\beta+\|s(L)\|\,\left\\|Y\right\\|_{\sup}$
		$\displaystyle\leq B_{1}\beta,$

for some $B_{1}=B_{1}({\mathcal{U}})>0$ , because by Proposition A.5, $|v|\leq\eta$ , $|s(t)|\leq 3\eta$ and $\eta=B\beta$ , so that

|v|\leq B\beta,\qquad|s(t)|\leq 3B\beta.

A similar estimate holds for $d(\psi_{-L+v}(x),\psi_{-L}(y))$ and hence from (182),

d(\psi_{L}(w),\psi_{L}(y))+d(\psi_{-L}(w),\psi_{-L+v}(x))\leq 2AB_{1}\,\beta.

Replacing this in (162) we have that

\forall|s|\leq L,\qquad d(\psi_{s}(y),\psi_{s+v}(x))\leq D_{1}\,\beta\,\text{\rm\large e}^{-\lambda(L-|s|)},

where $D_{1}=2AB_{1}C$ .

By (182) and (162) we also have that

d(\psi_{s}(y),\psi_{s+v}(x))\leq AC\,\text{\rm\large e}^{-\lambda(L-|s|)}\,\big{[}d(\psi_{L}(y),\psi_{L+v}(x))+d(\psi_{-L}(y),\psi_{-L+v}(x))\big{]}.

Now take $D:=\max\{D_{1},\,B,\,3B,\,AC\,\}$ .

∎

A.8 Definition.

We say that $\psi|_{\Lambda}$ is flow expansive if for every $\eta>0$ there is $\overline{\alpha}=\overline{\alpha}(\eta)>0$ such that if $x\in\Lambda$ , $y\in M$ and there is $s:{\mathbb{R}}\to{\mathbb{R}}$ continuous with $s(0)=0$ and $d(\psi_{s(t)}(y),\psi_{t}(x))\leq\overline{\alpha}$ for all $t\in{\mathbb{R}}$ , then $y=\psi_{v}(x)$ for some $|v|\leq\eta$ .

A.9 Remark.

Observe that Proposition A.5 implies uniform expansivity in a neighbourhood of $(X,\Lambda)$ , namely there are neighbourhoods $X\in{\mathcal{U}}\subset{\mathfrak{X}}^{1}(M)$ and $\Lambda\subset U\subset M$ such that for every $\eta>0$ there is $\alpha=\alpha(\eta,{\mathcal{U}},U)>0$ such that if $x\in\Lambda^{Y}_{U}:=\cap_{t\in{\mathbb{R}}}\psi^{Y}_{t}(\overline{U})$ , $y\in M$ , $s:({\mathbb{R}},0)\to({\mathbb{R}},0)$ continuous and $\forall t\in{\mathbb{R}}$ , $d(\psi^{Y}_{s(t)}\big{(}y),\psi^{Y}_{t}(x)\big{)}<\alpha$ ; then $y=\psi^{Y}_{v}(x)$ for some $|v|<\eta$ . See also Fisher-Hasselblatt [17, cor. 5.3.5].

This also implies uniform h-expansivity of their time-one maps as in Definition A.11.

A.10 Definition.

Let $f:X\to X$ be a homeomorphism. For $\varepsilon>0$ and $x\in X$ define

\Gamma_{\varepsilon}(x,f):=\{\,y\in X\;|\;\forall n\in{\mathbb{Z}}\quad d(f^{n}(y),f^{n}(x))\leq\varepsilon\,\}.

We say that $f$ is entropy expansive or h-expansive if there is $\varepsilon>0$ such that

\forall x\in X\qquad h_{\text{top}}(\Gamma_{\varepsilon}(x,f),f)=0.

Such an $\varepsilon$ is called an h-expansive constant for $f$ .

A.11 Definition.

Let ${\mathcal{U}}$ be a topological subspace of $C^{0}(X,X)\supset{\mathcal{U}}$ and $Y\subseteq X$ compact. We say that ${\mathcal{U}}$ is uniformly h-expansive on $Y$ if there is $\varepsilon>0$ such that

\forall f\in{\mathcal{U}}\quad\forall y\in Y\qquad h_{\text{top}}(\Gamma_{\varepsilon}(y,f),f)=0.

In our applications ${\mathcal{U}}$ will be a $C^{1}$ neighbourhood of a diffeomorphism endowed with the $C^{0}$ topology. An h-expansive homeomorphism corresponds to ${\mathcal{U}}=\{f\}$ .

A.12 Definition.

Let $L>0$ , we say that $(T,\Gamma)$ is an $L$ -specification if

(a)

$\Gamma=\{x_{i}\}_{i\in{\mathbb{Z}}}\subset\Lambda$ .
(b)

$T=\{t_{i}\}_{i\in{\mathbb{Z}}}\subset{\mathbb{R}}$ and $t_{i+1}-t_{i}\geq L$ $\forall i\in{\mathbb{Z}}$ .

We say that the specification $(T,\Gamma)$ is $\delta$ -possible if

\forall i\in{\mathbb{Z}}\qquad d(\psi_{t_{i}}(x_{i}),\psi_{t_{i}}(x_{i-1}))\leq\delta.

A.13 Theorem.

Given $\ell>0$ there are $\delta_{0}=\delta_{0}(\ell)>0$ and $E=E(\ell)>0$ such that if $0<\delta<\delta_{0}$ and $(T,\Gamma)=(\{t_{i}\},\{x_{i}\})_{i\in{\mathbb{Z}}}$ is a $\delta$ -possible $\ell$ -specification on $\Lambda$ then there exist $y\in M$ and $\sigma:{\mathbb{R}}\to{\mathbb{R}}$ continuous, piecewise linear, strictly increasing with $\sigma(t_{0})=t_{0}$ and $|\sigma(t)-t|<E\,\delta$ such that

(183)

\forall i\in{\mathbb{Z}}\quad\forall t\in]t_{i},t_{i+1}[\qquad d\big{(}\psi_{\sigma(t)}(y),\psi_{t}(x_{i})\big{)}<E\,\delta.

Moreover, if the specification is periodic then $y$ is a periodic point for $\psi$ .

Theorem A.13 does not need that the hyperbolic set $\Lambda$ is locally maximal, but if not the point $y$ is not in $\Lambda$ . In Fisher-Hasselbaltt [17] the shadowing theorem A.13 is proved without a local maximality assumption and with the Lipschitz estimate (183) and $\sigma(t)$ a homeomorphism such that $\sigma(t)-t$ has Lipschitz constant $E\delta$ . But then proposition A.7 above proves the bound $|\sigma(t)-t|<E\delta$ and moreover, that $\sigma(t)-t$ can be taken constant on each interval $]t_{i},t_{i+1}[$ .

Theorem A.13 is proved in Bowen [4] (2.2) p. 6 with $\sigma(t)-t$ constant on each $]t_{i},t_{i+1}[$ and without the estimate $E\delta$ . A proof of theorem A.13 for flows without the local maximality hypothesis and with the explicit estimate $E\delta$ appears in Palmer [26] theorem 9.3, p. 188. In [26], [27] the theorem requires an upper bound on the lengths of the intervals in $T$ . This is because there the theorem is proven also for perturbations of the flow. Indeed by Proposition A.7 longer intervals in $T$ improve the estimate.

References

[1] Patrick Bernard, Existence of $C^{1,1}$ critical sub-solutions of the Hamilton-Jacobi equation on compact manifolds, Ann. Sci. École Norm. Sup. (4) 40 (2007), no. 3, 445–452, See also arXiv:math/0512018.
[2] Jairo Bochi, Genericity of periodic maximization: proof of Contreras’ theorem following Huang, Lian, Ma, Xu, and Zhang, manuscript, 2019.
[3] Rufus Bowen, Entropy-expansive maps, Trans. Amer. Math. Soc. 164 (1972), 323–331.
[4] by same author, Periodic orbits for hyperbolic flows, Amer. J. Math. 94 (1972), 1–30.
[5] by same author, Symbolic dynamics for hyperbolic flows, Amer. J. Math. 95 (1973), 429–460.
[6] Xavier Bressaud and Anthony Quas, Rate of approximation of minimizing measures, Nonlinearity 20 (2007), no. 4, 845–853.
[7] G. Contreras, A. Figalli, and L. Rifford, Generic hyperbolicity of Aubry sets on surfaces, Invent. Math. 200 (2015), no. 1, 201–261.
[8] G. Contreras, A. O. Lopes, and Ph. Thieullen, Lyapunov minimizing measures for expanding maps of the circle, Ergodic Theory Dynam. Systems 21 (2001), no. 5, 1379–1409.
[9] Gonzalo Contreras, Ground states are generically a periodic orbit, Invent. Math. 205 (2016), no. 2, 383–412.
[10] by same author, Generic Mañé Sets, Preprint, arXiv:1307.0559, arxiv.org, 2021.
[11] Gonzalo Contreras, Jorge Delgado, and Renato Iturriaga, Lagrangian flows: the dynamics of globally minimizing orbits. II, Bol. Soc. Brasil. Mat. (N.S.) 28 (1997), no. 2, 155–196, special issue in honor of Ricardo Mañé.
[12] Gonzalo Contreras and Renato Iturriaga, Convex Hamiltonians without conjugate points, Ergodic Theory Dynam. Systems 19 (1999), no. 4, 901–952.
[13] by same author, Global Minimizers of Autonomous Lagrangians, $22^{\text{o}}$ Coloquio Bras. Mat., IMPA, Rio de Janeiro, 1999.
[14] Gonzalo Contreras and Gabriel P. Paternain, Connecting orbits between static classes for generic Lagrangian systems, Topology 41 (2002), no. 4, 645–666.
[15] Sylvain Crovisier and Rafael Potrie, Introduction to partially hyperbolic dyanmics, lecture notes for a minicourse at ICTP School on Dynamical Systems 2015.
[16] Albert Fathi and Antonio Siconolfi, Existence of $C^{1}$ critical subsolutions of the Hamilton-Jacobi equation, Invent. Math. 155 (2004), no. 2, 363–388.
[17] Todd Fisher and Boris Hasselblatt, Hiperbolic Flows, Zurich Lectures in Advanced Mathematics, European Mathematical Society, Berlin, 2019.
[18] Boris Hasselblatt and Anatole Katok, Introduction to the modern theory of dynamical systems, Cambridge University Press, Cambridge, 1995, With a supplementary chapter by Katok and Leonardo Mendoza.
[19] Morris W. Hirsch, Charles C. Pugh, and Michael Shub, Invariant manifolds, Springer-Verlag, Berlin, 1977, Lecture Notes in Mathematics, Vol. 583.
[20] Wen Huang, Zeng Lian, Xiao Ma, Leiye Xu, and Yiwei Zhang, Ergodic optimization theory for a class of typical maps, preprint arXiv:1904.01915, 2019.
[21] by same author, Ergodic optimization theory for Axiom A flows, preprint arXiv:1904.10608, 2019.
[22] Douglas Lind and Brian Marcus, An introduction to symbolic dynamics and coding, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2021, Second edition.
[23] Ricardo Mañé, Generic properties and problems of minimizing measures of Lagrangian systems, Nonlinearity 9 (1996), no. 2, 273–310.
[24] by same author, Lagrangian flows: the dynamics of globally minimizing orbits, International Conference on Dynamical Systems (Montevideo, 1995), Longman, Harlow, 1996, Reprinted in Bol. Soc. Brasil. Mat. (N.S.) 28 (1997), no. 2, 141–153., pp. 120–131.
[25] John N. Mather, Action minimizing invariant measures for positive definite Lagrangian systems, Math. Z. 207 (1991), no. 2, 169–207.
[26] Kenneth James Palmer, Shadowing in dynamical systems, Mathematics and its Applications, vol. 501, Kluwer Academic Publishers, Dordrecht, 2000, Theory and applications. MR 1885537
[27] by same author, Shadowing lemma for flows, Scholarpedia 4 (2009), no. 4, 7918.
[28] Charles Pugh and Michael Shub, The $\Omega$ -stability theorem for flows, Invent. Math. 11 (1970), 150–158.
[29] Anthony Quas and Jason Siefken, Ergodic optimization of super-continuous functions on shift spaces, Ergodic Theory and Dynamical Systems 32 (2012), no. 6, 2071–2082.
[30] Steve Smale, Differentiable dynamical systems. I: Diffeomorphisms; II: Flows; III: More on flows; IV: Other Lie groups, Bull. Am. Math. Soc. 73 (1967), 747–792, 795–804, 804–808; 808–817; Appendix to I: Anosov diffeomorphisms by John Mather, 792–795.
[31] Guo-Cheng Yuan and Brian R. Hunt, Optimal orbits of hyperbolic systems, Nonlinearity 12 (1999), no. 4, 1207–1224.

	$\displaystyle A_{L+c}$	$\displaystyle(\gamma\|_{[a-s,b+s]})+\Phi_{c}(\gamma(b+s),\gamma(a-s))\leq$
		$\displaystyle\leq\lim_{n}\big{\{}\,A_{L+c}(\eta_{n}\|_{[T_{n}-s,T_{n}]})+A_{L+c}(\gamma\|_{[a,b]})\begin{aligned} &+A_{L+c}(\eta_{n}\|_{[0,s]})\,\big{\}}\\ &+\Phi_{c}(\gamma(b+s),\gamma(a-s))\end{aligned}$
		$\displaystyle\leq\begin{aligned} &-\Phi_{c}(\gamma(b),\gamma(a))\\ &+\lim_{n}\big{\{}\,A_{L+c}(\eta_{n}\|_{[0,s]})+A_{L+c}(\eta_{n}\|_{[s,T_{n}-s]})+A_{L+c}(\eta_{n}\|_{[T_{n}-s,T_{n}]})\,\big{\}}\end{aligned}$
		$\displaystyle\leq-\Phi_{c}(\gamma(b),\gamma(a))+\Phi_{c}(\gamma(b),\gamma(a))=0.$

	$\displaystyle A_{\mathbb{L}}($	$\displaystyle w_{1})+A_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}+\varepsilon,t_{0}+T-\varepsilon]})+A_{\mathbb{L}}(w_{2})<$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]})+A_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}-\varepsilon,t_{0}+\varepsilon]})+{\mathbb{A}}_{\mathbb{L}}(\pi\Gamma\|_{[t_{0}+\varepsilon,t_{0}+T-\varepsilon]})-\eta_{1}\,d([x(t),{\dot{x}}(t)],\Gamma(t_{0}))^{2}$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]})+\delta^{2}\,\gamma(\Gamma)^{2}-\eta_{1}\,d([x(t),{\dot{x}}(t)],\Gamma)^{2}$
		$\displaystyle<A_{\mathbb{L}}(x\|_{[t-\varepsilon,t+\varepsilon]}),\qquad\text{using~{}\eqref{posso3}.}$

Proof of the C2C^{2} Mañé’s conjecture on surfaces.

Abstract.

Key words and phrases:

1991 Mathematics Subject Classification:

1. Introduction.

1.1 Definition.

Theorem A.

Corollary B.

Theorem C.

Corollary D.

2. Preliminars.

2.1 Lemma (A priori bound).

Proof:.

2.2 Corollary.

Proof:.

2.3 Corollary.

Proof:.

2.4 Lemma.

Proof:.

3. Optimal specifications.

3.1 Lemma.

Proof:.

3.2 Proposition.

Proof:.

4. Optimal periodic orbits.

4.1 Lemma.

Proof:.

4.2 Lemma.

Proof:.

4.3 Proposition.

Proof:.

5. The perturbed minimizers.

5.1 Lemma (Mather [25, p. 186]).

5.2 Lemma.

5.3 Proposition.

5.4 Lemma.

Proof:.

Claim 5.4.1:

Claim 5.4.2:

Claim 5.4.3:

Appendix A Shadowing

A.1 Proposition.

A.2.

A.3.

A.4 Lemma.

Proof:.

A.5 Proposition.

Proof:.

A.6 Proposition.

Proof:.

A.7 Proposition.

Proof:.

A.8 Definition.

A.9 Remark.

A.10 Definition.

A.11 Definition.

A.12 Definition.

A.13 Theorem.

References

Proof of the $C^{2}$ Mañé’s conjecture on surfaces.