Proximity effect of pair correlation in the inner crust of neutron stars
Abstract
We study proximity effect of pair correlation in the inner crust of neutron stars by means of the Skyrme-Hartree-Fock-Bogoliubov theory formulated in the coordinate space. We describe a system composed of a nuclear cluster immersed in neutron superfluid, which is confined in a spherical box. Using a density-dependent effective pairing interaction which reproduces both the pair gap of neutron matter obtained in ab initio calculations and that of finite nuclei, we analyze how the pair condensate in neutron superfluid is affected by the presence of the nuclear cluster. It is found that the proximity effect is characterized by the coherence length of neutron superfluid measured from the edge position of the nuclear cluster. The calculation predicts that the proximity effect has a strong density dependence. In the middle layers of the inner crust with baryon density fm fm-3, the proximity effect is well limited in the vicinity of the nuclear cluster, i.e. in a sufficiently smaller area than the Wigner-Seitz cell. On the contrary, the proximity effect is predicted to extend to the whole volume of the Wigner-Seitz cell in shallow layers of the inner crust with fm-3, and in deep layers with fm-3.
D10,D11,D13,D41
1 Introduction
The inner crust of neutron stars is an exotic inhomogeneous matter consisting of a lattice of neutron-rich nuclear clusters which is immersed in neutron superfluid Chamel-Haensel2008 . One of the central issues of the physics of the inner crust is interplay between the superfluidity and the inhomogeneity, which influences various properties of the inner crust such as the specific heat, the thermal conductivity, and the pinning and unpinning of vortices. These are essential factors to understand astrophysical issues, such as the cooling and the glitch phenomenon of the neutron stars.
Microscopic many-body approaches to these phenomena have been pursued in the framework of the Hartree-Fock-Bogoliubov (HFB) theory, which has a capability to describe microscopically the inhomogeneous pair-correlated system. It has been argued for instance that the presence of the nuclear cluster modifies the quasiparticle excitation spectrum and the average pair gap, leading to a sizable difference in the specific heat of the inner crust from that of the uniform neutron superfluid Pizzochero2002 ; sandulescu2004 ; Monrozeau2007 ; chamel2010 ; Pastore2015 . evaluate the pinning energy of superfluid vortices Avogadro2008 ; Wlazlowski2016 ; Jin2017 . Recent interest also concerns with a dynamical aspect of the issues, i.e. the interaction between the vibrational motion of the nuclear cluster and the phonon excitation (the Anderson-Bogoliubov collective mode) of the neutron superfluid. This is one of the key ingredients which influence the thermal conductivity of the inner crust in magnetars aguilera2009 ; Pethick10 ; Cirigliano11 ; Page-Reddy2012 ; Chamel13 . In an attempt to analyze this dynamical coupling from a microscopic viewpoint, we have investigated the collective excitation of the inner crust matter by means of the quasiparticle random phase approximation based on the HFB theory inakura2017 ; inakura2019 . We found that the dynamical coupling between the collective motions of the nuclear cluster and of the neutron superfluid is weak.
In the present study, we intend to reveal the interplay between the nuclear cluster and the neutron superfluid but from a different viewpoint, i.e. the proximity effect of the pairing correlation gennes1964 ; gennesbook . The proximity effect is a general phenomenon which emerges around a border region of the system of a superconducting/superfluid matter in contact with normal matter (or matter with different pairing property). The pairing correlations in both matter are affected mutually in the border region since the Cooper pairs penetrate the border. The proximity effect in the inner crust matter is discussed in a few preceding works chamel2010 ; sandulescu2004 ; barranco1998 , but only in a qualitative manner. In the present study, we aim at characterizing the proximity effect quantitatively in order to reveal basic features of the pair correlation arising from the inhomogeneous structure of the inner crust matter.
As a theoretical framework to perform this study, we adopt the HFB theory using the Skyrme functional with a implementation of a few new features. One of the key elements in the HFB approach is the effective pairing interaction or the effective pairing functional, which generates the pair correlation in the system under study, and a density-dependent contact force, called the density-dependent delta interaction (DDDI), is often adopted. Note however that the inner crust matter consists of the neutron superfluid, whose density varies in a wide range from zero to that of the nuclear saturation, and the nuclear clusters, which resemble to isolated neutron-rich nuclei. In order to take into account this feature, we prepare a new parameter set of DDDI, which is required to describe the pairing gap of neutron superfluid obtained in ab initio calculations gezerlis2010 ; abe2009 as well as the experimental pairing gap in finite nuclei. Secondly, we quantify the range of the proximity effect by identifying the distance where the presence of the nuclear cluster influences the pairing property in neutron superfluid. Using this measure, we discuss in detail the dependence of the proximity effect on the density of the neutron superfluid, and clarify how large the proximity effect is in different layers of the inner crust.
In Section 2, we explain the adopted Skyrme-HFB model and the new parameter set of DDDI. In the present HFB all the nucleons are described as quasiparticles confined in a spherical box. If we adopt the box size equal to the Wigner-Seitz radius of the lattice cell, it is the same as the Wigner-Seitz approximation often adopted in the preceding works. However, the box truncation causes so called finite-size effect, and it make difficult to analyze the proximity effect. In Section 3, we examine the finite-size effect, and propose a different setting of the analysis using a large box truncation in place of the Wigner-Seitz approximation. Section 4 is devoted to a systematic analysis of the proximity effect. In subsection 4.1 we describe our scheme of the analysis that quantifies the range of the proximity effect, and justify the scheme with a systematic variation of the density of neutron superfluid immersing the nuclear cluster. In subsection 4.2, we apply the same analysis to various layers of a realistic configuration of the inner crust of neutron stars. Section 5 is devoted to the conclusions.
2 Model
2.1 Skyrme-Hartree-Fock-Bogolibov method in a spherical box
We adopt the Skyrme-Hartree-Fock-Bogoliubov method to describe the inner crust matter. Since the method is an extension of that is used in Refs. inakura2017 ; inakura2019 , we describe it briefly with emphasis on new aspects which are introduced in the present study.
We solve the HFB equation in a spherical box using the radial coordinate space and the partial wave expansion. The zero temperature is assumed and the spherical symmetry of solutions is imposed. Electrons are neglected. The radial HFB equation for a given angular quantum numbers reads
| (1) |
where is the quasiparticle wave function. Index denotes neutron or proton.
We discretize the radial coordinate with an interval fm as up to the edge of the box, and use the nine-point formula to represent the derivatives in the Hartree-Fock Hamiltonian . We impose the Dirichlet-Neumann boundary condition NV1973 , with which even-parity wave functions vanish at the edge of the box and the first derivatives of odd-parity wave functions vanish at the same position. Equation (1) is represented as a matrix eigenvalue problem where the wave function at the discretized coordinates is a -dimensional vector. We use routine DSYEVX in the LAPACK package to solve the eigenvalue problem for the symmetric matrix. If we treat the lattice configuration of the nuclear clusters by means of the Wigner-Seitz approximation, the box radius is chosen to be the size of the Wigner-Seitz cell. We shall also choose larger boxes fm or 200 fm, as we explain below. All the quasiparticle states up to a maximal quasiparticle energy MeV are included to calculate the number density, the pair density and all the quantities needed to calculate the selfconsistent potentials. We put also a cut-off on the angular momenta of the partial waves so that : for fm, and for fm, for example. We use the parameter set SLy4 chabanat for the selfconsistent Hartree-Fock potential in . We adopt the density-dependent delta interaction, as described below, to derive the pair potential . We vary the neutron Fermi energy to control the neutron density and we determine the proton Fermi energy to fix the proton number of the nuclear cluster. The other details are the same as in the previous study inakura2017 ; inakura2019 .
2.2 Density-dependent pairing interaction
As the pairing interaction, we use a density-dependent delta-interaction (DDDI), given as
| (2) |
for neutrons. Here is the density-dependent interaction strength, and is the projection operator for the spin singlet channel. The pair potential is then with the neutron pair density (the neutron pair condensate)
| (3) |
We consider the following three models for the interaction strength .
The first one, which we introduced in Refs. matsuo2006 ; matsuo2007 , is given as
| (4) |
with fm-3. Here the overall constant is determined to reproduce the scattering length =-18.5 fm in free space (i.e. at zero density) under the single-particle cut-off energy MeV. The dependence of the interaction strength on the neutron density is determined so that it reproduces the neutron pairing gap in pure neutron matter which is obtained in the BCS approximation using a bare nuclear force matsuo2006 ; matsuo2007 . We denote the parameterization, Eq. (4), as “DDDI-b” since it refers to the BCS gap with the bare nuclear force. (It is the same as the parametrization DDDI-G3RS in Ref. matsuo2006 .)
| DDDI-a1 | -458.4 | 0.08 | 0.59 | 1/3 | 0.06 | 2/3 | 0 | 1/3 |
| DDDI-a2 | -458.4 | 0.08 | 0.59 | 1/3 | 0.255 | 2/3 | -0.195 | 1/3 |
| DDDI-b | -458.4 | 0.08 | 0.845 | 0.59 | - | - | - | - |
In the present study we introduce more realistic modeling of the neutron pairing appropriate to the inner crust matter. Here we consider parametrizations of the DDDI that provide realistic pairing gap both in neutron matter and in finite nuclei. Concerning the neutron matter, it is known that the pairing gap is affected by medium effects beyond the BCS approximation, and many of theoretical studies trying to evaluate the medium effects predict a significant reduction from the BCS gap while the predicted values spread in a wide range Dean2003 ; Lombardo2001 ; Gandolfi-Gezerlis-Carlson ; Strinati2018 . Nevertheless, the pairing gap in the low-density limit is believed to be described reliably by a perturbative approach to the screening effect, discussed first by Gor’kov and Melik-Barkhudarov (GMB) gmb , and the pairing gap in the GMB framework gives a reduction of a factor of from the BCS pairing gapheiselberg2000 ; Pethick-Smith ; Strinati2018 . Recently, numerical ab initio calculations based on Monte-Carlo methods have been performed for pure neutron matter in low density region fm-3, and the predicted pairing gaps are reduced from the BCS gap by a factor of 1.5 - 2 gezerlis2010 ; abe2009 ; Gandolfi2008 ; Gandolfi-Gezerlis-Carlson . We can refer to these studies in requiring a new parametrization of the DDDI. It is also known that the pairing gap in finite nuclei cannot be described well by the BCS approximation applied to the bare nuclear force, and there is no ab initio evaluation of the gap in finite nuclei. Instead we will refer to experimental information on the pairing gap in finite nuclei.
In order to satisfy these conditions we introduce the following extended form of the density-dependent interaction strength:
| (5) |
The first term is introduced to describe the GMB gap appropriate to the low-density limit of the pure neutron matter. As discussed in Appendix A, the force strength of the contact force which reproduces the GMB pairing gap depends on the neutron Fermi momentum or the density of neutron matter. The dependence is expressed as a linear term proportional to or if it is expanded in powers of . Requiring that the GMB pairing gap is reproduced by the DDDI in the low-density limit . the parameters of the first term in Eq. (5) is fixed to and .
The second and third terms are introduced to represent the pairing gap of neutron matter at finite density and that in finite nuclei. In particular, the second term together with the first term is relevant to the pairing gap in neutron matter, and we assume that the second term has a power , i.e., the second power of neutron Fermi momentum . We then require that the coefficient of this term is consistent with the ab initio pairing gap of neutron matter obtained for fm fm-3 in the quantum Monte Carlo calculation by Gezerlis and Carlson gezerlis2010 and the determinantal lattice Monte Carlo calculation by Abe and Seki abe2009 . Note however that this requitement alone does not fix uniquely the coefficient since these ab initio calculations are slightly different with each other and there is no ab initio results for moderately low densities fm fm-3.
The third term dependent on the proton density represents a part of medium effects associated with systems with a proton fraction. For simplicity we assume that it is proportional to the proton Fermi momentum or the proton density . 111 A perturbative estimate of the medium effect in symmetric matter gives an attractive induced interaction proportional to heiselberg2000 . We use both the coefficient of this term and the uncertainty in to describe the pairing gap in finite nuclei. In practice, we require that the average neutron pairing gap in 120Sn obtained from our HFB model reproduces the experimental neutron gap MeV, extracted from the 3-point odd-even mass difference Satula1998 .
In the present study we prepare two different parameter sets to represent the remaining uncertainty of the neutron pair gap. In one case (we call “DDDI-a1” below), we choose and so that the neutron pairing gap in 120Sn is reproduced without . In this case, the pairing gap of neutron matter is close to that of Abe and Seki abe2009 , and the neutron matter pairing gap at moderately low density is rather large MeV, as shown in Fig. 1. It is remarked that the medium effect associated with the nuclear cluster or finite nuclei is effectively included in . In another parameter set (“DDDI-a2”), we consider a case that the neutron matter pairing gap at moderately low density is relatively small; we determine so as to make the neutron matter pairing gap vanish at as the BCS gap does. The parameter is then determined to reproduce the neutron gap in 120Sn. (Note that the neutron matter pairing gap reproduces approximately the result of Gezerlis and Carlson gezerlis2010 , as shown in Fig. 3.) The parameter sets of the three DDDI models are summarized in Table 1.
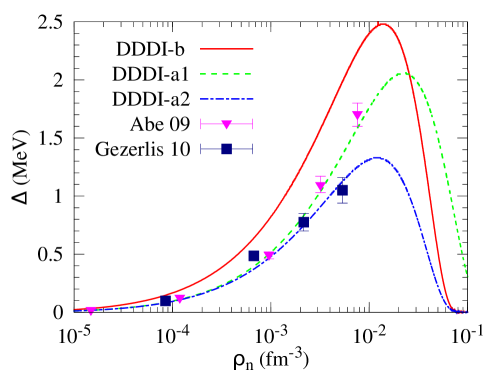
Figure 1 shows the neutron pairing gap in uniform neutron matter obtained from the Hartree-Fock plus BCS calculation using the DDDI models discussed above and the Skyrme functional with the parameter set SLy4. (The BCS calculation is briefly recapitulated in Appendix B, and we call it the uniform-BCS calculation in the following.) By construction, the pairing gaps obtained with the DDDI-a1 and the DDDI-a2 reproduce reasonably well the gap obtained with the ab initio calculations. The DDDI-a2 reproduces approximately the result of Gezerlis and Carlson gezerlis2010 for the density range fm-3. The gap of the DDDI-a2 at moderate density is small MeV, and vanishes at fm ( fm-1) corresponding to neutrons in the saturated nuclear matter. The neutron gap of the DDDI-a1 is very close to that of the DDDI-a2 up to fm-3, but deviate from it above fm-3, It is rather close to the gap of Abe and Seki abe2009 , and the neutron matter pairing gap at moderately low density is rather large MeV. The parameter set DDDI-b gives a larger pairing gap at low and moderately low densities than DDDI-a1 and DDDI-a2, while at densities around the saturation the gap becomes small and almost vanishing. 222The auxiliary-field diffusion Monte Carlo method Gandolfi2008 , another ab initio calculation, predicts the pairing gap close to the BCS gap in the density range . Thus it may be considered that the parameter set DDDI-b represents partly this result. We consider that DDDI-a1 and DDDI-a2 are more realistic than DDDI-b while the difference between DDDI-a1 and DDDI-a2 represents the uncertainty in modeling the realistic pairing correlation. We also use the model DDDI-b since it simulates the BCS gap, which is a robust baseline common to all the models of realistic bare nuclear force Dean2003 .
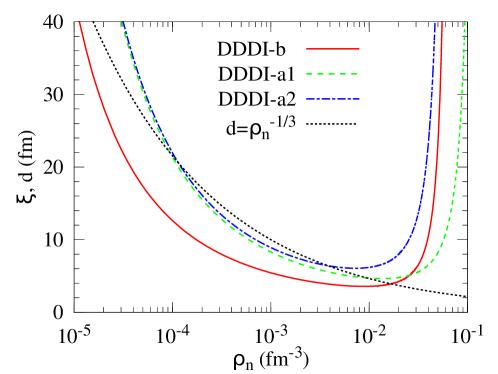
Figure 2 shows the coherence length of superfluid uniform neutron matter, calculated as described in Appendix B. The coherence length depends strongly on the neutron density. The coherence length is as short as fm at fm-3. The coherence length becomes long gradually as the neutron density decreases less than fm-3, and it also does rather sharply for increasing more than fm-3. The minimum value of the coherence length is fm for DDDI-b at neutron density corresponding to MeV, fm for DDDI-a1 at MeV, and fm for DDDI-a2 at MeV. The dotted curve in Fig. 2 shows the average inter-neutron distance . It is noted that the coherence length is shorter than the average inter-neutron distance at wide density interval fm-3 for DDDI-b, or comparable with at fm-3 for DDDI-a1 and DDDI-a2. The coherence length shorter than implies that the pair correlation at these densities is in the domain of the strong-coupling pairing, characterized as the BCS-BEC crossover phenomenon Strinati2018 .
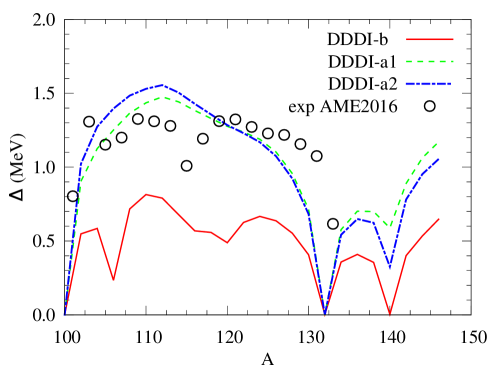
Figure 3 shows the average neutron pairing gap in Sn isotopes obtained in the present HFB code. The average neutron pairing gap in 120Sn calculated with DDDI-b, DDDI-a1 and DDDI-a2 is and 1.28 MeV, respectively. Note that the pair gap of DDDI-a1 and DDDI-a2 reproduces the experimental gap reasonably well over the long isotope chain while DDDI-b gives only a half of the experimental value.
3 Finite-size effect and large-box configuration
Since the present HFB calculation is performed in the radial coordinate space truncated with a finite box radius , obtained results depend on the box radius especially when is not large. This kind of dependence is often called the finite-size effect. If we adopt the Wigner-Seitz approximation, where the box size is chosen equal to the Wigner-Seitz radius of the lattice cell of the inner crust, results also include the finite-size effect. We shall examine how the Wigner-Seitz approximation is affected by the finite size effect. For this purpose, we here describe pure neutron matter using the same HFB code. For pure neutron matter, we can obtain an accurate numerical result by means of the uniform-BCS calculation, which corresponds to the limit of infinite size . Comparison with the uniform-BCS result makes it possible to evaluate the finite size effect.
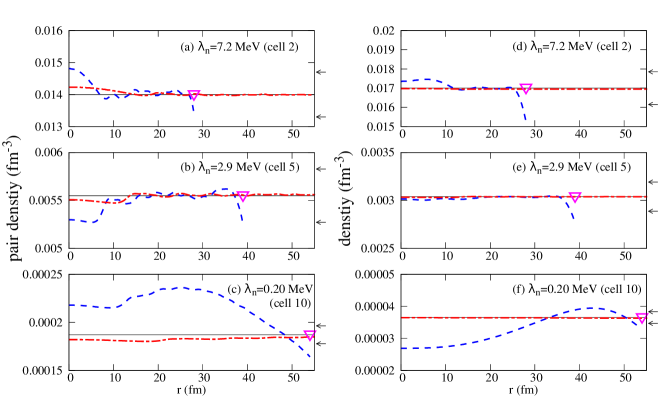
We have applied the present HFB model to the pure neutron systems by simply neglecting the proton contributions. Figure 4 shows a few example of the results, in which the neutron Fermi energy is chosen as , and 0.2 MeV corresponding to cells 2, 5 and 10 in Table LABEL:nvnuc, and the neutron density , and fm-3, respectively. The pairing interaction DDDI-a1 is adopted.
Dashed curves are the results for the calculation in which the box radius is set to the radius , 39 and 54 fm of the corresponding Wigner-Seitz cells. It is seen that both the number density and the pair density of neutrons deviate from the uniform-BCS results; the finite size effect in the pair density is not negligible and much larger than that for the number density. The deviation from the uniform-BCS result (horizontal lines) is more than 20% in cell 10 although it is less than about 5% in the other cells 2 and 5. The boundary condition with the finite box causes discretization of the energy spectrum of the quasiparticle states, and the pairing property is influenced by the discretization if the pair gap is not large enough than the energy spacing. It is also seen that the deviation from the uniform-BCS is worse at positions close to the origin than at far positions. A possible explanation is that the influence of the discretization of the quasiparticle energy spectrum may be stronger at small than at larger ; the number of contributing quasiparticle states is effectively small since the wave function of high- partial waves is suppressed at small .
The above results indicate that the Wigner-Seitz approximation to the inner crust matter may not be accurate enough to discuss the proximity effect. One needs to control the finite size effect in a better way. A desirable approach may be to take into account the lattice structure of the inner crust matter using the band theory method and the Bloch waves, where the continuity of the neutron quasiparticle spectrum is kept. However the band theory applied to the HFB calculation is presently quite limited chamel2010 , and a calculation with a large quasiparticle space is too demanding and difficult to be performed. Instead we adopt a simpler approach where a nuclear cluster is placed in a neutron superfluid confined in a large box, where the box size is chosen sufficiently large in order to reduce the finite-size effect as much as possible.
We find that fm gives the pair density convergent to the uniform-BCS with accuracy of around 1% for densities fm-3 as shown in Figure 2(a)(b), where we plot the results obtained with fm. In very-low-density cases fm-3, the pairing gap becomes very small MeV. In this case, influence of the discretization in quasiparticle levels is less negligible, and hence a larger box is required. For cell 10 (Fig. 2(c)), we obtained the agreement to the required accuracy with fm.
In the following we adopt this large-box configuration to discuss the proximity effect associated with the presence of the nuclear cluster.
4 Proximity effect
We shall now discuss the pair correlation in the inner crust matter. As discussed above we consider the system confined in a large box, at the center of which a nuclear cluster is placed. Using this setup, we shall investigate how the presence of the nuclear cluster influences the pair correlation of neutron superfluid in the neighborhood region around the cluster.
4.1 length of the proximity effect
In order to investigate general features of the proximity effect, we shall first examine cases where the density of the surrounding neutron superfluid is systematically varied while the proton number is fixed. In the next subsection we discuss realistic configurations of the inner crust matter, for which the proton number and the density of neutron superfluid are chosen to represent various layers of the inner crust.
The proton number is in all the examples in this subsection and we vary the neutron Fermi energy systematically from 0.2 MeV to 6 MeV, which corresponds to the density of the uniform neutron superfluid from fm-3 to fm-3.
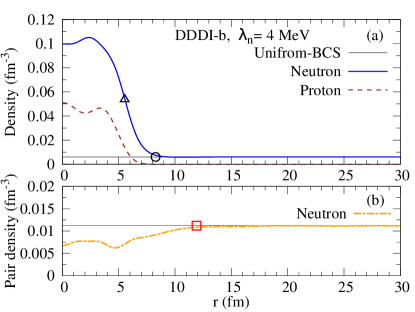
A typical result obtained for MeV ( fm-3) with DDDI-b is shown in Fig. 5, where plotted are the number densities of neutrons and protons, and , and the neutron pair density as a function of the radial coordinate . It is seen that the nuclear cluster is well localized in a central region as seen in the profile of the neutron density which converges rather quickly to a constant value at around fm (the proton density converges to zero around fm. ). The surface of the nuclear cluster may be quantified by fitting to the neutron density with a function of the Woods-Saxon type,
| (6) |
where defines the half-density surface, and represents the diffuseness of the surface. The constant is the neutron density obtained from the uniform-BCS performed for the same value of . The values of , and are extracted from a fitting. In addition we find it useful to consider “the edge” of the nuclear cluster to evaluate the area where the cluster exists. We define the nuclear edge by . The edge position is indicated by the black circle in Fig. 5, and it is seen that represents well the position where the neutron density converges to .
A most noticeable feature in Fig. 5 is that the neutron pair density exhibits behaviours different from those of the neutron number density . It is seen that the neutron pair density slowly converges and reaches the uniform-BCS value at around fm, deviating from by about 4 fm. In other words the influence of the nuclear cluster extends to the neighbour region beyond . This slow convergence is nothing but the proximity effect. In this example the neutron pair density inside the cluster is significantly smaller than that outside the cluster. This reflects the characteristic density dependence of the neutron pair gap of the DDDI-b model; the gap for the density inside the cluster () is very small MeV whereas that for the density of neutron superfluid ( fm) is relatively large MeV.
It has been argued that the proximity effect emerges in a region adjacent to the border with its length scale characterized by the coherence length of the superfluid/superconducting matter gennes1964 . We here assume that the border between the neutron superfluid and the nuclear cluster is approximated by the edge radius , rather than the half-density surface . If these considerations are reasonable, it is expected that the proximity effect is seen up to . In the case shown in Fig. 5, the position where the neutron pair density converges to the uniform-BCS value corresponds well to fm fm 11.9 fm, and the above argument appears to hold.
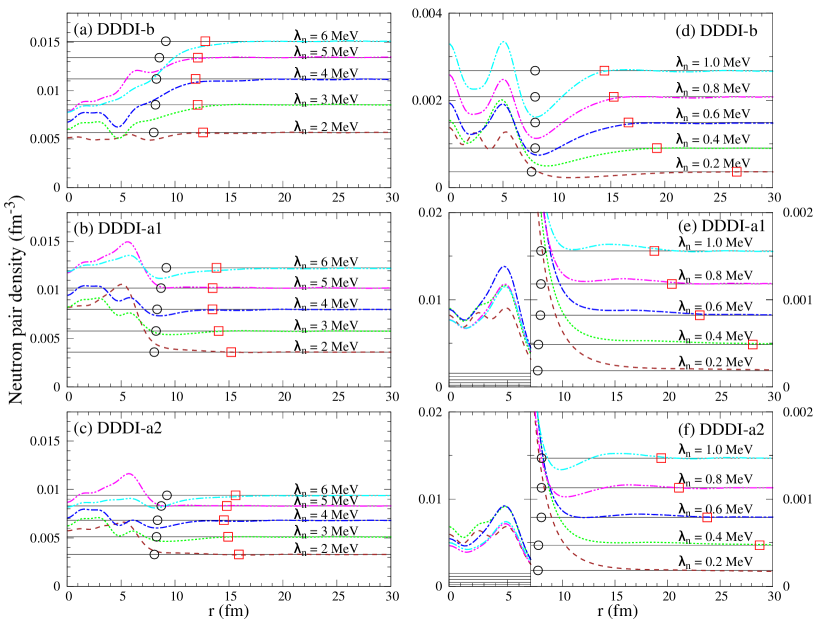
Figure 6 show systematic behaviours of the neutron pair densities calculated for various neutron Fermi energies and for three different pairing interactions: the DDDI-b (panel (a) in each figure), the DDDI-a1 (b), and the DDDI-a2 (c). Figure 6(a)(b)(c) shows the results for the neutron Fermi energy MeV corresponding the neutron density fm-3 (see Fig. 1), and Fig. 6(d)(e)(f) for ( fm-3).
The proximity effect is clearly visible in all the cases; the pair density converges to that of the uniform neutron superfluid at a position deviating significantly from the edge position of the nuclear cluster. It is also seen that the range of the proximity effect depends rather strongly on the neutron Fermi energy or the density of the neutron superfluid, especially at low neutron density fm-3 and MeV. It also depends on the three DDDI models. Despite the differences in the pairing properties, we confirm here that the range where the proximity effect reaches is described well by the position (marked with the square symbol), characterized by the coherence length measured from the edge of the nuclear cluster. (Note that the edge position of the nuclear cluster depends only weakly on the neutron Fermi energy, and there is essentially no dependence on the three choices of the pairing interaction. )
We here recall Fig. 2 where the coherence length is shown to become as small as fm at moderately low density fm-3 for the three DDDI’s. This brings about the short range of the proximity effect seen for MeV. This is related to the specific feature of the dilute neutron superfluid that the BCS-BEC crossover is about to occur at these densities.
A long range of the proximity effect seen for MeV can be related to the monotonic and considerable increase of the coherence length with decreasing neutron density for very low density fm-3. Note that for fm-3, the coherence length fm in the case of DDDI-b, fm for DDDI-a1 and fm for DDDI-a2. If the density of the external neutron superfluid decreases further, the range of the proximity effect is expected to exceed far beyond 50 fm.
4.2 Realistic inner crust configurations
Finally, we discuss the proximity effect for realistic situations of the inner crust of neutron stars. Here we refer to the Wigner-Seitz cells obtained in Negele and Vauthrin NV1973 for various layers of the inner crust. We perform the HFB calculation for the cells listed in Table LABEL:nvnuc using the large-box configuration. The proton number and the Wigner-Seitz radius of each cell is taken from Ref. NV1973 . The neutron Fermi energy , the control parameter of the neutron density, is chosen so that the obtained density of the external neutron superfluid reproduces approximately the density of the neutron gas in Ref. NV1973 . For simplicity we use a common value of for the three DDDI models. The box size is fm for most cells and 200 fm only for cell 1 with DDDI-b2, cell 10 with DDDI-a1 and cell 10 with DDDI-a2.
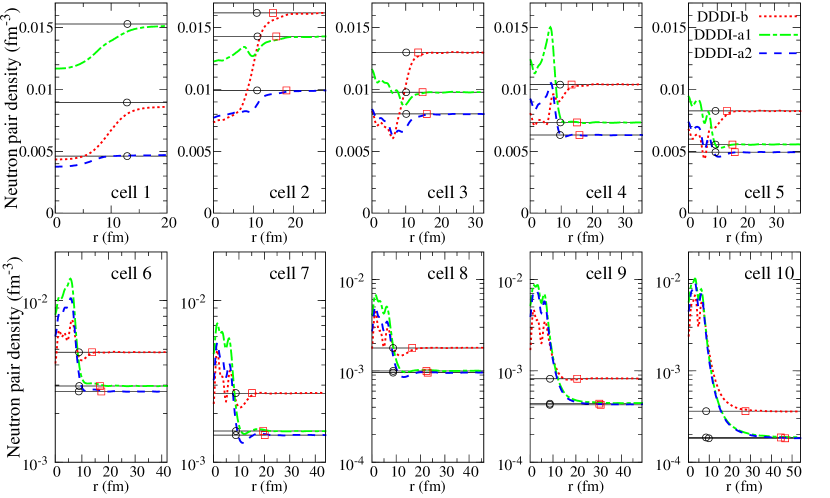
The calculated neutron pair density is shown in Fig. 8. The maximum of the plotted radial coordinate is the Wigner-Seitz radius for each cell. A noticeable feature is that in cells 3 to 8 the pair density converges to that of the uniform-BCS at a distance shorter than the half distance of the Wigner-Seitz radius. In other words the proximity effect is restricted only in a small area nearby the nuclear cluster. The area of uniform neutron superfluid and that of the nuclear cluster are well separated in these middle layers of the inner crust. This feature is common to the three DDDI pairing models. It is noted that the coherence length of external neutron superfluid is the smallest fm at cells 2-6 (for DDDI-b), cells 2-5 (for DDDI-a1), and cell 3 (for DDDI-a2), which are significantly smaller than the Wigner-Seitz radius of these cells at the middle layers.
In cells 9 and 10, where the external neutron superfluid is dilute ( fm-3), the proximity effect extends to a major area of the Wigner-Seitz cell, beyond the half length of the Wigner-Seitz radius, especially for DDDI-a1 and DDDI-a2. This reflects the long coherence length at such very low densities: fm for DDDI-a1 and DDDI-a2, and fm for DDDI-b. Note that the pairing gap of DDDI-a1 and DDDI-a2 in dilute neutron matter is reduced from the BCS value (corresponding to DDDI-b) by a factor of about 2, leading to a longer coherence length in these realistic gap models DDDI-a1 and DDDI-a2.
Another case where a long-range proximity effect is predicted is cell 1 at relatively high density, where the external neutron density fm is about a half of that of the saturated nuclear matter. The pair density deviates from that of the uniform neutron superfluid in the whole area of the Wigner-Seitz cell. In this cell with relatively high neutron density the predicted coherence length varies from 7 to 30 fm depending rather strongly on the pairing models, reflecting the uncertainty of the gap at such density. However, because of the relatively high baryon density and a large N/Z ratio, the Wigner-Seitz radius becomes small ( fm) and the edge position of the nuclear cluster becomes as large as fm due to a thick neutron skin of the cluster. Consequently the range of the proximity effect exceeds the Wigner-Seitz radius irrespective of the uncertainty of the pairing gap. Note that cell 1 corresponds to a deep layer of the inner crust, where a transition to the so called pasta phase is about to occur. The present result suggests strong proximity effect also for the pasta phase at higher baryon density. We remark also that the proximity effect in these deep layers might be even stronger than the present prediction because of the presence of adjacent nuclear clusters in the lattice configuration, but a quantitative evaluation is beyond the scope of the present study.
5 Conclusion
We have studied in detail the proximity effect of neutron pair correlation in the inner crust of neutron stars by applying the Skyrme-Hartree-Fock-Bogoliubov theory formulated in the coordinate representation. We describe a many-nucleon system consisting of protons (which form a nuclear cluster) and neutrons with a given positive Fermi energy, confined in a spherical box. If we choose the box radius equal to the Wigner-Seitz radius of the lattice cell, the calculation corresponds to the Wigner-Seitz approximation often adopted in preceding studies. We found however that for the realistic Wigner-Seitz radius fm of the inner crust matter, influence of the box truncation or the finite-size effect is not negligible for quantitative analysis of the proximity effect. We therefore use a large-box configuration where the box size is chosen sufficiently large fm. In other words, we considered a simplified model of the inner crust matter in which a single nuclear cluster is immersed in a uniform neutron superfluid, prepared in a sufficiently large box. As the effective interaction causing the pairing correlation, we introduced new parameterizations of the density-dependent delta interaction (DDDI-a1 and DDDI-a2) so that they reproduce the ab initio evaluations of the pair gap in low-density neutron matter as well as the experimental pair gap in finite nuclei.
Focusing on the neutron pair density (i.e. a locally defined pair condensate), we have examined how is affected by the presence of the nuclear cluster and how this quantity around the cluster converges to the limiting value of the immersing neutron superfluid. It is found from a systematic analysis that range of the proximity effect is characterized by the coherence length of neutron superfluid measured from the edge position of the cluster. An important feature is that the coherence length depends strongly on the density of neutron superfluid. The coherence length is as short as fm for density fm fm-3 while it increases gradually at lower density fm-3 and rather quickly at higher density fm-3.
Applying the above result to the realistic configurations of the inner crust, we predict that the proximity effect is well limited in the vicinity of the nuclear cluster, i.e. in a sufficiently smaller area than the Wigner-Seitz cell in the middle layers of the inner crust with baryon density fm fm-3. On the contrary, the proximity effect is predicted to extend to the whole volume of the Wigner-Seitz cell in the shallow layers of the inner crust with fm-3. Another region where the range of the proximity effect is expected to cover the whole Wigner-Seitz cell is deep layers of the inner crust with fm-3, where the Wigner-Seitz radius becomes small fm while the coherence length may becomes comparable or larger than . This observation indicates that in these layers there is no clear separation between the nuclear cluster and the immersing neutron superfluid as far as the pairing correlation is concerned. It implies that the phenomena originating from the pair correlation and superfluidity, such as the vortex pinning and the superfluid phonon excitations may also be affected by the proximity effect. It is noted also that theoretical approaches taking into account the lattice configuration is preferred for such cases. It is a subject to be pursued in future study.
Acknowledgement
We thank T. Inakura, K. Sekizawa, and K. Yoshida for valuable discussions. We also thank A. Ohnishi for a critical comment on the DDDI models. This work was supported by the JSPS KAKENHI (Grants Nos. 17K05436 and 20K03945).
Appendix A: Effective contact interaction for the GMB gap
Here we discuss the parameter set of DDDI which reproduces the pairing gap of Gor’kov Melik-Barkuhudarov (GMB) in the dilute limit of neutron matter. This is introduced by combining the known arguments on the GMB pairing gap heiselberg2000 ; Pethick-Smith and on the effective strength of the contact interaction Bertsch-Esbensen1991 ; Garrido1999 .
Let us first outline the relation between the strength of the contact interaction and the pairing gap in the BCS approximation. For the pairing interaction of the contact two-body force , the gap equation in the weak-coupling BCS approximation reads
| (7) |
where , , and is the single-particle energy, the Fermi energy (with the Fermi momentum ) and the pairing gap, respectively. To avoid the divergence inherent to the contact interaction, the sum is performed with a cut-off momentum or a cut-off single-particle energy . The force strength can be chosen so that the same interaction reproduces the zero-energy T-matrix , and the scattering length of the nucleon scattering in the channel. This requirement is expressed in terms of the Lippmann-Schwinger equation for the T-matrix, which can be written as
| (8) |
which determines the force strength as Bertsch-Esbensen1991 ; Garrido1999
| (9) |
The gap equation (7) combined with the T-matrix equation (8) is written as
| (10) |
The gap equation (10) is known to be solved analytically in the low-density limit satisfying and Marini1998 ; Papenbrock1999 . The right hand side of Eq. (10) is evaluated as , where is the single-particle level density at the Fermi energy. The paring gap in this limit is then given Marini1998 ; Papenbrock1999 ; Pethick-Smith ; Strinati2018 as
| (11) |
Note that the T-matrix plays a role of a renormalized interaction strength of the contact force.
It is known that the medium effect in the low-density limit can be evaluated perturbatively as originally discussed by Gor’kov and Melik-Barkhudarov gmb . The effect is represented as an induced interaction heiselberg2000 ; Pethick-Smith which modifies the interaction strength , where the numerical factor arises from an average of the Lindhard function. Similarly the left hand side of the gap equation (10) is modified as
| (12) |
and hence the GMB pairing gap valid in the low-density limit is given as
| (13) |
with a reduction of a factor of from the BCS gap.
Now, by combining the argument on the contact force, Eq. (8), and on the induced interaction modifying the l.h.s of the gap equation, Eq. (12), we find that an effective strength of the contact force which reproduces the GMB pairing gap is given by
| (14) |
which determines as
| (15) |
We note that the force strength depends on the Fermi momentum . Expanded in powers of , relevant to the low-density limit is the linear term in . It can be expressed also in terms of the density as
| (16) |
with
| (17) |
Appendix B: BCS calculation for uniform neutron matter
Here we describe the selfconsistent Hartree-Fock plus BCS approximation which is adopted to describe the pairing property of uniform neutron matter.
For a given value of the neutron Fermi energy , we numerically solve the coupled equations
| (18) |
| (19) |
| (20) |
where and are the Hartree-Fock potential and the effective mass of neutrons, obtained from the SLy4 functional.333In our previous publication inakura2017 , we made an approximation to Eq. (20) using a Fermi gas relation . Hence the result for neutron matter shown in Fig. 2 of Ref. inakura2017 is slightly different from that of the present study. The cut-off momentum is determined by so that it corresponds to the cut-off energy in the coordinate-space HFB calculation. The above scheme is called the uniform-BCS calculation in this paper.
The coherence length can be calculated by evaluating the size of the Cooper pair and is given
| (21) |
| (22) |
References
- (1) N. Chamel, and P. Haensel, Living Rev. Relativity, 11, 10 (2008). https://doi.org/10.12942/lrr-2008-10
- (2) N. Chamel, S. Goriely, J. M. Pearson, and M. Onsi, Phys. Rev. C 81, 045804 (2010). https://doi.org/10.1103/PhysRevC.81.045804
- (3) N. Sandulescu, N. V. Giai, and R. J. Liotta, Phys. Rev. C 69, 045802 (2004). https://doi.org/10.1103/PhysRevC.69.045802
- (4) C. Monrozeau, J. Margueron, N. Sandulescu, Phys, Rev. C 75, 065807 (2007). https://doi.org/10.1103/PhysRevC.75.065807
- (5) A. Pastore, Phys. Rev. C 91, 015809 (2015). https://doi.org/10.1103/PhysRevC.91.015809
- (6) P. M. Pizzochero, F. Barranco, E. Vigezzi, R. A. Broglia, Astrophys. J. 569, 381 (2002). https://doi.org/10.1086/339284
- (7) A. Avogadro, F. Barranco, R. A. Broglia, and E. Vigezzi, Nucl. Phys. A811, 378 (2008). https://doi.org/10.1016/j.nuclphysa.2008.07.010
- (8) G. Wlazłowski, K. Sekizawa, P. Magierksi, A. Bulgac, and M. N. Forbes, Phys. Rev. Lett. 117, 232701 (2016). https://doi.org/10.1103/PhysRevLett.117.232701
- (9) S. Jin, A. Bulgac, K. Roche, and G. Wlazłowski, Phys. Rev. C 95, 044302 (2017). https://doi.org/10.1103/PhysRevC.95.044302
- (10) D. N. Aguilera, V. Cirigliano, J. A. Pons, S. Reddy, and R. Sharma, Phys. Rev. Lett. 102, 091101 (2009). https://doi.org/10.1103/PhysRevLett.102.091101
- (11) C. J. Pethick, N. Chamel, and S. Reddy, Prog. Theor. Phys. Supple. 186, 9 (2010). https://doi.org/10.1143/PTPS.186.9
- (12) V. Cirigliano, S. Reddy, and R. Sharma, Phys. Rev. C 84, 045809 (2011). https://doi.org/10.1103/PhysRevC.84.045809
- (13) D. Page and S. Reddy, in Neutron Star Crust, ed. by C. Bertulani and J. Piekarewicz (Nova Science, 2012), p.281.
- (14) N. Chamel, D. Page, and S. Reddy, Phys. Rev. C 87, 035803 (2013). https://doi.org/10.1103/PhysRevC.87.035803
- (15) T. Inakura, and M. Matsuo, Phys. Rev. C 96, 025806 (2017). http://doi.org/10.1103/PhysRevC.96.025806
- (16) T. Inakura, and M. Matsuo, Phys. Rev. C 99, 045801 (2019). http://doi.org/10.1103/PhysRevC.99.045801
- (17) P. D. De Gennes, Rev. Mod. Phys. 36, 225 (1964). https://doi.org/10.1103/RevModPhys.36.225
- (18) P.G. de Gennes, Superconductivity of Metals and Alloys, (Advanced Book Program, Perseus Books, New York, N.Y., 1999).
- (19) E. Chabanat, P. Bonche, P. Heenen, J. Meyer, and R. Schaeffer, Nucl. Phys. A 635, 231 (1998). https://doi.org/10.1016/S0375-9474(98)00180-8
- (20) M. Matsuo, Phys. Rev. C 73, 044309 (2006). https://doi.org/10.1103/PhysRevC.73.044309
- (21) M. Matsuo, Y. Serizawa, and K. Mizuyama, Nucl. Phys. A 788, 307c (2007). https://doi.org/10.1016/j.nuclphysa.2007.01.017
- (22) D. J. Dean and M. Hjorth-Jensen, Rev. Mod. Phys. 75, 607 (2003). https://doi.org/10.1103/RevModPhys.75.607
- (23) G. C. Strinati, P. Pieri, G. Röpke, P. Schuck, M. Urban, Phys. Rep. 738, 1 (2018). https://doi.org/10.1016/j.physrep.2018.02.004
- (24) S. Gandolfi, A. Gezerlis, J. Carlson, Ann. Rev. Nucl. Part. Sci. 65, 303 (2015). https://doi.org/10.1146/annurev-nucl-102014-021957
- (25) U. Lombardo and H.-J. Schulze, in Physics of Neutron Star Interiors, edited by D. Blaschke, N. K. Glendenning, and A. Sedrakian, Vol. 578 of Lecture Notes in Physics (Springer, New York, 2001), p.30.
- (26) L. P. Gor‘kov and T. K. Melik-Barkhudarov, Sov. Phys. JETP 13, 1018 (1961).
- (27) F. Barranco, R. A. Broglia, H. Esbensen, and E. Vigezzi, Phys. Rev. C 58, 1257 (1998). https://doi.org/10.1103/PhysRevC.58.1257
- (28) A. Gezerlis, and J. Carlson, Phys. Rev. C 81, 025803 (2010). https://doi.org/10.1103/PhysRevC.81.025803
- (29) T. Abe, and R. Seki, Phys. Rev. C 79, 054002 (2009). https://doi.org/10.1103/PhysRevC.79.054002
- (30) J. W. Negele, and D. Vautherin, Nucl. Phys. A 207, 298 (1973). https://doi.org/10.1016/0375-9474(73)90349-7
- (31) H. Heiselberg, C. J. Pethick, H. Smith, and L. Viverit, Phys. Rev. Lett. 85, 2418 (2000). https://doi.org/10.1103/PhysRevLett.85.2418
- (32) C. J. Pethick and H. Smith, Bose-Einstein Condensation in Dilute Gasses, (Cambridge Univ. Press, Cambridge, 2002).
- (33) S. Gandolfi, A. Yu. Illarionov, S. Fantoni, F.Pederiva, K.E.Schmidt, Phys. Rev. Lett. 101, 132501 (2008). https://doi.org/10.1103/PhysRevLett.101.132501
- (34) W. Satula, J. Dobaczewski, and W. Nazarewicz, Phys. Rev. Lett. 81, 3599 (1998). https://doi.org/10.1103/PhysRevLett.81.3599
- (35) G. F. Bertsch and H. Esbensen, Ann. Phys. (N.Y.) 209, 327 (1991). https://doi.org/10.1016/0003-4916(91)90033-5
- (36) E. Garrido, P. Sarriguren, E. Moya de Guerra, and P. Schuck, Phys. Rev. C 60, 064312 (1999). https://doi.org/10.1103/PhysRevC.60.064312
- (37) T. Papenbrock and G. F. Bertsch, Phys. Rev. C 59, 2052 (1999). https://doi.org/10.1103/PhysRevC.59.2052
- (38) M. Marini, F. Pistolesi, and G. C. Strinati, Eur. Phys. J. B 1, 151 (1998). https://doi.org/10.1007/s100510050165
- (39) The 2016 Atomic Mass Evaluation, http://amdc.in2p3.fr/web/masseval.html http://amdc.in2p3.fr/web/masseval.html