Proximity induced time-reversal topological superconductivity in Bi2Se3 films without phase tuning
Abstract
Many proposals to generate a time-reversal invariant topological superconducting phase are based on imposing a phase difference between the superconducting leads proximitizing a nanostructure. We show that this phase can be induced on a thin film of a topological insulator like Bi2Se3 in proximity to a single s-wave superconductor. In our analysis we take into account the parity degree of freedom of the electronic states which is not included in effective Dirac-like surface theories. We find that the topological phase can be reached when the induced interparity pairing dominates over the intraparity one. Application of an electric field perpendicular to the film extends the range of parameters where the topological phase occurs.
I Introduction
The interest in topological phases of matter and, in particular, in topological superconductors (TSs) has not ceased to grow review . In addition to their fundamental interest, TSs are predicted to host topologically protected Majorana zero modes (MZM) at the edges with potential applications in future quantum technologies QT .
Although topological superconductivity is expected to occur spontaneously in certain compounds like Sr2RuO4 sr2ruo4 ; actual vigorous experimental progress is coming from the side of artificial nanostructures. In particular, clear signatures of MZMs have been demonstrated in hybrid nanostructures combining semiconducting nanowires with strong spin orbit (like InAs or InSb) and conventional superconductors exps-nanowires-1 ; exps-nanowires-2 ; exps-nanowires-3 ; exps-nanowires-4 ; exps-nanowires-5 .
As in the case of other proposals based on arrays of magnetic impurities impurities these platforms constitute a realization of broken-time reversal (symmetry class D) 1D topological superconductivity. Although the time-reversal counterpart or class DIII superconductivity has attracted great theoretical interest oreg-review , its actual realization is still an experimental challenge. The zero energy excitations in this class of TSs are Kramers pairs of Majorana modes. While their braiding properties appear to be path dependent stern ; stern1 , they exhibit other exotic transport tritops-ber ; jose1 and spin kesel ; cam ; B-schaffer-2 ; fractio properties which render them objects of fundamental interest.
Intrinsic DIII superconductivity in two and three dimensional systems has been discussed in the literature (see for instance Refs. zhang ; fu-berg ; Schmalian ) but also in this case most theoretical proposals have been focused on proximitized nanostructures. These, in general, require two basic ingredients: a multichannel or multiband electronic structure and a mechanism for inducing opposite pairing amplitudes on these channels no-go-theorem . These include Rashba nanowires proximitized by a d-wave Wong or an Iron-based superconductor with pairing symmetry Zhang-Kane-Mele ; or two parallel nanowires with interwire pairing Flensberg ; Klinovaja ; Ebisu or subject to opposite Zeeman fields Reeg . Another scenario is spin orbit and many body interactions in proximity with ordinary superconductivity haim ; yuval1 . Induction of the DIII phase on the edge or surface states of a 2D or a 3D topological insulator (TI) has also been considered Fu-Kane ; Santos ; Klinovaja ; Liu ; Schrade ; Black-Schaffer . Refs. Liu ; Black-Schaffer suggest that for the case of a thin 3D TI film reaching the DIII phase requires forming a S/TI/S junction and imposing a -phase difference. These studies are based on effective 2D models describing the surface states on the 3D TI film.
In the present work we propose a new approach for the case of proximitized 3DTI thin films. In contrast to previous works which start from the projected 2D theory, we use a 3D model which keeps track of the parity degree of freedom. We show that the DIII-TS phase may arise naturally by proximity to a single s-wave superconductor when considering the presence of interparity pairing. We further show that the inclusion of an external electric field, breaking inversion symmetry, helps to stabilize this topological phase.
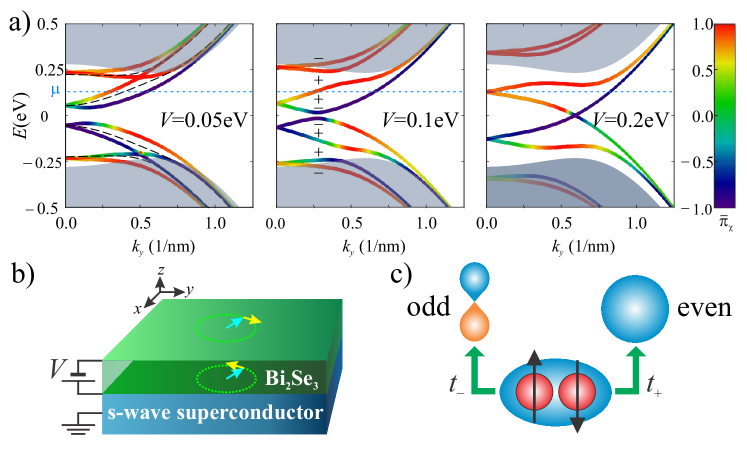
The main ingredients of the proposed mechanism are illustrated in Fig. 1. The surface states of a 3D TI are characterized by a well defined helicity, i.e. they are eigenstates of the helicity operator , where is the wave vector parallel to the surface and are Pauli matrices in spin space kp-Zhang . In addition, these states are also characterized by a certain parity pseudospin, which depends on the surface orientation and on the material. For instance, in films of the Bi2Se3 family grown along the axis, states on opposite surfaces have opposite helicities and opposite parity pseudospin Liu-Zhang . In sufficiently thin films, the surface states corresponding to oposite sides are not fully decoupled but hybridize to some extent Bi2Se3-films ; Niu and the helicity degeneracy can be broken by an electric field perpendicular to the film, as illustrated in Fig. 1(a). Therefore, when one of the surfaces is in contact with a superconductor as in Fig. 1(b), superconductivity is induced into the two surfaces in both parity channels, as well as interparity, as schematically depicted in Fig. 1(c). Interestingly, the interparity component induced on each helical channel tipically have opposite signs. Our goal is to show that for the case of an s-wave superconductor, the TS phase can be reached provided that the interparity component is large enough and inversion symmetry is broken.
II Model for a TI film and proximity effect
The low energy and long wavelength electronic properties of a TI of the Bi2Se3 family can be described by the Hamiltonian introduced in Ref. kp-Zhang in a basis of four states which are combinations of orbitals on the Bi and Se sites with even and odd parities. For analyzing the proximity effect it is convenient to perform a unitary transformation Liu-Zhang ; Silvestrov with respect to the model in Ref. kp-Zhang [see discussion in the Supplementary Material (SM), Ref. supplementary, ], which yields
| (1) | |||||
where parameters , while are Pauli matrices operating in parity space. This Hamiltonian commutes with the helicity operator, leading to the properties of the surface states commented above.
In order to describe the proximitized thin film we now switch into a tight-binding (TB) description of the electronic structure. For this purpose we follow Ref. acero and introduce a cubic lattice with parameter nm oriented along the -axis and consider the Hamiltonian as a long-wavelength expansion of this TB model. We shall consider the case of films of thickness and impose periodic boundary conditions on the directions. In the basis , where creates an electron with parallel momentum on the -layer within the film, parity and spin . The TB model adopts the form where
| (2) |
with . Within this model the eigenstates are again helicity degenerate (with the helicity operator properly extended to the discrete case) but this degeneracy is broken when an electric field along the direction, , is introduced.
To include the effect of induced pairing correlations on the film we consider the Bogoliubov de Gennes (BdG) Hamiltonian, expressed in the basis . It reads
| (3) |
where is the chemical potential, and are Pauli matrices in the particle-hole space. Although this model allows for more general configurations we shall focus in this work in the case depicted in Fig. 1(b), where pairing is induced on the layer only, i.e. . has intra () and inter () parity components,
| (4) |
The pairing potentials depend on the coupling of the TI with the superconductor underneath. As discussed in the SM supplementary , they would typically have the form and , where is the superconductor Fermi level density of states and are hopping parameters coupling the TI orbitals with parity and the superconductor. These parameters may have oposite signs. In particular, when the ordinary superconductor is contacted to the bottom of the film one expects , which implies that has an overall sign with respect to . On the contrary, when the superconductor is contacted to the top surface, and thus and have the same sign.
It should be stressed that the above expressions are fully compatible with time-reversal symmetry. Regarding the size of , while a non-interacting model suggests , the presence of moderate local Coulomb repulsion on the Bi and Se sites would yield the condition which is necessary for stabilizing the DIII-TS phase as we show below.
III Topological invariant
In the limit of weak coupling, the topological character of the proximitized TI film can be fully determined by the normal electronic properties at the Fermi level Zhang-invariant . The topological invariant introduced in Ref. Zhang-invariant is given by
| (5) |
where with denoting complex conjugation, is the time-reversal operator, runs over all bands crossing the Fermi energy, is the number of TRI points enclosed by a band and is the eigenstate on band at the Fermi surface. In TIs of the Bi2Se3 family the only TRI point enclosed by the surface bands is the point so that . On the other hand, due to the gap isotropy Eq. (5) can be evaluated along any direction in the plane.
As a paradigmatic example we shall examine the case . Details on the calculations are presented in the SM supplementary , where we also discuss the peculiar case. The spectrum for consists of four bands with positive energy which, expanded in , are given by
| (6) |
is a band index, , , , with and we have defined the parameters as , and . The bands and their evolution with voltage are shown in Fig 1(a). We focus on a chemical potential as indicated in Fig. 1(a), intersecting the bands with . A non-trivial value of the invariant in the present case (i.e. ) implies simply different signs of the projected pairing in the two helicity channels,
| (7) |
In this expression we have introduced the quantities , and , which are defined from the components of the eigenstates of on the bottom surface, i.e. we have , where and , and are the eigenstates of the helicity operator, so that measures the relative weight of the two parity sector components on the bottom surface. We then see that for having a non-trivial value of the topological invariant, the necessary (however not sufficient) condition is (or equivalently ) having different signs for the two helicities. An analytic expression for is given in supplementary .
As can be observed in Fig. 1(a), the parameter evolves differently along the lowest bands with opposite helicities, which are split due to the action of the electric field. While it remains negative for the band for all values of the chemical potential within the TI gap, in the band it evolves from negative to positive above a certain critical value of the momentum. As a consequence, for a chemical potential within this energy range and depending on the bias potential , the effective pairing of Eq. (V.5) may have different signs on the two helicity bands leading to a non-trivial value of the invariant, provided that, in addition, . (see SM supplementary for further details). In the following we study the occurence of the TS phase as a function of the parameters and which determine the relative size of the intra and interparity pairing. We take as the reference energy.
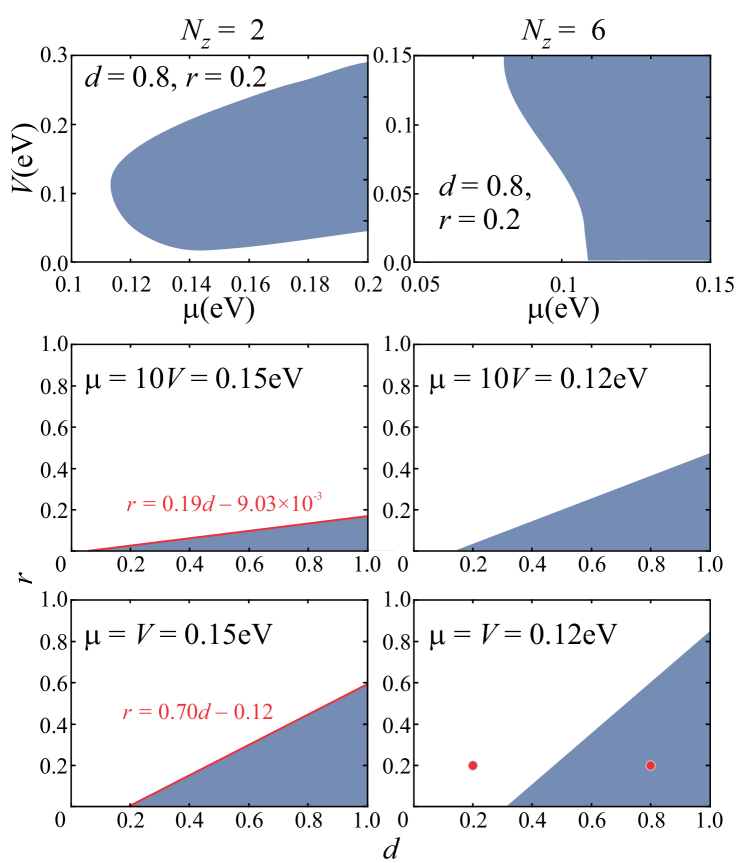
In the Fig. 2 we show the phase diagrams in the and in the planes for the and cases. As can be observed in the upper panels, the topological phase appears for above a certain value which decreases for increasing , corresponding to the closing of the hibridization gap between the surface states. On the other hand should not exceed a value where higher bands start to be populated. In addition we observe that a finite is needed in order to extend the stability of the topological phase in the plane. For small values (middle panels in Fig. 2) the stability is restricted to the regions and but these regions grow when , gradually reaching the optimal case where the TS phase appears for .
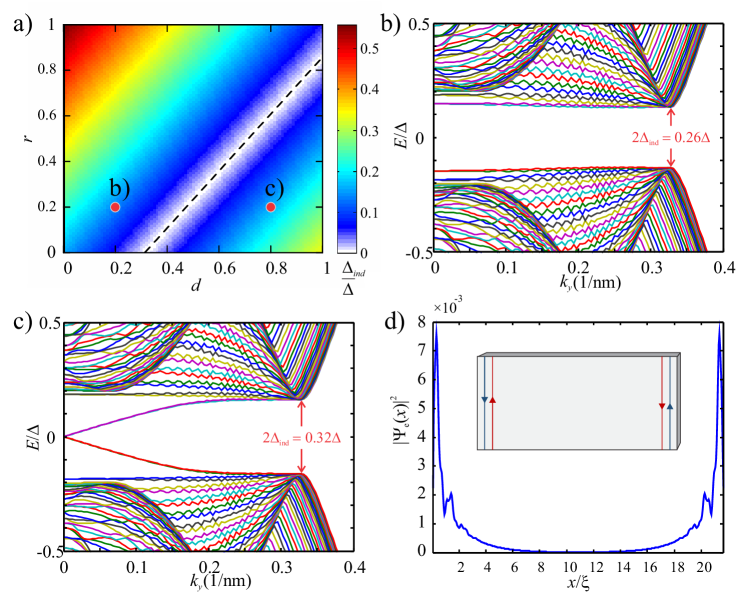
Another important aspect of the proximity effect in the TI film is the size of the induced gap parameter , which is determined by the smaller value of at the Fermi surface. As shown in Fig. 3(a) this quantity drops to zero at the boundary between the trivial and the TS region at the plane, as expected for a topological transition, and increases when departing from this boundary. The size of can be more clearly appreciated in Figs. 3(b,c) where we show the BdG spectrum for a film of finite width in the direction. The two cases correspond to parameters within the trivial and the topological regions, as indicated by the two dots in the lower right panel of Fig. 2 and in Fig. 3(a). In the former case the spectrum exhibits a pair subgap states, droping to zero energy for . The corresponding wavefunction, exhibiting localization at the edges of the film, is plotted in Fig. 3(d). Notice that the localization length is of the order of , which coincides with an effective coherence length . As expected for a TS-DIII phase, these states correspond to Kramers pairs of Majorana modes.
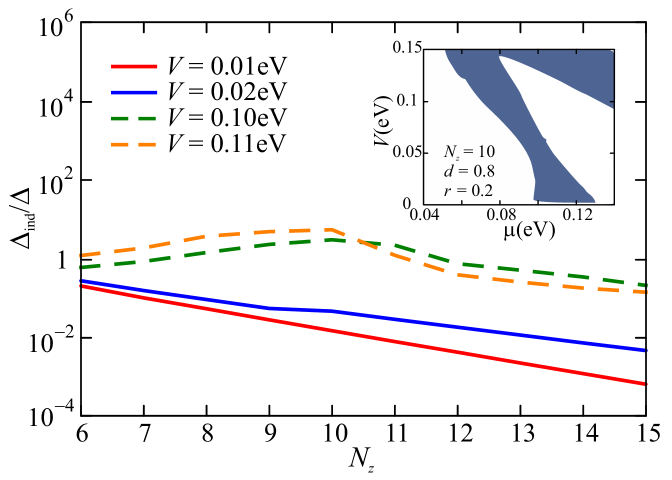
The above results correspond to very thin TI layers with . When is further increased the DIII-TS phase can still be reached for certain parameters values, but the topological region shrinks and the phase diagram starts to exhibit disconnected regions, as shown in the inset of Fig. 4 for . The behavior of the induced gap with depends on the value. While for small values, i.e., outside the topological region, it decreases exponentially with ; for larger it exhibits a non-monotonic behavior, first increasing and eventually decreasing for , as can be observed in the main frame of Fig. 4. This behavior is associated to the fact that higher bands start to cross the chemical potential.
A word of caution is in order regarding the reliability of the precise quantitative predictions of our model, which can nevertheless be trusted at a qualitative level. It is also important to remark that when the film is contacted to a superconductor through both surfaces, thus recovering the inversion symmetry, the topological phase disappears supplementary .
IV Conclusions
We have shown that a time reversal invariant TS phase can be induced on a TI film of the Bi2Se3 family proximitized by a conventional superconductor. In contrast to previous proposals our mechanism does not rely on tuning the phase difference in a S/TI/S junction but arises from the induced interparity pairing which naturally occurs at the S/TI interface. The mechanism requires breaking the spatial inversion symmetry and a certain degree of hybridization between the TI surface states. Application of an electric field perpendicular to the layers helps to stabilize the TS phase for thicker fims in a broader parameter space. Notice that such fields appear spontaneously at the interface between a TI film and its substrate due to charge accumulation Bi2Se3-films .
As a final remark let us mention that proximitized Bi2Se3 films have been analyzed in several experiments, either through Josephson effect goldhaber ; brinkman or by tunnel spectroscopy yang ; finck . We hope that our work could motivate further experimental studies on this type of devices.
Acknowledgments: We thank L. Brey and J. Schmalian for useful comments on the manuscript. This work has been supported by Spanish MINECO through Grants No. FIS2014-55486-P, FIS2017-84860-R and through the “María de Maeztu” Programme for Units of Excellence in R&D (MDM-2014-0377). LA thanks support from CONICET and SECyT from Argentina, as well as the Alexander von Humboldt foundation from Germany. WJH and OEC acknowledge funding from COLCIENCIAS, project No. 110165843163 and doctorate Scholarship 617.
References
- (1) M. Sato and Y. Ando, Topological Superconductors: a review. Rep. Prog. Phys. 80, 076501 (2017).
- (2) S. Vijay, T. H. Hsieh and L. Fu, Majorana Fermion Surface Code for Universal Quantum Computation, Phys. Rev. X 5, 041038 (2015); S. Plugge, A. Rasmussen, R. Egger and K. Flensberg, Majorana Box Qubits, New J. Phys. 19, 012001 (2017).
- (3) A. P. Mackenzie and Y. Maeno, The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing, Rev. Mod. Phys. 75, 657 (2003).
- (4) V. Mourik, K. Zuo, S. M. Frolov, S. R. Plissard, E. P. a. M. Bakkers, and L. P. Kouwenhoven, Signatures of Majorana fermions in in hybrid superconductor-semiconductor nanowire devices, Science 336, 1003 (2012).
- (5) A. Das, Y. Ronen, Y. Most, Y. Oreg, M. Heiblum, and H. Shtrikman, Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions, Nat. Phys. 8, 887 (2012).
- (6) S. M. Albrecht, A. P. Higginbotham, M. Madsen, F. Kuem- meth, T. S. Jespersen, J. Nyg, P. Krogstrup, and C. M. Marcus, Exponential protection of zero modes in Majorana islands, Nature 531, 206 (2016).
- (7) M. Deng, S. Vaitiekenas, E. Hansen, J. Danon, M. Leijnse, K. Flensberg, J. Nygard, P. Krogstrup, and C. Marcus, Majorana bound state in a coupled quantum-dot hybrid- nanowire system, Science 354, 1557 (2016).
- (8) H. J. Suominen, M. Kjaergaard, A. R. Hamilton, J. Sha- bani, C. J. Palmstrm, C. M. Marcus, and F. Nichele, Scalable Majorana Devices, Phys. Rev. Lett. 119, 176805 (2017).
- (9) S. Nadj-Perge, I.K. Drozdov, J. Li, H. Chen, S. Jeon, J. Seo, A. H. MacDonald, B. A. Bernevig, and A. Yazdani, Topological matter. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor, Science 346, 602 (2014).
- (10) For a recent review see A. Haim and Y. Oreg, Time Reversal-Invariant Topological Superconductivity, cond-mat 1809.06863.
- (11) K. Wölms, A. Stern, and K. Flensberg, Local Adiabatic Mixing of Kramers Pairs of Majorana Bound States, Phys. Rev. Lett. 113, 246401 (2014).
- (12) K. Wölms, A. Stern, and K. Flensberg, Braiding properties of Majorana Kramers pairs, Phys. Rev. B 93, 045417 (2016).
- (13) J. Li, W. Pan, B.A. Bernevig, R.M. Lutchyn, Detection of Majorana Kramers pairs using a quantum point contact Phys. Rev. Lett. 117, 046804 (2016).
- (14) C. Schrade, L. Fu, Parity-controlled Josephson effect mediated by Majorana Kramers pairs, Phys. Rev. Lett. 120, 267002 (2018).
- (15) A. Keselman, L. Fu, A. Stern, and E. Berg, Inducing Time-Reversal-Invariant Topological Superconductivity and Fermion Parity Pumping in Quantum Wires, Phys. Rev. Lett. 111, 116402 (2013).
- (16) A. Camjayi, L. Arrachea, A. Aligia and F. von Oppen, Fractional Spin and Josephson Effect in Time-Reversal-Invariant Topological Superconductors, Phys. Rev. Lett. 119, 046801 (2017).
- (17) M. Mashkoori, A. G. Moghaddam, M. H. Hajibabaee, A. M. Black-Schaffer, F. Parhizgar, Impact of topology on the impurity effects in extended s-wave superconductors with spin-orbit coupling, arXiv:1805.11885.
- (18) A. Aligia and L. Arrachea, Entangled end states with fractionalized spin projection in a time-reversal-invariant topological superconducting wire, arXiv:1806.06104.
- (19) X.-L. Qi, T.L. Hughes, S. Raghu, and S.-C. Zhang, Time-Reversal-Invariant Topological Superconductors and Superfluids in Two and Three Dimensions, Phys. Rev. Lett. 102, 187001 (2009).
- (20) L. Fu and E. Berg, Odd-parity topological superconductors: Theory and application to CuxBi2Se3, Phys. Rev. Lett. 105, 097001 (2010).
- (21) Ma. S. Scheurer and J. Schmalian, Topological superconductivity and unconventional pairing in oxide interfaces, Nature Comm. 6, 6005 (2015).
- (22) A. Haim, E. Berg, K. Flensberg, Y. Oreg, No-go theorem for a time-reversal invariant topological phase in noninteracting systems coupled to conventional superconductors, Phys. Rev. B 94, 161110 (2016).
- (23) C. L. M. Wong and K. T. Law, Majorana Kramers doublets in dx2-y2-wave superconductors with Rashba spin-orbit coupling Phys. Rev. B 86, 184516 (2012).
- (24) F. Zhang, C. L. Kane, and E. J. Mele, Time-Reversal-Invariant Topological Superconductivity and Majorana Kramers Pairs Phys. Rev. Lett. 111, 056402 (2013).
- (25) E. Gaidamauskas, J. Paaske, and K. Flensberg, Majorana Bound States in Two-Channel Time-Reversal-Symmetric Nanowire System, Phys. Rev. Lett. 112, 126402 (2014).
- (26) J. Klinovaja, A. Yacoby, and D. Loss, Kramers pairs of Majorana fermions and parafermions in fractional topological insulators, Phys. Rev. B 90, 155447 (2014).
- (27) H. Ebisu, B. Lu, J. Klinovaja and Y. Tanaka, Theory of time-reversal topological superconductivity in double Rashba wires: symmetries of Cooper pairs andAndreev bound states, Prog. Theor. Exp. Phys. 2016, 083I01 (2016).
- (28) C. Reeg, C. Schrade, J. Klinovaja, D. Loss, DIII Topological Superconductivity with Emergent Time-Reversal Symmetry, Phys. Rev. B 96, 161407 (2017).
- (29) Arbel Haim, Anna Keselman, Erez Berg, Yuval Oreg, Time-Reversal Invariant Topological Superconductivity Induced by Repulsive Interactions in Quantum Wires, Phys. Rev. B 89, 220504(R) (2014).
- (30) Arbel Haim, Konrad Wölms, Erez Berg, Yuval Oreg, Karsten Flensberg, Interaction-driven topological superconductivity in one dimension, Phys. Rev. B 94, 115124 (2016).
- (31) L. Fu and C. Kane, Superconducting proximity effect and majorana fermions at the surface of a topological insulator, Phys. Rev. Lett. 100, 096407 (2008).
- (32) L. Santos, T. Neupert, C. Chamon and C. Mudry, Superconductivity on the surface of topological insulators and in two-dimensional noncentrosymmetric materials, Phys. Rev. B 81, 184502 (2010).
- (33) C.-X. Liu Tand B. Trauzettel, Helical Dirac-Majorana interferometer in a superconductor/topological insulator sandwich structure, Phys. Rev. B 83, 220510 (2011).
- (34) C. Schrade, A.A. Zyuzin, J. Klinovaja, and Daniel Loss, Proximity-Induced Josephson Junctions in Topological Insulators and Kramers Pairs of Majorana Fermions, Phys. Rev. Lett. 115, 237001 (2015).
- (35) F. Parhizgar and A. M. Black-Schaffer, Highly tunable time-reversal- invariant topological superconductivity in topological insulator thin films, Scientific Reports 7, 9817 (2017).
- (36) H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Topological insulators in Bi2Se3,Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface, Nature Phys. 5, 438 (2009).
- (37) C.-X. Liu, X.-L. Qi, H. Zhang, X. Dai, Z. Fang, and S.-C. Zhang, Model hamiltonian for topological insulators, Phys. Rev. B 82, 045122 (2010).
- (38) Y. Zhang et al., Crossover of the three-dimensional topological insulator Bi to the two-dimensional limit, Nature Phys. 6, 584 (2010).
- (39) H.-Z. Lu, W.-Yu Shan, W. Yao, Q. Niu and S.-Q. Shen, Massive Dirac fermions and spin physics in an ultrathin film of topological insulator, Phys. Rev. B 81, 115407 (2010).
- (40) P. G. Silvestrov, P. W. Brouwer, and E. G. Mishchenko, Spin and charge structure of the surface states in topological insulators, Phys. Rev. B 86, 075302 (2012).
- (41) Supplementary Information.
- (42) According to Ref. Liu-Zhang appropriate parameters for Bi2Se3, obtained from fits to ab initio calculations are eV, eVÅ , eVÅ, eVÅ2 and eVÅ2.
- (43) S. Acero, L. Brey, W.J. Herrera, and A. Levy Yeyati, Transport in selectively magnetically doped topological insulator wires, Phys. Rev. B 92, 235445 (2015).
- (44) X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Topological invariants for the fermi surface of a time-reversal-invariant superconductor, Phys. Rev. B 81, 134508 (2010).
- (45) J. R. Williams et al., Unconventional Josephson effect in hybrid superconductor-topological insulator devices, Phys. Rev. Lett. 109, 056803 (2012).
- (46) M. Snelder, C.G. Molenaar, Y. Pan, D. Wu, Y. K. Huang, A. de Visser, A. A. Golubov, W.G. van der Wiel, H. Hilgenkamp, M.S. Golden and A. Brinkman, Josephson supercurrent in a topological insulator without a bulk shunt. Supercond. Sci. Technol. 27, 104001 (2014).
- (47) F. Yang et al., Proximity-effect-induced superconducting phase in the topological insulator Bi2Se3. Phys. Rev. B 86, 134504 (2012).
- (48) A. Finck, C. Kurter, Y. Hor and D. Van Harlingen, Phase coherence and Andreev reflection in topological insulator devices. Phys. Rev. X 4, 041022 (2014).
V Supplemental material
Supplemental material: Proximity induced time-reversal topological superconductivity in Bi2Se3 films without phase tuning. Oscar E. Casas Liliana Arrachea William J. Herrera Alfredo Levy Yeyati
V.1 Unitary transformation on the model of Ref. [1]
According to Ref. kp-Zhang the low-energy and long-wavelength electronic properties of Bi2Se3 can be described by a Hamiltonian written in a basis of four states which are combinations of orbitals of Bi and Se with even and odd parities given by
| (8) |
where and and are Pauli matrices operating in different pseudospin spaces. While matrices refer to the P1 and P2 orbitals which are mainly located on the Bi and Se sublattices respectively kp-Zhang , the matrices do not correspond exactly to the real spin but are related to it by Silvestrov
| (9) |
For analyzing proximity induced superconductivity it is convenient to write the system Hamiltonian in a basis where the matrices correspond to the real spin. For this purpose one can perform the following unitary transformation Silvestrov
| (10) |
where is a unitary vector along the axis. Applying this transformation to Hamiltonian (8) for one obtains the model given in Eq. (1) of the main text.
V.2 Origin of intra and inter parity pairing
The description of the superconducting proximity effect used in this work can be considered as the low-energy theory arising from integrating out the degrees of freedom of the proximitized superconductor in the Green’s function formalism. After this integration the proximity effect is encoded in a self-energy stanescu
| (11) |
where , where are the hopping amplitudes from the SC to the parity orbitals on the first layer of the TI, denote the Pauli matrices in particle-hole space, and is the superconductor Green function, which for the BCS case is given by
| (12) |
where is the pairing potential of the parent superconductor and denotes its Fermi level density of states. The parameters and in the main text thus arise from the elements in the limit .
V.3 Limit
The aim of this section is to show that the model we are considering contains the ingredients for topological superconductivity even in the extreme limit of a single monolayer in proximity to an ordinary superconductor.
We consider the Hamiltonian of Eq. (2) of the main text with
| (13) |
where we have defined . We introduce the Nambu spinor , where is a spinor of the basis of .
The matrix for the Bogoliubov de Gennes Hamiltonian of the monolayer of the Hamiltonian of Eq. (3) of the main text with induced superconductivity reads
We can now introduce a rotation with respect to the axis in the parity space such that and and focus on the case with . The resulting Hamiltonian reads
| (15) | |||||
We see that along the directions and this Hamiltonian has an identical structure as the 1D model ladder model introduced by Keselman et al in Ref. kesel, , upon identifying the two parity projections (even, odd) with the two legs of the ladder Hamiltonian of that paper. Importantly, the Hamiltonian of Eq. (15) has different signs of the pairing and of the spin orbit interaction in the two different parity channels of the rotated basis. Therefore, we know from Ref. kesel, that it hosts a topological phase.
V.4 Model and symmetries for
Here we consider the case , for which we can obtain some analytical results, specially for the topological invariant. The two layers are labeled with the indices (up) and (down). The matrix for the model Hamiltonian can be written as follows
where , , are Pauli matrices in the surface space, and , while is the scalar potential, representing a potential difference of between the opposite surfaces of the film.
We introduce the discretized version of the helicity operator . The Hamiltonian (V.4) commutes with this operator, . Thus, the states can be labeled with , which correspond to the two eigenstates of the helicity operator , , with .
The Hamiltonian (V.4) is time-reversal invariant, i.e. . For it also has inversion symmetry with . Therefore, the eigenstates with eigenenergies satisfy the following properties
| (17) | |||||
| (18) |
and for
| (19) | |||||
| (20) |
We also consider the Bogoliubov de Gennes Hamiltonian for the bilayer system in proximity to superconductors in the most general case, where the induced pairing potential has different amplitudes in the two layers, . The corresponding matrix reads
| (21) |
with
where and , where the pairings in the parity basis are given by .
In addition to time-reversal, this model Hamiltonian exhibits charge conjugation, with , and chiral symmetry with . This means that this system belongs to the Altland-Zirnbauer class DIII. For and , it has, in addition, inversion symmetry with .
V.5 topological invariant
We now consider the Hamiltonian of Eq. (V.4) and focus on the direction . The eigenstates of are expressed as , with and . From the equation we get that the components of the spinor , are real constants satisfying
where , , , , , . The energy bands are given by the expressions
Here defines a band index and we have introduced the definition . Fig.1 (a) of the main text illustrates the behavior of the ratios for different values of the potential . Notice that for the bands are degenerate in helicity. In fact, for the factor and then do not depends on .
We now focus on the superconductivity induced only in the surface, , . This implies , and in Eq.(21). By calculating the expectation value of with the surface states we obtain Eq. (7) in the main text, i.e.
Here, we have defined as well as the factor
| (25) |
As discussed in the main text, the invariant of Eq. (5) has a non-trivial value when the quantity (V.5) has different signs for the bands at the Fermi surface. In turn, a necessary condition is that has opposite signs for the two helicities. If we have for one band (which warrants ) the topological phase may exist in a range of parameters satisfying and for the opposite helicity. Notice that depends only on the intrinsic parameters, as well as on and , while depends also on the pairing parameters and . Hence, the general strategy we follow to define the existence of the topological phase is to identify the range of and for which
| (26) |
Notice that the maximum value for occurs for and corresponds to . In such a case, the change of sign in Eq. (V.5) occurs for .
Interestingly, for , there are two limits where Eq. (V.5) simplifies significantly and we can analytically determine the conditions for a topological phase. (i) For , the explicit calculation of the different coefficients casts , excluding the possibility of a topological phase. (ii) For we have
| (27) |
Focusing on , we see that , while for . Fixing the chemical chemical potential to satisfy this condition for and , we find the range of for the topological phase. Then, given a particular within such range, we can find the conditions to be satisfied for leading to .
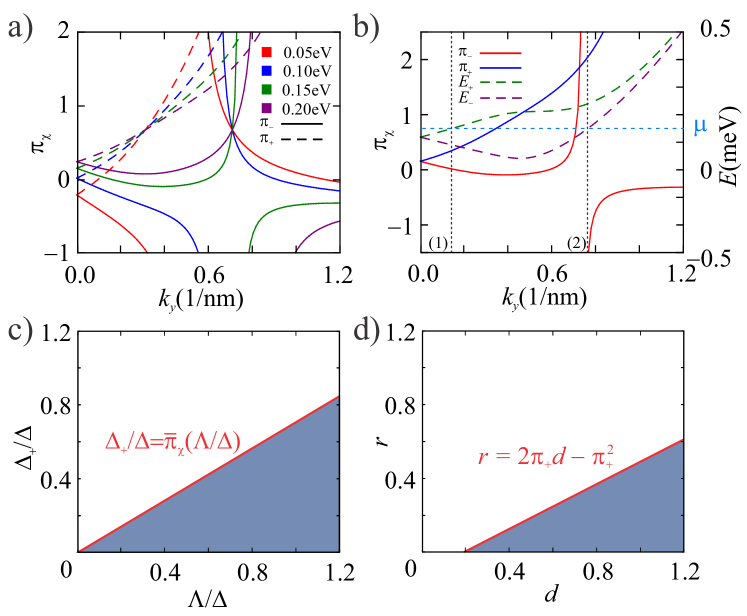
In the more general case, it is difficult to draw conclusions on the behavior of on the basis of the analytical expressions, but the procedure is similar than above. Examples are shown in Fig. 5 of this Suplemental Material (SM). In panels (a) and (b) Fig. 5 the behavior of as a function of is shown for different values of . We see that for most of the cases (notice that only in the case with eV this is not satisfied close to ). Instead shows a discontinuity with a vertical asymptote at , which implies a change of sign at . In panel (b) we focus on eV and we superimpose the plots of the energy bands. In this way, we can easily identify the portions of the dispersion relation where the conditions and are simultaneously satisfied for a certain value of the chemical potential .
Panels (c) and (d) in Fig. 5 correspond to the phase diagram in the space of the pairing parameters and for eV. The panel (c) corresponds to and the boundary separating the topological and non-topological phases is defined from the conditions of Eq. (26), which in this case is given by . In the panel (b) we illustrate the case with . As in the main text, we define and . The boundary between the topological and non-topological phases in this case is given by .
For the pairing only in the up-surface we can repeat the previous analysis by changing , . Finally, in the case of symmetric junction with two identical superconductors contacting the TI film and in the absence of an electric field, the system recovers the inversion symmetry and the topological phase is lost since the contribution to the topological invariant from both surface states has the same sign. While a finite electric field does break this symmetry it does not lead to a robust topological phase, at least for small values, when both surfaces are contacted to a superconductor.
References
- (1) C.-X. Liu, X.-L. Qi, H. Zhang, X. Dai, Z. Fang, and S.-C. Zhang, “Model hamiltonian for topological insulators”, Phys. Rev. B 82, 045122 (2010).
- (2) P. G. Silvestrov, P. W. Brouwer, and E. G. Mishchenko, “Spin and charge structure of the surface states in topological insulators”, Phys. Rev. B 86, 075302 (2012).
- (3) P. Sitthison and T. Stanescu, “Robustness of topological superconductivity in proximity-coupled topological insulator nanoribbons”, Phys. Rev. B 90, 035313 (2014).
- (4) Anna Keselman, Liang Fu, Ady Stern, Erez Berg, “Inducing time reversal invariant topological superconductivity and fermion parity pumping in quantum wires”, Phys. Rev. Lett. 111, 116402 (2013)