Pseudo-spin rotation symmetry breaking by
Coulomb interaction terms in spin-orbit coupled systems
Abstract
By transforming from the pure-spin-orbital () basis to the spin-orbital entangled pseudo-spin-orbital basis, the pseudo-spin rotation symmetry of the different Coulomb interaction terms is investigated under SU(2) transformation in pseudo-spin space. While the Hubbard and density interaction terms are invariant, the Hund’s coupling and pair-hopping interaction terms explicitly break pseudo-spin rotation symmetry systematically. The form of the symmetry-breaking terms obtained from the transformation of the Coulomb interaction terms accounts for the easy - plane anisotropy and magnon gap for the out-of-plane mode, highlighting the importance of mixing with the nominally non-magnetic =3/2 sector, and providing a physically transparent approach for investigating magnetic ordering and anisotropy effects in perovskite () and other pseudo-spin compounds.
pacs:
75.30.Ds, 71.27.+a, 75.10.Lp, 71.10.FdI Introduction
Arising from a novel interplay between crystal field, spin-orbit coupling (SOC) and intermediate-strength Coulomb interactions, the emergent quantum states which essentially determine the electronic and magnetic properties of the iridium based transition-metal oxides involve correlated motion of electrons in spin-orbital entangled states.krempa_AR_2014 ; rau_AR_2016 ; bertinshaw_AR_2018 In the spin-orbit Mott insulator with configuration, electronic states near the Fermi energy have dominantly =1/2 character, and important magnetic properties such as in-plane canted antiferromagnetic (AFM) order and magnon excitations have been extensively discussed in terms of the effectively single pseudo orbital (=1/2) picture.kim_PRL_2008 ; kim_Science_2009 ; watanabe_PRL_2010 ; kim1_PRL_2012 Finite-interaction and finite-SOC effects are responsible for the strong zone-boundary magnon dispersion measured in resonant inelastic X-ray scattering (RIXS) studies, highlighting the observable effect of mixing between =1/2 and 3/2 sectors.iridate_one
The Dzyaloshinskii-Moriya (DM) and pseudo-dipolar (PD) anisotropic interactions in the sector, although weakly affected by the tetragonal splitting,kim_PRL_2012 are not the source of true anisotropy in , as they yield pseudo-spin canting with no magnon gap due to compensation. True anisotropy has been ascribed to the Hund’s coupling term () using strong-coupling expansion (including virtual excitations to =3/2 states) and numerical self-consistent calculation.jackeli_PRL_2009 ; igarashi_PRB_2013 ; perkins_PRB_2014 ; vale_PRB_2015 ; igarashi_JPSJ_2014 While Coulomb interactions were considered within the pure-spin-orbital basis ( orbitals, pure spins) in above approaches, their treatment within a pseudo-spin-orbital basis, and the role of weak magnetism in the other two pseudo orbitals (=3/2 sector) on the -induced easy-plane magnetic anisotropy and magnon gap ( meV), as measured in recent resonant inelastic X-ray scattering (RIXS) studies,kim_NATCOMM_2014 ; pincini_PRB_2017 ; porras_PRB_2019 have not been elucidated. Furthermore, the pseudo-spin-orbital based approach can allow for a unified study of both intra-orbital (magnon) and inter-orbital (spin-orbit exciton) excitations within a single formalism.
Magnetic anisotropy is generally associated with spin rotation symmetry breaking. Therefore, a general pseudo-spin rotation symmetry analysis of the different Coulomb interaction terms, treating all three pseudo orbitals on the same footing, can provide additional insight into the origin of true magnetic anisotropy in arising from the interplay of spin-orbital entanglement and Coulomb interaction. Due to the spin-orbital entanglement, the same pseudo-spin rotation for all three pseudo orbitals () corresponds to different pure-spin rotations for the three pure () orbitals. This follows directly from the relation between the fermionic field operators in the pure-spin-orbital basis () and pseudo-spin-orbital basis (), where the Pauli matrices corresponding to the three pure orbitals . The same SU(2) transformation for all three pseudo orbitals corresponds to different SU(2) transformations for the three pure orbitals due to the orbital dependence of .
Therefore, the question of how the different Coulomb interaction terms transform under same pseudo-spin rotation for all three pseudo orbitals assumes importance. In other words, while all Coulomb interaction terms are invariant under same pure-spin rotation for all three pure orbitals, does this invariance hold under same pseudo-spin rotation in the pseudo-spin-orbital basis? Pseudo-spin rotation symmetry breaking by any Coulomb interaction term would imply true magnetic anisotropy and gapped magnon spectrum.
In this paper, we will show that while the Hubbard and density interaction terms do preserve pseudo-spin rotation symmetry, the Hund’s coupling () and pair-hopping () interaction terms explicitly break this symmetry systematically. This symmetry breaking results in (on-site) anisotropic interactions between moments in the =1/2 and =3/2 sectors, highlighting the importance of the weak magnetism in the nominally filled =3/2 sector as well as the mixing between the two sectors. Magnetic anisotropy will not survive in the large SOC limit when the two sectors become effectively decoupled. The physically transparent approach for investigating magnetic ordering and anisotropy effects will be illustrated for the perovskite compound , where the sign of =3/2 sector moments directly yields easy - plane anisotropy.
The structure of this paper is as below. After introducing the transformation between the pure-spin-orbital and pseudo-spin-orbital bases in Sec. II, a symmetry analysis of the individual Coulomb interaction terms is carried out in Sec. III, where the Hund’s coupling and pair hopping interaction terms are shown to explicitly break pseudo-spin rotation symmetry. The transformed Coulomb interaction terms are obtained in Sec. IV, explicitly showing that the symmetry breaking terms account for the easy - plane anisotropy in , as illustrated for the ground state energy in Sec. V, and for magnon excitations and anisotropy gap in Sec. VI. Comparison with an independent orbital based approach is discussed in Sec. VII, which provides confirmation of the above symmetry analysis and also illustrates the significant simplification achieved in the pseudo-spin-orbital basis. After a critical comparison (Sec. VIII) of different but equivalent approaches for studying magnetic anisotropy in , some conclusions are finally presented in Sec. IX.
II Pseudo-spin-orbital basis
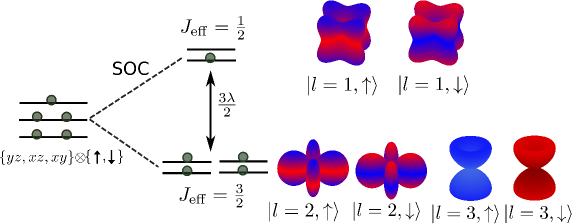
Due to large crystal-field splitting (3 eV) in the octahedra, low-energy physics in iridates is effectively described by projecting out the empty levels which are well above the levels. Spin-orbit coupling (SOC) further splits the states into =1/2 doublet () and =3/2 quartet (), with an energy gap of (Fig. 1). Nominally, four of the five electrons fill the =3/2 states, leaving one electron for the =1/2 sector, rendering it magnetically active in the ground state.
In the (,,,,) basis, the SOC Hamiltonian becomes block diagonal with two [] blocks. There is no mixing between the () and () sectors, which can therefore be treated as pseudo spins and for the three doubly degenerate eigenstates (pseudo orbitals).watanabe_PRL_2010 Corresponding to the three Kramers pairs above, the pseudo-spin-orbital basis states for the three pseudo orbitals (), with pseudo spins () each, have the form:
| (1) |
where , , are the t2g basis states and the signs correspond to spins . The coherent superposition of different-symmetry orbitals, with opposite spin polarization between / and levels implies spin-orbital entanglement, and also imparts unique extended 3D shape to the pseudo-orbitals , as shown in Fig 1. The pseudo-spin dynamics in iridate heterostructures are gaining interest as their magnetic properties are much more sensitive to structural distortion compared to pure spin systems due to spin-orbital entanglement.meyers_SREP_2019 ; mohapatra_PRB_2019
Taking the conjugate to express the above basis transformation in terms of the and states, and rewriting in terms of the corresponding fermionic field operators:
| (2) |
involving the annihilation operators for the pseudo orbitals (, ) and the orbitals (, ), we obtain (using Pauli matrices):
| (3) |
Inverting the above transformation yields the basis states represented in terms of the pseudo-spin-orbital basis states:
| (4) |
The above equations are convenient for transforming the hopping and Coulomb interaction terms to the pseudo-spin-orbital basis, and can be expressed in the compact form:
| (5) |
where for the three orbitals , respectively, and the (real) transformation coefficients are explicitly shown in Eq. (4).
III Pseudo-spin rotation symmetry breaking
We consider the on-site Coulomb interaction terms in the basis ():
| (6) | |||||
including the intra-orbital and inter-orbital density interaction terms, the Hund’s coupling term , and the pair hopping interaction term =. Here and are the creation and annihilation operators for site , orbital , spin , the density operator , the total density operator , and . All interaction terms above are SU(2) invariant and thus possess pure-spin rotation symmetry. In the following, we consider the transformation of individual Coulomb interaction terms to the pseudo-spin-orbital basis using Eq. (5), and examine their SU(2) transformation behavior in pseudo-spin space.
III.1 Total density operator
For the total density operator (for site ), we obtain using Eq. (5):
| (7) |
where we have used and . Now, under the SU(2) transformation in pseudo-spin space (same for all three pseudo orbitals ):
| (8) |
the terms are invariant, and the total density operator is therefore SU(2) invariant. Therefore, the density interaction terms () in Eq. (6) and the Hubbard interaction terms () (using ) are SU(2) invariant and possess spin rotation symmetry in pseudo-spin space.
III.2 Pair hopping interaction term
For the pair hopping interaction term (for site ), we obtain:
| (9) | |||||
which is SU(2) invariant and possesses spin-rotation symmetry in pure-spin space. However, SU(2) invariance is lost in pseudo-spin space, as shown below. Again, using Eq. (5) to transform to the pseudo-spin-orbital basis, we obtain:
| (10) |
where we have taken , to illustrate the operations with Pauli matrices. Now, under the SU(2) transformation in pseudo-spin space (Eq. 8), the last term in Eq. (10):
| (11) |
showing that is not SU(2) invariant. The pair hopping interaction term therefore explicitly breaks pseudo-spin rotation symmetry.
III.3 Hund’s coupling term
For this term involving the pure-spin rotationally symmetric interaction , we consider the spin density operator (for site ), and obtain using Eq. (5):
| (12) |
which transforms under the SU(2) transformation (Eq. 8) to:
| (13) |
We now consider the term in brackets above for the case ( orbital) and represent it in terms of a rotation operation in spin space:
| (14) |
where
| (15) |
shows the spin rotation by the rotation matrix corresponding to the SU(2) transformation , and
| (16) |
is the rotation matrix corresponding to rotation about the axis.
Similarly, for the operator with ( orbital), we will obtain the product . Therefore, the interaction term will yield the matrix product:
| (17) |
where is the transpose of and we have used for the diagonal matrix. Finally, since
| (18) |
as , the Hund’s coupling term is not pseudo-spin SU(2) invariant and therefore does not possess pseudo-spin rotation symmetry.
The above symmetry analysis shows that the Hund’s coupling and pair hopping interaction terms explicitly break pseudo-spin rotation symmetry. It is important to note here that the spin rotation symmetry is broken systematically. In other words, it is broken for each term in involving the summations over and for and in Eq. (12), and similarly for the pair hopping interaction term in Eq. (10).
IV Transformed Coulomb interaction terms
In the following, we illustrate the transformation of the different Coulomb interaction terms to the pseudo-spin-orbital basis, starting with =1 (=1/2) sector of the intra-pseudo-orbital interaction terms. Similar transformation to the basis has been discussed recently, focussing only on the density interaction terms.martins_JPCM_2017 Considering first the pair-hopping interaction term (Eq. 9), and retaining only the ====1 terms (indicated by below), we obtain:
| (19) | |||||
Similarly, for the Hund’s coupling term in Eq. (6), we obtain:
| (23) | |||||
as the product is identical for all three orbital pairs, and for the rotation matrices (Eq. 16), we have . Although the pair-hopping and Hund’s coupling interaction terms generally break pseudo-spin rotation symmetry, within the magnetically active =1 (=1/2) sector, they individually yield classically isotropic terms of the form . This follows from the special symmetry within this sector, as reflected by the identical coefficients for all three orbitals for (Eq. 4).
Finally, from the remaining term (in the term of Eq. 6), again retaining only the term, we obtain (using Eq. 7 for site ):
| (24) | |||||
where we have used and . Collecting all the interaction terms resulting from the pair-hopping, Hund’s coupling, and density interaction terms corresponding to , as obtained in Eqs. 19, 23, 24, yields an exact cancellation.
Similarly, considering the other two intra-pseudo-orbital cases () in the sector, we obtain from the three explicitly interaction terms:
| (25) |
explicitly showing the symmetry breaking contributions from the pair-hopping and Hund’s coupling interaction terms, as expected from the SU(2) transformation analysis in Sec. III, in the absence of the special symmetry in the sector. However, since for all three components of quantum spin operators , there is no true magnetic anisotropy even if classically anisotropic terms such as are present, as in Eq. (25).
Substituting in Eq. (25) yields an exact cancellation of the three explicitly interaction terms in the sector also. Therefore, the Hubbard like (or equivalently ) intra-pseudo-orbital interaction terms in all three sectors result only from the and terms in Eq. (6). Using similar analysis as above, and dropping one-particle density terms as in Eq. (24), one obtains (for site ):
| (26) |
From the above discussion it follows that true magnetic anisotropy results only from the inter-orbital anisotropic interaction terms such as with . Including inter-pseudo-orbital cases such as =, = and =, = in Eqs. (19) and (23), and keeping all interaction terms relevant for the present study (Hubbard, Hund’s coupling, and density), we obtain (for site ):
| (27) | |||||
where and are the spin and charge density operators. Using the spherical symmetry condition (=-), the transformed interaction Hamiltonian (27) simplifies to:
| (28) | |||||
In the above equation, the Hubbard-like terms , the Hund’s-coupling-like term , and the density terms , are all invariant under pseudo-spin rotation and the corresponding SU(2) transformation . Therefore, only the interaction terms and between moments in the =1/2 and =3/2 sectors are responsible for the magneto-crystalline anisotropy in , highlighting the importance of the weak magnetism in the nominally filled =3/2 sector due to the mixing between the two sectors. Magnetic anisotropy will not survive in the large SOC limit when the two sectors become effectively decoupled. As shown below, an easy - plane anisotropy is obtained from the dominant term () due to opposite sign of =3/2 sector moment.
V Easy x-y plane anisotropy
We consider the various interaction terms in Eq. (28) in the Hartree-Fock (HF) approximation, focussing on the staggered field terms corresponding to () ordered AF state on the square lattice. For general ordering direction with components = , the staggered field term for sector in the pseudo-orbital basis is given by:
| (29) |
where , for the two sublattices A/B, and the staggered field components are self-consistently determined from:
| (30) |
in terms of the staggered pseudo-spin magnetization components . In practice, it is easier to choose set of and self-consistently determine the Hubbard-like interaction strengths such that and using Eq. (30). The interaction strengths are related by .
Transforming the staggered-field term back to the three-orbital basis , and including the crystal field, SOC and band terms,watanabe_PRL_2010 we have considered in our band structure and spin fluctuation analysis, where
| (31) |
in the composite three-orbital, two-sublattice basis. The crystal field induced tetragonal splitting is included as the orbital energy offset from the degenerate orbitals. The different hopping terms in Eq. (31) connecting the same () and opposite () sublattice(s) are given by:
| (32) |
Here , , are respectively the first, second, and third neighbor hopping terms for the orbital. For the () orbital, and are the NN hopping terms in and directions, respectively. Mixing between and orbitals is represented by the NN hopping term . We have taken values of the tight-binding parameters (, , , , , , , ) = (1.0, 0.5, 0.25, 1.028, 0.167, 0.2, -0.7, 1.35) in units of , where the energy scale = 280 meV. Using above parameters, the calculated electronic band structure shows AFM insulating state and mixing between pseudo-orbital sectors.watanabe_PRL_2010 ; iridate_one
For the band dispersion terms in Eq. (31) and henceforth, we have used the crystal (global) coordinate axes referred to as for convenience. The spin coordinate axes are chosen to align with the crystal axes. If required, a site-dependent spin rotation allows one to transform back to the local spin coordinate axes common with the octahedral axes due to SOC.
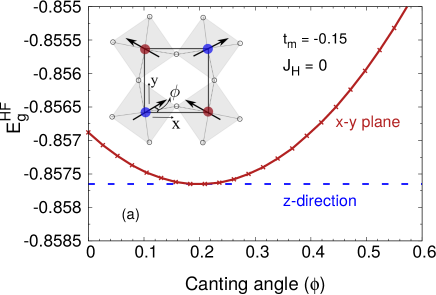
Canted AFM state
The octahedral-rotation-induced orbital mixing hopping term () between and orbitals generates PD () and DM [] anisotropic interactions in the strong coupling limit.iridate_one However, the AFM-state energy is invariant with respect to change of ordering direction from axis to - plane provided spins are canted at the optimal canting angle, thus preserving the gapless Goldstone mode. Fig. 2(a) shows the variation of AFM-state energy with canting angle () for ordering in the - plane. The energy minimum at the optimal canting angle is exactly degenerate with the energy for -direction ordering. This absence of true anisotropy in due to octahedral rotation alone is consistent with the general gauge transformation analysis showing that the spin-dependent hopping terms arising from the orbital-mixing terms in the three-orbital model can be gauged away.
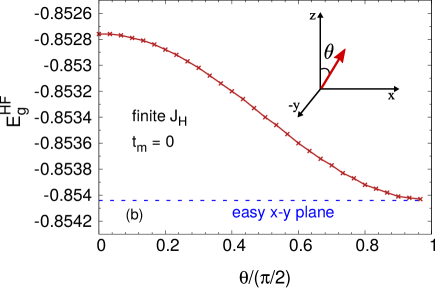
-induced easy-plane anisotropy
The Hund’s-coupling-induced easy-plane magnetic anisotropy is explicitly shown in Fig.2(b) by the variation of AFM-state energy with polar angle corresponding to staggered field orientation in the - plane, with and . Here represents the spin-rotationally-symmetric part of the staggered field and is the symmetry-breaking term, as seen from Eq. (30). We have taken =0.9, =, and the orbital mixing hopping term has been set to zero for simplicity. Converting from energy per state as shown in Fig.2 to simply energy per site (10 occupied states for each ), yields the magnetic anisotropy energy , which is comparable to the magnitude. The simplified analysis presented in this section, with staggered field only for the =1 orbital, serves to explicitly illustrate the magnetic anisotropy features within our three-band-model calculation.
VI Magnon excitations and anisotropy gap
In view of the Hund’s-coupling-induced easy - plane anisotropy as discussed above, we consider the -ordered AFM state. The magnon propagator corresponding to transverse spin fluctuations should therefore yield one gapless mode ( direction) and one gapped mode ( direction). Accordingly, we consider the time-ordered magnon propagator:
| (33) |
involving the transverse components of the pseudo-spin operators and for pseudo orbitals and at lattice sites and .
In the random phase approximation (RPA), the magnon propagator is obtained as:
| (34) |
where the bare particle-hole propagator:
| (35) |
was evaluated in the composite spin-orbital-sublattice basis (2 spin components 3 pseudo orbitals 2 sublattices A,B) by integrating out the fermions in the ordered state. Here and are the eigenvalues and eigenvectors of the Hamiltonian matrix in the pseudo-orbital basis, the indices correspond to the orbital-sublattice subspace, and the superscript refers to particle (hole) energies above (below) the Fermi energy. The amplitudes were obtained by projecting the states in the three-orbital basis on to the pseudo-orbital basis states corresponding to the and sector states, as given below:
| (36) |
in terms of the amplitudes in the three-orbital basis .
The rotationally invariant Hubbard- and Hund’s coupling-like terms having the form are diagonal in spin components (). The on-site Coulomb interaction terms are also diagonal in the sublattice basis (). The interaction matrix in Eq. (34) is therefore obtained as:
| (37) |
in the pseudo-orbital basis. While the first interaction term above preserves spin rotation symmetry, the second interaction term (corresponding to the terms in Eq. 28) breaks rotation symmetry and is responsible for easy - plane anisotropy. The spin wave energies are calculated from the pole condition of Eq. 34, where are the eigenvalues of the matrix. The matrix was evaluated by performing the sum over the 2D Brillouin zone divided into a 300 300 mesh.
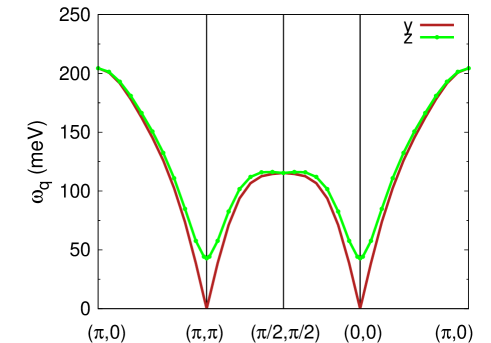
The calculated magnon energies in the -ordered AFM state are shown in Fig. 3. Here we have taken staggered field values in units of , which ensures self-consistency for all three orbitals, with the given relations ==+. Using the calculated sublattice magnetization values =(0.65,0.005,-0.038), we obtain =(0.80,0.83,0.83) eV, which finally yields =+=0.93 eV for =0.1 eV.
The magnon dispersion clearly shows the Goldstone mode and the gapped mode, corresponding to transverse spin fluctuations in the and directions, respectively. The easy - plane anisotropy arising from Hund’s coupling results in energy gap meV for the out-of-plane () mode. The two modes are degenerate at and . The excitation energy at is approximately twice that at , and the strong zone-boundary dispersion in this iridate compound was ascribed to finite- and finite-SOC effects.iridate_one The calculated magnon dispersion and energy gap are in very good agreement with RIXS measurements.kim1_PRL_2012 ; kim_NATCOMM_2014 ; pincini_PRB_2017 ; porras_PRB_2019
The electron fillings in the different pseudo orbitals are obtained as . Finite mixing between the =1/2 and 3/2 sectors is reflected in the small deviations from ideal fillings (1,2,2) and also in the very small magnetic moment values for as given above, which play a crucial role in the expression of magnetic anisotropy and magnon gap in view of the anisotropic interaction terms in Eq. (28). The values =0.38 eV, =0.93 eV, and =0.1 eV taken above lie well within the estimated parameter range for .igarashi_PRB_2014 ; zhou_PRX_2017
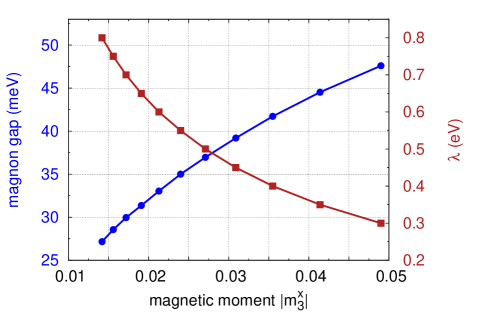
We have investigated the crucial role of the small =3/2 sector magnetic moment on the magnon gap by studying the variation with SOC strength which effectively controls the mixing between =1/2 and 3/2 sectors. Fig. 4 shows that the magnon gap sharply increases with the dominant magnetic moment , highlighting the finite-SOC effect on the experimentally observed out-of-plane magnon gap in . The opposite sign of the magnetic moment as compared to (due to spin-orbital entanglement) plays a vital role in the easy-plane anisotropy. It should be noted that the tetragonal splitting weakly affects the magnon gap through the =3/2 sector magnetic moments.
The magnon gap in Fig. 3 is related to the anisotropy term (see discussion of Fig. 2), and we consider here an analytical expression relating the two which can be derived for a simple model. For the anisotropic Hubbard model,chatterji_PRB_2007 using the spin fluctuation analysis for the AFM state on the square lattice,singh_PRB_1990 we obtain:
| (38) |
in the strong coupling limit ), where , and is the anisotropy term included in the Hubbard model. With (as in Fig. 2(b) discussion) and for simplicity, the ratio is obtained as , which is in good agreement with Fig. 3. It should be noted that a magnon gap of meV (one-tenth of that in Fig. 3) would correspond to an anisotropy term (one-hundredth of above), which is about 0.03 meV using the hopping energy scale meV.
VII Comparison with pure orbital based approach
A fully self-consistent approach within the pure () orbital basis, wherein all orbital off-diagonal spin and charge condensates are included (along with the diagonal condensates) in the Coulomb interaction contributions, has been applied recently to the compound with electron filling to investigate the complex interplay due to intimately intertwined roles of SOC, Coulomb interactions, and structural distortions.ruthenate_one We discuss below the relevant results obtained by extending this approach to the compound with .
| (s) | ||||
|---|---|---|---|---|
| (A/B) | 0.24 | 0.0 | 0.0 | 1.62 |
| (A/B) | 0.24 | 0.0 | 0.0 | 1.62 |
| (A/B) | 0.18 | 0.0 | 0.0 | 1.75 |
| (s) | ||||
|---|---|---|---|---|
| (A/B) | 0.69 | 0.0 | 0.0 | 1.04 |
| (A/B) | 0.006 | 0.0 | 0.0 | 1.99 |
| (A/B) | 0.023 | 0.0 | 0.0 | 1.97 |
Most importantly, we have explicitly confirmed the induced easy-plane anisotropy. The anisotropy is completely absent when =0 even for finite , and the fully self consistent calculation (with octahedral rotation turned off for simplicity) yields degenerate solutions corresponding to arbitrary orientation of the (=1) pseudo-spin moment, confirming that finite is not the source of any anisotropy. Moreover, we do not find any indication of easy-axis anisotropy within the basal plane even in the combined presence of Hund’s coupling (), octahedral rotation (), and tetragonal distortion (). When a small octahedral tilting about crystal axis is included, we obtain easy-axis anisotropy along crystal axis and pseudo-spin canting in the direction, which can be understood in terms of the induced DM interaction resulting from the interplay between octahedral tilting and SOC.ruthenate_one
The simplicity in the pseudo orbital basis is illustrated by comparing the magnetization and density values for the pure and pseudo orbitals. The projected amplitudes (Eq. 36) were used to convert from pure to pseudo orbitals. The results are presented in Table I, showing the much simpler structure in the pseudo orbital basis, with only =1 sector magnetically active and nearly nominal density values. Furthermore, while the orbital off-diagonal condensates in the pure orbital basis are finite and yield the Coulomb SOC renormalization, all off-diagonal condensates in the pseudo orbital basis were found to be negligible, which is expected as the SOC term is diagonal. The Coulomb renormalized SOC gap in this basis is directly obtained from the orbital diagonal terms.mohapatra_JMMM_2020 The reduced value for =3 in Table I compared with the previous section (see Fig. 4) is consistent with the Coulomb enhanced SOC value (from to 0.6 eV) in the fully self consistent calculation.
VIII Discussion
Finally, a critical comparison with other approaches for studying magnetic anisotropy in is presented below. In Ref. [10], the octahedral rotation induced PD and DM terms were considered as the dominant anisotropic interactions, which were shown to be gauged out by a site-dependent rotation of the spin operators (), resulting in no true magnetic anisotropy in the absence of Hund’s coupling. After including the induced corrections, the resulting anisotropic interaction terms were obtained as:
| (39) |
in terms of the rotated spin operator , where the sign corresponds to bond along the direction. Presence of tetragonal distortion was found to affect the coefficient .
Together with the Heisenberg AFM interaction, the first term with leads to easy plane magnetic ordering and magnon gap for out-of-plane fluctuations, whereas the much smaller easy-axis anisotropy and magnon gap for in-plane fluctuations were ascribed to the second term (). In Ref. [17], the large (40 meV) magnon gap measured for out-of-plane fluctuations was explained in terms of the above induced anisotropy term , although was not explicitly mentioned in the very brief discussion, as the main focus was on resolving the small ( 3 meV) magnon gap corresponding to the easy-axis anisotropy and basal-plane fluctuations via high-resolution RIXS and inelastic neutron scattering (INS). The proposed mechanism for the easy-axis anisotropy involve interlayer coupling and orthorhombic distortion which are beyond the scope of this work.
For the easy-plane anisotropy, our conclusions are in agreement with the above analysis, including no true anisotropy in the absence of , and the tetragonal distortion term only affecting the magnitude and not being the source of anisotropy. In terms of symmetry breaking, the above induced easy-plane anisotropy term obtained via strong coupling expansion is equivalent to our local anisotropic interaction term (dominantly ) derived using the transformation. The major difference is that while in Ref. [17] the value was treated as a fitting parameter in the 40 meV magnon gap analysis, in our work the explicit form of the anisotropic interaction term [] has been derived, and the magnon gap is determined using the same microscopic Hamiltonian parameters which account for the high energy magnon feature (strong zone boundary dispersion) within a unified scheme. Furthermore, all physical terms are treated on the same footing, which is especially important for the weakly correlated systems.iridate_one In general, the nature of magnetic anisotropy depends, through the sign and magnitude of the =3/2 sector moments and , on the lattice, band structure, and magnetic ordering, which is of particular interest for the honeycomb lattice compounds and -.
IX Conclusion
While all Coulomb interaction terms are invariant under same pure-spin rotation for all three pure () orbitals, the Hund’s coupling and pair hopping interaction terms were shown to explicitly break pseudo-spin rotation symmetry systematically due to the spin-orbital entanglement. Transformation of the various Coulomb interaction terms to the pseudo-spin-orbital basis formed by the =1/2 and 3/2 states therefore provides a physically transparent approach for investigating magnetic ordering and anisotropy effects in the perovskite () and other pseudo-spin compounds. Explicitly pseudo-spin symmetry-breaking terms were obtained (dominantly ), resulting in easy - plane anisotropy and magnon gap for the out-of-plane mode, highlighting the importance of mixing with the nominally non-magnetic =3/2 sector in determining the magnetic properties of .
References
- (1) W. Witczak-Krempa, G. Chen, Y. B. Kim, and L. Balents, Correlated Quantum Phenomena in the Strong Spin-Orbit Regime, Annu. Rev. Condens. Matter Phys. 5, 57 (2014).
- (2) J. G. Rau, E. Kin-Ho Lee, and H.-Y. Kee, Spin-Orbit Physics Giving Rise to Novel Phases in Correlated Systems: Iridates and Related Materials, Annu. Rev. Condens. Matter Phys. 7, 195 (2016).
- (3) J. Bertinshaw, Y. K. Kim, G. Khaliullin, and B. J. Kim, Square Lattice Iridates, Annu. Rev. Condens. Matter Phys. 10, 315 (2019).
- (4) B. J. Kim, H. Jin, S. J. Moon, J.-Y. Kim, B.-G. Park, C. S. Leem, J. Yu, T. W. Noh, C. Kim, S.-J. Oh, J.-H. Park, V. Durairaj, G. Cao, and E. Rotenberg, Novel Mott State Induced by Relativistic Spin-Orbit Coupling in , Phys. Rev. Lett. 101, 076402 (2008).
- (5) B. Kim, H. Ohsumi, T. Komesu, S. Sakai, T. Morita, H. Takagi, and T. Arima, Phase-Sensitive Observation of a Spin-Orbital Mott State in , Science 323, 1329 (2009).
- (6) H. Watanabe, T. Shirakawa, and S. Yunoki, Microscopic Study of a Spin-Orbit-Induced Mott Insulator in Ir Oxides, Phys. Rev. Lett. 105, 216410 (2010).
- (7) J. Kim, D. Casa, M. H. Upton, T. Gog, Y.-J. Kim, J. F. Mitchell, M. van Veenendaal, M. Daghofer, J. van den Brink, G. Khaliullin, and B. J. Kim, Magnetic Excitation Spectra of Probed by Resonant Inelastic X-Ray Scattering: Establishing Links to Cuprate Superconductors, Phys. Rev. Lett. 108, 177003 (2012).
- (8) S. Mohapatra, J. van den Brink, and A. Singh, Magnetic Excitations in a Three-Orbital Model for the Strongly Spin-Orbit Coupled Iridates: Effect of Mixing Between the and Sectors, Phys. Rev. B 95, 094435 (2017).
- (9) B. H. Kim, G. Khaliullin, and B. I. Min, Magnetic Couplings, Optical Spectra, and Spin-Orbit Exciton in Electron Mott Insulator , Phys. Rev. Lett. 109, 167205 (2012).
- (10) G. Jackeli and G. Khaliullin, Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models, Phys. Rev. Lett. 102, 017205 (2009).
- (11) J-i Igarashi and T. Nagao, Strong Coupling Theory of Spin and Orbital Excitations in , Phys. Rev. B 88, 104406 (2013).
- (12) N. B. Perkins, Y. Sizyuk, and P. Wölfle, Interplay of Many-Body and Single-Particle Interactions in Iridates and Rhodates, Phys. Rev. B 89, 035143 (2014).
- (13) J. G. Vale, S. Boseggia, H. C. Walker, R. Springell, Z. Feng, E. C. Hunter, R. S. Perry, D. Prabhakaran, A. T. Boothroyd, S. P. Collins, H. M. Rønnow, and D. F. McMorrow, Importance of Anisotropy in Revealed by Magnetic Critical Scattering Experiments, Phys. Rev. B 92, 020406(R) (2015).
- (14) J-i Igarashi and T. Nagao, Interplay between Hund’s Coupling and Spin-Orbit Interaction on Elementary Excitations in , J. Phys. Soc. Jpn. 83, 053709 (2014).
- (15) J. Kim, M. Daghofer, A. H. Said, T. Gog, J. van den Brink, G. Khaliullin, and B. J. Kim, Excitonic Quasiparticles in a Spin–Orbit Mott Insulator, Nat. Commun. 5, 4453 (2014).
- (16) D. Pincini, J. G. Vale, C. Donnerer, A. de la Torre, E. C. Hunter, R. Perry, M. Moretti Sala, F. Baumberger, and D. F. McMorrow, Anisotropic Exchange and Spin-Wave Damping in Pure and Electron-Doped , Phys. Rev. B 96, 075162 (2017).
- (17) J. Porras, J. Bertinshaw, H. Liu, G. Khaliullin, N. H. Sung, J.-W. Kim, S. Francoual, P. Steffens, G. Deng, M. Moretti Sala, A. Effimenko, A. Said, D. Casa, X. Huang, T. Gog, J. Kim, B. Keimer, and B. J. Kim, Pseudospin-Lattice Coupling in the Spin-Orbit Mott Insulator , Phys. Rev. B 99, 085125 (2019).
- (18) D. Meyers, Y. Cao, G. Fabbris, N. J. Robinson, L. Hao, C. Frederick, N. Traynor, J. Yang, J. Lin, M. H. Upton, D. Casa, J.-W. Kim, T. Gog, E. Karapetrova, Y. Choi, D. Haskel, P. J. Ryan, L. Horak, X. Liu, J. Liu, and M. P. M. Dean, Magnetism in Iridate Heterostructures Leveraged by Structural Distortions, Sci. Rep. 9, 4263 (2019).
- (19) S. Mohapatra, S. Aditya, R. Mukherjee, and A. Singh, Octahedral Tilting Induced Isospin Reorientation Transition in Iridate Heterostructures, Phys. Rev. B 100, 140409(R) (2019).
- (20) S. Boseggia, Ph.D. Thesis, Magnetic order and excitations in perovskite iridates studied with resonant X-ray scattering techniques (2014).
- (21) C. Martins, M. Aichhorn, and S. Biermann, Coulomb Correlations in and Oxides from First Principles— or How Spin– Orbit Materials Choose Their Effective Orbital Degeneracies, J. Phys.: Condens. Matter 29, 263001 (2017).
- (22) J-i Igarashi and T. Nagao, Analysis of Resonant Inelastic X-ray Scattering from in an Itinerant-Electron Approach, Phys. Rev. B 90, 064402 (2014).
- (23) S. Zhou, K. Jiang, H. Chen, and Z. Wang, Correlation Effects and Hidden Spin-Orbit Entangled Electronic Order in Parent and Electron-Doped Iridates , Phys. Rev. X 7, 041018 (2017).
- (24) S. Mohapatra and A. Singh, Magnetic Reorientation Transition in a Three Orbital Model for — Interplay of Spin-Orbit Coupling, Tetragonal Distortion, and Coulomb Interactions, J. Phys.: Condens. Matter 32, 485805 (2020).
- (25) S. Mohapatra and A. Singh, Correlated Motion of Particle-Hole Excitations Across the Renormalized Spin-Orbit Gap in , J. Magn. Magn. Mater 512, 166997 (2020).
- (26) T. Chatterji, S. Ghosh, A. Singh, L. P. Regnault, M. Rheinstadter, G.J. Mcintyre, and T. Lonkai, Spin Dynamics of studied via Inelastic Neutron Scattering and the Anisotropic Hubbard Model, Phys. Rev. B 76, 144406 (2007).
- (27) A. Singh and Z.Teššanović, Spin Fluctuations in an Itinerant Antiferromagnet, Phys. Rev. B 41, 11457 (1990).