PyramidFlow: High-Resolution Defect Contrastive Localization
using Pyramid Normalizing Flow
Abstract
During industrial processing, unforeseen defects may arise in products due to uncontrollable factors. Although unsupervised methods have been successful in defect localization, the usual use of pre-trained models results in low-resolution outputs, which damages visual performance. To address this issue, we propose PyramidFlow, the first fully normalizing flow method without pre-trained models that enables high-resolution defect localization. Specifically, we propose a latent template-based defect contrastive localization paradigm to reduce intra-class variance, as the pre-trained models do. In addition, PyramidFlow utilizes pyramid-like normalizing flows for multi-scale fusing and volume normalization to help generalization. Our comprehensive studies on MVTecAD demonstrate the proposed method outperforms the comparable algorithms that do not use external priors, even achieving state-of-the-art performance in more challenging BTAD scenarios.
1 Introduction
Due to the uncontrollable factors in the complex industrial manufacturing process, unforeseen defects will be brought to products inevitably. As the human visual system has the inherent ability to perceive anomalies[25], quality control relies on manual inspection for a long time.
However, large-scale images and tiny defects are challenging for manual inspection, so increasing research is focused on automated machine vision inspection. Among all the methods, supervised deep learning has achieved great success. It relies on annotated datasets to learn discriminative features, effectively overcoming the hand-crafted shortcomings. However, because of insufficient negative samples, the high demand for labels, and the absence of prior knowledge, those approaches based on supervised learning may suffer in identifying unseen defects in practices,
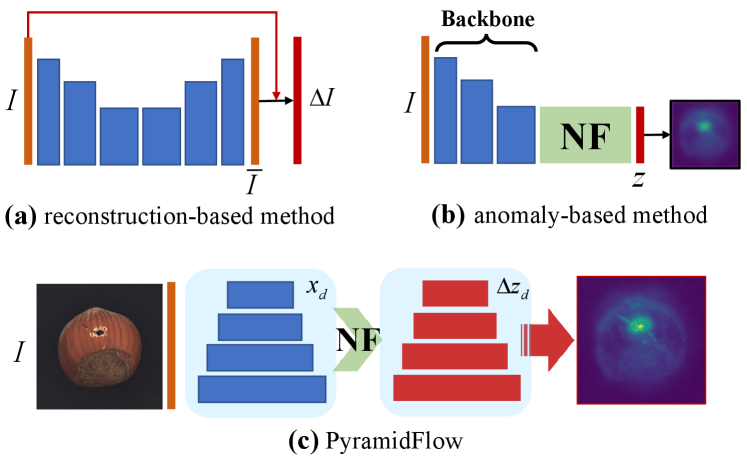
Recently, unsupervised methods have been applied to defect detection, as shown in Fig. 1(a,b). Reconstruction-based methods[4, 15, 23, 29] are the most famous, which take reconstructed images as templates and then apply explicit contrast in image space to achieve high-resolution localization. However, reconstructing using decoders is an ill-posed inverse problem, it is hard to reconstruct complex details. To overcome the above limitations, anomaly-based methods[7, 6] utilizing texture-aware pre-trained models achieves high image-level performance, which also damages pixel-level visual performance. One of the most promising methods is convolutional normalizing flows[27, 10, 22], which models the probability distribution further from pre-trained features, earning higher performance.
In this paper, a Pyramid Normalizing Flow (PyramidFlow) is proposed. It develops the idea of templates from image space into latent space by normalizing flow, then performing contrast for high-resolution anomaly localization, as shown in Fig. 1(c). Specifically, we propose the multi-scale Pyramid Coupling Block, which includes invertible pyramid and volume normalization, as the critical module to construct volume-preserving PyramidFlow. To the best of our knowledge, PyramidFlow is the first UNet-like fully normalizing flow specifically designed for anomaly localization, analogous to UNet[19] for biomedical image segmentation. Our main contributions can be summarized as follows.
-
•
We propose a latent template-based defect contrastive localization paradigm. Similar to the reconstruction-based methods, we perform contrast localization in latent space, which avoids the ill-posedness and reduces intra-classes variance efficiently.
-
•
We propose PyramidFlow, which includes invertible pyramids and pyramid coupling blocks for multi-scale fusing and mapping, enabling high-resolution defect localization. Additionally, we propose volume normalization for improving generalization.
-
•
We conduct comprehensive experiments to demonstrate that our advanced method outperforms comparable algorithms that do not use external priors, and even achieves state-of-the-art performance in complex scenarios.
2 Related Work
2.1 Deep learning-based Defect Localization
With the rise of deep learning, numerous works apply generalized computer vision methods for defect detection. Some works are based on object detection[14, 31, 30, 28, 13], which relies on annotated rectangular boxes, enabling locating and classifying defects end-to-end. The other is applying semantic segmentation[18, 24, 5], which enables pixel-level localization, suit for complex scenarios with difficult-to-locate boundaries. However, these works still rely on supervised learning, they attempt to collect sufficient defective samples to learn well-defined representations.
Recently, some promising work has considered the scarcity of defects in real-world scenarios, where defect-free samples are only obtained. These methods can be classified as reconstruction-based and anomaly-based. The reconstruction-based method relies on generative models such as VAE or GAN, which encode a defective image and reconstruct it to a defect-free image, then localize the defect with the contrast of these two images. The reconstruction-based method performs well on single textural images, but they cannot generalize to non-textural images for ill-posedness and degeneracy[25]. The anomaly-based method treats defects as anomalous, applying neural networks to discriminate between normality and anomalous. These methods extract pre-trained features, then estimate their probability density using Mahalanobis distances or K-NearestNeighbor, while the lower probability indicates where the image patches are abnormal. Although anomaly-based methods had achieved great success in defect detection, it locates defects with low pixel-level resolution compared with reconstruction-based methods, usually 1/16th or even lower, which greatly limits practical industrial applications.
To overcome existing shortcomings, we propose a latent template-based defect contrastive localization paradigm, which breaks the limitation of low-frequency texture-aware-only models, enabling more accurate results.
2.2 Normalizing Flow
Normalizing flow is a kind of invertible neural network with bijective mappings and traceable Jacobi determinants. It was first proposed for nonlinear independent component estimation[8] and applied to anomaly detection[21] recently for its invertibility helps prevent mode collapse. The normalizing flow comprises coupling blocks, these basic modules for realizing nonlinear mappings and calculating Jacobi determinants. Originally, NICE[8] proposed the additive coupling layer with unitary Jacobi determinants, while RealNVP[9] further proposed the affine coupling layer that enables the generation of non-volume-preserving mappings. However, redundant volume degrees of freedom can lead to increased optimization complexity, creating a domain gap between maximum likelihood estimation and anomaly metrics, which may potentially compromise the generalization performance in anomaly detection.
Previous works[21, 10, 27] on anomaly localization usually follow the methods proposed in RealNVP, but some challenges remain. Some studies[22] have found that convolutional normalizing flow focuses on local rather than semantic correlations, which are usually addressed by image embeddings[12]. Hence, earlier studies[21] adopted pre-trained backbones, while recent trends used pre-trained encoders to extract image patches[22, 10, 27]. However, pre-trained-based methods rely on task-irrelevant external priors, which limit generalization in unforeseen scenarios.
To address the above challenges, we propose a pyramid-like normalizing flow called PyramidFlow, which utilizes volume normalization to preserve volume mappings that include task-relevant implicit priors. Additionally, our method offers the option of using pre-trained models, and we have observed that external priors from pre-trained models can improve generalization performance. We will discuss these contributions in Sec. 4.3 and Sec. 4.4.
3 Methodology
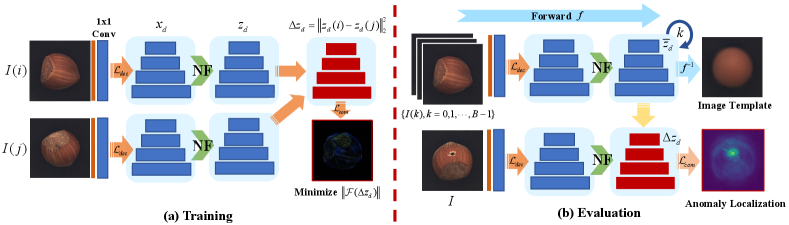
Our algorithm consists of two processes, training and evaluation, as shown in Fig. 2. The training process is similar to siamese networks, the model is optimized by minimizing the Frequency differences within the image pair. For the evaluation process, latent templates are obtained through inference at the total training dataset, then latent contrast and pyramid composition are applied to obtain an anomaly localization map. The details are shown in the following sections.
3.1 Invertible Pyramid
Defect images contain various frequency components. Usually, the low-frequency components represent the slow gradient background, while the high-frequency components correspond to details or defects. To decouple the frequency components and identify each frequency component independently, we propose invertible pyramids, which enable multi-scale decomposition and composition for a single feature. To facilitate feature learning, previous work applies pre-trained encoders to extract features. Although pre-trained methods with external priors help performance improvement, to fully explore the advantages of our approach in our primary study, let’s consider a baseline without any pre-trained model.
For a three-channel image , apply orthogonally initialized convolution to the image for obtain features . Given a feature and a positive integer , the pyramid decomposition is a mapping from features to feature sets , where is the level pyramid can be calculated as
| (1) |
where and are arbitrary linear upsampling and downsampling operators, while represents repeated downsampling times. If Eq. 1 is further satisfied , then the inverse operation of the pyramid decomposition can be described as
| (2) |
Differing from Gaussian pyramid, Eq. 2 indicates that there is always an inverse operation for pyramid decomposition, which is called pyramid composition. The method based on Eqs. 1 and 2, enabling perform multi-scale feature decomposition and composition, is a critical invertible module for PyramidFlow.
3.2 Pyramid Coupling Block
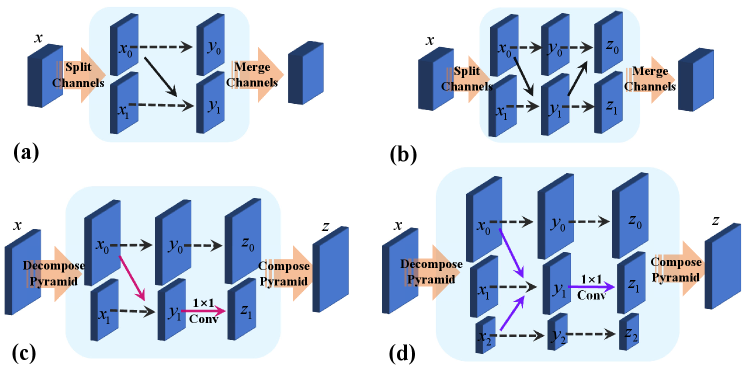
Invertible Modules. Invertible modules are the essential elements to implementing invertible neural networks. The invertible modules introduced in this paper are invertible convolution, invertible pyramid, and affine coupling block. The affine coupling block is the basic module that constitutes the normalizing flow. It is based on feature splitting for invertible nonlinear mappings with easily traceable Jacobian determinants and inverse operations.
As shown in Fig. 3(a), the conventional affine coupling block splits a single feature along the channel dimension, where one sub-feature keeps its identity while another is performed affine transformation controlled by it. Denote the splitted features are and its outputs are , then the corresponding transformation can be described as
| (3) | ||||
where are affine parameters, can be estimated by zero-initialized convolutional neural networks. For formula(3), there is an explicit inverse transformation:
| (4) | ||||
Denote the element at position of as . As the Jacobian matrix of transformation(3) is a triangular matrix, its logarithmic determinant can be estimated as
| (5) |
Eqs. 3, 4 and 5 are the basis of all affine coupling blocks. However, the coupling block shown in Fig. 3(a) remains identical for one part. Therefore the reverse cascade architecture is proposed in NICE[8] such that both parts are transformed, as shown in Fig. 3(b). The previous works construct the holistic invertible normalizing flow by iterative applying the structure shown in Fig. 3(b).
Implementation. Our method decomposes a single feature along the scale and realizes multi-scale feature fusion based on Eqs. 3, 4 and 5. In our implementation, the multi-scale affine parameters are estimated using a convolutional neural network with two linear layers, where bilinear interpolation is applied to match the target shape.
In addition, we employ invertible 1x1 convolution[11] for feature fusion within features. Specifically, denoting the full rank matrix corresponding to the invertible convolution as , which can be decomposed by PLU as
| (6) |
where is a frozen permutation matrix, is a lower triangular matrix with unit diagonal elements, is an upper triangular matrix with zero diagonal elements, and is the -th eigenvalue of the matrix , which always holds nonnegativity. The matrix is always invertible during optimization, then its logarithmic Jacobian determinant can be estimated as
| (7) |
In summary, Eqs. 3, 4, 5, 6 and 7 describe proposed pyramidal coupling block mathematically, as shown in Fig. 3(c). First, multi-scale feature fusion(3-5) is performed, and then apply linear fusion(6-7) for shuffle channels. Furthermore, we propose a dual coupling block as shown in Fig. 3(d), which is equivalent to the reverse parallel of the coupling block in Fig. 3(c). The dual coupling block is reparameterized in our implementation, and its affine parameters are estimated from concatenated features.
Volume Normalization. Suppose that the invertible transformation maps the variable to the latent variable . Previous works have assumed that the latent variable follows basic probability distribution (e.g. Gaussian distribution), then estimates sample probability density based on the following equation:
| (8) |
However, this approach relies on the basic distribution assumption and ignores the effect of the implicit prior in the probability density transform on generalization. When such approaches are applied to anomaly detection, the inconsistency between the training objectives and the anomaly evaluation results in domain gaps.
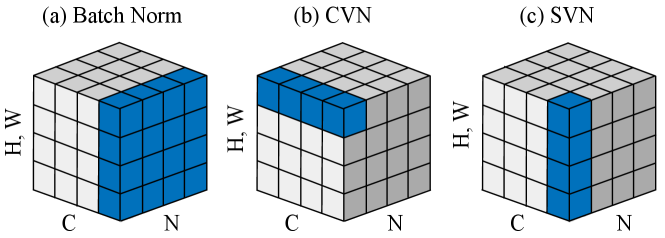
Similar to batch normalization or instance normalization in deep learning, the proposed volume normalization will be employed for volume-preserving mappings, as illustrated in Fig. 4. Particularly, for the affine coupling block, the parameter is subtracted from its mean value before performing Eq. 3; for the invertible convolution, the parameter is subtracted from its mean value before calculating the matrix based on Eq. 6. Depending on the statistical dimension, we propose Spatial Volume Normalization (SVN) and Channel Volume Normalization (CVN). SVN performs mean statistics along the spatial dimension, while CVN is along the channel dimension. Various volume normalization methods contain different priors, then we will explore their impact in Sec. 4.2.
3.3 Pyramid Normalizing Flow
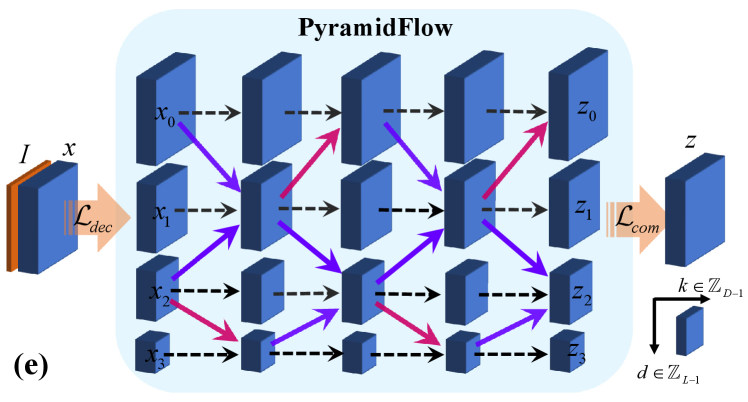
Architecture. Our PyramidFlow can be obtained by stacking the pyramid coupled blocks of Fig. 3(c,d) along the depth times and along the layer times, as shown in Fig. 3(e). Specifically, PyramidFlow boosts the image to feature using matrix , then performs the pyramid decomposition based on Eq. 1. The pyramid coupling blocks described in Eqs. 3, 4, 5, 6 and 7 are calculated in the order described in Fig. 3(e) to obtain potential pyramid features , which are finally composed into latent variables according to Eq. 2.
Loss Function. In the cases with volume normalization, the loss function excludes the probability density coefficients. Moreover, the logarithmic Jacobian determinant of the semi-orthogonal matrix is sample-independent, so its effect could be ignored during training.
Suppose a training batch with 2 normal samples, its latent variables are . Previous studies train neural networks using spatial difference . However, it ignored the impact of high-frequency defects. To address the above shortcoming, we propose the following Fourier loss function.
| (9) |
where is the fast Fourier transform of the image. Training the normalizing flow using Eq. 9 enables the model to focus on the high-frequency, allowing faster convergence. We will discuss this trick in Sec. 4.3.
Defect Localization. Previous studies[22, 27] usually localize defects with obvious differences based on category-independent zero templates. In our method, the defects are modeled as anomalous deviations with respect to the template. Then, the anomaly of the latent pyramid is defined as , where is mean of the latent pyramid. Finally, the total anomaly can be estimated as
| (10) |
The Eq. 10 shows that the total anomaly is a composition of anomalies at various scales, which is consistent with the empirical method proposed by Rudolph, et al. [22].
Image Template Estimation. The image template is a prototype of normal samples, a visualization of the latent template. Our fully normalizing flow is based on convolution instead of pre-trained encoders, maintaining end-to-end and near-invertibility, thus the flow’s input can be retrieved using Eq. 2 and Eq. 4 from latent mean , then solve the least square problem for image template .
4 Experiment and Discussion
In this chapter, we perform unsupervised anomaly localization experiments on MVTec Anomaly Detection Dataset[2] (MVTecAD) and BeanTech Anomaly Detection Dataset[16] (BTAD). MVTecAD contains 15 categories of industrial defect images, five of which are textural images and the other ten are object images. The object images contain three classes (grid, metal nut, screw) without rough registration and one class (hazelnut) without fine registration, and we will discuss these cases in Sec. 4.5. The BTAD contains three types of real-world and industry-oriented textural images, which is more challenging for pixel-level localization.
All experiments take Area Under the Receiver Operating characteristic Curve (AUROC) and Area Under the Per Region Overlap (AUPRO) as evaluation metrics. AUROC is the most widely used anomaly evaluation metric, and higher values indicate that various thresholds have less impact on performance. However, AUROC prefers larger anomalies and may fail in small proportions of anomalies. Thus, we further evaluate AUPRO for localization metric, similar to Intersection Over Union (IoU) commonly used in semantic segmentation. Detailed definitions can be found in [2].
4.1 Complexity Analysis
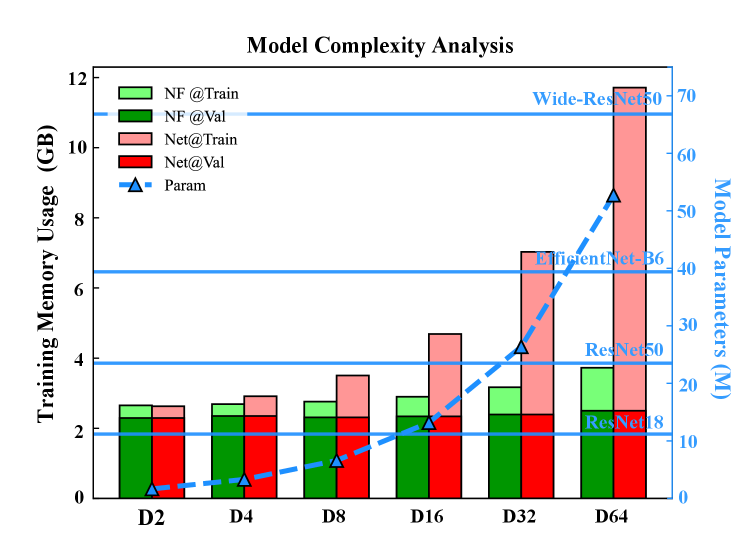
The normalizing flow based on Eqs. 3 and 4 is computationally invertible, which indicates that only one copy of the variables is necessary for all stages. This feature decreases the memory footprint during backpropagation from linear to constant complexity. We have analyzed the above characteristics based on a fixed number of pyramid layers , image resolution with , and channels , then changed the number of stacked layers to explore the trends of memory usage and model parameters. The forward and memory-saving backpropagation is implemented based on the self-developed PyTorch-based[17] framework autoFlow. All indicators are recorded during steady-state training, then plotted as bar and line graphs, as shown in Fig. 5.
The memory usage based on auto-differentiation increases linearly with depth , while the implementation based on normalizing flow achieves approximate depth-independent memory usage. The memory superiority enables the proposed method to be trained in memory-constrained devices below 4G without powerful hardware. The line graph shows the exponential trends between model parameters and depth, while the horizontal line represents the parameters of the usual pre-trained model. We mainly adopt methods with or even shallower, where the number of parameters is far smaller than popular pre-training-based methods. In summary, in scenarios of memory constraint, the proposed PyramidFlow enables dealing with larger images and requires fewer parameters than others.
4.2 Study on Volume Normalization
In this subsection, based on MVTecAD, we investigate the impact of volume normalization on generalization. The experiment without data augmentation, fixed pyramid layers , channels , and linear interpolated image to . During the training, the volume normalization applies sample mean normalization and updates the running mean with 0.1 momenta, while in the testing, the volume normalization is based on the running mean. We sufficiently explored the volume normalization methods proposed in Sec. 3.2. Some representative categories are shown as Tab. 1.
| Classes | CVN | SVN | ||
| AUROC | AUPRO | AUROC | AUPRO | |
| capsule | 96.1(+2.6) | 93.1(+5.1) | 93.5(+0.0) | 88.0(+0.0) |
| pill | 96.2(+1.8) | 96.3(+1.4) | 94.4(+0.0) | 94.9(+0.0) |
| toothbrush | 98.9(+2.5) | 97.9(+4.3) | 96.4(+0.0) | 93.6(+0.0) |
| carpet | 88.9(+0.0) | 88.3(+0.0) | 90.8(+1.9) | 91.0(+2.7) |
| grid | 86.2(+0.0) | 84.5(+0.0) | 94.2(+8.0) | 92.7(+8.2) |
| zipper | 92.2(+0.0) | 91.9(+0.0) | 95.4(+3.2) | 95.1(+3.2) |
The result in Tab. 1 shows the performance differences between the various volume normalization methods: CVN outperforms SVN for the first three classes, while the latter behaves the opposite. We further visualize these defect distributions in Fig. 6, which shows that SVN-superior classes are commonly textural images with a larger range of defects, while CVN-superior classes are object images.

SVN with larger receptive fields achieves non-local localization by aggregating an extensive range of texture features, while CVN realizes accurate localization by shuffling channels. In a word, different volume normalization techniques implicitly embody distinct task-specific priors. Furthermore, our ablation study in Sec. 4.3 shows that volume normalization does help to improve average performance.
4.3 Ablation Study
This subsection discusses the impact of some proposed methods on performance. The study is conducted on full MVTecAD, and other settings are the same as Sec. 4.2. We ablate four methods from baseline individually. In particular, experiment I is based on latent Gaussian assumption and Eq. 8 without volume normalization. For experiment II , the category-independent zero template is applied. Then, Experiment III does not adopt the method of Eq. 10 but composes the pyramid first and localizes its difference later. Finally, experiment IV adopts a spatial version of the loss function instead of Eq. 9. The result of the above ablation experiments is shown in Tab. 2.
| Method | Classes | MEAN | |
| Texture | Object | ||
| Ours (baseline) | 95.2(+0.0) | 95.7(+0.0) | 95.5(+0.0) |
| 95.1(+0.0) | 93.5(+0.0) | 94.0(+0.0) | |
| I. w/o Volume Normalization | 89.4(-5.8) | 85.2(-10.5) | 86.6(-8.9) |
| 87.5(-7.6) | 83.6(-9.9) | 84.9(-9.1) | |
| II. w/o Latent Template | 93.1(-2.1) | 90.7(-5.0) | 91.5(-4.0) |
| 91.9(-3.2) | 84.7(-8.8) | 87.1(-6.9) | |
| III. w/o Pyramid Difference | 87.8(-7.4) | 93.1(-2.6) | 91.3(-4.2) |
| 87.8(-7.3) | 89.4(-4.1) | 88.9(-5.1) | |
| IV. w/o Fourier Loss | 92.0(-3.2) | 93.3(-2.4) | 92.9(-2.6) |
| 92.8(-2.3) | 91.9(-1.6) | 92.2(-1.8) | |
Tab. 2 demonstrates that experiments I -IV present various performance degradation. Experiment I has the largest average degradation, with the object classes being more affected. Although the non-volume-preserving enables larger outputs and higher Image-AUROC performance, the implicit prior in volume normalization discussed in Sec. 4.2 is more helpful for generalization. For experiment II , it shows that the latent template benefits the performance, and object classes are improved greatly. It is because the category-specific latent template reduces intra-class variance, helping convergence during training. Then, experiment III suggests that multi-scale differences had a more pronounced impact on textural classes, as higher-level operators with larger receptive fields correspond to large defects. Finally, Experiment IV reveals that Fourier loss (9) is the icing on the cake that helps performance improvement. To summarize, methods I -III are critical for the proposed model, while tricks IV help further improvements.
4.4 Anomaly Localization
| External Prior | Methods | carpet | leather | tile | wood | bottle | cable | capsule | hazelnut | pill | toothbrush | transistor | zipper | MEAN |
| AnoGAN[23] | 54.2 | 64.1 | 49.7 | 62.1 | 85.8 | 78.0 | 84.1 | 87.1 | 86.8 | 90.0 | 79.9 | 78.1 | 75.0 | |
| 20.4 | 37.8 | 17.7 | 38.6 | 62.0 | 38.3 | 30.6 | 69.8 | 77.6 | 74.9 | 54.9 | 46.7 | 47.4 | ||
| Vanilla VAE[15] | 62.0 | 83.5 | 52.0 | 69.9 | 89.4 | 81.6 | 90.7 | 95.1 | 87.9 | 95.3 | 85.1 | 77.5 | 80.8 | |
| 61.9 | 64.9 | 24.2 | 57.8 | 70.5 | 77.9 | 77.9 | 77.0 | 79.3 | 85.4 | 61.0 | 60.8 | 66.6 | ||
| AE-SSIM[4] | 87.0 | 78.0 | 59.0 | 73.0 | 93.0 | 82.0 | 94.0 | 97.0 | 91.0 | 92.0 | 80.0 | 88.0 | 84.5 | |
| 64.7 | 56.1 | 17.5 | 60.5 | 83.4 | 47.8 | 86.0 | 91.6 | 83.0 | 78.4 | 72.4 | 66.5 | 67.3 | ||
| Ours | 90.8 | 99.6 | 97.9 | 93.8 | 95.9 | 92.1 | 96.1 | 98.0 | 96.2 | 98.9 | 97.4 | 95.4 | 96.0 | |
| (FNF) | 91.0 | 99.7 | 95.8 | 96.2 | 94.0 | 86.4 | 93.1 | 97.3 | 96.3 | 97.7 | 91.4 | 95.1 | 94.5 | |
| Res18 | S-T[3] | 93.5 | 97.8 | 92.5 | 92.1 | 97.8 | 91.9 | 96.8 | 98.2 | 96.5 | 97.9 | 73.7 | 95.6 | 93.7 |
| 87.9 | 94.5 | 94.6 | 91.1 | 93.1 | 81.8 | 96.8 | 96.5 | 96.1 | 93.3 | 66.6 | 95.1 | 90.6 | ||
| WRes50 | SPADE[6] | 97.5 | 97.6 | 87.4 | 88.5 | 98.4 | 97.2 | 99.0 | 99.1 | 96.5 | 97.9 | 94.1 | 96.5 | 95.8 |
| 94.7 | 97.2 | 75.9 | 87.4 | 95.5 | 90.9 | 93.7 | 95.4 | 94.6 | 93.5 | 97.4 | 92.6 | 92.4 | ||
| WRes50 | PaDiM[7] | 99.1 | 99.2 | 94.1 | 94.9 | 98.3 | 96.7 | 98.5 | 98.2 | 95.7 | 98.8 | 97.5 | 98.5 | 97.5 |
| 96.2 | 97.8 | 86.0 | 91.1 | 94.8 | 88.8 | 93.5 | 92.6 | 92.7 | 93.1 | 84.5 | 95.9 | 92.3 | ||
| EffiB5 | CS-Flow[22] | 98.0 | 98.4 | 93.9 | 88.6 | 90.9 | 95.3 | 97.9 | 96.3 | 95.7 | 96.3 | 95.5 | 96.4 | 95.3 |
| 98.0 | 98.5 | 94.5 | 92.9 | 88.7 | 94.0 | 96.1 | 95.1 | 91.1 | 89.9 | 96.9 | 95.4 | 94.2 | ||
| DTD | DRÆM[29] | 94.9 | 96.6 | 99.6 | 97.3 | 97.6 | 95.4 | 94.0 | 99.2 | 95.0 | 98.1 | 90.0 | 94.4 | 96.0 |
| 96.1 | 97.9 | 99.7 | 97.9 | 97.2 | 90.4 | 96.5 | 98.7 | 93.7 | 97.1 | 92.9 | 94.7 | 96.1 | ||
| Res18 | Ours | 97.4 | 98.7 | 97.1 | 97.0 | 97.8 | 91.8 | 98.6 | 98.1 | 96.1 | 98.5 | 96.9 | 96.6 | 97.1 |
| 97.2 | 99.2 | 97.2 | 97.9 | 95.5 | 90.3 | 98.3 | 98.1 | 96.1 | 97.9 | 94.7 | 95.4 | 96.5 |
MVTecAD. We performed defect localization for 12 registered classes in MVTecAD. In our comparisons, the method based on pre-trained models or using external datasets is viewed as requiring external prior, corresponding to the first column of Tab. 3. In our implementation, we augment textural classes with flips and rotations, each with a probability of 0.5, while object categories do not undergo any augmentation operation. It is worth noting that those base on complex augmentation or weak supervision is not considered in our comparisons, as our approach is capable of incorporating these techniques to improve performance. The detailed results are shown in Tab. 3.
First, we take three methods based on image contrast, AnoGAN[23], Vanilla VAE[15], and AE-SSIM[4]. They are not dependent on external datasets, so it is fair to compare them with our FNF model. Furthermore, we also compared our method to those that utilize external priors, such as S-T, SPADE, etc. All methods were reproduced based on the official implementation or AnomaLib[1]. For fair comparisons, we adapted the convolution to the pre-trained encoder, where the pre-trained encoder is the first two layers of ResNet18 for extracting the image into features of original 1/4 size and with 64 channels.
As shown in Tab. 3, our FNF method greatly outperforms the comparable methods without external priors, even exceeding S-T, SPADE, and CS-Flow that using external priors. Most of the reconstruction-based methods in Tab. 3 suffer from ill-posedness in complex scenarios (e.g., tile and wood.), while our method achieves the best AUPRO score owing to high-resolution contrast in latent space. However, a larger resolution implies larger intra-class variance, which degrades the overall AUROC performance for hard-to-determine anomaly boundaries. Furthermore, Fig. 7(a) visualizes representative examples of MVTecAD anomaly localization, which shows that our method achieves precise localization with reasonable scale.

BTAD. To fully illustrate our superiority, we experimented on the more challenging BTAD dataset without any data augmentation, and other settings are the same as MVTecAD. The detailed result in Tab. 4 shows that our method also achieves state-of-the-art performance, and Fig. 7(b) visualizes representative examples of BTAD anomaly localization.
| Methods | Classes | MEAM | ||
| 01 | 02 | 03 | ||
| VT-ADL[16] | 97.6 | 71.0 | 82.6 | 83.7 |
| 99.0 | 94.0 | 77.0 | 90.0 | |
| P-SVDD[26] | 95.7 | 72.1 | 82.1 | 83.3 |
| 91.6 | 93.6 | 91.0 | 92.1 | |
| SPADE[6] | 91.4 | 71.4 | 99.9 | 87.6 |
| 97.3 | 94.4 | 99.1 | 96.9 | |
| PatchCore[20] | 90.9 | 79.3 | 99.8 | 90.0 |
| 95.5 | 94.7 | 99.3 | 96.5 | |
| PaDiM[7] | 99.8 | 82.0 | 99.4 | 93.7 |
| 97.0 | 96.0 | 98.8 | 97.3 | |
| Ours (Res18) | 100.0 | 88.2 | 99.3 | 95.8 |
| 97.4 | 97.6 | 98.1 | 97.7 | |
4.5 Study on unregistered categories
In principle, template-based methods require pixel-level registration between images and templates, which is typically satisfied in most real-world scenarios, but may fail in some cases. This subsection explores the performance of the proposed method on unregistered (e.g. rotation, shift) categories (e.g. grid, metal nut, screw, and hazelnut), as shown in Tab. 5. The reconstruction-based AE-SSIM heavily relies on pixel-level contrast, which decreases the average localization accuracy (AUPRO%). In contrast, the anomaly-based SPADE avoids registration issues and achieves better performance. Fortunately, our ResNet18-based method, which utilizes normalizing flow to reduce patch variance, remains competitive in unregistered scenes, although it falls short of state-of-the-art performance. We visualize these categories in Fig. 7(c).
5 Conclusion
In this paper, we propose PyramidFlow, the first fully normalizing flow method based on the latent template-based contrastive paradigm, utilizing pyramid-like normalizing flows and volume normalization, enabling high-resolution defect contrastive localization. Our method can be trained end-to-end from scratch, similar to UNet, and our comprehensive experiments demonstrate that it outperforms comparable algorithms that do not use external priors, even achieving state-of-the-art performance in complex scenarios. While experiments on unregistered categories show that our method falls short of state-of-the-art, it still exhibits competitive performance. Future research will focus on improving performance in such scenarios.
Acknowledgment. We would like to extend sincere appreciation to Jiabao Lei for his valuable guidance and insightful suggestions, which greatly contributed to the success of this work.
References
- [1] S. Akcay, D. Ameln, A. Vaidya, B. Lakshmanan, N. Ahuja, and U. Genc. Anomalib: A deep learning library for anomaly detection. In 2022 IEEE International Conference on Image Processing (ICIP), pages 1706–1710.
- [2] Paul Bergmann, Michael Fauser, David Sattlegger, and Carsten Steger. Mvtec ad–a comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 9592–9600.
- [3] Paul Bergmann, Michael Fauser, David Sattlegger, and Carsten Steger. Uninformed students: Student-teacher anomaly detection with discriminative latent embeddings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 4183–4192.
- [4] Paul Bergmann, Sindy Löwe, Michael Fauser, David Sattlegger, and Carsten Steger. Improving unsupervised defect segmentation by applying structural similarity to autoencoders. In VISIGRAPP (5: VISAPP), 2019.
- [5] Jakob Božič, Domen Tabernik, and Danijel Skočaj. Mixed supervision for surface-defect detection: From weakly to fully supervised learning. Computers in Industry, 129:103459, 2021.
- [6] Niv Cohen and Yedid Hoshen. Sub-image anomaly detection with deep pyramid correspondences. CoRR, abs/2005.02357, 2020.
- [7] Thomas Defard, Aleksandr Setkov, Angelique Loesch, and Romaric Audigier. Padim: a patch distribution modeling framework for anomaly detection and localization. In International Conference on Pattern Recognition, pages 475–489. Springer.
- [8] Laurent Dinh, David Krueger, and Yoshua Bengio. NICE: non-linear independent components estimation. In Yoshua Bengio and Yann LeCun, editors, 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Workshop Track Proceedings, 2015.
- [9] Laurent Dinh, Jascha Sohl-Dickstein, and Samy Bengio. Density estimation using real NVP. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net, 2017.
- [10] Denis Gudovskiy, Shun Ishizaka, and Kazuki Kozuka. Cflow-ad: Real-time unsupervised anomaly detection with localization via conditional normalizing flows. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pages 98–107.
- [11] Durk P Kingma and Prafulla Dhariwal. Glow: Generative flow with invertible 1x1 convolutions. Advances in neural information processing systems, 31, 2018.
- [12] Polina Kirichenko, Pavel Izmailov, and Andrew G Wilson. Why normalizing flows fail to detect out-of-distribution data. Advances in neural information processing systems, 33:20578–20589, 2020.
- [13] Feng Li, Feng Li, and QingGang Xi. Defectnet: Toward fast and effective defect detection. IEEE Transactions on Instrumentation and Measurement, 70:1–9, 2021.
- [14] J. Luo, Z. Yang, S. Li, and Y. Wu. Fpcb surface defect detection: A decoupled two-stage object detection framework. IEEE Transactions on Instrumentation and Measurement, 70:1–11, 2021.
- [15] Takashi Matsubara, Kazuki Sato, Kenta Hama, Ryosuke Tachibana, and Kuniaki Uehara. Deep generative model using unregularized score for anomaly detection with heterogeneous complexity. IEEE Transactions on Cybernetics, 2020.
- [16] P. Mishra, R. Verk, D. Fornasier, C. Piciarelli, and G. L. Foresti. Vt-adl: A vision transformer network for image anomaly detection and localization. In 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), pages 01–06.
- [17] Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. Automatic differentiation in pytorch. 2017.
- [18] R. Ren, T. Hung, and K. C. Tan. A generic deep-learning-based approach for automated surface inspection. IEEE Transactions on Cybernetics, 48(3):929–940, 2018.
- [19] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, pages 234–241. Springer, 2015.
- [20] Karsten Roth, Latha Pemula, Joaquin Zepeda, Bernhard Schölkopf, Thomas Brox, and Peter Gehler. Towards total recall in industrial anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14318–14328.
- [21] Marco Rudolph, Bastian Wandt, and Bodo Rosenhahn. Same same but differnet: Semi-supervised defect detection with normalizing flows. In Proceedings of the IEEE/CVF winter conference on applications of computer vision, pages 1907–1916.
- [22] Marco Rudolph, Tom Wehrbein, Bodo Rosenhahn, and Bastian Wandt. Fully convolutional cross-scale-flows for image-based defect detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pages 1088–1097.
- [23] Thomas Schlegl, Philipp Seeböck, Sebastian M Waldstein, Ursula Schmidt-Erfurth, and Georg Langs. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International conference on information processing in medical imaging, pages 146–157. Springer.
- [24] Domen Tabernik, Samo Šela, Jure Skvarč, and Danijel Skočaj. Segmentation-based deep-learning approach for surface-defect detection. Journal of Intelligent Manufacturing, 31(3):759–776, 2020.
- [25] Xian Tao, Xinyi Gong, Xin Zhang, Shaohua Yan, and Chandranath Adak. Deep learning for unsupervised anomaly localization in industrial images: A survey. IEEE Transactions on Instrumentation and Measurement, 2022.
- [26] Jihun Yi and Sungroh Yoon. Patch svdd: Patch-level svdd for anomaly detection and segmentation. In Proceedings of the Asian Conference on Computer Vision.
- [27] Jiawei Yu, Ye Zheng, Xiang Wang, Wei Li, Yushuang Wu, Rui Zhao, and Liwei Wu. Fastflow: Unsupervised anomaly detection and localization via 2d normalizing flows. CoRR, abs/2111.07677, 2021.
- [28] Xuyi Yu, Wentao Lyu, Di Zhou, Chengqun Wang, and Weiqiang Xu. Es-net: Efficient scale-aware network for tiny defect detection. IEEE Transactions on Instrumentation and Measurement, 71:1–14, 2022.
- [29] Vitjan Zavrtanik, Matej Kristan, and Danijel Skočaj. Draem-a discriminatively trained reconstruction embedding for surface anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 8330–8339, 2021.
- [30] N. Zeng, P. Wu, Z. Wang, H. Li, W. Liu, and X. Liu. A small-sized object detection oriented multi-scale feature fusion approach with application to defect detection. IEEE Transactions on Instrumentation and Measurement, 71:1–14, 2022.
- [31] Jiabin Zhang, Hu Su, Wei Zou, Xinyi Gong, Zhengtao Zhang, and Fei Shen. Cadn: A weakly supervised learning-based category-aware object detection network for surface defect detection. Pattern Recognition, 109:107571, 2021.