QCD sum rule determination of the charm-quark mass

Progress on the theoretical QCD1 -QCD12 , as well as on the experimental information EXP1 -EXP4 on the vector current correlator has allowed for a considerable improvement on the accuracy of QCD sum rule determinations of the charm-quark mass K -hoang . The analysis of K is based on inverse (Hilbert) moment QCD sum rules, requiring QCD knowledge of the vector correlator in the low energy, as well as in the high energy region. In charm an alternative approach was used which involves only QCD information at short distances, together with (a) a simple integration kernel $p(s)=1-s/s_{0}$ (local constraint), and (b) Legendre-type polynomial kernels (global constraint). In this paper we describe an improved analysis based on the use of direct as well as inverse moment kernels of the form $p(s)=1-(s_{0}/s)^{n}$, with $n\geq 1$. These kernels enhance considerably the impact of the well known narrow resonances, as compared with e.g. a simple kernel $p(s)=1/s^{2}$ , or $p(s)=1-s/s_{0}$. They also provide a welcome stronger suppression of the contribution of data in the range $s\simeq 20-25\;\mbox{GeV}^{2}$. In comparison with simple inverse moments without pinching, this means that results are less sensitive to assumptions about the onset of perturbative QCD (PQCD), as well as to the treatment of the higher resonance data. For instance, changes in $s_{0}$ in the range $s_{0}\simeq 15-23\;\mbox{GeV}^{2}$ lead to a variation in $\overline{m}_{c}(3\;\mbox{GeV})$ of only $4\;\mbox{MeV}$ (for $n=2$) as opposed to a variation of $14\;\mbox{MeV}$ for $p(s)=1/s^{2}$, as used in K

We consider the vector current correlator

where $V_{\mu}(x)=\bar{c}(x)\gamma_{\mu}c(x)$. From the residue theorem in the complex s-plane ($-q^{2}\equiv Q^{2}\equiv s$) it follows

where $p(s)$ is an integration kernel, and

with $R_{c}(s)$ the standard R-ratio for charm production. The PQCD expansion of $\Pi(s)$ at short distances can be written as

where $e_{c}=2/3$ is the charm-quark electric charge, and

and $\overline{m}_{c}\equiv\overline{m}_{c}(\mu)$ is the running charm-quark mass in the $\overline{MS}$-scheme. Up to order $\cal{O}$ $[\alpha_{s}^{2}(\bar{m}_{c}^{2}/s)^{6}]$ the function $\Pi(s)_{PQCD}$ has been calculated in QCD1 , and exact results for $\Pi_{0}^{(3)}$ and $\Pi_{1}^{(3)}$ have been found in QCD2 . The function $\Pi_{2}^{(3)}$ is known exactly up to a constant QCD3 . At five-loop order $\cal{O}$$(\alpha_{s}^{4})$ the full logarithmic terms for $\Pi_{0}^{(4)}$ may be found in QCD5 , and for $\Pi_{1}^{(4)}$ in QCD6 . Since there is incomplete knowledge at this loop-order we shall use the available information as a measure of the truncation error in PQCD. The low energy expansion of the vector correlator around $s=0$ can be written as

where $z=s/(4\overline{m}_{c}^{2})$. The coefficients $\overline{C}_{n}$ can be expanded in powers of $\alpha_{s}(\mu)$

where $l_{m}\equiv\ln(\bar{m}_{c}^{2}(\mu)/\mu^{2})$. Up to three loop level the coefficients up to $n=30$ of $\bar{C}_{n}$ are known QCD8 -QCD9 . At four-loop level we have $\bar{C}_{0}$ and $\bar{C}_{1}$ from QCD8 , QCD10 , $\bar{C}_{2}$ from QCD9 , and $\bar{C}_{3}$ from QCD11 . We will choose $p(s)$ so that no coefficients $\bar{C}_{4}$ and above contribute to the residue at $s=0$, $\text{Res}[\Pi(s)\,p(s),s=0]$.

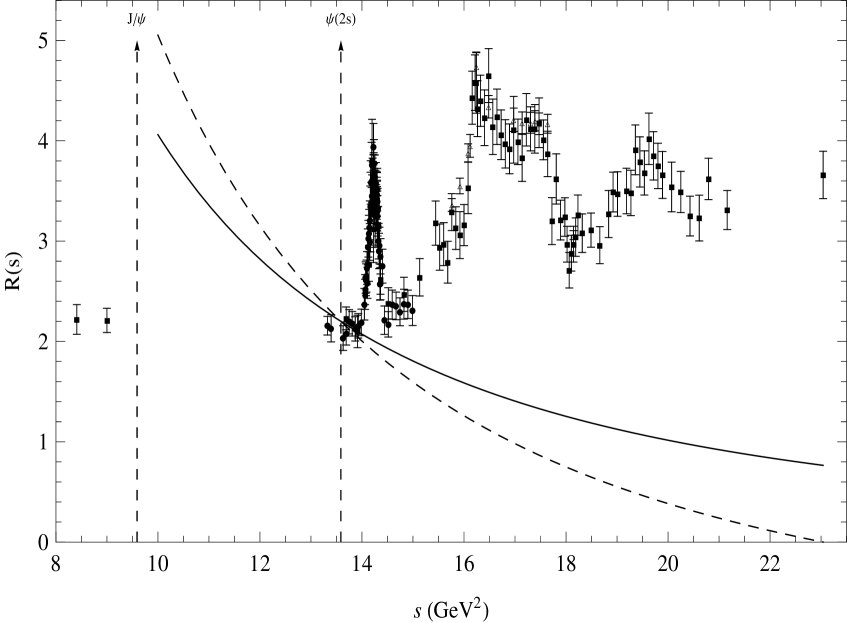
Apart from the quark mass, the fundamental QCD parameters are the running strong coupling $\alpha_{s}(\mu^{2})$, and the gluon condensate. For the strong coupling we use the world average from BETH2 , which agrees with lattice QCD results LATT , $\alpha_{s}(M_{Z}^{2})=0.1184\pm 0.0007$. However, we will consider other values when comparing results for $\overline{m}_{c}$ with other analyses. In the non-perturbative sector the leading power correction in the Operator Product Expansion (OPE) involves the gluon condensate, i.e. $\left<(\alpha_{s}/\pi)G^{2}\right>$ whose value has been extracted COND from the ALEPH data on $\tau$-decays. While the gluon condensate is renormalization group invariant, its determination from QCD sum rules involves a difference between integrals of PQCD and integrated experimental data. This leads to an unavoidable dependence of the gluon condensate on the value of $\alpha_{s}$ used in the PQCD expression of the correlator. Extrapolating the results of COND to include current values of $\alpha_{s}$ BETH2 , PICH , leads to $\left<(\alpha_{s}/\pi)G^{2}\right>=(0.01\pm 0.01)\;\text{GeV}^{4}$. This large uncertainty in the value of the gluon condensate has only a very small impact on our results for $\bar{m}_{c}$.
Turning to the experimental data, we follow closely the analysis of K . For the first two narrow resonances we use the latest data from the Particle Data Group PDG , $M_{J/\psi}=3.096916(11)\;\mbox{GeV}$, $\Gamma_{J/\psi\rightarrow e^{+}e^{-}}=5.55(14)\;\mbox{keV}$, $M_{\psi(2s)}=3.68609(4)\;\mbox{GeV}$, $\Gamma_{\psi(2s)\rightarrow e^{+}e^{-}}=2.35(4)\;\mbox{keV}$. These two narrow resonances are followed by the open charm region where the contribution from the light quark sector $R_{uds}$ needs to be subtracted from the total R-ratio $R_{tot}$. We perform this subtraction as in MC2 . In the region $3.97\;\mbox{GeV}\leq\sqrt{s}\leq 4.26\;\mbox{GeV}$ we only use CLEO data EXP4 as they are the most precise. In connection with the three data sets from BES EXP1 -EXP3 , we assume that the systematic uncertainties are not fully independent and add them linearly, rather than in quadrature. However, we treat these data as independent from the CLEO data set EXP4 , and thus add errors in quadrature. There is no data in the region $s=25-49\;\mbox{GeV}^{2}$, and beyond there is CLEO data up to $s\simeq 110\;\mbox{GeV}^{2}$. The latter data is fully compatible with PQCD.
We discuss next the integration kernels $p(s)$ in Eq.(2), which we choose as

with $n\geq 1$. As discussed in K , inverse moments $p(s)=1/s^{n}$ should not involve too large values of $n$. In fact, the convergence of PQCD deteriorates with increasing $n$, the gluon condensate contribution increases sharply for $n>2$, and the uncertainties in $\alpha_{s}$ and the renormalization scale $\mu$ have a greater impact on the total error of the charm-quark mass. On the other hand, direct kernels of the form $p(s)=s^{n}$, with $n\geq 1$, pose problems. Indeed, the high energy expansion of the vector correlator is incompletely known at $\mathcal{O}[\alpha^{3}_{s}]$, so that the greater the value of $n$ the greater is the contribution of the higher order mass corrections at this order in PQCD. Already with $n=1$ one would need a Pade approximation for the term $\mathcal{O}[\alpha^{3}_{s}\bar{m}_{c}^{6}]$. Hence, in order to avoid any approximation up to this order in PQCD we restrict ourselves to direct moments with $n=0$, and include inverse powers in an attempt to enhance the contribution of the well known narrow resonances, $J/\psi$ and $\psi(2S)$, and at the same time suppressing the broad resonance region. We found that Eq.(8) with $n=2$ is the optimal kernel as explained next. In Fig.1 we show the experimental data for the ratio $R(s)$ together with the kernel Eq.(8) with $n=2$ and $s_{0}\simeq\;23\;\mbox{GeV}^{2}$, and the simple kernel $p(s)=1/s^{2}$ normalized such that both kernels coincide at the peak of the second narrow resonance $\psi(2S)$, i.e. $s\simeq 13.6\;\mbox{GeV}^{2}$. One can easily appreciate that in comparison with the latter, the former kernel leads to a welcome enhancement of the weight of the $J/\psi$, as well as to a strong suppression of the broad resonance region, and particularly the region near the onset of the continuum. Quantitatively, the ratio of the area under the hadronic spectral function weighted with $p(s)$, in the narrow resonance region, ${\cal{I}}_{nr}$, and in the broad resonance region and beyond, ${\cal{I}}_{br}$, is ${\cal{I}}_{nr}/{\cal{I}}_{br}=3.6$ for $p(s)=1/s^{2}$, and ${\cal{I}}_{nr}/{\cal{I}}_{br}=7.7$ for Eq.(8) with $n=2$. Other values of $n$ lead to slightly less enhancement. In addition, the kernel Eq.(8) with $n=2$ leads to final results for $\overline{m}_{c}$ which are fairly insensitive to the choice of $s_{0}$. For instance, in the range $s_{0}\simeq\;15.0-23.0\;\mbox{GeV}^{2}$, $\overline{m}_{c}(3\;\mbox{GeV})$ changes by about $4.0\;\mbox{MeV}$, while using the kernel $p(s)=1/s^{2}$ it changes by $14.0\;\mbox{MeV}$.

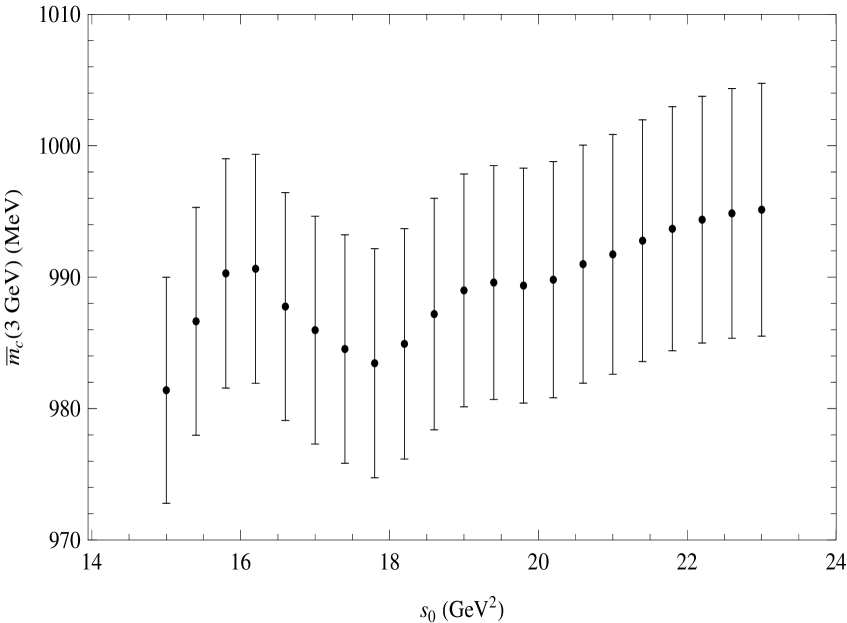
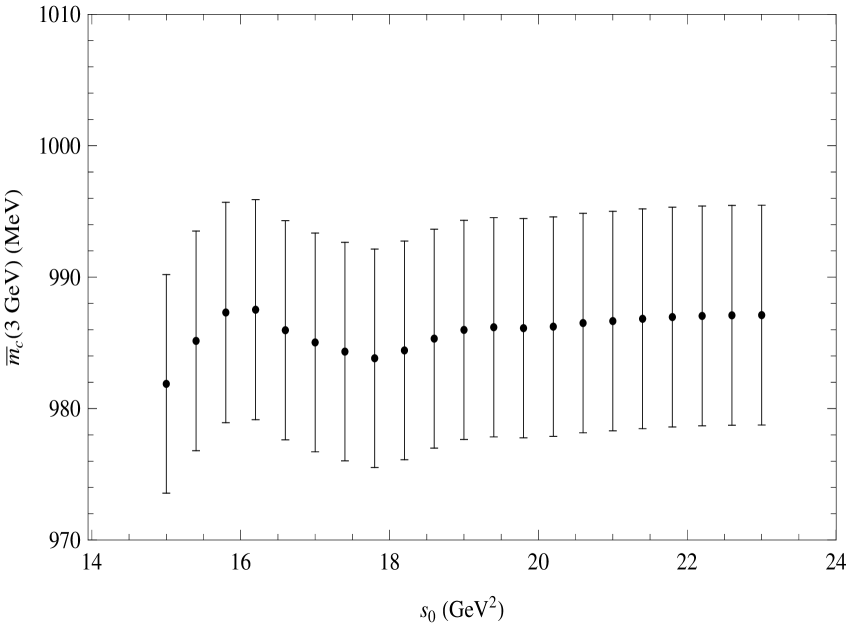
Proceeding to our determination we list in Table 1 the results for $\overline{m}_{c}(3\;\mbox{GeV})$ at different orders in perturbation theory, and using two integration kernels. The results for the kernel $p(s)=1/s^{2}$ differ from K as we use now a slightly different value of the strong coupling, of the gluon condensate, and of the $\psi(2S)$ parameters as given above, and we include the CLEO data EXP4 . The various errors associated to the final value of $\overline{m}_{c}(3\;\mbox{GeV})$ are given in Table 2. Results from Fixed Order Perturbation Theory (FOPT) are essentially the same as using Contour Improved Perturbation Theory (CIPT) to integrate around the circle of radius $s_{0}$ in the complex s-plane. In Fig.2 we show the results for $\overline{m}_{c}(3\;\mbox{GeV})$ as a function of $s_{0}$ for the kernel $p(s)=1/s^{2}$, and in Fig. 3 for the kernel Eq.(8) with $n=2$, the latter exhibiting improved stability.

The convergence pattern in $\alpha_{s}$ of the PQCD integral as a function of $\overline{m}_{c}$ can be studied by computing

with these integrals being functions of both $\overline{m}_{c}$ and $\alpha_{s}$. Using $\overline{m}_{c}(3\;\mbox{GeV})=987\;\mbox{MeV}$, and Eq.(8) with $n=2$ we find reasonable convergence, i.e. ${\cal{I}}^{(0)}=91.4\;\mbox{GeV}^{2}$, ${\cal{I}}^{(1)}=62.0\;\mbox{GeV}^{2}$, ${\cal{I}}^{(2)}=57.0\;\mbox{GeV}^{2}$, and ${\cal{I}}^{(3)}=56.3\;\mbox{GeV}^{2}$, where the upper index in ${\cal{I}}^{(j)}$ indicates the power of $\alpha_{s}$.

Our final result using the optimal kernel, Eq.(8), with $n=2$ is

in good agreement within errors with the result from inverse moment QCD sum rules K , other recent determinations charm -hoang , MC2 , SIGNER , as well as lattice QCD LATT . Translated into a scale invariant mass, the above result gives $\bar{m}_{c}(\bar{m}_{c})=1278\,\pm\,9\;\mbox{MeV}$ for the value used here for the strong coupling.