qeirreps: an open-source program for Quantum ESPRESSO to compute irreducible representations of Bloch wavefunctions
Abstract
Bloch wavefunctions in solids form a representation of crystalline symmetries. Recent studies revealed that symmetry representations in band structure can be used to diagnose the topological properties of weakly interacting materials. In this work, we introduce an open-source program qeirreps that computes the representation characters in a band structure based on the output file of Quantum ESPRESSO. Our program also calculates the index, i.e., the sum of inversion parities at all time-reversal invariant momenta, for materials with inversion symmetry. When combined with the symmetry indicator method, this program can be used to explore new topological materials.
keywords:
Quantum ESPRESSO; Irreducible representations; Non-symmorphic space groups.PROGRAM SUMMARY
Program title: qeirreps
Catalogue identifier:
Licensing provisions: GNU General Public Licence 3.0
Programming language: Fortran 90
Computer: any architecture with a Fortran 90 compiler
Operating system: Unix, Linux
RAM: Variable, depends on the complexity of the problem
External routines/libraries used:
-
1.
BLAS (http://www/netlib.org/blas)
-
2.
LAPACK (http://www.netlib.org/lapack)
Nature of problem: Irreducible representations of Bloch wavefunctions
Solution method: Linear algebra calculation for Bloch wavefunctions
Running time: 1 min - 1 h (strongly depends on the complexity of the problem)
1 Introduction
One of the main goals in condensed matter physics is to predict the properties of materials of our interest by solving the Schrödinger equation. In practice, this challenging problem is reduced to a manageable one in two ways. The first is to map the interacting system to a free (i.e., noninteracting) electronic system, as is done in the Kohn-Sham density functional theory (DFT) [1]. The other simplification utilizes the symmetry of the system. For example, the lattice translation symmetry of an ideal crystal that is free from impurities or disorders allows us to block-diagonalize the Hamiltonian by switching to the momentum space. The original problem of interacting electrons is thereby transformed into the one within the standard band theory. The electronic structure of an enormous number of weakly interacting materials has been successfully computed in this way.
In addition to the lattice translation symmetry, a perfect crystal tends to have other symmetries such as a spatial inversion and a discrete rotation. The set of symmetry operations of a crystal forms a group, called space group. In three dimensions, there are 230 different space groups, and the spatial symmetry of the crystal at work falls into one of them. Crystalline symmetries help us to a better understanding on the electronic band structure. Bloch wavefunctions form a representation of the space group, and the representation puts constraints on how many energy bands degenerate at each momentum and how energy bands at different momenta connect with each other. Furthermore, there has been an increasing number of evidence that the space group representation also informs us of the topological aspects of the Bloch wavefunction.
Since the discovery of the topological insulator [2, 3], topological materials have attracted researchers around the world. In the early stage of the study of topological phases, the focus was on the phases protected by internal symmetries: the time-reversal, the particle-hole, and the chiral symmetry [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]. These pioneering studies were united into the celebrated topological periodic table [19, 20, 21]. They were followed by a large number of studies that take into account the various types of crystalline symmetries [22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38]. It turned out that there exist various novel topological phases protected by crystalline symmetries [22, 27, 28, 29, 30, 31, 39, 40, 41, 42], such as mirror Chern insulators [43, 44], higher-order topological insulators [39, 41, 42, 45, 46, 47, 48], and topological semimetals of the Dirac [49] and Weyl [50] type. These topological materials host robust surface states and exhibits unique bulk responses, which could be leveraged for new low-power devices. Therefore, discovering new candidates of topological materials is one of the important tasks both for the fundamental physics and for the application.
At this moment, listing up the full set of topological invariants, for a given symmetry setting, that completely characterize all possible topological phases is still a pending problem. Furthermore, even if we know the mathematical definition of topological invariants, it is sometimes difficult to compute them directly using their definitions [28, 31, 32]. These issues can be resolved with the help of crystalline symmetries. By using the information of the representations of the Bloch wavefunctions at a set of crystalline momenta, it is sometimes possible to judge the topology encoded in the Bloch wavefunctions quite easily. The prototypical example is the Fu-Kane formula [9], which determines the invariant based on the inversion parities. Recently, this idea has been extended to a wider class of topological (crystalline) insulators and semimetals in all 230 space groups. The generalized schemes are nowadays known as the method of “symmetry indicators” [51, 52] and “topological quantum chemistry” [53]. Their usefulness in the search for realistic topological materials was clearly demonstrated by the recent comprehensive survey of topological materials among existing databases of inorganic substances [54, 55, 56, 57, 58]. As a result of this survey, thousands of candidates of topological (crystalline) insulators and semimetals have been identified. The theory of symmetry indicators has also been extended to magnetic space groups [59] and superconductors [60, 61, 62, 63, 64, 65], and further investigation of topological magnetic materials and superconductors is awaiting us.
Having in mind these applications, it is evidently important to make it possible to automatically compute irreducible representations of Bloch wavefunctions by using DFT. Although the authors of Refs. [54, 55, 56, 57, 58, 66] implemented this function for WIEN2k [67] and VASP [68], these softwares require paid licenses. In contrast, for the Quantum ESPRESSO [69, 70], which is a free, open-source package, the existing program can handle only one type of space groups, called “symmorphic” space groups, and does not work for the other type, called “non-symmorphic.” Given this situation, we develop an open-source code, named qeirreps, that works equally for symmorphic and non-symmorphic space groups. This would allow everyone to compute the band structure and determine the irreducible representations by themselves, and when combined with the method of symmetry-indicator, would help our search of novel topological materials like topological superconductors as partially demonstrated in Ref. [71].
The rest of this paper is organized as follows. In Sec. 2, we briefly review the theoretical background of space groups and their representations. In Sec. 3, we explain the installation and usage of qeirreps. After providing some examples: bismuth, silicon, NaCdAs, and PbPt3 in Sec. 4, we conclude in Sec. 5.
2 Theoretical background
We start with reviewing the basics of space groups and their representations.
2.1 Space group action on the real and momentum space
Let us consider a space group . An element moves to
| (1) |
where represents the point group part and represents the translation part of . The product of two elements and is defined by
| (2) |
In general, is not necessarily a lattice vector. If we can choose the origin of in such a way that becomes a lattice vector simultaneously for all , the space group is symmorphic; otherwise, it is nonsymmorphic. Nonsymmorphic space groups typically contain either screw axes or glide planes.
A space group always has a subgroup composed of lattice translations. An element of can be characterized by a lattice vector . We introduce the wavevector through the representation of the translation symmetry .
An element changes to . We say is invariant under when with a reciprocal lattice vector . For each , the set of that leaves invariant, i.e., , forms a subgroup of called the little group . Since is also an infinite group due to its translation subgroup , sometimes the finite group , called “little co-group [72],” is discussed instead. In this work, we always consider the little group .
2.2 Crystalline symmetries of band structures
The space group symmetry can be encoded in the single-particle Hamiltonian in momentum space by requiring
| (3) |
for each , where is a unitary matrix forming a representation of . For spinful electrons, relevant representations become ‘projective’ (in contrast to the ordinary ‘linear’ representation) and ’s satisfy
| (4) |
for . The projective factor is not unique, and we choose it as in Eq. (9). For spin-rotation invariant systems, can be set by neglecting the spin degree of freedom.
There is a way of treating projective representations of as linear representations of an enlarged group who has the doubled number of elements. This method is known as ‘double group,’ and is commonly used, for example, in Ref. [73]. In this treatment, contains both for each element of , and the product of and is defined by . See C for an example. Whether one handles projective representations directly, as we do in our program, or via the double group method does not affect the physical conclusion. See more detailed discussions on the relationship between projective representations and double groups in Refs. [74, 75].
The single-particle Hamiltonian can be diagonalized as
| (5) |
where () is the -th energy level of and is the identity matrix whose size is given by the order of degeneracy of . The unitary matrix is composed of all eigenvectors of . When is an element of , can also be block-diagonalized by as
| (6) |
Here, is the representation of of the -th band. Although the specific representation depends on the detailed choice of , its character
| (7) |
is basis independent. The output of our program is the list of characters for each the energy level at each high-symmetry point .
In the absence of accidental degeneracy or symmetries other than , the representation is automatically irreducible. That is, the character of the -th band coincides with one of the characters of irreducible representations of . Otherwise, can be decomposed into irreducible representations as , where the multiplicity of each irreducible representation is given by the formula
| (8) |
Our output file provides the list of and in irreps_list.dat and irreps_number.dat, respectively. 111Note that the output of our program is the character of representations of , not , and one should not confuse them. Irreducible representations of and are related to each other by a simple rule, and one can convert one to the other easily.
2.3 Application
The sum of integers in Eq. (8) over all filled bands, i.e., , counts the irreducible representation below the Fermi level at each high-symmetry point . The integers can be used, for example, to diagnose the topology of band insulators through the method of symmetry indicators [51, 52] or the topological quantum chemistry [53]. These methods diagnose the topology of the target material by comparing its irreducible representations with those of atomic insulators. Useful formulas of topological indices in terms of are provided in Refs. [76, 77, 78, 60].
For the user’s convenience, we implemented the function that automatically computes the index as the sum of the inversion parities of all occupied bands at all the time-reversal invariant momenta (TRIMs). The index can detect not only strong topological insulators but also topological crystalline insulators such as mirror Chern insulators or higher-order topological insulators [77, 78]. See Sec. 4.1 for an example. Other symmetry indicators can also be computed in the same way using the output of our program. We discuss several examples in Sec. 4.4.
2.4 Conventions
Let us summarize our conventions that are necessary to compare the output of our program with that of others. There are three sources of ambiguities that affect the U(1) phase of the representation : (i) the choice of representatives of , (ii) the choice of the coordinates, and (iii) the choice of spin rotation matrices. Readers not interested in the details can skip to Sec. 3.
2.4.1 The choice of representatives of
Although the number of elements of is infinite because of its translation subgroup, in the actual calculation, it is sufficient to discuss a finite number of elements by choosing one for each . This is because, if differs from by its translation part (i.e., and for a lattice vector ), the little-group representation of is simply given by . The choice of ’s is not unique, and in our program, they are automatically selected by Quantum ESPRESSO based on the input file. The chosen elements of are stored in our output files: the list of ’s is in pg.dat and the list of the corresponding ’s is in tg.dat.
2.4.2 The choice of the coordinates
When using Quantum ESPRESSO, one needs to prepare an input file that contains the information of the coordinates of atomic positions. In Quantum ESPRESSO, the fixed point of point group symmetries is always set to , and the input file must be carefully prepared. For a given material, even after fixing the symmetry operation, there can still be multiple choices of the coordinates, and the irreducible representations can in general be affected by this choice. In our examples discussed in Sec. 4, the information of the chosen coordinates is stored in the input file named *.scf.in.
To see this subtlety through a simple example, let us consider the inversion symmetric 1D system illustrated in Figure 1. In this model, there are two atoms A and B in a unit cell. In the panel (a), the atom A is placed at the origin and the coordinate of the atom B is . In the panel (b), the atom B is placed at the origin and the coordinate of the atom A is . This is the ambiguity of the coordinates mentioned above. In both cases, the inversion symmetry is about the origin , but the atom at the fixed point is different. This means that the inversion in (a) and that in (b) are physically different operations. As a consequence, their representations are not the same and are related by .
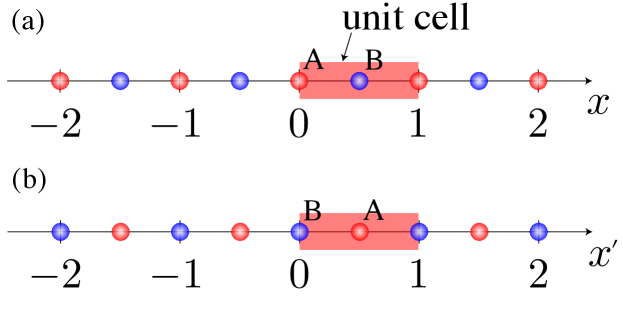
2.4.3 The choice of the spin rotation
As is well-known, the correspondence between a point group element and the spin rotation matrix has a sign ambiguity. Namely, when denotes a spin rotation matrix corresponding to the point group , is also an equally valid choice of the spin rotation matrix, and there is no unique way of resolving the ambiguity. Our choice of is stored in srg.dat.
Given the choice of for each , we fix the projective factor in Eq. (4) by
| (9) |
The information of is stored in factor_system_spin.dat.
3 Installation and usage
Here we explain how to install and use qeirreps. The flowchart of the calculations is shown in Figure 2.
3.1 Compiling environment for qeirreps
A Fortran 90 compiler, BLAS, and LAPACK libraries are required for the installation of qeirreps. Quantum ESPRESSO must also be installed in advance. In addition, the program qe2respack [79] 222This program qe2respack is a part of the program package RESPACK [79]. qe2respack in the latest version of RESPACK does not support DFT calculations with spin-orbit coupling. For calculations with spin-orbit coupling, we need the specific version of qe2respack described in this section. is required, which can be downloaded or cloned from the branch of respack “maxime2” in the GitHub repository (https://github.com/mnmpdadish/respackDev/). The program qe2respack.py is in the directory util/qe2respack.
3.2 Installation of qeirreps
Our program qeirreps is released at GitHub (https://github.com/qeirreps/qeirreps). The program files which contain source files, documents, and examples can be cloned or downloaded from this repository. The file qeirreps/src/Makefile must be edited to specify the compiler and libraries in your compiling environment. By typing $ make in the source directory qeirreps/src/, the executable binary qeirreps.x is compiled.
3.3 Preparing input files of qeirreps
Our program qeirreps works based on the output of Quantum ESPRESSO. To prepare input files of qeirreps, the following three steps are needed to be done one by one:
-
1.
Self-consistent first-principles (scf) calculation of a target material.
-
2.
Non-self-consistent first-principles (nscf) calculation of the material for each high-symmetry momentum.
-
3.
Data conversion from Quantum ESPRESSO output files to qeirreps input files.
The first two steps can be carried out by the standard functions of Quantum ESPRESSO. The result of the scf calculation is used in the successive nscf calculation. The set of high-symmetry points to be included in the calculation depends on the purpose of the calculation and the space group of the target material. When one applies the results of qeirreps to symmetry indicators or topological quantum chemistry, the minimum set of high-symmetry points are listed in Refs. [78, 57, 58].
We refer to the directory that stores the wavefunction data computed by the nscf calculation OUTDIR/PREFIX.save below. For the moment, qeirreps requires norm-conserving calculations. Pseudo-potentials must be optimized for norm-conserving calculations (for example, Optimized Norm-Conserving Vanderbilt Pseudopotential [80] is available in PseudoDojo (http://www.pseudo-dojo.org) [81]) and the option wf_collect should be set .TRUE. in the input files for DFT calculations.
The output files in OUTDIR/PREFIX.save must be converted by qe2respack into the form of input files of qeirreps. The work directory is referred to as DIRECTORY_NAME here. Then, type the following in the work directory:
where PATH_OF_qe2respack is the path to the directory util/qe2respack. qeirreps reads the files produced by qe2respack.py in the dir-wfn directory. The contents of these files are summarized in Table 1.
| File name | Information |
|---|---|
| dat.atom_position | The positions of atoms |
| dat.bandcalc | The energy cutoff for the wavefunction, Fermi energy, and total energy |
| dat.sample_k | The high-symmetry momenta |
| dat.eigenvalue | The energy level of each band |
| dat.nkm | The number of reciprocal lattice vectors used in |
| the expansion of wavefunctions at each momentum | |
| dat.kg | The set of reciprocal lattice vectors used in |
| the expansion of wavefunctions at each momentum | |
| dat.wfn | The Bloch wavefunction of each band |
| dat.lattice | The lattice vectors |
| dat.symmetry | The symmetry operators |

3.4 Running qeirreps
To run qeirreps, a directory named output must be created in the directory DIRECTORY_NAME above. Then type
where PATH_OF_qeirreps is the path to the directory qeirreps/src. There should be 12 output files in output. Seven of them named *.dat contain the following information: (i) the list of the point group part in pg.dat, (ii) the list of the translation part in tg.dat, (iii) the list of the spin rotation part in srg.dat, (iv) the factor system associated with the electronic spin in factor_system_spin.dat, (v) the representation characters of Bloch wavefunctions in character.dat, (vi) the characters of irreducible representations of in irreps_list.dat, and (vii) the numbers of irreducible representations of in the -th energy level in irreps_number.dat. The contents of these files are summarized in Table 2. Five of them named *_import.txt are the corresponding files for Mathematica usage. The standard output that appears during this calculation shows the lattice vectors, reciprocal lattice vectors, operation type of each symmetry operators, and so on.
For materials with inversion symmetry, qeirreps also implements the automatic evaluation of the index. To do this, an option of filling should be added to the command as
Here, z4 is the option to obtain the index and FILLING is the number of electrons per unit cell of the target material and is shown in the standard output of scf calculation by Quantum ESPRESSO as “number of electrons = FILLING.” Then, the program generates an additional output named z4.dat that contains the value of the index.
Our program qeirreps also provides the input file for the tool CheckTopologicalMat (https://www.cryst.ehu.es/cgi-bin/cryst/programs/topological.pl) [57]. Our program exports the input file named Bilbao.txt with the following command
where ctm is the option to obtain the input file. The tool CheckTopologicalMat tells us topological properties such as the value of symmetry indicators and gaplessness.
| File name | Information |
|---|---|
| pg.dat | The point group part () of each symmetry operation |
| tg.dat | The translation part () of each symmetry operation |
| srg.dat | The spin rotation part () of each symmetry operation |
| factor_system_spin.dat | The factor system () associated with the electric spin |
| character.dat | The character tables of irreducible representations of Bloch wavefunctions |
| irreps_list.dat | The characters () of irreducible representations of |
| irreps_number.dat | The numbers () of irreducible representations of in the -th energy level |
| z4.dat# | The index |
| Bilbao.txt# | The input file for CheckTopologicalMat [57] |
4 Examples
In this section, we discuss several examples to demonstrate the usage of qeirreps. We also explain how to compute topological indices based on the output of qeirreps. In all the examples, we use the primitive unit cell in the calculation of the band structure and the space group representations in the band structure.
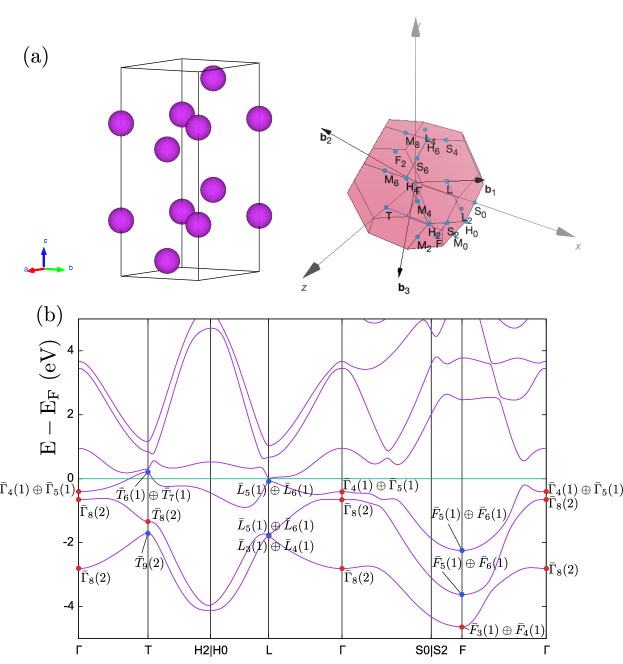
4.1 Bismuth
Our first example is bismuth. The space group (No.) contains the inversion symmetry . We obtain the crystal structure data of bismuth [Figure 3 (a)] from Material Project [82] and converted it into the form of an input file for Quantum ESPRESSO (included in A.1) by SeeK-path [83, 84] 333In this particular example, we manually shifted positions of atoms in the primitive unit cell so that we can compare our results with the one in Ref. [57].
We compute the irreducible representations of wavefunctions by qeirreps, taking into account the spin-orbit coupling. Our results are shown in the band structure in Figure 3 (b). The correspondence between the labels and characters of irreducible representations is included in B.1. These results are consistent with previous studies [57, 73].
We also compute the index [77, 78] using the option explained in Sec. 3.4. The output (z4.dat) shows
| sum of parities for 8 k-points: | ||
| -7.99999999999963 | ||
| z4 index: | ||
| 2 |
Namely, the index for bismuth with significant spin-orbit coupling is , indicating that this material is a higher-order topological insulator [85, 58, 57, 86]. The sample input files for bismuth are available in the directory qeirreps/example.
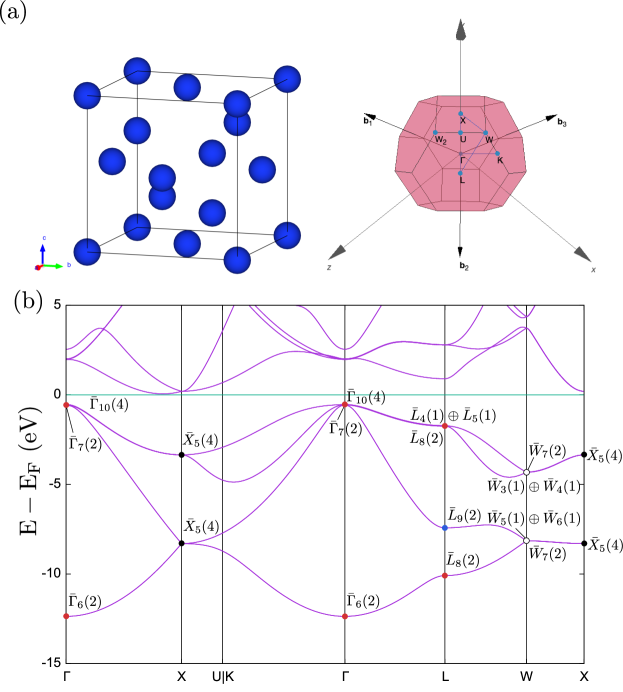
4.2 Silicon
To demonstrate that qeirreps equally works for nonsymmorphic space groups, let us discuss silicon. Its space group is (No. ), which also contains the inversion symmetry . The calculation procedure is completely the same as those for bismuth in Sec. 4.1. Our results of irreducible representations are in Figure 4 (b). The index is found to be zero. These results are consistent with the previous study in Ref. [57]. Sample input files for silicon are also in the directory qeirreps/example.
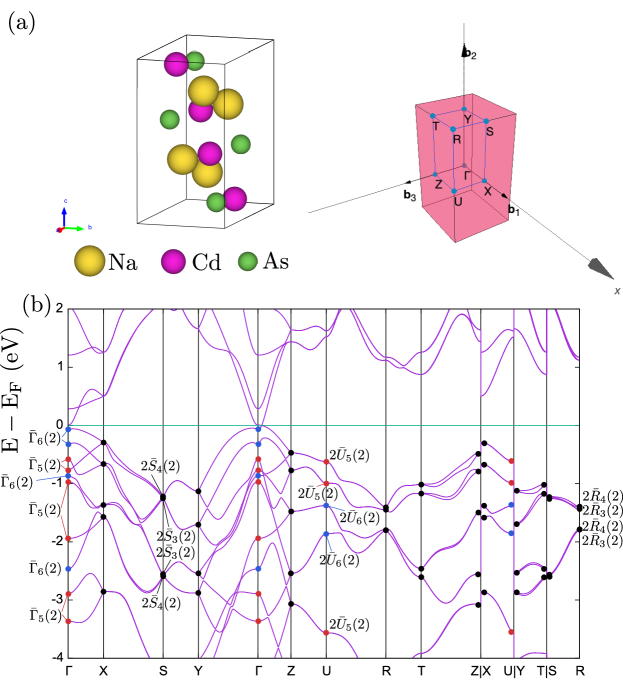
4.3 NaCdAs
Here we discuss NaCdAs as an example of topological materials with nonsymmorphic space group symmetries. Its space group is (No. ) which has the inversion symmetry . Irreducible representations computed in the presence of spin-orbit coupling are shown in Figure 5 (b). The index is 1, indicating that this material is a candidate of the strong topological insulator. These results are consistent with the previous study in Ref. [57]. (The index in Ref. [57] is 3 because their definition of the index includes an additional minus sign.) Sample input files for NaCdAs are contained in the directory qeirreps/example.
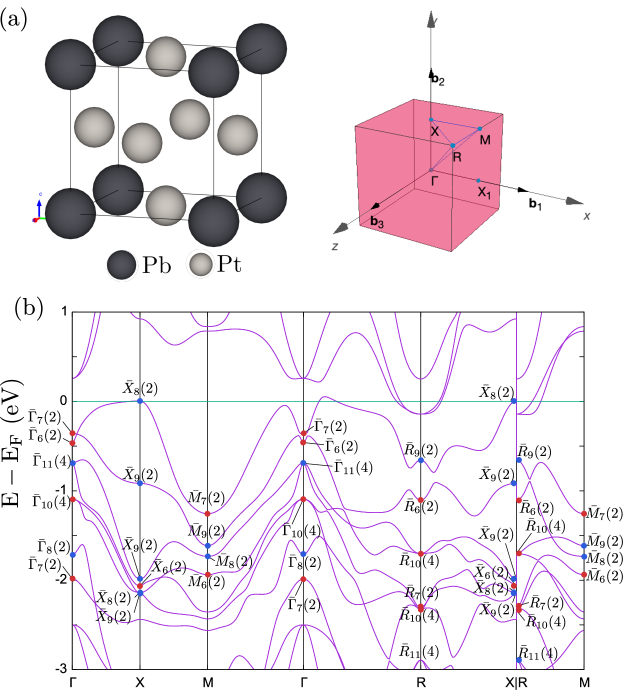
4.4 PbPt3
As our fourth example, let us discuss PbPt3, whose space group (No. ). This space group contains various elements such as the inversion , the rotoinversion about the -axis , and the mirror symmetries. We also assume the time-reversal symmetry. Our results of irreducible representations in the presence of spin-orbit coupling are in Figure 6 (b).
In this symmetry settings, we can define a index (other than the sum of the inversion parities) and a index by [87, 77, 78]
| (10) | ||||
| (11) |
where represents the number of occupied states that have irreducible representations of , and the set of is included in B.8. denotes four momenta invariant under the . Although our program qeirreps does not offer an automated calculation of these indices, one can compute them manually by using character.dat or uploading Bilbao.txt to CheckTopologicalMat [57]. In this example, we find , which is consistent with Ref. [57]. According to Ref. [77, 78], these values indicate nontrivial mirror Chern numbers. Sample input files for PbPt3 are included in qeirreps/example.
5 Conclusions
In conclusion, we developed a new open-source code qeirreps for computing irreducible representations in band structures based on the output of Quantum ESPRESSO. We explained the installation of the program and demonstrated its usage through examples. When combined with the symmetry indicator method, the output of this program can be used to diagnose the topological property of weakly interacting materials. Since Quantum ESPRESSO is a free, widely-used software, qeirreps should accelerate the exploration of new topological materials.
Acknowledgement
We thank Ryotaro Arita and Motoaki Hirayama for frutuful discussions. We also thank Luis Elcoro for useful and kind correspondence. We are very grateful to the anonymous referee of this manuscript for his or her constructive comments and suggestions. All DFT calculations in this work has been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo. The work of AM and SO is supported by Materials Education program for the future leaders in Research, Industry, and Technology (MERIT). SO is also supported by the ANRI Fellowship and JSPS KAKENHI Grant No. JP20J21692. The work of YN is supported by JSPS KAKENHI Grant No. 16H06345, 17K14336, 18H01158, 20K14423. The work of HW is supported by JSPS KAKENHI Grant No. JP17K17678 and by JST PRESTO Grant No. JPMJPR18LA.
Appendix A Samples of Quantum ESPRESSO input
A.1 For the scf calculation of bismuth
A.2 For the nscf calculation of bismuth
A.3 For the scf calculation of silicon
A.4 For the nscf calculation of silicon
A.5 For the scf calculation of NaCdAs
A.6 For the nscf calculation of NaCdAs
A.7 For the scf calculation of
A.8 For the nscf calculation of
Appendix B Information of irreducible representations
The notations of irreducible representations in the following tables follow Ref. [73]. Note that some characters have different values due to the choice of fractional translations and spin rotation matrices .
B.1 Character tables for bismuth [73]
table
table
table
table
B.2 Irreducible representations of bismuth
table
| 30 | |
|---|---|
B.3 Character tables for silicon [73]
table
| 0 | |||||||
| 0 | |||||||
| 0 | 0 | 0 | 0 | ||||
| 0 | |||||||
| 0 | 0 | 0 | 0 |
table
| 2 | 2 | -2 | -2 | 4 | -4 | ||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
table
table
table
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 |
B.4 Irreducible representations of silicon
table
| 8 | |
|---|---|
B.5 Character tables for NaCdAs [73]
table
table
table
table
table
table
table
table
B.6 Irreducible representations of NaCdAs
table
| 176 | |
|---|---|
B.7 Character table for [73]
table
| 0 | |||||||
| 0 | |||||||
| 0 | 0 | 0 | 0 | ||||
| 0 | |||||||
| 0 | 0 | 0 | 0 |
table
| 2 | 2 | -2 | -2 | 4 | -4 | ||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
table
table
| 0 | |||||||
| 0 | |||||||
| 0 | 0 | 0 | 0 | ||||
| 0 | |||||||
| 0 | 0 | 0 | 0 |
table
| 2 | 2 | -2 | -2 | 4 | -4 | ||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
| 1 | 1 | 1 | |||||
table
B.8 Irreducible representations of
table
| 68 | |
|---|---|
Appendix C Double group
Here we provide an example of projective representations to clarify the relation to the double group.
C.1 Definition of the group
We discuss the point group , which is isomorphic to . As a set, contains four elements: , where is the identity and , , and are, respectively, the two-fold rotation about , , and axis. The group product is defined by
| (12) | |||
| (13) | |||
| (14) | |||
| (15) |
C.2 Linear representations of the group
Linear representations of must satisfy
| (16) |
There are four linear representations of , which are all 1D representations. They are given by , , , and , where and .
C.3 Projective representation of the group
Projective representations of must satisfy
| (17) |
for a projective factor obeying the co-cycle condition for .
As an example, let us set
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) |
There is only one projective representation for this particular , which reads , , , . Here, is the 2D identity matrix and , , and are the Pauli matrices.
The choice of is not unique. For example, one can instead use
| (23) | |||
| (24) |
When all other components are unchanged, the corresponding projective representation is given by , , , . Other possible choices of can also be generated by the replacement and . ( must be chosen in such a way that the co-cycle condition is respected.)
C.4 Definition of the double group of the group
In the double group approach, we consider the linear representation of an enlarged group . contains both and for each element of . Hence, has eight elements in total. Given a projective factor , the group product of is defined by
| (25) |
Clearly, the very definition of the double group (i.e., the product rule itself) depends on the choice of .
C.5 Linear representation of the double group of the group
Let us assume our first choice of above. There are four 1D linear representations of , given by , , , and , where , , and . There is also one 2D linear representation of , given by , , , for .
In the double group treatment of the projective representation, one must choose linear representations of that satisfy for every and . Hence in this example, the valid choice is given by the 2D representation. The projective representation of we obtained in C.3 can be reproduced by setting for each .
References
- Kohn and Sham [1965] W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965).
- Kane and Mele [2005a] C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005a).
- Kane and Mele [2005b] C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 226801 (2005b).
- Bernevig et al. [2006] B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006).
- König et al. [2007] M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X.-L. Qi, and S.-C. Zhang, Science 318, 766 (2007).
- Fu and Kane [2006] L. Fu and C. L. Kane, Phys. Rev. B 74, 195312 (2006).
- Fu et al. [2007] L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007).
- Moore and Balents [2007] J. E. Moore and L. Balents, Phys. Rev. B 75, 121306 (2007).
- Fu and Kane [2007] L. Fu and C. L. Kane, Phys. Rev. B 76, 045302 (2007).
- Hsieh et al. [2008] D. Hsieh, D. Qian, L. Wray, Y. Xia, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature 452, 970 (2008).
- Liu et al. [2008] C. Liu, T. L. Hughes, X.-L. Qi, K. Wang, and S.-C. Zhang, Phys. Rev. Lett. 100, 236601 (2008).
- Qi et al. [2008] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Phys. Rev. B 78, 195424 (2008).
- Hsieh et al. [2009] D. Hsieh, Y. Xia, D. Qian, L. Wray, J. H. Dil, F. Meier, J. Osterwalder, L. Patthey, J. G. Checkelsky, N. P. Ong, A. V. Fedorov, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature 460, 1101 (2009).
- Xia et al. [2009] Y. Xia, D. Qian, D. Hsieh, L. Wray, A. Pal, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature Physics 5, 398 (2009).
- Roy [2009] R. Roy, Phys. Rev. B 79, 195322 (2009).
- Yu et al. [2010] R. Yu, W. Zhang, H.-J. Zhang, S.-C. Zhang, X. Dai, and Z. Fang, Science 329, 61 (2010).
- Knez et al. [2011] I. Knez, R.-R. Du, and G. Sullivan, Phys. Rev. Lett. 107, 136603 (2011).
- Chang et al. [2013] C.-Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L.-L. Wang, Z.-Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S.-C. Zhang, K. He, Y. Wang, L. Lu, X.-C. Ma, and Q.-K. Xue, Science 340, 167 (2013).
- Schnyder et al. [2008] A. P. Schnyder, S. Ryu, A. Furusaki, and A. W. W. Ludwig, Phys. Rev. B 78, 195125 (2008).
- Kitaev [2009] A. Kitaev, AIP Conference Proceedings 1134, 22 (2009).
- Ryu et al. [2010] S. Ryu, A. P. Schnyder, A. Furusaki, and A. W. W. Ludwig, New Journal of Physics 12, 065010 (2010).
- Fu [2011] L. Fu, Phys. Rev. Lett. 106, 106802 (2011).
- Freed and Moore [2013] D. S. Freed and G. W. Moore, Annales Henri Poincaré 14, 1927 (2013).
- Morimoto and Furusaki [2013] T. Morimoto and A. Furusaki, Phys. Rev. B 88, 125129 (2013).
- Chiu et al. [2013] C.-K. Chiu, H. Yao, and S. Ryu, Phys. Rev. B 88, 075142 (2013).
- Chiu and Schnyder [2014] C.-K. Chiu and A. P. Schnyder, Phys. Rev. B 90, 205136 (2014).
- Shiozaki and Sato [2014] K. Shiozaki and M. Sato, Phys. Rev. B 90, 165114 (2014).
- Shiozaki et al. [2015] K. Shiozaki, M. Sato, and K. Gomi, Phys. Rev. B 91, 155120 (2015).
- Shiozaki et al. [2016] K. Shiozaki, M. Sato, and K. Gomi, Phys. Rev. B 93, 195413 (2016).
- Shiozaki et al. [2017] K. Shiozaki, M. Sato, and K. Gomi, Phys. Rev. B 95, 235425 (2017).
- Wang et al. [2016] Z. Wang, A. Alexandradinata, R. J. Cava, and B. A. Bernevig, Nature 532, 189 (2016).
- Fang and Fu [2015] C. Fang and L. Fu, Phys. Rev. B 91, 161105 (2015).
- Song et al. [2017a] H. Song, S.-J. Huang, L. Fu, and M. Hermele, Phys. Rev. X 7, 011020 (2017a).
- Kruthoff et al. [2017] J. Kruthoff, J. de Boer, J. van Wezel, C. L. Kane, and R.-J. Slager, Phys. Rev. X 7, 041069 (2017).
- Thorngren and Else [2018] R. Thorngren and D. V. Else, Phys. Rev. X 8, 011040 (2018).
- Huang et al. [2017] S.-J. Huang, H. Song, Y.-P. Huang, and M. Hermele, Phys. Rev. B 96, 205106 (2017).
- [37] K. Shiozaki, M. Sato, and K. Gomi, arXiv:1802.06694 .
- [38] Z. Song, S.-J. Huang, Y. Qi, C. Fang, and M. Hermele, arXiv:1810.02330 .
- Song et al. [2017b] Z. Song, Z. Fang, and C. Fang, Phys. Rev. Lett. 119, 246402 (2017b).
- Langbehn et al. [2017] J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen, and P. W. Brouwer, Phys. Rev. Lett. 119, 246401 (2017).
- Benalcazar et al. [2017a] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Science 357, 61 (2017a).
- Fang and Fu [2019] C. Fang and L. Fu, Science Advances 5, eaat2374 (2019).
- Tanaka et al. [2012] Y. Tanaka, Z. Ren, T. Sato, K. Nakayama, S. Souma, T. Takahashi, K. Segawa, and Y. Ando, Nature Physics 8, 800 (2012).
- Hsieh et al. [2012] T. H. Hsieh, H. Lin, J. Liu, W. Duan, A. Bansil, and L. Fu, Nature Communications 3, 982 (2012).
- Schindler et al. [2018a] F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Science Advances 4, aat0346 (2018a).
- Benalcazar et al. [2017b] W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Phys. Rev. B 96, 245115 (2017b).
- Matsugatani and Watanabe [2018] A. Matsugatani and H. Watanabe, Phys. Rev. B 98, 205129 (2018).
- Trifunovic and Brouwer [2019] L. Trifunovic and P. W. Brouwer, Phys. Rev. X 9, 011012 (2019).
- Young et al. [2012] S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele, and A. M. Rappe, Phys. Rev. Lett. 108, 140405 (2012).
- Wan et al. [2011] X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, Phys. Rev. B 83, 205101 (2011).
- Po et al. [2017] H. C. Po, A. Vishwanath, and H. Watanabe, Nat. Commun. 8, 50 (2017).
- Po [2020] H. C. Po, Journal of Physics: Condensed Matter 32, 263001 (2020).
- Bradlyn et al. [2017] B. Bradlyn, L. Elcoro, J. Cano, M. G. Vergniory, Z. Wang, C. Felser, M. I. Aroyo, and B. A. Bernevig, Nature 547, 298 (2017).
- Tang et al. [2019a] F. Tang, H. C. Po, A. Vishwanath, and X. Wan, Nat. Phys. 15, 470 (2019a).
- Tang et al. [2019b] F. Tang, H. C. Po, A. Vishwanath, and X. Wan, Sci. Adv. 5 (2019b).
- Zhang et al. [2019] T. Zhang, Y. Jiang, Z. Song, H. Huang, Y. He, Z. Fang, H. Weng, and C. Fang, Nature 566, 475 (2019).
- Vergniory et al. [2019] M. G. Vergniory, L. Elcoro, C. Felser, N. Regnault, B. A. Bernevig, and Z. Wang, Nature 566, 480 (2019).
- Tang et al. [2019c] F. Tang, H. C. Po, A. Vishwanath, and X. Wan, Nature 566, 486 (2019c).
- Watanabe et al. [2018] H. Watanabe, H. C. Po, and A. Vishwanath, Sci. Adv. 4, eaat8685 (2018).
- Ono and Watanabe [2018] S. Ono and H. Watanabe, Phys. Rev. B 98, 115150 (2018).
- Ono et al. [2019] S. Ono, Y. Yanase, and H. Watanabe, Phys. Rev. Res. 1, 013012 (2019).
- Skurativska et al. [2020] A. Skurativska, T. Neupert, and M. H. Fischer, Phys. Rev. Research 2, 013064 (2020).
- [63] K. Shiozaki, arXiv:1907.13632 .
- Ono et al. [2020a] S. Ono, H. C. Po, and H. Watanabe, Science Advances 6, eaaz8367 (2020a).
- Geier et al. [2020] M. Geier, P. W. Brouwer, and L. Trifunovic, Phys. Rev. B 101, 245128 (2020).
- Gao et al. [2020] J. Gao, Q. Wu, C. Persson, and Z. Wang, “Irvsp: to obtain irreducible representations of electronic states in the VASP,” (2020), arXiv:2002.04032 .
- Blaha et al. [2001] P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, and J. Luitz, WIEN2K, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universität Wien, Austria, 2001).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
- Giannozzi et al. [2009] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch, Journal of Physics: Condensed Matter 21, 395502 (2009).
- Giannozzi et al. [2017] P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu, and S. Baroni, Journal of Physics: Condensed Matter 29, 465901 (2017).
- Ono et al. [2020b] S. Ono, H. C. Po, and K. Shiozaki, “-enriched symmetry indicators for topological superconductors in the 1651 magnetic space groups,” (2020b), arXiv:2008.05499 .
- Bradley and Cracknell [1972] C. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids (Oxford University Press, 1972).
- Elcoro et al. [2017] L. Elcoro, B. Bradlyn, Z. Wang, M. G. Vergniory, J. Cano, C. Felser, B. A. Bernevig, D. Orobengoa, G. de la Flor, and M. I. Aroyo, Journal of Applied Crystallography 50, 1457 (2017).
- Watanabe et al. [2016] H. Watanabe, H. C. Po, M. P. Zaletel, and A. Vishwanath, Phys. Rev. Lett. 117, 096404 (2016).
- Watanabe et al. [2015] H. Watanabe, H. C. Po, A. Vishwanath, and M. Zaletel, Proceedings of the National Academy of Sciences (2015), 10.1073/pnas.1514665112, https://www.pnas.org/content/early/2015/11/09/1514665112.full.pdf .
- Song et al. [2018a] Z. Song, T. Zhang, and C. Fang, Phys. Rev. X 8, 031069 (2018a).
- Khalaf et al. [2018] E. Khalaf, H. C. Po, A. Vishwanath, and H. Watanabe, Phys. Rev. X 8, 031070 (2018).
- Song et al. [2018b] Z. Song, T. Zhang, Z. Fang, and C. Fang, Nat. Commun. 9, 3530 (2018b).
- Nakamura et al. [2020] K. Nakamura, Y. Yoshimoto, Y. Nomura, T. Tadano, M. Kawamura, T. Kosugi, K. Yoshimi, T. Misawa, and Y. Motoyama, arXiv preprint arXiv:2001.02351 (2020).
- Hamann [2013] D. R. Hamann, Phys. Rev. B 88, 085117 (2013).
- [van Setten] et al. [2018] M. [van Setten], M. Giantomassi, E. Bousquet, M. Verstraete, D. Hamann, X. Gonze, and G.-M. Rignanese, Computer Physics Communications 226, 39 (2018).
- Jain et al. [2013] A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, and K. a. Persson, APL Materials 1, 011002 (2013).
- Hinuma et al. [2017] Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba, and I. Tanaka, Computational Materials Science 128, 140 (2017).
- Togo and Tanaka [2018] A. Togo and I. Tanaka, arXiv preprint arXiv:1808.01590 (2018).
- Schindler et al. [2018b] F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, H. Bouchiat, S. Guéron, A. Yazdani, B. A. Bernevig, and T. Neupert, Nature Physics 14, 918 (2018b).
- Hsu et al. [2019] C.-H. Hsu, X. Zhou, T.-R. Chang, Q. Ma, N. Gedik, A. Bansil, S.-Y. Xu, H. Lin, and L. Fu, Proceedings of the National Academy of Sciences 116, 13255 (2019).
- Fang et al. [2012] C. Fang, M. J. Gilbert, and B. A. Bernevig, Phys. Rev. B 86, 115112 (2012).