Quadrupole Moment of 37K
Abstract
The electric quadrupole coupling constant of the ground state of 37K( = 3/2+, = 1.22 s) in a tetragonal KH2PO4 single crystal was measured to be MHz using the -ray detecting nuclear quadrupole resonance technique. The electric quadrupole moment of 37K was determined to be efm2, where the known electric quadrupole coupling constant of stable 39K in the KH2PO4 crystal was used as a reference. The present experimental result is larger than that predicted by shell-model calculations in the or the and model spaces. A possible variation of effective charges was explored to explain the discrepancy.
keywords:
37K , electric coupling constant , quadrupole moment , -ray detecting nuclear magnetic resonance (NMR) , -ray detecting nuclear quadrupole resonance (NQR) , shell modelPACS:
21.10.Ky , 21.60.Cs , 27.30. +t , 27.40.+z , 29.27.Hj , 29.38.-c, , , , , , and
1 Introduction
The spectroscopic electric-quadrupole moment () provides a direct measure of the deviation of the charge distribution in a nucleus from spherical symmetry. Proton and neutron effective charges are used in shell-model calculations to obtain quadrupole moments. Within a given shell-model space, the effective charges represent 2, = 2+ excitations of the core nucleons to valence orbits [1] and reflect the virtual excitation of the isoscalar and isovector giant quadrupole resonances. Values of effective charges for -shell nuclei have been obtained from a systematic analysis of experimental 2 matrix elements [1, 2] and give reasonable agreement between experimental and theoretical quadrupole moments. However, some nuclei show significant disagreement between experiment and theory. The neutron-rich B isotopes, for example, show a reduction of the neutron effective charge [3] because the loosely-bound valence neutrons, far removed from the core, have less probability to excite the core than well bounded neutrons. Neutron-deficient nuclei, especially those with small proton separation energies, may also be expected to show variation of effective charges. Experimental of such neutron-deficient nuclei are still scarce, even in the shell. Additional systematic data of of neutron-deficient nuclei are important to further improve our knowledge about the exotic structure of dripline nuclei.
The previously measured quadrupole moment of neutron-deficient 37K, (37K) = 11 4 efm2, was obtained from the hyperfine coupling constant of the state of the 37K atom [4]. In the evaluation of K), the coupling constant of the 39K [5] atom and K) evaluated with a calculated electric field gradient [6] were used as reference. The OXBASH shell-model calculation code [7] in the model space with the USDA interaction [8] gives (37K)theory=7.5 efm2. The experimental value is larger in magnitude, but within 1 error of the shell-model result.
K) was remeasured using a newly-developed -ray detecting nuclear quadrupole resonance ( NQR) technique, to improve the precision of the previous measurement and to clarify the possible deviation from shell-model expectations. The new result, K) = 10.6 0.4 efm2, is well away from the shell-model result calculated in the model space. An extension of the shell-model space to include both and shells also does not account for the large observed for the 37K ground state. A possible variation of effective charges from the traditional values was explored to explain the discrepancy between theory and experiment.
2 Experiment
The K) measurement was performed at National Superconducting Cyclotron Laboratory (NSCL) at Michigan State University. 37K ions were produced from a primary beam of 36Ar accelerated to 150 MeV/nucleon by the coupled cyclotrons and impinging on a 564 mg/cm2 9Be target. A charge pick-up reaction (36Ar + p 37K) was employed to produce 37K because a large nuclear polarization is expected at the peak of the momentum-yield curve of the fragment [9]. The primary beam was steered at an angle of relative to the normal beam axis at the production target in order to produce the polarized beam. 37K ions were separated from other reaction products by the A1900 fragment separator [10]. The full angular acceptance () of the A1900 was used. An achromatic wedge (1200 mg/cm2 Al) was placed at the second intermediate dispersive image to separate 37K based on relative energy loss in the wedge. The central momentum of the 37K beam was selected with a 1% momentum acceptance to optimize the polarization. A typical counting rate of 37K ions at the experimental apparatus was 50 particles/s/pnA and 40 pnA of primary beam was available. The major contamination in the secondary beam following the A1900 was stable 36Ar, which did not adversely impact the -NMR measurement.
The polarized 37K ions were delivered to the -NMR apparatus [11] and implanted into a tetragonal KH2PO4 (KDP) single crystal. The crystal was 2 mm thick and tilted by 45∘ relative to the -detector surface. An external magnetic field of = 0.45 T was applied parallel to the direction of polarization and orthogonal to the beam direction to provide the Zeeman splitting field and to maintain the polarization in KDP. 37K decays to the daughter 37Ar by emitting rays with a half life of 1.226 s. The branching ratio to the ground state ( = 3/2+) is 98.2%. The maximum -ray energy is 5.13 MeV. The asymmetry parameter for direct decay to the 37Ar ground state is = 0.57. rays from the stopped 37K ions were detected by a set of plastic scintillator telescopes placed at 0∘(u) and 180∘(d) relative to the external field direction. The counting rate between u and d counters is asymmetric for a polarized source. The angular distribution,
| (1) |
depends on the polarization , and the angle between the direction of momentum of decaying ray and the polarization axis.
The KDP crystal used for implantation had its c-axis set parallel to the external magnetic field. The electric field gradient, , at the K lattice site in KDP is axially symmetric (asymmetry parameter ) and parallel to the c-axis. The magnetic sub-level energies, , of the 37K implanted in KDP are given in this condition by
| (2) |
where is the magnetic quantum number, is the nuclear factor, is the normalized electric coupling constant, where is the electric coupling constant, and is the angle between the c-axis and external magnetic field. Eq. (2) is given to the first-order of , taking the electric interaction as a perturbation to the main magnetic interaction. Since the 37K nucleus implanted into KDP has a large electric interaction, the electric interaction can not be considered as a perturbation to the magnetic interaction. Higher-order terms of the electric interaction have to be considered. However, Eq. (2) and (3) derived later may be used for the system with and , where the first order perturbation calculation gives the exact transition frequencies. The first term in Eq. (2) indicates the magnetic sublevels separated by a fixed energy value due solely to the magnetic interaction (Zeeman splitting). These sublevels are further shifted by the electric interaction and the energy spacing between adjacent sublevels is no longer constant. The 2 separate transition frequencies that appear due to the electric interaction are determined as
| (3) |
The transition frequencies correspond to the energy difference between two adjacent energy levels in Eq. (2), since the allowed transitions have . Here is the Larmor frequency.
The NMR signal is obtained from a double ratio defined as
| (4) |
where the subscript, off(on), stands for without(with) RF applied and is the measured change in polarization between RF on and off conditions. The NMR signal can be most effectively searched by applying the 2 transition frequencies in Eq. (3) simultaneously, as a function of the electric coupling constant. Such application ensures total destruction (, where is the initial polarization produced in the nuclear reaction) of the polarization at the actual electric coupling constant and makes the measurement efficient. The NMR signal for a nucleus with = 3/2 is 10 times bigger for than that obtained by applying a single transition frequency, where only a partial destruction of can be achieved. A one day measurement with the multiple frequency technique would be at least a 100 days measurement with the single frequency technique. In this calculation, a linear distribution of populations in is assumed as and , where is a constant. This multiple frequency version of the -NMR technique is known as the -ray detecting nuclear quadrupole resonance ( NQR) technique and is discussed in detail elsewhere [12].
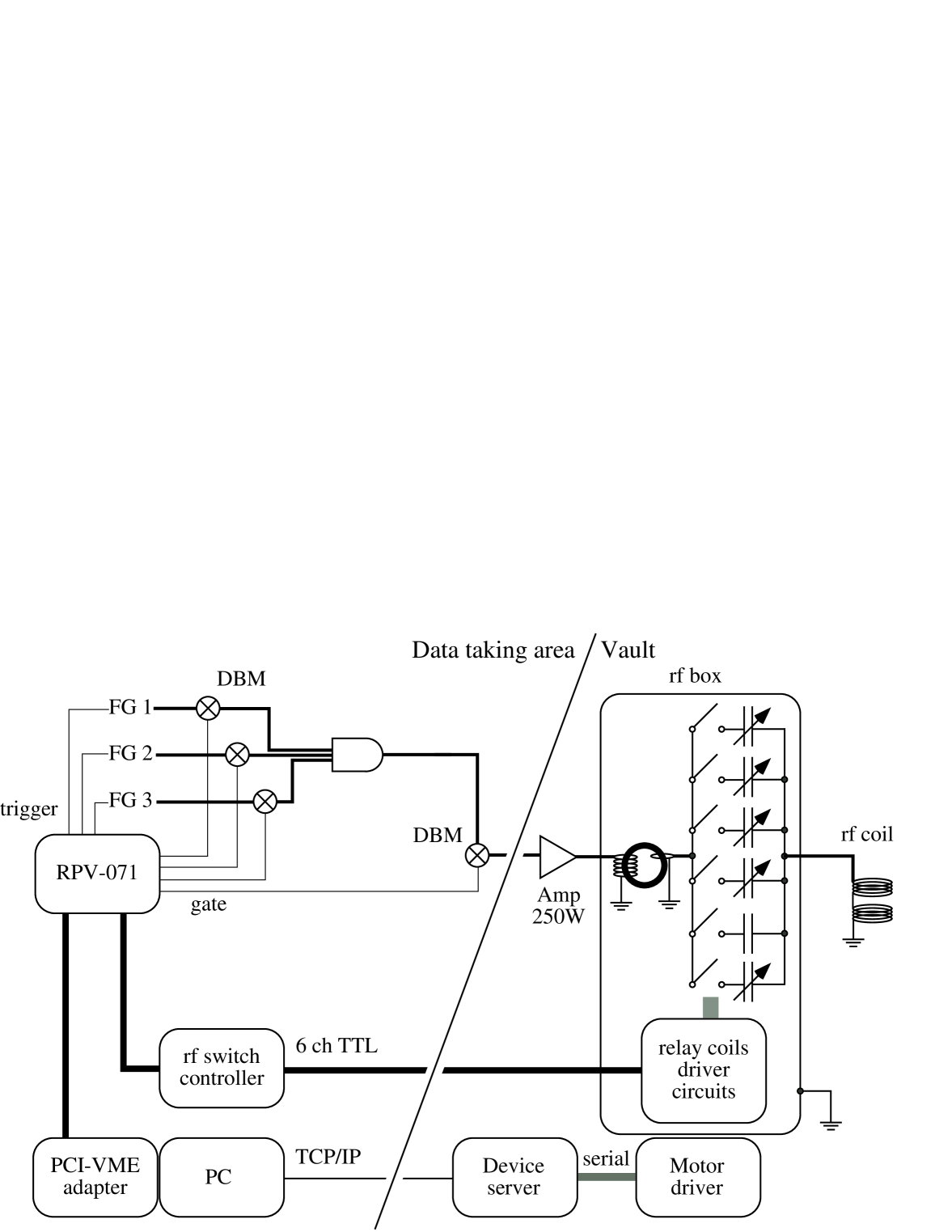
A schematic of the -NQR system at NSCL is shown in Fig. 1. An RF signal generated by a function generator (labeled FG 1) is selected by a gate (labeled DBM) and sent to an RF amplifier. The amplified signal is then applied to an RF coil, which is part of an LCR resonance circuit, with an impedance matching transformer and one of five variable capacitors and one fixed ( 10000 pF) capacitor. After 100 ms irradiation time, the frequency from FG 2 is selected by a gate signal and sent to the same LCR resonance circuit. A different capacitor, which has been tuned to the second frequency to satisfy the LCR resonance condition, is selected by the fast switching relay system. The system ensures sufficient power for any set of three transition frequencies over the expected search region of 1.9 4.0 MHz, so that a high transition probability is achieved. The transition frequency search range spans from 0.465 MHz to 2.465 MHz, as deduced from Eq. (3).
The electric coupling constant of 37K in KDP was searched by applying three transition frequencies to the 37K ions. The three transition frequencies for each electric coupling constant calculated using Eq. (3) were repeatedly applied, in sequence, through the RF coil. Each signal was frequency modulated (FM = 20 kHz) to cover a certain region of the electric coupling constant. The signal was frequency modulated at a rate of 50 Hz, and each signal was applied for 100 ms. The oscillating magnetic field strength was 0.6 mT. The 37K ions were continuously implanted into KDP and data were collected for consecutive RF on and off periods of 30 s each.
3 Result
The -NQR spectrum of 37K in KDP is shown in Fig. 2, where the NMR signal, , is plotted as a function of the electric coupling constant. The solid circles are the experimental data and the electric coupling constant of each point corresponds to a set of three transition frequencies, as noted earlier. The horizontal bar on each point is the range of electric coupling constant covered by the frequency modulation of the applied frequencies. The shaded area is the baseline of the resonance obtained from the data outside the resonance region. The solid line is a Gaussian fit to the data. The centroid of the fit gives the electric coupling constant of 37K in KDP:
| (5) |
The dashed line is a theoretical line shape taking into account the frequency modulation of each transition frequency and the distribution of the electric field gradient . The latter broadens the natural line width and may lead to a different centroid. The in KDP at the K lattice site is not known but several percent is expected in ionic crystals [13]. It is difficult to fit the theoretical line shape to data with as a fitting parameter since the data around the resonance are too sparse. Therefore, the theoretical line shape was obtained with an assumption of = 3%, giving reasonable reproduction of the data. The systematic error in the coupling constant reflects the difference between the centroids obtained with the Gaussian and theoretical line shape fits.
The electric coupling constant of 39K in KDP was measured by the conventional NMR technique as MHz [14]. The ratio of the electric quadrupole coupling constants of 37K and 39K in KDP was determined to be:
| (6) |
K) can be extracted from Eq. (6) if K) is known. Ab initio calculations were performed to obtain the electric field gradient of the state in the 39K atom [6]. Applying the electric field gradient to the electric coupling constant of the state [15], efm2 was deduced. This K) was used to deduce K) reported here. The method to extract from the measured with a precisely calculated has been successfully applied to many atomic systems [16]. Other reported values of K) obtained from the 4, 5 or 6 hyperfine coupling constants of the 39K atom [5] with the Sternheimer correction [17], and from molecular microwave spectra combined with calculations of electric field gradient [18] are available as well. The latter gives values, which are consistent with and as precise as the ab initio calculations. The values obtained with Sternheimer correction are subject to rather large error bars due to the accuracy of the correction [5]. However, these values of are in good agreement within quoted errors and do not increase the systematic error of the present result.
was extracted from Eq. (6) and K) discussed above as
| (7) |
The error includes the statistical and systematic errors that resulted from the line shape of the -NQR spectrum presented in Fig. 2. A temperature dependence of the electric field gradient at the K lattice site in KDP was reported in Ref. [14]. The temperature dependence was not considered for the K) reported here, since its contribution is smaller than the uncertainty in the present result.
The present value of K) is consistent and more precise than the previous value, = 11 4 efm2, which was extracted from the hyperfine coupling constant of the state of 37K atom, MHz reported in Ref. [4], with the coupling constant of 39K atom, MHz [5] and K) = 6.01 0.15 efm2 evaluated with a calculated electric field gradient [6].
4 Discussion
Theoretical calculations were performed using the OXBASH shell-model code [7] in the -model space with the USDA interaction [8] and Woods-Saxson single-particle wave functions. Theoretical quadrupole moments were calculated with , where is the bare quadrupole moment of the proton (neutron) and and are the effective charges for the proton and neutron, respectively. Values of = 1.3 and = 0.5 were used for the shell-model results. These effective charges are typical for shell nuclei [1, 2]. The experimental and theoretical results are summarized in Table 1 and shown in Fig. 3 for the K isotopes ( = 19) and their mirror nuclei (the = 19 isotones). Calculations with the USD [20] or the USDB [8] interactions gave results within the expected theoretical uncertainty and therefore only the results of the calculations performed with USDA interaction are discussed here. The quadrupole moments of the mirror nuclei were obtained by exchanging the bare quadrupole moments of the proton and neutron, assuming charge symmetry. The theoretical result K)theory = 7.5 efm2 is significantly smaller than the present experimental value [Eq. (7)]. The theoretical ratio [K)/K)]theory = 1.1 also disagrees with the experimental result [Eq.(6)] as well. Finally, the experimental trend of K isotopes is poorly reproduced by the shell model results as depicted in Fig. 3.
The smaller theoretical ratio of K) to K) than deduced from experiment is understood as follows. An increase in K)theory is expected when two neutrons are removed from 39K. This is realized from the value reported in Table 1. However, a decrease in is also calculated between 39K and 37K, which is nearly half the increase in . The reduction of is attributed to two neutrons coupled to 2+ in the shell. The wave function of the ground state of 37K is approximated by
| (8) |
where and represent the ground and first excited states, respectively. Eq. (4) can be rewritten as . The amplitudes of these states, and , are calculated to be 0.76 and 0.16, respectively. The covers 92% of all the possible wave functions in the model space. The contribution from each term to the can be evaluated as and , where is the quadrupole operator. The factors 1 and 0.6 in the righthand side of each equation are the phase factors given by the initial and final state spins. The opposite sign of the term to that of the term reduces the of 37K compared to that of 39K, where the term is dominant. The neutron configuration in 37K counteracts the and the reduction results in the small increase of the overall K)theory relative to K)theory. Consequently, the experimental ratio, namely the trend in , would be difficult to reproduce in this framework of the shell model, even if other interactions are considered.
Cross shell (2p-2h) excitations were considered for protons and neutrons with the Monte Carlo Shell Model (MCSM) in the and model space with the SDPF-M interaction [21]. The fractions of valence protons and neutrons excited to the shell in the calculation are 0.29 and 0.28 for 37K and 0.32 and 0.42 for 39K, respectively. The resulting [K)/K)]theory = 1.1 and (37K)theory = 7.47 efm2 are still significantly smaller than experimental values. The MCSM results are surprisingly similar to the OXBASH result ( [K)/K)]theory = 1.1 and (37K)theory = 7.52 efm2, respectively), which were limited to the model space. Although 30% of all the nucleons in the MCSM calculation are excited to the shell, the K)theory is not increased, compared to that calculated in the model space. The contribution of the 2p-2h excitations to (37K)theory can therefore be considered negligible.
The experimental result may be better reproduced by the shell-model calculations discussed above with an adjustment of the effective charges. A quadrupole deformation of the valence orbitals will lead to a self-consistent polarization of the core. The deformation is described as the coupling of 2, =2+ excitations of the core to the valence orbits [1] and is represented within the model space as effective charges for protons and neutrons. As discussed in the introduction, there is evidence of reduced effective neutron charges in the B isotopes near the neutron dripline [3]. But no precedent has been established for changes in effective charges in neutron-deficient nuclei like 37K.
The experimental ratio between K) and K) may be used as a guide in estimating effective charges. The ratio can be represented as:
| (9) |
where the = 20 neutron core in 39K couples to 0+. The ratio of the effective charges can be extracted as 1.14, using Eq. (6) and the bare quadrupole moments reported in Table 1. The typical effective charges , give . An increase in and/or a decrease in is required to reproduce the experimental K)/K) [Eq. (6)].
The suggestion of alternate effective charges is also seen in the experimental quadrupole moments of mirror nuclei near 37K. 39K and 39Ca have one proton hole and one neutron hole, respectively, in doubly-magic 40Ca. The simple shell-model configurations of these nuclei give the effective charge as the ratio of experimental and bare quadrupole moments for protons (39K) and neutrons (39Ca). The effective charges obtained in this approach are 1.13 and 0.71. The increase in and decrease in , relative to the typical values, lead to [K)/K)] and K)theory = 7.9 efm2. These values are increased relative to the shell-model results with the typical values of effective charges, but still remain smaller than the experimental values. The evaluated with these new effective charges derived from the = 39, = 1/2 mirror partners are summarized in Table 1.
The driving force for the variation of effective charges may lie in the interaction between the valence neutrons and core protons. The effective charges can be expanded to include the isoscalar, , and isovector, , polarization charges arising from the virtual excitation of the isoscalar and isovector giant quadrupole resonances of the core:
| (10) |
The is well determined from the 2 matrix elements between low-lying states [2], which is dominated by the isoscalar component, and can be derived from typical effective charges as . Therefore, using obtained by considering the ratio of experimental of 37K and 39K given in Eq. (9), a value is determined, much larger than the value from the typical effective charges, and . The large indicates stronger coupling to the isovector quadrupole giant resonance. It is also noted here that such a large has also been discussed for the = 51 mirror nuclei [22], which reside in the shell.
An alternative way to evaluate is by a collective model approach. The ground state wave function of 37K given in Eq. (4) may also be considered as a single-hole configuration in the shell interacting with the 2+ vibrational state of the 38Ca core. The influence of particle-core coupling can be calculated as a correction to the by taking into account the effect induced by the collective 2 operator. A simple relation between in the coupled particle-core system and the of the single particle configuration can be derived [23] as:
| (11) | ||||
The neutron-dependent proton effective charge, , can be derived from the experimental and excitation energy of the first-excited state in the 38Ca core. Eq. (11) can be evaluated using the values, fm2, 13 fm2, 40 MeV, = 2.21 0.01 MeV and fm4 [24], to obtain efm2. This collective approach using empirical data gives a larger value of than the shell model. The agreement with the present experimental result is improved, however, the error is large. A with higher precision would be useful for further discussion.
The large experimental K) and relatively small proton separation energy of 37K, MeV, would be an indication of extended valence proton orbit or even the development of a proton halo [25, 26]. In such a proton halo system, should converge to 1 due to a smaller probability of the valence protons to polarize the core. Though the experimental K)/K) may indicate a smaller , a corresponding increase in is essential to better reproduce K) and the ratio K)/K) as discussed above. Also, the mean-square charge radius of 37K relative to that of 39K is known [4] and does not show evidence of an extended distribution of protons. Therefore, the large K), the small and the small proton separation energy of 37K are not attributed to an extended proton orbit or a proton halo. The angular momentum of the valence nucleon () and the large atomic number ( = 19) are expected to suppress an extended proton orbit in 37K, due to large centrifugal and Coulomb barriers, respectively.
5 Summary
A newly-developed -NQR system was used at NSCL to measure the charge distribution of the neutron-deficient nucleus 37K. The electric quadrupole coupling constant of 37K, implanted in a tetragonal KDP single crystal, was measured to be = 2.99 0.07 MHz. Together with the known electric quadrupole coupling constant of 39K in KDP and quadrupole moment of 39K, the quadrupole moment of 37K was deduced as = 10.6 0.4 efm2. The present result is consistent with and significantly more precise than the previous value (11 4 efm2), evaluated from the hyperfine coupling constant measured by laser spectroscopy. Shell-model results in the or the and model spaces are not able to reproduce the large K) value. A increased neutron effective charge and a decreased proton effective charge relative to the typical values in the shell are required for a better agreement between experiment and theory. Such changes in the effective charges for the of neutron-deficient 37K indicate that the well bound valence neutrons strongly polarize the core protons. More substantial coupling to the isovector giant resonance is inferred, beyond that indicated by the typical effective charges for the shell nuclei.
Acknowledgement
This work was supported in part by the National Science Foundation, Grant PHY06-06007. The authors would like to express their thanks to the NSCL operations staff for providing the primary and secondary beams and the electronics group for their help in developing the RF system.
References
- [1] H. Sagawa and B. A. Brown, Nucl. Phys. A 430 (1984) 84.
- [2] B. A. Brown and B. H. Wildenthal, Ann. Rev. Nucl. Part. Sci. 38 (1988) 29.
- [3] H. Ogawa et al., Phys. Rev. C 67 (2004) 064308.
- [4] J. A. Behr et al., Phys. Rev. Lett. 79 (1997) 375.
- [5] E. Arimondo et al., Rev. Mod. Phys. 49 (1977) 31.
- [6] D. Sundholm et al., J. Chem. Phys. 98 (1993) 7152.
- [7] B. A. Brown et al., MSU-NSCL Report No. 1289.
- [8] B. A. Brown and W. A. Richter, Phys. Rev. C 74 (2006) 034315.
- [9] D. E. Groh et al., Phys. Rev. Lett. 90 (2003) 202502.
- [10] D. J. Morrissey, Nucl. Instrum. Methods Phys. Res. B 126 (1997) 316.
- [11] P. F. Mantica et al., Phys. Rev. C 55 (1997) 2501.
- [12] K. Minamisono et al., Nucl. Instrum. Methods Phys. Res. A in press.
- [13] T. Minamisono, Y. Nojiri and K. Sugimoto, Nucl. Phys. A 236 (1984) 416.
- [14] J. Seliger and V. Zagar, Phys. Rev. B 49 (1994) 14918.
- [15] G. Spprott and R. Novick, Phys. Rev. Lett. 21 (1968) 336.
- [16] M. Tokman et al., Chem. Phys. Lett. 291 (1998) 414, and references therein.
- [17] R. M. Sternheimer and R. F. Peierls, Phys. Rev. A 3 (1971) 837.
- [18] V. Kello and A. J. Sadlej, Chem. Phys. Lett. 292 (1998) 403.
- [19] N. J. Stone, At. Data Nucl. Data Tables 90 (2005) 75.
- [20] B. H. Wildenthal, Phys. Rev. C 28 (1983) 1343.
- [21] Y. Utsuno et al., Phys. Rev. C 60 (1999) 054315.
- [22] R. du Rietz et al., Phys. Rev. Lett. 93 (2004) 222501.
- [23] G. Neyens et al., Nucl. Phys. A 625 (1997) 668.
- [24] P. D. Cottle et al., Phys. Rev. C 60 (1999) 031301.
- [25] T. Minamisono et al., Phys. Rev. Lett. 69 (1992) 2058.
- [26] T. Sumikama et al., Phys. Rev. C 74 (2006) 024327.
| nucleus | (efm2) | (efm2) | Ref. | |||
|---|---|---|---|---|---|---|
| , | , | |||||
| 1.3, 0.5 | 1.13, 0.71 | |||||
| 39K | 5.32 | 0 | 6.92 | 6.01 | 6.01 0.15 | [6] |
| 37K | 3.94 | 4.80 | 7.52 | 7.86 | 10.6 0.4 | present |
| 35K | 4.71 | 2.91 | 7.58 | 7.39 | - | |
| 39Ca | 0 | 5.32 | 2.66 | 3.78 | 3.8 0.65 | [19] |
| 37Ar | 4.80 | 3.94 | 8.21 | 8.22 | 7.6 0.9 | [19] |
| 35S | 2.91 | 4.71 | 6.14 | 6.63 | 4.71 0.09 | [19] |