Quandles versus symmetric quandles for oriented links
Abstract.
Given a quandle, we can construct a symmetric quandle called the symmetric double of the quandle. We show that the (co)homology groups of a given quandle are isomorphic to those of its symmetric double. Moreover, quandle coloring numbers and quandle cocycle invariants of oriented links and oriented surface-links can be interpreted by using symmetric quandles.
Key words and phrases:
Quandle, Symmetric quandle, Oriented link2020 Mathematics Subject Classification:
Primary 57K12; Secondary 57K181. Introduction
A quandle is an algebraic system independently introduced by D. Joyce [10] and S. Matveev [15] in 1982. There are several studies using quandles in knot theory. Especially quandle cocycle invariants [2] (see also [3]), introduced by J. S. Carter et al. in 2003, are very useful for studies of oriented links and oriented surface-links, refer to [8, 14, 16, 19, 20, 21, 22, 23, 24] for example. Here, we note that in order to define quandle cocycle invariants, it is essential that links or surface-links are oriented. In 2007, S. Kamada [11] (see also [13]) introduced symmetric quandle cocycle invariants for links and surface-links. In order to define symmetric quandle cocycle invariants, it is not required that links or surface-links are oriented or orientable, and therefore, this enabled us to consider quandle cocycle invariants for links or surface-links which are not necessarily oriented or orientable. There are several studies using symmetric quandle colorings and symmetric quandle cocycle invariants, see [4, 9, 12, 13, 17, 18] for example.
In this paper, we focus on a symmetric quandle which is called the symmetric double of a given quandle. We show that the (co)homology groups of a given quandle are isomorphic to those of the symmetric double of the quandle (Section 4). We also show that for a given quandle, the quandle coloring numbers and the quandle cocycle invariants of oriented (surface-)links can be interpreted by using the symmetric double of the quandle (Sections 5 and 6).
This paper is organized as follows. In Section 2, we review the definitions of quandles, quandle (co)homology groups, and link invariants using quandles. In Section 3, we review the definitions of symmetric quandles, symmetric quandle (co)homology groups, and link invariants using symmetric quandles. In Section 4, we define the symmetric double of a given quandle, and we prove that the (co)homology groups of a quandle are isomorphic to those of its symmetric double. In Section 5, we discuss oriented link invariants using quandles. Especially, we show that quandle coloring numbers, quandle homology invariants and quandle cocycle invariants for oriented links can be interpreted by using symmetric quandles. In Section 6, we summarize the same properties as shown in Section 5 for oriented surface-links.
2. Quandles and invariants for oriented links
In this section, we review the definitions of quandles, quandle (co)homology groups, link invariants using quandles.
2.1. Quandles
A quandle [10, 15], see also [6], is a set with a binary operation satisfying the following axioms.
-
(Q1)
For any , .
-
(Q2)
For any , there exists a unique element such that .
-
(Q3)
For any , .
The unique element in the second axiom is denoted by . For a quandle , when we specify the quandle operation , we also denote by the quandle .
The proof of the next lemma is straightforward, and we leave it to the reader.
Lemma 2.1.
Let be a quandle. For any and , it holds that
where in this paper means .
Example 2.2.
A trivial quandle is a non-empty set with the trivial operation, that is, for any . A trivial quandle consisting of elements is denoted by .
Example 2.3.
The dihedral quandle of order for an integer is with the operation for any . We denote it by .
Example 2.4.
A conjugation quandle is a group with the operation for any . We denote it by .
2.2. Quandle (co)homology theories
Carter et al. [2] defined homology groups of quandles, which are deeply related to homology groups of racks due to Fenn et al. [7], and various versions are introduced so far, see [1, 3]. In this paper, we adopt the definition of the homology group of a quandle with an -set . We note that when is a singleton, the homology group concides with that defined in [2], and when , the homology group coincides with that defined in [3].
The associated group of a quandle is
where we note that any element of can be regarded as an element of through the map . An -set is a set equipped with a right action by the associated group . In this paper, we use the same symbol for the operation of a given quandle and the action on a given -set by , that is, we denote by the image of an element acted on by .
Let be a quandle and an -set. The same proof as in Lemma 2.1 works for the next lemma, and we leave it to the reader.
Lemma 2.5.
For any , and , it holds that
Let be the free abelian group generated by -tuples when is a positive integer, and let otherwise. The boundary homomorphism is defined by
for and otherwise, where represents that is removed. Then is a chain complex.
Let be the subgroup of generated by the elements of
Then is a subchain complex of . Let , and we denote by the induced boundary homomorphism . The quotient chain complex leads to the quandle homology group of and defined by .
For an abelian group , we define the chain complex . The homology groups are denoted by . Note that when , represents . We also define the cochain group and the coboundary homomorphism by and , respectively. The quandle cohomology group with coefficients in is defined by . We denote by and the cocycle group and the coboundary group , respectively.
2.3. Quandle colorings
A link is a disjoint union of circles embedded in . Two links are said to be equivalent if there exists an orientation-preserving self-homeomorphism of which maps one link onto the other. A diagram of a link is its image, via a generic projection from to , equipped with the height information around the crossings. The height information of a diagram of a link is given by removing regular neighborhoods of the lower crossing points, and thus, the diagram is regarded as a disjoint union of connected compact parts. We call each connected component an arc of the diagram. The -dimensional space is separated into several connected regions by a diagram. We call each connected region a complementary region of the diagram.
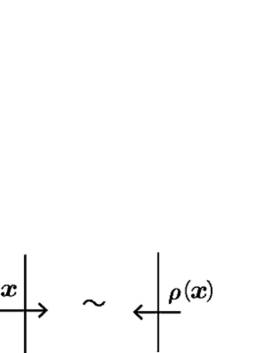
Let be a quandle. Let be an oriented link diagram, that is, a pair of a link diagram and an orientation of . In this paper, we often use normal orientations of arcs for representing the orientation of as in Figure 1, where for an arc of , the pair of the orientation and the normal orientation of the arc always forms the right-handed orientation of .

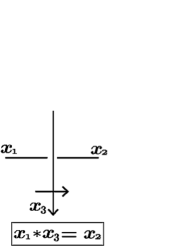
An -coloring of is an assignment of an element of to each arc satisfying the following condition.
-
•
Suppose that two arcs and which are under-arcs at a crossing are labeled by and , respectively, and the over arc, say , of is labeled by . We assume that the normal orientation of points from to . Then holds. See the left of Figure 2.
We denote by the set of -colorings of . We then have the following lemma.
Lemma 2.6 (cf. [2, 3]).
Let and be diagrams of oriented links. If and represent the same oriented link, then there exists a one-to-one correspondence between and .
This implies that , that is the cardinality of , is an invariant for oriented links, and hence, we also denote it by and call it the quandle coloring number of when is finite, where is an oriented link which represents. We note that in this paper, when a diagram represents an oriented link, we use the same symbol for the orientation of the oriented link.
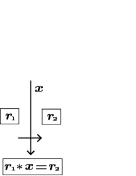
Let be an -set. An -coloring of is an -coloring of with an assignment of an element of to each complementary region of satisfying the following condition.
-
•
Suppose that two complementary regions and are adjacent over an arc , and , and are labeled by , and , respectively. We assume that the normal orientation of points from to . Then holds. See the right of Figure 2.
We denote by the set of -colorings of . Then we have the following lemma.
Lemma 2.7 (cf. [2, 3]).
Let and be diagrams of oriented links. If and represent the same oriented link, then there exists a one-to-one correspondence between and .
This implies that , that is the cardinality of , is an invariant for oriented links.
2.4. Quandle cocycle invariants of oriented links
In this subsection, we review the definition of a quandle cocycle invariant of an oriented link. We remark that several variations for quandle cocycle invariants are introduced so far, see [2, 3], and we adopt the definition of a shadow quandle cocycle invariant with a quandle and an -set . We note that when is a singleton, the shadow quandle cocycle invariant coincides with the quandle cocycle invariant with defined in [2], and when , the shadow quandle cocycle invariant coincides with that defined in [3].
Let be a quandle and an -set. Let be a diagram of an oriented link and an -coloring of . For each crossing of , we extract a weight as follows. Let and denote the under-arc and the over-arc of , respectively, such that the normal orientation of points from , and the complementary region of around which the normal orientations of and point from. We suppose that , and are labeled by , and , respectively. Then the weight of the crossing is , where if is positive and if is negative, see Figure 3. We note that a crossing is positive if the pair of the normal orientations of the over-arc and an under-arc of matches the right-handed orientation of , and is negative otherwise. Let denote the sum of the weights of all the crossings, and then, is a -cycle of . Define
as a multi-set, where a multi-set is a collection of elements which may appear more than once.
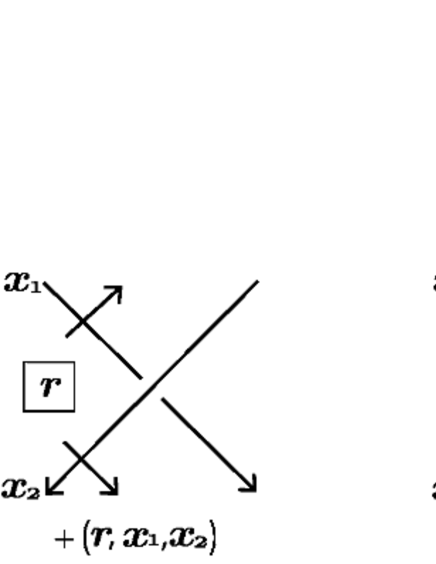
For an abelian group , let be a quandle -cocycle. We define the multi-set by
We also denote these invariants by and , respectively, and call them the quandle homology invariant of by and and the quandle cocycle invariant of by and , respectively.
3. Symmetric quandles and invariants for unoriented links
In this section, we review the definitions of symmetric quandles, symmetric quandle (co)homology groups, link invariants using symmetric quandles. We note again that while link invariants using quandles need orientations of links, link invariants using symmetric quandles do not use orientations of links (or surface-links). This enabled us to consider quandle invariants for links (or surface-links) which are not necessarily oriented or orientable.
3.1. Symmetric quandles
A symmetric quandle [11], see also [13], is a pair of a quandle and a good involution of , where an involution is said to be good if
| (GI1) and (GI2) |
for any . For a symmetric quandle , when we specify the symmetric quandle operation , we also denote by the symmetric quandle .
Example 3.1.
Let be a trivial quandle. Any involution is a good involution of .
Example 3.2.
Let be a group. The inversion is a good involution of the conjugation quandle .
3.2. Symmetric quandle (co)homology theories
Kamada [11], see also [13] in detail, defined (co)homology groups of symmetric quandles. In this subsection, we review the definition of a symmetric quandle homology group.
The associated group of a symmetric quandle is
An -set is a set equipped with a right action of the associated group . In this paper, we use the same symbol for the operation of a given symmetric quandle and the action on a given -set by , that is, we denote by the image of an element acted on by .
Let be a symmetric quandle and be an -set. The chain group , the boundary homomorphism , and the subgroup of are defined as in Subsection 2.2.
Let be the subgroup of generated by the elements of
Then is a subchain complex of . Let , and we denote by the induced boundary homomorphism . The quotient chain complex leads to the symmetric quandle homology group of and defined by .
For an abelian group , we define the chain complex . The homology groups are denoted by . Note that when , represents . We also define the cochain group and the coboundary homomorphism by and , respectively. The symmetric quandle cohomology group with coefficients in is defined by , and we denote by and the cocycle group and the coboundary group , respectively.
3.3. Symmetric quandle colorings
Let be a symmetric quandle and an (unoriented) link diagram. A semi-arc of is a connected component after removing the regular neighborhoods of the crossings of .
An -coloring of is the equivalence class of an assignment of a normal orientation and an element of to each semi-arc satisfying the following conditions.
-
•
Suppose that two semi-arcs coming from an over-arc of at a crossing are labeled by and . If the normal orientations are coherent, then , otherwise . See the left upper half of Figure 4.
-
•
Suppose that two semi-arcs and which are under-arcs at a crossing are labeled by and , respectively, and suppose that one of the semi-arcs coming from the over arc, say , of is labeled by . We assume that the normal orientation of points from to . If the normal orientations of and are coherent, then holds, otherwise holds. See the left lower half of Figure 4.
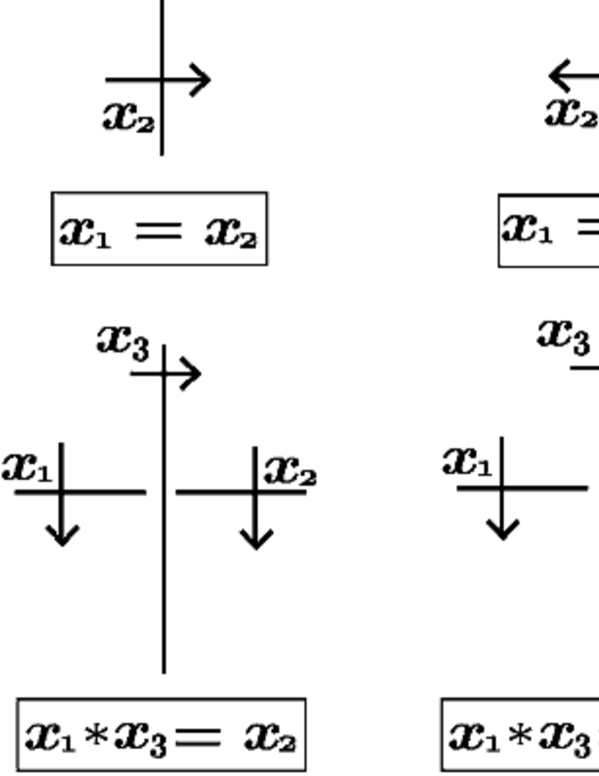
Here the equivalence relation is generated by basic inversions which are operations of replacing the normal orientation of a semi-arc with the inverse one and the element , assigned to the semi-arc, with , see Figure 5.
We denote by the set of -colorings of . We then have the following lemma.
Lemma 3.3 ([11, 13]).
Let and be diagrams of (unoriented) links. If and represent the same link, then there exists a one-to-one correspondence between and .
This implies that , that is the cardinality of , is an invariant for links, and hence, we also denote it by and call it the symmetric quandle coloring number of when is finite, where is a link which represents.
Let be an -set. An -coloring of is an -coloring of with an assignment of an element of to each complementary region of satisfying the following condition.
-
•
Suppose that two complementary regions and are adjacent over a semi-arc , and , and are labeled by , and , respectively. We assume that the normal orientation of points from to . Then holds. See the right of Figure 4.
We denote by the set of -colorings of . Then we have the following lemma.
Lemma 3.4 ([11, 13]).
Let and be diagrams of (unoriented) links. If and represent the same link, then there exists a one-to-one correspondence between and .
This implies that , that is the cardinality of , is an invariant for links.
3.4. Symmetric quandle cocycle invariants of (unoriented) links
Let be a symmetric quandle and an -set. Let be a diagram of an (unoriented) link and an -coloring of . For each crossing of , we extract a weight as follows. For a crossing of , there are four complementary regions of around . We choose one of the regions, say , and call it the specified region for . Let and denote the under-semi-arc and the over-semi-arc of , respectively, which faces the specified region . By basic inversions, we may assume that the normal orientations and of and , respectively, point from . Let , and be the labels of , and , respectively. Then the weight of the crossing is , where if the pair of the normal orientations and assigned to and , respectively, matches the right-handed orientation of , then , otherwise , see Figure 6.
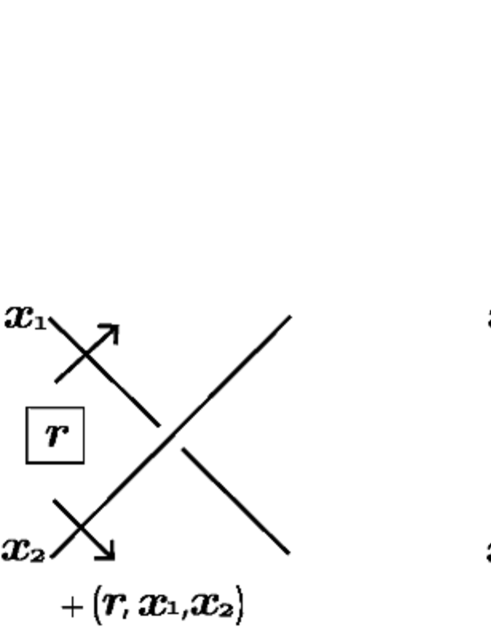
Let denote the sum of the weights of all the crossings, and then, is a -cycle of . Define
as a multi-set.
For an abelian group , let be a symmetric quandle -cocycle. We define the multi-set by
We also denote these invariants by and , respectively, and call them the symmetric quandle homology invariant of by and and the symmetric quandle cocycle invariant of by and , respectively.
4. Quandle homology groups are interpreted as symmetric quandle homology groups
In this section, we show that for any quandle and any -set , the quandle homology groups of and is obtained as symmetric quandle homology groups.
4.1. The symmetric double of a quandle
Let be a quandle. We set two copies and of by
and let . For , we call the sign of . Define a binary operation by
Lemma 4.1.
The set is a quandle with the operation .
Proof.
(Q1) For any , we have . (Q2) For any , we set and , and then we have . If we have two elements such that and , then holds, which implies and . (Q3) For any , by Lemma 2.1, we have . ∎
We call the quandle the double of .
Lemma 4.2.
The subset (resp. ) of forms a subquandle of . Moreover, we have (resp. ).
Proof.
It is easily seen that the quandle operation on preserves the sign , and thus, is a subquandle of . The isomorphism is given by . ∎
Define a map by .
Lemma 4.3.
The map is a good involution of the double of .
Proof.
(GI1) For any , we have . (GI2) For any , we have , and hence, holds. ∎
We call the symmetric quandle the symmetric double of .
Example 4.4.
Let be an odd integer and the dihedral quandle . The double of is isomorphic to the dihedral quandle , where the isomorphism is defined by
Set by for , where we note that this is a good involution of . Then the symmetric double of is isomorphic to the symmetric quandle .
Let be an -set. For the associated groups and , we define the group homomorphism by for . Note that represents in and represents the inverse of in . The next property can be proven by an easy verification as in Lemmas 2.1 and 2.5.
Lemma 4.5.
is a -set by the right action
Remark 4.6.
For , and hold, which imply that for and , we may apply the multiplication to the signs.
4.2. The homology groups of a quandle and its symmetric double
In this subsection, we show that the homology group of a given quandle and that of the symmetric double are isomorphic. This property is very important for applying symmetric quandle cocycle invariants for oriented (or unoriented orientable) links and saying that symmetric quandle cocycle invariants are a generalization of quandle cocycle invariants.
For simplicity, in this subsection, we omit parenthesis of operations or actions such as means , and means .
Let be a quandle, the symmetric double of , and an -set. We note that by Lemma 4.5, is regarded as a -set.
For each , apply the following process (Step 0)-(Step 2), say the canonicalization, while .
-
•
(Step 0) Set the singed -tuple by , and . Go to (Step 1).
-
•
(Step 1) If the th sign is , replace with
(1) and then, denote by the replaced signed -tuple (1). Go to (Step 2).
-
•
(Step 2) Set . Go to (Step 1).
We note that applying the canonicalization should be finished once we have with . Then we have an element , where we note that the transformation in (Step 1) comes from the generators of the subgroup of . This implies that any -tuple in is represented by a single term , that is,
We call the resultant element the canonical form of .
Example 4.7.
For , we apply the canonicalization until all the signs of the last three components become . Since we have the transformations
the canonical form of is .
Define a homomorphism by
for and otherwise, where is the canonical form of . Define a homomorphism by
for and otherwise.
Lemma 4.8.
and are inverses of each other, and thus, they are isomorphisms.
Proof.
First, we will check the well-definedness of . We temporarily regard this map as . We may show that for any and ,
| (2) | |||
| (3) |
Let denote the elements of such that and . Assume . For the -tuple , apply the canonicalization while . We note that applying the canonicalization should be finished once we have with . We then have the transformation
which implies that
where is the resultant by the above canonicalization, that is, and
For the -tuple , that is , apply the canonicalization while . We note that applying the canonicalization should be finished once we have with . We then have the transformation
which implies that
where is the resultant by the above canonicalization, and by Lemmas 2.1 and 2.5, we have
for ,
and for . Thus we have
and hence, the equation (2) holds. In the case that , the equation (2) also holds, and we leave the proof to the reader. Thus for any element , holds. For any such that for some , the canonical form of satisfies that , and hence, we have
and hence, the property (3) holds. Thus for any element , holds. As a consequence, we see that the map is well-defined.
We can easily check the well-definedness of as follows. We temporarily regard this map as . For any such that for some , we have , and hence,
Thus, for any , holds, which implies that is well-defined.
Finally, the property follows from
where is the canonical form of . The property follows from
This completes the proof. ∎
Remark 4.9.
As shown in above, any -tuple is represented by a single term , which implies that is generated by the elements of . Therefore, the isomorphism is, in other words, defined by
Lemma 4.10.
and are chain maps, and therefore by Lemma 4.8, they are isomorphisms between the chain complexes and .
Proof.
For any ,
Thus is a chain map from to .
Since is the inverse homomorphism of for any ,
which implies that is a chain map from to . ∎
Let be an abelian group. We have the following property.
Theorem 4.11.
For any , we have
and
Proof.
(1) By Lemma 4.10, since is an isomorphism from to , induces the isomorphism
where the inverse homomorphism is
Similarly, since we have the isomorphism from to , we have the induced isomorphism
(2) By Lemma 4.10, since is an isomorphism from to , induces the isomorphism
the inverse homomorphism is
∎
Corollary 4.12.
Let and be homomorphisms such that
Then is an -cocycle if and only if is an -cocycle, that is,
5. Invariants for oriented (or unoriented) links using quandles can be interpreted by using symmetric quandles
In this section, we discuss oriented link invariants using quandles. Especially, we show that quandle coloring numbers, quandle homology invariants and quandle cocycle invariants for oriented links can be interpreted by using symmetric quandles.
5.1. An interpretation of quandle coloring numbers by using symmetric quandle colorings
Let be a quandle and the symmetric double of .
By performing a finite number of basic inversions, we can see that any -coloring of a diagram of an unoriented link is uniquely represented by an assignment of a normal orientation and an element of to each semi-arc of , see Figure 7. We call the assignment the canonical form of (or of ).
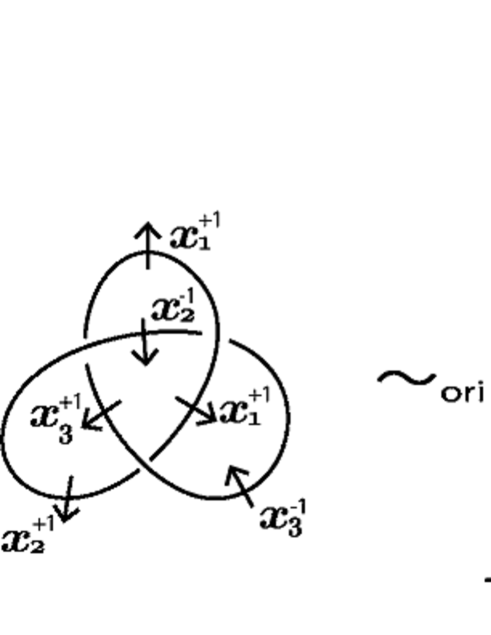
Let be a diagram of an unoriented link and a -coloring of . For a semi-arc of and the normal orientation assigned to for the canonical form of , we set the orientation of so that the pair matches the right-handed orientation of . Since for the canonical form of a -coloring of , any two semi-arcs of coming from the same component of have the coherent normal orientations, the above orientations for the semi-arcs of induce an orientation of , see the upper half of Figure 8.
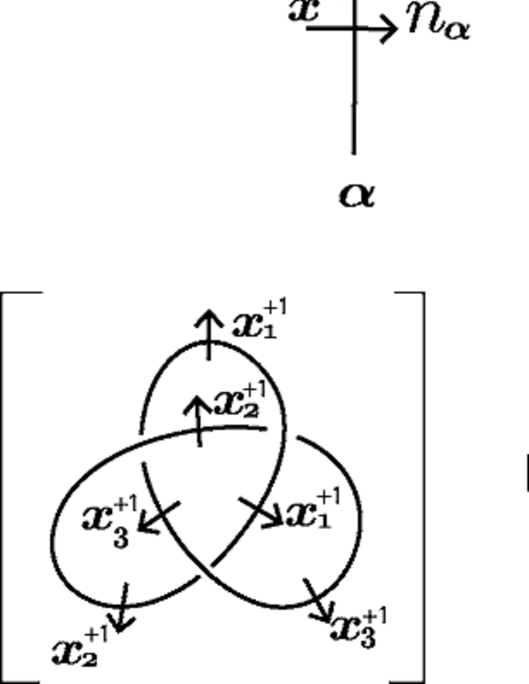
We call the orientation of the orientation induced by the canonical form of and the diagram the oriented diagram induced by the canonical form of . Let and be -colorings of . We say that and are orientation equivalent if the orientation induced by the canonical form of coincides with that of . We denote by the orientation equivalence class of a -coloring .
In this paper, means the set of orientations of . The transformation map from to is the map
and this induces the transformation map from to :
see the lower half of Figure 8. We then have the following property.
Lemma 5.1.
is bijective.
Proof.
The injectivity is clear, and hence, we show the surjectivity. Let and . For each semi-arc of , we assign the element and the normal orientation to so that the pair matches the right-handed orientation of . Then we can see that the assignment is the canonical form of a -coloring of and the equivalence class of the -coloring satisfies that . ∎
Any -colored diagram uniquely induces an oriented, -colored diagram by setting on the orientation induced by the canonical form of and replacing, for the canonical form of , the assigned element of each (semi-)arc with , see the upper half of Figure 9.
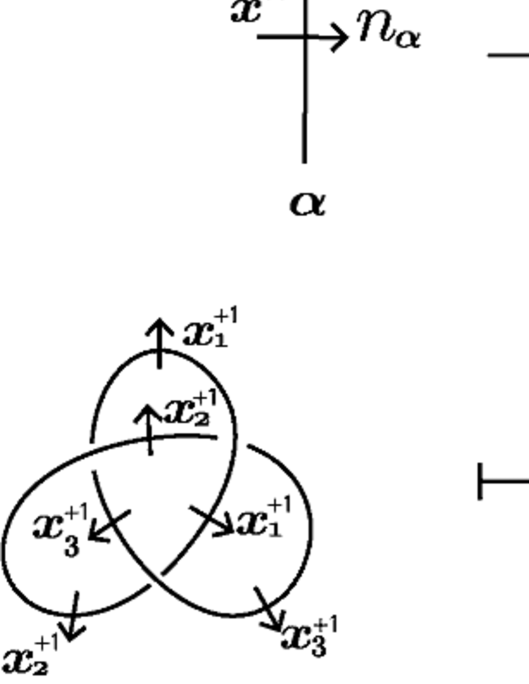
We call such the oriented, -colored diagram induced by the canonical form of . The transformation map from to is the map
see the lower half of Figure 9.
Lemma 5.2.
is bijective.
Proof.
Any oriented, -colored diagram uniquely induces a -colored diagram as follows. For each arc of , replace the orientation for with the normal orientations of the semi-arcs included in such that matches the right-handed orientation of and replace the assigned element of for with for the semi-arcs included in . Lemma 4.2 shows that the replaced assignment of the unoriented diagram represents a -coloring of . Thus we have the inverse map of :
∎
The next theorem implies that quandle coloring numbers for oriented links can be interpreted by using symmetric quandle colorings.
Theorem 5.3.
Let be a diagram of an oriented link and take such that . Then there exists a one-to-one correspondence between the sets and , and thus, we have
Proof.
By the definition of the bijective translation map , we have the restriction
which is bijective. Clearly this map gives a one-to-one correspondence between and . ∎
For an unoriented link , by considering all the orientations of and taking for each orientation , we can define an invariant of . More precisely, for a diagram of , the multi-set
is an invariant of . The next property implies that quandle coloring numbers for unoriented links can be also interpreted by using symmetric quandle colorings.
Corollary 5.4.
Let be a diagram of an unoriented link. As multi-sets, we have
5.2. An interpretation of quandle coloring numbers by using symmetric quandle colorings II
In this subsection, we will see that the properties shown in Subsection 5.1 are extended to the cases of -colorings and -colorings. Note that for simplicity, we use the same notation and names as in Subsection 5.1.
Let be a quandle, the symmetric double of , and an -set. By Lemma 4.5, we can also regard as a -set. Each -coloring of an oriented diagram is also regarded as the -coloring, say also , of by forgetting the assignment by . Similarly, for each -coloring of an unoriented diagram is also regarded as the -coloring, say also , of by forgetting the assignment by . Hence, the canonical form of a -coloring (or of a -colored diagram ) is defined by the assignment which is the canonical form of the -coloring when we forget the assignment by . Moreover, as in the case of Subsection 5.1, a -colored diagram induces an orientation (resp. an oriented diagram ) by considering the orientation (resp. the oriented diagram) induced by the canonical form of .
Let be a diagram of an unoriented link. Let and be -colorings of the diagram . We say that and are orientation equivalent if the orientation induced by the canonical form of coincides with that of . We denote by the orientation equivalence class of a -coloring .
The transformation map from to is the map
and this induces the transformation map from to :
see Figure 10.
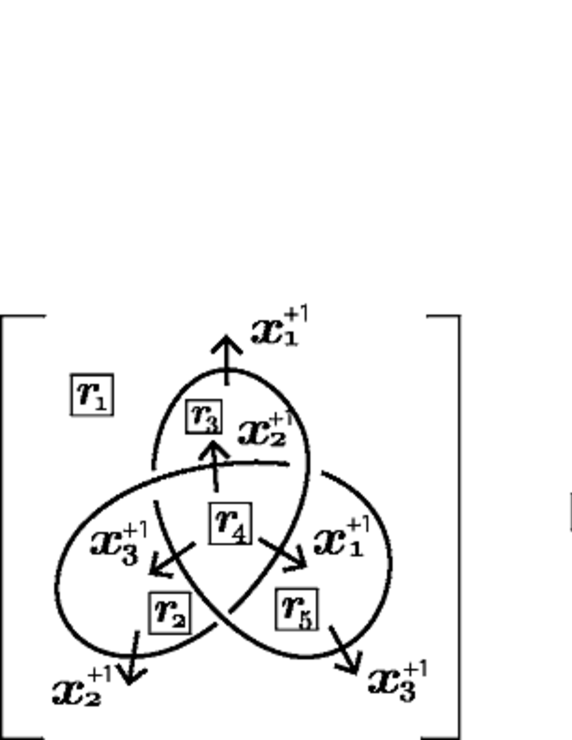
We then have the following property.
Lemma 5.5.
is bijective.
Any -colored diagram uniquely induces an oriented, -colored diagram by setting on the orientation induced by the canonical form of , replacing, for the canonical form of , the assigned element of each (semi-)arc with , and leaving the assignment by as it is, see Figure 11.
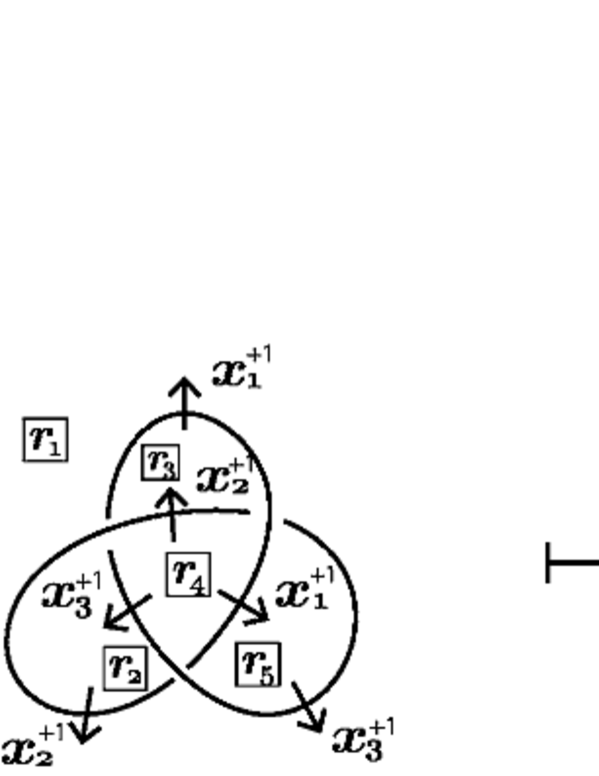
We call such the oriented, -colored diagram induced by the canonical form of . The transformation map from to is the map
see Figure 11.
Lemma 5.6.
is bijective.
We have the following theorem.
Theorem 5.7.
Let be a diagram of an oriented link and take such that . Then there exists a one-to-one correspondence between and , and thus, we have
Proof.
5.3. An interpretation of quandle cocycle invariants by using symmetric quandle cocycle invariants
Let be a quandle, the symmetric double of , and an -set. We note again that by Lemma 4.5, we can also regard as a -set.
For a diagram of an unoriented link and , we denote by the multi-set
where for a -colored diagram , we denote by the sum of the weights of all the crossings as in Subsection 3.4, and note that . The next theorem shows that the quandle homology invariant of an oriented link can be also interpreted by using symmetric quandles.
Theorem 5.8.
Let is a diagram of an oriented link and take such that . Then as multi-sets, we have
Proof.
For , let such that . Since is obtained from by giving on the orientation induced by the canonical form of , replacing, for the canonical form of , the assigned element of each (semi-)arc with , and leaving the assignment by as it is, when we have a weight for a crossing of , we have the weight for the same crossing of , see Figure 12. This implies that , and moreover, , and thus, we have .
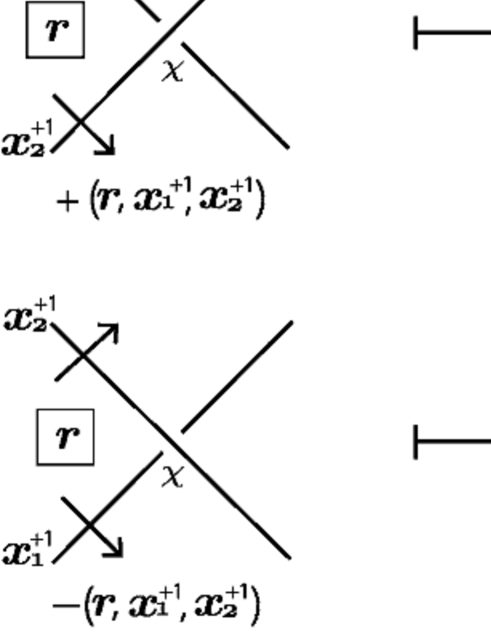
∎
For an unoriented link , by considering all the orientations of and taking the quandle homology invariant for each orientation , we can define an invariant of . More precisely, for a diagram of , the multi-set
is an invariant of . The next property implies that the quandle homology invariants of an unoriented link can be also interpreted by using symmetric quandles.
Corollary 5.9.
Let be a diagram of an unoriented link. As multi-sets, we have
Let be an abelian group. Let and be a quandle -cocycle and a symmetric quandle -cocycle, respectively, such that .
For a diagram of an unoriented link and , we denote by the multi-set
We note that .
The next theorem shows that the quandle cocycle invariant of an oriented link can be also interpreted by using symmetric quandles.
Theorem 5.10.
Let be a diagram of an oriented link and take such that . As multi-sets, we have
Proof.
For an unoriented link , by considering all the orientations of and taking the quandle cocycle invariant for each orientation , we can define an invariant of . More precisely, for an diagram of , the multi-set
is an invariant of . The next property implies that the quandle cocycle invariants of an unoriented link can be also interpreted by using symmetric quandles.
Corollary 5.11.
Let be a diagram of an unoriented link. As multi-sets, we have
Remark 5.12.
As a consequence of the results of this section, it is no exaggeration to say that symmetric quandles are also useful for oriented links, and symmetric quandles are not less than quandles in the case of considering coloring numbers and cocycle invariants for oriented links.
6. Invariants for surface-links using quandles and symmetric quandles
For oriented (or orientable, unoriented) surface-links, we have the same properties, that is, quandle coloring numbers, quandle homology invariants and quandle cocycle invariants are interpreted by using symmetric doubles of quandles. In this section, we summarize our results for surface-links.
6.1. Surface-links
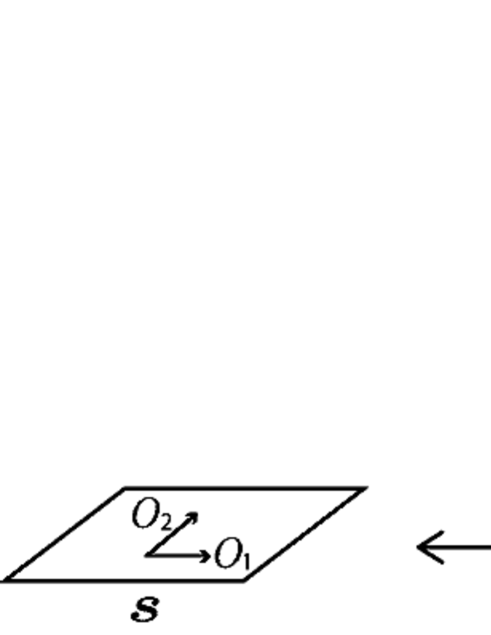
A (orientable) surface-link is a disjoint union of orientable closed surfaces locally-flatly embedded in . Two surface-links are said to be equivalent if there exists an orientation-preserving self-homeomorphism of which maps one surface-link onto the other. A diagram of a surface-link is its image, via a generic projection from to , equipped with the height information around the double point curves. The height information is given by removing the regular neighborhoods of the lower double points. Then a diagram is regarded as a disjoint union of connected compact surfaces, each of which is called a sheet. A connected component after removing the regular neighborhoods of all double points from the diagram is called a semi-sheet. The -dimensional space is separated into several connected regions by a diagram. We call each connected region a complementary region of the diagram. Refer to [2, 3, 5, 13] for more details. For an oriented surface-link diagram , we often use a normal orientation for a sheet to represent the orientation such that the triple matches the right-handed orientation of , see Figure 13.
6.2. Coloring numbers using quandles and symmetric quandles for oriented surface-links
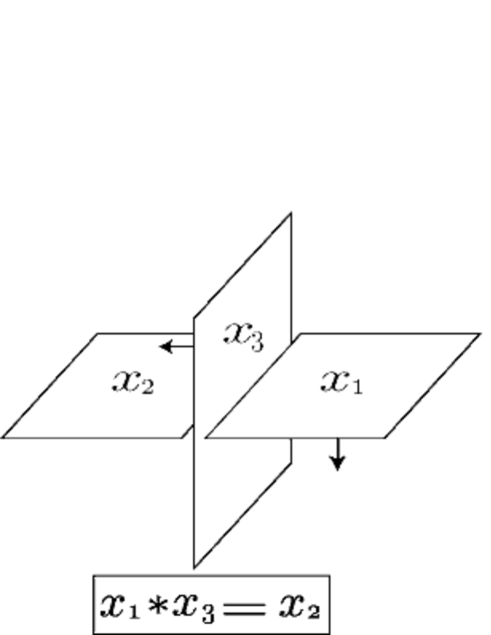
An -coloring of an oriented surface-link diagram for a given quandle is defined as an assignment of an element of to each sheet satisfying the condition depicted in the left of Figure 14 around double point curves. We denote by the set of -colorings of . An -coloring of an oriented surface-link diagram for a given quandle and a given -set is an -coloring of with an assignment of an element of to each complementary region of satisfying the condition depicted in the right of Figure 14 around semi-sheets. We denote by the set of -colorings of . Refer to [2, 3] for more details.
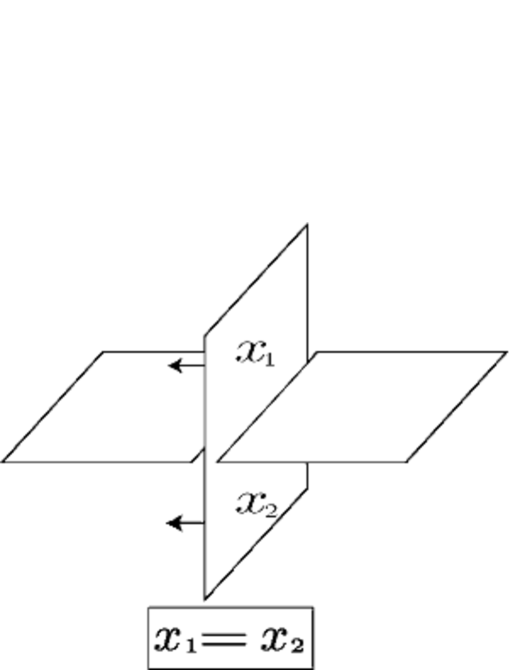
An -coloring of a surface-link diagram for a given symmetric quandle is defined as an equivalence class of an assignment of an element of and a normal orientation to each semi-sheet satisfying the conditions depicted in Figures 14 and 15 around double point curves, where the equivalence relation is generated by basic inversions depicted in Figure 16. We denote by the set of -colorings of . An -coloring of a surface-link diagram for a given symmetric quandle and a given -set is an -coloring of with an assignment of an element of to each complementary region of satisfying the condition depicted in the right of Figure 14 around semi-sheets. We denote by the set of -colorings of . Refer to [13] for more details.
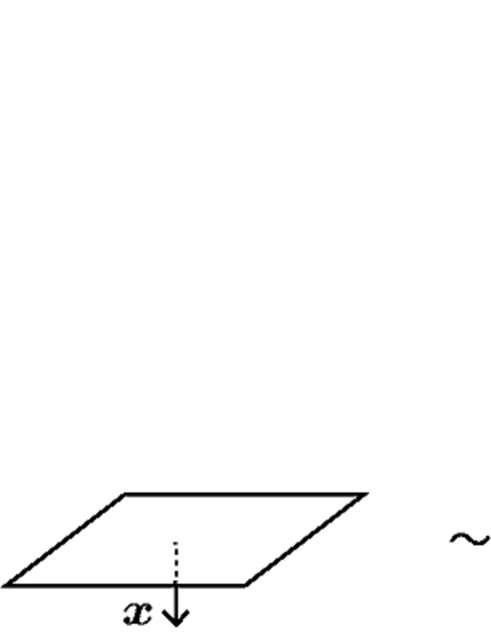
Let be a quandle and the symmetric double of . As in the case of links, by performing basic inversions, any -coloring of a diagram of an unoriented surface-link is uniquely represented by an assignment of a normal orientation and an element of to each semi-sheet of . We call the assignment the canonical form of .
Let be a diagram of an unoriented surface-link and a -coloring of . For a semi-sheet of and the normal orientation assigned to for the canonical form of , we set the orientation of so that the triple matches the right-handed orientation of , see Figure 13. Such orientations determine an orientation of , and we call the orientation the orientation induced by the canonical form of and the oriented diagram the oriented diagram induced by the canonical form of . Let and be -colorings of . We say that and are orientation equivalent if the orientation induced by the canonical form of coincides with that of . We denote by the orientation equivalence class of a -coloring . The transformation map from to is the map
The next theorem implies that quandle coloring numbers for oriented surface-links are interpreted by using symmetric quandle colorings.
Theorem 6.1.
Let be a diagram of an oriented surface-link and take such that . Then there exists a one-to-one correspondence between and , and thus, we have
The next corollary implies that the quandle coloring numbers of an (orientable, unoriented) surface-link can be also interpreted by using symmetric quandles.
Corollary 6.2.
Let be a diagram of an unoriented surface-link. As multi-sets, we have
Similarly we have the following transformation map from to .
where we use the same symbol for simplicity. We have the following theorem.
Theorem 6.3.
Let be a diagram of an oriented surface-link and take such that . Then there exists a one-to-one correspondence between and , and thus, we have
6.3. Cocycle invariants using quandles and symmetric quandles for oriented surface-links
The quandle homology invariant of an oriented surface-link for a quandle and an -set is defined by taking the sum of the weights of triple points for each -coloring, and collecting the weight sums for all the -colorings, refer to [2, 3] for more details, where the weight of a triple point is obtained as depicted in Figure 17. The symmetric quandle homology invariant of an (unoriented) surface-link for a symmetric quandle and an -set is also defined by taking the sum of the weights of triple points for each -coloring, and collecting the weight sums for all the -colorings, refer to [13] for more details, where the weight of a triple point is obtained as depicted in Figure 17.
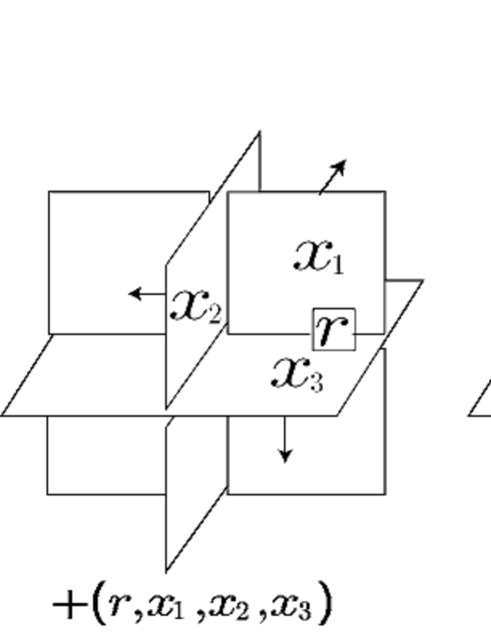
The quandle cocycle invariant of an oriented surface-link for a quandle , an -set and a quandle -cocycle is defined by taking the sum of the weights of triple points for each -coloring, and setting the multi-set of the images, by , of the weight sums for all the -colorings, refer to [2, 3]. The symmetric quandle cocycle invariant of an (unoriented) surface-link for a symmetric quandle , an -set and a symmetric quandle -cocycle is also defined by taking the sum of the weights of triple points for each -coloring, and setting the multi-set of the images, by , of the weight sums for all the -colorings, refer to [13].
Let be a quandle, the symmetric double of , and an -set. By Lemma 4.5, we can also regard as a -set. We have the next theorem, which shows that the quandle homology invariant of an oriented surface-link can be interpreted by using symmetric quandles.
Theorem 6.5.
Let is a diagram of an oriented surface-link and take such that . Then as multi-sets, we have
The next corollary shows that the quandle homology invariant of an (orientable, unoriented) surface-link can be also interpreted by using symmetric quandles.
Corollary 6.6.
Let be a diagram of an unoriented surface-link. As multi-sets, we have
Let be an abelian group. Let and be a quandle -cocycle and a symmetric quandle -cocycle, respectively, such that . The next theorem shows that the quandle cocycle invariant of an oriented surface-link can be also interpreted by using symmetric quandles.
Theorem 6.7.
Let is a diagram of an oriented surface-link and take such that . As multi-sets, we have
The next corollary shows that the quandle cocycle invariant of an (orientable, unoriented) surface-link can be also interpreted by using symmetric quandles.
Corollary 6.8.
Let be a diagram of an unoriented surface-link. As multi-sets, we have
Remark 6.9.
Remark 6.10.
As a consequence of the results of this section, it is no exaggeration to say that symmetric quandles are also useful for oriented surface-links, and symmetric quandles are not less than quandles in the case of considering coloring numbers and cocycle invariants for oriented surface-links.
Acknowledgments
This work was supported by JSPS KAKENHI Grant Number 16K17600.
References
- [1] J. S. Carter, M. Elhamdadi, M. Graa, and M. Saito, Cocycle knot invariants from quandle modules and generalized quandle homology, Osaka J. Math., 42, (2005), 499–541.
- [2] J. S. Carter, D. Jelsovsky, S. Kamada, L. Langford, and M. Saito, Quandle cohomology and state-sum invariants of knotted curves and surfaces, Trans. Amer. Math. Soc., 355, (2003), 3947–3989.
- [3] J. S. Carter, S. Kamada, and M. Saito, Surfaces in -space, Encyclopaedia of Mathematical Sciences 142, (2004), Low-Dimensional Topology, III. Springer-Verlag, Berlin, xiv pp.
- [4] J. S. Carter, K. Oshiro, and M. Saito, Symmetric extensions of dihedral quandles and triple points of non-orientable surfaces, Topology Appl., 157, (2010), 857–869.
- [5] J. S. Carter and M. Saito, Knotted surfaces and their diagrams, Mathematical Surveys and Monographs 55, (1998), American Mathematical Society, Providence, RI.
- [6] R. Fenn and C. Rourke, Racks and links in codimension two, J. Knot Theory Ramifications, 1, (1992), 343–406.
- [7] R. Fenn, C. Rourke, and B. Sanderson,and Trunks and classifying spaces, Appl. Categ. Structures, 3, (1995), 321–356.
- [8] M. Iwakiri, The lower bound of the -indices of surface-links via quandle cocycle invariants, Trans. Amer. Math. Soc., 362, (2010), 1189–1210.
- [9] Y. Jang and K. Oshiro, Symmetric quandle colorings for spatial graphs and handlebody-links, J. Knot Theory Ramifications, 21, (2012), 1250050, 16 pp.
- [10] D. Joyce, A classifying invariant of knots, the knot quandle, J. Pure Appl. Alg., 23, (1982), 37–65.
- [11] S. Kamada, Quandles with good involutions, their homologies and knot invariants, Intelligence of low dimensional topology 2006, 101–108, Ser. Knots Everything, 40, (2007), World Sci. Publ., Hackensack, NJ.
- [12] S. Kamada, Quandles and symmetric quandles for higher dimensional knots, Knots in Poland III. Part III, 145–158, Banach Center Publ., 103, (2014), Polish Acad. Sci. Inst. Math., Warsaw.
- [13] S. Kamada and K. Oshiro, Homology groups of symmetric quandles and cocycle invariants of links and surface-links, Trans. Amer. Math. Soc., 362, (2010), 5501–5527.
- [14] K. Kawamura, K. Oshiro, and K. Tanaka, Independence of Roseman moves including triple points, Algebr. Geom. Topol., 16, (2016), 2443–2458.
- [15] S. V. Matveev, Distributive groupoids in knot theory, Mat. Sb. (N.S.), 119 (161), (1982), 78–88.
- [16] T. Nosaka, Homotopical interpretation of link invariants from finite quandles, Topology Appl., 193, (2015), 1–30.
- [17] K. Oshiro, Triple point numbers of surface-links and symmetric quandle cocycle invariants, Algebr. Geom. Topol., 10, (2010), 853–865.
- [18] K. Oshiro, Homology groups of trivial quandles with good involutions and triple linking numbers of surface-links, J. Knot Theory Ramifications, 20, (2011), 595–608.
- [19] K. Oshiro and S. Satoh, -colored -knot diagram with six colors, Hiroshima Math. J., 44, (2014), 63–74.
- [20] K. Oshiro and K. Tanaka, On rack colorings for surface-knot diagrams without branch points, Topology Appl., 196, (2015), 921–93.
- [21] S. Satoh, Sheet numbers and cocycle invariants of surface-knots, Intelligence of low dimensional topology 2006, 287–291, Ser. Knots Everything, 40, (2007), World Sci. Publ., Hackensack, NJ.
- [22] S. Satoh, The length of a -cocycle of the -dihedral quandle, Algebr. Geom. Topol., 16, (2016), 3325–3359.
- [23] S. Satoh and A. Shima, The -twist-spun trefoil has the triple point number four, Trans. Amer. Math. Soc., 356, (2004), 1007–1024.
- [24] K. Tanaka, Inequivalent surface-knots with the same knot quandle, Topology Appl., 154, (2007), 2757–2763.