Quantitative uniform exponential acceleration of averages along decaying waves
Abstract
In this study, utilizing a specific exponential weighting function, we investigate the uniform exponential convergence of weighted Birkhoff averages along decaying waves and delve into several related variants. A key distinction from traditional scenarios is evident here: despite reduced regularity in observables, our method still maintains exponential convergence. In particular, we develop new techniques that yield very precise rates of exponential convergence, as evidenced by numerical simulations. Furthermore, this innovative approach extends to quantitative analyses involving different weighting functions employed by others, surpassing the limitations inherent in prior research. It also enhances the exponential convergence rates of weighted Birkhoff averages along quasi-periodic orbits via analytic observables. To the best of our knowledge, this is the first result on the uniform exponential acceleration beyond averages along quasi-periodic or almost periodic orbits, particularly from a quantitative perspective.
Keywords: Weighted averaging method, decaying waves, quantitative uniform exponential convergence, numerical simulation
2020 Mathematics Subject Classification: 37A25, 37A30, 37A46
1 Introduction
As one of the foundational theories in dynamical systems, ergodic theory first originated from Birkhoff and von Neumann. This seminal work has given rise to an array of diverse formulations and has been extensively applied across various domains. It is a well-established fact, as noted by Krengel [16], that the convergence rates of Birkhoff averages in ergodic theory are generally slow, and can even be arbitrarily slow for certain counterexamples. Similar assertions were reaffirmed by Ryzhikov [36], while recent results on the convergence rate within the Birkhoff ergodic theorem can be found in Podvigin’s comprehensive survey [24]. Furthermore, Yoccoz’s counterexamples [39, 40], constructed via rotations that are extremely Liouvillean–nearly rational–on the finite-dimensional torus, deserve mentioning. Such slow convergence is ubiquitous in ergodic theory and is intrinsically inescapable, and it would be at most in non-trivial cases with time length , i.e., the observables are non-constant, as detailed by Kachurovskiĭ [13]. More frustratingly, the pursuit of high-precision numerical results may demand computational durations on the order of billions of years, a point elaborated by Das and Yorke in [5].
Given the acknowledged slow convergence in ergodic theory, the weighting method is crucial for accelerating computations in both mathematics and mechanics. There is a growing interest in identifying suitable weighting functions to enhance the convergence rates of ergodic averages. To investigate quasi-periodic perturbations of quasi-periodic flows, Laskar employed a weighting function to accelerate computational processes, as detailed in [17, 18, 19]. Furthermore, Laskar claimed that a specific exponential weighting function possesses superior asymptotic characteristics, although he did not implement it or provide evidence of its convergence properties, as noted in [19]. It is worth highlighting that the resulting convergence rate can be demonstrated to exceed that of any arbitrary polynomial, which we shall detail later. To be more precise, Laskar employed the following weighting function to investigate ergodicity within dynamical systems:
| (1.1) |
and the corresponding weighted Birkhoff average of an sufficiently smooth observable evaluated along a trajectory of length reads
| (1.2) |
provided , and is a quasi-periodic mapping on the -torus with , is an initial point. It is evident that and the integral . From a statistical standpoint, this approach effectively reduces the impact of the initial and terminal data, thereby highlighting those in the central range. This emphasis aligns with the concept of averaging, consequently leading to an intuitively rapid uniform convergence to the spatial average . However, there are more profound reasons behind this phenomenon, which have been illustrated by the authors in [34].
Back to the main topic, following Laskar’s significant numerical discovery, Das and Yorke [5] provided rigorous proofs for quasi-periodic systems with Diophantine rotations. To be more precise, they demonstrated that under observables, the weighted Birkhoff averages can achieve rapid convergence of arbitrary polynomial order. However, more rigorous theoretical work is still lacking in this area. To this end, inspired by the fundamental work of Das and Yorke, the authors recently made interesting findings in [34, 35, 33]–namely that universally–or saying in terms of full measure, the weighted Birkhoff averages (as well as the Cesàro weighted averages) exhibit exponential convergence as long as the observables are analytic and irrespective of finite dimensions (quasi-periodic) or infinite dimensions (almost periodic). This comes somewhat unexpectedly since it can break through what is known as “curse of dimensionality”–a common phenomenon in high-dimensional systems where complexity grows exponentially with each additional dimension. More generally, the authors also discussed abstract scenarios admitting weaker nonresonance and regularity and present certain balancing criteria to achieve rapid convergence. Due to brevity considerations, these details are not elaborated upon here.
Based on these theoretical foundations, many researchers have utilized this weighting method to perform numerical calculations on various physical systems which has significantly increased their efficiency. On this aspect, see Calleja et al. [4], Das et al. [6], Sander and Meiss [27, 28, 29], Meiss and Sander [22], Duignan and Meiss [9], Blessing and Mireles James [3] among several others; these contributions provide strong evidence supporting rapid convergence. Specifically, Duignan and Meiss [9] employed this weighting method to distinguish between regular (in fact, quasi-periodic there) and chaotic systems. To be more precise, under the weighted Birkhoff averages via (1.1), regular systems typically demonstrate a rapid exponential convergence. In contrast, chaotic systems exhibit at most an one-order polynomial slow convergence. This raises an intriguing question: what other scenarios might these so-called regular systems applicable to weighted Birkhoff averages encompass?
The primary motivations behind this work are twofold: (M1) We aim to delve deeper into the practical applications of weighted Birkhoff averages beyond quasi-periodic and almost periodic systems which admit zero Lyapunov exponents. We believe at least that, for dynamical systems having negative maximal Lyapunov exponents, Birkhoff averages along trajectories, once weighted by the function (1.1), should also exhibit exponential convergence under certain generic conditions. (M2) Currently, the analysis of the convergence rates for the weighted Birkhoff averages with the weighting function (1.1) is almost entirely qualitative (at least, not particularly precise when compared with numerical simulations of the convergence rates). We suspect that this imprecision is due to limitations in previous techniques. Therefore, we aim to develop new approaches to provide a quantitative version of these convergence rates.
Based on the above considerations, we first start with some typical examples, namely exponentially decaying waves (e.g., and with certain and ), which constitute some fundamental solutions among others for linear matrix differential equations described as (other solutions have more polynomial parts than these, depending on the multiplicity of the eigenvalues, see Section 6), where all eigenvalues of the constant matrix lie inside the unit circle . Such decaying waves can also be interpreted as projections onto planes from spiral waves within -dimensional space. For further insights into the connections between decaying waves and dynamics systems, we refer readers to Liu et al. [20, 21], Wang et al. [37], Xing et al. [38] inclusive of their references which provide an exploration into this domain. As a main contribution, we demonstrate that Laskar’s weighted averaging method not only significantly accelerates the Birkhoff averages along quasi-periodic or almost periodic orbits, but also proves effective for other scenarios, involving weighted Birkhoff averages of decaying waves, with extremely rapid exponential convergence rates contrasting with the universal one-order polynomial type observed in unweighted cases (Theorem 1.1 and Remark 1.1). Specifically, our quantitative convergence rates prove to be remarkably precise, as evidenced by the numerical simulations illustrated in Figure 1 within Section 8. Furthermore, we proceed to discuss more general decaying waves in series forms and arrive at optimal results somewhat unexpectedly (Theorem 1.2).
Before delving into the main subject, let us first introduce some basic notations for the sake of simplicity. We define that in the limit process as , the statements and imply there exists a positive constant , such that and , respectively. We also denote by the -th derivative of a sufficiently smooth function . Additionally, for any fixed number , we define as the distance to the closest element of the set , or equivalently, it represents the metric on the standard torus identified with .
In what follows, we proceed to present our main results. Consider the unweighted time average of the decaying wave as
as well as the -weighted type given by
The first main result in this paper is stated as follows.
Theorem 1.1.
(I) For any fixed and ,
uniformly holds with , where . In particular, the control coefficient is independent of , and is uniformly bounded for large .
(II) However, for any fixed and , there exists infinitely many such that
whenever .
Remark 1.1.
For fixed and , the set of such has at most zero Lebesgue measure. Therefore, the convergence for the unweighted decaying waves is universal, or commonly referred to as almost certain. This is completely consistent with the zero-one law in [24].
Theorem 1.1 provides an upper bound on the convergence rate of the weighted Birkhoff average , which depends simultaneously on the decaying parameter and the rotating parameter . As we will demonstrate in the numerical simulation within Section 8, this estimate is remarkably precise.
The following conclusion concerning the averages of superimposed waves is a direct corollary of Theorem 1.1.
Corollary 1.1.
For , define , where and . Then for any sequence , the time average of the superimposed wave converges uniformly (with respect to ) and exponentially to .
Indeed, when the decaying parameters , Corollary 1.1 covers the cases of decaying quasi-periodic or decaying almost periodic. For a given set of rotation parameters with (), if for any , , then the motion exhibited is quasi-periodic (almost periodic). See [33] for further characterization of these two concepts, as well as specific examples in Kozlov [15], for instance. However, the control coefficient in Theorem 1.1 may tend to as the decaying parameter tends to . Therefore, if the case considered in Corollary 1.1 allows the decaying parameters to tend to (acting similarly to Bessel functions), then with the variation in the arithmetic properties of the rotation parameters , more complicated small denominator problems may arise. This needs to be dealt with in combination with the techniques in [33, 34, 35] (see also Section 7), which we prefer not to discuss here.
To enhance the applicability of our results, we present the quantitative Theorem 1.2 below. Prior to this, we denote by the space consisting of continuous functions on having an absolutely convergent Fourier series, i.e., the functions for which . With the norm defined by , is a Banach space isometric to with algebra property, see Katznelson [14] for instance. For , we denote by the space of -Hölder functions endowed with the norm
We also denote by the space of functions on with -order continuous derivatives, where .
Theorem 1.2.
Let , be given.
-
(I)
For any observable , it holds uniformly with respect to that
(1.3) where . A sufficient case is with . In particular, for any trigonometric polynomial of order on without the Fourier constant term, i.e., , the index of the exponential rate in (1.3) could be improved to .
-
(II)
For any analytic observable on , it holds uniformly with respect to that
(1.4) where . In particular, for any polynomial of order , i.e., , the index of the exponential rate in (1.4) could be improved to , provided
and
-
(III)
For any observable on with for some and , it holds uniformly with respect to that
where . A sufficient case is satisfying for and .
Remark 1.2.
Remark 1.3.
For trigonometric series, the absolute summability in (I) is almost optimal in order to guarantee the uniform convergence with respect to in (1.3). For example, considering and , we construct the counterexample as . Then . Taking and sufficiently close to , the weighed decaying wave becomes , which exhibits non-uniform convergence for such .
Recall that in [22, 5, 33], achieving fast convergence of the weighted Birkhoff average necessitates strong regularity for the observable, e.g., the regularity or even analyticity. However, as shown for the decaying wave in (I), incorporating the decaying part compensates for the lack of regularity, thereby naturally achieving the exponential convergence. Moreover, the observable in (III) could admit very weak regularity, for example, discontinuity except of .
The remainder of this paper is organized as follows. To highlight the ideas underlying our proof, we provide a detailed analysis of Theorem 1.1 in Section 2. Building upon this foundation, we give a more concise proof for Theorem 1.2 in Section 4. We also quantitatively discuss more general weighting functions in Section 5 and demonstrate their potential to lead exponential convergence of weighted Birkhoff averages, thereby providing theoretical validation for the numerical results by Das et al. [6], Duignan and Meiss [9], and Calleja et al. [4], among others. Although Theorems 1.1 and 1.2 consider discrete cases, we illustrate in Section 6 that such results extend naturally to continuous cases as well, and indeed, even simpler. In addition to the exponentially decaying waves addressed in Theorems 1.1 and 1.2, our newly developed techniques are also applicable to the weighted Birkhoff averages associated with more general types of decaying waves, especially orbits from certain nonlinear dynamical systems having negative maximum Lyapunov exponents, as detailed in Section 6. In Section 7, following careful approaches introduced in this paper, we revisit the exponential convergence rates of weighted Birkhoff averages along quasi-periodic orbits as initially discussed in [33], contributing an enhanced quantitative result (Theorem 7.1) to the existing research. As part of the main contributions, we show that:
- •
Finally, we present in Section 8 numerical simulation for a universal example which showcase the precision of our results, from a quantitative perspective.
2 Proof of Theorem 1.1
2.1 Proof of (I): Exponential convergence of the weighted type
We first prove (I). With the Poisson summation formula (see [11, 30] for instance), we have
and this leads to
| (2.1) |
This eliminates the influence of the initial phase parameter . By integrating by parts, it is evident to get
Note that and . Then it follows that
| (2.2) |
Next, we need certain accurate asymptotic estimates for , as demonstrated in the following Lemma 2.1.
Lemma 2.1.
There exist absolute constants , such that for all ,
| (2.3) |
Proof.
Note that is locally holomorphic. Fix , let us choose some such that for , it holds that
where . Then, using Cauchy’s integral formula and the triangle inequality, we have that for ,
| (2.4) |
We mention that (2.4) serves as an extension of Problem 4* in Chapter 5 of [30]. Following (2.4), one can also prove that is in a Denjoy-Carleman class (see the definition in [2]). With (2.4), we derive that
| (2.5) |
The crucial point is to estimate the asymptotic behavior of the integral in (2.5). For , consider the parameterized integral defined by
Utilizing the Cauchy-Schlömilch transformation, one can verify that is independent of , and it is indeed equal to . Then for any given and , it holds
On the one hand,
| (2.6) |
On the other hand,
| (2.7) |
One notices that the right hand side of (2.7) contains at most terms, and the power terms of can be dominated by due to , and those derivatives with respect to will eventually generate . On these grounds, there exists some absolute constant (independent of ) such that
| (2.8) |
Combining (2.5), (2.6), (2.7), (2.8) (with and ) and utilizing Stirling’s approximation as , we obtain the desired estimate with some :
∎
It is evident that there exists some absolute constant such that . Therefore, with (2.1), (2.2) and Lemma 2.1, we have that
| (2.9) |
holds for and
In the next lemma, we will demonstrate that exhibits exponential decay with respect to . The crucial insight in the proof is that by adjusting the time of integration by parts (with respect to the parameters , etc.), we can minimize within the permissible range, leading to its eventual exponential decay. Furthermore, we will employ a truncation method to demonstrate that the summation over does not affect the overall exponential decay.
Lemma 2.2.
There exists some absolute constant , such that
holds for sufficiently large.
Proof.
For the sake of brevity, define , where
According to monotonicity analysis, we have . Then by setting as , we arrive at
| (2.10) |
for some absolute constant (independent of ). To estimate , we consider partitioning into a union of two disjoint sets, namely with
Now, by utilizing (2.10), we obtain that
| (2.11) |
For convenience, we declare that the following absolute positive constants through are independent of . On the one hand,
| (2.12) |
On the other hand,
| (2.13) |
Now, substituting (2.12) and (2.13) into (2.11) yields
due to , which completes the proof. ∎
2.2 Proof of (II): convergence of the unweighted type
As to (II), it is evident to calculate that
This leads to convergence of whenever , which proves (II) of Theorem 1.1.
3 Proof of Corollary 1.1
Corollary 1.1 is a direct consequence of Theorem 1.1, for which we provide a brief proof here. According to part (I) of Theorem 1.1, for each decaying wave , it converges uniformly to at least at an exponential rate after weighted averaging due to the uniform lower bound on , and the control coefficient is independent of . Consequently, the absolute summability of the sequence allows for the interchange of order, thus completing the proof.
4 Proof of Theorem 1.2
We emphasize that the dependence of the control coefficient in Theorem 1.1 on the parameters is essential to prove Theorem 1.2.
Proof of (I): We only prove the latter two conclusions, as the first conclusion remains the same. In view of with , we write . In what follows, we prove that the Fourier series is indeed absolutely summable, which is known as the Bernstein Theorem. Below we provide a brief proof for the completeness. For any , define for . Then it can be verified that
This leads to
| (4.1) |
with some , where the Hölder continuity is used in (4.1). Then by Cauchy’s inequality, we have
By summing up with and utilizing , we obtain the absolute summable Fourier series of , which is converges pointwise to on .
For an individual with , the weighted average of the decaying wave admits exponential convergence in Theorem 1.1 with the decaying index . Therefore, by summing up and utilizing , we prove the first claim in (I). One notices that for general , we cannot obtain a more precise decaying index under this approach, as in Theorem 1.1, replacing by (the proof is completely same) and taking , we arrive at the decaying index here. Another reason is that as increases, has a subsequence that tends to (whether is rational or irrational), and therefore it does not have a positive bound from below. However, for any trigonometric polynomial of order on without the Fourier constant term, the decaying index of the exponential rate could be improved to , in a similar way. To be more precise, for any trigonometric part, the corresponding decaying index in Theorem 1.1 has a uniform lower bound, as for all .
Proof of (II): As to (II), the analyticity of yields for all , and . Note that for , we have
| (4.2) |
Then it is evident to verify that the summation of the coefficients of the trigonometric polynomial does not exceed . Therefore, with , the strict monotonicity of with respect to and and Theorem 1.1, we deduce the desired conclusion in (II) as follows:
where . When considering polynomials of order , i.e., , it can be observed from the trigonometric part in (4.2) that for with , the even case and the odd case are indeed different. For the even case, the lowest convergence rate is with
due to the existence of the constant term. While for the odd case where the constant term vanishes, we obtain the lowest convergence rate as , provided with
Combining the above two convergence rates we complete the proof of (II).
Proof of (III): The analysis is actually similar to (II), whenever we observe that
which yields the convergence rate with , as desired.
5 Further discussions on general exponential weighting functions
Historically, there have been various types of weighting functions for weighted Birkhoff averages. For instance, Laskar [17, 18, 19] utilized , and Das et al. [6] as well as the authors [34] employed for comparative purposes (in relation to (1.1)). It is also worth mentioning that very recently, Ruth and Bindel [25] introduced a co-called “tuned filter” that possesses similar desirable properties to (1.1) in applications. However, some weighting functions may not possess the property of being smoothness, which is crucial for achieving universal arbitrary polynomial or even exponential convergence. As a result, under such weighting functions, the weighted Birkhoff averages typically only exhibit convergence up to finite polynomial order. We do not intend to discuss them, but instead focus on some analogues of (1.1) that have been verified in numerical simulations to exhibit significantly superior exponential acceleration effects; see Das et al. [6], Duignan and Meiss [9], and Calleja et al. [4] on this aspect.
5.1 Exponential weighting function with two regularity parameters
For , consider a general exponential weighting function on defined by
In particular, . We refer to and as regularity parameters, because they characterize the asymptotic properties of the weighting function at the boundaries of the compact support. It also preserves the elementary properties of , as and . Das et al. [6] and Calleja et al. [4] utilized this weighting function with to find rotation numbers (the latter concerned the spin-orbit problem with tidal torque), and observed the so-called super-convergence. For general , it is evident to prove the arbitrary polynomial convergence via in weighted Birkhoff averages, however, it is non-trivial to obtain the exponential convergence. The authors provided in [33, 34, 35] a useful approach to achieve the exponential convergence by estimating for sufficiently large , following the spirit of induction. Unfortunately, it becomes much more difficult when dealing with the weighting function for from induction, as integrating by parts multiple times will lead to more complicated parts. More importantly, according to this method, it is almost impossible to obtain such precise convergence rate estimates in our paper (Theorems 1.1 and 1.2). Consequently, there does not exist any theoretical result that guarantees the exponential convergence of the weighted Birkhoff averages in [6, 4]. It is therefore natural that ones should consider the following questions:
- (Q1)
-
(Q2)
How about the convergence rates of the weighted decaying waves via ?
The answer for question (Q1), is positive. We first establish a quantitative lemma for , as an extension of Lemma 5.3 in [33] concerning . This approach is entirely distinct from the ones in [5, 6, 33], yet it proves to be highly effective. Subsequently, the theoretical exponential convergence discussed in [33, 34, 35] via can be obtained directly, by replacing in Lemma 5.3 in [33] with any number greater than .
Lemma 5.1.
For , there exists some such that for any ,
Proof.
Following a similar method in Lemma 2.1, we have that for fixed , there exists some such that
| (5.1) |
Then it follows from (5.1) and the symmetry that
| (5.2) |
where is the standard Gamma function. In view of Stirling’s approximation as , the right side of (5.2) admits an equivalent form as
provided with
Therefore, it is evident that there exists some such that
∎
Regarding question (Q2), it is somewhat interesting that ones could derive the following theorem, at least for :
Theorem 5.1.
5.2 Exponential weighting function with a width parameter
Finally, we would like to mention the weighting function utilized by Duignan and Meiss in [9], namely a various version of with a width parameter :
They compared numerically the impact of different width parameters on the convergence rate for the two-wave Hamiltonian system (e.g., to illustrate the converse KAM method that detects the breakup of tori [8, 22]), and they observed that, for different cases (such as varying orbits), it is difficult to obtain a uniform optimal to accelerate the convergence rate. Therefore, it is necessary to theoretically provide quantitative exponential convergence rates for all . It should be noted that even in the analysis of weighted Birkhoff averages, estimating the convergence rate of the weighting function is somewhat difficult in the previous techniques (see [33] for instance), let alone quantitatively.
Here we do not intend to delve into detailed discussions, but from the results, the difference with lies in, for example, the parameter in the exponential convergence rate of Theorem 1.1 being replaced by (noting only that the exponential part in (2.5) in Lemma 2.1 becomes , which yields the exponential part in (2.3) with the weighting function ).
It is worth emphasizing that increasing cannot make practical computations faster indefinitely, as the control coefficient for the exponential convergence will inevitably tend to infinity, leading to lack of uniformity (otherwise, when , the weighted average tends to rather than the spatial average). This is consistent with the views of Duignan and Meiss in [9]. However, for a given system, we can provide a feasible approach to the unsolved problem of finding the optimal width parameter in [9], by quantitatively estimating the exponential convergence rate (calculating the control coefficient quantitatively as well), thereby choosing the optimal to minimize the upper bound of the error.
6 Further applicability: the continuous case and the general decaying case
6.1 The continuous case
We first would like to emphasize that all results in this paper can be extended to the continuous case, i.e., in a integral form. The proofs become simpler, as we do not need to employ the Poisson summation formula, and thus do not require the elaborate summation estimates as in Lemma 2.2. Additionally, it is worth mentioning that the uniform exponential convergence rates obtained will be faster in certain cases, as in those cases, the term in the conclusions (see Theorem 1.1 for instance) will be replaced by (note that for all ), eliminating the need for the Poisson summation formula. Another distinction in terms of the conclusions between the continuous and discrete cases is the polynomial convergence condition for the unweighted type. Define in a similar way,
as well as the -weighted type,
Then, admits uniform exponential convergence as mentioned previously. However, through simple calculations, we can prove that as if , which differs from (II) in Theorem 1.1. To enable readers to understand the aforementioned analysis more clearly, we present the following theorem as a continuous form of Theorem 1.1 and provide a brief outline of its proof.
Theorem 6.1.
(I) For any fixed and ,
uniformly holds with , where . In particular, the control coefficient is independent of , and is uniformly bounded for large .
(II) However, for any fixed and , there exists infinitely many such that
whenever .
Proof.
We only show the strategy of (I). Unlike the discrete case, which requires the application of the Poisson summation formula, we only need to perform integration by parts on the weighted integral , with variable integration time denoted as . Therefore, this indeed corresponds to a segment of the discrete case; specifically, it does not involve within (2.2). Consequently, fundamentally this resembles Lemma 2.2 without necessitating partitioning of summations; one simply needs to select as to complete the proof of (I). ∎
Next, we further discuss analogues of Theorem 1.2. Similarly, in the continuous case, as long as the observable belongs to , the corresponding time average along the weighted decaying wave admits uniform exponential convergence. This is in stark contrast to the unweighted Birkhoff integrals. See Forni [10] for instance, given an irrational rotation in each coordinate on observed by an observable with bounded variation, the upper bound for all of the difference between the time average and the spatial average can often only be estimated as using the Denjoy-Koksma inequality and the metric theory of continued fractions, where is arbitrarily fixed. See also Dolgopyat and Fayad [7] for a more precise description of this aspect. This bound includes an additional logarithmic term beyond the optimal convergence rate achievable in sufficiently smooth cases, through a Fourier argument based on the co-homological equation. Consequently, our results are somewhat unexpected, as we achieve uniform exponential convergence from observables with very weak regularity.
6.2 The general decaying case
Finally, let us discuss weighted Birkhoff averages along general decaying waves. It should be noted that the approaches in this paper are not limited to weighted averages of exponentially decaying waves, but also extend to more general decay, such as the polynomial decay, exponential plus polynomial decay, super-exponential decay, etc. Specifically, the exponential plus polynomial decay, exemplified by where and , has a distinctive background as elucidated in the Introduction; it serves as a fundamental solution of the linear differential equation , where the constant matrix only admits eigenvalues within the unit circle –or equivalently, with negative maximal Lyapunov exponents, and the degree of the polynomial part depends on the multiplicity of the eigenvalues of . Furthermore, the techniques developed in this paper are applicable to weighted Birkhoff averages along trajectories of certain nonlinear systems that can be smoothly conjugated to linear ones, e.g.,
although in such cases, one must investigate the regularity of the conjugations. If only arbitrary polynomial convergence rates are desired when the conjugation is , the analysis will be straightforward–indeed, a slight modification of [5, 6, 33, 34, 35] or the approaches presented in this paper can achieve the desired conclusion; however, for the quantitative exponential convergence rates as considered in this paper (which will change form for more general decay), some essential estimates need to be established as in Lemma 2.1. In order to highlight our approaches more clearly, we prefer to focus on the exponentially decaying waves in this paper, without delving into the details of these more general cases, as they do not differ significantly in terms of conceptual framework. For this reason, we only present the following qualitative exponential convergence theorem with a brief outline of the proof.
Theorem 6.2.
(I) Consider the continuous nonlinear dynamical system
| (6.1) |
where satisfies , and all eigenvalues of lie inside the unit circle . Assume there exists a neighbourhood of and a conjugation such that , , and that , where is the flow of with the same initial of (6.1). Then for any flow starting from the initial point , the weighted Birkhoff averages
converge uniformly (with respect to ) and exponentially to .
(II) Consider the discrete nonlinear dynamical system
where satisfies , and all eigenvalues () of are simple and lie inside the unit circle . Moreover, is locally , and the following nonresonant condition holds:
Then there exists a neighbourhood of , such that for any iterated sequence starting from the initial point , the weighted Birkhoff average
converges uniformly (with respect to ) and exponentially to . In particular, the convergence rate is , where .
Proof.
We only prove (II), as the analysis for (I) is similar. For convenience, we only consider the case where . By utilizing Sternberg’s linearization theorem [31, 32], we obtain a local diffeomorphism such that , with and . Then it is evident that for any sufficiently close to , it holds
Generally, we set with and (indeed, in the discrete case here, but it may vary in the continuous case), then one observes that (this is actually a generalized version of the inverse Lagrange theorem), where
and
This leads to
for some universal . Both and converge uniformly (with respect to ) and exponentially to , as the components of and are exponentially decaying waves which we have discussed in Theorems 1.1 and 1.2. To be more precise, from the nonresonant condition for eigenvalues, we have for . Consequently, the smallest decaying parameter of such waves is , which leads to the exponential convergence of with , similar to the proof of (III) in Theorem 1.2. As for the continuous case, may be more complicated as may contain Jordan blocks, however, the components of are decaying waves with exponential plus polynomial decay, hence the weighted Birkhoff average along it still converges exponentially since the polynomial parts could be well dominated by the exponential parts in the proof. ∎
We end this section by emphasizing the followings: (i) Both two cases in (I) and (II) could be extended to the smoothly-observed case as discussed in Theorem 1.2; (ii) the existence of the conjugation in (I) can be guaranteed by the classical Hartman-Grobman theorem, but the regularity is generally at most of Hölder type below , regardless of how high the regularity of is, as detailed in Arnold’s book [1]; (iii) The regularity of in (II) allows for a finitely differentiable type depending on the nonresonant conditions of the eigenvalues, see Sternberg [31, 32]. For a more explicit exposition on Sternberg’s result, we would also like to mention the work of Zhang et al. [42].
7 Exponential acceleration in analytic quasi-periodic dynamical systems revisited
This section is mainly devoted to improve a previous qualitative result obtained by the authors in [33] to a quantitative one. Consider a quasi-periodic weighted Birkhoff average
as that in (1.2), where the -torus is modified to with for brevity, the initial point , the quasi-periodic mapping is specified by with the nonresonant rotation vector , and is a smooth observable on . One of the most important (which we say universal) results from [33], Corollary 3.1, states that if is analytic, then for almost all (in the sense of full Lebesgue measure) rotation vectors , the weighted Birkhoff error term
| (7.1) |
exhibits qualitative uniform (with respect to ) exponential convergence , where are certain universal constants. It is worth noting that, for qualitative considerations, [33] provides a strict lower bound for as , although this is not explicitly stated there. Our motivation in the forthcoming Theorem 7.1 is to refine this bound and demonstrate a variety of representative scenarios, utilizing the innovative techniques developed throughout this paper. We emphasize that if one is only interested in arbitrary polynomial convergence, one can follow the ideas presented in Das and Yorke [5] (or Das et al. [6]), making the complicated approaches employed here entirely unnecessary. The main difficulty lies in properly dealing with small divisors to quantify the exponential convergence, which still remains unexplored.
Theorem 7.1.
Consider the weighted Birkhoff error term in (7.1).
-
(I)
If is analytic, then for almost all rotations and all , we have
where is some universal constant.
-
(II)
If is analytic, then for rotations with Diophantine exponent of ***It is well known that such rotations only form a set of zero Lebesgue measure in ., namely
we have
where is some universal constant.
-
(III)
If is a finite trigonometric polynomial, then for almost all rotations, we have
where is some universal constant.
Proof.
To begin, we provide a thorough demonstration for (I), serving as the foundation for the proofs of (II) to (IV).
Denote by the thickened torus, and define the norm . Then, it is well known that if is analytic, its Fourier coefficients satisfy for all , where is the analytic radius of , see Salamon [26] for instance. Next, for any fixed , we establish a nonresonant condition from Herman [12] that is satisfied by almost all rotations (as varies):
| (7.2) |
Below we estimate the Birkhoff error in (I).
Note . Then it follows that
| (7.3) |
where the truncated order will be specified later.
For the truncated term , we first estimate . With the Poisson summation formula, we obtain
| (7.4) |
where for fixed and . For any truncated order with , set the time of integration by parts as
where is the constant given in Lemma 5.1. Then we have
| (7.5) | ||||
| (7.6) |
and similarly,
| (7.7) |
because , can be dominated by (7.5), and
Combining (7.6), (7.4), (7.7) and utilizing , , we arrive at the estimate for the truncated term as
| (7.8) |
As for the remainder term , it is evident that
| (7.9) |
provided with any .
Finally, by choosing the truncated order as
| (7.10) |
we have
which leads to
with some universal constant , and so does the Birkhoff error by recalling (7.3). This proves (I).
The proofs of (II) and (III) only require minor modifications to the proof of (I). It is noted that the nonresonant condition in (II) corresponds to the case where in (7.2), and indeed, it does not affect the subsequent analysis in (I) as is still analytic. Therefore, the Birkhoff error in (II) admits an upper bound as , where is some universal constant. Regarding (III), which specifically considers that is merely a finite trigonometric polynomial and is applied for almost all rotations, the truncation technique in (I) is unnecessary. In other words, , , and the reminder term does not exist. Consequently, the estimate for the truncated term in (7.8) directly yields in (III) with some universal constant . ∎
We end this section by mentioning that the above analysis can be adapted to address the almost periodic case (though more complex), as discussed in [35]. This is achieved by utilizing the infinite-dimensional spatial structure provided by Montalto and Procesi [23], among others. We plan to delve into this topic in future research.
8 Numerical simulation and analysis of convergence rates
In this section, we present an example to illustrate our quantitative estimates of the convergence rates as stated in Theorem 1.1. Let the decaying parameter be , the rotating parameter be , and the initial phase parameter be . In this case,
It can be verified that , and
Therefore, Theorem 1.1 tells us that the unweighted average exhibits polynomial convergence of , while the weighted average demonstrates exponential convergence as given by
| (8.1) |
We would like to emphasize that (8.1) is exceptionally precise. For , (8.1) provides an upper bound on the absolute error of approximately , while the actual error is around , as illustrated in Figure 1; for , (8.1) yields an upper bound on the absolute error of approximately , compared to the actual error of approximately , however, due to the extremely small nature of these values, they are not provided in the figure.
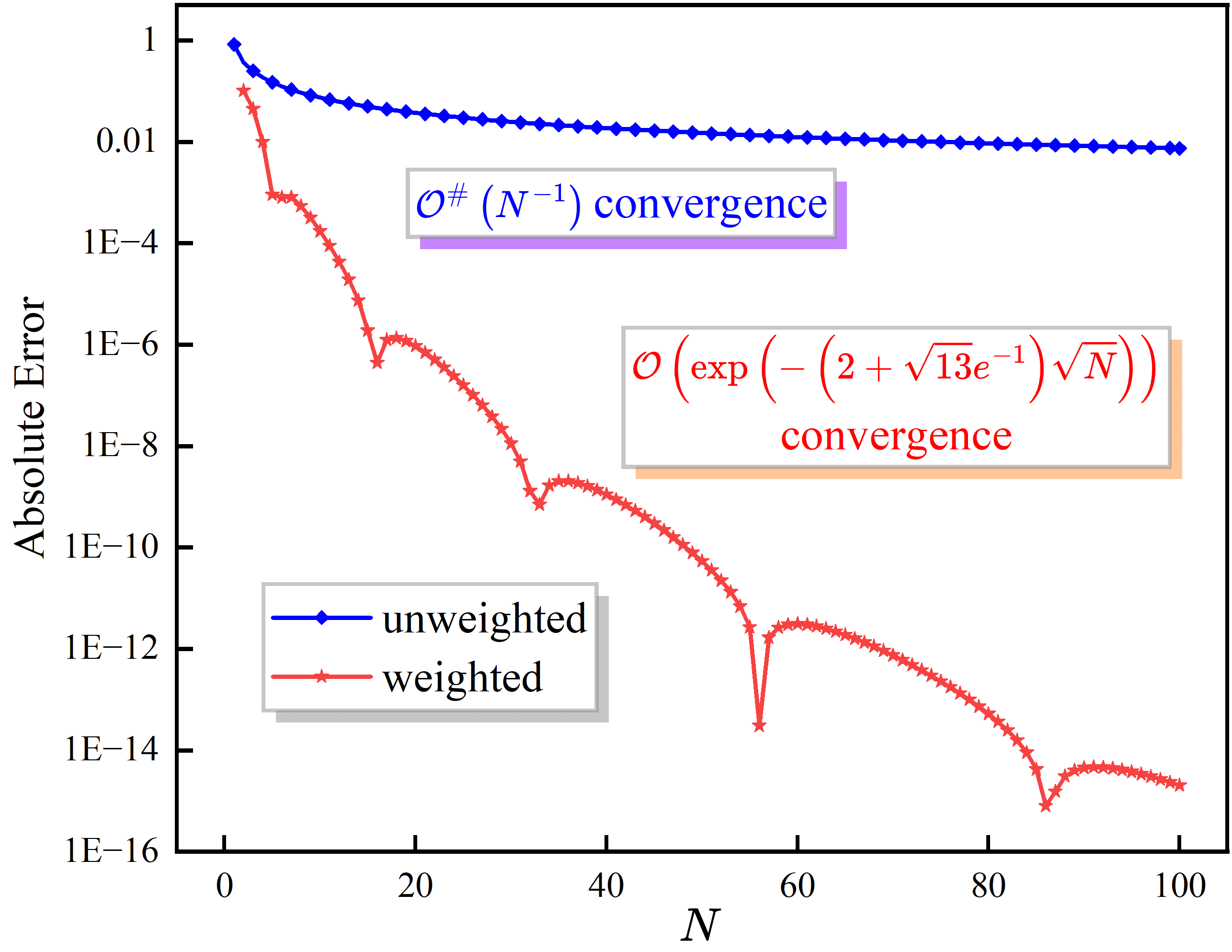
Actually, on the standard torus , the rotation number with respect to the rotating parameter in this case is , which admits a Diophantine exponent of ***Indeed, for any irrational with an exact Diophantine exponent, admits the same exact Diophantine exponent as , provided that are rational and . As a consequence, admits the same exact Diophantine exponent as , as seen in the equivalent expression ., i.e.,
for some , see Zeilberger and Zudilin [41] for a more accurate estimate on this aspect. We intentionally avoided using the constant type (with exact Diophantine exponent †††It is well known that such rotation numbers only form a set of zero Lebesgue measure in .) rotation numbers that would have further accelerated the convergence rate. Instead, we select a less irrational (more universal) alternative as . We also refer to Das et al. [6] for a numerical comparison of the two cases in the weighted Birkhoff average with rotation numbers (having the same Diophantine exponent as ) and (the constant type).
Acknowledgements
This work was supported in part by National Basic Research Program of China (Grant No. 2013CB834100), National Natural Science Foundation of China (Grant Nos. 12071175, 11171132, 11571065, 12471183), Project of Science and Technology Development of Jilin Province (Grant Nos. 2017C028-1, 20190201302JC), and Natural Science Foundation of Jilin Province (Grant No. 20200201253JC). The first author was deeply grateful to Professors Wolfgang M. Schmidt, Paul Vojta, Doron Zeilberger, Wadim Zudilin for their valuable email assistance on Diophantine approximation, and Maximilian Ruth and David Bindel for their valuable email discussions on the accurate convergence rates in weighted Birkhoff averages.
References
- [1] V. Arnold, Ordinary differential equations. Springer-Verlag, Berlin, 1992. pp. 334.
- [2] A. Belotto da Silva, E. Bierstone, A. Kiro, Sharp estimates for blowing down functions in a Denjoy-Carleman class. Int. Math. Res. Not. IMRN 2022, pp. 9685–9707. https://doi.org/10.1093/imrn/rnaa367
- [3] D. Blessing, J. D. Mireles James, Weighted Birkhoff Averages and the Parameterization Method. arXiv:2306.16597
- [4] R. Calleja, A. Celletti, J. Gimeno, R. de la Llave, Accurate computations up to breakdown of quasi-periodic attractors in the dissipative spin-orbit problem. J. Nonlinear Sci. 34 (2024), Paper No. 12, pp. 38. https://doi.org/10.1007/s00332-023-09988-w
- [5] S. Das, J. Yorke, Super convergence of ergodic averages for quasiperiodic orbits. Nonlinearity 31 (2018), pp. 491–501. https://doi.org/10.1088/1361-6544/aa99a0
- [6] S. Das, Y. Saiki, E. Sander, J. Yorke, Quantitative quasiperiodicity. Nonlinearity 30 (2017), pp. 4111–4140. https://doi.org/10.1088/1361-6544/aa84c2
- [7] D. Dolgopyat, B. Fayad, Deviations of ergodic sums for toral translations II. Boxes. Publ. Math. Inst. Hautes Études Sci. 132 (2020), pp. 293–352. https://doi.org/10.1007/s10240-020-00120-2
- [8] N. Duignan, J. D. Meiss, Nonexistence of invariant tori transverse to foliations: an application of converse KAM theory. Chaos 31 (2021), Paper No. 013124, pp. 19. https://doi.org/10.1063/5.0035175
- [9] N. Duignan, J. D. Meiss, Distinguishing between regular and chaotic orbits of flows by the weighted Birkhoff average, Phys. D 449 (2023), Paper No. 133749, pp. 16. https://doi.org/10.1016/j.physd.2023.133749
- [10] G. Forni, Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math. (2) 155 (2002), pp. 1–103. https://doi.org/10.2307/3062150
- [11] L. Grafakos, Classical Fourier analysis. Third edition. Graduate Texts in Mathematics, 249. Springer, New York, 2014. xviii+638 pp.
- [12] M.-R. Herman, Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations, Inst. Hautes Études Sci. Publ. Math., 49 (1979), pp. 5–233. http://www.numdam.org/item?id=PMIHES_1979__49__5_0
- [13] A. Kachurovskiĭ, Rates of convergence in ergodic theorems. (Russian) Uspekhi Mat. Nauk 51 (1996), pp. 73–124; translation in Russian Math. Surveys 51 (1996), pp. 653–703. https://doi.org/10.1070/RM1996v051n04ABEH002964
- [14] Y. Katznelson, An introduction to harmonic analysis. Third edition. Cambridge Mathematical Library. Cambridge University Press, Cambridge, 2004. xviii+314 pp. https://doi.org/10.1017/CBO9781139165372
- [15] V. V. Kozlov, On the ergodic theory of equations of mathematical physics. Russ. J. Math. Phys. 28 (2021), pp. 73–83. https://doi.org/10.1134/S1061920821010088
- [16] U. Krengel, On the speed of convergence in the ergodic theorem. Monatsh. Math. 86 (1978/79), pp. 3–6. https://doi.org/10.1007/BF01300052
- [17] J. Laskar, Frequency analysis for multi-dimensional systems. Global dynamics and diffusion. Phys. D 67 (1993), pp. 257–281. https://doi.org/10.1016/0167-2789(93)90210-R
- [18] J. Laskar, Frequency analysis of a dynamical system. Qualitative and quantitative behaviour of planetary systems (Ramsau, 1992). Celestial Mech. Dynam. Astronom. 56 (1993), pp. 191–196. https://doi.org/10.1007/BF00699731
- [19] J. Laskar, Introduction to frequency map analysis. Hamiltonian systems with three or more degrees of freedom (S’Agaró, 1995), pp. 134–150, NATO Adv. Sci. Inst. Ser. C: Math. Phys. Sci., 533, Kluwer Acad. Publ., Dordrecht, 1999.
- [20] G. Liu, Y. Li, X. Yang, Existence and multiplicity of rotating periodic solutions for resonant Hamiltonian systems. J. Differential Equations 265 (2018), pp. 1324–1352. https://doi.org/10.1016/j.jde.2018.04.001
- [21] G. Liu, Y. Li, X. Yang, Existence and multiplicity of rotating periodic solutions for Hamiltonian systems with a general twist condition. J. Differential Equations 369 (2023), pp. 229–252. https://doi.org/10.1016/j.jde.2023.06.001
- [22] J. D. Meiss, E. Sander, Birkhoff averages and the breakdown of invariant tori in volume-preserving maps. Phys. D 428 (2021), Paper No. 133048, pp. 20. https://doi.org/10.1016/j.physd.2021.133048
- [23] R. Montalto, M. Procesi, Linear Schrödinger equation with an almost periodic potential. SIAM J. Math. Anal. 53 (2021), pp. 386–434. https://doi.org/10.1137/20M1320742
- [24] I. Podvigin, On the pointwise rate of convergence in the Birkhoff ergodic theorem: recent results. Ergodic Theory and Dynamical Systems: Proceedings of the Workshops University of North Carolina at Chapel Hill 2021, edited by Idris Assani, Berlin, Boston: De Gruyter, 2024, pp. 117–126. https://doi.org/10.1515/9783111435503-005
- [25] M. Ruth, D. Bindel, Finding Birkhoff Averages via Adaptive Filtering. https://arxiv.org/abs/2403.19003
- [26] D. Salamon, The Kolmogorov-Arnold-Moser theorem. Math. Phys. Electron. J. 10 (2004), Paper 3, pp. 37.
- [27] E. Sander, J. D. Meiss, Birkhoff averages and rotational invariant circles for area-preserving maps. Phys. D 411 (2020), 132569, pp. 19. https://doi.org/10.1016/j.physd.2020.132569
- [28] E. Sander, J. D. Meiss, Rotation Vectors for Torus Maps by the Weighted Birkhoff Average. https://arxiv.org/abs/2310.11600
- [29] E. Sander, J. D. Meiss, Computing Lyapunov Exponents using Weighted Birkhoff Averages. https://arxiv.org/abs/2409.08496
- [30] E. Stein, R. Shakarchi, Fourier analysis. An introduction. Princeton Lectures in Analysis, 1. Princeton University Press, Princeton, NJ, 2003. xvi+311 pp.
- [31] S. Sternberg, Local contractions and a theorem of Poincaré. Amer. J. Math. 79 (1957), pp. 809–824. https://doi.org/10.2307/2372437
- [32] S. Sternberg, On the structure of local homeomorphisms of euclidean -space. II. Amer. J. Math. 80 (1958), pp. 623–631. https://doi.org/10.2307/2372774
- [33] Z. Tong, Y. Li, Exponential convergence of the weighted Birkhoff average. J. Math. Pures Appl. (9) 188 (2024), pp. 470–492. https://doi.org/10.1016/j.matpur.2024.06.003
- [34] Z. Tong, Y. Li, A note on exponential convergence of Cesàro weighted Birkhoff average and multimodal weighted approach. To appear in Acta Math. Sin. (Engl. Ser.).
- [35] Z. Tong, Y. Li, Universal exponential pointwise convergence for weighted multiple ergodic averages over . https://arxiv.org/abs/2405.02866
- [36] V. V. Ryzhikov, Slow convergences of ergodic averages. (Russian) Mat. Zametki 113 (2023), pp. 742–746; translation in Math. Notes 113 (2023), pp. 704–707. https://doi.org/10.4213/sm9844
- [37] S. Wang, Y. Li, X. Yang, Synchronization, symmetry and rotating periodic solutions in oscillators with Huygens’ coupling. Phys. D 434 (2022), Paper No. 133208, pp. 22. https://doi.org/10.1016/j.physd.2022.133208
- [38] J. Xing, X. Yang, Y. Li, Lyapunov center theorem on rotating periodic orbits for Hamiltonian systems. J. Differential Equations 363 (2023), pp. 170–194. https://doi.org/10.1016/j.jde.2023.03.016
- [39] J.-C. Yoccoz, Sur la disparition de propriétés de type Denjoy-Koksma en dimension . C. R. Acad. Sci. Paris Sér. A–B 291 (1980), pp. A655–A658.
- [40] J.-C. Yoccoz, Centralisateurs et conjugaison différentiable des difféomorphismes du cercle. Petits diviseurs en dimension . Astérisque No. 231 (1995), pp. 89–242.
- [41] D. Zeilberger, W. Zudilin, The irrationality measure of is at most 7.103205334137…. Mosc. J. Comb. Number Theory 9 (2020), pp. 407–419. https://doi.org/10.2140/moscow.2020.9.407
- [42] W. Zhang, K. Lu, W. Zhang, Differentiability of the conjugacy in the Hartman-Grobman theorem. Trans. Amer. Math. Soc. 369 (2017), pp. 4995–5030. https://doi.org/10.1090/tran/6810
- [43] A. Zygmund, Trigonometric series. 2nd ed. Vols. I, II. Cambridge University Press, New York, 1959. Vol. I. pp. xii+383; Vol. II. pp. vii+354.