Quantum correlation between a qubit and a relativistic boson in an expanding spacetime
Abstract
We use the quantum correlation of both logarithmic negativity and mutual information between a qubit and a relativistic boson to analyze the dynamics of universe expansion. These dynamical quantum correlations can encode the information about underlying spacetime structure, which suggests a promising application in observational cosmology. We find that the dynamics of both logarithmic negativity and mutual information between the qubit and the boson are very similar. They decrease monotonically with the growth of the expansion volume and the expansion rate. Smaller momentum and medium-sized mass of boson are more favourable for extracting the information about history of universe expansion. The quantum correlation between the qubit and the antiboson however has very different behavior: The logarithmic negativity is always zero and the mutual information can be generated through the expansion of universe. Smaller momentum and medium-sized mass of antiboson are beneficial for the production of mutual information. Finally, the trigger phenomenon and conservation for mutual information are witnessed.
Keywords: logarithmic negativity, mutual information, expanding spacetime
pacs:
04.70.Dy, 03.65.Ud,04.62.+vI Introduction
Quantum entanglement plays an important role in quantum information theory. It is a resource for quantum information tasks, such as quantum communication, teleportation and various computational tasks, and has applications in quantum control and quantum simulations L1 ; L2 ; L3 ; L4 . Though the study about quantum entanglement is originated initially from the nonrelativistic realm, extending it to the relativistic domain is ultimately necessary because the world can never escape the influence of gravity. In fact, many settings, such as photons in the realization of quantum information L5 ; L6 ; L7 ; L8 ; L9 ; L10 ; wsm1 ; L11 ; L12 ; L13 ; L14 ; L15 ; L16 ; L17 ; LL15 ; wsm2 ; wsm3 , involve relativistic effects. Moreover, quantum entanglement plays a prominent role in the information loss problem and in black hole thermodynamics L18 ; L19 ; L20 ; L21 .
In fact, the notion of relativistic quantum information includes two branches: the special relativity effect Moradpour2015 and the general relativity (acceleration and gravity) effect. In the latter case, people mainly concern two aspects: (i) Study the influence of gravity or acceleration on quantum resources or quantum settings, such as quantum entanglement, quantum coherence, quantum key distribution and quantum communication L5 ; L6 ; L7 ; L8 ; L9 ; L10 ; wsm1 ; L11 ; L12 ; L13 ; L14 ; L15 ; L16 ; L17 ; LL15 ; wsm2 ; wsm3 ; (ii) Probe the property of spacetime via quantum effect L22 ; L23 ; L24 . Quantum entanglement subject to gravitational effect shows that conceptually important qualitative differences from the nonrelativistic perspective arise. For example, quantum entanglement depends on the motional state of the observer and degrades from the perspective of accelerated observers L5 ; L6 ; L7 ; L8 ; L9 ; L10 . These results imply that quantum resources in relativistic settings might not be an invariant concept.
In this paper, we consider an entangled state between a qubit and a relativistic boson. The latter is transformed, via the expansion of a Robertson-Walker spacetime, to a superposition of different number states of boson and antiboson. We then study, in the final state, the pairwise quantum correlation (i.e.,logarithmic negativity and mutual information) between the qubit and the boson, or between the qubit and the antiboson. The dynamics, redistribution and conservation of the underlying quantum correlations in the expansion of universe are our research focuses. Such researches not only deepen our understanding about quantum correlations but also provide the prospect of employing quantum correlations as a tool to study the property of curved spacetime, because the dynamical quantum correlations contain information about the history of the expanding spacetime, affording the possibility of deducing cosmological parameters of the underlying spacetime. This novel way of obtaining information about cosmological parameters could both theoretically and experimentally provide new insight into the early universe LL24 ; LLL24 . Actually, it has been shown that quantum correlations play an important role in the thermodynamic properties of Robertson-Walker type spacetime, and can be used to distinguish different spacetimes, and probe spacetime fluctuations L25 ; L26 ; L27 .
The paper is organized as follows. In Sec. II, we present curtly the quantization of scalar fields in expanding spacetime. Sec. III is the main part of the paper, where the dynamics, redistribution and conservation of quantum correlations in the expanding spacetime are investigated. The last section is devoted to the brief conclusion.
II Quantization of scalar fields in expanding spacetime
Let us consider a two-dimensional Robertson-Walker spacetime with the line element described by the metric L28 ; L29 ; L30
| (1) |
where is the scale factor. Introducing the conformal time that is related to the cosmological time by
| (2) |
then the metric has the form
| (3) |
Following the standard notation, the conformal scale factor has specific form
| (4) |
where is positive real parameter controlling the total expansion volume, and is positive real parameter controlling the expansion rate. The conformal scale factor conveniently shows that the spacetime undergoes a period of smooth expansion for the universe, and becomes flat in the distant past [] and in the far future []. For convenience, the distant past and far future are referred to as the asymptotic “in”-region and “out”-region, respectively.
In the background of the expanding spacetime, a bosonic field obeys the Klein-Gordon equation
| (5) |
Solving this equation, we obtain two sets of complete modes in the asymptotic past and the asymptotic future
| (6) | |||||
| (7) |
where
| (8) | |||||
| (9) |
with the hypergeometric function, and
| (10) |
The in and out modes are related by the Bogoliubov transformationL29 ; Birrell1982
| (11) |
with Bogoliubov coefficients given by
| (12) | |||||
| (13) |
In accordance with Eq.(11), the Bogoliubov relationship between the operators of the in and out modes is
| (14) |
where is the bosonic annihilation operator acting on the state in the asymptotic past, and and are the bosonic annihilation and antibosonic creation operators acting on the states in the asymptotic future. This allows us to write the in-vacuum state as L28 ; L29 ; L30 ; Birrell1982
| (15) |
where represents the bosons and represents the antibosons. This equation clearly shows that the in-vacuum state evolves into a two-mode entangled state in the asymptotic future. Acting the Hermitian conjugate of Eq.(14) on the above in-vacuum state, one obtains L31
| (16) |
III Logarithmic negativity and mutual information in an expanding spacetime
Consider an entangled state between a qubit (shared by Alice) and a boson of momentum (shared by Bob) in the asymptotic past
| (17) |
where is a state parameter which runs from 0 to 1, and and denote the basis states of the qubit. In the simulation experiment, we consider a single qubit (A) and the boson (B) in their respective cavities. The two cavities are assumed to be the same otherwise except that they are separated by a spacelike distance. Then, we close Alice’s cavity through the switching function and turn on Bob’s switching function. When the boson evolves from the asymptotic past to the asymptotic future in a cavity, the bipartite state becomes mixed and can be measured by the decoherence factor. Using Eqs.(15) and (16), we can rewrite the entangled state as
| (18) |
In this way, the entangled state encodes historical information concerning the expanding spacetime. We can understand the properties of the underlying spacetime structure by analysing the quantum properties of this state, such as logarithmic negativity and mutual information. For simplicity, we omit the subscript “out” below.
III.1 Logarithmic negativity and mutual information between qubit and boson
We first study the quantum correlations between the qubit and the boson with momentum . By tracing over the antiboson mode , we obtain the density operator for the system of qubit and boson
| (19) | |||||
with .
There are many special approaches to the detection of quantum entanglement, among them the Peres-Horodecki positive partial transpose (PPT) criterion Peres1996 ; Horodecki1996 and the afterwards logarithmic negativityL32 are widely used, due to the simplicity of calculations. In this paper, we use the logarithmic negativity as the detection of entanglement, which is defined as , where the trace norm is given by and denotes the partial transpose of the bipartite density matrix with respect to its one party. It is worthwhile to point out that logarithmic negativity is only the sufficient condition of entanglement and is not necessarily a guarantee of detecting all the entanglement in any case. However, it is indeed a feasible indicator for the conjecture of universe expansion.
Performing partial transpose on density matrix with respect to the qubit, then the transposed density matrix has the eigenvalues
with . Due to , thus and , which means that there must be negative eigenvalues and the state is always entangled. The logarithmic negativity of the state is
| (20) |
We can also study the total correlation in the state by calculating the mutual information, which is defined as L33
| (21) |
where is the von Neumann entropy of the density matrix . From the expression of Eq.(19), we obtain the von Neumann entropies for the joint system and each subsystems as
| (22) |
| (23) |
and
| (24) |
respectively. Due to , we thus have and .
Eqs.(20) and (21) suggest that logarithmic negativity and mutual information depend on the cosmological parameters and , as well as the bosonic mass and momentum . Assuming that we live in the universe corresponding to the asymptotic future of the spacetime. Then we can find the historical information about the spacetime expansion by inspecting the evolution of logarithmic negativity and mutual information. The historical information shows a promising application in observational cosmology and presents a way to simulate the expansion of universe.
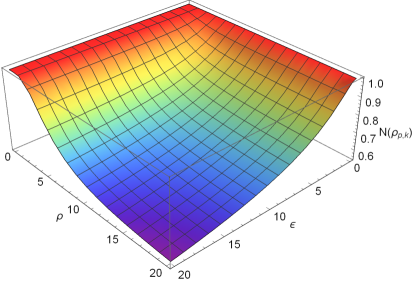
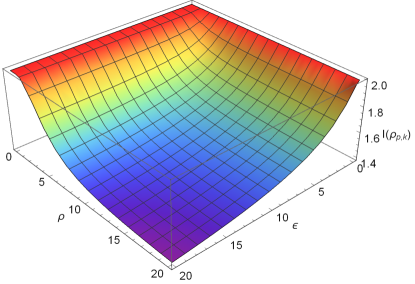
In Fig.1, we show the logarithmic negativity (left panel) and mutual information (right panel) between qubit and boson as functions of the expansion volume or the expansion rate . It is shown that the change of mutual information is very similar to the change of logarithmic negativity . They reduce monotonically with respect to both the expansion volume and the expansion rate .
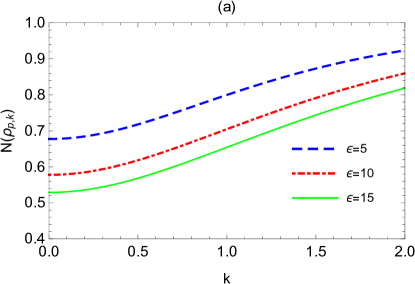
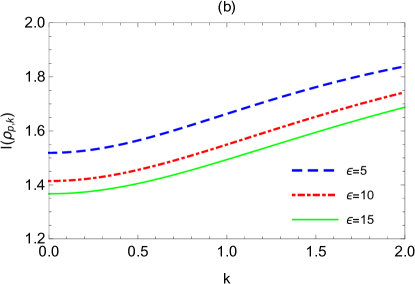
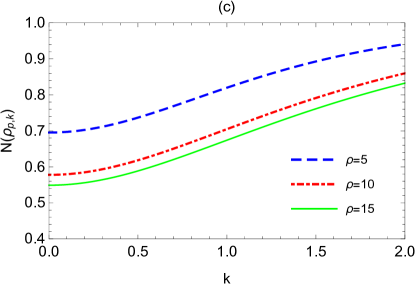
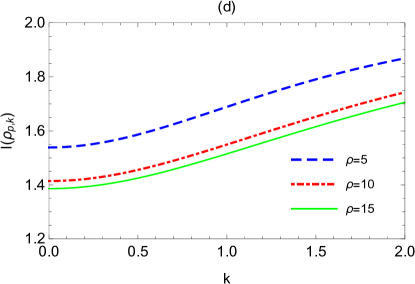
Fig.2 shows the dependency of logarithmic negativity and mutual information on the momentum , where the expansion volume and expansion rate are set to be three typical values according to Fig.1. We find that both the logarithmic negativity and the mutual information increase monotonically with the growth of momentum . For infinite , we have
Note that and are respectively the initial values of logarithmic negativity and mutual information in the state of Eq.(17), we thus conclude that, for boson with very large momentum, its logarithmic negativity and mutual information with the qubit are very little affected by the expanding spacetime. If we want to extract historical information about the expanding spacetime, the boson modes with smaller momentum are most preferable.
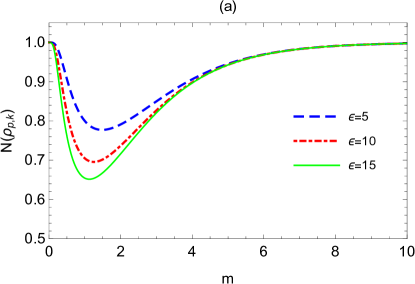
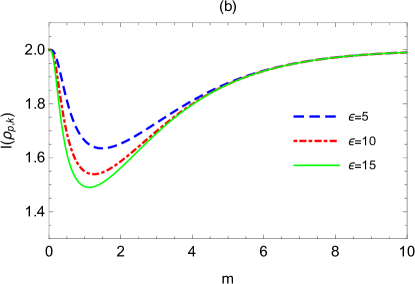
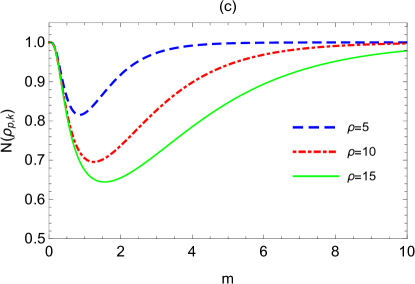
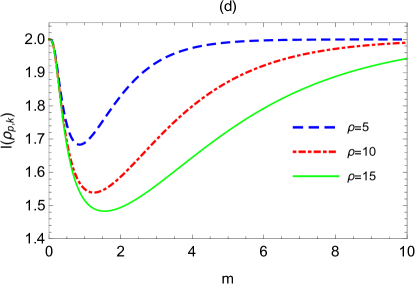
Fig.3 shows the change of logarithmic negativity and mutual information versus the mass for different expansion volume and different expansion rate . It is shown that logarithmic negativity and mutual information firstly decrease to the minimum and then asymptotically recover to their initial values with the increasing of mass . The fact that logarithmic negativity and mutual information asymptotically recover to their initial values can also be demonstrate through the analytical calculations
This result suggests that logarithmic negativity and mutual information between the qubit and the boson with very large or very small mass are less affected by the expanding spacetime. There is an optimal mass that is most prone to extract the information about the expanding spacetime. Note that the optimal mass decreases slightly with the growth of the expansion volume , and increases slightly with the growth of the expansion rate .
III.2 Logarithmic negativity and mutual information between qubit and antiboson
In order to study the redistribution of quantum correlations, we need to calculate logarithmic negativity and mutual information between qubit and the antiboson . Tracing over the mode in state of Eq.(18), we obtain the density matrix
| (25) | |||||
The partial transpose of this density matrix with respect to qubit has the eigenvalues
with and Thus the logarithmic negativity between the qubit and antiboson is
| (26) |
This means that spacetime expanding can not generate logarithmic negativity between the qubit and antiboson. However, this does not mean that quantum state between qubit and antiboson is not without quantum correlation. The correlated quantum coherence is nonlocal coherence and is regarded as a kind of quantum correlation. Through simple calculation, we find that the correlated quantum coherence can be generated by the spacetime expanding wsm32 .
The mutual information between the qubit and the antiboson is given by
| (27) |
where is given by Eq.(23), and and are given by
and
Eq.(27) is positive in general, meaning that spacetime expanding can generate mutual information between the qubit and the antiboson.
In Fig.4, we plot the mutual information between the qubit and the antiboson as a function of the expansion volume and the expansion rate . It is shown that the mutual information increases monotonically with both and , but the change is more sensitive to the beginning of and . This means that smaller and are more favorable from the consideration of extracting information.
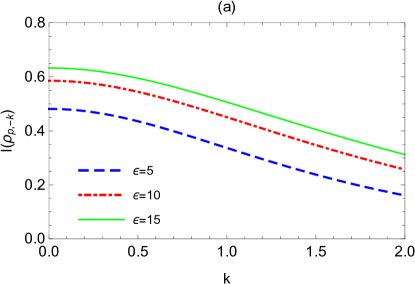
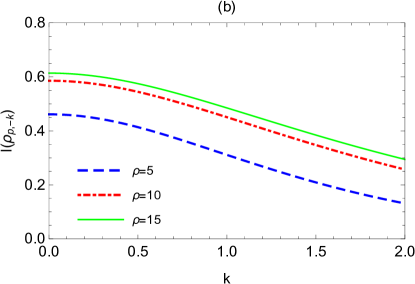
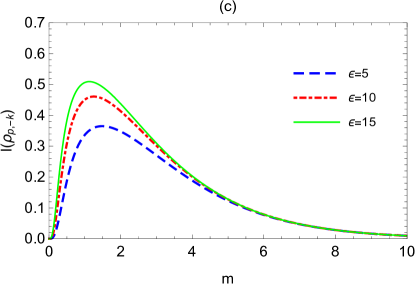
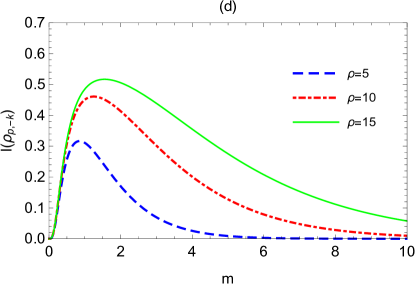
Fig.5 shows the change of mutual information versus the momentum or mass , where the expansion volume and expansion rate are set as the typical values according to Fig.4. We can see that reduces monotonically with the growth of the momentum [see Fig.5(a) and 5(b)]. In the limit of infinite momentum, we have (through analytic calculation). This means that the smaller the momentum we pick out, the more the generated mutual information is, which is more favourable for extracting information of spacetime expansion.
From Fig.5(c) and 5(d), we see that the generated mutual information increases from zero to a maximum and then reduces again to zero with the growth of the mass , i.e., satisfying
This means that there are some medium-sized masses which can produce more mutual information between the qubit and the antiboson and thus are more conducive to extract information about the expanding of universe. As displayed by Fig.3, the optimal mass decreases with the growth of the expansion volume , and increases with the growth of the expansion rate . In fact, we can demonstrate (see III.3 below) that the optimal mass displayed here is actually consistent with that in Fig.3.
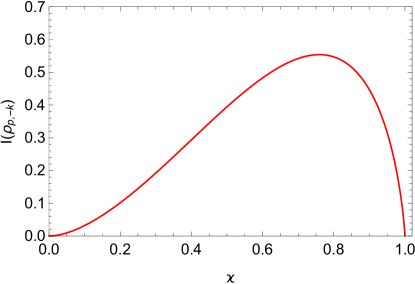
III.3 Trigger and monogamy of mutual information
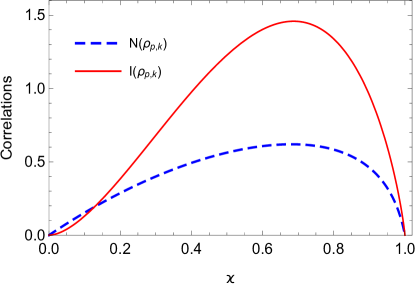
From the above discussion, we find that the expansion of universe can not produce logarithmic negativity , but can produce mutual information between the qubit and the antiboson. However, the production of requires some initial conditions. In Fig.6, we plot the logarithmic negativity , the mutual information and as functions of the initial parameter . It is shown that the production of the mutual information needs the trigger of the initial logarithmic negativity or initial mutual information . With no these triggers, the mutual information can not be generated. The more the trigger logarithmic negativity or the mutual information is, the more the generated mutual information is.
In fact, the trigger phenomenon of mutual information is obviously. We can view the boson and antiboson as a bipartite system. If there is no initial mutual information between the qubit and the boson, then also no initial mutual information between the qubit and the bipartite system. As no interaction exists between the qubit and the bipartite system in the expanding of spacetime, the mutual information between them always remains zero. Thus no mutual information exists between the qubit and the antiboson. What’s interesting is that the more the trigger mutual information, the more the generated mutual information , and this trigger phenomenon does not take place in the logarithmic negativity.
From Figs.1-5, we find that the changes of and are always opposite: Whenever the mutual information between the qubit and the boson degrades, then the mutual information between the qubit and the antiboson increases. After careful inspection of Eqs.(21) and (27), we find the monogamy relationship
| (28) |
where is the initial mutual information for the state of Eq.(17). This implies that the mutual information is re-distributable: The initial mutual information is redistributed into and , but the total mutual information is conserved in the expansion of universe. This is evidenced by the numerical simulations, i.e., the value of in Fig.3(b)(d) plus the value of in Fig.5(c)(d), for the same and , is equal to 2. This conservation also demonstrates that the optimal mass appeared in Fig.3(b)(d) and Fig.5(c)(d) coincide.
III.4 Entanglement entropy of boson
Ball firstly studied the entanglement entropy of bosonic field in an expanding spacetime L28 . Then, the comparison between fermionic and bosonic entanglement entropy for free field modes was studied L8 ; L29 . It is shown that the more information about cosmological parameters can be extracted by using fermionic entanglement entropy. Next, Li studied decoherence and disentanglement of scalar fields for Unruh-Wald qubit detector model in an expanded spacetime L31 . The results show that the expansion of the spacetime in its history destroys the entanglement between the qubits. Based on these work, Moradi investigated spin-particles entanglement between two modes of Dirac field in Robertson-Walker spacetime wsm33 . The analysis highlight the role of polarization of particles and compare the polarization results with those obtainable without accounting for it. Mohammadzadeh studied entropy production due to Lorentz invariance violation (LIV) in an expanding spacetime wsm34 , and Liu used the optimal estimation of parameters for scalar fields to extract information in expanding universe exhibiting LIV L30 . The extracted information about the past existence of LIV might be useful in recovering the quantum structure of gravity. Really, the occurrence of a peak in the behavior of entanglement entropy for a specific momentum can provide information about the expansion parameters. Therefore, the information about the LIV parameter is codified in this peak.
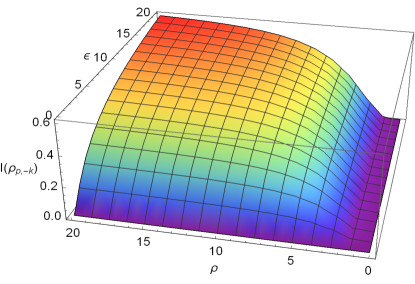
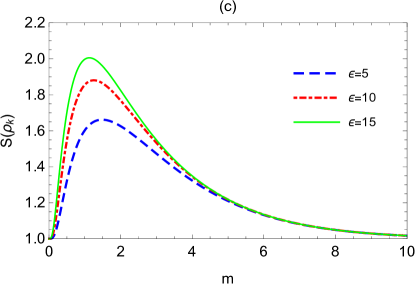
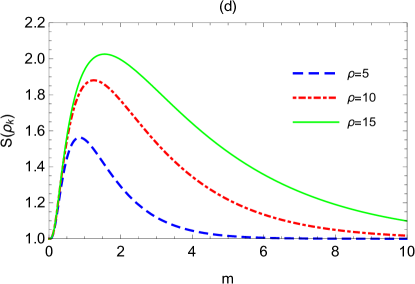
In III.1, we use the logarithmic negativity and mutual information between the qubit and the boson to detect the law of universe expansion, because they contain the information about universe expansion. In fact, we find from Eq.(24) that the entanglement entropy (i.e. von Neumann entropy) of the boson also contains the information about universe expansion, thus it also can be used to detect the law of universe expansion. As the whole system (qubit, boson and antiboson) is always a pure state in the universe expansion, describes actually the quantum correlation of the boson with the qubit and the antiboson. In Fig.7, we plot the entanglement entropy as a function of the expansion volume and the expansion rate , where the parameters are chosen as the same as in Fig.4. It is shown that the evolution of is also similar to that of in Fig.4. increases monotonically with both and , and the change is more sensitive to the beginning of and , meaning that smaller and are more favorable for the extraction of information.
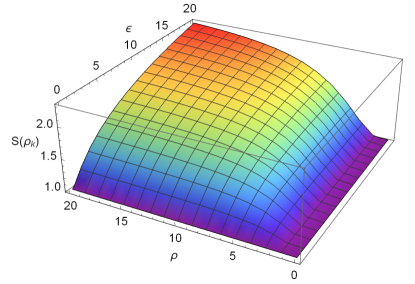
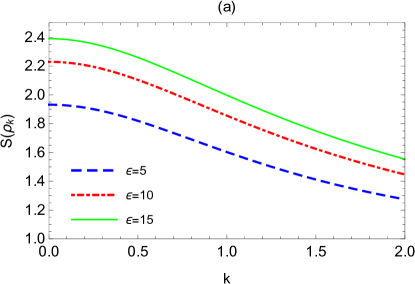
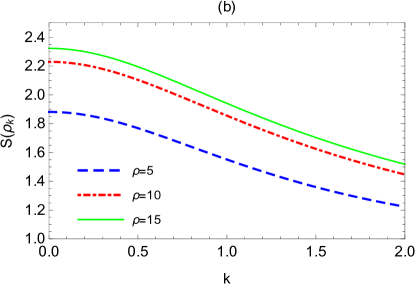
Fig.8 shows the change of entanglement entropy versus the momentum or mass , where the parameters are chosen as the same as in Fig.5. We see that Fig.8 is also very similar to Fig.5. reduces monotonically with the growth of the momentum [Fig.8(a) and 8(b)]. In the limit of infinite momentum, we have (through analytic calculation). This means that the smaller the momentum we pick out, the more the generated entanglement entropy is, which is more favourable for extracting information of spacetime expansion.
From Fig.8(c) and 8(d), we see that the generated entanglement entropy increases from zero to a maximum and then reduces again to zero with the growth of the mass , i.e., satisfying
This means that there are some medium-sized masses which can produce more entanglement entropy for the boson and thus are more conducive to extract information about the universe expansion. Also, the optimal mass decreases slightly with the growth of the expansion volume , and increases slightly with the growth of the expansion rate . However, this optimal mass is conceptually not the same thing as that in Fig.5(c)(d) for .
The ability to recover information about the cosmological parameters which are given access the generated mutual information between the qubit and the antiboson as well as entanglement entropy, were analysed in the limit of small mass . In this limit, we find an approximate relation between the generated mutual information and the mass
We can see that the generated mutual information is a monotonically increasing function of the expansion volume , and is a monotonically decreasing function of the momentum . We can also see that the generated mutual information is a increasing function of the mass for smaller . However, for bigger mass , the generated mutual information is a decreasing function of the mass . In this same limit, the expansion rate can be related to the variation of the generated mutual information
where is the energy of the -momentum mode. Unfortunately, for , the generated mutual information is almost zero due to the conformal symmetry of the theory. Therefore, the generated mutual information of massive states in our simple toy universe encodes the complete information about the cosmological parameters.
In the hopes of stimulating further research into the relation between the generated mutual information and universe expansion, we conclude with some discussion of further simulation avenues in this area. We discuss the possibility of the cosmic neutrino background that possesses quantum entanglement and mutual information from the early universe and surviving all the way to the present because of its weak coupling to matter. We can also discuss the importance of analogue experimental models providing a laboratory-accessible testbed for cosmological models. Finally, we can use quantum entanglement and mutual information as a tool for theoretical and experimental cosmology.
Perhaps, it may be applied in the modeling of universe expansion with superconducting circuit Zehua2017 . We theoretically propose a setup to realize Jackiw-Teitelboim expansion universe as solitons of sine-Gordon. Note that our configuration can be similar to the superconducting coplanar waveguide. However, each capacitor in our configuration is parallel with an identical superconducting quantum interference devices. It is the added superconducting quantum interference device providing a nonlinear potential to the Lagrangian of fluxes in the superconducting coplanar waveguide, which plays a very crucial role in the simulation of expansion universe. Each superconducting quantum interference device consists of two identical parallel Josephson junctions. Besides, the geometric size of superconducting quantum interference devices loop is assumed to be small enough such that its selfinductance is negligible compared to its kinetic inductance. In this case, each superconducting quantum interference device can be referred to as an effective Josephson junction with a junction capacitance and a tunable Josephson energy. We can realize the Jackiw-Teitelboim expansion universe as solitons of sine-Gordon equation in our setup. Thus, it allows us to understand the mechanics of solitons and especially the duality between Jackiw-Teitelboim gravity and sine-Gordon soliton from the perspective of experiment. The analogous dynamic behavior of quantum fields under the expanding universe in principle could be implemented in the setup. By appropriately adjusting the external magnetic flux through the superconducting quantum interference device loop, we can simulate the behavior of the conformal scale factor. Therefore, the analogous dynamic behavior of quantum fields under an expanding universe in principle could be implemented in setup. The in-mode and out-mode are two particular solutions in the past and future, respectively. Physically, these two particular solutions are a description of two different vacuum and excited states in the two asymptotic regions. We consider the boson (B) that is affected by the simulated spacetime expanding and the qubit (A) entangled with boson in shielding environment.
IV Conclusions
The effects of the expansion universe on quantum correlations (including logarithmic negativity and mutual information) between a qubit and a relativistic boson have been investigated. We have found that the dynamics for both the logarithmic negativity and mutual information between the qubit and the boson are very similar. Both of them reduce with the growth of the expansion rate and the expansion volumes. The degradation of quantum correlations also depends on the nature of the boson. The less the boson momentum is, the more serious the quantum correlations reduce. The dependency of quantum correlations on the mass of boson is however non-monotonic. Very small and very large mass of bosons have little influence, and some medium mass of bosons induce large reduction of quantum correlations.
We have found that, in the expanding of universe, logarithmic negativity between the qubit and the antiboson always remains zero, but the mutual information between them can be generated. With the growth of the expansion rate and the expansion volume, the generated mutual information becomes large and large. Smaller momentum and medium mass of bosons are more beneficial to generate mutual information between the qubit and the antiboson. Interestingly, the production of the mutual information between the qubit and the antiboson requires a trigger of initial quantum correlations. The more the trigger quantum correlations, the more the generated mutual information.
Further study has suggested that the mutual information is re-distributable. In the expansion of universe, the mutual information between the qubit and the boson reduce, at the same time the mutual information between the qubit and the antiboson is generated, where the total mutual information is conserved. This result is different from logarithmic negativity, which is not re-distributable and has no conservation property. We have also studied the effect of universe expansion on the entanglement entropy of the boson. With the growth of the expansion rate and the expansion volume, the entanglement entropy of boson is generated and becomes large and large. Smaller momentum and medium mass of bosons are more beneficial for the generation of the entanglement entropy.
In the expansion of universe, quantum correlation dynamics encode the information about the underlying spacetime structure, which suggests a promising application in observational cosmology. The results in this paper suggest that small momentum and medium mass of bosons can more sensitively highlight the changes of quantum correlations and thus are more beneficial for extracting the historical information about the underlying spacetime expansion. Of course, the scheme may be restricted by the current technology, because of the strict assumption that the qubit is shielded from any external influence in the expanding of universe, except for the initial entanglement with the boson. We expect our research can present helps for the relativistic quantum information processing and the observational cosmology.
Acknowledgements.
This work is supported by the National Natural Science Foundation of China (Grant Nos. 1217050862, 11275064), the Construct Program of the National Key Discipline, and BNUXKJC2017.
The authors declare no conflict of interest.
References
- (1) Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A and Wootters W K 1993 Phys. Rev. Lett. 70 1895
- (2) Huegla S F, Plenio M B and Vaccaro J A 2002 Phys. Rev. A 65 042316
- (3) Dodd J L, Nielsen M A, Bremner M J and Thew R T 2002 Phys. Rev. A 65 040301
- (4) The Physics of Quantum Information, edited by D. Bouwmeester, A. Ekert, A. Zeilinger (Springer-Verlag, Berlin, 2000).
- (5) Fuentes-Schuller I and Mann R B 2005 Phys. Rev. Lett. 95 120404
- (6) Alsing P M, Fuentes-Schuller I, Mann R B and Tessier T E 2006 Phys. Rev. A 74 032326
- (7) Li Y, Mao Q and Shi Y 2019 Phys. Rev. A 99 032340
- (8) Fuentes I, Mann R B, Martín-Martínez E and Moradi S 2010 Phys. Rev. D 82 045030
- (9) Hwang M R, Park D and Jung E 2011 Phys. Rev. A 83 012111
- (10) Wang J and Jing J 2011 Phys. Rev. A 83 022314
- (11) Wu S M and Zeng H S 2020 Class. Quantum Grav. 37 115003
- (12) Xu S, Song X K, Shi J D and Ye L 2014 Phys. Rev. D 89 065022
- (13) Dai Y, Shen Z and Shi Y 2016 Phys. Rev. D 94 025012
- (14) Qiang W C, Sun G H, Dong Q and Dong S H 2018 Phys. Rev. A 98 022320
- (15) Torres-Arenas A J, Dong Q, Sun G H, Qiang W C and Dong S H 2019 Phys. Lett. B 789 93
- (16) Liu X, Tian Z, Wang J and Jing J 2018 Phys. Rev. D 97 105030
- (17) Tian Z, Chä S Y and Fischer U R 2018 Phys. Rev. A 97 063611
- (18) Wang J, Wen C, Chen S and Jing J 2020 Phys. Lett. B 800 135109
- (19) Grochowski P T, Rajchel G, Kiałka F and Dragan A 2017 Phys. Rev. D 95 105005
- (20) Wu S M and Zeng H S 2019 Quantum Inf. Process 18 305
- (21) Wu S M, Zeng H S and Liu T H 2019 Results Phys. 14 102398
- (22) Ahn D, Moon Y, Mann R and Fuentes-Schuller I 2008 J. High Energy Phys. 06 062
- (23) Bombelli L, Koul R K, Lee J and Sorkin R D 1986 Phys. Rev. D 34 373
- (24) Horowitz G T and Maldacena J 2004 J. High Energy Phys. 02 008
- (25) Lloyd S 2006 Phys. Rev. Lett. 96 061302
- (26) Moradpour H, Maghool S and Moosavi S A 2015 Quantum Inf. Process 14 3913
- (27) Ge X H and Kim S P 2008 Class. Quantum Grav. 25 075011
- (28) Pan Q and Jing J 2008 Phys. Rev. D 78 065015
- (29) Ahn D and Kim M 2007 Phys. Lett. A 366 202
- (30) Uhlmann M, Xu Y and Schtzhold R 2005 New J. Phys. 7 248
- (31) Jain P, Weinfurtner S, Visser M and Gardiner C W 2007 Phys. Rev. A 76 033616
- (32) VerSteeg G and Menicucci N C 2009 Phys. Rev. D 79 044027
- (33) Müller R and Lousto C O 1995 Phys. Rev. D 52 4512
- (34) Han M, Olson S J and Dowling J P 2008 Phys. Rev. A 78 022302
- (35) Ball J L, Fuentes-Schuller I and Schuller F P 2006 Phys. Lett. A 359 550
- (36) Martín-Martínez E and Menicucci N C 2012 Class. Quantum Grav. 29 224003
- (37) Liu X, Jing J, Wang J and Tian Z 2020 Quantum Inf Process 19 26
- (38) Birrell N D and Davies P C W Quantum Fields in Curved Space (Cambridge University Press, 1982).
- (39) Li Y, Dai Y and Shi Y 2017 Eur. Phys. J. C 77 598
- (40) Peres A 1996 Phys. Rev. Lett. 77 1413
- (41) Horodecki M, Horodecki P and Horodecki R 1996 Phys. Lett. A 223 1
- (42) Plenio M B 2005 Phys. Rev. Lett. 95 090503
- (43) Nielsen M A and Chuang I Quantum Computation and Quantum Information (Cambridge University, Cambridge, England, 2000).
- (44) Ma T, Zhao M J, Zhang H J, Fei S M and Long G L 2017 Phys. Rev. A 95 042328
- (45) Moradi S, Pierini R and Mancini S 2014 Phys. Rev. D 89 024022
- (46) Mohammadzadeh H, Farahmand M and Maleki M 2017 Phys. Rev. D 96 024001
- (47) Tian Z, Jing J and Dragan A 2017 Phys. Rev. D 95 125003