Quantum critical properties of Bose-Hubbard models
Abstract
The Mott insulator-to-superfluid transition exhibited by the Bose-Hubbard model on a two-dimensional square lattice occurs for any value of the chemical potential, but becomes critical at the tips of the so-called Mott lobes only. Employing a numerical approach based on a combination of high-order perturbation theory and hypergeometric analytic continuation we investigate how quantum critical properties manifest themselves in computational practice. We consider two-dimensional triangular lattices and three-dimensional cubic lattices for comparison, providing accurate parametrizations of the phase boundaries at the tips of the respective first lobes. In particular, we lend strong support to a recently suggested inequality which bounds the divergence exponent of the one-particle correlation function in terms of that of the two-particle correlation function, and which sharpens to an equality if and only if a system becomes critical.
1 Introduction
The application of the theory of critical phenomena [1, 2, 3] to the description of the lambda transition undergone by liquid helium at about 2.18 K is still confronting physicists with a seemingly minor, yet annoying challenge: Owing to measurements performed under zero-gravity conditions in Earth orbit in order to reduce the rounding of the transition caused by gravitationally induced pressure gradients, the critical exponent describing the singularity of the specific heat could be determined with exceptional accuracy [4], finally resulting in the value . On the other hand, theoretical calculations so far have not managed to reproduce this figure to an accuracy compatible with the experimental uncertainty, despite substantial effort [5, 6, 7, 8, 9]. To our knowledge, the currently most accurate theoretical value has been reported by Campostrini et al. [8], based on finite-size scaling analyses of high-statistics Monte Carlo simulations and resummations of 22nd-order high-temperature expansions for the lattice model and the dynamically diluted model, giving . Since this comparison of measurement with calculation constitutes a core test of the renormalization group theory, the remaining discrepancy needs to be taken seriously.
It is therefore of interest to observe that the quantum phase transition exhibited at zero temperature by the Bose-Hubbard model [10] may contribute to solving this long-standing puzzle. In a grand-canonical setting this model depends on two dimensionless parameters, the scaled chemical potential and the scaled strength of hopping between adjacent lattice sites. Keeping fixed at a noninteger positive value, and increasing from zero to positive values, the -dimensional model features a transition from an incompressible Mott insulator to a superfluid at a certain . For almost all that transition is mean field-like, but at particular multicritical points corresponding to the tips of the so-called Mott lobes the transition falls into the universality class of the -dimensional model [10]. In particular, the comparatively simple -dimensional Bose-Hubbard model then belongs to the -dimensional universality class, the same class which also covers the lambda transition of liquid helium. Thus, in principle it should be possible to deduce the critical exponents of the lambda transition from a 2-dimensional Bose-Hubbard system [11].
We have previously outlined a strategy to exploit this connection: Utilizing numerically executed strong-coupling perturbation theory to high orders, in the guise of Eckardt’s process-chain approach [12], one obtains divergent-series representations of the model’s -particle correlation functions ; these divergent series can then be analytically continued with the help of generalized hypergeometric functions, taking up a recent suggestion by Mera et al. [13] The locus in the – parameter plane where the correlation functions diverge then marks the phase boundary; the manner how they diverge at the multicritical points provides information on the critical exponents [14, 15]. Applied to the 2-dimensional Bose-Hubbard model on a square lattice, the first hard test of this strategy indeed has yielded a fairly good estimate of the critical exponent [14]. Thus, the combination of high-order perturbation theory with hypergeometric analytic continuation provides an alternative, self-contained “bootstrap technique” for computing critical exponents that is independent from other approaches; it is hoped that further refinements of this technique will contribute to resolving the current discrepancy between the experimental and theoretical benchmark data [4, 8]. Here we report further results of our approach not only for the 2-dimensional square lattice, but also for the triangular lattice [16]. As an essential consistency check we also consider the Bose-Hubbard model on a 3-dimensional cubic lattice, which falls into the 4-dimensional class and therefore should not become critical at all.
2 Technical background
We start by summarizing the technical details of our procedure: Employing the repulsion energy of a pair of bosons occupying a common lattice site as reference energy, we write the Bose-Hubbard Hamiltonian in the dimensionless form
| (1) |
where the indices , label individual sites, and the operators and are bosonic annihilation and creation operators, obeying the canonical commutation relation
| (2) |
Moreover,
| (3) |
denotes the number operator which counts the particles on site . Thus, the first two terms of the Hamiltonian (1) specify, respectively, the total scaled on-site repulsion energy, and the system’s coupling to the chemical potential. The sum in the third term ranges over all pairs of sites , that are connected by a tunneling contact, as indicated by the symbol , describing the hopping of Bosons from sites to . Taken together, these three terms constitute the conventional Bose-Hubbard model that has been studied in great detail by many authors, using a wide variety of techniques [17, 18, 19, 20, 21, 22]. The fourth term represents spatially homogeneous sources and drains which explicitly break particle number conservation; this allows one to introduce an effective potential depending on the source strength by means of a Legendre transformation [23]. We expand the intensive ground-state energy , that is, the ground-state energy per lattice site of the extended model (1), as a power series in ,
| (4) |
and then apply the process-chain approach [12] for estimating the -particle correlation functions
| (5) |
To this end, we start from the ground state of the site-diagonal first two terms of the system (1), and include the other two terms as perturbations [24, 25, 26]. The computation of then prompts one to account for creation and annihilation processes; invoking perturbation theory to th order, with , therefore allows one to include tunneling processes. After evaluating the series (5) for given to an achievable order in the hopping strength , we fit this approximant by hypergeometric functions , allowing us to determine both the respective transition point and the exponent which governs the divergence of at that point [15],
| (6) |
From general arguments invoking neither the dimension nor the geometry of the underlying lattice we have inferred the inequality
| (7) |
which is expected to reduce to an exact equality if and only if the system becomes critical [14]. Thus, a comparison of the divergence exponents and , computed independently for a given variant of the model, enables one to detect quantum criticality. One of the main purposes of the present paper is to lend further support to this relation (7), which indicates quantum criticality through equality of both sides, by reporting the results of large-scale numerical calculations for three variants of the Bose-Hubbard model.
3 Accurate parametrization of phase boundaries
We first consider the phase boundary which, in accordance with the asymptotic relation (6), can already be deduced from alone. This study is motivated by a suggestion due to Freericks et al. [27], claiming that the two values limiting a Mott lobe with integer filling factor can be parametrized by the scaling ansatz [27]
| (8) |
where , and , , and the scaling polynomial are certain polynomials which have been stated for a 2-dimensional square lattice and as Eq. (104) in Ref. [27], and is the critical exponent which governs the correlation length [8]. This is an interesting suggestion, implying that accurate knowledge of the phase boundary suffices to determine .
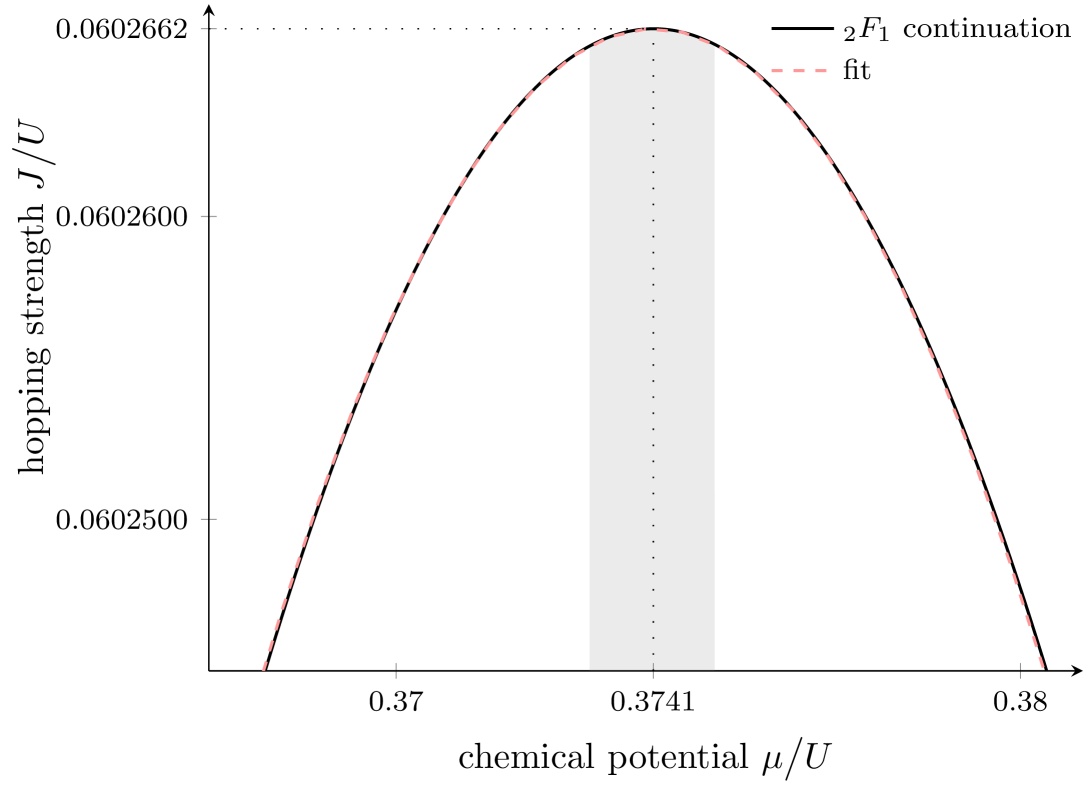
We therefore have made a precise computation of the phase boundary for the first Mott lobe of a 2-dimensional Bose-Hubbard model on a square lattice by combining process-chain calculations to th order in with hypergeometric analytic continuation based on [14, 15], and have plotted the very tip of this lobe in Fig. 1; here we consider as a function of . We then have taken 100 data points computed in a fairly narrow interval of size around the lobe tip, and have fitted them to a function of the form
| (9) |
obtaining
| (10) |
The deviation of the exponent “measured” here from the exponent 2 of a perfect parabola is fully accounted for by the limits to our numerical accuracy; clearly, the quality of our fit is not compatible with the suggested appearance of the critical exponent . Instead, according to our numerical data the phase boundary right at the tip appears to be given by a smooth square root function.
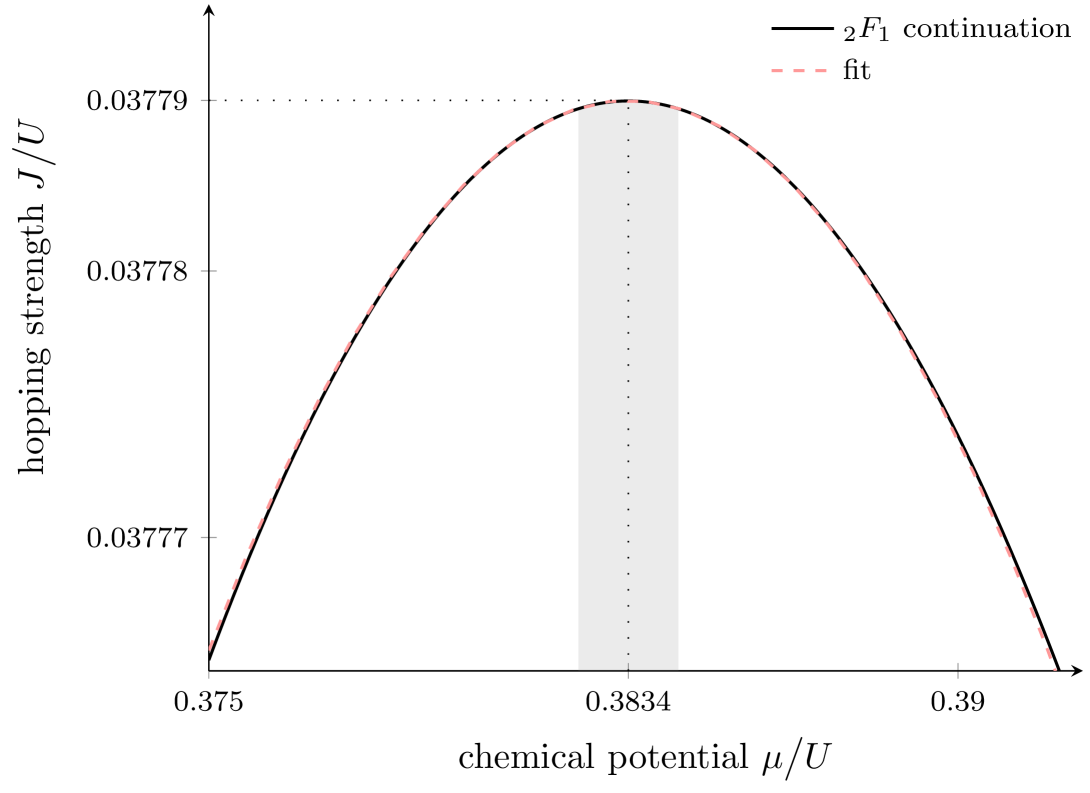
We have also performed such calculations for a triangular lattice: While each site of a square lattice is linked by a tunneling contact to four nearest neighbors, each site is surrounded by even six nearest neighbors on a triangular one. The results are shown in Fig. 2. As expected on the grounds of the respective coordination number, in comparison with the square lattice the lobe tip shifts to lower in the triangular case [16]. Again selecting an interval of width around the lobe tip, and taking 100 equidistant fit points, the ansatz (9) yields
| (11) |
likewise suggesting that the lobe tip is well approximated by an exact parabola, without correction involving a critical exponent.
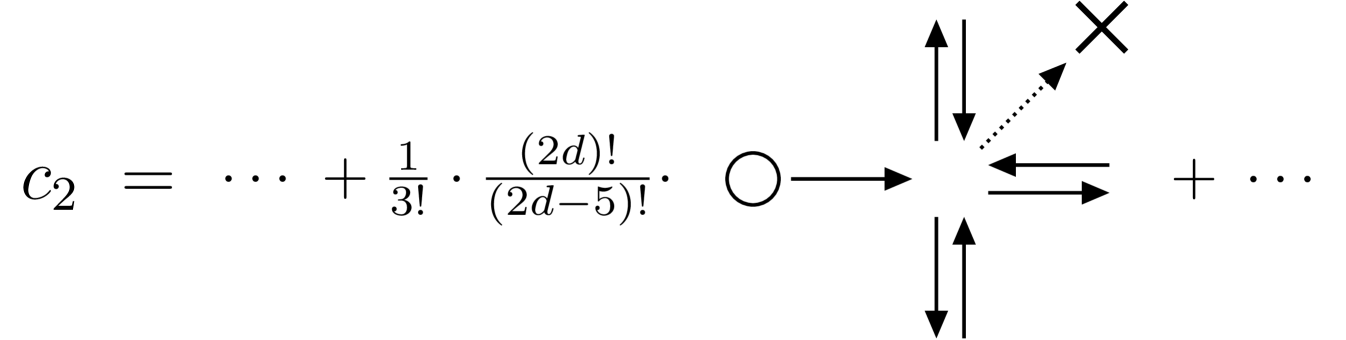
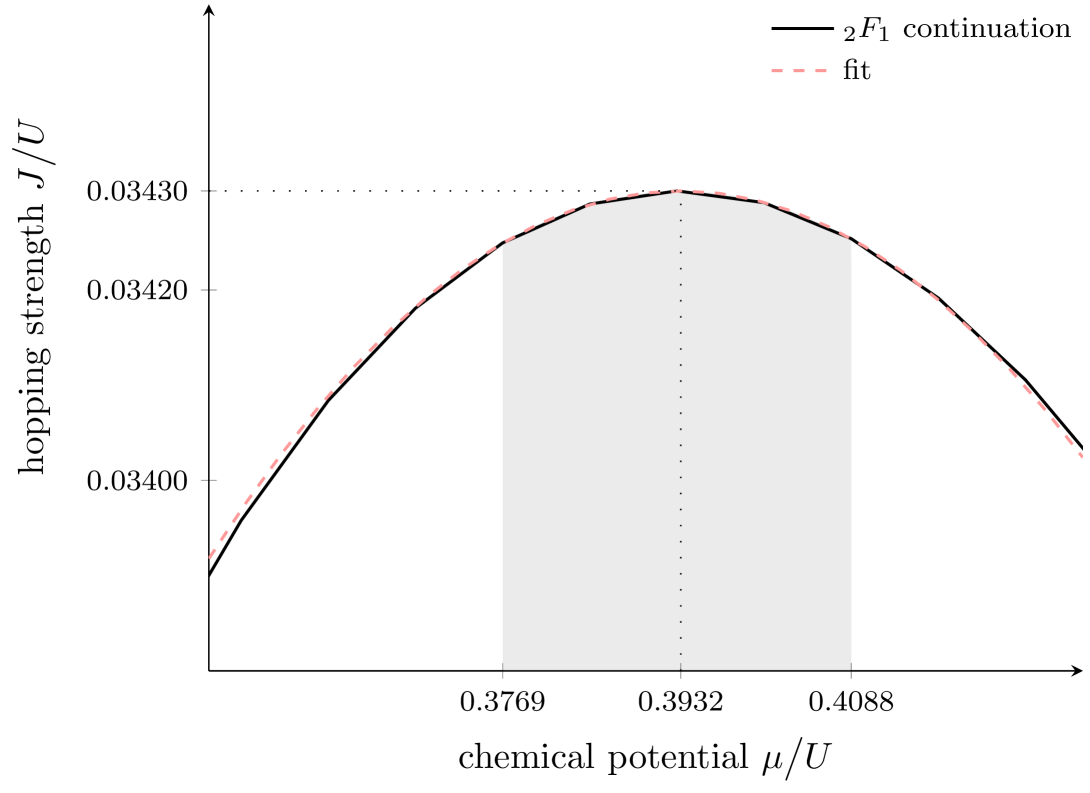
For comparison, we also have considered a 3-dimensional cubic lattice, for which the Mott transition does not become critical [10]. From the perspective of perturbation theory, the process chains defining for the 2-dimensional square lattice and those for the cubic lattice are virtually the same up to and including the 7th order in , with only different weight factors accounting for the different dimensions. Starting with the order additional diagrams begin to appear in three dimensions, such as depicted exemplarily in Fig. 3. The tip of the first Mott lobe is displayed in Fig. 4, together with the fit
| (12) |
to the ansatz (9). We emphasize that this fit results from the evaluation of merely 5 data points taken from a comparatively wide interval , more than 15 times as large as employed in Fig. 1. Yet, the deviation of the observed exponent from the parabola exponent 2 is not significant.
4 Manifestation of quantum criticality
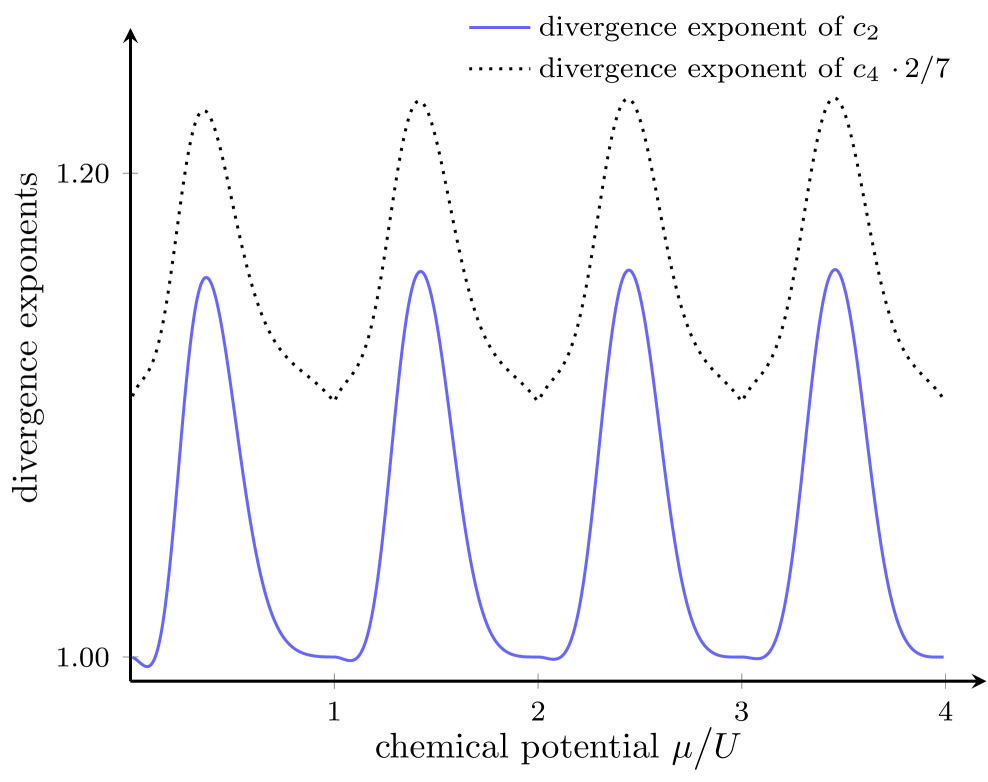
Since it does not appear to be feasible to recognize criticality by inspection of the phase boundary alone, we now turn to the more demanding criterion (7), prompting us to evaluate besides . We start with the 3-dimensional cubic lattice: Figure 5 shows both the divergence exponent , and the divergence exponent multiplied by , for chemical potentials covering the lowest four Mott lobes, . To produce this figure, the one-particle correlation function has been computed to 9th order in , and the two-particle correlation function to 7th order, amounting to the evaluation of perturbation theory to 11th order in both cases. Evidently the inequality (7) is well satisfied, equality being excluded for all . This is a fairly important consistency check, vindicating the recognition that the 3-dimensional Bose-Hubbard model does not become critical even at the tips of its Mott lobes [10, 11].
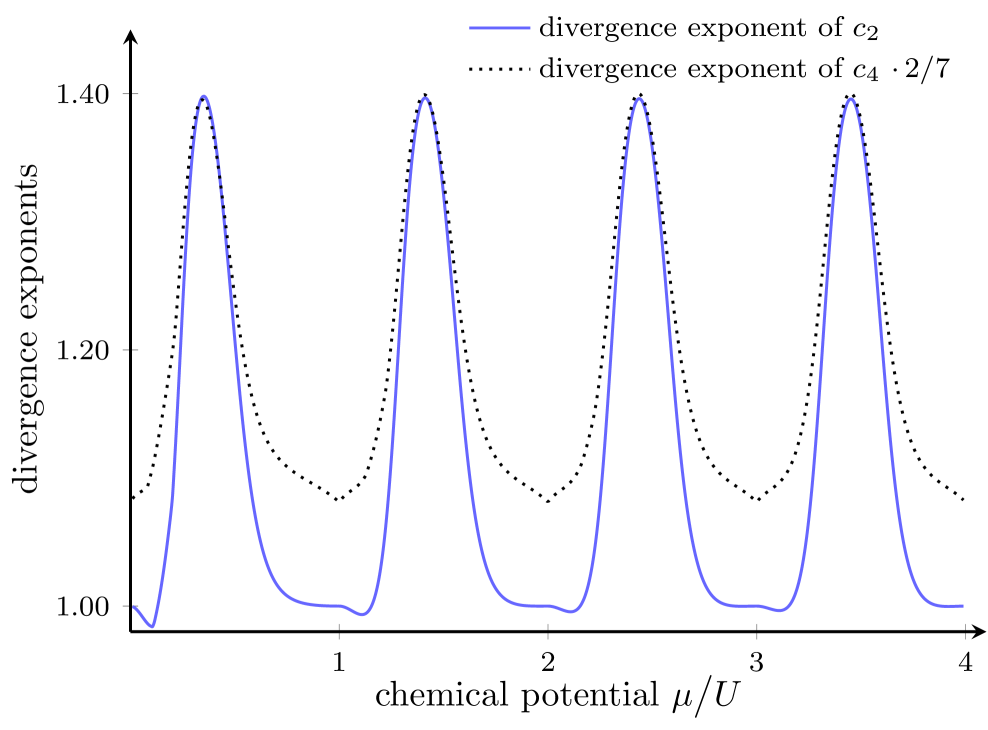
In contrast, the 2-dimensional models do become critical at the lobe tips. The corresponding comparison of and for the square lattice is shown in Fig. 6. In marked contrast to Fig. 5, here the two lines touch each other at the lobe tips to within numerical accuracy [14], so that the inequality (7) reduces to an equality at these points, thereby heralding criticality.
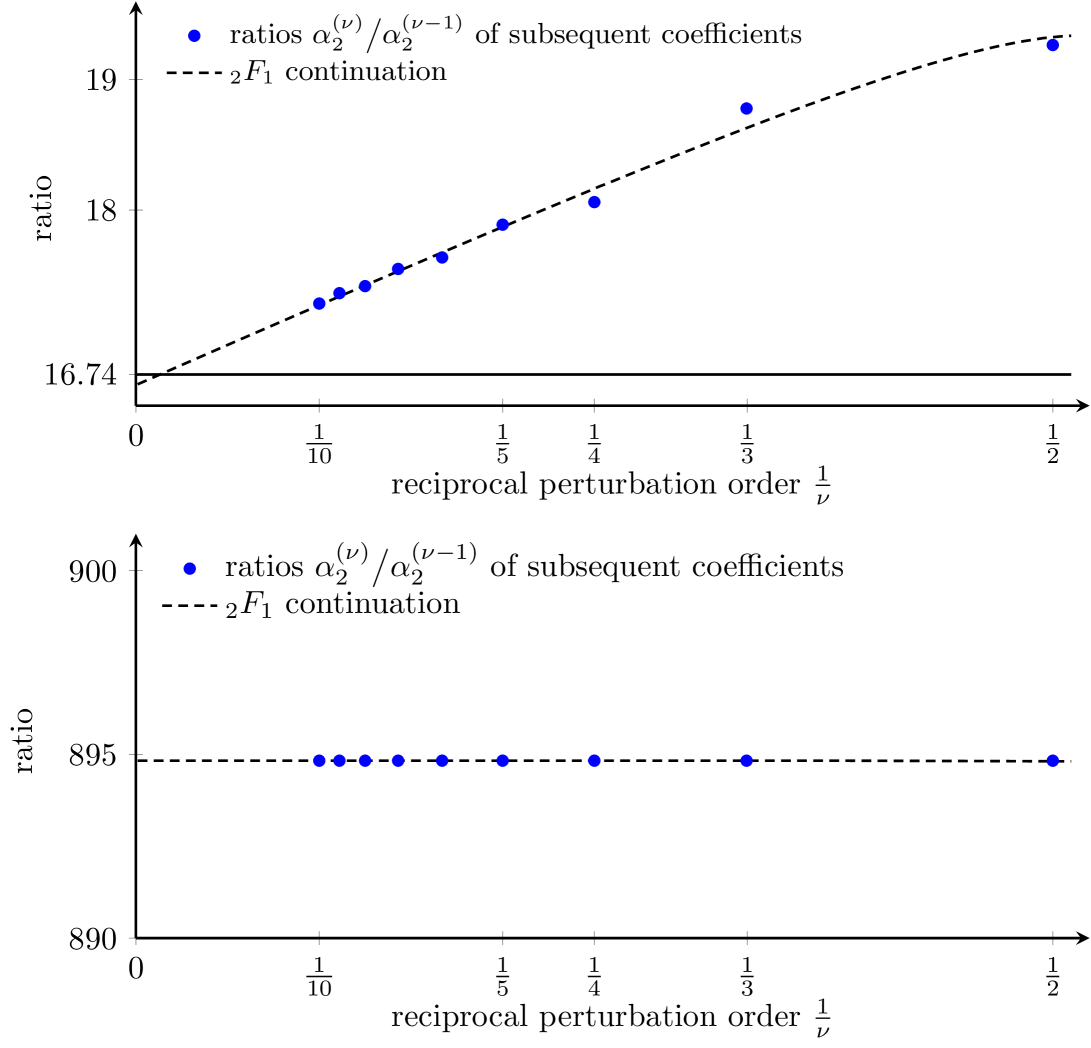
For gaining insight into the working principles of hypergeometric analytic continuation it is instructive to inspect the behavior of the coefficients constituting the series (5). To this end, we plot in Fig. 7 the ratios for (upper panel) and (lower panel). In the latter case, for close to the upper edge of the lowest lobe, the series representation (5) of is close to geometric, allowing for a comparatively simple and reliable determination of the limit [24, 25]. In the former case however, close to the critical lobe tip, the ratios decrease markedly with increasing hopping order , and appear to oscillate slightly around a common mean trend, so that their fit to a Gaussian hypergeometric function , or to generalized hypergeometric functions , indeed is indispensable for correctly estimating the limit [15].
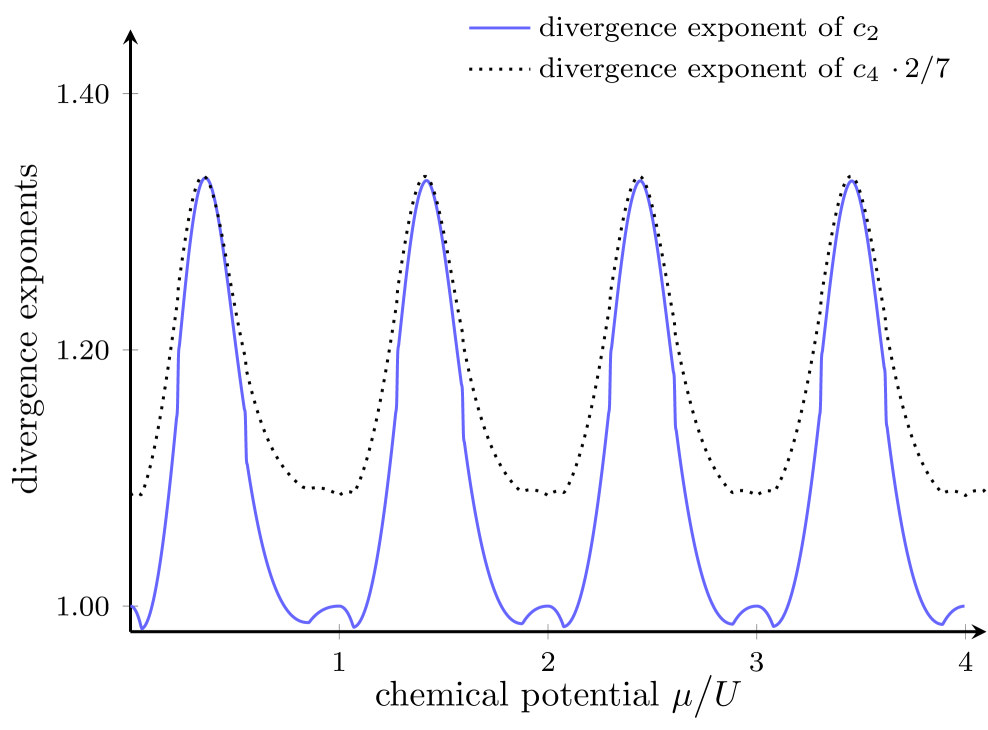
It is now of major interest to check the crucial inequality (7) for the triangular lattice. The numerical data shown in Fig. 8, where once again we have plotted both sides of this inequality, are fairly convincing indeed: To within numerical accuracy, the inequality (7) is confirmed, with exact equality being reached, again to within numerical accuracy, at the lobe tips. Thus, an approach based on high-order perturbation theory combined with hypergeometric analytic continuation definitively is sensitive to quantum criticality.
5 Discussion
The most important findings of the present numerical study are encoded in Figs. 5, 6, and 8, representing a computationally rather demanding verification of the divergence-exponent inequality (7) previously surmised in Ref. [14]: In general, the divergence exponent which characterizes the one-particle correlation function at the phase transition is smaller than times the divergence exponent of , but both sides become equal if and only if the system becomes critical.
Yet, there is one more issue that is at stake here. At criticality one expects the relation for the critical exponent of the order parameter [14]; together with , this yields the remarkable identity
| (13) |
Indeed, reading off from the lobe tips seen in Fig. 6 for the square lattice with its coordination number , and dividing by four, one obtains fairly good agreement with the expected value reported by Campostrini et al. [8]. While we do no yet reach the numerical accuracy level of this benchmark value, this may become feasible after honing our method still further, possibly allowing for a rather stringent test of the universality hypothesis of statistical physics. But the same procedure applied to the data depicted in Fig. 8 for the triangular lattice with coordination number yields the markedly different value
| (14) |
This is an interesting observation, suggesting that critical exponents of the Mott insulator-to-superfluid quantum phase transition in the Bose-Hubbard model depend not only on the dimensionality, but also on the coordination number of the respective lattice. The experimental verification of this prediction, possibly with ultracold atoms in optical lattices [28], could provide important guidance for the further development of the theory.
References
References
- [1] A. Pelissetto and E. Vicari, Critical phenomena and renormalization-group theory, Phys. Rep. 368, 549 (2002).
- [2] J. Zinn-Justin, Quantum Field Theory and Critical Phenomena, fourth edition (Clarendon Press, Oxford, 2002).
- [3] D. J. Amit and V. Martín-Mayor, Field Theory, the Renormalization Group, and Critical Phenomena: Graphs to Computers, third edition (World Scientific, Singapore, 2005).
- [4] J. A. Lipa, J. A. Nissen, D. A. Stricker, D. R. Swanson, and T. C. P. Chui, Specific heat of liquid helium in zero gravity very near the lambda point, Phys. Rev. B 68, 174518 (2003).
- [5] H. Kleinert, Theory and satellite experiment for critical exponent of -transition in superfluid helium, Phys. Lett A 277, 205 (2000).
- [6] H. Kleinert and V. Schulte-Frohlinde, Critical properties of theories (World Scientific, Singapore, 2001).
- [7] E. Burovski, J. Machta, N. Prokof’ev, and B. Svistunov, High-precision measurement of the thermal exponent for the three-dimensional universality class, Phys. Rev. B 74, 132503 (2006).
- [8] M. Campostrini, M. Hasenbusch, A. Pelissetto, and E. Vicari, Theoretical estimates of the critical exponents of the superfluid transition in 4He by lattice methods, Phys. Rev. B 74, 144506 (2006).
- [9] A. I. Sokolov and M. A. Nikitina, Pseudo- expansion and critical exponents of superfluid helium Physica A 444, 177 (2016).
- [10] M. P. A. Fisher, P. B. Weichman, G. Grinstein, and D. S. Fisher, Boson localization and the superfluid-insulator transition, Phys. Rev. B 40, 546 (1989).
- [11] A Rançon and N. Dupuis, Nonperturbative renormalization group approach to strongly correlated lattice bosons, Phys. Rev. B 84, 174513 (2011).
- [12] A. Eckardt, Process-chain approach to high-order perturbation calculus for quantum lattice models, Phys. Rev. B 79, 195131 (2009).
- [13] H. Mera, T. G. Pedersen, and B. K. Nicolić, Nonperturbative quantum physics from low-order perturbation theory, Phys. Rev. Lett. 115, 143001 (2015).
- [14] S. Sanders and M. Holthaus, Hypergeometric continuation of divergent perturbation series: I. Critical exponents of the Bose-Hubbard model, New J. Phys 19, 103036 (2017).
- [15] S. Sanders and M. Holthaus, Hypergeometric continuation of divergent perturbation series: II. Comparison with Shanks transformation and Padé approximation, J. Phys. A: Math. Theor. 50, 465302 (2017).
- [16] N. Teichmann, D. Hinrichs, and M. Holthaus, Reference data for phase diagrams of triangular and hexagonal bosonic lattices, EPL 91, 10004 (2010).
- [17] J. K. Freericks and H. Monien, Strong-coupling expansions for the pure and disordered Bose-Hubbad model, Phys. Rev. B 53, 2691 (1996).
- [18] D. van Oosten, P. van der Straten, and H. T. C. Stoof, Quantum phases in an optical lattice, Phys. Rev. A 63, 053601 (2001).
- [19] L. Pollet, S. Rombouts, K. Heyde, and J. Dukelsky, Bosons confined in optical lattices: The numerical renormalization group revisited, Phys. Rev. A 69, 043601 (2004).
- [20] B. Capogrosso-Sansone, N. V. Prokof’ev, and B. V. Sistunov, Phase diagram and thermodynamics of the three-dimensional Bose-Hubbard model, Phys. Rev. B 75, 134301 (2007).
- [21] T. P. Polak and T. K. Kopeć, Quantum rotor description of the Mott-insulator transition in the Bose-Hubbard model, Phys. Rev. B 76, 094503 (2007).
- [22] B. Capogrosso-Sansone, S. Güneş Söyler, N. V. Prokof’ev, and B. V. Sistunov, Monte Carlo study of the two-dimensional Bose-Hubbard model, Phys. Rev. A 77, 015602 (2008).
- [23] F. E. A. dos Santos and A. Pelster, Quantum phase diagram of bosons in optical lattices, Phys. Rev. A 79, 013614 (2009).
- [24] N. Teichmann, D. Hinrichs, M. Holthaus, and A. Eckardt, Bose-Hubbard phase diagram with arbitrary integer filling Phys. Rev. B 79, 100503(R) (2009).
- [25] N. Teichmann, D. Hinrichs, M. Holthaus, and A. Eckardt, Process-chain approach to the Bose-Hubbard model: Ground-state properties and phase diagram Phys. Rev. B 79, 224515 (2009).
- [26] C. Heil and W. von der Linden, Strong coupling expansion for the Bose-Hubbard and Jaynes-Cummings lattice models, J. Phys.: Condens. Matter 24, 295601 (2012).
- [27] J. K. Freericks, H. R. Krishnamurthy, Y. Kato, N. Kawashima, and N. Trivedi, Strong-coupling expansion for the momentum distribution of the Bose-Hubbard model with benchmarking against exact numerical results, Phys. Rev. A 79, 053631 (2009).
- [28] Xibo Zhang, Chen-Lung Hung, Shih-Kuang Tung, and Cheng Chin, Observation of quantum criticality with ultracold atoms in optical lattices, Science 335, 1070 (2012).