Quantum half-orphans in kagomé antiferromagnets
Abstract
We numerically study the effects of non-magnetic impurities (vacancies) in the spin- Heisenberg antiferromagnet on the kagomé lattice. For a range of low but nonzero temperatures, and spin values that extend down to , we find that the magnetization response to an external magnetic field is consistent with the response of emergent “half-orphan” degrees of freedom that are expected to dominate the response of the corresponding classical magnet in a similar temperature range whenever there are two vacancies on the same triangle. Specifically, for all spin values we have considered (from to ), there is a large enhancement of the local susceptibility of the lone spin on such a triangle with two vacancies; in the presence of a uniform magnetic field , this lone-spin behaves effectively as an almost free spin in an effective field . Quite remarkably, in the zero temperature limit, the ground state in the presence of a half-orphan has a non-zero total spin value that shows a trend similar to when . These qualitative aspects of the response differ strikingly from the more conventional response of diluted samples without such half-orphan degrees of freedom. We discuss how these findings could be checked experimentally.
I Introduction
The low-temperature physics of frustrated quantum magnets is controlled by the interplay between the geometric frustration, quantum fluctuations, entropic effects, and quenched disorder. In many interesting cases Savary and Balents (2016), the geometric frustration renders the leading exchange interactions unable to drive magnetic ordering even at temperatures much lower than the scale of these interactions. Instead, in a semiclassical picture, they confine the system to a manifold of minimally frustrated configurations, which can admit a description in terms of emergent degrees of freedom as in the case of classical spin ice Castelnovo et al. (2008). The low temperature physics is then controlled by how these emergent degrees of freedom behave in the presence of subdominant interactions as well as quantum and thermal fluctuations. In the extreme quantum limit, frustrated magnets can provide an arena for the physics of quantum number fractionalization; the Majorana fermion excitations of Kitaev’s honeycomb model being a celebrated example Kitaev (2006).
Interestingly, quenched disorder, i.e. non-magnetic substitutional impurities or lattice imperfections that affect the bond strengths in their vicinity, can provide a powerful probe of these emergent excitations and their unusual quantum numbers. For instance, the emergent magnetic monopole excitations of classical spin ice can be nucleated in the ground state of a disordered sample. Similarly, vacancies in Kitaev’s honeycomb model nucleate a Majorana fermion-Z2 flux complex in their vicinity. More generally, a wide variety of features can be probed or created by non-magnetic impurities in magnetic systems, depending on the nature of the underlying state. If the clean system is a spin liquid, then non-magnetic impurities can lead to spinon deconfinement Poilblanc et al. (2006) or even spin-charge separation if they are mobile Läuchli and Poilblanc (2004). More conventional ordering patterns can also be characterized by the response to non-magnetic impurities Alloul et al. (2009). An enhancement of local correlations is often observed near spinless impurities in antiferromagnets Martins et al. (1997). In valence bond crystals, that break lattice symmetries, or valence bond solids that are non-degenerate, non-magnetic impurities generically induce a localized spin texture around them Poilblanc et al. (2006). In systems with competing phases at low temperatures, non-magnetic impurities can furthermore reveal or seed competing orders Kaul et al. (2008). Quantum critical systems have also been shown Sachdev and Vojta (2003); Höglund et al. (2007) to host responses characteristic of their criticality to the inclusion of spinless defects. All these different physical behaviors and the corresponding local textures or responses have been detected in magnetic compounds using local probe techniques, such as nuclear magnetic resonance (NMR). Let us for instance mention the spin “polaron” observed in the two-dimensional doped material, SrCu2(BO3)2 material Haravifard et al. (2006); Yoshida et al. (2015), the imaging of spin-1/2 edge excitations in spin 1 Haldane compound Y2BaNi1-xMgxO5 Tedoldi et al. (1999), the magnetic response around an impurity observed in a kagomé compound (herbertsmithite) Olariu et al. (2008) and the localized bound states generated by impurities in topological magnets Yin et al. (2020).
Coming back to frustrated magnets, the SrCr9pGa12-9pO19 (SCGO) compound, in which Cr3+ moments lie on the vertices of the pyrochlore-slab (bilayer kagomé) lattice, provides another striking example of the interplay between impurities and the underlying physical state Obradors et al. (1988); Ramirez et al. (1990); Limot et al. (2002). Even in the best samples of SCGO, nonmagnetic Ga atoms disrupt the corner-sharing network of triangles and tetrahedra formed by the Cr ions; these Ga impurities can be modeled as static vacancies in the Heisenberg antiferromagnet on this lattice. At a classical level, the Heisenberg model on the pyrochlore slab lattice remains disordered down to , providing an interesting example of a classical spin liquid with full SU(2) symmetry of interactions Moessner and Berlinsky (1999); Moessner and Chalker (1998).
Following an earlier phenomenological analysis Schiffer and Daruka (1997) of experimental results on SCGO, Henley Henley (2001) described the liquid state in terms of an emergent fluctuating polarization field and noted that a triangle with two vacancies led to a lone or “orphan” spin on that triangle which behaves as a source (charge) for this polarization field. The polarization field of this charge leads, in this description, to an oscillating spin texture with a power-law envelope. Even without a detailed computation of this texture, this effective theory predicts that the classical spin- Heisenberg model on the pyrochlore slab lattice will have a net spin polarization of in the direction of an infinitesimal external magnetic field at .
Motivated by this factor of two, which is suggestive of spin fractionalization, Henley dubbed this combination of the lone spin and the resulting spin-texture a “half-orphan”, modifying the terminology of “orphan spins” introduced in the earlier phenomenological studies Schiffer and Daruka (1997). In closely related work Moessner and Berlinsky (1999) that studied the classical Heisenberg antiferromagnet on the pyrochlore and pyrochlore-slab lattices, Moessner and Berlinsky also recognized the special role of these half-orphan degrees of freedom in dominating the low temperature magnetic response, and used this insight to model the experimental results on SCGO within a single-unit approximation that used as input properties of individual simplices (triangles and tetrahedra) with various degrees of dilution.
This striking prediction of a saturation magnetization of for the system with two vacancies on the same triangle led immediately to the questions: Does the low-temperature susceptibility show signatures of this “spin fractionalization” ? In other words, does the impurity susceptibility of this orphan-texture complex correspond to that of a classical spin object? If yes, how is this response resolved spatially ? Motivated by these questions, Ref. Sen et al., 2011 used a hybrid large-N field-theory as well as direct Monte-Carlo simulations to study the low but nonzero temperature behaviour. Perhaps surprisingly, the answer turns out to be in the affirmative, with an interesting spatial structure that will be important in our present study: At low temperatures in the spin-liquid regime, each lone spin on a triangle with two vacancies “sees” an effective magnetic field that has magnitude (where is the applied external field) and responds to it as a free spin in this field at temperature . Exactly half of this paramagnetic response is cancelled off by the net diamagnetic response of the surrounding spin texture for which this orphan spin serves as a source, giving rise to a net susceptibility that equals the susceptibility of a spin at temperature .
In conjunction with subsequent work Sen et al. (2012) that also characterized the entropic interactions between these half-orphan degrees of freedom, this approach provides a fairly detailed picture of both the orphan-texture complex and its susceptibility, as well as interactions between orphans, including a theory for low temperature glassy behaviour in the multi-orphan case. Importantly, it provides a reasonably satisfactory fit to NMR data on SCGO Limot et al. (2002); Bono et al. (2004), that could not previously be accounted for by more conventional ideas. We provide more details on orphan physics in the classical case in the Appendix for completeness, along with classical Monte Carlo simulations for kagomé systems, as starting from now we will focus on kagomé planes (and not bilayers).
While one expects that the classical physics of half-orphans would be reflected in some form in a semiclassical treatment of the corresponding quantum magnet with large but finite spin , this expectation has thus far not been shored up by an actual controlled calculation of corrections to the classical picture. Nor has the fairly impressive success of classical descriptions of frustrated magnets such as SCGO been quantitatively examined from this point of view.
Spin kagomé magnets such as Herbertsmithite Mendels and Bert (2011); Khuntia et al. (2020) also feature some degree of dilution by nonmagnetic vacancies. Since it is well known that the classical kagomé magnet has a fairly broad low-temperature spin liquid regime, extending upwards from a lower cutoff of (that marks a subtle crossover to an ordered regime below this temperature Chern and Moessner (2013); Zhitomirsky (2008); Huse and Rutenberg (1992)), one expects that half-orphans seeded by vacancy-pairs should be fairly well-defined at the classical level in this regime. These observations provide the central motivation for the present study, in which we ask: Do these emergent half-orphan degrees of freedom nucleated by pairs of vacancies on the same triangle survive quantum effects in the Heisenberg antiferromagnet on the kagomé lattice?
The presence of nonmagnetic impurities in some of the best-known experimental realizations of frustrated quantum magnets on the kagomé lattice has motivated several studies of vacancy effects, which we build on here with our work. For instance, a single non-magnetic impurity is known to induce local dimer order in the spin-1/2 case Dommange et al. (2003) and does not generate a localized spin in the spin-3/2 case either Läuchli et al. (2007), while a finite concentration could lead to valence bond glass in the spin-1/2 case Singh (2010). Using a combination of series expansion and variational wavefunction studies, Gregor and Motrunich Gregor and Motrunich (2008) have also modeled inhomogeneous Knight shifts in compounds such as Herbertsmithite Mendels and Bert (2011) by studying the response of the kagomé antiferromagnet to nonmagnetic impurities. Again, there is no evidence that single vacancies induce the kind of dramatic enhancement that pairs of vacancies do in the classical picture.
In this manuscript, we study the finite-temperature as well as ground-state signatures of orphan physics in the spin- quantum Heisenberg model on the kagomé lattice for a large set of spin values ranging from up to , allowing us to discuss the quantum to classical crossover. One striking result of our study is that the ground state of the quantum system with two vacancies on the same triangle has nonzero spin quantum number . This tracks , which is the total quantum spin value (allowed to exist in the system) which is the closest to , i.e. we find down to . This provides a dramatic quantum manifestation of half-orphan physics at . In some way, this result is reminiscent of the end-spins in cut Haldane gap chains, which provide the clearest and experimentally relevant signature of the underlying symmetry-protected topological order in these systems. However, this is qualitatively different: The presence of quantum half-orphans in the ground state of samples with two vacancies on the same triangle is blind to the integer or half-integer nature of elementary spin , and is perhaps best thought of as a semiclassical effect that survives to surprisingly low values of . Indeed, there is no obvious underlying topological order at the heart of this effect.
In our finite temperature studies, we find that the local susceptibility offers a very clear signature of orphan physics down to . We attribute this to presence of quantum half-orphans in the ground state of these systems. From other probes such as the magnetization curve, we find that orphan physics can be detected to even lower values of quantum spin (down to ), with specific signatures not present for other types of impurity patterns. We also present an analysis of the histogram of spin magnetization due to a distribution of impurities, akin to a NMR Knight shift experiment, specific to the experimentally relevant situation. Our results are obtained with a finite-temperature method working in Krylov bases generated by an appropriate number of randomly distributed initial states (see details below), as well as Lanczos exact diagonalization (ED) and Density Matrix Renormalization Group (DMRG) for the study of ground-state properties.
The layout of this manuscript is as follows: In Sec. II we first study the ground state and present our results on the ground-state polarization, as well as spin textures obtained through ED and DMRG computations. We begin Section III with a brief description of the finite-temperature random sampling technique used to simulate thermodynamics of the quantum system, and then present finite-temperature results for orphan physics, including the local susceptibility response, the magnetization curve, as well as experimental predictions for the NMR Knight shift. Finally, Sec. IV summarizes our results along with a discussion of some outstanding issues. For completeness, in the Appendix, we also present the results of finite-temperature Monte Carlo simulations of vacancy effects in the classical Heisenberg model on the kagomé lattice, and identify the temperature regime in which orphan physics is clearly visible in the classical case.
II Ground State Physics in the Quantum Case
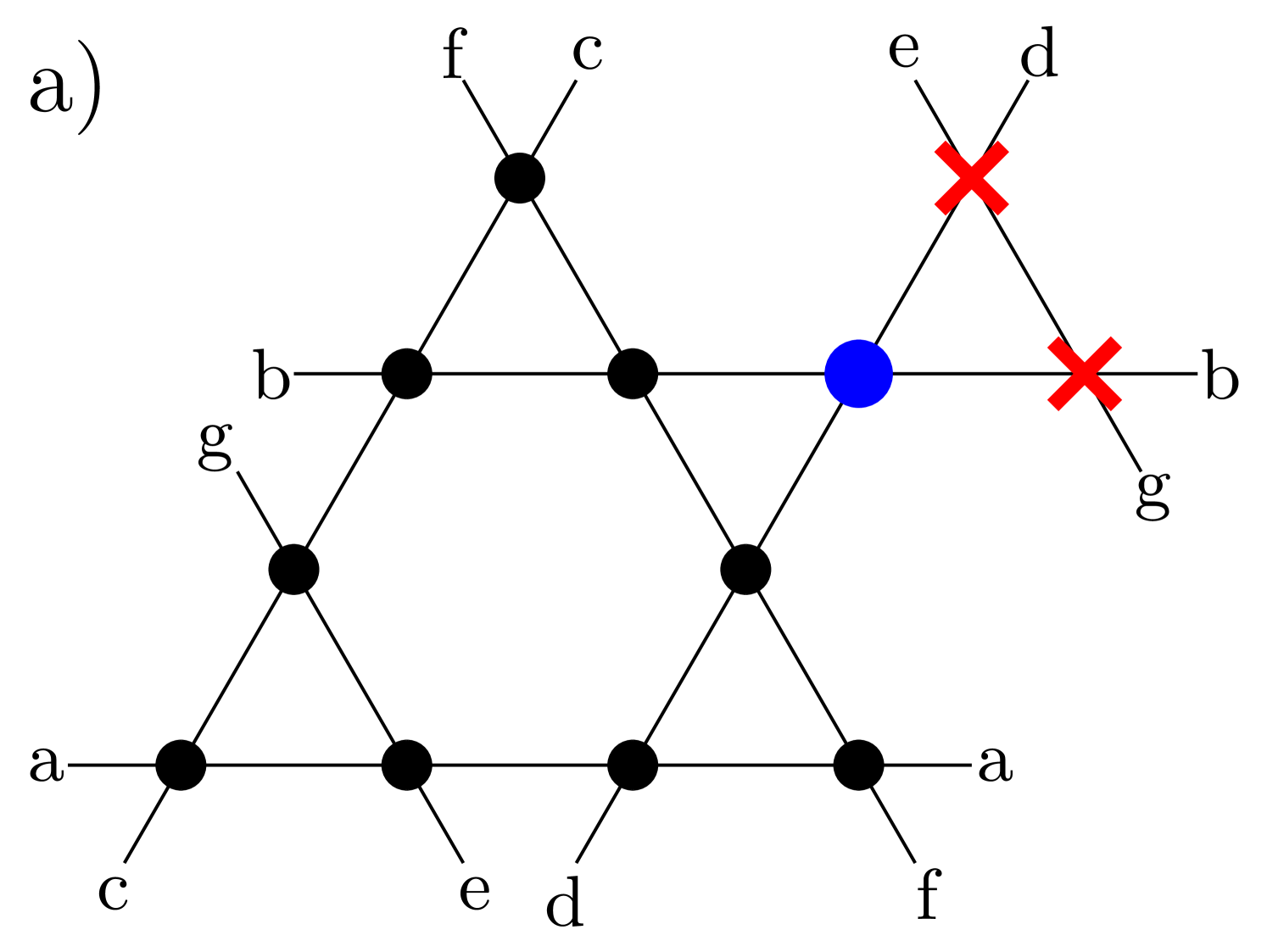
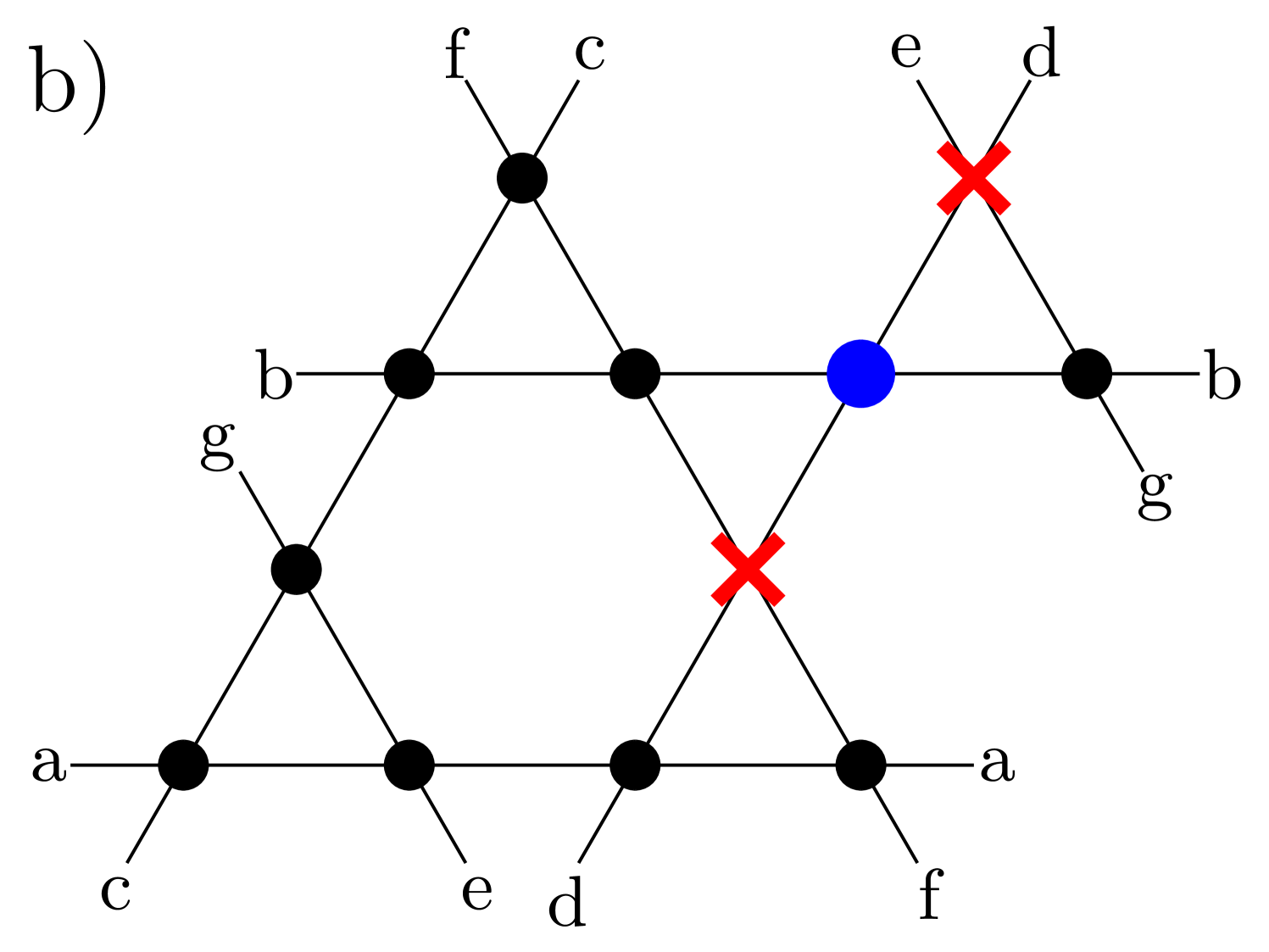
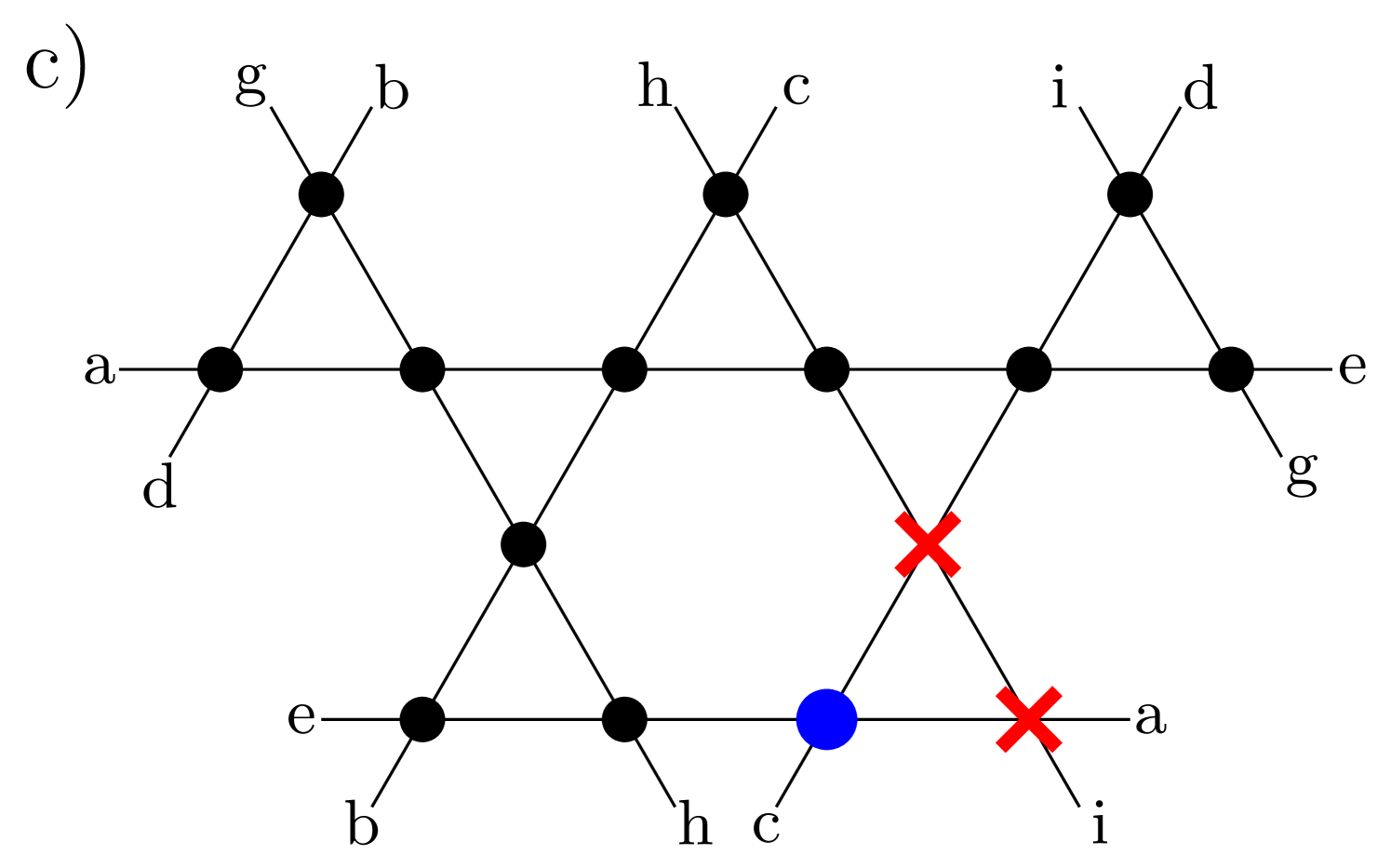
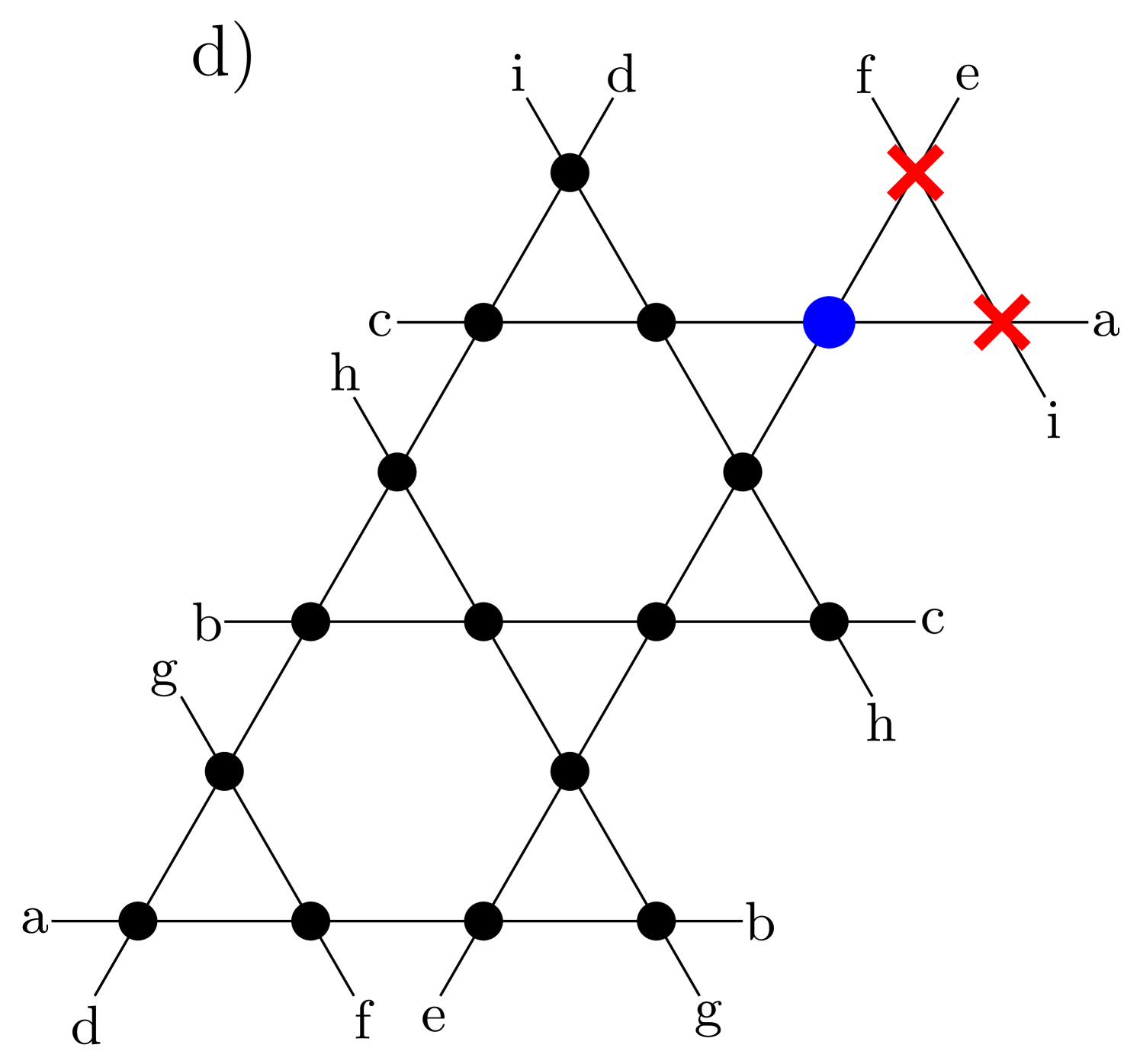
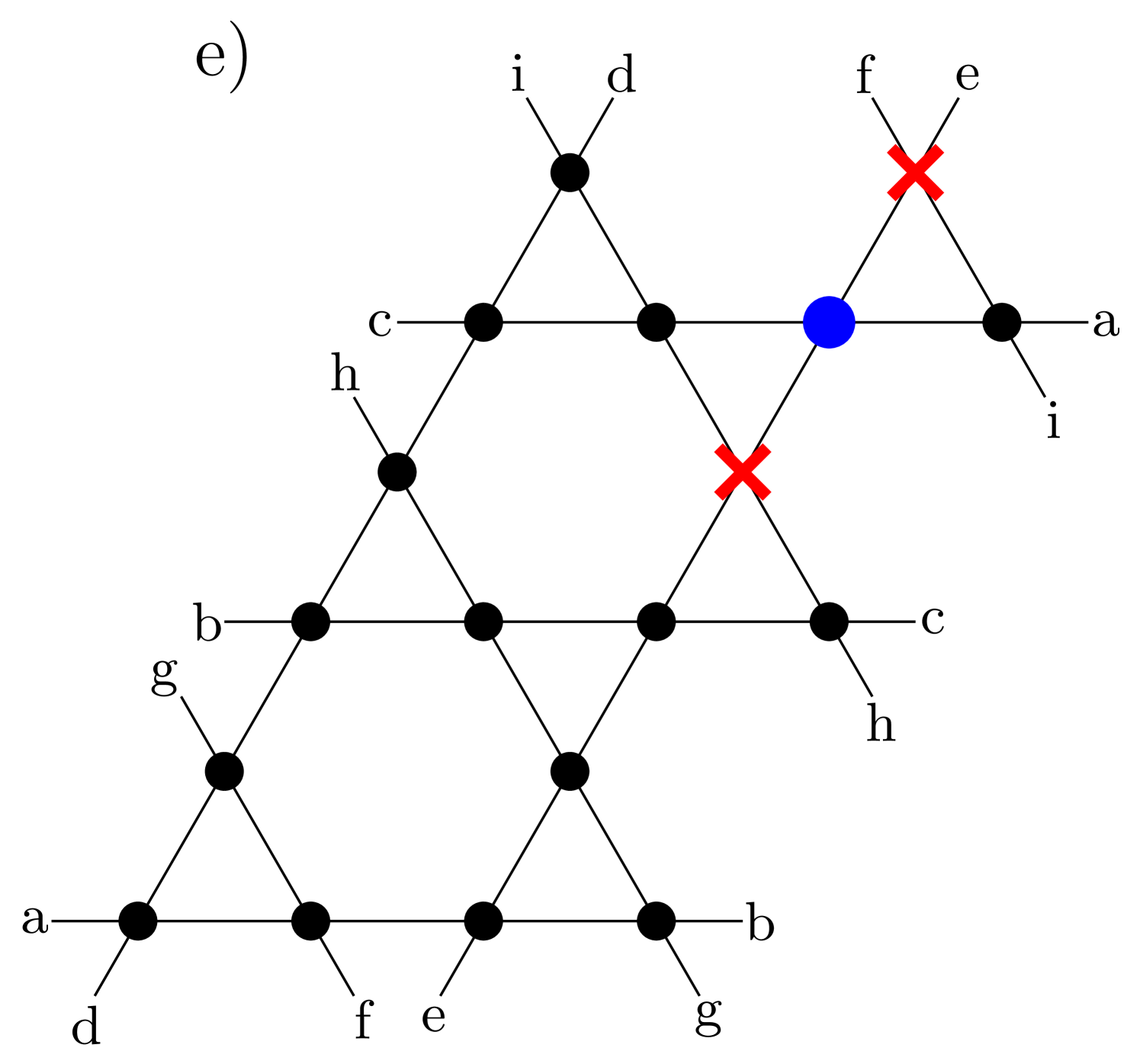
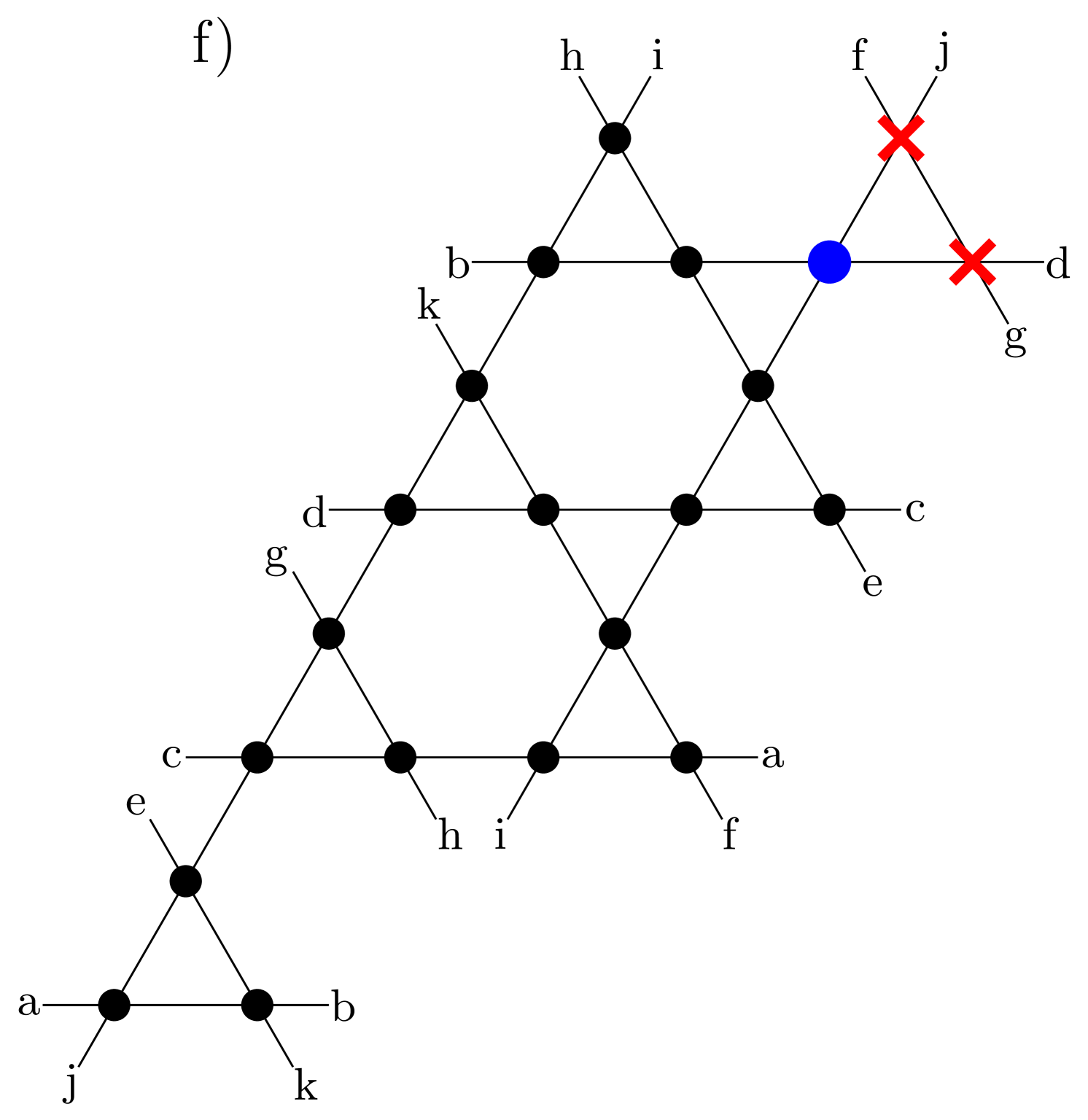
We begin with perhaps the simplest question that gets to the heart of the intriguing conundrum posed by Henley, Moessner and Berlinksy’s classical argument for a saturation magnetization of that reflects the presence of a half-orphan nucleated by two vacancies on a triangle: What is the ground state spin quantum number of a spin- quantum antiferromagnet on a kagomé lattice with two vacancies on one triangle of the lattice?
To answer this question for the kagomé magnet with Hamiltonian
| (1) |
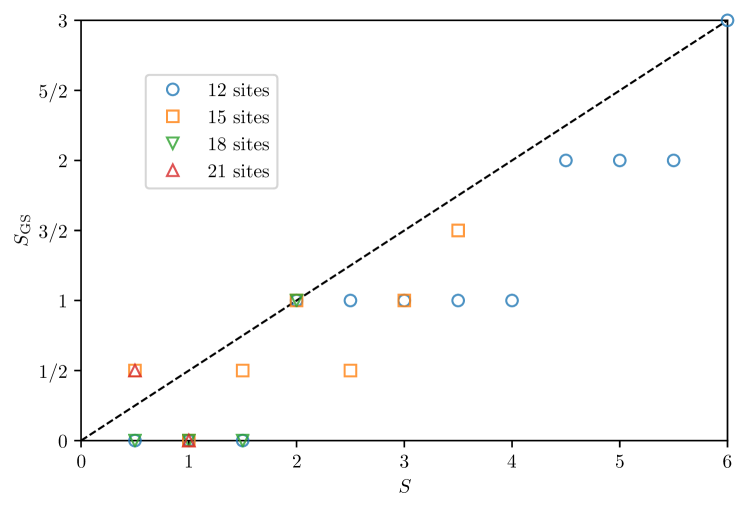
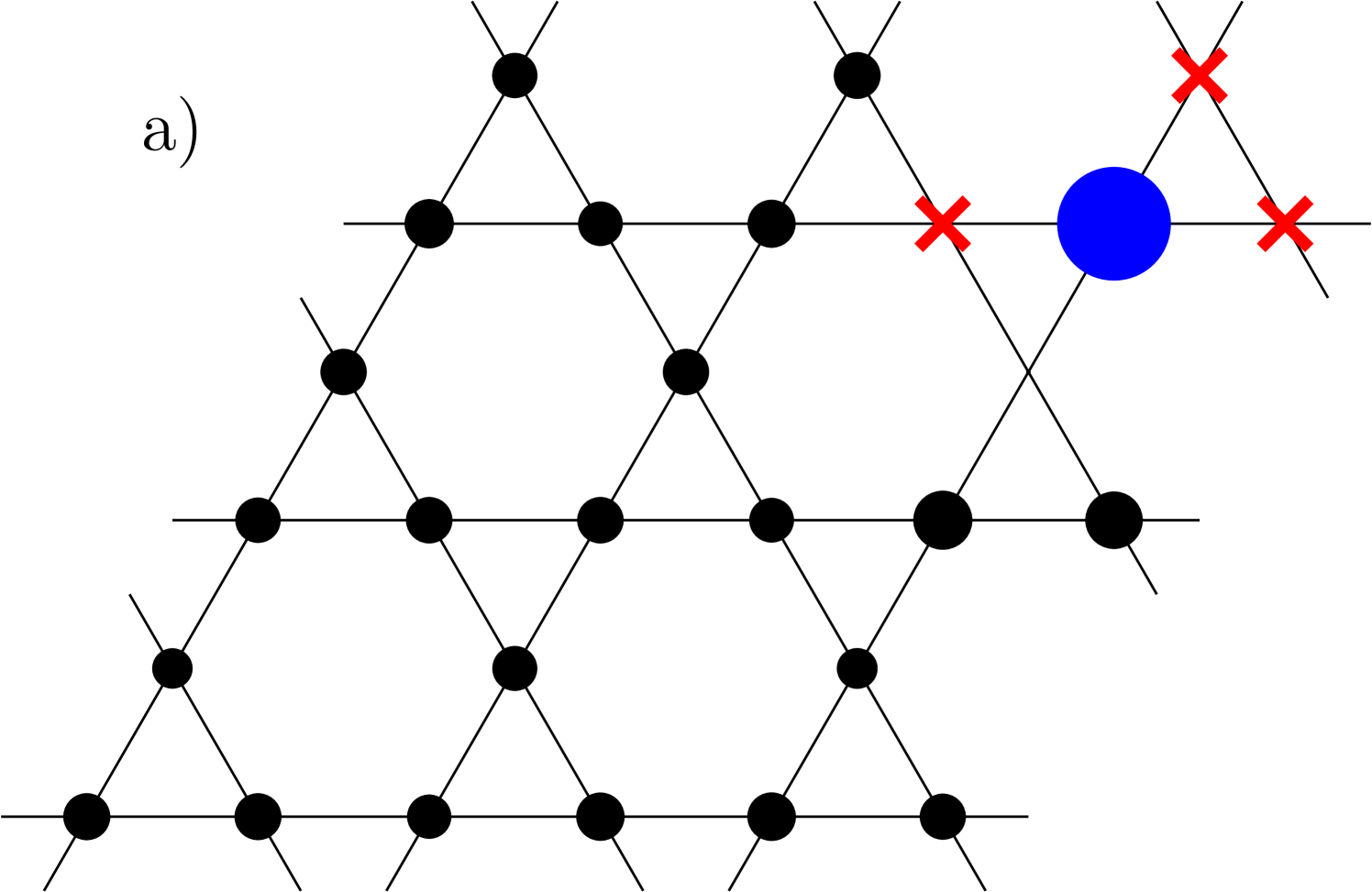
we first compute the total spin of the ground-state for some of the lattices shown in Fig. 1. This is done using Lanczos diagonalization for kagomé samples with an orphan spin, up to . This is represented in Fig. 2, where we find that starting from , the ground-state is no longer a singlet. We compare the total spin of the ground state to (dashed line in Fig. 2) and find an overall trend towards this classical prediction. In particular, the ground state spin tracks in most cases the (half-)integer closest to which is allowed in the sample. The results in Fig. 2 are mostly for the -sites samples with a pair impurity, but we find the same for the few larger clusters which we are able to simulate. In particular, we find for spin-2 lattices of sizes 15 and 18 with an orphan impurity. We were able to check also a combination of spin and lattice size where the global total spin is half integer . Note for instance the case of spins on a -sites sample with a pair impurity (13 sites effective) where we find that , which is indeed the allowed value closest to the classical prediction.
These results should be contrasted with all other cases we have tested, such as the pure case and different arrangements of the impurities (for one or two non-magnetic impurities). In these more conventional configurations, we always find the ground state to be of the lowest possible spin (a global singlet when the total number of spins is even). This is consistent with what is expected for conventional antiferromagnets.
In addition to this, we also study the ground state texture for cases where it is not a global singlet. This can be done by calculating for all sites on the lattice in the highest polarized state in the ground state multiplet. This is shown explicitly in Fig. 3 for . Since the ground-state has total spin (see Fig. 2), we have measured the distribution of magnetization in the sector. There is clearly a larger effect at the orphan site which tapers off with increasing distance, but due to the relative small size of the lattice, other sites are affected as well.
In Fig.4, we present other magnetization profiles for much larger system sizes using DMRG simulations White (1992); Schollwöck (2011); Fishman et al. (2020). We have chosen a spin so that the ground-state is polarized and we measure the local values in the ground-state. Typically, we have kept up to states (using only U(1) quantum number corresponding to the conservation of ) to achieve a discarded weight below . As often used in such simulations, we have chosen cylinder geometries, i.e. periodic boundary conditions in the short direction and open ones in the other. From these plots, it is clear that the spin texture is well localized around the orphan spin. Moreover, the numerical values found in these larger clusters are within of the ones obtained by ED on a much smaller 12-site cluster with 2 impurities.
[clean]sz_XC(0.11)
\lbl28,300; (a)
{lpic}[clean]sz_YC(0.11)
\lbl-50,300; (b)
In order to make contact with experiments, we now move to the finite-temperature regime to see if signatures of orphan spins remain and how to characterize them.
III Thermodynamics for the Quantum Version
In this section, we study the thermodynamics of the quantum version of the Heisenberg model in Eq. 1, for various values of the spin ranging from up to , on samples of the kagomé lattice containing one or several non-magnetic impurities, some of which are depicted in Fig. 1.
While a full computation of the thermodynamic properties does require the complete set of eigenvalues (to get the partition function), or even eigenstates (to compute observables), it has been known for a long-time that finite-temperature properties can be approximated using only a few well-chosen pure states in the correct energy window, as done in the finite-temperature Lanczos method Jaklič and Prelovšek (1994). This is rooted at the foundations of statistical mechanics since a pure state with energy of a large system has the same local properties as a thermodynamic mixed state at the related temperature. These ideas have been put on more rigorous grounds over the years, and are known as quantum typicality Hams and De Raedt (2000); Goldstein et al. (2006); Popescu et al. (2006); Reimann (2007).
In most of our results, we thus use a typicality scheme based on the exact application of the Hamiltonian to a random initial vector . Rather than using a power-method with repeated applications of the Hamiltonian Sugiura and Shimizu (2013, 2012) which has a slower convergence, we use the formulation in the Krylov basis , and choose large enough (typically between 100 and 500) such that at least two of the lowest energy states are converged. We found that this criterion implies large-enough Krylov spaces to ensure convergence at the lower temperature. Several previous works show that these approaches are particularly successful to study thermodynamic properties of frustrated magnets on lattices larger than those available with full diagonalization methods Shimokawa and Kawamura (2016); Schnack et al. (2018); Wietek et al. (2019); Prelovšek and Kokalj (2020), and we refer to them for details about this method. Despite using exact (machine precision) application of , all the data presented using this technique present error bars, which results from averaging over a finite number of initial random vectors . In our simulations, we use between and initial random vectors, depending on the system size, which is quite a high number (see discussion in Ref. Schnack et al. (2020) which averages over initial states). The error bars are computed using standard jackknife techniques to correctly take into account the important correlations between the numerator and denominators in all thermal expectations values Aichhorn et al. (2003); Schnack et al. (2020).
Specific aspects of our computations are: (i) the presence of impurities imply the absence of translation symmetries (for some impurity patterns, a reflection symmetry is still present), (ii) we measure expectation values of observables (such as the orphan magnetization ) which do not commute with , hence requiring to store all Krylov vectors Wietek et al. (2019). Even though we use total magnetization conservation and spin inversion symmetry, the first point implies very large Hilbert spaces, especially for large spin values. The second point implies a much larger memory requirement than for most applications of the typicality method which deal with observables which commute with the Hamiltonian. We mitigate this by storing all Krylov vectors in parallel for the largest samples. Both computationally demanding points limit the typicality method to kagomé samples with a relatively small number of spins. We can nevertheless reach samples with up to spins for and up to spins for .
In the following, we will present results for the total susceptibility of the sample , the local susceptibility, defined as (see e.g. Gregor and Motrunich (2008)) , or the magnetization curve . Here is the magnetization at an orphan site.
III.1 Local Susceptibility
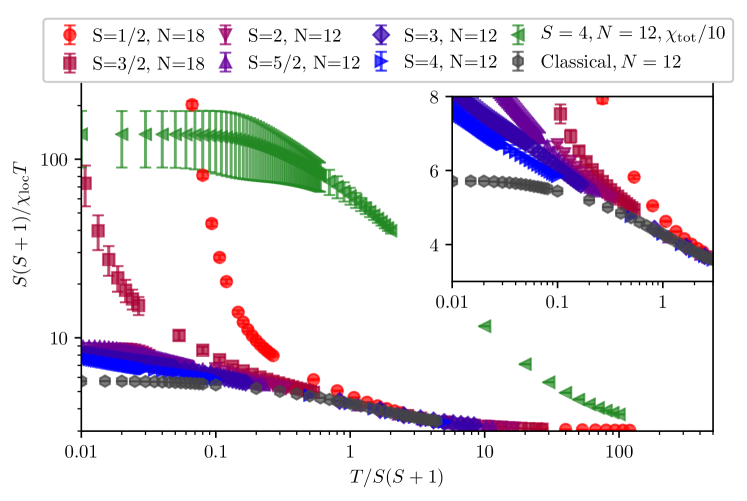
We compute the magnetic response of the spin closest to non-magnetic impurities: it is in most cases the orphan spin (such as in Figs. 1a, 1c, 1d, and 1f), but we also consider the closest spin for other impurity patterns (such as in Fig. 1b and 1e). Motivated by the classical expectations outlined in the Introduction, we study the local susceptibility as a sensitive probe of orphan physics.
We compare in particular in Fig. 5 the local susceptibility of the orphan spin for the -sites kagomé sample with a pair of impurities (Fig. 1a) for various values of spin to the classical result. To provide a simple comparison, we scale and , in analogy with the classical case. We find an agreement between the classical version for a range of temperatures lying between a (spin-dependent) minimum temperature and arbitrarily large temperatures. The inset of Fig. 5 allows us to identify the dependence on the spin of the typical temperature scale above which the local susceptibility is almost indistinguishable from the classical response. As expected, this temperature decreases with increasing spin , but note that it does so, even when rescaled by . More strikingly, we find that for , the inverse local susceptibility appears to converge to a finite value (around , depending on ), relatively close to the one of the classical case ( in theory, around for the -site samples, as shown in the Appendix). The lower spin values ( and ), for which we can use a larger 18-sites sample, depart earlier from the classical case (as expected); the major difference lying at low temperatures where the inverse response diverges. Clearly, this difference has its origins in the fact that the ground state for these cases does not host a half-orphan, i.e. is a spin singlet and does not lie in the total spin sector .
A clear signature of the orphan spin is found by comparing its local (inverse) susceptibility to the averaged (inverse) susceptibility per site, also represented for in Fig. 5: as is readily seen in this figure, the orphan spin is approximately an order of magnitude more sensitive to magnetic field at low temperatures. This is justified by assuming that a large portion of the magnetic response of the entire system is provided by the orphan spin, implying that the averaged susceptibility is times the orphan susceptibility, where is the number of spins ( in this case). It is important to understand whether this signature is unique to the orphan spin, or could also be found for spins close to the non-magnetic impurities for other impurity patterns. To answer this question, we study two other kinds of impurities (i) a single site impurity and (ii) two impurities on neighboring plaquettes (this case corresponds to Figs. 1b and 1e).
For the former case, we consider the local susceptibility of any spin close to the impurity, while for the latter, we consider the spin in between the two impurities (blue dot in Figs. 1b and 1e). The corresponding three scaled inverse local susceptibilities are represented in Fig. 6 for (representative of the generic case) as well as for . In both cases, we find the magnetic response to be significantly stronger for the orphan spin for low to medium () temperatures.
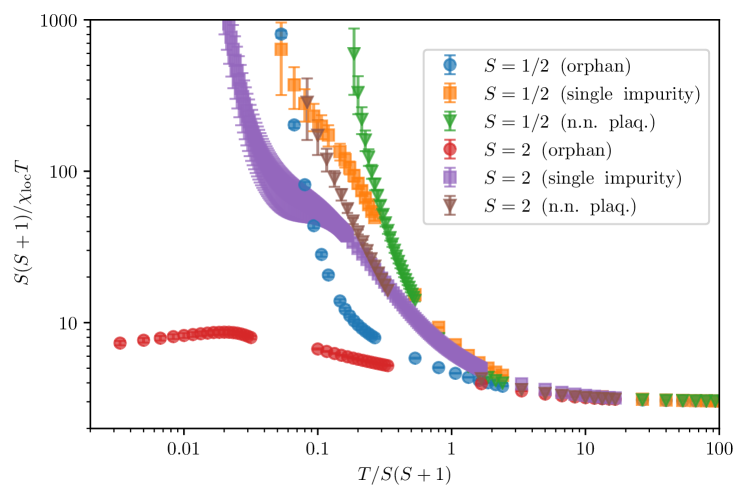
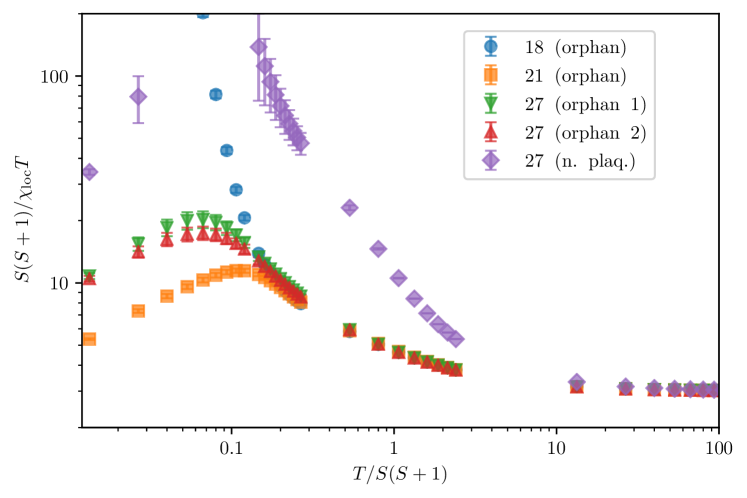
The spin- case is of special importance for several compounds Hiroi et al. (2001); Mendels et al. (2007); Mendels and Bert (2011); Arh et al. (2020), for which local magnetic responses can be probed by NMR. Motivated by this, we study in more details the case for a larger variety of sample sizes and impurity patterns. In Fig. 7, we study the orphan spin configuration for an -site kagomé sample (with effectively spins), a -site sample ( spins effective) and a -site sample with two orphan spins which are maximally separated ( spins effective), as well as the same -site sample with inpurities on neighboring plaquettes ( sites effective). All of these configurations are shown in Figs. 1 and 12. When the number of spins is even, the ground-state can be and is a global singlet. This feature is absent in all other cases with an odd number of spins, leading to a divergence in at low temperatures. Besides the lattice independent behavior in the high temperature range, we observe a clear distinction in the medium to high-temperature range in the local response between the orphan spin and other spins close to impurities, before the low-temperature signal (dominated by the ground-state nature) eventually appears. For the case of the lattice with two orphan impurities, both orphans are chosen to be equivalent from the perspective of lattice geometry and we expect that they should have identical behavior, which is what we observe within error bars.
III.2 Orphan magnetization curve and effects of the screening cloud
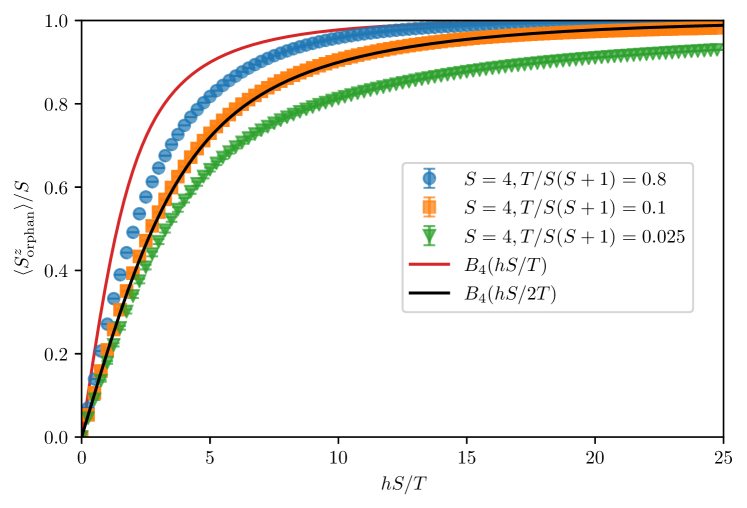
Another important feature of orphan physics which is important to test for in the quantum case is the effect of the screening cloud on the orphan spin itself. As discussed in the Introduction, in the classical case the cloud screens half of the applied magnetic field, implying that the orphan spin responds like a free spin in a magnetic field . This description should work only in the temperature range where quantum and thermal effects are not strong, i.e, in an intermediate temperature range with respect to , the coupling value.
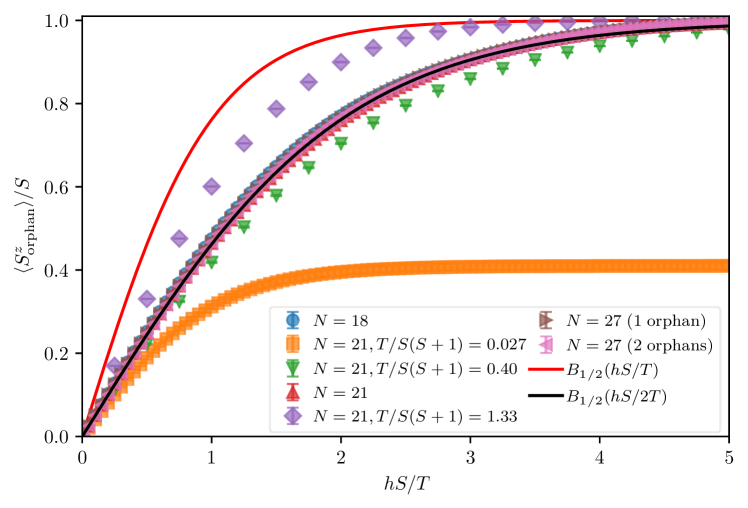
Fig. 8 displays a comparison between the scaled magnetization curve of the orphan spin for the spin kagomé -sites sample for three different temperatures, and compares it to the expected Brillouin functions for the full field or half-field , where
is the response to a magnetic field of a free spin- at temperature . We find good agreement between the typicality data and the half-field response for a temperature , and expected deviations at low and high temperature. We discuss below how to quantify the temperature scale for which the agreement is the best. We find similar behavior for lower spins, all the way down to spin-1/2.
In particular, motivated by the specific signature of the orphan local susceptibility in Fig. 7, we also study the field dependent response of the orphan impuritiy complexes at different temperatures for the low-spin case . Once again, we find a temperature range where the screening cloud of the orphan provides a net cancellation of half the magnetic field, making the response of the orphan spin consistent with a free spin- in a magnetic field . This can be observed in Fig. 9, for a different set of lattice sizes where the adherence to the half-field Brillouin function is consistent for different samples with the same temperature scale. An interesting feature to note here is the behavior of the orphan impurity complexes in the -sites sample with two such complexes. The screening cloud appears to be highly local as each of the two orphan spins respond exactly as a lattice with only one orphan spin. Furthermore, we find a plateau at low temperatures in the orphan response as well as an approach to its saturation value through a series of plateaus at higher fields (not shown in Fig. 9). This is due to the discrete nature of the finite-size spectrum on such a small lattice (and at such low temperature) and appears without any relationship to other well-known quantized plateaus that exist in the clean case Schulenburg et al. (2002); Cabra et al. (2005); Nishimoto et al. (2013); Capponi et al. (2013a).
The field dependence discussed above only appears for a particular temperature range which is controlled by thermal and quantum correlations. At high temperatures, the thermal correlation length is too short for the texture to survive, and at low temperatures the quantum correlation length is too long for the classical orphan description to work. It was noted in Ref. Sen et al., 2011, that in the classical case, the expectation that the orphan texture in the SCGO bilayer provides exactly shielding, works at temperatures below . In the case of the kagomé lattice, the classical results presented in the Appendix indicate that the orphan physics is slightly less stable to temperature (see Fig. 14) and we must thus expect a lower bound. This sets an approximate upper bound of temperature congruent with orphan physics for the quantum case as well for large spin-.
To make a more quantitative prediction for this temperature range, we define the integrated square of the difference between the numerical data obtained with the typicality method and the expected form of the field response of the orphan. Considering the analytical Brillouin function for spin- in magnetic field , we compute the integral
| (2) |
where is fixed. This quantity approaches zero only when the data fits the function to high accuracy in the window defined above. For numerical convenience, we define the integral to run from to an satisfying . We have checked that this does not affect conclusions.
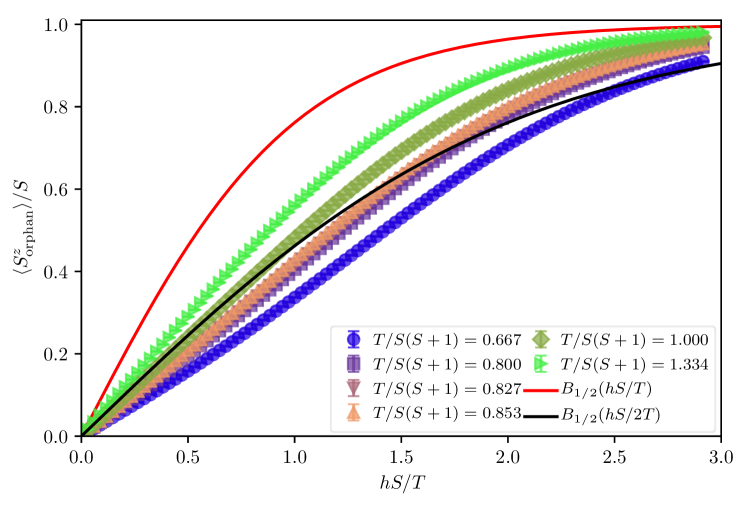
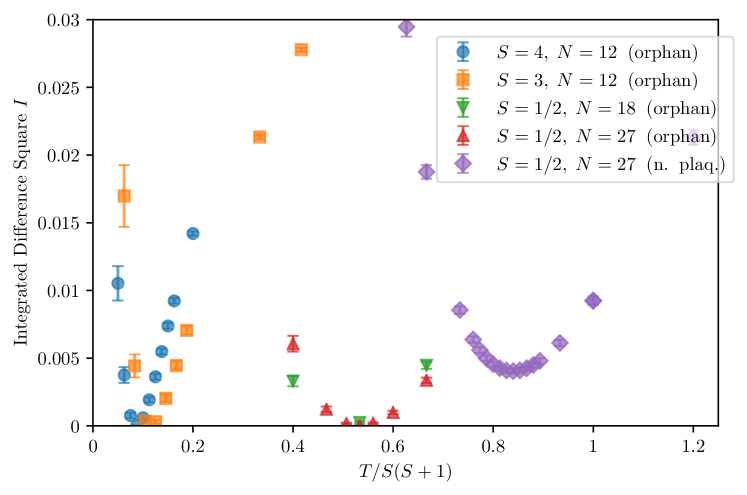
We show results for the quantum case in Fig. 11, for and on the -site lattice with an orphan spin, along with results on larger lattices. For all spin values, we find a temperature range where the data are extremely close to the half-field Brillouin function. This region can also be estimated directly from Fig. 5 by comparing the susceptibility with the expected value for the orphan defect. The deviations from orphan behavior at high temperatures arise from the same thermal fluctuations which melt orphan defects for the classical case, whereas the deviations at low temperatures arise from strong quantum fluctuations expected to render the spin liquid description inapplicable. We chose in Figs. 8 and 9 the temperature close to the minima of for and respectively, but let us emphasize that displaying data at temperatures corresponding to values of (respectively ) would result in curves which would not be distinguishable for (respectively ) on the scale of Figs. 8 and 9. Based on the numerical evidence provided in Fig. 11, this leaves a fair range of temperatures where the orphan physics could be probed experimentally with local probes for instance.
As can be furthermore noted in Fig. 11, there is no significant difference between and -sites samples for , implying that the orphan shielding is fairly local (as also expected from Refs. Sen et al. (2011, 2012)). We also compare to the case where the two impurities are on neighboring plaquettes to show that a strong shielding does not occur for any temperature range in this case. Although there is a minimum in the integrated difference square measure, the values at the minimum are significantly larger than corresponding values in cases where orphan spins are present. The corresponding magnetization curves are also quite distinct from the half-field Brillouin function (as seen in Fig. 10).
III.3 Local susceptibility distribution for doped kagomé systems
In order to make connections with possible experimental detection of orphan physics using NMR, we develop in this section a crude estimate for the distribution of local susceptibilities on large kagomé samples for the case .
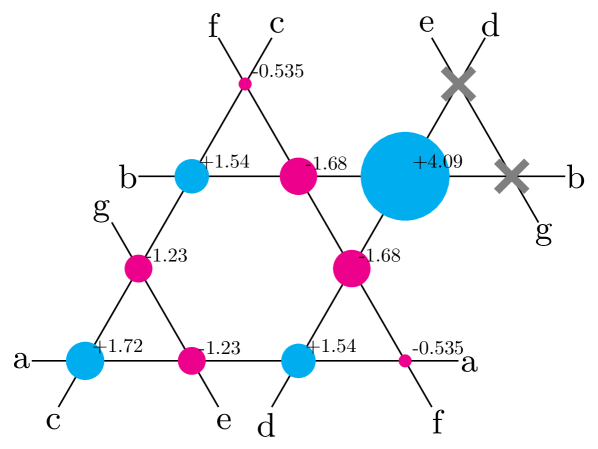
The procedure we consider is as follows. We work with a large lattice with sites to be representative of the thermodynamic limit. On this lattice, we randomly pick sites to host a non-magnetic impurity with probability . This non-magnetic impurity doping fraction of is chosen to ensure that we get a sizeable number of orphans. The choice of temperature is guided by Fig. 9, where we see that (or ) yields a good agreement with the orphan picture. At this temperature, we study a range of impurity patterns on the -sites sample and find that only certain impurity patterns produce a local susceptibility which differs significantly from that of the pure system. Using this information, we find in particular that there are only six patterns which are relevant for sites which host a magnetic ion, some of which are presented pictorially in Fig. 12. The motivation to create this simple division is driven by the observation that for a temperature , quantum correlations are quite weak and the impurities do not influence significantly the sites that are separated by more than one bond, confirming that the physics is very local. In increasing order of probabilities of occurrence and together with a description of their magnetic response, these six patterns are:
-
P1.
All four neighbors of the ion are non-magnetic impurities. This implies that the spin is completely decoupled from the lattice, and acts as a free spin .
-
P2.
Three neighbors are non-magnetic impurities: this is the situation where an orphan spin has an additional non-magnetic impurity next to it (see Fig. 12a). We find that the response of this spin is only slightly stronger than that of the orphan spin.
-
P3.
Two neighbors are non-magnetic impurities (Fig. 12b): this is the orphan spin which response has been detailed earlier in this section.
-
P4.
Two neighbors are non-magnetic impurities on neighboring plaquettes but do not form an orphan (see Fig. 12c). This has a response which is slightly stronger than the pure case.
-
P5.
Only one neighbor is a non-magnetic impurity (Fig. 12d which displays two of these cases). We find also that this situation behaves similarly to the pure case with a slightly stronger response.
-
P6.
No impurities are in the nearest neighbors. Response is well approximated by the pure case.

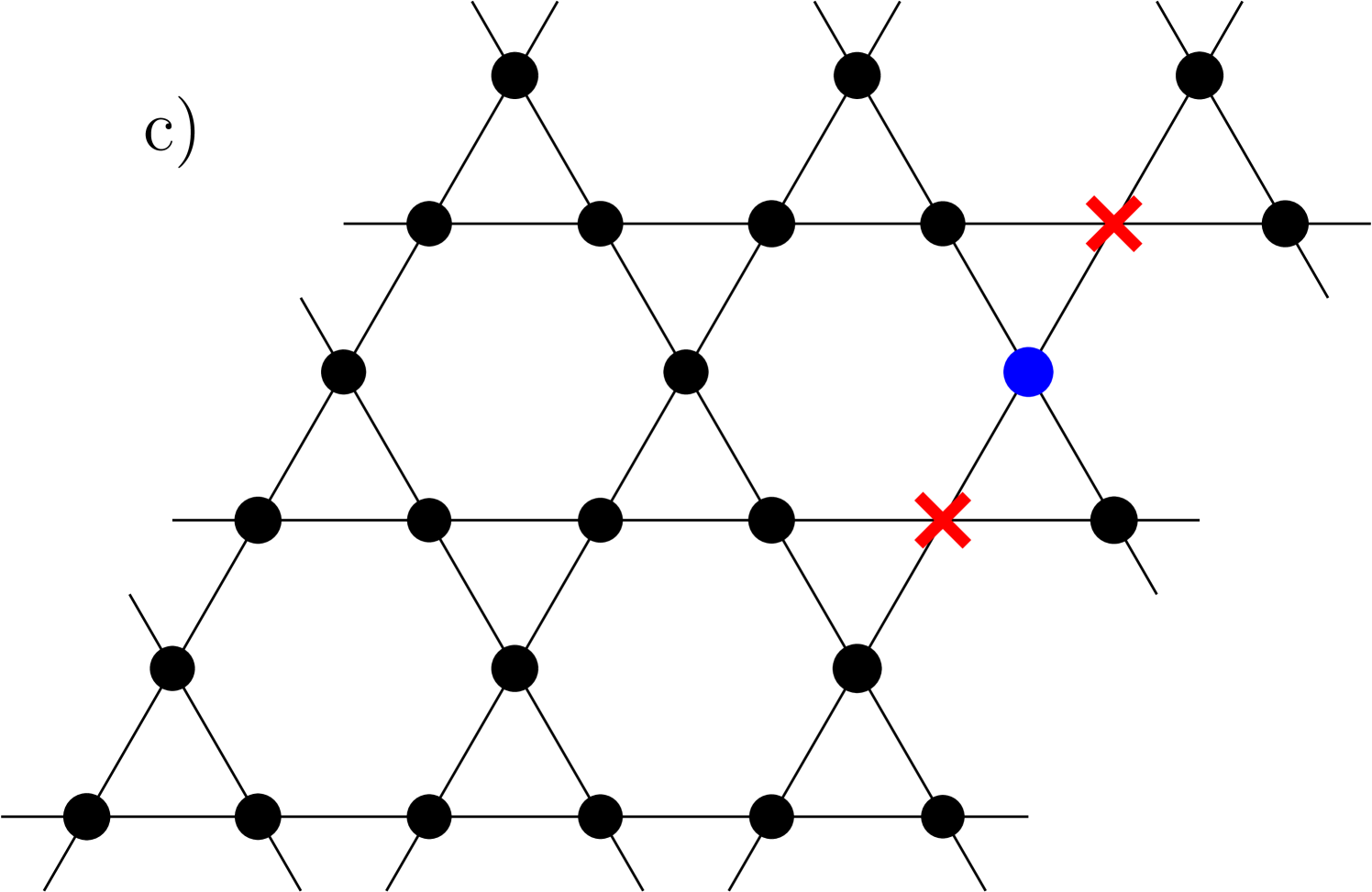

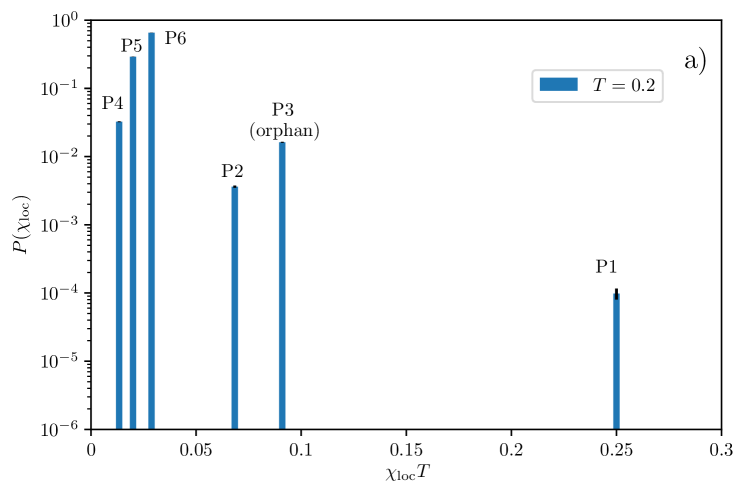
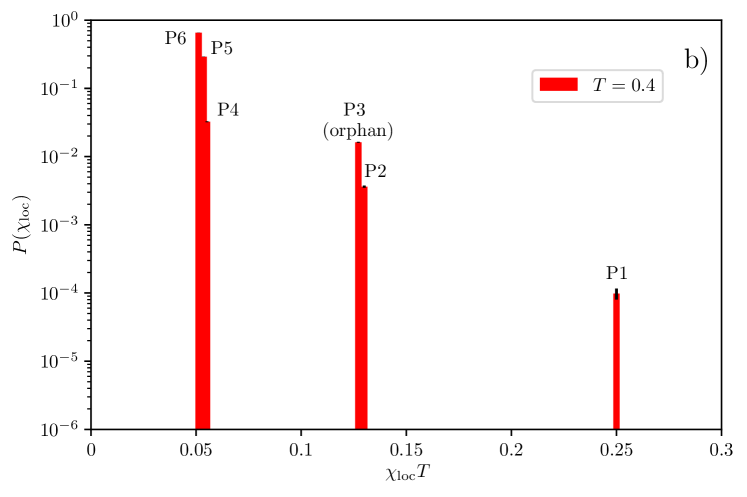
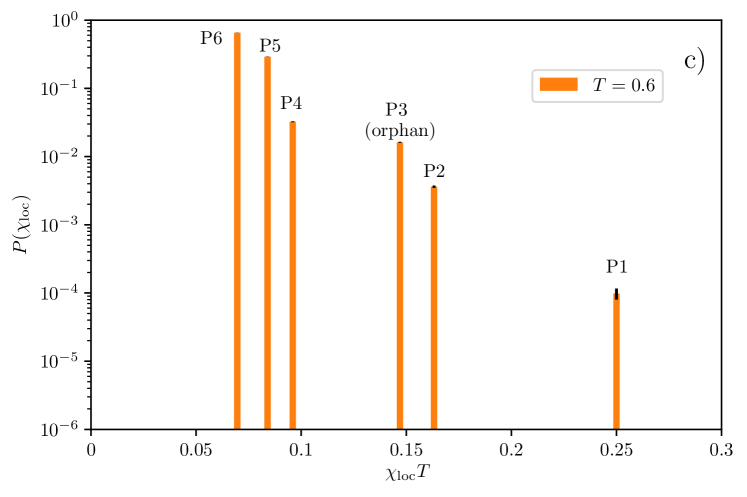
The six cases mentioned above lead to six peaks in the local susceptibility distribution , as displayed in the middle panel of Fig 13 and ranked right to left (the free spin has obviously the largest local susceptibility). Given the very similar responses, it might be hard to distinguish the three left-most peaks which are likely to form a main broad peak and correspond to the pure case as well as few impurities non-orphan physics. Note that in theses cases, the impurity susceptibility is smaller (respectively larger) than the pure one at low (respectively high) temperature, in agreement with recent series expansion results Bernu et al. (2020). The orphan physics is manifested through the presence of secondary peak (where the cases and might also be hard to resolve too). While this secondary peak is about only of the main peak in strength, it is well separated from it, which gives hope for a possible experimental detection. Also shown in Fig. 13 are results for and , which show the variation of the histogram with slight variations of the temperature away from the temperature () which best fits the orphan picture. For , the quantum correlations may be too strong for the approximations to strictly apply.
IV Conclusions
In this work, we have investigated whether and how the physics of half-orphans, originally described using a classical theory, survives quantum effects and leads to clearly identifiable signatures in the response of quantum spin- Heisenberg antiferromagnets on the kagomé lattice when nearest-neighbours non-magnetic impurities are present. We found that orphan-specific signatures are evident in local susceptibility data in an intermediate temperature range. We also found that the classical predictions for the screening cloud around an orphan spin are justified in the quantum case. Indeed the resulting spin texture is a more robust signature than the local susceptibility of the orphan spin itself, and appears to provide a window to orphan physics even in the case. Another striking result, for samples with a single orphan, is the strong dependence of the ground state spin quantum number on the spin- of the local moment itself. In complete agreement with the classical expectation, we found that the kagomé antiferromagnet with an orphan impurity complex has a ground state spin which is the nearest (half-)integer to allowed in most cases. Finally, we also presented experimental predictions for NMR Knight shifts on kagomé systems doped with non-magnetic impurities, which point to the possibility of observing the enhanced orphan-induced magnetic response through a small, but resolvable, secondary peak.
In the appropriate temperature regime corresponding to spin liquid behaviour, these classical results on half-orphan spins are also expected to apply mutatis mutandis to other corner-sharing lattices such as the pyrochlore. Our results, taken in conjunction with this expectation, therefore provide strong motivation for other related studies. For instance, one follow-up suggested by our work is to consider whether the nonzero ground-state spin quantum number that we find in samples with an orphan impurity complex is also present for the Heisenberg model with sufficiently large spin- on other corner-sharing lattices, for which the original arguments go through unchanged. We hope to report on this in the near future.
A noteworthy feature of the orphan-induced spin texture studied here is that it appears to be a very local feature that exists in an intermediate temperature window, and this feature seems largely independent of the nature of the ground state, whose character can vary with the spin value . For example, the Heisenberg kagomé antiferromagnet with spin-1/2 has a ground state which is non-magnetic but the precise nature of this spin liquid (gapless vs gapped) is still debated Jiang et al. (2008); Evenbly and Vidal (2010); Yan et al. (2011); Depenbrock et al. (2012); Iqbal et al. (2013); Capponi et al. (2013b); He et al. (2017); Liao et al. (2017); in the spin-1 case, the ground state is also non-magnetic although whether it breaks lattice symmetries Changlani and Läuchli (2015); Liu et al. (2015) or not Nishimoto and Nakamura (2015) is still a matter of debate; for larger values of , spin-wave analysis, coupled-cluster or series expansions methods point to an ordered phase Chubukov (1992); Götze et al. (2011); Oitmaa and Singh (2016) while a large- analysis, which generalizes the symmetry from SU(2) to a larger symmetry group, leads to a non-magnetic state Sachdev (1992).
It would be worth understanding how to incorporate the quantum orphan features found in our work in various effective field theories for these putative ground states Gregor and Motrunich (2008). Indeed, preliminary results suggest that some signatures of orphan physics are already present when samples with orphan impurity complex are studied using relatively crude extensions of variational treatments inspired by such effective field theories. It would also be interesting to complement our study of quantum half-orphans by series expansion methods; this may be particularly fruitful since the textures induced by the orphans are relatively compact in the temperature range of their existence.
Acknowledgements.
We thank Ph. Mendels and L. Messio for discussions and A. Wietek for useful insights about the typicality method. KD would like to gratefully acknowledge earlier collaborations on closely related topics with R. Moessner, A. Sen, and S. Sanyal, which provided part of the motivation for this work. This work benefited from the support of the project LINK ANR-18-CE30-0022-04 of the French National Research Agency (ANR). We acknowledge the use of HPC resources from CALMIP (grants 2019-P0677 and 2020-P0677) and GENCI (grant x2020050225). We use the libraries ITensor for DMRG simulations Fishman et al. (2020) (available at http://itensor.org), and PETSc Balay et al. (1997, 2017), SLEPc Hernandez et al. (2005); Roman et al. (2017) for the typicality computations. We gratefully thank J. Roman for improving the Krylov methods implementation in SLEPc to further ease typicality computations.References
- Savary and Balents (2016) Lucile Savary and Leon Balents, “Quantum spin liquids: a review,” Reports on Progress in Physics 80, 016502 (2016).
- Castelnovo et al. (2008) Claudio Castelnovo, Roderich Moessner, and Shivaji L Sondhi, “Magnetic monopoles in spin ice,” Nature 451, 42–45 (2008).
- Kitaev (2006) Alexei Kitaev, “Anyons in an exactly solved model and beyond,” Annals of Physics 321, 2–111 (2006).
- Poilblanc et al. (2006) Didier Poilblanc, Andreas Läuchli, Matthieu Mambrini, and Frédéric Mila, “Spinon deconfinement in doped frustrated quantum antiferromagnets,” Phys. Rev. B 73, 100403 (2006).
- Läuchli and Poilblanc (2004) Andreas Läuchli and Didier Poilblanc, “Spin-charge separation in two-dimensional frustrated quantum magnets,” Phys. Rev. Lett. 92, 236404 (2004).
- Alloul et al. (2009) H. Alloul, J. Bobroff, M. Gabay, and P. J. Hirschfeld, “Defects in correlated metals and superconductors,” Rev. Mod. Phys. 81, 45–108 (2009).
- Martins et al. (1997) George Balster Martins, Markus Laukamp, José Riera, and Elbio Dagotto, “Local enhancement of antiferromagnetic correlations by nonmagnetic impurities,” Phys. Rev. Lett. 78, 3563–3566 (1997).
- Kaul et al. (2008) Ribhu K. Kaul, Roger G. Melko, Max A. Metlitski, and Subir Sachdev, “Imaging bond order near nonmagnetic impurities in square-lattice antiferromagnets,” Phys. Rev. Lett. 101, 187206 (2008).
- Sachdev and Vojta (2003) Subir Sachdev and Matthias Vojta, “Quantum impurity in an antiferromagnet: Nonlinear sigma model theory,” Phys. Rev. B 68, 064419 (2003).
- Höglund et al. (2007) Kaj H. Höglund, Anders W. Sandvik, and Subir Sachdev, “Impurity induced spin texture in quantum critical 2d antiferromagnets,” Phys. Rev. Lett. 98, 087203 (2007).
- Haravifard et al. (2006) S. Haravifard, S. R. Dunsiger, S. El Shawish, B. D. Gaulin, H. A. Dabkowska, M. T. F. Telling, T. G. Perring, and J. Bonča, “In-gap spin excitations and finite triplet lifetimes in the dilute singlet ground state system SrCu2-xMgx(BO3)2,” Phys. Rev. Lett. 97, 247206 (2006).
- Yoshida et al. (2015) M. Yoshida, H. Kobayashi, I. Yamauchi, M. Takigawa, S. Capponi, D. Poilblanc, F. Mila, K. Kudo, Y. Koike, and N. Kobayashi, “Real space imaging of spin polarons in Zn-doped SrCu2(BO3)2,” Phys. Rev. Lett. 114, 056402 (2015).
- Tedoldi et al. (1999) F. Tedoldi, R. Santachiara, and M. Horvatić, “89 Y NMR imaging of the staggered magnetization in the doped haldane chain Y2BaNi1-xMgxO5,” Phys. Rev. Lett. 83, 412–415 (1999).
- Olariu et al. (2008) A. Olariu, P. Mendels, F. Bert, F. Duc, J. C. Trombe, M. A. de Vries, and A. Harrison, “17O NMR study of the intrinsic magnetic susceptibility and spin dynamics of the quantum kagome antiferromagnet ZnCu3(OH)6Cl2,” Phys. Rev. Lett. 100, 087202 (2008).
- Yin et al. (2020) Jia-Xin Yin, Nana Shumiya, Yuxiao Jiang, Huibin Zhou, Gennevieve Macam, Hano Omar Mohammad Sura, Songtian S Zhang, Zi-Jia Cheng, Zurab Guguchia, Yangmu Li, et al., “Spin-orbit quantum impurity in a topological magnet,” Nature Communications 11, 1–6 (2020).
- Obradors et al. (1988) X. Obradors, A. Labarta, A. Isalgué, J. Tejada, J. Rodriguez, and M. Pernet, “Magnetic frustration and lattice dimensionality in srcr8ga4o19,” Solid State Communications 65, 189 – 192 (1988).
- Ramirez et al. (1990) A. P. Ramirez, G. P. Espinosa, and A. S. Cooper, “Strong frustration and dilution-enhanced order in a quasi-2d spin glass,” Phys. Rev. Lett. 64, 2070 (1990).
- Limot et al. (2002) L. Limot, P. Mendels, G. Collin, C. Mondelli, B. Ouladdiaf, H. Mutka, N. Blanchard, and M. Mekata, “Susceptibility and dilution effects of the kagomé bilayer geometrically frustrated network: A Ga NMR study of SrCr9pGa12-9pO19,” Phys. Rev. B 65, 144447 (2002).
- Moessner and Berlinsky (1999) R Moessner and AJ Berlinsky, “Magnetic susceptibility of diluted pyrochlore and SrCr9-9xGa3+9xO19 antiferromagnets,” Phys. Rev. Lett. 83, 3293 (1999).
- Moessner and Chalker (1998) Roderich Moessner and John T Chalker, “Properties of a classical spin liquid: the heisenberg pyrochlore antiferromagnet,” Phys. Rev. Lett. 80, 2929 (1998).
- Schiffer and Daruka (1997) P. Schiffer and I. Daruka, “Two-population model for anomalous low-temperature magnetism in geometrically frustrated magnets,” Phys. Rev. B 56, 13712–13715 (1997).
- Henley (2001) C L Henley, “Effective hamiltonians and dilution effects in kagome and related anti-ferromagnets,” Canadian Journal of Physics 79, 1307–1321 (2001).
- Sen et al. (2011) Arnab Sen, Kedar Damle, and Roderich Moessner, “Fractional spin textures in the frustrated magnet SrCr9pGa12-9pO19,” Phys. Rev. Lett. 106, 127203 (2011).
- Sen et al. (2012) Arnab Sen, Kedar Damle, and R. Moessner, “Vacancy-induced spin textures and their interactions in a classical spin liquid,” Phys. Rev. B 86, 205134 (2012).
- Bono et al. (2004) D. Bono, P. Mendels, G. Collin, N. Blanchard, F. Bert, A. Amato, C. Baines, and A. D. Hillier, “ study of the quantum dynamics in the frustrated kagomé bilayers,” Phys. Rev. Lett. 93, 187201 (2004).
- Mendels and Bert (2011) Philippe Mendels and Fabrice Bert, “Quantum kagome antiferromagnet : ZnCu3(OH)6cl2,” Journal of Physics: Conference Series 320, 012004 (2011).
- Khuntia et al. (2020) P Khuntia, Matias Velazquez, Quentin Barthélemy, Fabrice Bert, Edwin Kermarrec, A Legros, Bernard Bernu, L Messio, Andrej Zorko, and P Mendels, “Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2,” Nature Physics 16, 469–474 (2020).
- Chern and Moessner (2013) Gia-Wei Chern and Roderich Moessner, “Dipolar order by disorder in the classical heisenberg antiferromagnet on the kagome lattice,” Phys. Rev. Lett. 110, 077201 (2013).
- Zhitomirsky (2008) Michael E Zhitomirsky, “Octupolar ordering of classical kagome antiferromagnets in two and three dimensions,” Phys. Rev. B 78, 094423 (2008).
- Huse and Rutenberg (1992) David A Huse and Andrew D Rutenberg, “Classical antiferromagnets on the kagomé lattice,” Physical Review B 45, 7536 (1992).
- Dommange et al. (2003) S. Dommange, M. Mambrini, B. Normand, and F. Mila, “Static impurities in the kagome lattice: Dimer freezing and mutual repulsion,” Phys. Rev. B 68, 224416 (2003).
- Läuchli et al. (2007) A. Läuchli, S. Dommange, B. Normand, and F. Mila, “Static impurities in the kagome lattice: Exact diagonalization calculations on small clusters,” Phys. Rev. B 76, 144413 (2007).
- Singh (2010) R. R. P. Singh, “Valence bond glass phase in dilute kagome antiferromagnets,” Phys. Rev. Lett. 104, 177203 (2010).
- Gregor and Motrunich (2008) Karol Gregor and Olexei I. Motrunich, “Nonmagnetic impurities in the spin-1/2 kagome antiferromagnet,” Phys. Rev. B 77, 184423 (2008).
- White (1992) S. R. White, “Density matrix formulation for quantum renormalization groups,” Phys. Rev. Lett. 69, 2863–2866 (1992).
- Schollwöck (2011) Ulrich Schollwöck, “The density-matrix renormalization group in the age of matrix product states,” Annals of Physics 326, 96 – 192 (2011).
- Fishman et al. (2020) Matthew Fishman, Steven R. White, and E. Miles Stoudenmire, “The ITensor software library for tensor network calculations,” arXiv:2007.14822 (2020).
- Jaklič and Prelovšek (1994) J. Jaklič and P. Prelovšek, “Lanczos method for the calculation of finite-temperature quantities in correlated systems,” Phys. Rev. B 49, 5065 (1994).
- Hams and De Raedt (2000) Anthony Hams and Hans De Raedt, “Fast algorithm for finding the eigenvalue distribution of very large matrices,” Phys. Rev. E 62, 4365–4377 (2000).
- Goldstein et al. (2006) Sheldon Goldstein, Joel L. Lebowitz, Roderich Tumulka, and Nino Zanghì, “Canonical typicality,” Phys. Rev. Lett. 96, 050403 (2006).
- Popescu et al. (2006) S. Popescu, A. Short, and A. Winter, “Entanglement and the foundations of statistical mechanics,” Nat. Phys. 2, 754 (2006).
- Reimann (2007) Peter Reimann, “Typicality for generalized microcanonical ensembles,” Phys. Rev. Lett. 99, 160404 (2007).
- Sugiura and Shimizu (2013) Sho Sugiura and Akira Shimizu, “Canonical thermal pure quantum state,” Phys. Rev. Lett. 111, 010401 (2013).
- Sugiura and Shimizu (2012) Sho Sugiura and Akira Shimizu, “Thermal pure quantum states at finite temperature,” Phys. Rev. Lett. 108, 240401 (2012).
- Shimokawa and Kawamura (2016) Tokuro Shimokawa and Hikaru Kawamura, “Finite-temperature crossover phenomenon in the s = 1/2 antiferromagnetic heisenberg model on the kagome lattice,” J. Phys. Soc. Jpn 85, 113702 (2016).
- Schnack et al. (2018) Jürgen Schnack, Jörg Schulenburg, and Johannes Richter, “Magnetism of the kagome lattice antiferromagnet,” Phys. Rev. B 98, 094423 (2018).
- Wietek et al. (2019) Alexander Wietek, Philippe Corboz, Stefan Wessel, B. Normand, Frédéric Mila, and Andreas Honecker, “Thermodynamic properties of the shastry-sutherland model throughout the dimer-product phase,” Phys. Rev. Research 1, 033038 (2019).
- Prelovšek and Kokalj (2020) P. Prelovšek and J. Kokalj, “Similarity of thermodynamic properties of the heisenberg model on triangular and kagome lattices,” Phys. Rev. B 101, 075105 (2020).
- Schnack et al. (2020) Jürgen Schnack, Johannes Richter, and Robin Steinigeweg, “Accuracy of the finite-temperature lanczos method compared to simple typicality-based estimates,” Phys. Rev. Research 2, 013186 (2020).
- Aichhorn et al. (2003) Markus Aichhorn, Maria Daghofer, Hans Gerd Evertz, and Wolfgang von der Linden, “Low-temperature lanczos method for strongly correlated systems,” Phys. Rev. B 67, 161103 (2003).
- Hiroi et al. (2001) Zenji Hiroi, Masafumi Hanawa, Naoya Kobayashi, Minoru Nohara, Hidenori Takagi, Yoshitomo Kato, and Masashi Takigawa, “Spin-1/2 kagomé -like lattice in volborthite Cu3V2O7(OH).2H2O,” J. Phys. Soc. Jpn. 70, 3377 (2001).
- Mendels et al. (2007) P. Mendels, F. Bert, M. A. de Vries, A. Olariu, A. Harrison, F. Duc, J. C. Trombe, J. S. Lord, A. Amato, and C. Baines, “Quantum magnetism in the paratacamite family: Towards an ideal kagomé lattice,” Phys. Rev. Lett. 98, 077204 (2007).
- Arh et al. (2020) T. Arh, M. Gomilšek, P. Prelovšek, M. Pregelj, M. Klanjšek, A. Ozarowski, S. J. Clark, T. Lancaster, W. Sun, J.-X. Mi, and A. Zorko, “Origin of magnetic ordering in a structurally perfect quantum kagome antiferromagnet,” Phys. Rev. Lett. 125, 027203 (2020).
- Schulenburg et al. (2002) J. Schulenburg, A. Honecker, J. Schnack, J. Richter, and H.-J. Schmidt, “Macroscopic magnetization jumps due to independent magnons in frustrated quantum spin lattices,” Phys. Rev. Lett. 88, 167207 (2002).
- Cabra et al. (2005) D. C. Cabra, M. D. Grynberg, P. C. W. Holdsworth, A. Honecker, P. Pujol, J. Richter, D. Schmalfuß, and J. Schulenburg, “Quantum kagomé antiferromagnet in a magnetic field: Low-lying nonmagnetic excitations versus valence-bond crystal order,” Phys. Rev. B 71, 144420 (2005).
- Nishimoto et al. (2013) S. Nishimoto, N. Shibata, and C. Hotta, “Controlling frustrated liquids and solids with an applied field in a kagome heisenberg antiferromagnet,” Nat. Comm. 4, 2287 (2013).
- Capponi et al. (2013a) Sylvain Capponi, Oleg Derzhko, Andreas Honecker, Andreas M. Läuchli, and Johannes Richter, “Numerical study of magnetization plateaus in the spin- kagome heisenberg antiferromagnet,” Phys. Rev. B 88, 144416 (2013a).
- Bernu et al. (2020) Bernard Bernu, Laurent Pierre, Karim Essafi, and Laura Messio, “Effect of perturbations on the kagome antiferromagnet at all temperatures,” Physical Review B 101, 140403 (2020).
- Jiang et al. (2008) H. C. Jiang, Z. Y. Weng, and D. N. Sheng, “Density matrix renormalization group numerical study of the kagome antiferromagnet,” Phys. Rev. Lett. 101, 117203 (2008).
- Evenbly and Vidal (2010) G. Evenbly and G. Vidal, “Frustrated antiferromagnets with entanglement renormalization: Ground state of the spin- heisenberg model on a kagome lattice,” Phys. Rev. Lett. 104, 187203 (2010).
- Yan et al. (2011) Simeng Yan, David A. Huse, and Steven R. White, “Spin-liquid ground state of the kagome heisenberg antiferromagnet,” Science 332, 1173 (2011).
- Depenbrock et al. (2012) Stefan Depenbrock, Ian P. McCulloch, and Ulrich Schollwöck, “Nature of the spin-liquid ground state of the heisenberg model on the kagome lattice,” Phys. Rev. Lett. 109, 067201 (2012).
- Iqbal et al. (2013) Yasir Iqbal, Federico Becca, Sandro Sorella, and Didier Poilblanc, “Gapless spin-liquid phase in the kagome spin- heisenberg antiferromagnet,” Phys. Rev. B 87, 060405 (2013).
- Capponi et al. (2013b) Sylvain Capponi, V. Ravi Chandra, Assa Auerbach, and Marvin Weinstein, “ chiral resonating valence bonds in the kagome antiferromagnet,” Phys. Rev. B 87, 161118 (2013b).
- He et al. (2017) Yin-Chen He, Michael P. Zaletel, Masaki Oshikawa, and Frank Pollmann, “Signatures of dirac cones in a dmrg study of the kagome heisenberg model,” Phys. Rev. X 7, 031020 (2017).
- Liao et al. (2017) H. J. Liao, Z. Y. Xie, J. Chen, Z. Y. Liu, H. D. Xie, R. Z. Huang, B. Normand, and T. Xiang, “Gapless spin-liquid ground state in the kagome antiferromagnet,” Phys. Rev. Lett. 118, 137202 (2017).
- Changlani and Läuchli (2015) Hitesh J. Changlani and Andreas M. Läuchli, “Trimerized ground state of the spin-1 heisenberg antiferromagnet on the kagome lattice,” Phys. Rev. B 91, 100407 (2015).
- Liu et al. (2015) Tao Liu, Wei Li, Andreas Weichselbaum, Jan von Delft, and Gang Su, “Simplex valence-bond crystal in the spin-1 kagome heisenberg antiferromagnet,” Phys. Rev. B 91, 060403 (2015).
- Nishimoto and Nakamura (2015) Satoshi Nishimoto and Masaaki Nakamura, “Non-symmetry-breaking ground state of the heisenberg model on the kagome lattice,” Phys. Rev. B 92, 140412 (2015).
- Chubukov (1992) Andrey Chubukov, “Order from disorder in a kagomé antiferromagnet,” Phys. Rev. Lett. 69, 832 (1992).
- Götze et al. (2011) O. Götze, D. J. J. Farnell, R. F. Bishop, P. H. Y. Li, and J. Richter, “Heisenberg antiferromagnet on the kagome lattice with arbitrary spin: A higher-order coupled cluster treatment,” Phys. Rev. B 84, 224428 (2011).
- Oitmaa and Singh (2016) J. Oitmaa and R. R. P. Singh, “Competing orders in spin-1 and XXZ kagome antiferromagnets: A series expansion study,” Phys. Rev. B 93, 014424 (2016).
- Sachdev (1992) Subir Sachdev, “Kagome- and triangular-lattice heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons,” Phys. Rev. B 45, 12377 (1992).
- Balay et al. (1997) Satish Balay, William D. Gropp, Lois Curfman McInnes, and Barry F. Smith, “Efficient management of parallelism in object oriented numerical software libraries,” in Modern Software Tools in Scientific Computing, edited by E. Arge, A. M. Bruaset, and H. P. Langtangen (Birkhäuser Press, 1997) pp. 163–202.
- Balay et al. (2017) Satish Balay, Shrirang Abhyankar, Mark F. Adams, Jed Brown, Peter Brune, Kris Buschelman, Lisandro Dalcin, Victor Eijkhout, William D. Gropp, Dinesh Kaushik, Matthew G. Knepley, Lois Curfman McInnes, Karl Rupp, Barry F. Smith, Stefano Zampini, Hong Zhang, and Hong Zhang, PETSc Users Manual, Tech. Rep. ANL-95/11 - Revision 3.8 (Argonne National Laboratory, 2017).
- Hernandez et al. (2005) Vicente Hernandez, Jose E. Roman, and Vicente Vidal, “SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems,” ACM Trans. Math. Software 31, 351–362 (2005).
- Roman et al. (2017) J. E. Roman, C. Campos, E. Romero, and A. Tomas, SLEPc Users Manual, Tech. Rep. DSIC-II/24/02 - Revision 3.8 (D. Sistemes Informàtics i Computació, Universitat Politècnica de València, 2017).
- Lee and Young (2007) LW Lee and AP Young, “Large-scale monte carlo simulations of the isotropic three-dimensional heisenberg spin glass,” Phys. Rev. B 76, 024405 (2007).
*
Appendix A Classical orphan physics on the kagomé lattice
In this section, we expand on our introductory remarks on orphan spins on corner-sharing lattices and their main signatures in the finite-temperature properties of classical frustrated magnets, with particular emphasis on the kagomé antiferromagnet of interest to us here. To this end, we consider in this section classical spins (vectors of magnitude ), coupled by a bilinear Heisenberg interaction on a network of corner-sharing simplices. For nearest-neighbour interactions, the Hamiltonian can be rewritten in terms of frustrated plaquette terms Moessner and Berlinsky (1999); Henley (2001). We have:
| (3) |
where labels plaquettes in the lattice. This is true for kagomé and pyrochlore and pyrochlore-slab structures, and other structures where all pairs of spin within a plaquette are interacting.
The Hamiltonian written in plaquette language is minimized by setting for all plaquettes Henley (2001). Replacing spins by non-magnetic impurities reduces the number of spins participating in a plaquette term, but the energetic constraint can still be satisfied as long as there is more than one spin in a plaquette. The orphan spin situation illustrated in Fig 1a, corresponds to the case where only one spin is left after substitution with non-magnetic impurities.
As the orphan spin is released from the constraints coming from one plaquette (triangle for the kagomé lattice), one expects that this spin remains “partially free” in some sense. As summarized in the Introduction, this expectation found a precise expression in the idea of a half-orphan degree of freedom in the work of Henley, and of Moessner and Berlinsky Henley (2001); Moessner and Berlinsky (1999). The detailed characterization of the response Sen et al. (2011) indicates that the orphan behaves as a spin object that sees an external field when an external field of is applied. This paramagnetic response of the lone spin is partially screened by the net diamagnetic response of the surrounding spin texture, leading to a net low temperature susceptibility identical to that of a spin , as befits the response of an emergent half-orphan degree of freedom which behaves like a net spin- particle smeared across a few lattice spacings around the orphan Sen et al. (2011).
For the specific case of the kagomé lattice, there is a caveat: The classical spin liquid at intermediate temperatures gives way at low enough temperature to a weakly ordered coplanar state of the classical Heisenberg model, where the coplanarity is itself a symmetry-breaking crossover phenomenon that occurs at , and the subsequent entropically driven choice of coplanar ordered state by anharmonic fluctuations only becomes apparent at even lower temperatures Chern and Moessner (2013); Zhitomirsky (2008); Huse and Rutenberg (1992). The smallness of is fortuitous from the point of view of orphan physics: In the very broad temperature regime in which there is spin liquid behaviour, we expect a pair of vacancies on the same triangle to again nucleate an emergent half-orphan degree of freedom. Below, we confirm via classical Monte Carlo simulations that this is indeed true, although the temperature window in which half-orphan physics is well-established classically is seen to be smaller compared to the pyrochlore-slab lattice Sen et al. (2011).
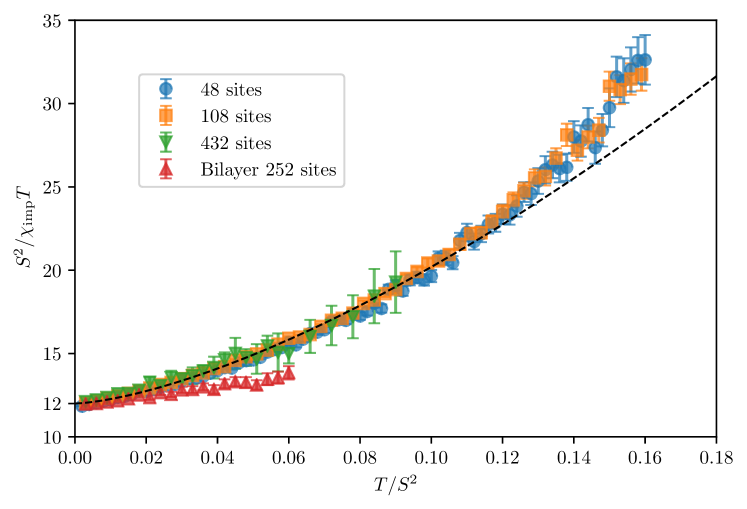
Ref. Sen et al., 2011 showed in the pyrochlore-slab magnet that the difference, denoted in Ref. Sen et al., 2011, of the total magnetic susceptibility between a pure sample (with no impurities) and an otherwise pure sample with two nearest-neighbour non-magnetic impurities (thus creating a single orphan) indeed corresponds to the response of a free spin of length . As for a single free spin, we should analogously expect to see at low temperatures a difference of the form on the kagomé lattice at intermediate temperatures well above the extremely low-temperature crossover to coplanar ordering, but well below the temperature scale set by .
We have computed this difference for several kagomé samples using classical Monte Carlo simulations and standard Metropolis, Wolff cluster and over-relaxation Lee and Young (2007) updates to ensure ergodicity. Our results are displayed in Fig. 14 where we plot as function of to check the dependence with temperature in a clear manner. Data at the lower end of our temperature range converge to the expected constant , and we find a size-independent and smooth deviation away from this result. For sake of completeness, we also reproduced the results of Ref. Sen et al., 2011 for the bilayer with 252 sites, where we find the approach to the limit to be even flatter.
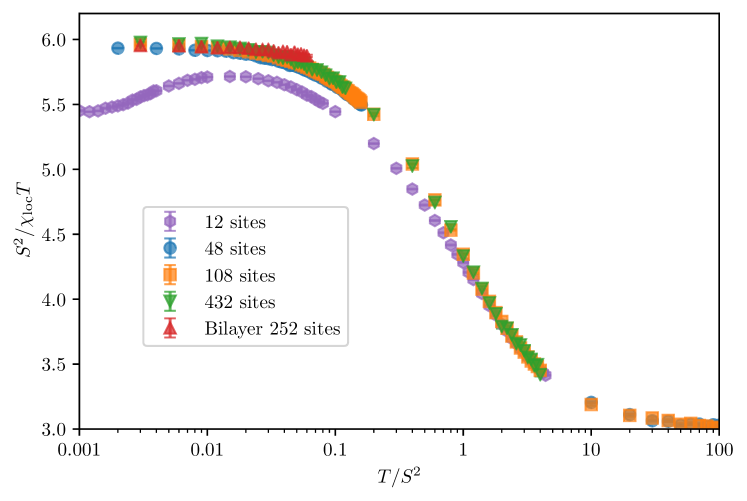
The local susceptibility , should reflect that the orphan spin behaves as a free spin of length in a magnetic field of strength (where is the applied external field). This is expected due to the screening of the magnetic field by the neighbors of the orphan spin Sen et al. (2012). In the low-field linear regime, we thus expect at sufficiently low but not-too-low temperature. Our Monte-Carlo simulations (Fig. 15) are in good agreement with this expectation at low temperatures, with an approximately size-independent peel-off towards the high temperature result of a free spin- at temperature : the data once again displayed as clearly exhibits a crossover from the value (obtained for spin-) at low-temperature to the high-temperature spin- value . Fig. 15 also represents data for the small size cluster of 12 sites which is shown to be already close to the thermodynamic limit (with at most a difference less than 10%). This particular 12-site sample (which is represented in Fig. 1a, along with the location of impurities and the orphan spin) is useful to compare with the quantum simulations reported in the main text, as we are limited to small sizes in our studies of the quantum problem.