Quantum Hall effect originated from helical edge states in Cd₃As₂

Introduction - Since the discovery of the quantum Hall effect in 2D electron gases Klitzing et al. (1980); Thouless et al. (1982), tremendous efforts have been devoted to generalizing the exotic phase of matter to higher dimensions Halperin (1987); Zhang and Hu (2001); Zilberberg et al. (2018), in the absence of magnetic fields Yu et al. (2010); Chang et al. (2013), or nonlinear-response regime Sodemann and Fu (2015); Low et al. (2015); Ma et al. (2019); Kang et al. (2019); Du et al. (2018, 2019). Recently, quantized Hall conductance plateaus have been observed in the topological Dirac semimetal Cd₃As₂, with sample thickness ranging from tens to hundreds of nanometers Zhang et al. (2017, 2019); Nishihaya et al. (2019); Lin et al. (2019); Schumann et al. (2018); Galletti et al. (2018); Uchida et al. (2017); Nishihaya et al. (2018); Kealhofer et al. (2020). One of the mechanisms is a 3D quantum Hall effect supported by the Fermi-arc surface states in the topological semimetal Wang et al. (2017); Lu (2018), which also can support a quantum oscillation Potter et al. (2014); Moll et al. (2016); Zhang et al. (2016). Nevertheless, because the samples are grown along various directions, the nature of the quantum Hall effect in 3D topological semimetals is still in debates (Tab. 1) and has been attracting growing attention.

In this Letter, we report a new mechanism of the quantum Hall effect in topological semimetals. We numerically calculate the Hall conductance of the Dirac-semimetal Cd₃As₂ slabs grown along three experimentally accessible and widely investigated crystallographic directions. For the slab grown along the [001] direction, the magnitude of the quantized Hall conductance increases with the increasing magnetic field, as a result of the Zeeman splitting of the helical edge states on the side surfaces [Fig. 1]. The mechanism was previously ignored and is originated from the nontrivial topology of the confinement induced bulk subbands characterized by the spin Chern number. In contrast, for the slab grown along the [110] direction, the Hall plateaus decrease with the increasing magnetic field, due to the Fermi-arc 3D quantum Hall effect Wang et al. (2017). As a result, the Hall conductance in the slab grown along the [112] direction can be understood as a competition between the helical edge states and Fermi-arc surface states, with Hall plateaus decreasing in the weak-field region but growing in the strong-field region.

Model and method - We start with an effective Hamiltonian for the Dirac semimetal Cd₃As₂ Wang et al. (2013), which reads

where $k_{\pm}=k_{x}\pm ik_{y}$, $\varepsilon_{0}(\mathbf{k})=C_{0}+C_{1}k_{z}^{2}+C_{2}(k_{x}^{2}+k_{y}^{2})$, and $M(\mathbf{k})=M_{0}+M_{1}k_{z}^{2}+M_{2}(k_{x}^{2}+k_{y}^{2})$. The $x$, $y$, and $z$ axes in the Hamiltonian are defined along the [100], [010], and [001] crystallographic directions, respectively. The model hosts two pairs of Weyl nodes at $\mathbf{k}=\left(0,0,\pm k_{\text{w}}\right)$ with the energy $E_{\text{w}}=C_{0}-C_{1}M_{0}/M_{1}$ and $k_{\text{w}}=\sqrt{\left|M_{0}/M_{1}\right|}$. We take the parameters for Cd₃As₂ as $C_{0}=-0.0145$ eV, $C_{1}=10.59$ eVŲ, $C_{2}=11.5$ eVŲ, $M_{0}=0.0205$ eV, $M_{1}=-18.77$ eVŲ, $M_{2}=-13.5$ eVŲ, $A=0.889$ eVÅ Cano et al. (2017). The samples of Cd₃As₂ are usually cleaved or grown along the [110] Schumann et al. (2016), [001] Kealhofer et al. (2020), or [112] directions Nishihaya et al. (2018, 2019). To obtain the dispersion of the Dirac semimetal slab along an arbitrary growth direction, we rotate the $y$ axis to the $y^{\prime}$ axis through the rotation matrix

The [110], [112], and [001] directions correspond to $\left(\theta,\alpha\right)=\left(0,-\pi/4\right)$, $\left(\arctan{\sqrt{2}},-\pi/4\right)$, and $\left(\pi/2,-\pi/4\right)$, respectively. We include a magnetic field always normal to the cleave surface $\mathbf{B}=\left(0,B,0\right)$. The Zeeman term has the form $H_{\text{Zeeman}}=\frac{\mu_{B}}{2}({\bm{\sigma}}\cdot\mathbf{B})\otimes\frac{1}{2}[g_{s}(\sigma_{0}+\sigma_{z})+g_{p}(\sigma_{0}-\sigma_{z})]$, where $\mu_{B}$ is the Bohr magneton, $g_{s}=18.6$ and $g_{p}=2$ are the $g$ factors Jeon et al. (2014).

The Hall conductance for a slab of thickness $L$ can be found as $\sigma_{\mathrm{H}}=\sigma L$, where the Hall conductivity can be found from the Kubo formula Zhang et al. (2014)

where $e$ is the elementary charge, $\hbar$ is the reduced Planck constant, $V_{\text{eff }}$ is the volume of the slab, $\left|\Psi_{\delta}\right\rangle$ is the eigenstate of energy $E_{\delta}$ for $H$ in the $y^{\prime}$-direction magnetic field and open boundaries at $y^{\prime}=\pm L/2,v_{x}$ and $v_{z}$ are the velocity operators, $f(x)$ is the Fermi distribution.

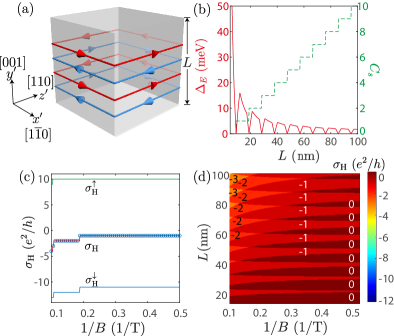
The [001] slab - For a Cd₃As₂ slab grown along the [001] direction, the bulk spectrum is quantized into discrete gapped subbands (See Sec. SI of Sup ) because of the quantum confinement effect Xiao et al. (2015); Pan et al. (2015); Chen et al. (2017). The spectrum opens a gap, which decays with increasing $L$ (probably with an oscillation as well). The effective Hamiltonian $\mathcal{H}_{nn}$ for each subband $n(=1,2,\ldots)$ is equivalent to a quantum spin Hall insulator Qi and Zhang (2011); Hasan and Kane (2010); Bernevig et al. (2006) characterized by the spin Chern number Lu et al. (2010); Sheng et al. (2006); Li et al. (2010) $C_{s}^{n}=(C_{n}^{\uparrow}-C_{n}^{\downarrow})/2$, where $C_{n}^{\uparrow,\downarrow}=\pm\frac{1}{2}\left[\text{sign}\left(M_{0}+M_{1}n^{2}\pi^{2}/L^{2}\right)-\text{sign}\left(M_{2}\right)\right]$ Lu et al. (2010) are the valence-band Chern numbers of the spin-up and spin-down blocks of the $n$-th subband. Each Chern number $C_{n}^{\uparrow/\downarrow}$ represents a chiral edge state circulating around the side surfaces [Fig. 1(a)]. The total spin Chern number $C_{s}=\sum_{n}{C_{s}^{n}}$ is equal to the number of pairs of helical edge states. As shown in Fig. 1(b), the oscillatory decay of the band gap with increasing $L$ is always accompanied by the variation of the spin Chern number $C_{s}$ at each dip. In the Dirac semimetal Na₃Bi, a topological phase transition to the quantum spin Hall state has been observed Collins et al. (2018).

However, the spin Chern number is not measurable because the measurable Hall conductance is associated with the total Chern number $\sigma_{\text{H}}=\frac{e^{2}}{h}\sum_{n,s=\uparrow,\downarrow}{C_{n}^{s}}$, which is zero in the absence of the magnetic field because of time-reversal symmetry. A magnetic field can break time-reversal symmetry as well as the balance between $C^{\uparrow}_{n}$ and $C^{\downarrow}_{n}$, leading to measurable Hall conductance $\sigma_{\text{H}}$ whose magnitude increases with increasing magnetic field, as shown in Figs. 1(c-d). We also plot the Hall conductance $\sigma_{\text{H}}^{\uparrow,\downarrow}$ for the spin-up and spin-down blocks of the Hamiltonian [Fig. 1(c)], which confirms that the non-zero quantum Hall conductance is originated from the field-induced imbalance between counter-propagating chiral edge states. Also, Fig. 1(d) shows that the Hall conductance approaches zero for thinner slabs because of the mixing of counter-propagating chiral edge states. This mechanism due to the splitting of helical edge states was previously ignored and could benefit the further experimental explorations.

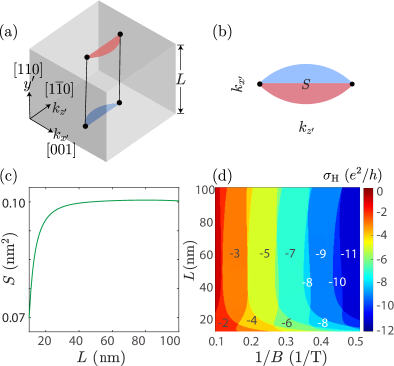
The [110] slab - In contrast to the above [001] case, for a semimetal slab grown along the [110] and equivalent [100] or [011] direction, there exists a 3D quantum Hall effect Wang et al. (2017); Li et al. (2020) arising from the Fermi-arc surface states Potter et al. (2014); Zhang et al. (2016). On each of the top and bottom surfaces of a Weyl semimetal, there are topologically-protected surface states, which can be regarded as half of a 2D electron gas. Their open Fermi surfaces are dubbed as the Fermi arcs. The 2D Fermi-arc surface states on opposite surfaces can be connected through the bulk states to form a complete 2D electron gas with a 3D spatial distribution and closed Fermi surface [Figs. 2(a)-(c), red for top and blue for bottom surfaces], to support a “3D” quantum Hall effect Wang et al. (2017). A Dirac semimetal can be regarded as two time-reversed Weyl semimetals to host two copies of the Fermi-arc quantum Hall effect. In addition, in a Dirac semimetal, the Fermi-arc surface states and their time-reversal partners on a single surface can form a 2D electron gas Kargarian et al. (2016), to support a quantum Hall effect as well. For both cases, the Hall conductance plateaus are supposed to decrease with increasing magnetic field, much like those in conventional 2D electron gases Klitzing et al. (1980), where the magnetic field presses the occupation of electrons to lower Landau levels, as shown in Figure 2(d) for different slab thickness $L$.

Moreover, Fig. 2(d) shows that the width of the quantized plateaus is stable for thicker slabs ($L>50$ nm), while show obvious variations for ultrathin slabs ($L<20$ nm) with decreasing thickness. This can be understood using Figs. 2(b-c), where the area of the Fermi loop $S$ converges to a constant for thick slabs but decreases exponentially with decreasing $L$, due to the hybridization of the opposite surfaces in ultrathin slabs. According to the Lifshitz-Onsager relation, $S$ determines the plateau width of the Hall conductance, which explains the quantized pattern in Fig. 2(d). Moreover, in Dirac semimetals $E_{\text{F}}$ shifts away from $E_{\text{w}}$ as the Zeeman effect splits $E_{\text{w}}$ (See Sec. SIII of Sup ), leading to a systematic shift of the Hall plateaus with increasing thickness [Fig. 2(d)].

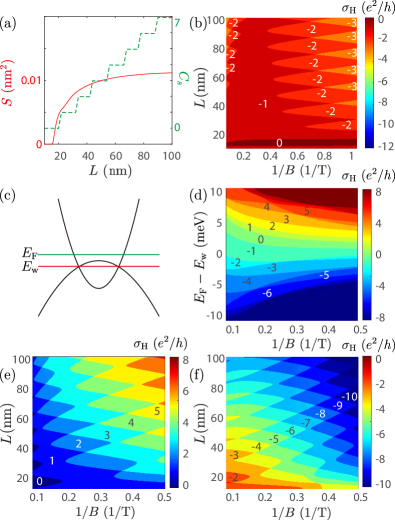
The [112] slab - The slabs along the [112] direction inherits the properties of both the confinement-induced helical edge states in the [001] slab and Fermi-arc surface states in the [110] slab. Figure 3(b) shows the Hall conductance of the slab along the [112] direction as a function of $1/B$ for different $L$. For weak magnetic fields [$1/B>0.4\text{ (1/T)}$], the oscillation pattern of the quantized Hall conductance is similar to that of the [110] slab, that is, the Hall plateaus decrease with increasing magnetic field, which indicates the quantized conductance is mainly originated from the Fermi-arc surface states. Compared to the [110] slab, the width of the plateaus is larger because of the smaller area enclosed by the Fermi arc $S$ [Fig. 3(a)]. For strong magnetic fields [$1/B<0.4\text{ (1/T)}$], the Hall conductance increases with increasing magnetic field, similar to that in the [001] slab, indicating that it is mainly contributed by the imbalance of the helical edge states.

Above, the Fermi energy is assumed to cross the Weyl nodes, i.e., $E_{\text{F}}=E_{\text{w}}$ [see Fig. 3(c) for the definitions of $E_{\text{F}}$ and $E_{\text{w}}$]. Figure 3(d) shows $\sigma_{\text{H}}$ in the $\left(E_{\text{F}}-E_{\text{w}},1/B\right)$ plane with $L=50$ nm. For the Fermi energies far away from the Weyl nodes, the quantum Hall effect is originated from the confinement-induced bulk subbands [Figs. 3(e)-(f)], and the Hall conductance monotonically decreases with increasing magnetic field for different thickness and Fermi energies, different from the non-monotonic dependence when $E_{\text{F}}=E_{\text{w}}$ or small $E_{F}-E_{w}$.

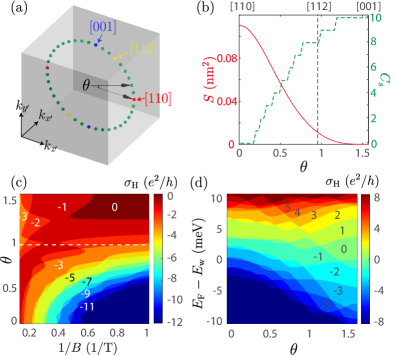
The angle dependence - Figure 4(a) illustrates the dependence on $\theta$, the angle between the line connecting the Dirac nodes and the $k_{x^{\prime}}$-$k_{z^{\prime}}$ plane. For example, the Dirac nodes are located on the $k_{x^{\prime}}$-$k_{z^{\prime}}$ plane when $\theta=0$ [Figs. 2(a-b)]. Figure 4(b) shows that $S$ decreases and $C_{s}$ increases with increasing $\theta$, indicating the competition between the Fermi-arc surface states and side-surface helical edge states. Figure 4(c) shows $\sigma_{\text{H}}$ as a function of $\theta$ and $1/B$ for $L=100$ nm. For $\theta=0$ ([110] direction) and $\theta=\pi/2$ ([001] direction), the quantized conductance is only contributed by the Fermi-arc surface states and imbalanced helical edge states, respectively. For other $\theta$, the quantized Hall conductance originates from both the Fermi-arc surface states and the helical edge states. Furthermore, $\sigma_{\text{H}}$ as a function of $\left(E_{\text{F}}-E_{\text{w}},\theta\right)$ [Fig. 4(d)] shows that the quantum Hall effect may be due to the confinement-induced bulk subbands, giving another origin for the experimentally observed quantum Hall effect in Cd₃As₂ Uchida et al. (2017); Nishihaya et al. (2018). In experiments, it may be difficult to distinguish whether the thickness dependent conductance plateaus are consequences of the bulk subbands or the Fermi-arc surface states. The non-monotonic dependence of $\sigma_{\text{H}}$ on the magnetic field may play another significant role to detect the side-surface helical edge states or Fermi-arc 3D quantum Hall effect in a [112] Dirac semimetal slab.

Discussion - Above, we have shown that the Hall plateaus can be attributed to the Fermi-arc surface states, confinement-induced bulk subbands, and helical side-surface edge states. It may be challenging to distinguish them in a standard Hall-bar device. The helical side-surface edge states can be identified through the nonlocal measurements Roth et al. (2009). Furthermore, in Sec. SIV of Sup , we propose two different local transport devices, which may help revealing the mechanism of the observed quantum Hall effects in experiments.

Note Added. - Recently, we became aware of a complementary study, which focuses on the quantum Hall states in topological semimetals confined in different directions Nguyen et al. (2021).