Quantum Many-body Scars through the Lens of Correlation Matrix
Abstract
Quantum many-body scars (QMBS)—rare eigenstates that evade thermalization—are typically characterized by their low entanglement entropies compared to surrounding thermal eigenstates. However, due to finite-size effects in systems accessible via exact diagonalization, this measure can be ambiguous. To address this limitation, we propose using the correlation matrix spectrum as an alternative probe to identify QMBS. In cases of exact QMBS with either known analytic expressions or can be captured by various frameworks of QMBS, we find the dimensionality of the null space of the correlation matrix—an integer value, and thus immune to finite-size effects—can qualitatively isolate QMBS. Beyond serving as a diagnostic tool, the correlation matrix method enables easy manipulation of the QMBS subspace. For approximate QMBS, such as those in the PXP model, we observe that the correlation matrix spectrum features numerous approximate zero eigenvalues, distinguishing these states. We demonstrate the effectiveness and utility of this method with several paradigmatic QMBS examples.
Introduction. With rapid advances in preparing and manipulating quantum states across various artificial quantum platforms, there has been growing interest in understanding how a generic isolated quantum system thermalizes after a quench [1, 2, 3, 4, 5, 6]. The universal thermalization imposes stringent constraints on the eigenstates of generic interacting quantum systems, and a widely accepted framework is the eigenstate thermalization hypothesis (ETH), which posits that locally an eigenstate encodes the information of a thermal ensemble [7, 8, 9, 10, 11]. Except for systems that are integral [12, 13, 14] or with emergent integrability such as the many-body localized systems [15, 16, 5], the validity of ETH has been confirmed in numerous numerical studies [17, 3]. Moreover, it was believed that the ETH applies in the strong sense that it holds for every eigenstate with finite energy density [18].
However, the ETH has recently been challenged by persistent oscillations of local observables after a quench in a Rydberg atom chain [19]. Shortly after, it is shown that the ETH in the effective PXP model is valid only in the weak sense: it breaks down for a measure-zero subset of eigenstates [20, 21]. These special outliers, drawing analogy to single-particle phenomena [22], were dubbed quantum many-body scars (QMBS), or simply scar states. This discovery sparked intense ongoing research, significantly expanding our understanding of QMBS [23, 24, 25]. For example, Shiraishi and Mori have constructed a framework to embed a target space spanned by scar states in a nonintegrable model [26]. Families of Hamiltonians hosting QMBS with closed analytic expressions and equidistant energy separation have also been constructed from symmetry and quasisymmetry perspectives [27, 28, 29, 30, 31, 32]. In parallel, in the spirit of -paring states in the Hubbard model [33, 34], the Mark–Lin–Motrunich (MLM) framework [35] and the equivalent spectrum generating algebra (SGA) formalism [36] have provided unified explanations of scar states discovered across different models [37, 38, 39, 40, 41, 42, 43].
However, due to the varying principles underlying those constructions, a unified framework for QMBS is still lacking [24]. As a result, the origin of QMBS in specific models is often addressed on a case-by-case basis. Moreover, theoretical analysis can often become quite involved, making it difficult to identify potential connections between different frameworks. For example, it is unclear whether the second family of QMBS in the spin-1 XY model can be captured by existing formalisms [41, 44]. Additionally, controlling the scar subspace is often challenging. On the numerical side, the entanglement entropy is commonly used to identify QMBS due to their characteristic low-entanglement nature [45]. However, because of the limited system sizes accessible via exact diagonalization, finite-size effects can make it difficult to reliably distinguish QMBS using this approach.
In this Letter, we show that these problems can be well addressed using the correlation matrix spectrum as a tool for characterizing and diagnosing QMBS. For exact QMBS, including those not captured by previous formalisms, we find the dimensionality of the kernel of the correlation matrix—being an integer and immune to finite-size effects— differs from that of thermal eigenstates. This number thus provides a sharp qualitative probe of QMBS, superior to the quantitative probe of entanglement entropy. For approximate QMBS, such as those in the PXP model, the distinct feature of numerous approximate zero eigenvalues in the correlation matrix spectrum also allow us to single out QMBS from thermal eigenstates.
Correlation Matrix. Our work is primarily motivated by the information perspective of the ETH. According to this hypothesis, the diagonal matrix element of a local observable, , with respect to a thermal eigenstate approaches the thermal ensemble average as the system size increases [8, 9, 3]
| (1) |
where is the partition function and represents the inverse temperature (with ). This implies that a thermal eigenstate encodes sufficient information to infer the underlying Hamiltonian, consistent with the fact that a wavefunction has exponentially many components, while a local Hamiltonian has only extensively many parameters. In other words, one might not able to reconstruct the Hamiltonian from a low-entangled QMBS. These ideas are solidified by using the correlation matrix, originally introduced in [46], as an operational tool for reconstructing the underlying local Hamiltonian from a single eigenstate. Let be a wave function, and let denote a real vector space of Hermitian operators spanned a set of operator basis that acts on . For an arbitrary Hermitian operator , we have the the following inequality
| (2) |
where , and is orthogonal to , i.e., . This inequality can be casted into a quadratic form
| (3) |
where is a vector of coefficients, and is the real symmetric correlation matrix defined as
| (4) |
The correlation matrix is positive semidefinite, and equality in the quadratic form is attained only when belongs to its null space, . In this case, the corresponding is referred to as an eigenoperator of , meaning . Let denote the dimensionality of the null space of . We can then construct linear-independent eigenoperators of . If the original Hamiltonian belongs to the chosen operator space , then the uniqueness of Hamiltonian reconstruction from thermal eigenstates is equivalent to [46]. We shall see below exact QMBS are characterized by a often much larger .
Exact QMBS. A paradigmatic model that hosts exact QMBS is the one-dimensional Affleck–Kennedy–Lieb–Tasaki (AKLT) Hamiltonian
| (5) |
where is the spin-1 operator at site , and is the identity operator [47, 37, 38]. The known series of QMBS have eigenenergies of and are captured by the SGA formalism. Their explicit form is given by
| (6) |
where is the ground state of the AKLT model and with being the spin-1 raising operator at site [36, 35]. Interestingly, this scar tower is stable against certain disorder perturbations: they persist as eigenstates of the following disordered Hamiltonian ,
| (7) |
where indexes lattice sites, and are restricted to take in the summation, are arbitrary complex numbers, and inside the parenthesis is the total spin , total magnetization state of two spins at sites and [35].
To show that the number of correlation matrix zeros can distinguish scar states from thermal eigenstates, we start with simple range-2 local basis . Just like Pauli matrices for spin- systems, we can use the standard generators of the SU(3) group, the eight Gell-Mann matrices , together with the identity matrix to define the operator bases ,
| (8) |
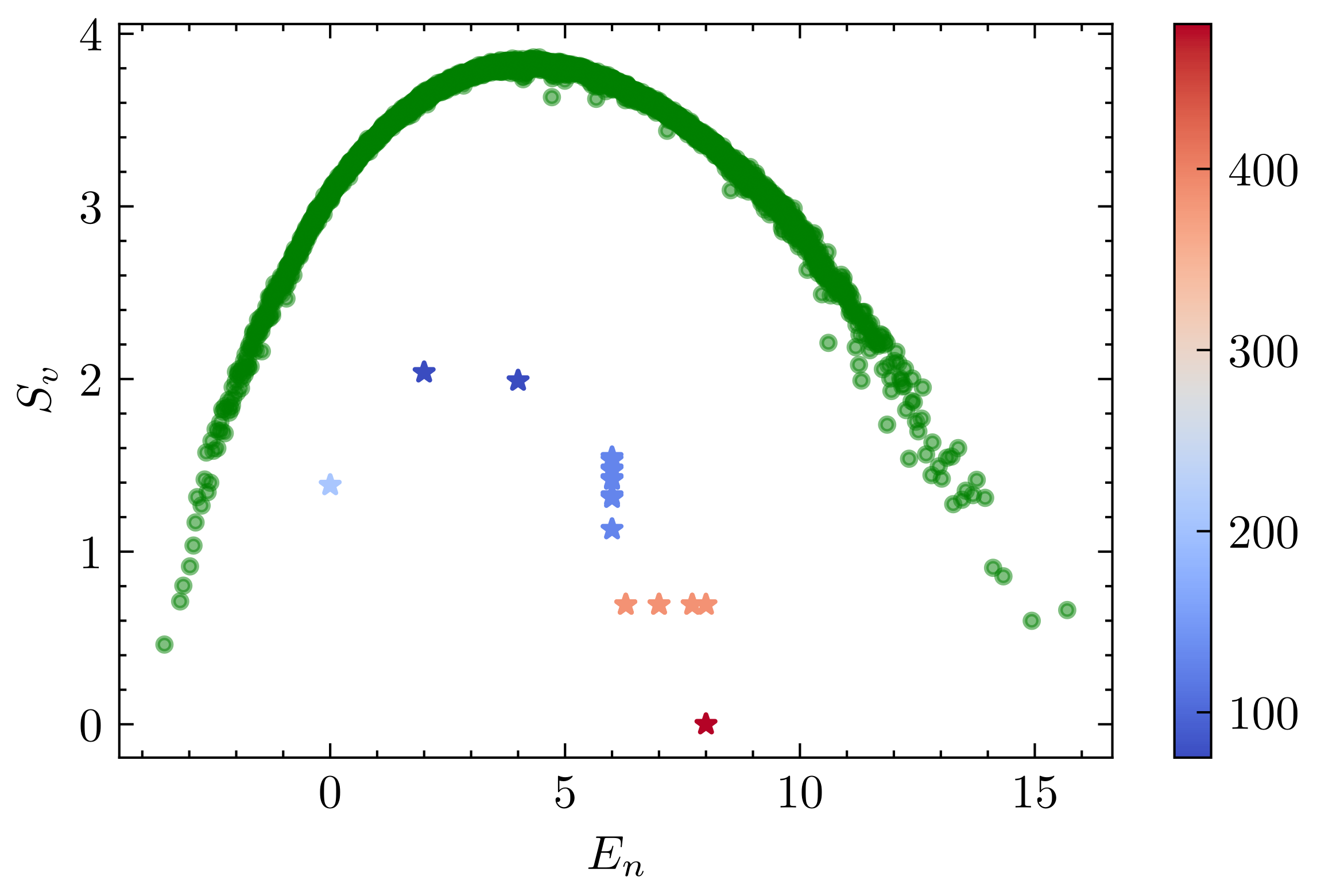
where labels the lattice sites ( is identified as ) and acts nontrivially only on sites and . Here and so that we include all single-site and two-site operators but exclude the trivial identity operator, which makes the correlation matrix of dimension . Since we can linearly combine to construct the Hamiltonian (7), we have for every eigenstate. As illustrated in Fig. 1, eigenstates with energies indeed exist and are numerically check to correspond to SGA scar states . Additionally, other scar states with anomalously low bipartite entanglement entropies are observed. On the side of correlation matrix spectrum, all thermal eigenstates unanimously have , meaning the original Hamiltonian can be reconstructed from a single thermal eigenstate [46]. In contrast, all the scar states exhibit larger values of , making the correlation matrix zeros a reliable qualitative probe for scar states. This stands in contrast to the quantitative probe of entanglement entropy, which is prone to finite-size effects.
Furthermore, analytical results otherwise difficult to derive can be obtained. Further analysis shows that, at least for , the minimal number of of SGA scar states satisfies . This number has to be compared with the known Hermitian eigenoperators of the SGA scar state: the Hamiltonian ; the total magnetization ; Hermitian disorder terms in . This means there is an additional linearly independent range-2 operator, denoted as , that is the eigenoperator of all SGA scar states. Thus, the most general range-2 Hamiltonian hosting the SGA scar states is where is an arbitrary real number. The explicit form of is given by
| (9) |
where in matrix representation reads
| (10) |
with accurate to machine precision. We have also tested that for even system sizes ranging from to , the constructed operator annihilates all the SGA scars in the AKLT model. Although the prime numbers appearing in suggest the difficulty of deriving this result analytically, it can be easily obtained by analyzing the null space of the correlation matrix numerically. For the additional scar states, we have successfully obtained their analytical expressions as well 111The theoretical analysis is quite involved, and the detailed study in left in Appendix A.. In short, these states are highly excited states of the AKLT Hamiltonian that are preserved under inclusion of the disorder term .
Scar Embedding and Compatibility. In addition to providing a qualitative diagnosis of scar states, the correlation matrix framework enables flexible manipulation of the scar state subspace and offers insight into its internal structure. Let denote the eigenoperator space of , which is the operator space spanned by , where is the null eigenvector of the correlation matrix constructed from . Given two eigenstates and of a Hamiltonian , if , then we can always select an operator from and add it to the original Hamiltonian to construct a new Hamiltonian,
| (11) |
of which but not remains an eigenstate. To illustrate this, we use the disordered AKLT model (7) as an example. Scar states in this model include the ferromagnetic state where , the single-magnon state,
| (12) |
where in the summation and () is the quasimomentum, and several other families such as the SGA tower 222Refer to Appendix A for details.. A detailed analysis of the eigenoperator spaces reveals that,
| (13) |
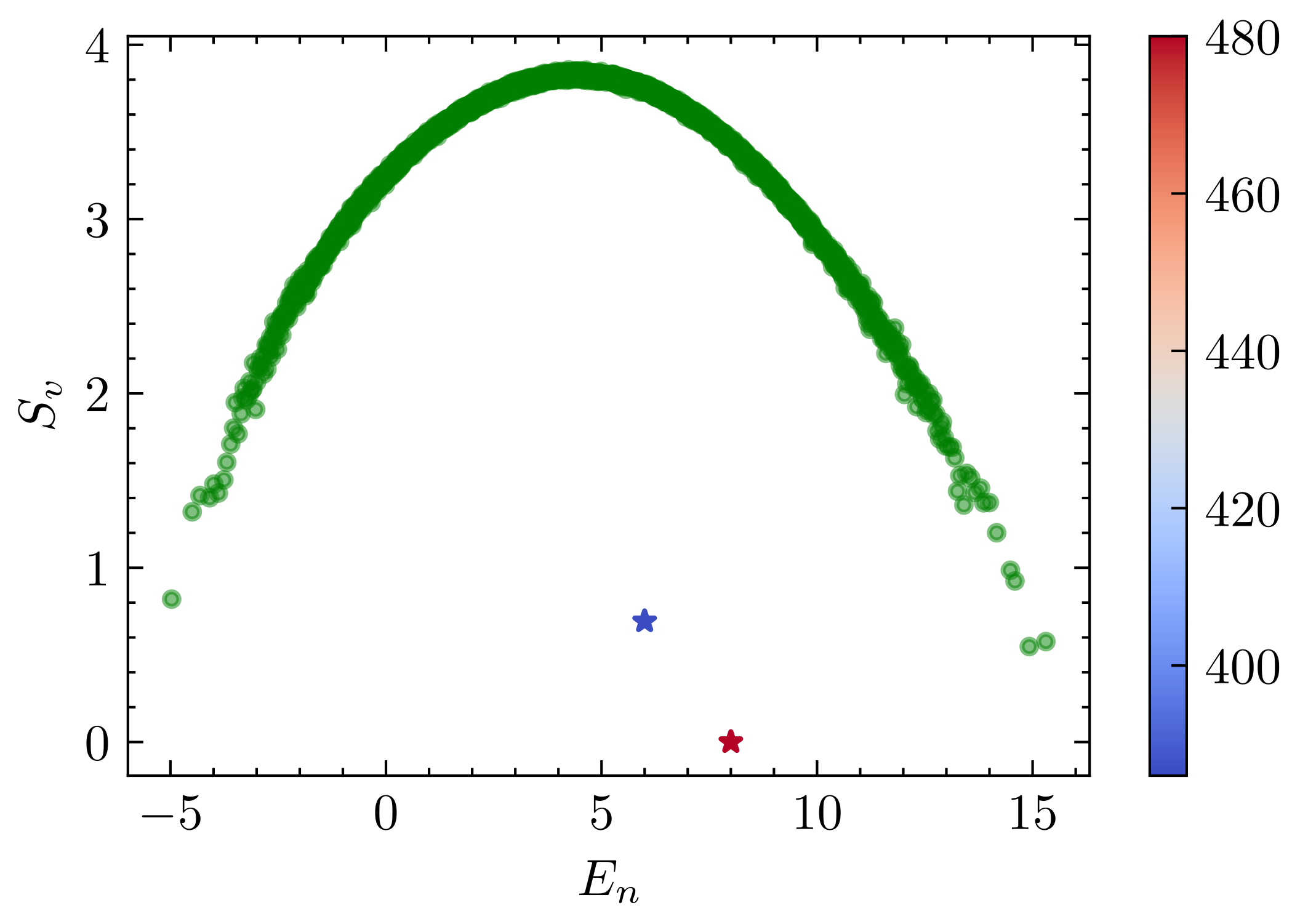
and that is not a subset of the eigenoperator space of any other scar. Moreover, although the dimension of is the same for all , their individual eigenoperator spaces are different. This means that we can construct a Hamiltonian to retain any given and as the only scar states. We can also add terms to make the unique scar state. However, for Hamiltonian with with on-site and nearest-neighbor interactions, if is a scar state, is necessarily an eigenstate. As shown in Fig. 2, we can construct a Hamiltonian where and are random numbers to embed scar space spanned by and . Similarly, since the eigenoperator space is not a subset of any other scar, we can construct a Hamiltonian with as the only scar state 333Refer to Appendix B for an in-depth analysis of the scar eigenoperator spaces and scar embedding examples..
Unification and Generality. Our method of using correlation matrix zeros to probe exact QMBS unifies many mathematical frameworks. To illustrate the generality of our approach, we consider three prominent examples: the Shiraishi–Mori framework, the non-Abelian Lie algebra construction, and the SGA formalism. In the Shiraishi–Mori formalism [26], the scarring Hamiltonian takes the following form
| (14) |
where are a set of local projectors that annihilate the scar subspace , are some local Hermitian operators, and is some Hamiltonian that satisfies . It follows that for any scar state , the projector is an eigenoperator of and each contributes a zero eigenvector to the correlation matrix for appropriate large operator space . This means that for any scar state where is the number of projectors , which distinguish it from thermal eigenstates. Similarly, in the “tunnels to towers” construction [32], the scarring Hamiltonian take the following form
| (15) |
where is a Hamiltonian with non-Abelian symmetry to endow the spectrum with a degenerate subspace, consists of a linear combination of generators in the Cartan subalgebra to lift the degeneracy, and a final Hamiltonian that annihilates a targeted subspace is needed to break symmetries and promote to a scar subspace. In this case, is also an eigenoperator for the scar states, making it detectable via the correlation matrix approach.
To demonstrate that our method also captures QMBS in the SGA formalism [36], it is convenient to use the equivalent Mark–Lin–Motrunich (MLM) framework [35]
| (16) |
where is the scar subspace, is the Hamiltonian, and is the ladder operator that repeatedly acts on a reference eigenstate to generates the whole scar tower . Therefore, as long as and are sum of local operators with maximum range , the left hand, denoted as , of (16) is of sum of local operators. Although is in general not Hermitian, this can be easily remedied by choose the operator basis to be non-Hermitian and subsequently modify the form of correlation matrix as
| (17) |
The correlation matrix is then a positive semidefinite Hermitian matrix and annihilator is also one-to-one correspondence with the null eigenvector of . In fact, as demonstrated in the disordered AKLT model, even using a Hermitian operator basis with a real symmetric is often sufficient in detecting scar states.
Approximate QMBS. For several paradigmatic exact QMBS we have tested 444Refer to Appendix C for extra examples of QMBS in the spin-1 XY model which also includes references [54]. , all scar states distinguish themselves from thermal eigenstates by having a much larger . However, for approximate scars with neither known analytic expressions nor can be captured by previous mathematical formalisms, the single number may be inadequate. A prime example of this is the well-known PXP model, described by the following Hamiltonian [20, 21]
| (18) |
where is the projection operator at site , and and are standard Pauli operators. Except for special eigenstates in the middle of the spectrum, the analytic expressions of QMBS are, in general, unavailable [52]. In our correlation matrix study, we choose the matrix representation of range- operator basis acting on lattice sites as
| (19) |
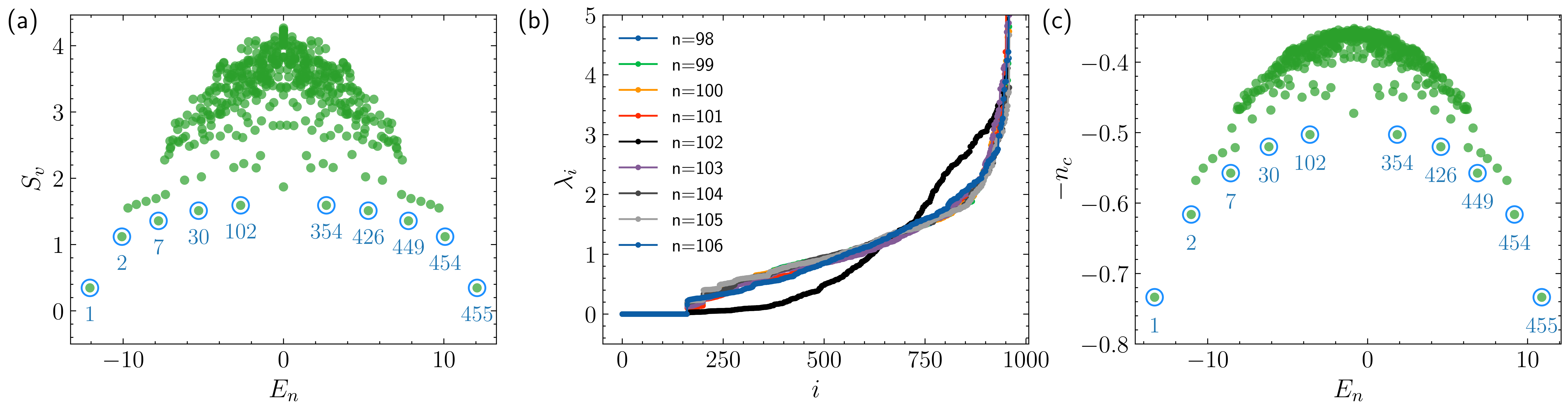
where denotes identity and three Pauli matrices for and , respectively. As before, is restricted to while other take . This ensures that our operator basis excludes trivial identity operators but includes all nontrivial local operators up to range . We employ periodic boundary conditions in our study. As shown in Fig. 3(b), the scar state (colored black) has the same as those of thermal eigenstates, which is associated with the Rydberg blockade condition. However, the correlation matrix spectrum reveals marked differences between the scar states and the thermal states. To quantify these differences, we introduce the following measure analogous to the role of entanglement entropy in quantifying quantum entanglement
| (20) |
to characterize the correlation matrix spectrum, where the summation over is restricted to nonzero values and is the total number of nonzero . As can be seen from Fig. 3(c), the introduced quantity effectively distinguishes scar states from thermal eigenstates. Moreover, is less sensitive to finite-size effects compared to entanglement entropy, making it a more reliable probe.
Summary. We have introduced a new method to detect quantum many-body scars (QMBS) using the correlation matrix spectrum. For exact QMBS, we demonstrate that the integer , the number of zero eigenvalues, can qualitatively distinguish scar states from thermal eigenstates. In this regard, functions similarly to how symmetry and topological numbers are used to classify phases of matter. Our method not only unifies many previous framework of QMBS, similar to the recent commutant algebra formalism [53] which we learned after the main idea is developed, but also is quite accessible and flexible. It enables the straightforward derivation of otherwise obscure analytic results, manipulation of the scar subspace, and insights into its internal constraints. For approximate QMBS where may fall short, one can introduce quantities such as to characterize scar states, leveraging the presence of multiple approximate zero eigenvalues in the spectrum. Given the versatility of the correlation matrix approach, we anticipate that its applications will extend beyond the study of QMBS.
Acknowledgments. We thank Hui Zhai, Lei Pan, and Shang Liu for numerous useful discussions. We also thank Shang Liu for carefully reading our manuscript and valuable feedback. We acknowledge support by NSFC Grant No. 12304288 (Z. Y.), No. 12247101 (Z. Y.), and No. 12374477 (P. Z.).
.1 Appendix A: The Nature of Additional QMBS in the Disordered AKLT Model
As discussed in the main text, we discovered additional QMBS in the disordered AKLT model, , beyond the known SGA scar states. For convenience, we shall reproduce the Hamiltonian here,
| (21) |
where is the standard AKLT Hamiltonian, the summation over and is restricted to , and are arbitrary complex numbers. Given that a series of low-entanglement eigenstates beyond the ground state have been recently identified [37], we hypothesize that some of these states remain eigenstates with the addition of the disordered term . In the following, we demonstrate that this is indeed the case. To facilitate this analysis, we first introduce the Schwinger boson representation. Since we are dealing with spins, the Schwinger boson creation (annihilation) operators () and () at site satisfy the following constraint,
| (22) |
The local basis () are then obtained by acting on the vacuum state of no bosons with Schwinger boson creation operators
| (23) |
For assist theoretical analysis, we introduce some graphical notations: a labeled circle represents a local site, an up arrow for , a down arrow for , and an right line with middle arrow connecting sites and , , for the singlet operator . The state is then obtained by acting the operators on the boson vacuum state . For example, according to (23), the state represented by the following figure
in the spin basis reads
| (24) |
And the ground state of the standard AKLT Hamiltonian can be represented as
| (25) |
With these notations in place, we now proceed to demonstrate that certain low-entangled eigenstates are annihilated by the disordered term , meaning they remain eigenstates of the disordered AKLT Hamiltonian.
The ferromagnetic state
The fully polarized ferromagnetic state is an eigenstate of the Hamiltonian with eigenenergy , as , and is annihilated by the disordered term. The action of on the ground state can be illustrated as
| (26) |
and thus . The highest SGA scar state, , corresponds to when is even, but does not exist when is odd. Therefore, as long as is even, we have a series of scar states with energies , and we shall ascribe as part of SGA scar family for convenience.
Single-magnon state
The single-magnon state defined below (normalization which are unimportant are omitted from below)
| (27) |
where with is the lattice momentum, and in the spin basis reads
| (28) |
This state is known to be the eigenstate of the AKLT Hamiltonian . Since is a sum of projectors , where projects onto the total spin state between neighboring sites, it follows that,
| (29) |
where we have used and , with subscripts suppressed for clarity. Equation (29) describes a single-particle hopping model, making an eigenstates of . Furthermore, since the total any neighboring spins is either one or two, is annihilated by disorder terms, for . Therefore, also remains an eigenstate of the disordered AKLT Hamiltonian . The eigenenergy of is . Alongside the SGA scars, which have eigenenergies , these states account for all scar states except for the degenerate ones at .
state
The state with
| (30) |
is another family of low-entangled eigenstates of the AKLT Hamiltonian . The maximum is for even and for odd . Here the two-dimer basis graphically reads (configurations at irrelevant sites suppressed)
| (31) | ||||
| (32) |
for and , and for
| (33) |
From this Schwinger boson representation, it is evident that with remains the eigenstate of . This is because the minimum for any pair of neighboring sites is one, and therefore is annihilated by the disorder term . The building block of is given by
| (34) |
where irrelevant site configurations have been omitted for clarity, and the first and the last term cancel upon summation. In the local spin basis representation, when considering the action of on , only the bonds and are relevant. For the bond , we have
| (35) |
and for the bond , we have
| (36) |
Neither of these bonds contains components of . Hence is annihilated by the disorder term , and remains an eigenstate of . However, the state in local spin basis reads
| (37) |
and in can not be annihilated by , meaning ceases to be an eigenstate of the disordered AKLT model.
state
One can also superpose to form the following eigenstate of the AKLT Hamiltonian
| (38) |
where the lattice momentum has to satisfy for even and for odd . The total number of states is therefore . Given that and with are all annihilated by the disorder term as discussed previously, all these states remain eigenstates of . Nevertheless, not all these states are linearly independent with previously discussed scar states, in particular we have the following relation [37]
| (39) |
state
The previously discussed states, , , , and , are all highest weight states within families of eigenstates of the AKLT Hamiltonian . By acting on these states with the global spin ladder operator , one generates additional eigenstates of with reduced total magnetization. Given the relations and , any neighboring spins of state only contain components of and . Consequently, this state is annihilated by the disorder term, . Therefore, remains an eigenstate of the disordered AKLT Hamiltonian .
state
The previously discussed states account all but one scar state in the disordered AKLT model. To reveal the nature of the missing one, it is easier to start with the following state
| (40) |
This state is an eigenstate of as does not contain component of . However, is linearly dependent with previously discussed scar states, and the missing scar state is actually . To demonstrate this, it suffices to show that
| (41) |
which would imply that is annihilated by the disorder part . We can rewrite this relation as follows (for ),
where the factor arises because the components of neighboring spins in only contain and . Moreover, the combination does not contain a component, proving that for . Thus, is annihilated by the disorder term and is an eigenstate of the disordered AKLT Hamiltonian .
From this, it is also evident why is not an eigenstate: has overlap with in .
This concludes our discussion of all the numerically identified scar states in the disordered AKLT model. To summarize, the scar states are as follows:
-
•
SGA scar states , where we include the ferromagnetic state in this tower for odd ;
-
•
with a total number ;
-
•
with if is even and if is odd;
-
•
with a total number ;
-
•
Two additional states: and , where .
Since is linearly dependent with and , the total number of scars state is if is even, and if is odd. This has been confirmed numerically for .
.2 Appendix B: Scar Eigenoperator Spaces in Disordered AKLT Model
In this section, we provide further details on the eigenoperator spaces of QMBS in the disordered AKLT model (21). As mentioned in the main text, the minimal of the SGA scars is . Specifically, for tested system sizes ranging from to , the correlation matrices of the scar states have a common null space of dimension . Moreover, this space is a proper subset of the intersection of null spaces of the other SGA scars, , which is of dimension . This means that there exists an eigenoperator that can be added to the Hamiltonian to destroy the middle SGA scars . This operator is a sum of local operators
| (42) |
and the expression of depends on whether is even or odd. Omitting the subscript for simplicity, we have
| (43) |
for odd , and
| (44) |
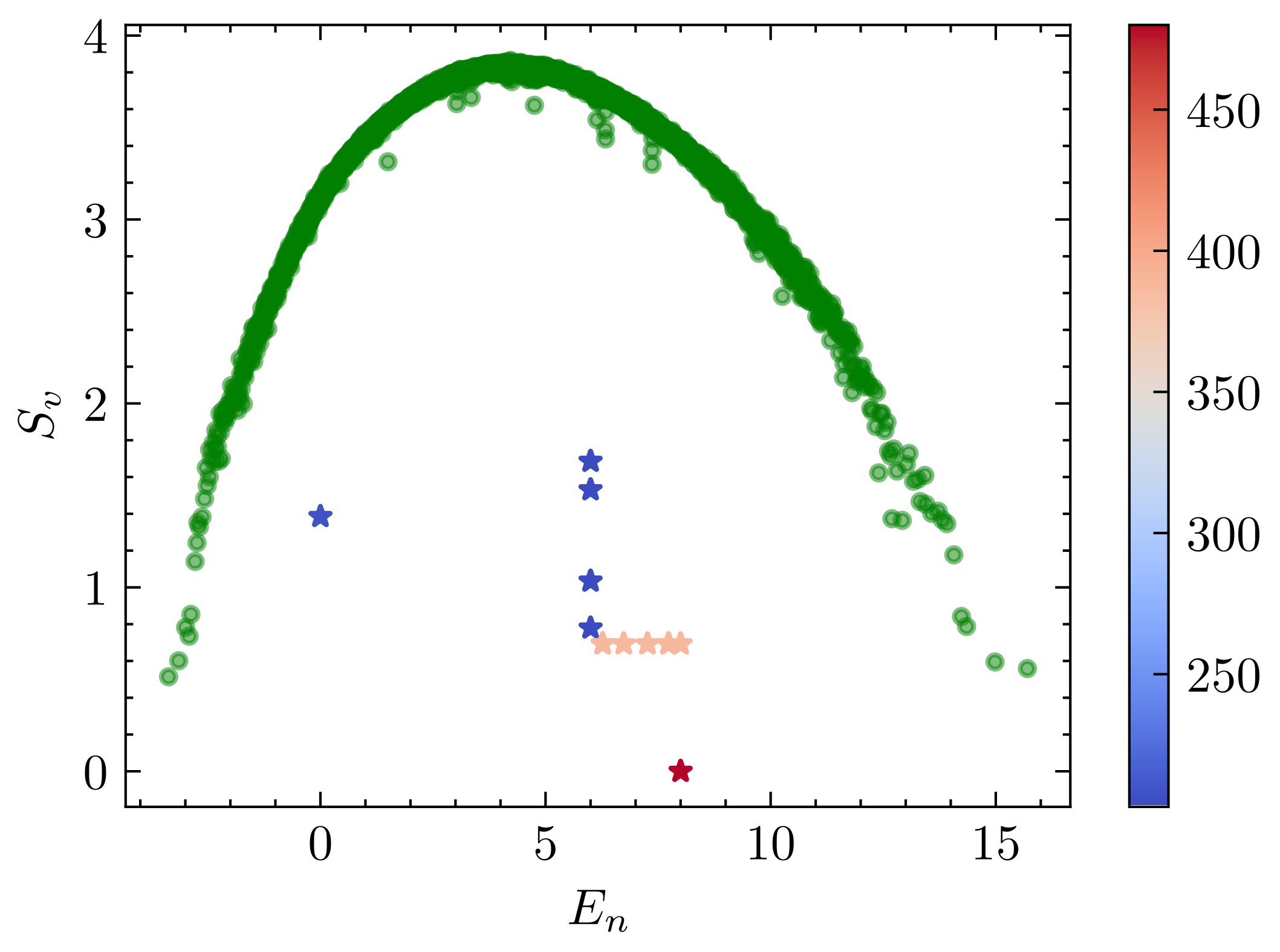
for even . Although we have used and to make the expression as simple as possible, the final expressions remain cumbersome and difficult to interpret. Conversely, these intricate expressions demonstrate the strength and flexibility of our method. As shown in Fig. 4, the middle SGA scars are indeed destroyed when () is added to the original Hamiltonian.
The ferromagnetic state , owing to its simplicity, has the largest eigenoperator space dimension. On the other hand, the ground state of the AKLT Hamiltonian, , is unique in that its null space is not a subset of any other scar states, including the ferromagnetic state. This implies that we can construct a Hamiltonian of the form
| (45) |
where are random real numbers and are eigenoperators that embeds as the only scar state. As shown in Fig. 5, such embedding Hamiltonian successfully isolates as the only scar state.
.3 Appendix C: Exact Scars in the Spin-1 XY Model
We next apply our method to the one-dimensional spin-1 XY model whose Hamiltonian is given by
| (46) |
where () are spin-1 operators at site , denote nearest neighbors, is the external magnetic field strength, and is the anisotropy parameter. The last term, which couples spins at sites and , is included to break a nonlocal SU(2) symmetry under open boundary conditions (OBC) [54]. We shall first focus on OBC, where the scar states admit the following analytic expression,
| (47) |
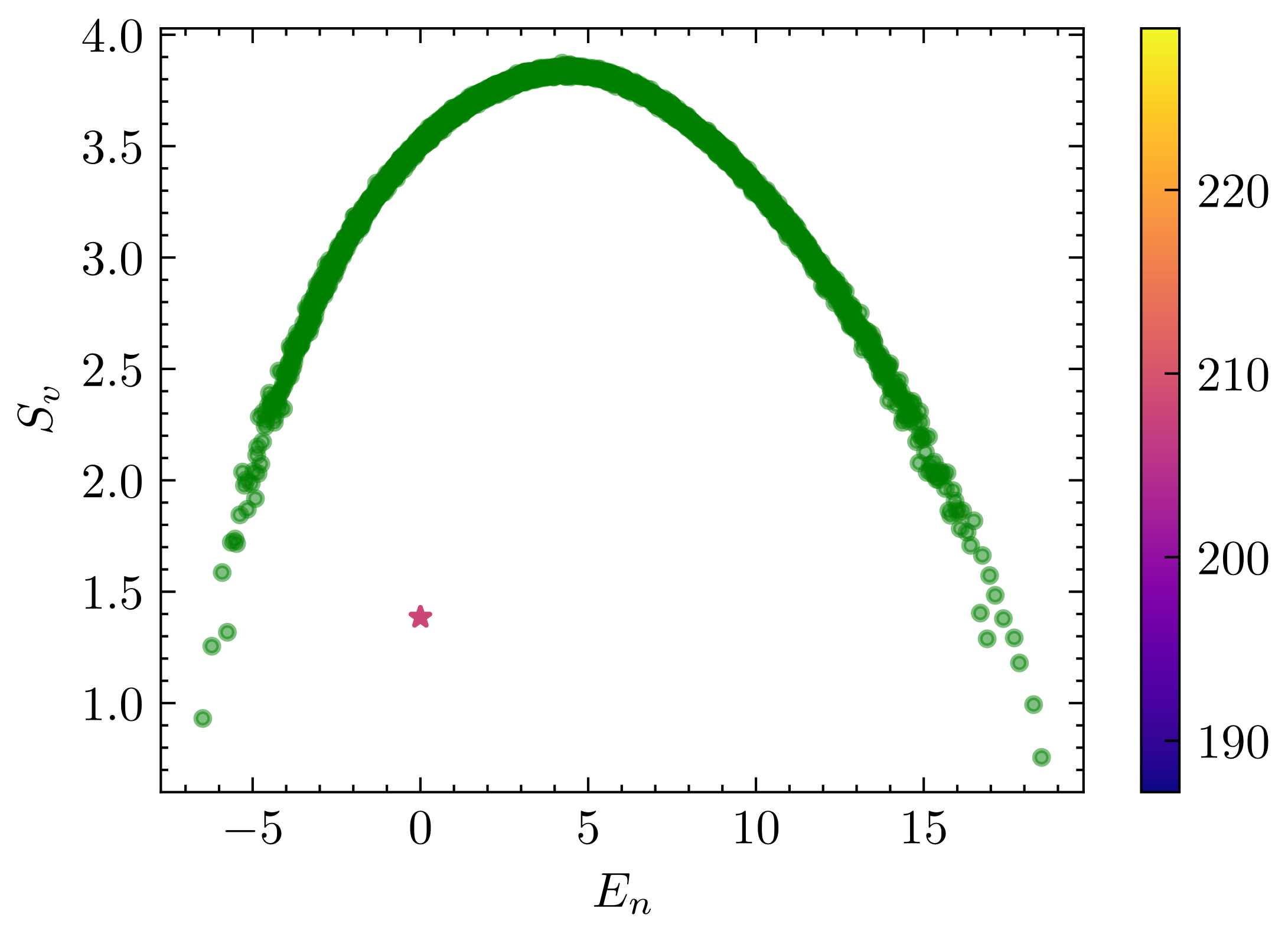
Here , is the fully polarized down state, where is the ladder operator at site . The normalization factor is not essential for our discussion. Under OBC, the system exhibits both spatial reflection symmetry and spin inversion symmetry in the zero total magnetization sector, and we shall perform computation in symmetry-resolved sectors. The operator basis is chosen to be the same as that of the spin-1 AKLT model. Since the last term of the Hamiltonian (46) does not belong the operator space , the Hamiltonian will not manifest itself as a null vector of the correlation matrix. As shown in Fig. 6, all thermal eigenstates have correlation matrix zero , which corresponds to the eigenoperator of total magnetization operator . In contrast, the scar state has a significantly larger .
For periodic boundary conditions with , the model admits another family of scar states [41]
| (48) |
However, due to a twisted SU(2) symmetry in even magnetization sectors, we study the following modified Hamiltonian
| (49) |
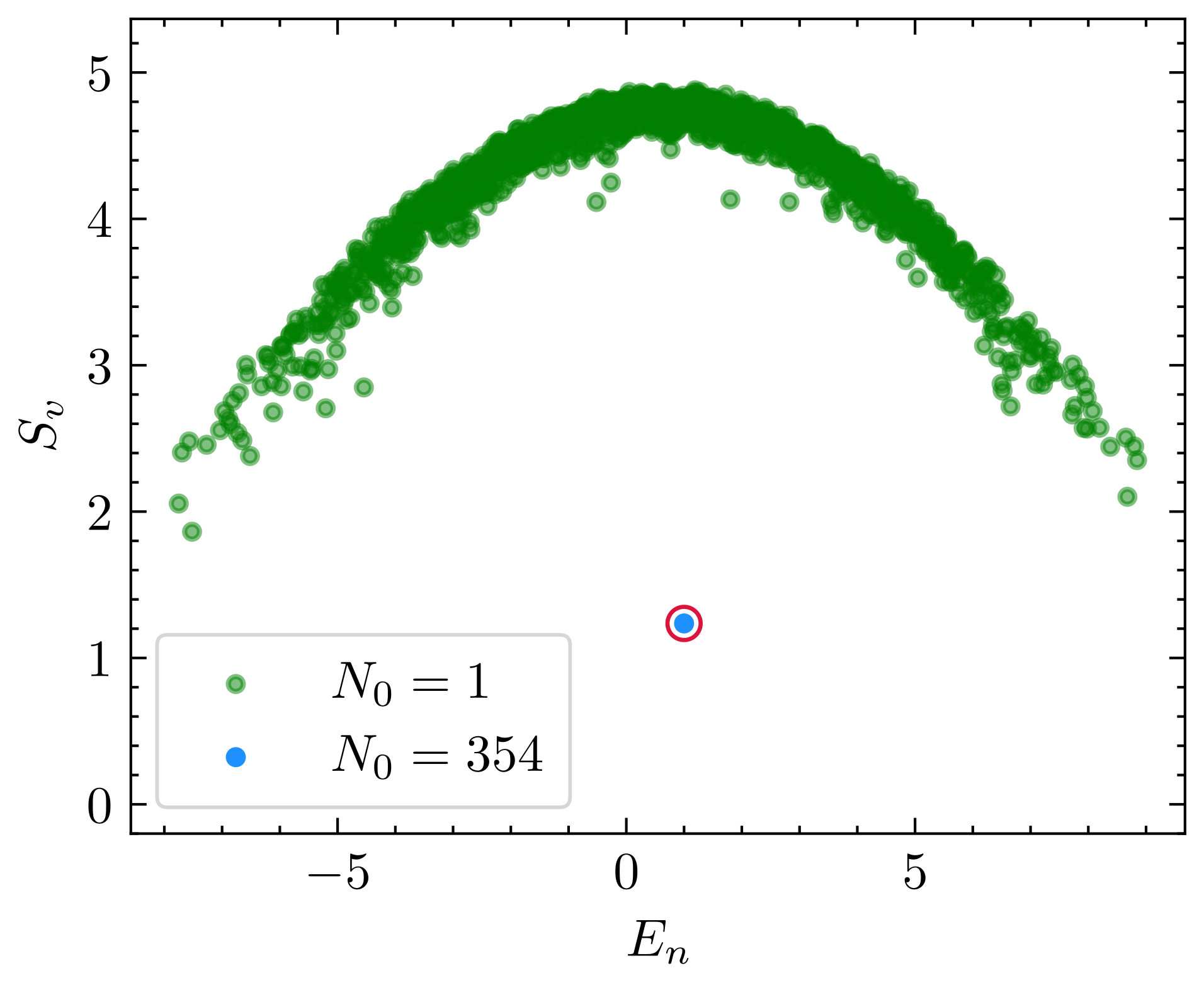
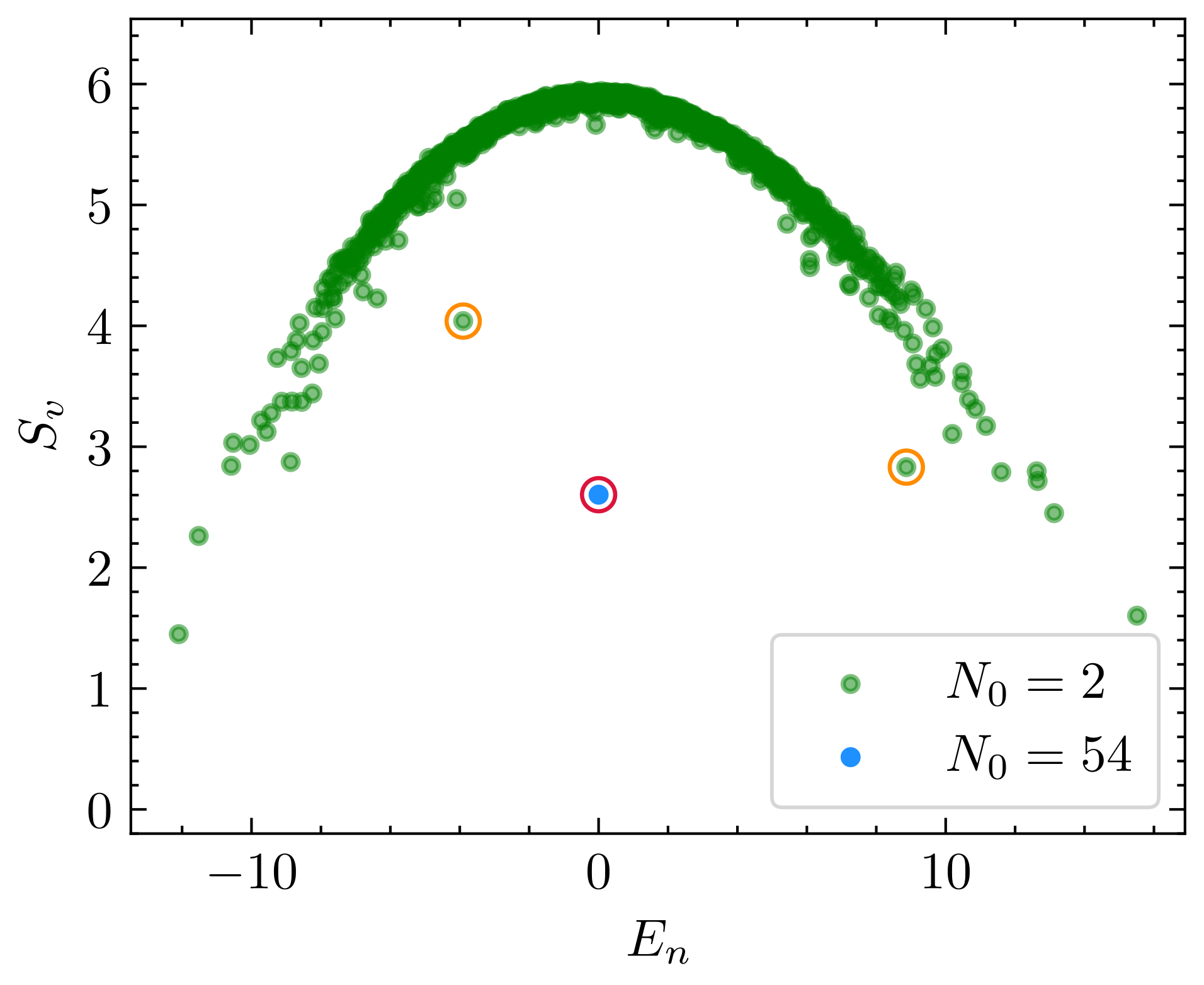
where the last term serves to break integrability [44]. This system preserves several symmetries: conservation of total magnetization , lattice translation, spacial reflection, and spin inversion (which maps to at site ). For our analysis, we focus on the , lattice momentum , and both spatial reflection and spin inversion symmetric sector. The operator basis is chosen to be the same as the disordered AKLT model. As seen in Fig. 7, the thermal eigenstates uniformly have , corresponding to the original Hamiltonian and the total magnetization operator . The scar state is distinguished by having a much larger . Although this scar state can be identified by its low entanglement entropy, the correlation matrix zero provides a qualitative probe rather than a quantitative one. Additionally, finite-size effects make it challenging to conclude whether the points circled in orange are scar states or not.
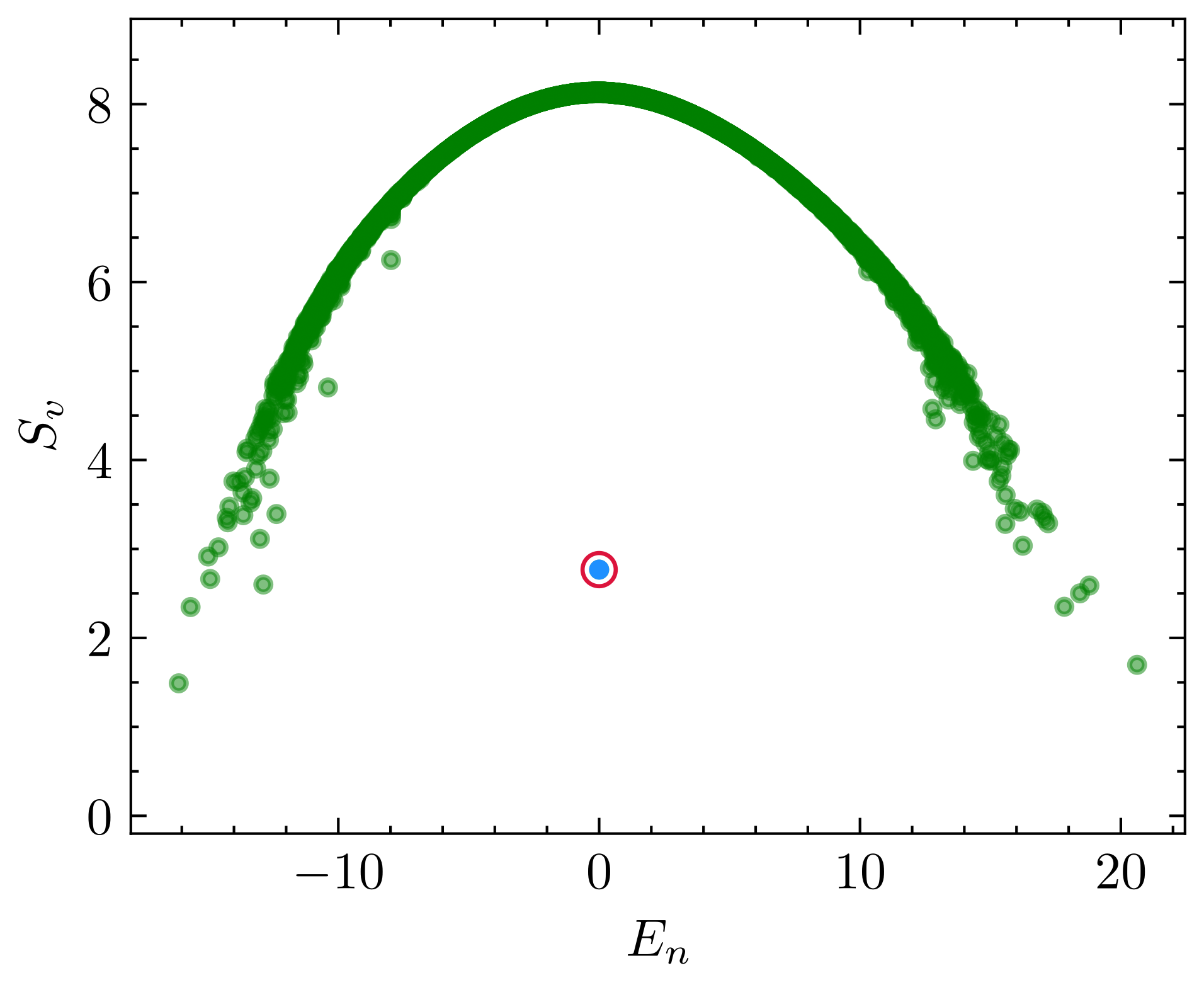
After refining our algorithm, we successfully extended the entanglement entropy spectrum calculation to system size . As can be seen from Fig. 8, only the state (circled red) has anomalously low entanglement entropy compared to those of surrounding thermal eigenstates, which reinforces our confidence that the points circled in orange in Fig. 7 are not QMBS.
References
- Nandkishore and Huse [2015] R. Nandkishore and D. A. Huse, Many-Body Localization and Thermalization in Quantum Statistical Mechanics, Annu. Rev. Condens. Matter Phys. 6, 15 (2015).
- Borgonovi et al. [2016] F. Borgonovi, F. Izrailev, L. Santos, and V. Zelevinsky, Quantum chaos and thermalization in isolated systems of interacting particles, Phys. Rep. 626, 1 (2016).
- D’Alessio et al. [2016] L. D’Alessio, Y. Kafri, A. Polkovnikov, and M. Rigol, From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics, Adv. Phys. 65, 239 (2016).
- Mori et al. [2018] T. Mori, T. N. Ikeda, E. Kaminishi, and M. Ueda, Thermalization and prethermalization in isolated quantum systems: A theoretical overview, J. Phys. B: At. Mol. Opt. Phys. 51, 112001 (2018).
- Abanin et al. [2019] D. A. Abanin, E. Altman, I. Bloch, and M. Serbyn, Colloquium: Many-body localization, thermalization, and entanglement, Rev. Mod. Phys. 91, 021001 (2019).
- Ueda [2020] M. Ueda, Quantum equilibration, thermalization and prethermalization in ultracold atoms, Nat. Rev. Phys. 2, 669 (2020).
- Deutsch [1991] J. M. Deutsch, Quantum statistical mechanics in a closed system, Phys. Rev. A 43, 2046 (1991).
- Srednicki [1994] M. Srednicki, Chaos and quantum thermalization, Phys. Rev. E 50, 888 (1994).
- Srednicki [1999] M. Srednicki, The approach to thermal equilibrium in quantized chaotic systems, J. Phys. A: Math. Gen. 32, 1163 (1999).
- Dunjko and Olshanii [2012] V. Dunjko and M. Olshanii, Thermalization from the Perspective of Eigenstate Thermalization Hypothesis, in Annual Review of Cold Atoms and Molecules, Annual Review of Cold Atoms and Molecules, Vol. 1 (World Scientific, Singapore, 2012) pp. 443–471.
- Deutsch [2018] J. M. Deutsch, Eigenstate thermalization hypothesis, Rep. Prog. Phys. 81, 082001 (2018).
- Franchini [2017] F. Franchini, An Introduction to Integrable Techniques for One-Dimensional Quantum Systems (Springer, Cham, 2017).
- Rigol et al. [2007] M. Rigol, V. Dunjko, V. Yurovsky, and M. Olshanii, Relaxation in a Completely Integrable Many-Body Quantum System: An Ab Initio Study of the Dynamics of the Highly Excited States of 1D Lattice Hard-Core Bosons, Phys. Rev. Lett. 98, 050405 (2007).
- Vidmar and Rigol [2016] L. Vidmar and M. Rigol, Generalized Gibbs ensemble in integrable lattice models, J. Stat. Mech. 2016, 064007 (2016).
- Gornyi et al. [2005] I. V. Gornyi, A. D. Mirlin, and D. G. Polyakov, Interacting Electrons in Disordered Wires: Anderson Localization and Low- Transport, Phys. Rev. Lett. 95, 206603 (2005).
- Basko et al. [2006] D. M. Basko, I. L. Aleiner, and B. L. Altshuler, Metal–insulator transition in a weakly interacting many-electron system with localized single-particle states, Ann. Phys. 321, 1126 (2006).
- Rigol et al. [2008] M. Rigol, V. Dunjko, and M. Olshanii, Thermalization and its mechanism for generic isolated quantum systems, Nature 452, 854 (2008).
- Kim et al. [2014] H. Kim, T. N. Ikeda, and D. A. Huse, Testing whether all eigenstates obey the eigenstate thermalization hypothesis, Phys. Rev. E 90, 052105 (2014).
- Bernien et al. [2017] H. Bernien, S. Schwartz, A. Keesling, H. Levine, A. Omran, H. Pichler, S. Choi, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić, and M. D. Lukin, Probing many-body dynamics on a 51-atom quantum simulator, Nature 551, 579 (2017).
- Turner et al. [2018a] C. J. Turner, A. A. Michailidis, D. A. Abanin, M. Serbyn, and Z. Papić, Weak ergodicity breaking from quantum many-body scars, Nat. Phys. 14, 745 (2018a).
- Turner et al. [2018b] C. J. Turner, A. A. Michailidis, D. A. Abanin, M. Serbyn, and Z. Papić, Quantum scarred eigenstates in a Rydberg atom chain: Entanglement, breakdown of thermalization, and stability to perturbations, Phys. Rev. B 98, 155134 (2018b).
- Heller [1984] E. J. Heller, Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits, Phys. Rev. Lett. 53, 1515 (1984).
- Serbyn et al. [2021] M. Serbyn, D. A. Abanin, and Z. Papić, Quantum many-body scars and weak breaking of ergodicity, Nat. Phys. 17, 675 (2021).
- Moudgalya et al. [2022] S. Moudgalya, B. A. Bernevig, and N. Regnault, Quantum many-body scars and Hilbert space fragmentation: A review of exact results, Rep. Prog. Phys. 85, 086501 (2022).
- Chandran et al. [2023] A. Chandran, T. Iadecola, V. Khemani, and R. Moessner, Quantum Many-Body Scars: A Quasiparticle Perspective, Annu. Rev. Condens. Matter Phys. 14, 443 (2023).
- Shiraishi and Mori [2017] N. Shiraishi and T. Mori, Systematic Construction of Counterexamples to the Eigenstate Thermalization Hypothesis, Phys. Rev. Lett. 119, 030601 (2017).
- Pakrouski et al. [2020] K. Pakrouski, P. N. Pallegar, F. K. Popov, and I. R. Klebanov, Many-Body Scars as a Group Invariant Sector of Hilbert Space, Phys. Rev. Lett. 125, 230602 (2020).
- Pakrouski et al. [2021] K. Pakrouski, P. N. Pallegar, F. K. Popov, and I. R. Klebanov, Group theoretic approach to many-body scar states in fermionic lattice models, Phys. Rev. Res. 3, 043156 (2021).
- Sun et al. [2023] Z. Sun, F. K. Popov, I. R. Klebanov, and K. Pakrouski, Majorana scars as group singlets, Phys. Rev. Res. 5, 043208 (2023).
- Ren et al. [2021] J. Ren, C. Liang, and C. Fang, Quasisymmetry Groups and Many-Body Scar Dynamics, Phys. Rev. Lett. 126, 120604 (2021).
- Ren et al. [2022] J. Ren, C. Liang, and C. Fang, Deformed symmetry structures and quantum many-body scar subspaces, Phys. Rev. Research 4, 013155 (2022).
- O’Dea et al. [2020] N. O’Dea, F. Burnell, A. Chandran, and V. Khemani, From tunnels to towers: Quantum scars from Lie algebras and -deformed Lie algebras, Phys. Rev. Research 2, 043305 (2020).
- Yang [1989] C. N. Yang, pairing and off-diagonal long-range order in a Hubbard model, Phys. Rev. Lett. 63, 2144 (1989).
- Yang and Zhang [1990] C. N. Yang and S. Zhang, SO4 symmetry in a Hubbard model, Mod. Phys. Lett. B 04, 759 (1990).
- Mark et al. [2020] D. K. Mark, C.-J. Lin, and O. I. Motrunich, Unified structure for exact towers of scar states in the Affleck-Kennedy-Lieb-Tasaki and other models, Phys. Rev. B 101, 195131 (2020).
- Moudgalya et al. [2020a] S. Moudgalya, N. Regnault, and B. A. Bernevig, -pairing in Hubbard models: From spectrum generating algebras to quantum many-body scars, Phys. Rev. B 102, 085140 (2020a).
- Moudgalya et al. [2018a] S. Moudgalya, S. Rachel, B. A. Bernevig, and N. Regnault, Exact excited states of nonintegrable models, Phys. Rev. B 98, 235155 (2018a).
- Moudgalya et al. [2018b] S. Moudgalya, N. Regnault, and B. A. Bernevig, Entanglement of exact excited states of Affleck-Kennedy-Lieb-Tasaki models: Exact results, many-body scars, and violation of the strong eigenstate thermalization hypothesis, Phys. Rev. B 98, 235156 (2018b).
- Moudgalya et al. [2020b] S. Moudgalya, E. O’Brien, B. A. Bernevig, P. Fendley, and N. Regnault, Large classes of quantum scarred Hamiltonians from matrix product states, Phys. Rev. B 102, 085120 (2020b).
- Mark and Motrunich [2020] D. K. Mark and O. I. Motrunich, -pairing states as true scars in an extended Hubbard model, Phys. Rev. B 102, 075132 (2020).
- Schecter and Iadecola [2019] M. Schecter and T. Iadecola, Weak Ergodicity Breaking and Quantum Many-Body Scars in Spin-1 XY Magnets, Phys. Rev. Lett. 123, 147201 (2019).
- Iadecola and Schecter [2020] T. Iadecola and M. Schecter, Quantum many-body scar states with emergent kinetic constraints and finite-entanglement revivals, Phys. Rev. B 101, 024306 (2020).
- Shibata et al. [2020] N. Shibata, N. Yoshioka, and H. Katsura, Onsager’s Scars in Disordered Spin Chains, Phys. Rev. Lett. 124, 180604 (2020).
- Chattopadhyay et al. [2020] S. Chattopadhyay, H. Pichler, M. D. Lukin, and W. W. Ho, Quantum many-body scars from virtual entangled pairs, Phys. Rev. B 101, 174308 (2020).
- Papić [2022] Z. Papić, Weak Ergodicity Breaking Through the Lens of Quantum Entanglement, in Entanglement in Spin Chains: From Theory to Quantum Technology Applications, edited by A. Bayat, S. Bose, and H. Johannesson (Springer, Cham, 2022) pp. 341–395.
- Qi and Ranard [2019] X.-L. Qi and D. Ranard, Determining a local Hamiltonian from a single eigenstate, Quantum 3, 159 (2019).
- Affleck et al. [1987] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Rigorous results on valence-bond ground states in antiferromagnets, Phys. Rev. Lett. 59, 799 (1987).
- Note [1] The theoretical analysis is quite involved, and the detailed study in left in Appendix A.
- Note [2] Refer to Appendix A for details.
- Note [3] Refer to Appendix B for an in-depth analysis of the scar eigenoperator spaces and scar embedding examples.
- Note [4] Refer to Appendix C for extra examples of QMBS in the spin-1 XY model which also includes references [54].
- Lin and Motrunich [2019] C.-J. Lin and O. I. Motrunich, Exact Quantum Many-Body Scar States in the Rydberg-Blockaded Atom Chain, Phys. Rev. Lett. 122, 173401 (2019).
- Moudgalya and Motrunich [2023] S. Moudgalya and O. I. Motrunich, Exhaustive Characterization of Quantum Many-Body Scars using Commutant Algebras (2023), arXiv:2209.03377 [cond-mat, physics:math-ph, physics:quant-ph] .
- Kitazawa et al. [2003] A. Kitazawa, K. Hijii, and K. Nomura, An SU(2) symmetry of the one-dimensional spin-1 XY model, J. Phys. A: Math. Gen. 36, L351 (2003).