Quantum Searches in a Hard 2SAT Ensemble
Abstract
Using a recently constructed ensemble of hard 2SAT realizations, that has a unique ground-state we calculate for the quantized theory the median gap correlation length values along the direction of the quantum adiabatic control parameter . We use quantum annealing (QA) with transverse field and a linear time schedule in the adiabatic control parameter . The gap correlation length diverges exponentially in the median with a rate constant , while the run time diverges exponentially with . Simulated classical annealing (SA) exhibits a run time rate constant that is small and thus finds ground-states exponentially faster than QA. There are no quantum speedups in ground state searches on constant energy surfaces that have exponentially large volume. We also determine gap correlation length distribution functions over the ensemble that at are close to Weibull functions with i.e., the problems show thin catastrophic tails in . The inferred success probability distribution functions of the quantum annealer turn out to be bimodal.
keywords:
Spin Glass , Monte Carlo , Quantum Adiabatic Computation1 Introduction
The purpose of the paper is to elaborate on the aspects of search efficiency’s in quantum ground state searches in specific models, toy models for that matter. We expand our theoretical knowledge and consider a mathematical theory, namely two-satisfiability (2SAT) that within Cook’s classification [1] of mathematical complexity lies in for sure. In that case mathematical rules of calculation are known, that solve any problem as a function of the number of degrees of freedom just in polynomial time. To be specific: Any 2SAT problem is mapped to a directed graph of implications, which then is analyzed for logical collisions: A task that algorithmically can be accomplished in polynomial compute time and knowing all collisions actually determines the ground-state in satisfiable instances. A comparable situation is encountered in the planar Ising glass without external field, where also algorithms exist that find ground-states in polynomial time, see [2].
The current work complements a recent work on synthetic ensembles of hard 2SAT [3] problems, which in vicinity of the satisfiability threshold of random 2SAT at [4], and for satisfiable instances are designed to hide a unique ground state of the 2SAT Hamiltonian at energy from a vast number of non-solutions at the energy gap . Biasing toward hard problems follows an idea of Znidaric [5, 6] for 3-SAT, which is worked out further in [3] for K-SAT with . The ensemble of hard 2SAT realizations has a exponential divergence
| (1.1) |
for the density of states function in the median of the ensemble at energy . The numeric value of the rate constant for 2SAT equals the entropy density at energy one and is a numeric model parameter without physical meaning. It parametrizes a doubling of the number of energy one configurations if about two new spins are added to the theory. Thus any stochastic search for the single ground state at within the energy one surface is expected to have serious problems. We expect this to be true for simulated annealing (SA) [7] as well as well for quantum annealing (QA) [8, 9, 10, 11, 12, 13] and we consider quantum adiabatic computations [14] to be a version of quantum annealing. It is important to note that our problems are not generated by heuristics but have a proper partition function representation.
Our study is part of a research effort that studies quantum annealing for the Ising Hamiltonian in terms of local Pauli matrices and two-point spin couplings at finite magnetic field :
| (1.2) |
where the first two terms denote the problem Hamiltonian. The particular 2SAT Hamiltonian of this work, and after a trivial reduction step from logical literals to Ising spins, has in fact the exact form of the problem part in eq.(1.2). The ensemble of problems has non-vanishing magnetic fields , frustration via sign alternating two-point couplings , bounded couplings and , a finite classical energy gap of unity and is defined on a non-planar connectivity graph at rather sparse connectivity: there are only two-point couplings at spin number . If anything: The satisfiability problem as studied here represent a particular hard and simple synthetic problem class for physical annealers within the set of all realizations of the form .
Within the last decade it has been argued [11, 14, 15, 16] that quantum annealing in general and in particular for frustrated Ising degrees of freedom can show faster convergence to the ground state of the problem Hamiltonian than classical annealing, see also the extensive reviews [17, 18]. We think however that as of today it is fair to say that for Hamiltonian’s of the form eq.(1.2) there is no convincing demonstration, that any frustrated Ising theory on non-planar connectivity graphs shows in fact a speedup in quantum annealing over classical annealing in the limit of large , a view that is also shared in [19] and even is experimentally studied [20, 21] on an existing annealing device with negative finding. Recent quantum annealing numerical studies in the 2D glass enhance the skepticism [22]. The findings of this work also do not suggest that quantum speedups are easy to obtain. In fact: The Ising model realizations of this work exhibit a clear and indisputable exponential speedup of simulated annealing over quantum annealing. We note that additional studies in other satisfiability theories like 3-XORSAT [24, 25, 26] and 3-SAT [23, 6, 27] showed, that quantum annealing does not solve these theories efficiently either.
Finally an important motivation of the current work is the presentation of precise numerical data for the energy gap at the quantum transition, which can be confronted to other approaches that deal with quantum search complexity. These include the semi-perturbative evaluation of the quantum energy gap [28], Quantum Monte Carlo annealing [11, 29, 15, 30] as well as annealing studies under Schrödinger wave function dynamics [31, 32]. We expect that algorithmic studies e.g. studies of simulated quantum annealing can profit as the problem ensemble here has small number of spins, while at the same time the maximal quantum gap correlation length is as large as for a theory with only spins.
2 Theory, Observables and Basic Observations on Annealing
2.1 Theory
We consider 2SAT problems with Boolean variables and clauses. In 2-satisfiability one tries to find a truth assignment to the variables that makes the conjunctive normal form
| (2.1) |
of clauses true, if that is possible in which case a problem is satisfiable. There are literals with and . Each literal being a variable or its negation and if the assignment of variables to literals and possible negations are chosen at random the issue is non-trivial. The problem is equivalent to finding ground-states at energy of the Hamiltonian
| (2.2) |
where
| (2.3) |
with . The matrix elements with and take the value if a variable is negated and otherwise and denotes a map from literals to Ising spins with . The Hamiltonian has an equally spaced discrete energy spectrum with a ground-state energy for satisfiable instances and a first excited energy gap of value one and, we will only consider satisfiable instances in this work . Physically the Hamiltonian describes an infinite dimensional Ising spin glass of the Edwards Anderson type with two values of frustration in a finite magnetic random field. The coordination number can be tuned by , the connectivity is free and thus planar as well as non-planar connectivity graphs can be involved.
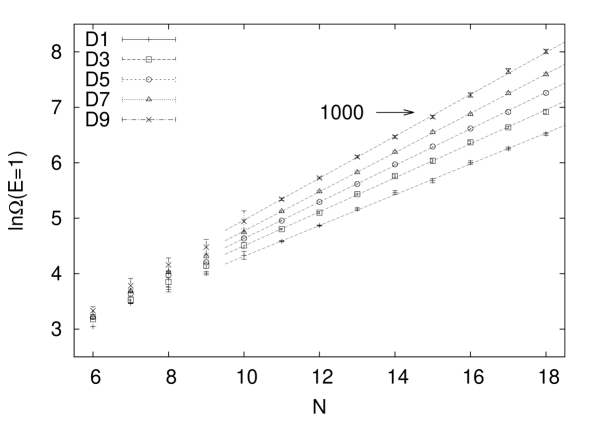
| 1 | 10 | 0.277 ( 2 ) | 0.57 |
|---|---|---|---|
| 3 | 10 | 0.306 ( 2 ) | 0.89 |
| 5 | 10 | 0.329 ( 2 ) | 0.36 |
| 7 | 10 | 0.353 ( 2 ) | 0.22 |
| 9 | 10 | 0.377 ( 2 ) | 0.39 |
We employ special 2SAT problems with unique ground-state i.e., density of states function from a recently constructed synthetic ensemble [3]. The hard 2SAT problem ensemble is designed to hide the ground state at energy from a large number of non-solutions at energy and has a clause-to-variable ratio for , that asymptotically for large approaches the satisfiability threshold of random 2SAT. The situation is depicted in Fig. 1) where a selected set of quantiles i.e., Deciles of the quantity on the cumulative problem distribution is displayed as a function of . It can be witnessed that diverges exponentially in , the straight lines in Fig. 1), in accord with eq.(1.1). The fifth decile (D5) is the median and a fit with and the form eq.(1.1) readily yields the rate constant at a for the fit, see also Table 1). There is a certain spread of the energy one entropy density , which for the first decile D1 ranges from up to at D9, which is a characteristic of underlying catastrophic statistics. The bias toward the hard 2SAT problem set was implemented in [3] via a systematic Monte Carlo study of a generating partition function
| (2.4) |
at fluctuating -value, where is a multicanonical weight [33]. The Monte Carlo process then generates at the hard 2SAT problem ensemble. Unfortunately and as of today it was not possible to generate problems at larger values of than . The reason being: The Monte Carlo moves on random 2SAT require calculations of which by itself creates an exponentially large compute barrier. We have spend some time to alleviate the situation but in essence were not successful.
2.2 Quantum Annealing
We find the unique ground state of the hard 2SAT instances via quantum annealing [8, 9, 10, 11, 12, 13] and use in particular the quantum adiabatic computations [14] . Conventional adiabatic quantum computation (QAC) assumes a linear interpolation between the problem Hamiltonian of eq.(2.2) and a non-commuting driver Hamiltonian , the transverse field term where is the -component Pauli matrix. The linear interpolation is:
| (2.5) |
The quantum adiabatic parameter is defined on the compact interval and in a physical annealing device becomes a smoothly varying function of physical time such that and . The time denotes the annealing time of single annealing trajectories and, as well as on devices and in theory trajectories are repeated many times yielding a success probability with for successful ground-state searches. Clearly a single annealing run of possible short duration may miss the ground-state but the repetition of many results into finite success. Combinatorics then tells us that
| (2.6) |
is the mean physical run-time for the successful ground-state searches at a parametric given target success-rate , which may be as close to unity as desired. The run times naturally pend on the presence and properties of singularities at the quantum phase transition within the quantum partition function as a function of on . To a lesser extent one expects dependencies on the annealing schedule which we choose for reasons of simplicity to be i.e., the linear schedule.
a)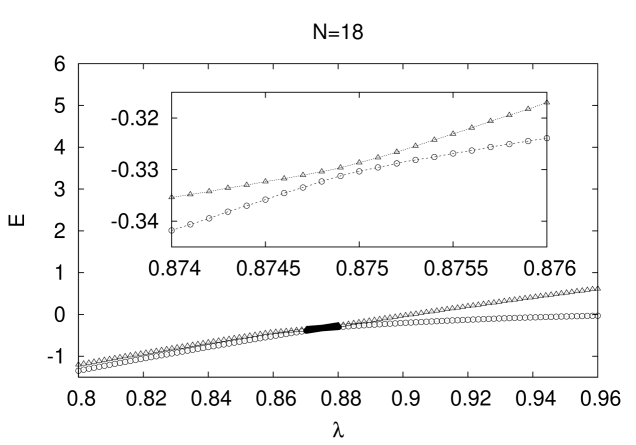
b)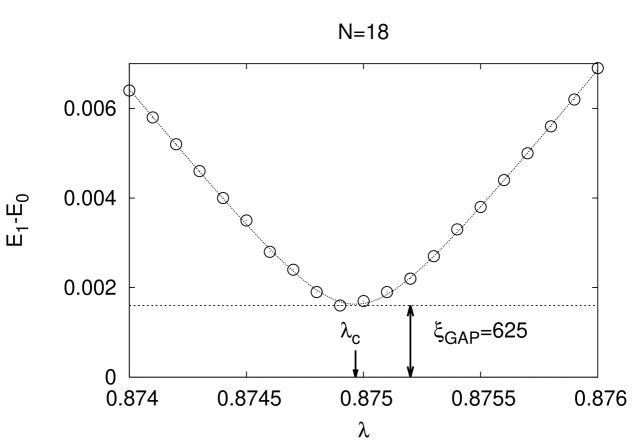
For realizations with a number of spins ranging in-between and we have computed levels of the instantaneous energy spectrum of the quantum adiabatic Hamiltonian in eq.(2.5). We determine the two lowest energy levels: the ground-state at energy and the first excited state at energy . We use the Lanczos algorithm and analyze either about or problem realizations at each with on a grid of discrete values. For the smaller values we have less statistics at about problems only. We consumed core hours on a parallel computer.
For purposes of illustration and, for a representative median complexity instance at , we show in Fig. 2a) energy eigenvalues and , while Fig 2b) contains the energy gap . The limiting values of the gap in Fig 2b) are for the driver Hamiltonian at and at for the problem Hamiltonian and are outside the range of the figure. Limiting values have been checked for any single problem. There is an important lesson to learn: The theory exhibits just one quantum phase transition as signaled by a unique minimum energy gap value at the transition point for any given instance numbered by and, all the energy gap’s are in fact extremely well described by the three-parametric form
| (2.7) |
in vicinity of the critical point 111The critical region at the LZ transition is of size , where r is of . The fits are performed on the critical region, which requires fine -spacing on the -grid. see e.g. the curve in Fig 2b). This is the canonical form at an Landau-Zener (LZ) avoided level crossing. The presence of an isolated Landau-Zener level crossing at the quantum phase transition without further structure on relates to particular aspects of the spectrum which turn out to be simple: The model does not possess a possible cascade of avoided and actual level crossings beyond for as in [17] and, also the energy gap does not close in vicinity of : The classical ground state is non-degenerate and as such there are no tunneling events in-between degenerate vacua. The three parameters and are determined for any single instance of the problem set.
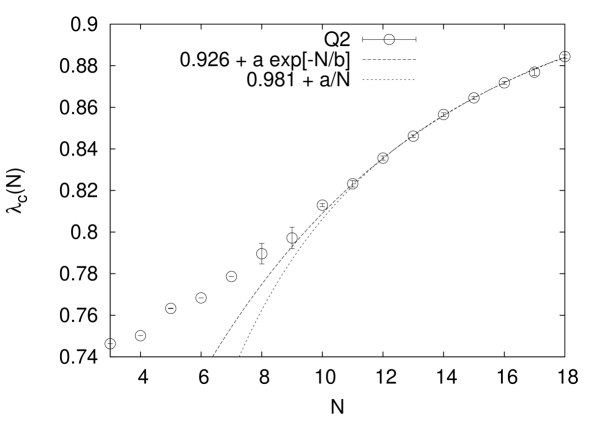
The positions of the avoided level crossings have been determined in the median of the ensembles. They are displayed in Fig. 3). However, and as there is no established finite size scaling (FSS) theory for these class of phase transitions, we feel unable to predict the critical point in the thermodynamic limit! We note that we have experimented with the FSS forms as well as , parameterizing exponential small as well as polynomial small corrections. Both Ansätze do in fact yield reasonable -values if data with are included into corresponding fits, see the two curves displayed in Fig. 3). However, the disparity in the parameters or reflects our ignorance on the critical point position .
The obvious presence of a single Landau Zener avoided level crossing at the critical point leads us to consider Landau Zener theory [34, 35] for the dynamical success rates of eq.(2.6), which becomes exact in the limit of infinite slow adiabatic state changes. For finite time schedules there will be corrections due to transitions to higher energy eigen-states, which in a first step are dropped here. Following these works the two energy level approximation to the diabatic success rate is
| (2.8) |
with
| (2.9) |
Using the adiabatic success rate one then has
| (2.10) |
and inserting the linear schedule one finds
| (2.11) |
During this work we will drop all irrelevant factors from and use
| (2.12) |
as the primary physical observable: the run-time which quantifies quantum search complexity. It is understood that physical dimensions and trivial pre-factors can be restored. The quantities are easily determined from the fits to the energy gap see eq.(2.7) for any problem of the problem set. Finally we also introduce the root
| (2.13) |
and the static gap correlation length
| (2.14) |
which in the path integral formulation denotes the maximal correlation length in-between spins at the quantum phase transition. For linear schedules and regular coefficients the singular part in the run-time then is carried by the singular contribution in
| (2.15) |
The two hereby denotes the quadratic Landau Zener run-time pole, which dominates the run-time as the energy gap closes.
The run-times and correlation length as well as all are distributed on the problem set as labeled by . Typically we can only afford twelve bins in histograms at while otherwise the resulting PDF’s turn out to be too irregular. We also apply statistical errors of magnitude if a bin has entries.
We remark that the problem set generation as given in eq.(2.4) picks improbable problems at from a distribution that otherwise and at the satisfiability threshold of 2SAT is centered at large -values and therefore catastrophic statistics can be applicable. We consider here a two parametric class of Weibull and Frechet functions
| (2.16) |
| (2.17) |
which pend on parameters and scales .
3 Simulated Annealing
We have employed simulated annealing (SA) [7] as an additional and conceptually different measure of complexity for the considered problem set. In its bare version simulated annealing is just an algorithm to solve problems. However, and as simulated annealing employs the canonical partition function , where is the temperature, one can expect that statistical properties determine the run-times in simulated annealing. Again there remains the fundamental issue in how far Monte Carlo pseudo-dynamics approximates physical dynamics under the solution of the equations of motion. For a failure under more physical dynamics than Monte Carlo namely Fokker Planck dynamics see [36].
In SA we set up the canonical partition function at inverse temperature where is the problem Hamiltonian. We choose a random initialized spin-configuration and perform local Metropolis spin updates in a multi-spin coded computer program [37, 38]. We employ compute time farming on a parallel computer with a parallel random number generator of Marsaglia [39]. The annealing procedure is similar to the one used in [3], however we use a different schedule in 2SAT. Each annealing trajectory is started at the high temperature
| (3.1) |
and terminates after Sweeps i.e., Monte Carlo steps where is the spin number. We use a multiplicative temperature schedule
| (3.2) |
that lowers the temperature after each sweep, and after sweeps reaches low temperature already. We repeat the annealing trajectories times with different random numbers and determine the mean success probability of successful ground-state searches after the sweep . Our measure of SA search run-time is
| (3.3) |
at target success rate one-half : . The procedure is repeated for a possible realizations and at all values of .
4 Success Probability Distributions
From the point of view of a quantum annealing PDF’s of gap correlation length values are not direct measurements. Quantum annealers yield measurements for success-rates of instances at problem index and, if statistics over an ensemble is accumulated: the probability distribution function is a measurable observable. The latter probability contains a static measure of run-time complexity which then under the specific dynamics is propagated into successes.
Within LZ-theory we can simply separate statics and dynamics, see the final result in eq.(4.6): At first we note that of eq.(2.13) is a static quantity which we will assume to have a probability distribution
| (4.1) |
The function can numerically be estimated here also by binning, and as the regular contributions of eq.(2.15) turn out to only have smoothly varying dependencies, its overall shape is close to the one of . At second we observe that
| (4.2) |
with
| (4.3) |
constitutes a one parametric map from the static quantifier to the success rate as a function of . It is important to realize here that is a free parameter for annealing devices that may be scaled by scale factors to any value either by scaling the physical annealing time , or by ”formally” combining repetitions of single annealing runs into one combined success probability! A short calculation yields for the inverse map
| (4.4) |
and for the Jacobian
| (4.5) |
The desired probability distribution function can now be written down and up to an irrelevant normalization factor is
| (4.6) |
where it is understood that the inverse eq.(4.4) is applied. This is an interesting finding and a comment is in order:
If from the functions of eq.(2.16) and eq.(2.17) one singles out the Frechet function at k=2
| (4.7) |
then terms cancel with corresponding terms from the Jacobian and, one can find a value of such that i.e., is constant. We find that quantum systems with with Frechet distributed and with an LZ quantum phase transition ought to exhibit constant success probability distributions in quantum annealing for linear time schedules, if the annealing times are tuned to the point of mean success . Scanning the parameter space of eq.(2.16) and eq.(2.17) in-between and as models for , and always tuning to the point of mean success one half, we find for the Frechet case bimodal success probability distribution functions at while for these turn out to be uni-modal. A corresponding watershed line does not exist for the Weibull case for which all probability distributions are bimodal in . Within the scope of this work we will numerically determine values and PDF’s for the given problem set and with the help of eq.(4.6) fold them into corresponding success probability distributions.
5 Findings
5.1 Problem Set Correlations of Observables
Our numerical study provides a wealth of observables that quantify quantum as well as classical search complexity for each incidence on the problem set. These are for QA the gap correlation length , the run-time , its root and success rates . For SA run-times in Sweeps , corresponding success-rates and a free energy are given. The observables either are exact as in the case of , carry numerical errors of relative magnitude like for , or have small statistical errors as for . We transform any set of success probabilities via
| (5.1) |
to the point of mean equal success rate one half by an appropriate choice of . The considerations on the shapes of success PDF’s of the last section then apply. One of the interesting issues now are correlations in-between observables for a given problem set at fixed , which we choose to discuss on a semi-quantitative level.
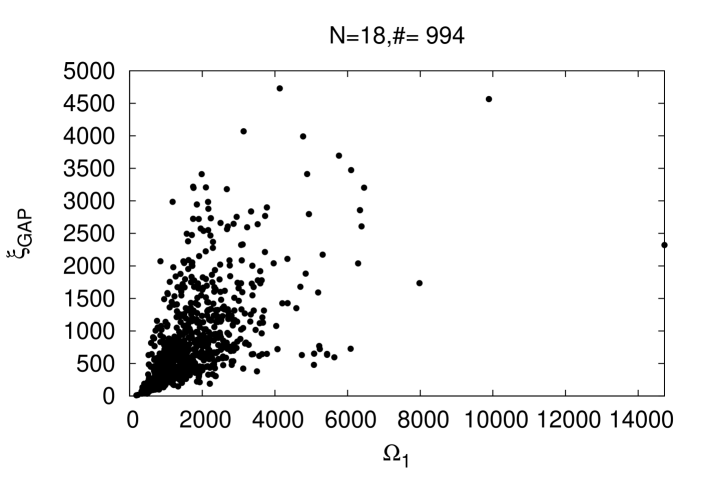
The run time behavior in SA and QA on the problem set can, problem by problem either be correlated, or correlations may fall apart in which case different run-time scaling in is possible. Recalling and to be static quantifiers of QA and SA search complexity we display in Fig. 4) a scatter plot of both for spins. Similar figures can be obtained at smaller . It is quite evident: The gap correlation length and the energy one degeneracy are to a large extent un-correlated. For reasons of completeness we cite the maximum gap correlation length from the union of all problems, which at was found to have the value
| (5.2) |
We remark that such large correlation length values constitute an impasse to any Quantum Monte Carlo (QMC) simulation for the spectrum. Whether the same holds true for simulated quantum annealing studies with QMC methods, is an open question.
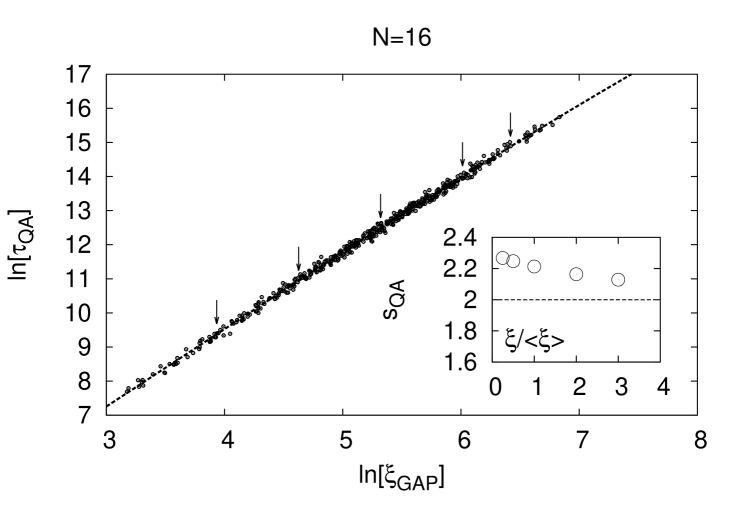
The situation however, as far as correlations are concerned turns around from largely un-correlated to correlated when correlations of static search quantifiers respectively with their corresponding dynamic counterparts, namely run-times and are considered. On the quantum annealing side we display in Fig. 5) and observables for the problem set in a common scatter plot at logarithmic scale. Both quantities show an almost linear correlation in-between the logarithms, the small open circles in the figure. A closer inspection yields, see the inset in Fig. 5), that the slopes of the logarithmic run-time derivatives slightly overshoot the quadratic LZ pole value: . The margin is about percent for easy problems at small . The difference to the pole value then vanishes for the very hard problems. For the linear run-time schedules as considered here, these run-time corrections are induced by the coefficients of eq.(2.12). In the logarithmic derivatives they turn out to be regular. We calculated the derivatives numerically. For this purpose a 3-rd order polynomial is fitted to the data, which then is differentiated.
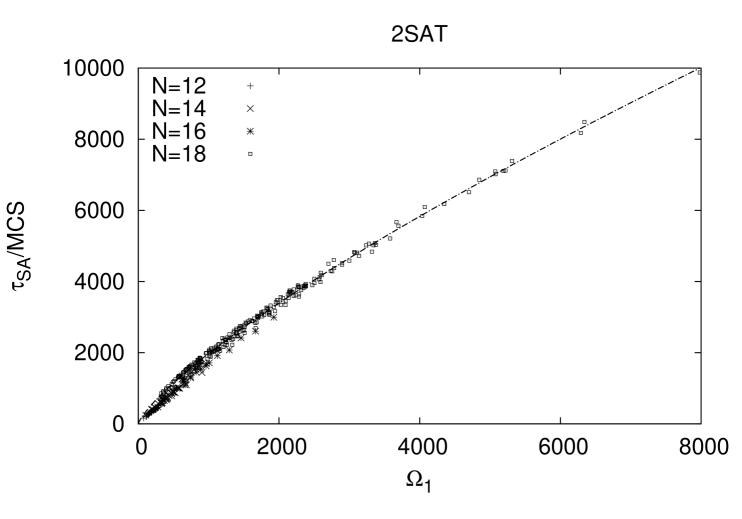
On the classical annealing side we display in Fig. 6) and observables for the and problem sets in a common scatter plot at linear scale. The data show a band of allowed correlations, which is significant and is not caused by the statistical errors of the SA simulation as errors are small. We suspect internal structure on the energy one surface relative to the ground-state in terms of spin flip distances and their stochastic distribution. We fit the correlation by the Ansatz and obtain . A representative scaling form is displayed in Fig. 6), the curve in the figure. We mention, that the performance of different classical annealer’s in case of Dwave is used to question the quantum nature of the search process [40, 41, 42]. It is inconceivable that for our toy model classical annealer’s would not have as static quantifier. If however classical dynamics can model Dwave, then criticism to the effect that the machine is operating classical has to be taken more serious.
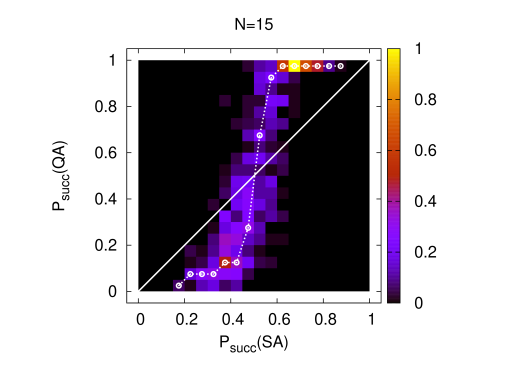
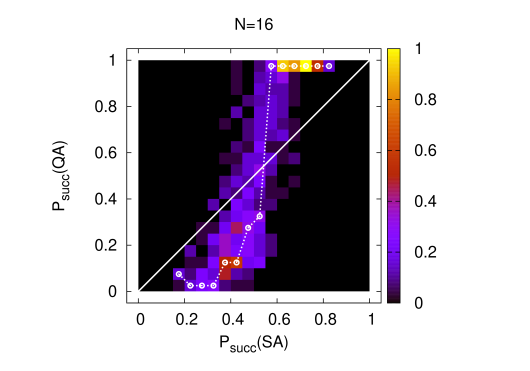
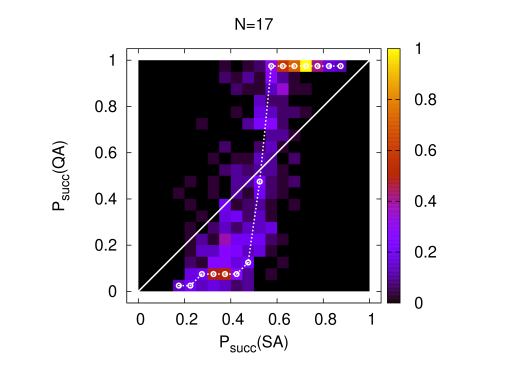
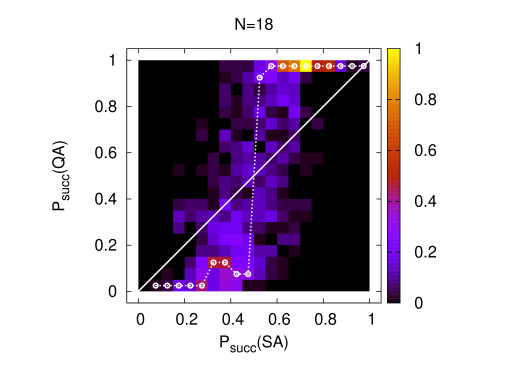
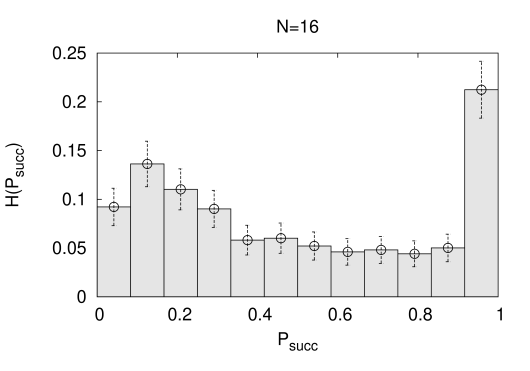
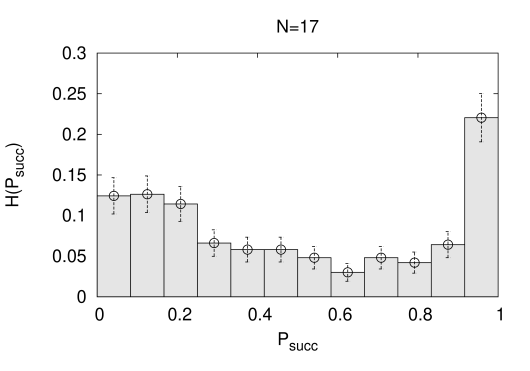
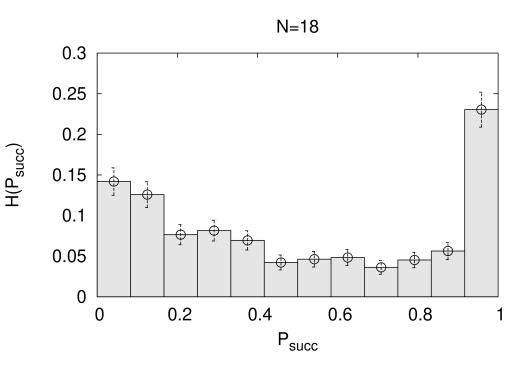
Finally a comprehensive pictorial representation of different quantum versus classical search complexities is obtained in terms of correlations in-between success probabilities for QA and for SA, which both are compactified observables on the interval . It is straightforward to construct a double histogram on the problem set, which counts entry’s into bins and is normalized to unity at the bin of maximal frequency. The data are displayed in Fig. 7) for the largest spin numbers. There is a band of events which parts form the linear correlation, see the straight lines in Fig. 7), and clearly forms a step-like structure at an value of . It is clear, and with reference to the arguments of the last section, that we can attribute this step to the presence of catastrophic statistics in the distribution of the quantifier in eq.(4.6). This issue and the probability distributions of , and of observables will be discussed in the next section. The work [20] presents similar success rate correlations in-between Dwave and SA again. The step there, see Fig. 2c) of the paper, turns out to be less symmetric with a larger amount of statistical noise. However, the theories definitely are different and nothing quantitative can be concluded from the comparison.
5.2 Probability Distribution Functions, PDF’s
| 10 | 4.12 | 1.11(3) | 3.02(29) | 6.94 | 1.23(6) | 2.82(28) |
|---|---|---|---|---|---|---|
| 11 | 3.88 | 1.18(4) | 2.84(20) | 2.28 | 1.24(4) | 2.19(14) |
| 12 | 6.22 | 1.18(6) | 2.70(21) | 5.21 | 1.24(6) | 2.17(16) |
| 13 | 3.53 | 1.26(5) | 2.31(14) | 3.00 | 1.27(5) | 1.90(11) |
| 14 | 1.97 | 1.26(4) | 1.98(09) | 0.52 | 1.28(2) | 1.67(04) |
| 15 | 2.44 | 1.25(6) | 1.65(09) | 1.36 | 1.26(5) | 1.40(07) |
| 16 | 0.53 | 1.25(3) | 1.58(06) | 0.62 | 1.28(4) | 1.43(06) |
| 17 | 0.36 | 1.34(3) | 1.40(05) | 0.71 | 1.36(5) | 1.34(06) |
| 18 | 1.61 | 1.37(7) | 1.24(07) | 0.66 | 1.39(5) | 1.15(04) |
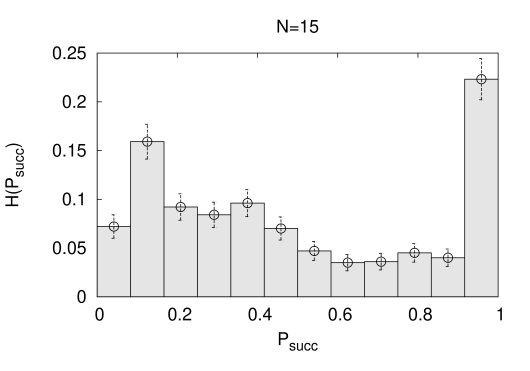
The discretized numerical success probability distribution functions of the quantum annealing processes on the problem set are bimodal, they span the whole compact interval without any tendency of self-averaging at increasing , and are displayed in Fig. 8) for and . These distributions constitute theoretical predictions for quantum annealer’s that run the linear schedule in the large annealing time limit. The success probability distributions of simulated annealing (SA) are unimodal, as in the case of Dwave [20, 21].
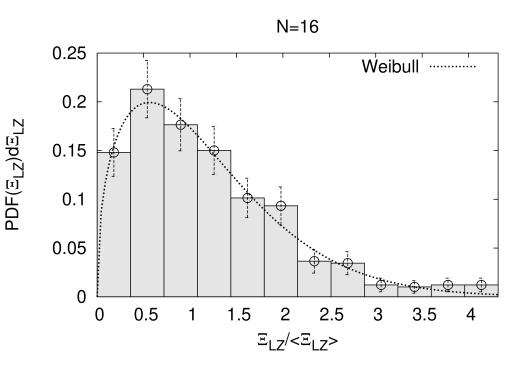
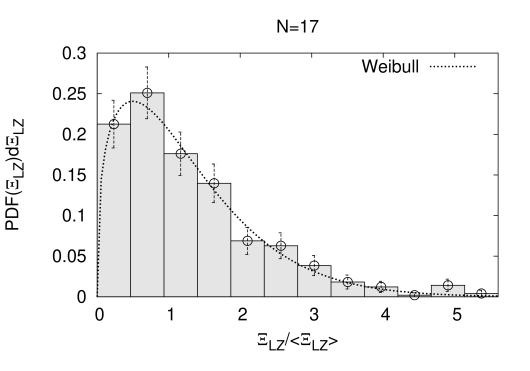
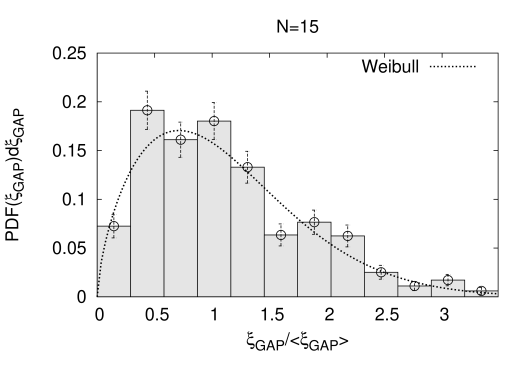
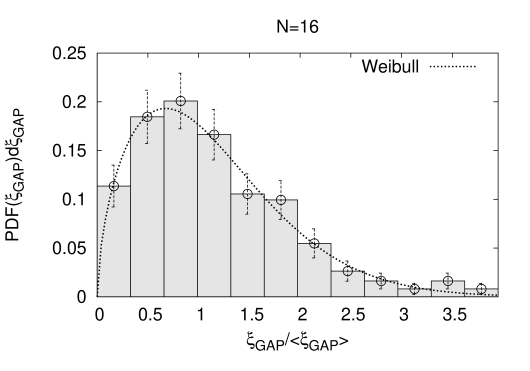
For the linear time schedule the static distributions of are relevant, while the gap correlation length distributions at the quantum phase transition anyhow are fundamental. Both kind of probability distributions are displayed Fig. 9): the top row contains at and , while the bottom row contains at and . On the main diagonal of the figure at one can compare and PDF’s for an identical problem set. All distributions are plotted as a function of their corresponding variable in units of the median as denoted by . One notices that the distributions of and at do not differ much, when plotted as a function of median normalized x-coordinates. We have performed fits to the distribution data employing the catastrophic functions and of eq.(2.16) and eq.(2.17). The qualities of the fits single out Weibull functions as the better models for data and, thus we fit e.g. the Ansatz
| (5.3) |
to the distribution. The fit-results for parameters , scales and correspondingly and scales are all collected in Table 2), together with the values for the fits. The fitted curves are also displayed in Fig. 9), see the curves in the figure. Most importantly we find that for our largest systems at Weibull functions describe the PDF’s to good precision, see the values in Table 2). This implies thin catastrophic distribution function tails in the variables or . The value of slowly decreases from respectively at , to respectively at and possible assumes at infinite . None of the distributions has reached its stationary shape. We mention that a duality in-between and implies, that Weibull distributions for gap correlation length values turn into Frechet distributed energy gap distributions at . Neither the semi Poisson distribution of nearest neighbor levels in randomly distributed energies , nor Wigner’s surmise [43] of energy gaps aka random matrix theory for quantum level repulsion in the bulk are appropriate models here. If actually takes the asymptotic value , then is predicted with a fat tail in ! Znidaric in [44] found a Poisson distribution for the energy gaps in 3SAT with a thin tail in however.
5.3 Run Time Singularities
| 1 | 12 | 0.293 ( 4 ) | 0.9 |
|---|---|---|---|
| 3 | 12 | 0.311 ( 6 ) | 4.4 |
| 5 | 12 | 0.330 ( 5 ) | 1.9 |
| 7 | 12 | 0.351 ( 3 ) | 0.8 |
| 9 | 12 | 0.364 ( 3 ) | 0.5 |
There is a simple question: does quantum annealing with the help of quantum fluctuations perform differently, than classical annealing under the use of thermal fluctuations for a given problem set ? Or on the practical side: Can quantum annealing outperform classical annealing ? The issue here is narrowed down to the very specific comparison of the findings in LZ theory (QA) to the numerical data of simulated annealing (SA). The scope of the comparison is limited and can possibly be broadened in sub-sequent work. On the quantum side neither finite run-time corrections to LZ-theory via the excitations to higher energy levels, nor the corrections due to non-linear schedules are accounted. On the classical side physical dynamics is approximated by Monte Carlo pseudo dynamics which one may conjecture to perform faster than genuine classical dynamics. We think that neither restriction is relevant here as efficiencies turn out to be grossly different and likely can not be leveled by corrections.
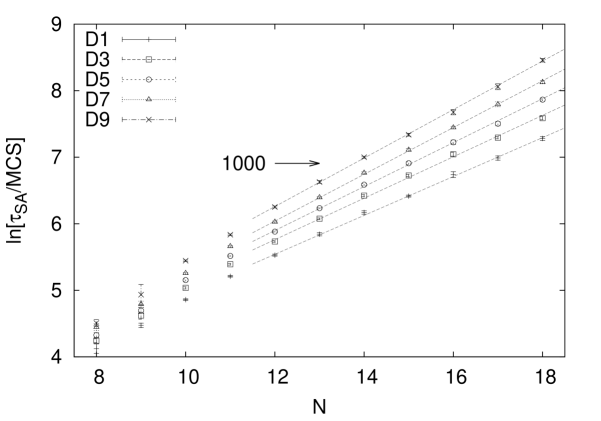
We display in Fig. 10) our findings with respect to classical dynamics. The logarithmic search time of eq.(3.3) in units of Monte Carlo steps is displayed as a function of the spin number for a selected sub-set of Deciles on the problem set. For spin numbers up to we find a exponential run time singularity of the form
| (5.4) |
and the fitted rate constants for various Deciles and are presented in Table 3). Statistical error bars have been determined with jack-knife binning methods. The numerical rate constant value in the median (D5) is and turns out to be identical with the value of the corresponding singularity in the density of states . There is a certain spread in the rate constant values pending on the Decile value, which however is bounded and thus our problem ensemble is pure: There is no indication for an admixture of problems, that for small Deciles would either show polynomial, or otherwise different from exponential run time behavior at large Deciles. A similar conclusion can be obtained for the quantum case.
a)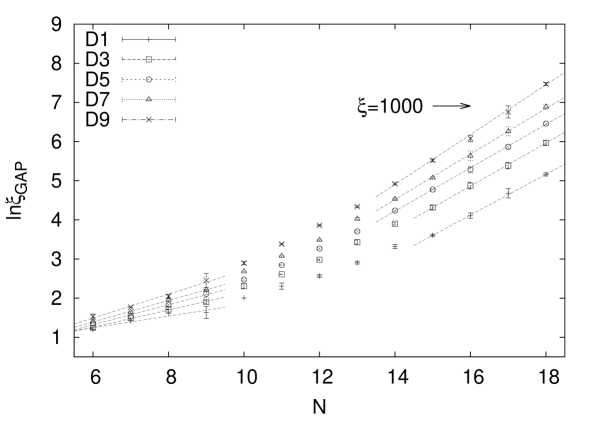
b)
| 1 | 15 | 0.519 ( 04 ) | 0.07 | 0.567 ( 8 ) | 0.12 |
|---|---|---|---|---|---|
| 3 | 15 | 0.549 ( 06 ) | 0.06 | 0.584 ( 9 ) | 0.07 |
| 5 | 14 | 0.553 ( 06 ) | 0.30 | 0.592 ( 8 ) | 0.23 |
| 7 | 14 | 0.581 ( 12 ) | 0.80 | 0.625 ( 6 ) | 0.19 |
| 9 | 14 | 0.636 ( 09 ) | 0.85 | 0.669 ( 8 ) | 0.28 |
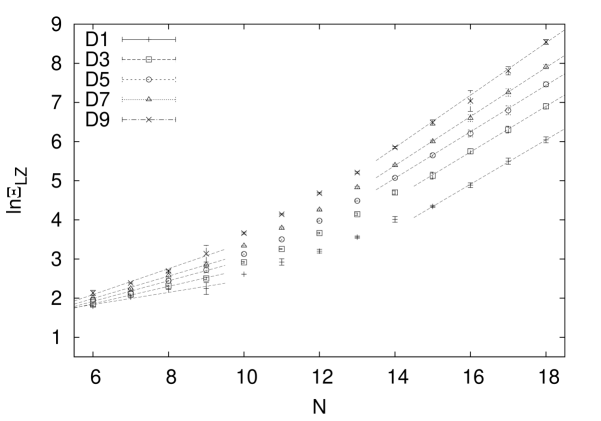
We display in Figures 11 a) and 11 b) our findings with respect to quantum search complexity. The logarithmic gap correlation length is given in Fig. 11 a) while the logarithmic run time root with is given in Fig. 11 b). Again we present data for a selected set of Deciles including the median. We observe a crossover behavior from weak singular behavior at small turning to strong singular behavior at largest . For spin numbers and for both observables the data are consistent with exponential singularities
| (5.5) |
and
| (5.6) |
Exponential singular behavior in run-times was also observed by Znidaric in [6] for 3SAT with a strength of the singularity that at given however was weaker then the one in this paper. The numerical rate constant values in the median (D5) as obtained from fits to the data with are and and are given in Table 4). The fitted values of rate constants for other Deciles and corresponding fit quality values can also be found in Table 4). The rate constant turns out to be ten percent larger than and all the fits have -values of indicating good quality data modeling.
Summarizing, using a conventional standard quantum adiabatic algorithm with a transverse field and a linear time schedule we find a ground state quantum search complexity for the ensemble of hard 2SAT problems [3] with a super hard
| (5.7) |
run time singularity at , that even exceeds the singularity of trivial enumerations. The corresponding singularity in classical, i.e. simulated annealing (SA) searches has a rate constant which only is a fraction . A compute time wall of such magnitude for an adiabatic quantum algorithm designed to solve the 2SAT problem is theoretically interesting, but from an algorithmic point of view can only be termed an failure. Finally, and recalling that our problems are actually in , we state the obvious fact that quantum annealing, as well as classical annealing are not able to recognize a mathematical structure which otherwise and using calculus makes the problem solvable in polynomial time. It is unclear as to which basis for the degrees of freedoms, or which Hamiltonian had to be chosen in 2SAT in order that annealing can succeed in polynomial time, or whether that is possible at all.
6 Conclusion
Within the scope of the present work we study the quantum search complexity within hard 2SAT which is mapped to an ensemble of Ising models. We hide a unique ground state at energy zero from an exponentially large number of configurations at the classical energy gap value (). The situation corresponds to a search for an needle in a haystack, where the haystack extents over the energy one surface. For our theory the free energy landscape at energy one is simple and all configurations there are connected by single spin flips. There are concurrent proposals for Ising models [45] i.e., physical glasses e.g. the 3D EA glass with less trivial connectivity properties in vicinity of the ground state energy, which are conjectured to be candidate models for quantum speed ups over classical annealing. However, for the specific problem set here we find a quantum search run-time , that scales unfavorable to large values of with an exponential singularity. The rate constant of the singular behavior turns out to be larger than of trivial phase space enumerations ! Thus even a simple enumeration wins over quantum annealing for large i.e., finds ground states faster than QA. In addition stimulated annealing finds ground states faster than enumeration. We do not expect that gradual changes to the algorithm: neither alternate annealing schedules, nor alternate driver or problem Hamiltonian’s can change this ranking as long as energies above and at the ground state are populated like a needle in a haystack.
A quantum search algorithm, that for an tractable theory in blatantly fails with compute times that exceed Ising enumeration provokes a question: Is there place for a loophole that could possibly restore confidence too some degree into the efficiency of quantum annealing ? For the specific case of 2SAT we note that the mathematical search for logical collisions on 2SAT’s implication graph can actually be shaped into the form of an alternate quantum adiabatic algorithm. The algorithm checks for logical collisions i.e., the connectivity of literals with anti-literals on the directed implication graph. Whether such a quantum algorithm yields better efficiency is currently not known.
We have taken effort to predict the shape of success probability distributions in quantum annealing, which turn out to be bimodal at mean success one half. These probabilities are important functions as for annealing devices they correspond to direct physical observations. We then identify the origin of the bimodal property. Within LZ theory it is caused by a Weibull distributed static quantifier , which is propagated with the help of the quadratic Landau Zener run-time pole into a bimodal distribution. However, the Weibull distribution by itself is not predicted by theory. It rather characterizes the problem set. We also add the interesting general remark that quantifier distributions of the Frechet type at would yield constant success probability distribution functions, which however is not the case for our problem set. We expect that a similar mechanism generates the bimodal successes for the EA glass on Dwave [20]. The different shapes of PDF’s here and there are likely caused by different quantifier distributions of the catastrophic type, which on Dwave are not yet known.
We also note that our problems can be mapped onto the Dwave computer. The procedure is not elegant and will require problem embedding on Dwave’s Chimera topology. Should the machine follow quantum dynamics at low temperatures, then the scaling of the run times with ought to exhibit the failure of the quantum search quite clearly, as we know now that compute time barriers for the quantum search are substantially harder than for the classical search. A failure of this kind would actually be welcome and it would support recent findings on the quantum nature of the search process [46]. It is however equally reasonable to expect that the machine could solve the hard 2SAT problems with ease, in which case this would hint at a classical search mode on the machine, consistent with [41, 42]. We hope to actually perform the quantum computer experiment in the near future.
Finally we remark that [3] contains several KSAT theories with and corresponding hard KSAT problems. For , e.g. 3SAT these can be mapped via polynomial transformations to maximal independent set (MIS) [47] with an alternate Ising problem Hamiltonian. As the models at appear even harder we expect even more pronounced failures of quantum annealing with increasing if searches are quantum.
Acknowledgment: Calculations were performed under the VSR grant JJSC02 and an Institute account SLQIP00 at Jülich Supercomputing Center on various computers.
References
- [1] S. A. Cook, Proc. Third Annual ACM Symposium on the Theory of Computing, (ACM, New York, 1971) 151.
- [2] J. Stat. Phys. , 144, Issue 3, (2011) 519.
- [3] T. Neuhaus, ”Monte Carlo Search for Very Hard KSAT Realizations for Use in Quantum Annealing”, preprint, November 2014.
- [4] B. Bollobas, C. Borgs, J. T. Chayes, J. H. Kim and D. B. Wilson, ”The scaling window of the 2-SAT transition”, Random Structures and Algorithms 18, Issue 3, (2001) 201.
- [5] M. Znidaric, "Single-solution Random 3-SAT Instances", arXiv:cs/0504101 (2005) preprint.
- [6] M. Znidaric, Phys. Rev. A 71 (2005) 062305.
- [7] S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, New Series, Vol. 220, No. 4598, 671 (1983).
- [8] A. Apolloni, C. Carvalho and D. de Falco, Stoc. Proc. Appl. 33,(1989) 233-244.
- [9] P. Amara, D. Hsu and J.E. Straub, J. Phys. Chem. 97 (1993) 6715.
- [10] A.B. Finnila, M.A. Gomez, C. Sebenik, C. Stenson and J.D. Doll, Chem. Phys. Lett. 219 (1994) 343.
- [11] T. Kadowaki and H. Nishimori, Phys. Rev. E 58, (1998) 5355.
- [12] T. Morita and H. Nishimori, J. Math. Phys. 49 (2008) 125210.
- [13] M. Ohzeki and H. Nishimori, ”Quantum annealing: An introduction and new developments”, Journal of Computational and Theoretical Nanoscience 8, Number 6 (2011).
- [14] E. Farhi, J. Goldstone, S. Gutmann, and M. Sipser, arXiv:quant-ph/0001106, (2001); E. Farhi, J. Goldstone, S. Gutmann, J. Lapan, A. Lundgren, and D. Preda, Science 292, (2001) 472.
- [15] G. E. Santoro, R. Martonak, E. Tosatti, and R. Car, Science 295 (2002) 2427.
- [16] R. Martonak, G. E. Santoro, E. Tosatti, Phys. Rev. B 66 (2002) 094203.
- [17] G. E. Santoro and E. Tosatti, J. Phys A 39 (2006) R393.
- [18] A. Das and B. K. Chakrabarti, Rev. Mod. Phys. 80 (2008) 1061.
- [19] B. Altshuler, H. Krovi and J. Roland, ”Anderson localization makes adiabatic quantum optimization fail”, PNAS 107 no. 28 (2010) 12446.
- [20] S. Boixo, T. F. Ronnow, S. V. Isakov, Z. Wang, D. Wecker, D. A. Lidar, J. M. Martinis and M. Troyer, Nature Physics 10 (2014) 218.
- [21] T. F. Ronnow, Z. Wang, J. Job, S. Boixo, S. V. Isakov, D. Wecker, J. M. Martinis, D. A. Lidar and M. Troyer, Science 345 (2014) 420.
- [22] B. Heim, T: F. Ronnow, S: V. Isakov, M. Troyer, “Quantum versus Classical Annealing of Ising Spin Glasses”, arXiv:1411.5693 (2014).
- [23] D. A. Battaglia, G. E. Santoro and E. Tosatti, Phys. Rev. E 71 (2005) 066707.
- [24] A. P. Young, S. Knysh, and V. N. Smelyanskiy, Phys. Rev. Lett. 101, 170503 (2008) and Phys. Rev. Lett. 104, 020502 (2010).
- [25] I. Hen and A. P. Young, Phys. Rev. E 84 (2011) 061152.
- [26] E. Farhi, D. Gosset, I. Hen, A. W. Sandvik, P. Shor, A. P. Young and F. Zamponi Phys. Rev. A 86 (2012) 052334 .
- [27] T. Neuhaus, M. Peschina, K. Michielsen and H. De Raedt, Phys. Rev. A 83 (02011) 012309.
- [28] M. H. Amin, A. Y. Smirnov, N. G. Dickson and M. Drew-Brook "Approximate diagonalization method for large-scale Hamiltonians", Phys. Rev. A 86, (2012) 052314.
- [29] J. Brooke, D. Bitko, T.F. Rosenbaum and G. Aeppli, "Quantum annealing in a disordered magnet", Science 284 (1999) 779.
- [30] T. Neuhaus, "Statistical Analysis for Quantum Adiabatic Computations: Quantum Monte Carlo Annealing", Physics Procedia 15 (2011) 71.
- [31] H. de Raedt, Europhys. Lett. 3 (1987) 139.
- [32] Y. Matsuda, H. Nishimori and H. G. Katzgraber, "Ground-state statistics from annealing algorithms: Quantum vs classical approaches", New J. Phys. 11 (2009) 073021.
- [33] B. A. Berg and T. Neuhaus, Phys. Rev. Lett. 68, 9 (1992).
- [34] L. Landau, Physikalische Zeitschrift der Sowjetunion 2, (1932) 46.
- [35] C. Zener, Proceedings of the Royal Society of London A 137 (1932) 696.
- [36] O. Melchert and A.K. Hartmann, ”Ground states of 2d +-J Ising spin glasses via stationary Fokker-Planck sampling”, J. Stat. Mech. P10019 (2008).
- [37] S. Wansleben, J. G. Zabolitzky and C. Kalle, J. of Statist. Phys. 37, Issue 3-4 (1984) 271.
- [38] G. Bhanot, D. Duke and R. Salvador, J. Stat. Phys. 44, Issue 5-6 1986) 985.
- [39] G. Marsaglia, J. Stat. Software 8, 14, (2003) 1.
- [40] D. Browne, ”Quantum computation: Model versus machine”, Nature Physics 10 (2014) 179.
- [41] J. A. Smolin and G. Smith, ”Classical signature of quantum annealing”, preprint arXiv:1305.4904 [quant-ph] (2013).
- [42] S. W. Shin, G. Smith, J. A. Smolin and U. Vazirani, ”How Quantum is the D-Wave Machine?”, preprint arXiv:1401.7087 [quant-ph] (2014).
- [43] E. P. Wigner, in Conference on Neutron Physics by Time-of-Flight (Oak Ridge National Laboratory Report No. 2309, 1957) p. 59.
- [44] M. Znidaric, Phys. Rev. A 72 (2005) 052336.
- [45] H. G. Katzgraber, F. Hamze and R. S. Andrist, "Glassy Chimeras could be blind to quantum speedup: Designing better benchmarks for quantum annealing machines", Phys. Rev. X 4 (2014) 021008.
- [46] W. Vinci, T. Albash, A. Mishra, P. A. Warburton and D. A. Lidar in "Distinguishing Classical and Quantum Models for the D-Wave Device", arXiv:1403.4228 [quant-ph] (Submitted on 17 Mar 2014).
- [47] V. Choi in "Adiabatic Quantum Algorithms for the NP-Complete Maximum-Weight Independent Set, Exact Cover and 3SAT Problems", preprint arXiv:1004.2226 [quant-ph] (Submitted on 13 Apr 2010).