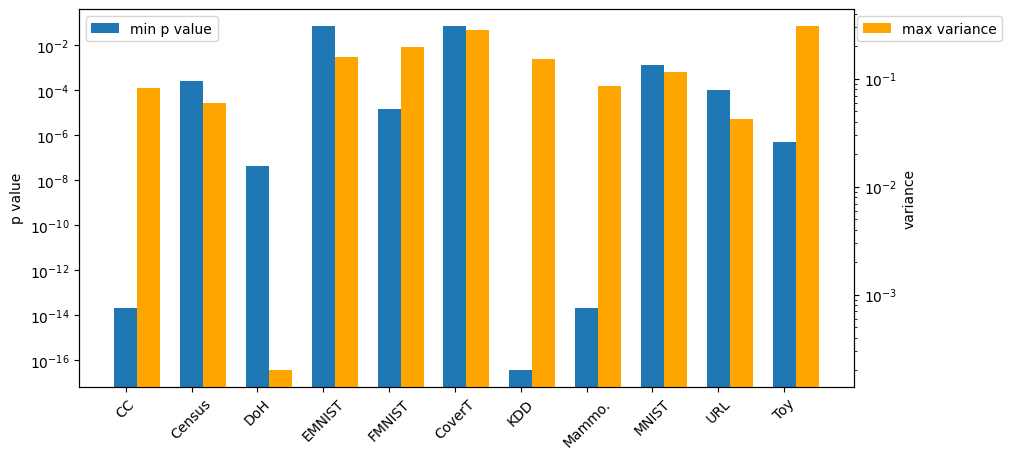Quantum Support Vector Regression for Robust Anomaly Detection
Abstract
Anomaly Detection (AD) is critical in data analysis, particularly within the domain of IT security. In recent years, Machine Learning (ML) algorithms have emerged as a powerful tool for AD in large-scale data. In this study, we explore the potential of quantum ML approaches, specifically quantum kernel methods, for the application to robust AD. We build upon previous work on Quantum Support Vector Regression (QSVR) for semisupervised AD by conducting a comprehensive benchmark on IBM quantum hardware using eleven datasets. Our results demonstrate that QSVR achieves strong classification performance and even outperforms the noiseless simulation on two of these datasets. Moreover, we investigate the influence of – in the NISQ-era inevitable – quantum noise on the performance of the QSVR. Our findings reveal that the model exhibits robustness to depolarizing, phase damping, phase flip, and bit flip noise, while amplitude damping and miscalibration noise prove to be more disruptive. Finally, we explore the domain of Quantum Adversarial Machine Learning and demonstrate that QSVR is highly vulnerable to adversarial attacks and that noise does not improve the adversarial robustness of the model.
Index Terms:
benchmark, semisupervised learning, noise, hardware, adversarial attacks, robustness, quantum kernel methods, quantum machine learningI Introduction
Quantum Machine Learning (QML) merges Quantum Computing (QC) and Machine Learning (ML) to exploit potential advantages of QC for ML. Recently, Quantum Kernel Methods (QKMs) have gained attention for their potential to replace many supervised QML models and their ability to surpass variational circuits, as evidenced by Schuld [1]. Theoretical findings further prove that QKMs can potentially address classification problems intractable for classical ML, such as the discrete logarithm problem [2].
Anomaly Detection (AD) is crucial in the realm of IT security, as it identifies deviations from normal patterns in areas like network intrusion and fraud detection [3]. However, it is important to note that ML models employed in security-sensitive contexts are susceptible to adversarial attacks, where small, carefully crafted perturbations in inputs can result in misclassification. (Quantum) Adversarial Machine Learning (QAML/AML) explores techniques for both generating these adversarial attacks and defending against them.
Given the potential of QML to address problems challenging for classical methods, the application of QML to AD is a tempting progression. In 2023, Tscharke et al. [4] proposed a semisupervised AD approach based on the reconstruction loss of a Quantum Support Vector Regression (QSVR) equipped with a quantum kernel. The authors compared the performance of the QSVR against a Quantum Autoencoder (QAE), a classical Support Vector Regression (CSVR) with a Radial Basis Function (RBF) kernel, and a classical autoencoder (CAE), using ten real-world and one synthetic dataset. Their simulated QSVR demonstrated comparable performance to CSVR, with marginal superiority over the other models. However, the implementation of their QSVR on hardware was left open, a gap tackled by this paper.
In today’s Noisy Intermediate-Scale Quantum (NISQ) era, noise limits the application of QC for industrial tasks, underscoring the need for a comprehensive understanding of how noise affects quantum algorithms. Noise impacts QML models by affecting predictive performance and, in QAML, altering robustness against adversarial attacks [5, 6].
The remainder of this work is structured as follows: The next subsection I-A offers a comprehensive review of research related to QKMs, the impact of noise on QML, and QAML. Our contributions are detailed in subsection I-B. The following Background (section II) provides a foundation for understanding QKMs, noisy QC, and adversarial attacks. Next, the Methods (section III) describe the implementation of the QSVR on hardware, the noise simulation, and the adversarial attacks generation. In Results and Discussion (section IV), we analyze the results of the hardware experiments and investigate the influence of noise and adversarial attacks on the model’s performance. Finally, Conclusion and Outlook (section V) highlights the key results of this work and provides future research directions.
I-A Related Work
In 2019, Havlicek et al. [7] introduced a quantum Support Vector Machine (QSVM) for binary classification on a two-qubit NISQ device. Since then, QSVMs have been applied to many areas, including remote sensing image classification [8], mental health treatment prediction [9], and breast cancer prediction [10]. Kyriienko and Magnusson [11] extended this to unsupervised fraud detection with a simulated one-class QSVM, and Tscharke et al. [4] developed a QSVR for semisupervised AD in 2023. However, to the best of our knowledge, a QSVR for semisupervised AD has not yet been set up on hardware.
Research has also explored the influence of noise in QML models [12, 13, 14], focusing on noise robustness [15, 16] or beneficial use of noise [17, 18]. However, as far as we know, the influence of noise on a QSVR for semisupervised AD has not yet been evaluated.
Finally, the link between quantum noise and QAML was established by Du et al. [5] in 2021, who found that adding depolarization noise can increase adversarial robustness. Building on this, Huang and Zhang [6] improved the adversarial robustness of Quantum Neural Networks by adding noise layers in 2023. To date, there have been no published results involving adversarial attacks on semisupervised QML models for AD.
I-B Contributions
The goal of our work is to gain further insight into the potential of QSVR for semisupervised AD in the NISQ era, which we accomplish through these contributions:
-
1.
We investigate how the model performs on hardware and report that the QSVR achieves good classification performance on a 27-qubit IBM device, even outperforming a noiseless simulation on two out of ten real-world datasets.
-
2.
We show that the QSVR is largely robust to noise by training and evaluating over 500 noisy models. We further observe that amplitude damping and miscalibration have the most damaging effect on the model’s performance and that the artificial Toy dataset, constructed to be linearly separable, suffers the most from noise.
-
3.
Finally, we investigate the robustness of the QSVR against adversarial attacks and find it highly vulnerable, with performance on real-world datasets dropping by up to an order of magnitude for a weak attack strength of . Introducing noise into the QSVR does not clearly improve the model’s adversarial robustness.
II Background
II-A Quantum Kernel Methods
A kernel is a positive, semidefinite function on the input set . It uses a distance measure between two input vectors to create a model that captures the properties of a data distribution. A feature map maps input vectors to a Hilbert or feature space . They are of great importance in ML, as they map input data in a higher-dimensional space with a well-defined metric. The feature map can be a nonlinear function that changes the relative position of the data points. As a result, the dataset can become easier to classify in feature space, and even linearly separable. We associate feature maps with kernels by defining a kernel via
| (1) |
where is the inner product defined on .
With the exponentially large Hilbert space of QCs, the use of QKMs for ML is close at hand. A quantum feature map is implemented via a feature-embedding circuit , which acts on a ground state of a Hilbert space as . The distance measure in the quantum kernel is the absolute square of the inner product of the quantum states. On hardware, this can be realized by the inversion test, where a sample is encoded in the unitary , followed by the adjoint encoding the second sample and measuring the probability of the all-zero state. Thus, the quantum kernel is defined as
| (2) |
and returns the overlap or fidelity of the two states. A more in-depth description of quantum kernels can be found in [19, 20].
There exist many different encoding techniques for the circuit realizing the quantum feature map, but for this work, we will focus on angle encoding because of its advantageous complexity with respect to the number of gates for an input vector x of dimension . Angle encoding is a special form of time-evolution encoding, where a scalar value is encoded in the unitary evolution of a quantum system governed by a Hamiltonian . The unitary of time-evolution encoding is given by
| (3) |
In the case of angle encoding, the Pauli matrices with are used in the Hamiltonian .
II-B Noisy Quantum Computing
Real quantum systems are never completely isolated from the environment; for example, an electron realizing a qubit will interact with other charged particles. Moreover, quantum computers are programmed by an external system and thus can never be a closed system [21, 22].
In the current NISQ-era, noise significantly limits the performance of quantum algorithms, primarily through coherent and incoherent noise. Coherent noise arises from systematic, reversible errors that lead to predictable but undesired evolution of the states, often caused by imperfect calibrations or imprecise control signals [23]. Coherent noise is an unitary evolution of the system, characterized by having only one operation element in the operator-sum representation introduced below [24, 25].
Incoherent noise, on the other hand, is characterized by random, stochastic processes caused by insufficient isolation of the system from its environment. These uncontrolled interactions between system and environment lead to deviations between the desired and the actual evolution and to a loss of coherence in the system [23, 22].
Quantum noise can be modeled by a quantum channel, where the term ”channel” is drawn from classical information theory [21]. In the operator-sum representation, a channel is described by the map with operation elements (or Kraus operators) mapping the density operator to another density operator .
| (4) |
In the following, selected types of single-qubit noisy channels are described, and their operation elements are listed. For a more detailed explanation of the noisy quantum channels, we refer to [21, 26, 24].
-
1.
Amplitude Damping channel: describes the effect of energy loss, such as when an atom emits a photon. The channel acts on the quantum system and the environment as follows: if both and are in their ground state , nothing happens. If is in the excited state , a photon will be emitted with probability , leading to the excitation of the environment and causing the transition , while drops to the ground state, i.e. . The evolution caused by the channel can be summarized as:
(5) This is achieved by the operation elements:
(8) (11) -
2.
Bitflip channel: flips the state of a qubit from to and vice versa with probability . The operators are:
(14) (17) -
3.
Depolarizing channel: the qubit remains intact with probability , while an error occurs with probability . If an error occurs, the state is replaced by a uniform ensemble of the three states . This is a symmetric decoherence channel defined by operation elements:
(20) (23) (26) (29) -
4.
Miscalibration channel: a coherent noise channel applying an ”overrotation” to the rotation gate with . This can be caused by an imperfect calibration of the device [23]. Since the channel is unitary, it has only one operation element:
(30) -
5.
Phase Damping channel: the phase damping or dephasing channel models the effect of random environmental scattering on a qubit, such as photon interactions in a waveguide or atomic states perturbed by distant charges. This channel causes a partial loss of phase information without energy loss. It produces the same effect as the phase flip channel, with the phase damping related to the phase flip probability by
(31) -
6.
Phaseflip channel: applies a phase of to the -state with probability and leaves the -state unchanged. It has the operation elements:
(34) (37) The channel has the following effect on the state’s density matrix :
(42) From this, we can see that the phase flip channel destroys superposition by decaying the off-diagonal terms of the density matrix while the on-diagonal terms remain invariant.
II-C Adversarial Attacks
QML models are typically trained using a hybrid quantum-classical approach. In this framework, the model parameters are optimized using a classical optimization algorithm, while the quantum part is limited to the evaluation of the loss, which is (partially) done by the quantum computer or simulator. This hybrid approach allows us to easily extend the concept of adversarial attacks from classical ML to QML, which has already been successfully demonstrated in [27].
An adversarial attack is a small, carefully crafted perturbation of the -dimensional input that causes the model to misclassify the input [28, 29]. An untargeted adversarial sample is created by maximizing the model’s loss while keeping the perturbation small enough to be imperceptible to humans, e.g., by ensuring for some small . In general, the ideal perturbation is given by
| (43) |
where is the model, are the model’s optimized parameters after training, and is the target.
One of the most widely used methods for generating adversarial samples is Projected Gradient Descent (PGD) [30]. PGD iteratively maximizes the model’s prediction error while ensuring that the perturbation remains within a predefined range. This approach has become a standard tool for evaluating the robustness of models to adversarial threats. The perturbed input is determined by
| (44) |
where represents the perturbed data at step , clips the perturbed data into the range of the normalized input set , and is the step size.
A straightforward strategy to increase the adversarial robustness is adversarial training, where adversarial samples are included in the training set.
III Methods
The experiments performed in this work are threefold. First, we benchmarked the QSVR for semi-supervised AD on hardware. Second, we evaluated the influence of noise on the classification performance of the QSVR, and third, we investigated the influence of noise on the adversarial robustness of the QSVR. An overview of the datasets used in the experiments is given in Table VI in Appendix A in the appendix. The datasets were reduced to five dimensions using Principal Components Analysis. For a more detailed description of the model, the datasets, and the preprocessing techniques, we refer to [4].
III-A Quantum Support Vector Regression Model
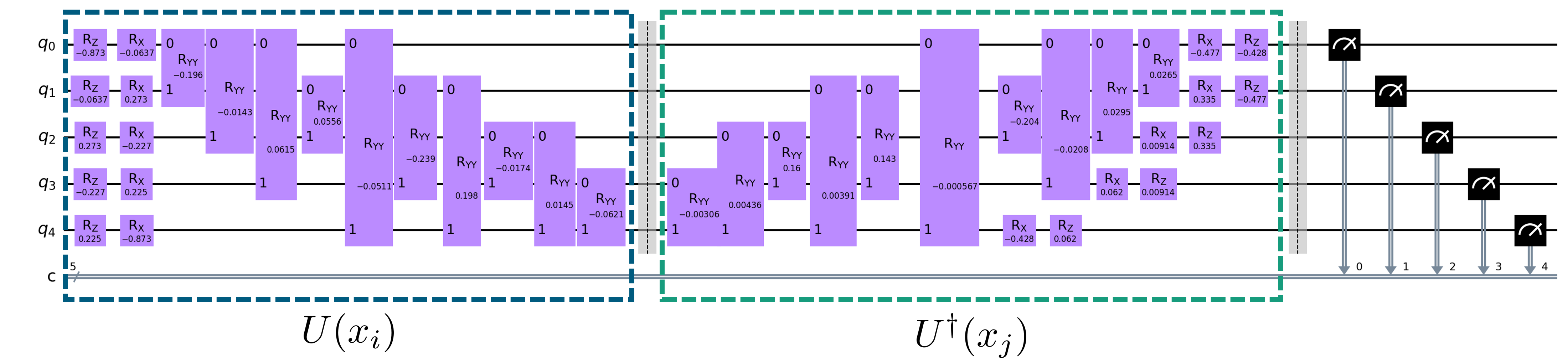
The QSVR for semi-supervised AD is described in detail in [4] , and the kernel circuit is displayed in Fig. 1. The first data point is encoded by the unitary , followed by its inverse encoding the second data point . The unitary consists of a layer of RZ gates and a layer of RX gates, followed by a layer of IsingZZ111https://docs.pennylane.ai/en/stable/code/api/pennylane.IsingZZ.html gates to create entanglement. Each of the single-qubit gates encodes one feature, while the parameter of the IsingZZ gate is a product of two features. The kernel entry is obtained by measuring the probability of the all-zero state after applying both unitaries.
III-B Hardware Experiments
In the hardware experiments, we used a training set of size 30 from the normal class and a test set of size 50 with equal class ratio, following [4].
III-B1 Device Specifications
The experiments were performed on the IBM System One in Ehningen, Germany, in January 2024. The system is a 27-qubit superconducting quantum computer with a quantum volume of 64. The QSVR was implemented using qiskit [31] with default error mitigation techniques. Further specifications of the system are listed in table I.
| Spec | Value |
|---|---|
| Name | IBM Quantum System One at Ehningen |
| System type | Superconducting |
| Number of qubits | 27 |
| Quantum Volume | 64 |
| Processor type | Falcon |
| Deployment year | 2021 |
| Coherence time | s |
| Single qubit error | |
| Two qubit gate error | |
| Operation time of 2 qubit gate | ns for CNOT |
III-B2 Reference Models
III-C Generation of Noise
The influence of noise on the QSVR for semisupervised AD was evaluated by applying six noise channels with different strengths to the quantum circuit that computes the kernel. The seven noise probabilities used in the experiments are and the five noise channels are [bitflip, phaseflip, depolarizing, phase damping, amplitude damping]. This leads to a total of models per dataset. For the miscalibration channel, the noise probability is the overrotation in radians in 20 linear steps between 0 and . For the DoH dataset subject to adversarial attacks of strength , additional evaluations were performed in the region close to . The noisy QSVR was simulated using PennyLane [33]. We used a training set of size 100 from the normal class and a test set of size 100 with a balanced class ratio.
III-D Generation of Adversarial Attacks
We created 100 adversarial samples of the test set (50 from each class) using PGD with the parameters listed in Table II. The attacks targeted the noiseless models and were then applied to the noisy models. For adversarial training, we create adversarial samples of the training set and train the model using the adversarial training set of size 100.
| Spec | Values |
|---|---|
| Attack strength | [0.01, 0.1, 0.3] |
| Iterations | 50 |
IV Results and Discussion
In this study, we first benchmarked our QSVR on the 27-qubit IBM Ehningen device (labeled qc-QSVR) and compared its performance against the simulated quantum baseline models QSVR (simulated version of our model, see [4]) and QAE (based on [32]), as well as CSVR and CAE as classical baselines. Second, six different noise channels of varying strength were introduced to evaluate the influence of noise on the QSVR algorithm. Third, the adversarial robustness of the model was examined, and the influence of noise on the adversarial robustness was evaluated by exposing the (noisy) models to adversarial attacks. The simulations show no error bars because the SVR is a deterministic model and pennylane’s default.mixed222https://docs.pennylane.ai/en/stable/code/api/pennylane.devices.default_mixed.DefaultMixed.html device used to calculate the kernels computes exact outputs.
IV-A Hardware Results
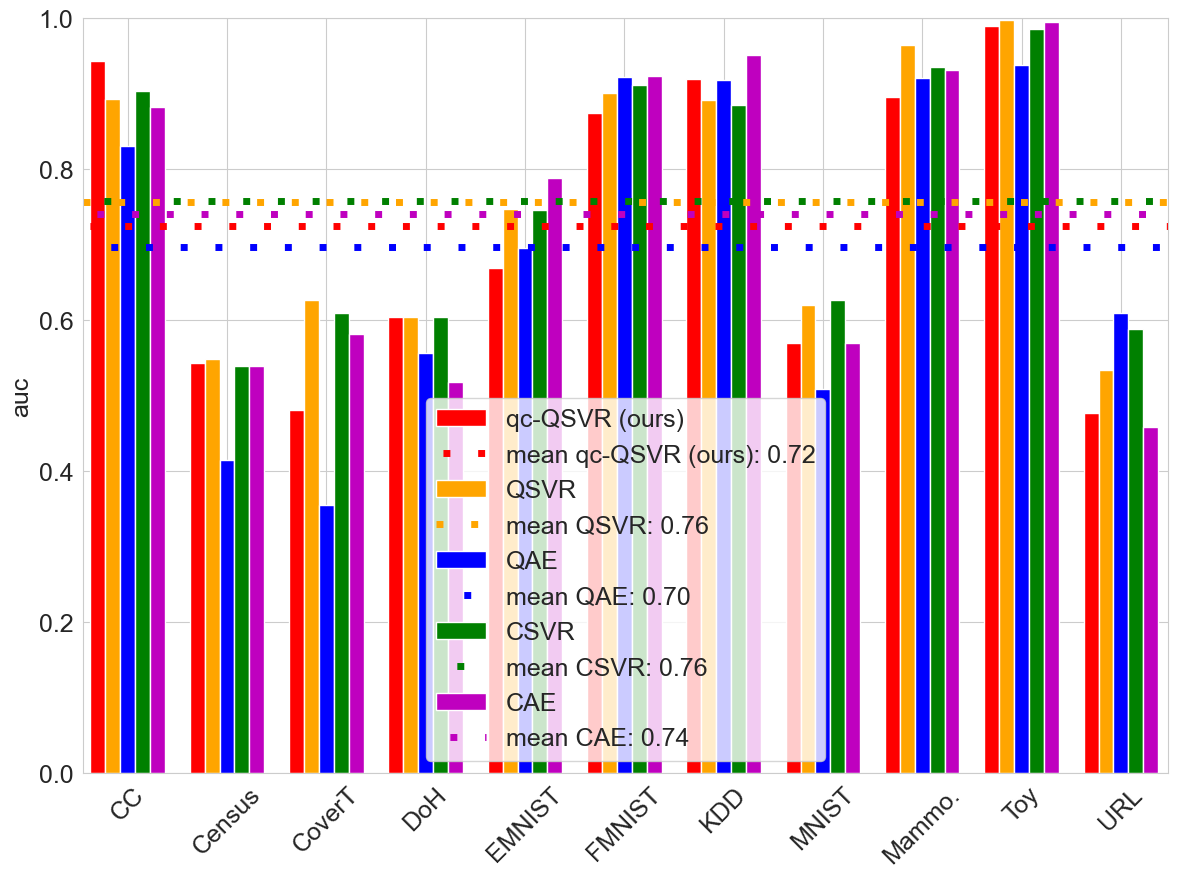
Figure 2 compares model performance on eleven datasets using area under the ROC curve (AUC), a commonly used metric in AD that measures the trade-off between the true and false positive rates independent of a detection threshold. An AUC of 1.0 indicates perfect classification of the dataset, and a random classifier achieves an AUC of 0.5 on balanced binary datasets. The datasets include Credit Card Fraud (CC), Census, Forest Cover Type (CoverT), Domain Name System over HTTPS (DoH), EMNIST, Fashion MNIST (FMNIST), Network Intrusion (KDD), MNIST, Mammography (Mammo), URL, and our constructed dataset Toy. The models included in the study are qc-QSVR (ours), QSVR, QAE, CSVR, and CAE. The average performance of each model across all datasets is represented by a dotted line, while the bars indicate the models’ performance on individual datasets.
On average, our qc-QSVR exhibits an AUC decrease of 0.04 compared to the simulated QSVR. In 8 out of 11 datasets, the simulated model outperforms the qc-QSVR, with the performance gap explained by hardware noise. On the DoH datasets, both models perform identically, while on the CC and KDD datasets, the qc-QSVR surprisingly outperforms its simulated counterpart. On these two datasets, hardware-induced noise appears to enhance model performance, an effect we attribute to improved generalization. Specifically, the perturbations introduced by the noisy gates mimic the corruptions applied in denoising autoencoders, a technique shown to yield superior generalization compared to standard autoencoders [34]. Our results are consistent with those of other authors who observe that noise can improve the performance of QML models under certain circumstances [35, 36].
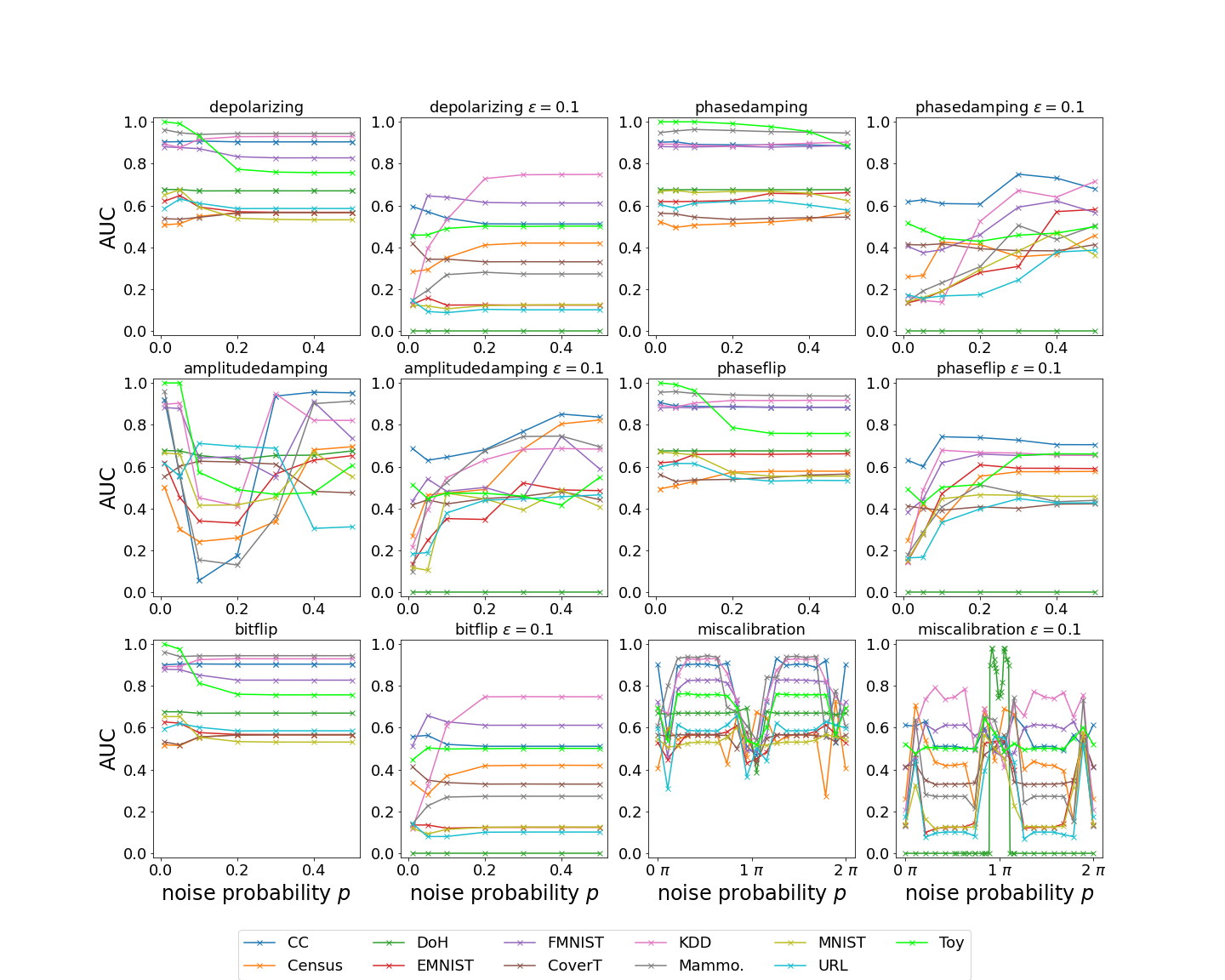
IV-B Influence of Noise on the Model Performance
The hardware results show that noise in NISQ devices affects the performance of QSVR. Therefore, in this section, we examine the influence of six noise channels on the QSVR based on the performance on eleven datasets. Figure 3 shows the AUC of noisy simulations with the noise channels described in Section II-B as well as the influence of adversarial attacks of strength on the noisy simulations. The model’s robustness against noise is now analyzed, and the adversarial robustness is investigated in Section IV-C. The QSVR is largely robust against depolarizing, phase damping, phaseflip , and bitflip noise, as the AUC for these noise types remains rather stable with increasing noise probability. A theoretical analysis of the robustness of quantum classifiers done by LaRose and Coyle [37] proves that single-qubit classifiers are robust against precisely these noise channels. Taking into account the findings of Schuld [1] that many short-term and fault-tolerant quantum models can be replaced by a general support vector machine whose kernel computes distances between data-encoding quantum states, we expect these results to transfer to our QSVR.
Amplitude damping has a large effect on the model’s behavior as the AUC decreases for all datasets except CoverT and URL at and . At higher , the AUC partially recovers, approaching 0.5. This shows that the QSVR is very sensitive to amplitude damping , and at high noise levels the model becomes a random classifier. These results are also supported by LaRose and Coyle’s [37] analysis, who found that quantum classifiers are generally not robust against amplitude damping noise.
The curves of the models subject to miscalibration noise show a periodicity of approximately , with dips at about for , and plateaus in between. Small levels of miscalibration degrade the performance of the model, but when the noise level is above about , the AUC reaches a plateau at a level similar to the one for zero noise until the curve dips again around . We conclude that small degrees of miscalibration reduce model performance, and that this type of noise should be avoided in hardware.
IV-C Adversarial Robustness
AD is often used in security-critical areas such as credit card fraud detection or network intrusion detection. Therefore, ML models used for AD must be robust to adversarial attacks. For low-dimensional, tabular data sets, it is possible that a sample can be completely and effectively transformed into a sample of a different class at high attack strengths. In these cases, the effect on the AUC may be exaggerated and should be interpreted only as an upper bound on the performance drop.
IV-C1 Noise-Free Adversarial Attacks
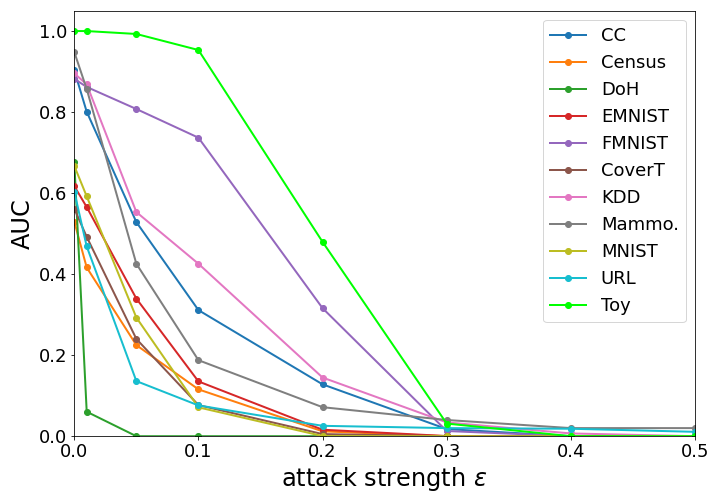
First, we consider the noise-free model and plot the obtained results of the PGD attacks up to a strength of in Figure 4. The noise-free QSVR is highly vulnerable to adversarial attacks, as evidenced by the decrease in AUC for small attack strengths of for all datasets except Toy. The largest decrease is in the AUC of the DoH dataset, which drops by an order of magnitude from 0.67 to 0.06 for the attack. As the attack strength increases, the AUC continues to decrease for all datasets until it approaches 0.0 for . We conclude that techniques to increase the adversarial robustness of the model should be investigated.
The unchanged AUC of Toy for can be explained by the creation process of the dataset. The dataset was created to be linearly separable with a separation distance of 0.4 between the classes, so the data points must be shifted a large distance in feature space to be misclassified. However, since the AUC drops to 0.0 for , which is smaller than the separation distance, we might conclude that the QSVR is susceptible to overfitting.
IV-C2 Noisy Adversarial Attacks
Second, the performance of the noisy QSVR when subjected to adversarial perturbations of strength is shown in Figure 3. Omitting miscalibration, we find that for noise levels below , the AUC is low for most noise types and datasets, following the trend of high adversarial vulnerability observed in Figure 4. At higher noise levels, however, the AUC typically recovers to some extent, reaching a plateau at about an AUC of 0.5. This indicates that the model transitions to a random classifier, showing that the adversarial attacks are so powerful that quantum noise cannot improve performance beyond that of a random classifier. Other researchers report similar results, noting that random noise and adversarial noise are fundamentally different, and that models resilient to random noise are often still vulnerable to adversarial noise [38].
Miscalibration noise affects both models under attack and models not under attack, similarly, resulting in spikes around for in most datasets. Interestingly, for adversarially attacked models, as opposed to models that are not under attack, these spikes can be lower than the adjacent plateaus, depending on the dataset. Between these spikes, the AUC generally remains stable, forming plateau regions.
The DoH dataset is an outlier, with an AUC of 0.0 across almost all noise types and strengths, which is explained by its extreme vulnerability to adversarial attacks seen in Figure 4. This vulnerability can be explained by Figure 5 in Appendix B in the appendix, showing the p-value from the Kolmogorov–Smirnov test and the maximum feature variance within the test set. The DoH dataset has a relatively high p-value combined with a very low variance. The high p-value indicates a high probability that the normal and anomalous samples originate from the same distribution, while the low variance suggests a high degree of similarity between all samples, especially between the normal and anomalous data. As a result, the DoH dataset is difficult to classify, and even tiny adversarial attacks of strength lead to manipulations a magnitude greater than the variance within the dataset.
Notably, the AUC for the DoH dataset with miscalibration noise is over nearly all noise levels and peaks only around , where it approaches . An analysis of the adversarial test kernels for the DoH dataset subject to miscalibration noise is shown in Table III and highlights major differences between a high-performing run (, ) and a low-performing run (, ) for both classes. The mean kernel values for the high-AUC run are four orders of magnitude larger than those for the low-AUC run. In addition, the disparity between kernel values of classes 0 and 1 is greater in the high-performing scenario, allowing for easier distinction by the SVR and thus improved model AUC. Considering that the kernel entries represent the probability of measuring the all-zero state, we observe that miscalibration noise with a strength close to shifts the DoH-embedding states closer to the all-zero state, thus increasing the kernel values.
Since the overrotation introduced by miscalibration noise is independent of the data, this type of noise can be thought of as additional fixed parameter rotation gates in the circuit. Because the parameters of these gates have a significant impact on model performance, we highlight the importance of using kernels tailored to the dataset, such as trainable kernels.
| p | AUC | class | mean kernel value |
|---|---|---|---|
| 2.9 | 0.98 | 0 | 1.743e-01 5.157e-02 |
| 1 | 1.734e-01 5.121e-02 | ||
| 1.7 | 0.00 | 0 | 1.800e-05 7.360e-06 |
| 1 | 1.796e-05 7.395e-06 |
The models attacked with and do not provide new insights, as they exhibit similar behavior to the attacks above, and can be obtained from the authors upon reasonable request.
We conclude that quantum noise is not suited for increasing the adversarial robustness of the QSVR. This finding is consistent with prior research [14], where the authors suggest that adding noise to QML models to increase the adversarial robustness is unlikely to be beneficial in practice.
IV-C3 Adversarial Training
Adversarial training is a straightforward approach to increasing the adversarial robustness of supervised learning algorithms. Table IV reveals that adversarial training increases the AUC for the adversarial test set on seven out of eleven datasets, and the average AUC over all datasets rises from 0.28 to 0.31. However, the increase in AUC is small, and except for FMNIST and Toy, the AUC remains below 0.5. For the test set without adversarial samples, the AUC decreases through adversarial training on six out of eleven datasets, and the average declines from 0.75 to 0.71. Table V shows the ratio of correctly classified normal samples to the total number of normal samples, as well as the same ratio for the anomalies. For normal data, the ratio is , and for the anomalies it is . We observe that retraining increases the classification ratio for the normal data of the Toy dataset from 0.78 to 0.94, while the ratio for the anomalies remains unchanged at 1.00. For KDD, we report similar results, but the increase in the classification ratio of the normal data through retraining is smaller. This shows that adversarial retraining can lead to more normal samples being classified correctly without influencing the classification of the anomalies, since the latter are not contained in the training set. However, this was not observed for other datasets and was most pronounced for the synthetic dataset, suggesting this behavior requires a large separation distance between the two classes.
We conclude that adversarial training cannot be used to reliably harden the QSVR against adversarial attacks. We attribute this to the semisupervised setting, meaning that only normal samples are available during training.
| Dataset | Test AUC w/ retraining | Test AUC w/o retraining | Adv AUC w/ retraining | Adv AUC w/o retraining |
| CC | 0.85 | 0.90 | 0.37 | 0.31 |
| Census | 0.62 | 0.53 | 0.05 | 0.12 |
| DoH | 0.68 | 0.68 | 0.00 | 0.00 |
| EMNIST | 0.63 | 0.62 | 0.17 | 0.14 |
| FMNIST | 0.91 | 0.88 | 0.73 | 0.74 |
| CoverT | 0.44 | 0.56 | 0.18 | 0.08 |
| KDD | 0.71 | 0.90 | 0.46 | 0.43 |
| Mammo. | 0.74 | 0.95 | 0.22 | 0.19 |
| MNIST | 0.62 | 0.67 | 0.11 | 0.07 |
| URL | 0.59 | 0.60 | 0.08 | 0.08 |
| Toy | 1.00 | 1.00 | 1.00 | 0.95 |
| Mean | 0.71 | 0.75 | 0.31 | 0.28 |
| Dataset | retraining | no retraining | ||
|---|---|---|---|---|
| norm. | anom. | norm. | anom. | |
| CC | 0.96 | 0.28 | 0.98 | 0.24 |
| Census | 1.00 | 0.00 | 1.00 | 0.00 |
| DoH | 1.00 | 0.00 | 1.00 | 0.00 |
| EMNIST | 1.00 | 0.02 | 0.98 | 0.02 |
| FMNIST | 0.86 | 0.66 | 0.86 | 0.68 |
| CoverT | 1.00 | 0.00 | 1.00 | 0.00 |
| KDD | 1.00 | 0.34 | 0.96 | 0.34 |
| Mammo. | 0.96 | 0.18 | 1.00 | 0.14 |
| MNIST | 1.00 | 0.00 | 1.00 | 0.00 |
| URL | 0.96 | 0.08 | 0.98 | 0.04 |
| Toy | 0.94 | 1.00 | 0.78 | 1.00 |
| Mean | 0.97 | 0.23 | 0.96 | 0.22 |
V Conclusion and Outlook
We first benchmarked our QSVR for semisupervised AD on 27-qubits IBM hardware and found that the average AUC was slightly lower than that of the noiseless simulation (0.72 compared to 0.76). However, the QSVR outperformed the noiseless simulation on two out of eleven datasets.
Second, the influence of six noise channels on the performance of the QSVR was evaluated, revealing that the QSVR is largely robust against deporarizing, phasedamping, phase flip and bit flip noise. Amplitude damping, on the other hand, results in the most significant degradation of the model and miscalibration noise also has the potential to impact performance.
Finally, the adversarial robustness of the (noisy) model was assessed, and it was observed that the QSVR is highly vulnerable to adversarial attacks. Even weak PGD attacks with a strength of can reduce the AUC by up to an order of magnitude. Introducing quantum noise does not yield any beneficial effect, neither on the unattacked model’s performance nor on its adversarial robustness. Moreover, adversarial training does not reliably improve the adversarial robustness of the model. Consequently, we conclude that the QSVR demonstrates potential for semisupervised AD in the NISQ era, however, special attention should be paid to the vulnerability to adversarial attacks and amplitude damping and miscalibration noise.
We emphasize the importance of employing dataset-specific kernels and recommend exploring trainable kernels to further enhance the performance of QML models. Future research directions could also include expanding the model to more qubits, and finally, future work may also focus on techniques to enhance the adversarial robustness of the QSVR and defend against such attacks.
Acknowledgment
The research is part of the Munich Quantum Valley, which is supported by the Bavarian state government with funds from the Hightech Agenda Bayern Plus.
References
- [1] Maria Schuld “Supervised quantum machine learning models are kernel methods”, 2021 arXiv:2101.11020 [quant-ph]
- [2] Yunchao Liu, Srinivasan Arunachalam and Kristan Temme “A rigorous and robust quantum speed-up in supervised machine learning” In Nature Physics 17 Nature Research, 2021, pp. 1013–1017 DOI: 10.1038/s41567-021-01287-z
- [3] Lukas Ruff et al. “A Unifying Review of Deep and Shallow Anomaly Detection” In Proceedings of the IEEE 109.5, 2021, pp. 756–795 DOI: 10.1109/JPROC.2021.3052449
- [4] K. Tscharke, S. Issel and P. Debus “Semisupervised Anomaly Detection using Support Vector Regression with Quantum Kernel” In 2023 IEEE International Conference on Quantum Computing and Engineering (QCE) Los Alamitos, CA, USA: IEEE Computer Society, 2023, pp. 611–620 DOI: 10.1109/QCE57702.2023.00075
- [5] Yuxuan Du et al. “Quantum noise protects quantum classifiers against adversaries” In Phys. Rev. Res. 3 American Physical Society, 2021, pp. 023153 DOI: 10.1103/PhysRevResearch.3.023153
- [6] Chenyi Huang and Shibin Zhang “Enhancing adversarial robustness of quantum neural networks by adding noise layers” In New Journal of Physics 25.8 IOP Publishing, 2023, pp. 083019 DOI: 10.1088/1367-2630/ace8b4
- [7] Vojtěch Havlíček et al. “Supervised learning with quantum-enhanced feature spaces” In Nature 567.7747, 2019, pp. 209–212
- [8] Amer Delilbasic et al. “Quantum Support Vector Machine Algorithms for Remote Sensing Data Classification” In 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, 2021, pp. 2608–2611 DOI: 10.1109/IGARSS47720.2021.9554802
- [9] Syed Farhan Ahmad, Raghav Rawat and Minal Moharir “Quantum Machine Learning with HQC Architectures using non-Classically Simulable Feature Maps” In 2021 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), 2021, pp. 345–349 DOI: 10.1109/ICCIKE51210.2021.9410753
- [10] Mhlambululi Mafu and Makhamisa Senekane “Design and Implementation of Efficient Quantum Support Vector Machine” In 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), 2021, pp. 1–4 DOI: 10.1109/ICECET52533.2021.9698509
- [11] Oleksandr Kyriienko and Einar B. Magnusson “Unsupervised quantum machine learning for fraud detection”, 2022 arXiv:2208.01203 [quant-ph]
- [12] Diego García-Martín, Martín Larocca and M. Cerezo “Effects of noise on the overparametrization of quantum neural networks” In Phys. Rev. Res. 6 American Physical Society, 2024, pp. 013295 DOI: 10.1103/PhysRevResearch.6.013295
- [13] Yifan Zhou and Peng Zhang “Noise-Resilient Quantum Machine Learning for Stability Assessment of Power Systems” In IEEE Transactions on Power Systems 38.1, 2023, pp. 475–487 DOI: 10.1109/TPWRS.2022.3160384
- [14] David Winderl, Nicola Franco and Jeanette Miriam Lorenz “Quantum Neural Networks under Depolarization Noise: Exploring White-Box Attacks and Defenses”, 2023 arXiv:2311.17458 [quant-ph]
- [15] Nam H Nguyen, Elizabeth C Behrman and James E Steck “Quantum learning with noise and decoherence: a robust quantum neural network” In Quantum Machine Intelligence 2.1, 2020, pp. 1
- [16] Jiahao Yao et al. “Noise-Robust End-to-End Quantum Control using Deep Autoregressive Policy Networks” In Proceedings of the 2nd Mathematical and Scientific Machine Learning Conference 145, Proceedings of Machine Learning Research PMLR, 2022, pp. 1044–1081 URL: https://proceedings.mlr.press/v145/yao22a.html
- [17] Keyi Ju et al. “Harnessing Inherent Noises for Privacy Preservation in Quantum Machine Learning” In ICC 2024 - IEEE International Conference on Communications, 2024, pp. 1121–1126 DOI: 10.1109/ICC51166.2024.10622663
- [18] David Winderl, Nicola Franco and Jeanette Miriam Lorenz “Constructing Optimal Noise Channels for Enhanced Robustness in Quantum Machine Learning”, 2024 arXiv: https://arxiv.org/abs/2404.16417
- [19] Maria Schuld and Francesco Petruccione “Machine Learning with Quantum Computers”, Quantum Science and Technology Cham: Springer International Publishing, 2021 DOI: 10.1007/978-3-030-83098-4
- [20] Maria Schuld and Nathan Killoran “Quantum Machine Learning in Feature Hilbert Spaces” In Phys. Rev. Lett. 122 American Physical Society, 2019, pp. 040504 DOI: 10.1103/PhysRevLett.122.040504
- [21] Michael A. Nielsen and Isaac L. Chuang “Quantum Computation and Quantum Information: 10th Anniversary Edition” Cambridge University Press, 2010
- [22] Dieter Suter and Gonzalo A. Álvarez “Colloquium: Protecting quantum information against environmental noise” In Rev. Mod. Phys. 88 American Physical Society, 2016, pp. 041001 DOI: 10.1103/RevModPhys.88.041001
- [23] Noah Kaufmann, Ivan Rojkov and Florentin Reiter “Characterization of Coherent Errors in Noisy Quantum Devices”, 2023 arXiv:2307.08741 [quant-ph]
- [24] John Preskill “Lecture Notes for Ph219/CS219: Quantum Information Chapter 3” California Institute of Technology, 2018
- [25] Joel Wallman, Chris Granade, Robin Harper and Steven T Flammia “Estimating the coherence of noise” In New Journal of Physics 17.11 IOP Publishing, 2015, pp. 113020 DOI: 10.1088/1367-2630/17/11/113020
- [26] Mark M. Wilde “Quantum Information Theory” Cambridge University Press, 2013 DOI: https://doi.org/10.1017/CBO9781139525343
- [27] Maximilian Wendlinger, Kilian Tscharke and Pascal Debus “A Comparative Analysis of Adversarial Robustness for Quantum and Classical Machine Learning Models”, 2024 arXiv:2404.16154 [cs.LG]
- [28] Christian Szegedy et al. “Intriguing properties of neural networks”, 2014 arXiv:1312.6199 [cs.CV]
- [29] Ian J. Goodfellow, Jonathon Shlens and Christian Szegedy “Explaining and Harnessing Adversarial Examples”, 2015 arXiv:1412.6572 [stat.ML]
- [30] Aleksander Madry et al. “Towards Deep Learning Models Resistant to Adversarial Attacks”, 2019 arXiv:1706.06083 [stat.ML]
- [31] Ali Javadi-Abhari et al. “Quantum computing with Qiskit”, 2024 DOI: 10.48550/arXiv.2405.08810
- [32] Korbinian Kottmann, Friederike Metz, Joana Fraxanet and Niccolò Baldelli “Variational quantum anomaly detection: Unsupervised mapping of phase diagrams on a physical quantum computer” In Phys. Rev. Res. 3 American Physical Society, 2021, pp. 043184 DOI: 10.1103/PhysRevResearch.3.043184
- [33] Ville Bergholm et al. “PennyLane: Automatic differentiation of hybrid quantum-classical computations”, 2022 arXiv:1811.04968 [quant-ph]
- [34] Pascal Vincent, Hugo Larochelle, Yoshua Bengio and Pierre-Antoine Manzagol “Extracting and composing robust features with denoising autoencoders” In Proceedings of the 25th International Conference on Machine Learning, ICML ’08 Helsinki, Finland: Association for Computing Machinery, 2008, pp. 1096–1103 DOI: 10.1145/1390156.1390294
- [35] Erik Terres Escudero, Danel Arias Alamo, Oier Mentxaka Gómez and Pablo García Bringas “Assessing the Impact of Noise on Quantum Neural Networks: An Experimental Analysis” In Hybrid Artificial Intelligent Systems Springer Nature Switzerland, 2023, pp. 314–325 DOI: 10.1007/978-3-031-40725-3˙27
- [36] L. Domingo, G. Carlo and F. Borondo “Taking advantage of noise in quantum reservoir computing” In Scientific Reports 13.1, 2023, pp. 8790 DOI: 10.1038/s41598-023-35461-5
- [37] Ryan LaRose and Brian Coyle “Robust data encodings for quantum classifiers” In Phys. Rev. A 102 American Physical Society, 2020, pp. 032420 DOI: 10.1103/PhysRevA.102.032420
- [38] Alhussein Fawzi, Seyed-Mohsen Moosavi-Dezfooli and Pascal Frossard “Robustness of classifiers: from adversarial to random noise”, 2016 arXiv: https://arxiv.org/abs/1608.08967
- [39] Andrea Dal Pozzolo, Olivier Caelen, Reid A. Johnson and Gianluca Bontempi “Calibrating Probability with Undersampling for Unbalanced Classification” In 2015 IEEE Symposium Series on Computational Intelligence, 2015, pp. 159–166 DOI: 10.1109/SSCI.2015.33
- [40] Dheeru Dua and Casey Graff “UCI Machine Learning Repository”, 2017 URL: http://archive.ics.uci.edu/ml
- [41] Jock A. Blackard and Denis J. Dean “Comparative accuracies of artificial neural networks and discriminant analysis in predicting forest cover types from cartographic variables” In Computers and Electronics in Agriculture 24.3, 1999, pp. 131–151 DOI: https://doi.org/10.1016/S0168-1699(99)00046-0
- [42] Mohammadreza MontazeriShatoori, Logan Davidson, Gurdip Kaur and Arash Habibi Lashkari “Detection of DoH Tunnels using Time-series Classification of Encrypted Traffic” In 2020 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), 2020, pp. 63–70 DOI: 10.1109/DASC-PICom-CBDCom-CyberSciTech49142.2020.00026
- [43] Gregory Cohen, Saeed Afshar, Jonathan Tapson and André Schaik “EMNIST: Extending MNIST to handwritten letters” In 2017 International Joint Conference on Neural Networks (IJCNN), 2017, pp. 2921–2926 DOI: 10.1109/IJCNN.2017.7966217
- [44] Han Xiao, Kashif Rasul and Roland Vollgraf “Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms”, 2017 arXiv:1708.07747 [cs.LG]
- [45] Mahbod Tavallaee, Ebrahim Bagheri, Wei Lu and Ali A. Ghorbani “A detailed analysis of the KDD CUP 99 data set” In 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, 2009, pp. 1–6 DOI: 10.1109/CISDA.2009.5356528
- [46] Y. Lecun, L. Bottou, Y. Bengio and P. Haffner “Gradient-based learning applied to document recognition” In Proceedings of the IEEE 86.11, 1998, pp. 2278–2324 DOI: 10.1109/5.726791
- [47] KEVIN S. WOODS et al. “COMPARATIVE EVALUATION OF PATTERN RECOGNITION TECHNIQUES FOR DETECTION OF MICROCALCIFICATIONS IN MAMMOGRAPHY” In International Journal of Pattern Recognition and Artificial Intelligence 07.06, 1993, pp. 1417–1436 DOI: 10.1142/S0218001493000698
- [48] Mohammad Saiful Islam Mamun et al. “Detecting Malicious URLs Using Lexical Analysis” In Network and System Security Cham: Springer International Publishing, 2016, pp. 467–482
Appendix A Overview of the Datasets
| Dataset | Reference | Normal class | Anomalous class |
|---|---|---|---|
| CC | [39] | Normal | Anomalous |
| Census | [40] | 50k | 50k |
| CoverT | [41] | 1-4 | 5-7 |
| DoH | [42] | Benign | Malicious |
| EMNIST | [43] | A-M | N-Z |
| FMNIST | [44] | 0-4 | 5-9 |
| KDD | [45] | Normal | Anomalous |
| MNIST | [46] | 0-4 | 5-9 |
| Mammo | [47] | Normal | Malignant |
| Toy | / | Normal | Anomalous |
| URL | [48] | Benign | Non-benign |
Appendix B Analysis of the DoH Dataset