Quaternary-singlet State of Spin-1 Bosons in Optical Lattice

Without the magnetic dipole-dipole interaction or for the intra-site pure spin-1 condensate $(\hat{H}_{0}=C\mathbf{\hat{F}}^{2})$, the simplest ground state for the F=1 spinor ²³Na condensates $(C>0)$ is a spin singlet formed by two spin-1 particles described as

with $F=F_{1}+F_{2}=0$ is the total spin, $m=m_{1}+m_{2}=0$ is the total z component, $G$ is the Clebsch-Gordon coefficient.

The operator $\hat{A}^{{\dagger}}\equiv(\hat{a}_{0}^{{\dagger}})^{2}-2\hat{a}_{1}^{{\dagger}}\hat{a}_{-1}^{{\dagger}}$ describe a singlet pair creating operator formed by two identical spin-1 bonsons, and the ground state of N particles is $(\hat{A}^{{\dagger}})^{N/2}\left|0\right\rangle.$ G is the CG coefficient. The particle density matrix $(\hat{\rho})_{\alpha\beta}=\left\langle\hat{a}_{\alpha}^{{\dagger}}\hat{a}_{\beta}\right\rangle$ is

with $\alpha,\beta$=$1,0,-1.$This matrix has three equal macroscopic eigenvalues called “superfragmented state”Ho and Yip . A weak external magnetic field along z $(\hat{H}_{0}=C\mathbf{\hat{F}}^{2}-p\hat{F}_{z})$ can break the pairs and polarize the system fragment1 ; fragment2 with the ground state described as

The particle numbers on the three Zeeman levels are redistributed as

with the 0-component distribution shrink rapidly as S increases.

For the subspace of exactly one particle per well, the Mott-insulator ground state of one-dimensional optical lattice has been confirmed to be a dimmer statesYip with the form,

where the state

The operator $\hat{\Theta}_{12}^{{\dagger}}\equiv\hat{a}_{0}^{{\dagger}}\hat{b}_{0}^{{\dagger}}-\hat{a}_{1}^{{\dagger}}\hat{b}_{-1}^{{\dagger}}-\hat{a}_{-1}^{{\dagger}}\hat{b}_{1}^{{\dagger}}$ describe a singlet pair creating operator formed by two spin-1 bonsons in the different site.

For more or at least two particles per well, the ground states are more complicated.

For simplify, we first consider $3\Lambda\hat{F}_{1z}\hat{F}_{2z}=0$, which serves as reference case for the complete discussion.

It can be rewrited aslizhibing ; Xuone ; Xutwo ; zj ; zj2 ; shiyu ; shiyu2

with $a=C_{1}-\Lambda/2$, $b=C_{2}-\Lambda/2$, and $c=\Lambda/2,\mathbf{\hat{F}}=\mathbf{\hat{F}}_{1}+\mathbf{\hat{F}}_{2}$ is the total spin operator. The eigenstates of (17) are the common eigenstates for the commuting operators $\mathbf{\hat{F}}_{1}^{2},\mathbf{\hat{F}}_{2}^{2},\mathbf{\hat{F}}^{2}$, and $\hat{F}_{z}$, given by

with the uncoupled basis states $\left|F_{1},m_{1}\right\rangle$ ($\left|F_{2},m_{2}\right\rangle)$ generated from equation (13) by a repeat using lowering operator $\hat{F}_{1-},$ and they can span a Hilbert space of dimension $(N_{1}+1)(N_{1}+2)/2$ MK . $C$ is the Clebsch-Gordon coefficient. The corresponding eigenenergy is

Given $N_{j}$, the allowed values of $F_{j}$ are $F_{j}=0,2,4,\cdots N_{j}$ if $N_{j}$ is even; and $F_{j}=1,3,5,\cdots N_{j}$ if $N_{j}$ is odd, satisfying $\left|F_{1}-F_{2}\right|\leqslant F\leqslant F_{1}+F_{2}$.

We will next consider the special case of $N_{1}=N_{2}=N$ and for $N$ even.

Fig. 1 shows the development of the four order parameters

for $\Lambda$ (in the unit of $\left|C_{1}\right|$) with even particles per well ( take $N_{1}=N_{2}=6$).We find that in the $\Lambda<\frac{-({2N-1})C_{2}}{C_{1}N}$ region, $\mathbf{\bar{F}}_{1}^{2},$ $\mathbf{\bar{F}}_{2}^{2},$ and $\mathbf{\bar{F}}_{1}\cdot\mathbf{\bar{F}}_{2}$ are all polarized to the maximum with the system being ferromagnetic. In the region $\Lambda\in\left[-C_{1}-C_{2},C_{1}+C_{2}\right]$, the two sites are essentially independent for a weak inter-sites dipole-dipole interaction. This phase is a total spin singlet $\mathbf{\bar{F}}^{2}=0$ described by the direct product of the polar ground state $(\hat{A}^{{\dagger}})^{N/2}(\hat{B}^{{\dagger}})^{N/2}\left|0\right\rangle$ giving rise to $\mathbf{\bar{F}}_{1}^{2}=0$ $\mathbf{\bar{F}}_{2}^{2}=0$and $\mathbf{\bar{F}}_{1}\cdot\mathbf{\bar{F}}_{2}=0.$When $\Lambda>\frac{({2N-1})C_{2}}{C_{1}({N+1})}$ they are polarized to the maximum but in the opposite directions with $\mathbf{\bar{F}}^{2}=0$ and $-2\mathbf{\bar{F}}_{1}\cdot\mathbf{\bar{F}}_{2}=\mathbf{\bar{F}}_{1}^{2}+\mathbf{\bar{F}}_{2}^{2}\neq 0$.We find interestingly that in this state the total spin vanishes, while the sites spins satisfy $\mathbf{\bar{F}}_{1}^{2}=\mathbf{\bar{F}}_{2}^{2}=N(N+1)$ .

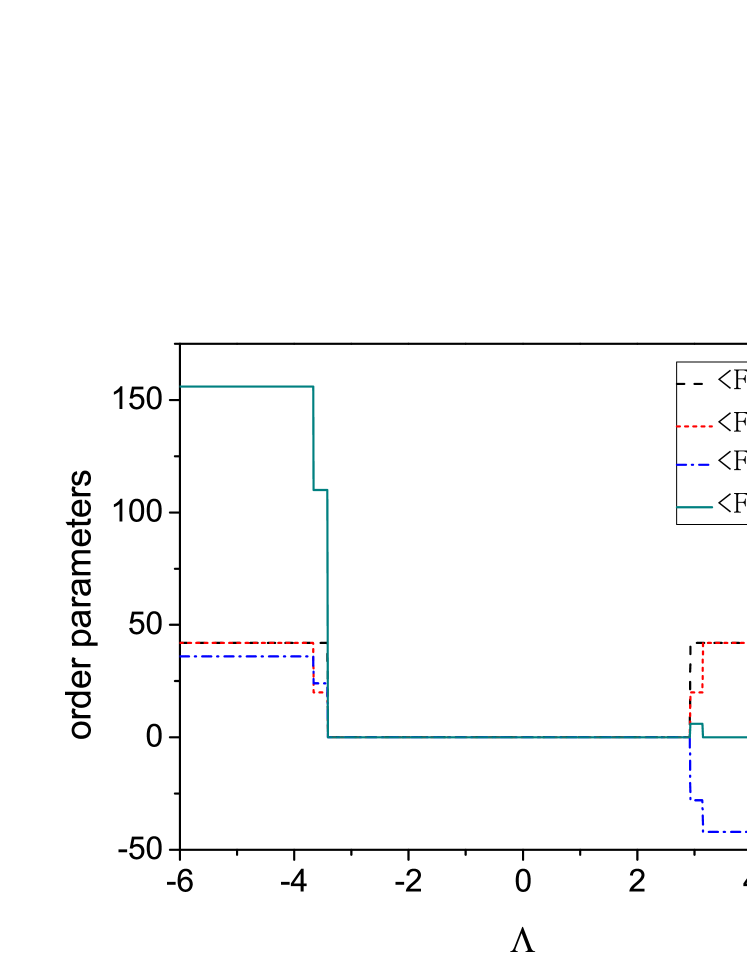
The ground state in the region $\Lambda>\frac{({2N-1})C_{2}}{C_{1}({N+1})}$ is a singlet, with all basis states obeying the condition $m_{1}+m_{2}=0$. All channels of total spin zero have to be taken

into account and we have

If we take $N_{1}$=$N_{2}$=$2$ for example, we find that

Compared to the “superfragmented state” $(\hat{A}^{{\dagger}})^{N/2}\left|0\right\rangle=((\hat{a}_{0}^{{\dagger}})^{2}-2\hat{a}_{1}^{{\dagger}}\hat{a}_{-1}^{{\dagger}})^{N/2}\left|0\right\rangle$Ho and Yip , this quaternary-singlet states has the similar appearance. However it is not the direct product of the two conventional singlet pairs, $\left|2,2,0,0\right\rangle\neq\hat{A}^{{\dagger}}\hat{B}^{{\dagger}}\left|0\right\rangle.$ The difference between $\left|N,N,0,0\right\rangle$ and $(\hat{A}^{{\dagger}})^{N/2}(\hat{B}^{{\dagger}})^{N/2}\left|0\right\rangle$ can be easily find in the phase diagram (Fig.1).

We notice that

and it is easy to understand that $\mathbf{\hat{F}}^{2}(\hat{\Theta}_{12}^{{\dagger}})^{N}\left|0\right\rangle=0.$ In this section, we will talk about three different singlet states, the quaternary-singlet state $\left|N,N,0,0\right\rangle,$ the dimer state $(\hat{\Theta}_{12}^{{\dagger}})^{N}\left|0\right\rangle$ and the direct product singlet state $(\hat{A}^{{\dagger}})^{N/2}(\hat{B}^{{\dagger}})^{N/2}\left|0\right\rangle,$ the properties such as

are shown in Fig.1.

As a exceptional case, all eigenvectors $\left|N,m_{1}\right\rangle$ in (18) can be expressed in terms of the Fock states Ying Wu , which are defined as

For the state $\left|N,N,0,0\right\rangle,$we calculate the particle numbers and number fluctuations on the Fock states and find that the average numbers of atoms in the six components are exactly all equal, $\left\langle n_{1}^{(j)}\right\rangle=\left\langle n_{0}^{(j)}\right\rangle=\left\langle n_{-1}^{(j)}\right\rangle=N/3$. The fluctuations are given explicitly

which approximatively satisfy $\left\langle\Delta n_{1}^{(j)}\right\rangle=2\left\langle\Delta n_{0}^{(j)}\right\rangle=\left\langle\Delta n_{-1}^{(j)}\right\rangle$ for large $N$zj , as opposed to $2\left\langle\Delta n_{1}\right\rangle=\left\langle\Delta n_{0}\right\rangle=2\left\langle\Delta n_{-1}\right\rangle$ for the single species or intra-site singlet state $(C_{1,2}>0)$ Ho and Yip .

The difference between these states are obvious. As total spin F vanishes, the number distributions are all $\left\langle n_{1}^{(j)}\right\rangle=\left\langle n_{0}^{(j)}\right\rangle=\left\langle n_{-1}^{(j)}\right\rangle=N/3,$ but the number fluctuation distribution in these states are quite different, it has been shown that for the state $Z^{1/2}(\hat{A}^{+})^{N_{1}}(\hat{B}^{+})^{N_{2}}\left|0\right\rangle$ Ho and Yip , they are

For the state $Z^{1/2}(\hat{\Theta}_{12}^{{\dagger}})^{N}\left|0\right\rangle,$ according to the multinomial theorem

with $c_{nlk}=n!/\left(l!(k-l)!(n-k)!\right)$, we find that the state $(\hat{\Theta}_{12}^{{\dagger}})^{N}\left|0\right\rangle$ can be described by the Fock state $\left|n_{1}^{(1)},n_{0}^{(1)},n_{-1}^{(1)}\right\rangle\otimes\left|n_{1}^{(2)},n_{0}^{(2)},n_{-1}^{(2)}\right\rangle$ as

where we have used the property $\left(\hat{a}^{{\dagger}}\right)^{N}\left|0\right\rangle=\sqrt{N!}\left|N\right\rangle$. We find that the number fluctuations are equally distributed, i.e.

For the real Hamiltonian (9), the last term plays an important role in domain formation and can polarize the spin to the same direction. This interaction offers a effect extra uniform weak field to the nearby site and breaks the singlet states. The ground state can be constructed using the quaternary-singlet state $\left|N,N,0,0\right\rangle$ and direct product singlet state $(\hat{A}^{{\dagger}})^{N/2}(\hat{B}^{{\dagger}})^{N/2}\left|0\right\rangle.$

In the region $\Lambda\in\left[-C_{1}-C_{2},C_{1}+C_{2}\right]$, since the spin singlet operator commutes with the spin   

and it does not change total spin and any spin components but just add two particles. Therefore, we can construct the unnormalized spin state for N particlesbefore2 : first, write down a state with necessary spin for a small number of particles; second, apply $\hat{A}^{{\dagger}}(\hat{B}^{{\dagger}})$ as many times as needed to get the desired number of particles. We got

with the fixed number in the two sites satisfied $T_{1,2}=(N_{1,2}-S_{1,2})/2.$

For the region $\Lambda>\frac{({2N-1})C_{2}}{C_{1}({N+1})},$ if we let $\left|N,N,0,0\right\rangle=Z^{1/2}(\hat{Q}^{{\dagger}})^{2N}\left|0\right\rangle,$the ground state for the Hamiltonian (9) is

In the $\Lambda<\frac{-({2N-1})C_{2}}{C_{1}N}$ region, the system is polarized to the ferromagnetic phase, the ground state is