Qudit entanglers using quantum optimal control
Abstract
We study the generation of two-qudit entangling quantum logic gates using two techniques in quantum optimal control. We take advantage of both continuous, Lie algebraic control and digital, Lie group control. In both cases, the key is access to a time-dependent Hamiltonian which can generate an arbitrary unitary matrix in the group SU(). We find efficient protocols for creating high-fidelity entangling gates. As a test of our theory, we study the case of qudits robustly encoded in nuclear spins of alkaline earth atoms and manipulated with magnetic and optical fields, with entangling interactions arising from the well-known Rydberg blockade. We applied this in a case study based on a dimensional qudit encoded in the nuclear spin in 87Sr, controlled through a combination of nuclear spin-resonance, a tensor AC-Stark shift, and Rydberg dressing, which allows us to generate an arbitrary symmetric entangling two-qudit gate such as CPhase. Our techniques can be used to implement qudit entangling gates for any encoded in the nuclear spin. We also studied how decoherence due to the finite lifetime of the Rydberg states affects the creation of the CPhase gate and found, through numerical optimization, a fidelity of , , , and for , , , and respectively. This provides a powerful platform to explore the various applications of quantum information processing of qudits including metrological enhancement with qudits, quantum simulation, universal quantum computation, and quantum error correction.
I Introduction
In the standard paradigm of quantum information processing (QIP) one encodes information in qubits, the quantum analog of classical bits, by isolating two well-chosen energy levels of the system. In many platforms, one has access and control over multiple levels, which can enhance our ability to do QIP in a variety of ways Wang et al. (2020); Blok et al. (2021); Gross (2021); Puri et al. (2020); Gottesman et al. (2001). In particular, one can encode information in base- using -level qudits Wang et al. (2020). With a larger state space per subsystem, qudits offer potential advantages for quantum communication Fujiwara et al. (2003), quantum algorithms Luo et al. (2014); Luo and Wang (2014); Li et al. (2013a); Lu et al. , and topological quantum systems Cui and Wang (2015); Cui et al. (2015); Bocharov et al. (2015) . Quantum computation with qudits can also reduce circuit complexity and can be advantageous in a variety of NISQ-era applications Brylinski and Brylinski (2002); Lu et al. ; Luo and Wang (2014); Li et al. (2013a); Zobov and Ermilov (2012); Weggemans et al. (2022); González-Cuadra et al. (2022).
Qudits may also provide significant advantages in quantum error correction and fault-tolerant quantum computation Campbell (2014); van Dam and Howard (2011); Gottesman (1999); Campbell et al. (2012); Kapit (2016). Of particular importance is reducing the physical resources needed to encode logical qubits. In the standard paradigm, logical qubits are encoded in multiple physical qubits, such as in the well-known surface code Fowler et al. (2012), which has a substantial overhead. An alternative approach is to encode a logical qubit in a single qudit. This has been a powerful tool, e.g., in encoding a logical qubit in the multiple harmonic levels of a bosonic mode Gottesman et al. (2001), and has been theoretically considered in high dimensional spin qudits in atoms Gross (2021); Omanakuttan and Gross (2023), molecules Albert et al. (2020), and in solid state devices Gross et al. (2021). Developing general methods for quantum control and entanglement of qudits would greatly expand the tools at our disposal.
In the gate-based approach to quantum computation with qubits, a universal gate set consists of single-qubit gates that generate the group SU and one entangling two-qubit gate, such as CNOT DiVincenzo (1995). This generalizes simply for qudits. The universal gate-set consists of the generators of single-qudit gates in SU() and an entangling two-qudit gate Muthukrishnan and Stroud (2000a); Zhou et al. (2003); Brennen et al. (2005). Unlike qubits, where native Hamiltonians can be used to naturally implement the desired gate set, qudits require more complex protocols. The gates that are necessary for the implementation of the universal gate set have been recently implemented for qudits in superconducting transmon Blok et al. (2021); Goss et al. (2022); Fischer et al. (2022) as well as in trapped ions Ringbauer et al. (2022); Hrmo et al. (2022) up to dimension . In these experiments, one implements qudit gates using constructive methods through a prescribed set of Givens rotations Brennen et al. (2005); Li et al. (2013b). While there has been substantial progress, much work remains to be done to efficiently implement a high-fidelity universal qudit gate set.
In this article, we study an alternative approach based on quantum optimal control. Quantum optimal control was originally developed in NMR Vandersypen and Chuang (2005) and for coherent control of chemistry Rabitz et al. (2000); sha (2011), and has been extensively used in quantum information processing Koch et al. (2022). We consider both continuous Hamiltonian control (Lie algebraic) and digital gate-based control (Lie group). Quantum optimal control has been experimentally implemented in a wide range of platforms ranging from ion traps Poulsen et al. (2010), neutral atoms Treutlein et al. (2006); Goerz et al. (2014a); Lysne et al. (2020), superconductors Rebentrost et al. (2009); Goerz et al. (2014b), and nitrogen vacancy (NV) centers Waldherr et al. (2014); Scheuer et al. (2014). Its use in implementing single-qudit gates was demonstrated in the seminal experiments of Jessen Anderson (2013) with information encoded in the hyperfine states of cesium and studied in Omanakuttan et al. (2021) for qudits encoded in the nuclear spin of alkaline-earth atoms. In this work, we extend these techniques to the implementation of entangling gates between two qudits. We study qudit entangling gates for any within the -dimensional Hilbert space of each subsystem.
As a concrete example that demonstrates the power of the method, we present here an optimal control scheme to implement entangling gates in qudits encoded in the nuclear spin of 87Sr atoms. The nuclear spin is a good memory for use in quantum information processing given its weak coupling to the environment and resilience to other background noise Barnes et al. (2022); Daley et al. (2008); Daley (2011). The ground state of the 87Sr is also studied in a recent paper as a possible candidate for qudit encoding with entangling interaction enabled by the Rydberg blockade Zache et al. (2023) Also, the recent significant achievements of quantum information processing using the Rydberg blockade Levine et al. (2019); Bluvstein et al. (2022); Graham et al. (2022) make this an ideal platform for exploring quantum computation. Using a combination of a tunable radio-frequency magnetic field and interactions that arise when atoms are excited to high-lying Rydberg states, the atomic qudit is fully controllable. We find that one can use quantum optimal control to implement high-fidelity entangling qudit gates even in the presence of decoherence arising from the finite Rydberg-state lifetime.
The remainder of this article is organized as follows. In Sec. II we review the fundamentals of quantum control and define two approaches: Lie algebraic and Lie group theoretic protocols for the generation of any arbitrary qudit entangling gates. In Sec. III, we study how control is achieved using numerical optimization based on the well-known GRAPE algorithm Khaneja et al. (2005) and obtain control waveforms using the Lie algebraic method. We also use a gradient-based approach to find a digital sequence of unitary maps that achieves the desired gate using a Lie group theoretic method. Finally, we study how decoherence affects the fidelity of these gates. We give conclusions and outlook of our approach in Sec. IV.
II Controllability
A complete universal gate set for qudits requires one entangling gate. A standard choice is the CPhase gate, which is the generalization of CZ gate for qubits, defined
| (1) |
where , the -th primitive root of identity for a subsystem of dimension . We can see that for we recover the CZ gate. This gate is locally equivalent to the qudit-analog of the CNOT gate, known as CSUM gate,
| (2) |
by the Hadamard gate for qudits, . Previous works have studied how to implement these gates through a well-defined sequence of maps generated by one-qudit and two-qudit Hamiltonians Brennen et al. (2005); Muthukrishnan and Stroud (2000b); Vlasov (2002); Brylinski and Chen (2002). We study here the use of numerical optimization and the theory of optimal control.
II.1 Lie algebraic approach

In the Lie algebraic approach to quantum control, we consider a Hamiltonian of the form , where is the set of time-dependent classical control waveforms, and is called the drift Hamiltonian. The system is said to be “controllable” if the set of Hamiltonians, , are generators of the desired Lie algebra, e.g., . Then such that for any target unitary in desired Lie Group, e.g., . In addition, we require , where is known as the “quantum speed limit time,” which sets the minimal time needed for the system to be fully controllable.
We consider here open-loop control determined by a well-defined Hamiltonian of the general form,
| (3) |
where are time-dependent Hamiltonians acting on the individual subsystems, and is the interaction that entangles them. Here we include the time dependence in the Hamiltonian that acts on the individual system as these will be generally easier to implement experimentally. In this formulation, , is the drift Hamiltonian. However, one could in principle include time dependence in the entangling Hamiltonian as well and this may achieve faster gates.
II.2 Lie group approach
In the digital, Lie group approach to quantum control, we consider a family of unitary maps in the desired group that are easily implementable, , where are the parameters that specify the unitary matrices at our disposal. The relevant Lie group of interest here is , the group of two-qudit unitary matrices in dimensions, where the overall phase is removed. The system is controllable if , such that . Similar to the Lie algebraic quantum control approach, the goal is to find through numeric optimization, e.g., via gradient-based methods.
For the case of two-qudit gates, a controllable Lie group structure is given as,
| (4) |
where and . Thus, we can achieve the target gate to the desired fidelity by intertwining a sequence of local gates and the available entangling interaction in alternating layers of single qudit gates and entangling gates, as shown in Fig. 1(b). This approach is similar to the construction based on Givens rotation Ringbauer et al. (2022). Here, the possibility of accessing arbitrary local gates makes this protocol very powerful. A schematic comparison of both these approaches is shown in Fig. 1.
II.3 Physical Platform: Rydberg atoms
To make these ideas concrete, we consider the implementation of entangling gates in neutral atoms using the strong van der Waals interactions between atoms in high-lying Rydberg states. We use the Rydberg dressing paradigm in which one adiabatically superposes the Rydberg state into the ground states to introduce interactions between dressed ground states Johnson and Rolston (2010); Keating et al. (2015); Jau et al. (2016); Zeiher et al. (2016, 2017); Borish et al. (2020). Rydberg dressing has been studied with multiple applications including the dynamics of interacting spin models Zeiher et al. (2016, 2017); Borish et al. (2020) as well as to prepare metrologically-useful states Kaubruegger et al. (2019). Entanglement between neutral atoms via Rydberg dressing has been theoretically proposed for creating qubit entangling gates Keating et al. (2015); Mitra et al. (2020, 2022) and experimentally implemented Jau et al. (2016); Martin et al. (2021); Schine et al. (2022).
We study here encoding a qudit in the spin of 87Sr. In the ground state there is neither orbital nor spin angular momentum in the electrons, , and only nuclear spin, , giving us ten possible levels in which to encode our qudit, labeled from . The nuclear spin is highly isolated from the environment and thus serves as a robust memory for quantum information. In Omanakuttan et al. (2021) we studied how we could implement single qudit gates in these systems through a combination of a laser-induced tensor light-shift and radio frequency (rf)-induced Larmor precession. We generalize to the two-qudit case here.
To implement entangling two-qudit control, we will make use of the excitation to the Rydberg series from the metastable first excited states. The choice of energy levels depends on practical considerations. By choosing the metastable state , the total electron angular momentum gives rise to a large magnetic dipole moment, which substantially increases the speed of gates, but this comes at the cost of increased sensitivity to background magnetic fields and residual tensor light shifts from the trapping lasers. By choosing the metastable clock state, one retains the robustness of having at the cost of much slower gates, since the magnetic coupling is now solely to the nuclear spin. We consider here coherently transferring qudits from the ground state to the state hyperfine states of the manifold, which provides for faster and more flexible control Trautmann et al. (2022), putting technical noise aside.
To achieve the entangling interaction, we consider Rydberg dressing, generalizing the mechanism discussed in Jau et al. (2016); Keating et al. (2015); Mitra et al. (2020). The AC Stark shift (light shift) associated with a dressed state when a laser is tuned near a Rydberg resonance is modified for two atoms because of the Rydberg blockade. The deficit between the two-atom light shift and twice the one-atom light shift determines the entangling energy Keating et al. (2015). For the case of qudits, the same physics holds, but now with a multilevel structure and a spectrum of entangling energies. When the spectrum is nonlinear, the system is controllable.

Fig. 2 depicts the basic scheme. Those levels of the qudit that we chose to participate in the gate are excited from the ground to the first excited state. The Rydberg states in 87Sr have well-resolved hyperfine splitting. We consider UV dressing laser near the resonance between the , hyperfine manifold and the , Rydberg hyperfine states. In the presence of a bias magnetic field, due to the difference in the g-factors, the two manifolds will be differently Zeeman shifted. The different magnetic sublevels that define the qudit will thus be differently detuned to the Rydberg magnetic sublevels. Due to this and the Clebsch-Gordan coefficients associated with the different transitions, each sublevel will be differently dressed (equivalently, there is a tensor light shift). When two atoms are dressed, the effect of the Rydberg blockade modifies the spectrum as discussed above.
An example of two sublevels (one from each atom) is shown in Fig. 2(b). Diagonializing this atom-laser Hamiltonian under the approximation of a perfect Rydberg blockade yields the representation
| (5) |
where the tilde indicates dressed states,
| (6) |
and are the light shifts originating from these interactions. The spectrum of the entangling Hamiltonian shown in Fig. 2(c) gives us insight into the controllability of the system. In the chosen order, the spectrum reveals the structure of quadratic potentials arising from a combination of the tensor light shift and Rydberg blockade. This nonlinearity makes the Hamiltonian controllable; further details are discussed in Appendix (B).
The time-dependent Hamiltonian necessary for the Lie algebraic control can be chosen as phase-modulated Larmor precession, , with the magnetic dipole vector operator, and where . Defining the auxilary subspace, , for the levels in hyperfine manifold and the subspace, , for the levels in the Rydberg hyperfine manifold, we have . Thus defining the Zeeman shift , the Larmor precession frequency , and choosing rf drive on resonance in the -manifold, , in the co-rotating frame at , the Hamiltonian is
| (7) | ||||
where are the spin angular momentum operators in the respective subspaces along axis .
As the acts on the laser-dressed states defined in Eq. (6), which are superpositions of and states that have different -factors, one needs to find the action of the magnetic interaction in the dressed basis. Due to the nonlinearity, the action of the rf-magnetic driving on the dressed states is no longer simple Larmor precession. Considering a global rf-magnetic interaction, the acts on both qudits as
| (8) | ||||
Thus in the dressed basis, the Hamiltonian is , where the action of the magnetic field in the dressed basis is given by the Hamiltonian,
| (9) | ||||
By modulating the phase one can generate any target unitary gate.
III Numerical Methods
We consider encoding a -dimensional qudit in the dimensional Hilbert space associated with magnetic sublevels of the nuclear spin of 87Sr. To implement gates based on optimal control for , we use techniques based on the structure of partial isometries. A partial isometry of dimension in a physical system of dimension is defined as,
| (10) |
where are two orthonormal bases for the qudit. The unitary of maps of interest then has the form,
| (11) |
where acts on the orthogonal subspace, with dimension . To find the control waveform, one then optimizes the fidelity between the target isometry and the isometry generated using quantum control Pedersen et al. (2007)
| (12) |
III.1 Numerical results for Lie algebraic approach
As discussed in Sec. IIc, one can implement an arbitrary entangling gate through a combination of Rydberg dressing and phase-modulated Larmor precession driven by rf-fields. Because our control Hamiltonian is symmetric with respect to the exchange of the qudits, we consider here symmetric gates, with global control. We seek, through numerical optimization, the time-dependent rf-phase, . To achieve this we employ the well-known GRAPE algorithm Khaneja et al. (2005). To implement GRAPE, we discretize the control waveform, , and numerically maximize the fidelity by gradient ascent. We choose here a piecewise constant parameterization (as in Anderson (2013)) and write the control waveform as a vector where and . The waveform is thus a series of square rf-pulses with constant amplitude and phase over the duration .
The minimum number of elements in the control vector is determined by the number of parameters needed to specify the target isometry. A -dimensional partial isometry is defined by the columns in a -dimensional unitary matrix. Hence, to find the number of free parameters for a -dimensional isometry one can count the number of parameters needed to specify orthonormal vectors uniquely in a -dimensional vector space. This is given by
| (13) | ||||
where in the first line, we subtracted one from the parameter count in since the overall phase of the isometry is neglected. Eq. (13) recovers well-known limits. When and , , which is the number of free parameters needed to specify a pure state in a -dimensional Hilbert space. When , , which is the number of free parameters needed to specify a special unitary map in -dimensions.
In the Lie algebraic protocol for designing entangling gates, the control Hamiltonian, as well as the target unitary matrices, are symmetric under the exchange of qudits. In this case, one can work in the symmetric subspace for two qudits. Using the hook length formula Frame et al. (1954), the dimension of the symmetric subspace of the total vector space and isometry is,
| (14) |
Thus, using Eq. (13), we find the number of free parameters required for the two-qubit entangling unitary given in Table 1.
| 2 | 320 |
| 3 | 623 |
| 5 | 1424 |
| 7 | 2295 |

Proof-of-principle numerical examples of waveforms that generate the CPhase gate are given in Fig. 3. The figure gives the as a piecewise constant function of time, obtained using the GRAPE algorithm. We consider prime-dimensional qudits, the cases of most interest in quantum algorithms. Fig. 3(a) shows the case of the , a qutrit encoded in . The total time is , which is divided into intervals for the quantum control. Fig. 3(b) shows an example waveform for the case of . Here, the total time is , divided into intervals. Similarly, Fig. 3(c) shows the case of in our level system. The total time is , divided into 2500 time intervals. This controllable Hamiltonian can also be used to generate other two-qudit gates. The qudit generalization of the Mlmer-Srensen gate, as is given in the Appendix C.
The waveforms found here are a proof-of-principle set of square pulses and are not intended to be taken as the best choice for experimental implementation. In practice, one can design and optimize for much smoother waveforms using well-known techniques by imposing additional constraints on bandwidth and slew rate. Alternatively, one can optimize in the Fourier domain or in any other complete basis of functions using the techniques of gradient optimization of analytic controls (GOAT) Machnes et al. (2018).
III.2 Numerical results for Lie group approach
In the Lie group control protocol discussed in Sec.IIc we parameterize the target unitary map as
| (15) | ||||
The control parameters consist of the set of times and the parameters , , which specify each of the local unitary maps. We can parameterize these according to
| (16) |
where is the generalized Gell-Mann matrices that span the Lie algebra . The matrices can be categorized as,
| symmetric: | (17) | |||
| anti-symmetric: | ||||
| diagonal: |
The task of the numerical optimization, thus, is to find the set of times of the entangling interaction , and the expansion coefficients of the Gell-Mann matrices and . We denote this whole set of parameter as .
We define one layer of the control as consisting of a pair of local SU gates followed by the entangling Hamiltonian for a time . The total number of free parameters for a CPhase gate is , as follows from Eq. (14) for a symmetric gate in . Thus, the minimum number of layers required to obtain the CPhase gate is given by
| (18) | ||||
The numerical results for the minimum number of layers needed in the system are given in Table 2 for the cases of and . In practice, we find that one needs more than this minimum number of layers to implement the target unitary gate with high fidelity. This improves the optimization landscape for gradientascent Larocca et al. (2018).
For our case under study, we choose the same entangling Hamiltonian as we used in the Lie algebraic approach given in Eq. (5). However, unlike that approach, we interleave the entangling interaction with local single-qudit SU() gates. Implementation of this requires another layer of optimization. As we do not have access to native Hamiltonians proportional to the Gell-Mann matrices, to implement local qudit gates we can employ local SU() optimal control Omanakuttan et al. (2021). From a practical perspective, this might be implemented directly in the manifold, either through a combination of tensor-light shift and rf-driven Larmor precession similar to Omanakuttan et al. (2021), or alternatively through a combination of microwave-driven Rabi oscillations between different hyperfine levels in and rf-driven Larmor procession as in Anderson (2013). In either case, optimal control can be used to find the relevant experimental waveform that generates the desired local gates.
| 3 | 3 | 6 | 7 |
| 5 | 7 | 10 | 12 |
| 7 | 13 | 14 | 15 |
In this analysis, we included locally addressable control on each qudit. Though the CPhase gate is symmetric under exchange, we find that this symmetry breaking is necessary for effective optimization of this parameterization, similar to that seen in Choquette et al. (2021). An alternative protocol is to employ symmetric global control of the local unitaries, , but to reverse the sign of the entangling Hamiltonian in alternating layers. This allows for effective optimization, and the corresponding result is given in Table (2).
III.3 Decoherence
In a closed quantum system, quantum optimal control employing either the Lie algebraic or the Lie group approaches can be used in principle to implement any qudit entangling gate to any desired fidelity. In our numerical optimization, we took the target infidelity to be . In the absence of decoherence, we could achieve that target in a reasonable time for . For , more time is required. However, the fundamentally achievable fidelity is limited by decoherence associated with the particular physical platform. For the system at hand, decoherence occurs due to the finite lifetime of the Rydberg states, which predominantly leads to leakage and loss outside the computational basis. In that case, we can model the gate as generated by a non-Hermitian effective Hamiltonian, , where the Hermitian part is the control Hamiltonian and the anti-Hermitian represents decay out of the Rydberg states. The fidelity of interest is given by
| (19) |
where . Here the decay amplitude from a dressed state is , which in turn gives the effective Hamiltonian as
| (20) |
With this model for decoherence in hand, the numerical results for the Lie algebraic approach are given in Fig. 4, which shows the infidelity as a function of time for a CPhase gate for different dimension isometries. We focus here on the case of the prime dimensional qudits. In contrast to closed-system control, in the presence of decoherence, infidelity decreases at first and then increases. This is due to the fact there is an optimal time of evolution, larger than the quantum speed limit, but not too large when compared to the coherence time of the system. As expected, one needs more time as the qudit dimension increases, which in turn results in an increase in the minimum infidelity one could achieve in each of these cases as shown in Fig. 4. We obtain a maximum fidelity of 0.9985, 0.9980, 0.9942, and 0.9800 for , , , and respectively for the CPhase gate. Note, the values of fidelity for different dimensional qudits should be considered in the context of a particular application. For example, the threshold for fault tolerance for qudits, in general, is larger for larger Anwar et al. (2014); Watson et al. (2015). For the particular scheme considered in Anwar et al. (2014), the threshold for , , , and are close to , , , and respectively. Hence, the proof-of-principle fidelity obtained here is promising and can be further optimized.

In the Lie group approach, we can use the effective Hamiltonian to describe the evolution when the Rydberg dressing is employed. In this case, we have,
| (21) | ||||
We neglect here any decoherence associated with the local SU() gates. Thus the fidelity including the decoherence effects is given as,
| (22) |

A comparison of the fidelities achieved based on the Lie algebraic and Lie group approaches is given in Fig. 5 for and . The results suggest that the Lie algebraic protocol slightly outperforms the Lie group protocol in the presence of decoherence.
This difference in the performance can be attributed to the time spent in the Rydberg state for these two approaches, as shown in Fig. 6. Fundamentally, we can understand this from the fact that the Lie algebraic approach has more control parameters as compared to the Lie group protocol. Thus, based on the Magnus expansion Merkel (2009); Jurdjevic and Sussmann (1972); Brockett (1973), the nested commutators which are at the heart of controllability become easier to achieve. Both approaches yield high fidelities in large dimensional qudits. Nevertheless, the Lie group approach may be preferable when considering the complexity necessary for experimental control.
In general, a key experimental consideration for the successful implementation of open-loop quantum control is the effect of uncertainties in Hamiltonian parameters. These can be mitigated to some degree using the tools of robust quantum control Anderson et al. (2015); Goerz (2015); Glaser et al. (2015); Koch (2016). Such techniques are generalizations of spin-echo type composite pulses which can be useful when there is sufficient coherence time. With a detailed understanding of the dominant inhomogeneities, robust optimal control can be used to implement suitable composite waveforms for qudit entanglers on any platform.
The specific experimental foundation of this proposal is well-motivated by existing literature, particularly the work of the Jessen group Anderson (2013). One particular issue discussed above is the trap-induced differential light shifts between the ground state and excited state manifold Trautmann et al. (2023). It will be necessary to mitigate motional dephasing arising from vector- and tensor-shifts, which induce an -dependence on polarizability, thus inducing possible motional dephasing between levels. The easiest way around this problem is to operate with a linearly-polarized optical trap, with polarization vector aligned at the “magic angle” Norcia et al. (2018) and corresponding magic wavelength Ye et al. (2008) for the transition. This allows intra-state coherence within the (and other -levels) manifold, and inter-state (i.e., optical qubit) coherence between the and . We can also mitigate motional effects via high-fidelity ground-state cooling Kaufman et al. (2012); Thompson et al. (2013); Lester et al. (2014).

IV Conclusion and Outlook
Quantum computation with qudits has potential advantages when compared with architectures employing qubits. Implementing gates for qudit-based quantum computation is fundamentally more challenging, as the generators for these gates are not native Hamiltonians on physical platforms. One way to overcome this challenge is to use the tools of quantum optimal control, whereby we combine native Hamiltonians with time-dependent waveforms that drive the system in order to implement a universal gate set with high fidelity.
In this work, we introduced two classes of numerical methods of quantum optimal control for implementing the qudit entangling gates, an essential component of the universal gate set. The first approach is based on continuous-time driving given a controllable Hamiltonian with tunable parameters and uses the Lie algebraic structure of the control problem. The second approach is more “digital,” using the Lie group structure to design a family of unitary maps that can be applied in sequence to achieve any nontrivial entangling gate of interest.
As a specific example, we studied encoding a qudit in the nuclear spin of 87Sr, a species of atoms that is particularly important in quantum information processing. The nuclear spin can accommodate a qudit of dimension . We have previously studied protocols for implementing single-qudit gates in SU(). To implement entangling gates we studied how we make two atoms interact using the well-known Rydberg blockade mechanism, and in particular, we studied Rydberg dressing schemes. Using this we are able to generate any two-qudit entangling gate, both using the Lie algebraic and Lie group based approaches.
We also studied how the fundamental effects of decoherence introduced by the finite lifetime of the Rydberg states reduce the gate fidelity. To model this we used a nonHermitian Hamiltonian and found that even when including decoherence, one could achieve high fidelity for these qudit entanglers. Given the flexibility of arbitrary control, we can seek the best approach to encoding qudits and mitigating errors.
Finally, while we have studied a particular case study in the context of neutral-atom quantum computing, the general methods we have developed here can be applied in other platforms, including trap ions transmon qudits, and nanomagnets Petiziol et al. (2021); Chiesa et al. (2021), which also have natural encoding and control Hamiltonians.
Acknowledgements.
This work was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project numbers 20200015ER and 20210116DR, and the NSF Quantum Leap Challenge Institutes program, Award No. 2016244. The authors acknowledge fruitful discussions with Sri Datta Vikas Buchemmavari, Milad Marvian, Pablo Poggi, Jonathan Gross, Irfan Siddiqi, and Noah Goss during various stages of this work.Appendix A Hyperfine structure of Rydberg states and Clebsch-Gordan coefficients

As described in the Sec. IIc, to create entanglement we promote the population from the ground state to the first excited state, with the hyperfine quantum number , and then consider a UV laser to excite the atoms to the Rydberg series to implement the interaction between atoms with adiabatic dressing (see Fig. 2). The Rabi frequency characterizing the coupling of the different levels in the hyperfine manifold to the Rydberg states will be different due to the Clebsch-Gordon Coefficients for these transitions. Let be the Rabi frequency on the ( transition). The Rabi frequency experienced by the other levels is then
| (23) |
where we have chosen and , and a -polarized light. In Fig. 7 the Rabi frequencies of the different levels are given as a function of , whose parabolic shape describes the tensor light shift, thus giving a natural nonlinearity which arises solely due to well-defined hyperfine structure of 87Sr.
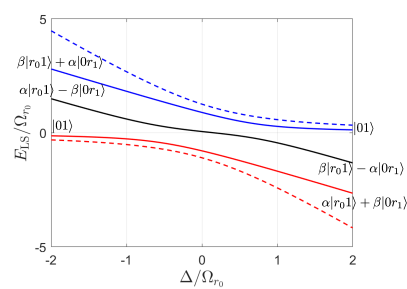
Consider the Rydberg dressing scheme in Fig. 2. In the perfect blockade regime, the two-atom Hamiltonian coupling of two magnetic sublevels labeled and is described by a three-level system, governed by the Hamiltonian,
| (24) | ||||
where determines the detunings due to the differential Zeeman shit. Fig. 8 shows the resulting AC Stark shifts on the three dressed states after diagonalizing this Hamiltonian. The dressed ground state is shown in red; the other two dressed states represent Autler-Townes splitting. In the absence of the van der Waals interaction the AC Stark shift (light shift) is the sum of the light shifts of each atom independently (dashed line in Fig. 8. The difference between these is the entangling energy.
One can understand the entangling power of the Hamiltonian by studying the properties of the dressed energy levels as a function of detuning. Figure 8 shows the particular case of , for the Hamiltonian in Eq. (24), where and . On the red side of detuning and for large detuning, as we start with the bare state and we adiabatically sweep through resonance, the state maps to the superposition of the two Rydberg states. Note, this is not an equal superposition as seen in Mitra et al. (2020) due to the fact that the states and couple with different Rydberg Rabi frequency and detuning to the Rydberg states.
Appendix B Controllability
The quantum system is said to be controllable if, given a time-dependent Hamiltonian , there exist a time-dependent set of waveforms , such that the one can generate an arbitrary unitary map. Here we consider those two-qudit unitary maps generated by an entangling Hamiltonian that is symmetric under the exchange of the qudits and thus does not require local addressing. To show that a Hamiltonian is controllable, we use the operator basis of irreducible spherical tensors on spin defined as Sakurai and Napolitano (2014); Klimov and Espinoza (2002),
| (25) |
These satisfy the fundamental commutation relations,
| (26) | ||||
The set of operators form a complete orthonormal operator basis. Merkel et al. Merkel (2009) showed that given a generating set of Hamiltonians , if
| (27) |
for , the system is fully controllable. That is, the set generates the whole Lie algebra of interest, which thus allows us to implement an arbitrary unitary map on the spin of the system using quantum control.
We consider two-qudit systems, where the relevant Lie Group is ; here . We expand the entangling Hamiltonian in the operator basis of spherical tensors with , spanning the space of dimension . Fig. 9 shows operator decomposition of the entangling Hamiltonian in different orders of spherical tensors. One can see in this figure that there are contributions from higher rank tensors, making the system controllable.

Appendix C Creating other symmetric qudit entanglers for the Lie algebraic approach

Since the Hamiltonian described in Eq.(3) can be used to create any symmetric two-qudit Hamiltonian, we can also generate the Mlmer-Srenson gate for qudits defined as,
| (28) |
where the total angular momentum operator for the two qudits is
| (29) |
We employ the same procedure for optimal control as we discussed in the main text in designing the waveforms to implement the CPhase gate. Numerical examples of the waveforms that create the Mlmer-Srenson gate for are given in Fig. 10. The figure shows , the piecewise constant of the control waveform, obtained using the GRAPE algorithm. Fig. 3(a) shows the case of the the qutrit encoded in . The total time is and we divide the time into time steps for the quantum control. In Fig. 3(b) we plot an example waveform for the case of the into our level system. We have a total time of and we divide the time into time steps for the quantum control. In Fig. 3(c) we plot an example for the case of the into our level system. We have a total time of and we divide the time into time steps for the quantum control.
References
- Wang et al. (2020) Yuchen Wang, Zixuan Hu, Barry C Sanders, and Sabre Kais, “Qudits and high-dimensional quantum computing,” Frontiers in Physics 8, 589504 (2020).
- Blok et al. (2021) M. S. Blok, V. V. Ramasesh, T. Schuster, K. O’Brien, J. M. Kreikebaum, D. Dahlen, A. Morvan, B. Yoshida, N. Y. Yao, and I. Siddiqi, “Quantum information scrambling on a superconducting qutrit processor,” Phys. Rev. X 11, 021010 (2021).
- Gross (2021) Jonathan A. Gross, “Designing codes around interactions: The case of a spin,” Phys. Rev. Lett. 127, 010504 (2021).
- Puri et al. (2020) Shruti Puri, Lucas St-Jean, Jonathan A. Gross, Alexander Grimm, Nicholas E. Frattini, Pavithran S. Iyer, Anirudh Krishna, Steven Touzard, Liang Jiang, Alexandre Blais, Steven T. Flammia, and S. M. Girvin, “Bias-preserving gates with stabilized cat qubits,” Science Advances 6, eaay5901 (2020), https://www.science.org/doi/pdf/10.1126/sciadv.aay5901 .
- Gottesman et al. (2001) Daniel Gottesman, Alexei Kitaev, and John Preskill, “Encoding a qubit in an oscillator,” Phys. Rev. A 64, 012310 (2001).
- Fujiwara et al. (2003) Mikio Fujiwara, Masahiro Takeoka, Jun Mizuno, and Masahide Sasaki, “Exceeding the classical capacity limit in a quantum optical channel,” Phys. Rev. Lett. 90, 167906 (2003).
- Luo et al. (2014) Ming-Xing Luo, Xiu-Bo Chen, Yi-Xian Yang, and Xiaojun Wang, “Geometry of quantum computation with qudits,” Scientific reports 4, 1–5 (2014).
- Luo and Wang (2014) MingXing Luo and XiaoJun Wang, “Universal quantum computation with qudits,” Science China Physics, Mechanics & Astronomy 57, 1712–1717 (2014).
- Li et al. (2013a) Bin Li, Zu-Huan Yu, and Shao-Ming Fei, “Geometry of quantum computation with qutrits,” Scientific reports 3, 2594 (2013a).
- (10) Hsuan-Hao Lu, Zixuan Hu, Mohammed Saleh Alshaykh, Alexandria Jeanine Moore, Yuchen Wang, Poolad Imany, Andrew Marc Weiner, and Sabre Kais, “Quantum phase estimation with time-frequency qudits in a single photon,” Advanced Quantum Technologies 3, 1900074, https://onlinelibrary.wiley.com/doi/pdf/10.1002/qute.201900074 .
- Cui and Wang (2015) Shawn X Cui and Zhenghan Wang, “Universal quantum computation with metaplectic anyons,” Journal of Mathematical Physics 56, 032202 (2015).
- Cui et al. (2015) Shawn X Cui, Seung-Moon Hong, and Zhenghan Wang, “Universal quantum computation with weakly integral anyons,” Quantum Information Processing 14, 2687–2727 (2015).
- Bocharov et al. (2015) Alex Bocharov, Shawn X. Cui, Martin Roetteler, and Krysta M. Svore, “Improved quantum ternary arithmetics,” (2015), arXiv preprint arXiv:1512.03824.
- Brylinski and Brylinski (2002) Jean-Luc Brylinski and Ranee Brylinski, “Universal quantum gates,” Mathematics of quantum computation 79 (2002).
- Zobov and Ermilov (2012) VE Zobov and AS Ermilov, “Implementation of a quantum adiabatic algorithm for factorization on two qudits,” Journal of Experimental and Theoretical Physics 114, 923–932 (2012).
- Weggemans et al. (2022) Jordi R Weggemans, Alexander Urech, Alexander Rausch, Robert Spreeuw, Richard Boucherie, Florian Schreck, Kareljan Schoutens, Jiří Minář, and Florian Speelman, “Solving correlation clustering with qaoa and a rydberg qudit system: a full-stack approach,” Quantum 6, 687 (2022).
- González-Cuadra et al. (2022) Daniel González-Cuadra, Torsten V. Zache, Jose Carrasco, Barbara Kraus, and Peter Zoller, “Hardware efficient quantum simulation of non-abelian gauge theories with qudits on rydberg platforms,” Phys. Rev. Lett. 129, 160501 (2022).
- Campbell (2014) Earl T. Campbell, “Enhanced fault-tolerant quantum computing in -level systems,” Phys. Rev. Lett. 113, 230501 (2014).
- van Dam and Howard (2011) Wim van Dam and Mark Howard, “Noise thresholds for higher-dimensional systems using the discrete wigner function,” Phys. Rev. A 83, 032310 (2011).
- Gottesman (1999) Daniel Gottesman, “Fault-tolerant quantum computation with higher-dimensional systems,” in Quantum Computing and Quantum Communications, edited by Colin P. Williams (Springer Berlin Heidelberg, Berlin, Heidelberg, 1999) pp. 302–313.
- Campbell et al. (2012) Earl T. Campbell, Hussain Anwar, and Dan E. Browne, “Magic-state distillation in all prime dimensions using quantum reed-muller codes,” Phys. Rev. X 2, 041021 (2012).
- Kapit (2016) Eliot Kapit, “Hardware-efficient and fully autonomous quantum error correction in superconducting circuits,” Phys. Rev. Lett. 116, 150501 (2016).
- Fowler et al. (2012) Austin G. Fowler, Matteo Mariantoni, John M. Martinis, and Andrew N. Cleland, “Surface codes: Towards practical large-scale quantum computation,” Phys. Rev. A 86, 032324 (2012).
- Omanakuttan and Gross (2023) Sivaprasad Omanakuttan and Jonathan Gross, “Multispin clifford codes for angular momentum errors in spin systems,” arXiv preprint arXiv:2304.08611 (2023).
- Albert et al. (2020) Victor V. Albert, Jacob P. Covey, and John Preskill, “Robust encoding of a qubit in a molecule,” Phys. Rev. X 10, 031050 (2020).
- Gross et al. (2021) Jonathan A Gross, Clément Godfrin, Alexandre Blais, and Eva Dupont-Ferrier, “Hardware-efficient error-correcting codes for large nuclear spins,” arXiv preprint arXiv:2103.08548 (2021).
- DiVincenzo (1995) David P. DiVincenzo, “Two-bit gates are universal for quantum computation,” Phys. Rev. A 51, 1015–1022 (1995).
- Muthukrishnan and Stroud (2000a) Ashok Muthukrishnan and C. R. Stroud, “Multivalued logic gates for quantum computation,” Phys. Rev. A 62, 052309 (2000a).
- Zhou et al. (2003) D. L. Zhou, B. Zeng, Z. Xu, and C. P. Sun, “Quantum computation based on d-level cluster state,” Phys. Rev. A 68, 062303 (2003).
- Brennen et al. (2005) Gavin K. Brennen, Dianne P. O’Leary, and Stephen S. Bullock, “Criteria for exact qudit universality,” Phys. Rev. A 71, 052318 (2005).
- Goss et al. (2022) Noah Goss, Alexis Morvan, Brian Marinelli, Bradley K Mitchell, Long B Nguyen, Ravi K Nail, Larry Chen, Christian Jünger, John Mark Kreikebaum, David I Santiago, et al., “High-fidelity qutrit entangling gates for superconducting circuits,” arXiv preprint arXiv:2206.07216 (2022), 10.48550/arXiv.2206.07216.
- Fischer et al. (2022) Laurin E Fischer, Alessandro Chiesa, Francesco Tacchino, Daniel J Egger, Stefano Carretta, and Ivano Tavernelli, “Towards universal gate synthesis and error correction in transmon qudits,” arXiv preprint arXiv:2212.04496 (2022), 10.48550/arXiv.2212.04496.
- Ringbauer et al. (2022) Martin Ringbauer, Michael Meth, Lukas Postler, Roman Stricker, Rainer Blatt, Philipp Schindler, and Thomas Monz, “A universal qudit quantum processor with trapped ions,” Nature Physics 18, 1053–1057 (2022).
- Hrmo et al. (2022) Pavel Hrmo, Benjamin Wilhelm, Lukas Gerster, Martin W van Mourik, Marcus Huber, Rainer Blatt, Philipp Schindler, Thomas Monz, and Martin Ringbauer, “Native qudit entanglement in a trapped ion quantum processor,” arXiv preprint arXiv:2206.04104 (2022).
- Li et al. (2013b) Chi-Kwong Li, Rebecca Roberts, and Xiaoyan Yin, “Decomposition of unitary matrices and quantum gates,” International Journal of Quantum Information 11, 1350015 (2013b).
- Vandersypen and Chuang (2005) L. M. K. Vandersypen and I. L. Chuang, “Nmr techniques for quantum control and computation,” Rev. Mod. Phys. 76, 1037–1069 (2005).
- Rabitz et al. (2000) Herschel Rabitz, Regina de Vivie-Riedle, Marcus Motzkus, and Karl Kompa, “Whither the future of controlling quantum phenomena?” Science 288, 824–828 (2000), https://www.science.org/doi/pdf/10.1126/science.288.5467.824 .
- sha (2011) Quantum Control of Molecular Processes (John Wiley & Sons, Ltd, 2011) Chap. 17, pp. 463–490, https://onlinelibrary.wiley.com/doi/pdf/10.1002/9783527639700.ch17 .
- Koch et al. (2022) Christiane P Koch, Ugo Boscain, Tommaso Calarco, Gunther Dirr, Stefan Filipp, Steffen J Glaser, Ronnie Kosloff, Simone Montangero, Thomas Schulte-Herbrüggen, Dominique Sugny, et al., “Quantum optimal control in quantum technologies. strategic report on current status, visions and goals for research in europe,” EPJ Quantum Technology 9, 19 (2022).
- Poulsen et al. (2010) Uffe V. Poulsen, Shlomo Sklarz, David Tannor, and Tommaso Calarco, “Correcting errors in a quantum gate with pushed ions via optimal control,” Phys. Rev. A 82, 012339 (2010).
- Treutlein et al. (2006) Philipp Treutlein, Theodor W. Hänsch, Jakob Reichel, Antonio Negretti, Markus A. Cirone, and Tommaso Calarco, “Microwave potentials and optimal control for robust quantum gates on an atom chip,” Phys. Rev. A 74, 022312 (2006).
- Goerz et al. (2014a) Michael H. Goerz, Eli J. Halperin, Jon M. Aytac, Christiane P. Koch, and K. Birgitta Whaley, “Robustness of high-fidelity rydberg gates with single-site addressability,” Phys. Rev. A 90, 032329 (2014a).
- Lysne et al. (2020) Nathan K. Lysne, Kevin W. Kuper, Pablo M. Poggi, Ivan H. Deutsch, and Poul S. Jessen, “Small, highly accurate quantum processor for intermediate-depth quantum simulations,” Phys. Rev. Lett. 124, 230501 (2020).
- Rebentrost et al. (2009) P. Rebentrost, I. Serban, T. Schulte-Herbrüggen, and F. K. Wilhelm, “Optimal control of a qubit coupled to a non-markovian environment,” Phys. Rev. Lett. 102, 090401 (2009).
- Goerz et al. (2014b) Michael H Goerz, Daniel M Reich, and Christiane P Koch, “Optimal control theory for a unitary operation under dissipative evolution,” New Journal of Physics 16, 055012 (2014b).
- Waldherr et al. (2014) Gerald Waldherr, Y Wang, S Zaiser, M Jamali, T Schulte-Herbrüggen, H Abe, T Ohshima, J Isoya, JF Du, P Neumann, et al., “Quantum error correction in a solid-state hybrid spin register,” Nature 506, 204–207 (2014).
- Scheuer et al. (2014) Jochen Scheuer, Xi Kong, Ressa S Said, Jeson Chen, Andrea Kurz, Luca Marseglia, Jiangfeng Du, Philip R Hemmer, Simone Montangero, Tommaso Calarco, Boris Naydenov, and Fedor Jelezko, “Precise qubit control beyond the rotating wave approximation,” New Journal of Physics 16, 093022 (2014).
- Anderson (2013) Brian Eric Anderson, “Unitary transformations in a large hilbert space,” (2013).
- Omanakuttan et al. (2021) Sivaprasad Omanakuttan, Anupam Mitra, Michael J. Martin, and Ivan H. Deutsch, “Quantum optimal control of ten-level nuclear spin qudits in ,” Phys. Rev. A 104, L060401 (2021).
- Barnes et al. (2022) Katrina Barnes, Peter Battaglino, Benjamin J Bloom, Kayleigh Cassella, Robin Coxe, Nicole Crisosto, Jonathan P King, Stanimir S Kondov, Krish Kotru, Stuart C Larsen, et al., “Assembly and coherent control of a register of nuclear spin qubits,” Nature Communications 13, 1–10 (2022).
- Daley et al. (2008) Andrew J. Daley, Martin M. Boyd, Jun Ye, and Peter Zoller, “Quantum computing with alkaline-earth-metal atoms,” Phys. Rev. Lett. 101, 170504 (2008).
- Daley (2011) Andrew J Daley, “Quantum computing and quantum simulation with group-ii atoms,” Quantum Information Processing 10, 865–884 (2011).
- Zache et al. (2023) Torsten V Zache, Daniel González-Cuadra, and Peter Zoller, “Fermion-qudit quantum processors for simulating lattice gauge theories with matter,” arXiv preprint arXiv:2303.08683 (2023).
- Levine et al. (2019) Harry Levine, Alexander Keesling, Giulia Semeghini, Ahmed Omran, Tout T. Wang, Sepehr Ebadi, Hannes Bernien, Markus Greiner, Vladan Vuletić, Hannes Pichler, and Mikhail D. Lukin, “Parallel implementation of high-fidelity multiqubit gates with neutral atoms,” Phys. Rev. Lett. 123, 170503 (2019).
- Bluvstein et al. (2022) Dolev Bluvstein, Harry Levine, Giulia Semeghini, Tout T Wang, Sepehr Ebadi, Marcin Kalinowski, Alexander Keesling, Nishad Maskara, Hannes Pichler, Markus Greiner, et al., “A quantum processor based on coherent transport of entangled atom arrays,” Nature 604, 451–456 (2022).
- Graham et al. (2022) TM Graham, Y Song, J Scott, C Poole, L Phuttitarn, K Jooya, P Eichler, X Jiang, A Marra, B Grinkemeyer, et al., “Multi-qubit entanglement and algorithms on a neutral-atom quantum computer,” Nature 604, 457–462 (2022).
- Khaneja et al. (2005) Navin Khaneja, Timo Reiss, Cindie Kehlet, Thomas Schulte-Herbrüggen, and Steffen J. Glaser, “Optimal control of coupled spin dynamics: design of nmr pulse sequences by gradient ascent algorithms,” Journal of Magnetic Resonance 172, 296–305 (2005).
- Muthukrishnan and Stroud (2000b) Ashok Muthukrishnan and C. R. Stroud, “Multivalued logic gates for quantum computation,” Phys. Rev. A 62, 052309 (2000b).
- Vlasov (2002) Alexander Yu Vlasov, “Noncommutative tori and universal sets of nonbinary quantum gates,” Journal of Mathematical Physics 43, 2959–2964 (2002).
- Brylinski and Chen (2002) Ranee K Brylinski and Goong Chen, Mathematics of quantum computation (CRC Press, 2002).
- Johnson and Rolston (2010) J. E. Johnson and S. L. Rolston, “Interactions between rydberg-dressed atoms,” Phys. Rev. A 82, 033412 (2010).
- Keating et al. (2015) Tyler Keating, Robert L. Cook, Aaron M. Hankin, Yuan-Yu Jau, Grant W. Biedermann, and Ivan H. Deutsch, “Robust quantum logic in neutral atoms via adiabatic rydberg dressing,” Phys. Rev. A 91, 012337 (2015).
- Jau et al. (2016) Y-Y Jau, AM Hankin, T Keating, IH Deutsch, and GW Biedermann, “Entangling atomic spins with a rydberg-dressed spin-flip blockade,” Nature Physics 12, 71–74 (2016).
- Zeiher et al. (2016) Johannes Zeiher, Rick Van Bijnen, Peter Schauß, Sebastian Hild, Jae-yoon Choi, Thomas Pohl, Immanuel Bloch, and Christian Gross, “Many-body interferometry of a rydberg-dressed spin lattice,” Nature Physics 12, 1095 (2016).
- Zeiher et al. (2017) Johannes Zeiher, Jae-yoon Choi, Antonio Rubio-Abadal, Thomas Pohl, Rick van Bijnen, Immanuel Bloch, and Christian Gross, “Coherent many-body spin dynamics in a long-range interacting ising chain,” Phys. Rev. X 7, 041063 (2017).
- Borish et al. (2020) V. Borish, O. Marković, J. A. Hines, S. V. Rajagopal, and M. Schleier-Smith, “Transverse-field ising dynamics in a rydberg-dressed atomic gas,” Phys. Rev. Lett. 124, 063601 (2020).
- Kaubruegger et al. (2019) Raphael Kaubruegger, Pietro Silvi, Christian Kokail, Rick van Bijnen, Ana Maria Rey, Jun Ye, Adam M. Kaufman, and Peter Zoller, “Variational spin-squeezing algorithms on programmable quantum sensors,” Phys. Rev. Lett. 123, 260505 (2019).
- Mitra et al. (2020) Anupam Mitra, Michael J. Martin, Grant W. Biedermann, Alberto M. Marino, Pablo M. Poggi, and Ivan H. Deutsch, “Robust mølmer-sørensen gate for neutral atoms using rapid adiabatic rydberg dressing,” Phys. Rev. A 101, 030301 (2020).
- Mitra et al. (2022) Anupam Mitra, Sivaprasad Omanakuttan, Michael J Martin, Grant W Biedermann, and Ivan H Deutsch, “Practical and fundamental limits of neutral atom entanglement using rydberg dressing,” arXiv preprint arXiv:2205.12866 (2022).
- Martin et al. (2021) Michael J Martin, Yuan-Yu Jau, Jongmin Lee, Anupam Mitra, Ivan H Deutsch, and Grant W Biedermann, “A mølmer-sørensen gate with rydberg-dressed atoms,” arXiv e-prints , arXiv–2111 (2021).
- Schine et al. (2022) Nathan Schine, Aaron W Young, William J Eckner, Michael J Martin, and Adam M Kaufman, “Long-lived bell states in an array of optical clock qubits,” Nature Physics 18, 1067–1073 (2022).
- Trautmann et al. (2022) Jan Trautmann, Dimitry Yankelev, Valentin Klüsener, Annie Jihyun Park, Immanuel Bloch, and Sebastian Blatt, “The magnetic quadrupole transition in neutral strontium,” arXiv preprint arXiv:2211.02470 (2022).
- Pedersen et al. (2007) Line Hjortshøj Pedersen, Niels Martin Møller, and Klaus Mølmer, “Fidelity of quantum operations,” Physics Letters A 367, 47–51 (2007).
- Frame et al. (1954) J Sutherland Frame, G de B Robinson, and Robert M Thrall, “The hook graphs of the symmetric group,” Canadian Journal of Mathematics 6, 316–324 (1954).
- Machnes et al. (2018) Shai Machnes, Elie Assémat, David Tannor, and Frank K. Wilhelm, “Tunable, flexible, and efficient optimization of control pulses for practical qubits,” Phys. Rev. Lett. 120, 150401 (2018).
- Larocca et al. (2018) Martín Larocca, Pablo Poggi, and Diego Wisniacki, “Quantum optimal control: Landscape structure and topology,” arXiv preprint arXiv:1802.05683 (2018).
- Choquette et al. (2021) Alexandre Choquette, Agustin Di Paolo, Panagiotis Kl. Barkoutsos, David Sénéchal, Ivano Tavernelli, and Alexandre Blais, “Quantum-optimal-control-inspired ansatz for variational quantum algorithms,” Phys. Rev. Research 3, 023092 (2021).
- Anwar et al. (2014) Hussain Anwar, Benjamin J Brown, Earl T Campbell, and Dan E Browne, “Fast decoders for qudit topological codes,” New Journal of Physics 16, 063038 (2014).
- Watson et al. (2015) Fern H. E. Watson, Hussain Anwar, and Dan E. Browne, “Fast fault-tolerant decoder for qubit and qudit surface codes,” Phys. Rev. A 92, 032309 (2015).
- Merkel (2009) Seth Merkel, “Quantum control of d-dimensional quantum systems with application to alkali atomic spins,” arXiv preprint arXiv:0906.4790 (2009), 10.48550/arXiv.0906.4790.
- Jurdjevic and Sussmann (1972) Velimir Jurdjevic and Héctor J Sussmann, “Control systems on lie groups,” Journal of Differential equations 12, 313–329 (1972).
- Brockett (1973) Roger W Brockett, “Lie theory and control systems defined on spheres,” SIAM Journal on Applied Mathematics 25, 213–225 (1973).
- Anderson et al. (2015) B. E. Anderson, H. Sosa-Martinez, C. A. Riofrío, Ivan H. Deutsch, and Poul S. Jessen, “Accurate and robust unitary transformations of a high-dimensional quantum system,” Phys. Rev. Lett. 114, 240401 (2015).
- Goerz (2015) Michael Hartmut Goerz, Optimizing robust quantum gates in open quantum systems, Ph.D. thesis (2015).
- Glaser et al. (2015) Steffen J Glaser, Ugo Boscain, Tommaso Calarco, Christiane P Koch, Walter Köckenberger, Ronnie Kosloff, Ilya Kuprov, Burkhard Luy, Sophie Schirmer, Thomas Schulte-Herbrüggen, et al., “Training schrödinger’s cat: quantum optimal control,” The European Physical Journal D 69, 1–24 (2015).
- Koch (2016) Christiane P Koch, “Controlling open quantum systems: tools, achievements, and limitations,” Journal of Physics: Condensed Matter 28, 213001 (2016).
- Trautmann et al. (2023) J. Trautmann, D. Yankelev, V. Klüsener, A. J. Park, I. Bloch, and S. Blatt, “ magnetic quadrupole transition in neutral strontium,” Phys. Rev. Res. 5, 013219 (2023).
- Norcia et al. (2018) M. A. Norcia, A. W. Young, and A. M. Kaufman, “Microscopic control and detection of ultracold strontium in optical-tweezer arrays,” Phys. Rev. X 8, 041054 (2018).
- Ye et al. (2008) Jun Ye, H. J. Kimble, and Hidetoshi Katori, “Quantum state engineering and precision metrology using state-insensitive light traps,” Science 320, 1734–1738 (2008), https://www.science.org/doi/pdf/10.1126/science.1148259 .
- Kaufman et al. (2012) Adam M Kaufman, Brian J Lester, and Cindy A Regal, “Cooling a single atom in an optical tweezer to its quantum ground state,” Physical Review X 2, 041014 (2012).
- Thompson et al. (2013) Jeffrey Douglas Thompson, TG Tiecke, Alexander S Zibrov, V Vuletić, and Mikhail D Lukin, “Coherence and raman sideband cooling of a single atom in an optical tweezer,” Physical review letters 110, 133001 (2013).
- Lester et al. (2014) Brian J Lester, Adam M Kaufman, and Cindy A Regal, “Raman cooling imaging: Detecting single atoms near their ground state of motion,” Physical Review A 90, 011804 (2014).
- Petiziol et al. (2021) Francesco Petiziol, Alessandro Chiesa, Sandro Wimberger, Paolo Santini, and Stefano Carretta, “Counteracting dephasing in molecular nanomagnets by optimized qudit encodings,” npj Quantum Information 7, 133 (2021).
- Chiesa et al. (2021) A Chiesa, F Petiziol, E Macaluso, S Wimberger, P Santini, and S Carretta, “Embedded quantum-error correction and controlled-phase gate for molecular spin qubits,” AIP Advances 11, 025134 (2021).
- Sakurai and Napolitano (2014) J Sakurai and J Napolitano, “Modern quantum mechanics. 2-nd edition,” Person New International edition (2014).
- Klimov and Espinoza (2002) A B Klimov and P Espinoza, “Moyal-like form of the star product for generalized su(2) stratonovich-weyl symbols,” Journal of Physics A: Mathematical and General 35, 8435 (2002).