Quorums Quicken Queries: Efficient Asynchronous Secure Multiparty Computation
Abstract
We describe an asynchronous algorithm to solve secure multiparty computation (MPC) over players, when strictly less than a fraction of the players are controlled by a static adversary. For any function over a field that can be computed by a circuit with gates, our algorithm requires each player to send a number of field elements and perform an amount of computation that is . This significantly improves over traditional algorithms, which require each player to both send a number of messages and perform computation that is .
Additionaly, we define the threshold counting problem and present a distributed algorithm to solve it in the asynchronous communication model. Our algorithm is load balanced, with computation, communication and latency complexity of , and may be of independent interest to other applications with a load balancing goal in mind.
1 Introduction
Recent years have seen a renaissance in secure multiparty computation (MPC), but unfortunately, the distributed computing community is in danger of missing out. In particular, while new MPC algorithms boast dramatic improvements in latency and communication costs, none of these algorithms offer significant improvements in the highly distributed case, where the number of players is large.
This is unfortunate, since MPC holds the promise of addressing many important problems in distributed computing. How can peers in Bittorrent auction off resources without hiring an auctioneer? How can we design a decentralized Twitter that enables provably anonymous broadcast of messages. How can we create deep learning algorithms over data spread among large clusters of machines?
In this paper, we take a first step towards solving MPC for large distributed systems. We describe algorithms that require each player to send a number of messages and perform an amount of computation that is , where is the number of players and is the number of gates in the circuit to be computed. This significantly improves over current algorithms, which require each player to both send a number of messages and perform computation that is . We now describe our model and problem.
Model There are players, with a private and authenticated channel between every pair of players. Communication is via asynchronous message passing, so that sent messages may be arbitrarily and adversarially delayed. Latency in this model is defined as the maximum length of any chain of messages (see [11, 3]).
We assume a Byzantine adversary controls an unknown subset of up to of the players. These players are bad (i.e. Byzantine) and the remaining players are good. The good players run our algorithm, but the bad players may deviate in an arbitrary manner. Our adversary is static, i.e. it must select the set of bad players at the start of our algorithm. The adversary is computationally unbounded. Thus, we make no cryptographic hardness assumptions.
MPC Problem: Each player, , has a private input . All players know a -ary function . We want to ensure that: 1) all players learn the value of on the inputs; and 2) the inputs remain as private as possible: each player learns nothing about the private inputs other than what is revealed by the output of and the player’s private value .
In the asynchronous setting, the problem is challenging even with a trusted third party. In particular, the trusted party can not determine the difference between a message never being sent and a message being arbitrarily delayed, and so the bad players can always refrain from sending any messages to the trusted party. Thus, the trusted party must wait to receive inputs. Then it must compute the function using default values for the missing inputs, and send the output back to the players as well as the number of received inputs.111We send back only the number of inputs used, not the set of players whose inputs are used. This is required to ensure scalability; see Section 6. The goal of an asynchronous MPC protocol is to simulate the above scenario, without the trusted third party.
The function to be computed is presented as a circuit with gates. For convenience of presentation, we assume each gate has fan-in two and fan-out at most two. For any two gates and in , if the output of is input to , we say that is a child of and that is a parent of . We also assume that all computations in the circuit occur over a finite field ; The size of depends on the specific function to be computed but must always be . All the inputs, outputs and messages sent during the protocol are elements of , and consequently, messages will be of size .
Our MPC result requires solutions to the following two problems, which may be of independent interest.
Threshold Counting There are good players each with a bit initially set to . At least of the players will eventually set their bits to . The goal is for all the players to learn when the number of bits with values is at least .
Quorum Formation There are players, up to of whom may be bad. A quorum is a set of players for some constant . A quorum is called good if the fraction of bad players in it is at most for a fixed positive . We want all players to agree on a set of good quorums, and we want the quorums to be load-balanced: each player is mapped to quorums.
1.1 Our Results
The main result of this paper is summarized by the following theorem.
Theorem 1.1
Assume there are players, less than a fraction of which are bad for some fixed , and an -ary function, that can be computed by a circuit of depth with gates. If all good players follow Algorithm 1, then with high probability (w.h.p.), they will solve MPC, while ensuring:
-
1.
Each player sends at most field elements,
-
2.
Each player performs computations, and
-
3.
Expected total latency is .
Our additional results are given by the following two theorems.
Theorem 1.2
Assume good players follow Algorithm -Counter. Then w.h.p., the algorithm solves the threshold counting problem, while ensuring:
-
1.
Each player sends at most messages of constant size,
-
2.
Each player receives at most messages,
-
3.
Each player performs computations,
-
4.
Total latency is .
Theorem 1.3
Assume players, up to of whom are bad, for fixed . If all good players follow the Create-Quorum protocol, the following are ensured w.h.p.:
-
1.
The players agree on good quorums,
-
2.
Each player sends at most bits,
-
3.
Each player performs computations,
-
4.
Total latency is .
In the rest of the paper we discuss the algorithms and ideas involved in obtaining these results. Detailed proofs are deferred to the full version [16].
2 Related Work
The study of secure computation started in 1982 with the seminal work of Yao [27]. Later Goldrich, Micali, and Wigderson [20] proposed the first generic scheme for solving a cryptographic notion of MPC. This work was followed by some unconditionally-secure schemes in late 1980s [6, 10, 26, 5, 21, 22, 4]. Unfortunately, these methods all have poor communication scalability that prevents their wide-spread use. In particular, if there are players involved in the computation and the function is represented by a circuit with gates, then these algorithms require each player to send a number of messages and perform a number of computations that is (see [18, 19, 17]).
Recent years have seen exciting improvements in the cost of MPC when is much larger than [12, 14, 13]. For example, the computation and communication cost for the algorithm described by Damgård et al. in [13] is plus a polynomial in . However, the additive polynomial in is large (e.g. ) and so these new algorithms are only efficient for relatively small . Thus, there is still a need for MPC algorithms that are efficient in both and .
We first introduced the notion of using quorums for local communication to decrease the message cost in a brief announcement [15]. In that paper, we described a synchronous protocol with bit complexity of per player that can tolerate a computationally unbounded adversary who controls up to fraction of the players for any fixed positive . This paper improves our previous result by handling asynchronous communication. One important challenge in the asynchronous communication model is to ensure that at least inputs are committed to, before the circuit evaluation. To address this issue we introduce and solve the threshold counting problem.
Boyle, Goldwasser, and Tessaro [8] describe a synchronous cryptographic protocol to solve MPC problem that is also based on quorums. Their algorithm uses a fully homomorphic encryption (FHE) scheme and thus, tolerates a computationally-bounded adversary that can take control of up to () fraction of players for any fixed positive . Their protocol requires each player to send messages of size bits and requires rounds. Interestingly the cost of the protocol is independent of the circuit size.
Counting Networks Threshold counting can be solved in a load-balanced way using counting networks, which were first introduced by Aspnes, Herlihy, and Shavit [2]. Counting networks are constructed from simple two-input two-output computing elements called balancers connected to one another by wires. A counting network can count any number of inputs even if they arrive at arbitrary times, are distributed unevenly among the input wires, and propagate through the network asynchronously. Aspnes, Herlihy, and Shavit [2] establish an upper bound on the depth complexity of counting networks. Since the latency of counting is dependent to the depth of the network, minimizing the network’s depth is a goal for papers in this area. A simple explicit construction of an -depth counting network, and a randomized construction of an -depth counting networkwhich works with high probability is described in [24, 25]. These constructions use the AKS sorting network [1] as a building block. While the AKS sorting network and the resulting counting networks have depth, large hidden constants render them impractical. We note that the threshold counting problem is simpler than general counting.
3 Preliminaries
We say an event occurs with high probability (w.h.p), if it occurs with probability at least , for some and sufficiently large . We assume all computations occur over a finite field . Every time we use a mask during the protocol, we assume the mask is a value chosen uniformly at random from .
We now describe protocols that we use as building blocks in this paper.
Secret Sharing In secret sharing, a player, called the dealer, wants to distribute a secret amongst a group of participants, each of whom is allocated a share of the secret. The secret can be reconstructed only when a sufficient number of shares are combined together and each of the shares reveals nothing to the player possessing it. If a method is used to ensure the dealer sends shares of a real secret and not just some random numbers, then the new scheme is called Verifiable Secret Sharing (VSS). As our model is asynchronous, we use the asynchronous VSS (or AVSS) scheme described by Benor, Canneti and Goldreich in [5]. We denote the sharing phase by Avss-Share and the reconstruction phase by Avss-Rec. The protocol of [5] works correctly even if up to of the players are bad. The latency of the protocols is and the communication cost is , where is the number of players participating in the protocol. In this paper, we will use the protocols only among small sets of players (quorums) of logarithmic size, so will be and the communication cost per invocation will be .
Heavy-Weight MPC We use a heavy-weight asynchronous algorithm for MPC donated by Hw-MPC. This algorithm, due to Ben-Or et al. [5], is an errorless MPC protocol that tolerates up to bad players. Let be the number of players who run a Hw-MPC to compute a circuit with gates. The expected latency of Hw-MPC is and the number of messages sent . In this paper, we will use Hw-MPC only for logarithmic number of players and gates, i.e. , and the communication cost per invocation is .222To make sure our algorithm has the expected total latency equal to , every time we need to run the Hw-MPC algorithm, we run same copy of it each for steps.
Asynchronous Byzantine Agreement In the Byzantine agreement problem, each player is initially given an input bit. All good players want to agree on a bit which coincides with at least one of their input bits. Every time a broadcast is required in our protocol, we use an asynchronous Byzantine agreement algorithm from [9], which we call Asynch-BA.
4 Technical Overview
We briefly sketch the ideas behind our three results.
Quorum-Based Gate Evaluation The main idea for reducing the amount of communication required in evaluating the circuit is quorum-based gate evaluation. Unfortunately, if each player participates in the computation of the whole circuit, it must communicate with all other players. Instead, in quorum-based gate evaluation, each gate of the circuit is computed by a gate gadget. A gate gadget consists of three quorums: two input quorums and one output quorum. Input quorums are associated with the gate’s children which serve inputs to the gate. Output quorum is associated with the gate itself and is responsible to create a shared random mask and maintain the output of the quorum for later use in the circuit. As depicted in Figure 1, these gate gadgets connect to form the entire circuit. In particular, for any gate , the output quorum of ’s gadget is the input quorum of the gate gadget for all of ’s parents (if any).

The players in each gate gadget run Hw-MPC among themselves to perform the gate operation. To make sure the computation is correct and secure, each gate gadget maintains the invariant that the value computed by the gadget is the value that the corresponding gate in the original circuit would compute, masked by a uniformly random element of the field. This random number is not known to any individual player. Instead, shares of it are held by the members of the output quorum. Thus, the output quorum can participate as an input quorum for the evaluation of any parent gate and provide the masked version of the inputs and shares of the mask.
This gate gadget computation is continued in the same way for all gates of the circuit until the final output of whole circuit is evaluated. This technique for evaluating a gate of the circuit using quorums, is illustrated in Figure 5.2 and the details are described in Section 5.1.
Threshold Counting Our interest in threshold counting for this paper is to ensure that at least inputs are committed to, before the circuit evaluation occurs. To solve the threshold counting problem, we design a new distributed data structure and algorithm called -Counter. The -Counter enables threshold counting with asynchronous communication, and may be of use for other problems beyond MPC.
To give intuition, we first consider a naive approach for counting in asynchronous model. Assume a complete binary tree where each player sends its input to a unique leaf node when it is set to . Then, for every node , each child of sends a message showing the number of inputs it has received so far and it sends the updated message every time this number changes. The problem with this approach is that it is not load-balanced: each node at depth has descendants in the tree, and therefore, in the worst case, sends and receives messages. Thus, a child of the root sends messages to the root and receives the same number of messages from its children. To solve the load-balancing problem, we use a randomized approach which ensures w.h.p. that each leaf of the data structure receives at least messages and does not communicate with its parent until it has done so. Subsequnt messages it receives are not forwarded to its parent but rather to other randomly chosen leaves to ensure a close to uniform distribution of the messages. The details of our algorithm are described in Section 5.1 and more formally in Algorithm 2. Theorem 1.2 describes the resource complexity of the algorithm.
Asynchronous Quorum Formation Recently, King et al. [23] described an efficient algorithm to solve the quorum formation problem, w.h.p., in the synchronous model with full information. Our new algorithm, Create-Quorum, builds on the result of [23] to solve the quorum formation problem in the asynchronous model, with private channels. The properties of Create-Quorum, are described by Theorem 1.3. The algorithm and the proof are deferred to the full version [16] due to space restrictions.
5 Our Algorithm
Our algorithm makes use of a circuit graph, , which is based on the circuit that computes . We assume the gates of the circuit are numbered , where the gate numbered 1 is the output gate. The circuit graph is a directed acyclic graph over nodes. There are of these nodes, one per player, that we call input nodes. There are remaining nodes, one per gate, that we call gate nodes. For every pair of gate nodes and , there is an edge from to iff the output of the gate represented by node is an input to the gate represented by node . Also, for any input node and gate node , there is an edge from to if the player represented by gate node has an input that feeds into the gate represented by node . Similar to our definition in , for any two nodes and in , if has an edge to , we say that is a child of and that is a parent of . Also, for a given node , we will say the height of is the number of edges on the longest path from to any input node in . For each node in , we define the following variables. is the quorum associated with node . is the output of the gate corresponding to . Finally, is a random mask and is the masked output associated with node , i.e. .
We number the nodes of canonically in such a way that the input node numbered corresponds to player . We refer to the node corresponding to the output gate as the output node.
Algorithm 1 consists of four parts. The first part is to run Create-Quorum in order to agree on good quorums. The second part of the algorithm is Input-Commitment in which, quorums form the count tree. Then, each player commits its input values to quorum at the leaf nodes of the count tree and finally the players in that quorum decide whether these values are part of the computation or not. The details of this part of the algorithm is described in Section 5.1. The third part of the algorithm is evaluation of the circuit, described in detail in Section 5.2). Finally, the output from the circuit evaluation is sent back to all the players by quorums arranged in a complete binary tree.
-
1.
All players run Create-Quorum,
-
2.
All players run Input-Commitment,
-
3.
All players run Circuit-Eval,
-
4.
Propagate the output by quorums arranged in a complete binary tree.
5.1 Input-Commitment
In this section we describe a Monte Carlo algorithm, called -Counter that performs threshold counting for a threshold .
The algorithm consists of up and down stages. For the up stage the players are arranged in a (pre-determined) tree data structure consisting of a root node with children, each of which is itself the root of a complete binary tree; these subtrees have varying depths. The players in the trees count the number of -inputs, i.e. the number of players’ inputs that are set to . As a result, the root can decide when the threshold is reached. In the down stage, the root notifies all the players of this event via a complete binary tree of depth . Note that the trees used in the up and down stages have the same root. In what follows, unless otherwise specified, “tree” will refer to the tree data structure used for the up stage.
Let . Note that . The root of our tree has degree . Each of the children of the root is itself the root of a complete binary subtree, which we will call a collection subtree. For , the th collection subtree has depth . Player 1 is assigned to the root and players 2 to , are assigned to its children, i.e. the roots of the collection subtrees, with player being assigned to the th child. The remaining nodes of the collection trees are assigned players in order, starting with , left to right and top to bottom. One can easily see that the entire data structure has fewer than nodes, (in fact it has fewer than nodes) so some players will not be assigned to any node.
The leaves of each collection subtree are collection nodes while the internal nodes of each collection tree are adding nodes.
When a player’s input is set to , it sends a message, which we will sometimes simply refer to as a flag, to a uniformly random collection node from the first collection subtree. Intuitively, we want the flags to be distributed close to evenly among the collection nodes. The parameters of the algorithm are set up so that w.h.p. each collection node receives at least messages.
Each collection node in the th collection tree waits until it has received flags. It then sends its parent a message. For each additional flag received, up to , it chooses a uniformly random collection node in the st collection subtree and forwards a flag to it. If then it forwards these flags directly to the root. Subsequent flags are ignored. Again, we use the randomness to ensure a close to even distribution of flags w.h.p.
Each adding node waits until it has received a message from each of its children. Then it sends a message to its parent. We note that each adding node sends exactly one message during the algorithm. The parameters of the algorithm are arranged so that all the messages that are sent in the the th collection subtree together account for of the -inputs. Thus all the messages in all the collection subtrees together account for of the -inputs. At least -inputs remain unaccounted for. These and upto more are collected as flags at the root.
When player 1, at the root, has accounted for at least -inputs, it starts the down stage by sending the message to players 2 and 3. For , when player receives the message, it forwards to players and . Thus, eventually the message reaches all the players, who then know that the threshold has been met. The formal algorithm is shown in Algorithm 2.
is the number of players, is the threshold.
-
1.
Setup (no messages sent here):
-
(a)
Build the data structure:
-
•
Player 1 is the root.
-
•
For , player is a child of the root and the root of the th collection subtree, which has depth .
-
•
The remainder of the nodes in the collection subtrees are assigned to players left to right and top to bottom, starting with player .
-
•
-
(b)
Let for the root.
-
(a)
-
2.
Up stage
-
(a)
Individual Players: upon input change to choose a uniformly random collection node from collection subtree 1 and send a to .
-
(b)
Collection nodes in collection subtree :
-
•
Upon receiving s from collection subtree , if , or from individual players if , send parent a message.
-
•
Upon subsequently receiving a , send it to a uniformly random collection node in collection subtree , if . If then send these directly to the root. Do this for up to flags. Then ignore all subsequent messagess.
-
•
-
(c)
Adding nodes: Upon receiving messages from both children, send parent a message.
-
(d)
Root: While
-
•
Upon receiving a message from the root of collection subtree , increment by
-
•
Upon receiving a message, add one to .
-
•
-
(a)
-
3.
Down stage (now )
-
(a)
Player 1 (the root): Send to Players 2 and 3, then terminate.
-
(b)
Player for : Upon receiving from Player , forward it to Players and (if they exist) and then terminate.
-
(a)
The algorithm Input-Commitment is based on -Counter assuming that the nodes in the data structure are assigned quorums. We assume that the quorums have a canonical numbering and the role of “player” in -Counter is played by quorum . When we say quorum sends a message to quorum , we mean that every (good) player in quorum sends to every player in quorum . A player in quorum is said to have received from if it receives from at least of the players in .
Run the following algorithms in parallel:
-
1.
Algorithm IC-Player.
-
2.
Algorithm IC-Input.
-
3.
Algorithm -Counter with and with quorums as participants.
Run by player with input
-
1.
the quorum at the leaf node associated with input of player
-
2.
Sample a uniformly random value from and set to this value.
-
3.
-
4.
Send to all the players in
-
5.
Run Avss-Share to commit the secret value to the players in .
Run by player in Quorum associated with node responsible for the input of
-
1.
After receiving and a share of , participate in the Avss-Share verification protocol and agreement protocol to determine whether consistent shares for and the same are sent to everyone.
-
2.
If the Avss-Share verification protocol and the agreement protocol end and it is agreed that was the same for all and shares of are valid and consistent, set and you are ready to start the -Counter algorithm with message.
-
3.
Upon receiving from your parent quorum, participate in 5/8-Majority using as your input. If it returns FALSE, reset to the default value and your share of to 0.
The -Counter is used for input commitment in the following way. Let denote the input node associated with player who holds input . Quorum is assigned to this node. Player samples uniformly at random from , sets to and sends to all players in . Next, player uses Avss-Share to commit to the secret value to all players in . Once player has verifiably completed this process for the values and , we say that player has committed its masked value to , and each player in then sets a bit to 1. If player ’s shares fail the verification process, then the ’s are set to 0, which is also the default value. Note that the quorum ’s input for -Counter will be if 5/8 of the are 1. The quorums acting as nodes in the -Counter data structure, run Algorithm 2 with threshold of to determine when at least inputs have been committed. Note that when a quorum has to select a random quorum to communicate with, they must agree on the quorum via a multiparty computation.
Based on the down stage in -Counter, when at least inputs have been detected at the root node, it sends a message to all the quorums via a complete binary tree. When a player who is a member of quorum receives the message, participates in a Hw-MPC with other members of , using as its input. This Hw-MPC determines if at least 5/8 of the bits are set to 1. If they are, then the quorum determines that the -th input () is part of the computation and uses the received value of and shares of as their input into Gate-Eval. Otherwise, they set to the default input and the shares of to 0. We call this the 5/8-Majority step.
5.2 Evaluating the Circuit
We assign nodes of to quorums in the following way. The output node of is assigned to quorum ; then every node in numbered (other than the output node) is assigned to quorum number , where . Assume player is in quorum at the leaf node of count tree, which is the same quorum assigned to input node in . The circuit evaluation phase of the protocol for player starts after the completion of the 5/8-Majority step for node in Input-Commitment. After this step, for each input node , players in know the masked input and each has a share of the random element , although the actual input and mask are unknown to any single player.
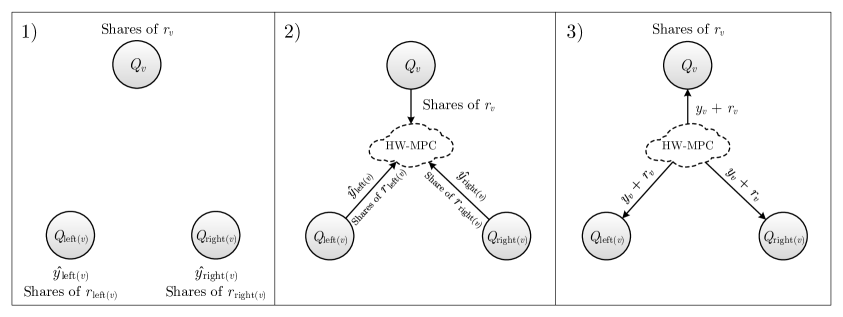
The first step is to generate shares of uniformly random field elements for all gate nodes. If player is in a quorum at gate node , he generates shares of , a uniformly random field element, by participating in the Mask-Generation algorithm. These shares are needed as inputs to the subsequent run of Hw-MPC.
Run by each player in a quorum associated with each node
-
1.
For each input node , after finishing Input-Commitment with and a share of as output, uses these as inputs to Gate-Eval on each parent node of .
-
2.
For each gate node :
-
(a)
runs Mask-Generation on and gets a share of as output
-
(b)
runs Gate-Eval on with its share of as the input and gets as output
-
(c)
runs Gate-Eval on each parent node of with input and ’s share of
-
(a)
-
3.
After finishing computation of the gate represented by the output node, the players at the output node run Output-Rec to reconstruct the output.
This protocol is run by each player in a quorum associated with each gate node to generate .
-
1.
Choose uniformly at random an element (this must be done independently each time this algorithm is run and independently of all other randomness used to generate shares of inputs etc.)
-
2.
Run Avss-Share to create verifiable secret shares of for each player in the quorum associated with and deal these shares to all the players in the quorum associated with including itself.
-
3.
Participate in the Avss-Share verification protocol for each received share. If the verification fails, set the particular share value to zero.
-
4.
Add together all the shares (including the one dealt by yourself). This sum will be player ’s share of the value .
Next, players form the gadget for each gate node with children and to evaluate the gate associated with using Gate-Eval as depicted in Figure 2. The values and are the inputs to the gate associated with , and is the output of as it would be computed by a trusted party. First section of figure describes the initial conditions of the gate quorum and two input quorums before participating in Hw-MPC. Each player in gate quorum has a share of the random element (via Mask-Generation). Every player in the left input quorum has the masked value and a share of (resp. for the right input quorum). In the second section, all the players of the three quorums run Hw-MPC, using their inputs, in order to compute , which is equal to . Third section shows the output of the gate evaluation after participating in Hw-MPC. Each player in now knows 1) the output of the gate plus the value of ; and 2) shares of . Thus, players in now have the input to perform the computation associated with the parents of (if any). Note that both and themselves are unknown to any individual.
The gate evaluation is performed for all gate nodes from the bottom of the to the top. The output of the quorum associated with the output node in is the output of the entire algorithm. Thus, this quorum will unmask the output via Output-Rec. The last step of the algorithm is to send this output to all players. We do via a complete binary tree of quorums, rooted at the output quorum.
This protocol is run for each gate node with children and , the participants are the players in , and .
-
1.
If you are a player in , (resp. ) use (resp. ) as your input to Hw-MPC. If you are a player in , use as your input to Hw-MPC.
-
2.
Participate in Hw-MPC.
-
3.
value returned by Hw-MPC.
This protocol is run by all players in .
-
1.
Reconstruct from its shares using Avss-Rec.
-
2.
Set the circuit output message: .
-
3.
Send to all players in the quorums numbered and .
6 Some Remarks
As described in the introduction, the goal of MPC is to simulate a trusted third party in computation of the circuit and then send back the computation result to the players. Let denote the set of players from whom input is received by the (simulated) trusted party. Recall that .333We allow because the adversary is not limited to delivering one message at a time; two or more messages may be received simultaneously. Thus, for an arbitrary a description of requires bits, and cannot be sent back to the players using only a scalable amount of communication. Therefore, we relax the standard requirement that be sent back to the players. Instead, we require that at the end of the protocol each good player learns the output of ; whether or not their own input was included in ; and the size of .
Also note that although we have not explicitly included this in Input-Commitment, it is very easy for the players to compute the size of the computation set . Once each input quorum has performed the 5/8-Majority step and agreed on the bit they can simply use an addition circuit to add these bits together and then disperse the result. This is an MPC, all of whose inputs are held by good players, since each input bit is jointly held by the entire quorum and all the quorums are good. Thus the computation can afford to wait for all inputs and computes the correct sum.
In the protocol proposed in this paper, it may be the case that a player participates more than one time in the quorums performing a single instance of Hw-MPC. In such a case, we allow to play the role of more than one different players in the MPC, one for each quorum to which belongs. This ensures that the fraction of bad players in any instance of Hw-MPC is always less than . Hw-MPC maintains privacy guarantees even in the face of gossiping coalitions of constant size. Thus, player will learn no information beyond the output and its own inputs after running this protocol.
7 Conclusion
We have described a Monte Carlo algorithm to perform asynchronous secure multiparty computation in an scalable manner. Our algorithms are scalable in the sense that they require each player to send messages and perform computations. They tolerate a static adversary that controls up to a fraction of the players, for any positive constant.
Many problems remain open including the following. Can we prove lower bounds for the communication and computation costs for Monte Carlo MPC? Can we implement and adapt our algorithm to make it practical for a MPC problem such as the beet auction problem described in [7]. Finally, can we prove upper and lower bounds for resource costs to solve MPC in the case where the adversary is dynamic, able to take over players at any point during the algorithm?
8 Acknowledgments
This work was supported by the NSF under grants CCR-0313160 and CAREER Award 0644058. We are grateful to Tom Hayes, Mahdi Zamani and the anonymous reviewers for useful suggestions and comments.
References
- [1] M. Ajtai, J. Komlós, and E. Szemerédi. An 0(n log n) sorting network. In Proceedings of STOC’83, pages 1–9, New York, NY, USA, 1983. ACM.
- [2] J. Aspnes, M. Herlihy, and N. Shavit. Counting networks and multi-processor coordination. In Proceedings of STOC’91, pages 348–358. ACM, 1991.
- [3] H. Attiya and J. Welch. Distributed Computing: Fundamentals, Simulations and Advanced Topics (2nd edition), page 14. John Wiley Interscience, March 2004.
- [4] Z. Beerliova and M. Hirt. Efficient multi-party computation with dispute control. In Theory of Cryptography Conference, 2006.
- [5] M. Ben-Or, R. Canetti, and O. Goldreich. Asynchronous secure computation. In Proceedings of STOC’93, 1993.
- [6] M. Ben-Or, S. Goldwasser, and A. Wigderson. Completeness theorems for non-cryptographic fault-tolerant distributed computing. In Proceedings of STOC’88, pages 1–10, 1988.
- [7] P. Bogetoft, D. Christensen, I. Damgård, M. Geisler, T. Jakobsen, M. Krøigaard, J. Nielsen, J. Nielsen, K. Nielsen, J. Pagter, et al. Secure multiparty computation goes live. Financial Cryptography and Data Security, pages 325–343, 2009.
- [8] E. Boyle, S. Goldwasser, and S. Tessaro. Communication locality in secure multi-party computation: how to run sublinear algorithms in a distributed setting. In Proceedings of TCC’13, pages 356–376, Berlin, Heidelberg, 2013. Springer-Verlag.
- [9] R. Canetti and T. Rabin. Fast asynchronous byzantine agreement with optimal resilience. In Proceeding of STOC’93, pages 42–51, 1993.
- [10] D. Chaum, C. Crépeau, and I. Damgård. Multiparty unconditionally secure protocols. In Proceedings of STOC’88, pages 11–19, 1988.
- [11] B. Chor and C. Dwork. Randomization in Byzantine agreement. Advances in Computing Research, 5:443–498, 1989.
- [12] I. Damgård and Y. Ishai. Scalable secure multiparty computation. Proceedings of CRYPTO’06, pages 501–520, 2006.
- [13] I. Damgård, Y. Ishai, M. Krøigaard, J. Nielsen, and A. Smith. Scalable multiparty computation with nearly optimal work and resilience. Proceedings of CRYPTO’08, pages 241–261, 2008.
- [14] I. Damgård and J. Nielsen. Scalable and unconditionally secure multiparty computation. In Proceedings of CRYPTO’07, pages 572–590. Springer-Verlag, 2007.
- [15] V. Dani, V. King, M. Movahedi, and J. Saia. Breaking the o(nm) bit barrier: Secure multiparty computation with a static adversary. In Proceedings of PODC’12, 2012.
- [16] V. Dani, V. King, M. Movahedi, and J. Saia. Quorums quicken queries: Efficient asynchronous secure multiparty computation. 2013.
- [17] W. Du and M. Atallah. Secure multi-party computation problems and their applications: a review and open problems. In Proceedings of the 2001 workshop on New security paradigms, pages 13–22. ACM, 2001.
- [18] K. Frikken. Secure multiparty computation. In Algorithms and theory of computation handbook, pages 14–14. Chapman & Hall/CRC, 2010.
- [19] O. Goldreich. Secure multi-party computation. Manuscript., 1998.
- [20] O. Goldreich, S. Micali, and A. Wigderson. How to play any mental game. In Proceedings of STOC’87, pages 218–229. ACM, 1987.
- [21] M. Hirt and U. Maurer. Robustness for free in unconditional multi-party computation. In Advances in Cryptology-CRYPTO ’01, pages 101–118. Springer, 2001.
- [22] M. Hirt and J. Nielsen. Upper bounds on the communication complexity of optimally resilient cryptographic multiparty computation. Advances in Cryptology-ASIACRYPT 2005, pages 79–99, 2005.
- [23] V. King, S. Lonergan, J. Saia, and A. Trehan. Load balanced scalable byzantine agreement through quorum building, with full information. In International Conference on Distributed Computing and Networking (ICDCN), 2011.
- [24] M. Klugerman and C. G. Plaxton. Small-depth counting networks. In Proceedings of STOC’92, pages 417–428, 1992.
- [25] M. R. Klugerman. Small-depth counting networks and related topics, 1994.
- [26] T. Rabin and M. Ben-Or. Verifiable secret sharing and multiparty protocols with honest majority. In Proceedings of STOC’89, pages 73–85. ACM, 1989.
- [27] A. Yao. Protocols for secure computations. In Proceedings of FOCS’82, pages 160–164, 1982.