Radiation in Systems with Near Zero Dielectric Constant

Introduction. Recently, systems with near zero dielectric permittivity(ENZ) become a subject of investigation because of their interesting properties Ziol ; SeEn ; ASSE . One can find such materials at teraherz, infrared and optical frequencies among semiconductors, metals as well as dielectrics. In the present paper we consider some radiation effects in the systems with near zero $\varepsilon$. The main underlying physical idea is that in such media the pseudophoton momentum $k=\omega\sqrt{\varepsilon}/c$ is small and therefore is scattered on the inhomogeneties more effectively. Hence one can expect an enhancement of intensity in radiation mechanisms caused by scattering of pseudophotons. Below we discuss two such radiation mechanisms: transition(TR) and diffusive(DR). In former case TR from a charged particle traversing an interface between vacuum and an ENZ medium is investigated. In latter case we consider DR from a charged particle crossing a random stack with near zero average dielectric constant.

Transition Radiation. Transition Radiation originates when a charged particle crosses an interface between two homogeneous media GTs . Its intensity depends on dielectric constants of media as well as on particle velocity. In the simplest case of traversing of particle from vacuum into a ENZ medium the backward spectral-angular TR intensity into vacuum is determined as follows GTs

where $\beta=v/c$, $\theta$ is the angle between velocity directed normally to the interface and observation direction, $\varepsilon(\omega)$ is the dielectric permittivity of a homogeneous medium. Note that Eq.(1) is obtained from the basic expression for TR intensity GTs in the limit $\beta\ll 1$ and $\varepsilon\ll 1$ . Relativistic case $\beta\sim 1$ will be investigated elsewhere. It follows from Eq.(1) that the intensity has peak at angles

Reflection coefficient of a photon polarized in the plane of incidence from the interface between vacuum and $\varepsilon$- medium is determined as LanLif

As it follows from Eqs.(2) and (3) maximum of TR intensity is achieved at the angles for which the corresponding reflection coefficient is maximal $r=1$. The incident on the interface pseudophotons fulfilling the condition Eq.(2) are completely reflected from the surface, separate from the charge and convert into real photons. Reflection coefficient Eq.(3) becomes minimal $r=0$ at Brewster’s angleLanLif

Pseudophotons fulfilling the condition Eq.(4) does not reflect and separate from the charge. Therefore corresponding TR intensity is minimal for the angles and frequencies satisfying the Eq.(4). These two values for ENZ medium are close to each other. Therefore one will has a sharp peak in spectral-angular TR intensity, see Fig.1. The width of peak on angle can be estimated as

In conventional media an ENZ conditions can be created in vicinity of frequencies of lattice longitudinal vibrations(optical phonons) or collective oscillations of ensemble of free electrons(plasmons). The above mentioned peak is associated with the properties of the medium and does not depend on the particle energy. Its height for ENZ medium significantly exceeds the maximum of conventional TR intensity in the limit $|\varepsilon|\to\infty$ GTs

This enhancement, see Fig.(1) is caused by the resonance interaction of the electromagnetic field induced by a charged particle with the vibrations of a lattice or with collective oscillations of a plasma of free electrons. During this interaction a part of energy of lattice vibrations or plasma oscillations is transformed into the energy of transversal electromagnetic wave. We make numerical estimates using Eq.(1) and the following expression for the dielectric constant at frequencies close to the plasmon frequencies of weakly doped InSb Agr

where $\varepsilon_{\infty}$ and $\varepsilon_{0}$ are high frequency and static dielectric constants,respectively, $\omega_{T}$ is the transversal optical phonon frequency,$\gamma_{-}$ and $\Gamma$ are the plasmon and optical phonon decay rates, respectively. As follows from Eq.(7), at frequencies close to plasmon frequency $\omega\sim\omega_{p}$, one can reach small values of real and imaginary parts of dielectric constant provided that $\gamma_{-}/\omega\ll 1$ and $\Gamma/\omega_{T}\ll 1$.

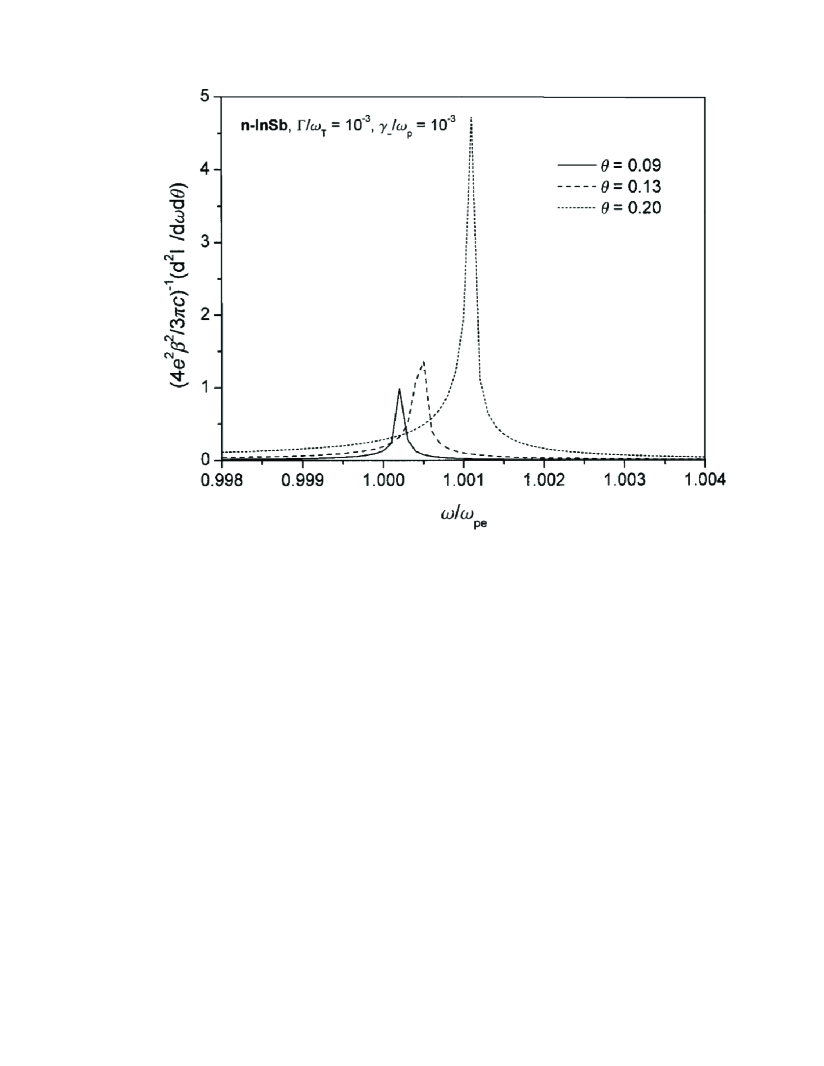
As follows from Fig.(1) TR photons from the interface between vacuum and InSb belong to THz region. In Fig.1 TR intensity from ENZ medium is normalized to the TR intensity value from a medium with $|\varepsilon|\to\infty$. Therefore TR intensity from ENZ medium exceeds TR from a metal almost $4-5$ times. Another advantage is that angular distribution is quite narrow compared to the metal case. Hence TR from a ENZ medium can be considered as a promising source of THz radiation.

Diffusive Radiation. A charged particle passing through a stack of plates placed in a homogeneous medium is known to be radiating electromagnetic waves. Radiation originates because of the scattering of electromagnetic field on the plates. Considering this problem theoretically it was shown ZH98 ; ZH06 that when the conditions of diffusional scattering of pseudophotons are fulfilled its contribution to the radiation intensity is the dominant one

where $\theta$ is the observation angle, $\vec{v}$ is the particle velocity which is directed normally to the plates on $z$, $\varepsilon$ is the average dielectric constant (see below), $\gamma=(1-v^{2}\varepsilon/c^{2})^{-1/2}$ is the Lorentz factor in the medium, $l,l_{in}$ are pseudophoton elastic and inelastic mean free paths,respectively. Inelastic mean free path is mainly associated with the absorption of electromagnetic field in the medium. Elastic mean free path is associated with the photon refraction on plates. It depends on the photon incidence angle on plates. In case of normally incident photon elastic mean free path is determined as follows ZH98

where $B$ is the correlation function of random dielectric constant field created by randomly located plates

Here $n=N/L_{z}$ is concentration of plates in the system, $a$ is their thickness, $b$ is their dielectric constant and $L_{z}$ is is the system size in the $z$ direction. It follows from Eq.(10) that when $ka\gg 1$, $B(2k)/B(0)\sim 1/(ka)^{2}\ll 1$. Therefore in both cases $ka\gg 1$ and $ka\ll 1$ photon mean free path has the form

where $B(0)=k^{4}(b-\varepsilon)^{2}na^{2}/\varepsilon^{2}$. Substituting this expression into Eq.(11) and taking into account that $k=\omega\sqrt{\varepsilon}/c$, we have

Remind that $\varepsilon$ is the average dielectric constant of the system which for a layered stack has the form:

Here $\varepsilon_{0}$ is the dielectric constant of a homogeneous medium into which plates with dielectric constant $b(\omega)$ and thickness $a$ are randomly embedded. If a homogeneous medium is vacuum then $\varepsilon_{0}\equiv 1$. Choosing for plates materials with $b(\omega)<0$ one can make the average dielectric constant of the system quite small $\varepsilon\ll 1$. Correspondingly, the photon elastic mean free path will be small and the radiation intensity will be large in a such system. Let us now estimate the inelastic mean free path $l_{in}$. If the spacing between the plates is vacuum then $l_{in}$ is determined by the absorption by plates. Absorption in a plate is characterized by the imaginary part of dielectric constant of a plate $Imb(\omega)$. Two regimes are possible. When $\varepsilon\gg fImb$, where $f$ is the linear fraction of plates in the system, $l_{in}$ can be estimated as

In the opposite regime $\varepsilon\ll fImb$, $l_{in}$ is estimated as

Substituting Eqs.(14),(15) and Eq.(12) into Eq.(8) one can be convinced that $I_{D}\sim\varepsilon^{-3}$ or $I_{D}\sim\varepsilon^{-2}$ depending which regime is realized. In any case obviously radiation intensity enhances in the limit $\varepsilon\to 0$. Let us now make some numerical estimates.

In alkali halide crystals, in semiconductors like $GaP,InSb,$ and etc. the dielectric constant is negative in the region between the frequencies of transversal and longitudinal optical phonons, see Agr . For example, for the compound $MgO$ in the frequency region $550-650cm^{-1}$ the real part of dielectric constant take values in the interval $-6,-2$ and the imaginary part in the interval $0.6-0.2$. The above mentioned interval lies in the far infrared region. It follows from Eq.(12) that in case $2\pi a\leq\lambda$ the minimum of mean free path and therefore the maximum of radiation intensity is achieved for average plate thickness $a\sim\lambda/2\pi$. For the above mentioned frequencies this is about $20\mu m$. Choosing such values for average thickness of plates one can reach the localization limit $\lambda/2\pi$ And ; Arya which is a minimal value for photon elastic mean free path $l$. One needs $l_{in}$ in order to estimate the number of emitted photons using Eq.(8). Taking $f\sim 0.1$, $Imb\sim 0.4$ and $\varepsilon\sim 0.5$, one gets from Eq.(14), $l_{in}\sim 557\mu m$. Using Eq.(8) one can estimate the integrated over all angles number of emitted photons in the interval $\Delta\omega$ as

where $\alpha$ is the fine structure constant. Because $l\ll l_{in}$ the exponential decaying factor in Eq.(8) plays important role only for very large angles $\theta\approx\pi/2$. Therefore we ignored it when estimating the total number of emitted photons. Substituting $l_{in}\sim 562\mu m$, $l\sim\lambda/2\pi\sim 17\mu m$ into Eq.(16)and taking $\Delta\omega\sim\omega$ one has approximately $N_{ph}\sim 167$ infrared photons per one electron. This implies that using commercially available $5-6MeV$, $1mA$ linear accelerator a total output power of $2.4mW(10^{18}photon/s)$ can be produced.

We have considered radiation effects in systems with near zero dielectric constant by example of transition and diffusive radiations. An enhancement of intensity is demonstrated in both cases. Numerical estimates for specific systems show that ENZ systems can be used for generation of light in the THz and infrared regions.