Random Graph Matching in Geometric Models: the Case of Complete Graphs
Abstract
This paper studies the problem of matching two complete graphs with edge weights correlated through latent geometries, extending a recent line of research on random graph matching with independent edge weights to geometric models. Specifically, given a random permutation on and iid pairs of correlated Gaussian vectors in with noise parameter , the edge weights are given by and for some link function . The goal is to recover the hidden vertex correspondence based on the observation of and . We focus on the dot-product model with and Euclidean distance model with , in the low-dimensional regime of wherein the underlying geometric structures are most evident. We derive an approximate maximum likelihood estimator, which provably achieves, with high probability, perfect recovery of when and almost perfect recovery with a vanishing fraction of errors when . Furthermore, these conditions are shown to be information-theoretically optimal even when the latent coordinates and are observed, complementing the recent results of [DCK19] and [KNW22] in geometric models of the planted bipartite matching problem. As a side discovery, we show that the celebrated spectral algorithm of [Ume88] emerges as a further approximation to the maximum likelihood in the geometric model.
1 Introduction
Graph matching (or network alignment) refers to finding the best vertex correspondence between two graphs that maximizes the total number of common edges. While this problem, as an instance of quadratic assignment problem, is computationally intractable in the worst case, significant headways, both information-theoretic and algorithmic, have been achieved in the average-case analysis under meaningful statistical models [CK16, CK17, DMWX21, BCL+19, FMWX19a, FMWX19b, HM20, WXY21, GM20, GML22, MRT21b, MRT21a]. One of the most popular models is the correlated Erdős-Rényi graph model [PG11], where both observed graphs are Erdős-Rényi graphs with edges correlated through a latent vertex matching; more generally, in the correlated Wigner model, the observations are two weighted graph with correlated edge weights (e.g. Gaussians [DMWX21, DCK19, FMWX19a, Gan21a]). Despite their simplicity, these models inspired a number of new algorithms that achieve strong performance both theoretically and practically [DMWX21, FMWX19a, FMWX19b, GM20, GML22, MRT21b, MRT21a]. Nevertheless, one of the major limitations of models with independent edges is that they fail to capture graphs with spatial structure [AG14], such as those arising in computer vision datasets (e.g. mesh graphs obtained by triangulating 3D shapes [LRB+16]). In contrast to Erdős-Rényi-style model with iid edges, geometric graph models, such as random dot-product graphs and random geometric graphs, take into account the latent geometry by embedding each node in a Euclidean space and determines edge connection between two nodes by the proximity of their geographical location. While the coordinates are typically assumed to be independent (e.g. Gaussians or uniform over spheres or hypercubes), the edges or edge weights are now dependent. The main objective for the present paper is to study graph matching in correlated geometric graph models, where the network correlation is due to that of the latent coordinates.
1.1 Model
Given two point clouds and in , we construct two weighted graphs on the vertex set with weighted adjacency matrices and as follows. For each , let and , for some probability transition kernel . The coordinates are correlated through a latent matching as follows: Consider a Gaussian model
where ’s are iid vectors and is uniform on , the set of all permutations on . In matrix form, we have
| (1) |
where are matrices whose rows are ’s, ’s and ’s respectively, denotes the permutation matrix corresponding to , and is the collection of all permutation matrices. Given the observation and , the goal is to recover the latent correspondence .
Of particular interest are the following special cases:
-
•
Dot-product model: The observations are complete graphs with pairwise inner products as edge weights, namely, and . As such, the weighted adjacency matrices are and , both Wishart matrices. It is clear that from and one can reconstruct and respectively, each up to a global orthogonal transformation on the rows. In this light, the model is also equivalent to the so-called Procrustes Matching problem [MDK+16, DL17, GJB19], where in (1) undergoes a further random orthogonal transformation – see Appendix A for a detailed discussion.
-
•
Distance model: The edge weights are pairwise squared distances and . This setting corresponds to the classical problem of multi-dimensional scaling (MDS), where the goal is to reconstruct the coordinates (up to global shift and orthogonal transformation) from the distance data (cf. [BG05]).
-
•
Random Dot Product Graph (RDPG): In this model, the observed data are two graphs with adjacency matrices and , where and conditioned on and , and is some link function, e.g. . In this way, we observe two instances of RDPG that are correlated through the underlying points and the latent matching. See [AFT+17] for a recent survey on RDPG.
-
•
Random Geometric Graph (RGG): Similar to RDPG, conditioned on for some link function applied to the pairwise distances. The second RGG instance is constructed in the same way using . A simple example is for some threshold , where each pair of points within distance is connected [Gil61]; see the monograph [Pen03] for a comprehensive discussion on RGG.
Let us mention that the model where the two point clouds are directly observed has been recently studied by [DCK19, DCK20] in the context of feature matching and independently by [KNW22] as a geometric model for the planted matching problem, extending the previous work in [CKK+10, MMX21, DWXY21] with iid weights to a geometric (low-rank) setting. In this model, and in (2) are observed and the maximum likelihood estimator (MLE) of amounts to solving
| (2) |
which is a linear assignment (max-weight matching) problem on the weighted complete bipartite graph with weight matrix . In the sequel we shall refer to this setting as the linear assignment model, which we also study in this paper for the sake of proving impossibility results for the more difficult graph matching problem, as the coordinates are latent and only pairwise information are available.
Fig. 1 elucidates the logical connections between the aforementioned models. Among these, linear assignment model is the most informative, followed by the dot product model and the distance model, whose further stochastically degraded versions are RDPG and RGG, respectively. As a first step towards understanding graph matching on geometric models, in this paper we study the case of weighted complete graphs in the dot product and distance models.
1.2 Main results
By analyzing the MLE (2) in the stronger linear assignment model (1), [KNW22] identified a critical scaling of dimension at :
-
•
In the low-dimensional regime of , accurate reconstruction requires the noise level to be vanishingly small. More precisely, with high probability, the MLE (2) recovers the latent perfectly (resp. with a vanishing fraction of errors) provided that (resp. ).
-
•
In the high-dimensional regime of , it is possible for to be as large as . Since the dependency between the edges weakens as the latent dimension increases,111For the Wishart matrix, it is known [JL15, BG18] that the total variation between the joint law of the off-diagonals and their iid Gaussian counterpart converges to zero provided that . Analogous results have also been obtained in [BDER16] showing that high-dimensional RGG is approximately Erdős-Rényi. this is consistent with the known results in the correlated Erdős-Rényi and Wigner model. For example, to match two GOE matrices with correlation coefficient , the sharp reconstruction threshold is at [Gan21b, WXY21].
In this paper we mostly focus on the low-dimensional setting as this is the regime where geometric graph ensembles are structurally distinct from Erdős-Rényi graphs. Our main findings are two-fold:
-
1.
The same reconstruction thresholds remain achievable even when the coordinates are latent and only inner-product or distance data are accessible.
-
2.
Furthermore, these thresholds cannot be improved even when the coordinates are observed.
To make these results precise, we start with the dot-product model with and , and according to (1). In this case the MLE turns out to be much more complicated than (2) for the linear assignment model. As shown in Appendix B, the MLE takes the form
| (3) |
where the integral is with respect to the Haar measure on the orthogonal group , based on the SVD , and similarly for . It is unclear whether the above Haar integral has a closed-form solution,222The integral in (3) can be reduced to computing for a diagonal , which, in principle, can be evaluated by Taylor expansion and applying formulas for the joint moments of in [Mat13, Theorem 2.2]. let alone how to optimize it over all permutations. Next, we turn to its approximation.
As we will show later, in the low-dimensional case of , meaningful reconstruction of the latent matching is information-theoretically impossible unless vanishes with at a certain speed. In the regime of small , Laplace’s method suggests that the predominant contribution to the integral in (3) comes from the maximum over . Using the dual form of the nuclear norm , where denotes the sum of all singular values of , we arrive at the following approximate MLE:
| (4) |
We stress that the above approximation to the MLE (3) is justified for the low-dimensional regime where is small. In the high-dimensional (high-noise) case, the approximate MLE actually takes on the form of a quadratic assignment problem (QAP), which is the MLE for the well-studied iid model [CK16]; in the special case of the dot-product model, it amounts to replacing the nuclear norm in (4) by the Frobenius norm. We postpone this discussion to Section 4.
To measure the accuracy of a given estimator , we define
as the fraction of nodes whose matching is correctly recovered. The following result identifies the threshold at which the approximate MLE achieves perfect or almost perfect recovery.
Theorem 1 (Recovery guarantee of AML in the dot-product model).
Assume the dot-product model with . Let be the approximate MLE defined in (4).
-
(i)
If , the estimator achieves perfect recovery with high probability:
(5) -
(ii)
If , the estimator achieves almost perfect recovery with high probability:
(6)
A few remarks are in order:
-
•
In fact we will show the following nonasymptotic estimate that implies (6): For all sufficiently small , if , then with probability tending to one.
- •
-
•
Unlike linear assignment, it is unclear how to solve the optimization in (4) over permutations efficiently. Nevertheless, for constant we show that it is possible to find an approximate solution in time that is polynomial in that achieves the same statistical guarantee as in Theorem 1. Indeed, note that (3) is equivalent to the double maximization
(7) Approximating the inner maximum over a suitable discretization of , each maximization over for fixed is a linear assignment problem, which can be solved in time. In Section 3, we provide a heuristic that shows (7) can be further approximated by the classical spectral algorithm of Umeyama [Ume88] which is much faster in practice and achieves good empirical performance. For that grows with , it is an open question to find a polynomial-time algorithm that attains the (optimal, as we show next) threshold in Theorem 1.
Next, we proceed to the more difficult distance model, where and . Deriving the exact MLE in this model appears to be challenging; instead, we apply the estimator (4) to an appropriately centered version of the data matrices. Let denotes the all-one vector and define . Then and , where and . Strictly speaking, the vectors and are correlated with the ground truth , since can be viewed as a noisy version of ; however, we expect them to inform very little about because such scalar-valued observations are highly sensitive to noise (analogous to degree matching in correlated Erdős-Rényi graphs [DMWX21, Section 1.3]). As such, we ignore and by projecting and to the orthogonal complement of the vector . Specifically, we compute, as commonly done in the MDS literature (see e.g. [SRZF03, OMK10]),
| (8) |
It is easy to verify that and , where and consist of centered coordinates and respectively, with and . Overall, we have reduced the distance model to a dot product model where the latent coordinates are now centered.
One can show that the MLE of given the reduced data is of the same Haar-integral form (3). Using again the small- approximation, we arrive at the following estimator by applying (4) to the centered data and :
| (9) |
Theorem 2 (Recovery guarantee in the distance model).
Finally, we state an impossibility result for the linear assignment model, proving that the perfect and almost perfect recovery threshold of and obtained by analyzing the MLE in [KNW22] are in fact information-theoretically necessary. Complementing Theorem 1 and Theorem 2, this result also establishes the optimality of the estimator (4) and (9) for their respective model.
Theorem 3 (Impossibility result in the linear assignment model).
Consider the linear assignment model with .
-
(i)
If there exists an estimator that achieves perfect recovery with high probability, then .
-
(ii)
If there exists an estimator that achieves almost perfect recovery with high probability, then .
Furthermore, in the special case of , necessary conditions in and can be improved to and , respectively.
Theorem 3(i) slightly improves the necessary condition for perfect recovery in [KNW22] from to . For almost perfect recovery, the negative result in [KNW22] is limited to MLE, while Theorem 3 holds for all algorithms. Moreover, the necessary condition in Theorem 3(ii) was conjectured in [KNW22, Conjecture 1.4, item 1], which we now resolve in the positive. Finally, while our focus is in the low-dimensional case of , we also provide necessary conditions that hold for general . (See Appendix E for details).
In view of Fig. 1, since the negative results in Theorem 3 are proved for the strongest model and the positive results in Theorem 2 are for the weakest model, we conclude that for all three models, namely, linear assignment, dot-product, and distance model, the thresholds for exact and almost perfect reconstruction is given by and , respectively.
2 Outline of proofs
2.1 Positive results
The positive results of Theorem 1 and Theorem 2 are proved in Appendix C and Appendix D. Here we briefly describe the proof strategy in the dot product model. Suppose we want to bound the probability that the approximate MLE in (4) makes more than number of errors. Denote by the Hamming distance between two permutations . Without loss of generality, we will assume that . By the orthogonal invariance of , we can assume, for the sake of analysis, that and . Applying (7),
| (10) |
For each fixed and , averaging over the noise yields, for some absolute constant ,
| (11) |
In the remaining argument, there are three places where the structure of the orthogonal group plays a crucial role:
-
1.
The quantity in (11) turns out to depend on through its cycle type and on through its eigenvalues. Crucially, the eigenvalues of an orthogonal matrix lie on the unit circle, denoted by , with . We then show that the error probability in (11) can be further bounded by, for some absolute constant ,
(12) where is the number of fixed points in and is the total number of cycles.
-
2.
In order to bound (10), we take a union bound over and another union bound over an appropriate discretization of . This turns out to be much subtler than the usual -net-based argument, as one needs to implement a localized covering and take into account the local geometry of the orthogonal group. Specifically, note that the error probability in (11) becomes larger when is near and when is near (i.e. the phases ’s are small); fortunately, the entropy (namely, the number of such and such within a certain resolution) also becomes smaller, balancing out the deterioration in the probability bound. This is the second place where the structure of is used crucially, as the local metric entropy of in the vicinity of is much lower than that elsewhere.
-
3.
Controlling the approximation error of the nuclear norm is another key step. Note that for any matrix norm of the dual form , where is the dual norm of , the standard -net argument (cf. [Ver18, Lemma 4.4.1]) yields a multiplicative approximation , where is any -net of the dual norm ball. In general, this result cannot be improved (e.g. for Frobenius norm); nevertheless, for the special case of nuclear norm, this approximation ratio can be improved from to , as the following result of independent interest shows. This improvement turns out to be crucial for obtaining the sharp threshold.
Lemma 1.
Let be a -net in operator norm of the orthogonal group . For any ,
(13)
The proof of Theorem 1 is completed by combining (12) with a union bound over a specific discretization of , whose cardinality satisfies the desired eigenvalue-based local entropy estimate, followed by a union bound over which can be controlled using moment generating function of the number of cycles in a random derangement.
2.2 Negative results
The information-theoretic lower bounds in Theorem 3 for the linear assignment model are proved in Appendix E. Here we sketch the main ideas. We first derive a necessary condition for almost perfect recovery that holds for any via a simple mutual information argument [HWX17]: On one hand, the mutual information can be upper bounded by the Gaussian channel capacity as . On the other hand, to achieve almost perfect recovery, needs be asymptotically equal to the full entropy which is . These two assertions together immediately imply that , which further simplifies to when . However, for constant , this necessary condition turns out to be loose and the main bulk of our proof is to improve it to the optimal condition . To this end, we follow the program recently developed in [DWXY21] in the context of the planted matching model by analyzing the posterior measure of the latent given the data .
To start, a simple yet crucial observation in [DWXY21] is that to prove the impossibility of almost perfect recovery, it suffices to show a random permutation sampled from the posterior distribution is at Hamming distance away from the ground truth with constant probability. As such, it suffices to show there is more posterior mass over the bad permutations (those far away from the ground truth) than that over the good permutations (those near the ground truth) in the posterior distribution. To proceed, we first bound from above the total posterior mass of good permutations by a truncated first moment calculation applying the large deviation analysis developed in the proof of the positive results. To bound from below the posterior mass of bad permutations, we aim to construct exponentially many bad permutations whose log likelihood is no smaller than . A key observation is that can be decomposed according to the orbit decomposition of :
| (14) |
where denotes the set of orbits in and for any orbit ,
| (15) |
Thus, the goal is to find a collection of vertex-disjoint orbits whose total lengths add up to and each of which is augmenting in the sense that . Here, a key difference to [DWXY21] is that in the planted matching model with independent edge weights studied there, short augmenting orbits are insufficient to meet the total length requirement; instead, [DWXY21] resorts to a sophisticated two-stage process that first finds many augmenting paths then connects then into long cycles. Fortunately, for the linear assignment model in low dimensions of , as also observed in [KNW22] in their analysis of the MLE, it suffices to look for augmenting -orbits and take their disjoint unions. More precisely, we show that there are many vertex-disjoint augmenting -orbits. This has already been done in [KNW22] using a second-moment method enhanced by an additional concentration inequality. It turns out that the correlation among the augmenting -orbits is mild enough so that a much simpler argument via a basic second-moment calculation followed by an application of Turán’s theorem suffices to extract a large vertex-disjoint subcollection. Finally, these vertex-disjoint augmenting -orbits give rise to exponentially many permutations that differ from the ground truth by .
Finally, we briefly remark on perfect recovery, for which it suffices to focus on the MLE (2) which minimizes the error probability for uniform . In view of the likelihood decomposition given in (14), it further suffices to prove the existence of an augmenting -orbit. This can be easily done using the second-moment method. A similar strategy was adopted in [DCK19], but our first-moment and second-moment estimates are tighter and hence yield nearly optimal conditions.
3 Experiments
In this section we present preliminary numerical results on synthetic data from the dot product model. As observed in [GJB19], the form of the approximate MLE in (7) as a double maximization over and naturally suggests an alternating maximization strategy by iterating between the two steps: (a) For a fixed , the -maximization is a linear assignment; (b) For a fixed , the -maximization is the so-called orthogonal Procrustes problem and easily solved via SVD [Sch66]. However, with random initialization this method performs rather poorly falling short of the optimal threshold predicted by Theorem 1. While more informative initialization (such as starting from a obtained by the doubly-stochastic relaxation of QAP [GJB19]) can potentially help, in this section we focus on methods that are closer to the original approximate MLE.
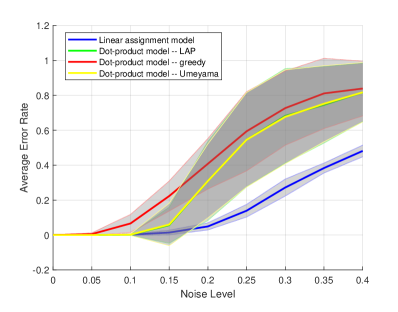
As the proof of Theorem 1 shows, as far as achieving the optimal threshold is concerned it suffices to consider a finely discretized . This can be easily implemented in , since any orthogonal matrix is either a rotation or reflection of the form: or . We then solve (7) on a grid of values, by solving the -maximization for each such and reporting the solution with the highest objective value. As shown in Fig. 2(a) for , the performance of the approximate MLE in the dot-product model (green) follows closely that of the MLE in the linear assignment model (blue). Using the greedy matching algorithm (red) in place of the linear assignment solver greatly speeds up the computation at the price of some performance degradation.
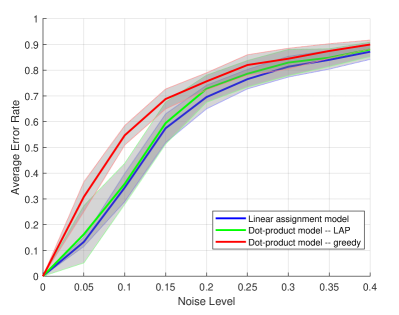
As the dimension increases, it becomes more difficult and computationally more expensive to discretize . Instead, we take a different approach. Note that in the noiseless case (), as long as all singular values have multiplicity one, we have for some in
| (16) |
As such, in the noiseless case it suffices to restrict the inner maximization of (7) to the subgroup corresponding to coordinate reflections. Since the noise is weak in the low-dimensional setting, we continue to apply this heuristic by computing
| (17) |
which turns out to work very well in practice. Taking this method one step further, notice that in the low-dimensional regime, all non-zero singular values of and are tightly concentrated on the same value . If we ignore the singular values and simply replace and by their left singular vectors and , (17) can be written more explicitly as
| (18) |
which, somewhat unexpectedly, coincides with the celebrated Umeyama algorithm [Ume88], a specific type of spectral method that is widely used in practice for graph matching. In Fig. 2(b) we compare for and . Consistent with Theorem 1, the error rates in the dot-product model and the linear assignment model are both near zero until exceeds a certain threshold, after which the former departs from the latter. Finally, comparing Fig. 2(a) and Fig. 2(b) confirms that the reconstruction threshold improves as the latent dimension increases as predicted by Theorem 1.
4 Discussion
In this paper we studied the problem of graph matching in the special case of correlated complete weighted graphs in the dot product and distance model, as a first step towards the more challenging case of random dot-product graphs and random geometric graphs. Within the confines of the present paper, there still remain a number of interesting directions and open problems which we discuss below.
Non-isotropic distribution
The present paper assumes the latent coordinates ’s and ’s are isotropic Gaussians. For the linear assignment model, [DCK19, DCK20] has considered a more general setup where for some covariance matrix . As explained in [DCK19, Appendix A], it is not hard to see, based on a simple reduction argument (by scaling both ’s and ’s with and add noise if needed), that as long as the singular values of are bounded from above and below, the information-theoretic limits in terms of remain unchanged. For the dot product or distance model, this is also true but less obvious – see Appendix F for a proof.
While the statistical limits in the nonisotropic case remain the same, potentially it allows more computationally tractable algorithms to succeed. For example, the spectral method recently proposed in [FMWX19a, FMWX19b] finds a matching by rounding the so-called GRAMPA similarity matrix
| (19) |
Here and are the SVD of the observed weighted adjacency matrices, and is a small regularization parameter. In the isotropic case, applying this algorithm to the dot-product model is unlikely to achieve the optimal threshold in Theorem 1. The reason is that in the low-dimensional regime of small , both and and rank- and all singular values ’s and ’s are largely concentrated on the same value of . As such, the similarity matrix (19) degenerates into , where and are the row-sum vectors. Rounding to a permutation matrix is equivalent to “degree-matching”, that is, finding the permutation by sorting and , which can only tolerate type of noise level, for constant independent of the dimension , due to the small spacing in the order statistics [DMWX21]. However, in the nonisotropic case where has distinct singular values, we expect and to have descent spectral gaps and the spectral method (19) may succeed at the dimension-dependent thresholds of Theorem 1. A theoretical justification of this heuristic is outside the scope of this paper.
High-dimensional regime
Recall the exact MLE (3), wherein the objective function is an average over the Haar measure on , can be approximated by (4) for small . Next, we derive its large- approximation. Rewriting the objective function in (3) as for a random uniform and taking its second-order Taylor expansion for large , we get
where we applied , , and . This expansion suggests that for large (which can be afforded in the high-dimensional regime of ), the MLE is approximated by the solution to the following QAP:
| (20) |
This observation aligns with the better studied correlated Erdős-Rényi models or correlated Gaussian Wigner models, where the MLE is exactly given by the QAP (20).
To further compare with the estimator (4) that has been shown optimal in low dimensions, let us rewrite (20) in a form that parallels (7):
| (21) |
In contrast, the dual variable in (7) is constrained to be an orthogonal matrix, which, as discussed in the proof sketch in Section 2.1, is crucial for the proof of Theorem 1. Overall, the above evidence points to the potential suboptimality of QAP in low and moderate-dimensional regime of and its potential optimality in the high-dimensional regime of .
Practical algorithms
As demonstrated by extensive numerical experiments in [FMWX19a, Sec. 4.2], for correlated random graph models with iid pairs of edge weights, the Umeyama algorithm (18) significantly improves over classical “low-rank” spectral methods involving only the top few eigenvectors, but still lags behind the more recent spectral methods such as the GRAMPA algorithm (19) that uses all pairs of eigenvalues and eigenvectors. Surprisingly, in the low-dimensional dot product model with , while the GRAMPA algorithm is expected to perform poorly, empirical result in Section 3 indicates that the Umeyama method actually works very well in this setting. In fact, it is not hard to show that the Umeyama algorithm returns the true permutation with high probability in the noiseless case of ; however, understanding its theoretical performance in the noisy setting remains open.
Appendix A Further related work
The present paper bridges several streams of literature such as planted matching, feature matching, Procrustes matching, and graph matching, which we describe below.
Planted matching and feature matching
The planted matching problem aims to recover a perfect matching hidden in a weighted complete bipartite graph, where the edge weights are independently drawn from either or depending on whether edges are on the hidden matching or not. Originally proposed by [CKK+10] to model the application of object tracking, a sharp phase transition from almost perfect recovery to partial recovery is conjectured to exist for the special case where is a folded Gaussian and is a uniform distribution over . A recent line of work initiated by [MMX21] and followed by [SSZ20, DWXY21] has successfully resolved the conjecture and characterized the sharp threshold for general distributions.
Despite these fascinating advances, they crucially rely on the independent weight assumption which does not account for the latent geometry in the object tracking applications. As a remedy, the linear assignment model (1) was proposed and studied by [KNW22] as a geometric model for planted matching, where the edge weights are pairwise inner products and no longer independent. In the low-dimensional setting of , the MLE is shown to achieve perfect recovery when and almost perfect recovery when . Further bounds on the number of errors made by MLE and recovery guarantees in the high-dimensional setting are provided. However, the necessary conditions derived in [KNW22] only pertain to the MLE, leaving open the possibility that almost perfect recovery might be attained by other algorithms at lower threshold. This is resolved in the negative by the information-theoretic converse in Theorem 3, showing that is necessary for any algorithm to achieve almost perfect recovery. Along the way, we also slightly improve the necessary condition for perfect recovery from to .
The linear assignment model (1) was in fact studied earlier in [DCK19, DCK20] in a different context of feature matching, where ’s and ’s are viewed as two correlated Gaussian feature vectors in and the goal is to find their best alignment. It is shown in [DCK19] that perfect recovery is possible when , and impossible when and .333While the impossibility result in [DCK19, Theorem 2] only states the assumption that , its proof, specifically the proof of [DCK19, Lemma 4.5], implicitly assumes which further implies . In comparison, the necessary condition in Theorem 5 is tighter and holds for any , agreeing with their sufficient condition within an additive factor. It is also shown in [DCK20] that almost perfect recovery is possible when in the high-dimensional regime for a small constant . This matches our necessary condition in Proposition 1 with a sharp constant.
Related problems on feature matching were also studied in the statistics literature. For example, [CD16] studies the model of observing and , where are two independent random Gaussian matrices and is deterministic. The minimum separation (in Euclidean distance) of rows of needed for perfect recovery, denoted by , is shown to be on the order of . Note that in the low-dimensional regime , this condition is comparable to our threshold for perfect recovery , as the typical value of scales as when is Gaussian. However, the average-case setup is more challenging as can be atypically small due to the stochastic variation of .
Procrustes matching
Our dot-product model is also closely related to the problem of Procrustes matching, which finds numerous applications in natural language processing and computer vision [RCB97, MDK+16, DL17, GJB19]. Given two point clouds stacked as rows of and , Procrustes matching aims to find an orthogonal matrix and a permutation that minimizes the Euclidean distance between the point clouds, i.e., . As observed in [GJB19], this is equivalent to , which further reduces to . Thus our approximate MLE (4) under the dot-product model is equivalent to Procrustes matching on and . A semi-definite programming relaxation is proposed in [MDK+16] and further shown to return the optimal solution in the noiseless case when is generic and asymmetric [MDK+16, DL17]. In contrast, the more recent work [GJB19] proposes an iterative algorithm based on the alternating maximization over and with an initialization provided by solving a doubly-stochastic relaxation of the QAP . Its performance is empirically evaluated on real datasets, but no theoretical performance guarantee is provided. Since the dot-product model is equivalent to the statistical model for Procrustes matching, where for a random permutation and orthogonal matrix , our results in Theorem 1 and Theorem 3 thus characterize the statistical limits of Procrustes matching.
Graph matching
There has been a recent surge of interest in understanding the information-theoretic and algorithmic limits of random graph matching [CK16, CK17, HM20, WXY21, DMWX21, BCL+19, FMWX19a, FMWX19b, GM20, GML22, MRT21b, MRT21a], which is an average-case model for the QAP and a noisy version of random graph isomorphism [BES80]. Most of the existing work is restricted to the correlated Erdős-Rényi-type models in which are iid pairs of two correlated Bernoulli or Gaussian random variables. In this case, the maximum likelihood estimator reduces to solving the QAP (20). Sharp information-theoretic limits are derived by analyzing this QAP [CK16, CK17, Gan21b, WXY21] and various efficient algorithms are developed based on its spectral or convex relaxations [Ume88, ZBV08, ABK15, VCL+15, LFF+16, DML17, FMWX19a, FMWX19b]. However, as discussed in Section 4, for geometric models such as the dot-product model, the QAP is the high-noise approximation of the MLE (3), which differs from the low-noise approximation (3) that is shown to be optimal in the low-dimensional regime of . This observation suggests that for geometric models one may need to rethink the algorithm design and move beyond the QAP-inspired methods.
Appendix B Maximal likelihood estimator in the dot-product model
To compute the “likelihood” of the observation given the ground truth , it is useful to keep in mind of the graphical model
where is related via (1), , and .
Note that are are rank-deficient. To compute the density of conditioned on meaningfully, one needs to choose an appropriate reference measure and evaluate the relative density . Let us choose to be the product of the marginal distributions of and , which does not depend on . For any rank- positive semidefinite matrices and , define and based on the SVD and , where and (the Stiefel manifold). We aim to show
| (22) |
for some fixed function , where the integral is with respect to the Haar measure on . This justifies the MLE in (3) for the dot-product model.
To show (22), denote by and neighborhoods of and respectively. (Their specific definitions are not crucial.) Consider a -neighborhood of of the following form:
and similarly define . Write the SVD for as , where and the diagonal matrix are mutually independent; in particular, is uniformly distributed over . Then for constant ,
where is defined by
Note that this function is continuous, strictly positive, and right-invariant, in the sense that for any . Thus, as , we have for some constant ,
proving (22).
Appendix C Analysis of approximate maximum likelihood
In this section we prove Theorem 1 for the dot product model. The proof of Theorem 2 for the distance model follows the same program and is postponed to Appendix D.
C.1 Discretization of orthogonal group
We first prove Lemma 1 on the approximation of nuclear norm on a discretization of .
Proof of Lemma 1.
Consider the singular value decomposition , where and is diagonal. Then the nuclear norm is attained at . Pick an element with , where . By orthogonality of and , we have
| (23) |
Note that
| (24) |
Also, we have
Adding the above equations and applying (23)-(24) yield
This implies
which completes the proof. ∎
Next we give a specific construction of a -net for that is suitable for the purpose of proving Theorem 1. Since orthogomal matrices are normal, by the spectral decomposition theorem, each orthogonal matrix can be written as , where with for all and is an unitary matrix. To construct a net for , we first discretize the eigenvalues uniformly and then discretize the eigenvectors according to the optimal local entropy of orthogonal matrices with prescribed eigenvalues.
For any fixed , let . Then the set
is a -net in norm for the set of all possible spectrum . For each , let denote the set of orthogonal matrices with a prescribed spectrum , i.e.
where ’s are the eigenvalues of sorted in the counterclockwise way from to . Similarly, define to be the set of unitary matrices with a given spectrum
Then . Let be the optimal -net in operator norm for , and let be the projection (with respect to ) of to . Define
| (25) |
We claim that is a -net in operator norm for the orthogonal group.
Lemma 2.
The set defined in (25) is a -net in operator norm for .
Proof.
Given , let its eigenvalue decomposition be . where . Then there exists where , such that . By definition, there exists such that and . Let denote the projection of . Then
where the second inequality follows from projection. ∎
The size of this -net is estimated in the following lemma.
Lemma 3 (Local entropy of ).
For each where , we have
| (26) |
Proof.
Note that
For any matrix , we have
where is the the operator norm with respect to . This implies
where is the operator norm ball centered at with radius . As a normed vector space over , the space of complex matrices has dimension since . Then the desired result follows from a standard volume bound (c.f. e.g. [Pis99, Lemma 4.10]) for the metric entropy
∎
C.2 Moment generating functions and cycle decomposition
Based on the reduction (55), it suffices to estimate
where
| (27) |
This moment generating function (MGF) is estimated in the following lemma.
Lemma 4.
For any fixed , let denote the set of orbits of the permutation and be the number of orbits with length . Let and denote by the eigenvalues of , where . Then
| (28) |
where
| (29) |
satisfying, for all ,
| (30) |
Furthermore,
| (31) |
where is a universal constant independent of .
Proof.
For simplicity, denote . Let be the vectorization of , and note that . Through the vectorization, we have
Let , then
| (32) |
Note that the eigenvalues of are
This leads to
| (33) |
Through a cycle decomposition, the spectrum of is the same as a block diagonal matrix of the following form
where is the number of -cycles in , and is a circulant matrix given by
It is well known that the eigenvalues of are the -th roots of unity . Therefore, the spectrum of is the following multiset
| (34) |
Recall that are the eigenvalues of . Note that the eigenvalues of are the complex conjugate of the eigenvalues of . Combined with (33) and (34), we have
| (35) |
Define
To simplify , let and so that and . Thus,
Note that
Multiplying the above two equations gives us
which implies
Note that , and therefore we have shown (29). In particular,
| (36) |
Since for , we have
Consequently, this gives us (31). In general, note that
which completes the proof for (30). To see this, define which is increasing in . Then
where the last inequality holds because for . Finally, (28) follows from (35). ∎
Based on the above representation via cycle decomposition, we have the following estimate for the moment generating function. This estimate is a key result in this paper as it is the basis of both Theorem 1 and Lemma 6.
Lemma 5.
Suppose . For some , let and be the -net defined in (25).
-
(i)
If , then
(37) -
(ii)
For any , if , then the following is true
(38)
Proof.
(i) For any fixed , combining (30) and (31) yields
| (39) |
Note that by Lemma 3, we have
| (40) |
Using Lemma 4 and (39), this leads to
where the second line follows from Lemma 3 and the fourth line follows from the fact that the number of permutations with fixed points is at most .
Recall that and . For any fixed ,
If , we have
| (41) |
Therefore, let and where , then
| (42) |
where the last line follows from and .
On the other hand, for ,we decompose it into two parts , where
We first show that the contribution of is negligible. To see this, note that
Recall that and . Therefore we have . Moreover, a simple observation is that . This concludes that is negligible and it suffices to bound . Note that for we have . Therefore, this implies
For , we have since . Consequently, in this regime we have
Thus, for , we have
| (43) |
For , we use a trivial bound
In this case,
| (44) |
Thus, (43) and (44) together imply
| (45) |
Combining (42) and (45) together, we obtain
which completes the proof.
(ii) Due to the stronger noise level, we need to be more careful in (39):
| (46) |
For simplicity, denote by the number of non-fixed points of . Let be the restriction of the permutation on its non-fixed points, which by definition is a derangement. Denote the number of cycles of a permutation by . An observation is that . Then Lemma 4 and (46) yield
Denote . Using (40) and rearranging the above inequality give us
| (47) |
Note that
where the expectation is taken for a uniformly random permutation . To bound the above truncated generating function, recall that the generating function of is given by (see, e.g., [FS09, Eq. (39)])
| (48) |
Pick some to be determined later and obtain the following
Choosing , we have
| (49) |
Recall that
For , each term is bounded by (43) and (44). On the other hand, if , we control via (41). Here in the case of almost perfect recovery, combined with (49), the assumption on yields a superexponentially decaying term in the summation (47). Specifically, combined this with (47) and (49), we obtain
where
Let where . Recall that . Then applying Stirling’s approximation gives us
| (50) |
and
| (51) |
Combining (50) and (51) implies
which completes the proof. ∎
The estimate of the moment generating functions results in the following lemma, which plays a crucial rule in the probability reduction estimate (55).
Lemma 6.
For some , let and be the -net defined in (25).
-
(i)
If , for any constant , the following inequality is true with high probability
(52) -
(ii)
For any , if , the following is true for any fixed constant with high probability
(53)
C.3 Proof of Theorem 1
Proof.
For fixed and , we have
Note that we have the following observations
and
Therefore,
| (54) |
Consider the following events
It is well known that , and by Lemma 6 we also have . On the events and , the previous estimate (54) for reduces to
| (55) |
By Lemma 5, the reduction (55) and a union bound, we have
This implies that the ground truth is the approximate MLE with probability , i.e.,
which shows the success of perfect recovery with high probability.
Appendix D Proof for the distance model
In this section, we prove Theorem 2. Let , and . Recall that the approximate MLE for the distance model is given by (9). As in the proof of Theorem 1, thanks to the orthogonal invariance of the nuclear norm , we may assume and without loss of generality, so that
Following the arguments for the dot-product model in Appendix C, a key step is to extend the estimate for in (27) to the following MGF:
| (56) |
where and . The following lemma gives a comparison between the MGF for the distance model and that for the dot-product model defined in (27), the latter of which was previous estimated in Lemma 4.
Lemma 7.
Fix a permutation matrix . For , denote by the eigenvalues of , where . Then
| (57) |
Proof.
Let . Denote by the vectorization of and recall that satisfies . Then
Denote , then
It suffices to compute the eigenvalues of . Recall that the spectrum of is given by (34). We claim that the spectrum of is the following multiset
| (58) |
where is the spectrum of defined in Lemma 4, given by
Now we prove (58). As shown in (34), has eigenvalue with multiplicity , where denote the number of cycles. We denote these by . Using the cycle decomposition and the block diagonal structure as in Lemma 4, we know that the eigenvectors corresponding to are of the following form
where the number of ’s equals the length of the corresponding cycle. In particular, due to the block diagonal structure, the blocks in ’s do not overlap. Therefore, we know that the vector is in the eigenspace of . Using the Gram-Schmidt process, we can construct vectors such that is a orthonormal basis of the eigenspace, i.e.
Pick an arbitrary eigenvalue of with eigenvector , and also pick an arbitrary eigenvalue of with eigenvector . Based on the arguments above, if , then , and therefore
| (59) |
For the eigenpair , we have
| (60) |
Combining (59) and (60), we conclude that for and , the eigenvalue of remains to be an eigenvalue of , while the eigenvalues of are replaced by in the spectrum of . Hence we have shown (58) is true.
Lemma 8.
Suppose . For some , let and be the -net defined in (25).
-
(i)
If , then
(61) -
(ii)
For any , if , then the following is true
(62)
Proof.
Lemma 8 implies the following high probability estimates. The proof is the same as in Lemma 6 via Chernoff bound and therefore we omit it here.
Lemma 9.
Suppose . For some , let and be the -net defined in (25).
-
(i)
If , for any constant , the following inequality is true with high probability
(64) -
(ii)
For any , if , the following is true for any fixed constant with high probability
(65)
Now we are ready to prove Theorem 2 . Similarly as in the dot-product model (see the remark following Theorem 1), for almost perfect recovery, we actually prove a stronger nonasymptotic bound: For all sufficiently small , if , then with high probability, which clearly implies Theorem 2 by taking .
Proof of Theorem 2.
(i) Let be the -net for defined in (25). Following the same argument as in Theorem 1
For fixed and , we have
Since the entries of are not independent, we need to be more careful:
because and commutes with any permutation matrix . Therefore, similarly as in (54),
| (66) |
Consider the events
We claim that . To see this, note that
For each , we have , where is the -th column of . By Hanson-Wright inequality (see e.g. [RV13, Theorem 1.1]), for each ,
Taking and simplifying the above inequality yield
| (67) |
Note that (67) is true for every , and the columns ’s are independent. This immediately gives us . Moreover, by Lemma 9 we also have . On the events and , the estimate (66) reduces to
| (68) |
Combining this with Lemma 8 and applying a union bound, we have
This implies with high probability, which completes the proof.
Appendix E Information-theoretic necessary conditions
In this section, we derive necessary conditions for both almost perfect recovery and perfect recovery for the linear assignment model (1). These conditions also hold for the weaker dot-product and distance models.
E.1 Impossibility of almost perfect recovery
We first derive a necessary condition for almost perfect recovery that holds for any via a simple mutual information argument. Then we focus on the special case where is a constant and give a much sharper analysis, improving the necessary condition from to . Note that achieving a vanishing recovery error in expectation is equivalent to that with high probability (see e.g. [HWX17, Appendix A]). Thus without loss of generality, we focus on the expected number of errors in this subsection.
Proposition 1.
For any , if there exists an estimator such that , then
| (69) |
The necessary condition (69) further specializes to:
- •
-
•
:
- •
Proof.
Since form a Markov chain, by the data processing inequality of mutual information, we have
| (71) |
On the one hand, note that . Moreover, for any fixed realization of , the number of such that is , where denotes the number of derangements of elements, given by
and denotes rounding to the nearest integer. Therefore,
Furthermore, takes values in . Thus from the chain rule,
| (72) |
On the other hand, the information provided by the observation about satisfies
| (73) |
where follows from the Gaussian channel capacity formula and the fact that the mutual information in the Gaussian channel under a second moment constraint is maximized by the Gaussian input distribution. Combining (71)–(73), we get that
arriving at the desired necessary condition (69). ∎
While the negative result in Proposition 1 holds for any , the necessary condition (69) turns out to be loose for bounded . The following result gives the optimal condition in this case.
Theorem 4.
Assume for any constant . There exists a constant that only depends on such that for any estimator and all sufficiently large ,
Theorem 4 readily implies that for constant , is necessary for achieving the almost perfect recovery, i.e., . To prove Theorem 4, we follow the program in [DWXY21] of analyzing the posterior distribution. The likelihood function of given is proportional to . Therefore, conditional on , the posterior distribution of is a Gibbs measure, given by
and is the normalization factor.
As observed in [DWXY21, Section 3.1], in order to prove the impossibility of almost perfect recovery, it suffices to consider the estimator which is sampled from the posterior distribution . To see this, given any estimator , and are equal in law, and hence
which shows that is optimal within a factor of two. Thus it suffices to bound from below.
To this end, fix some to be specified later and define the sets of good and bad solutions respectively as
By the definition of , we have
Next we show two key lemmas, which bound the posterior mass of and from above and below, respectively.
Lemma 10.
Assume for any constant . For any constant such that , with probability at least ,
| (74) |
Lemma 11.
Assume for some constant . There exist constants and that only depend on such that for all and sufficiently large , with probability at least ,
| (75) |
E.2 Upper bounding the posterior mass of good permutations
In this section, we prove Lemma 10 by a truncated first moment calculation. We need the following key auxiliary result.
Lemma 12.
Assume that . Then for any ,
Proof.
It follows from (30) in Lemma 4 that
where is the number of non-fixed points, is the restriction of the permutation on its non-fixed points, and denotes the number of cycles of . It follows that
where , the expectation is taken for a uniformly random permutation , and the last inequality follows from (49). ∎
Proof of Lemma 10.
Note that
where
for some to be specified. Next we bound and separately.
First, the number of permutations such that has non-fixed points is
| (76) |
where . Thus
| (77) |
Furthermore, for any ,
| (78) |
where the first equality holds due to and and the second equality follows from .
To bound , the calculation above shows that directly applying the Markov inequality is too crude since . Note that although is negatively biased, when is atypically large it results in an excessive contribution to the exponential moments. Thus we truncate on the following event:
for some threshold to be chosen.
Then for any ,
| (80) |
To bound the first term, note that for any ,
By choosing , we get that
Recall from Lemma 12, we have that
Therefore, it follows from a union bound that
| (81) |
where the last equality holds by choosing .
E.3 Lower bounding the posterior mass of bad permutations
In this section, we prove Lemma 11. We aim to construct exponentially many bad permutations whose log likelihood is no smaller than . It turns out that can be decomposed according to the orbit decomposition of as per (14). Thus, following [DWXY21], we look for vertex-disjoint orbits whose total lengths add up to and each of them is augmenting in the sense that .
In the planted matching model with independent weights [DWXY21], a great challenge lies in the fact that short augmenting orbits (even after taking their disjoint unions) are insufficient to meet the total length requirement. As a result, one has to search for long augmenting orbits of length . However, due to the excessive correlations among long augmenting orbits, the second-moment calculation fundamentally fails. To overcome this challenge, [DWXY21] invents a two-stage finding scheme which first finds many but short augmenting paths and then patches them together to form a long augmenting orbit using the so-called sprinkling idea. Fortunately, in our low-dimensional case of , as also observed in [KNW22], it suffices to look for augmenting -orbits and take their disjoint unions. More precisely, the following lemma shows that there are vertex-disjoint augmenting -orbits, from which we can easily extract exponentially many different unions of total length . In contrast, to prove the failure of the MLE for almost perfect recovery in [KNW22], a single union of vertex-disjoint augmenting -orbits is sufficient.
Lemma 13.
If , then there exist constants , , and that only depend on and such that for all , with probability at least , there are at least many vertex-disjoint augmenting -orbits.
This lemma is proved in [KNW22, Section 4] using the so-called concentration-enhanced second-moment method. For completeness, here we provide a much simpler proof via the vanilla second-moment method combined with Turán’s theorem.
Proof.
Let denote the indicator that is an augmenting -orbit and . To extract a collection of vertex-disjoint augmenting -orbits, we construct a graph , where the vertices correspond to for which , and and are connected if and share a common vertex. By construction, any collection of vertex-disjoint -orbits corresponds to an independent set in . By Turán’s theorem (see e.g. [AS08, Theorem 1, p. 95]), there exists an independent set in of size at least . It remains to bound from below and from above.
Note that . For all sufficiently large, and it follows from [KNW22, Prop. 4.3] that
Therefore,
| (83) |
Under the assumption that , it follows that for some constant that only depends on and . Moreover,
where the second equality holds because and are independent when . Recall that . Moreover, it follows from [KNW22, Prop. 4.5] that
Combining the last three displayed equation yields that
| (84) |
Under the assumption that , it follows that for some that only depends on and . By Chebyshev’s inequality,
Moreover,
and hence
By Markov’s inequality, with probability at least . Therefore, with probability at least ,
for some constant that only depends on and . ∎
E.4 Impossibility of perfect recovery
In this section, we prove an impossibility condition of perfect recovery.
Theorem 5.
Suppose that and
| (85) |
for a constant . Then there exists a constant that only depends on such that for any estimator , .
Theorem 5 immediately implies that if there exists an estimator that achieves perfect recovery with high probability, then
| (86) |
In comparison, it is shown in [DCK19, Theorem 1] that perfect recovery is possible if . Thus our necessary condition agrees with their sufficient condition up to an additive factor. Our necessary condition (86) further specializes to
- •
-
•
:
-
•
:
Note that the previous work [DCK19] shows that is necessary for perfect recovery, under the additional assumption that . The analysis therein is based on showing the existence of an augmenting -orbit via the second-moment method. We follow a similar strategy, but our first and second moment estimates are sharper and thus yield a tighter condition.
Proof.
Recall that denote the indicator that is an augmenting -orbit and . For the purpose of lower bound, consider the Bayesian setting where is drawn uniformly at random. Then the MLE given in (2) minimizes the probability of error. Hence, it suffices to bound from below . Note that on the event , there exists at least one permutation whose likelihood is at least as large as that of and hence the error probability of MLE is at least . Therefore,
It remains to bound from below. To this end, we first bound . In view of (84),
By assumption and (85), it follows from (83) that
Moreover,
where holds because for all and holds due to assumption (85),
Combining the last three displayed equation yields that for some constant that only depends on . By the Paley-Zygmund inequality,
∎
Appendix F Recovery thresholds in the nonisotropic case
In this section we argue that Theorem 1 continues to hold under the same conditions in the nonisotropic case of , provided that for some absolute constant . In the general nonisotropic case, we denote by the moment generating function given by (27) to highlight the dependency on the covariance matrix and the noise level . As in the proof of Lemma 5, recall denotes the vectorization of . Since , the vector has distribution . Note that . Modifying (32) accordingly, we have
where and . This shows that the MGF satisfies the same estimates (30), (31) and Lemma 5 for the isotropic case with the original noise replaced by a constant multiple of it . This constant multiplicative factor keeps satisfying the same noise threshold in Theorem 1, which implies both prefect recovery and almost perfect recovery can still be achieved for the nonisotropic case under the same conditions, hence confirming our claim in Section 4.
Acknowledgment
The authors are grateful to Zhou Fan, Cheng Mao, and Dana Yang for helpful discussions.
Y. Wu is supported in part by the NSF Grant CCF-1900507, an NSF CAREER award CCF-1651588, and an Alfred Sloan fellowship. J. Xu is supported in part by the NSF Grant CCF-1856424 and an NSF CAREER award CCF-2144593.
References
- [ABK15] Yonathan Aflalo, Alexander Bronstein, and Ron Kimmel. On convex relaxation of graph isomorphism. Proceedings of the National Academy of Sciences, 112(10):2942–2947, 2015.
- [AFT+17] Avanti Athreya, Donniell E Fishkind, Minh Tang, Carey E Priebe, Youngser Park, Joshua T Vogelstein, Keith Levin, Vince Lyzinski, and Yichen Qin. Statistical inference on random dot product graphs: a survey. The Journal of Machine Learning Research, 18(1):8393–8484, 2017.
- [AG14] Ayser Armiti and Michael Gertz. Geometric graph matching and similarity: A probabilistic approach. In Proceedings of the 26th International Conference on Scientific and Statistical Database Management, pages 1–12, 2014.
- [AS08] Noga Alon and Joel H. Spencer. The Probabilistic Method. Wiley-Interscience Series in Discrete Mathematics and Optimization, 3 edition, 2008.
- [BCL+19] Boaz Barak, Chi-Ning Chou, Zhixian Lei, Tselil Schramm, and Yueqi Sheng. (nearly) efficient algorithms for the graph matching problem on correlated random graphs. In Advances in Neural Information Processing Systems, pages 9186–9194, 2019.
- [BDER16] Sébastien Bubeck, Jian Ding, Ronen Eldan, and Miklós Z Rácz. Testing for high-dimensional geometry in random graphs. Random Structures & Algorithms, 49(3):503–532, 2016.
- [BES80] László Babai, Paul Erdös, and Stanley M Selkow. Random graph isomorphism. SIAM Journal on computing, 9(3):628–635, 1980.
- [BG05] Ingwer Borg and Patrick JF Groenen. Modern multidimensional scaling: Theory and applications. Springer Science & Business Media, 2005.
- [BG18] Sébastien Bubeck and Shirshendu Ganguly. Entropic clt and phase transition in high-dimensional wishart matrices. International Mathematics Research Notices, 2018(2):588–606, 2018.
- [CD16] Olivier Collier and Arnak S Dalalyan. Minimax rates in permutation estimation for feature matching. The Journal of Machine Learning Research, 17(1):162–192, 2016.
- [CK16] Daniel Cullina and Negar Kiyavash. Improved achievability and converse bounds for Erdös-Rényi graph matching. In Proceedings of the 2016 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Science, pages 63–72. ACM, 2016.
- [CK17] Daniel Cullina and Negar Kiyavash. Exact alignment recovery for correlated Erdös-Rényi graphs. arXiv preprint arXiv:1711.06783, 2017.
- [CKK+10] M. Chertkov, L. Kroc, F. Krzakala, M. Vergassola, and L. Zdeborová. Inference in particle tracking experiments by passing messages between images. PNAS, 107(17):7663–7668, 2010.
- [DCK19] Osman E Dai, Daniel Cullina, and Negar Kiyavash. Database alignment with Gaussian features. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 3225–3233. PMLR, 2019.
- [DCK20] Osman Emre Dai, Daniel Cullina, and Negar Kiyavash. Achievability of nearly-exact alignment for correlated gaussian databases. In 2020 IEEE International Symposium on Information Theory (ISIT), pages 1230–1235. IEEE, 2020.
- [DL17] Nadav Dym and Yaron Lipman. Exact recovery with symmetries for procrustes matching. SIAM Journal on Optimization, 27(3):1513–1530, 2017.
- [DML17] Nadav Dym, Haggai Maron, and Yaron Lipman. DS++: a flexible, scalable and provably tight relaxation for matching problems. ACM Transactions on Graphics (TOG), 36(6):184, 2017.
- [DMWX21] Jian Ding, Zongming Ma, Yihong Wu, and Jiaming Xu. Efficient random graph matching via degree profiles. Probability Theory and Related Fields, 179(1):29–115, 2021.
- [DWXY21] Jian Ding, Yihong Wu, Jiaming Xu, and Dana Yang. The planted matching problem: Sharp threshold and infinite-order phase transition. arXiv preprint arXiv:2103.09383, 2021.
- [FMWX19a] Zhou Fan, Cheng Mao, Yihong Wu, and Jiaming Xu. Spectral graph matching and regularized quadratic relaxations I: The Gaussian model. arxiv preprint arXiv:1907.08880, 2019.
- [FMWX19b] Zhou Fan, Cheng Mao, Yihong Wu, and Jiaming Xu. Spectral graph matching and regularized quadratic relaxations II: Erdős-Rényi graphs and universality. arxiv preprint arXiv:1907.08883, 2019.
- [FS09] Philippe Flajolet and Robert Sedgewick. Analytic combinatorics. Cambridge University Press, 2009.
- [Gan21a] Luca Ganassali. Sharp threshold for alignment of graph databases with Gaussian weights. Mathematical and Scientific Machine Learning (MSML21), 2021. arXiv preprint arXiv:2010.16295.
- [Gan21b] Luca Ganassali. Sharp threshold for alignment of graph databases with gaussian weights. In MSML21 (Mathematical and Scientific Machine Learning), 2021.
- [Gil61] Edward N Gilbert. Random plane networks. Journal of the society for industrial and applied mathematics, 9(4):533–543, 1961.
- [GJB19] Edouard Grave, Armand Joulin, and Quentin Berthet. Unsupervised alignment of embeddings with wasserstein procrustes. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 1880–1890. PMLR, 2019.
- [GM20] Luca Ganassali and Laurent Massoulié. From tree matching to sparse graph alignment. arXiv preprint arXiv:2002.01258, 2020.
- [GML22] Luca Ganassali, Laurent Massoulié, and Marc Lelarge. Correlation detection in trees for planted graph alignment. In 13th Innovations in Theoretical Computer Science Conference (ITCS 2022). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2022.
- [HM20] Georgina Hall and Laurent Massoulié. Partial recovery in the graph alignment problem. arXiv preprint arXiv:2007.00533, 2020.
- [HWX17] B. Hajek, Y. Wu, and J. Xu. Information limits for recovering a hidden community. IEEE Trans. on Information Theory, 63(8):4729 – 4745, 2017.
- [JL15] Tiefeng Jiang and Danning Li. Approximation of rectangular beta-laguerre ensembles and large deviations. Journal of Theoretical Probability, 28(3):804–847, 2015.
- [KNW22] Dmitriy Kunisky and Jonathan Niles-Weed. Strong recovery of geometric planted matchings. In Proceedings of the 2022 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 834–876. SIAM, 2022.
- [LFF+16] Vince Lyzinski, Donniell Fishkind, Marcelo Fiori, Joshua Vogelstein, Carey Priebe, and Guillermo Sapiro. Graph matching: Relax at your own risk. IEEE Transactions on Pattern Analysis & Machine Intelligence, 38(1):60–73, 2016.
- [LRB+16] Z Lähner, Emanuele Rodolà, MM Bronstein, Daniel Cremers, Oliver Burghard, Luca Cosmo, Andreas Dieckmann, Reinhard Klein, and Y Sahillioglu. SHREC’16: Matching of deformable shapes with topological noise. Proc. 3DOR, 2(10.2312), 2016.
- [Mat13] Sho Matsumoto. Weingarten calculus for matrix ensembles associated with compact symmetric spaces. Random Matrices: Theory and Applications, 2(02):1350001, 2013.
- [MDK+16] Haggai Maron, Nadav Dym, Itay Kezurer, Shahar Kovalsky, and Yaron Lipman. Point registration via efficient convex relaxation. ACM Transactions on Graphics (TOG), 35(4):1–12, 2016.
- [MMX21] Mehrdad Moharrami, Cristopher Moore, and Jiaming Xu. The planted matching problem: Phase transitions and exact results. The Annals of Applied Probability, 31(6):2663–2720, 2021.
- [MRT21a] Cheng Mao, Mark Rudelson, and Konstantin Tikhomirov. Exact matching of random graphs with constant correlation. arXiv preprint arXiv:2110.05000, 2021.
- [MRT21b] Cheng Mao, Mark Rudelson, and Konstantin Tikhomirov. Random graph matching with improved noise robustness. In Proceedings of Thirty Fourth Conference on Learning Theory, volume 134 of Proceedings of Machine Learning Research, pages 3296–3329, 2021.
- [OMK10] Sewoong Oh, Andrea Montanari, and Amin Karbasi. Sensor network localization from local connectivity: Performance analysis for the MDS-MAP algorithm. In 2010 IEEE Information Theory Workshop on Information Theory (ITW 2010, Cairo), pages 1–5. IEEE, 2010.
- [Pen03] Mathew Penrose. Random geometric graphs, volume 5. OUP Oxford, 2003.
- [PG11] Pedram Pedarsani and Matthias Grossglauser. On the privacy of anonymized networks. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 1235–1243. ACM, 2011.
- [Pis99] G. Pisier. The volume of convex bodies and Banach space geometry. Cambridge University Press, 1999.
- [RCB97] Anand Rangarajan, Haili Chui, and Fred L Bookstein. The softassign procrustes matching algorithm. In Biennial International Conference on Information Processing in Medical Imaging, pages 29–42. Springer, 1997.
- [RV13] Mark Rudelson and Roman Vershynin. Hanson-Wright inequality and sub-Gaussian concentration. Electron. Commun. Probab., 18:no. 82, 9, 2013.
- [Sch66] Peter H Schönemann. A generalized solution of the orthogonal procrustes problem. Psychometrika, 31(1):1–10, 1966.
- [SRZF03] Yi Shang, Wheeler Ruml, Ying Zhang, and Markus PJ Fromherz. Localization from mere connectivity. In Proceedings of the 4th ACM international symposium on Mobile ad hoc networking & computing, pages 201–212, 2003.
- [SSZ20] Guilhem Semerjian, Gabriele Sicuro, and Lenka Zdeborová. Recovery thresholds in the sparse planted matching problem. Physical Review E, 102(2):022304, 2020.
- [Ume88] Shinji Umeyama. An eigendecomposition approach to weighted graph matching problems. IEEE Transactions on Pattern Analysis and Machine Intelligence, 10(5):695–703, 1988.
- [VCL+15] Joshua T Vogelstein, John M Conroy, Vince Lyzinski, Louis J Podrazik, Steven G Kratzer, Eric T Harley, Donniell E Fishkind, R Jacob Vogelstein, and Carey E Priebe. Fast approximate quadratic programming for graph matching. PLOS one, 10(4):e0121002, 2015.
- [Ver18] Roman Vershynin. High-Dimensional Probability: An Introduction with Applications in Data Science. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, 2018.
- [WXY21] Yihong Wu, Jiaming Xu, and Sophie H. Yu. Settling the sharp reconstruction thresholds of random graph matching. arXiv preprint2102.00082, 2021.
- [ZBV08] Mikhail Zaslavskiy, Francis Bach, and Jean-Philippe Vert. A path following algorithm for the graph matching problem. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(12):2227–2242, 2008.