Random walks on Coxeter interchange graphs
Abstract.
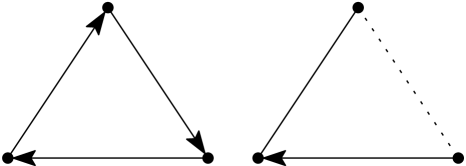
A tournament is an orientation of a graph. Vertices are players and edges are games, directed away from the winner. Kannan, Tetali and Vempala and McShine showed that tournaments with given score sequence can be rapidly sampled, via simple random walks on the interchange graphs of Brualdi and Li. These graphs are generated by the cyclically directed triangle, in the sense that traversing an edge corresponds to the reversal of such a triangle in a tournament.
We study Coxeter tournaments on Zaslavsky’s signed graphs. These tournaments involve collaborative and solitaire games, as well as the usual competitive games. The interchange graphs are richer in complexity, as a variety of other generators are involved. We prove rapid mixing by an intricate application of Bubley and Dyer’s method of path coupling, using a delicate re-weighting of the graph metric. Geometric connections with the Coxeter permutahedra introduced by Ardila, Castillo, Eur and Postnikov are discussed.
Key words and phrases:
Coxeter permutahedra, digraph, graphical zonotope, majorization, Markov chain Monte Carlo, MCMC, mixing time, oriented graph, paired comparisons, permutahedron, root system, score sequence, signed graph, tournament2010 Mathematics Subject Classification:
05C20, 11P21, 17B22, 20F55, 51F15, 51M20, 52B05, 60J10, 62J151. Introduction
A tournament is an orientation of a graph. We think of vertices as players and edges as games, the orientation of which indicates the winner. Tournaments are related to the geometry of the permutahedron , which is a classical polytope in discrete convex geometry. See, e.g., Stanley [33], Ziegler [38], and Kolesnik and Sanchez [20].
Classical combinatorics is related to the root system of type . Coxeter combinatorics is concerned with extensions to the other roots systems of types , and (and sometimes also the finite, exceptional types , , , and ). For example, works by Galashin, Hopkins, McConville and Postnikov [10, 11] have investigated Coxeter versions of the chip-firing game (the sandpile model).
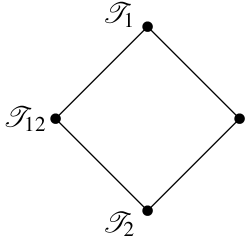
Recently, Kolesnik and Sanchez [19] introduced the Coxeter analogue of graph tournaments, which are associated with orientations of signed graphs, as in Zaslavsky [37], and the Coxeter permutahedra , recently introduced by Ardila, Castillo, Eur and Postnikov [2]. Coxeter tournaments involve collaborative and solitaire games, as well as the usual competitive games in graph tournaments.
In this work, we show (see Theorem 4 below) that random walks rapidly mix on the sets of Coxeter tournaments with given score sequence, that is, on the fibers of the Coxeter permutahedra . Informally, this means that the walk is close to uniform in the fiber after a short amount of time, yielding an efficient way to sample from this set of interest.
Many combinatorial properties of these structures remain mysterious. The purpose of this work is to explore the associated Coxeter interchange graphs, which encode their combinatorics, via random walks. These graphs, introduced by Kolesnik, Mitchell and Przybyłowski [18], generalize the interchange graphs introduced by Brualdi and Li [6]. Rapid mixing in the classical setting was established by Kannan, Tetali and Vempala [16] and McShine [25]. We recover these results by our general strategy.
Let us emphasize that even the classical interchange graphs appear to be difficult to describe in general. Indeed, Brualdi and Li [6, p. 151] state that they have “a rich and fascinating combinatorial structure and that much remains to be determined.” Even counting the number of vertices is of “considerable interest and considerable difficulty” [6, p. 143].
Beginning with Spencer [32], and subsequent works by McKay [23], McKay and Wang [24], and Isaev, Iyer and McKay [15], asymptotic estimates for the number of vertices in the interchange graphs have been found only for fibers of points near the center of . In the other extreme, Chen, Chang and Wang [9] showed that, for certain points near the boundary of , the interchange graph is the classical hypercube.
The Coxeter interchange graphs are richer still. Therefore, in broad terms, we show in this work that random walks rapidly mix on a wide and intricate class of graphs.
Rapid mixing can sometimes be used to approximately count sets of interest. Roughly speaking, this is because the uniform measure on a set is related to the size of the set . See, e.g., Sinclair [31] for more details. The current work might serve as a first step towards developing efficient approximate counting schemes for the fibers of the Coxeter permutahedra .
As this work touches on a variety of subjects (combinatorics, geometry, algebra and probability), some preliminaries are required before we can state our results precisely. In Section 1.1, we discuss the literature related to tournaments and the standard permutahedron (of type ). Our results are discussed informally in Sections 1.2 and 1.3. Further background on tournaments, root systems, signed graphs and combinatorial geometry is in Section 2 and in the previous works in this series [20, 19, 18]. Our main result is stated formally in Section 3. See Sections 4, 5 and 6 for the proofs. Finally, a number of open problems and future directions are listed in Section 7.
We hope that this work will serve as an invitation to step into the Coxeter “worlds” (of types , and ). We believe that Coxeter combinatorics is fertile ground, where algebraists, combinatorialists, geometers and probabilists can open new lines of fruitful communication. In particular, many problems in discrete probability likely have a Coxeter analogue, waiting to be discovered.
1.1. Context
A tournament is an orientation of the complete graph , encoded as some with all . Each edge in is oriented as if or if . We think of each edge as a game, directed away from the winner. The win sequence
lists the total number of wins by each player, where are the standard basis vectors. We let denote the standard win sequence, corresponding to the transitive (acyclic) tournament in which for all . In a sense, and its permutations are as “spread out” as possible.
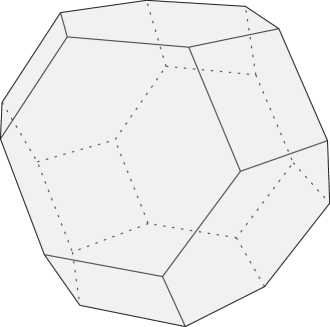
Results by Rado [29] and Landau [21] imply that the set of all win sequences is precisely the set of lattice points in the permutahedron , that is, . We recall that is a classical polytope in discrete geometry (see, e.g., Ziegler [38]), obtained as the convex hull of and its permutations, see Figure 1. By Stanley [33], win sequences are in bijection with spanning forests . (The volume of is the number of spanning trees .) See Postnikov [28] for generalizations.
It is convenient to make a linear shift
| (1) |
where . Note that this re-centers the polytope at the origin . The score sequence
associated with the win sequence of a tournament , is given by
| (2) |
This shift corresponds to awarding a point for each win/loss. We let denote the set of all possible score sequences.
Although the set has a simple, geometric description, the set , of tournaments with given score sequence , appears to be quite combinatorially complex.
Kannan, Tetali and Vempala [16] investigated simple random walk as a way of sampling from . However, rapid mixing was proved only for sufficiently close to . McShine [25] established rapid mixing in time , for all , by an elegant application of Bubley and Dyer’s [7] method of path coupling, which was relatively new at the time. See Section 2.3 below for an overview. We note that Sarkar [30] has shown that mixing takes for some sequences.
More specifically, in [16, 25], the random walks are on the interchange graphs introduced by Brualdi and Li [6]. Any two tournaments with the same score sequence have the same number of copies of the cyclic triangle (see Figure 5). Moreover, if some contains a copy of , then the tournament , obtained by reversing the orientation of all edges in , has the same score sequence as . These observations are the key to exploring . The graph has a vertex for each and two are neighbors if for some copy of . It can be shown that is connected. In this sense, generates the set .
The permutahedron is related with the standard root system of type , as the symmetric group is the Weyl group of type . We refer to, e.g., the standard text by Humphreys [14] for background on root systems. We recall that Killing [17] and Cartan [8] classified all (irreducible, crystallographic) root systems (up to isomorphism) as the infinite families , , and and the finite exceptional types , , , and .
Coxeter permutahedra , recently studied by Ardila, Castillo, Eur and Postnikov [2], are obtained by replacing the role of in the definition of with the Weyl group of a root system . See, e.g., Figure 2.
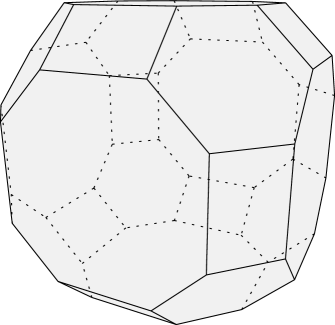
The previous works in this series [19, 18] studied the connection between the polytopes and Coxeter tournaments, which are related to orientations of signed graphs, as developed by Zaslavsky [35, 36, 37]. As mentioned above, these tournaments involve collaborative and solitaire games, as well as the usual competitive games in classical graph tournaments.
1.2. Purpose
In this work (see Theorem 4) we show that simple random walks mix rapidly on the Coxeter interchange graphs . These graphs encode the combinatorics of the sets , of Coxeter tournaments with a given score sequence , and give structural information about the fibers of the Coxeter permutahedra . We focus on the non-standard types , and .
We also show (see Theorem 5) that all Coxeter interchange graphs are connected and we bound their diameter. In constructing our random walk couplings, we uncover various other fine, structural properties of the graphs , and hence the sets , which might be of independent (algebraic, geometric, etc.) interest.
1.3. Discusssion
Path coupling is a powerful method for establishing rapid mixing (see Section 2.3). As already mentioned, path coupling was used in [25]. We will also use this method, however, the application in the Coxeter setting is significantly more delicate.
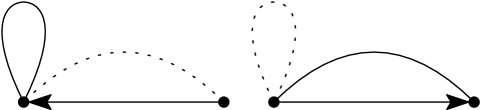
As discussed above, the interchange graphs in type are generated by a single neutral tournament, namely, the cyclic triangle . On the other hand, in the Coxeter setting, there are a number of other generators which play a role (see Figures 6, 7 and 5). A fascinating interplay arises, as these generators can interact in a variety of interesting ways. As such, the Coxeter interchange graphs are much richer in complexity. Likewise, the analysis of random walks on these structures is more involved.
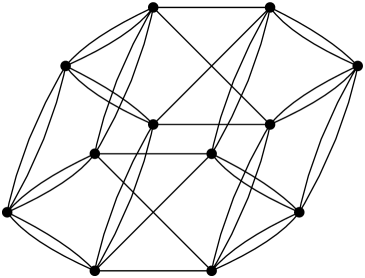
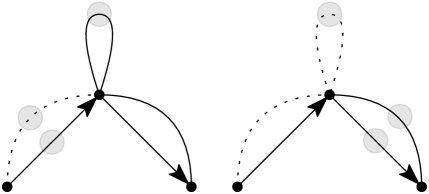
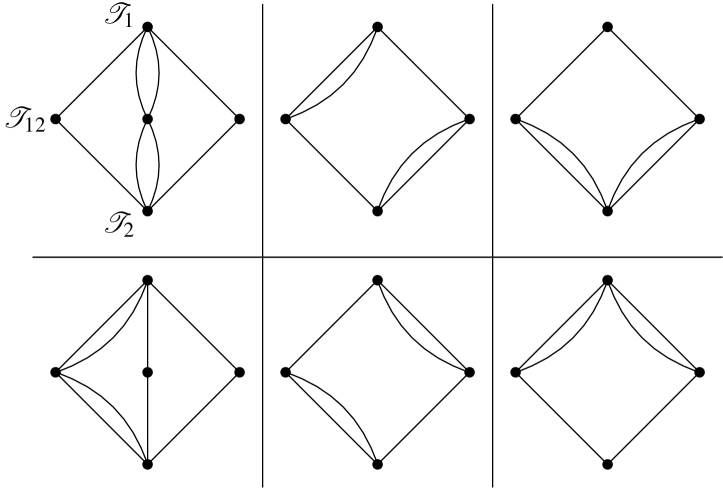
The types increase in difficulty in order , , , . Type is especially challenging, due to the presence of loops in some of the generators, which we call clovers (see Figure 7). These generators correspond to double edges in an interchange graph. In particular, a special type of structure, which we call a crystal (see Figure 25), can appear in type interchange graphs. The crystal arises in when . Crystals can also be found as subgraphs in larger type interchange graphs, for instance, in the snare drum in Figure 3, when . In other examples, such as the tambourine in Figure 4, when is the center of the polytope, there are no crystals, but interesting structure nonetheless.
The presence of crystals in type interchange graphs leads to two main issues. The first is in extending certain natural couplings on various small subgraphs (the extended networks discussed in Sections 5.1 and 5.2) to a unified coupling on the entire interchange graph. To overcome this difficulty, we will prove a number of detailed combinatorial properties of the Coxeter interchange graphs. We classify the types of subgraphs (see Figures 14, 17 and 25), which together form the full graph, and study the ways in which they can intersect. For example, one crucial property (see Lemma 21) is that any two crystals can share at most one single edge. Without this property, it seems that a path coupling argument would not be possible.
The second issue caused by crystals is in obtaining a “contractive” (see Section 2.3) coupling. In applying path coupling, we will need to re-weight the graph metric in a specific way, which accounts for the occurrence of crystals. Loosely speaking, the choice of weights is related to the fact that, in our random walk couplings, crystals work like “switches,” that convert single edges to double edges, and vice versa.
The overall coupling used to establish rapid mixing in the Coxeter setting is quite elaborate. See, e.g., Figures 28, 29 and 30 below. The classical type result [16, 25] is a special case of the argument depicted in Figure 27.
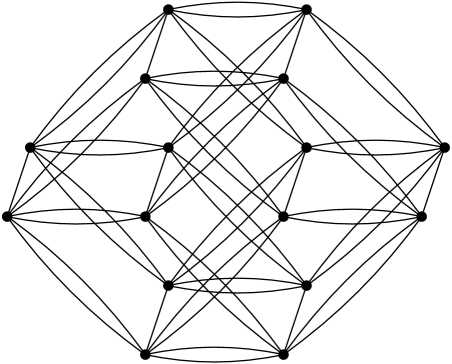
2. Background
We refer to [2], Humphreys [14], Zaslavsky [35, 36, 37], and the previous works in this series [19, 18] for a detailed background on root systems, signed graphs and their connections to discrete geometry. In this section, we will only recall what is used in the current work.
2.1. Coxeter tournaments
A signed graph on has a set of signed edges . The four possible types of edges are:
-
•
negative edges between two vertices and ,
-
•
positive edges between two vertices and ,
-
•
half edges with only one vertex , and
-
•
loops at a vertex .
We note that classical graphs correspond to signed graphs with only negative edges.
In this work, we focus on the complete signed graphs of types , and . These signed graphs contain all possible negative and positive edges . In type (resp. ), all possible half edges (resp. loops ) are also included. We call a signed graph a -graph if .
Most of the results in the literature on classical (type ) graph tournaments restricts to the case that is the complete graph . We note that the signed graph with all possible negative edges (and no other types of signed edges) corresponds to the classical complete graph .
A Coxeter tournament on a signed graph is an orientation of . When is unspecified, our default assumption will be that . More formally, , with all . We think of each as a game, and as indicating its outcome. (We think of as having a natural ordering, so that holds all information about the orientation of under . However, we could, somewhat pedantically, instead write .)
The score sequence is given by, cf. (2),
where is the vector corresponding to the signed edge , given by , and . In other words:
-
•
negative edges are competitive games in which one of wins and the other loses a point,
-
•
positive edges are collaborative games in which both win or lose a point,
-
•
half edges are (half edge) solitaire games in which wins or loses a point, and
-
•
loops are (loop) solitaire games in which wins or loses point.
If we say that is neutral.
We let denote the standard score sequence corresponding to the Coxeter tournament in which all . We note that, in some contexts, is called the Weyl vector. It is also the sum of the fundamental weights of the root system . See, e.g., [14, 13] for more details.
As discussed in [2], the Coxeter -permutahedron is the convex hull of the orbit of under the Weyl group of type . Thus is a distinguished vertex of . Note that the symmetric group is the Weyl group of standard type and the Weyl vector is , so (see (1) above) is the -permutahedron of standard type .
In [19], we showed that is precisely the set of all possible mean score sequences of random Coxeter tournaments, thereby establishing a Coxeter analogue of a classical result of Moon [26]. The next work in this series [18] focused on deterministic Coxeter tournaments. The set of all score sequences of Coxeter tournaments was classified, generalizing the classical result of Landau [21] discussed above.
The precise characterization of is somewhat technical, involving a certain weak sub-majorization condition and additional parity conditions in types and . The proof is constructive, in that it shows how to build a Coxeter tournament with any given score sequence. See [18, Theorem 4] for more details.
2.2. Interchange graphs
The set of all Coxeter tournaments on with given score sequence was also investigated in [18]. Coxeter analogues of the interchange graphs discussed above were introduced. Recall that the sets are generated by the cyclic triangle . In the Coxeter setting, there are additional generators.
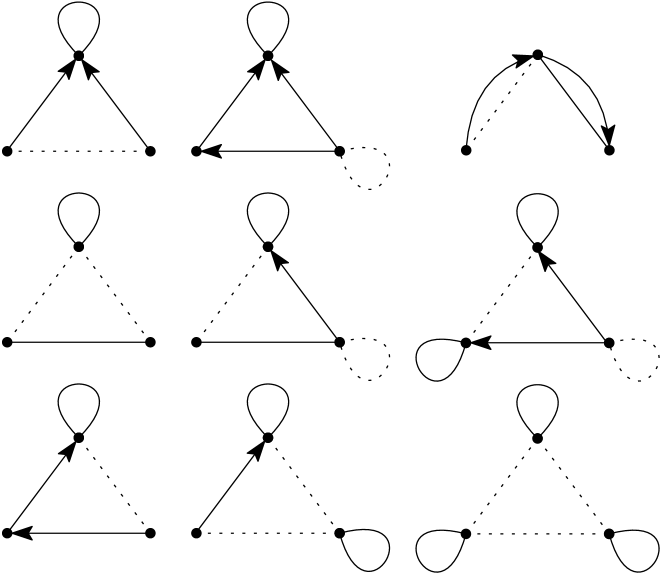
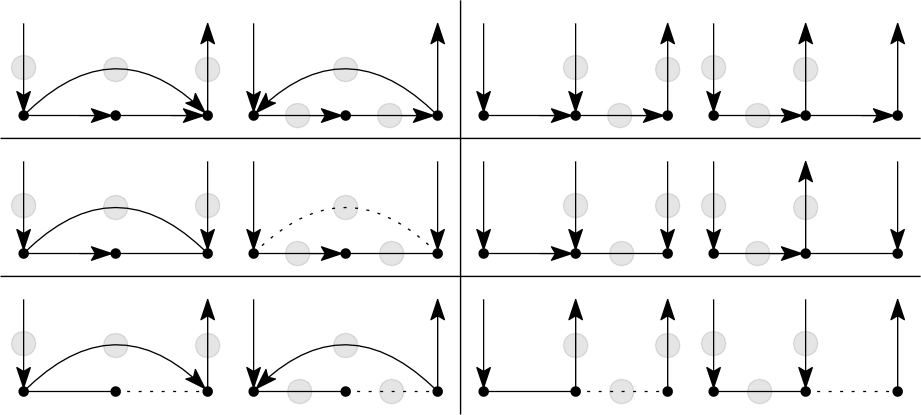
In all types , and , in addition to , we also require a balanced triangle . In type , there are also three neutral pairs , and . On the other hand, in type , there are also two neutral clovers and . See Figures 5, 6 and 7. In figures depicting Coxeter tournaments, we will draw:
-
•
competitive games as edges directed away from their winner,
-
•
collaborative games as solid/dotted lines if won/lost,
-
•
half edge solitaire games as half edges directed away/toward from their (only) endpoint if won/lost, and
-
•
loop solitaire games as solid/dotted loops if won/lost.

The reversal of a Coxeter tournament on is obtained by reversing the outcome of all games in . That is, , where . If , we let denote the Coxeter tournament obtained from by reversing the outcome of all games in . In particular, .
The Coxeter interchange graph has a vertex for each . Vertices are neighbors if , for some copy of a type generator. If is a neutral clover, we add a double edge, and otherwise we add a single edge.
For instance, the “snare drum,” in Figure 3 above, is when .
The decision to represent clovers as double edges might seem arbitrary at first sight, however, there is a good reason. As it turns out, rather miraculously, this adjustment makes the type interchange graphs degree regular. Furthermore, the degree of is related to distances in in the following way. Let denote the squared length of .
Recall that is the set of all possible score sequences of Coxeter tournaments on . As discussed above, this set is classified in [18].
Theorem 1 ([18]).
Let , or . Fix any . Then the Coxeter interchange graph is regular, with degree given by
where is the standard score sequence.
In particular, .
We observe that, as moves closer to the center of the polytope , the degree of increases. This is in line with the intuition that Coxeter tournaments with closer to (i.e., closer to being neutral) should contain more copies of the (neutral) generators.
Let us note that with are precisely the vertices of . For such , we have , in line with the fact there is a unique Coxeter tournaments with score sequence . Indeed, such a tournament is transitive, in the sense that it contains no copy of a neutral generator, and so its interchange graph is single isolated vertex.
In [18], we observed that such a result also holds for graph tournaments, in relation to the standard permutahedron, yielding a geometric interpretation of the classical result (see, e.g., Moon [27]) that any two tournaments with the same win/score sequence have the same number of cyclic triangles.
In closing, let us emphasize the the neutral generators in Figures 5, 6 and 7 were identified in [18]. Theorem 1, proved therein, identifies the degree of the interchange graphs. However, in the current work, we will show (see Theorem 5 below) that the interchange graphs are connected. It is this result that justifies calling these structures “generators,” in the sense that the entire space is obtained by iteratively reversing copies of these specific neutral structures.
2.3. Path coupling
We recall that an aperiodic, irreducible discrete-time Markov chain on a finite state space has a unique equilibrium on such that, for all ,
as . We note that is the asymptotic proportion of time spent at state . The maximal total variation distance from by time ,
is non-increasing. The mixing time is defined as
A Markov chain is said to be rapidly mixing if is bounded by a polynomial in .
Path coupling was introduced by Bubley and Dyer [7]. See, e.g., Aldous and Fill [1, Sec. 12.1.12] or Levin, Peres and Wilmer [22, Sec. 14.2] for reformulations of the original result that are closer in appearance to that of the following.
Consider a connected graph . The graph distance is the minimal number of edges in a path between and . The diameter is is the maximal length of such a path in .
Definition 2.
We say that is weighted by if each edge is assigned some weight . The weighted distance is the minimal total weight path between and . Likewise, is the weighted diameter.
The usual graph distance corresponds to the for which for all .
Theorem 3 (Path coupling, [7]).
Consider a Markov chain on a connected graph , weighted by . Suppose that, for some , for each there is a coupling with so that
Then mixes in time .
Often this result is applied with , and, indeed, this will suffice for us in types and . In this case, path coupling has the intuitive interpretation that if the chain is “contractive” in expectation, then it is rapidly mixing.
On the other hand, in the more complicated type , we will select a careful re-weighting that takes into account some of the more intricate features in the interchange graphs of this type.
Finally, note that the type interchange graphs are, in fact, multigraphs. Specifically, some pairs of vertices (corresponding to clover reversals) are joined by double edges, as in Figures 3 and 4 above. This is for technical convenience, as it makes the graph regular, and thereby our coupling procedure easier to explain. We note that Theorem 3 still applies, since a Markov chain on a multigraph with some double edges is equivalent to the Markov chain on the graph , obtained by collapsing each double edge in into a single edge, and combining the two associated edge crossing probabilities.
3. Main result
Our main result shows that random walks rapidly mix on the Coxeter interchange graphs.
Theorem 4.
Let , or . Fix any . Then lazy simple random walk on mixes in time if or , and in time if .
Rapid mixing in type , proved in [16, 25], follows as a special case of our proof of this result in type .
We note that the classification of in [19] is constructive, which allows us to initialize the random walk in the first place.
In fact, we will prove sharper bounds (see Theorem 23 and 24 below). In types and , we will show that , where is the degree (see Theorem 1 above) of the interchange graph . The result above follows, since . In type , we will show that , where is a certain quantity (see Lemma 22) satisfying . We call the maximal crystal degree of the interchange graph. Roughly speaking, it is maximal number of crystals, all containing the same double edge. This quantity is related to the re-weighting that we will use in applying Theorem 3 in type . We note that re-weighting arguments have been used before, e.g., in the work of Wilson [34].
4. Connectivity
Before proving Theorem 4, we will first establish the following combinatorial result, giving further structural information (beyond its regularity, given by Theorem 1) about the Coxeter interchange graphs.
Theorem 5.
Let , or . Fix any ). The Coxeter interchange graph is connected and its diameter .
This result is a corollary of Lemma 13 (the “reversing lemma”) proved at the end of this section. A number of preliminaries are required. First, in the next subsection, we will find a way of encoding Coxeter tournaments as special types of directed graphs.
4.1. Z-frames
Oriented signed graphs were studied by Zaslavsky [37]. From this point of view (see [37, Fig. 1]), each oriented signed edge in an oriented signed graph is the union of at most two directed half edges. We modify this idea, by adding a named endpoint to each half-edge, which we call a match. This will allow us to prove certain structural facts using graph theory techniques. We call such a structure a Z-frame.
Definition 6.
A Z-frame is a directed, bipartite multigraph on disjoint sets of players and matches , such that every match has degree or .
This concept is fairly general, and not all Z-frames correspond to a Coxeter tournament on some . However, each such has a unique representation as a Z-frame . We think of as revealing the “inner directed graph structure” of . Players in correspond to vertices in . Recall that each game in corresponds to an oriented signed edge. Each such game is associated with a match in .
We will think of edges directed away/toward players as positively/negatively charged. (That being said, positive/negative edges in a Z-frame should not be confused with positive/negative edges in a Coxeter tournament.)
We say that is neutral if all players have net zero charge, i.e., , where is the number of positive/negative edges incident to . We put . Note that, if is neutral then is even.
Definition 7.
Let be a Coxeter tournament on a signed graph on . Let be the Z-frame on and , with the following directed edges:
-
•
If a competitive game between players and is won (resp. lost) by in , we include two directed edges (resp. ).
-
•
If a collaborative game between players and is won (resp. lost) in , we include two directed edges (resp. ).
-
•
If a half edge solitaire game by player is won (resp. lost) in , we include one directed edge (resp. ).
-
•
If a loop solitaire game by player is won (resp. lost) in , we include two directed edges (resp. ).
See Figure 8 for an example of a Coxeter tournament and its corresponding Z-frame .

The reason for the above terminology is that directed edges in with a positive/negative charge correspond to positive/negative contributions to the score sequence . Note that, in competitive/collaborative games, the two charges are opposing/aligned (regardless of the outcome of the game). See Figure 1.
| 1 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 0 |
4.2. Decomposing Z-frames
Our aim is to decompose neutral Coxeter tournaments into irreducible neutral parts. In this section, we will do this for Z-frames in general.
Recall that a trail is a walk in which no edge is visited twice.
Definition 8.
We call a trail of (directed) edges in a Z-frame closed if it starts and ends at the same vertex, and otherwise we call it open. A trail is neutral if the two consecutive edges at each player have opposite charges. The length of a trail is its number of matches.
Note that the edges along a trail in a -frame do not repeat, and are connected to each other in alternation by a player/match. Also note that neutral open trails start and end at distinct final matches (the left and rightmost matches along the trail). See Figure 9.

Lemma 9.
Any neutral Z-frame can be decomposed into an edge-disjoint union of closed neutral trails and open neutral trails, such that no two open trails have a common final match.
Proof.
Let . Since Z is neutral, . Therefore we may pair each edge directed away from with an edge directed toward . Note that any such pair is a neutral trail. We let denote the set of all such pairs. Then is a decomposition of into an edge-disjoint union of neutral trails. Select a decomposition with the minimal number of neutral trails. Open trails in this decomposition cannot have a common final match, as otherwise they could be concatenated to form a single longer trail, contradicting minimality. ∎
Let be a neutral Z-frame. We say that is reducible if it contains a non-empty neutral . Otherwise, is irreducible.
Each vertex in a neutral trail has even degree, since and . As discussed, vertices in a neutral have even . Our next result observes that if is irreducible, then all .
Lemma 10.
Let be an irreducible neutral Z-frame. Then is a neutral trail and for all .
Proof.
By Lemma 9, is a neutral trail, and so all are even. If is an isolated vertex that plays no solitaire games, then . Otherwise, if is non-trivial, we will argue that are the only possibilities. To see this, start at any along the trail, and then follow the trail. Consider the charges of the edges incident to , in the order in which they are visited by the trail. If the first and second charges are opposing, then the trail is complete with . Otherwise, suppose they are both positive (the other case is symmetric). Since is neutral, the 3rd charge is negative. Finally, consider the 4th charge. If it were positive, then the sub-trail between the third negative edge incident to and the forth positive edge incident to would be neutral. Therefore, the 4th charge is negative, and so the trail is complete with . ∎
4.3. Reversing Coxeter tournaments
Applying the results of the previous section, we obtain the following result for Z-frames of Coxeter tournaments .
Lemma 11.
Let , or . Let be the Z-frame of a neutral Coxeter tournament on a signed -graph . Consider a decomposition into neutral trails given by Lemma 9. If or then all trails are closed. If then possibly some are open.
Proof.
This result follows by noting that if is of type or then all matches in are degree 2. Therefore, there are no open neutral trails in the decomposition, so each is closed. On the other hand, in type it is possible to have open and closed trails, since in this case possibly some matches are degree 1. ∎
Note that a tournament on a signed graph is neutral if and only if its Z-frame is neutral. Naturally, we call such a irreducible if is irreducible, and reducible otherwise.
Lemma 12.
Suppose that is a -graph in which all players have degree four. Then any neutral tournament on is reducible.
Proof.
The proof is by contradiction. Suppose that on is neutral and that is irreducible. By Lemma 9, is in fact a single neutral trail, which for convenience we will denote by . Following the consecutive edges of , we can find a closed trail which:
-
•
starts and ends at some player ,
-
•
visits no player more than once along the way,
-
•
and is neutral everywhere except at .
Let us assume that the two directed edges in incident to are positive, since the other case is symmetric.
Consider the extension of , as it departs via some negatively charged directed edge, until it eventually returns to some player for the first time. Note that , as else, since is irreducible, it would follow that , and then that there are degree 2 vertices in along . Since is neutral at , the edges in incident to have opposing charges. Let , where is the trail between and which includes the positive/negative edge in incident to , as in Figure 10. To conclude, consider the charge of the directed edge in along which is revisited. To obtain the required contradiction, note that if this charge is positive (resp. negative) then (resp. ) is a neutral trail. ∎
Finally, we turn our attention to the main result of this section.
Lemma 13 (Reversing lemma).
Let , or . Let be a tournament on the complete signed graph , and let be a neutral sub-tournament. If has games then can be reversed in a series of at most type generator reversals.
The assumption that is on is crucial, since not all of the games in the generators used to reverse will be in itself. However, after the series of reversals, only the games in will have been reoriented, i.e., all games in will be restored to their initial orientations.
Proof.
Without loss of generality we may assume that is irreducible. In this case, by Lemma 9, the Z-frame is a single neutral trail. For simplicity, we will speak of as a tournament and trail interchangeably.
We first address the simplest case of open neutral trails, which appears only in type . We proceed by induction on the length . The smallest open trails, with , are the neutral pairs (as in Figure 6) themselves, which are clearly reversible in a single reversal. For longer open neutral trails , consider any (half edge) solitaire game in played by some in , which is not an endpoint of the trail. Using , we can first reverse either the part of the trail that is to the “left” of or else the part which is to the “right.” We can do this using the inductive hypothesis, as one of the parts is neutral and both have length smaller than . Then, using the reversal of this game , we can reverse the other part of the trail in turn. See Figure 11 for an example.
Next, we turn to the case of closed neutral trails. Recall that closed trails do not have solitaire half edge games, so from this point on we assume that or . If is a generator, then the result clearly holds. If it is not, then let be the number of vertices in . If , one can verify directly that the result holds. See Figure 12.
For , we aim to find a pair of vertices , in which do not play a game with each other in . Once we find such a pair, the argument is similar to the case of open trails above; the difference being that, in the case of closed trails, we will either first reverse the “top/bottom” (instead of the “left/right”) of the trail, and then the other side in turn, as in Figure 13.

To this end, suppose that every pair of vertices in plays at least one game with each other. As , this implies that the degree of every player in is at least . Moreover, if some in plays a loop game, then . However, as is neutral and irreducible, this would contradict Lemma 10. Thus, is a -regular -graph. But this is also impossible, by Lemma 12. Therefore, for all , there exists a pair of players which do not play a game with each other, and this concludes the proof. ∎
Finally, using the reversing lemma, we will prove the main result of this section.
Proof of Theorem 5.
Let . The distance between and is the smallest number of the generator reversals which transforms into . The games in the difference are precisely those which need to be reversed. Since , it follows that is neutral. Therefore, by Lemma 13, there is a path from to in of length . Hence is connected and its diameter . ∎
5. Interchange networks
In this section, for ease of exposition, we will speak of Coxeter tournaments and their corresponding vertices in interchangeably.
Definition 14.
For at distance two in , we define the interchange network to be the union over all paths of length two between .
Note that each path of length two between such corresponds to a way of reversing the difference between and .
5.1. Classifying networks
In this section, we will classify the possibilities for . As we will see, this is the key to applying path coupling (Theorem 3 above) in Section 6 below. In the classical case of type there is only one possibility for (a “single diamond”), and this is the reason why such a simple contractive coupling (as in Figure 27 below) is possible. As it turns out, this continues to hold in types and , but the underlying reasons are more complicated. Type , on the other hand, is significantly more complex, as then the structure of can take various other forms.
It can be seen that any two distinct generators are either disjoint or else have exactly one game in common . In this case, we say that are adjacent.
Note that if a path of length two from to passes through some , then there are two generators such that , for . In this way, every such path of length two from to is determined by a midpoint and a pair of generators .
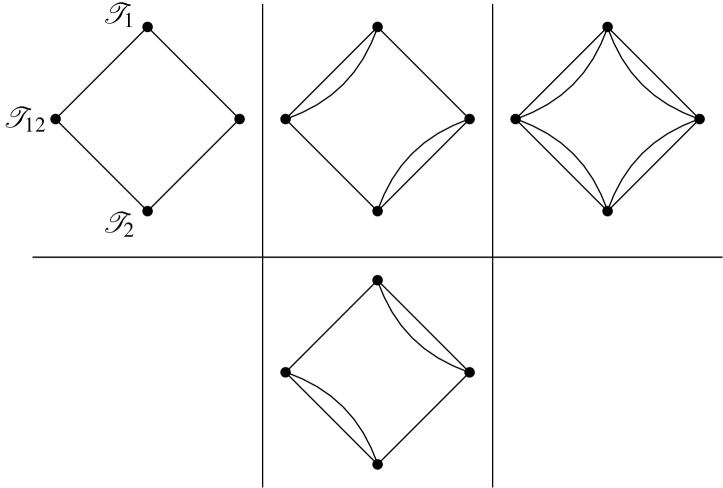
There are three possible networks when are disjoint. We call these the single, double and quadruple diamonds. See Figure 14. Recall that double edges in correspond to neutral clover reversals. All other types of reversals (neutral triangles and pairs) are represented as single edges.

The following result classifies the types of networks when are disjoint.
Lemma 15.
Suppose that there is a path of length two between in that passes through midpoint , with associated generators such that . Suppose that are disjoint. Then if exactly zero, one or two of the are clovers then the network is a single, double or quadruple diamond, respectively.
Proof.
Clearly, there are exactly two paths from to . These paths correspond to reversing the disjoint generators in series, in one of the two possible orders. See Figure 15. ∎
The case that are adjacent is more involved. It is useful to note that, in this case, the difference is a neutral tournament with exactly four games on either three or four vertices. Even so, there are a number of cases to consider, and the key to a concise argument is grouping symmetric cases together. For a Coxeter tournament , we define its projection graph to be the graph obtained by changing each:
-
•
oriented negative/positive edge (i.e., competitive/collaborative game) into an undirected edge,
-
•
oriented half edge (i.e., half edge solitaire game) into an undirected half edge,
-
•
oriented loop (i.e., loop solitaire game) into an undirected loop.
There are a number of ways that two generators can be adjacent. However, there are only four possibilities for their projected difference . We call these the square, tent, fork and hanger, as in Figure 16. The following observation is essentially self-evident, and can be verified by an elementary case analysis. We omit the proof.

Lemma 16.
Assume the same set up as Lemma 15, except that instead are adjacent. Let . Then:
-
(1)
If are neutral triangles on four/three vertices then is a square/tent.
-
(2)
If are neutral clovers then is a tent.
-
(3)
If is a neutral pair and is a neutral pair or triangle then is a fork.
-
(4)
If is a neutral clover and is a neutral triangle then is a hanger.
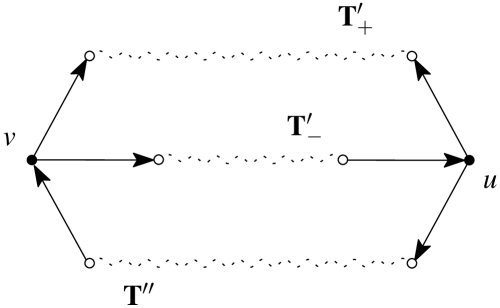
In addition to the single and double diamond networks in Figure 14, there are two additional networks that can occur when are adjacent. We call these the split and heavy diamonds, see Figure 17.
The following result classifies the types of networks when are adjacent.
Lemma 17.
Assume the same set up as Lemma 16 (with are adjacent). Let and . Then:
-
(1)
If or , then is a single diamond.
-
(2)
If and is a square, then is a single diamond.
-
(3)
If and is a tent, then is a split diamond.
-
(4)
If and is a hanger, then is a double or heavy diamond.
Proof.
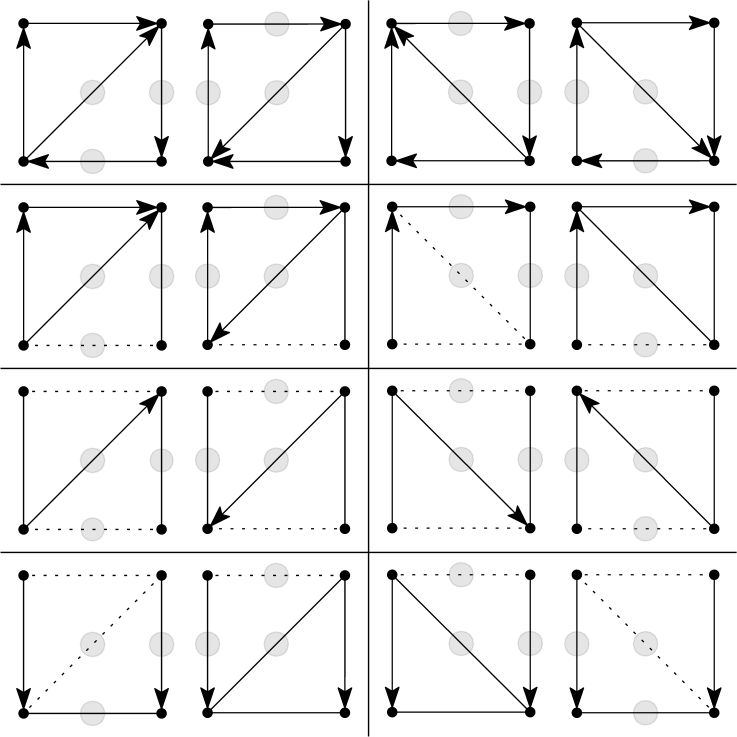
Case 1a. We start with the simplest case that or and are adjacent neutral triangles on four vertices, so that is a square. Note that, to reverse in two steps, we must reverse exactly two edges in in each step. As such, no neutral pairs will be involved in reversing in two steps. There are exactly two ways to reverse . For each pair of “antipodal” vertices in , consider the two games played between the pair. Exactly one of the two games allows us to reverse the games in on one “side” of . Then, in turn, we can use to reverse the other two games in . See Figure 18 for all the possible cases of .
Case 1b. Suppose that or and are adjacent neutral triangles on three vertices, so that is a tent. In this case, both of the (competitive and collaborative) games between the “base” vertices lead to a way of reversing . See Figure 19.

Case 1c. Suppose that and that one of is a neutral pair and the other is an adjacent neutral pair or triangle, so that is a fork. Then the half edge game played by the “middle” vertex and exactly one of the games between the “base” vertices lead to ways of reversing . See Figure 20.
By Cases 1a–c, statement (1) follows, that is, in types and the network is always a single diamond, as in Figure 21.
Case 2. In type , the case that is a square follows by the same argument as in types and . Indeed, recall that any reversal of in two steps will involve reversing exactly two games in in each step. Therefore, no clovers will be involved in such a reversal of , and so once again is a single diamond, yielding statement (2).
Case 3a. Suppose that and that is a tent formed by two adjacent neutral triangles on three vertices. Then by Case 1b, contains a single diamond. However, using the loop game played by the “middle” vertex, we obtain an additional path of length two between . We can use to reverse the two games on one “side” of the tent. Then, in turn, we can use to reverse the other two games. See Figure 22. Hence is a split diamond in this case.
Case 3b. Suppose that and that is a tent formed by two adjacent neutral clovers. Then is on three vertices, and so by Case 1b, we find that is a split diamond, once again.
By Cases 3a–b, statement (3) follows. The difference between Cases 3a and 3b are depicted in the first column of Figure 23.
Case 4. Finally, suppose that and that is a hanger. We will argue that this case corresponds to the second and third columns in Figure 23.
Note that, in this case, exactly one of is a neutral clover and the other is an adjacent neutral triangle. Suppose that the loop game in is played by vertex and that the other two vertices in are . Note that any way of reversing in two steps will involve reversing exactly once, and so each path of length two from to will contain exactly one double edge.
The four cases in the second and third columns in Figure 23 can be seen by considering the other games played between and that are not in . Depending on their outcomes, each such game either creates a clover with loop at or else forms a neutral triangle together with the two “opposite” games in . After this clover/triangle is reversed, the triangle/clover, which was not initially, becomes present. See Figure 24.
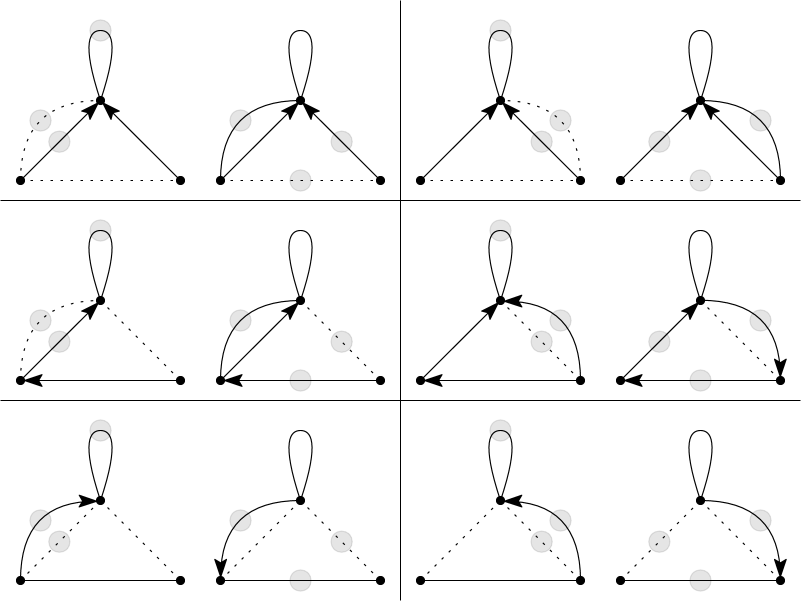
The proof is complete. ∎
5.2. Extended networks
Lemmas 15 and 17 above classify the types of interchange networks . Recall that such a network contains all paths of length two between .
Definition 18.
We define the extended interchange network to be the union of over all “antipodal” pairs in at distance two.
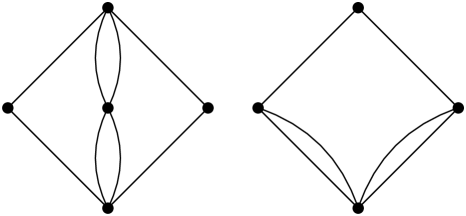
Single, double and quadruple diamonds are “stable,” in the sense that . In contrast, split and heavy diamond networks extend to a type of structure, which we call a crystal. See Figure 25.
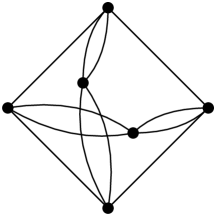
Remark.
All of the interchange networks that we have described, except the single diamond, can be found in Figure 3 above. This demonstrates how interchange networks can overlap and mesh together to form the interchange graph of a given score sequence.
Lemma 19.
Suppose that are at distance two in . Let and .
-
(1)
If is a single, double or quadruple diamond, then the extended interchange network .
-
(2)
Otherwise, if is a split or heavy diamond, then the extended interchange network is a crystal.
Proof.
Statement (1) is clear, and can be seen by inspection. On the other hand, statement (2) follows by repeated application of Lemma 17, considering the various antipodal pairs in .
Case 1. If is a split diamond, as in the first column of Figure 23, then consider in that are incident to only single edges in . By Lemma 17, it follows that is a split diamond, and therefore is a crystal.
Case 2. If is a heavy diamond, as in the third column of Figure 23, then consider in , each of which incident to exactly one single edge and one double edge in . By Lemma 17, it follows that is a split diamond, and therefore there is a path of length two between them consisting of two single edges in . Then, applying Lemma 17, once again, but this time to the midpoint along this path and in that is incident to two single edges in , we find that is a crystal, as claimed. ∎
Recall that two generators are either disjoint or have exactly one game in common. A similar property holds for extended networks.
Lemma 20.
Any two distinct extended networks are either edge-disjoint or have exactly one single or double edge in common.
Proof.
By Lemma 19 there are only four types of extended networks. By an elementary case analysis, it can be seen that any two antipodal (distance two) vertices in an extended network give rise to the same extended network . That is, , for any such . From this observation the result follows, since if two extended networks share at least three vertices, then they necessarily have at least one antipodal pair of vertices in common. ∎
5.3. Properties of crystals
In this section, we obtain two key properties of crystals, which will play a crucial role in the type couplings discussed in Section 6.2 below.
First, we note that crystals cannot share a single edge. We will use this, together with Lemma 20, to extend natural couplings on networks to a coupling on the full interchange graph.
Lemma 21.
Suppose that are distinct crystals in an interchange network . Then , are either edge-disjoint or share a double edge. That is, no such share a single edge.
Proof.
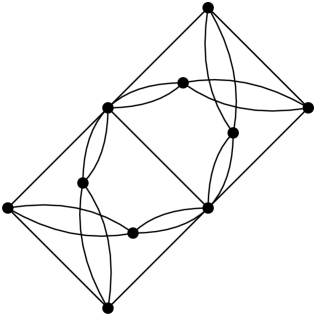
The previous result shows that single edges can be in at most one crystal. Double edges, on the other hand, can be in more than one. The following result gives an upper bound on this number, which is related to the re-weighting of the graph metric, discussed in Section 6.2, under which our coupling will be contractive.
Recall that is the degree of .
Lemma 22.
Any given double edge in an interchange network is contained in at most crystals.
Proof.
Consider a double edge between some . By Lemma 20, each crystal containing it corresponds to an additional double edge or two single edges incident to . It follows that there are at most such crystals.
The second bound is somewhat more complicated. Recall, as noted in the proof of Lemma 21, that each crystal is associated with three players. Suppose that a double edge between some is associated with a neutral clover involving players . We claim that, for any other player , there are at most two crystals associated with . To see this, observe that, if there were three, then one of would be incident to four single edges in these crystals. However, this would imply that in one of there are four neutral triangles on , which is impossible. Indeed, as noted in the proof of Lemma 21, there can be at most two. Therefore, there are at most crystals containing any given double edge. (In fact, the upper bound can be proved, but involves a more careful analysis.) ∎
6. Rapid mixing
Using the results of the previous section, we show that simple random walk on any given is rapidly mixing. The idea is to first define couplings on extended networks . We then argue that these couplings are compatible, and extend to a full coupling.
In types and , rapid mixing then follows by Theorem 3, using the standard weighting given by the graph distance in . In type , we will need to select a special re-weighting , accounting for the presence of crystals in the interchange graphs of this type.
For a tournament , we let denote the set of edges in incident to .
6.1. Coupling in and
We begin with the simplest cases of types and . These types are the most straightforward, since then all networks are single diamonds, and no re-weighting of the graph metric is necessary.
Theorem 23.
Let or . Fix any . Then lazy simple random walk on the Coxeter interchange graph is rapidly mixing in time .
Proof.
Let or . Consider two copies of lazy simple random walk and on , started from neighboring . Then for some type generator . In this sense, the random walks start at distance 1.
We will construct a contractive coupling of , such that the expected distance between is strictly less than , for every choice of . In fact, in this coupling, the will coincide with probability , and otherwise remain at distance .
More specifically, we couple using the natural bijection from to , which fixes the edge and pairs “opposite” edges in each single diamond containing . By Lemmas 15 and 17, for each type generator , the network is a single diamond. As such, there are exactly two paths of length two from to . One such path passes through . We let
| (3) |
be the first edge along the other such path. By Theorem 1 and Lemmas 19 and 20, is a bijection from to .
Finally, we define the coupling of as follows. Let be a uniformly random edge in and a Bernoulli random variable (i.e., a fair “coin flip”). If , we put if and if . In this case, the coupling contracts. On the other hand, if we put and if , and and if , where is given by the bijection in (3). See Figure 27.

Remark.
Rapid mixing for classical (type ) tournaments follows as a special case of the argument above.
6.2. Coupling in
Finally, we investigate mixing in type .
Recall that, in types and , the coupling was determined by an edge pairing, given by a bijection from to , where are neighboring tournaments in . The coupling in type is also determined by such a , however, since there are a number of different networks in type , the pairing is more involved.
The fact (see Lemma 21) that distinct crystals cannot share a single edge is crucial. Otherwise it would not be possible to extend couplings on extended networks to a full coupling. Roughly speaking, this is because (see Case 1b in the proof of Theorem 24 below) single edges in a crystal will need to be paired with one of the edges in a double edge of the same crystal. As such, if there were two crystals with the same single edge, a bijective pairing would not be possible.
Furthermore, there is an additional complication in type . As it turns out, the pairing does not lead to a contractive coupling, with respect to the graph distance in . The problem concerns the case that the initial starting positions are joined by a single edge in a crystal. In this case, the natural coupling is only “neutral” (i.e., with in Theorem 3), rather than contractive.
There are (at least) three ways to overcome this difficulty, leading to increasingly better bounds on the mixing time. The first way is to apply Bordewich and Dyer’s [5] path coupling without contraction, leading to an upper bound . It is also possible to apply path coupling at time , since at this point the coupling (with respect to the usual graph metric) becomes contractive. In doing so, the key is to observe that, in the problematic case that are joined by a single edge in a crystal, if stays within the crystal then the pairing (described below) selects a in the crystal such that are now joined by a double edge. This argument leads to an upper bound of .
We will present a third strategy, by re-weighting the metric, which yields a better bound.
Recall (see Lemma 21) that single edges in are contained in at most one crystal. Double edges, on the other hand, can be contained in more than one. We define the crystal degree of a double edge to be the number of crystals containing it. We let denote the maximal crystal degree, over all double edges. By Lemma 22, we have that , where is the degree of .
We will assume throughout that . Indeed, if , then there are no crystals in the interchange graph. In this case, a straightforward modification of the proof of Theorem 23 (using the standard graph metric) shows that .
We will prove the following result, using the weighting that puts on each edge in a double edge and on each single edge.
To be clear, this choice of re-weights the graph distance between neighboring vertices joined by single edges, but not those joined by double edges. Specifically, if are joined by a single edge then , and if are joined by a double edge then each edge is given weight , and so the weighted distance between remains (see Definition 2).
Theorem 24.
Let . Fix any . Then lazy simple random walk on the Coxeter interchange graph is rapidly mixing. If there are no crystals in (when ) then . Otherwise, we have .
In particular, this result implies that .
Proof.
As discussed, let us assume that , as otherwise a simple adaptation of the general reasoning in types and (the proof of Theorem 23) shows that .
Consider two copies of lazy simple random walk and on , started from neighbors . Let be such that .
The first step is to obtain an edge pairing , which will associate a to each possible . Then we will show that this coupling is contractive, with respect to the re-weighting on single edges and on each edge in double edges. The key in this regard will be the classification of extended networks, established in Section 5.
By Lemma 21, there are three cases to consider:
-
(1)
is a neutral triangle, and the edge is in
-
(a)
no crystal,
-
(b)
exactly one crystal.
-
(a)
-
(2)
is a neutral clover, and the double edge between is in crystals.
In these cases, we will construct couplings with the following properties:
-
•
In Case 1a, either , or else are again joined by a single edge.
-
•
In Case 1b, either are joined by a double edge in the crystal, or else are joined by a single edge.
-
•
In Case 2, either are joined by a single edge in some crystal containing the double edge between , or else are joined by a double edge.
Note that, under these couplings, crystal networks work like “switches,” in that they move single edges to double edges, and vice versa. Also note that, it is Cases 1b and 2 in which the choice of is crucial. We put weight on single edges so that, as we will see, the couplings in these cases are contractive.
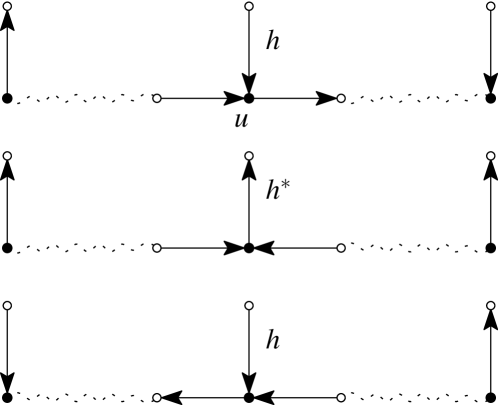
Case 1a. Suppose that is a neutral triangle, and that the single edge is not contained in a crystal. Then, by Lemmas 15 and 17, all extended networks containing are single and double diamonds. As such, it is only slightly more complicated to construct a contractive coupling in this case, than it was in types and above. We proceed as depicted in Figure 28 (cf. Figure 27).

Once again (as in the proof of Theorem 23), using Theorem 1 and Lemmas 19 and 20, we find a bijection from from to that fixes the edge and pairs “opposite” edges in single and double diamonds containing . and so correspond to the same generator.
For each edge in a single diamond containing , we let
| (4) |
be the “opposite” edge in .
Likewise, for each double edge, consisting of two copies , with , of the same edge in a double diamond network containing , we let
| (5) |
with , be the “opposite” edges in .
We couple as follows. Let be a uniformly random edge in and a Bernoulli. (Note that, this is a uniformly random edge, not generator. Indeed, neutral clovers corresponding to double edges are twice as likely to be selected as neutral triangles .) If , we put if and if . On the other hand, if , we put and if and and if , where is given by the bijection , defined in (4) or (5) above.
Note that with probability . Otherwise, are again joined by a single edge. As such
| (6) |
Case 1b. Suppose that is a neutral triangle, and that the single edge is contained in exactly one crystal. Once again, by Lemma 20, all single and double diamonds and the one crystal containing are otherwise edge-disjoint. In this case, the bijection can no longer fix , as in Case 1a. Rather, we will need to use this edge in a non-trivial way in order to define the edge pairing within the crystal.
The bijection , in this case, is defined in the same way as in Case 1a for the edges in each single and double diamond. On the other hand, for the edges in the crystal, we define as indicated in Figure 29. That is, the two single edges in the crystal incident to (one of which is ) are paired with the double edges in the crystal incident to , and vice versa. By Theorem 1, is a bijection from to . We stress here that pairs edges, not generators, and it is critical, in this case, that there is only one crystal containing (since it can only be paired once).

To couple , we let be a uniformly random edge in and a Bernoulli. If , we put and . If , we put and , where is given by the bijection .
In this case, with probability the pair remains in the crystal, but are now joined by a double edge. Otherwise, are again joined by a single edge. Therefore,
| (7) |
since .
Case 2. Finally, suppose that is a neutral clover. Suppose that is contained in crystals.
By Lemmas 15 and 17, all extended networks containing are double and quadruple diamonds and crystals. As in the previous cases, we define in this case by pairing “opposite” edges in the double and quadruple diamonds. In this case, fixes the two edges in the double edge between . Note that if is in a crystal, then one of is incident to two single edges in the crystal and the other is incident to a double edge in the crystal. We define on each such crystal by pairing these edges, as indicated in Figure 30. Once again, applying Theorem 1, we see that is a bijection from to .
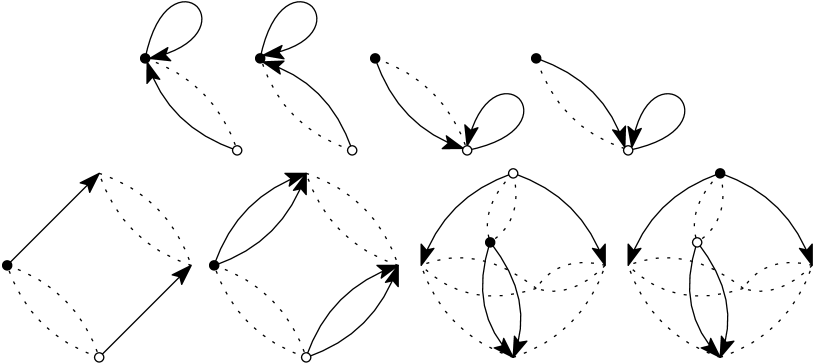
To couple , we let be a uniformly random edge in and a Bernoulli. If , we put if and if . Otherwise, if , we put and if and and if , where is given by the bijection .
In this case, with probability . With probability , the pair move within one of the crystals containing , and are then joined by a single edge. Otherwise, with probability , remain joined by a double edge. Therefore,
| (8) |
since .
7. Future directions
We conclude with a list possibilities for future study.
-
(1)
It remains open to find lower bounds for the mixing time, and to determine whether our bounds are sharp. In types , and , we might conjecture so, at least up to logarithmic factors.
Recall that, in these types, we have shown that , for any score sequence, where is the degree of the interchange graph. In type , Sarkar [30] has shown that for a special class of score sequences with and a “bottleneck” that is simple to analyze. A similar argument also works in the other types , and . Perhaps at least can be shown to hold in general.
As discussed, in type , Chen, Chang and Wang [9] have shown that the interchange graph is the hypercube, for some very specific score sequences. This shows, at least in some cases, that the bound is sharp, with the logarithmic factor.
In type , on the other hand, we have used a re-weighting of the metric to show that , where is the maximal crystal degree. Perhaps other techniques can lead to an improvement. However, we think that crystals in type are a genuine obstacle, so it might be surprising if, in fact, also in this type.
-
(2)
Recall that Theorem 5 shows that the interchange graphs are connected with diameter . It might be of theoretical interest to find a precise formula for , or at least good bounds, as a function of . Note that Theorem 1 above (proved in [18]) gives such a formula for the degree . We also note that in [6] some results are proved about the diameter in type .
-
(3)
Recall that each edge in the interchange graph corresponds to a generator reversal. Generators are the smallest neutral structures. It might be interesting to consider a generalization, in which neutral structures up to a given size can be reversed in a single step, and to quantify the decrease in the mixing time.
-
(4)
A graphical zonotope is a polytope obtained as a Minkowski sum of line segments, where the sum is indexed by the edges of the graph (see, e.g., Ziegler [38]). The permutahedron
is the graphical zonotope of the complete graph . Likewise, the Coxeter versions are obtained as sums indexed by the edges in the complete signed graphs . It could be interesting to study random walks on the fibers of other graphical zonotopes.
That being said, our current arguments take full advantage of the symmetry of . Once some edges become unavailable, it is more challenging (or even impossible) to show connectivity (and bound the diameter) of the interchange graph, and to devise a path coupling (which we have accomplished, via a non-trivial edge pairing argument).
-
(5)
Rapid mixing can be a starting point for approximate counting. It would be interesting if our result could help with counting the number of vertices in interchange graphs, for a general score sequence. As already discussed, these have been approximated (see [32, 23, 24, 15]) only in type and when is close to the center of .
-
(6)
In this work, we have studied random walks on interchange graphs associated with score sequences. However, one could also, quite naturally, try to study random walks on the set of score sequences itself. In type , all lattice points are score sequences. In types , and the score sequences are more complicated sets of points, characterized in the previous work in this series [18].
-
(7)
Finally, we recall that the interchange graphs in Figures 3 and 4 are Cartesian products. Also recall that, in type , some interchange graphs are the hypercube [9], which are a simple example of a product graph. It might be enlightening to investigate the product structure of interchange graphs more generally.
8. Acknowledgements
We thank Christina Goldschmidt, James Martin, Sam Olesker-Taylor, Oliver Riordan and Matthias Winkel for helpful conversations. We thank the two anonymous reviewers for their many insightful comments and suggestions for future work.
This publication is based on work (MB; RM) partially supported by the EPSRC Centre for Doctoral Training in Mathematics of Random Systems: Analysis, Modelling and Simulation (EP/S023925/1).
TP was supported by the Additional Funding Programme for Mathematical Sciences, delivered by EPSRC (EP/V521917/1) and the Heilbronn Institute for Mathematical Research.
This work was carried out while BK was at the University of Oxford. BK gratefully acknowledges the support provided by a Florence Nightingale Bicentennial Fellowship (Department of Statistics) and a Senior Demyship (Magdalen College).
References
- 1. D. Aldous and J. A. Fill, Reversible markov chains and random walks on graphs, 2002, Unfinished monograph, recompiled 2014, available at http://www.stat.berkeley.edu/˜aldous/RWG/book.html.
- 2. F. Ardila, F. Castillo, C. Eur, and A. Postnikov, Coxeter submodular functions and deformations of Coxeter permutahedra, Adv. Math. 365 (2020), 107039, 36.
- 3. S. Backman, Riemann-Roch theory for graph orientations, Adv. Math. 309 (2017), 655–691.
- 4. by same author, Partial graph orientations and the Tutte polynomial, Adv. in Appl. Math. 94 (2018), 103–119.
- 5. M. Bordewich and M. Dyer, Path coupling without contraction, J. Discrete Algorithms 5 (2007), no. 2, 280–292.
- 6. R. A. Brualdi and Q. Li, The interchange graph of tournaments with the same score vector, Progress in graph theory (Waterloo, Ont., 1982), Academic Press, Toronto, ON, 1984, pp. 129–151.
- 7. R. Bubley and M. Dyer, Path coupling: A technique for proving rapid mixing in Markov chains, Proc. 38th IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, 1997, pp. 223–231.
- 8. E. Cartan, Sur la Reduction a sa Forme Canonique de la Structure d’un Groupe de Transformations Fini et Continu, Amer. J. Math. 18 (1896), no. 1, 1–61.
- 9. A.-H. Chen, J.-M. Chang, and Y.-L. Wang, The interchange graphs of tournaments with minimum score vectors are exactly hypercubes, Graphs Combin. 25 (2009), no. 1, 27–34.
- 10. P. Galashin, S. Hopkins, T. McConville, and A. Postnikov, Root system chip-firing I: interval-firing, Math. Z. 292 (2019), no. 3-4, 1337–1385.
- 11. by same author, Root system chip-firing II: central-firing, Int. Math. Res. Not. IMRN (2021), no. 13, 10037–10072.
- 12. E. Gioan, Enumerating degree sequences in digraphs and a cycle-cocycle reversing system, European J. Combin. 28 (2007), no. 4, 1351–1366.
- 13. B. Hall, Lie groups, Lie algebras, and representations, second ed., Graduate Texts in Mathematics, vol. 222, Springer, Cham, 2015, An elementary introduction.
- 14. J. E. Humphreys, Reflection groups and Coxeter groups, Cambridge Studies in Advanced Mathematics, vol. 29, Cambridge University Press, Cambridge, 1990.
- 15. M. Isaev, T. Iyer, and B. D. McKay, Asymptotic enumeration of orientations of a graph as a function of the out-degree sequence, Electron. J. Combin. 27 (2020), no. 1, Paper No. 1.26, 30.
- 16. R. Kannan, P. Tetali, and S. Vempala, Simple Markov-chain algorithms for generating bipartite graphs and tournaments, Random Structures Algorithms 14 (1999), no. 4, 293–308.
- 17. W. Killing, Die Zusammensetzung der stetigen endlichen Transformationsgruppen, Math. Ann. 36 (1890), no. 2, 161–189.
- 18. B. Kolesnik, R. Mitchell, and T. Przybyłowski, Coxeter interchange graphs, preprint (2024), available at arXiv:2312.04532.
- 19. B. Kolesnik and M. Sanchez, Coxeter tournaments, preprint (2023), available at arXiv:2302.14002.
- 20. by same author, The geometry of random tournaments, Discrete Comput. Geom. 71 (2024), 1343–1351.
- 21. H. G. Landau, On dominance relations and the structure of animal societies. III. The condition for a score structure, Bull. Math. Biophys. 15 (1953), 143–148.
- 22. D. A. Levin, Y. Peres, and E. L. Wilmer, Markov chains and mixing times, American Mathematical Society, Providence, RI, 2009, With a chapter by James G. Propp and David B. Wilson.
- 23. B. D. McKay, The asymptotic numbers of regular tournaments, Eulerian digraphs and Eulerian oriented graphs, Combinatorica 10 (1990), no. 4, 367–377.
- 24. B. D. McKay and X. Wang, Asymptotic enumeration of tournaments with a given score sequence, J. Combin. Theory Ser. A 73 (1996), no. 1, 77–90.
- 25. L. McShine, Random sampling of labeled tournaments, Electron. J. Combin. 7 (2000), Research Paper 8, 9.
- 26. J. W. Moon, An extension of Landau’s theorem on tournaments, Pacific J. Math. 13 (1963), 1343–1345.
- 27. by same author, Topics on tournaments, Holt, Rinehart and Winston, New York-Montreal, Que.-London, 1968.
- 28. A. Postnikov, Permutohedra, associahedra, and beyond, Int. Math. Res. Not. IMRN (2009), no. 6, 1026–1106.
- 29. R. Rado, An inequality, J. London Math. Soc. 27 (1952), 1–6.
- 30. S. Sarkar, Mixing times of tournaments, undergraduate thesis, Georgia Institute of Technology, 2020.
- 31. A. Sinclair, Algorithms for random generation and counting, Progress in Theoretical Computer Science, Birkhäuser Boston, Inc., Boston, MA, 1993, A Markov chain approach.
- 32. J. H. Spencer, Random regular tournaments, Period. Math. Hungar. 5 (1974), 105–120.
- 33. R. P. Stanley, Decompositions of rational convex polytopes, Ann. Discrete Math. 6 (1980), 333–342.
- 34. D. B. Wilson, Mixing times of Lozenge tiling and card shuffling Markov chains, Ann. Appl. Probab. 14 (2004), no. 1, 274–325.
- 35. T. Zaslavsky, The geometry of root systems and signed graphs, Amer. Math. Monthly 88 (1981), no. 2, 88–105.
- 36. by same author, Signed graphs, Discrete Appl. Math. 4 (1982), no. 1, 47–74.
- 37. by same author, Orientation of signed graphs, European J. Combin. 12 (1991), no. 4, 361–375.
- 38. G. M. Ziegler, Lectures on polytopes, Graduate Texts in Mathematics, vol. 152, Springer-Verlag, New York, 1995.