Rare Decays in LHCb

The LHCb experiment  lhcb has provided preliminary results in the measurement of the forward-backward asymmetry, fraction of longitudinal polarization and differential branching fraction of $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ kstmm and the measurement of the ${\cal B}(B^{0}_{s}\!\rightarrow\phi\gamma)$ phiG . LHCb has also provided upper limits in ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ and ${\cal B}(B^{0}\rightarrow\mu^{+}\mu^{-})$ bsmm . Sect. 2 sumarizes the analysis and results obtained by LHCb in the study of $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$. Sect. 3 sumarizes the measurement of ${\cal B}(B^{0}_{s}\!\rightarrow\phi\gamma)/{\cal B}(B^{0}\!\rightarrow K^{*0}\gamma)$ and Sect. 4 sumarizes the analysis and results of $B^{0}_{(s)}\rightarrow\mu^{+}\mu^{-}$.

The rare decay $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ is a $b\rightarrow s$, flavour changing neutral current decay, mediated by electroweak box and penguin diagrams in the Standard Model (SM). In models beyond the SM, new particles can enter in competing loop-order diagrams resulting in large deviations from SM predictions (see for example Refs. Ali:1991is ; Altmannshofer:2008dz ).

$B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ candidates are selected by first applying a loose pre-selection based on the $B^{0}$ lifetime, daughter impact parameters and a requirement that the $B^{0}$ points back to one of the primary vertices in the event. A tighter multivariate selection, based on a boosted decision tree (BDT), is then applied to select a clean sample of $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ candidates, with a signal-to-background ratio in a 100${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ window around the reconstructed $B^{0}$ mass of about three-to-one. The BDT is based on the $B^{0}$ kinematics, $B^{0}$ vertex quality, daughter track quality, impact parameter and kaon, pion and muon particle identification. The offline selection criteria are explicitly chosen to minimise angular acceptance effects. The multivariate selection was trained using $B^{0}_{d}\rightarrow J/\psi K^{*0}$ candidates from the 2010 data as a proxy for the signal and $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ candidates from the upper mass sideband of the 2010 data for the background. Specific vetoes are used in order to eliminate non combinatorial background.

The trigger, reconstruction and offline selection can all bias the measured angular distribution of $B^{0}\!\rightarrow K^{*0}\mu^{+}\mu^{-}$ candidates. The detection acceptance is accounted for by weighting events when fitting for $A_{FB}$, $F_{L}$ and $\mathrm{d}BF/\mathrm{d}q^{2}$ (where $q^{2}$ is the di-muon mass squared). Event weights are calculated on a per-event basis in a small phase space window around each candidate, using fully simulated Monte Carlo (MC) simulation events. Simulated events are re-weighted to account for known data-MC differences in PID performance, impact parameter resolution, tracking efficiency and track multiplicity.

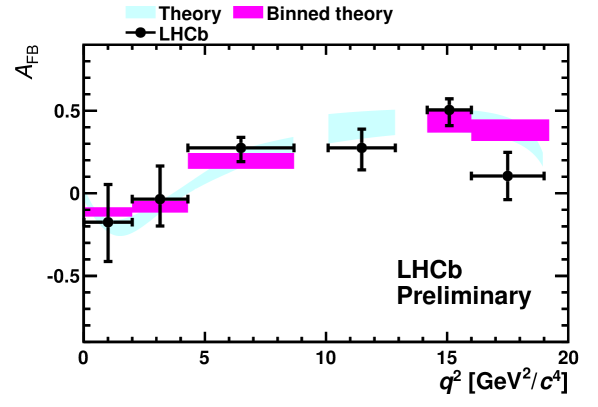
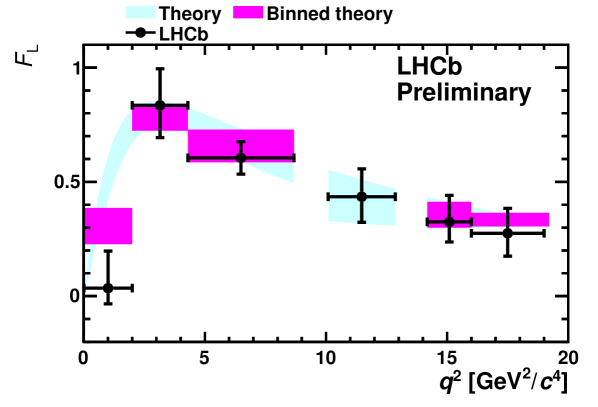
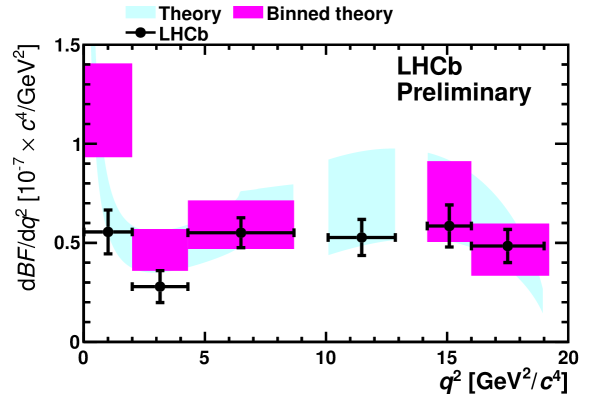
The fit results for $A_{FB}$, $F_{L}$ and $\mathrm{d}BF/\mathrm{d}q^{2}$, and their comparison with theoretical predictions Bobeth:2011gi , are shown in Fig. 1.

The systematic error on $A_{FB}$, $F_{L}$ and $\mathrm{d}BF/\mathrm{d}q^{2}$ is typically $\sim 30\%$ of the statistical error. In the high-$q^{2}$ region, the dominant contribution to the systematic uncertainty comes from the overall uncertainty on the acceptance correction which is dictated by the limited simulation statistics. This can clearly be improved for future analyses. Throughout, a sub-dominant contribution comes from the data-derived performance corrections. In particular, from knowledge of the PID performance and tracking efficiency in data. This is again statistically limited and can also be improved with larger datasets. When fitting for $A_{FB}$ and $F_{L}$ the signal and background mass model and the angular model for the background have been varied and yield corrections at the level of 10-20% of the statistical uncertainty. The uncertainty on the differential branching fraction includes the $\sim 4\%$ uncertainty coming from the measured $B^{0}\!\rightarrow{J\mskip-3.0mu/\mskip-2.0mu\psi\mskip 2.0mu}K^{*0}$ and ${J\mskip-3.0mu/\mskip-2.0mu\psi\mskip 2.0mu}\rightarrow\mu^{+}\mu^{-}$ branching fractions PDG . These measurements are current world best, and don’t confirm previous hints of a non-SM value of $A_{FB}$ at low $q^{2}$.

In the SM, the amplitude of these $b\rightarrow s\gamma$ penguin transitions is dominated by a virtual intermediate top quark coupling to a $W$ boson. Extensions of the SM predict new heavy particles that may propagate virtually within the loop and modify the dynamics of the transition. Therefore, these radiative modes are promising laboratories that could reveal the presence of new phenomena beyond the SM with the precise measurement of the branching ratios, asymmetries or angular distributions. The offline selection of both the $B^{0}\!\rightarrow K^{*0}\gamma$ and $B^{0}\!\rightarrow\phi\gamma$ decays is performed with the strategy of maximizing the cancellation of systematic uncertainties when performing the ratio. The analysis of $\sim 341\mbox{\,pb}^{-1}$ of LHCb data gives:

Where $f_{d}$ ($f_{s}$) are the probabilities of the $b$ quark to hadronize into $B^{0}$ ($B^{0}_{s}$). This results is compatible within 1.6 standard deviations with the theory prediction.

Combining the ratio of branching fractions in 1 with the World Average measurement for the $\cal B$($B^{0}\!\rightarrow K^{*0}\gamma$) from HFAG , we obtain,

which agrees within 1.6 standard deviations with the previous experimental measuremen, and wich correspond to the most precise measurement of this $BR$ to date.

The SM predictions for the branching fractions of the FCNC decays $B^{0}_{s}\rightarrow\mu^{+}\mu^{-}$ and $B^{0}\rightarrow\mu^{+}\mu^{-}$ are ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ = $(3.2\pm 0.2)\times 10^{-9}$ and ${\cal B}(B^{0}\rightarrow\mu^{+}\mu^{-})$ = $(0.10\pm 0.01)\times 10^{-9}$ Buras2010 . However, contributions from new processes or new heavy particles can significantly enhance these values. For example, within Minimal Supersymmetric extensions of the SM (MSSM), in the large $\tan\beta$ regime, ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ receives contributions proportional to $\tan^{6}\beta$ MSSM , where $\tan\beta$ is the ratio of the vacuum expectation values of the two neutral $C\!P$-even Higgs fields, and can differ significantly from the SM prediction. The LHCb analysis is done by clasifying $B^{0}_{(s)}\rightarrow\mu^{+}\mu^{-}$ candidates in bins of a 2D parameter space made by the invariant mass and a multivariate clasifier which condensates geometrical and kinematical information of the event. The signal expectation in each bin is calculated using data from control channels such as $B^{0}_{(s)}\rightarrow h^{+}h^{{}^{\prime}-}$ and $B^{+}\rightarrow J/\psi K^{+}$. The background expectation is calculated by interpolating from mass sidebands. The $B^{0}_{(s)}\rightarrow h^{+}h^{{}^{\prime}-}$ peaking background yield is calculated using $\pi\rightarrow\mu$ and $K\rightarrow\mu$ misidentification probabilities obtained from data using decays such as $\Lambda\rightarrow p\pi^{-}$ and $D^{0}\rightarrow K^{+}\pi^{-}$. The signal and background expectations are compared with the distribution of observed events, and the limits are set using the $\textrm{CL}_{\textrm{s}}$ method  Junk_99 ; Read_02 . The ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ and ${\cal B}(B^{0}\rightarrow\mu^{+}\mu^{-})$ upper limits obtained are:

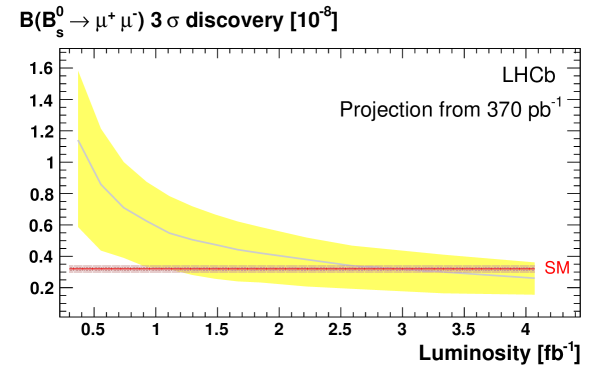
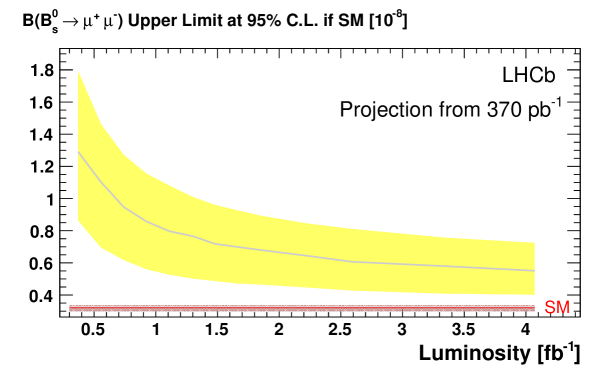
Fig. 2 shows the luminosity needed to impose stronger limits or to achieve a 3$\sigma$ evidence of $B^{0}_{s}\rightarrow\mu^{+}\mu^{-}$.

As can be seen in Fig. 1, there is good agreement between recent SM predictions and LHCb’s measurement of $A_{FB}$, $F_{L}$ and $\mathrm{d}BF/\mathrm{d}q^{2}$ in the six $q^{2}$ bins. In a $1<q^{2}<6\mathrm{\,Ge\kern-1.00006ptV}^{2}$ bin, LHCb measures $A_{FB}=-0.10^{+0.14}_{-0.14}\pm 0.05$, $F_{L}=0.57^{+0.11}_{-0.10}\pm 0.03$ and $\mathrm{d}BF/\mathrm{d}q^{2}=0.39\pm 0.06\pm 0.02$, to be compared with theoretical predictions of $A_{FB}=-0.04^{+0.03}_{-0.03}$, $F_{L}=0.74^{+0.06}_{-0.07}$ and $\mathrm{d}BF/\mathrm{d}q^{2}=(0.50^{+0.11}_{-0.10})\times 10^{-7}$ respectively. The experimental uncertainties are presently statistically dominated, and will improve with a larger data set. Such a data set would also enable LHCb to explore a wide range of new observables  Egede:2008uy .

In 340 pb^-1 of $pp$ collisions at a centre of mass energy of $\sqrt{s}=7$ TeV the most precise measurement of ${\cal B}(B^{0}\!\rightarrow\phi\gamma)$ has been performed, giving:

The ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ and ${\cal B}(B^{0}\rightarrow\mu^{+}\mu^{-})$ upper limits obtained by LHCb are:

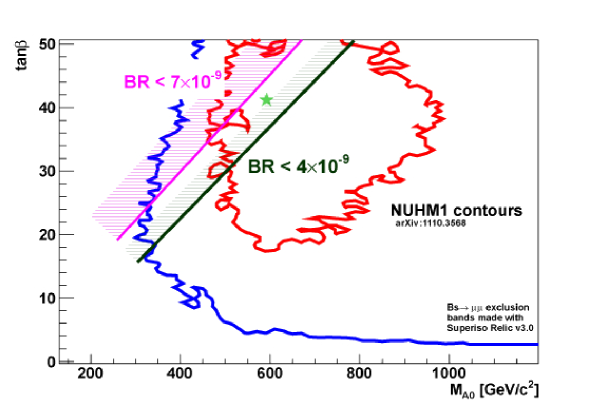
In Fig. 2 the luminosity needed for a 3$\sigma$ evidence as a function of ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ is shown. Approximately $\sim 2\mbox{\,fb}^{-1}$ are needed in the case that the value is equal to the SM prediction, but statistical fluctuations can make it possible with $\sim 1\mbox{\,fb}^{-1}$. Fig. 2 also shows that exclusions of ${\cal B}(B^{0}_{s}\rightarrow\mu^{+}\mu^{-})$ down to the ($2\times)$ SM level would impose important constraints in region around the current NUHM1 best fit point  MC7 . All the results presented here are current world best.